A simulation-free approach to assessing the performance of the continual reassessment method

Abstract

The continual reassessment method (CRM) is an adaptive design for Phase I trials whose operating characteristics, including appropriate sample size, probability of correctly identifying the maximum tolerated dose, and the expected proportion of participants assigned to each dose, can only be determined via simulation. The actual time to determine a final “best” design can take several hours or days, depending on the number of scenarios that are examined. The computational cost increases as the kernel of the one-parameter CRM design is expanded to other settings, including additional parameters, monitoring of both toxicity and efficacy, and studies of combinations of two agents. For a given vector of true DLT probabilities, we have developed an approach that replaces a simulation study of thousands of hypothetical trials with a single simulation. Our approach, which is founded on the consistency of the CRM, very accurately reflects the results produced by the simulation study, but does so in a fraction of time required by the simulation study. Relative to traditional simulations, we extensively examine how our method is able to assess the operating characteristics of a CRM design for a hypothetical trial whose characteristics are based upon a previously published Phase I trial. We also provide a metric of nonconsistency and demonstrate that although nonconsistency can impact the operating characteristics of our method, the degree of over- or under-estimation is unpredictable. As a solution, we provide an algorithm for maintaining the consistency of a chosen CRM design so that our method is applicable for any trial.

1 |. BACKGROUND

The purpose of traditional Phase I clinical trials is to suggest a dose, or several doses, of a potential new treatment that are safe, and therefore assumed to be worth pursuing in future efficacy (Phase II) trials. These dose-finding studies typically enroll participants for whom no other treatment options exist and tend to start enrollment on low doses rather than use randomization. Higher doses are assigned to future participants adaptively, meaning that the experience of earlier participants is used to inform which dose is assigned to future participants. As the trial reaches the end of accrual, it is expected that the adaptive design has directed dose assignments toward a “desirable” dose, commonly known as the maximum tolerated dose (MTD) or recommended Phase II dose (RP2D).

There are an abundance of Phase I trial designs,¹ which fall generally into two classes. The first class includes the 3+3 design,² the cumulative cohort design,³ and the k-in-a-row design,⁴ all of which use an algorithm to determine dose assignments from the toxicity profile of currently enrolled participants. The second class includes designs in which dose assignments are based upon the results of a statistical model used to estimate the probability of dose-limiting toxicity (DLT) for each dose. These designs include the Bayesian optimal interval design,⁵ the modified toxicity probability interval design,⁶ escalation with overdose control,⁷ and the continual reassessment method (CRM),⁸ which is the precursor of most other model-based designs.

An excellent tutorial of the CRM has been published by Garrett-Mayer,⁹ as well as a more recent presentation by Wheeler et al.¹⁰ The CRM design begins by first eliciting an a priori value for the probability of DLT for each dose; the vector of these values is known as the “skeleton.” The first participant or cohort of participants is assigned to a dose and each participant is followed for the occurrence of DLT over a predefined window of time. For agents that are given repeatedly in cycles, often DLTs are only assessed in the first cycle. Although the original formulation of the CRM recommended the dose for the first cohort should be the one believed a priori to be the MTD, later modifications to the CRM suggested for participant safety reasons that the starting dose should be the lowest dose,¹¹ which has become standard convention in most applications of the CRM.

In the CRM, the probability of DLT for each of the doses under study is assumed to follow a one-parameter model. In the Bayesian formulation of the CRM, a prior distribution is placed on the model parameter and the observed proportions of DLT at each dose are used to compute the posterior distribution for the model parameter. The posterior mean is then inserted in the CRM model to estimate the posterior probability of DLT for each dose. Subject to escalation and/or deescalation constraints, the next cohort of participants is then assigned to the MTD, which is the dose with posterior probability of DLT closest to the target DLT probability. The posterior estimates of the DLT probabilities are continually updated with each successive cohort and enrollment stops once the desired sample size is reached, at which point the final determination of the MTD or RP2D is made.

The CRM has a number of “tuning parameters,” including the skeleton, prior variance, maximum sample size, and potential stopping rules, that need to be defined by the user. Furthermore, there are no closed-form expressions that quantify how each tuning parameter impacts operating characteristics of the CRM, including the probability of correctly identifying the MTD and the expected proportion of participants assigned to each dose. Although assessment for a single design can be performed in several minutes on a personal computer using the titesim function included in the R library package dfcrm,¹² or online at https://uvatrapps.shinyapps.io/crmb¹³ or https://trialdesign.org, the actual time to determine a final “best” design among all tuning parameters can take several hours or days, depending upon how many features of the design are allowed to vary and the number of settings of true DLT probabilities that are considered.

For a given set of parameter settings, we have developed an approach that uses a single simulation to replicate information that, until now, could only be produced by a simulation study that examines thousands of hypothetical trials. Our approach very accurately reflects the results that would have been produced by the simulation study, but does so in a fraction of time required by the simulation study. In Section 2, we first present the necessary details for the CRM, and in Section 3, we follow with a description of our approach and its underlying theory. In Section 4, we demonstrate how our approach can be used in the design of a new trial and compare computation speed and results relative to a traditional simulation study. We summarize our current and ongoing work in Section 5.

2 |. REVIEW OF CRM

2.1 |. Model and design

The design of a Phase I trial starts with J dose levels of an investigational treatment and the targeted probability of a DLT, denoted as θ. A one-parameter model, denoted as p_j = f(d_j; β), is used to associate dose d_j, j = 1, 2, …, J, with its corresponding DLT probability, p_j, in which d_j is a numeric value assigned to dose j. The two most-commonly used models in the CRM are the power (or empiric) model, $p_j=d_j^{\text{exp}\left(\beta \right)}$, and the logistic model, log(p_j/[1 − p_j]) = 3 + exp(β)d_j, in which β is the unknown model parameter. The remainder of this article will focus on the power model, but we emphasize that our method is applicable to any one-parameter model.

We let π_j denote an a priori DLT probability for dose j; collectively, the vector, π = {π₁, π₂, …, π_J}, is called the skeleton. As suggested earlier, the value of d_j is not the actual clinical dose, but is a value solved using the assumed model, f(d_j; β). Once π is specified, we set β equal to its prior mean, denoted as μ, and we use π_j and f(d_j; β) to solve for d_j, that is, d_j = π_j/exp(μ) for the power model.

In the Bayesian formulation of the CRM, a prior distribution, g(β), is assumed for β, such that β has support on the real line. We emphasize that in our model we exponentiate the value of β because we assume that the probability of DLT must increase with dose. If the support of g(β) is already constrained to the positive line, then β can be used directly in the model rather than exp(β). The dose assignment for each cohort is determined adaptively based upon the dose assignments and DLT outcomes observed on previously enrolled participants.

Specifically, if we have enrolled k participants, in which participant i = 1, 2, …, k has dose assignment d_[i], which is one of the values in {d₁, d₂, … d_J}, and a binary indicator of DLT Y_i, we can compute the posterior mean for β as

$$\widehat{\beta }=\frac{{\int }_{-\infty }^{\infty }\beta L(\beta \mid \mathbf{\text{Y}},\mathbf{\text{D}})g(\beta )d\beta }{{\int }_{-\infty }^{\infty }L(\beta \mid \mathbf{\text{Y}},\mathbf{\text{D}})g(\beta )d\beta },$$ (1)

where

$$L(\beta \mid \mathbf{\text{Y}},\mathbf{\text{D}})=\prod _{i=1}^{k}f{\left(d_{[i]};\beta \right)}^{Y_i}{\left[1-f\left(d_{[i]};\beta \right)\right]}^{1-Y_i}$$ (2)

$$=\prod _{i=1}^k{\left[d_{[i]}^{\beta }\right]}^{Y_i}{\left[1-d_{[i]}^{\beta }\right]}^{1-Y_i}$$ (3)

is the likelihood for β, Y={Y₁, Y₂, … Y_k}, and D={d_[1], d_[2], … d_[k]}. We can then compute a posterior DLT probability for each dose as ${\widehat{p}}_j=d_j^{\widehat{\beta }}$.

The dose level, j*, recommended for the next enrolled cohort is the dose with the estimated DLT probability closest to θ. After observing the DLT outcomes for this most-recently enrolled cohort, we use Equation (1) to update ${\widehat{p}}_j$ and update which dose has a DLT probability closest to the targeted DLT probability. At the end of the study, we determine the MTD as the index j* based upon the data from all N participants, where N is selected either as a feasible number of participants that can be enrolled, or based upon published sample size calculations.^14,15

2.2 |. Consistency of CRM

The selection of the MTD at the end of the study is founded on the belief that the probability of correctly identifying the MTD increases with the sample size, so that dose assignments begin to focus on a single dose, which is more and more likely to be the MTD. This so-called consistency of the CRM was first explored by Shen and O’Quigley¹⁶ and later expanded upon by Cheung and Chappell¹⁷ and O’Quigley.¹⁸ The original consistency requirement of Shen and O’Quigley¹⁶ begins with the support of the model parameter β being divided into J nonoverlapping intervals ${\mathcal{B}}_1,{\mathcal{B}}_2,\cdots {\mathcal{B}}_J$. Assuming that β has support on the real line, and defining b₁ = −∞ and b_{J +1} = ∞, we have ${\mathcal{B}}_j=\left(b_j,b_{j+1}\right)$ such that b_j, j = 2, 3, … J solves f(d_j−1; b_j) + f(d_j; b_j) = 2θ. Essentially, interval ${\mathcal{B}}_j$ contains the values of β that lead to dose j having a modeled DLT probability closest to the targeted DLT probability θ. Thus, for a given model, these intervals are a function only of the skeleton and the targeted DLT probability.

If we have a vector of true DLT probabilities, α = {α₁, α₂, …, α_J}, where α_j is the true DLT probability of dose j, we can find a value for the model parameter β, denoted ${\beta }_j^{*}$, at which the modeled DLT probability is equivalent to the true DLT probability, that is, ${\alpha }_j=f\left(d_j;{\beta }_j^{*}\right)$. Certainly the CRM is consistent if there exists a unique value, ${\beta }_0^{*}$, such that ${\beta }_0^{*}={\beta }_1^{*}={\beta }_2^{*}=\cdots ={\beta }_J^{*}$, that is, the model is correct. However, even if the model is incorrect, the CRM can still be consistent as follows.

First, from the values in α, we know which dose is the true MTD, that is, the dose for which |α_j − θ| is smallest. We denote this dose with the subscript ℓ ∈ {1, 2, …, J}, with corresponding interval ${\mathcal{B}}_{\ell }$. Consistency for the CRM will occur if ${\beta }_j^{*}\in {\mathcal{B}}_{\ell }$ for every dose. As an example, which will be explored more in Section 4, suppose we have a study of J = 6 doses with a target DLT probability of θ = 0.25, and that dose 4 is the true MTD. If we adopt the skeleton π = (0.03, 0.11, 0.25, 0.42, 0.58, 0.71), we have the intervals ${\mathcal{B}}_1=(-\infty ,-0.692)$, ${\mathcal{B}}_2=(-0.692,-0.223)$, ${\mathcal{B}}_3=(-0.223,0.245)$, ${\mathcal{B}}_4=(0.245,0.714)$, ${\mathcal{B}}_5=(0.714,1.183)$, and ${\mathcal{B}}_6=(1.183,\infty )$ based upon our assumed power model. With true DLT probabilities α = (0.01, 0.03, 0.11, 0.25, 0.41, 0.57), we have, ${\beta }_1^{*}=0.376$, ${\beta }_2^{*}=0.415$, ${\beta }_3^{*}=0.447$, ${\beta }_4^{*}=0.469$, ${\beta }_5^{*}=0.483$, and ${\beta }_6^{*}=0.492$. Therefore, α is consistent with π because ${\beta }_j^{*}\in {\mathcal{B}}_4$ for all j. By contrast, consistency is violated if dose 3 has true DLT probability α₃ = 0.18, because now ${\beta }_3^{*}=0.212$ which is outside the bounds of ${\mathcal{B}}_4$.

3 |. PROPOSED METHODOLOGY

3.1 |. Approximating simulations

As we stated earlier, a CRM design is examined in a simulation study in which many, perhaps 5000, hypothetical trials are run assuming a vector of true DLT probabilities α. For each of the simulations, we record the dose assigned to each participant and the dose selected as the MTD at the end of the study. The performance of the CRM is often summarized by (i) the proportion of simulations in which each dose is selected as the MTD, and (ii) the average proportion of participants assigned to each dose. The value in (i) corresponding to the true MTD is known as the probability of correct selection (PCS); the consistency of the CRM implies that PCS increases to 1 as the sample size increases, which implies that each of the other doses is selected with a probability that decreases to 0 as the sample size increases. We also desire that the largest value in (ii) corresponds to the true MTD and that the values in (ii) are relatively small for doses larger than the true MTD as a measure of overdosing. Our goal is to compute values for these three quantities without the need for simulations.

To do this, we first return to the intervals ${\mathcal{B}}_1,{\mathcal{B}}_2,\dots {\mathcal{B}}_J$ that divide the support of the model parameter β. In any single simulation, when we have collected data on n ≤ N participants, we will have a posterior distribution for β and we define ω_jn to be the amount of posterior mass in ${\mathcal{B}}_j$, such that ${\sum }_j{\omega }_{jn}=1$. Thus, ω_j0 is the amount of a priori mass contained in ${\mathcal{B}}_j$ and ω_jN is the amount of posterior mass contained in ${\mathcal{B}}_j$ at the end of the study. If dose ℓ is the true MTD, then the consistency of the CRM implies that ω_ℓN converges to 1 as N goes to infinity. Thus, both PCS and ω_ℓN converge to 1 as N goes to infinity.

In a simulated trial, each participant supplies a single indicator of DLT for a single dose. For our method to mimic many simulations simultaneously, we generate a J-vector of outcomes for each participant, with one outcome for each dose, and we use these multivariate data to determine the MTD. However, instead of generating a vector of binary DLT indicators for each dose, we instead assign each participant the vector α, that is, each participant’s DLT indicator for each dose is replaced with its expected value. The idea of using a multivariate vector of outcomes for each participant is similar to the nonparametric optimal design¹⁹ that provides an upper bound on the PCS of the CRM.

At this point, without further adjustment, we have JN observations to determine the MTD instead of the N observations in an actual trial. We solve this issue as follows. Per corollary 1 in O’Quigley,¹⁸ we know that if the posterior mean of β based upon data from k participants lies in interval ${\mathcal{B}}_j$, then dose j would be assigned to participant (k + 1). Therefore, we can interpret ω_jk to be the posterior propensity that dose j would be assigned to participant (k + 1), and we incorporate these propensities as weights into the likelihood used by the CRM. For each participant k + 1, we adaptively change the weights based upon the results occurring from participants i = 1, 2, … k. Explicitly, the likelihood in Equation (2) changes to

$$\begin{gathered} L(\beta \mid \mathit{\alpha })=\prod _{i=1}^k\prod _{j=1}^J{\left\{f{\left(d_j;\beta \right)}^{{\alpha }_j}\right\}}^{w_{(j-1),i}}{\left\{{\left[1-f\left(d_j;\beta \right)\right]}^{\left(1-{\alpha }_j\right)}\right\}}^{{\omega }_{(j-1),i}} \\ =\prod _{i=1}^k\prod _{j=1}^J{\left\{f{\left(d_j;\beta \right)}^{{\alpha }_j}{\left[1-f\left(d_j;\beta \right)\right]}^{\left(1-{\alpha }_j\right)}\right\}}^{{\omega }_{(j-1),i}} \end{gathered}$$ (4)

Thus, in this “likelihood,” every participant has the same vector of outcomes, quantified by α, but each participant has a different set of weights. The posterior distribution of β is recursively updated with each new participant, which produces a new set of weights, and we repeat this process for all N participants. From this one simulation of N participants, we have generated the operating characteristics of the CRM. Specifically, if dose ℓ is the true MTD, then ω_ℓN is the estimate of the PCS, and ${\sum }_{i=1}^N{\omega }_{\ell i}$ is the estimated expected number of participants assigned to dose ℓ.

Let us now examine this algorithm with our previous example. Recall that we have a study of J = 6 doses with a target DLT probability of θ = 0.25, and that dose 4 is the true MTD. We choose to use the CRM with the power model and adopt a skeleton π = (0.03, 0.11, 0.25, 0.42, 0.58, 0.71) and vector of true DLT probabilities α = (0.01, 0.03, 0.11, 0.25, 0.41, 0.57), which is consistent with π. If we give β a normal prior distribution with mean 0 and variance 1.00, then we have the a priori weights ω₁₀ = 0.251, ω₂₀ = 0.133, ω₃₀ = 0.150, ω₄₀ = 0.186, ω₅₀ = 0.122, and ω₆₀ = 0.158, where ω_j0 is the a priori mass in interval ${\mathcal{B}}_j$. These values are the weights assigned to the first participant.

If we enroll participants in cohorts of size 1, then we use Equation (4) with these weights to produce a posterior distribution for β. For each dose j, we now compute the a posteriori mass in ${\mathcal{B}}_j$, giving us new weights ω₁₁ = 0.173, ω₂₁ = 0.173, ω₃₁ = 0.217, ω₄₁ = 0.201, ω₅₁ = 0.138, and ω₆₁ = 0.098. These values are the weights assigned to the second subject. This process continues with each consecutive participant; weights for the first 25 participants can be found in Table 1. After 25 participants, the final updated weights, which are the weights for the hypothetical 26th participant, are the final probabilities that each dose is selected as the MTD. Thus, for dose 4 (the true MTD), the weight ω_26,4 = 0.626 is the estimated PCS with 25 participants. Moreover, the final row in Table 1 is the sum of the weights for each dose across all 25 participants, which provides an estimate of the expected number of participants that would be assigned to each dose. Thus, for this design, we expect that 10 or 11 participants would be assigned to the MTD.

TABLE 1.

Posterior probabilities placed on each of six doses during a Phase I trial using the CRM

Participant	Dose number
ID	1	2	3	4	5	6
1	0.244	0.167	0.185	0.166	0.119	0.118
2	0.173	0.173	0.217	0.201	0.138	0.098
3	0.122	0.170	0.241	0.234	0.151	0.082
4	0.086	0.161	0.260	0.263	0.161	0.068
5	0.061	0.149	0.275	0.291	0.168	0.056
6	0.043	0.135	0.286	0.317	0.172	0.046
7	0.030	0.122	0.294	0.341	0.175	0.038
8	0.021	0.109	0.299	0.364	0.176	0.031
9	0.015	0.096	0.302	0.385	0.176	0.026
10	0.011	0.085	0.304	0.405	0.174	0.021
11	0.008	0.074	0.304	0.424	0.173	0.017
12	0.005	0.065	0.303	0.442	0.170	0.014
13	0.004	0.057	0.301	0.460	0.167	0.011
14	0.003	0.049	0.299	0.476	0.164	0.009
15	0.002	0.043	0.295	0.491	0.161	0.008
16	0.001	0.037	0.292	0.506	0.157	0.006
17	0.001	0.032	0.287	0.521	0.153	0.005
18	0.001	0.028	0.283	0.534	0.150	0.004
19	0.000	0.024	0.278	0.547	0.146	0.003
20	0.000	0.021	0.273	0.560	0.142	0.003
21	0.000	0.018	0.268	0.572	0.139	0.002
22	0.000	0.016	0.263	0.584	0.135	0.002
23	0.000	0.014	0.258	0.595	0.131	0.002
24	0.000	0.012	0.253	0.606	0.128	0.001
25	0.000	0.010	0.248	0.616	0.125	0.001
26	0.000	0.009	0.243	0.626	0.121	0.001
Sum of
Rows 1–25	0.831	1.867	6.868	10.901	3.851	0.672

Note: Dose 4 is the true MTD and is indicated by the vertical double lines. The skeleton is π = (0.03, 0.11, 0.25, 0.42, 0.58, 0.71) and the vector of true DLT probabilities is α = (0.01, 0.03, 0.11, 0.25, 0.41, 0.57). Each row corresponds to the weight that would be produced after that subject’s data are incorporated into the posterior calculations. The dose with the largest weight would be assigned to the next subject. The sum of the first 25 rows provides information on the expected number of participants assigned to each dose in a trial.

Abbreviations: CRM, continual reassessment method; MTD, maximum tolerated dose.

The CRM is also often designed with a limit on escalation, whereby a dose cannot be assigned to a new participant unless all lower doses have been assigned to previous participants. Such a restriction could be applied to our method by simply adding the weights of doses that cannot be currently assigned to the weight of the highest dose that can be assigned. With this restriction, for example, row 1 in Table 1 would have a 1.000 for dose 1 and 0.000 for all other doses, while row 2 in Table 1 would have a value of 0.727 for dose 2 and 0.000 for doses 3 to 6 (dose 1 would be unchanged).

We note that our description assumed that dose assignments were done sequentially with each individual participant. However, mostly due to historical references to the 3+3 design,² the CRM is sometimes implemented to enroll participants in cohorts of three participants, with each participant in the cohort assigned to the same dose. Our method is able to accommodate this feature by simply giving each participant in the cohort the same weights before computing the posterior distribution for β and updating the weights, rather than updating the weights after each individual participant. Thus, our method is able to quickly examine the impact that cohort size has on the CRM operating characteristics, with only one simulation necessary for each cohort size.

Furthermore, appropriate sample sizes for Phase I trials using the CRM have been traditionally based on extensive simulation studies, although approximations have been published recently by both Cheung,¹⁴ who uses PCS as a metric, and Braun,¹⁵ who uses posterior credibleinterval length as a metric. The elegance of our proposed method lies in its ability to quickly determine PCS after every consecutive participant, so that PCS can be estimated for a multitude of sample sizes in one simulation, with computations that are faster and do not require approximations used Cheung and Braun.

More generally, our method applies to any design parameter whose “optimal” value is traditionally calibrated through simulation. For example, Lee and Cheung^20,21 present a systematic way of calibrating values for both the skeleton and model parameter prior variance, but both algorithms eventually incorporate simulation into their approach. Instead, our method could be used to replace the simulation step in each algorithm and promote greater use of their methods in the design of actual Phase I trials.

Last, our method is able to quickly assess any stopping rule that is based upon accumulated dose assignments. For example, if the lowest dose is assigned to several participants, this may suggest in reality that all doses are too toxic and enrollment should be paused or the study should end. Or, further accrual could be terminated once a specific number of participants are all assigned the same dose, which is likely the dose selected as the MTD. Examination of a stopping rule is presented in conjunction with the hypothetical trial designed in Section 4.

3.2 |. Lack of consistency between skeleton and true DLT probabilities

Our method hinges on the assumption that the true DLT probabilities examined are consistent with the selected skeleton. Thus, one must first select a skeleton and then select a set of true DLT probabilities that are consistent with that skeleton. Although such a process confirms that the CRM will eventually converge its dose assignments to the MTD, often studies are designed in reverse, that is, the true DLT probabilities are selected first and then a skeleton is examined with those true DLT probabilities; see James et al²² for an example.

Nonetheless, if one has a specific vector of true DLT probabilities to examine, a given skeleton that is inconsistent can be modified to become consistent using the following algorithm:

1. From the vector α of true DLT probabilities, determine which dose is the MTD; denote this dose as ℓ;

2. From the vector π of skeleton DLT probabilities and target DLT probability θ, compute the intervals ${\mathcal{B}}_1,{\mathcal{B}}_2,\dots {\mathcal{B}}_J$ as described in Section 2.2; denote interval ${\mathcal{B}}_{\ell }=\left(b_{\ell },b_{\ell +1}\right)$;

3. Determine the values ${\beta }_1^{*},{\beta }_2^{*},\dots ,{\beta }_J^{*}$ as described in Section 2.2;

4. For j = 1,2, … J, compute an indicator of consistency, that is, determine if ${\beta }_j^{*}\in {\mathcal{B}}_{\ell }$;

5. If all doses indicate consistency, then stop and use current skeleton.

6. If at least one dose indicates lack of consistency:

   1. For k = 1, 2, …, ℓ − 1, update ${\beta }_k^{*}=b_{\ell }+\left({\beta }_{\ell }^{*}-b_{\ell }\right)k/\ell$;
   2. For k = ℓ + 1, ℓ + 2, …, J, update ${\beta }_k^{*}={\beta }_{\ell }^{*}+\left(b_{\ell +1}-{\beta }_{\ell }^{*}\right)(k-\ell )/(J-\ell +1)$;
   3. For j = 1, 2, …, J, update the dose value d_j that solves ${\alpha }_j=f\left(d_j;{\beta }_j^{*}\right)$ and convert d_j to the corresponding skeleton value π_j;

7. Repeat steps (2) to (6) until consistency occurs for all doses.

In step (6a), we consider doses lower than the true MTD. We replace their corresponding value of ${\beta }_k^{*}$ with the expected value of the kth of (ℓ − 1) order statistics drawn uniformly over the interval $\left(b_{\ell },{\beta }_{\ell }^{*}\right)$, which is simply the shifted and scaled mean of a Beta random variable. Likewise, for doses higher than the MTD, in step (6b) we replace their corresponding value of ${\beta }_k^{*}$ with the expected value of the (J − k)th of (J − ℓ) order statistics drawn uniformly over the interval $\left({\beta }_{\ell }^{*},b_{\ell +1}\right)$, which is also a shifted and scaled mean of a Beta random variable. We then derive the skeleton values that correspond to these updated values and repeat the process until we generate a skeleton that is consistent with the desired vector of true DLT probabilities. Convergence usually occurs within one or two iterations.

Recall in our earlier example that we had a skeleton π = (0.03, 0.11, 0.25, 0.42, 0.58, 0.71). If the true DLT probabilities were α = (0.04, 0.09, 0.18, 0.26, 0.40, 0.70), this skeleton would not be consistent because of the values assigned to doses 1, 2, 3, and 6. The greatest impact is from α₃, which hampers the ability of the CRM to differentiate between whether dose 3 or 4 is the MTD. After two iterations of the algorithm above, we create the modified skeleton π = (0.10, 0.19, 0.32, 0.42, 0.58, 0.83) which is now consistent with α.

4 |. APPLICATION TO DESIGN OF A NEW TRIAL

We now present an application of our method in the design a Phase I trial. Our trial setting is one presented in Infante et al,²³ which is a Phase I trial of eleven doses of LCL161, a promoter of cancer cell death, in participants with advanced solid tumors. Based upon the trial summary data presented in the article, which collapsed the six lowest doses into a single dose, we assume our trial has a more manageable set of six doses. At the end of the actual study, the investigators decided that the fourth dose was the RP2D, and we will assume this dose is the true MTD. The original study targeted a desired DLT probability between 0.16 and 0.33, so we have selected a target of θ = 0.25. Thus, we assume the true DLT probabilities are α = (0.01, 0.03, 0.11, 0.25, 0.41, 0.57). We also assume that the maximum planned sample size is N = 30.

Using the getprior function in the R library dfcrm, the code getprior(0.08, 0.25, 3, 6) produces a skeleton of π = (0.03, 0.11, 0.25, 0.42, 0.58, 0.71) which happens to be consistent with α. The value of 0.08 used in the function is one we use in practice to produce skeleton values that are reasonably spaced so as to provide a distinct a priori MTD. We model the association between dose and the probability of DLT with the power model whose model parameter, β, has a log-normal distribution with log(β) having mean 0 and standard deviation σ. Our first goal is to determine an appropriate value for σ. One approach²¹ is to find the value of σ, among a grid of values, that leads to nearly equal prior probability placed on each dose being the MTD. Using this approach produces a value of σ = 1.00; note that the default value in the titecrm function in the R library dfcrm is $\sigma =\sqrt{1.34}=1.16$.

However, because of the speed of our method, it is possible to quickly find an appropriate value for σ that makes PCS as large as possible. Among the 141 candidate values in (0.70, 0.71, …, 2.10), we found that any value between 0.73 and 0.89 led to the largest value of PCS; this search took 18 seconds on a MacBook Pro with a 2.8 GHz processor with 16 GB of memory. We also ran 5000 simulations for each candidate value of σ using the crmsim function in the R library dfcrm; this search took 6.3 hours. Among the candidate values of σ, the difference in PCS computed from our method and traditional simulations was no more than two percentage points. Moreover, the two methods differed by no more than two participants assigned to the true MTD by the end of the study among all values of σ, with 88% of values for σ having a difference of no more than one subject. Thus, we have very strong evidence for the concordance of operating characteristics of our method and those produced with traditional simulations. Furthermore, we have conclusive evidence that our method is valid for any reasonable value of σ, even though the consistency of the CRM was founded in maximum likelihood (frequentist) methods.

At this point in our design, we adopt σ = 0.85 and wish to determine how the operating characteristics of the CRM might vary among other skeletons, each that is consistent with α. We do this by first randomly selecting with equal probability one of doses 2, 3, 4, and 5 to be the a priori MTD. For the a priori MTD, we then select a DLT probability randomly in the interval (0.20, 0.30), which is five percentage points on either side of our target θ = 0.25. We then select ordered DLT probabilities uniformly from the intervals (0.05, 0.20) and (0.30, 0.95) for doses below and above the a priori MTD, respectively. The resulting skeleton is then assessed for consistency; if it is not consistent, it is modified using the algorithm in Section 3.2.

Using our method, we were able to examine 1000 skeletons in just over 2 minutes. By contrast, examining these 1000 skeletons via 5000 simulations each took nearly 2 days. Figure 1 contains boxplots of the difference in both PCS and number of participants assigned to the MTD after 30 participants among the 1000 skeletons used with the two methods. In Figure 1, although there are differences among a few skeletons, for a majority of skeletons, we have excellent concordance between the two methods, again providing strong evidence that our method replicates the results produced in traditional simulations.

FIGURE 1.

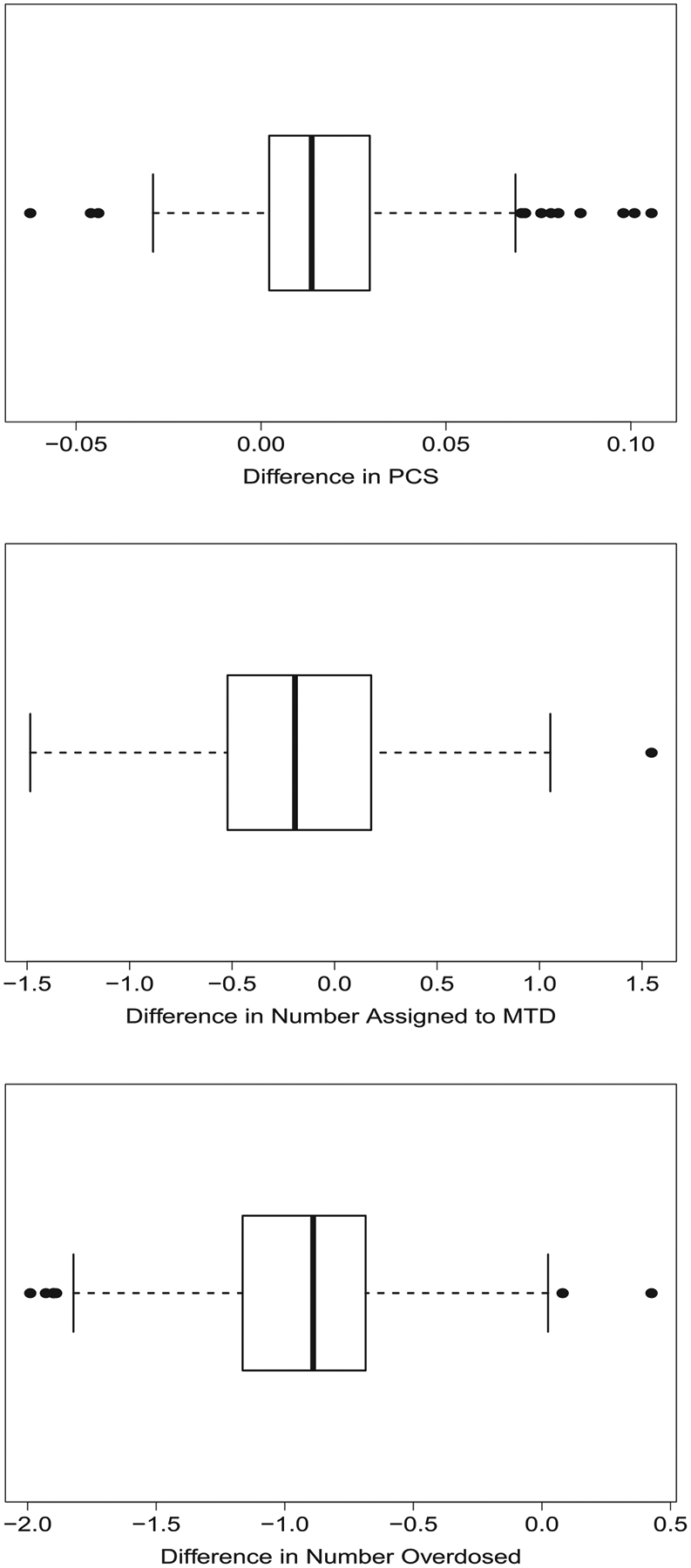
Boxplots of differences in operating characteristics of a CRM design with 30 participants produced by a traditional simulation study of 5000 simulations and the proposed method over 1000 different consistent skeletons. The vector of true DLT probabilities is α = (0.01, 0.03, 0.11, 0.25, 0.41, 0.57). The upper plot presents the difference in the probability of correct selection (PCS) of the maximum tolerated dose (MTD); the middle plot presents the difference in the average number of participants assigned to the MTD; the lower plot presents the difference in the average number of participants assigned to doses above the MTD. Difference is computed as result from proposed method minus result from traditional simulations. CRM, continual reassessment method

For a given skeleton and value for σ, we can also examine the operating characteristics for our design across many possible vectors of true DLT probabilities, as long as each is consistent with our skeleton. The consistency of the CRM described in Section 2.2 implies that once the skeleton and the location of the MTD are specified, each dose has an interval of probabilities in which its true DLT probability must exist. For our setting, those intervals are ${\mathcal{I}}_1=(0.00,0.01)$, ${\mathcal{I}}_2=(0.01,0.06)$, ${\mathcal{I}}_3=(0.06,0.17)$, ${\mathcal{I}}_4=(0.17,0.33)$, ${\mathcal{I}}_5=(0.33,0.50)$, ${\mathcal{I}}_6=(0.50,0.65)$, for doses 1 to 6, respectively. For each dose, we drew 1000 DLT probabilities uniformly from its corresponding interval to produce 1000 vectors for α and used our method to compute the operating characteristics for each of those 1000 vectors with a sample size of 30 participants. See Figure 2 for distributions of PCS and expected numbers of participants assigned to the MTD and doses higher than the MTD.

FIGURE 2.

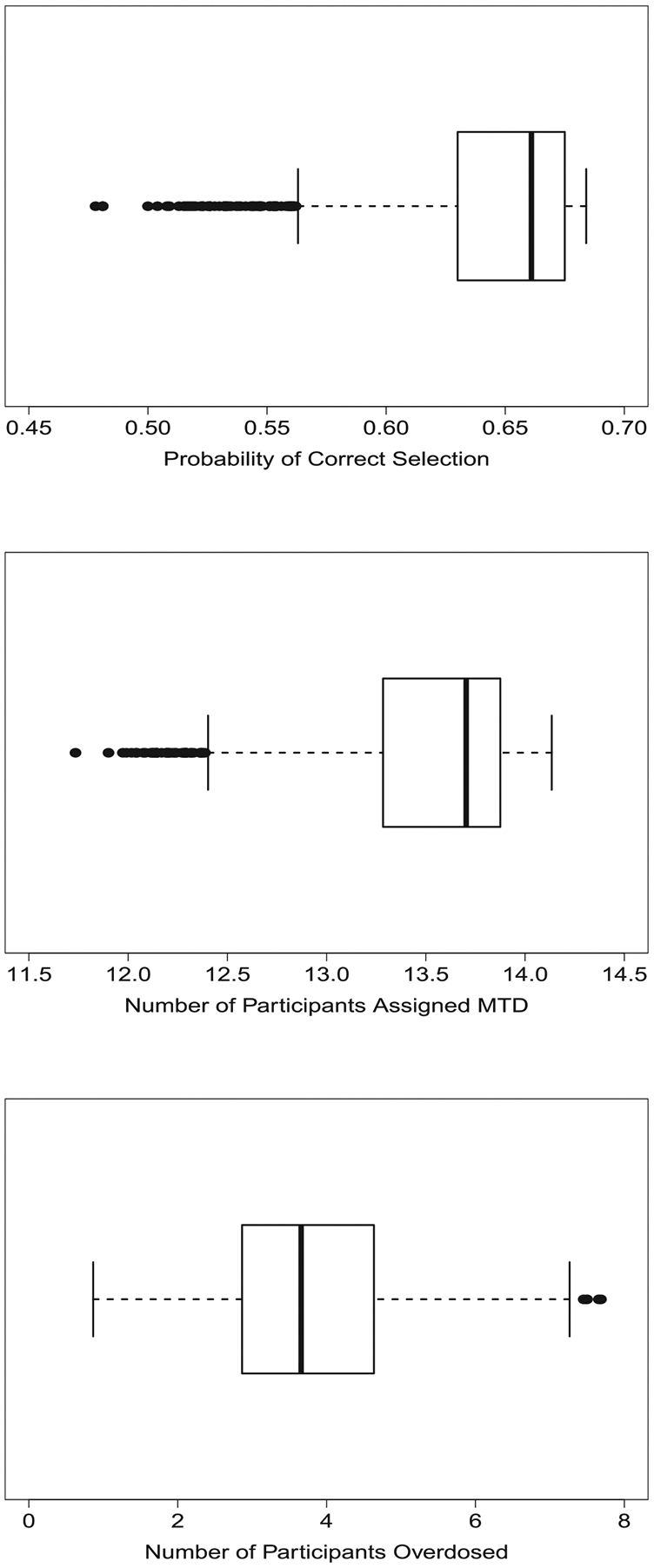
Boxplots of operating characteristics of a CRM design with 30 participants produced by the proposed method over 1000 different consistent vectors of true DLT probabilities using a skeleton o π = (0.03, 0.11, 0.25, 0.42, 0.58, 0.71). The upper plot presents the probability of correct selection (PCS) of the maximum tolerated dose (MTD); the middle plot presents average number of participants assigned to the MTD; the lower plot presents the average number of participants assigned to doses above the MTD. CRM, continual reassessment method

Because our method is able to compute PCS and number of subjects assignedto the MTD after each consecutive participant, determining an appropriate sample size can also be done quickly. Across the 1000 vectors of true DLT probabilities just examined, we used our method to compute PCS for any sample size up to 100 participants to determine the sample sizes necessary for producing PCS of both 0.70 and 0.80 across many possible true settings. Figure 3 presents boxplots of the sample sizes that provide PCS of 0.70 and 0.80 among the 1000 settings examined; we note that such a plot would be nearly impossible to provide using traditional simulations. The figures provide a range of sample sizes that could be proposed, and perhaps the median could be suggested as the final sample size, rather than one sample size generated from one specific value for α. We note that, in a handful of settings, we compared our sample sizes to those generated from a traditional simulation study (results not shown) to confirm the accuracy of our results, as verifying all 1000 settings would have required a prohibitive amount of computational expense.

FIGURE 3.

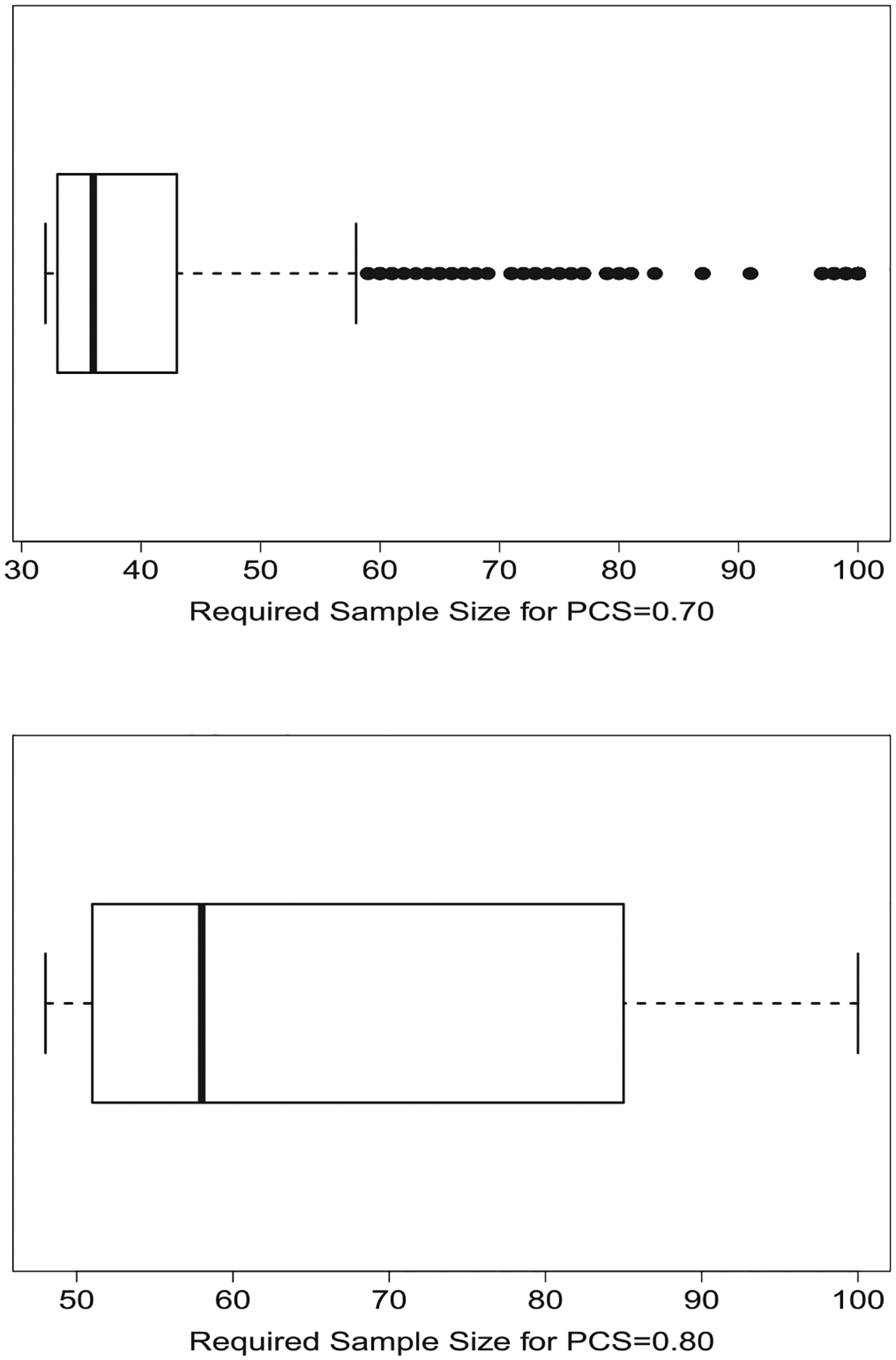
Boxplots of maximum sample sizes required for PCS of 0.70 (upper plot) and 0.80 (lower plot) across 1000 different vectors of true DLT probabilities of a CRM design for a study of six doses with a skeleton of π = (0.03, 0.11, 0.25, 0.42, 0.58, 0.71) and vector of true DLT probabilities α = (0.01, 0.03, 0.11, 0.25, 0.41, 0.57). CRM, continual reassessment method; PCS, probability of correct selection

As a reference, we compared our sample sizes to those resulting from the methods of Cheung,¹⁴ which are contained in the function getn in the titecrm library. This function requires the user to supply an odds ratio that summarizes the pattern in the true DLT probabilities, which becomes less and less accurate as the true DLT probabilities deviate from a linear pattern on a log-odds scale. For example, when α = (0.01, 0.03, 0.17, 0.20, 0.45, 0.58), whose values are summarized well with an odds ratio of 2.35, using the getn function produced sample sizes of 32 and 51 for PCS of 0.70 and 0.80, which are close to 33 and 49, the corresponding sample sizes generated by our method. By contrast, when α = (0.01, 0.03, 0.15, 0.27, 0.48, 0.61), the best fitting odds ratio is 2.43, which leads to sample sizes of 30 and 48 using the getn function, but actually requires sample sizes of 46 and 75 based upon our method, for PCS of 0.70 and 0.80, respectively.

We would also like to assess the impact of a safety stopping rule that halts accrual once five participants have been assigned to the lowest dose. If the vector of true DLT rates is α = (0.28, 0.36, 0.50, 0.67, 0.83, 0.90), the first stopping rule leads to a median of 10 enrolled participants before the stopping criterion is met. This value of 10 compares favorably to the value of 11 participants that was produced from 5000 simulations. Thus, the study is expected to halt enrollment quite early and potentially terminate after approximately one-third of the planned accrual. If we increase the true DLT rates to α = (0.38, 0.48, 0.58, 0.68, 0.78, 0.88), the median number of participants drops further to eight participants for both our method and traditional simulations.

We emphasize that our method assumes that the skeleton and the vector of true DLT probabilities are consistent with each other. In practice, it is common for individuals to select one skeleton and then assess the operating characteristics for a handful of vectors of true DLT probabilities, without any consideration of consistency. In fact, it is likely not possible to find one skeleton that would be consistent with all the vectors of true DLT probabilities. We now seek to compare the operating characteristics of our design with those of traditional simulations when the skeleton is not consistent for all vectors of true DLT probabilities examined.

Continuing with our same skeleton and prior standard deviation, we consider seven vectors of true DLT rates, whose lack of consistency is quantified as follows. As explained in Section 3.2, if dose ℓ ∈ {1, 2, …, J} is the MTD, there is a corresponding interval ${\mathcal{B}}_{\ell }=\left({\beta }_1,{\beta }_2\right)$ of values for the model parameter. Consistency for the CRM will occur if ${\beta }_j^{*}\in {\mathcal{B}}_{\ell }$ for every dose, where ${\beta }_j^{*}$ is the value of the model parameter that mades the modeled DLT probability for dose j equal to its true DLT probability. We define the measure of nonconsistency

$${\varphi }_{\text{NC}}=\sum _{j:{\beta }_j^{*}<{\beta }_1}{\left({\beta }_j^{*}-{\beta }_1\right)}^2+\sum _{j:{\beta }_j^{*}>{\beta }_2}{\left({\beta }_j^{*}-{\beta }_2\right)}^2,$$

which is a sum of Euclidean distances of each ${\beta }_j^{*}$ from the interval ${\mathcal{B}}_{\ell }$, depending on whether ${\beta }_j^{*}$ is to the left or right of ${\mathcal{B}}_{\ell }$. By definition ϕ_NC = 0 when consistency exists.

Table 2 summarizes how our measure of nonconsistency is related to the differential between traditional simulations and our method in their values of both PCS and the average proportion of subjects assigned to the MTD. In scenarios 1 and 2, in which dose 4 is the MTD, we see that our method overestimates the operating characteristics of the CRM because it is unable to replicate the fact that dose 5 is selected as the MTD and is assigned more often in traditional simulations. In scenarios 3 and 4, although the degree of nonconsistency is greater than in scenarios 1 and 2, we see our method produces operating characteristics comparable to traditional simulations. By contrast, in scenarios 5 and 6, we now have the MTD at dose 3, although the DLT probability of dose 2 is also close to the target of 0.25. In both of these scenarios, our method places greater weight on dose 2 than on dose 3, while traditional simulations do the same, but to a lesser degree. Finally, in scenario 7, we see there is little difference between the DLT probabilities of doses 2 and 3, although dose 2 is the MTD. Thus, traditional simulations are selecting and assigning dose 3 as the MTD about as often as dose 2, while our method greatly prefers dose 2 to dose 3.

TABLE 2.

Comparison of operating characteristics between proposed method (New) and traditional simulations (Trad) when the skeleton (0.03, 0.11, 0.25, 0.42, 0.58, 0.71) and the vector of true DLT probabilities α are not consistent with each other

		Prob of select			Prop assigned
Scenario	Method	At MTD	Below MTD	Above MTD	At MTD	Below MTD	Above MTD
1
α =(0.01, 0.06, 0.12, 0.21, 0.30, 0.45)	New	0.68	0.15	0.17	0.47	0.38	0.15
ϕNC = 0.03	Trad	0.52	0.18	0.31	0.41	0.35	0.25
2
α =(0.01, 0.10, 0.12, 0.20, 0.35, 0.40)	New	0.68	0.18	0.14	0.46	0.42	0.11
ϕNC = 0.12	Trad	0.55	0.20	0.25	0.42	0.37	0.21
3
α =(0.01, 0.03, 0.06, 0.12, 0.24, 0.48)	New	0.59	0.36	0.05	0.38	0.59	0.03
ϕNC = 0.27	Trad	0.62	0.32	0.06	0.41	0.52	0.07
4
α =(0.01, 0.05, 0.07, 0.15, 0.30, 0.35)	New	0.43	0.57	0.00	0.29	0.71	0.00
ϕNC = 0.38	Trad	0.43	0.50	0.07	0.30	0.64	0.06
5
α =(0.07, 0.16, 0.18, 0.26, 0.41, 0.46)	New	0.31	0.69	0.00	0.25	0.75	0.00
ϕNC = 0.49	Trad	0.42	0.50	0.08	0.32	0.58	0.10
6
α =(0.09, 0.18, 0.20, 0.28, 0.43, 0.48)	New	0.15	0.85	0.00	0.16	0.84	0.00
ϕNC = 0.63	Trad	0.34	0.61	0.05	0.28	0.65	0.08
7
α =(0.17, 0.26, 0.28, 0.36, 0.51, 0.56)	New	0.70	0.12	0.17	0.53	0.22	0.26
ϕNC = 0.94	Trad	0.38	0.18	0.43	0.34	0.23	0.43

Note: Seven scenarios of true DLT probabilities are presented in order of increasing level of nonconsistency as quantified by ϕ_NC.

Abbreviation: MTD, maximum tolerated dose.

In summary, we see that the amount of nonconsistency does not necessarily predict whether our method will over- or under-estimate the operating characteristics of the CRM, nor by how much discrepancy will occur. In scenario 7, we see the greatest amount of nonconsistency and our method vastly overestimates both the PCS and the proportion of participants assigned to the MTD. However, in scenarios 5 and 6, which have less nonconsistency than scenario 7, our method now underestimates both PCS and the proportion of participants assigned to the MTD. Moreover, in scenarios 3 and 4, although nonconsistency exists, the performance of our method is actually comparable to traditional simulations.

5 |. CONCLUDING REMARKS

We have developed methodology that reduces the need for simulations to determine common operating characteristics of the CRM. From our method, we can develop several summary measures, including PCS, the average number of participants assigned to each dose, desired sample size, and the average dose value assigned to each patient. We have also developed methods that produce a skeleton that is compatible with a given vector of true DLT probabilities so that the CRM will be consistent. However, two challenges to our method are (i) the inability to estimate the probability of stopping early as is done in traditional simulations, and (ii) the need for consistency between the skeleton and vector of true DLT probabilities. With regard to the latter limitation, we have attempted to provide one metric for the degree of nonconsistency, but it was unable to predict the differential between operating characteristics of our method and traditional simulations. We are pursuing different approaches for quantifying nonconsistency that better inform our method and potentially allow direct adjustment of any over- or under-estimation of PCS.

Cheung and Chappell¹⁷ developed a weaker definition of consistency based upon the expectation that the CRM will do well whenever the true DLT probabilities are sufficiently steep around the MTD. In general, for a given skeleton, their methods allow for a broader set of true DLT probabilities. However, a crucial component of our method is the consistency intervals ${\mathcal{B}}_1,{\mathcal{B}}_2,\dots {\mathcal{B}}_J$, which are not part of the weaker consistency definition. As a result, our method is not necessarily applicable to any vector of true DLT probabilities that meet the weaker consistency definition, but not the stronger definition, which we confirmed using the settings presented in Section 4 (results not shown).

We expect that our method will prove impactful beyond the traditional CRM and will be useful for any Bayesian adaptive design that has foundations in the CRM. This includes the bivariate CRM,²⁴ the partial order CRM,²⁵ the CRM with Bayesian model averaging,²⁶ the time-to-event CRM,²⁷ and the two-agent combination design of Braun and Jia.²⁸ All of these approaches are even more computation-intensive than the original CRM, and we expect that our method could provide even greater computational savings over traditional simulations when determining operating characteristics for these designs.

Nonetheless, general use of our method remains an open problem to solve. For example, one of the modifications to the CRM proposed by Neuenschwander et al²⁹ was to replace the fixed value of the intercept in the logistic model to instead be a parameter, α with its own prior distribution, so that both the intercept and the slope were estimated through their posterior distributions. Through a log-log transformation to the power model, we have log[−log(p_j)] = β + log[−log(d_j)], which can be generalized to the two-parameter model log[−textlog(p_j)] = β + α log[−log(d_j)], where now α serves as a slope parameter. For either model, we can compute the intervals ${\mathcal{B}}_1,{\mathcal{B}}_2,\dots {\mathcal{B}}_J$ for a given value of α. Thus, the intervals will change as α changes, making it possible to find joint bivariate regions for (α, β) for each dose, although it is unclear how those regions relate to the requirement of consistency necessary for our method. We also continue to develop a process for adjusting our method directly for nonconsistency of the skeleton and vector of true DLT probabilities so that PCS and assignment to the true MTD better reflect what results from simulations.

Through our work, we have also discovered in practice that there is a general lack of appreciation that the skeleton and the vector of true DLT probabilities should be selected in relationship to each other so that consistency of the CRM is maintained. This issue has been examined in greater detail,^30,31 but the message has fallen mostly on deaf ears. Instead, most applications of the CRM first identify the skeleton and the true DLT probabilities independent from each other and then examine the operating characteristics via simulation, without any consideration that the CRM may not be consistent in the first place. Such a practice needs to be eliminated, and can be mitigated with our proposed algorithm.

APPENDIX

1. R function for computing operating characteristics of CRM; example found at end of function

##############START FUNCTION#############
crm_oc <− function (my_skel , ptox_true , theta , Nsubj , cohort_size , sigma ,
start_dose=1, restrict=T , d1_maxn=Nsubj , cum_maxn=Nsubj )
{
 #This function computes operating characteristics for the CRM for a given
 #set of true DLT rate s and design parameters.
 #Currently the function only uses the power ( empiric ) model

 #my_skel = vector of DLT probabilities
 #ptox_true = vector of true DLT probabilities
 #theta = targeted DLT probability
 #Nsubj = maximum number of participants to enroll
 #cohort_size = number of participants enrolled together as a cohort
 #sigma = prior standard deviation for model parameter
 #start_dose = dose assigned to first participant
 #restrict = restrict escalation from untried doses
 #d1_maxn = number of participants assigned to dose 1 to invoke stopping
 #cum_maxn = number of particpants assigned to same dose to invoke stopping

 #Function to determine which dose has largest weight
 get_maxw <− function (rownum) ( 1 : ndose )[w[rownum,]==max(w[rownum , ] ) ]
 
 #Likelihood function used for posterior computations 11h <− function ( beta )
 {
   11h <− 1
   for ( i in 1: length ( Yout ))
   {
     p <− Dout [ i ] ^exp ( beta )
     11h <− 11h*p^ (Wout[ i ]*Yout [ i ])*(1 − p) ^ (Wout[ i ]*(1 − Yout [ i ] ) )
   }
   11h*dnorm( beta , 0 , sigma )
 }

 #Function to compute consistency intervals
 get . consist . int <− function (my_skel , theta )
 {
   zz <− function ( beta , i , dd , theta )
     dd[ i ] ^exp ( beta ) + dd[ i +1]^exp ( beta ) – 2*theta

   ndose <− length (my_ skel )
   1b <− −Inf
   for ( i in 1 : ( ndose −1))
    1b <− c ( 1b , uniroot ( zz , interval=c( −100 ,100) , i=i , theta=theta , dd=my_ skel ) $ root )
   ub <− c ( 1b [ 2 : ndose ] , Inf )

   list ( 1b=1b , ub=ub)
 }

 #Number of doses
 ndose <− length (my_ skel )

 #Computing bounds on consistency intervals
 ci <− get . consist . int (my_skel , theta )

 #Computing prior mass for each interval
 w <− pnorm( ci $ub , 0 , sigma ) − pnorm( ci $lb , 0 , sigma )
  if ( restrict==T) w <− as . numeric ( ( 1 : ndose)==start_dose )
 w <− matrix ( rep (w, cohort_size ) , nrow=cohort_ size , byrow=T)
 
 #Run computations for each subject
 ntot <− cohort_size
 while ( ntot <= Nsubj )
 {
   Wout <− c ( t (w))
   Yout <− rep ( ptox_true , ntot )
    Dout <− rep (my_skel , ntot )
   pm <− rep (0 , ndose )
   for (k in 1: ndose )
    pm[k] <− integrate ( 11h , ci $ 1b [k ] , ci $ub[k ]) $ value
   new_w <− pm/sum(pm)
   if ( restrict==T)
   {
     currmax <− get_maxw( ntot )
     newmax <− min( ndose , currmax+1)
     new_w[newmax] <− sum(new_w[newmax: ndose ])
     new_w[ ( 1 : ndose )>newmax] <− 0
   }
   w <− rbind (w, matrix ( rep (new_w, cohort_size ) , nrow=cohort_ size , byrow=T))
   ntot <− ntot+cohort_size
 }
 pcs <− w[ seq (1 , Nsubj+cohort_size , by=cohort_ size ) ,][ −1 ,]
 rownames( pcs ) <− 1 : ( Nsubj / cohort_size )
 colnames( pcs ) <− paste ( “Dose ” ,1: ndose , sep=“ ” )
 
 nassn <− apply (w[−(Nsubj +(1: cohort_size ) ) , ] , 2 , cumsum)
 nassn <− nassn [ seq ( cohort_size , Nsubj , by=cohort_size ) ,]
 rownames( nassn ) <− 1 : ( Nsubj / cohort_size )
 colnames( nassn ) <− paste ( “Dose” ,1: ndose , sep=“ ” )
 
 nstp_tox <− ( 1 : Nsubj )[ apply (w[ 1 : Nsubj , ] , 2 , cumsum) [ , 1 ] >=d1_maxn]
 nstp_tox <− ifelse ( length ( nstp_tox )==0, Nsubj , nstp_tox )
 nstp_cum <− apply (w[ 1 : Nsubj , ] , 2 , cumsum)>=cum_maxn
 nstp_cum <− row( nstp_cum)*nstp_cum
 nstp_cum <− ( nstp_cum==0)*Nsubj + ( nstp_cum>0)*nstp_cum
 nstp_cum <− min( apply ( nstp_cum, 2 , min))
 list ( pcs=pcs [nrow( pcs ) ,] , nassn=nassn [nrow( nassn ) ,] ,
       nstp_tox=nstp_tox , nstp_cum=nstp_cum, accum_pcs=pcs , accum_nassn=nassn )
}
##############END FUNCTION#############

##################EXAMPLE#################
my_skel <− c (0.03 , 0.11 , 0.25 , 0.42 , 0.58 , 0.71)
 ptox_true <− c (0.01 , 0.03 , 0.11 , 0.25 , 0.41 , 0.57)
 theta <− 0.25
 Nsubj <− 30
 cohort_ size <− 2
 sigma <− 0.85

 my_oc <− crm_oc (my_skel , ptox_true , theta , Nsubj , cohort_size , sigma ,
  start_dose=1, restrict=T , d1_maxn=5, cum_maxn=10)

2. R function for assessing skeleton for consistency and modifying, if necessary; example found at end of function

##############START FUNCTION#############
consist_skel <− function (my_skel , ptox_true , theta )
{
  #This function assesses the consistency of a given skeleton and vector
  #of true DLT probabilities ; f consistency does not exist ,
  #recursively develops consistent skeleton

  #my_skel = vector of DLT probabilities
  #ptox_t rue = vect or of true DLT probabilities
  #theta = targeted DLT probability

  #Algorithm to compute consistency interval bounds
  get . consist . int <− function (my_skel , theta )
  {
    zz <− function ( beta , i , dd, theta)
     dd [ i ] ^exp ( beta ) + dd [ i + 1] ^exp ( beta ) – 2*theta

    ndose <− length (my_skel )
    1b <− −Inf
    for ( i in 1 : ( ndose −1))
     1b <− c ( 1b , uniroot ( zz , interval=c ( −100 ,100) , i=i , theta=theta , dd=my_skel ) $ root )
    ub <− c ( 1b [2: ndose ] , Inf )

    list ( 1b=1b , ub=ub)
  }

  #Determine which dose is the true MTD
  ndose <− length (my_skel )
  delta <− abs ( ptox_true −theta )
  mtd_true <− ( 1 : ndose ) [ delta==min( delta ) ]

  #Computing bounds on consistency in tervals
  ci <− get . consist . int (my_skel , theta )

  #Check for consistency
  mu1 <− cbind (my_skel^exp ( ci $ub [mtd_true ] ) , my_skel^exp ( ci $ 1b [mtd_true ] ) )
  consist <− sum( ptox_true>=mu1[ , 1 ] & ptox _true<=mu1[ ,2])==ndose

  while ( ! consist )
  {
    #Compute parameter value f or each dose so that skelet on and truth are equal
    beta_star <− log ( log ( ptox_ true ) / log (my_ skel ) )

    #Determine how many doses are above and below the true MTD
    n_below <− mtd_true −1
    n_above <− ndose −(n_below+1)
    beta_below <− beta_above <− NULL
    a_below <− a_above <− b_below <− b_above <− NULL
   
    if (n_below>0)
    {
      a_below <− ci $ 1b [mtd_true ]
      b_below <− beta_star [mtd_true ]
      beta_below <− ( b_below−a_below )*( 1 :n_below ) / (n_below+1) + a_below
    }

    if (n_above>0)
    {
      a_above <− beta_star [mtd_true ]
      b_above<− ci $ub [mtd_true ]
      beta_above <− ( b_above−a_above )*( 1 :n_above ) / (n_above +1) + a_above
    }

    beta_star <− c ( beta_below , beta_star [mtd_true ] , beta_above )

    #Compute skeleton corresponding to beta values
    my_skel <− exp ( log ( ptox_true ) /exp( beta_star ) )
    #Determine if consistency now exists for each dose

    ci <− get . consist . int (my_skel , theta )
    mu1 <− cbind (my_skel^exp ( ci $ub [mtd_true ] ) , my_skel^exp ( ci $ 1b [mtd_true ] ) )
    consist <− sum( ptox_true>=mu1[ , 1 ] & ptox_true<=mu1[ ,2])==ndose
  }
  my_skel
}
#############END FUNCTION#############

##################EXAMPLE#################
my_skel <− c ( 0. 03 , 0 . 1 1 , 0. 2 5 , 0 . 4 2 , 0. 5 8 , 0.71)
theta <− 0.25

#Vector of true DLT rates where skeleton is consistent
ptox_true1 <− c ( 0. 01 , 0 . 03 , 0. 11 , 0 . 25 , 0. 41 , 0.57)
new_skel1 <− consist_skel (my_skel , ptox_true1 , theta )
 print (new_skel1 )

#Two other vectors of true DLT rates where skelet on is non−consistent
ptox_true2 <− c ( 0. 05 , 0 . 08 , 0. 12 , 0 . 18 , 0. 25 , 0.35)
new_skel2 <− consist_skel (my_skel , ptox_true2 , theta )
 print (new_skel2 )

ptox_true3 <− c ( 0. 15 , 0 . 25 , 0. 35 , 0 . 45 , 0. 55 , 0.65)
new_skel3 <− consist_skel (my_skel , ptox_true3 , theta )
 print (new_skel3 )

DATA AVAILABILITY STATEMENT

The appendix contains R code for two functions, one to produce operating characteristics and one to generate a consistent skeleton. The author will also provide, upon request, any code used to generate the simulation results presented in this article. A future R library of functions is in development.