Abstract
Cilia are microscopic hair-like external cell organelles that are ubiquitously present in nature, also within the human body. They fulfill crucial biological functions: motile cilia provide transportation of fluids and cells, and immotile cilia sense shear stress and concentrations of chemical species. Inspired by nature, scientists have developed artificial cilia mimicking the functions of biological cilia, aiming at application in microfluidic devices like lab-on-chip or organ-on-chip. By actuating the artificial cilia, for example by a magnetic field, an electric field, or pneumatics, microfluidic flow can be generated and particles can be transported. Other functions that have been explored are anti-biofouling and flow sensing. We provide a critical review of the progress in artificial cilia research and development as well as an evaluation of its future potential. We cover all aspects from fabrication approaches, actuation principles, artificial cilia functions – flow generation, particle transport and flow sensing – to applications. In addition to in-depth analyses of the current state of knowledge, we provide classifications of the different approaches and quantitative comparisons of the results obtained. We conclude that artificial cilia research is very much alive, with some concepts close to industrial implementation, and other developments just starting to open novel scientific opportunities.
Bioinspired artificial cilia can provide microfluidic functions like flow generation, particle transport and flow sensing. This critical review broadly describes the progress in artificial cilia research and evaluates its future potential.
1. Introduction
Cilia are slender protrusions of cells, which are ubiquitously present in nature, acting both as actuators and sensors. The cilia can be viewed as micro-hairs or flexible rods, which can have a typical length between 1 and 30 μm. They cover the outer surface of many micro-organisms, such as paramecia, and by concerted oscillation of the cilia, paramecium swims.1 Cilia are also present in our body, enabling transport – for example in the fallopian tube cilia transport the ovum along the ovary duct, and in the trachea they clear the airways from mucus. During embryonic development, cilia in the embryonic node induce fluid flow, which is critical to the determination of the vertebrate left/right body axis.2 Cilia also provide sensing, for example in the inner ear, acting as sensors for sound and gravity, or in the kidney as shear stress sensors.3–5
Inspired by nature, scientists have developed artificial cilia mimicking the functions of biological cilia. The research on artificial cilia started over a decade ago and is still rapidly expanding. Many research groups have developed microscopic actuators resembling cilia, actuated to move under the influence of different stimuli such as electrostatic fields,6 magnetic fields,7–15 and even light16 and pH.17 Mimicking the impressive functionalities of biological cilia, researchers have been exploring the capabilities of the developed artificial cilia in applications such as microrobots,18–20 microsensors,21,22 the manipulation of light, droplets and particles,23–25 self-cleaning and antifouling surfaces,26–28 microfluidic mixing,6 and predominantly, microfluidic pumping with integrated on-chip artificial cilia in microfluidic devices.29 Many of the results of this research are highly promising, especially with regard to application in microfluidic chips such as lab-on-chip (LOC) and organ-on-chip (OOC) devices, and it seems just a matter of time until artificial cilia will be integrated into commercial microfluidic products. At the same time, novel applications such as biological cell manipulation including on-chip mechano-stimulation of cell cultures and tissues are being explored.
The current stage of development of this exciting field, therefore, asks for a critical review of its progress as well as an evaluation of its future potential. This is what we provide in this review. Different from existing reviews of artificial cilia,29,30 we carry out comprehensive and in-depth analyses of the current state of knowledge, providing classifications of the different approaches as well as quantitative comparisons of the results published. The focus is on functions and applications relevant to microfluidic devices: transport of fluids and particles, as well as flow sensing.
We start with a brief overview of cilia in biology with the aim to review the appearance and function of natural cilia. Then, we describe how these biological functions can be mimicked, in a general sense, to create functions relevant to microfluidic applications. Subsequently, we review, classify and compare the various principles that have been proposed to actuate artificial cilia. Next, we give an overview of fabrication approaches used to create artificial cilia, and we evaluate their pros and cons. We then review the functions studied the most, namely flow generation and particle manipulation, respectively, and assess the published results quantitatively. The use of artificial cilia as flow sensors, which historically was actually the first application developed but has not experienced a widespread introduction in the microfluidics field up to date, is included in this review as well. Most of these aspects concern experimental developments, but modeling artificial cilia using numerical approaches is important to understand the experimental results and to guide future experiments; hence, we also give a brief overview of the main computational approaches to model artificial cilia. We close the review with a general summary and an outlook in which we describe the steps that need to be taken for further development, as well which future exciting opportunities artificial cilia can offer.
2. Cilia in biology
In 1675, Antonie van Leeuwenhoek first observed hair-like external cell organelles which we now know as cilia.31 Biological cilia are ubiquitous, occurring in many different organisms and tissues. After their discovery, not much was further established about their role and existence for a very long period of time. With the development in microscopy and imaging techniques, the beating/motile nature of cilia began to be observed in the 1930's.32 From that moment onwards, a great deal of work has been done deepening the understanding of cilia in all their aspects. Cilia fulfill many different roles and exhibit widely varying attributes such as length, motility or molecular structure. The fact that cilia have survived evolution and appear in such a variety of places and shapes suggests that these sub-cellular structures are highly efficient at carrying out tasks at the micro-scale.
2.1. Size and location
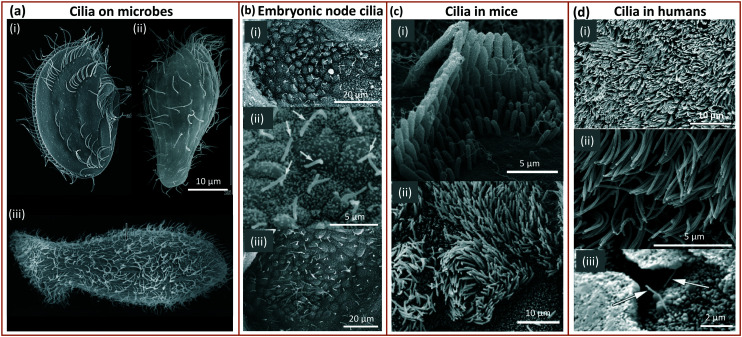
Cilia can be found at the smallest scales of life, having first been discovered on protozoa.33 Having persisted during evolution into complex organisms, cilia have been observed in many animals including zebrafish,34,35 rats36 and humans;37–40 some examples are shown in Fig. 1. Cilia appear in nearly every tissue of the human body, with varying functions in different organs, such as the lungs,37 kidneys39,41 or reproductive systems.38,42 Non-motile cilia have lengths varying from 1 μm in chondrocytes to 30 μm on kidney epithelial cells.43 Some of the smallest motile cilia exist in the embryonic node of mice with a length of around 3–5 μm and a diameter of 0.3 μm beating at a frequency of 10 to 15 Hz.31,44 The biggest motile cilia in different mammals grow longer than the non-motile cilia with 10's of microns in length such as the singular cilia called flagella present on sperm cells.31
Fig. 1. Cilia in nature: (a) (i) ciliary pattern on the body of Leptopharynx costatus. Reproduced from ref. 45 with permission from John Wiley and Sons. (ii) Cilia on the body of Platyophrya bromelicola. Reproduced from ref. 46 with permission from Elsevier. (iii) Closely spaced cilia on Spathidium spathula. Reproduced from ref. 47 with permission from Elsevier. (b) (i and ii) Cilia in the mouse embryonic node at an embryo age of 7.5 days. Reproduced from ref. 48 and 49 respectively with permission from Elsevier. (iii) Ciliated mouse embryonic node. Reproduced from ref. 50 with permission from Springer Nature. (c) (i) Stereocilia staircase structure in mouse cochlear. Reproduced from ref. 51 with permission from Springer Nature. (ii) Cilia on mouse tracheal epithelial cells. Reproduced from ref. 52 with permission under open license CC BY. (d) (i) Human tracheal epithelial cilia. Reproduced from ref. 53 with permission under open license CC BY. (ii) Cilia on human nasal epithelial cells. Reproduced from ref. 54 with permission under open license CC BY. (iii) Sensing cilia in the renal tubule (kidney). Reproduced from ref. 39 with permission from John Wiley and Sons.
2.2. Structure and function
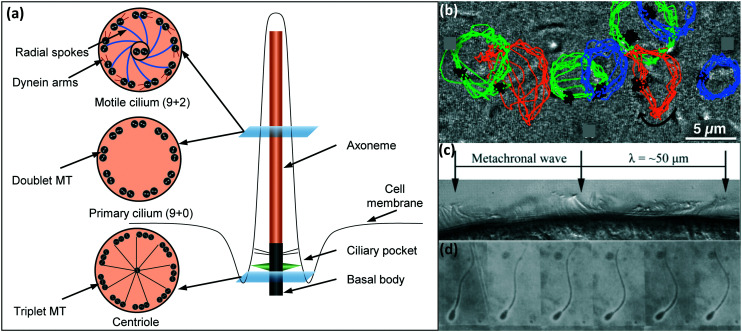
The molecular structure and function of biological cilia are closely related. On the molecular scale, a cilium is comprised of a basal body and an axoneme, see Fig. 2(a). The basal body consists of 9 triplets of microtubules which turn into doublets at the distal end, and serves as a connector of the axoneme to the cell membrane. The axoneme itself consists of 9 peripheral pairs of microtubules, either with (9 + 2) or without (9 + 0) two central singlet microtubules. Despite this generally simple molecular buildup, cilia exists in a wide variety of shapes and sizes, allowing them to perform a great number of tasks.
Fig. 2. (a) Schematic representation of the molecular structure of a cilium. The main components (basal body and axoneme) consist of microtubule (MT) doublets or triplets. For motile cilia, the axoneme possesses two central microtubules as well as upper and lower dynein arms. (b) Image showing a cilium performing a tilted conical motion along with the tracer lines of nodal cilia where the positions of the root are indicated in black, and the different tips in blue, green, and orange. Presence of cilia base/root close or on to the cilia tip trajectory indicate a tilted conical motion. Reproduced from the open access ref. 55. (c) Cilia on the epithelium of a flatworm (planarian) are shown here to display a metachronal motion, where individual cilia exhibit a whipping motion with consecutive cilia moving slightly out of phase. Reproduced from ref. 56 with permission from the American Society for Cell Biology. (d) Wavy motion of a flagellum shown in a sequence of frames of a sperm cell performing wavy motion. Reproduced from ref. 57 with permission from Elsevier.
As indicated in Fig. 2(a), cilia can be subdivided into two categories: primary (non-motile) cilia (9 + 0 axoneme) and motile cilia (9 + 2 axoneme). Primary cilia are involved in mechanosensing and chemosensing, relaying information about blood flow, compressive forces or Ca2+ concentration by triggering intracelular signaling pathways.41,58–61 Motile cilia provide active forces to a cell's surrounding liquids, either through rotational motion or planar whip-like motion, see Fig. 2(b and c).62 To achieve this motion, the axonemes of motile cilia possess two central microtubules as well as dynein arms (motor protein complexes). It is quite common for motile cilia to have macro-scale coordination, in which, in larger patches of cilia, consecutive cilia beat slightly out of phase to create metachronal waves, Fig. 2(c). This type of cilia allows for instance the clearance of mucus in the airways40 as well as the transportation of oocytes through the fallopian tube.38 Additionally, some single-cell organisms as well as sperm cells have singular motile cilia called flagella with lengths of 50 to 60 microns.31 These flagella feature motor complexes on their basal bodies to generate wavy or rotational corkscrew motion, as shown in Fig. 2(d).63
Cilia function is clearly crucial for our health, and many studies have shown that ciliary defects can cause a wide range of medical conditions and diseases called ciliopathies.64 For example, malfunction of the motile cilia in the embryonic node during embryonic development can lead to situs inversus,65 having the heart or even multiple internal organs mirrored to the wrong side of the body; defective cilia in the airways can lead to chronic airway disease; and malfunctioning cilia in the fallopian tube or flagella on sperm cells cause infertility.66–68
In moving fluids, cilia in nature operate under so called ‘low Reynolds number’ or ‘Stokes flow’ conditions due to their small size and relatively low frequencies of operation. This means that inertial effects are not important and the flow is dominated by viscous effects.69 Consequently, to generate any net flow, the motion of the cilia must be asymmetric, i.e. having a different forward trajectory compared to the backward trajectory during one cycle. This is indeed apparent in the various ways natural cilia move – in rotational motion, cilia rotate along a tilted cone, moving closer to the surface during the backward stroke than during the forward stroke (Fig. 2(b)); the whipping motion made by other cilia is also asymmetric: they move forward with a more straightened shape and backward in a more bent state (Fig. 2(c)). If their motion was symmetric, cilia would just displace fluid back and forth without any net flow, even in the case of temporal asymmetry (moving faster forwards than backwards).
The abundant persistence of cilia in biology indicates that these hair-like structures are highly efficient at moving liquids and sensing ion concentrations or shear forces on the micrometer-scale, with cilia sizes ranging between 2 and 60 μm.31 These attributes of cilia provide a good motivation for the use of artificial cilia in microfluidic devices.
3. Artificial cilia: microfluidic applications
Microfluidics is the science and technology of manipulating, processing and analyzing small volumes of fluids. Microfluidic devices typically contain chambers connected by microchannels of sizes between micros and millimeters. Originally developed in the 1990's for miniaturized chemical analysis, microfluidic technology has advanced to applications in medical diagnostics, high-throughput screening, and as a research tool to study biological and biochemical processes.70,71 Microfluidics is especially suitable for ‘lab-on-chip’ devices, and for analyzing processes at the level of single cells,72,73 or the behavior of micro-tissues that mimic the (patho-)physiological response of human organs, ‘organ-on-chip’.74–76
Even though microfluidics-based applications are being commercialized especially in medical diagnostics, the field of microfluidics is still in development with different technological approaches, materials, and principles being explored simultaneously. In the last two decades, many researchers spent much effort to develop single microfluidic components such as micropumps,77 microvalves,78 micromixers,79 and microfluidic liquid handling devices in general. However, a consistent fabrication and interfacing technology as a prerequisite for the efficient development of microfluidic systems is often still missing. This gap can only be bridged by establishing a microfluidic platform approach, which allows the fast and easy implementation of (bio-)chemical protocols based on common building blocks within a well-defined fabrication technology. Mark et al.80 have given an overview and evaluation of microfluidic platforms under development, the most important ones being droplet-based, centrifugal, electrokinetic, capillary, acoustic, and microfluidic large-scale integration platforms. The latter is the most advanced platform, based on pneumatically driven elastomeric microvalves81 integrated in a microfluidic channel network.82
In biology, as we have discussed in the previous section, cilia provide a ubiquitous and consistent solution to fluid and particle manipulation at the micrometer scale, i.e. they form a biological microfluidic platform. Their size of tens of μm is in perfect match with requirements in microfluidic devices, and they provide in nature many of the functions needed in microfluidic applications, such as pumping, mixing, particle and cell transport, and sensing. Hence, mimicking these functions by artificial cilia that are integrated in microfluidic chips may offer an attractive novel microfluidic platform. For example, nano-scale artificial cilia can be used in microfluidic chips to increase the surface area in an immuno-assay and enhance the limit of detection of a crucial marker in myocardial infarction (cTnI).83 In another study, magnetic artificial cilia are used to eliminate the biofouling in a desired area in a microfluidic device that results from the growth of algae.28 This system can be potentially used to clean sensors to detect environmental factors in micro-organism culture dishes. Orbay et al. also used an acoustic field to actuate cilia in a microfluidic chip and induce micro-mixing on demand.84 Advantages of artificial cilia compared to conventional approaches may be that they provide a fully integrated solution that does not require direct connection to external sources using tubing or wires in particular if magnetic field or light is used for actuation, that they enable local, in addition to global, active control of fluids and particles, and that they are biomolecule- and cell-friendly in contrast to some existing micro-pumps. However, artificial cilia development is still very diverse with different actuation principles and fabrication approaches used, hence we are still far off from a commercial artificial cilia-based microfluidic platform technology. In the remainder of this review we will explore which approaches may be most promising towards eventual implementation, and whether artificial cilia could in the end form the basis of a versatile microfluidic platform or if they would rather be more suitable to serve particular niche applications.
It is important to note here, that the inspiration by nature to develop artificial cilia does not imply that we literally copy the biological cilia; we rather borrow the general principle. Hence artificial cilia may be larger (or smaller) than their biological counterparts, they may have different shapes (e.g. flap-like rather than hair-like), they may move faster or in a different way, and so forth. Taking this freedom means that we can even overcome limitations of the biological cilia that could hamper microfluidic applications. One such limitation is the restriction to the Stokes flow regime, explained in section 2. For artificial cilia, both the size and, especially, the speed of motion can be designed to be larger, which takes them out of the Stokes regime so that inertial effects become relevant and can be exploited (in addition to motion asymmetry) for fluid manipulation. In the following, we will see a number of examples of such effects.
4. Artificial cilia actuation principles
A variety of principles have been proposed for the actuation of artificial cilia, ranging from the use of magnetic field, to light, to electric field, to pneumatics. This section reviews and evaluates these principles, or sources of energy, while listing their pros and cons. Next, we will analyze how artificial cilia actuation scales with size, which is relevant for the application in microfluidics. The type of artificial cilia motion that can be generated is strongly related to the actuation principle used and therefore these are discussed in the last part of this section.
4.1. Energy sources for artificial cilia actuation
With the exception of some applications as sensors, artificial cilia need some form of energy input to create active motion for applications such as flow generation, mixing or other types of active manipulation of substances. We will next discuss these one by one.
4.1.1. Magnetic field
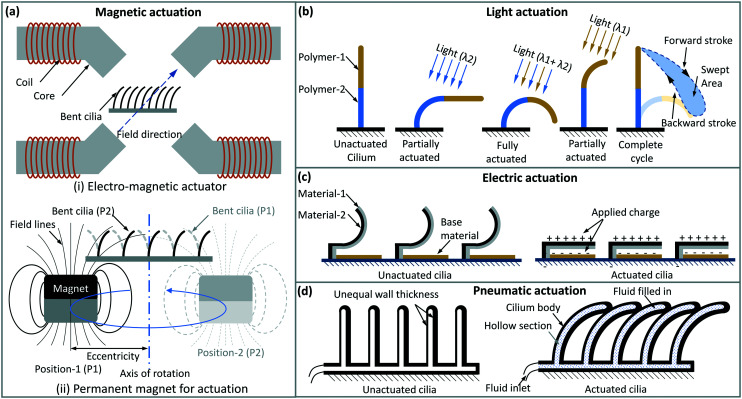
The most common way to actuate artificial cilia is by using an external magnetic field, schematically depicted in Fig. 3(a). This has a number of advantages. First, it does not require any mechanical connection from the artificial cilia to the external source, providing design flexibility and reducing the risk of contamination. Second, flexible magnetic artificial cilia can be made in a relatively straightforward way, including molding with a mixture of magnetic micro- or nanoparticles and a polymeric matrix, usually an elastomer such as polydimethylsiloxane (PDMS),15,19,85 self-assembling of dispersed magnetic particles in a dispersion utilizing magnetic dipole interaction in an external field,10,12,86 or direct photolithography processes9,87 – more details can be found in section 5. Third, most microfluidic components, cells and chemicals do not interact with magnetic fields, making it possible to treat magnetic artificial cilia and their external actuators as an auxiliary system, and providing a level of freedom in designing and integration of artificial cilia into an application environment.
Fig. 3. Actuation principles of artificial cilia. (a) Magnetic actuation with (i) electromagnets and (ii) a moving permanent magnet; the cilia orientation follows the magnetic field direction. (b) Light driven motion of artificial cilia; two segments of the cilia body can be made to deflect under two different wavelengths of light irradiation, creating an asymmetrical motion with an appropriate sequence. (c) Electrostatic cilia can be made to deflect with an electric field, and they relax elastically when the field is removed; these cilia can be actuated relatively fast (up to hundreds of Hz). (d) Pneumatic or hydraulic actuation. Hollow, elastic cilia with asymmetric structures can be made to deflect and relax back when gas or liquid is pumped in a pulsating manner; when individually addressed, they can create a metachronal wave.
However, when designing devices that make use of magnetic artificial cilia, compromises have to be made between versatility in cilia motion and the accessible space and field strength. A set of electromagnets (see Fig. 3(a)) can provide the most versatile control over the direction and strength of the time-dependent field, able to facilitate a wide range of motions (see section 4.3), but the size of the working space that has a unidirectional and homogeneous field is usually small, and it can be difficult and/or costly to obtain strong, high frequency fields because of inductance, core losses, flux through neighbouring poles and unfavorable scaling of field strength over the size of the coil. Moreover, the arrangement of the electromagnetic poles can easily block optical access or hinder sample handling. These restrictions make it necessary to take careful considerations when designing an electromagnetic actuator for artificial cilia, where some compromises are often made. Using a rotating permanent magnet to generate the field, on the other hand (see Fig. 3(a)), provides much cheaper access to a strong and high frequency field, and leaves a largely free space for easier access to the microfluidic device, but at the same time this approach severely reduces the flexibility in controlling the amplitude and shape of the time-dependant magnetic field. Hence an actuator solution employing a permanent magnet often needs ‘design for purpose’, meaning that the end application needs to have a clear and largely fixed requirement over the cilia motion and the corresponding field.
4.1.2. Light
Light responsive liquid crystal polymers have also been used for making cilia-like structures.16 These polymers contain photoresponsive components such as azobenzene that reversibly change molecular conformation upon exposure to light, usually in the UV-range. Through the aligned network of liquid crystal molecules, these molecular changes present themselves macroscopically in bending of the film-like artificial cilia, as schematically shown in (Fig. 3(b)). In addition, these artificial cilia may have two sections along their length, each responding to a different wavelength of light by design of the photoresponsive component. By inducing bending of these two sections with the appropriate wavelengths in the right sequence, the cilia can be driven to mimic asymmetrical motion of natural cilia. The use of light is attractive since, like for magnetic actuation, it can be applied without any mechanical connection to the cilia or to the chip in which they may be integrated. However, the frequency at which they can be driven is relatively low, i.e. in the order of 1 Hz or lower, which is not sufficient for meaningful flow generation fitful for microfluidic applications.
4.1.3. Electric field
One of the first examples of artificial cilia used in microfluidics was made to respond to electric field.6 The principle is depicted in Fig. 3(c). The artificial cilia consist of a bi-layer of a polymer film (polyimide) and a conductive film (chromium), and they are curled upwards in the non-actuated state. When applying a voltage between the chromium film and an electrode embedded in the surface, the cilia roll out due to the electrostatic force acting on them. After switching off the voltage, the cilia curl back up due to elastic recovery. They can be driven at a high frequency up to hundreds of Hz, and generate high fluid velocities and perform highly effective mixing in a microfluidic channel. In contrast to biological cilia, the electrostatic artificial cilia show hardly any motion asymmetry, and it turned out that inertial effects play a crucial role owing to the high speed of cilia motion in combination with their relatively large size (100 μm in length).88 An important disadvantage of the use of electrical field, however, is that high electric fields are needed for actuation (up to 100 V), limiting the use of electrostatic artificial cilia in conductive medium, and in applications involving handling of biological samples.
4.1.4. Pneumatic actuation
Hollow artificial cilia made from elastomeric polymers can be driven pneumatically through connected tubes, and bend back and forth in a predetermined direction thanks to asymmetrical internal structures, as sketched in Fig. 3(d).89,90 By connecting the neighbouring cilia separately and addressing them in a sequence, a metachronal wave can be created to generate a flow. Asymmetrical motion can also be realized by having multiple pressure channels that facilitate different modes of bending in one cilium and addressing these channels in sequence.91 With tunable individual control, these cilia can help in understanding the relation between fluid propulsion and metachronic patterns.92 The pneumatically driven artificial cilia have been shown to be able to generate large fluid flow velocities. However, it is difficult to miniaturize such hollow structures, and so far only millimeter sized cilia have been demonstrated in literature.
4.1.5. Other actuation principles
Acoustic, temperature, pH and capillary force are also used to create motion of artificial cilia. Acoustically actuated cilia can assist in mixing fluids in microfluidic channels with the use of a piezoelectric actuator.84 In the cases of temperature and pH, cilia deflections are picked up as sensing signals17 or used in a feedback loop for mimicking homeostasis,93 rather than used as a mechanism for creating fluid flow. In the case of capillary force, carefully engineered cilia-like structures can self-assemble into different configurations during drying of the surrounding fluid, and can grab small objects during that process.94
4.2. Scaling of the forces acting on artificial cilia
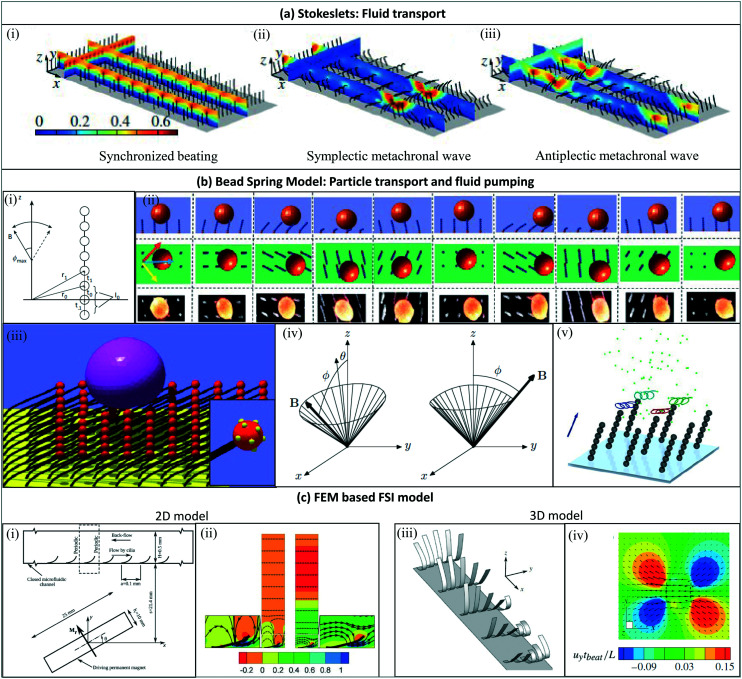
It is worthwhile to briefly discuss the forces on the cilia, i.e. the resistance forces of fluid drag and elasticity of the cilia, as well as the actuation forces which drive the cilia motion. Since magnetic artificial cilia are the predominant type, and the only one having practical examples across different length scales, we will limit the discussion to the magnetic actuation.
For the purpose of a general discussion, we employ here a reduced-order approach. More in-depth analysis can be found in the literature, including detailed theoretical and numerical modeling of the motion of cilia, see section 9. Here we focus on how the forces scale with the dimensions of the cilia, which is particularly relevant for microfluidics and LOC applications.
4.2.1. Fluid drag
The fluid drag on the cilia in a microfluidic environment, which usually has a low Reynolds number so that we can neglect inertia effects, can be approximated by the drag force on a slender cylinder:95
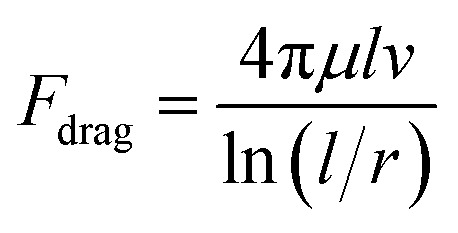 |
1 |
where l and r are the length and the radius of cilia, μ is the fluid dynamic viscosity, and v is the relative speed of the cilia with respect to the surrounding fluid, which can be approximated by half of the speed of the cilia tip and hence scales with the length (when the frequency and the shape of the motion are kept the same when scaling). Note, that eqn (1) provides a first order approximation, and a numerical treatment is typically required for obtaining a more accurate result.96
It can be seen from eqn (1) that, keeping the aspect ratio of the cilia the same, Fdrag scales with l2, assuming one wants to achieve similarity in the shape of cilia during motion, regardless of length scales, and maintain the same frequency of movement. In such case, the fluid speed close to the cilia body will also scale with l, meaning larger cilia will generate larger flow speed. However, the volumetric flow rate will be more complicated, since one also needs to take into account the channel dimensions, cilia arrangement and the overall flow resistance.
4.2.2. Elastic force
Bending creates an elastic shear force in the cilium at location x, which indicates the distance from the base of that cilium, which can be estimated by classical Euler–Bernoulli beam theory:
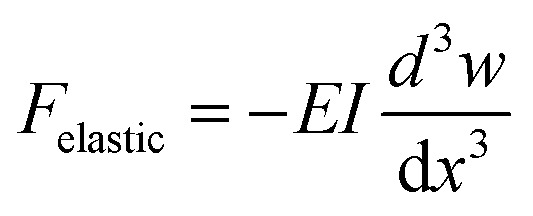 |
2 |
where E is the elastic modulus, I is the second moment of area of the cilium cross section equal to πr4/2, and w is the deflection perpendicular to the cilia length direction. Here we assume that the cross section of the cilia does not change along the length, and the material has a constant modulus E.
It can be deducted from eqn (2) that Felastic scales with l2, if the deflection of the cilia w is made to scale with l, i.e. the shape of the motion remains the same, and keeping the cilia aspect ratio constant. Hence, the scaling with cilia size of the elastic shear force is analogous to that of the fluid drag.
4.2.3. Magnetic actuation force
The response of magnetic cilia, which are usually much smaller than the source of the field (either electromagnetic coils or a permanent magnet), and with relative small curvatures during actuation, can be approximated by:97
| Fmag = (m·∇)B | 3 |
and
| Tmag = m × B | 4 |
where Fmag is the translational magnetic force acting on a cilium, Tmag is the magnetic torque acting on a cilium, m is the magnetization of a cilium and B is the magnetic flux density measured at the location of the cilium. Fmag is usually too small for cilia actuation, as the field gradient ∇B is only big enough close to the surface of the magnetic source and decreases quickly with distance. Instead, the motion of most magnetic artificial cilia is driven by the torque Tmag.
The magnetization m depends on the material and geometry of the cilia. The magnetic component in these cilia can be superparamagnetic particles, such as ferrite or magnetite nanoparticles8,86,98 and carbonyl iron microparticles,13,15 or ferromagnetic particles, such as neodymium powder.19,85 For superparamagnetic cilia, m is determined by the magnitude of the external field B and its angle with respect to the long axis of the cilia, with the largest torque Tmax generated at an angle around 45°.‡ Ferromagnetic cilia, on the other hand, can be pre-magnetized in a field much larger than the actuation field and carry a remanent magnetization. The maximum torque Tmax is then generated when the cilia remanent field and the actuation field are at an angle of 90°.
For the scaling analysis on magnetic force with respect to cilia size, we assume that the same external magnetic field B is always applied and that the cilia are always made of the same material. In this case the torque Tmag scales with m regardless of the type of magnetic materials, which in turn scales with the volume of cilia, or l3 (keeping the cilia aspect ratio constant). For easier comparison with other forces, we convert the magnetic torque to force,
| Fmagnetic = |Tmag|/l, | 5 |
which then scales with l2.
4.2.4. Scaling for magnetic cilia
We can now draw a conclusion that, for magnetic artificial cilia, the actuation, fluid drag and elastic forces all scale with l2, meaning that similarity in the motion of cilia can be obtained on different scales. This property of magnetic artificial cilia is important for applications on different length scales, where the flexibility and frequency in motion are usually important, and the magnetic actuation force cannot be easily increased by other means, e.g. the apparent susceptibility of magnetic particles is usually comparable for different materials (a few times greater than that of air), their concentration cannot be too high, and the magnetic field is usually constrained in the range from tens up to a few hundreds of milliTesla in all practical situations.
The above arguments are based on maintaining the aspect ratio of cilia on different scales. It is a valid assumption, based on the observation from literature and our own experience, that the aspect ratio of the magnetic artificial cilia for practical applications is always in the order of 10, despite large differences in their overall sizes.7,11–15,98 An aspect ratio much smaller will make the cilia too rigid, while an aspect ratio too large will make the cilia behave like flagella, with a much reduced tip movement, which is interesting in itself,86 but can result in reduced effectiveness if one's purpose is to actuate fluids.100
4.3. Types of artificial cilia motion and shapes
Due to their small sizes, just like biological cilia, microscopic artificial cilia often operate in low Reynolds number environments, where inertia plays an insignificant role.69 In order to generate net flows, which are required for pumping and mixing applications, some form of spatial asymmetry in motion is therefore necessary. Such asymmetry can be from non-reciprocal, individual cilia motion, such as a tilted conical motion or a 2D asymmetric motion, or it can be realized by creating a metachronal wave, in which an array of cilia beat with a regular phase difference between neighbours. All these types of motion are inspired by nature (see Fig. 2), and in some studies, flow generated by artificial cilia is used to understand the mechanism of their natural counterparts.
On the other hand, as mentioned in section 3, both the size and the speed of motion can be larger for artificial cilia, which takes them out of the Stokes regime so that inertial effects become relevant and can be used (in addition to motion asymmetry) for fluid flow generation.
Two types of cilia shapes are commonly seen in the literature. One is more cylindrical, the other is shaped like a flap. Both of them have been shown to effectively generate flow and mixing with appropriate actuation. Cylindrical shaped cilia can be actuated to exhibit both 2D or 3D motions, while flap-like cilia can only be actuated to perform 2D motion. Below, we will discuss these different types of motion.
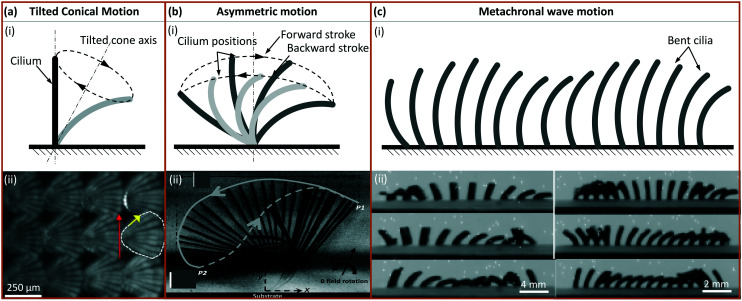
4.3.1. 3D tilted conical motion
Tilted conical motion is mostly employed by magnetic cilia. A 3D rotating field is used to drive the cilia into a conical motion with a tilting angle, as illustrated in Fig. 4(a). In this way, the cilia push more fluid when they are moving in a more upright position – the ‘effective stroke’, and pull less fluid back when they are moving in a more inclined position, hence the ‘recovery stroke’. Spatial asymmetry in the motion is achieved, which creates a net flow in the effective stroke direction.
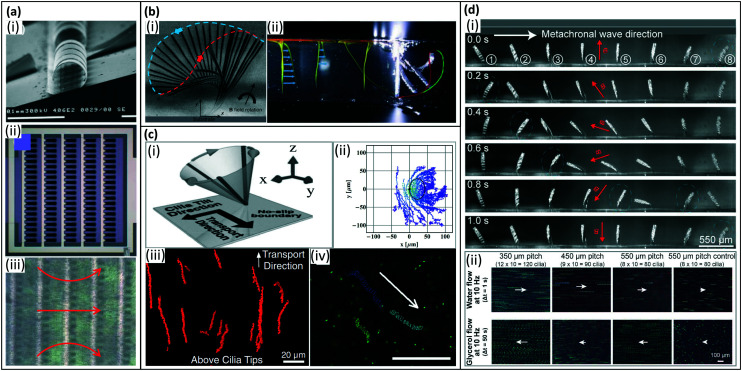
Fig. 4. Artificial cilia motion types. (a) (i) Tilted conical motion; (ii) time-lapse image showing top-view of cilia under tilted conical motion, where the red arrow indicates the direction of effective stroke and the yellow arrow indicates the rotation direction. Reproduced from ref. 27 with permission from John Wiley and Sons. (b) (i) 2D asymmetric motion with the swept area between the dotted lines representing forward and backward stroke; (ii) side-view image where the solid line indicates the effective stroke and the dashed line indicates the recovery stroke. Reproduced from ref. 101 with permission from the Royal Society of Chemistry. (c) (i) Metachronal wave motion and (ii) time-sequence images from showing the wave propagation. Reproduced from ref. 19 with permission under open license CC BY.
4.3.2. 2D asymmetric motion
There are two types of asymmetry in 2D asymmetric motion, namely (1) spatial asymmetry, meaning cilia move in different shapes for different parts of the motion cycle; and (2) temporal asymmetry, in which the speed is different, depending if cilia are moving forward or backward.
2D spatially asymmetrical motion is achieved by all the above-mentioned actuation principles, i.e. magnetic, light, electrostatic and pneumatic actuation, in which the cilia move in a more straightened up posture in one direction (the effective stroke), pushing more fluid forward, and in a more curled shape when they move in the other direction (the recovery stoke), pulling less fluid backwards, as illustrated in Fig. 4(b). For light and pneumatic actuation, this mechanism is built in the structure of the cilia, as explained in the earlier section 4.1.2 and 4.1.4.
For magnetic cilia, spatial asymmetric 2D motion can be achieved by using rotating magnetic fields.102 During the effective part of the motion cycle, the cilia follow the direction of the field in more straight-up conformation. As the cilia bend further and accumulate elastic energy, they eventually overcome the magnetic torque and move back in the recovery stroke, which is typically in a more curled-up shape. A similar mechanism is also at work for the electrostatic cilia, contributing to the net flow generation.6
Temporal asymmetry is a result of the different speeds during the two strokes, and this typically happens with magnetic cilia that are a few hundreds of micrometers long or larger. The local Reynolds number can be larger than 1, especially during the elastic stroke, where cilia tend to move more abruptly. The electrostatic cilia6 also showed similar behavior, resulting in a significant inertial effect.
Note that for 2D actuation of large cilia, quite often the two types of asymmetries coexist. This can result in some cases for them to cancel out their effects on flow generation, even leading to flow reversal at different scales.103
Natural cilia sometimes exhibit both 3D tilted conical motion and 2D asymmetric motion,48 achieving a maximized efficiency in generating flow and locomotion. This level of optimization in motion is not yet realized in artificial cilia.
4.3.3. Metachronal wave motion
Even if individual cilia move with complete reciprocity, a net flow can still be generated if an array of cilia moves in a metachronal wave, as illustrated in Fig. 4(c). This has been achieved in pneumatically actuated cilia by actuating them individually.89 Metachronal wave motion of smaller cilia has also been achieved by magnetic actuation using two different methods. One is to allow the neighbouring cilia to have different magnetic torque in the same magnetic field, by pre-magnetization,19 internal particle alignment,28 or cilia having different shapes.104 The other one is to actuate with a locally varying magnetic field.105,106
The direction of the flow, however, is less straightforward to predict than for the above two types of motion. Numerical and experimental studies show that both symplectic (in the direction of wave propagation) and antiplectic (the opposite) flow are possible, and this is determined by the interplay between multiple factors including the cilia pitch, wave speed, and channel geometry. There is not yet a general rule that can be used to predict the flow direction, although it appears that antiplectic flow occurs more often than symplectic flow in nature.
5. Artificial cilia fabrication
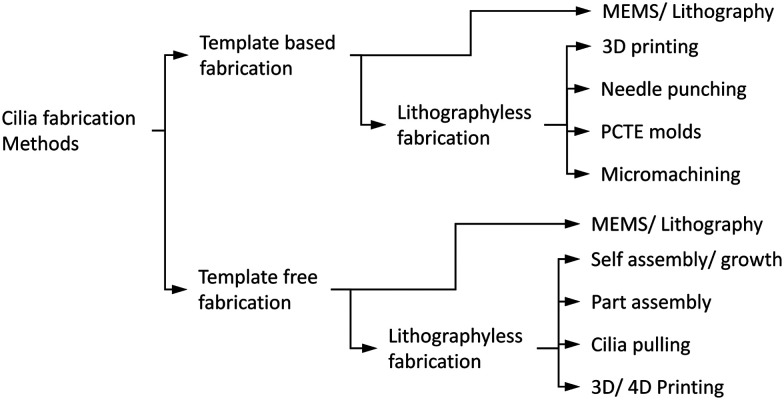
Appreciating the diverse shapes, sizes and functionalities of cilia existing in nature, a number of different artificial cilia fabrication methods have been developed over the last couple of decades. The fabrication methods have not only improved and gotten closer to mimicking different aspects of cilia but have also resulted in the development of a range of engineering devices with applications stretching beyond the ones observed in nature. The earliest attempts to fabricate cilia involved the use of ‘micro electro mechanical systems’ (MEMS) techniques to achieve a functioning (deflection sensitive) artificial cilia structure as sensor.107,108 Combining different MEMS techniques like thin film deposition, photolithography, thermal oxidation, coating, reactive ion etching (RIE) and deep reactive ion etching (DRIE) etc., and deploying them on a flat silicon substrate, thin rectangular strips of typically 10 μm thickness and 100 s of microns long and wide were obtained. Continuing with the MEMS based fabrication methods, the thin rectangular shaped artificial cilia were succeeded by cylindrical ones109,110 and often integrated with a sensing element to act as a sensor. After a short period of a few years, the MEMS based fabrication of primary artificial cilia as sensors was followed by the fabrication of a motile cilia structures capable of inducing flow and mixing in the surrounding fluid medium.6 This property of the artificial cilia structures to act as actuators, reported in a key publication6 that employed electrostatically actuated polymer structures, would go on to become a representative property of the artificial cilia. The complexity of inducing motion capabilities in structures at micro and nano scales has resulted in a wide range of fabrication methods developed for obtaining motile artificial cilia structures while other methods have focused on making sensory cilia structures. A complete classification of cilia fabrication methods is shown in Fig. 5, and schematic representations of the methods are depicted in Fig. 6. In general, the cilia fabrication methods can be broadly classified into template-based and template-free fabrication methods.30
Fig. 5. Flow chart showing the classification of the artificial cilia fabrication methods. The fabrication is broadly divided into template-based and template-free fabrication which is further divided into MEMS based (mostly involving lithography processes) and lithographyless fabrication methods. All the methods shown here are further represented in a tabular form in the ESI† Table S1 along with the referred papers.
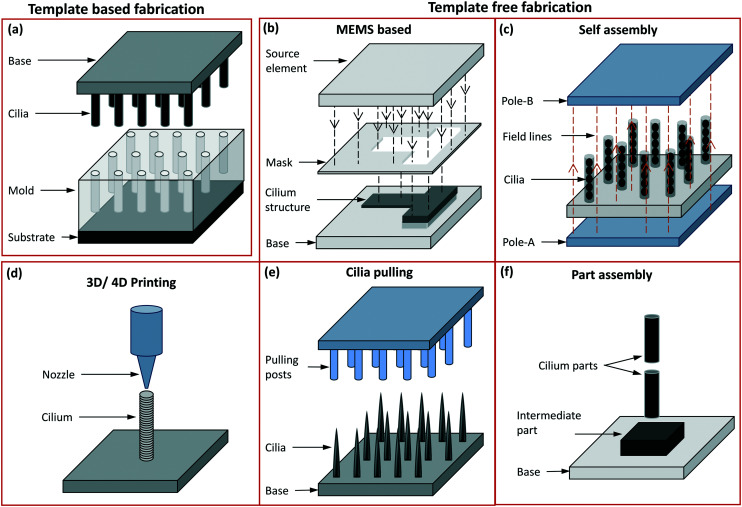
Fig. 6. Schematic representation of different fabrication methods: (a) template-based fabrication where the mould is on the bottom side and the demoulded cilia on the top side with the base material made of either the same as cilia material or a different one. (b) The template free fabrication based on MEMS processes like thin film deposition, photolithography and etching, accompanied by other chemical treatment processes are used to mostly fabricate in-plane flap-shaped cilia structures. The source element shown here may either be a UV source or a source for metal coating etc. The mask may either be a separate unit or one deposited on the device surface itself. (c) The poles in the self assembly process are permanent or electro magnets used to align and assemble magnetic cilia structures, or can form an electric field aligning conducting material. (d) In 3D printing, the nozzle dispenses a material to form the cilia while, optionally (‘4D’), an external magnetic field imposes alignment of magnetic particles in the cilia during fabrication. (e) In cilia pulling, the pulling posts shown here may either be formed by solid structures (mostly PDMS) or by electrodes, which pull out hairlike structures from a liquid precursor film either by direct contact or by a localized electric field. (f) In part assembly, different units of the entire cilia structure are assembled to form a fully functional unit.
5.1. Template-based fabrication methods
In Fig. 6(a), the template based fabrication methods are summarized in a single panel since these all employ cilia fabrication using a mould. In both the template based and template free fabrication approaches, the use of MEMS processes has been adopted to produce primary and motile artificial cilia of different sizes and aspect ratios. A main MEMS process is photolithography, used to pattern different material layers on a substrate followed by etching of sacrificial layers to release the final structures,6,107 as well as to produce templates/moulds in photo-polymers like SU8.15 Another is the use of DRIE to create master moulds in a silicon substrate.111,112 The techniques to prepare moulds through lithographyless methods include 3D printing,19,113 the creation of tapered holes in a base material using sewing needles,113 using commercially available ‘polycarbonate track etched membranes’ (PCTE) with different pore sizes,7,98 micro-machining processes like micro milling and drilling,114,115 and laser machining.116 3D printing has recently been used to create molds for fabricating cilia structures of defined geometries with however sizes in the millimeter range.19,117 The needle punching method of mould preparation allows fabrication of tapered as well as inclined cilia structures and has been utilized to make moulds in a material like polyethylene (PE).118 The PCTE membrane based fabrication method has proved very successful in fabricating cilia structures of the smallest sizes equivalent to ones found in nature.7,98 The PCTE moulds are commercially available with extremely small pore sizes of 10 s of nanometers in diameter and allow the release of moulded structures by their dissolution in chemical solvents like DMSO (dimethylsulfoxide) and chloroform, therefore making it the right candidate for fabricating the smallest artificial cilia capable of undergoing extreme deflection and motility. The dissolution/sacrificing of the PCTE moulds bypasses the need to demould the cilia structures through a commonly used lift/peel-off process employed in many other methods that involve a non-sacrificial mould. Employing a lift/peel-off process to demould cilia structures with extremely small sizes is either not compatible with the materials used to fabricate motile cilia, or puts the cilia under extreme stresses therefore resulting in their wear and tear. Another class of fabrication methods used to create the moulds is micromachining, such as micro-milling or drilling114,115 and laser machining.116 The cilia fabricated through micromachining usually result in sizes larger than the ones fabricated through the other template based methods discussed above, but they allow for the seeding of directionality (e.g. magnetization alignment varying between individual cilia in an array) and therefore enable complex motion profiles displayed by fabricated cilia structures such as metachrony.
5.2. Template-free fabrication methods
In the template free fabrication method, the use of MEMS techniques has been used to directly fabricate in-plane flap-shaped artificial cilia structures and not for preparing moulds as done in the template based method. The cilia fabricated here are mostly thin strips/flaps with a rectangular shape and they are made from materials actuated through a magnetic104,105 or electric6 field. Through this method it is easy to control the relative sizes of the individual rectangular flaps using a mask as shown in Fig. 6(b) which is for example utilized to achieve metachronal motion of the artificial cilia.105,104 Another greatly used template-free method of fabricating artificial cilia is the self-assembly method involving the use of a magnetic or electric field to shape the material into long strands as schematically shown in Fig. 6(c). The external applied magnetic field is either used to align magnetic micro-particles into chains followed by their bonding with each other,10,12,119 or to align a magnetic fluid, a mixture of magnetic particles and a fluid polymer, into multiple thin spikes,120–123 which subsequently are solidified to make the artificial cilia structure. The self-assembly method has the advantage of employing simple steps to shape the magnetic particles or fluids into micro hair-like spikes but lacks in controlling the precise placement, shape and size of the cilia structures produced. Cilia fabricated through the self assembly method have been shown to be capable of generating net flow in the surrounding fluids.124 Self assembly through electrically induced processes have been shown to produce branched artificial cilia.125 To precisely control the shape and location of cilia structures, the 3D/4D printing method has been employed,126,127Fig. 6(d). When printing polymers containing magnetic microparticles for creating magnetic artificial cilia, “4D” printing involves inducing directionality in the magnetic chains/field in individual cilia while printing them using a conventional 3D fabrication method.126,127 Seeding/programming directional behaviour to the external magnetic field helps in achieving complex motion profiles of the cilia, enabling to mimic crawling and metachronal motions. The cilia pulling method, schematically shown in Fig. 6(e), involves pulling a fluid film at multiple points simultaneously, by means of micropillars that are in touch with the fluid surface and are subsequently moved upwards,14 or by localizing an electric field by means of conducting needles to pull a polymer film up in the form of elongated streaks or cilia.128 The cilia pulling method is an effective method to produce cilia over a large surface area, but careful tuning of the fluid properties is critical to achieve the final shape of the artificial cilia fabricated. Some of the artificial motile cilia actuated by principles like electro-osmosis and thermal actuation have been demonstrated to work for relatively large scale cilia and were therefore fabricated using a part-assembly method,129,130 see Fig. 6(f). This method is mostly used to assemble different parts like the sensing or actuating mechanisms, the cilium structure, etc., to make fully functional cilia units. A complete classification of the fabrication methods along with related papers is shown in ESI† Table S1. Images of artificial cilia fabricated using the different methods, collected from different papers, are shown in Fig. 7.
Fig. 7. Images of artificial cilia made with different fabrication approaches. (a) SEM image of cilia (i) fabricated from a mould prepared from SU-8 using photolithography (MEMS) process. Reproduced from ref. 15 with permission from Elsevier. (ii) shows cilia fabricated using PCTE as template/mould to shape a magnetic polymer into micro/nanoscale cilia structures. Reproduced from ref. 98 with permission under open license CC BY-NC-ND. (b) SEM image of an actuable polymer cilia structure (i) fabricated using different MEMS process like vapour deposition, sputter coating, lithography etc. Reproduced from ref. 6 with permission from the Royal Society of Chemistry. (ii) shows an array of rectangular shaped nickel–iron magnetic artificial cilia fabricated using two-mask lithography process. Reproduced from ref. 105 with permission from the American Chemical Society. Magnetic artificial cilia of different sizes fabricated using a photolithographic process from a photoreactive copolymer are shown in (iii). Reproduced from ref. 87 with permission from John Wiley and Sons. (c) Cilia in (i) are made from super-paramagnetic beads by self-aligning them using an external magnetic field. Reproduced from ref. 10 with permission from Proceedings of the National Academy of Sciences. Cilia fabricated by aligning cobalt particles mixed with an elastomer by a magnet are shown in (ii). Reproduced from ref. 131 with permission from the American Chemical Society. (iii) shows cilia fabricated by placing iron particles dispersed in a thermo-plastic polyurethane between two magnets to shape into the cilia structures. Reproduced from ref. 121 with permission from John Wiley and Sons. (d) (i) shows the alignment of iron-carbonyl particles in different directions in the cilia structures fabricated using 4D printing process. Reproduced from the free access ref. 127. 3D printed cilia structures with each cilium having particles aligned in different directions is shown in (ii). Reproduced from ref. 126 with permission under open license CC BY. (e) (i) and (ii) show cilia fabricated from a polymer by pulling them out of the plane using field effect spinning. Needles used to pull the cilia are shown in (i). Reproduced from ref. 128 with permission from the American Chemical Society. PDMS posts (iii) on a roller used to pull a precursor material to shape them into cilia structures shown in (iv). Reproduced from ref. 14 with permission from the Royal Society of Chemistry. (f) The cilium structure fabricated separately shown in (i) is one part of a complete unit.129 (ii) Shows cilia made from PMMA attached to the base through an epoxy resin to complete the device assembly. Reproduced from the open access ref. 130. A bistable buckled beam held between two clips that forms the cilium structure when attached to a fixed base is shown in (iii). Reproduced from ref. 132 with permission from the Institute of Electrical and Electronics Engineers.
6. Flow generation by artificial cilia
As explained in section 3, fluid pumping and mixing are of paramount importance in microfluidic applications.70 Conventional microfluidic pumping relies either on large peripherals, such as pneumatic control systems or syringe pumps, or on expensive and/or cumbersome components. Efficient microfluidic mixing, on the other hand, is very challenging. This is due to low Reynolds number conditions resulting from the small channel sizes which prevent the flow from becoming turbulent, while the channel size is often too large for molecular diffusion to be effective in mixing within a reasonable time. Inspired by the highly efficient fluid manipulation capabilities of biological cilia, researchers came up with the idea of using artificial cilia to create on-chip integrated micro-pumps and micro-mixers.29Table 1 summarizes most previously reported artificial cilia in terms of fluid pumping. A dimensionless parameter, the normalized flow speed δ, is used to fairly compare their pumping efficiency. This parameter is defined as:
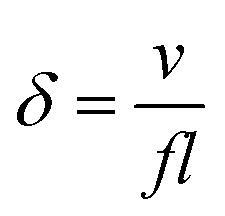 |
6 |
Fluid pumping capabilities of artificial cilia reported in the literature. In the table, these artificial cilia are arranged according to their length from small to large. The best ones in terms of generated absolute maximum flow speed and normalized flow speed are marked in bold and italic, respectively. (μ) MAC = (microscopic) magnetic artificial cilia.
| Cilia type | Fabrication method | Cilia geometry | Actuation method | Cilia motion | Working fluid | Maximum flow speed | Beating frequency | Local Remax | Normalized flow speed | Fluid pumping mechanism |
|---|---|---|---|---|---|---|---|---|---|---|
| l × w × t [μm3] | v [m s−1] | f [Hz] | ρvl/μ | δ = v/fl | ||||||
| l × d [μm2] | ||||||||||
| μMAC12b | Self-assembly | 20 × 3 | Uniform rotating magnetic field | 3D tilted conical motion | Water | 3 | 5 | 0.01 | 0.030 | 3D non-reciprocal motion |
| μMAC8a | Tracked-etched polycarbonate membranes as templates | 25 × 0.7 | Uniform rotating magnetic field | 3D tilted conical motion | Water | 8 | 34 | ≦0.025 | 0.009 | 3D non-reciprocal motion |
| μMAC10a | Self-assembly | 31 × 4.4 | Uniform rotating magnetic field | 3D tilted conical motion | Water | 5 | 0.5 | <1 | 0.0323 | 3D non-reciprocal motion |
| μMAC102a | Photolithography techniques | 70 × 20 × 0.4 | Uniform rotating magnetic field | 2D non-reciprocal motion | Water | — | 50 | <1 | — | 2D non-reciprocal motion |
| μMAC11a | Photolithography techniques | 70 × 20 × 0.4 | Non-uniform rotating magnetic field | 2D non-reciprocal motion | Water | 130 | 10 | <1 | 0.186 | 2D non-reciprocal motion |
| Electrostatic cilia6a | Micro-systems technology processing | 100 × 20 × 1 | AC voltage | 2D non-reciprocal motion | Silicone oil | 600 | 200 | 1 | 0.030 | Inertia |
| μMAC104b | Two-mask lithographic process | 200 × 20 × 0.07 | Nearly uniform rotating magnetic field | 2D non-reciprocal motion | Water | 1350 | 62 | 0.09–0.6 | 0.109 | 2D non-reciprocal motion |
| μMAC14b | Continuous roll-pulling method | Conical shape 250 | Uniform rotating magnetic field | 3D tilted conical motion | Water | 120 | 20 | 6 | 0.024 | 3D non-reciprocal motion |
| μMAC13b | Magnetic fiber drawing (self-assembly) | 300 | Uniform rotating magnetic field | 3D tilted conical motion | Water | 70 | 50 | — | 0.005 | 3D non-reciprocal motion |
| μMAC9b | Photolithography techniques | 300 × 100 × 15 | Uniform rotating magnetic field | 2.5D non-reciprocal motion | Water | 500 | 50 | <1 | 0.033 | 2.5D non-reciprocal motion |
| μMAC15b | Micro-molding | 350 × 50 | Uniform rotating magnetic field | 3D tilted conical motion | Water | 260 | 40 | 15 | 0.018 | 3D non-reciprocal motion |
| 2D metachronal μMAC138b | Micro-molding | 350 × 50 | Non-uniform periodical magnetic field | 2D non-reciprocal motion | Water | 3000 | 100 | 920 | 0.086 | 2D non-reciprocal motion + inertia + metachrony |
| 2D metachronal μMAC20b | Micro-molding | 350 × 50 | Uniform rotating magnetic field | 2D symmetric motion | Water | 220 | 10 | 50–700 | 0.063 | Inertia + metachrony |
| 2D metachronal MAC85a | Hand-assembly | 1000 × 550 × 100 | Uniform rotating magnetic field | 2D non-reciprocal motion | Glycerol | 450 | 2.5 | <0.1 | 0.180 | 2D non-reciprocal motion + metachrony |
| 3D metachronal MAC19a | Molding | 4000 × 800 | Uniform rotating magnetic field | 3D non-reciprocal motion | Glycerol | 83 | 0.083 | <1 | 0.250 | 3D non-reciprocal motion + metachrony |
| 2D metachronal pneumatic metachronal cilia89a | Moulding | 8000 × 1000 | Pneumatically | 2D non-reciprocal motion | Water | 19 000 | 30 | 3480 | 0.079 | 2D non-reciprocal motion + inertia + metachrony |
| 2D metachronal pneumatic metachronal cilia91a | Moulding | 14 000 × 1000 | Pneumatic-hydraulic pressure | 2D non-reciprocal motion | Glycerol | 500 | 0.25 | 0.04 | 0.143 | 2D non-reciprocal motion + metachrony |
Maximum local flow above the cilia tips.
Maximum global flow in the channel. Note that the normalized flow speed is calculated regardless the chip geometry and the amount of cilia.
In this equation, v is the velocity of the generated fluid flow, f is the cilia beating frequency, and l is the cilia length. Hence, δ represents the flow velocity generated per beating cycle scaled by cilia size. We will see that the most efficient artificial cilia reported so far are the self-assembled microscopic magnetic artificial cilia by Vilfan et al. in 2009:10 even though the absolute fluid velocities induced are low (5 μm s−1) so that they may be unsuitable for many microfluidic applications, relative to their size and beating frequency they perform best.
6.1. Fluid pumping
Net fluid pumping by artificial cilia can be achieved by actuating them in various ways, which are possibly combined, as explained in section 4 and schematically shown in Fig. 4. First, like biological cilia, the shape of the artificial cilia motion may be non-reciprocal, i.e. with an effective stroke during which the effect of the cilia on the fluid is maximized and a recovery stroke during which the effect is minimized. The cilia beating may be 3-D, often exhibiting a tilted conical motion as sketched in Fig. 4(a); this was demonstrated by Downton and Stark in 2009 to be a simple yet effective non-reciprocal motion to generate net fluid flows.133 The cilia beating may also be 2-D, i.e. in a single plane usually perpendicular to the surface as in Fig. 4(c). Using numerical simulations, Khaderi et al. found that, for such 2D cilia motion, the net fluid flow generated scales with the so-called swept area, which is the area enclosed by the path traced by the cilia tip in one beating cycle, shown as the dashed curve in Fig. 4(c).134 Second, for relatively large cilia, inertia can play a role if there is temporal non-reciprocity in the cilia beating in which one of the strokes is much faster than the returning stroke. A net flow may then be generated in the fast stroke direction; such inertial flow generation does not happen for biological cilia (see section 2). Third, metachronal beating with neighboring cilia beating out of phase (see Fig. 4(c)) may contribute to fluid flow generation; the specific metachrony is termed symplectic, antiplectic and laeoplectic when the metachronal wave travels in the same, opposite and perpendicular direction as the effective stroke, respectively.135 Finally, it should be noted that tot total flow generated is influenced by the number and areal density of the artificial cilia. The net flow increases with the number of cilia, however depending on the areal density this increase is not proportional (i.e. sub-linear) due to hydrodynamic interactions between the cilia.14
The earliest artificial cilia for creating flows, reported by us in 2008, were micro-flaps fabricated from bilayer films of polyimide and chromium on the surface of ITO glass using MEMS technologies, see Fig. 8(a).6 These 100 μm sized cilia were able to generate a translational flow speed up to 500 μm s−1 in a microfluidic chamber when actuated electrostatically by applying an AC voltage of 75 V/1 kHz with on–off frequencies at 50 Hz. The main mechanism at work was inertia, since the cilia beating speed was very high.88 In 2007, Evans et al. reported the first magnetic artificial cilia with a size similar to biological cilia (with diameters ranging from 200 nm to 1 μm and aspect ratios as high as 125) fabricated with track-etched polycarbonate membranes as templates.7 In 2010, these bio-mimetic cilia were demonstrated to be able to simultaneously generate two sharply segregated regimes of fluid flow: directional flow above the cilia tips, with generated flow speeds of 8 μm s−1, and mixing flow below the tips, when they were actuated using an off-axis rotating permanent magnet to perform tilted conical motion at 34 Hz (Fig. 8(ciii)).8 The first self-assembled magnetic artificial cilia, having a typical length of 31 μm, were reported by Vilfan et al. in 2009, and were able to induce a net flow of 5 μm s−1 by performing a tilted conical motion at 0.5 Hz.10 In our group, we optimized the fabrication process of cylindrical microscopic magnetic artificial cilia and enhanced the fluid pumping properties from 2013 to 2018 to bring the idea of using the cilia as on-chip integrated micropumps closer to real life applications,12–15 reaching induced flow speeds of 260 μm s−1 for 350 μm long cilia performing tilted conical motion. In 2018, Hanasoge et al. further increased the pumping efficiency of microscopic magnetic artificial cilia to a maximum flow speed of 1350 μm s−1 when the 200 μm long cilia performed a 2D non-reciprocal motion (Fig. 8(bi)).104
Fig. 8. Artificial cilia used for fluid pumping. (a) Fluid flow generated by inertia effects of 2D reciprocal motion of electrostatic artificial cilia. (i) SEM image of the electrostatic artificial cilia; (ii) top view schematic of the layout of an array of electrostatic artificial cilia: the cilia are arranged in 5 columns of 20 cilia, and they are covered with a 0.5 mm thick film of silicone oil (viscosity 9.3 mPa s), containing TiO2 tracer particles; and (iii) snapshot of the flow generated by the electrostatic artificial cilia, the red arrows indicate the flow direction, the black dots are TiO2 tracer particles. Reproduced from ref. 6 with permission from the Royal Society of Chemistry. (b) Fluid flow generated by 2D non-reciprocal motion. (i) Overlay of experimental images showing magnetic cilium motion over one beating cycle, the blue and red dashed lines indicate the cilium tip trajectory during the effective stroke and recovery stroke, respectively, which also demonstrate the difference in swept area by the cilium during the two strokes. Reproduced from ref. 104 with permission from the Royal Society of Chemistry. (ii) Superimposed images of the dye tracing test of the initial situation and the situation after 130 beating cycles for 2D non-reciprocal motion of pneumatic artificial cilia, showing the generated net flow in the same direction as the effective stroke (indicated by the blue curve). Reproduced from ref. 90 with permission from John Wiley and Sons. (c) Fluid flow generated by 3D non-reciprocal tilted conical motion. (i) Schematic of the cilia motion. Reproduced from ref. 8 with permission from the National Academy of Sciences. (ii) Traces of particles above the cilium. The cilium is fixed at (0, 0) and the black solid line denotes the calculated path of the cilium tip. Reproduced from ref. 124 with permission from the American Institute of Physics. (iii) Trajectory of tracer particles above the tips (z = 30 m), showing unidirectional flow. Reproduced from ref. 8 with permission from the National Academy of Sciences. (iv) Traces of 1 μm fluorescent tracer particles in the horizontal plane, 40 mm above the bottom substrate, showing a net flow. The scale bar is 100 μm. Reproduced from ref. 12 with permission from the Royal Society of Chemistry. (d) Fluid flow generated by 2D metachronal motion. (i) Snapshots of a metachronal motion of one row of MAC during one beating cycle at 1 Hz in water. (ii) Trajectories of tracer particles in both water and glycerol. The arrows indicate the relative speed and direction of the generated flow. Reproduced from ref. 20 with permission under open license CC BY-NC-ND.
All above-mentioned artificial cilia beat in phase and synchronously. However, as explained in section 2, biological cilia often exhibit metachronal motion. Numerical modeling has demonstrated that metachronal motion can be more efficient than synchronous motion in terms of fluid pumping.102,103,136,137 These findings have motivated researchers to explore manmade analogs of natural cilia that are capable of performing metachronal motion. The mechanism of creating metachronal cilia can be summarized into two categories (see also section 4.3.3): (i) applying different forces to each cilium within an array of cilia, and (ii) designing an array of cilia with different responses to a uniformly applied stimulus such as a uniform magnetic field. In 2020, Zhang et al. experimentally demonstrated the first metachronal microscopic magnetic artificial cilia (350 μm long) that could generate a flow speed 30 times higher than that generated by a synchronous motion, namely up to 3000 μm s−1, but inertial effects played an important role too.138 The reported metachronal motion was realized by applying a non-uniform but periodical magnetic field using, however, a relatively cumbersome actuation setup with a moving belt containing many small permanent magnets. To solve this issue, in 2021, Zhang et al. reported an array of metachronal microscopic magnetic artificial cilia where neighboring cilia have different magnetic properties, and thus beat out-of-phase in a simple uniform rotating magnetic field (Fig. 8(d)).20 These metachronal magnetic artificial cilia showed 3 times higher fluid pumping capabilities than synchronously beating cilia, with generated fluid velocities of 220 μm s−1. Gu et al. reported magnetically actuated artificial cilia carpets that exhibit metachronal waves in dynamic magnetic fields. The metachronal waves are achieved by programmable magnetization patterns coming from stretching and folding onto curved templates.19 Milana et al. developed pneumatic cilia performing metachronal waves by pressurizing with a dedicated pressure source. The net flow speed increased by 50%, compared to synchronous beating, when cilia move in an antiplectic wave with phase shift of −π/3 but the flow decreased for symplectic waves (Fig. 8(bii)).90 Dong et al. investigated the quantitative relationship between metachronal coordination and the induced fluid flow, and found that only antiplectic metachronal waves with specific wave vectors could enhance fluid flows compared with the synchronized case.85Fig. 8 shows representative examples of artificial cilia and the typical flow patterns and/or velocities they can generate.
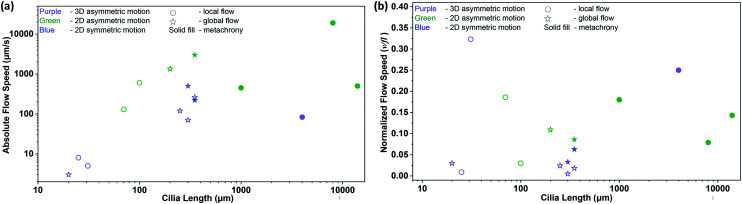
Table 1 summarizes the fluid pumping capabilities of the artificial cilia published up to date. Fig. 9 shows both the absolute flow speed and the relative flow speed as a function of the cilia length for all the publications listed in the table. The data should be compared with care, since these include both local flow measured closely above the cilia tips and global flow measured far away from the ciliated area, as indicated in the figure. Clearly, there is a correlation between the cilia size and actuation frequency on one hand, and the absolute value of the generated fluid flow speed on the other hand, with higher speeds for larger or faster artificial cilia. The highest absolute speed is generated by the pneumatically controlled artificial cilia of Gorissen et al.,89 namely 19 000 μm s−1, but their large size (8 mm) prohibits application in microfluidic devices. The relative flow speed (Fig. 9(b)), on the other hand, does not show a clear correlation with cilia size. The artificial cilia most effective in generating flow, relative to size and beating frequency as measured by the normalized flow speed δ, are the small artificial cilia developed by Vilfan et al.10 since these have the largest δ of 0.323; however the absolute value of the fluid velocity generated by these artificial cilia, 5 μm s−1, is too low for many practical microfluidic applications. A good compromise is offered by the various mid-sized (100 s of μm) magnetic artificial cilia that can generate typical fluid flow velocities of 100 s of μm s−1, which is the range relevant for microfluidic devices.
Fig. 9. Summary of the net flow generated by previously reported artificial cilia listed in Table 1. (a) Absolute flow speed as a function of cilia length. The color of the symbols indicates cilia motion with purple, green and blue indicating 3D non-reciprocal motion, 2D non-reciprocal motion and 2D reciprocal motion, respectively. The circle and star symbols indicate whether the associated publication reports the local flow above the cilia tips or the global flow measured far away from the ciliated area, respectively. Solid filled data indicate the existence of a metachronal wave. (b) Normalized flow speed, δ = v/fl, as a function of cilia length (see Table 1 for the corresponding references). The symbols have the same meaning as in panel (a).
6.2. Mixing
Compared to microfluidic pumping, research on microfluidic mixing using artificial is more limited. The earliest report is by den Toonder et al. in 2008, shown in Fig. 10(a).6 The reported electrostatic cilia could create efficient mixing in a Y-shape microfluidic device. Oh et al. created resonance-actuated artificial cilia in 2009,139 and showed in 2010 that the cilia mixer reduced the mixing time by 8.0- and 1.4 times compared to diffusion- and vibration mixers, respectively.140 Chen and co-workers experimentally and theoretically studied the effect of microscopic magnetic artificial cilia motion on the mixing efficiency.115,141,142 Superior mixing performance could be achieved when the cilia perform a figure-of-eight motion, as shown in Fig. 10(b).141 Finally, studies have shown that metachrony potentially enhances microfluidic mixing.85,92
Fig. 10. Fluid mixing with artificial cilia. (a) Fluid mixing with electrostatically actuated artificial cilia: (i) design of Y-shape microfluidic channel, (ii) optical image of the Y-shaped microfluidic device with two inlets for pumping in liquids and one outlet, (iii and iv) snapshots from a mixing experiment using dyed silicone oils; the mixing is complete within 1.5 cycles traveling distance in the main flow direction. Reproduced from ref. 6 with permission from the Royal Society of Chemistry. (b) Fluid mixing with MAC: (i) design of T-shape microfluidic channel, (ii) and (iii) SEM image of the MAC, (iv and v) snapshots from a mixing experiment using glycerol aqueous dye solutions; the insert shows the trajectory made by the cilia tip. Reproduced with permission from Chen 2013. Reproduced from ref. 141 with permission from the Royal Society of Chemistry.
7. Particle and droplet manipulation by artificial cilia
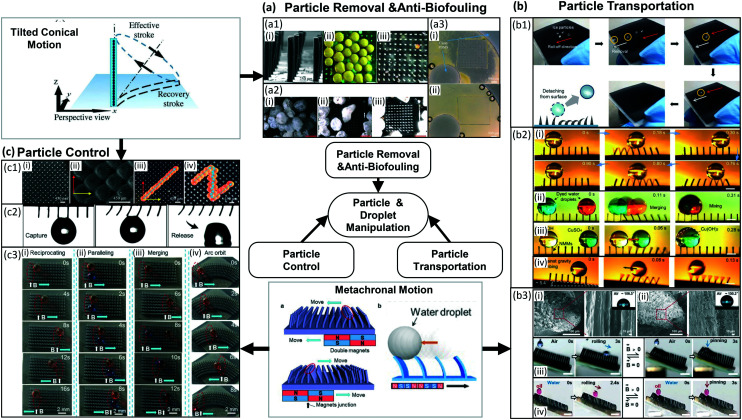
The manipulation of particles and droplets is an important function to realize in microfluidic devices for a number of applications, such as bioanalysis, disease diagnostics, drug delivery and self-cleaning surfaces.27,28,143 Recently, researchers have found inspiration in the ways that biological cilia manipulate particles, and have created versatile particle and droplet manipulation approaches using artificial cilia.24,27,28,30,120,144–146 Initially, numerical studies showed that artificial cilia are promising for manipulating particles.147–153 In recent years, increasingly experimental studies have been published exploring the particle manipulation capabilities of artificial cilia, where especially magnetically actuated artificial cilia have been used.24,25,27,28,30,120,144–146,154–161 The reported artificial cilia can not only remove particles, grains of sand, and microalgae27,28 (see Fig. 11(a)) to create self-cleaning and anti-biofouling surfaces, but they can also transport particles (see Fig. 11(b)).146,158,159 Moreover, by tuning the artificial cilia motion, more intricate control of the motion patterns of particles or droplets can be achieved (see Fig. 11(c)).25,155,158
Fig. 11. Particle and droplet manipulation by artificial cilia. (a) Particle removal, self-cleaning and anti-biofouling by artificial cilia exhibiting tilted conical motion (upper left panel). Reproduced from ref. 27 with permission from John Wiley and Sons. (a1) Use of magnetic artificial cilia to remove PLA particles in water. (i) SEM image of the MAC used in the article. (ii) shows the state of the surface before cleaning, (iii) is the state of the surface after actuating MAC for 60 s. (a2) Removal of natural sand grains by magnetic artificial cilia. (i)–(iii) show the cleaning process after 0 s 16 s and 30 s, respectively. a1 and a2 reproduced from ref. 27 with permission from John Wiley and Sons. (a3) Anti-biofouling by magnetic artificial cilia. (i) Broader bright-field microscopy image of the ciliated part after 28 days actuation, showing that the central unciliated area is almost perfectly clean. (ii) Broader bright-field microscopy image of a control experiment after 28 days, showing that the complete channel is fouled indiscriminately. Reproduced from ref. 28 with permission under open license CC BY-NC-ND. (b) Particle transport by artificial cilia exhibiting tilted conical motion (upperleft panel). (b1) Transport of ice particles by magnetically responsive film-like cilia. Because of the superhydrophobic wetting properties, ice particles form with nearly perfect spherical shapes. Reproduced from ref. 159 with permission under open license CC BY. (b2) (i) Transporting droplets back and forth on a superhydrophobic magnetically responsive microplate array. (ii) Process of directional propulsion, merging, and mixing of water droplets on the surface. (iii) A simple chemical reaction based on the rapid droplet horizontal propulsion and microscopic positioning and merging. (iv) A water droplet (volume around 3 μL) climbing up an inclined superhydrophobic magnetically responsive microplate array surface at an inclination angle of around 5.4°. Reproduced from ref. 158 with permission from the American Chemical Society. (b3) (i and ii) Morphology and corresponding water droplet contact angles of the magnetic microcilia before and after superhydrophobic modification, respectively. (iii) A water droplet can be switched between states of rolling down and pinning on an inclined surface by changing the magnetic field. (iv) Oil droplet manipulation in water on an inclined surface. Reproduced from ref. 146 with permission under open license CC BY. (c) Particle control by artificial cilia exhibiting metachronal motion (lower middle panel). Reproduced from ref. 155 and 158 with permission from the American Chemical Society. (c1) (i) Magnetic artificial cilia with size of 50 μm in diameter, 350 μm in height. (ii) Top view of tilted conical motion shown by actuated cilia. (iii and iv) Top-view time-lapse trajectory of a particle transported along controlled directions. Reproduced from ref. 25 with permission under open license CC-BY-NC-ND. (c2) Water droplet capture and on-demand release by a superhydrophobic magnetically responsive microplate array surface. Reproduced from ref. 158 with permission from the American Chemical Society. (c3) (i) Water droplet moves reciprocally on a magnetic responsive cilia surface. (ii) Two droplets moving in parallel on a surface. (iii) Merging of droplets. (iv) Directional stable transportation of a droplet along a circular orbit. Reproduced from ref. 155 with permission from the American Chemical Society.
7.1. Particle removal, self cleaning, and anti-biofouling
Quite a number of numerical studies have shown the potential of using artificial cilia to create self-cleaning and antifouling surfaces by removing particles.26,147–150,152,153,162 Based on these results, some experimental studies have been reported in recent years. In 2019, Zhang et al. demonstrated that their magnetic artificial cilia can remove viscoelastic polylactic acid (PLA) particles from the ciliated surfaces when the artificial cilia perform the tilted conical motion in water, as shown in Fig. 11(a1);27 the size range of the particles was 30 μm to 500 μm. The main mechanism for this self-cleaning effect, proposed by the authors, is that the actuated cilia induce strong hydrodynamic and mechanical forces on the particles, overcoming the adhesion force between the particles and the substrate or the cilia. In addition, the authors studied the efficiency of the self-cleaning for particles with different sizes. They demonstrated that the cleanness was above 80% for all particle sizes except for the particles with a diameter similar to the pitch between the cilia. Moreover, in both water and air the artificial cilia could remove naturals and grains, which have arbitrary shapes and higher density (Fig. 11(a2)). In 2020, Zhang et al. demonstrated that the same magnetic artificial cilia can remove real biofouling agents, microalgae, due to hydrodynamic shear forces acting on the algae, hence creating anti-biofouling surfaces, see Fig. 11(a3). This was a meaningful step towards real life applications.28
7.2. Particle and droplet transportation
Transporting particles and droplets on a surface is another important application of artificial cilia. To control the interaction between the particles or droplets and the artificial cilia, the cilia surface can be treated to modify their surface energy. In particular, they can be turned superhydrophobic by various treatments such as superhydrophobic spraying, immersion in a solution, and femtosecond laser modification.146,155,158,159 Making use of the superhydrophobic nature of a magnetic artificial cilia array treated by coating of carbon nanoparticles, Kim et al.159 studied the transportation of ice particles. As the cilia bend along the magnetic field direction, they form an open channel on the surface. Combined with the superhydrophobicity of the surface, droplets are then transported smoothly. The ice particles form nearly perfect spherical shapes on the superhydrophobic surface, which can also be easily removed by actuating the cilia as shown in Fig. 11(b1). Artificial cilia can also be actuated to exhibit metachronal motion (see section 4), which can be used to transport particles or droplets. Hu et al.158 actuated magnetic artificial in the form of microplates treated with hydrophobic spraying, by moving an array of connected magnets underneath the ciliated surface. In this way, they successfully transported droplets on a horizontal surface and they even realized simple chemical reactions on the surface (see Fig. 11(b2) (i)–(iii)). In addition, they were able to transport a droplet upward on a tilted surface, against gravity (see Fig. 11(b2) (iv)). The successful transportation relied on the metachronal cilia motion, droplet inertia and the local high adhesion to the microplates. Also Jiang et al.146 realized droplet transportation by artificial cilia on an inclined surface. In this case, not only water droplets but also oil droplets could be transported. By immersing the cilia array in different solutions, either a superhydrophobic or a superoleophobic surface could be obtained (see Fig. 11(b3) (i and ii)). For the transportation (b3(iii and iv)), the force balance between the left and right side of the droplets was crucial.
7.3. Particle and droplet control
Beyond transportation in one direction, more intricate particle control can be realized by controlling the artificial cilia motion, enabling to move particles along a designated orbit. Zhang et al.25 employed magnetic artificial cilia exhibiting a tilted conical motion to control the motion of PLA particles placed on top of the cilia tips. As illustrated in Fig. 11(c1), the particles could be transported by the coordination of the pulling force provided by the anteriorcilia and the pushing forces applied by the posterior ones, guided by the rotation of the external magnetic field. By changing the rotation and/or the tilting direction of the cilia, the particles could be transported along any designed route over the ciliated area. These experiments were confirmed by numerical simulations.25 Artificial cilia can also be used to capture and release droplets,158,161 as shown in Fig. 11(c2). A magnetically responsive array of microplate-shaped artificial cilia was treated with superhydrophobic spray so that the cilia obtained local high-adhesion spots, key to capturing droplets, and thus the cilia array could be used to capture water droplets. The water droplets could be released by deforming the microplate array with an external magnetic field. Finally, cilia arrays exhibiting metachronal motion caused by the translation of a permanent magnet have been shown to induce stable transportation of droplets. This means that, by controlling the direction of the magnetic array translation causing a unidirectional wave, droplets can be transported along any wanted route or stopped on demand.146,155,158,159 For instance, the droplets can move along a straight or arch orbit as shown in Fig. 11(c3). Moreover, two droplets can also move in a parallel way or merge. This precise control was achieved by the ingenious design combining the anisotropic characteristics of microgrooves and the active oscillation of the artificial cilia. ESI† Table S2 compares the reported artificial cilia particle and droplet manipulation techniques quantitatively.
8. Flow sensing by artificial cilia
In nature, the majority of the cilia types present ubiquitously inside and outside bodies of living organisms exist as sensory/primary cilia (see section 2). The sensing impetus may either be a mechanical deformation (called mechanosensing) or a change in the chemical concentration/species around or on the cilia surfaces (called chemosensing). The earliest research works on artificial cilia were in fact inspired by the sensing properties of the cilia specifically present on insect bodies or in the fish lateral line.107,108 In these first publications, a rectangular cantilever type structure (in-plane or out-of-plane) acts as a signal receptor while the base to which the cantilever/cilium is connected was modified to act as a piezoresistive sensing unit (strain gauges)107,108 as schematically shown in Fig. 12(a) and the SEM images in Fig. 13(a). Soon after the development of this strain gauge based artificial cilia sensor, capable of measuring flow of air and/or water when immersed, the sensing receptor was modified through micromachining processes to a cylindrical geometry, and the sensing base was further modified to sense low frequency vibrations thus increasing its sensitivity. This property was exploited to develop an artificial cilia system capable of sensing sound vibrations underwater, therefore acting as a hydrophone, as well as the direction of the sound wave propagation, by arranging the piezoresistive units circularly at the base around the sensing cilium.163,164 Use of artificial cilia to create hydrophones with improved sensitivity and for specific applications, accompanied with improvements of their ease of fabrication, continued to grow over the succeeding years.165–167 With the use of piezoresistive units to convert the mechanical input into an electric signal, the artificial cilia based sensors were designed to also mimic a specific configuration of cilia where a bundle of cilia are covered with a signal transferring accessory structure called cupula.168 This type of artificial system contains a flexible cilia bundle made of a compliant polymer, embedded in a liquid/gel with an integrated sensor together making a sensing unit capable of detecting changes in the surrounding environment. The majority of the cilia based sensors developed have chosen the piezoresistive devices as the sensing units for their very fast response time, see ESI† Table S3. Recent modifications in the piezoresistive sensing units have come in the form of carbon nanotubes (CNT) based piezoresistors with high sensitivity to low deformations169,170 and graphene based flexible strain gauges for making all flexible cilia sensors.117,171 In terms of the sizes of the piezoresistive based cilia sensors, because of the fabrication processes involved, most of them have cilia lengths falling in the milliscale range (above 1 mm) and only a very few of them in the sub-mm range, see ESI† Table S3. The very few micro-cilia sensors based on piezoresistive sensors have been fabricated from stiff materials with stiff and brittle silicon substrates making them less suitable for microfluidic applications in which low flow speeds must be measured for which flexibility is required.107–109,165
Fig. 12. Schematic representation of: (a) piezoresistive and piezoelectric cilia sensors where the cilium structure may be attached to one or multiple sensors/elements arranged either in its base or within the cilium structure. The sensors may experience deflection like represented by the bent configuration A and B depending on their type of arrangement around the cilium structure. (b) A capacitance based sensor integrated in the cilium base may be triggered by the bending of the cilium in the same manner as shown for the piezo sensors (configuration A and B). (c) A GMR or GMI sensor is placed under the cilia made from a magnetic material. Minute change in the magnetic field due to the deflection of magnetic cilia bought about by the surrounding fluid flow or vibrations is sensed by the sensor placed in the base.
Fig. 13. Artificial cilia based sensors: (a) SEM image of a piezoresistive sensor based cilium with the piezoresistive element in the base (image-i) designed as per the configuration B shown in the schematic Fig. 12(a). Reproduced from ref. 108 with permission from the Institute of Physics. In image-ii the sensing element is integrated within the cilium structure. Reproduced from ref. 165 with permission from Elsevier. (b) SEM images of arras of cilia with a capacitive sensor integrated in the base both in image-i and ii, reproduced from ref. 175 and 176 respectively with permission from the Institute of Physics. (c) Magnetic artificial cilia containing magnetic nanowires embedded in PDMS (image-i) and SU-8 (image-ii) for measuring flow. Image-i reproduced from ref. 180 with permission from the Royal Society of Chemistry. Image-ii reproduced from ref. 184 with permission from the Institute of Electrical and Electronics Engineers.
Attempting to avoid the use of brittle silicon as a substrate, the polymer PVDF (polyvinylidene fluoride) integrated with electrodes working as piezoelectric units has been proposed to be used in artificial sensory cilia systems.172 In the form of micro and nano fibers, the piezoelectric PVDF was linked to multiple cilia tips in a hydrogel cupula making a highly sensitive sensing system with threshold detecting flow limit of 8 μm s−1.173 Another configuration of piezoelectric PVDF fibres and a co-polymer of PVDF as a sensor in a cilia system involved its use in rather simplified fabrication processes with the fibers typically present around the central cilium base as schematically shown Fig. 12(a).130,167 More recently, an artificial cilium has been presented working as a hydrophone using leadzirconate titanate (PZT) as a piezoelectric sensor.174 Apart from the sensor with cilia tips connected with the PVDF fibers in a cupula,173 the cilia lengths of other piezoelectric based sensors are again larger than 1 mm, but since the cupula has multiple cilia covered in a hydrogel drop, the effective size of this sensor also falls in the millimeters scale. This makes these artificial cilia sensors less suitable for application in microfluidics.
Along with the development of piezoresistive and piezoelectric cilia sensors, capacitance based sensors have been proposed simultaneously to mimic the ‘arrayed’ nature of the cilia as acoustic175 and flow sensors.176 The capacitive sensors are integrated in the base of each cilium, as shown in Fig. 12(b) and 13(b) and these generate an electric response to the mechanical stimuli. These sensors were initially made in a silicon substrate and the cilia themselves from the stiff SU-8 polymer.175–177 An entirely compliant cilia sensor using an internal core of liquid metal as a capacitive unit surrounded by a soft silicon body has also been developed,178 but its size also falls well into the millimeter scale, again not fitting to microfluidic applications.
To develop a truly micro/nanoscale artificial ciliary sensor, the concept of measuring changes around a magnetic sensor brought about by the deflection of a micro/nano magnetic cilia like structure as schematically shown in Fig. 12(c) has been shown to be highly promising. Using a giant magnetoresistive (GMR) under a thick carpet of iron-gallium nano wires, a transducer was developed with however a complex packaging procedure.179 Mixing iron nanowires with poly(dimethylsiloxane) (PDMS) and casting it into the pores of a poly(methyl methacrylate) (PMMA) mold, flexible micro-sized cilia for flow sensing have already been developed,180 see Fig. 13(c). The mold was prepared in a PMMA sheet using a CO2 laser and the deflection of the magnetic artificial cilia was sensed by giant magnetoimpedance (GMI) sensors. The use of GMR and GMI sensors along with the magnetic composites suitable for molding into smaller and smaller cilia sizes could be seen as the right candidate for developing microfluidic flow and sound sensors.
Apart from the types of sensors discussed above, sensing of the cilia received inputs have also been achieved by the use of other sensors like force sensitive resistors (FSR),181 ionic polymer metal composite (IPMC)182 and more recently, resonance based sensors183 as listed in the ESI† Table S3. The cilia sizes in all these sensing systems are however equal to or above 1 mm. Cilia with sizes falling in the micro range are listed in Table 2, along with the relevant details.
Sensing artificial cilia based on different sensing principles and with biggest feature size less than 1 mm are listed here. The list is sorted as per the cilia sizes, from smallest to largest. A more complete list is given in the ESI† Table S3.
| Ref. | Flow sensing principle | Material | Size* □: l × w × t μm, ○: l × d μm | Medium | Flow velocity | Flow measurement resolution |
|---|---|---|---|---|---|---|
| 185 | Magnetic | PPy NW | 1 × 0.08–0.2 | Air | — | — |
| 186 | Magnetic | Fe–Ga NW | 5 × 0.1 | Air | — | — |
| 179, 187 | Magnetic | Fe–Ga NW | 25–100 × 0.02–0.2 | Liquids | 400 Hz–10 kHz | — |
| 188 | Magnetic | Co NW | 50 × 0.7 | Water/air | 6 mL min−1 | 136 μL min−1 |
| 173 | Piezoelectric | SU-8 | 400–800 × 50 | Water | 1–5 Hz | — |
| 177 | Capacitive | SU-8 | 500 × 50 | Air | — | — |
| 180, 184 | Magnetic | Fe NW, PDMS/SU-8 | 500 × 100, 20 × 5 | Water | 0.6 m s−1 | 0.56 mm s−1 |
| 109 | Piezoresistive | SU8 | 600 × 80 | Air/water | — | <1 m s−1 |
| 165 | Piezoresistive | AlN3 + Mo | (200–600) × 100 × 0.7 | Water | 0.3 bar | 0.025 bar |
| 107 | Piezoresistive | — | 800 × 400 × 250 | Air | 10 s of cm s−1 to 2 m s−1 | — |
| 108 | Piezoresistive | Permalloy | 820 × 0–10 × 100 | Water | 1 m s−1 | — |
| 176 | Capacitive | SU-8 | 900 × 50 | Air | — | — |
| 189 | Piezoresistive | Red wax | 1000 × 100 × 40 | Water | — | 184.2 dB |
| 190 | Magnetic | Fe–Ga NW | — × 0.001–0.1 | Air | 300 Hz–5 kHz | — |
| 172 | Piezoelectric | PVDF | — × 25 | Air | — | — |
| 175 | Capacitive | SU-8 | 1000 × — | Air | 0.1–1 m s−1 | — |
9. Modeling artificial cilia
Modeling the motion of artificial cilia under the influence of an applied stimulus and its effect on the surrounding fluid and/or neighbouring or contacting particles is challenging. This is due to the complexity of the problem, which involves the coupled interactions between multiple physical domains, such as solid mechanics, fluid mechanics, involving fluid structure-interaction, electromagnetism, etc. Hence, only a few theoretical models that go beyond the scaling analyses presented in section 2 have been reported.
One theoretical model describes the bending of magnetic artificial cilia containing paramagnetic particles by balancing the applied magnetic torque (Tmag) with the opposing deformation torque Tdef.191 The magnitude of the magnetic torque is given by:
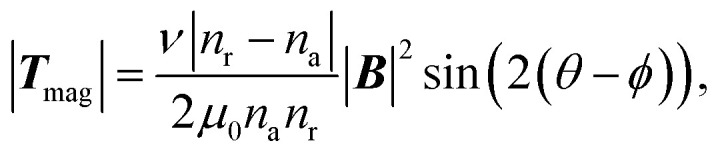 |
7 |
which assumes a negligible magnetic gradient as well as a cilium aspect ratio dominated induced magnetic moment, which holds if the magnetic susceptibility is high.192,191 In the above expression, ν is the total volume of magnetic particles in the cilium, na and nr are the geometry demagnetization factors along and perpendicular to the cilium long axis respectively, and B is the magnetic flux density. ϕ and θ are the angle of the magnetic field and the angle of the cilium from the vertical, hence B makes an angle (ϕ − θ) with the long axis of the cilium. Tmag is balanced by the counteracting deformation torque, of which the magnitude is given by:
 |
8 |
where r is the cilium radius, l its length, and E its Youngs modulus.191Eqn (8) assumes that the cilium bends with a constant radius of curvature while undergoing large deformation.7 Magnetic cilia bending experiments have shown good correspondence with this model.98,191
The flow generated by artificial cilia performing a known tilted conical motion, as shown in Fig. 4(a) and 8(c), has been described by a semi-quantitative theoretical model that is valid in low Reynolds number conditions. In this model, the volume of fluid transported in each cycle is proportional to sin Θ sin2 Φ, with Θ the tilt angle of the cone axis and Φ the cone opening angle.133 This model has been extended to the situation in which the path traced by the cone is ellipsoidal rather than circular by including the aspect ratio α of the two ellipsoid axes, resulting in a generated fluid velocity of v = cfα sin Θ sin2 Φ with c being a proportionality constant and f the actuation frequency of the artificial cilia.13 This semi-quantitative model has been shown to describe experimental results well.13,133
More complex situations, such as different artificial cilia motions than tilted conical rotation, or cases that include nonlinear interactions, cannot be sufficiently captured in purely theoretical models to make quantitative predictions. Over the years, therefore, various computational techniques have been utilized to model the actuation of artificial cilia and the associated fluid dynamics. Such models are relevant for understanding the observed phenomena, but also for providing guidance to the design of novel artificial cilia systems for specific applications. It is challenging to resolve the coupled dynamics of fluid–cilia interaction in numerical models, which is due to the computational complexity attributed to the non-linear nature of the equations to be solved as well as the requirement of two-way coupling between the cilia deformation and fluid flow to be accounted for. The fluid dynamics is governed by the Navier–Stokes (NS) equations and the non-linearity of the problem depends on the Reynolds number (Re). As mentioned in the previous sections, many applications fall in the category of low Re flow and that plays a significant role in the solution strategies. For instance, at low Re (≪1) the inertial effects are negligible and the non-linear terms (i.e. the advection terms in the NS equations) vanish. Therefore, the basic nature of fluid flow is dominated by viscous effects and in that case one has to solve the Stokes equation, which relieves some of the computational complexity. The structural dynamics of the artificial cilia, however, still exhibits non-linear behaviour because large scale deformation is observed while the cilia are subjected to externally applied loads such as magnetic and fluid forces.
We briefly discuss the computational techniques that are employed to tackle different classes of problems involving fluid–cilia interaction. The method of regularized Stokeslets193 is widely used to compute the Stokes flow generated by beating cilia.194 A cilium is approximated by regularized Stokeslets along its centreline193 and to satisfy the no-slip boundary condition at the plane wall, image Stokeslets are used.195,196 The distribution and strength of Stokeslet varies with time and position on the cilium.194 The exact solution of the Stokes equation is determined by the Stokeslet, the primary Greens function of Stokes flow and the superposition of these solutions provide the flow field.196 The method was used, for instance, to study the mixing and transport by an asymmetrically beating cilia carpet by considering the 2D kinematics of the cilia under the influence of metachronal waves as shown in Fig. 14(a).194
Fig. 14. Computational techniques utilized to resolve the fluid–cilia interaction. (a) The method of regularized Stokeslets is used to account for fluid transport: the shown velocity fields correspond to (i) synchronized cilia beating (ii) symplectic metachronal beating (iii) antiplectic metachronal beating. Reproduced from ref. 194 with permission from Cambridge University Press. (b) The bead-spring model is widely used to study particle transport and fluid pumping applications. (i) A schematic representation of an artificial cilium by spherical beads connected through springs. Reproduced from ref. 100 with permission from Springer Nature. (ii) The numerical results of particle transportation by magnetically actuated artificial cilia (top and side views first two rows) are compared with the experimental result (top view third row). Reproduced from ref. 25 with permission under open license CC BY-NC-ND. (iii) A soft particle transported by adhesive cilia. Reproduced from ref. 26 with permission from the American Chemical Society. (iv) The beating kinematics and pumping performance of a magnetically actuated artificial cilium. Reproduced from ref. 133 with permission from Europhysics Letters. (v) The flow velocity generated by rotating artificial cilia. Reproduced from ref. 10 with permission from the National Academy of Sciences. (c) Finite element based fully coupled 2D and 3D FSI solvers (i) a schematic of the problem in which magnetically actuated artificial cilia are used to generate the flow in a channel. (ii) The velocity fields are compared in the absence (left one) and in the presence of fluid inertia (right one). Image-i and ii are reproduced from ref. 205 with permission from the Royal Society of Chemistry. (iii) metachronal beating of 3D plate-like cilia: the magnetically actuated thin plate or shell like artificial cilia immersed in a semi-infinite fluid for generating the flow. (iv) The velocity field generated by the in-phase beating of 3D cilia. Image-i and ii are reproduced from ref. 206 with permission from Cambridge University Press.
To numerically mimic the beating pattern of magnetically actuated artificial cilia, bead-spring models10,100,133,197 have been developed to represent the actual cilium for applications like pumping,100 swimming197 and particle transport.25Fig. 14(b) shows examples. The spherical superparamagnetic beads are linked by springs to form a cilium. The springs account for bending and stretching forces between neighboring beads and the magnetic dipolar interactions subject to the external magnetic field are accounted for. The hydrodynamic interaction is considered between beads,100,197 assuming Stokes flow. The equations of motion of the cilia comprise all the forces acting on the beads (elastic, magnetic and hydrodynamic). The hydrodynamic interaction is accounted for by including the contribution of the Rotne–Prager mobility matrix.197 To account for the no-slip boundary condition at the plane wall, Blakes tensor195,196 is used.197 The bead-spring model coupled with the analytical solution of the Stokes equation is quite efficient in terms of computational cost for low Re applications;25,100,197 large-scale cilia deformation due to an external magnetic field can be captured in three dimensions, but is limited to non-inertial fluid–cilia interaction. Computational modeling of particle manipulation and fluid pumping applications have also been carried out by combining lattice Boltzmann based flow solvers with lattice spring models representing the cilia in a similar manner as the bead-spring models, except that the connected beads or lattice nodes are non-magnetic.26,147,150,152,153,198–200
Fully coupled fluid–structure interaction (FSI) models to resolve the structural dynamics of magnetically actuated artificial cilia interacting with the fluid have also been reported.103,134,201,202 The FSI model utilizes a coupled Eulerian–Lagrangian framework to solve the fluid–structure interactions. The Navier–Stokes equations are discretized by using a finite-element formulation on a Eulerian mesh, and the velocity and pressure are interpolated quadratically and linearly, respectively.134 The cilia are modeled by using Euler–Bernoulli beam elements in a Lagrangian framework that fully accounts for the geometric nonlinearity. The overall formulation is based on the principle of virtual work. A monolithic approach is employed to solve the fluid–structure dynamics simultaneously by incorporating the no-slip boundary condition at the fluid–cilia interface with the use of Lagrange multipliers.203 The magnetic actuation forces, acting as an external load to the cilia (that can be either permanently magnetic as well as superparamagnetic), are determined by solving the Maxwells equations. This FSI model has been employed to study two-dimensional microfluidic propulsion by using magnetically-driven artificial cilia in an open-loop and a closed-loop channel,102 the effect of metachronal beating within the Stokes regime,103 and the effect of fluid inertia on the propulsion performance, as illustrated in Fig. 14(c).204,205
A three-dimensional FSI model to study magnetically actuated plate like superparamagnetic cilia interacting within a semi-infinite fluid in the Stokes regime has been developed by Khaderi and Onck.206 Triangular shell elements are used to discretize the cilia and the low-Re fluid dynamics is accounted by using Greens functions195 in combination with a boundary element approach. The no-slip boundary condition is imposed at the fluid–cilia interface, and the drag force acts as an external point force distributed over the cilia surface. The model has been applied to study the effect of metachronal waves on fluid transport (see Fig. 14(c)),206 the swimming of artificial flagella207 and pneumatic cilia.92
10. Outlook and opportunities
Our review shows that most efforts in artificial cilia research have been aimed at generating fluid flow (section 6). Clearly, magnetic actuation is used the most for microfluidic pumping, and this indeed is the most promising approach for application in microfluidics since it offers many advantages:
• it does not require any physical connections such as tubes or current wires;
• the interference with fluids, molecules, cells, or tissues generally used in microfluidic applications is negligible, because these are not influenced by the magnetic field and, the other way around, the artificial cilia actuation is not influenced by them; the magnetic artificial cilia pumping is cell-friendly;
• the method is versatile: by control of the magnetic field, the flow can be controlled in space and in time such that, for example, pulsating flows or flow reversal can be achieved in a straightforward manner;15
• the artificial cilia pumping forms an integrated part of the device itself; and by design of the layout and location of artificial cilia in combination with the magnetic actuation protocol, local flow patterns can in principle be created, which is almost impossible to achieve with microfluidic flow driven by an external pump.
As we have shown in section 6, the mid-sized magnetic artificial cilia (100 s of μm) can generate flow speeds of 100 s of μm s−1, which is a range relevant for microfluidic devices, and the size of these cilia is compatible with integration in microfluidic devices for many applications. We are convinced that particularly for creating recirculating flows in microfluidic devices, magnetic artificial cilia can provide an optimal solution; such flows are for example required in organ-on-chip applications where fluids, containing nutrients and often cells, need to be recirculated over cells or between tissues, to mimic blood flow, provide nutrients, or to exchange factors between tissues.
Proof-of-principle of microfluidic flow generation by magnetic artificial cilia has been convincingly shown, as evidenced by the results summarized in section 6. However, towards implementation in real-world applications and commercial devices, work is needed on:
• fabrication methods that enable to produce the cilia, in the end, on an industrial scale. This means that current fabrication approaches need to be scaled up. This is, in principle, possible for a replication process such as the molding methods that are used often, but also for MEMS-based processing since this is already an established industrial approach;
• materials: currently, the basic material for many artificial cilia is PDMS. Even though this material has great advantages such as easy processability and flexibility, it also has disadvantages. Processing times are mostly long, absorption by PDMS of small molecules may be an issue in some applications (e.g. in drug testing), and the hydrophobic nature of PDMS can lead to practical issues such as bubble formation. Hence, work on other material opportunities is needed for further development of artificial cilia;
• in the research on magnetic artificial cilia, the magnetic actuation setups that are used to generate the required magnetic fields are still rather bulky, which is not convenient for a commercial product; therefore, miniaturization of the magnetic actuation device is needed to obtain a compact instrument that can interface with the microfluidic device;
• assembly steps in fabrication processes are often costly, and these are minimized as much as possible in industrial manufacturing; for artificial cilia, the assembly and integration in microfluidic devices therefore requires more attention.
Compared to microfluidic pumping, microfluidic mixing by artificial cilia has not been studied much (section 6). We believe that magnetic artificial cilia mixing could provide a good solution for mixing in microfluidic devices, especially when fluids must be mixed in microchambers with initially stagnant fluids, i.e. in the case when no flow is generated using external means. Examples are micro-reaction chambers in which biochemical reactions must take place, in which binding events must happen between targets and labels, or in which agents must be homogeneously distributed for optimal detection. By design of the artificial cilia configuration in such a chamber, in combination with a tuned magnetic actuation protocol, time-dependent flow patterns can be created that lead to effective micromixing by the generation of chaotic advection or stretching and folding flow patterns.208 Also, the use of metachrony can be powerful for enhancing mixing.92 To design the optimal cilia configuration and actuation protocol, numerical simulations will be of great help.
Particle and droplet manipulation (section 7) have been shown for relatively large cilia and particles. For meaningful applications in microfluidic devices, in which smaller particles such as cells need to be transported, further miniaturization is needed. Magnetic artificial cilia with suitable dimensions have already been developed (see section 5), and towards controlled cell manipulation the challenges are to create ciliated surfaces with sufficient areal density of cilia, and to obtain sufficient control of the motion of the cilia using a carefully designed magnetic actuation device. Anti-(bio)fouling, for example of sensor surfaces, is another possible microfluidic application of actuated cilia (section 7). Initial results show, indeed, that magnetic cilia motion can remove microalgae from surfaces, but in real life biofouling is a complex time-dependent process and more (field) experiments are needed mimicking realistic biofouling conditions to further tune and prove the anti-biofouling capacity of artificial cilia.
Even though flow sensing was the first application to be inspired by biological cilia, research into artificial cilia-based microfluidic flow sensing has been quite limited (section 8). Nevertheless, we believe that this is a very promising application especially, again, for magnetic artificial cilia for which the read-out of cilia deformation under flow is done using integrated magnetic sensors such as GMR or GMI. Such an approach is potentially very sensitive, does not interact with the environment, is non-invasive and has low noise. The challenges here are to further miniaturize and integrate smaller and smaller cilia as well as GMR or GMI sensors in the microfluidic devices. Being fully integrated in the device and providing real-time monitoring, the artificial cilia flow sensor signal can be part of a feedback loop that enables to fully control flow using an integrated artificial cilia pump. Such a possibility will be of great use for example in OOC applications where controlled fluid flow is essential.
The recent development of motile magnetic artificial cilia with truly biological sizes (tens of μm long)98 opens opportunities beyond technological applications for microfluidic control, namely for understanding the properties and behavior of biological cilia systems. Research on this topic can range from fundamental behavior at the cilia-level, to understanding (patho-)physiological function of human ciliated systems. An example of the former is the emergence of metachrony or even more complex collective dynamic behavior of ciliated systems; the question whether this is caused by hydrodynamic interactions between cilia, or by (mechanical) interaction through the common surface on which the cilia are located, is still not answered.209 Engineering artificial cilia experiments, carefully designed to study this effect, can help to gain understanding. An example of the latter, understanding (patho)physiological function of ciliated systems, is the study of the clearance of human respiratory tract induced by mucociliary transport. An in vitro microphysiological model based on artificial cilia, mimicking the structure and dynamics of the human mucociliary clearance apparatus could not only help understand this process, but could also be used to test potential treatments for individuals in which this process is impaired. A first model has been demonstrated,210 but this is still based on relatively large artificial cilia, and the challenge here is to shrink these to physiological dimensions and to include the layered structure of fluid representing the mucus film. A similar approach could be used to understand the clearance function of motile cilia present in the middle ear.211 Another example is to create an artificial embryonic node, to systematically investigate how the left–right asymmetry of the human body is induced by flow generated by the nodal cilia, a phenomenon that is also not fully understood.212 Artificial cilia models could also be used to understand mechanisms of sensing by primary cilia such as those in the kidney tubules by systematically studying cilia deformation due to applied flow.
Further, devices with integrated biologically sized artificial cilia could be applied as a tool to study mechanotransduction at the cellular level. Culturing individual cells, or layers of cells, on carpets of biologically sized artificial cilia would provide the opportunity to apply, in a controlled manner, local forces to cells (at subcellular scales) and measure reaction forces from the cells. This would facilitate the fundamental study of cellular mechanotransduction with unprecedented resolution, but it may also provide new insights into steering cell behavior, properties, or even differentiation, through applying mechanical stimuli.
Finally, in the present article we have focused on artificial cilia functions and applications related to microfluidics. But, beyond this field, there are many other areas in which artificial cilia can contribute, for example: control of friction and adhesion, tactile feedback surfaces, controlling optical surface properties, application in rheometry, for locomotion and propulsion in micro-robotics,19,20 target capture in biomedical assays, microbiology,213 (photo)catalysis and energy harvesting.30
11. Conclusions
The past decade has shown great progress of artificial cilia research, especially on the development of fabrication methods and on the control of cilia motion during actuation for fluid flow generation. Using magnetic actuation, which is used most, artificial cilia have been demonstrated to generate substantial fluid flow relevant to microfluidic applications, and at a scale that facilitates integration in microfluidic devices. Hence, microfluidic flow generation by magnetic artificial cilia is now ready for the transition towards implementation and use in real-world microfluidic applications such as LOC and OOC. This requires further development of fabrication methods and materials towards industrial levels, miniaturization of magnetic actuation devices, and effective assembly and integration methods.
Other microfluidic applications of artificial cilia such as particle manipulation, anti-(bio)fouling and flow sensing, have been convincingly demonstrated in academic research settings, but these ask for more basic and conceptual research before the transition to industrial implementation can be made.
The most recent developments open new opportunities, in particular those that have led to biologically sized magnetic artificial cilia with high motility. These artificial cilia could be used to create realistic in vitro models of biological cilia and ciliated systems, which then can be applied to investigate the functioning and the (patho)physiological behavior of natural cilia, important for understanding and eventually treating diseases related to cilia dysfunctioning, known as ciliopathies. Another application is the use of biologically sized artificial cilia to study mechanotransduction at the cellular level, or even to steer the behavior of biological cells in vitro.
In conclusion, artificial cilia research is very much alive, with some concepts close to industrial implementation, and other developments just starting to open novel scientific opportunities.
Author contributions
Conceptualization and supervision: JMJdT; investigation and writing of original draft: TuI, YW, IA, ZC, HEA, HG, RK, BBV, TW, SZ, PRO, JMJdT; writing – review & editing: JMJdT, PRO, YW, TuI.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
The research leading to this publication has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation Programme under Grant Agreement No. 833214. T. u. I. has been financially supported by the European Union's Horizon 2020 Research and Innovation Programme under Marie Sklodowska-Curie Grant 754462. S. Z. is financially supported by the Alexander von Humboldt Foundation. Z. C. is financially supported by the China Scholarship Council under grant no. 201706400061.
Biography
Front row, from left to right: Ye Wang, Zhiwei Cui, Jaap M. J. den Toonder, Tanveer ul Islam, Tongsheng Wang, and Bhavana B. Venkataramanachar. Back row, from left to right: Hemanshul Garg, Hossein Eslami Amirabadi, Shuaizhong Zhang, Patrick R. Onck, Roel Kooi, and Ishu Aggarwal.
Professor Jaap den Toonder of Eindhoven University of Technology and Professor Patrick Onck of the University of Groningen are pioneers in the field of artificial cilia. Their collaboration on this topic started when they jointly initiated the European project ARTIC in 2006, and they have continued to expand their joint artificial cilia research up to the present day. Their approaches are perfectly complementary. In the Microsystems research section of den Toonder, novel concepts are designed, innovative materials and microfabrication methods are developed, and experimental prototypes are tested and demonstrated. Jaap den Toonder received an ERC Advanced Grant on the subject in 2019. In the Onck research group, advanced numerical models are developed and applied to steer the conceptual design and to understand the observed phenomena. This review paper is written by the artificial cilia team from both groups, including PhD students and postdocs as well as assistant professor Ye Wang (Eindhoven University of Technology) who has been working on artificial cilia since 2011. First author Tanveer ul Islam is currently postdoctoral researcher at Eindhoven University of Technology.
Electronic supplementary information (ESI) available: Tables S1–S3. See DOI: https://doi.org/10.1039/d1lc01168e
Footnotes
A slender magnetic body such as a cilium has different susceptibility along different axes because of geometry-based demagnetization factors,99 with the preferred magnetization direction along its length. Assuming an angle θ between the cilium and the external field, it can be deducted that Tmag scales with sin 2θ, with a maximum at 45°.
Notes and references
- Sleigh M., Cilia and flagella, Academic Press, 1974 [Google Scholar]
- Nonaka S. Shiratori H. Saijoh Y. Hamada H. Nature. 2002;418:96–99. doi: 10.1038/nature00849. [DOI] [PubMed] [Google Scholar]
- Singla V. Reiter J. Science. 2016;313:629–633. doi: 10.1126/science.1124534. [DOI] [PubMed] [Google Scholar]
- Praetorius H. Spring K. J. Membr. Biol. 2001;184:71–79. doi: 10.1007/s00232-001-0075-4. [DOI] [PubMed] [Google Scholar]
- Wilmer M. Ng C. Lanz H. Vulto P. Suter-Dick L. Masereeuw R. Trends Biotechnol. 2016;34:156–170. doi: 10.1016/j.tibtech.2015.11.001. [DOI] [PubMed] [Google Scholar]
- den Toonder J. Bos F. Broer D. Filippini L. Gillies M. de Goede J. Mol T. Reijme M. Talen W. Wilderbeek H. et al. . Lab Chip. 2008;8:533–541. doi: 10.1039/B717681C. [DOI] [PubMed] [Google Scholar]
- Evans B. Shields A. Carroll R. L. Washburn S. Falvo M. Superfine R. Nano Lett. 2007;7:1428–1434. doi: 10.1021/nl070190c. [DOI] [PubMed] [Google Scholar]
- Shields A. R. Fiser B. L. Evans B. A. Falvo M. R. Washburn S. Superfine R. Proc. Natl. Acad. Sci. U. S. A. 2010;107:15670–15675. doi: 10.1073/pnas.1005127107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fahrni F. Prins M. W. J. van IJzendoorn L. J. Lab Chip. 2009;9:3413–3421. doi: 10.1039/B908578E. [DOI] [PubMed] [Google Scholar]
- Vilfan M. Potočnik A. Kavčič B. Osterman N. Poberaj I. Vilfan A. Babič D. Proc. Natl. Acad. Sci. U. S. A. 2010;107:1844–1847. doi: 10.1073/pnas.0906819106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hussong J. Schorr N. Belardi J. Prucker O. Rühe J. Westerweel J. Lab Chip. 2011;11:2017–2022. doi: 10.1039/C0LC00722F. [DOI] [PubMed] [Google Scholar]
- Wang Y. Gao Y. Wyss H. Anderson P. den Toonder J. Lab Chip. 2013;13:3360–3366. doi: 10.1039/C3LC50458A. [DOI] [PubMed] [Google Scholar]
- Wang Y. Gao Y. Wyss H. M. Anderson P. D. den Toonder J. M. J. Microfluid. Nanofluid. 2015;18:167–174. doi: 10.1007/s10404-014-1425-8. [DOI] [Google Scholar]
- Wang Y. den Toonder J. Cardinaels R. Anderson P. Lab Chip. 2016;16:2277–2286. doi: 10.1039/C6LC00531D. [DOI] [PubMed] [Google Scholar]
- Zhang S. Wang Y. Lavrijsen R. Onck P. R. den Toonder J. M. Sens. Actuators, B. 2018;263:614–624. doi: 10.1016/j.snb.2018.01.189. [DOI] [Google Scholar]
- van Oosten C. L. Bastiaansen C. W. M. Broer D. J. Nat. Mater. 2009;8:677–682. doi: 10.1038/nmat2487. [DOI] [PubMed] [Google Scholar]
- Zarzar L. D. Kim P. Aizenberg J. Adv. Mater. 2011;23:1442–1446. doi: 10.1002/adma.201004231. [DOI] [PubMed] [Google Scholar]
- Lu H. Zhang M. Yang Y. Huang Q. Fukuda T. Wang Z. Shen Y. Nat. Commun. 2018;9:3944. doi: 10.1038/s41467-018-06491-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu H. Boehler Q. Cui H. Secchi E. Savorana G. De Marco C. Gervasoni S. Peyron Q. Huang T.-Y. Pane S. Hirt A. M. Ahmed D. Nelson B. J. Nat. Commun. 2020;11:2637. doi: 10.1038/s41467-020-16458-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S. Cui Z. Wang Y. den Toonder J. ACS Appl. Mater. Interfaces. 2021;13:20845–20857. doi: 10.1021/acsami.1c03009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sniadecki N. J. Anguelouch A. Yang M. T. Lamb C. M. Liu Z. Kirschner S. B. Liu Y. Reich D. H. Chen C. S. Proc. Natl. Acad. Sci. U. S. A. 2007;104:14553–14558. doi: 10.1073/pnas.0611613104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sniadecki N. J. Lamb C. M. Liu Y. Chen C. S. Reich D. H. Rev. Sci. Instrum. 2008;79:044302. doi: 10.1063/1.2906228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Y. Antao D. S. Xiao R. Wang E. N. Adv. Mater. 2014;26:6442–6446. doi: 10.1002/adma.201401515. [DOI] [PubMed] [Google Scholar]
- Zhang S. Wang Y. Onck P. den Toonder J. Microfluid. Nanofluid. 2020;24:1–20. doi: 10.1007/s10404-019-2306-y. [DOI] [Google Scholar]
- Zhang S. Zhang R. Wang Y. Onck P. R. den Toonder J. M. ACS Nano. 2020;14:10313–10323. doi: 10.1021/acsnano.0c03801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balazs A. C. Bhattacharya A. Tripathi A. Shum H. J. Phys. Chem. Lett. 2014;5:1691–1700. doi: 10.1021/jz5004582. [DOI] [PubMed] [Google Scholar]
- Zhang S. Wang Y. Onck P. R. den Toonder J. M. Adv. Funct. Mater. 2019;29:1806434. doi: 10.1002/adfm.201806434. [DOI] [Google Scholar]
- Zhang S. Zuo P. Wang Y. Onck P. Toonder J. M. d. ACS Appl. Mater. Interfaces. 2020;12:27726–27736. doi: 10.1021/acsami.0c05403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- den Toonder J. Onck P. Trends Biotechnol. 2013;31:85–91. doi: 10.1016/j.tibtech.2012.11.005. [DOI] [PubMed] [Google Scholar]
- Zhang X. Guo J. Fu X. Zhang D. Zhao Y. Adv. Intell. Syst. 2020:2000225. [Google Scholar]
- Choksi S. P. Lauter G. Swoboda P. Roy S. Development. 2014;141:1427–1441. doi: 10.1242/dev.074666. [DOI] [PubMed] [Google Scholar]
- Gray J. Proc. R. Soc. London, Ser. B. 1930;107:313–332. [Google Scholar]
- Lane N. Philos. Trans. R. Soc., B. 2015;370:20140344. doi: 10.1098/rstb.2014.0344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X. Lu Q. Peng Y. Geng F. Shao X. Zhou H. Cao Y. Zhang R. Protein Cell. 2020;11:433–445. doi: 10.1007/s13238-020-00695-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thouvenin O. Keiser L. Cantaut-Belarif Y. Carbo-Tano M. Verweij F. Jurisch-Yaksi N. Bardet P.-L. van Niel G. Gallaire F. Wyart C. eLife. 2020;9:e47699. doi: 10.7554/eLife.47699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haemmerle C. A. D. S. Nogueira M. I. Watanabe I.-S. Front. Neuroanat. 2015;9:134. doi: 10.3389/fnana.2015.00134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S. G. Lee S.-N. Baek J. Yoon J.-H. Lee H. Acta Biomater. 2021;128:346–356. doi: 10.1016/j.actbio.2021.04.030. [DOI] [PubMed] [Google Scholar]
- Baczynska A. Funch P. Fedder J. Knudsen H. J. Birkelund S. Christiansen G. Hum. Reprod. 2007;22:968–979. doi: 10.1093/humrep/del455. [DOI] [PubMed] [Google Scholar]
- Deane J. A. Verghese E. Martelotto L. G. Cain J. E. Galtseva A. Rosenblum N. D. Watkins D. N. Ricardo S. D. Nephrology. 2013;18:161–168. doi: 10.1111/nep.12022. [DOI] [PubMed] [Google Scholar]
- Sears P. R. Thompson K. Knowles M. R. Davis C. W. Am. J. Physiol. 2013;304:L170–L183. doi: 10.1152/ajpcell.00078.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoder B. K. J. Am. Soc. Nephrol. 2007;18:1381–1388. doi: 10.1681/ASN.2006111215. [DOI] [PubMed] [Google Scholar]
- Wang X. Jin H. Han F. Cui Y. Chen J. Yang C. Zhu P. Wang W. Jiao G. Wang W. et al. . Clin. Genet. 2017;91:313–321. doi: 10.1111/cge.12857. [DOI] [PubMed] [Google Scholar]
- Saggese T. Young A. A. Huang C. Braeckmans K. McGlashan S. R. Cilia. 2012;1:1–12. doi: 10.1186/2046-2530-1-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirokawa N. Okada Y. Tanaka Y. Annu. Rev. Fluid Mech. 2009;41:53–72. doi: 10.1146/annurev.fluid.010908.165141. [DOI] [Google Scholar]
- Foissner W. Wolf K. W. Yashchenko V. Stoeck T. J. Eukaryotic Microbiol. 2011;58:134–151. doi: 10.1111/j.1550-7408.2011.00532.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foissner W. Wolf K. W. Eur. J. Protistol. 2009;45:87–97. doi: 10.1016/j.ejop.2008.07.003. [DOI] [PubMed] [Google Scholar]
- Foissner W. Eur. J. Protistol. 1991;27:313–330. doi: 10.1016/S0932-4739(11)80248-8. [DOI] [PubMed] [Google Scholar]
- Hirokawa N. Tanaka Y. Okada Y. Takeda S. Cell. 2006;125:33–45. doi: 10.1016/j.cell.2006.03.002. [DOI] [PubMed] [Google Scholar]
- Nonaka S. Tanaka Y. Okada Y. Takeda S. Harada A. Kanai Y. Kido M. Hirokawa N. Cell. 1998;95:829–837. doi: 10.1016/S0092-8674(00)81705-5. [DOI] [PubMed] [Google Scholar]
- Shinohara K. Kawasumi A. Takamatsu A. Yoshiba S. Botilde Y. Motoyama N. Reith W. Durand B. Shiratori H. Hamada H. Nat. Commun. 2012;3:1–8. doi: 10.1038/ncomms1624. [DOI] [PubMed] [Google Scholar]
- Delling M. Indzhykulian A. Liu X. Li Y. Xie T. Corey D. Clapham D. Nature. 2016;531:656–660. doi: 10.1038/nature17426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu F. Li T. Sui Y. Chen Q. Yang S. Yang J. Hong R. Li D. Yan X. Zhao W. et al. . Protein Cell. 2020;11:852–857. doi: 10.1007/s13238-020-00746-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakamura R. Katsuno T. Kishimoto Y. Kaba S. Yoshimatsu M. Kitamura M. Suehiro A. Hiwatashi N. Yamashita M. Tateya I. et al. . Sci. Rep. 2020;10:1–6. doi: 10.1038/s41598-019-56847-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luengen A. E. Kniebs C. Buhl E. M. Cornelissen C. G. Schmitz-Rode T. Jockenhoevel S. Thiebes A. L. Sci. Rep. 2020;10:1–11. doi: 10.1038/s41598-019-56847-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nonaka S. Yoshiba S. Watanabe D. Ikeuchi S. Goto T. Marshall W. F. Hamada H. PLoS Biol. 2005;3:e268. doi: 10.1371/journal.pbio.0030268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rompolas P. Patel-King R. S. King S. M. Mol. Biol. Cell. 2010;21:3669–3679. doi: 10.1091/mbc.e10-04-0373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindemann C. B. Rikmenspoel R. Exp. Cell Res. 1972;73:255–259. doi: 10.1016/0014-4827(72)90131-0. [DOI] [PubMed] [Google Scholar]
- Abdul-Majeed S. Moloney B. C. Nauli S. M. Cell. Mol. Life Sci. 2012;69:165–173. doi: 10.1007/s00018-011-0744-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin H. Burnette D. T. Bae Y.-K. Forscher P. Barr M. M. Rosenbaum J. L. Curr. Biol. 2005;15:1695–1699. doi: 10.1016/j.cub.2005.08.047. [DOI] [PubMed] [Google Scholar]
- Flaherty J. Feng Z. Peng Z. Young Y.-N. Resnick A. Biomech. Model. Mechanobiol. 2020;19:445–460. doi: 10.1007/s10237-019-01220-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreno E. Lightfoot J. W. Lenuzzi M. Sommer R. J. Proc. R. Soc. B. 2019;286:20191089. doi: 10.1098/rspb.2019.1089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Supatto W. and Vermot J., From cilia hydrodynamics to zebrafish embryonic development, Elsevier, 2011, vol. 95, pp. 33–66 [DOI] [PubMed] [Google Scholar]
- Nakamura S. Minamino T. Biomolecules. 2019;9:279. doi: 10.3390/biom9070279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fliegauf M. Benzing T. Omran H. Nat. Rev. Mol. Cell Biol. 2007;8:880–893. doi: 10.1038/nrm2278. [DOI] [PubMed] [Google Scholar]
- Smith D. J. Montenegro-Johnson T. D. Lopes S. S. Annu. Rev. Fluid Mech. 2019;51:105–128. doi: 10.1146/annurev-fluid-010518-040231. [DOI] [Google Scholar]
- Reiter J. Leroux M. Nat. Rev. Mol. Cell Biol. 2017;18:533–547. doi: 10.1038/nrm.2017.60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabriel G. C. Young C. B. Lo C. W. Semin. Cell Dev. Biol. 2021;110:2–10. doi: 10.1016/j.semcdb.2020.04.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gravesande K. S. V. Omran H. Ann. Med. 2005;37:439–449. doi: 10.1080/07853890510011985. [DOI] [PubMed] [Google Scholar]
- Purcell E. M. Am. J. Phys. 1977;45:3–11. doi: 10.1119/1.10903. [DOI] [Google Scholar]
- Whitesides G. M. Nature. 2006;442:368–373. doi: 10.1038/nature05058. [DOI] [PubMed] [Google Scholar]
- Sackmann E. K. Fulton A. L. Beebe D. J. Nature. 2014;507:181–189. doi: 10.1038/nature13118. [DOI] [PubMed] [Google Scholar]
- Ravetto A. Anderson P. Bouten C. den Toonder J. SM Journal of Biomedical Engineering. 2017;3:1016. [Google Scholar]
- Kim D.-H. Wong P. K. Park J. Levchenko A. Sun Y. Annu. Rev. Biomed. Eng. 2009;11:203–233. doi: 10.1146/annurev-bioeng-061008-124915. [DOI] [PubMed] [Google Scholar]
- Beebe D. J. Ingber D. E. den Toonder J. Lab Chip. 2013;13:3447–3448. doi: 10.1039/C3LC90080K. [DOI] [PubMed] [Google Scholar]
- van de Stolpe A. den Toonder J. Lab Chip. 2013;13:3449–3470. doi: 10.1039/C3LC50248A. [DOI] [PubMed] [Google Scholar]
- Bhatia S. N. Ingber D. E. Nat. Biotechnol. 2014;32:760–772. doi: 10.1038/nbt.2989. [DOI] [PubMed] [Google Scholar]
- Laser D. J. Santiago J. G. J. Micromech. Microeng. 2004;14:R35–R64. doi: 10.1088/0960-1317/14/6/R01. [DOI] [Google Scholar]
- Oh K. Ahn C. J. Micromech. Microeng. 2006;16:13–39. doi: 10.1088/0960-1317/16/5/R01. [DOI] [Google Scholar]
- Nguyen N.-T. Wu Z. J. Micromech. Microeng. 2004;15:R1–R16. doi: 10.1088/0960-1317/15/2/R01. [DOI] [Google Scholar]
- Mark D. Haeberle S. Roth G. von Stetten F. Zengerle R. Chem. Soc. Rev. 2010;39:1153–1182. doi: 10.1039/B820557B. [DOI] [PubMed] [Google Scholar]
- Unger M. A. Chou H. P. Thorsen T. Scherer A. Quake S. R. Science. 2000;288:113–116. doi: 10.1126/science.288.5463.113. [DOI] [PubMed] [Google Scholar]
- Melin J. Quake S. R. Annu. Rev. Biophys. Biomol. Struct. 2007;36:213–231. doi: 10.1146/annurev.biophys.36.040306.132646. [DOI] [PubMed] [Google Scholar]
- Wang Y. Zhao J. Zhu Y. Dong S. Liu Y. Sun Y. Qian L. Yang W. Cao Z. Microsyst. Nanoeng. 2021;7:65. doi: 10.1038/s41378-021-00291-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orbay S. Ozcelik A. Bachman H. Huang T. J. J. Micromech. Microeng. 2018;28:025012. doi: 10.1088/1361-6439/aaa0ae. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong X. Lum G. Z. Hu W. Zhang R. Ren Z. Onck P. R. Sitti M. Sci. Adv. 2020;6:eabc9323. doi: 10.1126/sciadv.abc9323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babataheri A. Roper M. Fermigier M. Du Roure O. J. Fluid Mech. 2011;678:5–13. doi: 10.1017/S002211201100005X. [DOI] [Google Scholar]
- Belardi J. Schorr N. Prucker O. Rühe J. Adv. Funct. Mater. 2011;21:3314–3320. doi: 10.1002/adfm.201100787. [DOI] [Google Scholar]
- Baltussen M. Anderson P. Bos F. den Toonder J. Lab Chip. 2009;9:2326–2331. doi: 10.1039/B901660K. [DOI] [PubMed] [Google Scholar]
- Gorissen B. de Volder M. Reynaerts D. Lab Chip. 2015;15:4348–4355. doi: 10.1039/C5LC00775E. [DOI] [PubMed] [Google Scholar]
- Milana E. Gorissen B. Peerlinck S. De Volder M. Reynaerts D. Adv. Funct. Mater. 2019;29:1900462. doi: 10.1002/adfm.201900462. [DOI] [Google Scholar]
- Milana E. Zhang R. Vetrano M. R. Peerlinck S. De Volder M. Onck P. R. Reynaerts D. Gorissen B. Sci. Adv. 2020;6:eabd2508. doi: 10.1126/sciadv.abd2508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang R. den Toonder J. Onck P. R. Phys. Fluids. 2021;33:092009. doi: 10.1063/5.0054929. [DOI] [Google Scholar]
- He X. Aizenberg M. Kuksenok O. Zarzar L. D. Shastri A. Balazs A. C. Aizenberg J. Nature. 2012;487:214–218. doi: 10.1038/nature11223. [DOI] [PubMed] [Google Scholar]
- Pokroy B. Kang S. H. Mahadevan L. Aizenberg J. Science. 2009;323:237–240. doi: 10.1126/science.1165607. [DOI] [PubMed] [Google Scholar]
- Cox R. G. J. Fluid Mech. 1970;44:791–810. doi: 10.1017/S002211207000215X. [DOI] [Google Scholar]
- van Leeuwen J. Aerts P. Lowe C. P. Philos. Trans. R. Soc. London, Ser. B. 2003;358:1543–1550. doi: 10.1098/rstb.2003.1340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowes F. J. Proc. R. Soc. London, Ser. A. 1974;337:555–567. [Google Scholar]
- Ul Islam T. Bellouard Y. den Toonder J. M. Proc. Natl. Acad. Sci. U. S. A. 2021;118:35. doi: 10.1073/pnas.2104930118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osborn J. A. Phys. Rev. 1945;67:351–357. doi: 10.1103/PhysRev.67.351. [DOI] [Google Scholar]
- Gauger E. M. Downton M. T. Stark H. Eur. Phys. J. E: Soft Matter Biol. Phys. 2009;28:231–242. doi: 10.1140/epje/i2008-10388-1. [DOI] [PubMed] [Google Scholar]
- Hanasoge S. Ballard M. Hesketh P. J. Alexeev A. Lab Chip. 2017;17:3138–3145. doi: 10.1039/C7LC00556C. [DOI] [PubMed] [Google Scholar]
- Khaderi S. N. Craus C. Hussong J. Schorr N. Belardi J. Westerweel J. Prucker O. Rühe J. Den Toonder J. Onck P. Lab Chip. 2011;11:2002–2010. doi: 10.1039/C0LC00411A. [DOI] [PubMed] [Google Scholar]
- Khaderi S. Den Toonder J. Onck P. Langmuir. 2012;28:7921–7937. doi: 10.1021/la300169f. [DOI] [PubMed] [Google Scholar]
- Hanasoge S. Hesketh P. J. Alexeev A. Soft Matter. 2018;14:3689–3693. doi: 10.1039/C8SM00549D. [DOI] [PubMed] [Google Scholar]
- Hanasoge S. Hesketh P. J. Alexeev A. ACS Appl. Mater. Interfaces. 2020;12:46963–46971. doi: 10.1021/acsami.0c13102. [DOI] [PubMed] [Google Scholar]
- Zhang S. Cui Z. Wang Y. den Toonder J. M. J. Lab Chip. 2020;20:3569–3581. doi: 10.1039/D0LC00610F. [DOI] [PubMed] [Google Scholar]
- Ozaki Y., Ohyama T., Yasuda T. and Shimoyama I., Proceedings IEEE Thirteenth Annual International Conference on Micro Electro Mechanical Systems (Cat. No. 00CH36308), 2000, pp. 531–536
- Fan Z. Chen J. Zou J. Bullen D. Liu C. Delcomyn F. J. Micromech. Microeng. 2002;12:655. doi: 10.1088/0960-1317/12/5/322. [DOI] [Google Scholar]
- Chen N. Tucker C. Engel J. M. Yang Y. Pandya S. Liu C. J. Microelectromech. Syst. 2007;16:999–1014. [Google Scholar]
- McGary P. D. Tan L. Zou J. Stadler B. J. Downey P. R. Flatau A. B. J. Appl. Phys. 2006;99:08B310. doi: 10.1063/1.2167332. [DOI] [Google Scholar]
- Glazer P. Leuven J. An H. Lemay S. Mendes E. Adv. Funct. Mater. 2013;23:2964–2970. doi: 10.1002/adfm.201203212. [DOI] [Google Scholar]
- Li M. Kim T. Guidetti G. Wang Y. Omenetto F. G. Adv. Mater. 2020;32:2004147. doi: 10.1002/adma.202004147. [DOI] [PubMed] [Google Scholar]
- Dai B. Li S. Xu T. Wang Y. Zhang F. Gu Z. Wang S. ACS Appl. Mater. Interfaces. 2018;10:42979–42984. doi: 10.1021/acsami.8b13419. [DOI] [PubMed] [Google Scholar]
- Wu Y.-A. Panigrahi B. Chen C.-Y. Microsyst. Technol. 2017;23:5893–5902. doi: 10.1007/s00542-017-3428-3. [DOI] [Google Scholar]
- Wu Y.-A. Panigrahi B. Lu Y.-H. Chen C.-Y. Micromachines. 2017;8:260. doi: 10.3390/mi8090260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marume R. Tsumori F. Kudo K. Osada T. Shinagawa K. Jpn. J. Appl. Phys. 2017;56:06GN15. doi: 10.7567/JJAP.56.06GN15. [DOI] [Google Scholar]
- Kamat A. M. Zheng X. Jayawardhana B. Kottapalli A. G. P. Nanotechnology. 2020;32:095501. doi: 10.1088/1361-6528/abcc96. [DOI] [PubMed] [Google Scholar]
- Wang Y. Chen X. Sun K. Li K. Zhang F. Dai B. Shen J. Hu G. Wang S. Sci. China Mater. 2019;62:236–244. doi: 10.1007/s40843-018-9302-4. [DOI] [Google Scholar]
- Breidenich J. L. Wei M. C. Clatterbaugh G. V. Benkoski J. J. Keng P. Y. Pyun J. Soft Matter. 2012;8:5334–5341. doi: 10.1039/C2SM25096A. [DOI] [Google Scholar]
- Demirörs A. F. Aykut S. Ganzeboom S. Meier Y. A. Hardeman R. de Graaf J. Mathijssen A. J. Poloni E. Carpenter J. A. Ünlü C. et al. . Adv. Sci. 2021:2102510. doi: 10.1002/advs.202102510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J. A.-C. Evans B. A. Tracy J. B. Adv. Mater. Technol. 2020;5:2000147. doi: 10.1002/admt.202000147. [DOI] [Google Scholar]
- Zhou Q. Ji B. Wei Y. Hu B. Gao Y. Xu Q. Zhou J. Zhou B. J. Mater. Chem. A. 2019;7:27334–27346. doi: 10.1039/C9TA10489E. [DOI] [Google Scholar]
- Sun L. Zheng Y. Front. Mater. Sci. 2015;9:178–184. doi: 10.1007/s11706-015-0291-y. [DOI] [Google Scholar]
- Kokot G. Vilfan M. Osterman N. Vilfan A. Kavčič B. Poberaj I. Babič D. Biomicrofluidics. 2011;5:034103. doi: 10.1063/1.3608139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugioka H. Ishikawa M. AIP Adv. 2020;10:055302. doi: 10.1063/1.5143700. [DOI] [Google Scholar]
- Shinoda H. Azukizawa S. Maeda K. Tsumori F. J. Electrochem. Soc. 2019;166:B3235. doi: 10.1149/2.0361909jes. [DOI] [Google Scholar]
- Azukizawa S. Shinoda H. Tokumaru K. Tsumori F. J. Photopolym. Sci. Technol. 2018;31:139–144. doi: 10.2494/photopolymer.31.139. [DOI] [Google Scholar]
- Jeong W. Jeong S.-M. Lim T. Han C.-Y. Yang H. Lee B. W. Park S. Y. Ju S. ACS Appl. Mater. Interfaces. 2019;11:35286–35293. doi: 10.1021/acsami.9b09571. [DOI] [PubMed] [Google Scholar]
- Kim C. Y., Lee H. S., Cho Y. H., Joh C., Choi P. and Park S. J., Smart Sensors, Actuators, and MEMS V, 2011, p. 80662F
- Hu X. Jiang Y. Ma Z. Xu Y. Zhang D. Sensors. 2019;19:5384. doi: 10.3390/s19245384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Timonen J. V. Johans C. Kontturi K. Walther A. Ikkala O. Ras R. H. ACS Appl. Mater. Interfaces. 2010;2:2226–2230. doi: 10.1021/am100244x. [DOI] [PubMed] [Google Scholar]
- Rossiter J., Stoimenov B. and Mukai T., 2006 IEEE International Symposium on MicroNanoMechanical and Human Science, 2006, pp. 1–6
- Downton M. Stark H. EPL. 2009;85:44002. doi: 10.1209/0295-5075/85/44002. [DOI] [Google Scholar]
- Khaderi S. Baltussen M. Anderson P. Ioan D. Den Toonder J. Onck P. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2009;79:046304. doi: 10.1103/PhysRevE.79.046304. [DOI] [PubMed] [Google Scholar]
- Machemer H. J. Exp. Biol. 1972;57:239–259. doi: 10.1242/jeb.57.1.239. [DOI] [PubMed] [Google Scholar]
- Osterman N. Vilfan A. Proc. Natl. Acad. Sci. U. S. A. 2011;108:15727–15732. doi: 10.1073/pnas.1107889108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elgeti J. Gompper G. Proc. Natl. Acad. Sci. U. S. A. 2013;110:4470–4475. doi: 10.1073/pnas.1218869110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y. Chen W. Zeng W. Lu Z. Zhou X. Cell Death Dis. 2020;11:1–13. doi: 10.1038/s41419-019-2182-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oh K. Chung J.-H. Devasia S. Riley J. J. Lab Chip. 2009;9:1561–1566. doi: 10.1039/B817409A. [DOI] [PubMed] [Google Scholar]
- Oh K. Smith B. Devasia S. Riley J. J. Chung J.-H. Microfluid. Nanofluid. 2010;9:645–655. doi: 10.1007/s10404-010-0578-3. [DOI] [Google Scholar]
- Chen C.-Y. Chen C.-Y. Lin C.-Y. Hu Y.-T. Lab Chip. 2013;13:2834–2839. doi: 10.1039/C3LC50407G. [DOI] [PubMed] [Google Scholar]
- Chen C.-Y. Hsu C.-C. Mani K. Panigrahi B. Chem. Eng. Process.: Process Intesif. 2016;99:33–40. doi: 10.1016/j.cep.2015.10.023. [DOI] [Google Scholar]
- Kirschner C. M. Brennan A. B. Annu. Rev. Mater. Res. 2012;42:211–229. doi: 10.1146/annurev-matsci-070511-155012. [DOI] [Google Scholar]
- Ben S. Tai J. Ma H. Peng Y. Zhang Y. Tian D. Liu K. Jiang L. Adv. Funct. Mater. 2018;28:1706666. doi: 10.1002/adfm.201706666. [DOI] [Google Scholar]
- Ben S. Yao J. Ning Y. Zhao Z. Zha J. Tian D. Liu K. Jiang L. Sci. China: Chem. 2020;63:347–353. doi: 10.1007/s11426-019-9660-5. [DOI] [Google Scholar]
- Ben S. Zhou T. Ma H. Yao J. Ning Y. Tian D. Liu K. Jiang L. Adv. Sci. 2019;6:1900834. doi: 10.1002/advs.201900834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tripathi A. Shum H. Balazs A. C. Soft Matter. 2014;10:1416–1427. doi: 10.1039/C3SM52156G. [DOI] [PubMed] [Google Scholar]
- Branscomb J. Alexeev A. Soft Matter. 2010;6:4066–4069. doi: 10.1039/C0SM00185F. [DOI] [Google Scholar]
- Masoud H. Alexeev A. Soft Matter. 2011;7:8702–8708. doi: 10.1039/C1SM05423F. [DOI] [Google Scholar]
- Ghosh R. Buxton G. A. Usta O. B. Balazs A. C. Alexeev A. Langmuir. 2010;26:2963–2968. doi: 10.1021/la902926w. [DOI] [PubMed] [Google Scholar]
- Dayal P. Kuksenok O. Bhattacharya A. Balazs A. C. J. Mater. Chem. 2012;22:241–250. doi: 10.1039/C1JM13787E. [DOI] [Google Scholar]
- Tripathi A. Bhattacharya A. Balazs A. C. Langmuir. 2013;29:4616–4621. doi: 10.1021/la400318f. [DOI] [PubMed] [Google Scholar]
- Bhattacharya A. Buxton G. A. Usta O. B. Balazs A. C. Langmuir. 2012;28:3217–3226. doi: 10.1021/la204845v. [DOI] [PubMed] [Google Scholar]
- Al-Azawi A. Hörenz C. Tupasela T. Ikkala O. Jokinen V. Franssila S. Ras R. H. AIP Adv. 2020;10:085021. doi: 10.1063/5.0012852. [DOI] [PubMed] [Google Scholar]
- Song Y. Jiang S. Li G. Zhang Y. Wu H. Xue C. You H. Zhang D. Cai Y. Zhu J. et al. . ACS Appl. Mater. Interfaces. 2020;12:42264–42273. doi: 10.1021/acsami.0c10034. [DOI] [PubMed] [Google Scholar]
- Cao M. Jin X. Peng Y. Yu C. Li K. Liu K. Jiang L. Adv. Mater. 2017;29:1606869. doi: 10.1002/adma.201606869. [DOI] [PubMed] [Google Scholar]
- Zhou Y. Huang S. Tian X. Adv. Funct. Mater. 2020;30:1906507. doi: 10.1002/adfm.201906507. [DOI] [Google Scholar]
- Jiang S. Hu Y. Wu H. Li R. Zhang Y. Chen C. Xue C. Xu B. Zhu W. Li J. et al. . Nano Lett. 2020;20:7519–7529. doi: 10.1021/acs.nanolett.0c02997. [DOI] [PubMed] [Google Scholar]
- Kim J. H. Kang S. M. Lee B. J. Ko H. Bae W.-G. Suh K. Y. Kwak M. K. Jeong H. E. Sci. Rep. 2015;5:1–10. doi: 10.1038/srep17843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang C. Wu L. Li G. ACS Appl. Mater. Interfaces. 2018;10:20150–20158. doi: 10.1021/acsami.8b04190. [DOI] [PubMed] [Google Scholar]
- Wang H. Zhang Z. Wang Z. Liang Y. Cui Z. Zhao J. Li X. Ren L. ACS Appl. Mater. Interfaces. 2019;11:28478–28486. doi: 10.1021/acsami.9b07941. [DOI] [PubMed] [Google Scholar]
- Mayne R. Whiting J. G. Wheway G. Melhuish C. Adamatzky A. BioSystems. 2017;156:46–52. doi: 10.1016/j.biosystems.2017.04.001. [DOI] [PubMed] [Google Scholar]
- Xue C. Chen S. Zhang W. Zhang B. Zhang G. Qiao H. Microelectron. J. 2007;38:1021–1026. doi: 10.1016/j.mejo.2007.09.008. [DOI] [Google Scholar]
- Guojun Z. Panpan W. Linggang G. Jijun X. Wendong Z. Microelectron. J. 2011;42:815–819. doi: 10.1016/j.mejo.2011.01.002. [DOI] [Google Scholar]
- Qualtieri A. Rizzi F. Todaro M. T. Passaseo A. Cingolani R. De Vittorio M. Microelectron. Eng. 2011;88:2376–2378. doi: 10.1016/j.mee.2011.02.091. [DOI] [Google Scholar]
- Guan L. Zhang G. Xu J. Xue C. Zhang W. Xiong J. Sens. Actuators, A. 2012;188:35–40. doi: 10.1016/j.sna.2012.01.018. [DOI] [Google Scholar]
- Bora M. Kottapalli A. G. P. Miao J. Triantafyllou M. S. NPG Asia Mater. 2017;9:e440. doi: 10.1038/am.2017.183. [DOI] [Google Scholar]
- Liu W. Li F. Stefanini C. Chen D. Dario P. Rob. Auton. Syst. 2010;58:1138–1148. doi: 10.1016/j.robot.2010.06.006. [DOI] [Google Scholar]
- Slinker K. A. Kondash C. Dickinson B. T. Baur J. W. Adv. Mater. Technol. 2016;1:1600176. doi: 10.1002/admt.201600176. [DOI] [Google Scholar]
- Sengupta D. Trap D. Kottapalli A. G. P. Nanomaterials. 2020;10:211. doi: 10.3390/nano10020211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamat A. M. Pei Y. Kottapalli A. G. Nanomaterials. 2019;9:954. doi: 10.3390/nano9070954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiting L., Bilsay S., Cesare S., Arianna M., Fei L., Dajing C., Paolo D., Metin S. and Xin F., 2008 IEEE International Conference on Robotics and Biomimetics, 2009, pp. 49–54
- Asadnia M. Kottapalli A. G. P. Karavitaki K. D. Warkiani M. E. Miao J. Corey D. P. Triantafyllou M. Sci. Rep. 2016;6:1–13. doi: 10.1038/s41598-016-0001-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi S. Geng W. Bi K. He J. Hou X. Mu J. Li F. Chou X. Sens. Actuators, A. 2020;313:112203. doi: 10.1016/j.sna.2020.112203. [DOI] [Google Scholar]
- Krijnen G. J. Dijkstra M. van Baar J. J. Shankar S. S. Kuipers W. J. de Boer R. J. Altpeter D. Lammerink T. S. Wiegerink R. Nanotechnology. 2006;17:S84. doi: 10.1088/0957-4484/17/4/013. [DOI] [PubMed] [Google Scholar]
- Dagamseh A. Wiegerink R. J. Lammerink T. S. Krijnen G. J. Bioinspiration Biomimetics. 2012;7:046009. doi: 10.1088/1748-3182/7/4/046009. [DOI] [PubMed] [Google Scholar]
- Izadi N. de Boer M. J. Berenschot J. W. Krijnen G. J. J. Micromech. Microeng. 2010;20:085041. doi: 10.1088/0960-1317/20/8/085041. [DOI] [Google Scholar]
- Wissman J. P. Sampath K. Freeman S. E. Rohde C. A. Sensors. 2019;19:2639. doi: 10.3390/s19112639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain R., McCluskey F. P. and Flatau A. B., IEEE Transactions on Components, Packaging and Manufacturing Technology, 2011
- Alfadhel A. Li B. Zaher A. Yassine O. Kosel J. Lab Chip. 2014;14:4362–4369. doi: 10.1039/C4LC00821A. [DOI] [PubMed] [Google Scholar]
- Engel J., Chen J., Chen N., Pandya S. and Liu C., SENSORS, 2005, IEEE, 2005, p. 4 [Google Scholar]
- Lei H., Li W. and Tan X., Electroactive Polymer Actuators and Devices (EAPAD) 2012, 2012, p. 83401A
- Guo X. Yang B. Li C. Liang Z. J. Micromech. Microeng. 2020;31:025001. doi: 10.1088/1361-6439/abce9d. [DOI] [Google Scholar]
- Alfadhel A., Li B. and Kosel J., SENSORS, 2014, IEEE, 2014, pp. 2066–2069 [Google Scholar]
- Schroeder P. Schotter J. Shoshi A. Eggeling M. Bethge O. Hütten A. Brückl H. Bioinspiration Biomimetics. 2011;6:046007. doi: 10.1088/1748-3182/6/4/046007. [DOI] [PubMed] [Google Scholar]
- Downey P. R., Flatau A. B., McGary P. D. and Stadler B. J., Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2008, 2008, p. 69320P
- Jain R., McCluskey F. P., Flatau A. B. and Stadler B. J., Nanosensors, Microsensors, and Biosensors and Systems 2007, 2007, p. 652805
- Hein M. A. Maqableh M. M. Delahunt M. J. Tondra M. Flatau A. B. Shield C. K. Stadler B. J. IEEE Trans. Magn. 2012;49:191–196. [Google Scholar]
- Chen P. Zhang G. Yang X. Ji S. Liang X. Lv T. Zhang X. Zhu S. Shang Z. Zhang W. Sens. Actuators, A. 2021;331:112575. doi: 10.1016/j.sna.2021.112575. [DOI] [Google Scholar]
- DiSabatino Jr R. J., McCluskey F. P., Flatau A. B. and Stadler B. J., Smart Structures and Materials 2006: Smart Electronics, MEMS, BioMEMS, and Nanotechnology, 2006, p. 617217
- Judith R. M. Fisher J. K. Spero R. C. Fiser B. L. Turner A. Oberhardt B. Taylor R. M. Falvo M. R. Superfine R. Lab Chip. 2015;15:1385–1393. doi: 10.1039/C4LC01478B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abbott J. J. Ergeneman O. Kummer M. P. Hirt A. M. Nelson B. J. IEEE Trans. Robot. 2007;23:1247–1252. [Google Scholar]
- Cortez R. SIAM J. Sci. Comput. 2001;23:1204–1225. doi: 10.1137/S106482750038146X. [DOI] [Google Scholar]
- Ding Y. Nawroth J. C. McFall-Ngai M. J. Kanso E. J. Fluid Mech. 2014;743:124–140. doi: 10.1017/jfm.2014.36. [DOI] [Google Scholar]
- Blake J. Proc. Cambridge Philos. Soc. 1971:303–310. doi: 10.1017/S0305004100049902. [DOI] [Google Scholar]
- Blake J. J. Fluid Mech. 1972;55:1–23. doi: 10.1017/S0022112072001612. [DOI] [Google Scholar]
- Gauger E. Stark H. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2006;74:021907. doi: 10.1103/PhysRevE.74.021907. [DOI] [PubMed] [Google Scholar]
- Alexeev A. Yeomans J. Balazs A. C. Langmuir. 2008;24:12102–12106. doi: 10.1021/la801907x. [DOI] [PubMed] [Google Scholar]
- Alexeev A. Ghosh R. Buxton G. A. Usta O. B. Balazs A. C. Proc. ASME Global Congr. NanoEng. Med. Biol. 2010:43–44. [Google Scholar]
- Bhattacharya A. Balazs A. C. Soft Matter. 2013;9:3945–3955. doi: 10.1039/C3SM00028A. [DOI] [Google Scholar]
- Khaderi S. Den Toonder J. Onck P. Biomicrofluidics. 2012;6:014106. doi: 10.1063/1.3676068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khaderi S. N. den Toonder J. M. Onck P. R. Adv. Appl. Mech. 2015;48:1–78. [Google Scholar]
- Lanczos C., The variational principles of mechanics, University of Toronto press, 2020 [Google Scholar]
- Khaderi S. Baltussen M. Anderson P. Den Toonder J. Onck P. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2010;82:027302. doi: 10.1103/PhysRevE.82.027302. [DOI] [PubMed] [Google Scholar]
- Khaderi S. Hussong J. Westerweel J. den Toonder J. Onck P. RSC Adv. 2013;3:12735–12742. doi: 10.1039/C3RA42068J. [DOI] [Google Scholar]
- Khaderi S. Onck P. J. Fluid Mech. 2012;708:303–328. doi: 10.1017/jfm.2012.306. [DOI] [Google Scholar]
- Namdeo S. Khaderi S. Onck P. Proc. R. Soc. A. 2014;470:20130547. doi: 10.1098/rspa.2013.0547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shanko E. van de Burgt Y. Anderson P. den Toonder J. Micromachines. 2019;10:731. doi: 10.3390/mi10110731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quaranta G. Aubin M. Tam D. Phys. Rev. Lett. 2015;115:year. doi: 10.1103/PhysRevLett.115.238101. [DOI] [PubMed] [Google Scholar]
- Pedersoli L. Zhang S. Briatico-Vangosa F. Petrini P. Cardinaels R. den Toonder J. Peneda Pacheco D. Biotechnol. Bioeng. 2021;118:3898–3913. doi: 10.1002/bit.27866. [DOI] [PubMed] [Google Scholar]
- Luo W. Yi H. Taylor J. Li J.-D. Chi F. Todd N. W. Lin X. Ren D. Chen P. Sci. Rep. 2017;7:45870. doi: 10.1038/srep45870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen D. Norris D. Ventikos Y. Med. Eng. Phys. 2011;33:857–867. doi: 10.1016/j.medengphy.2010.10.020. [DOI] [PubMed] [Google Scholar]
- Verburg T. Schaap A. Zhang S. den Toonder J. Wang Y. Biotechnol. Bioeng. 2021;118:2472–2481. doi: 10.1002/bit.27756. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.