Abstract
Variety identification of seeds is critical for assessing variety purity and ensuring crop yield. In this paper, a novel method based on hyperspectral imaging (HSI) and deep convolutional neural network (DCNN) was proposed to discriminate the varieties of oat seeds. The representation ability of DCNN was also investigated. The hyperspectral images with a spectral range of 874–1734 nm were primarily processed by principal component analysis (PCA) for exploratory visual distinguishing. Then a DCNN trained in an end-to-end manner was developed. The deep spectral features automatically learnt by DCNN were extracted and combined with traditional classifiers (logistic regression (LR), support vector machine with RBF kernel (RBF_SVM) and linear kernel (LINEAR_SVM)) to construct discriminant models. Contrast models were built based on the traditional classifiers using full wavelengths and optimal wavelengths selected by the second derivative (2nd derivative) method. The comparison results showed that all DCNN-based models outperformed the contrast models. DCNN trained in an end-to-end manner achieved the highest accuracy of 99.19% on the testing set, which was finally employed to visualize the variety classification. The results demonstrated that the deep spectral features with outstanding representation ability enabled HSI together with DCNN to be a reliable tool for rapid and accurate variety identification, which would help to develop an on-line system for quality detection of oat seeds as well as other grain seeds.
The excellent representation ability of deep spectral features enables hyperspectral imaging combined with deep convolutional neural network to be a powerful tool for large-scale seeds detection in modern seed industry.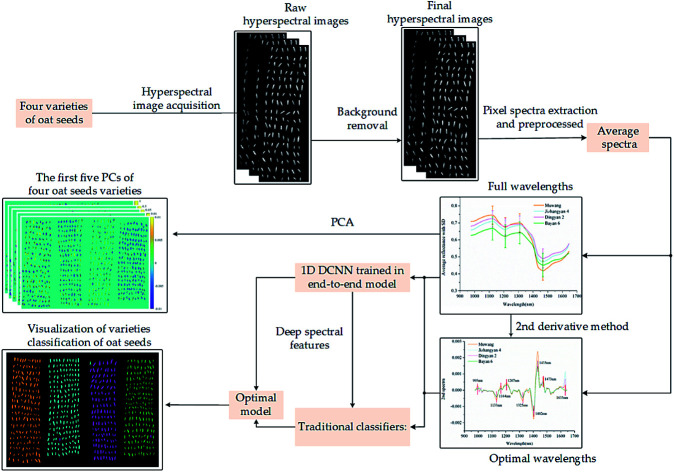
1. Introduction
As a widely cultivated cereal grain, oat (Avena sativa L.) has extremely high nutritional and medical value, and it is also utilized as animal feed. The plentiful chemical components such as dietary fiber and protein in oats can clear the intestinal waste and are friendly to most celiac individuals.1,2 The content of these chemical components in oats varies greatly due to many genetic and environmental factors, such as fertilization, rainfall, disease and management during storage, and variety is the determinate factor.3 In addition, the growth and the yield of oats are greatly influenced by the variety. However, the variety purity of oat seeds cannot be guaranteed because mixture between different varieties may occur during cultivation, harvest or storage. Therefore, strengthening the evaluation of variety purity before oat seeding is of great importance for obtaining the expected quality and yield, variety identification being a key.
Currently, the morphological detection method which is based on the appearance characteristics of seeds is commonly utilized to identify seed varieties. This manual inspection method is not only time consuming but also subjective. Other more accurate methods such as protein electrophoresis and DNA molecular marker technologies require professional knowledge and complex operations.4,5 Moreover, the treatment process is sample damaged and reagent dependent. These disadvantages limit their application in large-scale samples detection in modern seed industry. Thus, it is compelling to develop an automatic method capable of distinguishing oat seeds varieties in a rapid and accurate manner.
In recent years, spectroscopic and imaging technologies have been used as a rapid, non-destructive alternative to analyse and detect the chemical quality of agricultural products. Hyperspectral imaging (HSI) being an emerging technique has drawn raising attentions from researchers in the field of analytical chemistry due to the capacity of acquiring spectral and spatial information simultaneously.6,7 This leads to a derived advantage, namely visualization of category and chemical composition distribution of samples through combining the spectrum and the corresponding spatial location of each pixel in HSI image. In addition, batch detection is another superiority, making HSI very suitable to process large-scale samples. Because of these advantages, HSI has been successfully applied in various tasks involving seeds, such as classification of seed varieties, detection of seed vigor, identification of seed diseases.8–10 As far as we know, no research has reported the application of HSI on varieties identification of oat seeds.
In this study, rapid varieties discrimination of oat seeds using HSI was investigated. However, hyperspectral image is a cube matrix containing massive data. In order to extract useful information from such kind of data and obtain satisfying analytical results, variable selection methods such as second derivative (2nd derivative) method, principal component analysis (PCA) loadings method and successive projections algorithm (SPA) were often used to select discriminative wavelengths.11,12 These wavelengths often provided certain spectral fingerprint information, which reflected the chemical composition difference between different samples. Classical machine learning algorithms such as support vector machine (SVM), multiple logistic regression (MLR) and partial least squares discriminant analysis (PLS-DA) were usually employed to generate predictive results based on the selected optimal wavelengths.13,14
Deep learning (DL), a research focus in machine learning, has tremendously improved the state-of-art results in various data analysis tasks. DL originally called representative learning can represent data by automatically learning abstract deep features in a deep network. Deep convolutional neural network (DCNN), a deep structure consisting of multiple convolutional layers and pooling layers, enables end-to-end analysis of data and was widely used in various visual tasks.15,16 In the field of spectral analysis, DCNN was also gradually utilized in nitrogen concentration prediction of oilseed rape leaf, disease detection of wheat Fusarium head blight and crop classification in remote sensing images.17–19 Our previous research has also confirmed that DCNN can achieve satisfying results in Chrysanthemum varieties discrimination.20 However, all DCNNs ran in end-to-end manner in these studies, that is to say, data representation and classification were concentrated in one system. In fact, DCNN is essentially a deep representation of data, which can be combined with traditional classifiers.
Therefore, the main objectives of this study was to explore the feasibility of combining HSI and DCNN for varieties identification of oat seeds and further deeply investigate the representation ability of DCNN. Our specific objectives were to: (1) develop a suitable DCNN with end-to-end learning mode using full wavelengths, (2) select efficient wavelengths that benefit for variety identification, (3) compare the results of different discriminant models using deep spectral features and selected efficient wavelengths, and (4) visualize the classification results of oat seeds using the optimal model for variety purity assessment.
2. Materials and methods
2.1. Oat seeds samples
Four varieties of oat seeds named MuWang, Jizhangyan 4, Dingyan 2 and Bayan 6 were provided by Academy of Agricultural and Animal Sciences, Inner Mongolia, China. All seeds were harvested and nature dried in 2017. Before experiment, the seeds with poor conditions, such as damaged, moldy or shriveled were picked and removed. In total, 14 846 plump oat seeds (3519 of MuWang, 4250 of Jizhangyan 4, 3739 of Dingyan 2 and 3338 of Bayan 6) were used for hyperspectral images collection. To facilitate multivariate analysis and expression, oat seeds were encoded as 1, 2, 3, 4 for MuWang, Jizhangyan 4, Dingyan 2 and Bayan 6, respectively.
2.2. Hyperspectral image acquisition and correction
A line-scanning near-infrared HSI system with a resolution of 326 × 256 (spatial × spectral) pixels was set up in a laboratory and employed to collect the hyperspectral images of oat seeds. Multiple interconnected subcomponents organically formed this system: an ImSpector N17E imaging spectrograph (Spectral Imaging Ltd., Oulu, Finland) with a spectral range from 874.41 nm to 1733.91 nm, a Xeva 992 CCD camera equipped with an OLES22 lens (Spectral Imaging Ltd., Oulu, Finland), two 150 W tungsten halogen lamps (3900e Lightsource; Illumination Technologies Inc.; West Elbridge, NY, USA) placed symmetrically under the camera, and a miniature conveyer belt driven by a stepped motor (Isuzu Optics Corp., Taiwan, China). The whole system was located in a dark room and controlled by a data acquisition and preprocessing software (Xenics N17E, Isuzu Optics Corp., Taiwan, China) installed in a computer. The hyperspectral image of oat seeds acquired by this system was a three-dimensional cube matrix, in which each pixel corresponded to a spectral curve containing 256 wavelengths as well as a spatial geometric position.
A black plate with a reflectance close to 0 was placed on the conveyer belt and the oat seeds were placed on the plate. Three system parameters, the exposure time of the camera, the height of the camera lens from the black plate and the speed of the conveyer belt movement were set to 3 ms, 15.2 cm and 11.5 mm s−1, respectively, to collect clear and undistorted hyperspectral images.
Before collecting the oat seeds images, the white board correction and the black board correction were carried out to obtain the hyperspectral image of a white Teflon tile with a reflectance close to 100% and the hyperspectral image of a black cloth with a reflectance close to 0. Using these two reference images combined with the original hyperspectral image of oat seeds, the corrected hyperspectral image could be obtained by calculating the following formula, which removes the influence of dark current and other factors.
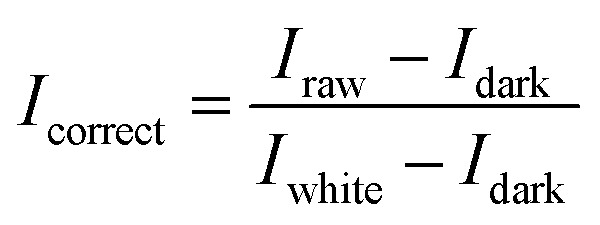 |
1 |
where Iraw represents the original hyperspectral image of oat seeds, Iwhite represents the white reference image, Idark represents the black reference image, Icorrect represents the corrected image.
2.3. Spectral data extraction and pretreatment
A threshold segmentation method was firstly carried out to separate oat seeds from black background. Then, the spectra of all pixels in each oat seed region, the region of the interest (ROI), were extracted. In order to reduce the noise caused by the instability of HSI system at the beginning and end of the image acquisition, a total of 56 wavelengths were removed from the head and tail of the spectral curves. Thus, the middle 200 wavelengths from 975 nm to 1646 nm were retained for the spectra of all pixels. These spectra were then processed one by one by wavelet transform (WT) with a basis function of Daubechies 6 and a decomposition scale of 3 to further eliminate the random noise. Finally, the average spectrum of each ROI was calculated and utilized as a sample in dataset. For the purpose of multivariate analysis, the dataset of each variety was randomly divided into a training set and a testing set at a ratio of 3 : 1. Thus, the average spectra of 11 134 oat seeds constituted the final training set, and the rest 3712 seeds formed the final testing set.
3. Data analysis
3.1. Principal component analysis
As a popular statistical analysis method in pattern recognition, PCA is often used for compression and visualization of high-dimensional data. The essence of PCA is a data transformation which is not intended to optimize class separability. The main idea of PCA is to find an orthogonal projection matrix to transform original data matrix into a new feature space so that the sample variance maximum. The variables in the new feature space also known as principal components (PCs) are linear combinations of the variables in the original data matrix and are orthogonal to each other. In general, the first few PCs reflect most of the variance in original data. Just because of this, these PCs are often selected to construct a low-dimensional matrix which is regarded as a new representation of the original high-dimensional data matrix. Therefore, PCA can extract the key information reflecting the internal structure of data through this way, which not only reduces redundancy but also removes noise. In addition, the score images of the first few PCs can also be utilized to explore the pattern differences between different samples. As a hyperspectral image consists of hundreds of spectral wavelengths which contain a lot of redundancy and collinear information, PCA is very suitable to analyse this kind of data. In this study, PCA was introduced to explore the pattern differences between different varieties of oat seeds in hyperspectral images.
3.2. Optimal wavelengths selection
As mentioned in previous section, hyperspectral images contain a mass of redundant information. In order to facilitate the spectra analysis and improve the prediction performance, variable selection methods are usually employed to pick the effective wavelengths which can provide spectral fingerprint information of different samples. Among many variable selection methods, 2nd derivative method obtains a second order (2nd) spectral curve by taking the second derivative of the original spectral curve. This 2nd spectral curve can reflect the concavity and convexity of the original spectral curve, and any fluctuations in the original spectral curve are mapped to the peaks and valleys in the 2nd spectral curve.21 A sharp undulation corresponds to a tall peak or a deep valley, whereas a gentle undulation corresponds to a short peak or a shallow valley. The wavelengths corresponding to the tall peaks and deep valleys with large differences between spectral curves are regarded as the optimal wavelengths and selected for further analysis of discriminant models.
3.3. Traditional discriminant models
LR, a statistical classification approach based on linear regression model, is widely used in various fields such as spectral analysis and medical diagnosis.13,22 Unlike the linear regression model with an output in entire real interval, LR outputs a discrete value in a limited range of [0, 1] which represents the probability of a certain category. To obtain such an output, a sigmoid function is appended to the linear regression model to map the entire real interval to the range of [0, 1], just like the softmax function followed the last full connected layer in DCNN. This is probably where the name “logistic regression” comes from. For the binary classification problem, a threshold need to be set. If the output probability is greater than this threshold, the input sample is considered to belong to the positive class, otherwise belongs to the negative class. For the multi-classification problem, multiple one-to-many classifiers are combined. The cross-entropy loss is defined as the cost function of LR, and a regularization term is introduced in the cost function. The optimized algorithm optimize_algo, the regularization term r and the regularization coefficient c′ needed to be adjusted according to specific dataset. To obtain the optimal parameters, a five-fold cross-validation operation and a simple grid-search program were carried out in this study. The searching range of optimize_algo, r and c′ were set to {newton-cg, lbfgs, liblinear and sag}, {L1, L2} and 2−8 to 28, respectively.
SVM with a stable classification performance is one of the most commonly-used discriminant approaches in spectral analysis. As a binary classification model, the main idea of SVM is to find a hyperplane to maximize the interval between positive and negative samples. Samples falling on the hyperplane are called support vectors and determine the classification performance. A regularized hinge loss can be regarded as the cost function of linear SVM. To solve the nonlinear problem, the kernel trick is introduced to implicitly transform the original nonlinear problem into a linear separable problem. Generally, the selection of kernel function often depends on the domain knowledge. In the field of spectral analysis, RBF kernel was frequently used to construct nonlinear SVM model. The optimal penalty coefficient c and the kernel parameter g were also calculated through a cross-validation operation and a grid-search program in this study. The searching range of c and g were both set to 2−8 to 28. For multi-classification problems, similar to the LR model, it is required to combine multiple one-to-many classifiers.
3.4. Deep convolutional neural network
DCNN is a popular deep learning algorithm. A typical DCNN includes five modules: input, convolution, pooling, fully connected and output. The convolution module generally contains one or more convolution layers and an activation function. The convolution of DCNN is operated by filters which are only calculated with a local region of previous layer. In other words, the neurons are not fully connected to the neurons in the previous layer. This local perception manner not only enables DCNN to learn local features of the input, but also significantly reduces the number of parameters. Moreover, the design of sharing parameters for multiple convolution kernels in a convolution layer further reduces the number of parameters. The pooling module also uses filters to reduce data dimension, and the fully connected module similar to traditional neural network completes the classification task. DCNN perfectly integrates feature learning, feature extraction, dimensionality reduction, and final classification in one system. The training process of DCNN often consists of two phases: forward learning and back propagation.
(1) Forward learning phase: a sample (1D, 2D, 3D matrix) was fed to the input module, and passed through the entire network by calculated with the parameters of all layers. Then the actual output can be obtained.
(2) Back propagation phase: the error between the actual output and the ground truth is calculated, and the loss function is propagated backward. Then the parameters of each layer are updated.
These two steps are repeated until the network's output is close to the ground truth.
In our previous study, a 1D CNN using ELU as activation function and batch normalization to alleviate the over-fitting problem was developed for discrimination of Chrysanthemum varieties.20 This DCNN achieved excellent performance. Thus, to explore the feasibility of combining HSI and DCNN for varieties identification of oat seeds, this kind of architecture was regarded as a mirror to build a new DCNN. According to the characteristics of spectral data of oat seeds, some hyper-parameters of DCNN needed to be re-adjusted by trial and error. The structure and the configuration of the new DCNN was shown in Fig. 1. It could be seen that the new DCNN was composed of four convolution groups (convolution and pooling) and two fully connected layers. The number of convolution filters in the first convolutional group was adjusted to 64, and was multiply increased as the groups going deeper. The outputs of the two fully connected layers were adjusted to 512 dimensions and 4 dimensions, respectively. The cross-entropy loss function combined with the Stochastic Gradient Descent (SGD) optimizer was still employed to train DCNN. To obtain satisfactory classification performance, two hyper-parameters: batch size b and training iterations epoch needed to be adjusted. Similar to SVM and LR, a cross-validation operation and a grid-search program were carried out to search optimal b, and the search range is {64, 128, 256, 512, 1024}. In order to find optimal epoch and terminate the training process in advance, DCNN was trained using the optimal b. And training accuracy and training loss under each epoch were recorded. The epoch with slow fluctuation of training accuracy was regarded as the optimal epoch. After end-to-end training, the category of each sample could be acquired directly from this DCNN when the average spectrum was input. This is one of the most competitive advantages of DCNN, that is, feature representation is done automatically without additional manual extraction.
Fig. 1. The structure of our DCNN and the flowchart of “deep spectral features + traditional classifiers”.
As deep learning is originally called representation learning and DCNN extracts the abstract deep feature through convolution and pooling layer-by-layer, a natural question is how to evaluate the representational ability of this deep feature. Can this deep feature be extracted and fed to the models commonly used in spectral analysis? Inspired by these questions, we reviewed the structure of the new DCNN developed for varieties identification of oat seeds and discovered the peculiarity of the first fully connected layer which was located between the last convolutional layer and the last fully connected layer. That is, the extraction of local features has been done before the first fully connected layer, and the sample category will be output after it. Therefore, the vector with size of 512 × 1 output by the first fully connected layer could be regarded as the deep spectral feature automatically learnt by DCNN.
For the purpose of extracting the deep spectral feature and evaluating its representation ability, DCNN which has been trained in end-to-end manner before was firstly introduced. Then, the spectral data in original training set and testing set were re-input into this DCNN without gradient derivation and back propagation, and the corresponding outputs of the first fully connected layer were extracted. Further, the deep spectral features of the training data and the corresponding category labels were utilized to train the traditional discriminant models such as SVM and LR, and the deep spectral features of the testing data and the corresponding labels were used to evaluate the overall classification performance. Finally, the performances of this “deep spectral features + traditional classifiers” were compared with those of “optimal wavelengths + traditional classifiers” and “DCNN trained in end-to-end manner”. The flowchart of “deep spectral features + traditional classifiers” was shown in Fig. 1.
3.5. Varieties visualization of oat seeds
The varieties visualization of oat seeds facilitates market regulators and seed companies to quickly inspect the seed variety and assess the variety purity, which is benefit for large-scale seeds detection in modern seed industry. The characteristic of collecting the spectral information and spatial location information simultaneously of HSI offers the feasibility of varieties visualization. In addition, a high robust and reliable discriminant model is necessary for accurate visualization of oat seeds. Therefore, the discriminant model with optimal performance was selected for varieties visualization in this study. The average spectrum of oat seed was extracted and input into the optimal model to obtain the variety category. Then, all pixels in the oat seed area in hyperspectral image were assigned to this category. Different colors were given to different varieties for intuitively and clearly inspecting the seed variety and calculating the variety purity.
3.6. Software tools
In order to remove irrelevant background and retain the oat seeds areas, Envi 4.6 (ITT Visual Information Solutions, Boulder, CO, USA) was utilized to crop the hyperspectral images. Matlab R2018a (The MathWorks, Natick, MA, USA) was employed to extract, denoise (WT), and exploratory analyze (PCA) the spectral data. The optimal wavelengths selection based on the 2nd derivative method was realized using Unscrambler 10.1 (CAMO AS, Oslo, Norway). All discriminant models were implemented in Spyder 3.2.6 (Anaconda, Austin, TX, USA) environment using python language. DCNN was built under the framework of Pytorch (Facebook, Menlo Park, CA, USA).
4. Results
4.1. Spectral characteristics of oat seeds
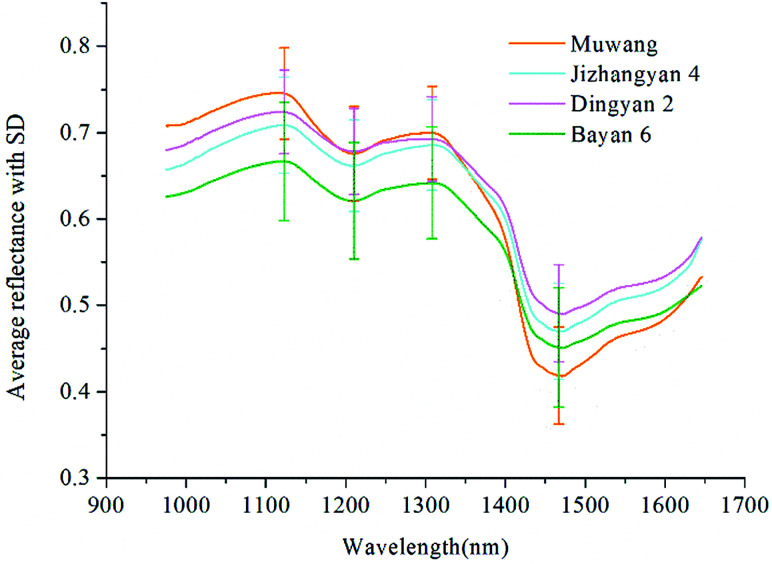
The average spectra with standard deviation (SD) of four varieties of oat seeds in the range of 975–1646 nm was shown in Fig. 2. The patterns of these spectral curves were similar to those of oat and groat samples in ref. 23, although differences existed in the position and amplitude of the curve fluctuations. In this study, the spectral curves of four varieties of oat seeds shared the same positions of peaks and valleys. The peak at 1123 nm and the valley at 1210 nm are related to the second overtone of C–H stretching vibrations of carbohydrates.12,24 The peak around 1308 nm is assigned for the combination of the first overtone of amide B and the fundamental amid vibrations, and the valley at 1467 nm is contributed to the protein resulting from the first overtone of the N–H stretching vibrations.24,25 Certain differences between four varieties of oat seeds could be observed from these peaks and valleys, which could be employed as the basis of further classification. However, fuzziness also existed. For example, the spectral curves in the range of 1150–1320 nm of Muwang and Dingyan 2 were almost overlap, making it difficult to tell them apart. Therefore, more accurate multivariate analysis is necessary.
Fig. 2. Average spectra of four varieties of oat seeds.
4.2. Principal component analysis
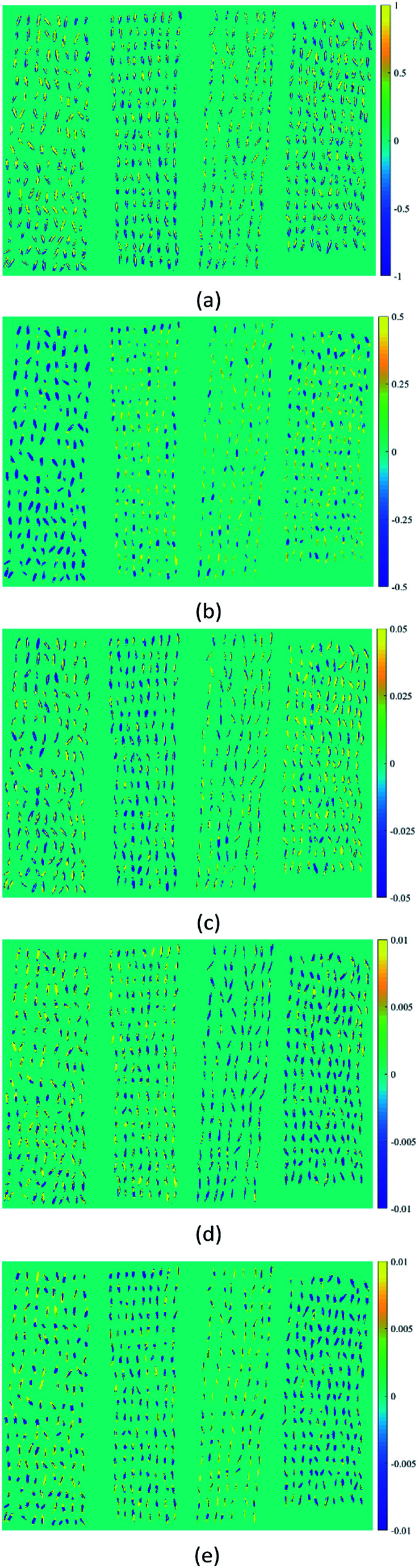
As a qualitative analysis method commonly used in the field of spectral analysis, PCA was introduced to find the spectral pattern differences between four varieties of oat seeds in this study. The orthogonal projection matrix was firstly calculated using the training set. Then the spectra data of a hyperspectral image randomly selected for each variety from the testing set was extracted and preprocessed. A principal component matrix could be obtained by multiplying the projection matrix and the spectra data matrix. The first five PCs explained 99.94% of spectral variance, including 91.77%, 7.60%, 0.45%, 0.08% and 0.04% for PC1, PC2, PC3, PC4, and PC5, respectively. Thus, the score images of these five PCs were investigated to identify and visualize the differences between varieties (Fig. 3). Although PC1 carried most of the variance information, it didn't show significant classification information between varieties, as it might reflect some common ingredients of oat seeds. The first visualization of varieties differences was observed in PC2. Muwang with negative scores of most pixels in sample regions could be easily discriminated from the other three varieties. In addition, the four varieties could be further divided into two categories (Muwang and Jizhangyan 4 as the first category, Dingyan 2 and Bayan 6 as the second category), since most pixels of Muwang and Jizhangyan 4 had negative scores in PC3 and positive scores in PC4 while Dingyan 2 and Bayan 6 exhibited the opposite patterns. As Muwang has been distinguished, Jizhangyan 4 in the first category could also be identified. The two varieties in the second category, Dingyan 2 and Bayan 6, could be discriminated using PC5. In summary, a preliminary varieties identification could be made by combining the manifestation of oat samples in these five PCs. This demonstrated the feasibility of using hyperspectral images to distinguish oat varieties. However, this process was crude and cumbersome, and more accurate discriminant models were needed for further quantitative analysis.
Fig. 3. Score images of the first five PCs of four varieties of oat seeds (form lest to right: Muwang, Jizhangyang 4, Dingyan 2, Bayan 6): (a) PC1, (b) PC2, (c) PC3, (d) PC4, (e) PC5.
4.3. Selection of optimal wavelengths
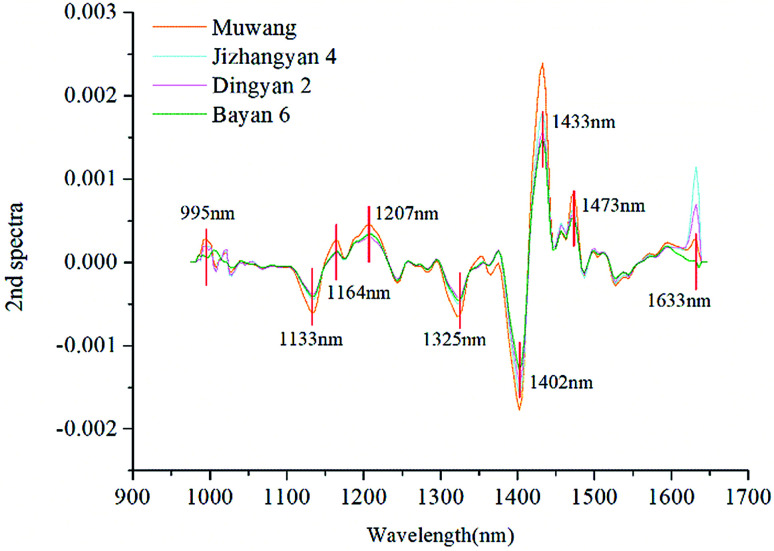
In this study, the spectral curves of oat seeds used for multivariate analysis contained 200 wavelengths, between which many correlations existed. In order to remove the redundant information and speed up the classification, variable selection was performed using 2nd derivative method. In the 2nd spectral curve, peaks and valleys with large differences between spectral curves were selected as the optimal wavelengths. As shown in Fig. 4, nine optimal wavelengths were selected and marked. The fingerprint information contained in near-infrared spectra is attributed to the stretching vibrations of chemical bonds such as C–N, C–H, and N–H in organic molecules.26,27 For example, the short peak at 995 nm may be related to the second overtone of N–H stretching.11 The bands at 1133, 1164 and 1207 nm are attributed to the second overtone of C–H stretching.11,24 The wavelength at 1325 nm is associated with the combination of the first overtone of amide B and the fundamental amid vibrations.25 The deep valley at 1402 nm and the tall peak at 1433 nm (around 1437 nm) may correspond to the first overtone of O–H stretching and the C O stretching from saturated and unsaturated carboxyl acids.24,28 The wavelength at 1473 nm (around 1473.9 nm) is assigned to the water bands, and the last optimal wavelength at 1633 nm is ascribed to the first overtone of C–H stretching.29,30 Different varieties of oat seeds exhibited different fingerprint information at these nine optimal wavelengths, which could be caused by composition differences determined by variety. Therefore, as a simplification of full wavelengths, these wavelengths contained the key information to distinguish different varieties, and could be combined with classical classifiers to perform further discriminant analysis.
Fig. 4. 2nd spectral curves of four varieties of oat seeds.
4.4. Discriminant analysis of different models
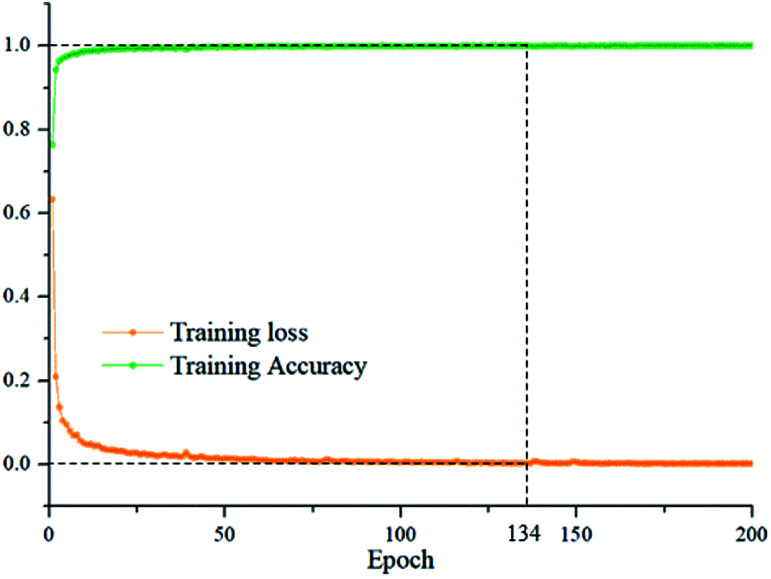
To evaluate the ability of DCNN in representing the spectral differences of oat seeds, an end-to-end DCNN was developed. Multiple models were established through combining the deep spectral features automatically learnt by DCNN with traditional classifiers such as RBF-SVM, LINEAR-SVM and LR. The discriminant models based on full wavelengths and optimal wavelengths were built for comparison. The major related parameters of discriminant models were determined through cross-validation and were summarized in Table 1. To find the optimal epoch for DCNN, the relationship between epoch and training accuracy and training loss were shown on Fig. 5. It can be seen that DCNN has converged and the training accuracy has fluctuated very little when epoch = 134. Thus, the optimal epoch was set to 134.
Varieties discrimination results of oat seeds using different modelsa.
| Models | Parameters | Training | Testing | ||
|---|---|---|---|---|---|
| Accuracy/% | Time/s | Accuracy/% | Time/s | ||
| Full wavelengths + RBF_SVM | (256, 0.0039) | 98.63 | 13.97 | 98.05 | 1.97 |
| Full wavelengths + LINEAR_SVM | — | 98.39 | 18.02 | 97.88 | 0.0026 |
| Full wavelengths + LR | (liblinear, L2, 256) | 98.94 | 11.63 | 98.69 | 0.0024 |
| Optimal wavelengths + RBF_SVM | (256, 0.16) | 89.82 | 4.58 | 87.31 | 0.22 |
| Optimal wavelengths + LINEAR_SVM | — | 84.62 | 6.38 | 84.21 | 0.0017 |
| Optimal wavelengths + LR | (Liblinear, L2, 74.66) | 85.30 | 3.83 | 84.92 | 0.0008 |
| Deep spectral features + RBF_SVM | (1.85, 0.0039) | 100 | 19.04 | 99.05 | 2.25 |
| Deep spectral features + LINEAR_SVM | — | 100 | 11.81 | 99.02 | 0.61 |
| Deep spectral features + LR | (Liblinear, L2, 0.54) | 100 | 18.02 | 98.72 | 0.0050 |
| DCNN trained in end-to-end manner | (256, 133) | 100 | 9701.63 | 99.19 | 7.96 |
Parameters of different discriminant models. (c, g) for RBF_SVM, (optimize_algo, r, c′) for LR, and (epoch) for DCNN trained in end-to-end manner.
Fig. 5. The relationship between epoch and training performance.
The classification accuracies of all models were also summarized in Table 1. As we can see, the performance of all DCNN-based models were better than that of traditional models based on full wavelengths and optimal wavelengths, showing accuracies close to 100% on training set and about 99% on testing set. It was just because of the abstract representation of multiple convolutional layers in DCNN that the deep spectral features were more distinguishable than the original full wavelengths. In addition, this also proved that the deep features automatically learnt by DCNN was more suitable than the manually selected optimal wavelengths in representing the spectral differences caused by the composition differences. Consistent with our previous findings, all models based on full wavelengths outperformed the corresponding models based on optimal wavelengths.20 As the quantity of information was reduced by 95.5% ((200 − 9)/200 × 100 = 95.5%), performance degradation was foreseeable.
Moreover, it could be observed that RBF_SVM performed better than LINEAR_SVM. RBF performing an implicit nonlinear transformation was more appropriate to deal with complex classification problems. This was also the reason why RBF_SVM was more commonly used in spectral analysis than LINEAR_SVM.11,12 As a classification model based on linear regression, the classification accuracy of LR was satisfying, especially it achieved an accuracy of 98.72% on testing set when combined with the deep spectral features. Among these models, DCNN trained in end-to-end manner wining the highest accuracy of 99.19% on testing set not only outperformed the traditional discriminant models, but also performed slightly better than the other three DCNN-based models. This might be caused by the end-to-end training mode, that is, feature extraction and classification were integrated in one system, and the optimal parameters were determined during training process.
The overall results demonstrated that it was feasible to combine DCNN and traditional classifiers for varieties identification of oat seeds based on HSI and such methods generally obtained good classification performance. Compared with original full wavelengths and the optimal wavelengths selected manually, the deep spectral features had superior representation capability. Trained in end-to-end manner, DCNN can be used as a reliable model for varieties identification of oat seeds.
4.5. Classification visualization of oat seeds
The ability of acquiring spectral information and spatial information simultaneously allows HSI to intuitively visualize the classification results of oat seeds. Fig. 6(a) showed the original hyperspectral images of four varieties of oat seeds randomly selected from testing set. It could be seen that most of the oat seeds differed litter in morphology and texture characteristics. Rapid discrimination of different varieties using human eyes was very difficult. To solve this problem, the optimal model in previous section, DCNN trained in end-to-end manner, combined with the spatial location information contained in hyperspectral images was utilized to classify these oat seeds and visualize the classification results. As shown in Fig. 6(b), the corresponding predicted results were marked in four colors (orange for Muwang, cyan for Jizhangyan 4, magenta for Dingyan 2 and olive for Bayan 6). The correct classification and misclassification of different varieties were clearly displayed in the prediction maps. Among the 654 oat seeds, only 1 were misclassified. That is to say, the accuracy of this visualization reached 99.85%, which was adequate for the variety detection and purity calculation in actual production process. The visualization results indicated that hyperspectral imaging together with DCNN was a promising technique to identify different varieties of oat seeds rapidly and accurately, which is expected to be a powerful tool for quality detection of large-scale seeds in modern seed industry.
Fig. 6. Classification visualization of oat seeds (from left to right: Muwang, Jizhangyan 4, Dingyan 2 and Bayan 6): (a) original gray images; (b) the prediction maps.
5. Discussion
As a popular deep learning algorithm, DCNN has dramatically improved the state-of-art results in various visual tasks. Compared with traditional classifiers, DCNN is prone to an over-fitting problem since the model has more parameters. In order to learn appropriate parameters for DCNN, a large number of training samples is indispensable. The characteristic of batch detection of HSI makes it possible to collect large-scale data, which has attracted many researchers to combine HSI with DCNN for data analysis.31–33 In this study, the training set contained spectral vectors of 11 134 oat seeds, and the testing set consisted of 3712 spectral vectors of other non-repetitive oat seeds. In addition, the DCNN developed in this study is relatively shallow, and a batch normalization layer which can reduce the offset effect was added behind each convolution layer and the first fully connected layer. Although a dropout layer was often added in similar positions in other DCNN, our previous attempts showed that this mechanism did not work well here.34 The accuracy on training set of DCNN-based models was 100% and the prediction result on testing set was also satisfactory. This indicated that our collected samples were sufficient to learn the appropriate parameters and the over-fitting problem didn't appear on our DCNN.
Although deep learning is originally called representation learning, to the best of our knowledge, there is no research to deeply investigate the representation ability of DCNN. In this study, the deep spectral features automatically learnt by DCNN were combined with three traditional classifiers, and compared with the discrimination models based on full wavelengths and optimal wavelengths. The results showed that all the models based on DCNN outperformed the traditional models based on full wavelengths and optimal wavelengths. This further confirmed the excellent ability of DCNN in representing the spectral differences between different samples. However, unlike expected, the classification ability of three models combining deep features with traditional classifiers was slightly worse than that of DCNN trained in end-to-end manner. This might be because the end-to-end training mode enables the optimal parameters to be determined during training process. While, for the other three models based on DCNN, the parameters of traditional classifiers could only be determined separately by a grid-search method. Thus, it was difficult for DCNN and traditional classifiers to achieve optimal state simultaneously. Integrating traditional classifiers into DCNN can be attempted in future to achieve end-to-end learning, which may improve the classification performance. Nevertheless, the excellent representation ability of deep spectral features once again proved that HSI combined with DCNN is a powerful tool for seed variety identification.
6. Conclusions
This paper aimed to study the feasibility of using HSI and DCNN for varieties identification of oat seeds and investigate the representation ability of DCNN. The score images drawn according to the results of PCA showed the divisibility of four varieties of oat seeds. The optimal wavelengths selected by the 2nd derivative method was proved to contain some crucial information about varieties discrimination. Three models combining deep spectral features with traditional classifiers were compared with the common models based on full wavelengths and optimal wavelengths as well as DCNN trained in end-to-end manner. All DCNN-based models obtained better performance than other models, confirming that the ability of DCNN in representing the spectral difference of different varieties of oat seeds was excellent. The unexpected results that DCNN trained in end-to-end manner achieved the highest accuracy on testing set showed the advantage of end-to-end training manner. How to integrate traditional classifiers into DCNN to implement end-to-end learning is an important issue to be studied in future. The overall results indicated that with the batch detection superiority of HSI and the outstanding representation ability of DCNN, HSI combined with DCNN becomes a powerful tool for large-scale seeds detection in modern seed industry. This study may be helpful to boost the research of DCNN in the field of spectral analysis.
Conflicts of interest
There are no conflicts of interest to declare.
Supplementary Material
Acknowledgments
This work was supported by National Key R&D Program of China (No. 2018YFD0101002).
References
- Anttila H. Sontag-Strohm T. Salovaara H. Viscosity of beta-glucan in oat products. Agric. Food Sci. 2004;13:80–87. doi: 10.2137/1239099041838012. [DOI] [Google Scholar]
- Mäkinen O. E. Sozer N. Ercili-Cura D. Poutanen K. Protein from oat: structure, processes, functionality, and nutrition. Sustainable Protein Sources. 2017:105–119. doi: 10.1016/B978-0-12-802778-3.00006-8. [DOI] [Google Scholar]
- Sunilkumar B. A. Tareke E. Review of analytical methods for measurement of oat proteins: the need for standardized methods. Crit. Rev. Food Sci. Nutr. 2017;57:1–19. doi: 10.1080/10408398.2017.1414029. [DOI] [PubMed] [Google Scholar]
- Shuaib M. Zeb A. Ali Z. Ali W. Ahmad T. Khan I. Characterization of wheat varieties by seed storage-protein electrophoresis. Afr. J. Biotechnol. 2007;6:497–500. [Google Scholar]
- Ye S. Wang Y. Huang D. Li J. Gong Y. Xu L. Liu L. Genetic purity testing of F1 hybrid seed with molecular markers in cabbage (Brassica oleracea var. capitata) Sci. Hortic. 2013;155:92–96. doi: 10.1016/j.scienta.2013.03.016. [DOI] [Google Scholar]
- Brereton R. G. Jansen J. Lopes J. Marini F. Pomerantsev A. Rodionova O. Roger J. M. Walczak B. Tauler R. Chemometrics in analytical chemistry—part II: modeling, validation, and applications. Anal. Bioanal. Chem. 2018;410:6691–6704. doi: 10.1007/s00216-018-1283-4. [DOI] [PubMed] [Google Scholar]
- Lasch P. Stämmler M. Zhang M. Baranska M. Bosch A. Majzner K. FT-IR hyperspectral imaging and artificial neural network analysis for identification of pathogenic bacteria. Anal. Chem. 2018;90:8896–8904. doi: 10.1021/acs.analchem.8b01024. [DOI] [PubMed] [Google Scholar]
- Zhao Y. Zhu S. Zhang C. Feng X. Feng L. He Y. Application of hyperspectral imaging and chemometrics for variety classification of maize seeds. RSC Adv. 2018;8:1337–1345. doi: 10.1039/C7RA05954J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kandpal L. M. Lohumi S. Kim M. S. Kang J. S. Cho B. K. Near-infrared hyperspectral imaging system coupled with multivariate methods to predict viability and vigor in muskmelon seeds. Sens. Actuators, B. 2016;229:534–544. doi: 10.1016/j.snb.2016.02.015. [DOI] [Google Scholar]
- Lee H. Kim M. S. Song Y. R. Oh C. S. Lim H. S. Lee W. H. Kang J. S. Cho B. K. Non-destructive evaluation of bacteria-infected watermelon seeds using visible/near-infrared hyperspectral imaging. J. Sci. Food Agric. 2017;97:1084–1092. doi: 10.1002/jsfa.7832. [DOI] [PubMed] [Google Scholar]
- Zhang C. Liu F. He Y. Identification of coffee bean varieties using hyperspectral imaging: influence of preprocessing methods and pixel-wise spectra analysis. Sci. Rep. 2018;8:2166. doi: 10.1038/s41598-018-20270-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng X. Peng C. Chen Y. Liu X. Feng X. He Y. Discrimination of CRISPR/Cas9-induced mutants of rice seeds using near-infrared hyperspectral imaging. Sci. Rep. 2017;7:15934. doi: 10.1038/s41598-017-16254-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Z. Wang Q. Plaza A. Li J. Sun L. Wei Z. Real-time implementation of the sparse multinomial logistic regression for hyperspectral image classification on GPUs. IEEE Geosci. Remote Sens. Lett. 2015;12:1456–1460. [Google Scholar]
- Kong W. Zhang C. Liu F. Nie P. He Y. Rice seed cultivar identification using near-infrared hyperspectral imaging and multivariate data analysis. Sensors. 2013;13:8916–8927. doi: 10.3390/s130708916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krizhevsky A., Sutskever I. and Hinton G., ImageNet classification with deep convolutional neural networks, Proceedings of the Conference on Neural Information Processing Systems, 2012, pp. 1106–1114 [Google Scholar]
- Chen L. C. Papandreou G. Kokkinos L. Murphy K. Yuille A. L. DeepLab: semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018;40:834–848. doi: 10.1109/TPAMI.2017.2699184. [DOI] [PubMed] [Google Scholar]
- Yu X. Lu H. Liu Q. Deep-learning-based regression model and hyperspectral imaging for rapid detection of nitrogen concentration in oilseed rape (Brassica napus L.) leaf. Chemom. Intell. Lab. Syst. 2018;172:188–193. doi: 10.1016/j.chemolab.2017.12.010. [DOI] [Google Scholar]
- Jin X. Jie L. Wang S. Qi H. J. Li S. W. Classifying wheat hyperspectral pixels of healthy heads and Fusarium head blight disease using a deep neural network in the wild field. Remote Sens. 2018;10:395. doi: 10.3390/rs10030395. [DOI] [Google Scholar]
- Ji S. Zhang C. Xu A. Shi Y. Duan Y. 3D convolutional neural networks for crop classification with multi-temporal remote sensing images. Remote Sens. 2018;10:75. doi: 10.3390/rs10010075. [DOI] [Google Scholar]
- Wu N. Zhang C. Bai X. Du X. He Y. Discrimination of Chrysanthemum varieties using hyperspectral imaging combined with a deep convolutional neural network. Molecules. 2018;23:2381. doi: 10.3390/molecules23092381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C. Jiang H. Liu F. He Y. Application of near-infrared hyperspectral imaging with variable selection methods to determine and visualize caffeine content of coffee beans. Food Bioprocess Technol. 2017;10:213–221. doi: 10.1007/s11947-016-1809-8. [DOI] [Google Scholar]
- Collins M. H. Martin L. J. Alexander E. S. Todd Boyd J. Sheridan R. He H. Pentiuk S. Putnam P. E. Abonia J. P. Mukkada V. A. Franciosi J. P. Rothenberg M. E. Newly developed and validated eosinophilic esophagitis histology scoring system and evidence that it outperforms peak eosinophil count for disease diagnosis and monitoring. Dis. Esophagus. 2017;30:1–8. doi: 10.1111/dote.12470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serranti S. Cesare D. Marini F. Bonifazi G. Classification of oat and groat kernels using NIR hyperspectral imaging. Talanta. 2013;103:276–284. doi: 10.1016/j.talanta.2012.10.044. [DOI] [PubMed] [Google Scholar]
- Ribeiro J. S. Ferreira M. M. C. Salva T. J. G. Chemometric models for the quantitative descriptive sensory analysis of Arabica coffee beverages using near infrared spectroscopy. Talanta. 2011;83:1352–1358. doi: 10.1016/j.talanta.2010.11.001. [DOI] [PubMed] [Google Scholar]
- Daszykowski M. Wrobel M. S. Czarnik-Matusewicz H. Walczak B. Near-infrared reflectance spectroscopy and multivariate calibration techniques applied to modelling the crude protein, fibre and fat content in rapeseed meal. Analyst. 2008;133:1523–1531. doi: 10.1039/B803687J. [DOI] [PubMed] [Google Scholar]
- Alishahi A. Farahmand H. Prieto N. Cozzolino D. Identification of transgenic foods using NIR spectroscopy: a review. Spectrochim. Acta, Part A. 2010;75:1–7. doi: 10.1016/j.saa.2009.10.001. [DOI] [PubMed] [Google Scholar]
- Li G. Li Y. Zhang M. Study on identification of rice seeds by chemical oscillation fingerprints. RSC Adv. 2015;5:96472–96477. doi: 10.1039/C5RA14126E. [DOI] [Google Scholar]
- Lammertyn J. Nicolaï B. Ooms K. Smedt V. D. Baerdemaeker J. D. Non-destructive measurement of acidity, soluble solids, and firmness of jonagold using NIR-spectroscopy. Trans. ASAE. 1998;41:1089–1094. [Google Scholar]
- Vance C. K. Tolleson D. R. Kinoshita K. Rodriguez J. Foley W. J. Near infrared spectroscopy in wildlife and biodiversity. J. Near Infrared Spectrosc. 2016;24:1–25. doi: 10.1255/jnirs.1199. [DOI] [Google Scholar]
- Chung H. Choi H. Ku M. Rapid identification of petroleum products by near-infrared spectroscopy. Bull. Korean Chem. Soc. 1999;20:1021–1025. [Google Scholar]
- Qiu Z. Chen J. Zhao Y. Zhu S. He Y. Zhang C. Variety identification of single rice seed using hyperspectral imaging combined with convolutional neural network. Appl. Sci. 2018;8:212. doi: 10.3390/app8020212. [DOI] [Google Scholar]
- Paoletti M. E. Haut J. M. Plaza J. Plaza A. A new deep convolutional neural network for fast hyperspectral image classification. ISPRS J. Photogramm. Remote Sens. 2018;145:120–147. doi: 10.1016/j.isprsjprs.2017.11.021. [DOI] [Google Scholar]
- Haut J. M. Paoletti M. E. Plaza J. Li J. Plaza A. Active learning with convolutional neural networks for hyperspectral image classification using a new bayesian approach. IEEE Trans. Geosci. Remote Sens. 2018;99:1–22. [Google Scholar]
- Cao X. Zhou F. Xu L. Meng D. Xu Z. Paisley J. Hyperspectral image classification with Markov random fields and a convolutional neural network. IEEE Trans. Image Process. 2018;27:2354–2367. doi: 10.1109/TIP.2018.2799324. [DOI] [PubMed] [Google Scholar]