Abstract
The poor predictive accuracy of current computational enzyme design methods has led to low success rates of producing highly active variants that target non-natural substrates. In this report, a quantitative assessment approach based on molecular dynamics (MD) simulations was developed to eliminate false-positive enzyme designs at the computational stage. Taking cephradine hydrolase as an example, the apparent Michaelis binding constant (Km) and catalytic efficiency (kcat/Km) of designed variants were correlated with binding free energies and activation energy barriers, respectively, as calculated by molecular mechanics/Poisson–Boltzmann surface area (MM/PBSA) and molecular mechanics/generalized Born surface area (MM/GBSA) methods with explicit water considered based on general MD simulation protocols. The correlation results showed that both the MM/GBSA and MM/PBSA methods with a protein dielectric constant (εp = 4) could rank the variants well based on the predicted binding free energies between enzyme and the substrate. Furthermore, the activation energy barriers calculated by the MM/PBSA method with an εp = 24 correlated well with kcat/Km. Thus, false-positive variants obtained by the enzyme design program PRODA were eliminated prior to experimentation. Therefore, MD simulation-based quantitative assessment of designed variants greatly enhanced the predictive accuracy of computational enzyme design tools and should facilitate the construction of artificial enzymes with high catalytic activities toward non-natural substrates.
A quantitative assessment method for computational enzyme design was developed to rank the active designs of cephradine hydrolase based on molecular dynamics simulation.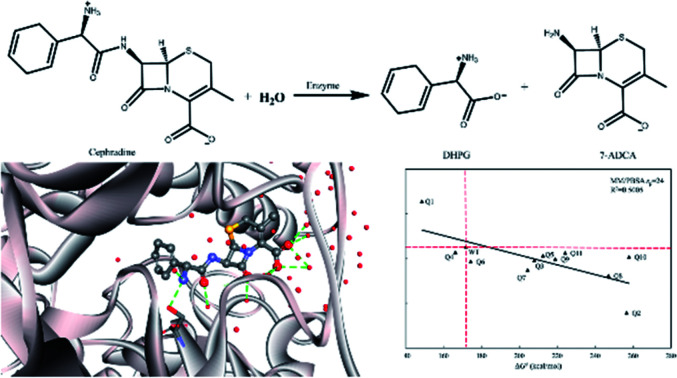
Introduction
As efficient biocatalysts, enzymes are used widely in industry to accelerate chemical reactions and obtain high selectivity and specificity under ambient conditions.1,2 However, native enzymes cannot meet the increasing demands of green process developments. The use of native enzymes toward non-natural substrates often suffers from low activity and production of worthless by-products.3 In the last two decades, directed evolution approaches have succeeded in adapting native enzymes to catalyze non-natural chemical transformations through high-throughput screening.1 An alternative and more economical way to adapt native enzymes is the structure-based computational enzyme design approach. With the help of molecular modeling and high-performance computing, researchers can optimize or create enzyme structures that preferentially stabilize the transition state relative to the ground state, thereby reducing the major free energy barrier along the reaction coordinate. Computational enzyme design can be divided into two subclasses: the de novo design of new active sites and the redesign of existing active sites. The de novo design approach requires the construction of an active site model (theozyme)4 for the new reaction. This model is then placed in a suitable protein scaffold5 and the binding pocket is redesigned to stabilize the anchored active site. De novo design has been used successfully to generate artificial enzymes for the Kemp elimination reaction,6 retro-aldol reaction,7 and Diels–Alder reaction.8 Although the catalytic activities of the de novo designed enzymes are always modest, this approach produces good starting points for further evolution of the enzyme by experimental approaches. In the redesign approach, the native enzyme active sites are tailored to catalyze reactions for non-natural substrates. The computational active site redesign strategy is capable of replacing the substantial workload of directed evolution to adapt native enzymes with enhanced activity and selectivity for non-natural substrates.9–14
Although the computational enzyme design strategy has been effective and shown potential in these cases, the success rate has not improved. Generally, assumptions such as a rigid backbone, discrete amino acid side chain rotamers and discrete ligand placement, and continuum solvent are adopted in current enzyme design algorithms. These trade-offs facilitate the search of the sequence space but sacrifice the model accuracy for a protein–ligand interaction. This results in the algorithms producing a large number of false positive variants besides the few beneficial variants. To filter out the false positive variants at the computational stage, various methods such as mixed quantum and molecular mechanics (QM/MM),15,16 semi-empirical valence bond17 and molecular dynamics (MD) simulations18–22 have been applied. The results of these studies show that MD simulations can be used to evaluate enzyme designs effectively.16 However, evaluation criteria applied in these studies such as active site root-mean-square deviations (RMSDs), water coordination numbers, hydrogen-bond distances and angles along the simulation trajectories can only be used to rank the designed variants qualitatively. In this report, we develop a direct way to correlate the free energy changes calculated based on the MD trajectories with kinetic parameters, i.e., the turnover number kcat and the apparent Michaelis constant Km, of the designed variants to rank these variants quantitatively. Several MD simulation based methods are developed to calculate ensemble averaged thermodynamic quantities, such as the linear interaction energy (LIE),23 thermodynamic integration (TI),24 free energy perturbation (FEP),25 and Molecular Mechanics/Generalized Born or Poisson–Boltzmann Surface Area (MM/GBSA and MM/PBSA).26,27 Although LIE, TI and FEP provide relatively accurate free energy calculations, the computational cost of these methods is very unfavorable. In contrast, the MM/GBSA and MM/PBSA methods are computationally economical and have been used successfully to predict ligand binding free energies28,29 to screen small molecule inhibitors in drug design. Here, we use MM/GBSA and MM/PBSA methods to calculate the binding free energies between enzyme active sites and the substrates at various states based on MD simulation trajectories to evaluate the designed variants quantitatively.
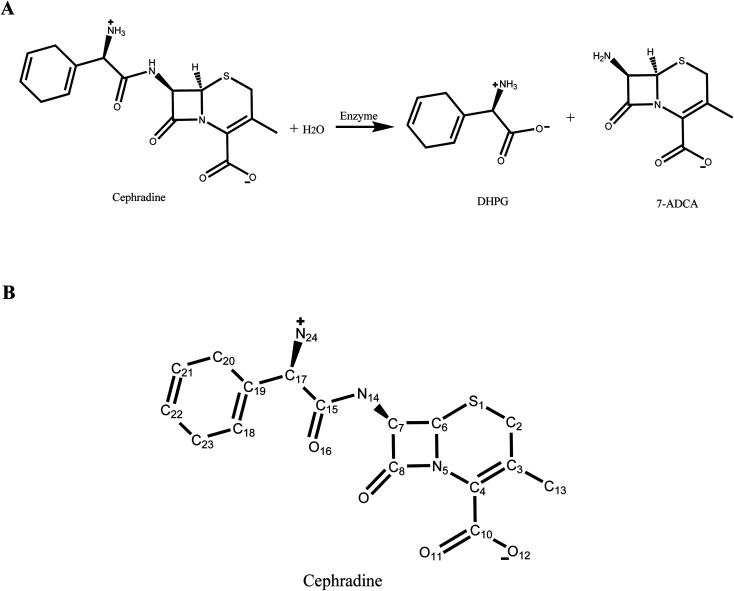
In our previous study,30 a new scaffold (PDB ID: 1JU3), which is a Rhodococcus sp. cocaine esterase (EC 3.1.1.84, Uniprot ID: Q9L9D7), was identified from structural databases to catalyze the hydrolysis and synthesis of cephradine, an important semi-synthetic β-lactam antibiotic. The hydrolytic reaction of cephradine catalyzed by the enzyme is shown in Fig. 1A. The catalytic hydrolysis of cephradine by the wild-type enzyme is low. Several hundred variants were designed by our computational enzyme design program PRODA to increase the activity31–34 and the kinetic parameters of the top-ranked eleven variants were experimentally measured. Among the eleven designed variants, only one variant showed higher catalytic efficiency (kcat/Km) than the wild-type enzyme, indicating a success rate of less than 10%. To eliminate all or at least part of the false positive predictions by PRODA, an MD simulation was used here to evaluate the active designs of cephradine synthase by MM/GBSA and MM/PBSA methods quantitatively.
Fig. 1. Hydrolysis of cephradine catalyzed by enzyme. (A) Reaction scheme. 7-ADCA: 7-aminodesacetoxycephalosporanic acid, DHPG: D-dihydrophenyl-glycine. (B) Structural formula of cephradine marked with heavy atom names.
Materials and methods
Structure modeling
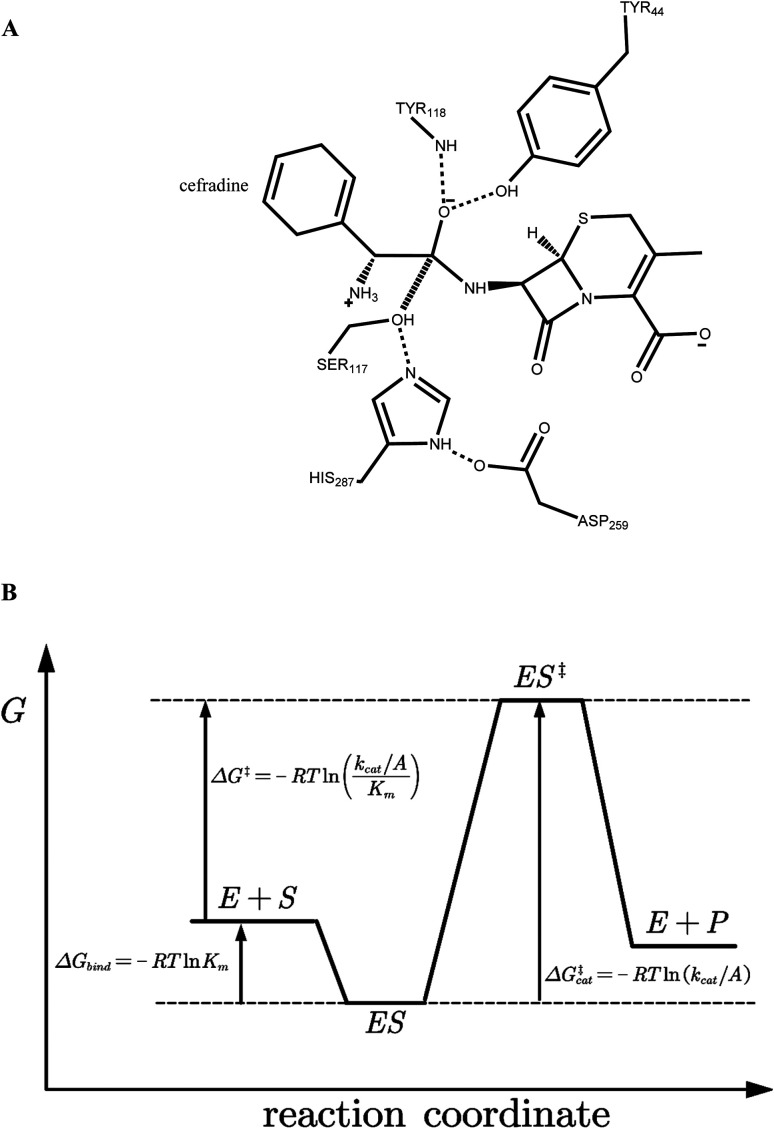
The crystal structure of wild-type cocaine esterase from Rhodococcus sp. (PDB ID: 1JU3) was taken directly from the Protein Data Bank (PDB) without further minimization. The water molecules were removed, and hydrogen atoms were added using PRODA by virtue of the topology parameters of the all-atom CHARMM 22 force field. The crystal structure of cephradine was taken directly from the Cambridge Structural Database and the heavy atom names of cephradine are shown in Fig. 1B. The geometries of cephradine in the transition and Michaelis binding states (Fig. 2A) were calculated by PRODA.
Fig. 2. (A) Catalytic geometrical constraints of cephradine hydrolase. The hypothesized bond between atoms C15 and OG is shown in hashed line. Hydrogen bonds are shown in dashed lines. (B) Reaction coordinate of enzymatic reaction. E + S represents the unbound form of enzyme and substrate, ES for the Michaelis binding state, and ES‡ for the transition state. R indicates the gas constant, Km is the apparent Michaelis parameter, kcat is the turnover number, and A is the pre-exponential factor.
The geometry of cephradine at the transition state (TS) is shown in Fig. 2A, where the central atom (C15) adopts a tetrahedral intermediate form. The catalytic geometrical relationships between the TS and the catalytic residues of the protein scaffold are shown in Fig. 2A. The catalytic triad (Ser117–His287–Asp259) forms the nucleophilic attacking group while the backbone amido group of Try118 and the hydroxyl group of Tyr44 constitute the oxyanion hole that stabilizes the negatively charged O16 atom. To represent the translational, rotational and conformational freedoms of the TS in the active site, a rotamer library of the TS with 5470 conformers was generated using the targeted small molecule placement approach developed in our earlier work,33 which is based on the catalytic geometrical constraints (Table S1†) and placing rules (Table S2†). The atomic parameters for cephradine were obtained from the model compounds of the CHARMM 22 force field and the atomic partial charges were assigned based on the PARSE model. In the active site of the protein scaffold, a total of 36 residues (N42, Y44, W52, T54, Q55, S56, H87, V116, S117, Y118, L119, V121, S140, M141, S143, L146, A149, P150, W151, A162, W166, L169, I170, W220, W235, D259, F261, E264, S265, W285, S286, H287, S288, L290, L407, F408) were subjected to side chain conformational optimization. A backbone-independent rotamer library compiled by Xiang and Honig,35 which contains 11 810 original rotamers, was used to model the side chain conformations of the design sites. The atomic and internal coordination parameters for amino acids were taken from the all-atom force field CHARMM 22. The protein–ligand interaction for the enzyme–TS complex in PRODA was calculated using the MM/GBSA form of the free energy function. The enzyme–TS complex was repacked and global minimum energy conformations (GMEC) were identified using the combinatorial optimization algorithm developed in our previous work.33 The optimized conformation was used as the starting geometry of cephradine for the subsequent MD simulations at the TS. The geometry of cephradine at the Michaelis binding state (Fig. 2B) was obtained in a similar way to that described above. However, the amide bond in the geometry of cephradine adopted the planar form and the distance between the C15 atom of cephradine and the OG atom of Ser117 was extended to van der Waals contact ranges. The catalytic geometrical constraints and placing rules for small molecular placement at the Michaelis binding state are presented in Tables S3 and S4,† respectively.
Molecular dynamics simulation
The MD simulations were carried out with the Desmond package.36 In each case, an orthorhombic solvent box was constructed with a distance of 10 Å from the solute, and up to 15 000 water molecules represented by TIP3P37 were added to the box. The charge of the system was neutralized by addition of an appropriate number of Na+ or Cl− counter ions to the solvent box. The atomic partial charges of cephradine were fitted using the RESP techniques38 by the AmberTools module antechamber, where the electrostatic potential of cephradine was calculated using the Hartree–Fock (H F)/6-31G* basis set by Gaussian 09.39 In the molecular mechanics energy calculation, the Amber force field ff99SB-ILDN40 was used for enzymes and the general Amber force filed gaff41 was used for cephradine. The system was relaxed at 10 K by 100 ps Brownian dynamics NVT simulation with restraints on the solute heavy atoms (50 kcal mol−1). The solvent box was then equilibrated at 10 K by 12 ps of NVT simulation and 12 ps of NPT simulation with restraints on the solute heavy atoms (50 kcal mol−1). The system was then heated to 300 K and full equilibration was performed in the NPT ensemble for 12 ps with restraints on the solute heavy atoms (50 kcal mol−1). The last relaxation procedure was a 24 ps NPT dynamics run at 300 K without restraints. Finally, unrestrained production runs were performed at 300 K for 20 ns, which is a length that is considered adequate for similar calculations.16 The M-SHAKE42 algorithm was used to restrain bonds involving hydrogen atoms to their equilibrium lengths. Non-bonded interactions were truncated at 9 Å and the Gaussian split Ewald method43 with a 60 × 40 × 60 mesh was used for electrostatic interactions. The constant temperature and pressure were controlled using a Berendsen thermostat or manostat.44 Approximately 20 000 snapshots were deposited with a time space of 1 ps. The Desmond built-in post-analysis utility Simulation Event Analysis was used to extract statistics information, including distances, angles and RMSDs from the MD records. The MD simulation was run on a computer cluster with 64 cores and usually took 35 h to finish.
Binding free energy calculations by MM/PBSA and MM/GBSA
In the MM/PBSA or MM/GBSA methods, the binding free energy (ΔGbind) between the substrate (S) and the enzyme (E) to form a complex ES is calculated as:
| ΔGbind = ΔEMM + ΔGpol + ΔGnp − TΔS | 1 |
where ΔEMM represents the gas-phase molecular mechanics energy, including bond stretching, angle bending, torsion rotation, van der Waals and electrostatic contributions, as:
| ΔEMM = ΔEbond + ΔEangle + ΔEtors + ΔEvdw + ΔEelec | 2 |
The ΔGpol term represents the polar contribution to the solvation free energy, while the ΔGnp term stands for the non-polar contribution. The ΔS term represents the conformational entropy, which can be estimated by normal-mode analyses. The conformational entropy contribution to the binding free energy is controversial45–47 and this term was neglected to reduce computational cost. In this work, the binding free energies were calculated using the single trajectory approach based on the MD simulation of the protein–ligand complex, as this computational strategy can reduce noise and errors in simulations.28 Therefore, the internal energy terms (ΔEbond, ΔEangle, ΔEtors) in eqn (2) cancel and the gas-phase interaction energy (ΔEMM) between the enzyme and the substrate is the sum of van der Waals (ΔEvdw) and electrostatic (ΔEelec) interaction energies. All analyses by MM/PBSA and MM/GBSA were implemented using the MMPBSA.py48 python script in the AmberTools17 package. The analyses were carried out on 100 evenly spaced snapshots extracted from the production MD run trajectory between 10 and 20 ns, where the trajectory files from Desmond were transformed into Amber coordinate files via VMD software.49 In MM/PBSA, the ΔGpol term was calculated by solving the linearized Possion–Boltzmann equation; the default finite-difference PB solver with default parameters was adopted. In MM/GBSA, the ΔGpol term was calculated by the modified GB models developed by Onufriev50 and his colleagues, where the atomic radii (igb = 5) were chosen. In both PB and GB calculations, the salt molar concentration was set at 0.1 M in solution. The ΔGnp term was determined based on the solvent accessible surface area (SASA): ΔGnp = surften × ΔSASA, where the default parameter (surften = 0.0072 kcal mol−1 Å−2) was adopted. In this work, explicit waters around the substrate were considered in the MM/PBSA and MM/GBSA analyses, and the corresponding MD trajectories were obtained using the Amber module cpptraj51 with the keyword “closest”, which retains the requested number (Nwat) of water molecules that are closest to the substrate.
Results and discussion
Validation of the MD simulation
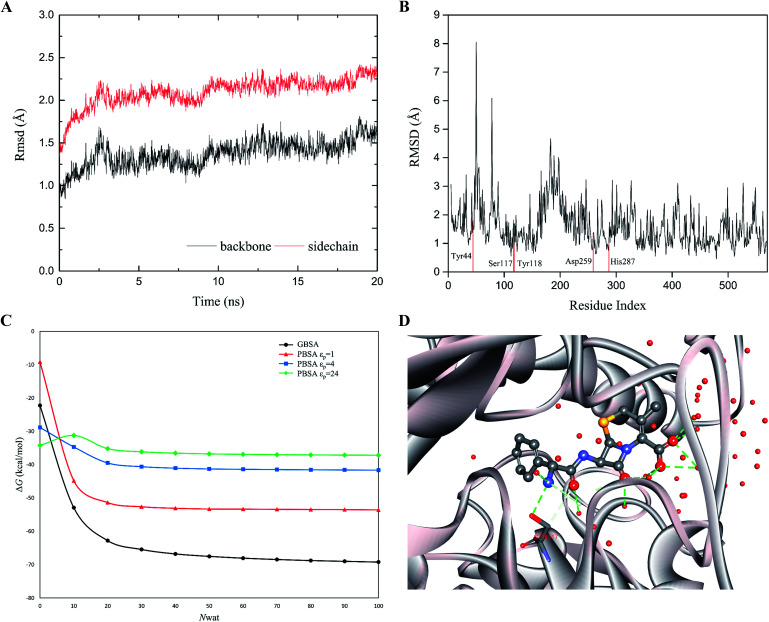
The rapid MD simulation protocols introduced in the preceding section were verified by testing the stability of the wild-type (WT) cocaine esterase (cocE). The ligand and the water molecules in the crystal structure (PDB ID: 1JU3) of cocE were removed. The RMSD of all backbone atoms and side chain atoms of cocE relative to their initial crystal structural positions were monitored over the course of 20 ns MD simulations, and the resulting plots of RMSDs are shown in Fig. 3A. After 10 ns, the observed RMSDs for backbone and side chain atoms lie within a low and narrow range of approximately 1.25–1.75 Å and 2.0–2.5 Å, respectively. The time averaged RMSD for each residue of cocE is shown in Fig. 3B, where the five catalytic residues are indicated by red lines. Ser117 is the most flexible residue in the active site with a RMSD value of 1.82 Å. Ser117 plays the nucleophilic attacking role in the catalytic machinery and its structural flexibility is consistent with this function. All other catalytic residues, i.e., His287 (1.00 Å), Asp259 (1.37 Å), Tyr44 (1.80 Å) and Tyr118 (0.96 Å), displayed very low RMSDs as they contribute hydrogen bonds to stabilize either the catalytic triad or the oxyanion. The whole structure and the active site geometries were well maintained during the simulation. Moreover, the system volume kept stable during the 20 ns MD simulations (Fig. S2†). We concluded that the MD simulation protocols recapitulate the crystal structure of cocE and this protocol should behave equally well in the presence of substrates.
Fig. 3. (A) The RMS deviations between the crystal structure and the MD snapshots for wild type cocE during 20 ns. The RMSDs of backbone atoms are represented by black line, while the RMSDs of sidechain atoms are shown in red line. (B) The 20 ns averaged RMSDs of heavy atoms are shown in per-residue form. Five catalytic residues Tyr44, Ser117, Tyr118, Asp259, and His287 are labeled in red. (C) The effect of number of explicit waters (Nwat) considered in MM/GBSA and MM/PBSA methods on the predicted binding free energies of WT. The black line indicates the results from the MM/GBSA method, while the red, blue, and green lines for results from the MM/PBSA methods based on εp = 1, 4, or 24. (D) The active site geometry with 50 explicit water molecules. The protein secondary structure is shown in silver ribbon. The cefradine is shown in ball-and-stick model. The hydrogen bonds are represented by green dashed lines. Oxygen atoms are colored in red, nitrogen atoms in cyan, and carbon atoms in grey.
The explicit waters around the substrate were considered in the binding free energy calculations by MM/PBSA or MM/GBSA. In addition, explicit water molecules that surround the substrate were considered in this study because these water molecules may influence energetic parameters. Computations were performed on the WT cocE–cephradine complex to probe the influence of the number of explicit water molecules on the calculated binding free energies. The calculated results of the binding free energies by MM/PBSA and MM/GBSA against the number of explicit waters from 0 to 100 with increments of 10 are presented in Fig. 3C. The calculated binding free energies decreased drastically when considering only a few explicit water molecules in the MM/PBSA and MM/GBSA methods. This result may be due to the closest water molecules forming hydrogen bonds with the substrate (Fig. 3D). The calculated binding free energies were essentially constant once the number of explicit water molecules (Nwat) increased above 30. Since changes in the electrostatic environment of the active site of cocE variants may change, 50 explicit waters were considered in the following binding free energy calculations by both MM/PBSA and MM/GBSA methods.
Ranking variants by calculated binding free energy
Wild-type cocE and its variants belong to the family of serine proteases. For the amide hydrolysis reaction that is catalyzed by serine proteases,52 the acylation process is always the rate-limiting step when compared with that of the deacylation process. Moreover, WT cocE and its variants are poor enzyme catalysts towards the hydrolysis of cephradine,30 indicating that the kinetics of cephradine hydrolysis is reaction-controlled rather than diffusion-controlled. This can be explained that the scaffold of the esterase cocE and its variants lacks of suitable hydrogen bonding acceptor to stabilize the leaving amino group of cephradine in the transition state for proton shuttling with His287 and results in low amidase activity.54,55 Therefore, the Michaelis–Menten equation for cephradine hydrolysis can be greatly simplified and the Michaelis constant, Km, can be approximated by the dissociation constant KS of the enzyme–substrate complex. The binding free energy ΔGbind corresponds to the Gibbs free energy change between the enzyme–substrate bound form (ES state in Fig. 2B) and the unbound form (E + S state in Fig. 2B). Based on the MD simulations, the binding free energies (ΔGbind) of WT cocE and variants were calculated by the MM/PBSA and MM/GBSA methods. Importantly, the MM/PBSA and MM/GBSA methods are used here to rank the binding free energies of the variants rather than give accurate predictions of the absolute binding free energies.
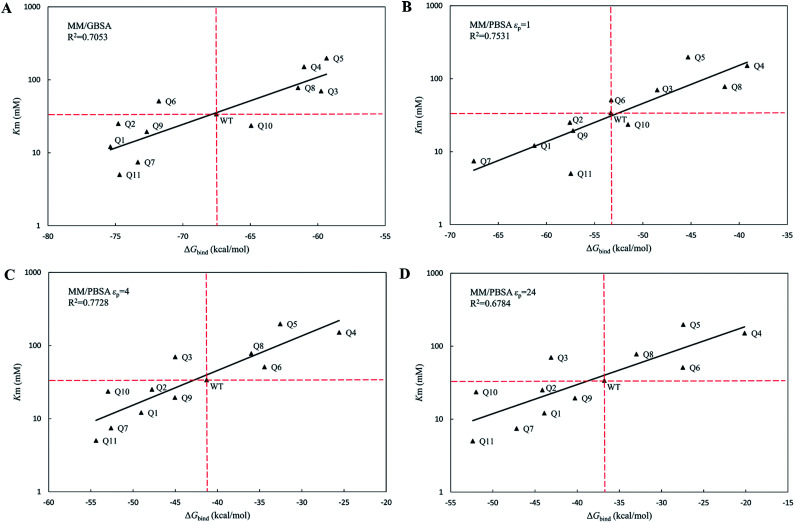
The calculated binding free energies (ΔGbind) were semi-log plotted against the experimentally measured Km values for the cocE WT and variants in Fig. 4A for the MM/GBSA method and Fig. 4B–D for the MM/PBSA method based on different protein dielectric constants εp. The results of the statistical significance test for these correlations were shown in Table S5,† and all these fits passed the t-test. In Fig. 4A, WT cocE and the majority of the variants concentrated around the regression line, resulting in a correlation coefficient of R2 = 0.7053. A hypothetical coordinate system with the WT protein as the origin was added to Fig. 4A, and the results of all variants, except Q6 and Q10, resided in the first and third quadrants, indicating that the MM/GBSA method can differentiate variants with that of the WT protein according to the predicted binding free energies between enzyme and the substrate. However, results for the variants lying in the first and third quadrants were widely distributed around the regression line, indicating that the MM/GBSA method cannot rank the variants well. Fig. 4B shows the predicted binding free energies calculated by the MM/PBSA method based on εp = 1, and the correlation coefficient improved (i.e., R2 = 0.7531) when compared with that of the MM/GBSA method. The results of all variants except Q10 in Fig. 4B resided in the first and third quadrants, and more importantly the results for these variants concentrated on the regression line, indicating that the MM/PBSA method not only can differentiate variants from that of the WT protein, but can also rank the variants. This can be attributed to the finite-difference Poisson–Boltzmann method embedded in the MM/PBSA method calculating the electrostatic component of the solvation energy more accurately than the generalized Born model. The active site of the enzyme is a typical anisotropic electrostatic environment and the dielectric constant in the active pocket should be higher than that in the hydrophobic core of the protein since it is always directly in contact with the polar solvent. In Fig. 4C and D, the binding free energies between enzymes and substrate were calculated by the MM/PBSA method based on εp = 4 and εp = 24, respectively. In Fig. 4C, the correlation coefficient R2 = 0.7728 was further improved. The results for all variants except Q3 reside in the first and third quadrants. Note that variant Q6, which was a false positive prediction in Fig. 4A, moved completely into the first quadrant, and variant Q10, which was a false negative prediction in Fig. 4B, moved into the third quadrant, indicating that these two variants were predicted correctly by the MM/PBSA method based on εp = 4. Moreover, variant Q11, whose apparent binding constant was the smallest among all variants, ranked best in Fig. 4C according to the predicted binding free energies. The predicted binding free energies by the MM/PBSA method deteriorated when the εp was increased to 24. The correlation coefficient decreased noticeably in Fig. 4D (R2 = 0.6784), indicating that selection of the appropriate protein dielectric constant is critical for the MM/PBSA method to correctly predict the binding free energies. In summary, a relatively high protein dielectric constant (εp = 4) is beneficial for ranking purposes using the MM/PBSA method, which is consistent with the suggestion from Hou and his colleagues.53
Fig. 4. The regression between the experimental Michaelis binding constants and the predicted binding free energies of WT and its eleven variants by MM/GBSA and MM/PBSA methods. The ordinate is scaled logarithmically, and the hypothetical coordination systems are shown in dashed lines with the WT as the origin. (A) MM/GBSA method; (B) MM/PBSA method based on εp = 1; (C) MM/PBSA method based on εp = 4; (D) MM/PBSA method based on εp = 24.
Ranking variants by the calculated activation energy barrier
On the reaction coordinate for enzymatic catalysis shown in Fig. 2B, the Gibbs free energy change (activation energy, ΔG‡cal) from the Michaelis binding state (ES) to the transition state (ES‡) corresponds to the turnover number (kcat). The activation process involves formation of a bond between the OG atom of Ser117 and the central C15 atom of cephradine during the acylation step for the hydrolytic reaction of cephradine, and that the molecular dynamics simulation using the ff99SB-ILDN force field cannot handle bond breaking and formation. Therefore, we cannot use the MM/GBSA method or the MM/PBSA method to calculate the activation energies of the variants. In fact, the experimental turnover numbers (kcat) and the calculated activation energies (ΔG‡cat) of WT and its eleven variants by MM/GBSA and MM/PBSA methods were poorly correlated (Fig. S1(A–D)†), and all fits did not pass the t-test but for MM/PBSA method based on εp = 24 (Table S5†). However, the acylated state is relatively stable when compared with that of the transition state and the bond between the OG atom of Ser117 and the central C15 atom of cephradine was formed. Therefore, the MD simulation can be run for this state. The MD simulation time (20 ns) is much longer than the actual lifetime of the intermediate state (∼fs). In the reference state (E + S), the solvation processes of the isolated enzyme (E) and substrate (S) can be performed by two individual MD simulations. Using the trajectories of the three individual MD simulations for E, S and ES‡, the free energy change (ΔG‡) between the transition state (ES‡) and the reference state (E + S) can be calculated by the MM/GBSA method or the MM/PBSA method. As this free energy change (ΔG‡) corresponds to the catalytic efficiency (kcat/Km) of the enzyme, we can use the calculated ΔG‡ to evaluate the variants. Note that the covalent bond energy between the enzyme and substrate was not included in the calculated free energy change (ΔG‡) and was cancelled during the evaluation of the variants. To obtain convergent results in the triple trajectories, water molecules within a 10 Å range to the OG atom of Ser117 were explicitly considered for the states (E) and (ES‡) during the calculation of the solvation energy, whereas the implicit method was used for the S state.
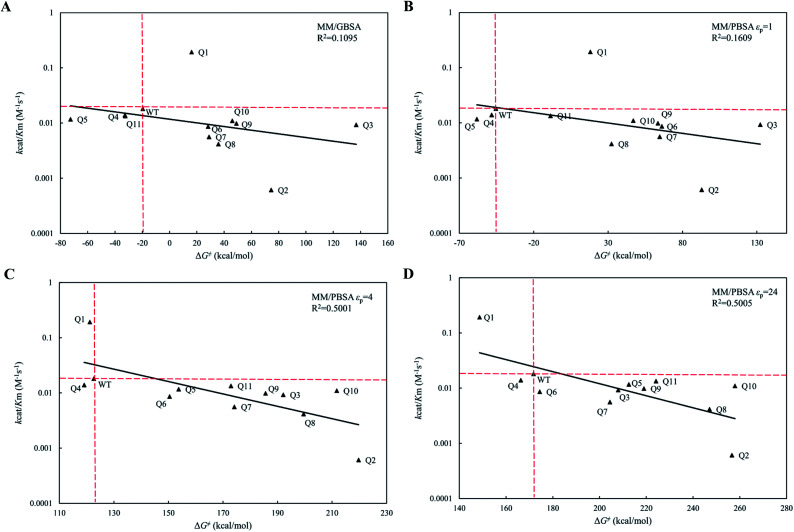
The calculated free energy changes (ΔG‡) are semi-log plotted against the experimentally measured catalytic efficiencies (kcat/Km) for WT cocE and variants in Fig. 5A for the MM/GBSA method and for the MM/PBSA method (Fig. 5B–D) based on different εp. In Fig. 5A, the MM/GBSA method showed a very poor correlation coefficient (R2 = 0.1095). The variants Q4, Q5 and Q11 appeared to be false positives because they showed even lower energy barriers than the WT enzyme even though their catalytic efficiencies were lower. Moreover, the best variant Q1 showed a ten-fold higher catalytic efficiency (kcat/Km) than the WT protein (Table 1), but this was a false negative because the predicted energy barrier of the variant was higher than that of the WT enzyme. In Fig. 5B, the MM/PBSA method based on εp = 1 yielded similar performances with only an improvement observed for variant Q10, i.e., the result was no longer in the false positive quadrant. These results indicate that the protein dielectric constant might be set too low (εp = 1) to correctly reflect the electrostatic environment in the active site of the enzyme. Moreover, the correlation between kcat/Km and ΔG‡ for MM/GBSA method and MM/PBSA method based on εp = 1 did not pass the t-test (Table S5†). In Fig. 5C and D, the εp was increased to 4 and 24, respectively. In Fig. 5C, the MM/PBSA method based on εp = 4 showed a better correlation coefficient (R2 = 0.5001) and most variants were distributed along the regression line. The best variant, Q1, ranked second among all variants and its relative position to that of the WT protein was predicted correctly, although the free energy gap was small. The worst variant Q2 was predicted to have the highest energy barrier, which is also consistent with its experimental catalytic efficiency. The variant Q4 was the only false positive prediction and no false negative prediction was observed. When the εp was increased to 24 in Fig. 5D, the best variant Q1 ranked top and its free energy gap relative to the WT enzyme increased when compared with the results in Fig. 5C. Although the correlation coefficient (R2 = 0.5005) did not improve, the better prediction results showed that the evaluation performance of the MM/PBSA method could be greatly improved if higher protein dielectric constants are selected in the active site. All eleven variants were predicted by PRODA to have higher catalytic efficiencies when compared with that of the WT enzyme, but the results shown in Table 1 indicate that all variants except Q1 were false positive predictions. Based on MD simulations, the energy barriers shown in Fig. 5D, which were calculated by the MM/PBSA method under a suitable εp (i.e., 24), can help to eliminate all false positive variants except Q4 before experiments were recorded. Therefore, MD based simulations can greatly improve the accuracy of energy-based sequence prediction tools, such as PRODA, for computational enzyme design.
Fig. 5. The regression between the experimental catalytic efficiencies and the predicted activation energy barries of WT and its eleven variants by MM/GBSA and MM/PBSA methods. The ordinate is scaled logarithmically, and the hypothetical coordination systems are shown in dashed lines with the WT as the origin. (A) MM/GBSA method; (B) MM/PBSA method based on εp = 1; (C) MM/PBSA method based on εp = 4; (D) MM/PBSA method based on εp = 24.
The kinetic parameters of the cephradine hydrolase and its variants predicted by PRODA. The data is taken from the ESI of the ref. 30. Reaction conditions are: pH 7.0 at 22 °C.
| Variants | Mutations | k cat (×10−3 s−1) | K m (mM) | k cat/Km (×10−3 M−1 s−1) |
|---|---|---|---|---|
| WT | — | 0.61 | 33.90 | 18.11 |
| Q1 | F261T | 2.33 | 12.10 | 192.72 |
| Q2 | Q55R | 0.02 | 25.16 | 0.61 |
| Q3 | F408L | 0.65 | 70.03 | 9.26 |
| Q4 | P150E | 2.11 | 151.34 | 13.93 |
| Q5 | F261T/F408L | 2.32 | 198.12 | 11.68 |
| Q6 | F261T/P150E | 0.44 | 51.16 | 8.63 |
| Q7 | F261T/L407Q | 0.04 | 7.46 | 5.61 |
| Q8 | F261T/L407H | 0.32 | 77.98 | 4.16 |
| Q9 | F261T/F408Y | 0.19 | 19.47 | 9.84 |
| Q10 | F261T/L407Q/F408Y | 0.26 | 23.68 | 10.99 |
| Q11 | F261T/L407H/F408Y | 0.07 | 5.02 | 13.41 |
Conclusions
In this paper, the computationally designed variants of a Rhodococcus sp. cocaine esterase for the hydrolysis of cephradine were assessed quantitatively by MM/GBSA and MM/PBSA methods based on MD simulations. The apparent Km of the variants correlated well with the binding free energies calculated by the MM/GBSA and MM/PBSA methods with explicit waters around the substrate considered. The catalytic efficiencies kcat/Km of the variants correlated poorly with the activation energy barriers calculated by the MM/GBSA and MM/PBSA methods when a low protein dielectric constant (εp = 1) was used. In contrast, when εp = 4 or 24 for the enzyme, the activation energy barriers calculated by the MM/PBSA method correlated well with the catalytic efficiencies (kcat/Km) of the variants, and most false positive predictions obtained by the computational enzyme design program PRODA could be eliminated prior to experimental analysis. Although the methods developed here need to be tested on more systems, we showed that MD-based quantitative assessment of cocE variants provided an effective and efficient screening tool for energy-based computational enzyme design.
Conflicts of interest
There are no conflicts of interest to declare.
Supplementary Material
Acknowledgments
We acknowledge the financial support from the National Natural Science Foundation of China (Grant Numbers: 21476123 and 21878170) and the Ministry of Science and Technology of China (Grant Number: 2012AA021204).
Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra02406a
References
- Bornscheuer U. T. Huisman G. W. Kazlauskas R. J. Lutz S. Moore J. C. Robins K. Nature. 2012;485:185–194. doi: 10.1038/nature11117. [DOI] [PubMed] [Google Scholar]
- Schmid A. Dordick J. S. Hauer B. Kiener A. Wubbolts M. Witholt B. Nature. 2001;409:258–268. doi: 10.1038/35051736. [DOI] [PubMed] [Google Scholar]
- Arnold F. H. Nature. 2001;409:253–257. doi: 10.1038/35051731. [DOI] [PubMed] [Google Scholar]
- Tantillo D. J. Jiangang C. Houk K. N. Curr. Opin. Chem. Biol. 1998;2:743–750. doi: 10.1016/S1367-5931(98)80112-9. [DOI] [PubMed] [Google Scholar]
- Zanghellini A. Jiang L. Wollacott A. M. Cheng G. Meiler J. Althoff E. A. Röthlisberger D. Baker D. Protein Sci. 2006;15:2785–2794. doi: 10.1110/ps.062353106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Röthlisberger D. Khersonsky O. Wollacott A. M. Jiang L. DeChancie J. Betker J. Gallaher J. L. Althoff E. A. Zanghellini A. Dym O. Albeck S. Houk K. N. Tawfik D. S. Baker D. Nature. 2008;453:190–195. doi: 10.1038/nature06879. [DOI] [PubMed] [Google Scholar]
- Jiang L. Althoff E. A. Clemente F. R. Doyle L. Rothlisberger D. Zanghellini A. Gallaher J. L. Betker J. L. Tanaka F. Barbas C. F. Hilvert D. Houk K. N. Stoddard B. L. Baker D. Science. 2008;319:1387–1391. doi: 10.1126/science.1152692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel J. B. Zanghellini A. Lovick H. M. Kiss G. Lambert A. R. St Clair J. L. Gallaher J. L. Hilvert D. Gelb M. H. Stoddard B. L. Houk K. N. Michael F. E. Baker D. Science. 2010;329:309–313. doi: 10.1126/science.1190239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon S. R. Stanley E. J. Wolf S. Toland A. Wu S. J. Hadidi D. Mills J. H. Baker D. Pultz I. S. Siegel J. B. J. Am. Chem. Soc. 2012;134:20513–20520. doi: 10.1021/ja3094795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khare S. D. Kipnis Y. Greisen P. J. Takeuchi R. Ashani Y. Goldsmith M. Song Y. Gallaher J. L. Silman I. Leader H. Sussman J. L. Stoddard B. L. Tawfik D. S. Baker D. Nat. Chem. Biol. 2012;8:294–300. doi: 10.1038/nchembio.777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel J. B. Smith A. L. Poust S. Wargacki A. J. Bar-Even A. Louw C. Shen B. W. Eiben C. B. Tran H. M. Noor E. Gallaher J. L. Bale J. Yoshikuni Y. Gelb M. H. Keasling J. D. Stoddard B. L. Lidstrom M. E. Baker D. Proc. Natl. Acad. Sci. U. S. A. 2015;112:3704–3709. doi: 10.1073/pnas.1500545112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wijma H. J. Floor R. J. Bjelic S. Marrink S. J. Baker D. Janssen D. B. Angew. Chem., Int. Ed. 2015;54:3726–3730. doi: 10.1002/anie.201411415. [DOI] [PubMed] [Google Scholar]
- Grisewood M. J. Hernández-Lozada N. J. Thoden J. B. Gifford N. P. Mendez-Perez D. Schoenberger H. A. Allan M. F. Floy M. E. Lai R.-Y. Holden H. M. Pfleger B. F. Maranas C. D. ACS Catal. 2017;7:3837–3849. doi: 10.1021/acscatal.7b00408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R. Wijma H. J. Song L. Cui Y. Otzen M. Tian Y. Du J. Li T. Niu D. Chen Y. Feng J. Han J. Chen H. Tao Y. Janssen D. B. Wu B. Nat. Chem. Biol. 2018;14:664–670. doi: 10.1038/s41589-018-0053-0. [DOI] [PubMed] [Google Scholar]
- Alexandrova A. N. Röthlisberger D. Baker D. Jorgensen W. L. J. Am. Chem. Soc. 2008;130:15907–15915. doi: 10.1021/ja804040s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiss G. Röthlisberger D. Baker D. Houk K. N. Protein Sci. 2010;19:1760–1773. doi: 10.1002/pro.462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frushicheva M. P. Cao J. Chu Z. T. Warshel A. Proc. Natl. Acad. Sci. U. S. A. 2010;107:16869–16874. doi: 10.1073/pnas.1010381107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osuna S. Jiménez-Osés G. Noey E. L. Houk K. N. Acc. Chem. Res. 2015;48:1080–1089. doi: 10.1021/ar500452q. [DOI] [PubMed] [Google Scholar]
- Privett H. K. Kiss G. Lee T. M. Blomberg R. Chica R. A. Thomas L. M. Hilvert D. Houk K. N. Mayo S. L. Proc. Natl. Acad. Sci. U. S. A. 2012;109:3790–3795. doi: 10.1073/pnas.1118082108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mollica L. Conti G. Pollegioni L. Cavalli A. Rosini E. J. Chem. Inf. Model. 2015;55:2227–2241. doi: 10.1021/acs.jcim.5b00535. [DOI] [PubMed] [Google Scholar]
- Jiménez-Osés G. Osuna S. Gao X. Sawaya M. R. Gilson L. Collier S. J. Huisman G. W. Yeates T. O. Tang Y. Houk K. N. Nat. Chem. Biol. 2014;10:431–436. doi: 10.1038/nchembio.1503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Q. Huang X. Zhu Y. J. Mol. Model. 2014;20:2314. doi: 10.1007/s00894-014-2314-5. [DOI] [PubMed] [Google Scholar]
- Åqvist J. Luzhkov V. B. Brandsdal B. O. Acc. Chem. Res. 2002;35:358–365. doi: 10.1021/ar010014p. [DOI] [PubMed] [Google Scholar]
- Pearlman D. A. Charifson P. S. J. Med. Chem. 2001;44:3417–3423. doi: 10.1021/jm0100279. [DOI] [PubMed] [Google Scholar]
- Price D. J. Jorgensen W. L. J. Comput.-Aided Mol. Des. 2001;15:681–695. doi: 10.1023/A:1012266200343. [DOI] [PubMed] [Google Scholar]
- Massova I. Kollman P. A. Perspect. Drug Discovery Des. 2000;18:113–135. doi: 10.1023/A:1008763014207. [DOI] [Google Scholar]
- Kollman P. A. Massova I. Reyes C. Kuhn B. Huo S. Chong L. Lee M. Lee T. Duan Y. Wang W. Donini O. Cieplak P. Srinivasan J. Case D. A. Cheatham T. E. Acc. Chem. Res. 2000;33:889–897. doi: 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- Hou T. Wang J. Li Y. Wang W. J. Chem. Inf. Model. 2011;51:69–82. doi: 10.1021/ci100275a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genheden S. Ryde U. Expert Opin. Drug Discovery. 2015;10:449–461. doi: 10.1517/17460441.2015.1032936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang X. Xue J. Zhu Y. Chem. Commun. 2017;53:7604–7607. doi: 10.1039/C7CC02270K. [DOI] [PubMed] [Google Scholar]
- Zhu Y. Ind. Eng. Chem. Res. 2007;46:839–845. doi: 10.1021/ie0605985. [DOI] [Google Scholar]
- Lei Y. Luo W. Zhu Y. Protein Sci. 2011;20:1566–1575. doi: 10.1002/pro.685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang X. Han K. Zhu Y. Protein Sci. 2013;22:929–941. doi: 10.1002/pro.2275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He J. Huang X. Xue J. Zhu Y. Green Chem. 2018;20:5484–5490. doi: 10.1039/C8GC03420F. [DOI] [Google Scholar]
- Xiang Z. Honig B. J. Mol. Biol. 2001;311:421–430. doi: 10.1006/jmbi.2001.4865. [DOI] [PubMed] [Google Scholar]
- Bowers K. J., Chow D. E., Xu H., Dror R. O., Eastwood M. P., Gregersen B. A., Klepeis J. L., Kolossvary I., Moraes M. A., Sacerdoti F. D., Salmon J. K., Shan Y. and Shaw D. E., in Proceedings of the ACM/IEEE SC 2006 Conference, 2006, pp. 43–43 [Google Scholar]
- Jorgensen W. L. Chandrasekhar J. Madura J. D. Impey R. W. Klein M. L. J. Chem. Phys. 1983;79:926–935. doi: 10.1063/1.445869. [DOI] [Google Scholar]
- Bayly C. I. Cieplak P. Cornell W. Kollman P. A. J. Phys. Chem. 1993;97:10269–10280. doi: 10.1021/j100142a004. [DOI] [Google Scholar]
- Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Mennucci B., Petersson G. A., Nakatsuji H., Caricato M., Li X., Hratchian H. P., Izmaylov A. F., Bloino J., Zheng G., Sonnenberg J. L., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Montgomery J. A., Peralta J. E., Ogliaro F., Bearpark M., Heyd J. J., Brothers E., Kudin K. N., Staroverov V. N., Kobayashi R., Normand J., Raghavachari K., Rendell A., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Rega N., Millam J. M., Klene M., Knox J. E., Cross J. B., Bakken V., Adamo C., Jaramillo J., Gomperts R., Stratmann R. E., Yazyev O., Austin A. J., Cammi R., Pomelli C., Ochterski J. W., Martin R. L., Morokuma K., Zakrzewski V. G., Voth G. A., Salvador P., Dannenberg J. J., Dapprich S., Daniels A. D., Farkas Ö., Foresman J. B., Ortiz J. V., Cioslowski J. and Fox D. J., Gaussian 09 Revision A.2, 2009
- Lindorff-Larsen K. Piana S. Palmo K. Maragakis P. Klepeis J. L. Dror R. O. Shaw D. E. Proteins. 2010;78:1950–1958. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J. Wolf R. M. Caldwell J. W. Kollman P. A. Case D. A. J. Comput. Chem. 2004;25:1157–1174. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Kräutler V. van Gunsteren W. F. Hünenberger P. H. J. Comput. Chem. 2001;22:501–508. doi: 10.1002/1096-987X(20010415)22:5<501::AID-JCC1021>3.0.CO;2-V. [DOI] [Google Scholar]
- Shan Y. Klepeis J. L. Eastwood M. P. Dror R. O. Shaw D. E. J. Chem. Phys. 2005;122:54101. doi: 10.1063/1.1839571. [DOI] [PubMed] [Google Scholar]
- Berendsen H. J. C. Postma J. P. M. van Gunsteren W. F. DiNola A. Haak J. R. J. Chem. Phys. 1984;81:3684–3690. doi: 10.1063/1.448118. [DOI] [Google Scholar]
- Yang T. Wu J. C. Yan C. Wang Y. Luo R. Gonzales M. B. Dalby K. N. Ren P. Proteins. 2011;79:1940–1951. doi: 10.1002/prot.23018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallnoefer H. G. Liedl K. R. Fox T. J. Comput. Chem. 2011;32:1743–1752. doi: 10.1002/jcc.21758. [DOI] [PubMed] [Google Scholar]
- Weis A. Katebzadeh K. Söderhjelm P. Nilsson I. Ryde U. J. Med. Chem. 2006;49:6596–6606. doi: 10.1021/jm0608210. [DOI] [PubMed] [Google Scholar]
- Miller B. R. McGee T. D. Swails J. M. Homeyer N. Gohlke H. Roitberg A. E. J. Chem. Theory Comput. 2012;8:3314–3321. doi: 10.1021/ct300418h. [DOI] [PubMed] [Google Scholar]
- Humphrey W. Dalke A. Schulten K. J. Mol. Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Onufriev A. Bashford D. Case D. A. Proteins. 2004;55:383–394. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- Roe D. R. Cheatham T. E. J. Chem. Theory Comput. 2013;9:3084–3095. doi: 10.1021/ct400341p. [DOI] [PubMed] [Google Scholar]
- Hedstrom L. Chem. Rev. 2002;102:4501–4524. doi: 10.1021/cr000033x. [DOI] [PubMed] [Google Scholar]
- Sun H. Li Y. Shen M. Tian S. Xu L. Pan P. Guan Y. Hou T. Phys. Chem. Chem. Phys. 2014;16:22035–22045. doi: 10.1039/C4CP03179B. [DOI] [PubMed] [Google Scholar]
- Syrén P.-O. Hult K. ChemCatChem. 2011;3:853–860. doi: 10.1002/cctc.201000448. [DOI] [Google Scholar]
- Syrén P.-O. FEBS J. 2013;280:3069–3083. doi: 10.1111/febs.12241. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.