The Relationship of Whole Human Vertebral Body Creep to Bone Density and Texture via Clinically Available Imaging Modalities

Abstract

Creep deformation of human vertebrae accumulates under physiological levels of load and is understood to contribute to the progression toward clinically observable vertebral fracture. However, little information is available in terms of clinically measurable predictors of creep behavior in human vertebrae. In this study, creep tests were performed on 22 human cadaveric T12 vertebrae (13 male, 9 female; age 41–90). Areal and volumetric bone density parameters were measured from the same specimens using dual x-ray absorptiometry and high resolution computed tomography. Image textural analyses (which probe the organization of image intensities within the cancellous bone in low resolution clinical imaging) were performed using digital tomosynthesis (DTS) images. Multiple regression models were constructed to examine the relationship between creep properties and bone density and DTS image textural parameters. For the standard clinical imaging configuration, models including DTS derived image textural parameters alone were generally more explanatory (adjusted R²: 0.14–0.682) than those with bone density parameters forced in the models (adjusted R²: 0.17–0.61). Metrics of textural heterogeneity and anisotropy presented as the most explanatory imaging markers for creep deformation and recovery from creep. These metrics of image texture may help provide, independent from bone mass, important clinically measurable indicators of the time dependent deformation of human vertebrae.

INTRODUCTION

Creep, the time-dependent deformation under a persistent load, is known to occur under physiologic levels of load, and contribute to progressive accumulation of deformation in human vertebral bone (Oravec et al., 2018; Pollintine et al., 2009; Yamamoto et al., 2006). Long-term exposure to creep is suggested to play a role in the accumulation of deformation that eventually appear as a vertebral fracture in vivo (Yamamoto et al., 2006).

Several studies reported relationships between creep behavior and trabecular microstructure in human and animal cancellous bone (Kim et al., 2011; Manda et al., 2016) and human vertebral bodies (Oravec et al., 2018). However, despite the potential importance of creep in development of vertebral fractures, little information is available in regards to clinically measurable predictors of creep properties in human vertebral bodies.

We consider digital tomosynthesis (DTS) as a clinically available imaging modality capable of measuring microstructural information relevant to vertebral creep. DTS is able to access the spine while combining a relatively high in-plane resolution (150–300 μm) with about 12–17% of radiation dose of a typical computed tomography exam (Mettler et al., 2008; Zhang et al., 2014). Previous work has demonstrated that cancellous bone microstructure can be quantified using DTS image texture (Kim et al., 2015), and that the textural information from DTS can predict cancellous bone stiffness (Kim et al., 2017) and whole vertebral body strength (Yeni et al., 2018). However, the extent to which DTS derived properties predict vertebral body creep properties has not been studied.

In the current study, we aimed to characterize the relationship between whole human cadaveric vertebral body creep and DTS-derived measures of cancellous bone texture, and determine their relative significance in the presence of bone mineral density (BMD) measures from dual energy x-ray absorptiometry (DXA) and high-resolution computed tomography (HRCT).

METHODS

The specimens used in this study were previously described (Oravec et al., 2018). Briefly, human cadaveric thoraco-lumbar spines were acquired from tissue banks under local IRB approval and thoracic 12 vertebrae were harvested from 22 donors. The donor set consisted of 13 men and 9 women between the ages of 41 and 90 (median age: 69, 25^th percentile: 59, 75^th percentile: 74). Donors with a history of HIV, hepatitis, diabetes, renal failure, metastatic cancer, osteomalacia, hyperparathyroidism, Paget’s disease of bone, spine surgery, cause of death involving trauma, and corticosteroid, anticonvulsant or bisphosphonate use were not included. Vertebral bodies were dissected, soft tissue and posterior elements were removed, and specimens were stored wrapped in saline-soaked gauze at −20 °C until imaging and testing were performed. Prior to imaging studies, specimens were aligned on custom radiolucent trays and placed in acrylic boxes immersed in 0.9% saline to simulate soft tissue contrast encountered in vivo.

The vertebral bodies were scanned using digital tomosynthesis (DTS; Shimadzu Sonialvision Safire II). Specimens were imaged in both coronal and lateral views while aligned axially (0°) or transversely (90°) to the superior-inferior axis of the vertebrae to account for the effect of scanning direction on the resolution of structures oriented parallel or perpendicular to the tomosynthesis sweep direction (Flynn et al., 2007; Notohara et al., 2009; Shibata et al., 2014). 74 projection images were acquired and reconstructed into a stack image with in-plane (coronal/lateral) pixel size of 0.279 mm with 1 mm slice spacing. A cuboidal volume of interest (VOI) was cropped from the cancellous centrum in each vertebral body within the DTS image-stack. Image textural parameters including fractal dimension (FD), mean lacunarity (λ, lacunarities averaged over the range of size scales), the slope lacunarity (S_λ, change of lacunarity with change in size scale), MIL, and LFD were calculated using the fractal, mean intercept length (MIL) and line fraction deviation (LFD) methods as previously described (Figure 1) (Kim et al., 2017). Image textural analyses were performed using DTS data from 22 specimens (one of the 23 specimens used in the previous study did not meet VOI size requirements for unbiased calculation of DTS textural outcomes, and was therefore excluded). Measures of anisotropy were calculated from MIL (A_MIL) and LFD (A_LFD) as the ratio of the principal measurements from respective analysis. Inter-slice standard deviation (SD) of each parameter was also recorded as measures of heterogeneity for that parameter (Figure 1). A description of image textural parameters is provided in Table 1.

Figure 1:

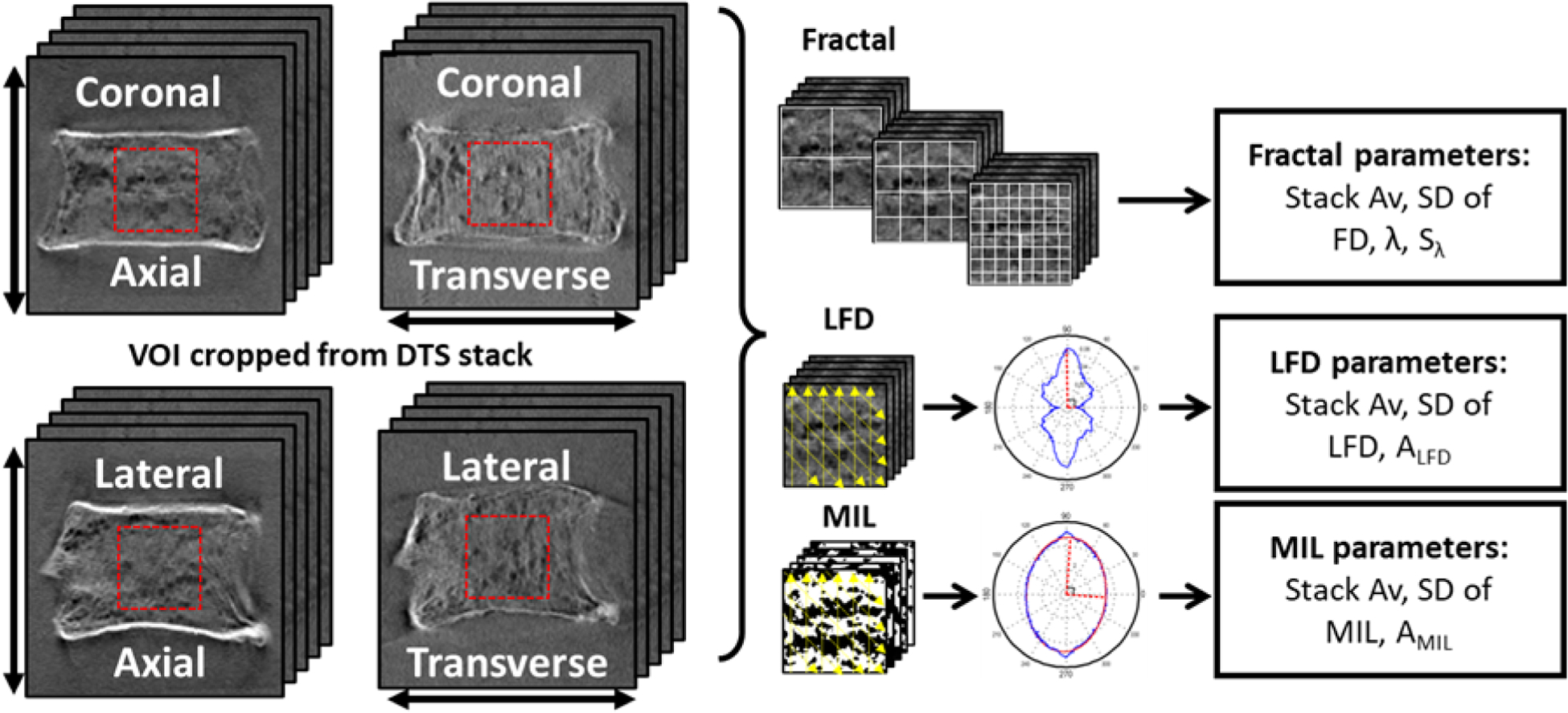
Measurements calculated from axial and transverse DTS images in coronal and lateral views (arrows indicate direction of tomosynthesis sweep). Cuboidal VOIs were extracted from the DTS stack. Fractal analysis, using the box-counting method on gray level images, was performed in Fraclac within ImageJ to calculate Fractal dimension (FD), lacunarity (λ) and lacunarity slope (S_λ) were calculated using the box-counting method. Line fraction deviation analysis (LFD) and mean intercept length (MIL) were calculated using a custom code within MATLAB.

Table 1.

Description of the independent variables measured from DTS, DXA and HRCT, to be correlated with creep properties.

Image Modality	Variable	Description
DTS	FD	Measure of complexity in gray level texture
	λ	Gappiness in gray level texture; a measure of heterogeneity
	Sλ	Rate of change in λ with size scale; alternate measure of texture heterogeneity
	LFD	Measure of maximum orientation in gray level texture
	ALFD	Anisotropy based on LFD
	MIL	Measure of average feature size in binarized texture
	AMIL	Anisotropy based on MIL
	SD-FD	Standard deviation of respective parameters among slices of the analysis volume, as measures of their heterogeneity
	SD-λ
	SD-Sλ
	SD-LFD
	SD-ALFD
	SD-MIL
	SD-AMIL
DXA	BMDAP	Areal BMD measured in AP view
	BMDLat	Areal BMD measured in lateral view
HRCT	cBMD	Cancellous volumetric BMD in HU
	iBMD	Integral cancellous and cortical volumetric BMD in HU
	shBMD	Volumetric BMD of the cortical shell in HU

Measures of areal and volumetric bone density were calculated using dual x-ray absorptiometry (DXA) and high resolution computed tomography (HRCT) images (Figure 2). Vertebral bodies were scanned using DXA in anteroposterior (AP) and lateral (Lat) orientations using a standard fast array lumbar spine protocol (Hologic Discovery-A). Bone mineral density (BMD) was measured from each view (BMD_AP, BMD_Lat) for each vertebra (g/cm²). In order to calculate volumetric BMD, specimens were scanned using high resolution computed tomography (HRCT) and reconstructed at 0.7 mm axial pixel spacing with 0.75 mm slice thickness (Siemens Sensation 64). Volume masks were segmented from HRCT images representing cancellous and cortical bone and multiplied with the original gray value images (Buie et al., 2007; Oravec et al., 2018), from which integral cancellous+cortical (iBMD), volumetric cancellous (cBMD), and shell (shBMD) bone mineral density (BMD) were calculated (Hounsfield units).

Figure 2:

Region definitions for measurement of bone density from CT (left) and DXA (right). Density measures (unit: Hounsfield units) were recorded from CT images within cancellous (cBMD), cortical shell (shBMD), and integral cancellous and cortical volumes (iBMD). Bone mineral density was measured from DXA images acquired in coronal (BMD_AP) and lateral (BMD_LM) orientations (unit: g/cm²).

Following imaging studies, creep tests were conducted in a materials test machine (Model 8850; Instron, Canton, MA) with specimens fully submerged in saline at 37°C as described previously (Oravec et al., 2018). Briefly, specimens were loaded to 1000N and held for 2 hours, load was removed, and recovery was recorded for another 2 hours. Vertebral endplates were potted prior to testing using dental stone to ensure flat and parallel boundary conditions and the vertebra-endcap construct was constrained in metal platens. Creep and recovery displacement parameters were calculated from displacement vs time data (Figure 3). Creep displacement (D_cr) and creep recovery displacement (R_cr) were selected as primary displacement outcomes and others were ignored due to their strong correlation with the selected variables (Oravec et al., 2018). Measured displacements were also normalized using the displacement at 1000N (i.e., D_cr-norm, R_cr-norm) to account for the dependence of creep displacement parameters on initial elastic behavior (i.e., to isolate the creep property from elastic properties such as vertebral stiffness). Residual displacement (D_r) was calculated as the final displacement after the 2 hour hold at 100 N. In addition, creep time constant (τ_cr), stretch exponent (n) and creep rate (C) were calculated from a curve fit of the creep portion of the displacement vs. time data using a function of the form “Displacement = a(1-EXP(−(t/τ_cr)ⁿ))+Ct” which was an excellent fit to the data (Oravec et al., 2018).

Figure 3:

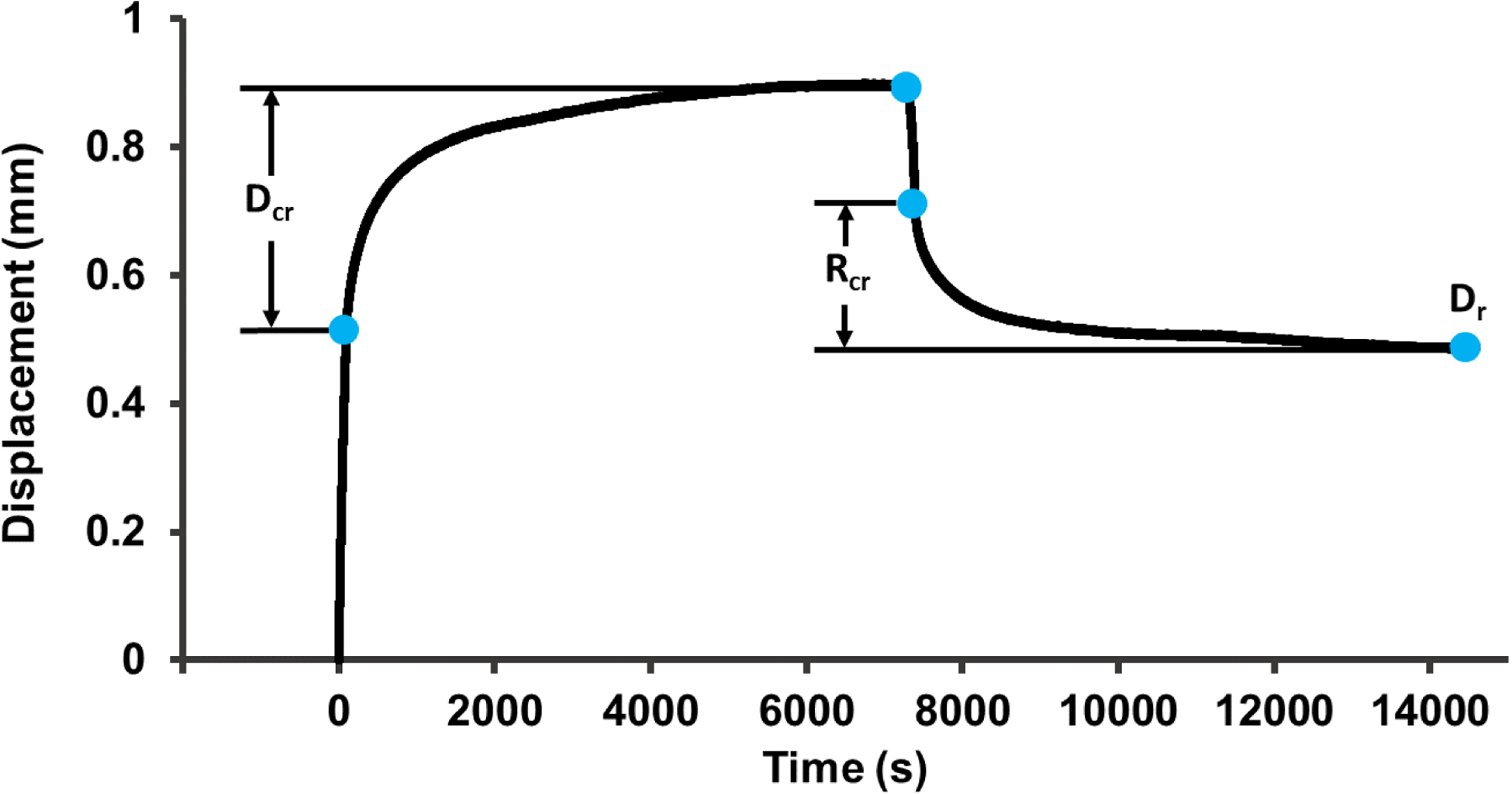
A representative creep curve (70/F). Creep displacement (D_cr) was calculated as that occurring in the 2 hour hold at 1000 N after initial loading. Recovery from creep (R_cr) was calculated as that occurring during the 2 hour hold at 100 N after elastic recovery. D_cr and R_cr were normalized using the displacement at the start of the 1000 N hold period as alternative outcomes to account for the dependence of these parameters on initial elastic deformation (D_cr-norm and R_cr-norm). Residual displacement (D_r) was calculated as the final displacement after the 2 hour hold at 100 N. Curve fitting was performed on the same data range used to calculate D_cr in order to calculate the creep time constant (τ_cr), stretch exponent (n), and creep rate (C).

Pearson product-moment correlations were evaluated between creep, DTS and BMD variables. Multiple regression models were constructed using a stepwise procedure to examine relationships between measures of creep and parameters. Two types of multiple regression models were run: the first with the most significant BMD variable forced as the first term in the model, and the second with DTS parameters only. The goal of the first models was to determine the effect of DTS variables independently from BMD in predicting creep outcomes. The goal of the second models was to examine the contribution of DTS variables alone. Each scanning configuration was examined separately. Multiple regression models were built in a forward fashion and limited to 2 predictor variables to avoid overfitting (Hair, 2009). Interaction terms were not included in the models. Only models passing a multicollinearity test (as determined by a variance inflation factor ≤ 5) were retained. Normality of the residuals was tested in multiple variable regressions by fitting a normal distribution to the residuals and using the Shapiro-Wilk W test. Heteroscedasticity was examined using the Brown-Forsythe test for unequal variances on residuals stratified by their median value. Significance was considered as p < 0.05. All analyses were performed in JMP (v10.0, SAS Institute, Inc., Cary, NC).

RESULTS

As previously noted (Oravec et al., 2018), three of 22 specimens failed catastrophically during the creep test. Creep deformations were not calculated for these three specimens. These specimens had the lowest bone densities in the sample (BMD_AP was 0.176–0.196 g/cm² for the three specimens, vs. 0.265–0.786 g/cm² for the remaining specimens). Fit parameters τ_cr and n were calculable for 3 failed specimens, and C was calculable for 2 of the 3. In total, creep displacements were calculated for 19 specimens, creep rate for 21 specimens, and time constant and stretch exponent for 22 specimens.

Among the DTS variables measured from 4 configurations, at least one variable was found to be significantly correlated with every creep outcome except time constant τ_cr. Significant correlations ranged from 0.43 to 0.67 in magnitude (p=0.002 to p=0.05) (Tables S1–4). Results from univariate correlations between creep and DTS variables are presented in supplemental data (Tables S1–4).

Stretch exponent n was negatively correlated with BMD_AP (R=−0.59, p<0.005) and BMD_LM (R=−0.57, p<0.007), and creep rate with iBMD (R=−0.64, p<0.002), shBMD (R=−0.59, p<0.005), cBMD (R=−0.57, p<0.008), BMD_LM (R=−0.59, p<0.005), and BMD_AP (R=−0.53, p<0.02). Other variables including the stiffness-normalized deformations did not correlate with any bone density measure (D_cr: p=0.057–0.354; D_cr-norm: p=0.159–0.472; R_cr: p=0.071–0.443; R_cr-norm: p=0.332–0.917; D_r: p=0.069–0.540; τ_cr: p=0.353–0.906). When the most significant BMD measure was forced into the multiple regression models, additional DTS variables were significant for n and C (Table 2).

Table 2.

Summary of the most explanatory multiple regression models (as determined by R²_adj) of creep measurements and for each DTS scanning configuration, in the presence of a significant BMD effect (n=19 for creep displacements, n=22 for τ_cr and n, and n=21 for C). Each cell shows R²_adj followed by the predictor(s) in the model (in the order of parameter name, standardized beta coefficient, and p-value in each row). For those models with multiple variables, p-values are shown for tests of normality (p_N) and heteroscedasticity (p_H). If no BMD variables were significantly correlated with a given creep variable, the inclusion of DTS variables was not pursued further (N/A).

	Coronal		Lateral
	Axial	Transverse	Axial	Transverse
Creep (Dcr)	N/A	N/A	N/A	N/A
D cr-norm	N/A	N/A	N/A	N/A
Recovery (Rcr)	N/A	N/A	N/A	N/A
R cr-norm	N/A	N/A	N/A	N/A
Residual (Dr)	N/A	N/A	N/A	N/A
Time Constant (τcr)	N/A	N/A	N/A	N/A
Stretch exponent (n)	R2adj = 0.42 BMDAP (−0.59) <0.003 Sλ (−0.37) <0.04 pN > 0.89 pK>0.89	R2adj = 0.45 BMDAP(−0.62) <0.002 MIL (−0.40) <0.03 pN > 0.09 pH > 0.18	R2adj = 0.46 BMDAP (−0.55) <0.003 Sλ (−0.41) <0.02 pN > 0.25 pH > 0.39	R2adj = 0.51 BMDAP (−0.62) <0.0007 Sλ (−0.47) <0.007 pN > 0.76 pH > 0.38
Creep rate (C	R2adj = 0.61 iBMD (−0.71) 0.0001 ALFD (+0.50) <0.003 pN > 0.66 pH > 0.32	R2adj = 0.38 iBMD (−0.64) <0.002	R2adj = 0.38 iBMD (−0.64) <0.002	R2adj = 0.38 iBMD (−0.64) <0.002

When variables from DTS alone were used in multiple regression models, all creep displacements had at least one significant model including one or more DTS predictor variables (Figure 4, Table 3). Models for curve-fit variables were generally less explanatory than those including BMD (Table 3). All regression models with multiple variables passed tests for normality and heteroscedasticity of residuals.

Figure 4:

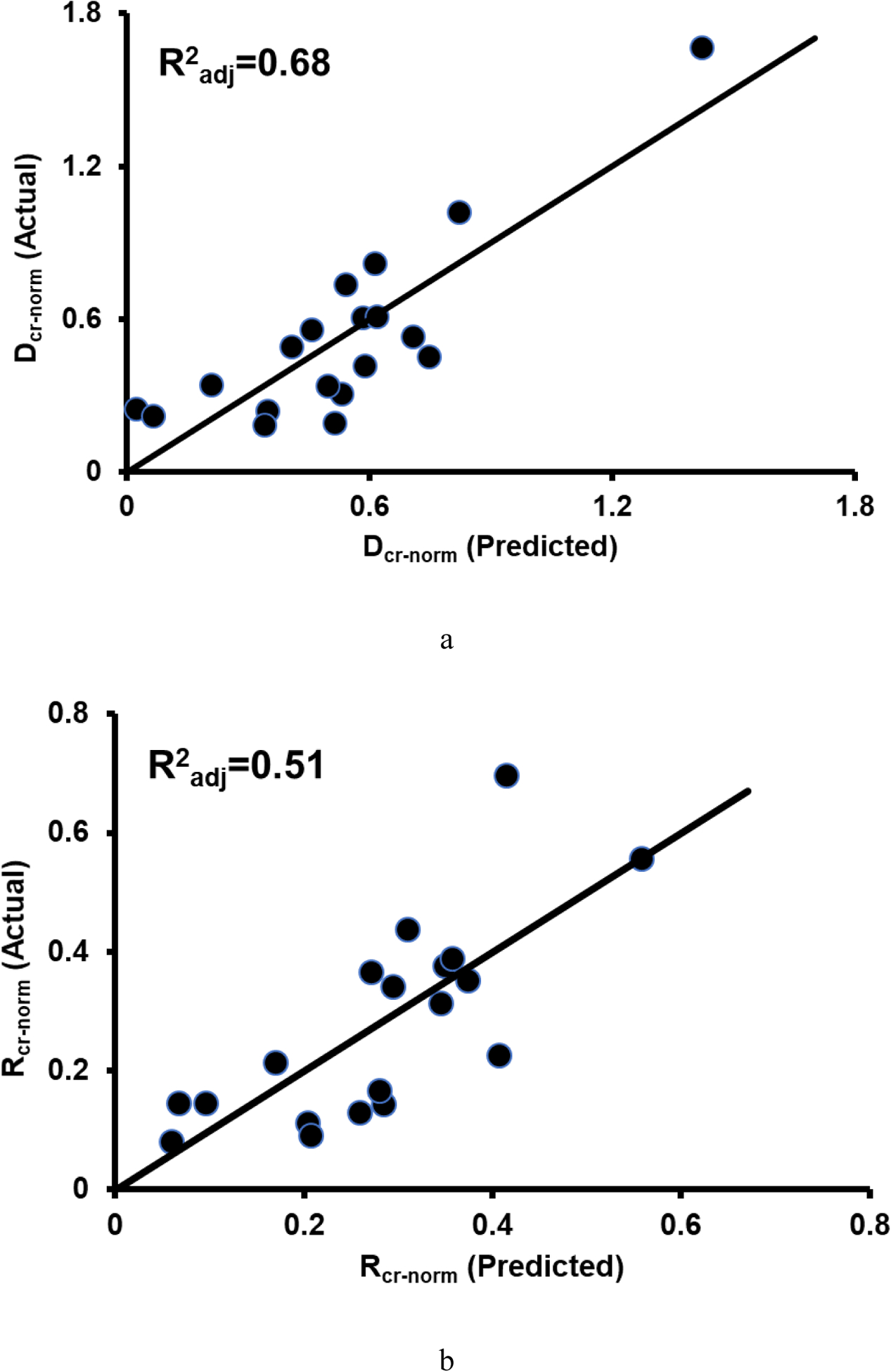
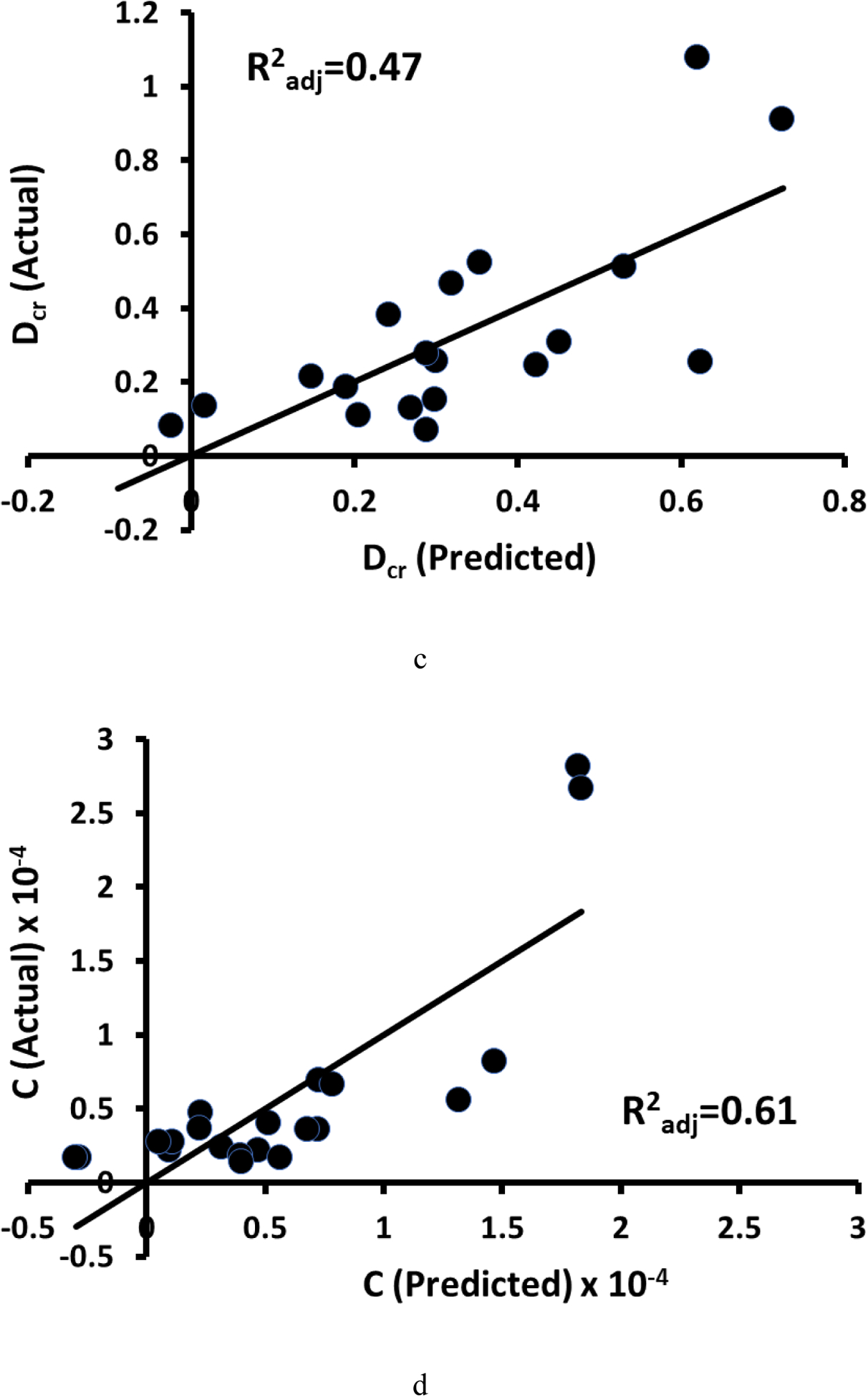
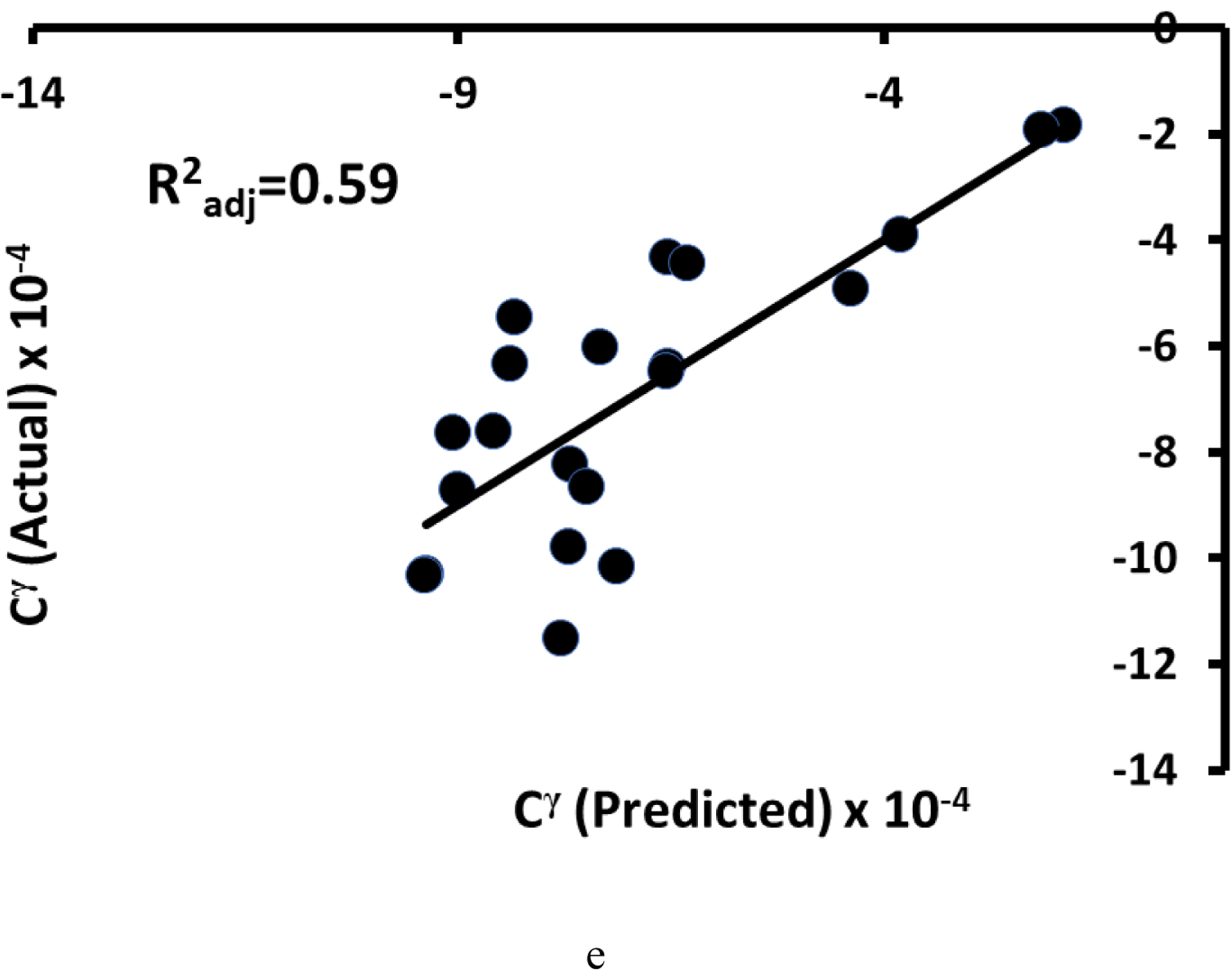
a) Actual vs. predicted normalized creep displacement (D_cr-norm = −6.94*A_MIL + 12.32*λ + 7.25), b) creep recovery displacement (R_cr-norm = −3.77*A_MIL + 3.53*λ + 4.24), and c) creep displacement (D_cr = −7.37*FD - 3.65*A_MIL). The actual vs. predicted fit for d) creep rate (C = −1.3e-6*iBMD + 4.8e-5*A_LFD) exhibited nonlinearity. e) When a Box-Cox transformation was applied to the variables, the fit was more linear (C^γ = −4.4e-7*iBMD^γ + 4.8e-5*A_LFD^γ, where γ = −0.6, −0.2, and 0.8 for C, iBMD, A_LFD, respectively). Multiple regression models for D_cr-norm and R_cr-norm contained λ and A_MIL and the model for D_cr contained FD and A_MIL. The model for C contained iBMD and A_LFD. The DTS variables in these models were measured from images acquired in the axial AP scanning configuration (n=19 for creep displacements, n=22 for τ_cr and n, and n=21 for C).

Table 3.

Summary of the most explanatory multiple regression models (as determined by R²_adj) of creep measurements and for each DTS scanning configuration, containing variables from DTS alone (n=19 for creep displacements, n=22 for τ_cr and n, and n=21 for C). Each cell shows R²_adj followed by the predictor(s) in the model (in the order of parameter name, standardized beta coefficient, and p-value in each row). For those models with multiple variables, p-values are shown for tests of normality (p_N) and heteroscedasticity (p_H). No significant models with DTS variables alone are indicated by NS.

	Coronal		Lateral
	Axial	Transverse	Axial	Transverse
Creep (Dcr)	R2adj = 0.466 FD (−0.73) <0.002 AMIL (−0.46) <0.03 pN > 0.75 pH > 0.74	R2adj = 0.246 FD (−0.54) <0.02	NS	NS
D cr-norm	R2adj = 0.682 λ (+0.80) <0.0001 AMIL (−0.66) <0.0003 pN > 0.07 pH > 0.07	NS	NS	NS
Recovery (Rcr)	R2adj = 0.492 AMIL (−0.74) <0.0008 λ (+0.51) <0.02 pN > 0.48 pH > 0.28	NS	NS	NS
R cr-norm	R2adj = 0.508 AMIL (−0.76) <0.0006 λ (+0.49) <0.02 pN > 0.32 pH > 0.35	NS	R2adj = 0.166 AMIL (−0.46) <0.05	NS
Residual (Dr)	R2adj = 0.47 FD (−0.75) <0.0009 SD-FD (−0.42) <0.05 pN>0.62 pH > 0.92	R2adj = 0.34 MIL (+0.61) <0.006	R2adj = 0.26 Sλ (+0.54) <0.02	R2adj = 0.36 FD (−0.62) <0.006 SD-λ (−0.42) <0.05 pN > 0.17 pH > 0.90
Time Constant (τcr)	NS	NS	NS	NS
Stretch Exponent (n)	NS	R2adj = 0.141 SD-λ, (−0.43) <0.05	R2adj = 0.168 Sλ (−0.46) <0.04	NS
Creep rate (C)	NS	NS	NS	NS

DISCUSSION

In the current study, we established relationships between creep properties of isolated human vertebrae and clinically measurable image texture parameters from digital tomosynthesis. To our knowledge, this is the first study in which clinically viable image texture measurements have been used to predict viscoelastic properties of vertebral bone.

DTS-derived variables of cancellous bone texture were associated with creep properties of human vertebrae independently from BMD variables. BMD was not significantly correlated with any creep displacements, and for those models including a BMD term (n and C) the underlying relationship with BMD was generally poor. The lack of correlation with BMD is an important distinction from the case of failure properties, where bone density accounts for 60–80% of the variation in vertebral strength (Ebbesen et al., 1999; Link et al., 1997; Moro et al., 1995). Those DTS derived textural parameters associated with creep properties generally represent aspects of microstructural orientation and heterogeneity. These findings suggest that very little is learned about creep behavior through standard bone density tests, whereas imaging biomarkers that quantify orientation and heterogeneity may be useful in this regard.

When creep displacements were normalized for initial elastic deformation to account for the contribution of vertebral stiffness, models for normalized creep displacements (i.e., D_cr-norm, R_cr-norm) with DTS variables alone were slightly more explanatory than D_cr and R_cr. Higher correlations between DTS texture and normalized creep displacements more strongly suggests a true association between texture variables and vertebral creep separate from the elastic properties of the vertebra.

DTS provides an image stack with large slice thickness and differing sensitivity in resolving features oriented parallel or perpendicular relative to the scanning direction (Flynn et al., 2007; Notohara et al., 2009; Shibata et al., 2014). The effect of view on image formation is evident in Figure 1, where structural features oriented perpendicular to the scanning direction are more prominent. In order to address this effect of scanning configuration, images were therefore acquired with the specimen aligned parallel or perpendicular to the scanning direction in both lateral and coronal views. The dependence of the measurements on DTS scan configuration was discussed in previous work, and was attributed to anisotropic resolution and slice thickness for a given view (Kim et al., 2017; Yeni et al., 2018). DTS variables were most strongly associated with creep displacements for the axial scan orientation in the AP view. This is fortunate as an axial sweep is readily achievable in vivo using most DTS systems. Transverse acquisitions are technically feasible on live patients, but not with the system used in this study. However, scanners with open geometries, such as those with ceiling suspended x-ray tubes, can accommodate a transverse scan if needed. However, in the interest of associations with creep parameters, transverse and lateral orientations add little to the explanatory value of those models with bone density and those with DTS variables alone (Tables 2–3).

A_MIL and lacunarity (λ) consistently appeared in models of D_cr and R_cr in the clinically more relevant axial coronal DTS scans. Lacunarity is a fractal measure related to the variability of the size of gaps in a porous texture (Dougherty, 2001), while A_MIL represents anisotropy of trabecular structure. The results indicate that increased pore heterogeneity and decreased trabecular anisotropy are associated with higher stiffness-adjusted creep and recovery displacements. These variables being significant for vertebral bone is consistent with the results of computational studies that reported significant effects of density, pore uniformity and loss of cell walls in the creep behavior of cellular materials (Ajdari et al., 2009; Andrews and Gibson, 2001; Huang and Gibson, 2003). Preferential loss of horizontal trabeculae with aging has been noted in vertebrae, and trabecular anisotropy is largely affected by this process (Mosekilde, 1988). It is therefore likely that changes in the anisotropy of the trabecular structure correspond to loss of cell walls noted in these computational studies. Lacunarity (Zaia et al., 2006) and anisotropy (Ciarelli et al., 2000; Mosekilde et al., 1985) are understood to significantly change with age and osteoporosis. These variables have also been shown to be among those with the lowest measurement error (2.1% and 9.1%, respectively) (Yeni et al., 2018), further supporting their use.

Although up to 68% variability in creep variables could be explained by clinically measurable imaging variables, and this explanatory capability is comparable to that achieved by μCT imaging (Oravec et al., 2018), explained variability was still relatively low. The findings of the current study are limited to a range of image texture parameters representing microstructural organization of cancellous bone. Though density and microstructural organization are known to affect the creep behavior of porous materials (Ajdari et al., 2009; Andrews and Gibson, 2001; Huang and Gibson, 2003), a portion of the viscoelastic behavior itself is attributable to the properties of mineral and organic composition in bone (Bowman et al., 1999; Ojanen et al., 2017). Associations of BMD and fractal variables derived from gray level texture with the shape parameters of the creep curve found in this study may be partially attributable to the underlying mineral composition. However, no direct measurement of tissue properties was attempted. As such, future work should include analysis options to extract information on mineral distribution from DTS, or supplement it with tests that include information on tissue composition or mechanics. Such tests might include in-situ reference point indentation (Bridges et al., 2012) and ex-situ micro-imaging such as Fourier transformed infrared and Raman spectroscopies and scanning and backscattered electron microscopies on a biopsy sample (Ciarelli et al., 2009; Gamsjaeger et al., 2011; Paschalis et al., 2001; Roschger et al., 1998).

The small sample size used in this study must be recognized as a limitation for model building efforts. Due to concern with overfitting, the models were limited to two effect variables (Hair, 2009). As such, it is possible there are additional and potentially more explanatory models that were not identified.

In conclusion, DTS imaging provides textural information associated with creep behavior of whole vertebral bodies. DTS derived lacunarity and anisotropy appear to be textural measures readily available from DTS which may serve as imaging markers for vertebral creep. The relationships of these measures of image texture with creep may help provide, independent from bone mass, important clinical indicators of the progression toward eventual vertebral deformity.