Discriminating memory disordered patients from controls using diffusion model parameters from recognition memory

Abstract

One hundred and five memory disordered (MD) patients and fifty seven controls were tested on item recognition memory and lexical decision tasks and diffusion model analyses were conducted on accuracy and response time (RT) distributions for correct and error responses. The diffusion model fit the data well for the MD patients and control subjects, the results replicated earlier studies with young and older adults, and individual differences were consistent between the item recognition and lexical decision tasks. In the diffusion model analysis, MD patients had lower drift rates (with mild Alzheimer’s (AD) patients lower than mild cognitive impairment (MCI) patients) as well as wider boundaries and longer nondecision times. These data and results were used in a series of studies to examine how well MD patients could be discriminated from controls using machine-learning techniques, linear discriminant analysis, logistic regression, and support vector machines (all of which produced similar results). There was about 83% accuracy in separating MD from controls; and within the MD group, AD patients had about 90% accuracy and MCI patients had about 68% accuracy (controls had about 90% accuracy). These methods might offer an adjunct to traditional clinical diagnosis. Limitations are noted including difficulties in obtaining a matched group of control subjects as well as the possibility of misdiagnosis of MD patients.

In this article, we examine the difference between controls and Alzheimer’s disease (AD) and mild cognitive impairment (MCI) patients (collectively memory-disordered (MD) patients) on performance on an item recognition task (“was this test word in the study list or not”) and on a lexical decision task (“was this letter string a word or not”). The experimental data are fit by the diffusion decision model (Ratcliff, 1978; Ratcliff & McKoon, 2008) and the model parameters are used to discriminate between MD patients and controls. The item recognition and lexical decision tasks were chosen for several reasons. First, accuracy is reasonably preserved under normal healthy aging and so decrements from moderately high performance levels can be detected. Second, both tasks have been well fit by the diffusion model which separates performance into components, providing an integrated view of accuracy and correct and error response time (RT) measures. Third, these and similar tasks have been used to examine both normal aging and memory disorders.

Memory is one of the hallmark abilities that is affected by AD and is impacted in many of the causes of those with MCI. Decrements in the speed of motor processing are also commonly present in AD and MCI. Both these components are extracted from behavioral data by diffusion model-based analyses. The diffusion model represents the cognitive processes involved in making simple two-choice decisions. Decisions are made by a noisy process that accumulates information over time from a starting point towards one of two decision criteria and the model separates the quality of evidence entering a decision from the decision criteria and from nondecision processes. Specifically, diffusion model analyses have separated the evidence (drift rate) used to drive the decision process from components representing the amount of evidence needed to make a decision (boundary separation) and the duration of processes other than the decision process (nondecision time). Ratcliff, Thapar, and McKoon (2010, 2011; we label these articles, RTM) found that drift rate in these item recognition and lexical decision tasks was almost unaffected by aging but differed with IQ. In contrast, the components representing the amount of evidence needed to make a decision and the duration of processes other than the decision process were affected by aging but not IQ. Ratcliff et al. (2011) also examined associative recognition (was this test pair of words studied in the same pair or in different pairs). However, they found that performance is severely degraded in older adults (Naveh-Benjamin, 2000; Ratcliff et al., 2011) and so the better-preserved item recognition paradigm was used in this study.

We use the diffusion model parameters in analyses to examine whether the model-based approach might be useful in discriminating between MD patients and normal older adults. We examine a number of different groups of subjects, different discrimination methods, and different combinations of model parameters and data. There have been a large number of studies to discriminate between MD patients and normal older adults, but fewer using model-based analyses. Tse et al. (2010) examined the differences between healthy older adults and mild AD patients in RT distributions in three tasks, Stroop, Simon, and switching tasks. Results showed that the main difference between the AD patients and healthy older adults was a spreading of the tail of the RT distributions operationalized as an increase in the tau parameter of the exGaussian distribution (see also Spieler, Balota, & Faust, 1996).

Two studies used discrimination methods to separate groups based on experimental measures (see also Wiecki, Poland, & Frank, 2015). Hutchison, Balota and Duchek (2010) examined the use of a Stroop task switching paradigm to discriminate between patients with mild AD and healthy older adults. The task involved presenting a word in color as the target and 1400 ms before the test word, a cue that indicates the task to be performed was presented (“word” or “color”). The task switched predictably every 2 trials from word to color then color to word. The subjects were 32 mild AD patients and 64 healthy controls and they received 144 trials of the task preceded by 8 practice trials (the task was embedded in a larger psychometric task battery). They used the incongruent error rate (from trials in which the color word and the color in which it was presented were not the same) in a logistic regression analysis and found 81% correct classification of the patients. They also found that only one of the 18 psychometric tasks used in the battery provided higher discriminability than the Stroop measure.

Houmani et al. (2018) presented results from a study to examine whether EEG markers were capable of separating groups of patients. They used EEG data collected with patients resting with their eyes closed. There were 169 patients with various disorders, namely subjective cognitive impairment (SCI), MCI, AD, and other pathologies, and they used features from measures of signal complexity and synchrony with a SVM classifier. Results showed a high separation accuracy of 91.6% for AD (N=49) versus SCI (N=22) patients but lower separation accuracy (81–88% correct) for three-way classification of AD versus SCI, versus others. In a four-way analysis, MCI patients were classified correctly about 60% of the time, which is similar to the result from our analysis for classification of MCI patients.

There have been a number of reviews of diagnostic tests and methods. Here we briefly discuss three, one that used all methods, one that used computerized tests, and one that used neuropsychological tests to screen for dementia.

Gaugler et al. (2013) presented results from an analysis and review of 41 meta-analyses and reviews selected from 507 abstracts in order to examine the accuracy of a range of diagnostic approaches. They examined results from studies that used clinical measures, cerebrospinal fluid-tau measures, positron emission tomography (PET), single-photon emission computed tomography (which uses photon emitting isotopes instead of radioisotopes used in PET), and structural MRI. These different methods produce accuracy in the range of 70–90% relative to neuropsychological diagnosis. However, Gaugler et al. questioned the quality of the studies they reviewed and concluded by suggesting that no firm conclusions could be drawn about the various methods they examined.

Aslam et al. (2018) examined the accuracy of tests that are automated and not subject to subjective interpretation. These were mainly cognitive/neuropsychological tests including tasks that involved testing various cognitive domains such as memory, language, visuospatial processing, executive functioning, and so on. Accuracy was in the range of 60%–90%. But one limitation of many of the studies reviewed was the small number of subjects and lack of replicability. The article concludes that it is hard to make recommendations on the clinical use of such computerized tests, at this time.

Hwang et al. (2019) examined various standard neuropsychological tests for detection of dementia and MCI in hospital patients. These were MMSE, cognitive performance scale, time and change task, clock-drawing task, and cognitive impairment test. Results were varied, with accuracy in the range of 70–90%. However, the authors were unable to recommend for or against the use of a specific instrument for screening for dementia or MCI in older hospital inpatients because single tests used in isolation were not reliable enough.

There were five main aims for the research in this article. First, we wanted to examine the performance of MD patients on lexical decision and item recognition tasks relative to control subjects. Second, we examined whether the diffusion model can fit data from these patients. Third, we compared diffusion model parameters between patients and controls to see what components of processing differ between the two groups. Fourth, we wanted to see if the MD patients (and controls) produced reliable individual differences by examining correlations between model parameters for the two tasks. In the RTM studies, diffusion model parameters (drift rate, boundary separation, and nondecision time) correlated between tasks. Fifth, we used discriminant methods to determine the accuracy with which the data or the model parameters allow the MD patients to be discriminated from controls. We used three different statistical/machine learning methods along with cross validation in these studies.

Experiment

Item recognition and lexical decision are tasks that engage central cognitive processes, especially memory and knowledge of words. In the tasks in our experiment, the independent variables were manipulated to produce a range of moderate to high accuracy values. Sweeping out RTs over a range of accuracy values provides maximal constraints on fitting the diffusion model to data (Ratcliff & Tuerlinckx, 2002).

One important feature of this experiment was the lack of error feedback. We had found in pilot work that with this population of MD patients, as well as the general population of older adults, feedback that told them they were wrong was dispiriting and caused some of them to terminate participation. This was true even in experiments designed to be easy and even if we told them college students were no more accurate than they were. Thus, we did not use explicit feedback and had the experimenter monitor their performance, providing them with encouraging feedback and guidance if they needed to be recalibrated to the task.

Method

Subjects.

For the MD patient group, 29 adults diagnosed with mild/early-stage Alzheimer’s disease (AD) and 76 adults diagnosed with mild cognitive impairment (MCI) participated in the experiment. They ranged in age from 53 to 89 years with a mean of 72.9 and a SD of 8.4 years. All subjects were recruited from and diagnosed by a neurologist at the Memory Disorders Clinic at The Ohio State University Wexner Medical Center and were paid for their participation. Patient characteristics are presented in Table 1.

Table 1:

Subject characteristics

Subjects	Mean age	SD age	Sex Female	Race White	Race Black	Ethnicity Hispanic	Mean MMSE	SD MMSE	Mean SAGE	SD SAGE
AD	74.8	7.0	44.8%	100%	0	0	22.9	2.9	13.5	4.2
MCI	72.0	8.6	44.7%	100%	0	1.3%	27.3	2.6	18.1	3.6
MD controls	68.9	6.6	68.4%	80.7%	15.8%	3.5%	28.9	1.4
RTMold	68.3	4.4	86.7%	88.9%	11.1%	4.4%	28.3	1.5
RTMvold	82.0	4.1	81.4%	90.7%	9.3%	2.3%	28.0	1.1

Note. Age in years. The percentage of Asian and Pacific Islanders is (100% - % White - %Black). AD means Alzheimer’s group, MCI means mild cognitive impairment group, and RTM are the older adults from Ratcliff, Thapar, and McKoon (2011).

Subjects with mild AD met the following inclusion criteria: a diagnosis of mild stage AD based on the presence of dementia with two or more cognitive domains impaired including memory; a gradual onset with progressive deterioration; loss of independence in some activities of daily living; onset between the ages of 40 and 90; and absence of other disorders that could account for the cognitive deficits. Subjects with MCI met the following inclusion criteria: a diagnosis of MCI based on subjective complaint of memory problems by the patient, preferably corroborated by an informant; greater-than-normal memory impairment detected with standard memory assessment tests; normal general cognitive function; generally normal activities of daily living; and absence of dementia. Inclusion in the MCI group was limited to those individuals who received a diagnosis of MCI and at the time of testing had not progressed to AD. Diagnostic cognitive evaluations included the following neuropsychological and other rating scales given to the patients: Mini-Mental Status Exam (MMSE; Folstein, Folstein, & McHugh, 1975), Self-Administered Gerocognitive Examination (SAGE; Scharre, Chang, Murden, et al., 2010), Consortium to Establish a Registry for Alzheimer’s Disease (CERAD), Clinical Dementia Rating Scale (CDR; Morris, 1993), and the Global Deterioration Scale (GDS; Reisberg et al., 1982).

To recruit patients, Dr. Scharre or one of his associates under his direction described the study to them. After discussion and if they agreed to participate and signed the informed consent documents approved by the Ohio State University’s Social and Behavioral Sciences Institutional Review Board, the research assistant from Ratcliff and McKoon’s laboratory conducted the experiment at the Memory Disorders Clinic using a laptop computer. To ensure that patients were able to provide consent, we asked them to recite a reasonable summary of what the study was about (they were given 2 tries to do this), and to answer correctly to 5 questions about the content of the consent form. All of the AD and MCI patients were able to pass this test.

We use the MMSE and SAGE tests in later analyses. The mean of the MMSE was 25.6 with a SD of 3.3 and the mean of the SAGE was 16.2 with a SD of 4.0. The scale of the MMSE is 0 to 30 with a score of 20 or above indicating inclusion in our study. The scale of the SAGE is from 0 to 22, with 17–22 considered normal, 15–16 indicating likely Mild Cognitive Impairment, and 14 and below indicating likely dementia.

Each subject participated in one 60-minute session which began with the lexical decision task. After 15 minutes of data collection, this task was terminated and the item recognition task was performed. This resulted in an average of 459 responses in lexical decision per subject and 471 responses in item recognition. For both tasks, subjects were instructed to respond quickly but not at the expense of making avoidable errors. For each task, an experimenter sat next to the subject and monitored their performance.

We used two control groups for the MD patient group. In the first, 52 older adults were recruited as part of a larger study using flyers in community centers, libraries, and senior centers, from word of mouth, and from the memory disorders clinic. We will call this the MD control group. The lexical decision and item recognition tasks were the first experiments in which the subjects participated so the amount of training was the same. Fifteen additional older adults were excluded after testing because either, they had participated in other experiments, had cognitive scores below our standard cutoffs (MMSE 25, IQ 80), had a major head/brain injury in the past, were not a native speaker of English, or had a medical condition that could affect performance. We also recruited 5 caregivers of the MD patients who matched the age ranges for the MD patient group and met the criteria above and these were included in the MD control group.

We had an additional control group for item recognition from data from 60–90 year old subjects from Ratcliff, Thapar, and McKoon (2011) who participated in three sessions with item and associative recognition and cued and free recall. The item recognition task was tested first in the sequence of tests without prior practice. We will call this the RTM control group. Although the MD patients were tested on lexical decision before item recognition, most of the changes in model parameters take place between sessions rather than within sessions. Thus, if the MD patients improved performance because of lexical decision practice, this would reduce discriminability between the MD patient groups and this group rather than improve it. There was one major difference between this group and the MD patients and MD control group: the RTM group was given RT feedback if a response had a RT greater than 900 ms. This was done to reduce the possibility of slower recollective processes in that experiment and produce responses based on the first information available. This may explain why drift rates are lower for this group than for the MD control group because the subjects were being driven to respond quickly and so they may not have processed the test item as completely as they would if they had more time (see Starns, Ratcliff, & McKoon, 2012). We perform analyses with and without this RTM group.

Stimuli.

For both the item recognition and lexical decision tasks, the stimuli were high, low, and very low frequency words. There were 800 high frequency words with frequencies from 78 to 10,600 per million (mean=325, SD=645, Kucera & Francis, 1967); 800 low frequency words, with frequencies of 4 and 5 per million (mean = 4.41, SD = 0.19); and 741 very low frequency words, with frequencies of 1 per million or no occurrence in the Kucera and Francis’ corpus (mean = .36; SD = .48). All of the very low frequency words occurred in the Merriam-Webster Ninth Collegiate Dictionary (1990), and they were screened by three undergraduate students; any words that they did not know were eliminated. For all three tasks, stimuli were chosen randomly without replacement from these pools. The stimuli were presented on the screen of a PC and responses were collected on the PC’s keyboard.

Lexical Decision.

Words were selected from the high, low, and very low frequency pools and nonwords were selected from a pool of 2341 pseudowords that were generated from words by randomly replacing all the vowels with other vowels (except for “u” after “q”). There were 30 blocks of trials with each block containing 30 letter strings: 5 high frequency words, 5 low frequency words, 5 very low frequency words, and 15 pseudo words. Subjects were asked to press the “/” key if the letter string was a word and the “z” key if it was not. There was no error feedback. On average, about 15 blocks were completed in the 15 minutes allocated to this task.

Item recognition.

There were 42 study-test blocks. For each block, the study list consisted of 6 high and 6 low frequency words displayed for 1 s each. One additional filler word, a very low frequency word, was placed at the end of the study list to serve as a buffer item. The test list immediately followed the study list and consisted of the 12 studied words plus 12 new words, 6 of them high frequency and 6 low frequency. The first two test words in the test list were fillers, either two new very low frequency words or one new very low frequency word and the last item of the study list (which was a filler item). Subjects were asked to press the “/” key if the test word had been presented in the immediately preceding study list and the “z” key if not. There was no error feedback. On average, about 16 study-test blocks were completed in the 30 minutes allocated to this task.

Data and code availability.

Data and code are available from the first author on reasonable request. This study was not preregistered.

Diffusion Model

The diffusion model is designed to explain the cognitive processes involved in making simple two-choice decisions. Expressions for predicted values of accuracy and RT distributions can be found in Ratcliff (1978) and Ratcliff and Tuerlinckx (2002). The model separates the quality of evidence entering a decision from the decision criteria and from nondecision processes. Decisions are made by a noisy process that accumulates information over time from a starting point z toward one of two response criteria, or boundaries, a and 0. The boundary setting represents how much evidence the subject requires in order to make a decision. When a boundary is reached, a response is initiated. The rate of accumulation of information is called the drift rate (v), and it is determined by the quality of the information extracted from the stimulus in perceptual tasks and the quality of match between the test item and memory in memory and lexical decision tasks. The mean of the distribution of times taken up by the nondecision component is labeled T_er. Nondecision time represents the time taken for encoding the stimulus, extracting the decision relevant information to produce drift rate, and response output. Within trial variability (noise) in the accumulation of information from the starting point toward the boundaries results in processes with the same mean drift rate terminating at different times, thus producing response time (RT) distributions, and sometimes at the wrong boundary (producing errors). For detailed descriptions of the diffusion model and applications, see Forstmann, Ratcliff, and Wagenmakers (2016), Ratcliff and McKoon (2008), and Ratcliff, Smith, Brown, and McKoon (2016).

The values of the components of processing vary from trial to trial, under the assumption that subjects cannot accurately set the exact same parameter values from one trial to another (e.g., Laming, 1968; Ratcliff, 1978). Across-trial variability in drift rate is normally distributed with SD η, across-trial variability in starting point is uniformly distributed with range s_z, and across-trial variability in the nondecision component is uniformly distributed with range s_t. Also, there are “contaminant” responses-- slow outlier response times as well as responses that are spurious in that they do not come from the decision process of interest (e.g., distraction, lack of attention). To accommodate these responses, we assume that, on some proportion of trials (p_o), a uniform distributed random RT between the minimum and maximum RT for the condition is the contaminant RT assumption (see Ratcliff & Tuerlinckx, 2002). The assumption of a uniform distribution is not critical; recovery of diffusion model parameters is robust to the form of the distribution and also to the form of the across-trial variability components (Ratcliff, 2008, 2013).

The values of all the parameters, including the variability parameters, are estimated simultaneously from data by fitting the model to all the data from all the conditions of each experiment. The model can successfully fit data from single subjects producing well-estimated drift rate, boundary separation, and nondecision time values if there are around 400–1000 total observations per subject (see Ratcliff & Childers, 2015, for a detailed analysis). Variability in these parameter estimates is much less than differences in the parameters across subjects (individual differences in these parameters) so that correlations are meaningful. The ability of the model to fit data from individual subjects and produce meaningful individual differences analyses is an important feature of the model because many models in cognitive psychology may fit group data adequately, but they have not been shown to provide information about individual differences. The model fit the data well and it did so with the assumption that only drift rate, not the nondecision component or the criteria, varied with the difficulty of experimental conditions. For instance, the slower and less accurate responses for low compared to high frequency words in lexical decision were explained by a difference only in their drift rates.

The diffusion model was fit to the data for each task and each subject by minimizing a chi-square value with a general SIMPLEX minimization routine that adjusts the parameters of the model until it finds the parameter estimates that give the minimum chi-square value (see Ratcliff & Tuerlinckx, 2002, for a full description of the method). The data entered into the minimization routine for each experimental condition were the .1, .3, .5, .7, .9 quantile RTs for correct and error responses and the corresponding accuracy values. The quantile RTs and the diffusion model were used to generate the predicted cumulative probability of a response by that quantile response time. Subtracting the cumulative probabilities for each successive quantile from the next higher quantile gives the proportion of responses between adjacent quantiles. For the chi-square computation, these are the expected values, to be compared to the observed proportions of responses between the quantiles (i.e., the proportions between 0, .1, .3, .5, .7, .9, and 1.0, which are .1, .2, .2, .2, .2, and .1) multiplied by the number of observations. Summing over (Observed-Expected)²/Expected for all conditions gives a single chi-square value to be minimized.

The diffusion model must explain accuracy, the shapes of the RT distributions for correct and error responses, and the relative speeds of correct and error responses and the model can be understood as decomposing these accuracy and RT data for correct and error responses into components of processing. In some models in psychology (signal detection theory, some kinds of dual process models), the model parameters are a simple transformation of the data from two data values to two parameters which results in an untestable theory. In contrast, the diffusion model must fit experimental data (RT distributions and how they change with accuracy) in order for the model parameters to be valid. Thus, the model has to pass a quality-of-fit test before it can be used to interpret processing.

Results: RTs and Accuracy

RTs less than 300 ms and greater than 5000 ms were eliminated from analyses. This excluded 1.1% and 1.5% of the data for the item recognition and lexical decision tasks respectively.

Table 2 shows accuracy and median RTs for item recognition as a function of the experimental variables. We present the results for the AD and MCI groups separately and then combined into a MD patient group (to help with comparisons). To perform statistical analyses for both tasks, we combined the conditions to provide single values of accuracy and mean correct RT for each subject and performed an analysis of variance on each variable with the three subject groups (AD, MCI, and controls) as the independent variable. We use Tukey’s HSD post hoc test to examine differences between pairs of subject groups.

Table 2:

Item recognition data: Probability correct and correct and error mean RTs

	High word freq “old”			Low word freq. “old”			High word freq “new”			Low word freq. “new”
Subjects	PrC	CRT	ERT	PrC	CRT	ERT	PrC	CRT	ERT	PrC	CRT	ERT
AD	0.691	1165	1298	0.688	1155	1276	0.501	1260	1262	0.652	1256	1340
MCI	0.637	1085	1266	0.721	1061	1294	0.711	1148	1275	0.804	1135	1368
MD	0.650	1105	1273	0.713	1082	1289	0.661	1168	1270	0.768	1159	1358
MD controls	0.682	886	1117	0.816	860	1138	0.851	946	1010	0.902	914	1070
RTM11	0.592	782	812	0.725	770	838	0.820	783	851	0.872	779	887

PrC is probability correct, CRT and ERT are correct and error mean RT, freq. means frequency. Subject groups as in Table 1.

For item recognition, for all the groups, there was a mirror effect with responses to low frequency words more accurate and faster than responses to high frequency words for both “old” and “new” items. The AD patients were slower and less accurate than the MCI patients and both groups were slower and less accurate than the MD control group. For the following analyses, mean accuracy values and mean RTs were combined over correct responses for old and new items (and word and nonword items for lexical decision). This produced a single value of accuracy and a single value of mean RT for each subject.

Using one-way analyses of variance (ANOVAS), there was a main effect of group on accuracy (F(2,159)=47.0, p<2×10⁻¹⁶, ƞ_p²=.371). The AD and MCI groups differed from each other (HSD p=.0002) and the MD control group differed from both AD and MCI groups (p’s < 10⁻⁶). There was a main effect on RT (F(2,159)=27.6, p=5.2×10⁻¹¹, ƞ_p²=.258). The difference between the AD and MCI groups did not quite reach significance (HSD p=.054) but the MD control group differed from both AD and MCI groups (p’s < 10⁻⁶).

The RTM control group was less accurate than the MD control group and only a little more accurate than the MD patient group. However, the RTM control group had responses that were much faster than the other two groups. The RTM and MD control groups also had a bias towards “new” responses that the MD patient group did not. We use this bias in our discrimination tests.

Table 3 shows results for the lexical decision task. Accuracy was very high for high frequency words, and lower for low frequency and nonwords, and about 85% correct for very low frequency words. Mean RTs were close to a second or longer for all responses (except for high frequency words for the MD control group) and error RTs were typically 200–400 ms longer than correct RTs. The AD and MCI groups had quite similar accuracy values and RTs, but the MD control group had shorter RTs. There was a main effect of subject group on accuracy (F(2,159)=5.1, p=.0072, ƞ_p²=.060). The AD and MCI groups did not differ from each other (HSD p=.23), the MCI and MD control group did not differ from each other (HSD p=.11), but the MD control group differed from the AD group (p=0.006). There was a main effect on RT (F(2,159)=18.4, p=6.5×10⁻⁸, ƞ_p²=.188), the difference between the AD and MCI groups was not significant (HSD p=.70), but the MD control group differed from both AD and MCI groups (p’s < 10⁻⁵).

Table 3:

Lexical decision: Probability correct and correct and error mean RTs

	High word freq			Low word freq.			Very low word freq			Nonword
Subjects	PrC	CRT	ERT	PrC	CRT	ERT	PrC	CRT	ERT	PrC	CRT	ERT
AD	0.978	989	1248	0.930	1179	1463	0.833	1271	1508	0.913	1385	1576
MCI	0.985	963	1338	0.947	1140	1513	0.862	1235	1573	0.913	1342	1527
MD	0.983	970	1308	0.942	1150	1497	0.855	1243	1554	0.913	1352	1359
MD controls	0.991	792	856	0.959	935	1178	0.878	1022	1266	0.942	1071	1223

Note. Abbreviations as in Table 2.

Diffusion Model Analyses

The diffusion model was applied to the data for each task for each subject individually. Mean parameter values for the two patient groups and control groups for both experiments are presented in Table 4. As would be expected from the accuracy and RT data for both experiments, boundary separation and nondecision times were smaller for the MD control group than for MD patients. For item recognition, the values from the RTM control group were lower than those for the MD control group. For item recognition, drift rates were lower for the MD patient groups. In the same way as for accuracy and mean RT, a single value of drift rate was produced in lexical decision by adding the drift rates for “word” responses and subtracting the drift rate for “nonword” responses (and taking the mean) and for item recognition by taking the average of the drift rates for “old” words and minus the (usually negative) drift rates for “new” words (and taking the mean). A drift rate bias was also computed for item recognition for the discriminant analyses presented later; this was the sum of the 4 drift rates for both tasks. This bias can be seen using the values in Table 4; for the MD control group and the RTM data, there is a bias towards “new” responses while there is little bias for the MD patients.

Table 4:

Diffusion model parameters for item recognition and lexical decision.

	a	Ter	η	sz	p0	st	z	v1	v2	v3	v4	χ2
AD Rn mean	0.217	0.734	0.208	0.121	0.002	0.318	0.124	0.106	0.097	−0.024	−0.127	48.5
MCI Rn mean	0.212	0.712	0.237	0.120	0.003	0.249	0.119	0.106	0.169	−0.157	−0.227	49.5
MD Rn mean	0.214	0.719	0.229	0.120	0.003	0.268	0.120	0.106	0.149	−0.120	−0.199	49.3
MD control Rn mean	0.179	0.647	0.311	0.099	0.004	0.192	0.107	0.130	0.276	−0.355	−0.436	51.5
RTM11 mean	0.123	0.598	0.191	0.043	0.001	0.204	0.060	0.081	0.191	−0.253	−0.309	68.6
AD Lex mean	0.250	0.629	0.133	0.035	0.023	0.245	0.147	0.413	0.217	0.135	−0.200	38.6
MCI Lex mean	0.261	0.651	0.127	0.071	0.012	0.246	0.151	0.391	0.227	0.143	−0.209	39.3
MD Lex mean	0.258	0.645	0.129	0.061	0.015	0.245	0.150	0.397	0.224	0.141	−0.207	39.1
MD control Lex mean	0.221	0.570	0.141	0.062	0.010	0.185	0.127	0.512	0.283	0.179	−0.279	37.8
AD Rn SD	0.054	0.148	0.098	0.057	0.003	0.151	0.038	0.104	0.086	0.114	0.116	13.0
MCI Rn SD	0.065	0.114	0.104	0.065	0.010	0.149	0.045	0.142	0.153	0.148	0.140	15.3
MD Rn SD	0.062	0.124	0.102	0.063	0.009	0.152	0.043	0.132	0.141	0.151	0.140	14.6
MD control Rn SD	0.050	0.068	0.056	0.054	0.012	0.096	0.034	0.135	0.134	0.135	0.143	17.9
RTM11 SD	0.032	0.087	0.099	0.031	0.010	0.100	0.027	0.145	0.145	0.136	0.157	23.3
AD Lex SD	0.072	0.141	0.073	0.079	0.038	0.174	0.053	0.153	0.086	0.063	0.107	18.8
MCI Lex SD	0.066	0.127	0.081	0.076	0.028	0.171	0.048	0.166	0.114	0.101	0.121	15.7
MD Lex SD	0.068	0.130	0.079	0.076	0.031	0.171	0.049	0.165	0.108	0.093	0.117	16.5
MD control Lex SD	0.067	0.082	0.074	0.078	0.024	0.124	0.042	0.142	0.110	0.096	0.138	17.3

Boundary separation is a, starting point is z, mean nondecision time is T_er , the SD in drift across trials is η, range of the distribution of starting point s_z , range of the distribution of nondecision times, s_t , and p_o is the proportion of contaminants. The subject groups are as in Table 1, Rn means item recognition, Lex means lexical decision. For item recognition, v₁ represents high frequency old words, v₂ represents low frequency old words, v₃ represents high frequency new words, and v₄ represents low frequency new words. For lexical decision, v₁ represents high frequency words, v₂ represents low frequency words, v₃ represents very low frequency words, and v₄ represents pseudowords.

For item recognition, there was a main effect of subject group on boundary separation (F(2,159)=6.5, p=.0020, ƞ_p²=0.75). The AD and MCI groups did not differ from each other (HSD p=.92) but the MD control group differed from both AD and MCI groups (p’s < .01). There was a main effect on nondecision time (F(2,159)=8.6, p=.00029, ƞ_p²=.098). The difference between the AD and MCI groups was not significant (HSD p=.65) but the MD control group differed from both AD and MCI groups (p’s < .002). There was a main effect of group on drift rate (F(2,159)=58.2, p<2×10⁻¹⁶, ƞ_p²=.423) and the differences between each pair of the three groups was significant (HSD p’s < .0008).

For lexical decision, there was a main effect on boundary separation (F(2,159)=5.7, p=.0040, ƞ_p²=.067). The AD and MCI groups did not differ from each other (HSD p=.997) but the MD control group differed from both AD and MCI groups (p’s < .04). There was a main effect on nondecision time (F(2,159)=7.7, p=.00060, ƞ_p²=.089). The difference between the AD and MCI groups was not significant (HSD p=.95) but the MD control group differed from both AD and MCI groups (p’s < .007). There was a main effect on drift rate (F(2,159)=8.7, p=.00026, ƞ_p²=.099). The difference between the AD and MCI groups was not significant (HSD p=.33) but the MD control group differed from both AD and MCI groups (p’s < .005).

From the model parameters for each subject, predicted values of accuracy and correct and error RT quantiles were generated for each experimental condition, and these were averaged in the same way over subjects. Figure 1 plots the 0.1, 0.3, 0.5, 0.7, and 0.9 RT quantiles vertically against their response proportions with the x’s the data and the o’s and lines the predictions. This provides information about how accuracy changes across conditions and how distribution shape changes as accuracy changes. The shapes of the RT distributions can be visualized by drawing equal area rectangles between the quantile RTs as shown in the second down left panel of Figure 1. The .1 quantile represents the leading edge of the distribution, the .5 quantile is the median, and the .9 quantile represents the tail of the distribution. Results show as in Ratcliff et al. (2010) that the change in mean RT across conditions is mainly a spread in the distribution for both tasks.

Figure 1.

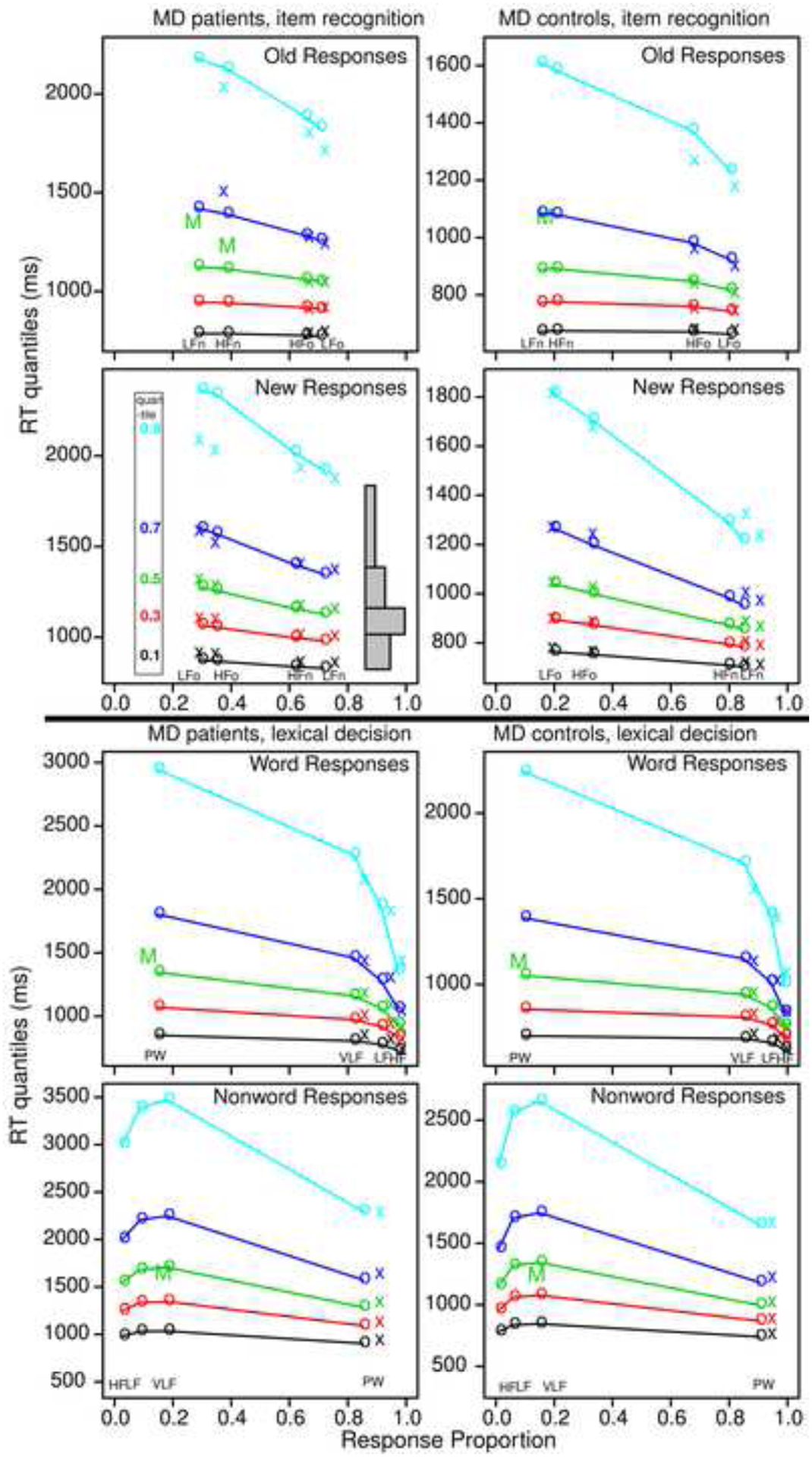
Quantile probability plots for item recognition and lexical decision tasks for data and model predictions for MD patients and the MD control group averaged over subjects in the same way. The x’s are the data and the o’s are the predictions joined by the lines. The five lines stacked vertically above each other are the values predicted by the diffusion model for the 0.1, 0.3, 0.5, 0.7, and 0.9 quantile RTs as a function of response proportion for the conditions of the experiments. The quantiles are labeled on the left-hand side of the second left plot and equal-area rectangles drawn between the quantiles are shown on the right side of that plot (which represent RT distributions). The M’s in the plots show the median RT because some subjects did not have enough error responses to compute quantiles.

The top four panels are for the item recognition task with the left two for the MD patients and the right two for the MD control group. In the top two panels, “old” responses are shown with the far right column of quantile RTs (in each plot) for studied (“old”) low frequency words and the next left for high frequency words. Errors to low frequency new words are to the far left (represented by a median RT) and errors to high frequency new words are the next to the left. The bottom two plots are a mirror image of the top right plot for correct responses to “new” words and errors to “old” words. For several of the plots, quantiles are not shown for some of the error conditions and in some cases, a single “M” is presented for the median RT (when there is at least a single RT for each subject in that condition). This is because there are fewer than 5 (or zero) responses for some of the subjects in those conditions so that quantiles cannot be computed. As discussed earlier, accuracy is lower for MD patients as shown by the columns of quantiles being closer to the center than for the MD control group. Also, the RTs are on different scales with the MD patients with longer RTs than the MD control group.

The bottom four panels show the same plots for the lexical decision task. The third row shows “word” responses in lexical decision, in these panels, the far right column of RT quantiles is for high frequency words, the next left, low frequency words, and the column nearest the middle, very low frequency words. The column on the far left represents error responses to nonwords and as for item recognition, only “M” is shown because some subjects have too few observations to compute quantiles. The bottom row shows nonword responses with correct responses to nonwords to the right and error responses to word to the left. Empirical values for the two far left conditions, errors to high and low frequency words, are not plotted because some subjects had no error responses so even median RTs could not be computed.

Chi-Square Goodness of Fit

We calculated chi-square goodness of fit values for each task for each subject and the means of the chi-square values are shown in Table 4. The degrees of freedom for the chi-square values were calculated as follows: For the 5 quantile RTs, there are 6 bins: 2 outside the 0.1 and 0.9 quantiles and 4 between the pairs of quantiles. This gives 12 degrees of freedom, minus 1 because the total probability adds to 1. Thus, for both tasks with 4 conditions, the number of degrees of freedom with 4 conditions and 11 parameters is 33 (44–11). The 0.95 critical value is 47.4 for a two-tailed test and 50.7 for a one-tailed test. The mean chi-square values are mainly below the one-tailed critical value for both tasks.

The chi-square statistic has the property that as the number of observations increases, the power of the test increases so that even the smallest deviation can lead to significance. To illustrate this: The chi-square value is the sum over all frequency classes of (O-E)²/E where O and E are the observed and expected frequencies. Suppose in our computations, the observed and expected proportions between two adjacent bins systematically miss by .1 (e.g., instead of the proportions being .2, one is .1 and the next is .3). Then the additional contribution from this miss to the chi-square is (N(.1–.2)²/.3+N(.3–.2)²/.1), where N is the number of observations in the condition. For the item recognition task with about N=114 observations per condition, the contribution to the chi-square from this systematic deviation would be 15.2. This helps explain why the mean chi-square value is larger for the RTM control group because it had a larger number of observations per condition than the experiment presented here. For example, for the MD control group, there were about 140 observations per condition, and for the RTM control group, there were about 260 observations per condition (as opposed to the 114 for the MD patients). Therefore, the lower values of chi-square in this article than Ratcliff et al. (2010, 2011) are the result of fewer observations rather than substantially better fits.

Evaluating the Control Group Based on Model Parameters

The subjects in the RTM studies have a range of IQ’s documented in those articles, which may or may not match our group of memory disordered patients, but they have an age range that matches. Given that in those prior studies, both lexical decision and item recognition drift rates varied as a function of IQ, without IQ measures we cannot be certain that differences are not due to IQ differences and there is no way to measure their preclinical IQs. However, there is a strong correlation of IQ with drift rates in lexical decision and item recognition, so we can examine whether the decrease in performance for the MD patients in the two groups relative to the MD controls is the same for lexical decision and item recognition or whether lexical decision performance would be relatively unimpaired in these patients, but recognition would be more impaired. In fact, lexical decision drift rates in the MD control group are about 1.3 times those of the two MD patient groups, which were not different. But for item recognition, drift rates for the MD control group were almost twice as large as those of the MCI group, which were almost twice as large as those of the AD group. Thus, evidence used to drive the decision process was more preserved for memory disordered patients in the lexical decision task than in the item recognition task. Thus, the large decline in memory performance cannot be attributed solely to pre-clinical differences between the MD patients and MD controls.

Correlations Among Model Parameters, Data, Age and Diagnostic Tests

In prior research (Ratcliff, Thapar, & McKoon, 2010, 2011; Ratcliff, Thompson, & McKoon, 2015), diffusion model parameters and data (accuracy and mean RT) correlated between tasks. Figures 2 and 3 show scatter plots of age, model parameters, and data for the item recognition and lexical decision tasks. With 105 MD patients and 57 MD controls in an individual differences analysis, even moderate values of the correlation coefficient will be significant because the critical values are 0.19 and 0.26 respectively. Note that the correlations are also sensitive to outliers so correlations near the critical value should be viewed with suspicion if the scatter plots show any evidence of outliers.

Figure 2.

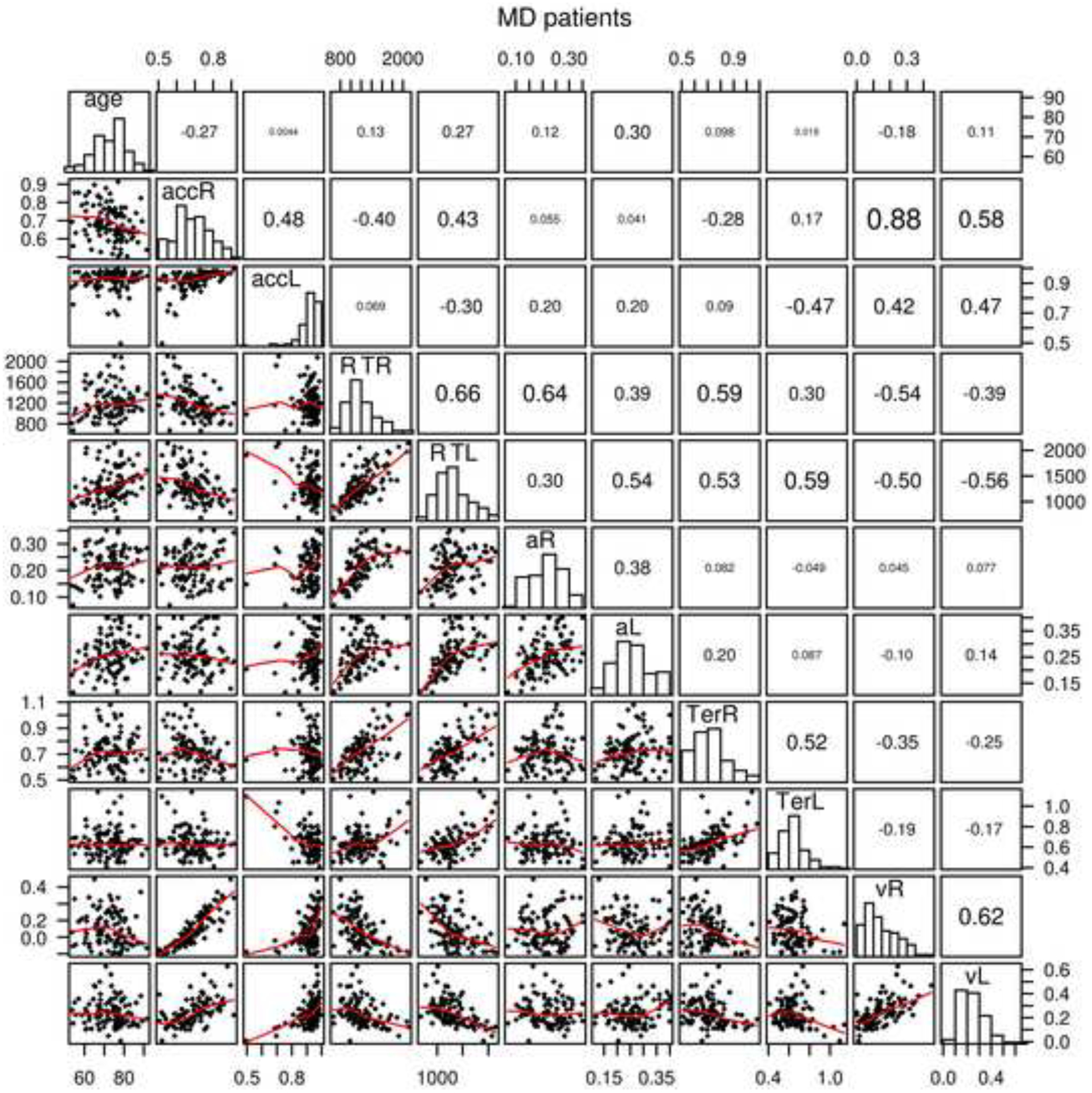
Scatter plots, histograms, and correlations for age, accuracy and mean RT, and diffusion model parameters, nondecision time, boundary separation, and drift rate averaged over conditions for the MD patients. acc represents accuracy, R represents item recognition, L represents lexical decision, a represents boundary separation, T_er represents nondecision time, and v represents mean drift rate averaged over conditions.

Figure 3.

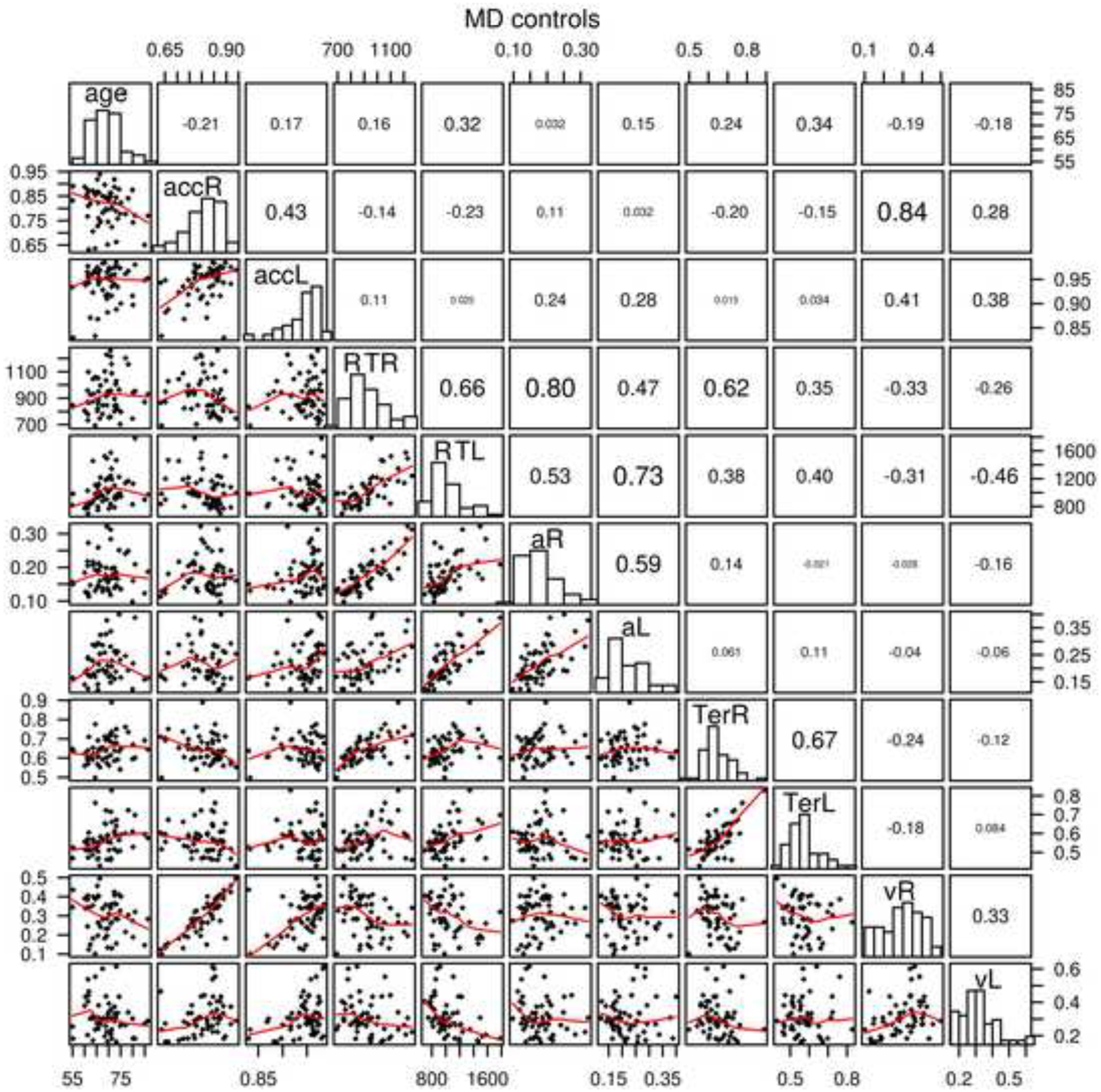
The same plot as in Figure 2 for the MD control group.

The correlations between diffusion model parameters in lexical decision and item recognition for boundaries (a) were 0.38 and 0.59 (for the MD patient and the MD control groups respectively - this same order is used for the following comparisons), nondecision time (T_er) 0.52 and 0.67, drift rates (v) 0.62 and 0.33, and across-trial SD in drift (η) 0.27 and 0.19 (across-trial SD in drift rate is not plotted in Figures 2 and 3). Thus, the main model parameters were reliably correlated across the two tasks for both the MD patient and MD control groups. For the data, for the MD patient and MD control groups respectively, mean RT was correlated 0.66 and 0.66 between the two tasks and accuracy was correlated 0.48 and 0.43.

As in the earlier research, drift rates were correlated with accuracy, and nondecision time and boundary separation were correlated with mean RT. There were also negative correlations between drift rate and RT suggesting that longer RTs were related to poorer evidence used in the decision process. These were the main correlations, but all are shown in in Figures 2 and 3. For the diagnostic tests for MD patients, SAGE and MMSE were correlated 0.67. We do not have the SAGE measure for the MD control group and the MMSE had a mean of 28.9 with a top score of 30, so the range of the MMSE was severely limited. This correlation between the MMSE and SAGE tasks showed a strong relationship suggesting that they measure similar aspects of performance. The MMSE and SAGE tasks correlated with drift rates for item recognition 0.52 and 0.52 and for lexical decision 0.40 and 0.46 respectively, which shows that the MMSE and SAGE scores measure similar abilities to those that produce evidence driving the decision process in these two tasks. The correlations between the MMSE and SAGE tasks for boundary separation were small, but for nondecision time the correlation was −0.28 averaged over the four combinations of tasks and measures. This latter result suggests a weak relationship between ability in these tasks and nondecision time, with higher ability related to shorter nondecision time.

These results show that for the patients and controls, we obtain similar patterns of individual differences as in earlier studies. This shows that the modeling and analysis produces interpretable individual differences because the main model parameters correlate across the two tasks and so appear to be measuring similar processes as in the earlier studies. Also, the MMSE and SAGE tests appear to measure the same cognitive abilities that evidence driving the two fast cognitive tasks (lexical decision and recognition) measures.

Discriminating Between Groups Based on Model Parameters or Data

The gold standard to which neuropsychological testing should aspire is to produce tests that separate patients into those that have a disorder and those that do not. It seems to be universally agreed that in many domains, the neuropsychological tests currently being used are not highly diagnostic at an individual level. Therefore, a high priority has to be to examine any task that shows differences between groups to determine if it is diagnostic at an individual level. As discussed earlier, the diffusion model is one of the few quantitative models in psychology that has been used to produce meaningful individual differences and has been applied to data from patients with a number of disorders, as well as aging and developmental research.

Here we use three statistical/machine learning methods to examine the accuracy with which the MD patients can be discriminated from controls. These methods are linear discriminant analysis (LDA), logistic regression (LR), and support vector machine (SVM). These methods use data or model parameters and a variable that specifies to which group the subject belongs. The algorithm then finds weights on model parameters or data that best separates the groups. LDA gives a categorical classification output for the two groups that we use here to represent accuracy of performance with this classifier. It also provides a score that allows us to change the hit rate and correct rejection rate (sensitivity and specificity scores). This score also tells us the degree to which subjects are more or less strongly classified in the two groups. LR and SVM give scores (rather than the categorical assignment that is available from the LDA method) that are used in the same way as the scores for LDA. Therefore, in order to determine the accuracy of these methods, it is necessary to find the criterion that gives the best classification accuracy. This is done by adjusting the criterion value to find a value that best separates the groups.

Linear discriminant analysis attempts to find a linear combination of variables with a linear decision boundary that finds the largest separation of the different groups. LDA assumes normal distributions of the independent variables and this is a reasonable assumption for the data and model parameters we use in the analysis (see the histograms in the diagonals of Figures 2 and 3). We use the linear discriminant analysis function (lda) in the MASS package in R (Venables & Ripley, 1994). We also tried quadratic discriminant analysis which produces a quadratic boundary between groups, but this only differs from LDA when there are more than two groups and the method produced similar results in the analyses with 3 or 4 groups. We also examined whether a second discrimination helped discrimination when we were examining 3 or 4 groups and results showed no improvement over the single discriminator.

For all these methods, we use cross validation to evaluate the method by training on a sample of about two thirds of the data/parameters and then testing the result on the other one third of the data (there are many possible choices of what sample sizes to use, we felt this 2/3 vs. 1/3 was a good compromise in comparison to accuracy when the whole data set was used). This avoids the problem of overfitting that might occur if all the values were used in classification. In our applications, this process is performed 1000 times and accuracy of the separation between groups and SDs in these values are presented. For the LR and SVM methods, a single criterion was used for all 1000 cross-validation studies. We present results from the cross validation study as well as results for application to the full data set in Table 5.

Table 5:

Classification Accuracy

		LDA			LR		SVM
Number	Groups	FD-acc	CV-acc	CV-SD	CV-acc	CV-SD	CV-acc	CV-SD
1	MD/MDC+RTM	0.836	0.832	0.035	0.829	0.033	0.826	0.037
2	AD/MCI	0.733	0.697	0.065
3	AD/MDC	0.942	0.909	0.047
4	MCI/MDC	0.789	0.754	0.056
5	MD/MDC	0.815	0.796	0.048
6	MD/RTM	0.860	0.851	0.037
7	MDC/RTM	0.786	0.763	0.054
8	MD/MDC/RTM	0.744	0.708	0.042
9	AD/MCI/MDC/RTM	0.636	0.591	0.049
10	MD/MDC+RTM, a, Ter, v	0.828	0.817	0.036
11	MD/MDC+RTM, Ter, v	0.732	0.725	0.041
12	MD/MDC+RTM, a, v	0.816	0.807	0.035
13	MD/MDC+RTM, a, Ter	0.788	0.781	0.039
14	MD/MDC+Lexical	0.833	0.802	0.047
15	MD/MDC+RTM, Data Rn	0.812	0.810	0.036	0.817	0.035	0.806	0.037
16	MC/MDC data Rn	0.772	0.766	0.045
17	MD/MDC, Lex data	0.728	0.708	0.040
18	MD/MDC 10 blocks	0.796	0.775	0.047
19	MD/MDC HDDM	0.809	0.791	0.047
20	MD/MDC Word Frequency	0.815	0.786	0.047

Note. LDA means linear discriminant analysis, LR means logistic regression, SVM means support vector machine, FD means full data, CV means cross validation, acc means accuracy, SD means standard deviation, AD means Alzheimer’s group, MCI means mild cognitive impairment group, MDC means MD caregiver group, and RTM are the older adults from Ratcliff, Thapar, and McKoon (2011).

These methods are applied to the following data sets (described earlier). First, there are the 105 MD patients tested on both item recognition and lexical decision (29 diagnosed as AD, 76 diagnosed as MCI). Second, there are the 57 subjects from the MD control group who were tested on both item recognition and lexical decision in the same way as the MD patients. We also used a control group from Ratcliff et al. (2011) as described above. The model parameters for the RTM group are presented in Table 4 (we combined two older age groups in the analyses but present them separately in Table 4) along with those from the patient and the MD control groups. It turns out that using this RTM set of data in the discriminant analysis improved discrimination between the AD, MCI, and the MD control groups. Results are presented in Table 5.

Diffusion model parameters.

The first 9 rows use diffusion model parameters for the item recognition task: boundary separation, nondecision time, the mean drift rate, and the bias in drift rate. The first row shows accuracy for the most important analysis, the separation of MD patients from all older adults. There is about 83% successful separation of the groups. Figure 4 top panel shows the separation for individual subjects. The top row plots each subject on the x-axis and the categorization on the y-axis. Although some of the dots merge, the ones that are misclassified are easy to see. For the 29 AD patients, only 3 out of 29 of them are misclassified (90% accuracy), for the 57 MD control group, 7 out of 57 are misclassified (88% accuracy), and 7 out of the 88 older adults from the RTM control group are misclassified (92% accuracy). The MCI patients were classified less accurately with 52 out of 76 correctly classified (68% accuracy). These results show that subjects that are clearly impaired or clearly unimpaired are accurately classified, but those that are less impaired are less accurately classified.

Figure 4.

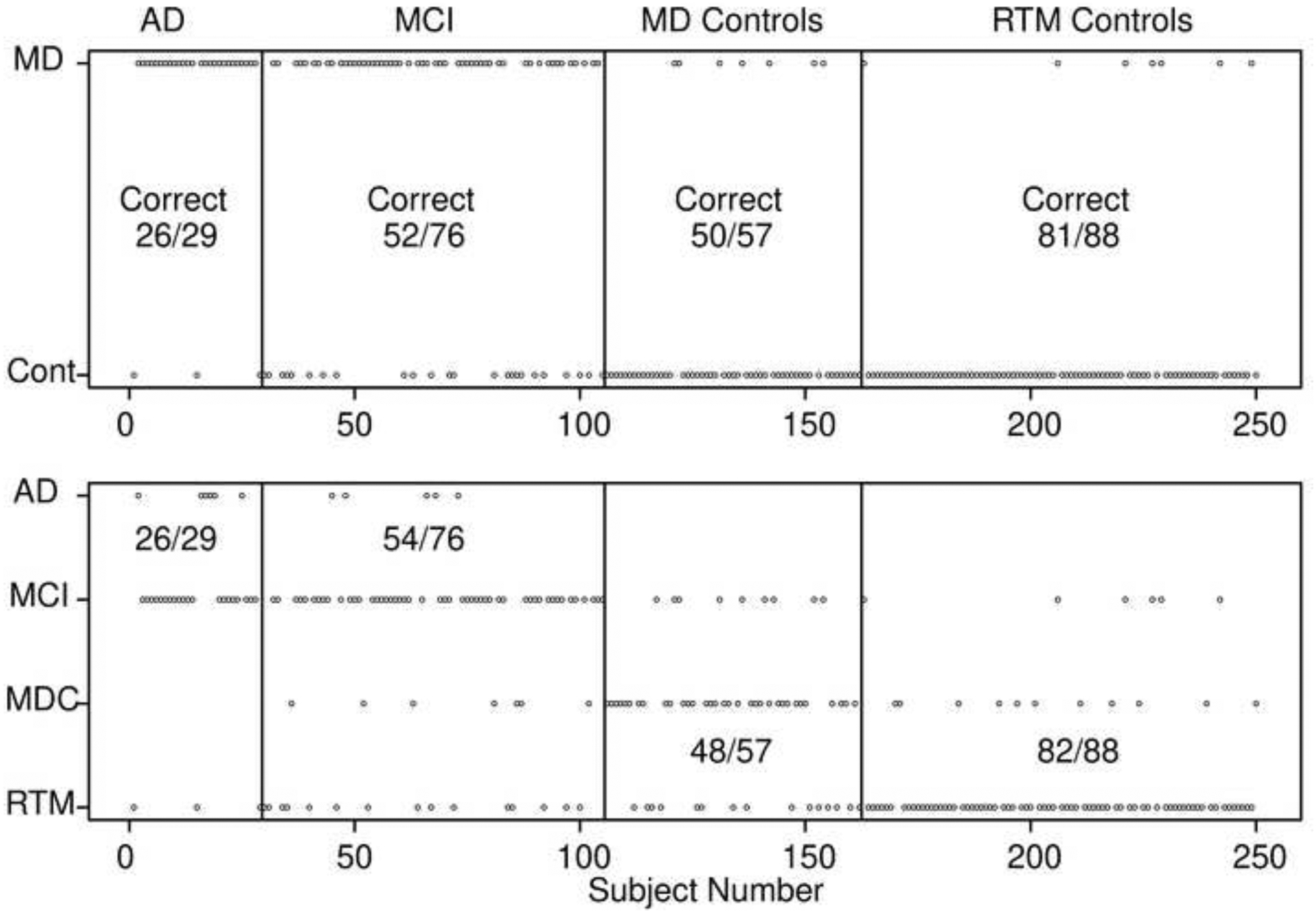
Classification scores for the LDA method for two-way classification (top figure) and four-way classification (bottom figure). Each small circle represents a single subject. The vertical lines divide the subject groups (with labels at the top) and the horizontal labels represent the classification (top MD patients versus controls, bottom, AD, MCI, the MD control group, and the RTM control group). The numbers in the plots represent correct classification and in the bottom plot, the classification is for AD and MCI groups combined for classification into either of those two groups and for controls, the classification is for classification into one of those two groups.

The first row also shows the results from the LR and SVM classifiers which give very similar results to the LDA results. This occurs probably because distributions of the classifier values (Figure 5 bottom right) are symmetrically distributed and there seems to be no way to classify the groups in a more complicated way. The 2nd through the 8th rows show comparisons between subgroups in which only the groups listed are trained and tested. The results generally support the analyses from the first row. The AD and MCI groups are relatively poorly separated from each other with about 70% accuracy. The MD patient group was separated from the MD control group with about 80% accuracy which shows that the addition of the RTM control group improved classification of these two groups. The MD patient group and RTM control group were more accurately classified with about 86% correct classification, but this is likely due to the speed feedback given to the older adults in the RTM group that was discussed earlier.

Figure 5.

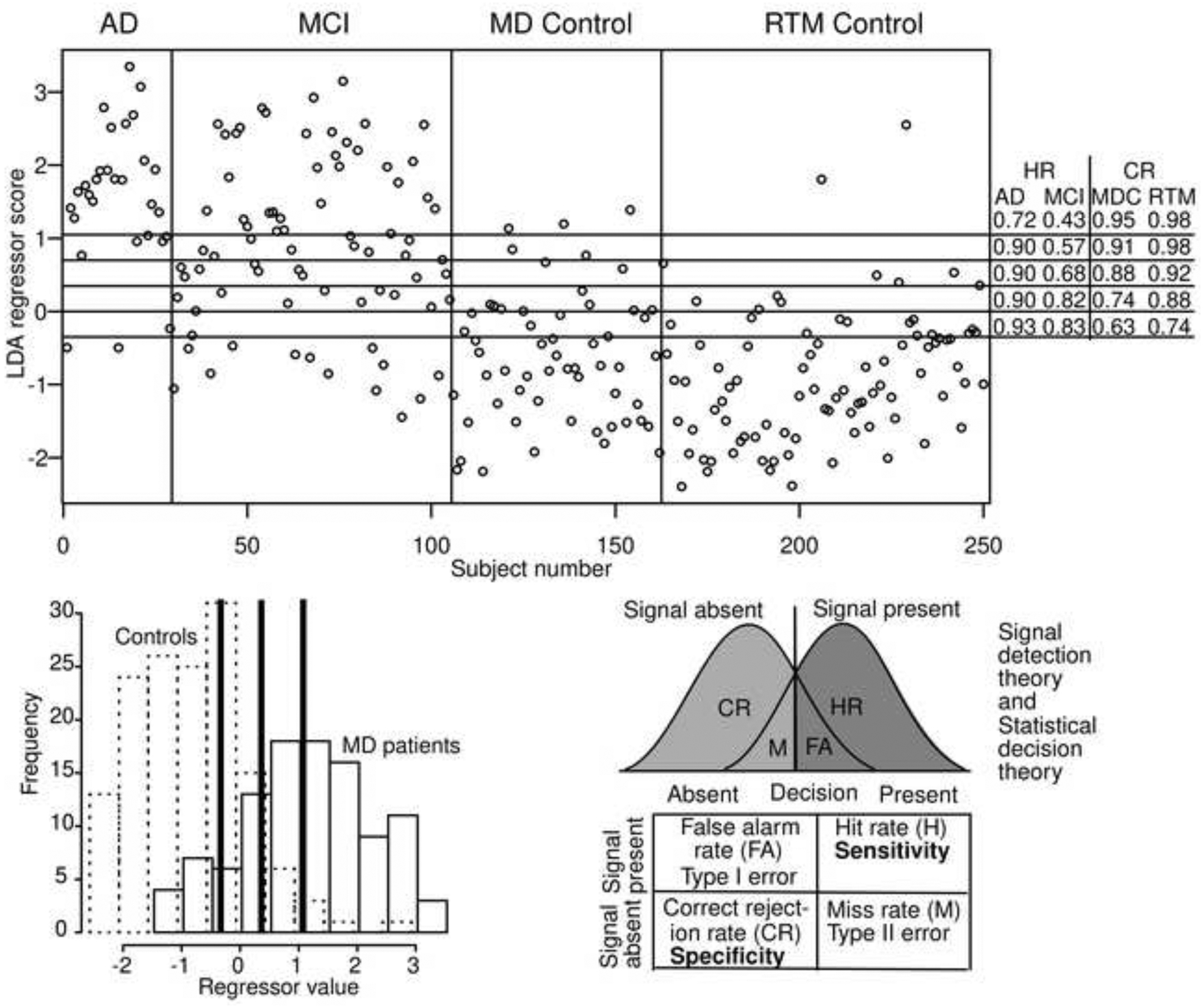
The top figure shows the values of the output of classifier for each subject from the top plot in Figure 4. The five horizontal lines show different criteria for classification corresponding to the hit rate (HR) and correct rejection rate (CR) shown on the right for the 4 subject groups. The bottom left plot shows histograms of the MD (solid lines) and controls (dashed lines) of the regressor values. The three heavy vertical lines correspond to the top and bottom horizontal lines and the middle line in the top panel. The bottom right shows a standard signal detection representation and a table of terms from signal detection, statistical decision theory, and sensitivity and specificity.

LDA is the method preferred for multi-group classification when the assumption of normally distributed variables is met and so we use this method for the following multi-group classifications. The 8th row shows classification with training and testing for three groups, MD patient group, MD control group and the RTM control group. Accuracy is about 71% mainly because of misclassification of the MCI group as above. The 9th row shows the classification into four groups, AD, MCI, MD control group and RTM control group. Accuracy of this classification is quite low, about 60%. The results are plotted in the second panel of Figure 4. The four rows show the classification and the numbers in the panels show the number classified into the AD/MCI group versus MD control/RTM control groups. The results from collapsing the four groups into two groups are very similar to the two-category classification shown in the top line of Table 5; only 1 out of the 250 subjects was better classified. (Three-way classification for AD, MCI, and MD control groups was also about 60% accurate with values within 1% of those in row 9.)

Rows 10 through 13 of Table 5 show the effects of using only some of the diffusion model predictor variables. Bias was taken out of the analyses and row 10 shows results from the three model parameters. Rows 11–13 show the results from pairs of variables. The results show that boundary separation is the best predictor (in terms of accuracy) followed by drift rate, and then nondecision time.

Adding lexical decision parameters.

Row 14 shows the result from adding boundary separation and nondecision time from the lexical decision task to boundary separation, nondecision time, drift rate and bias from item recognition. The RTM experiment did not have lexical decision data and so there was no RTM group for this analysis. Accuracy was increased over that from row 5 by less than 1%. The slight improvement could be because the values of boundary separation and nondecision time from lexical decision reduced the variability in those quantities relative to the values from item recognition alone (boundary separation and nondecision time were each correlated across the item recognition and lexical decision tasks, see Figures 2 and 3).

Using raw data in discrimination.

Row 15 shows results from classifying MD versus the MD control group plus the RTM control group. The results show that classification accuracy using RT and accuracy data is only 2% lower than for classification using diffusion model parameters (row 1). With more observations per experiment, we believe that the item recognition model parameters would be better estimated, and performance would increase over that for the raw data. We also ran LR and SVM on these data and results in row 15 show results that are quite similar to those presented in row 1, namely, the three methods give very similar results. Row 16 shows the results from classification of two groups, MD versus MD controls and the results also show about a 2% drop in classification accuracy (compared with row 5).

Row 17 shows the analysis (from row 5) discriminating MD patients from the MD control group using lexical decision data. As can be seen, discrimination accuracy drops considerably which shows that lexical decision is not as good of a task for discriminating MD patients from controls as item recognition.

Reducing the number of observations.

Our experiment used a lexical decision task followed by an item recognition task. This resulted in about a one-hour session. If the item recognition task and the methods presented here were to be used in diagnosis, then a smaller amount of time spent on data collection would make this approach more appealing. In the initial design, the lexical decision task provided data that might have helped in discrimination, but it also provided practice at using the computer system. If this were a clinical trial, then we could not draw conclusions about eliminating the lexical decision task because it would change the protocol. However, we can examine the effect of reducing the number of trials in the item recognition task and guess at what would happen if item recognition were run without the lexical decision task.

We generated quantiles and accuracy values for 10 study/test blocks, blocks 2–11. The average number of observations for each MD patient was 229 out of 240 (a few subjects completed less than 10 blocks and some responses were trimmed out) which was 49% of the data for this group. The average number of observations for each control subject was 238 out of 240 which was 43% of the data for this group. We fit the diffusion model in the same way as for the other fits and produced parameter values. These values were then used in the LDA analysis and results are presented in row 18 of Table 5 (to be compared with row 5). These results show a drop of about 2% in discrimination of MD versus MD control groups. If there is any effect of practice provided by the lexical decision task on the following item recognition task, it would be to improve performance on the item recognition task for the patients. Thus, we believe that eliminating the lexical decision task would only help discriminate MD patients from controls.

Hierarchical Bayesian parameter estimation.

Two reviewers suggested that modern Hierarchical modeling might have an advantage over non-hierarchical methods, or at least serve as a check on the model fitting approach used to this point. It does not make sense to fit the MD and control groups separately with hierarchical methods because of possible shrinkage that might artificially compress the groups, produce artificially larger differences between them, and so produce artificially better discrimination between the groups. To examine whether the hierarchical Bayesian method would benefit discrimination, we fit the MD group and MD control group for the item recognition task in one hierarchical model. We then conducted a LDA analysis exactly in the same way as above as in row 5 of Table 5 with point estimates for the MD patients versus controls. The results are shown in row 19 and show a decrease in accuracy of about 1% for the hierarchical model versus the G-square fitting method. Individual differences in model parameters are much smaller than variability in parameters that result from model fitting which means that individual differences dominate and as long as good fitting methods are used, results are likely to be similar as is observed here (see Ratcliff & Childers, 2015, for a brief investigation of hierarchical fits implemented in HDDM).

In the hierarchical Bayesian model fits done in HDDM, we found indeed that the SDs in the model parameters were lower relative to the SDs in the G-square values. The SDs for boundary separation for HDDM and the G-square methods were 0.060 and 0.052 (in the scaling with σ=0.1), the SDs for mean drift rate for HDDM and the G-square methods were 0.122 and 0.074 respectively, and the SDs for nondecision time for HDDM and the G-square methods were 0.081 and 0.112 respectively. Even though the variability is lower, there was no benefit to discrimination. The correlations in the G-square and HDDM model parameters were .75, .66, and .94 for boundary separation, drift rate, and nondecision time respectively.

There is a problem in using this hierarchical method and that is that if a new patient was to be discriminated, the whole hierarchical Bayesian analysis would have to be run again with that additional data set included. This is because fitting data from a new patient individually would likely produce biases in parameter estimates relative to the parameters obtained from that subject run in a hierarchical fit. Rerunning the analysis with HDDM with the new data included has a practical problem and that is fitting time. It took about 2.5 days to run the analyses with 250 data sets on a high-speed desktop machine. If this method was to be used in practice, 2.5 days (or more if more data were added) is too long to wait for a result. In contrast, the G-square method provides fits in a minute or so and the fits for each data set are independent so that refitting the whole data set is not needed.

Using word frequency drift rates.

Potentially, there is extra information in the experimental conditions, namely word frequency. We used boundary separation, nondecision time, and the four drift rates (high and low frequency words crossed with old and new test items, i.e., presented versus non-presented). Results for a LDA analysis using all these parameters are shown in row 20 in Table 5. Results are very similar to the results in row 5 and therefore using the drift rates for each individual word frequency condition did not improve discrimination.

Discussion

This article provides a number of results for performance of memory disordered patients and control subjects on two simple cognitive tasks, item recognition and lexical decision. First, data show standard patterns of results for the effects of word frequency on accuracy and RT. The RT distributions are right skewed and changes in accuracy are mirrored with a spreading of RT distributions. Error RTs are longer than correct RTs, which is typical of data from these tasks.

Second, the diffusion model was fit to the experimental data and the fits were about the same quality as fits to other data sets in the literature. Results for item recognition showed that the AD and MCI groups had similar parameter values with the major exception of drift rate. Mean drift rate for the AD group was slightly more than half the size of the drift rates for the MCI group (0.089 vs. 0.164). The MCI group had mean drift rates that were half as large as the MD control group (0.299). The MD control group also had lower boundary separation and shorter nondecision time than the MD patient group. The SD in drift rate across trials was also a little larger for the MD control group than the MD patient group. For the lexical decision task, similar results are obtained for boundary separation, nondecision time, and the SD in drift rate across trials, but drift rates were nearly the same for the AD and MCI groups (0.241 and 0.241) and only a little higher for the MD control group (0.313).

Third, there were strong correlations for each of the MD patient and MD control groups between the same model parameters on each task (drift rates, nondecision time, and boundary separation). Also, RT correlated with boundary separation and nondecision time, accuracy correlated with drift rate, and drift rate correlated with mean RT.

Fourth, we performed a series of discriminant analyses using diffusion model parameters for item recognition, lexical decision, and accuracy and mean RT data. The most important result was that item recognition parameters separated AD patients from the MD control group with about 90% accuracy. However, accuracy for MCI patients was worse, with about 68% correct classification. This shows that the extremes are well classified, but the MCI group is less well classified. Some of these MCI patients will progress to AD, but others will not. We aim to follow as many of these individuals as we can to examine whether the scores from the discriminant analysis are predictive.

Discrimination methods allow two (or more) groups to be separated on some dimension, in our examples here, a linear combination of diffusion model parameters. The usual terms to represent accuracy in discrimination in neuropsychological testing are specificity and sensitivity and here we show how they are related to statistical decision theory and signal detection theory in the context of our discrimination results (many people will already understand the relationship of course, e.g., Scharre et al., 2010).

The top of Figure 5 shows the discrimination scores for the 250 subjects that correspond to the top analysis in Figure 4. The horizontal lines represent possible criteria for separating MD patients from controls and the middle horizontal line is the cutoff that produced the classification in Figure 4 top. On the right-hand side of the plot are the discrimination scores for the four different groups as a function of the 5 criterion settings. The middle one with a hit rate of 0.90 and 0.68 for the AD and MCI groups, respectively, and correct rejection rates of 0.88 and 0.92 for the MD control group and RTM control group respectively corresponds to the proportions on the top of Figure 4. If the criterion were moved upwards, fewer controls are classified as memory disordered (with correct rejection rates of 96%), but also fewer MD patients are classified as disordered (hit rate a little above 50%). On the other hand, if the criterion is moved down, MD patients are classified as disordered with greater probability, but controls are also classified as disordered with greater probability.

The left bottom side of Figure 5 shows histograms of the values in the top panel with the solid histogram for scores from patients and the dotted histogram for controls (this is a more traditional way of representing data like these). The three thick vertical lines correspond to the top, middle, and lowest horizontal lines in the top panel. As the thick line moves from left to right, fewer individuals are classified as memory disordered. The bottom right of Figure 5 shows standard signal detection distributions to represent histograms (the distributions are plotted with equal areas, unlike the discrimination histograms) showing the hit rate, false alarm rate, miss rate, and correct rejection rate. Below the distributions is the decision table with type I and type II errors corresponding to false alarm and miss rates and sensitivity and specificity corresponding to hit and correct rejection rates.

The signal detection example makes the point that sensitivity and specificity can trade off with the criterion setting just as do hit and correct rejection rates. It is important to note that this example (and applications like it) applies to cases in which the variable upon which the decision is made is continuous. In other cases, for example, pregnancy tests and antibody tests for the coronavirus, the output is or might be categorical with only a discrete output produced. Then hit rate/sensitivity and correct rejection rate/specificity cannot be traded against each other.

One issue that is important to consider with the evaluation of any of these methods is how accurate is the clinical diagnosis. It is recognized that clinical diagnosis itself has a degree of variability that is not small. Results from post mortem studies suggest that an accuracy of 85–90% is about the best that can be expected from a clinical diagnosis of AD, especially when the patient has AD mixed with other dementias (e.g., 67% when mixed, Khan & Alkon, 2010). Furthermore, pathology studies show that there are older adults that have AD but show no symptoms (Beach et al., 2012). This means that we might expect a ceiling of around 90% on diagnosis, except for the most extreme cases (e.g., our AD versus control results in Table 5).

The other issue that is important in evaluating methods of diagnosis is how to select control subjects (which is glossed over in many publications). There are several issues. First, they must be treated in a very similar way to patients. They must not have been in other experiments because we know accuracy, RT, and model parameters change with practice (Dutilh, Vandekerckhove, Tuerlinckx, & Wagenmakers, 2009; Ratcliff, Thapar, & McKoon, 2006). Boundary separation and nondecision time are both reduced and drift rate can increase with practice, depending on the task. This means that by selecting subjects who had taken part in other tasks, we might obtain artificially better separation between impaired and control subjects. The second issue concerns how to equate characteristics of patients and controls. For example, if patients were high functioning adults and the controls were lower functioning adults, then ability might covary with the groups and discrimination might be inflated or deflated. Third, controls with problems that might impair performance such as concussions, traumatic brain injuries, strokes, low MMSE, or non-native speakers may lead to reduced performance of the control group leading to reduced discrimination. Also, there is always the possibility that a control subject may have an undiagnosed memory disorder. All these issues suggest that great care be taken in selecting control subjects.

Conclusions and Implications

The analysis presented here involves several features that might improve understanding of the effects of MCI and AD on cognition and might help improve diagnostic testing. First, cognitive tasks were used that have well-understood models of the processes involved in decision-making. The models extract components of processing that can be separately examined for how they change under disease. Second, by using several parameters that represent the components of processing, we were able to separate patients from controls with reasonable accuracy using statistical and machine learning methods. For data of this kind, the specific method did not matter much, with differences in accuracy less than 1%. Third, using simple correlational measures, we were able to determine which parameters and measures were measuring similar factors and which were more independent. For example, the MMSE and SAGE tests were correlated with each other and with drift rate in the memory task. However, drift rate was only the second most important model component that determined how well the groups were discriminated.

One important issue is that data of high quality are needed for use in methods such as the modeling approach taken in this research. The data should be collected with a research assistant observing the subject, monitoring performance, and giving feedback to guide how the task is to be done. In addition, it is important to collect enough data to reliably estimate accuracy and RT or model parameters on experimental tasks such as the simple memory task used here.

One important direction for future work is to determine whether additional measures, such as EEG measures, are independent (to a large degree) of behavioral measures. If they are, then they may provide a separate source of evidence and so behavioral and EEG (or multiple) measures collected while performing a memory task (as in Ratcliff, Sederberg, Smith, & Childers, 2016) might improve discrimination. Multiple measures could be studied with different machine learning techniques, for example, those presented in Table 5.

At this point the main behavioral diagnostic tools are standard simple neuropsychological ones, including many paper and pencil ones. Reviews (e.g., Hwang et al., 2019) have found that these have limited accuracy, but are quite good at discriminating between extreme cases. We believe that model-based analyses and more advanced methods of using multiple sources of evidence are worth significant investigation because we can hope that they will improve diagnosis, subject to the limitations of accurate clinical diagnosis.