A mathematical model for treatment using chemo-immunotherapy

Abstract

In this study, we investigated a mathematical model for chemoimmunotherapy (a combination of chemotherapy and immunotherapy) for brain cancer. In most cases, the standard protocol for cancer treatment is fixed in terms of treatment time intervals and dosages. We offer a wide range of non-fixed protocols, which essentially vary in terms of time intervals and dosages (i.e., personalised medicine). The functions that describe this treatment are explicit and analytical. Hence, the parameters of the function can be easily changed and a new protocol can be obtained. We compared different protocols and obtained an optimal solution. In addition, we applied the singular perturbed vector field (SPVF) method to determine the hierarchy of the system of equations, which enabled us to identify the equilibrium points of the mathematical model and investigate their stability.

Cancer protocol; Mathematical model; Dosage; Chemo-immunotherapy; GBM

1. Introduction

Cancer is the general name for a group of diseases characterised by the unrestrained growth of cells, which are tiny structures that make up the organs and tissues in the body. These cells differ in appearance and function; however, they regenerate in a similar manner, through division, to heal or rebuild damaged tissue.

Normally, cell division is orderly and controlled. However, in cancer cells, this process is uncontrolled, and cells continue to divide and multiply easily [1].

Below, selected facts regarding cancer from around the world are presented [2], [3], [4], [5], [6], [7], [8]:

Cancer is the second leading cause of death globally and is responsible for an estimated 9.6 million deaths annually. Approximately one in six deaths that occur globally is due to cancer.

Approximately 70% of the deaths from cancer occur in poor countries with low salaries.

Approximately one-third of cancer deaths is caused by five leading behavioural and dietary risks: high body mass index, low fruit and vegetable intake, lack of physical activity, tobacco use, and alcohol use. Tobacco use is responsible for approximately 22% of all cancer-related deaths.

Infections, such as hepatitis and human papillomavirus (HPV), can cause cancer, and can be responsible for up to 25% of cancer cases.

The economic impact of cancer is significant and increasing. The total annual economic cost of cancer in 2010 was estimated to be approximately 1.16 trillion USD.

There are many different types of cancer. Cancerous tumours can appear almost anywhere and in any organ of the body [9], [10], [11], [12], [13]. In this study, we focused on brain cancers. Brain tumours can be divided into two types. Tumours that begin to grow in the brain cells themselves, most often originating in glioma cells (Multi-shaped glioblastoma, GBM, is a type of cancer that develops in the brain from the brain cells themselves, called Glioma), can appear anywhere in the brain and usually do not send metastases out of the brain [14], [15], [16]. The standard treatment in these cases is surgery for tumour resection. Following surgery, radiation and/or chemo-immunotherapy are usually performed. If the tumour recurs, additional surgery can be performed to remove the tumour. In cases where surgical resection is impossible, medication or radiation therapy is necessary. The second type of brain tumours are those that grow in another organ in the body, such as the breast, lung, colon, etc., and metastasise to the brain.

In the present study, we discuss the first type of tumours, which are tumours that originate in the brain cells called glioma cells. These tumours include astrocytoma, pilocytic astrocytoma, low-grade astrocytoma, anaplastic astrocytoma, GBM, oligodendrogliomas, and ependymoma. Early detection of tumours can save lives [17].

Tumours of the brain can be treated with surgery for tumour resection, radiation (radiotherapy), chemotherapy (i.e., the use of anti-cancer drugs (cytotoxic) whose function is to damage cancer cells), treatment with alternating electric fields, targeted biological therapy (targeted therapy) targeted to tumour-specific genes, proteins, or to the tissue environment that contributes to tumour development, and immunotherapy [18], [19], [20]

From theoretical research to experimental investigations, scientists from all fields worldwide are searching for a solution to this disease [21], [22], [23], [24], [25], [26], [27], [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], and this solution can originate from several sources. Medical doctors, scientists such as biological physicists, and mathematicians are involved in cancer research

There are numerous possible approaches to cancer treatment. The main goal of cancer treatment is to cure the patient, if possible, or control the development of the disease as much as possible. In certain cases, the treatment is designed to relieve the symptoms of the disease and improve the patient's quality of life.

Examples of cancer treatments include surgery, chemical treatment (chemotherapy), radiation therapy (radiotherapy), immunological therapy, biological or molecular therapy, hormonal therapy, and a combination of several treatments.

In this study, we propose a therapeutic protocol from a mathematical perspective. The mathematical model focuses on chemo-immunotherapy using the immunological drug, Interleukin-2 ($IL-2$). This model also considers the interaction between chemotherapy and immunotherapy to create more effective chemotherapy treatments using an analytical function that describes the treatment and customisation of each patient. This function depends on the time of administration of the drug and different doses. After these interactions are presented using the mathematical model, we opted to perform an investigation in two directions. First, we numerically solved the model for different protocols (i.e., different parameters of the analytical function) and compared the results. Second, we applied the singular perturbed vector field (SPVF) method to the mathematical model [39]. This method exposes the hierarchy of a system by changing the coordinates of the original model. Once the hierarchy of the system is exposed, it can be divided into fast and slow subsystems. This division enables us to first determine the equilibrium points of the model and then analyse the stability of these equilibrium points.

2. Mathematical model

In this section, we present a mathematical model based on [44]. The mathematical model describes the interactions between dendritic cells D, cytotoxic T-cells, cytokines $IL-2$, and Interleukin-10 ($IL-10$), chemotherapy treatment, and cancer cells. The model is not suggested to accurately describe the complete reality. In reality, numerous additional cells in the body and immune system participate in the interaction of the body with cancer cells. However, the model is an acceptably sufficient approximation of reality that can address the hopes of patients with cancer.

The assumptions of the model are as follows: T-cells are activated via interactions with an antigen-presenting cell (APC) or accessory cell, which are considered dendritic cells D in this study. The D-cells interact with $I{L}_{10}$ and regulatory T-cells $T_R$ (Treg). Tregs modify dendritic cells by making them tolerogenic. These tolerogenic dendritic cells deactivate cytotoxic T-cells and create new Tregs from certain naive T-cells. These interactions are described by (1)–(3).

The cytotoxic T-cells $T_C$ are derived from the naive T-cell population $T_N$, which produces cytotoxic T cells. The population size of these cells indirectly depends on $IL-2$ [26].

The naive Tcells are created at a constant rate and die at a rate dependent on $I{L}_2$. Naive Tcells are activated by APCs. The interaction between a tolerogenic dendritic cell and a cytotoxic T-cell leads to non-responsiveness at a rate of d; this process is considered to occur in the same manner as death, as the T-cell no longer fulfils its function. This cell population also has a natural death rate. When cytotoxic cells interact with $IL-2$, they become activated; however, when they interact with $IL-10$, they become non-activated. Tregs, $T_R$, can be differentiated from the naive T-cell population upon interaction with a tolerogenic dendritic cell. The interaction between Tregs and $IL-2$ results in their expansion at a rate of c. Of note, Tregs also have a natural death rate ${\omega }_R$. These assumptions presented herein are described by equations (4)-(7).

Naive Tcells produce $IL-2$ at a constant rate; however, they decay at a constant rate ${\omega }_2$. The interaction of a cytotoxic Tcell with $IL-2$ causes the Tcell to release $IL-2$ at a rate of $a_2$. The interaction of naive $CD{4}^{+}$ T-cells with immature dendritic cells causes them to release $IL-10$ [27]. The Treg-CTL interaction also induces the production of $IL-10$ at a rate of $a_{10}$; otherwise, $IL-10$ is produced at the rate of ${\omega }_{10}$. These procedures are described by (8)-(9).

The immune system reacts when a tumour is present in the body. Activation of the immune system during cancerous growth occurs via cytotoxic T-cells. The rate at which cytotoxic cells kill tumour cells is $D_C$, where C is the size of the tumour [28]. This interaction is described by (10).

When modelling cancer treatment using a mathematical model, it is common to express the function of the treatment using a delta function, which describes the sudden and rapid introduction of the substance into the body. When a substance is present in the body, it interacts with the immune system and the tumour itself. Thereafter, part of the substance is absorbed by the body and other parts are passed from the body [29], [30], [31]; this occurs gradually and is considerably slower than the initial process. In this case, a function must be constructed such that up to a point $x_0$, it increases rapidly, beyond which it decreases more slowly and continuously, and is derivative at point $x_0$. Therefore, a delta function does not fit the description of the above process as it is not continuous and is not derivative at $x_0$. Here, we model the treatment using an analytical function that is continuous and derivative for all $x\in \mathbb{R}$ (the function of the treatment is denoted by $\mathcal{F}(q,t)$, where q is the quantity of chemotherapy and t is the time). As the function depends on the time and dosage, the dosage and time for each individual patient can be adjusted. The dynamics of chemotherapy drug decay are described by equation (11), where $C_H$ is the concentration of the chemotherapy drug [32].

In the present study, we discuss drug treatment after surgery to remove cancerous tumours.

Let $\overrightarrow{U}$ be the vector of the dynamic variables of the system: $\overrightarrow{U}=(D_I,D,D_T,T_N,T_C,T_{CP},T_R,I{L}_2,I{L}_{10},C,C_H)$.

The relationships between the dynamic variables of the system and the corresponding parameters are shown in Diagrams $1-6$

Under the above assumptions, the mathematical model includes a system of first-order nonlinear ordinary differential equations (ODEs), and has the following form:

$$\frac{d{D}_I}{dt}=-a{D}_I-a_T{D}_I\frac{T_R}{g_R+T_R}-{\omega }_I{D}_I-b_T{D}_I\frac{I{L}_{10}}{g_{10}+I{L}_{10}}-k_{D_I}{D}_I(1-e^{{\delta }_{D_I}{C}_H})\equiv F_1(\overrightarrow{U}),$$ (1)

$$\frac{dD}{dt}=a{D}_I-\omega D-k_{D_I}D(1-e^{{\delta }_D{C}_H})\equiv F_2(\overrightarrow{U}),$$ (2)

$$\frac{d{D}_T}{dt}=a_T{D}_I\frac{T_R}{g_R+T_R}-{\omega }_T{D}_T+b_T{D}_I\frac{I{L}_{10}}{g_{10}+I{L}_{10}}-k_{D_T}{D}_T(1-e^{{\delta }_{D_T}{C}_H})\equiv F_3(\overrightarrow{U}),$$ (3)

$$\frac{d{T}_N}{dt}={\alpha }_N-T_N\frac{{\omega }_N}{g_2+I{L}_2}-k_N{T}_N(1-e^{{\delta }_N{C}_H})\equiv F_4(\overrightarrow{U}),$$ (4)

$$\frac{d{T}_C}{dt}=a_C{T}_{N}D-d{D}_T{T}_C-a_{CP}{T}_C\frac{I{L}_2}{g_2+I{L}_2}+d_{CP}{T}_{CP}\frac{I{L}_{10}}{g_{10}+I{L}_{10}}-{\omega }_C{T}_C-k_C{T}_C(1-e^{{\delta }_C{C}_H})\equiv F_5(\overrightarrow{U}),$$ (5)

$$\frac{d{T}_{CP}}{dt}=a_{CP}{T}_C\frac{I{L}_2}{g_2+I{L}_2}-d_{CP}{T}_C\frac{I{L}_{10}}{g_{10}+I{L}_{10}}+\gamma T_{CP}-k_{CP}{T}_{CP}(1-e^{{\delta }_{CP}{C}_H})\equiv F_6(\overrightarrow{U}),$$ (6)

$$\frac{d{T}_R}{dt}=a_R{D}_T{T}_N+c{T}_R\frac{I{L}_2}{g_2+I{L}_2}-{\omega }_R{T}_R-k_R{T}_R(1-e^{{\delta }_{R}M})\equiv F_7(\overrightarrow{U}),$$ (7)

$$\frac{dI{L}_2}{dt}={\alpha }_2{T}_N-{\omega }_{2}I{L}_2+a_2{T}_C\frac{I{L}_2}{g_2+I{L}_2}\equiv F_8(\overrightarrow{U}),$$ (8)

$$\frac{dI{L}_{10}}{dt}={\alpha }_{10}{D}_I+a_{10}{T}_R{T}_C-{\omega }_{10}I{L}_{10}\equiv F_9(\overrightarrow{U}),$$ (9)

$$\frac{dC}{dt}=fC(1-hC)-D_{C}C-kC(1-e^{{\delta }_C{C}_H})\equiv F_{10}(\overrightarrow{U}),$$ (10)

$$\frac{d{C}_H}{dt}=-{\omega }_{C_H}{C}_H+\mathcal{F}(q,t)\equiv F_{11}(\overrightarrow{U}),$$ (11)

where $D_C=d{(L/C)}^l\cdot {(s+{(L/C)}^l)}^{-1}$ is the rate at which cytotoxic cells kill tumour cells [45].

The model is complete, subject to the initial conditions

$$\overrightarrow{U}(t=0)={\overrightarrow{U}}_0,$$ (12)

where $t=0$ refers to the initial treatment.

The analytical function $\mathcal{F}$ describes chemotherapy treatment, which is a combination of chemotherapy and immunotherapy. The function depends on time t and dosage q.

The function has the form:

$$\mathcal{F}(q,t)=\sum _{k=0}^{n}q(t-mk)\mathcal{H}(t-mk)e^{\frac{t-mk}{0.5}},$$ (13)

where n is the duration of the customised treatment for each patient, $\mathcal{H}$ is the unit step function, and m is the interval between treatments. For example, when $m=7$, the patient receives treatment every week.

The above mathematical model with function $\mathcal{F}$ describes a customised treatment protocol for each patient. Personalisation is performed by the analytical function described in equation (13), which depends on the time between treatments and the dose given to each patient. Any functional variable can be changed. Therefore, if the interval between treatments is to be changed, this can be carried out analytically. Similarly, if the dose from patient to patient needs to be changed, this can be also carried out analytically. These two parameters are fully controlled by a medical doctor.

The model can be written in abbreviated form as

$$\frac{d\overrightarrow{U}}{dt}=\overrightarrow{F}(\overrightarrow{U}),\overrightarrow{U}(0)={\overrightarrow{U}}_0,$$ (14)

where $\overrightarrow{F}(\overrightarrow{U})$ is the vector field of the model; that is, $\overrightarrow{F}(\overrightarrow{U})=(F_1(\overrightarrow{U}),...,F_{11}(\overrightarrow{U}))$.

The following parameters are used at the numerical simulation as well as at the application of the SPVF algorithm.

Model Parameters
Parameter	Value	Description
ω	0.19	Decay Rate of Immunogenic Dendritic Cells [25]
ωI	0.35	Decay Rate of Immature Dendritic Cells [25]
ωT	0.456	Decay Rate of Tolerogenic Dendritic Cells [25]
ωC	1.2 ⋅ 10−1	Decay Rate of Cytotoxic T-Cells [49]
ωN	1.12 ⋅ 10−2	Decay Rate of Naive T-Cells
ωR	2.34 ⋅ 10−2	Decay Rate of Regulatory T-Cells
ω2	23	Decay Rate of IL-2 [48]
ω10	123	Decay Rate of IL-10
${\omega }_{C_H}$	3.45 ⋅ 102	Decay Rate of Chemotherapy Medicine
kC	0.086	The relative size of tumor needed for half-maximal stimulation of Cytotoxic T-cells
c	.018	Max Growth Rate of T-regs [47]
aT	1.236	Activation Rate of Tolerogenic Dendritic Cells by Tregs
dCP	60	Deactivation Rate of Cytotoxic Analysis T-Cells by Tregs [34]
d	67	Deactivation Rate of Cytotoxic T-Cells by Dendritic Cells [49]
α2	0.021	Source Rate of IL-2 [47]
α10	0.34	Source Rate of IL-10 from Dendritic Cells [34]
αN	1.232	Source Rate of Naive T-cells
aCP	0.465	Activation Rate of Cytotoxic Cells by IL-2
gR	.018	Max Growth Rate of Tregs [47]
aR	6.984	Activation Rate of Tregs
g2	12	Growth Rate of Cytotoxic T-Cells
g10	56	Deactivation Rate of Cytotoxic T-Cells by Tregs
aC	0.768	Activation Rate of Naive T-Cells by Dendritic Cells [34]
$k_{D_I}$	3.848	The relative size of tumor needed for half-maximal stimulation of Immature dendritic cells
a	2.223	Activation Rate of Immature dendritic cells
$k_{D_T}$	87.646	The relative size of tumor needed for half-maximal stimulation of Tolerogenic dendritic cells
kN	0.0634	The relative size of tumor needed for half-maximal stimulation of Naive T-cells
a10	2.976	Activation Rate of Regulatory T-cells
a2	3.9578	Activation Rate of Cytotoxic T-cells by Interleukin 2 (IL-2)
δ()	∈[0.32 ⋅ 10−2,2.879 ⋅ 10−1]	Pure coefficient in exponential expression
kR	321	Level of Tregs necessary for half maximal activation of tolerogenic dendritic cells
bT	0.45	Activation Rate of Tolerogenic Dendritic Cells by IL-10
γ	12	Growth Rate of Cytotoxic T-Cells [49]
a10	0.453	Source Rate of IL-10 from Tregs

3. Analysis and results

In this section, we present the results of the two research objectives defined in the Introduction. The first is the application of the SPVF method, which determines the equilibrium points and investigates their stability. The second is a comparison of the results obtained by numerically solving the mathematical model for different treatment protocols using the analytical function (13), which considers different dosages and times.

3.1. Equilibrium points and stability analysis

One of the most important investigations in mathematical models describing realistic biological phenomena involves determining the equilibrium of the system. Based on the equilibrium of the system, there were no changes during a certain period of time. Such result is critical, particularly for the study of cancerous tumours [46]. Herein, we determined the equilibrium points of the mathematical model presented in Equations (1)-(11) with the initial conditions (12) and the function (13). Briefly, we first compared the right-hand side of equations (1)-(11) to zero, $\overrightarrow{F}(\overrightarrow{U})=0$, solved the algebraic equations to determine the equilibrium of the model, and finally verified the stability of each equilibrium point using the Jacobian matrix. As we are interested in equilibrium points ≠0, this system cannot be solved analytically, only numerically. Hence, an approximation is required. The first step of the approximation is to reduce the system of equations to decompose the model into fast and slow parts and study only the fast part when the slow part is frozen. Accordingly, the dynamical variables of the system that progress rapidly, and those that progress slowly must be known. However, based on the presentation of the model, the desired decomposition cannot be known without prior knowledge from experiments or intuition. Another method for discovering decomposition is the application of asymptotic mathematical methods. In this study, we applied the well-known SPVF method presented in [39]. An algorithm for the decomposition of a system of ODEs is presented in detail herein. The main function of the SPVF is to transfer the coordinates of the model, where the model can be decomposed into fast and slow subsystems at new coordinates. According to the SPVF method, to determine the equilibrium points of the system rewritten in new coordinates, the equilibrium points of only the fast subsystem can be found, while the slow subsystem remains constant. In addition, a stability analysis of the equilibrium points can be performed only for the fast subsystem. According to the SPVF method, the transformation and inverse transformation maintain stable equilibrium points, that is, the stable points remain stable in both the new and old coordinate systems under the transformation of the SPVF method.

By applying the SPVF algorithm, we obtain the eigenvalues of the system and new coordinates as follows:

$${\lambda }_1^f=2.6755\cdot {10}^{21},{\lambda }_2^f=1.9873\cdot {10}^{19},{\lambda }_3^f=5.6789\cdot {10}^{18},{\lambda }_4^f=6.5422\cdot {10}^{17},{\lambda }_5^s=86556.9783,{\lambda }_6^s=5685.5754,{\lambda }_7^s=4455.7854,{\lambda }_8^s=544.8077,{\lambda }_9^s=43.8889,{\lambda }_{10}^s=23.7655,{\lambda }_{11}^s=1.5459,$$ (15)

where f denotes $fast$ and s denotes $slow$, and are explained in the following paragraph. To avoid burdening the reader with algebraic expressions, we list the eigenvectors corresponding to the above eigenvalues as ${\overrightarrow{w}}_1,...,{\overrightarrow{w}}_{11}$.

According to the SPVF algorithm, the system of equations can be decomposed into fast and slow subsystems with respect to the maximal $gap=\frac{{\lambda }_i}{{\lambda }_j}$; that is, because the eigenvalues are arranged in descending order, the gap is the ratio of two consecutive eigenvalues. $MaxGap$ is the maximum ratio of any two consecutive eigenvalues. As observed from the above eigenvalues (equations (15)), the maximum gap is between ${\lambda }_4^f$ and ${\lambda }_5^s$ because $MaxGap\left\{\frac{{\lambda }_4^f}{{\lambda }_5^s}\right\}>>Gap\left\{\frac{{\lambda }_i}{{\lambda }_j}\right\}$ for all $i,j\in \{1,...,11\}$. Hence, the system of equations can be decomposed into the fast subsystem ${\tilde{D}}_I,\tilde{D},{\tilde{D}}_T,{\tilde{T}}_N$ and slow subsystem ${\tilde{T}}_C,{\tilde{T}}_{CP},{\tilde{T}}_R,{\tilde{I}}_2,{\tilde{I}}_{10},\tilde{C},{\tilde{C}}_H$, where $\tilde{\cdot }$ denotes the presentation of the dynamic variables at the new coordinates. Therefore, the stability analysis can concentrate on the fast subsystem, whereas the slow subsystem remains fixed. To determine the equilibrium points, we first formalise the transformation to new coordinates, where the decomposition into fast and slow subsystems is valid.

If we denote the new dynamical variables of the model in the new coordinates as $\overrightarrow{\tilde{U}}=({\tilde{D}}_I,\tilde{D},{\tilde{D}}_T,{\tilde{T}}_N,{\tilde{T}}_C,{\tilde{T}}_{CP},{\tilde{T}}_R,{\tilde{I}}_2,{\tilde{I}}_{10},\tilde{C},{\tilde{C}}_H)$, the model can be presented in the new coordinates using the eigenvectors as follows:

$$\overrightarrow{\tilde{U}}=W\cdot \overrightarrow{U},$$ (16)

where matrix W is the matrix whose columns are the transposes of the eigenvector, that is, $W=({\overrightarrow{w}}_1^t,...,{\overrightarrow{w}}_{11}^t)$. We take the derivative of the algebraic system (16) with respect to time t and substitute the system (14) as follows:

$$\frac{d\overrightarrow{\tilde{U}}}{dt}=W\cdot \frac{d\overrightarrow{U}}{dt}=W\cdot \overrightarrow{F}(\overrightarrow{U}).$$ (17)

To complete the presentation of the model in new coordinates, we multiply equation (16) from the left by the inverse matrix $W^{-1}$; this allows us to write the old dynamical variables of the model as a function of the new dynamical variables:

$$\overrightarrow{U}=W^{-1}\cdot \overrightarrow{\tilde{U}}.$$ (18)

Substituting equation (18) into (17), we obtain the complete model with the initial conditions rewritten in new coordinates as

$$\frac{d\overrightarrow{\tilde{U}}}{dt}=W\cdot \overrightarrow{F}(W^{-1}\cdot \overrightarrow{\tilde{U}})\equiv \overrightarrow{H}\left(\overrightarrow{\tilde{U}}\right),\overrightarrow{\tilde{U}}{|}_{t=0}=W\cdot \overrightarrow{U}{|}_{t=0}.$$ (19)

At these coordinates (model (19)), the model is decomposed into fast and slow subsystems, as follows:

$${\epsilon }_1\cdot \frac{d{\tilde{D}}_I}{dt}=H_{fast}\left(\overrightarrow{\tilde{U}}\right){\epsilon }_2\cdot \frac{d\tilde{D}}{dt}=H_{fast}\left(\overrightarrow{\tilde{U}}\right){\epsilon }_3\cdot \frac{d{\tilde{D}}_T}{dt}=H_{fast}\left(\overrightarrow{\tilde{U}}\right){\epsilon }_4\cdot \frac{d{\tilde{T}}_N}{dt}=H_{fast}\left(\overrightarrow{\tilde{U}}\right)$$ (20)

$$\frac{d{\tilde{T}}_C}{dt}=H_{slow}\left(\overrightarrow{\tilde{U}}\right)\frac{d{\tilde{T}}_{CP}}{dt}=H_{slow}\left(\overrightarrow{\tilde{U}}\right)\frac{d{\tilde{T}}_R}{dt}=H_{slow}\left(\overrightarrow{\tilde{U}}\right)\frac{d{\tilde{I}}_2}{dt}=H_{slow}\left(\overrightarrow{\tilde{U}}\right)\frac{d{\tilde{I}}_{10}}{dt}=H_{slow}\left(\overrightarrow{\tilde{U}}\right)\frac{d\tilde{C}}{dt}=H_{slow}\left(\overrightarrow{\tilde{U}}\right)\frac{d{\tilde{C}}_H}{dt}=H_{slow}\left(\overrightarrow{\tilde{U}}\right),$$ (21)

where $0<{\epsilon }_i<<1$ for $i=1,2,3,4$ are small parameters of the fast subsystem.

The main advantage of decomposing the system of equations into fast and slow subsystems is the ability to study only the fast subsystem without losing biological information in our case, and thus obtain a general picture of the entire process of the model. In this study, equilibrium and stability points were explored. Stability analysis is a biologically important investigation that can be performed to determine when a patient's medical condition stabilises in terms of the relevant parameters for treatment. Hence, the relevant subsystem is a system of equations (20). For convenience, the abbreviated representation of the system of equations (20)-(21) is:

$$\overrightarrow{\epsilon }\cdot \frac{d{v}_f}{dt}={\overrightarrow{\mathcal{H}}}_f({\overrightarrow{v}}_f,{\overrightarrow{v}}_s)$$ (22)

$$\frac{d{v}_s}{dt}={\overrightarrow{\mathcal{H}}}_s({\overrightarrow{v}}_f,{\overrightarrow{v}}_s),$$ (23)

where $(\overrightarrow{\epsilon },{\epsilon }_1,...,{\epsilon }_4)$, ${\overrightarrow{v}}_f=({\tilde{D}}_I,\tilde{D},{\tilde{D}}_T,{\tilde{T}}_N)$, and ${\overrightarrow{v}}_s=({\tilde{T}}_C,{\tilde{T}}_{CP},{\tilde{T}}_R,{\tilde{I}}_2,{\tilde{I}}_{10},\tilde{C},{\tilde{C}}_H)$.

To obtain the equilibrium points of the model, we must solve the fast subsystem (22) for the fast variables while setting all slow variables (system of equations (23)) as constant (the slow variables are “frozen” at their initial values; hence, we can take ${\overrightarrow{v}}_s={\overrightarrow{v}}_s(0)$ as the constants);

$${\overrightarrow{\mathcal{H}}}_f({\overrightarrow{v}}_f^{⁎},{\overrightarrow{v}}_s(0))=0.$$ (24)

After obtaining the equilibrium point solution from the fast subsystem (algebraic system (24)), we substitute these points into the slow subsystem and solve the algebraic system for solutions of the slow variables, that is,

$${\overrightarrow{\mathcal{H}}}_s({\overrightarrow{v}}_f^{⁎},{\overrightarrow{v}}_s^{⁎})=0.$$ (25)

Solving the system of equations (24) and then solving the system of equations (25) result in the equilibrium points of the model rewritten in new coordinates. The next step is to analyse the stability of each equilibrium point. Hence, we examined the sign of the real part of the eigenvalues of the following $Jacobian$ matrix at each equilibrium point.

$${\left(\begin{array}{c}\hfill \frac{\partial ({\overrightarrow{\mathcal{H}}}_f({\overrightarrow{v}}_f,{\overrightarrow{v}}_s),{\overrightarrow{\mathcal{H}}}_s({\overrightarrow{v}}_f,{\overrightarrow{v}}_s))}{\partial ({\overrightarrow{v}}_f,{\overrightarrow{v}}_s)}\hfill \end{array}\right)|}_{({\overrightarrow{v}}_f^{⁎},{\overrightarrow{v}}_s^{⁎})}.$$ (26)

The eigenvalues with negative real parts (obtained from equation (26)) are locally stable. Only one stable equilibrium point was found for each treatment protocol. Five protocols were studied. The first protocol did not include treatment, that is, $\mathcal{F}(q,t)=0$. In this case, there is no equilibrium point. For $\mathcal{F}(q,t)\ne 0$, we obtained an equilibrium point.

The model rewritten in the new coordinates using the eigenvectors does not have biological meaning as every dynamical variable in the new coordinates is a linear combination of the dynamical variables in the old coordinates. Hence, equilibrium points have no biological meaning. Therefore, to provide a biological interpretation of our results, we must invert the equilibrium points to the old coordinates, that is, we must apply the inverse matrix of the eigenvectors $W^{-1}$ to the equilibrium points:

$$W^{-1}\left(\begin{array}{c}\hfill {\overrightarrow{v}}_f^{⁎}\hfill \\ \hfill {\overrightarrow{v}}_s^{⁎}.\hfill \end{array}\right)$$ (27)

All equilibrium points (obtained from equation (27)) depend on the parameters and initial conditions of the model. For example, the equilibrium point of the dynamical variable of the tumour C for the protocol given to the patient twice with 28 days between treatments is

$$C^{⁎}=0.2537\cdot {\omega }_2{\alpha }_{10}{D}_I^0-0.8766\cdot \kappa {\omega }_{C_H}h{g}_2{D}^0+2.4564\cdot a_{CP}\gamma D_T^0+1.2342\cdot b_T{g}_{10}{\kappa }_{D_I}{\omega }_T{T}_N^0+1.6768\cdot \kappa a_2{a}_R{T}_C^0-0.0033\cdot {\omega }_{10}{d}_{CP}{T}_{CP}^0-9.7745\cdot {\omega }_{C_H}{a}_C{\omega }_T{T}_R^0+0.0090\cdot hf{\kappa }_{N}d\gamma I{L}_2^0-0.0978\cdot d_{CP}{\alpha }_N{g}_{2}I{L}_{10}^0+3.55{\omega }_{10}{C}^0+9.9968\cdot d{\omega }_C{\kappa }_R{C}_H^0.$$ (28)

Once we substitute the parameters of the model, we obtain the stable equilibrium point of the cancer tumour. Thus, the equilibrium point for the dynamic variable C is a combination of the remaining dynamic variables of the model, indicating that this is the optimal combination of variables for achieving a stable equilibrium point.

3.2. Numerical results

In this section, we present our numerical results relative to the experimental results (clinical results, [40], [41], [42]). We analysed the solution profiles of our results obtained by solving models (1)-(11), and applied a numerical simulation using the MATLAB ode45 packages.

According to a report from the Washington University School of Medicine in St. Louis, most patients with glioblastoma die less than 18 months after diagnosis [43]. However, a clinical trial of a personalised vaccine for glioblastoma revealed improvements in survival rates for such patients. A summary of this study is given below.

The trial included patients from different countries with brain tumours and glioblastomas at different stages. Some patients received a vaccine called DCVax-L, and some received a placebo. The vaccine is personalised and varies from one patient to another. All treatments were administered to patients who underwent a cancerous tumour removal procedure, and a small amount of tumour tissue was processed and then exposed to the patient's own immune cells, called dendritic cells. This procedure trains dendritic cells to follow and destroy tumour cells. Subsequently, these trained dendritic cells were re-injected into the patient. The treatment protocol was not fixed. An example of this protocol is as follows: Vaccine once every 3 weeks three times. The vaccine was then administered three times, once every two months, and then once every six months.

Patients in the trial had a median survival of just over 23 months, some had an average overall survival of 40.5 months, and generally, patients with an aggressive glioblastoma lived 15 to 17 months with standard treatment such as surgery for tumour removal, chemotherapy, and radiotherapy.

In addition to this type of treatment, patients reported minimal side effects compared to those associated with the standard treatment.

Figs. 2, 4, 6, and 8 present the function $\mathcal{F}(q,t)$ for one cycle at different treatment times. For example, Fig. 2 presents the function of a treatment every 7 days. The complete treatment cycle is 365 days.

Figure 2.

Plot of function $\mathcal{F}(q,t)$ describing chemotherapy treatment for cancer - one cycle only. Treatment cycle was every 7 days. In our analysis, we considered a constant dosage normalised to “1”. Full treatment cycle was 365 days.

Figure 4.

Plot of function $\mathcal{F}(q,t)$ describing chemotherapy treatment for cancer - one cycle only. Treatment cycle was every 14 days. In our analysis, we considered a constant dosage normalised to “1”. Full treatment cycle was 365 days.

Figure 6.

Plot of function $\mathcal{F}(q,t)$ describing chemotherapy treatment for cancer - one cycle only. Treatment cycle was every 28 days. In our analysis, we considered a constant dosage normalised to “1”. Full treatment cycle was 365 days.

Figure 8.

Plot of function $\mathcal{F}(q,t)$ describing chemotherapy treatment for cancer - one cycle only. Treatment cycle was every 56 days. In our analysis, we considered a constant dosage normalised to “1”. Full treatment cycle was 365 days.

Fig. 1 presents the solution profiles of cancer cells (solid line). We compared the results of the proposed model with clinical data. The model was solved using $\mathcal{F}(q,t)=0$, that is, no treatment was administered to the patient. As expected, the cancer cells began to grow after approximately 110 days.

Figure 1.

Solution profiles of cancer cells without treatment ($\mathcal{F}(q,t)=0$) - solid line compared to experimental (clinical) results.

In Fig. 3, we present the solution profiles of cancer cells (solid lines) for different parameter values. This figure relates to Fig. 2, where the treatments were administered to the patient every 7 days. Line 1 refers to the treatment with the highest mixed dosage $q_1$, and 4 refers to the treatment with the lowest mixed dosage $q_4$. These results are predictable because both doses are high and the time differences between treatments are relatively short, with a difference of 7 days between treatments. As a result, the cancer decreases relatively quickly to virtually zero after $40--85$ days for all doses. Because the dose $q_4$ (Line 4) is the lowest, it decreases more slowly to zero relative to the other doses.

Figure 3.

Solution profiles of cancer cells with treatment every 7 days. Solid lines: Line 1 refers to treatment with highest mixed dosage q₁ and Line 4 refers to treatment with lowest mixed dosage q₄. Lines 2,3 are intermediate dosages - compared to experimental (clinical) results

In Fig. 5, we present the solution profiles of cancer cells (solid lines) for different parameter values. This figure relates to Fig. 4, where the treatments were administered to the patient every 14 days. As depicted in these graphs, at the beginning of the treatment, there was a sharp decrease in the tumour size followed by an increase in the tumour size; such finding is due to the second dose being administered two weeks after the first dose. After the second dose, the tumour size decreased until approximately 180 days, when the tumour size reached zero.

Figure 5.

Solution profiles of cancer cells with treatment every 14 days. Solid lines: Line 1 refers to treatment with highest mixed dosage q₁ and Line 4 refers to treatment with lowest mixed dosage q₄. Lines 2,3 are intermediate dosages - compared to experimental (clinical) results

In Fig. 7, we present the solution profiles of cancer cells (solid lines) for different parameter values. This figure relates to Fig. 6, where the treatments were administered to the patient every 28 days. As depicted in the graphs, the behaviour is slightly different and unusual because, at the beginning of treatment, the cancer decreases rapidly with the administration of the drug. Subsequently, there was an increase in the tumour for 75 days, followed by a decrease to virtually zero after 190 days (190 days is approximately seven treatment cycles). Of note, the second dose is administered to the patient only after 28 days, and therefore requires time to significantly affect the tumour. Inexplicably, after 190 days, the tumour begins to grow to a maximum size that occurs after 270 days (270 days is a cycle of approximately ten treatments). Thereafter, the tumour again decreases to virtually zero after 340 days, which corresponds to 12 treatment cycles. The rational explanation for the increase and decrease is the relatively large intervals of the treatment itself, which allows the tumour to grow.

Figure 7.

Solution profiles of cancer cells with treatment every 28 days. Solid lines: Line 1 refers to treatment with highest mixed dosage q₁ and Line 4 refers to treatment with lowest mixed dosage q₄. Lines 2,3 are intermediate dosages - compared to experimental (clinical) results

In Fig. 9, the solution profiles of cancer cells (solid lines) for different parameter values are shown. This figure relates to Fig. 8, where the treatments were administered to the patient every 56 days. These results demonstrate a behaviour similar to that of the previous graph, where the treatment doses were administered at relatively large intervals. As observed at the beginning of the treatment, similar to all other results, the tumour decreases quickly and then begins to increase for 60 days. The next treatment is administered after 56 days, and the tumour begins to decrease after 80 days, which means that, in this case, the treatment affects the tumour virtually immediately. The tumour size decreases for 70 days, then starts increasing for 60 days, but to a considerably smaller size than its previous size. When another treatment cycle is performed, the tumour begins to decrease again; this cycle is repeated. In this case, a correlation was found between treatment and tumour size, and the effect was virtually immediate. After only a few days of treatment, tumour size decreased. After several weeks of treatment, the effect decreased and the tumour began to grow again. When the treatment was repeated, the tumour size began to decrease again. Unlike the previous case, the treatment and size of the tumour were virtually completely coordinated in terms of time.

Figure 9.

Solution profiles of cancer cells with treatment every 46 days. Solid lines: Line 1 refers to treatment with highest mixed dosage q₁ and Line 4 refers to treatment with lowest mixed dosage q₄. Lines 2,3 are intermediate dosages - compared to experimental (clinical) results

Fig. 10 shows the solution profiles of the cancer cells based on different values of the initial conditions $C(0)\in [{10}^3,{10}^{13}]$. According to the graphs, all cancer cells decreased with treatment time. As demonstrated by the results obtained after approximately 245 days, cancer cells reach a state of equilibrium.

Figure 10.

The solutions profiles of the cancer cells with different initial conditions.

Fig. 11 presents the dynamic variables of dendritic cells, that is, immature dendritic cells, immunogenic dendritic cells, and tolerogenic dendritic cells vs. cancer cells. As depicted in the graphs, the dendritic cells ($D_I,D_T$, and D) behave approximately the same only on a different scale in relation to the cancer cells. First, the dendritic cells decrease, and is followed by a very sharp increase that stabilises over time. Currently, the number of cancer cells is steadily declining.

Figure 11.

The graphs describe the dynamical variables D_T,D_I and D vs the cancer cells C.

Fig. 12 displays the plots of cytotoxic T-cells, naive T-cells, regulatory T-cells, and cytokine $IL-2$ vs. cancer cells. Cytotoxic T-cells behave similarly. At the beginning of the process, the T-cells decrease, and then increase and stabilise. Of note, these cells have negative values as the y-axis is set as a log, indicating the values of these cells between 0 and 1. The $IL-2$ cells remained stable throughout the process. However, at a given scale of the t-axis, the number of cancer cells decreased monotonically.

Figure 12.

The graphs describe the dynamical variables T_R,T_N and IL₂ vs the cancer cells C.

Fig. 13 shows the plots of cytotoxic T-cells, naive T-cells, regulatory T-cells, and cytokine $IL-10$ vs. cancer cells. The difference between this figure and the previous figure is the behaviour of $IL-10$. The cytokine $IL-10$ rises rapidly to a state of stabilisation.

Figure 13.

The graphs describe the dynamical variables T_R,T_N and IL₁₀ vs the cancer cells C.

Fig. 14 shows a heatmap of the dynamic variables of the mathematical model. Each square in the heatmap describes the correlation between the variable on the x-axis and the variable on the y-axis. The correlation used in our calculations was $Pearson-correlation$. As expected, on the diagonal of the heatmap, the correlation was 1, which indicates a linear correlation between the same dynamical variables. For example, the correlation between variables $D_T$ and $C_H$ is close to -1, which means that the correlation is a negative linear correlation. Thus, a direct opposite correlation exists, as one variable increases and the other decreases, and vice versa. Based on the heatmap, the matrix is symmetric with respect to the diagonal $y=x$. Further, the same variables are observed to be grouped in clusters, that is, D, T, etc. Such result indicates that the correlation between the variables in the same cluster is 1 (positive correlation), and the variables from different clusters have a negative correlation.

Figure 14.

The correlations between the dynamical variables of the model.

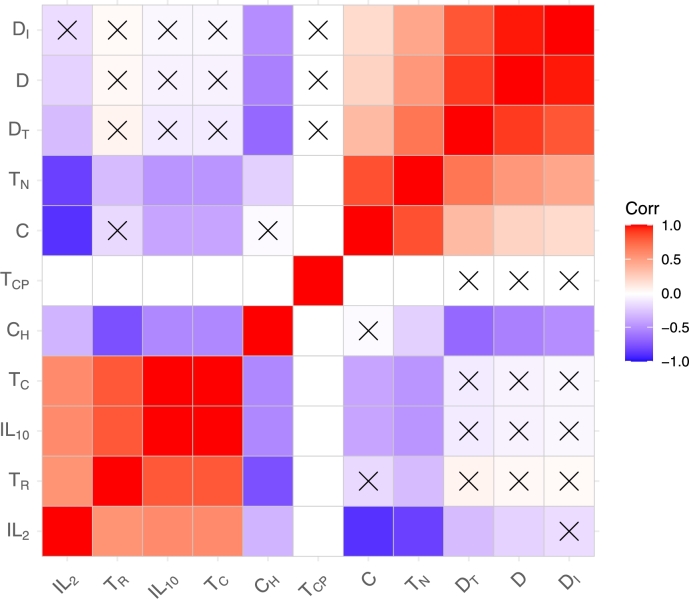
Fig. 15 contains a plot of the same heatmap of the dynamical variables of the mathematical model. In x, we emphasise the variables that are not significant. In our calculations, we set $p-value$ to 0.05. From this drawing, the relationship between variables that have a positive correlation and those that are significant are evident. The variables with negative correlations were not significant. This result can be used in future research where a large amount of data will be collected and artificial intelligence can be applied. Accordingly, the variables that are significant can be determined.

Figure 15.

The correlations between the dynamical variables of the model with significant variables which marked by X

Fig. 16 shows the same heatmap as the previous plots, but with another level of clusters. The $cell.type-bar$ shows sets of variables that behave similarly. Mathematical connections are not necessarily behaviour and biological connections. For example, the green bar represents a cluster of dendritic variables, which behave the same and reinforce the results presented in the previous graphs.

Figure 16.

The correlations between the dynamical variables of the model in different level.

Figure 17, Figure 18, Figure 19 displays the correlations between the different dynamic variables (present in the diagonal of the matrix) of the system. For example, in 18, the fourth column is the second column. The graph describes the correlation between the variables, $IL-2$ and $T_R$. In each graph in Figs. Figure 17, Figure 18, Figure 19, the correlation of the same variable was added to the variable of the cancer cells. The axes of these Figures are the diagonals of the matrix.

Figure 17.

The correlations between T-cells and the cancer cells. The axes are: the y axis is the considered dynamical variable and the x axis is the time

Figure 18.

The correlations between T-cells and IL − 10 and the cancer cells. The axes are: the y axis is the considered dynamical variable and the x axis is the time

Figure 19.

The correlations between all the dynamical variables of the model. The axes are: the y axis is the considered dynamical variable and the x axis is the time

4. Conclusions

In this study, a mathematical model for chemo-immunotherapy, which is a combination of chemotherapy and immunotherapy for brain cancer, was investigated. The system of equations included nonlinear first-order ODEs. The mathematical model considers the interaction of immune system cells with cancer cells and the treatment. The dynamic variables of the system are immature dendritic cells, immunogenic dendritic cells, tolerogenic dendritic cells, naive T-cells, cytotoxic T-cells, proliferating cytotoxic T-cells, Treg, $IL-2$, $IL-10$, cancer cells, and chemotherapy medicine. We proposed a new treatment protocol, which is essentially a new analytical function that depends on the time interval between treatment and dosage. Of note, the hierarchy of the system was hidden. To investigate the stability of the equilibrium points, it is necessary to solve the nonlinear algebraic equation related to the mathematical model, which, in this case, is impossible analytically. Hence, we applied the SPVF algorithm to transfer the mathematical model to a new coordinate with an explicit hierarchy and divided it into fast and slow subsystems. This procedure enabled us to investigate only the fast subsystem, without losing the biological information of the original model. We determined all equilibrium points of the model in the new coordinates and their stability. The equilibrium points have no biological meaning in the new coordinates; hence, we inverse-transformed only the stable equilibrium points into the original coordinates of the model (In the present paper we have presented one stable equilibrium point of the mathematical model (28)).

We investigated the mathematical model with our proposed treatment protocol, with constant dosage and different time intervals between treatments, that is, 7, 14, 28, and 56 days. Thereafter, we compared our analysis results with experimental (clinical) data. The optimal treatment was found to correspond to the protocol with a 7 day interval between treatments. The next step involved the application of the protocol with different dosages and time intervals simultaneously.

We examined the behaviour of cancer cells when the initial conditions were changed. All results were identified to reach a state of equilibrium at approximately the same time. Indeed, this is dependent on the treatment, which has been determined to vary in terms of dosage and time.

Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 clearly show the correlations between the variables of the mathematical model. Further, the variables with a positive correlation, when the Pearson correlation is close to 1; those with a negative correlation, a Pearson correlation close to -1; and those with a correlation of 0, which indicates a weak linear correlation between the two variables, can be clearly seen. Significant variables in the model were also found, which can be useful for the application of machine learning. Overall, we present graphs that represent the correlation of each variable with the graph of cancer cells, and explicitly illustrate the behavioural relationships of the variables, both biologically and mathematically.

Declarations

Author contribution statement

Ophir Nave: Conceived and designed the analysis; Analyzed and interpreted the data; Contributed analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

The data that has been used is confidential.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

Supplementary material related to this article can be found online at https://doi.org/10.1016/j.heliyon.2022.e09288.

No additional information is available for this paper.

Supplementary material

The following Supplementary material is associated with this article:

Diagram1.docx

The interaction of the dynamical variables of the mathematical model.