Abstract
The coronavirus disease 2019 (COVID-19) pandemic has posed substantial challenges to worldwide health systems in quick response to epidemics. The assessment of personal exposure to COVID-19 in enclosed spaces is critical to identifying potential infectees and preventing outbreaks. However, traditional contact tracing methods rely heavily on a manual interview, which is costly and time consuming given the large population involved. With advanced indoor localisation techniques, it is possible to collect people's footprints accurately by locating their smartphones. This study presents a new framework for the assessment of personal exposure to COVID-19 carriers using their fine-grained trajectory data. An integral model was established to quantify the exposure risk, in which the spatial and temporal decay effects are simultaneously considered when modelling the airborne transmission of COVID-19. Regarding the obstacle effect of the indoor layout on airborne transmission, a weight graph based on the space syntax technique was further introduced to constrain the transmission strength between subspaces that are less inter-visible. The proposed framework was demonstrated by a simulation study, in which external comparison and internal analysis were conducted to justify its validity and robustness in different scenarios. Our method is expected to promote the efficient identification of potential infectees and provide an extensible spatial–temporal model to simulate different control measures and examine their effectiveness in a built environment.
Keywords: Contact tracing, Space syntax, COVID-19, Visibility analysis, Spatio-temporal model
1. Introduction
The coronavirus disease 2019 (COVID-19) pandemic has caused a severe disaster and posed an unprecedented challenge to public health systems throughout the world [1,2]. Contact tracing is an effective tool to diminish the onward transmission of pandemics [3,4]. Contact tracing aims to identify risky individuals who have been recently exposed to infected persons, thus supporting the designation of instant tests and self-quarantine in case of further transmission [5,6]. At present, contact tracing is one of the mainstream practices for the regular prevention and control of COVID-19 in most parts of the world [7].
Traditionally, contact tracing is conducted by manual interview of the infected or diagnosed people regarding the areas they might have visited and others whom they might have contacted [8]. However, given the complexity of human behavior and the large population involved, manual interviews can cost huge amounts of time and human resources, which will delay the time for halting the transmission [9]. Digital contact tracing applications based on smartphones have been developed and applied worldwide [10,11]. As a result, users’ footprints and their risky contact can be recorded and analysed by authorised agencies, which offers considerable benefits to timely contact tracing [12].
Defining a risky contact is one of the critical issues in current digital contact tracing approaches [13]. The longer a person stays close to infected people, the higher risk of transmission is [14]. The World Health Organization (WHO) defines an interaction with a potential COVID-19 carrier within 1 m and for at least 15 min as a high risky contact [15]. Although the numeric setting may deviate from WHO's guidelines due to different environments and requirements, the basic idea of using specific proximity thresholds to distinguish close contacts is common in current studies.
However, adopting proximity thresholds assumes a crisp boundary between risky and safe interactions, which ignores the distance-decay effect of transmission risk [16]. The definition of WHO fails to identify contact within a distance of 10 m and a duration of 20 min, although such exposure may still be risky due to the aerosol diffusion of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) [17]. A larger threshold will still promote the exclusion of ‘safe enough’ people, and more individuals will be recognised as ‘close contact’, which will inevitably lead to overestimation in practice. Furthermore, contacts within the given proximity thresholds will be regarded as being uniformly risky in existing models. However, people who stay closer to or longer with an infected person should be theoretically at a higher risk [3]. In response to these problems, multiple levels of thresholds are adopted to attain a fine classification of risky contacts [[18], [19], [20]]. However, the problem of uniform risk remains unsolved at each risk level.
To estimate individual transmission risk more precisely thus supporting a fast identification and filtering highly risky people, this study develops an extensible and computational framework for the assessment of personal exposure to COVID-19 transmission, especially in public indoor spaces. As the primary place for people gathering and close interactions, public indoor spaces, such as supermarkets and hospitals, pose a transmission risk that is over 18 times higher than that of outdoor spaces [21]. With the popularity of public wireless services, advanced WiFi-based positioning techniques provide an effective solution for the collection of fine-grained individual trajectories [[22], [23], [24]], which supports the creation of more sophisticated contact tracing models. In this study, an explicit expression considering the effects of spatiotemporal decay was firstly derived to formulise the airborne transmission of SARS-CoV-2. Then, an integral model was proposed to quantify the exposure risks based on the spatiotemporal trajectories of exposed and infected individuals. With further consideration of the effect of obstacles, a weight graph was constructed based on the space syntax technique, which constrains the strength of transmission between less inter-visible subspaces, to model the topology of an indoor space. Finally, simulation experiments were conducted to verify the proposed method and test its effectiveness in different contexts. The proposed method will promote the efficient identification of risky exposure and contribute to smart indoor monitoring systems for the regular control of COVID-19 in the post-pandemic era.
The remainder of this article is organised as follows: Section 2 reviews the related works on contact tracing models. Section 3 introduces the methodology of this study. Section 4 describes the simulation experiments and analyses of the performance of the proposed method. Finally, Section 5 discusses and concludes this study.
2. Related works
2.1. Overview of digital contact tracing approaches
During the fight against COVID-19, a series of smartphone-based digital approaches has been implemented to facilitate contact tracing by recording the user's close exposure to a person who was later found to be infected. These approaches generally rely on QR codes, Global Positioning System (GPS), Bluetooth or WiFi technology [25]. These technologies are compared in Table 1 .
Table 1.
Comparison of different technological approaches for contact tracing.
| Technology | Indoor accuracy | Advantages | Disadvantages |
|---|---|---|---|
| QR code | Room level |
|
|
| GPS | Most likely not operating |
|
|
|
|
||
|
|
||
| Bluetooth | <2 m |
|
|
|
|
||
|
|
||
| WiFi | <1 m |
|
|
2.1.1. QR codes
QR codes are easily deployed and provide a cheap way to collect public mobility information for contact tracing. In China, people are instructed to scan a QR code when visiting public spaces. An alert will be pushed to smartphone users when they are found to be once co-located with an infected person [11]. Although this approach lacks focus on whether a close contact has actually occurred, it is a quick and effective response to the spread of COVID-19 given the vast population of China [26].
2.1.2. GPS
GPS can provide detailed footprints of users and thus support a finer-grained contact tracing than QR codes. Various smartphone GPS-based apps, such as ‘Care19’ from the US, ‘Corona Data’ from Germany or ‘Corona 100 m’ from South Korea, have been established; they allow the quick identification of possible locations of risky contact [10,27,28]. Wang et al. [29] demonstrated a typical example that presented a GPS-based system to reconstruct the spatiotemporal trajectory of a smartphone user in the past 14 days and evaluated the infection risk based on the user's historic visits to places that contained diagnosed patients. However, GPS data suffer from a profound signal loss caused by dense buildings or indoor environments [30]. In addition, given the inevitable positioning errors in GPS data, setting proper proximity thresholds for distinguishing risky contact is challenging [29].
2.1.3. Bluetooth
Another batch of studies attempted to use Bluetooth for contact tracing. Unlike GPS, which records the coordinates of users, the received signal strength (RSS) of a Bluetooth beacon is utilised to measure the distance between nearby devices. Although Bluetooth technology provides less information on user movement and actual geographic location, which is not conducive to studying the disease spread, user privacy can be largely preserved [31]. In addition, Bluetooth is not restricted by indoor or outdoor conditions. Given these advantages, Bluetooth technology has been widely implemented in contact-tracing apps, such as the ‘NHS COVID-19’ app from the UK and ‘COVIDSafe’ from Australia [32,33]. Although Bluetooth technology can generally achieve a 2 m accuracy in distance estimation [34], the measurement can be less reliable once the smartphone is deep in a pocket or handbag [25]. Furthermore, the technology cannot determine whether people are separated by walls or floors, which will induce a false level of spurious identification in contact tracing [25,35].
2.1.4. WiFi
WiFi can provide positioning data with higher accuracy in indoor spaces compared with GPS. This merit makes WiFi an effective technology for contact-tracing in indoor environments, such as hospitals, airports and supermarkets [35]. Once users enable the WiFi access on their devices, their locations can be timely computed based on the strength of signals between their devices and WiFi access points (WAPs). Similar to GPS-based contact tracing approach, social distance and duration thresholds are commonly used in WiFi-based approaches to identify close exposure [36]. Section 2.3 will introduce more details about the positioning performance of WiFi technology.
2.2. Spatial model of contact risk
The current methods for contact tracing are mostly qualitative and output only Boolean values to distinguish risky contacts based on predefined proximity thresholds [10,27,28]. However, given the distance-decay effect, contacts that satisfy given thresholds may present varying risks. Yin et al. [37] assumed the contact strength is inverse-distance weighted and introduced a distance-decay model to improve the calculation of encounter probability based on the spatiotemporal trajectories of agents. Nevertheless, only spatial distance was considered in this study, whilst the effect from temporal distance was overlooked.
With awareness of the elevated transmission risk during prolonged exposure, Ying and O'Clery [38] measured the risk of viral transmission by the duration when a customer was exposed to an infected person in the same zone of a supermarket. This kind of method, which substantially estimates the contact strength by the frequency of co-location, is common in current studies on COVID-19, especially in large-scale surveillances [[39], [40], [41]]. However, such co-location-based methods have been argued as being coarsely grained without consideration on the precise distance between individuals [38,42]. Moreover, given the airborne transmission property of SARS-CoV-2, even without direct contact with infected people, virus-laden aerosols remain risky to those who walk along the patient's path [17]. The above issues must be further considered when building a sophisticated risk model.
2.3. Indoor localisation technology
Advanced indoor localisation approaches offer new chances to develop better contact tracing methods. WiFi and active radio frequency identification (RFID) are essential technologies used in indoor real-time positioning [43]. Technically, WiFi and RFID share similar positioning principles, in which the location of a target device is estimated based on the geometric relationship between multiple RFID readers or WAPs with known positions. However, given the limited coverage of the RFID reader, RFID is often used only when room-level accuracy is required [44], such as the tracking of goods, whilst WiFi is more accurate and easily deployed to track people in a large and complex scenario [22,43].
WiFi-based localisation technology generally utilises the RSS to estimate the distance between a smartphone and a WAP: the higher the RSS value, the smaller the distance [24]. By combining the estimated distances to at least three reference points, the real-time location of a smartphone in a predefined coordinate system can be possibly obtain based on trilateration or the least square method [24]. The positioning accuracy of WiFi technology ranges within several meters in an unobstructed space and can be significantly improved to the centimetre level using ultra-wideband techniques [22,45].
To deal with highly obstructed indoor environments, Chen et al. [23] presented a frequency-hopping approach and achieved an accuracy of 5 cm with a standard bandwidth. In the recent study of Zhang et al. [46], an adaptive access point selection method, which can achieve a positioning accuracy within 2 cm, was proposed to deal with the positioning problem of smartphones with a low scanning frequency. Although the accuracy of WiFi-based localisation is affected by the environments and hardware, advanced studies have proven that WiFi technology can be readily used to collect people's fine-grained trajectory.
3. Methodology
3.1. Spatiotemporal decay in the airborne transmission of SARS-CoV-2
According to the study of Chu et al. [16], the absolute risk of SARS-CoV-2 infection is generally estimated at 12.8% with a physical distance (PD) of less than 1 m, and for every additional 1 m, the risk decreases approximately by half (change factor: 2.02). Hence, regardless of additional protection (e.g. face mask and goggles), the infection risk concerning spatial distance can be modelled as follows:
| (1) |
where and are the spatial coordinate vector of the exposed and infected persons, respectively. Notably, although the distance decay effect in Equation (1) is widely acknowledged in the scientific community [47,48], the coefficients 12.8% and 2.02 can be arguable because they are the result of regression from multiple clinical studies without consideration of the duration of exposure, size of droplets, and other factors, such as wearing of masks and face shields [16,49,50]. However, we kept these coefficients following the original paper because they have negligible impact on the assessment of the relative risk of transmission and can be easily amended in different scenarios.
In addition, previous studies revealed that the infectiousness of virus-laden aerosols decays along with time, whilst the decay rate can be affected by numerous environmental factors. According to the study of Dabisch et al. [51], temperature, humidity and simulated sunlight have a significant influence on the persistence of SARS-CoV-2 in aerosols, and the decay rate can be calculated as follows:
| (2) |
where is the decay rate of infectivity (), denotes the temperature (), refers to the relative humidity (%), and is the UVB irradiance ().
Let denote the starting time of aerosol formation. is the instantaneous risk at a given timestamp , which can be calculated as follows:
| (3) |
3.2. Integral model for the assessment of exposure risk
The exposure risk can be calculated based on Equation (3) by means of integration. The simplest scenario is shown in Fig. 1 , where the two agents are motionless, and the infected person's moving event ends before the exposed person's starts. Consequently, the exposed person will suffer from all the virus-laden aerosols formed during the movement of the infected people. In that sense, the individual risk for the exposed person can be expressed as follows:
| (4) |
Fig. 1.
Geometric interpretation of exposure risk calculation of the simplest scenario based on integration. Infected and exposed people are motionless and
However, given that locations and are not always static, and the moving event may start and end in different orders, using Equation (4) will lead to logic contradictions (e.g. exposure risk exists only after the action of infected people). Therefore, Equation (4) needs to be improved further to fit different cases.
Considering that the sampling interval of the WiFi-based localisation technique can be at the secondary level [24], this study assumed that the agent moves uniformly and straight between each two trace points. Thus, an agent's trajectory can be decomposed into multiple linear segments (i.e. moving events), and the agent's location can be possibly inferred at any timestamp. Without loss of generality, we used to denote the movement between two successive sampling timestamps, namely, and , and the agent's location at timestamp t () can be expressed as .
Notably, the risk exists only after the formation of aerosols. Therefore, given the movements and of exposed and infected people, respectively, six possible cases can be obtained when calculating the exposure risks by means of integration (Fig. 2 ).
Case 1
When , the exposed person gains no risk from this pair of movements given that his movement ends before the virus-laden aerosol forms.
Case 2
When , the exposed person suffers from the full aerosols formed by the infected person along all movements.
Case 3
When , given a timestamp (), the exposed person suffers only from the aerosols formed during to .
Case 4
When , such case can be treated as a combination of Cases 1 and 3 by taking as the cutting line of .
Case 5
When , such case can be treated as a combination of Cases 2 and 3 by taking as the cutting line of .
Case 6
When , such case can be treated as a combination of Cases 1, 2 and 3 by taking and as the cutting lines of .
Fig. 2.
Possible cases for the calculation of the exposure risks between two moving events. The integral equation will be different before and after the dashed line.
Based on the above discussion, the risk of viral transmission produced by moving events and can be expressed as follows:
| (5) |
Finally, given the trajectory of infected person , the risk of exposed person is computed by accumulating the values, which can be expressed as follows:
| (6) |
where and are the number of segments in the trajectory of the infected and exposed persons, respectively.
3.3. Weight graph accounting for the effect of obstacles
The premise of airborne transmission between two places is that virus-laden aerosols can float from one to the other. Therefore, given the complex topological structure of public indoor spaces, this study assumed that airborne transmission will only occur when people's locations are mutually visible. However, the computation of the visibility between each pair of trace points is enormous, especially when the results need to be applied to an integral function, i.e. Equation (6).
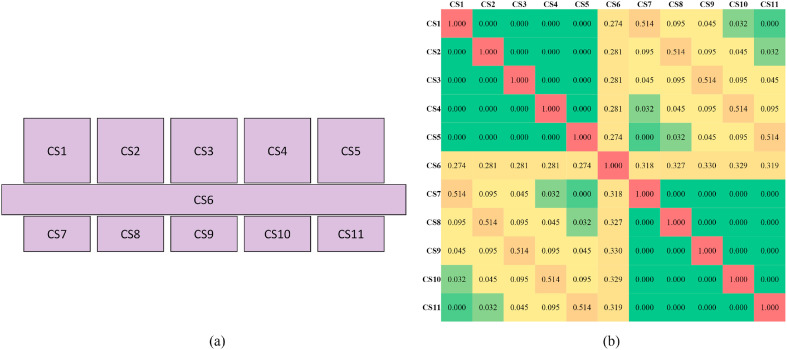
To deal with the effect of obstacle on transmission risk, this study introduced a simplified algorithm based on the concept of ‘convex space’ (CS) from the space syntax analysis. A CS is defined as a space where no cross exists between the perimeter and the line between any two of its points [52], such as spaces A, B and C in Fig. 3 . Notably, any two points in a CS are mutually visible. Therefore, the exposure risk can be directly calculated based on Equation (5) for any moving events that occur in the same CS. As for moving events that occur in two different CSs, a constant weight is firstly calculated based on the statistics of inter-visible point pairs between the CSs. With CSs A and B in Fig. 3 as the example, given a predefined size of grid cells, the weight from the transmission from A to B is defined as follows:
| (7) |
where and are the total number of grids in spaces A and B, respectively, and is the number of grids in space A that can be observed from grid in space B. The weight ranges from 0 to 1. The lower value of , the less inter-visible are the CSs. Notably, the weight graph is a symmetric matrix given that is always equal to .
Fig. 3.
Illustration of convex space. The indoor space was divided into three CSs: A, B and C.
Finally, a weight matrix can be constructed for any indoor space. Thus, Equation (6) is rewritten as follows:
| (8) |
where refers to the function that assigns the space ID to a moving event. The weighting term will constrain the magnitude of risks if the CSs are relatively less inter-visible. Notably, several indoor objects, such as tables and cabinets, may influence the airborne transmission. The effect of these objects can be modelled by assigning a fuzzy value, which corresponds the degree of obstacle, to each pair of grids during the visibility analysis. However, such an improvement requires more empirical information about the transport of airborne particles, which is beyond the scope of this study.
4. Simulation experiments
4.1. Experimental setup
Given the rarely available open WiFi positioning datasets, this study adopted a dataset simulated by the PedSim plug-in in Rhino7 [53]. In PedSim, we can easily control the entrance, exit, visit interest and velocity of agents. As shown in Fig. 4 , an indoor environment of a branching linear structure was created to represent a scenario in an underground shopping street, which is common in tunnels connecting public transportation systems (e.g., metro systems) and commercial centres. The indoor space had an accessible area of 895 with two exits, five restaurants and five stores.
Fig. 4.
3D layout of the made-up indoor space used in this study.
We designed three types of agents of different visiting interests in PedSim, that is, eating, shopping and passerby. As a result, we obtained 179 trajectories with a sampling interval of 1 s and a total duration of over 20 min. Table 2 summarises the detailed configuration for these agents. Fig. 5 displays the whole dataset.
Table 2.
Configuration of agents in this study.
| Agent's type | Number of shops to visit | Number of restaurants to visit | Number of trajectories | Average speed (m/s) | Average duration (s) |
|---|---|---|---|---|---|
| eating | 0 | 1 | 60 | 0.38 | 201 |
| shopping | 2 | 0 | 66 | 0.47 | 182 |
| passerby | 0 | 0 | 53 | 0.99 | 51 |
Fig. 5.
Overview of the simulated dataset.
Without the loss of generality, a specific indicator called ‘aggregate risk’ (AR) was defined to test the performance of our method in different scenarios. To calculate AR, we firstly sampled one of the agents as an infected person without replacement and simulated the corresponding transmission scenarios. Then, by repeating the sampling and simulation processes for times (no duplicated samples were allowed), AR can be expressed as follows:
| (9) |
where is the number of agents.
In addition, from the perspective of an individual, a personal aggregate risk score () is defined as follows:
| (10) |
To reduce the computational cost, we selected to demonstrate our method in the following experiments.
4.2. Construction of the weight graph
According to the ‘least and fattest’ principle for the construction of CSs [54], we obtained 11 CSs from the experimental region. Fig. 6 shows the CSs and the heatmap representing their weight matrix. Notably, we set the cell size of 0.25 m2 for the visibility analysis when calculating the weight matrix. The distant pair, such as CS5 and CS8, presented a significantly low weight, which meant that the transmission between these spaces was ignorable given that the diffusion of virus-laden aerosols was assumed to be largely blocked.
Fig. 6.
Construction of weight graph. (a) CSs of the made-up indoor space; (b) heatmap of the weight matrix.
Notably, in the following experiments, each moving event was assigned with a CS if the start point was within the space.
4.3. Performance in capturing spatiotemporal decay effect
To exemplify the performance of the proposed method in dealing with the spatiotemporal decay effect, we selected one passerby instance as the patient in this simulation. Fig. 7 (a) shows the estimated risks for each moving event of exposed people. The main risky areas were primarily located in the corridor along the trajectory of the patient, whilst the moving events within branching rooms were relatively safer given that they were distant from the patient.
Fig. 7.
(a) Estimation of the exposure risks of all agents when a passerby agent was assumed to be infected. (b) Temporal variation of the average risk in the corridor area.
The corridor area was used as an example to show the temporal decay effect. As shown in Fig. 7(b), no exposure risk was observed before the patient entered. Therefore, the agents who entered the space before the patient were not recognised as close contacts although they have visited the same place within a certain period. Then, the risk rapidly increased as the patient remained longer in this space, consistent with the notion that the longer a patient stays in a location, the more virus-laden aerosols are produced. After the patient left the shop, the space was still unsafe, whilst the average risk gradually decreased over time due to the reduction and dissipation of virus-laden aerosols.
4.4. Effectiveness of weight graph
As one of the main innovations of this study, the weight graph played an essential role in dealing with the obstacle effect in indoor spaces. To demonstrate the effectiveness of the weight graph, we compared the AR values estimated by Equations (6), (8). In the following discussion, we termed the model of Equation (6) as ‘Unweighted’ and that of Equation (8) as ‘CS-based weights’. In addition, to test the validity of using CS instead of finer coordinates (i.e., dense grid) to quantify the obstacle effect, we added the estimation based on a dense grid with a cell size of 0.25 m2 as the baseline model, termed as ‘Grid-based weights’. Notably, we selected a grid cell of 0.25 m2 to compute the ground truth because the maximum movement during a sampling interval (i.e., 1 s) of the agents in our simulation was approximately 0.5 m. Thus, each of the agent's movements can be mostly represented by one grid.
As shown in Table 3 , compared with the baseline, the AR was overestimated by 7.81% without weighting, whilst using CS-based weights underestimated the AR with a relative difference of 2.59% (100%–97.41%.). From the individual perspective, the relative error of PAR corresponding to CS-based weights was 4.41% on average. By contrast, this value increased to 11.32%, and the maximum was over 36.50% without weighting. These findings indicated that exposure risk may be largely overestimated if the obstacle effect is ignored, and using the proposed weight graph can significantly reduce the relative error.
Table 3.
Statistics of different weighting methods.
| Method |
AR (Ratio to the baseline) |
Relative error of PAR |
|||
|---|---|---|---|---|---|
| Average | Minimum | Median | Maximum | ||
| CS-based weights | 0.0246 97.41% |
4.41% | 0.55% | 4.26% | 16.70% |
| Unweighted | 0.0273 107.81% |
11.32% | 1.58% | 10.62% | 36.50% |
| Grid-based weights (baseline) | 0.0253 / |
/ | / | / | / |
Notably, although the use of a dense grid theoretically provides a more accurate result, the weight graph will be more efficient in practice because the spatial association of moving events to grid cells can be very costly, especially for large indoor spaces. In addition, overestimation from the obstacle effect will be exaggerated for environments with enclosed subspaces. Hence, finer-grained CSs will be an appropriate solution in practice as a balance between accuracy and computational cost.
4.5. Model validation
4.5.1. Validation with computational fluid dynamics (CFD) simulation
Computational fluid dynamics (CFD) simulation is a powerful tool in modelling the aerosol transport and has recently applied to the evaluation of COVID-19 transmission [55]. In this section, a CFD simulation was conducted using Autodesk CFD [56] to further validate the proposed method.
According to the conventional Wells-Riley model [57], which is widely adopted in assessing the risk of airborne transmissible diseases, the infection probability could be expressed as:
| (11) |
where is the concentration of virus-laden aerosols, p is volumetric flow rate of susceptible person's breath, and is the exposure duration. Without loss of generality, was set to 1 to factor out its effect, and the concentration is represented by the concentration of carbon dioxide [58,59].
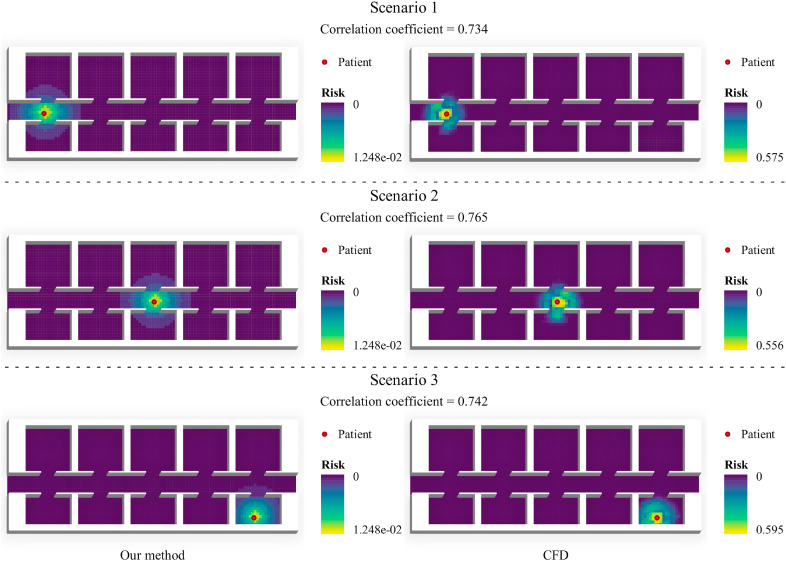
As shown in Fig. 8 , the spatial distribution of transmission risk estimated by CFD and our method are highly correlated with a Pearson correlation over 0.7 in different scenarios. For both methods, the transmission risk radiates out from the patient's location, and the strength generally declines as the distance increases. Also, both the methods are capable of capturing the obstacle effect by indicating a sharp change of risk close to the wall (most significant Scenario 2). One difference observed is that the dispersion of risks at the entrance of rooms is less significant in our method. This is mainly caused by the simplification of topology using the weight graph. However, such dispersion can be better modelled by using finer-grained convex spaces.
Fig. 8.
Comparison between the maps of transmission risk produced by CFD and our method in different scenarios. Each scenario represents the moment when a motionless patient stays at his location for 30 s. The risk of each grid cell is evaluated by assuming a motionless person at the cell's centroid with a duration of 1 s. Maps are colored based on Natural breaks.
According to our analysis, different evaluation standards between the two kinds of risks are the main factor affecting the specific value of correlation coefficient. As we currently focus on justifying the effectiveness of our method rather than its numeric consistency with CFD simulations, the conversion of these risks is beyond the scope of this study.
4.5.2. Visualization of the risks caused by moving object
To further verify our method in dealing with moving objects, we selected two agents as the patients, respectively, and plotted the spatial distribution of transmission risks at different timestamp during their movement.
As shown in Fig. 9 (a), the risk is radiatively distributed along the patient's path, and where the patient has not visited are relatively safe. By comparing Fig. 9 (b) and (c), a decay of risks can be observed after the patient left the indoor space. Similarly, in case 2, there is an increase of risk as the patient stayed longer in the bottom-right room (Fig. 9 (d)–(e)), and a decay after the patient left the space (Fig. 9 (e)–(f)). Different from the relatively uniform risk distribution along the patient's path in case 1, the bottom-right room is dominant in transmission risk because the patient spent most time on ‘eating’ in this room. The visual results are generally consistent with our common perception about the diffusion and decay of transmissible virus, which to some extent justifies our approach.
Fig. 9.
Map of the transmission risk for two selected cases in different scenarios. The risk is evaluated by assuming a motionless person at every specific grid cell with a duration of 1 s. Maps are colored based on Natural breaks.
4.6. Influence of data uncertainty
4.6.1. Positioning error
Positioning error is inevitable in WiFi localisation due to obstacles and signal interference. In this experiment, we applied errors obeying a normal distribution to the agents’ coordinates from 0.3 m to 1.8 m to investigate the effect of different magnitudes of positioning errors on PAR. Notably, to reduce the randomness effect, we ran each simulation with a specific for 20 times to obtain stable assessments.
The experimental results are shown in Fig. 10 , in which agents were ordered by their actual PAR for a better comparison. The exposure risks were generally underestimated with positioning errors. In addition, such underestimation became more significant as the value of increased, especially when . This finding is reasonable because according to the error propagation theorem, the expected distance between each pair of coordinates will be enlarged when normal errors are applied, especially when the error is larger than the actual distance measurement. As a result, the distance between agents will be generally overestimated, and the risk will drop due to the spatial decay effect.
Fig. 10.
Changes in PAR with different sizes of positioning error.
Kendall's , which measures the correlation between two rankings [60], was calculated for the mean observation and ground truth. The value of Kendall's was above 0.9 for all cases. Thus, despite the positioning errors at a certain level of uncertainty on risk evaluation, the estimations remained useful to distinguish risky contacts. Furthermore, the confidence interval was narrow for all cases, which proved the robustness of the proposed method for detecting randomness in people's movements.
4.6.2. Omission of positioning data
Data omission is another source of uncertainty in positioning data due to the loss of WiFi signal and shutdown of WiFi access. Intuitively, if a user's trace points are completely missed, we cannot evaluate neither his exposure risk nor his likelihood of infecting others. Hence, the complete omission of data is beyond the scope of this study.
In this experiment, we focused on a general scenario, in which people's trace points were partially lost. We randomly discarded the trace points with an omission ratio ranging from 0.2 to 0.8, and the effect of omission data was reflected by the changes in PAR. Notably, for each value, the simulation was run for 20 times to reduce the randomness effect.
As shown in Fig. 11 , the PAR values were generally lowered because several risky exposures had not been recorded due to omission, and the underestimation exacerbated with a higher omission ratio. However, in terms of the Kendall's over 0.97, the ranks of agents' PAR were almost unchanged, which indicated that our method remained effective in distinguishing highly risky exposure. These findings further verified the robustness of our method for uncertainties from positioning data.
Fig. 11.
Effect of data omission on PAR.
4.7. Influence of people's velocity on exposure risks
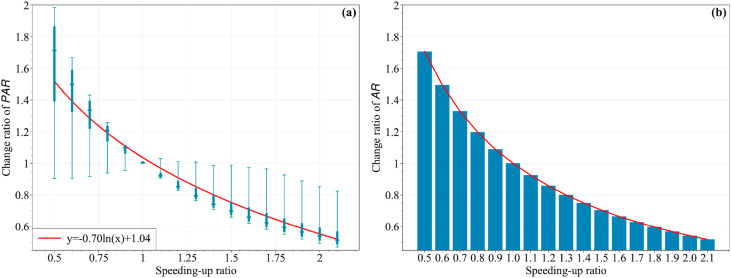
In addition to the evaluation of personal infection risk, our method can be applied to support better decision making regarding epidemic prevention and control. Reduction of eat-in services and rapid departure from public areas are common policies for preventing the transmission of COVID-19 [61]. Under these measures, people generally spend less time for shopping and eating. In this experiment, we simulated the effects of these policies by adjusting the people's velocity (equivalent to changing the stay duration). Firstly, a speeding-up ratio was applied to scale the time of the raw data to simulate the changes in velocities. Secondly, with the estimations corresponding to the original speed as the base, the change ratios of PAR and AR were calculated for further analysis.
Considering the limitation of people's walking speed, the speeding-up ratio ranged from 0.5 to 2 with a step of 0.1 in this experiment, where a ratio larger than 1 represents the scenario of speeding up, and that with a value lower than 1 indicates the scenario of slowing down. As shown in Fig. 12 , a high velocity led to relatively low exposure risks because people's interactions were shortened. From the individual respective, as labelled in Fig. 12(a), PAR generally underwent a logarithmic reduction as people's velocity increased. Thus, the exposure risk increased rapidly when people slowed down and spent more time in indoor spaces. A similar exponential trend can be observed in the change ratio of AR (Fig. 12(b)). These findings can be valuable for directing rational policies, such as the degree of eat-in limitation, and prompting pedestrians to reduce their duration in crowded areas reasonably.
Fig. 12.
Changes in risks with respect to different velocities. (a) Change ratio of PAR. (b) Change ratio of AR.
5. Limitations of this study
The proposed method was currently demonstrated with simulated datasets: its validity was justified by an external comparison to the results of CFD simulations, and its robustness was examined by a series of sensitivity analyses on data uncertainty. Even though the simulation results have proved the effectiveness of our method, it is worth conducting further validation with real-life data in our future research. It is worth mentioning that access to real trajectory data would be limited due to privacy concerns. Compared with Bluetooth and GPS, WiFi receives relative low privacy concerns and the highest uptake because most people are likely to enjoy the free wireless services in public spaces [25,34]. Existing studies also demonstrated the prospect of some encryption techniques in WiFi localisation preservation [62]. Thus, we believe that the privacy issue would not seriously hamper the application of our method in practice.
Since the scope of this study is limited to building a spatial-temporal model for fast evaluation and identification of risky exposure to COVID-19, some perturbing factors from the environment as well as human behavior are not fully considered. The current model assumes that the transmission risk is governed by five factors, namely, temperature, humidity, sunlight, PD and duration, which are insufficient to cover all the possible cases due to the complexity of the airborne transmission of COVID-19 in reality. The effect of several preventative measures that may expedite the decay of viral infectiousness, such as wearing of masks, ventilation and disinfection, if quantifiable, can be further incorporated into our model via modifications of Equations (1), (2). Furthermore, given that people's behaviour, such as coughing and touching, cannot be recorded by the positioning data, the risks raised by large droplets and fomite transmission have not been considered in the current model. Regardless, these transmissions are markedly less efficient than airborne transmission and can be significantly reduced by wearing of masks and self-disinfection [63].
Moreover, considering the aerosol diffusion microscopically, the height of a person, human thermal plume [64] and the change in airflow pattern caused by the movement of people [59] will have a certain influence on the transmission risk. One possible solution is to convert these complex fluid dynamic processes into empirical coefficients to incorporate them into our model. For example, given that thermal plume is related to the type of clothing [64], we may adjust the temporal decay rate in Equation (2) appropriately based on what people are wearing. Similarly, the effect of varying infectiousness of virus at different infection stages [65], if more clinical data are available, should be further integrated into our method by setting specific initial parameters for each patient differently regarding their infection status.
Lastly, this work did not consider secondary transmission, which may lead to a certain level of risk underestimation. In future work, epidemiological approaches, such as the susceptible-infected model [66], can be used together with the proposed framework for a more precise evaluation of exposure risk.
6. Discussion and conclusion
Grounded in the ‘1 m and 15 min’ guideline for close exposure of COVID-19 from WHO, various smartphone-based approaches have been established using spatial–temporal thresholds for fast contact tracing. However, these methods assumed a crisp boundary to determine risky interactions whilst ignoring that the exposure risk will increase with a shortened distance, prolonged duration and under the influence of environmental factors. Given the airborne transmission of SARS-CoV-2, people will be at a certain level of risk despite the absence of an evident space–time intersection with infected individuals.
This study introduced an extensible framework to evaluate the transmission risk of COVID-19 based on fine-grained individual trajectories in indoor environments. By means of integration, the proposed method can well capture the spatial–temporal decay of airborne transmission based on the epidemiological characteristics of SARS-CoV-2. A weight graph was also implemented based on the space syntax technique to make our method adaptive to open and obstructed spaces. The experimental results showed that our method is insensitive to the either omission or deviation in positioning data, and can presents stable result in distinguishing relatively high-risky people from a crowd. It was also found that the proposed weight graph can significantly reduce the overestimation of risk by considering the obstacle effect and theoretically more efficient than the division by a dense grid, which might lead to intensive computation during spatial indexing of the positing points.
Of interest, the proposed method can be easily adapted to simulate how different environmental factors, people's mobility patterns and indoor layout will influence the infection risk [[67], [68]]. Compared to the CFD simulation that focuses on the physical process of airborne transmission, our method offers a fast response to the spatial-temporal dynamics in people's interactions, which makes it suitable in modelling individual-level exposure risk among large-scale population in complex environments. This framework is also applicable to outdoor spaces when people's fine-grained trajectory is available. With the reopening of society, our method will contribute to efficient contact tracing and serve as a useful analytic tool for planners and policymakers in decision-making in post-pandemic societies.
CRediT authorship contribution statement
Pengfei Chen: Methodology, Visualization, Writing – original draft, Funding acquisition, Conceptualization. Dongchu Zhang: Software, Methodology, Conceptualization. Jianxiao Liu: Conceptualization, Investigation. Izzy Yi Jian: Writing – review & editing, Validation.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by the National Natural Science Foundation of China [grant number: 42101351] and the Hong Kong Polytechnic University [grant number:1-W19P].
References
- 1.Velavan T.P., Meyer C.G. The COVID-19 epidemic. Trop. Med. Int. Health. 2020;25:278. doi: 10.1111/tmi.13383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yuki K., Fujiogi M., Koutsogiannaki S. COVID-19 pathophysiology: a review. Clin. Immunol. 2020;215 doi: 10.1016/j.clim.2020.108427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Keeling M.J., Hollingsworth T.D., Read J.M. Efficacy of contact tracing for the containment of the 2019 novel coronavirus (COVID-19) J. Epidemiol. Community Health. 2020;74:861–866. doi: 10.1136/jech-2020-214051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Luo L., Liu D., Liao X., Wu X., Jing Q., Zheng J., Liu F., Yang S., Bi B., Li Z. MedRxiv; 2020. Modes of Contact and Risk of Transmission in Covid-19: a Prospective Cohort Study 4950 Close Contact Persons in Guangzhou of China. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ye Q., Wang B., Mao J., Fu J., Shang S., Shu Q., Zhang T. Epidemiological analysis of COVID-19 and practical experience from China. J. Med. Virol. 2020;92:755–769. doi: 10.1002/jmv.25813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yong S.E.F., Anderson D.E., Wei W.E., Pang J., Chia W.N., Tan C.W., Teoh Y.L., Rajendram P., Toh M.P.H.S., Poh C. Connecting clusters of COVID-19: an epidemiological and serological investigation. Lancet Infect. Dis. 2020;20:809–815. doi: 10.1016/S1473-3099(20)30273-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bradshaw W.J., Alley E.C., Huggins J.H., Lloyd A.L., Esvelt K.M. Bidirectional contact tracing could dramatically improve COVID-19 control. Nat. Commun. 2021;12:232. doi: 10.1038/s41467-020-20325-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Walrave M., Waeterloos C., Ponnet K. Ready or not for contact tracing? Investigating the adoption intention of COVID-19 contact-tracing technology using an extended unified theory of acceptance and use of technology model. Cyberpsychol., Behav. Soc. Netw. 2021;24:377–383. doi: 10.1089/cyber.2020.0483. [DOI] [PubMed] [Google Scholar]
- 9.Kretzschmar M.E., Rozhnova G., Bootsma M.C., van Boven M., van de Wijgert J.H., Bonten M.J. Impact of delays on effectiveness of contact tracing strategies for COVID-19: a modelling study. Lancet Public Health. 2020;5:e452–e459. doi: 10.1016/S2468-2667(20)30157-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kim H. COVID-19 apps as a digital intervention policy: a longitudinal panel data analysis in South Korea. Health Pol. 2021;125:1430–1440. doi: 10.1016/j.healthpol.2021.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wu J., Xie X., Yang L., Xu X., Cai Y., Wang T., Xie X. Mobile health technology combats COVID-19 in China. J. Infect. 2021;82:159–198. doi: 10.1016/j.jinf.2020.07.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ahmed N., Michelin R.A., Xue W., Ruj S., Malaney R., Kanhere S.S., Seneviratne A., Hu W., Janicke H., Jha S.K. A survey of COVID-19 contact tracing apps. IEEE Access. 2020;8:134577–134601. [Google Scholar]
- 13.Appelman J., Liebst L.S., Lindegaard M.R. Netherlands Institute for the Study of Crime and Law Enforcement; Amsterdam: 2021. How Common Are High-Risk COVID-19 Contacts? [Google Scholar]
- 14.Sun C., Zhai Z. The efficacy of social distance and ventilation effectiveness in preventing COVID-19 transmission. Sustain. Cities Soc. 2020;62:102390. doi: 10.1016/j.scs.2020.102390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.WHO . 2021. Covid-19 Strategy Update.https://www.who.int/publications/i/item/who-2019-nCoV-surveillanceguidance-2020.8 [Google Scholar]
- 16.Chu D.K., Akl E.A., Duda S., Solo K., Yaacoub S., Schünemann H.J., Chu D.K., Akl E.A., El-harakeh A., Bognanni A., Lotfi T., Loeb M., Hajizadeh A., Bak A., Izcovich A., Cuello-Garcia C.A., Chen C., Harris D.J., Borowiack E., Chamseddine F., Schünemann F., Morgano G.P., Muti Schünemann G.E.U., Chen G., Zhao H., Neumann I., Chan J., Khabsa J., Hneiny L., Harrison L., Smith M., Rizk N., Giorgi Rossi P., AbiHanna P., El-khoury R., Stalteri R., Baldeh T., Piggott T., Zhang Y., Saad Z., Khamis A., Reinap M., Duda S., Solo K., Yaacoub S., Schünemann H.J. Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: a systematic review and meta-analysis. Lancet. 2020;395:1973–1987. doi: 10.1016/S0140-6736(20)31142-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Prather K.A., Marr L.C., Schooley R.T., McDiarmid M.A., Wilson M.E., Milton D.K. Airborne transmission of SARS-CoV-2. Science. 2020;370:303–304. doi: 10.1126/science.abf0521. [DOI] [PubMed] [Google Scholar]
- 18.Zhang N., Chen W., Chan P.-T., Yen H.-L., Tang J.W.-T., Li Y. Close contact behavior in indoor environment and transmission of respiratory infection. Indoor Air. 2020;30:645–661. doi: 10.1111/ina.12673. [DOI] [PubMed] [Google Scholar]
- 19.The Austrian Federal Ministry . 2021. Frequently Asked Questions - Coronavirus.https://www.sozialministerium.at/dam/jcr:d36ce9e9-6f6d-40a5-9284-5caa9a7a9b0c/Frequently%20asked%20questions%20-%20Coronavirus.pdf [Google Scholar]
- 20.Ng P.C., Spachos P., Plataniotis K.N. COVID-19 and your smartphone: BLE-based smart contact tracing. IEEE Syst. J. 2021;15:5367–5378. doi: 10.1109/JSYST.2021.3055675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bulfone T.C., Malekinejad M., Rutherford G.W., Razani N. Outdoor transmission of SARS-CoV-2 and other respiratory viruses: a systematic review. J. Infect. Dis. 2021;223:550–561. doi: 10.1093/infdis/jiaa742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yang C., Shao H. WiFi-based indoor positioning. IEEE Commun. Mag. 2015;53:150–157. doi: 10.1109/MCOM.2015.7060497. [DOI] [Google Scholar]
- 23.Chen C., Chen Y., Han Y., Lai H.-Q., Liu K.R. Achieving centimeter-accuracy indoor localization on WiFi platforms: a frequency hopping approach. IEEE Internet Things J. 2016;4:111–121. [Google Scholar]
- 24.Zafari F., Gkelias A., Leung K.K. A survey of indoor localization systems and technologies. IEEE Commun. Surv. Tutor. 2019;21:2568–2599. doi: 10.1109/COMST.2019.2911558. [DOI] [Google Scholar]
- 25.Lo B., Sim I. Ethical framework for assessing manual and digital contact tracing for COVID-19. Ann. Intern. Med. 2021;174:395–400. doi: 10.7326/M20-5834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Huang Y., Wu Q., Wang P., Xu Y., Wang L., Zhao Y., Yao D., Xu Y., Lv Q., Xu S. Measures undertaken in China to avoid COVID-19 infection: internet-based, cross-sectional survey study. J. Med. Internet Res. 2020;22 doi: 10.2196/18718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Althoff K.N., Coburn S.B., Nash D. Contact tracing: essential to the public health response and our understanding of the epidemiology of coronavirus disease 2019. Clin. Infect. Dis. 2020;71:1960–1961. doi: 10.1093/cid/ciaa757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bresic D. CITIP Blog; 2021. The German Corona-Data-Donation-App as an Example of the Concept of Data Donation.https://www.law.kuleuven.be/citip/blog/the-german-corona-data-donation-app-as-an-example-of-the-concept-of-data-donation/ [Google Scholar]
- 29.Wang S., Ding S., Xiong L. A new system for surveillance and digital contact tracing for COVID-19: spatiotemporal reporting over network and GPS. JMIR MHealth UHealth. 2020;8 doi: 10.2196/19457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yao W., Liu Y., Zhou D., Pan Z., Till M.J., Zhao J., Zhu L., Zhan L., Tang Q., Liu Y. Impact of GPS signal loss and its mitigation in power system synchronized measurement devices. IEEE Trans. Smart Grid. 2016;9:1141–1149. [Google Scholar]
- 31.Radhakrishnan M., Misra A., Balan R.K., Lee Y. 2015 IEEE 12th Int. Conf. Mob. Ad Hoc Sens. Syst. IEEE; 2015. Smartphones and ble services: empirical insights; pp. 226–234. [Google Scholar]
- 32.Garrett P.M., White J.P., Lewandowsky S., Kashima Y., Perfors A., Little D.R., Geard N., Mitchell L., Tomko M., Dennis S. The acceptability and uptake of smartphone tracking for COVID-19 in Australia. PLoS One. 2021;16 doi: 10.1371/journal.pone.0244827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wymant C., Ferretti L., Tsallis D., Charalambides M., Abeler-Dörner L., Bonsall D., Hinch R., Kendall M., Milsom L., Ayres M. The epidemiological impact of the NHS COVID-19 App. Nature. 2021;594:408–412. doi: 10.1038/s41586-021-03606-z. [DOI] [PubMed] [Google Scholar]
- 34.Grekousis G., Liu Y. Digital contact tracing, community uptake, and proximity awareness technology to fight COVID-19: a systematic review. Sustain. Cities Soc. 2021;71:102995. doi: 10.1016/j.scs.2021.102995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shahroz M., Ahmad F., Younis M.S., Ahmad N., Kamel Boulos M.N., Vinuesa R., Qadir J. COVID-19 digital contact tracing applications and techniques: a review post initial deployments. Transport Eng. 2021;5 doi: 10.1016/j.treng.2021.100072. [DOI] [Google Scholar]
- 36.Tu P., Li J., Wang H., Wang K., Yuan Y. Epidemic contact tracing with campus WiFi network and smartphone-based pedestrian dead reckoning. IEEE Sensor. J. 2021;21:19255–19267. doi: 10.1109/JSEN.2021.3091135. [DOI] [Google Scholar]
- 37.Yin Z.-C., Jin Z.-H.-N., Ying S., Liu H., Li S.-J., Xiao J.-Q. Distance-decay effect in probabilistic time geography for random encounter. ISPRS Int. J. Geo-Inf. 2019;8:177. doi: 10.3390/ijgi8040177. [DOI] [Google Scholar]
- 38.Ying F., O'Clery N. Modelling COVID-19 transmission in supermarkets using an agent-based model. PLoS One. 2021;16 doi: 10.1371/journal.pone.0249821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lotfi M., Hamblin M.R., Rezaei N. COVID-19: transmission, prevention, and potential therapeutic opportunities. Clin. Chim. Acta. 2020;508:254–266. doi: 10.1016/j.cca.2020.05.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rambhatla S., Zeighami S., Shahabi K., Shahabi C., Liu Y. ArXiv Prepr. ArXiv201207283; 2020. Towards Accurate Spatiotemporal COVID-19 Risk Scores Using High Resolution Real-World Mobility Data. [Google Scholar]
- 41.Fan C., Lee S., Yang Y., Oztekin B., Li Q., Mostafavi A. Effects of population co-location reduction on cross-county transmission risk of COVID-19 in the United States. Appl. Netw. Sci. 2021;6:1–18. doi: 10.1007/s41109-021-00361-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Génois M., Barrat A. Can co-location be used as a proxy for face-to-face contacts? EPJ Data Sci. 2018;7:11. doi: 10.1140/epjds/s13688-018-0140-1. [DOI] [Google Scholar]
- 43.Papapostolou A., Chaouchi H. 2009 IEEE 20th Int. Symp. Pers. Indoor Mob. Radio Commun. IEEE; 2009. Exploiting multi-modality and diversity for localization enhancement: WiFi & RFID usecase; pp. 1903–1907. [Google Scholar]
- 44.Holm S. 2009 IEEE Int. Conf. RFID. IEEE; 2009. Hybrid ultrasound-RFID indoor positioning: combining the best of both worlds; pp. 155–162. [Google Scholar]
- 45.Campbell B., Dutta P., Kempke B., Kuo Y.-S., Pannuto P. Decawave: exploring state of the art commercial localization. Ann Arbor. 2015;1001 [Google Scholar]
- 46.Zhang W., Yu K., Wang W., Li X. A self-adaptive AP selection algorithm based on multiobjective optimization for indoor WiFi positioning. IEEE Internet Things J. 2021;8:1406–1416. doi: 10.1109/JIOT.2020.3011402. [DOI] [Google Scholar]
- 47.Tupper P., Boury H., Yerlanov M., Colijn C. Event-specific interventions to minimize COVID-19 transmission. Proc. Natl. Acad. Sci. Unit. States Am. 2020;117:32038–32045. doi: 10.1073/pnas.2019324117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Jenkins C., Sunjaya A. Social distancing as a strategy to prevent respiratory virus infections. Respirology. 2021;26:143–144. doi: 10.1111/resp.13990. [DOI] [PubMed] [Google Scholar]
- 49.McCarthy J.E., Dewitt B.D., Dumas B.A., McCarthy M.T. Modeling the relative risk of SARS-CoV-2 infection to inform risk-cost-benefit analyses of activities during the SARS-CoV-2 pandemic. PLoS One. 2021;16 doi: 10.1371/journal.pone.0245381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Chen W., Zhang N., Wei J., Yen H.-L., Li Y. Short-range airborne route dominates exposure of respiratory infection during close contact. Build. Environ. 2020;176 doi: 10.1016/j.buildenv.2020.106859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Dabisch P., Schuit M., Herzog A., Beck K., Wood S., Krause M., Miller D., Weaver W., Freeburger D., Hooper I., Green B., Williams G., Holland B., Bohannon J., Wahl V., Yolitz J., Hevey M., Ratnesar-Shumate S. The influence of temperature, humidity, and simulated sunlight on the infectivity of SARS-CoV-2 in aerosols. Aerosol Sci. Technol. 2021;55:142–153. doi: 10.1080/02786826.2020.1829536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Klarqvist B. A space syntax glossary. NA. 2015;6 [Google Scholar]
- 53.Wang P. 2017. PedSim, Food4Rhino.https://www.food4rhino.com/en/app/pedsim [Google Scholar]
- 54.Hillier B., Hanson J. Cambridge university press; 1989. The Social Logic of Space. [Google Scholar]
- 55.Li X., Lester D., Rosengarten G., Aboltins C., Patel M., Cole I. A spatiotemporally resolved infection risk model for airborne transmission of COVID-19 variants in indoor spaces. Sci. Total Environ. 2022;812:152592. doi: 10.1016/j.scitotenv.2021.152592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Autodesk CFD https://www.autodesk.com/campaigns/cfd2020 n.d.
- 57.Riley E.C., Murphy G., Riley R.L. Airborne spread of measles in a suburban elementary school. Am. J. Epidemiol. 1978;107:421–432. doi: 10.1093/oxfordjournals.aje.a112560. [DOI] [PubMed] [Google Scholar]
- 58.Vouriot C.V., Burridge H.C., Noakes C.J., Linden P.F. Seasonal variation in airborne infection risk in schools due to changes in ventilation inferred from monitored carbon dioxide. Indoor Air. 2021;31:1154–1163. doi: 10.1111/ina.12818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Wang C.C., Prather K.A., Sznitman J., Jimenez J.L., Lakdawala S.S., Tufekci Z., Marr L.C. Airborne transmission of respiratory viruses. Science. 2021;373 doi: 10.1126/science.abd9149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Marden J.I. Rank correlation methods. J. Am. Stat. Assoc. 1992;87:249–251. [Google Scholar]
- 61.Wang D., Yao J., Martin B.A. The effects of crowdedness and safety measures on restaurant patronage choices and perceptions in the COVID-19 pandemic. Int. J. Hospit. Manag. 2021;95 doi: 10.1016/j.ijhm.2021.102910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Zhao P., Liu W., Zhang G., Li Z., Wang L. Preserving privacy in WiFi localization with plausible dummy locations. IEEE Trans. Veh. Technol. 2020;69:11909–11925. doi: 10.1109/TVT.2020.3006363. [DOI] [Google Scholar]
- 63.Port J.R., Yinda C.K., Owusu I.O., Holbrook M., Fischer R., Bushmaker T., Avanzato V.A., Schulz J.E., Martens C., van Doremalen N. SARS-CoV-2 disease severity and transmission efficiency is increased for airborne compared to fomite exposure in Syrian hamsters. Nat. Commun. 2021;12:1–15. doi: 10.1038/s41467-021-25156-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Sun S., Li J., Han J. How human thermal plume influences near-human transport of respiratory droplets and airborne particles: a review. Environ. Chem. Lett. 2021;19:1971–1982. doi: 10.1007/s10311-020-01178-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Backer J.A., Eggink D., Andeweg S.P., Veldhuijzen I.K., van Maarseveen N., Vermaas K., Vlaemynck B., Schepers R., van den Hof S., Reusken C.B., Wallinga J. Shorter serial intervals in SARS-CoV-2 cases with Omicron BA.1 variant compared with Delta variant, The Netherlands, 13 to 26 December 2021. Euro Surveill. 2022;27 doi: 10.2807/1560-7917.ES.2022.27.6.2200042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Matouk A.E. Complex dynamics in susceptible-infected models for COVID-19 with multi-drug resistance. Chaos, Solit. Fractals. 2020;140:110257. doi: 10.1016/j.chaos.2020.110257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Ugail H., Aggarwal R., Iglesias A., Howard N., Campuzano A., Suárez P., Maqsood M., Aadil F., Mehmood I., Gleghorn S., Taif K., Kadry S., Muhammad K. Social distancing enhanced automated optimal design of physical spaces in the wake of the COVID-19 pandemic. Sustain. Cities Soc. 2021;68 doi: 10.1016/j.scs.2021.102791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Liu J., Shi W., Chen P. Exploring travel patterns during the holiday season—A case study of Shenzhen Metro system during the Chinese Spring festival. ISPRS Int. J. Geo-Inf. 2020;9(11):651. [Google Scholar]