Abstract
Mendelian randomization (MR) is often used to estimate effects of time-varying exposures on health outcomes using observational data. However, MR studies typically use a single measurement of exposure and apply conventional instrumental variable (IV) methods designed to handle time-fixed exposures. As such, MR effect estimates for time-varying exposures are often biased, and interpretations are unclear. We describe the instrumental conditions required for IV estimation with a time-varying exposure, and the additional conditions required to causally interpret MR estimates as a point effect, a period effect or a lifetime effect depending on whether researchers have measurements at a single or multiple time points. We propose methods to incorporate time-varying exposures in MR analyses based on g-estimation of structural mean models, and demonstrate its application by estimating the period effect of alcohol intake, high-density lipoprotein (HDL) cholesterol and low-density lipoprotein (LDL) cholesterol on intermediate coronary heart disease (CHD) outcomes using data from the Framingham Heart Study. We use this data example to highlight the challenges of interpreting MR estimates as causal effects, and describe other extensions of structural mean models for more complex data scenarios.
Keywords: Mendelian randomization analysis, instrumental variable, g-estimation, structural mean models
Introduction
Instrumental variable (IV) methods can be applied to observational data to estimate a causal effect of an exposure on an outcome.1 An increasingly used application of IV estimation is in Mendelian randomization (MR) studies, in which genetic variants are proposed as instrumental variables.2–4 Many MR studies are concerned with the effects of time-varying exposures (e.g., alcohol intake, blood lipids) but MR studies typically use a single measurement of exposure and apply conventional IV methods designed to handle time-fixed exposures. As a result, the validity and interpretation of MR effect estimates is unclear.5 Some authors interpret current MR estimates based on a single exposure measurement as the effect of life-long interventions on exposure that start at conception,6–8 but such interpretation requires strong unverifiable conditions.9
Ideally, MR estimates would incorporate longitudinal data on time-varying exposures into the analysis. However, even if information on time-varying exposures were available to researchers, the problem remains that conventional IV methods cannot appropriately use such information. Here we explore some alternatives for MR estimation with longitudinal data on time-varying exposures.
Our paper is organized as follows. We first describe the instrumental conditions required for IV estimation with a time-varying exposure. Next, we review the possible causal interpretations of MR estimates, depending on whether researchers have measurements of a time-varying exposure at a single time point or at multiple time points. We then use extensions of IV methods based on g-estimation of structural mean models (SMMs), which overcome the limitations of classical IV methods for time-varying exposures. As an illustration, we apply g-estimation of SMMs to MR analyses that compare markers of coronary heart disease (CHD) under sustained interventions on alcohol intake, low-density lipoprotein (LDL) cholesterol, and high-density lipoprotein (HDL) cholesterol using data from the Framingham Heart Study (FHS).
The instrumental conditions for time-varying exposures
IV methods require the existence of an instrumental variable, or instrument, that meets three conditions. Informally, these instrumental conditions are (1) the instrument is associated with the exposure; (2) the instrument does not affect the outcome except through its possible effect on the exposure; and (3) the instrument and the outcome do not share causes.1 Formal definitions of the three conditions are provided in eAppendix 1. Conditions (2) and (3) are not empirically verifiable. To identify the average causal effect of an exposure on an outcome in the population, a fourth condition of homogeneity is required1—a point we will return to when discussing IV estimation using g-estimation of structural mean models. However, these four conditions may still be insufficient to identify a causal effect of a time-varying exposure using IV estimation; as we discuss below, additional unverifiable conditions are generally needed.
For a time-fixed exposure, a possible set of relationships between a causal instrument , exposure , outcome and unmeasured confounders can be depicted using the canonical causal directed acyclic graph (DAG) in Figure 1A.1 For a time-varying exposure, these relationships are more accurately represented by the causal DAG in Figure 1B, in which the instrument Z is associated with the time-varying exposure at multiple time points between conception (m = 0) and the measurement of the outcome.9,10 With a causal instrument Z as depicted in Figure 1B, this causal diagram begins to illustrate the problems of MR analyses which consider only a single measurement of a time-varying exposure: instrumental condition (2) is violated with respect to the effect of Am on Y because Z has direct effects on the outcome Y through the exposure at time points other than m.5,9,11
Figure 1.

Causal diagram for instrumental variable analyses with a causal instrument and (A) a time-fixed exposure or (B) a time-varying exposure.
In the next two sections we consider three types of causal effects that can be targeted when the exposure is time-varying: the effect of exposure at a single time point on the outcome (point effect), the effect of exposure during a period on the outcome (period effect), and the effect of exposure throughout the lifetime on the outcome (lifetime effect). We explore the conditions required to identify these effects depending on whether researchers have measurements of a time-varying exposure at a single time point or at multiple time points. A summary is provided in Table 1.
Table 1.
Possible causal estimands in Mendelian Randomization studies of time-varying exposures and their identifiability assumptions
| Estimand (on the additive scale) | Assumptions required for identification | ||
|---|---|---|---|
| With a single exposure measurement | With multiple exposure measurements | ||
| Point effect | Difference in mean counterfactual outcomes had everyone received exposure at time versus had everyone received exposure at time : |
Instrumental conditions hold for the proposed instrument for exposure at time . For instrumental condition 2 to hold, each component of the time-varying exposure other than at time must be unaffected by the instrument or have no effect on the outcome.a | N/A |
| Period effect b | Instrumental conditions hold for the exposure, as a whole, between times and (i.e., each component of the time-varying exposure outside of this time period is unaffected by the instrument or has no effect on the outcome) | ||
| Generalized form | Difference in mean counterfactual outcomes had everyone received the exposure trajectory between times and versus had everyone received the exposure trajectory between times and : |
No realistic assumptions for identification in MR studies | All relevant exposure time points have been measured and at least as many instruments as the number of exposure time points are available. The association between instrument-exposure must vary between time points for at least one instrument. No realistic assumptions for identification in MR studies if not all relevant exposure time points have been measured. |
| Shift in exposure trajectories | Difference in mean counterfactual outcomes had everyone received the exposure trajectory between times and versus had everyone received the same exposure trajectory after shifting the exposure by one unit across the entire period |
1. The association between the instrument and the exposure is constant on the additive scale between times and
c 2. Instrumental conditions hold for the exposure trajectory between times and . For instrumental condition 2 to hold, each component of the time-varying exposure outside of this time period must be unaffected by the instrument or have no effect on the outcome.c |
If all relevant exposure time points have been measured and there are a sufficient number of instruments, no additional assumptions are needed. If only a subset of relevant exposure time points have been measured, the instrument-exposure association during unmeasured time points must be the same as the instrument-exposure association for at least one of the measured time points. |
The effect of a point exposure
Suppose that the following information is available for each individual in the study population: a causal genetic variant Z, a single measurement of of a time-varying exposure at age , and the outcome Y measured once at age . In this setting, the time-varying exposure is measured at a single time.
Let be the counterfactual (potential) outcome if the individual had received exposure level a at age m, and the mean counterfactual outcome had everyone received exposure level at . By consistency, the counterfactual outcome is equal to the observed outcome among individuals whose observed exposure at time is equal to for any value . The (average) point effect is the difference between the mean counterfactual outcome had everyone received exposure level at and the mean counterfactual outcome had everyone received exposure level at , that is,
Conventional IV estimation of the point effect requires that the genetic variant Z be an instrument for Am. This would be true if each component of the time-varying exposure other than is unaffected by the instrument (i.e., no arrow from Z into when ) or does not affect the outcome through (i.e., no arrow from when to Y), as illustrated using simulations in eAppendix 3.1.5,9,10 Neither scenario is likely to hold because genetic variants often have long-term effects (we expect arrows from the instrument to multiple exposure time points), and many outcomes in MR studies are chronic conditions with critical windows of exposure that span years or even decades (we expect arrows from multiple exposure time points to outcome Y).12
Now suppose that, for each individual in the study population, the time-varying exposure were measured at times: . If we conducted separate MR analyses, each using one of these exposure measurements, can we interpret the resulting MR estimates as an estimate of the point effect at each age? The answer is no, because we have, at best, a single instrument Z for all MR analyses. The answer would be yes if we had instruments, each satisfying the instrumental conditions for a distinct exposure time point for .
In summary, interpreting MR estimates for time-varying exposures as point effects require strong assumptions that are unlikely to hold in most settings, even when only a single exposure measurement is considered.
The effect of exposure during a period and the effect of exposure over a lifetime
Suppose we are interested in the average causal effect on the outcome Y of a hypothetical intervention on the exposure during the period . The (average) period effect is the difference between the mean counterfactual outcome had everyone received the exposure trajectory and the mean counterfactual outcome had everyone received the exposure trajectory between times and that is,
To identify any period effect using IV methods, the proposed instrument(s) must meet the three instrumental conditions for the exposure, as a whole, during this period (see eAppendix 1.2.2). To satisfy the second instrumental condition, each component of the time-varying exposure outside of the period must be either unaffected by the instrument or affect the outcome only through affecting subsequent exposure at time points to . This is a weaker exclusion restriction than that required for estimating a point exposure, which requires that the instrument affects the outcome only through the exposure at a single time point . However, this weaker assumption is only plausible if the period studied very closely mapped onto the critical period.9
Even when the weaker exclusion restriction holds, the types of period effects that can be identified by IV methods depend on the number of exposure measurements available during the period of interest and additional assumptions may be needed. First, suppose we have measured all relevant exposure time points during the period . Then, under the additional assumption of no interaction between the exposure at different time points, we can identify the controlled direct effects of each exposure time point during this period, that is for time where , as well as the overall period effect (see eAppendix 2.1–2.3). Our simulations illustrate the lack of bias (see eAppendix 3.2–3.3) except in the presence of exposure-exposure interaction (see eAppendix 3.4). These results are consistent with previously reported challenges in estimating interactions in MR studies.13,14
Next, suppose we only have one measurement of the exposure, for . Then we cannot disentangle the effect of the exposure from the effects of the exposure at other time points during the period (as illustrated using simulations in eAppendix 3.5). However, under additional assumptions, we can identify the effect of increasing exposure by one unit across the period—that is, the effect of shifting the entire exposure trajectory by one unit across this period
For a causal effect on the additive scale, the Z- association must be constant on the additive scale for , or, for a dichotomous instrument , must be the same for all in this period (see eAppendix 2.4 for the proof and eAppendix 3.6 for the simulations).9,15 This is unlikely to hold for many exposures, and is known not to hold for genetic variants for exposures such as body mass index (BMI)16–18, low-density lipoprotein cholesterol19, and blood pressure20,21 if the period is long. In fact, in the application we consider below, we also show important variation in the variant-exposure relationship over age (eFigure 4.1).
Last, suppose we have measured the exposure at some, but not all, time points during the period . Under the assumption that the Z- association is constant over this period, we can similarly identify the effect of shifting the exposure trajectory during this period (see simulations in eAppendix 3.8). However, we cannot identify controlled direct effects of the exposures time points considered in the SMM. In particular, variation in the association is needed to disentangle the effects of the exposure at one time point from another. Therefore, to identify additional types of period effects with multiple exposure time points, we must relax this homogeneity assumption, but only to the extent that changes in the Z- association during the period can be adequately captured by the exposure measures considered in the model. For example, if there are three relevant exposure time point and the exposure has been measured at the first and third time points, we can identify the controlled direct effect of the exposure at time 1, , and the effect of shifting the exposure trajectory by 1 unit across times 2 and 3, , if the association remains constant across times 2 and 3 (eAppendix 3.9). If, rather, the association remains constant across times 1 and 2, we can identify the effect of shifting the exposure trajectory by 1 unit across times 1 and 2, , and the controlled direct effect of the exposure at time 3, . That is, we can identify the effect of shifting the exposure trajectory across multiple time points within the period of interest if the exposure at some of those time points are unmeasured and the instrument–exposure association remains constant over those time points. In general, given the period with relevant exposure time points, of which are measured and are unmeasured, we can identify some period effects if the magnitude of the instrument–exposure association at each unmeasured exposure time point is equal to the magnitude of the instrument–exposure association for at least one of the measured exposure time points.
When the period starts at the time of conception and ends at the outcome recording time m, we refer to this special case of a period effect as the lifetime effect between conception and time m.22,23 In general, as the length of the period increases, fewer arrows from the causal diagram need to be removed to have a valid instrument, but more exposure measurements may be needed to minimize the additional homogeneity assumptions required to identify a period effect.
In summary, interpreting conventional MR estimates for time-varying exposures as period effects is achievable with an additional homogeneity assumption about the relationship between the instrument and the exposure over time.9 This assumption is relaxed when more measures of the time-varying exposure are considered. Next, we describe how to extend MR methods to accommodate multiple measures of an exposure.
Structural models for point, period, and lifetime effects
An additive structural mean model is a model for the expected difference in the counterfactual outcomes under two different exposure strategies. The SMM for the point effect of a time-varying exposure at age is
where is a function of instrument Z and exposure , indexed by the unknown parameter . For simplicity, we consider only the instrument and exposure , although the SMM could further incorporate measured covariates1,24—a point we will return to in the discussion. For a dichotomous exposure and instrument, the saturated parameterization of this SMM is
However, the parameters of this saturated model cannot be identified with IV estimation.1,24 That is, the model cannot be a function of the instrument Z, or . Therefore, we will parameterize the SMM as
where represents the point effect at m and equals the usual IV estimand and thus makes a homogeneity assumption of no additive effect modification of the exposure on the outcome by the instrument within levels of exposure.1
The SMM for a period effect between ages and is:
where and is a function of the exposure between age and age m indexed by the unknown (possibly vector-valued) parameter . Once we consider multiple time points, this model is also referred to as a structural nested mean model (SNMM) as it represents a series of nested equations, where each equation corresponds to an exposure time point.1 The first equation models the effect of receiving the exposure at the first time point and never again afterwards, the second equation models the effect of receiving the exposure at the second time point and never again afterwards, and so forth.
The constraints on the types of period effects that can be identified via IV are the result of having exhausted the constraints on the data distribution implied by the instrumental conditions. With one measurement of the exposure at time where and under the assumption that the instrument–exposure association is constant over this period, the period effect of shifting the exposure trajectory shift can be represented by in the SMM
With up to exposure measurements during the period , the model expands to include up to parameters.
In this SMM, each parameter corresponds to the controlled direct effect of its corresponding exposure time point. For a SMM which considers only a subset of the relevant exposure time points during the period, the parameterization of the SMM and the types of period effects that are modelled depend on the number of exposure measurements available, and how the instrument–exposure associations are assumed to be constant over this period.
In the case of a single IV and a single exposure measurement, it can be shown that the usual IV estimand used in MR studies equals from the additive SMM for the point estimate, and from the single parameter SMM for the period effect if the above assumptions hold.1,24,25 Next, we describe the process for estimating the parameters of a SMM.
Estimation
The parameters of SMMs can be estimated via g-estimation. Consider again the SMM for the point effect at time m
Under the instrumental conditions, it can be shown1,26 that
because the SMM is linear. For point effects, we can identify each one by individually applying the above equation to each time point and using an instrument which satisfies the instrumental conditions for that corresponding time point.
To identify the period or lifetime effect of shifting the entire exposure trajectory using a single exposure measurement, we consider the measured exposure for and use the same closed form estimator as shown above. Now consider an SMM for the period which considers exposure time points with vector-valued variables and where , and the vector-valued parameter . Then
The proof is provided in eAppendix 2.3. Here, we need at least as many instruments as the number of measured exposure time points to estimate . Confidence intervals for the g-estimate and for the point, period or lifetime effect can be estimated via bootstrapping. Next, we demonstrate an application of SMMs to an MR analysis to infer the period effects of alcohol intake, HDL cholesterol and LDL cholesterol on intermediate CHD outcomes using data from the Framingham Heart Study.
Application: The effect of alcohol and cholesterol on the risk of coronary heart disease
MR studies of alcohol intake, HDL cholesterol and LDL cholesterol have used only a single measurement of exposure to estimate their lifetime effects on CHD risk exposures, despite evidence that alcohol intake and blood lipid levels can change substantially over the life course.27–29 We used data from the Framingham Heart Study to estimate the period effect of a one drink/day shift in alcohol intake trajectory, a 10mg/dL shift in HDL cholesterol trajectory or a 10 mg/dL shift in LDL cholesterol trajectory on intermediate CHD outcomes. We compared estimates from SMMs with a single point exposure against a SMM with multiple point exposures, and defined the period of interest to be during the time of follow-up for participants.
Study population
This study was completed using fully anonymized data from the Framingham Heart Study (FHS) obtained through dbGAP (https://dbgap.ncbi.nlm.nih.gov, dbGAP study accession: phs000007). FHS is an ongoing prospective cohort study on cardiovascular disease.30 Our study included descendants of the Original Cohort who formed the Third Generation Cohort.31 At the time of analysis, data for two examination cycles were available: at baseline (or examination 1), and at the next follow-up examination completed 6 years after baseline (or examination 2). The analysis was restricted to individuals with no history of cardiovascular disease at baseline and with complete data on exposure at baseline, outcome, and all proposed instruments. This left an analytical sample of 2,938 participants for alcohol intake-related analyses and 2,920 participants for blood lipids-related analyses (Figure 2). All participants provided written consent to participate in the study, and all analyses described here were approved by the Harvard T. H. Chan School of Public Health Institutional Review Board.
Figure 2.

Inclusion and exclusion of study participants from the Framingham Heart Study (FHS) Third Generation (Gen III)
Proposed instruments
We proposed genetic variants of alcohol intake, HDL cholesterol and LDL cholesterol as instruments. Blood samples for DNA extraction were collected at examination 1. Participants were genotyped through an NHLBI funded SNP-Health Association resource project using the Affymetrix GeneChip Human Mapping 500K Array and 50K Human Gene Focused Panel. Genotyping methods, quality control, and imputation procedures have been previously described.32 Given the exploratory nature of GWAS and issues of multiple testing, we used previously identified genome-wide significant (p < 5×10−8) single nucleotide polymorphisms (SNPs) as candidate instruments for alcohol use33 and blood lipids34. To minimize potential pleiotropic effects of SNPs identified for alcohol intake, we excluded 130 variants that were also genome-wide significant for age of initiation of regular smoking, ever smoking, cigarettes per day and smoking cessation, which left 26 candidate SNPs for our analysis (eTable 4.2A).33 For blood lipids, 50 out of 60 genome-wide significant SNPs for HDL cholesterol and 25 out of 30 genome-wide significant SNPs LDL cholesterol remained after excluding those that were significant for both HDL and LDL cholesterol, or for triglycerides (eTables 4.2B–4.2C).34 For each individual genetic variant, we checked for violations of the instrumental inequalities by dichotomizing alcohol intake at ≤1 drink per day and >1 drink per day and blood lipids at the median, and categorizing outcomes into quartiles. 35 One alcohol intake-related variant, two HDL cholesterol-related variants and two LDL cholesterol-related variants were excluded for violating the instrumental inequalities (eTables 4.2A–4.2C).
Exposures
Alcohol intake was assessed via questionnaire36 and blood was drawn from participants after an overnight fast at both examination time points. HDL cholesterol concentrations were measured directly using standardized assays and LDL cholesterol concentrations were estimated from the standard lipid profile.37
Outcomes
C reactive protein (CRP), gamma-glutamyl transferase (GGT), and ankle-brachial index (ABI) were assessed at the second examination. CRP was measured in fasting blood samples using high-sensitivity nephelometric immunoassays (Dade Behring). Plasma GGT activity was measured using spectrophotometry (Quest Diagnostics, MedPath, Teterboro, NJ).38 ABI was calculated as the ratio of the average systolic blood pressure (SBP) measured at the ankles to the higher of the two brachial SBP measurements. CRP and GGT were normalized by using a log transformation.
Statistical analysis
We compared g-estimated period effects from SMMs which considered different exposure measurements in the analysis: (1) only the exposure measured at examination 1; (2) only the exposure measured at examination 2; (3) the average exposure level across the two examination time points; and (4) both exposure time points. This corresponded to the following SMMs:
| Model 1: |
| Model 2: |
| Model 3: |
| Model 4: |
In models 1 to 3, represents the period effect of shifting the exposure trajectory by one standardized increase in alcohol consumption, HDL cholesterol, or LDL cholesterol over the duration of the study period. The same period effect is represented in model 4 by . We g-estimated the parameters of the SMMs as described above. MR estimates from SMMs of log-transformed CRP or log-transformed GGT were exponentiated to represent multiplicative effects on the natural scale. We bootstrapped 1,000 samples to obtain 95% confidence intervals. All analyses were conducted in R 3.5.2 (www.r-project.org, R Core Development Team).
Results
At baseline, mean age at examination 1 was 40.3 years and ranged from 19 to 72 years (Table 2). Associations of proposed instruments with their respective exposures and outcomes are presented in eTables 4.4–4.6. We estimated the period effects of alcohol intake, HDL cholesterol and LDL cholesterol on CRP level, GGT levels and ABI using different SMM parameterizations (Figure 3). The choice of model had little impact on both the point estimate and its 95% confidence interval. The range of effect values that were very compatible with our data (as measured by the 95% confidence intervals) was wider for alcohol than for HDL and LDL cholesterol, which was expected because the proposed instrument–exposure association was weaker for alcohol than for HDL and LDL cholesterol (eTable 4.7). The point estimates for the effect on CRP of all three exposures were close to the null. The point estimates for the effect on GGT was close to the null for HDL and LDL cholesterol and around a 1.3-fold increase for alcohol. The point estimates for the effect on ABI were consistent with harm for all three exposures but the width of the 95% confidence intervals was wide.
Table 2.
Baseline characteristics of study participants
| Characteristics | Third Generation Cohort (n = 3,150) |
|
|---|---|---|
| Total n (% missing) | Summary statistic | |
| Age (years), mean ± SD | 3,150 (0.00) | 40.3 ± 8.7 |
| Sex, n (%) | 3,150 (0.00) | |
| Male | 1,467 (46.6) | |
| Female | 1,683 (53.4) | |
| Education, n (%) | 3,141 (0.29) | |
| High school / GED or less | 473 (15.1) | |
| Some college or equivalent, no degree | 525 (16.7) | |
| Bachelor’s degree or equivalent | 1,606 (51.1) | |
| Graduate or professional degree | 537 (17.1) | |
| Smoking status, n (%) | 3,148 (0.06) | |
| Never smoker | 1,835 (58.3) | |
| Former smoker | 862 (27.4) | |
| Current smoker | 451 (14.3) | |
| Number of cigarettes smoked (cigarettes/day), mean ± SD | 3,143 (0.22) | 6.6 ± 10.5 |
| Physical activity (hours/day), mean ± SD | ||
| Slight activity (e.g. standing, walking) | 3,132 (0.57) | 5.1 ± 2.7 |
| Moderate activity (e.g. housework, light sports) | 3,132 (0.57) | 3.5 ± 2.5 |
| Heavy activity (e.g. intensive sports) | 3,134 (0.51) | 1.3 ± 1.8 |
| BMI (kg/m2) | 3,148 (0.06) | 26.7 ± 5.4 |
| Blood pressure (mmHg), mean ± SD | ||
| Diastolic | 3,147 (0.10) | 75.2 ± 9.6 |
| Systolic | 3,150 (0.00) | 116.6 ± 14.1 |
| Ever prescribed antihypertensive medication, n (%) | 3,148 (0.06) | 274 (8.7) |
| Ever prescribed cholesterol-lowering medication, n (%) | 3,148 (0.06) | 227 (7.2) |
| Alcohol intake (g/day), mean ± SD | 2,938 (6.73) | 11.0 ± 15.2 |
| Lipids (mg/dL), mean ± SD a | ||
| Total cholesterol | 2,921 (0.07) | 188.9 ± 35.2 |
| HDL cholesterol | 2,920 (0.10) | 55.3 ± 16.2 |
| LDL cholesterol | 2,920 (0.10) | 112.5 ± 31.9 |
Percent missing calculated among participants who have never been prescribed cholesterol-lowering medication (n = 2,923)
Figure 3.
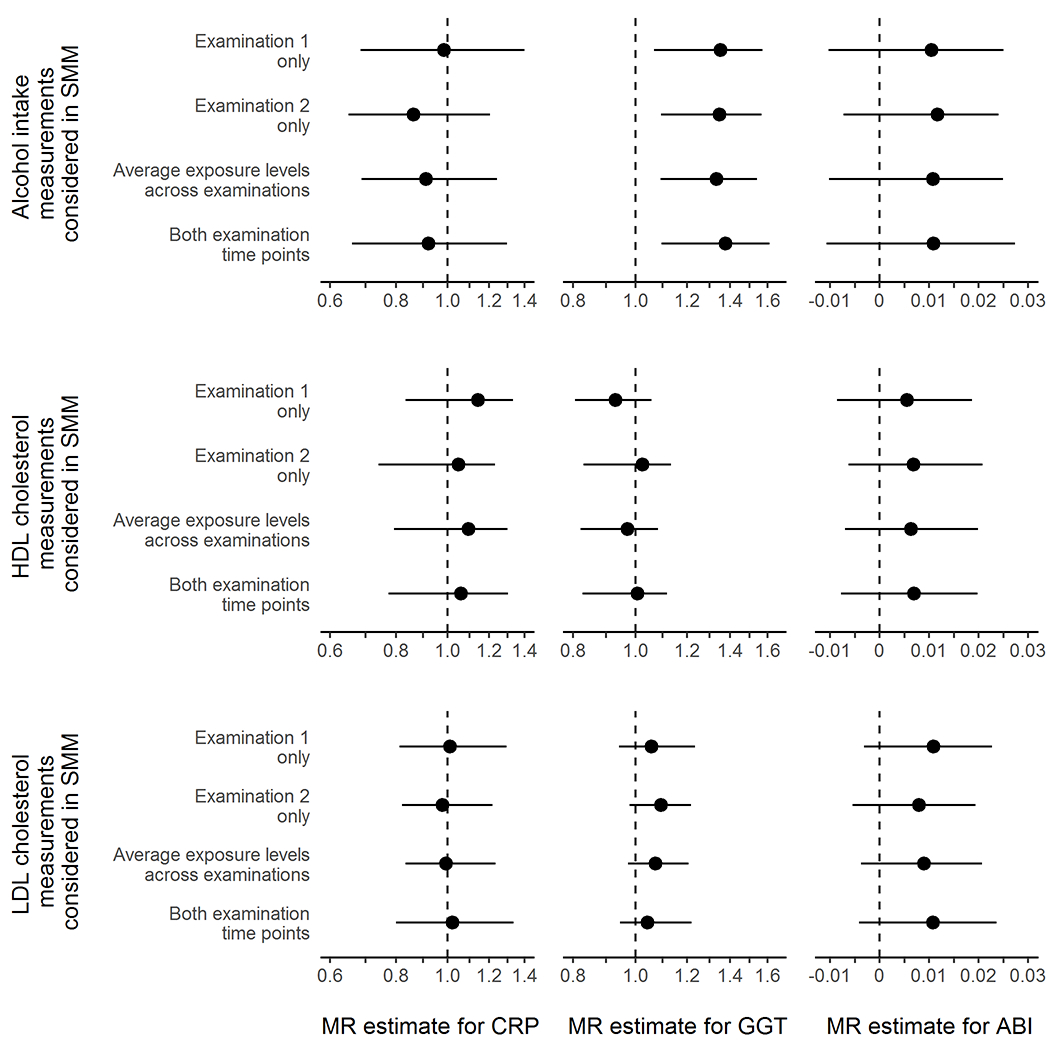
Comparison of different analytical approaches to obtain multiplicative (for c-reactive protein [CRP] and gamma-glutamyl transferase [GGT]) and additive (for ankle-brachial index [ABI]) period effects and 95% confidence intervals corresponding to one standardized increase in (A) alcohol intake per day, (B) high-density lipoprotein [HDL] cholesterol, and (C) low-density lipoprotein [LDL] cholesterol.
Discussion
When using MR, the causal estimand of interest may be a point effect or a period effect (including the lifetime effect), and the conditions for identifying these effects (including the second instrumental condition and several homogeneity conditions) will depend on the choice of causal estimand.
In general, the assumptions required for the second instrumental condition to hold are (i) biologically implausible when interpreting MR estimates as point effects, regardless of the number of exposure measurements available, and (ii) more plausible when interpreting MR estimates as period effects. If the second instrumental condition holds, additional homogeneity assumptions, which can be relaxed with more exposure measurements, are sufficient for certain period effects. The plausibility of these homogeneity assumptions will vary depending on duration of the period, patterns in the gene–exposure relationship over time, and the available data for analysis. For shorter periods or gene–exposure associations which do not change substantially over time, one or a few measurements may be sufficient to identify the period or lifetime effect. However, many exposures of interest in MR studies have age-varying associations with their proposed genetic instruments which span over years or decades,15 and therefore may require multiple measurements over long periods of follow-up.
We also described and demonstrated how to extend MR methods to accommodate multiple measures of an exposure by using SMMs. Although the MR estimates from additive SMMs and conventional IV estimators (e.g. ratio of coefficients, two-stage least squares) are numerically equivalent,1,24 SMMs make explicit the counterfactual contrasts of interest and can be extended in several ways.1,25,39 First, SMMs can use surrogate instruments, although the violations of instrumental conditions need to be redefined.9 Second, SMMs can include non-linear outcomes. Third, inverse probability of weighting can be used to account for selection bias due to loss to follow-up, although generally cannot address potential biases in most MR studies that result from conditioning on surviving up until the point of study entry.5,40,41 Last, SMMs can incorporate covariates to address potential violations of the third instrumental condition or allow for weaker versions of homogeneity assumptions.
Recent MR studies have used an alternative approach, multivariable MR, to disentangle the effects of an exposure across different periods of life.42,43 For individual-level data, multivariable MR relies on the two-stage least squares (2SLS) estimator.44 In the context of additive causal effects for continuous outcomes, g-estimation of structural mean models and 2SLS yield very similar MR estimates (eAppendix 3.3–3.4). However, there are two key advantages of SMMs. First, SMMs can be naturally extended to many settings, including accommodating binary and failure-time outcomes and estimating effects on the multiplicative scale.39 Second, SMMs are semi-parametric, and therefore avoid some of the parametric assumptions of 2SLS.1 In particular, SMMs are more robust to model misspecification for binary outcomes.45
Our data example resulted in imprecise estimates because of small sample size and short length of follow-up. Further applications of SMMs in MR studies with larger datasets are warranted. However, our analysis suffices to illustrate alternate approaches to standard MR methods, especially when the exposure is time-varying, and to highlight two key challenges in estimating and interpreting period effects from MR analyses.
The first is defining the period of interest. A well-formulated research question should target a specific and, hopefully, clinically relevant time period for the effect of the exposure on the outcome. However, available data for the types of MR analyses that can be conducted may not be fully compatible with the target research question—for example, we may not have sufficient measures of the exposure, or the IV conditions may be violated for the time period of interest. Here, we defined the period as the time under follow-up, but then key assumptions for estimating this period effect may not hold: our proposed instrument likely affects exposure outside of this period and prior exposure likely has direct effects on the outcome. Alternatively, we could have interpreted our estimates as lifetime effects, but the two exposure measurements, taken only 6 years apart, are unlikely to capture a lifetime’s worth of changes in exposure. In fact, the exposure levels at each time point were highly correlated, which may explain the similar estimates of the single- and multi-parameter SMMs.
The second challenge is the choice of time scale. Under the oft-made analogy between MR studies and randomized trials, the analogue of randomization would occur at conception and therefore age would be the natural time scale.5 Due to wide variations in age at first visit and short duration of follow-up, we were limited to using time since enrollment in the study as the time scale, which implies the added assumption that the period effect is homogeneous across age. The plausibility of this assumption is not only specific to the exposure–outcome relationship of interest, but also depends on the variability in age.
In conclusion, we present an application of structural mean models to estimate the effect of a time-varying exposure on an outcome using MR with repeated exposure measurements. Given the increasing popularity of MR as a method for answering causal questions, as well as increasing availability of longitudinal data in genetic studies, this work provides a basis for considering repeated measures of time-varying exposures in future MR studies.
Supplementary Material
Sources of financial support:
J.S. is supported by a UCB Fellowship. S.A.S. is supported by a NWO/ZonMW Veni grant (91617066). I.D.V. is supported by the Brigham Research Institute through the Fund to Sustain Research Excellence. M.A.H. is supported by a National Institutes of Health (NIH) grant R37 AI102634.
Footnotes
Conflicts of interest: None declared
Process of obtaining code and data: This study was completed using fully anonymized data from the Framingham Heart Study (FHS). Access to the data can be requested through dbGAP (https://dbgap.ncbi.nlm.nih.gov, dbGAP study accession: phs000007). Access to the code used in the simulations is available at Code for the simulations are available at https://github.com/joy-shi1/smms-and-iv.
References
- 1.Hernán MA, Robins JM. Causal Inference: What If. Boca Raton: Chapman & Hall/CRC; 2020. [Google Scholar]
- 2.Burgess S, Thompson SG. Use of allele scores as instrumental variables for Mendelian randomization. Int J Epidemiol. 2013;42(4):1134–1144. doi: 10.1093/ije/dyt093 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Burgess S, Small DS, Thompson SG. A review of instrumental variable estimators for Mendelian randomization. Stat Methods Med Res. 2017;26(5):2333–2355. doi: 10.1177/0962280215597579 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Smith GD, Hemani G. Mendelian randomization: genetic anchors for causal inference in epidemiological studies. Hum Mol Genet. 2014;23(R1). doi: 10.1093/hmg/ddu328 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Swanson SA, Tiemeier H, Ikram MA, Hernán MA. Nature as a Trialist?: Deconstructing the Analogy between Mendelian Randomization and Randomized Trials. Epidemiology. 2017;28(5):653–659. doi: 10.1097/EDE.0000000000000699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Smith GD, Ebrahim S. Mendelian randomization: prospects, potentials, and limitations. Int J Epidemiol. 2004;33(1):30–42. doi: 10.1093/ije/dyh132 [DOI] [PubMed] [Google Scholar]
- 7.Nitsch D, Molokhia M, Smeeth L, DeStavola BL, Whittaker JC, Leon DA. Limits to causal inference based on Mendelian randomization: a comparison with randomized controlled trials. Am J Epidemiol. 2006;163(5):397–403. doi: 10.1093/aje/kwj062 [DOI] [PubMed] [Google Scholar]
- 8.Ference BA. Mendelian randomization studies: Using naturally randomized genetic data to fill evidence gaps. Curr Opin Lipidol. 2015;26(6):566–571. doi: 10.1097/MOL.0000000000000247 [DOI] [PubMed] [Google Scholar]
- 9.Labrecque JA, Swanson SA. Interpretation and Potential Biases of Mendelian Randomization Estimates With Time-Varying Exposures. Am J Epidemiol. 2018;188(1):231–238. doi: 10.1093/aje/kwy204 [DOI] [PubMed] [Google Scholar]
- 10.Vanderweele TJ, Tchetgen Tchetgen EJ, Cornelis M, Kraft P. Methodological challenges in Mendelian randomization. Epidemiology. 2014;25(3):427–435. doi: 10.1097/EDE.0000000000000081 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Swanson SA, Labrecque J, Hernán MA. Causal null hypotheses of sustained treatment strategies: What can be tested with an instrumental variable? Eur J Epidemiol. 2018;33(8):723–728. doi: 10.1007/s10654-018-0396-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kuh D, Ben-Shlomo Y, Lynch J, Hallqvist J, Power C. Life course epidemiology. J Epidemiol Community Health. 2003;57(10):778–783. doi: 10.1136/jech.57.10.778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.North TL, Davies NM, Harrison S, et al. Using genetic instruments to estimate interactions in mendelian randomization studies. Epidemiology. 2019;30(6):E33–E35. doi: 10.1097/EDE.0000000000001096 [DOI] [PubMed] [Google Scholar]
- 14.Rees JMB, Foley CN, Burgess S. Factorial Mendelian randomization: Using genetic variants to assess interactions. Int J Epidemiol. 2020;49(4):1147–1158. doi: 10.1093/ije/dyz161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Labrecque JA, Swanson SA. Age-varying genetic associations and implications for bias in Mendelian randomization analyses. medRxiv. 2021. [Google Scholar]
- 16.Winkler TW, Justice AE, Graff M, et al. The Influence of Age and Sex on Genetic Associations with Adult Body Size and Shape: A Large-Scale Genome-Wide Interaction Study. PLoS Genet. 2015;11(10):1–42. doi: 10.1371/journal.pgen.1005378 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hardy R, Wills AK, Wong A, et al. Life course variations in the associations between FTO and MC4R gene variants and body size. Hum Mol Genet. 2010;19(3):545–552. doi: 10.1093/hmg/ddp504 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sovio U, Mook-Kanamori DO, Warrington NM, et al. Association between common variation at the FTO locus and changes in body mass index from infancy to late childhood: the complex nature of genetic association through growth and development. PLoS Genet. 2011;7(2):e1001307. doi: 10.1371/journal.pgen.1001307 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shirts BH, Hasstedt SJ, Hopkins PN, Hunt SC. Evaluation of the gene-age interactions in HDL cholesterol, LDL cholesterol, and triglyceride levels: the impact of the SORT1 polymorphism on LDL cholesterol levels is age dependent. Atherosclerosis. 2011;217(1):139–141. doi: 10.1016/j.atherosclerosis.2011.03.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Simino J, Shi G, Bis JC, et al. Gene-age interactions in blood pressure regulation: a large-scale investigation with the CHARGE, Global BPgen, and ICBP Consortia. Am J Hum Genet. 2014;95(1):24–38. doi: 10.1016/j.ajhg.2014.05.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shi G, Gu CC, Kraja AT, et al. Genetic effect on blood pressure is modulated by age: the Hypertension Genetic Epidemiology Network Study. Hypertens (Dallas, Tex 1979). 2009;53(1):35–41. doi: 10.1161/HYPERTENSIONAHA.108.120071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Smith GD, Ebrahim S. “Mendelian randomization”: Can genetic epidemiology contribute to understanding environmental determinants of disease? Int J Epidemiol. 2003;32(1):1–22. doi: 10.1093/ije/dyg070 [DOI] [PubMed] [Google Scholar]
- 23.Stitziel NO, Kathiresan S. Leveraging human genetics to guide drug target discovery. Trends Cardiovasc Med. 2017;27(5):352–359. doi: 10.1016/j.tcm.2016.08.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hernán MA, Robins JM. Instruments for causal inference: An epidemiologist’s dream? Epidemiology. 2006;17(4):360–372. doi: 10.1097/01.ede.0000222409.00878.37 [DOI] [PubMed] [Google Scholar]
- 25.Robins JM. The analysis of randomized and non-randomized AIDS treatment trials using a new approach to causal inference in longitudinal studies. Heal Serv Res Methodol a Focus AIDS 1989:113–159. [Google Scholar]
- 26.Robins JM. Correcting for non-compliance in randomized trials using structural nested mean models. Commun Stat methods. 1994;23(8):2379–2412. [Google Scholar]
- 27.Britton A, Ben-Shlomo Y, Benzeval M, Kuh D, Bell S. Life course trajectories of alcohol consumption in the United Kingdom using longitudinal data from nine cohort studies. BMC Med 2015;13(1). doi: 10.1186/s12916-015-0273-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Johnson FW, Gruenewald PJ, Treno AJ, Taff GA. Drinking over the life course within gender and ethnic groups: A hyperparametric analysis. J Stud Alcohol 1998;59(5):568–580. doi: 10.15288/jsa.1998.59.568 [DOI] [PubMed] [Google Scholar]
- 29.Duncan MS, Vasan RS, Xanthakis V. Trajectories of Blood Lipid Concentrations Over the Adult Life Course and Risk of Cardiovascular Disease and All-Cause Mortality: Observations From the Framingham Study Over 35 Years. J Am Heart Assoc 2019;8(11). doi: 10.1161/JAHA.118.011433 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Cupples LA, Arruda HT, Benjamin EJ, et al. The Framingham Heart Study 100K SNP genome-wide association study resource: overview of 17 phenotype working group reports. BMC Med Genet. 2007;8 Suppl 1(Suppl 1):S1. doi: 10.1186/1471-2350-8-S1-S1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Splansky GL, Corey D, Yang Q, et al. The Third Generation Cohort of the National Heart, Lung, and Blood Institute’s Framingham Heart Study: design, recruitment, and initial examination. Am J Epidemiol 2007;165(11):1328–1335. doi: 10.1093/aje/kwm021 [DOI] [PubMed] [Google Scholar]
- 32.Wang TJ, Zhang F, Richards JB, et al. Common genetic determinants of vitamin D insufficiency: A genome-wide association study. Lancet. 2010;376(9736):180–188. doi: 10.1016/S0140-6736(10)60588-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Liu M, Jiang Y, Wedow R, et al. Association studies of up to 1.2 million individuals yield new insights into the genetic etiology of tobacco and alcohol use. Nat Genet. 2019;51(2):237–244. doi: 10.1038/s41588-018-0307-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Willer CJ, Schmidt EM, Sengupta S, et al. Discovery and refinement of loci associated with lipid levels. Nat Genet. 2013;45(11):1274–1285. doi: 10.1038/ng.2797 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Diemer EW, Labrecque J, Tiemeier H, Swanson SA. Application of the Instrumental Inequalities to a Mendelian Randomization Study With Multiple Proposed Instruments. Epidemiology. 2020;31(1):65–74. doi: 10.1097/EDE.0000000000001126 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Elias PK, Elias MF, D’Agostino RB, Silbershatz H, Wolf PA. Alcohol consumption and cognitive performance in the Framingham Heart Study. Am J Epidemiol. 1999;150(6):580–589. http://dbgap.ncbi.nlm.nih.gov. Accessed October 21, 2018. [DOI] [PubMed] [Google Scholar]
- 37.Martin SS, Blaha MJ, Elshazly MB, et al. Comparison of a novel method vs the Friedewald equation for estimating low-density lipoprotein cholesterol levels from the standard lipid profile. JAMA. 2013;310(19):2061–2068. doi: 10.1001/jama.2013.280532 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lee DS, Evans JC, Robins SJ, et al. Gamma glutamyl transferase and metabolic syndrome, cardiovascular disease, and mortality risk: The Framingham Heart Study. Arterioscler Thromb Vasc Biol. 2007;27(1):127–133. doi: 10.1161/01.ATV.0000251993.20372.40 [DOI] [PubMed] [Google Scholar]
- 39.Vansteelandt S, Joffe M, others. Structural nested models and G-estimation: the partially realized promise. Stat Sci. 2014;29(4):707–731. [Google Scholar]
- 40.Swanson SA. A Practical Guide to Selection Bias in Instrumental Variable Analyses. Epidemiology. 2019;30(3):345–349. doi: 10.1097/EDE.0000000000000973 [DOI] [PubMed] [Google Scholar]
- 41.Vansteelandt S, Dukes O, Martinussen T. Survivor bias in Mendelian randomization analysis. Biostatistics. September 2017. doi: 10.1093/biostatistics/kxx050 [DOI] [PubMed] [Google Scholar]
- 42.Richardson TG, Sanderson E, Elsworth B, Tilling K, Smith GD. Use of genetic variation to separate the effects of early and later life adiposity on disease risk: Mendelian randomisation study. BMJ. 2020;369. doi: 10.1136/bmj.m1203 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gill D, Georgakis MK, Zuber V, et al. Genetically Predicted Midlife Blood Pressure and Coronary Artery Disease Risk: Mendelian Randomization Analysis. J Am Heart Assoc. 2020;9(14):e016773. doi: 10.1161/JAHA.120.016773 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Burgess S, Thompson SG. Multivariable Mendelian randomization: The use of pleiotropic genetic variants to estimate causal effects. Am J Epidemiol. 2015;181(4):251–260. doi: 10.1093/aje/kwu283 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Clarke PS, Windmeijer F. Instrumental variable estimators for binary outcomes. J Am Stat Assoc. 2012;107(500):1638–1652. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


