Physiologically Based Modeling to Predict Monoclonal Antibody Pharmacokinetics in Humans from in vitro Physiochemical Properties

ABSTRACT

A model-based framework is presented to predict monoclonal antibody (mAb) pharmacokinetics (PK) in humans based on in vitro measures of antibody physiochemical properties. A physiologically based pharmacokinetic (PBPK) model is used to explore the predictive potential of 14 in vitro assays designed to measure various antibody physiochemical properties, including nonspecific cell-surface interactions, FcRn binding, thermal stability, hydrophobicity, and self-association. Based on the mean plasma PK time course data of 22 mAbs from humans reported in the literature, we found a significant positive correlation (R = 0.64, p = .0013) between the model parameter representing antibody-specific vascular to endothelial clearance and heparin relative retention time, an in vitro measure of nonspecific binding. We also found that antibody-specific differences in paracellular transport due to convection and diffusion could be partially explained by antibody heparin relative retention time (R = 0.52, p = .012). Other physiochemical properties, including antibody thermal stability, hydrophobicity, cross-interaction and self-association, in and of themselves were not predictive of model-based transport parameters. In contrast to other studies that have reported empirically derived expressions relating in vitro measures of antibody physiochemical properties directly to antibody clearance, the proposed PBPK model-based approach for predicting mAb PK incorporates fundamental mechanisms governing antibody transport and processing, informed by in vitro measures of antibody physiochemical properties, and can be expanded to include more descriptive representations of each of the antibody processing subsystems, as well as other antibody-specific information.

Introduction

The ability to predict the pharmacokinetics (PK) of monoclonal antibodies (mAbs) in humans during the early screening of drug candidates would contribute significantly to the efficient development of therapeutic antibodies. The various factors that determine the disposition of mAbs in humans continue to be the subject of extensive investigation.^1,2 Recent studies have reported empirically derived relationships between antibody clearance and experimentally determined mAb physiochemical properties.^3–6 In this report, we propose a model-based approach for predicting mAb PK that incorporates the fundamental mechanisms that govern antibody transport and processing, coupled with in vitro assay measures of antibody physiochemical properties.

The in vivo disposition of antibodies is governed largely by their nonspecific off-target binding, affinity for neonatal Fc receptor (FcRn-IgG interaction), and target-mediated drug disposition (TMDD).⁷ Among these antibody-specific factors, FcRn-IgG interaction has been characterized by surface plasmon resonance (SPR), immunoassays, cell-based approaches, and solution-based methods among others.^3,8 Given that antibodies with common crystallizable fragment (Fc) regions and no TMDD display different PK behaviors,⁹ a number of approaches have been developed to screen antibodies for their nonspecific interactions. The approaches have included binding poly-specificity reagent (PSR), baculovirus particles (BVP), heparin, HEK293 cells, chaperone proteins, and cross-interaction chromatography.^1,10

Several groups have proposed empirically derived relationships relating antibody clearance to the aforementioned in vitro assays of physiochemical properties.^3–5 Avery et al.⁵ found the combination of biophysical assays assessing nonspecific interactions, self-association, and FcRn binding can be used to differentiate antibodies with lower and higher clearances. Goulet et al.⁴ proposed that FcRn binding together with thermal stability could predict in vivo half-life and clearance based on an analysis of eight antibodies. The study by Kraft et al.³ further delineated the role of nonspecific cell-surface interaction on in vivo clearance of IgG, using heparin chromatography as an in vitro surrogate. Grinshpun et al.¹¹ investigated 12 in vitro assays, of which several in combination were found to be able to categorize the clearance of 64 antibodies as slow or fast. Although the results reported in these studies have demonstrated predictive ability to characterize the clearance or half-life of mAbs as slow or fast, they cannot predict the full mAb PK time course in plasma or tissues of interest.

The ability of physiologically based pharmacokinetic (PBPK) models to describe the disposition of mAbs in humans and other species is now well established.^12–14 PBPK models of therapeutic antibodies that include subsystems representing the fundamental mechanisms responsible for antibody transport such as paracellular exchange, nonspecific binding, FcRn interaction and transcytosis, can be informed by in vitro assays designed to characterize these interactions and processes. The resulting models can be used to predict the plasma and tissue disposition of antibodies. For example, Jones and colleagues¹⁴ associated an affinity-capture self-interaction nanoparticle spectroscopy (AC-SINS) assay with a model parameter that represents nonspecific interaction affinity between mAbs and the cell membrane. In our previous study, an in silico-based metric representing the positive charge in antibody complementarity-determining region (PPC) was incorporated into a PBPK model for predicting antibody PK in humans.¹⁵

In the work reported herein, a PBPK modeling framework is used to explore the predictive potential of 14 in vitro assays designed to measure various antibody physiochemical properties, including nonspecific cell-surface interactions, FcRn binding, thermal stability, hydrophobicity, and self-association. The model is developed using mean plasma PK time course data of 22 mAbs from humans reported in the literature. For each antibody, model parameters related to paracellular transport, nonspecific binding, and FcRn interaction are then estimated. Potential relations between estimated model parameters and the different in vitro assay results for the 22 antibodies are explored. The established relations between antibody-specific parameters and in vitro assays are then used to conduct PBPK model-based predictions of the plasma PK time course of each antibody. The results demonstrate the utility of the proposed model-based framework that integrates physiochemical characteristics of antibodies to predict PK profiles in humans, with the goal of facilitating antibody screening and engineering in early development stages.

Results

The PBPK model used in this study is depicted in Figure 1 and described in detail in the Materials and Methods section.

Figure 1.

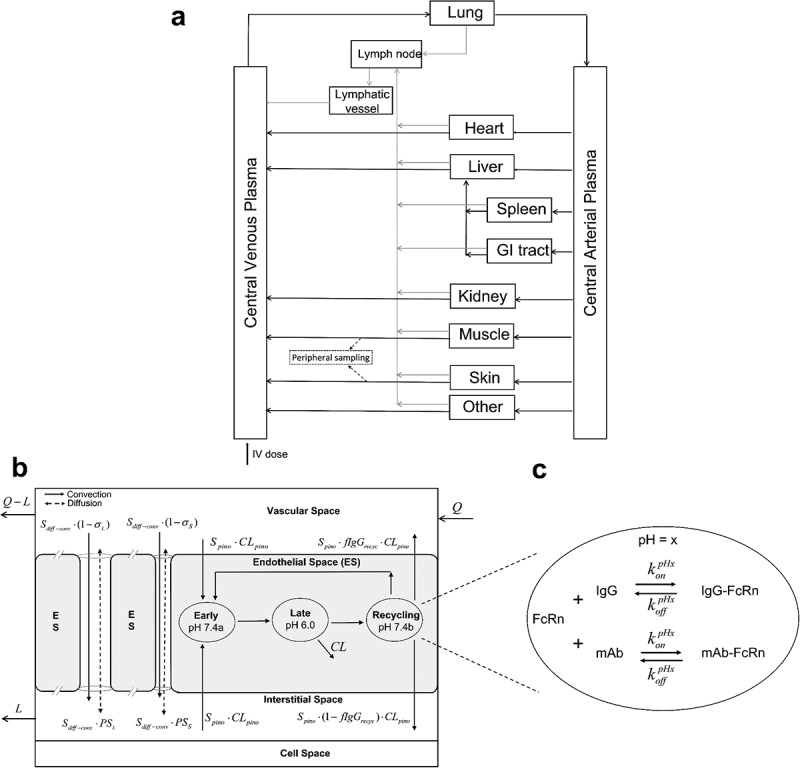
Schematic of the whole-body PBPK model for mAbs following IV administration. (a) overall circulatory model. (b) Organ-level structure of a typical tissue, including vascular space, endothelial space, interstitial space, and cell space. Paracellular transport via convection and diffusion through pores is depicted along with endothelial transport and process. (c) Endosomal subcompartments, showing the competition between endogenous IgG and mAb for FcRn at a specific pH value.

Long Description: Whole-body PBPK model diagrams. (a) An overall flow diagram with separate boxes representing different organs (such as lung, heart, liver), central venous plasma, central arterial plasma, lymph node, and lymphatic vessels. They are connected using solid lines via plasma flows and lymph flows anatomically. An arrow into central venous plasma labels an intravenous dose. In addition, dashed arrows drawn from muscle and skin point to a peripheral sampling site. (b) A box is divided into different spaces labeled as vascular space, endothelial space, interstitial space, cell space from top to bottom. Arrows labeled with Q and Q-L flow into and out of vascular space, respectively. Two solid flow arrows labeled with convection move from vascular space to interstitial space through a large pore and a small pore between endothelial space. Besides each of them is a dashed flow arrow labeled as diffusion, moving bi-directionally between vascular and interstitial spaces. Within endothelial space, three ellipses indicated as “Early pH 7.4a,” “Late pH 6.0,” and “Recycling pH 7.4b” are connected sequentially from left to right, with a recycling arrow from the last ellipse to the first one and an elimination arrow from the second ellipse. There are two arrows labeled as S_pino·CL_pino into the first ellipse from vascular space and interstitial space, respectively. From the last ellipse there are two arrows flowing into vascular space and interstitial space. Lastly, a flow termed as L moves out of interstitial space. (c) A zoomed ellipse of endothelial endosomal space. On the top within the ellipse, there are FcRn, plus sign, IgG on the left side of bi-directional arrows and IgG-FcRn on the right side. The arrow going from left to right is labeled with k_on^pHx and the reverse arrow labeled with k_off^pHx. On the bottom within the ellipse, there is same arrangement with FcRn, mAb, and mAb-FcRn.

Antibody-FcRn dissociation constant at pH = 6.0 ($K_d^{6.0}$)

The following exponential relation between $K_d^{6.0}$ and hFcRn_RT was determined based on the data from 37 mAbs:⁵ $K_d^{6.0}=K{0}_d^{6.0}\cdot e^{-\lambda \cdot hFcRn\mathrm{\_}RT}$, where $K{0}_d^{6.0}$= 1136, $\lambda$= 0.52 with R = 0.79 (Figure 2). Based on this relationship, the values for $K_d^{6.0}$ for the 22 mAbs (Table 1) that are subject of this study were calculated and are listed in Table 2.

Figure 2.

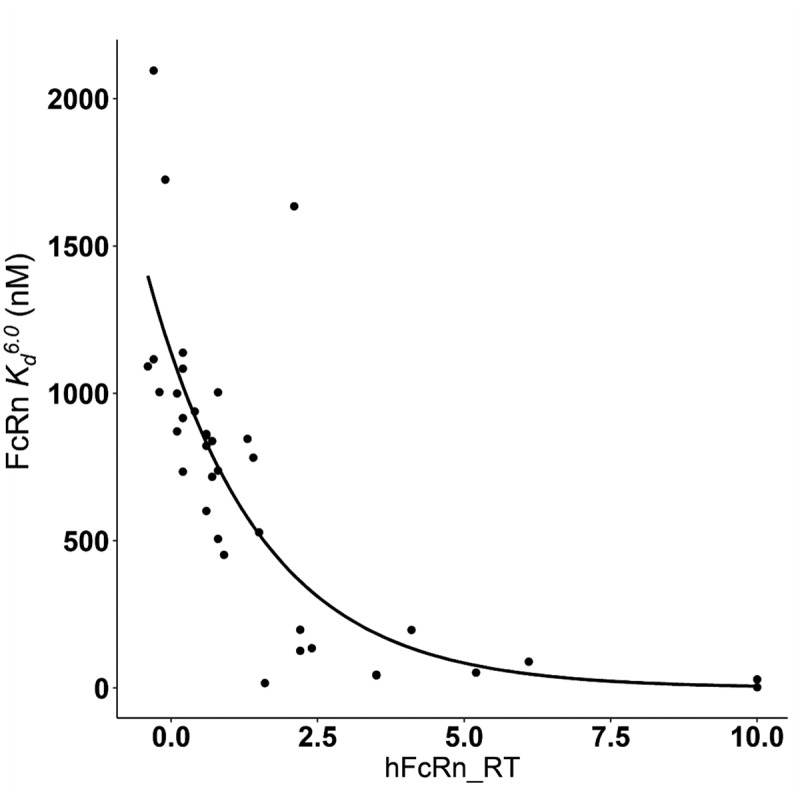
Observed and modeled relationship between FcRn $K_d^{6.0}$ and FcRn relative retention time (hFcRn_RT). The dots represent available assay results of 37 antibodies.⁵ The line indicates the nonlinear regression relationship: $K_d^{6.0}=1136\cdot e^{-0.52\cdot hFcRn\mathrm{\_}RT}$, R = 0.79.

ALT Text: A scatter plot with 37 points and a decaying fitting curve. Most points locate around the curve with four points away from it. The x axis is labeled with hFcRn_RT with a range of 0.0 to 10.0. The y axis has a title of “FcRn K_d^6.0 (nM)” ranging from 0 to 2000.

Table 1.

List of included mAbs

mAb (abbreviation)	Dosing	Reported clearance (ml/day)		Hep_RT	hFcRn_RT	Molecular weight (g/mol x 105)	Reference
Adalimumab (Ada)	0.25–5 mg/kg	210		0.79	1.04	1.44	24
Atezolizumab (Ate)	1–20 mg/kg; 1200 mg	239		0.53	1.16	1.45	25
Bapineuzumab (Bap)	5 mg/kg	216		0.86	−0.02	1.49	26
Benralizumab (Ben)	0.3 mg/kg	261		0.71	0.99	1.46	27
Bevacizumab (Bev)	5 mg/kg	201		0.55	0.69	1.49	28
Canakinumab (Can)	1–3 mg/kg; 600 mg	161		0.55	0.32	1.45	29
Daclizumab (Dac)	200, 400 mg	286		0.84	0.02	1.43	30
Emibetuzumab (Emi)	700, 1400 mg	250		0.84	0.86	1.44	31
Enokizumab (Eno)	0.3–9 mg/kg	137		0.54	0.41	1.48	32
Farletuzumab (Far)	200, 400 mg/m^2	188		0.49	0.17	1.45	33
Figitumumab (Fig)	10, 20 mg/kg	164		0.77	1.39	1.46	34
Fulranumab (Ful)	3–30 mg	233		0.90	1.09	1.45	35
Gevokizumab (Gev)	0.01–3 mg/kg	175		0.63	0.4	1.45	36
Guselkumab (Gus)	0.03–10 mg/kg	338		0.87	1.24	1.44	37
Mepolizumab (Mep)	250 mg	157		0.60	−0.03	1.49	38
Olokizumab (Olo)	3 mg/kg; 10 mg/kg	116		0.21	0.14	1.5	39
Ozanezumab (Oza)	0.1–15 mg/kg	221		0.64	0.69	1.45	40
Pertuzumab (Per)	2–15 mg/kg	258		0.59	0.37	1.48	41
Tildrakizumab (Til)	0.1–10 mg/kg	154		0.55	0.23	1.47	42
Tralokinumab (Tral)	150 mg	168		0.68	0.63	1.44	43
Trastuzumab (Tras)	6 mg/kg	225		0.66	0.46	1.48	44
Ustekinumab (Ust)	0.1–5 mg/kg	148		0.68	0.13	1.49	45

Table 2.

Estimated antibody-specific parameters

Abbreviation	$K_d^{6.0}$ (nM) (RSE%)	$S_{pino}$ (RSE%)	$S_{diff-conv}$ (RSE%)
Ada	663 (49)	1.17 (3.5)	1.08 (4.5)
Ate	623 (52)	0.93 (7.5)	0.81 (6.4)
Bap	1148 (28)	0.99 (2.2)	1.16 (8.0)
Ben	680 (48)	1.31 (4.2)	0.98 (7.1)
Bev	795 (41)	1.14 (2.2)	0.68 (8.7)
Can	963 (34)	0.90 (1.1)	0.88 (4.1)
Dac	1125 (29)	1.26 (1.4)	1.06 (5.7)
Emi	727 (45)	1.09 (17.9)	0.87 (9.9)
Eno	919 (35)	0.86 (2.4)	0.76 (4.0)
Far	1041 (31)	1.14 (8.1)	0.48 (14)
Fig	552 (59)	0.94 (1.9)	0.92 (6.6)
Ful	646 (50)	1.15 (2.4)	1.24 (4.5)
Gev	924 (35)	0.84 (2.6)	0.69 (3.7)
Gus	597 (54)	1.45 (1.2)	1.13 (2.9)
Mep	1154 (28)	0.95 (2.5)	0.48 (8.5)
Olo	1057 (31)	0.61 (2.4)	0.88 (4.1)
Oza	795 (41)	1.10 (1.3)	0.93 (5.0)
Per	938 (35)	1.09 (7.7)	0.90 (6.8)
Til	1009 (32)	0.81 (1.0)	0.75 (4.0)
Tral	820 (40)	0.94 (3.6)	0.55 (9.4)
Tras	895 (36)	1.02 (11.2)	0.61 (12)
Ust	1062 (31)	0.84 (1.6)	0.51 (5.3)

$K_d^{6.0}$: FcRn-mAb dissociation rate constant at pH = 6.0

$S_{pino}$^: scale factors for antibody-specific endothelial pinocytosis uptake rate

$S_{diff-conv}$: scale factors for antibody-specific paracellular transport rate

Antibody-specific scale factors for pinocytosis ($S_{pino}$) and diffusion-convection ($S_{diff-conv}$)

Using the plasma concentration-time data for each of the 22 mAbs resulted in estimates of the two antibody-specific model parameters $S_{pino}$ and $S_{diff-conv}$ listed in Table 2 for each antibody. The estimates of $S_{pino}$ ranged from 0.614 to 1.454 and those of $S_{diff-conv}$ between 0.475 to 1.24. The two parameters were estimated with good precision (RSE% < 20%) as indicated in Table 2. Figure 3 provides plots of the fitted concentration-time profiles, demonstrating good agreement between observed plasma concentrations and model predictions (R > 0.94 for all antibodies), indicating that the PBPK model can describe the plasma concentration time courses observed following the administration of these antibodies.

Figure 3.

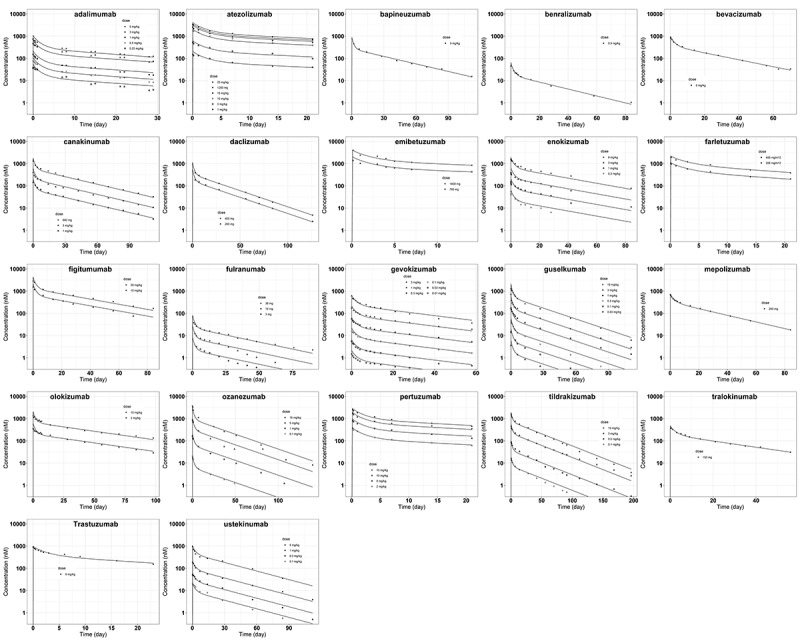
Model predicted and observed antibody plasma concentration versus time profiles following intravenous delivery. The solid lines are model predictions. The symbols represent digitized data at different dose levels from literature (Table 1).

ALT Text: 22 scatter plots arranged into five rows, with different antibody names on the top of each plot. Within each plot there are dots of different shapes labeled as different doses. A solid line is plotted corresponding to dots of each dose, with good agreement. The x axis has a title of “Time (day)” and y axis is in log scale with a title of “Concentration (nM).”

Biophysical determinants of antibody-specific model parameters

The results of the linear regression analyses relating the estimated values of $S_{pino}$ for each antibody to each of the in vitro physiochemical properties individually found that a significant relationship was obtained with only heparin relative retention time (Hep_RT) as shown in Figure 4a (R = 0.64, p = .0013). The p values for the other in vitro assays evaluated individually ranged from 0.093 to 0.93 (see Supplemental Material). Similarly, $S_{diff-conv}$ was found to be significantly associated only with heparin relative retention time (Figure 4b, r = 0.52, p = .012), but not with any of the other physiochemical properties (individual p ranges from 0.13 to 0.82, see Supplemental Material). Multiple regression relations were explored via stepwise regression, but no significant associations were identified with the addition of other physiochemical properties. For example, when “Slope for Accelerated Stability” was added to Hep_RT to describe the values of $S_{pino}$ obtained from the 22 antibodies, its regression coefficient was 0.99, with a standard error of 0.59 (p = .11). The addition of “HEK titer” in the regression to predict $S_{diff-conv}$ yielded its regression coefficient as −0.00067, with standard error of 0.00074 (p = .37).

Figure 4.

Association between the two estimated model parameters and antibody heparin relative retention time (Hep_RT). Estimated regression lines: (a) $S_{pino}=0.75\cdot Hep\mathrm{\_}RT+0.53$ (R = 0.64, p = .0013, residual standard error = 0.148). (b) $S_{diff-conv}=0.73\cdot Hep\mathrm{\_}RT+0.35$ (R = 0.52, p = .012, residual standard error = 0.197). Shaded areas represent 95% confidence region for the line of means.

ALT Text: Two scatter plots arranged into two columns. In each plot there are 22 dots, each labeled with an antibody abbreviation. An uptrend straight regression line is plotted with gray areas around it. The dots are located around the lines with some deviations in both plots. The x axis is labeled with Hep_RT with a range from 0.0 to 1.0. In (a) The y axis is labeled with Spino ranging from 0.0 to 1.5. (b) The y axis is labeled with Sdiff-conv ranging from 0.0 to 1.5.

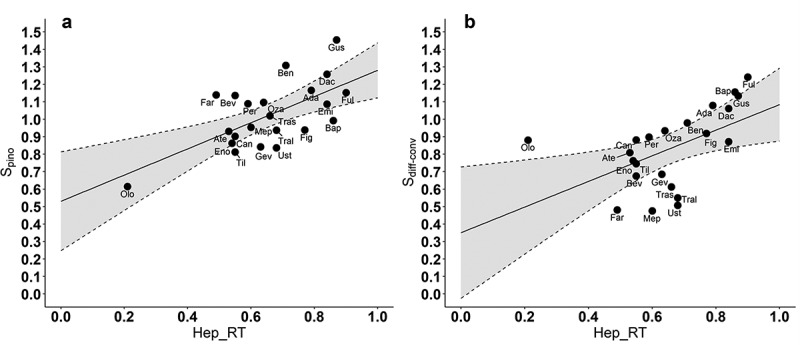
We note that Hep_RT also shows a significant but weaker positive association with several assays for nonspecific interaction (e.g., PSR, R = 0.47, p < 10⁻³; enzyme-linked immunosorbent assay (ELISA), R = 0.40, p < 10⁻³), as well as for self-association (AC-SINS, R = 0.37, p < 10⁻³), based on the values reported,¹⁰ indicating the concurrence between these in vitro assays.

Model-based prediction of antibody PK

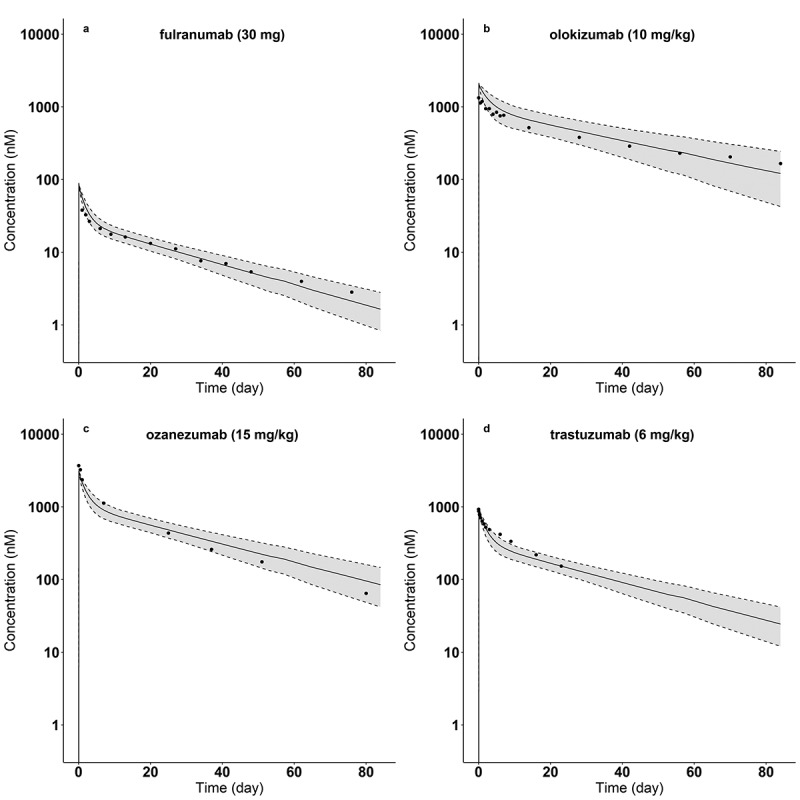
Using the identified regression relations between $S_{pino}$, $S_{diff-conv}$ and Hep_RT (Figure 4), each antibody’s Hep_RT, hFcRn_RT and molecular weight (MW) were used with the PBPK model to perform a population simulation of the plasma concentration for each of the 22 antibodies. Figure 5 shows the predictions for four antibodies with the smallest (Olokizumab) and largest (Fulranumab) Hep_RT values, as well as two with values of Hep_RT near the near the mean heparin relative retention times (Ozanezumab, Trastuzumab) of the 22 antibodies studied. The mean (±standard deviation) of $S_{pino}$ of these four antibodies (Fulranumab, Olokizumab, Ozanezumab, and Trastuzumab) are 1.21 (±0.16), 0.69 (±0.18), 1.01 (±0.15), and 1.03 (±0.15), respectively. In addition, the corresponding mean (±standard deviation) of $S_{diff-conv}$ of these four antibodies are 1.01 (±0.20), 0.50 (±0.20), 0.82 (±0.20), and 0.84 (±0.20), respectively. As indicated in the figure, the 5^th–95^th percentile ranges of the model-based PK predictions include the observed plasma concentrations of these antibodies.

Figure 5.

Model-predicted and observed plasma concentrations of four antibodies: (a) fulranumab (hep_RT = 0.90), (b) olokizumab (hep_RT = 0.21), (c) ozanezumab (hep_RT = 0.64), and (d) trastuzumab (hep_RT = 0.66) for the indicated doses. Dots are mean concentrations from literature (Table 1). Solid lines indicate the predicted median concentration from the population simulations. Dash lines display the 5th and 95th percentiles of the predicted plasma concentrations from the population simulations.

ALT Text: Four plots arranged into two rows and two columns, with about ten dots in each plot. A decaying curve is plotted in each panel surrounded with gray areas, showing a fast drop followed by a slower decaying phase. The grays areas include dots in each panel. The x axis title is “Time (day)” from 0 to 80. The y axis is in log scale ranging from 0 to 10000 with a title of “Concentration (nM).” Each panel has different titles on the top with: (a) fulranumab (30 mg); (b) olokizumab (10 mg/kg); (c) ozanezumab (15 mg/kg); (d) trastuzumab (6 mg/kg).

Internal validation of model parameter-assay correlation

The results of an internal validation using the heparin relative retention times of randomly selected subsets of 18 mAbs to construct new $S_{pino}$ and $S_{diff-conv}$ regression models are as follows. Of the 100 regression relations, 94 resulted in a significant association (p < .05) between $S_{pino}$ and Hep_RT, while 74 were found to yield a significant association between $S_{diff-conv}$ and Hep_RT. These results suggests that our finding of a significant association between $S_{pino}$ and Hep_RT and between $S_{diff-conv}$ and Hep_RT is likely independent of the specific antibodies within the subset of the 22 antibodies tested.

Discussion

Previous studies have established that stronger nonspecific antibody binding leads to increased pinocytotic uptake, resulting in greater lysosomal degradation of mAbs.^3,7 Consistent with these findings, we found a significant positive correlation (R = 0.64, p = .0013) between the model parameter representing antibody-specific vascular to endothelial clearance ($S_{pino}$) and heparin relative retention time (Hep_RT), an in vitro measure of the nonspecific binding. We also found that antibody-specific differences in paracellular transport due to convection and diffusion ($S_{diff-conv}$) could be partially explained by Hep_RT (R = 0.52, p = .012). Paracellular convection is determined by the vascular to tissue hydrostatic gradient and the sieving effect, with the latter dependent on pore physiology, as well as the size, shape, and charge shape of antibodies.¹⁶ This observed positive correlation, could be a consequence of the longer heparin retention time that results from the stronger binding of the more positively charged antibodies to the negative charges of the heparin column.

The results from 12 physiochemical property assays for nonspecific interaction, thermal stability, hydrophobicity and antibody self-association reported by Jain et al.¹⁰ for each of the 22 antibodies examined in our study were considered (see Supplemental Material), both individually and in combination, for their ability to predict the model-based estimates of $S_{pino}$ and $S_{diff-conv}$. These included assays related to cross-interaction (e.g. PSR, ELISA, BVP, CIC) and self-association (AC-SINS), which were reported¹⁰ to be predictive of clearance. None of these 12 assays, however, was found to be a significant predictor of either $S_{pino}$ or $S_{diff-conv}$ for the 22 antibodies we investigated. For example, although PSR had the strongest association with $S_{pino}$, among the 12 assays, it was not significant (R = 0.37, p = .095). Similarly, AC-SINS was not found to be associated with $S_{pino}$ (R = 0.101, p = .63) or with $S_{diff-conv}$ (R = 0.19, p = .40). Interestingly, several of these assays were positively correlated with Hep_RT (e.g., PSR, R = 0.47, p < 10⁻³; ELISA, R = 0.40, p < 10⁻³; AC-SINS, R = 0.37, p < 10⁻³), but unlike Hep_RT their association with the antibody-specific model parameters did not rise to the level of significance. ELISA and other assays measure direct interactions for heterogeneous surrogates, focusing on various non-covalent interactions with different degrees of involvement of charge and hydrophobicity interactions that do not appear to have the sensitivity to adequately describe cellular events. On the other hand, heparin chromatography isolates heparin as a homogenous surrogate for relevant cell surface-based component interaction, thus facilitating increased sensitivity to be connected to parameters such as $S_{pino}$, which are also focused on cellular events. In another study, Avery et al. used DNA- and insulin-binding assays to characterize nonspecific interactions and also considered FcRn interaction using SPR and column chromatography assays.⁵ However, since only four of the antibodies in our study were investigated by Avery et al., a predictive statistical analysis is not warranted.

Structure-based in silico metrics have previously been considered as predictors of PK during antibody screening. Accordingly, we also assessed 23 in silico metrics from the Molecular Operating Environment (MOE)¹⁷ and five from the Therapeutic Antibody Profiling (TAP) platform¹⁸ for their potential association with the estimates of the model-based pinocytosis and diffusion-convection parameters for the 22 antibodies in our study (see Supplemental Material). Only one in silico measure related to hydrophobicity was found to be a significant predictor of $S_{pino}$ (R = 0.74, p = .0053) for 12 of the antibodies in common between the two sets. In a further analysis of those antibodies reported with known Hep_RT values and in silico measures from MOE and TAP platforms (n = 59), we found that Hep_RT was positively associated with several charge-related and hydrophobicity-related metrics. In particular, Hep_RT was found to be associated with the charge-related metric pI_3D in combination with the hydrophobicity descriptor asa_hph (R = 0.82, p < 10⁻¹³). This suggests that Hep_RT may represent the combined effects of electrostatic and hydrophobic factors, as fundamental determinants of antibody-specificity.¹⁹ We note that a comprehensive investigation of various in vitro and in silico properties of 64 antibodies identified charge and hydrophobicity as important predictors of nonspecific antibody clearance based on statistical and machine learning analyses.¹¹

Physiologically based pharmacokinetics models have been used to predict disposition of mAbs in humans based on antibody physiochemical properties assessed via in vitro assays and in silico methods. In a study of 12 antibodies, an in vitro self-association score (AC-SINS) was used to predict antibody-specific binding affinity with cell membrane within a PBPK model.¹⁴ In our modeling analysis, however, we did not find a significant relationship between the values of AC-SINS reported by Jain et al.¹⁰ and the estimated pinocytosis scaling parameter ($S_{pino}$) values for the 22 antibodies considered (R = 0.109, p = .63). Since self-association interactions are mechanistically more directly related to the solubility, viscosity and opalescence of the antibody formulation than to nonspecific antibody interactions that occur in vivo, it may be more difficult to identify any potential associations between AC-SINS and PBPK model-based parameters characterizing nonspecific interactions.²⁰ Further PBPK studies using additional antibodies would be needed to explore AC-SINS as a model-based predictor of antibody PK in humans.

In our previous PBPK modeling work, a sequence-based in silico charge metric (patches of positive charge in the complementarity-determining region, PPC) was found to be positively associated with $S_{pino}$ in 16 mAbs (R = 0.73, p = .0013).¹⁵ The positive relation between $S_{pino}$ and the PPC metric is theoretically reasonable¹⁴ and consistent with other in vitro and in vivo studies.^21,22 However, we found no significant relationship between $S_{pino}$ and the PPC metric in the larger set of 22 mAbs evaluated in this work (R = 0.24, p > .2). Pooling the distinct antibodies from our current and previous work (n = 28), a borderline but statistically significant association was found between $S_{pino}$ and PPC (R = 0.44, p = .02). Taken together, these results suggest local charge in the complementarity-determining region may inform the model-based estimate of antibody pinocytotic transport, but other antibody properties not incorporated in the modeling analysis may make it difficult to detect any contribution of this charged-based property.²²

Although we found statistically significant associations between both the PBPK model parameters representing antibody nonspecific binding and that representing paracellular transport with an in vitro heparin chromatography assay, the resulting regression relationships involved notable variability as indicated by the regression line 95% confidence regions in Figure 4. Given that the modeling analysis was based on mean data reported for each of the 22 antibodies considered, we could not include subject specific factors that could account for some of the unexplained variability reflected in the regression relationships. Moreover, differences in subject disease states and FcRn expression, as well as antibody-specific differences in physical sizes and glycosylation patterns were not investigated as additional explanatory predictors

of $S_{pino}$ and $S_{diff-conv}$.²³ It should be noted that the antibodies selected have been approved or were evaluated in Phase 2 or Phase 3 clinical trials, and have thus have been selected for their desirable PK properties. This de facto selection bias yields a set of antibodies with smaller differences in physiochemical properties, as measured by the in vitro assays, making it more challenging to quantify any relationships between model-based antibody transport processes and in vitro readouts. An additional limitation of the work is the relatively small number of antibodies considered, and further investigation that includes more antibodies with available plasma and tissue concentration time course data is required to assess the suitability of the proposed model-based approach for predicting antibody plasma and tissue PK in humans. In addition, the Hep_RT values of the 22 mAbs were adopted from Kraft et al.,³ in which the variable domains of different antibodies where grafted onto a common IgG1 Fc. Although six of the antibodies included in this study where IgG2 and IgG4 isotypes, the correlation between $S_{pino}$ and Hep_RT and $S_{diff-conv}$ and Hep_RT remained significant even after excluding these six non-IgG1 mAbs (results not shown). Finally, the model represents antibody-specific differences in transport as linear scale factors, which may not represent these antibody-dependent processes with sufficient fidelity to reflect the full extent of any underlying differences in antibody disposition.

In contrast to other studies that have used empirically derived expressions to relate in vitro measures of antibody physiochemical properties directly to antibody clearance, we propose a PBPK model-based approach for predicting mAb PK that incorporates the mechanisms that govern antibody transport and processing, which are in turn informed by in vitro measures of antibody physiochemical properties. The underlying premise of this work is that the fundamental mechanisms responsible for antibody transport (paracellular exchange, nonspecific binding, FcRn interaction, transcytosis) are more directly relatable to the in vitro assays designed to characterize these interactions and processes than is overall systemic clearance. Given its physiological basis, the proposed PBPK model can be expanded to include more descriptive representations of each of the antibody processing subsystems such as TMDD in extracellular spaces, as well as other antibody-specific information.

Materials and methods

In vitro assay data

Results from a previously reported study by Kraft et al.³ were used to characterize antibody nonspecific cell-surface interaction and FcRn interaction. As described,³ the variable regions of 131 antibodies approved or in clinical development were grafted onto the identical IgG1 Fc domain and their relative retention times in heparin (Hep_RT) and on human FcRn (hFcRn_RT) columns were measured. In addition, results from 12 physiochemical property assays designed to assess nonspecific interaction, thermal stability, hydrophobicity, and antibody self-association were obtained from the report of Jain et al.¹⁰ The results from these 14 assays from Kraft et al.³ and Jain et al.¹⁰ for the 22 antibodies used in this work (see below) are provided in the Supplemental Material.

To determine antibody-FcRn dissociation constant at pH 6.0 ($K_d^{6.0}$) of the evaluated antibodies, measurements of antibody FcRn affinities (SPR assay) and human FcRn column retention time from 37 antibodies⁵ were used to construct an empirical relationship between $K_d^{6.0}$ and hFcRn_RT (data in Supplemental Material), from which the antibody-FcRn dissociation constants at pH 6.0 for the 22 antibodies in this study were calculated.

Clinical study data

For each of the 131 antibodies reported in Kraft et al.³ and the 137 antibodies in Jain et al.,¹⁰ a literature and database search was conducted to identify those mAbs with available plasma concentration-time profiles following intravenous (IV) administration. ELISAs were used in these previous studies to measure the concentration of antibodies. We digitized the reported mean plasma concentration-time course plots for those mAbs with linear kinetics (no obvious TMDD) and with frequent sampling. The 22 antibodies identified, of which 14 were approved, are listed in Table 1 along with their dosing, reported clearance, Hep_RT, hFcRn_RT and molecular weight. The PK data from 16 of these mAbs included two or more dose levels. Additional information (IgG subtype, mechanism of action, global status, and indications) about these 22 mAbs are provided in the Supplemental Material.

Model structure

The PBPK model used in this study (Figure 1) is based on that reported in our previous work,¹⁵ which itself extended and modified a mAb PBPK model reported by Glassman and Balthasar.¹⁴ Figure 1a depicts the whole-body circulatory system structure of the model, with antibody (and IgG) distribution to and from the indicated organs via convection shown by black lines and returned from the organs to the central venous plasma pool through convection via the lymphatic flow (gray lines).

Figure 1b shows the model used to represent administered mAb and endogenous IgG disposition in each organ/tissue, and includes vascular, endothelial, interstitial, and cellular spaces, with transcapillary exchange via paracellular transport and pinocytosis. For generality, and to allow for future extension, a two-pore model was used to describe the paracellular transport of endogenous IgG and administrated mAbs as detailed in our previous report¹⁵ (following that presented by Li and Shah⁴⁶). The following mass balance equations describe the organ vascular space concentrations of endogenous IgG ($CIg{G}_{vasc}^{Organ}$) and mAb ($CmA{b}_{vasc}^{Organ}$):

$$\begin{array}{rl}& V_{vasc}^{Organ}\cdot \frac{dCIg{G}_{vasc}^{Organ}}{dt}=Q^{Organ}\cdot CIg{G}_{vasc}^{Arterial}-(Q^{Organ}-L^{Organ})\cdot CIg{G}_{vasc}^{Organ}\\ & -C{L}_{pino}^{Organ}\cdot CIg{G}_{vasc}^{Organ}+fIg{G}_{recyc}\cdot C{L}_{pino}^{Organ}\cdot CIgF{c}_{recyc}^{Organ}\\ & -P{S}_L^{Organ}\cdot (CIg{G}_{vasc}^{Organ}-CIg{G}_{inter}^{Organ})\cdot \frac{P{e}_L}{e^{P{e}_L}-1}-P{S}_S^{Organ}\cdot (CIg{G}_{vasc}^{Organ}-CIg{G}_{inter}^{Organ})\cdot \frac{P{e}_S}{e^{P{e}_S}-1}\\ & -J_L^{Organ}\cdot (1-{\sigma }_L)\cdot CIg{G}_{vasc}^{Organ}-J_S^{Organ}\cdot (1-{\sigma }_S)\cdot CIg{G}_{vasc}^{Organ}\end{array}$$ (1)

$$\begin{array}{rl}& V_{vasc}^{Organ}\cdot \frac{dCmA{b}_{vasc}^{Organ}}{dt}=Q^{Organ}\cdot CmA{b}_{vasc}^{Arterial}-(Q^{Organ}-L^{Organ})\cdot CmA{b}_{vasc}^{Organ}\\ & -S_{pino}\cdot C{L}_{pino}^{Organ}\cdot CmA{b}_{vasc}^{Organ}+S_{pino}\cdot fIg{G}_{recyc}\cdot C{L}_{pino}^{Organ}\cdot CmAbF{c}_{recyc}^{Organ}\\ & -S_{diff-conv}\cdot P{S}_L^{Organ}\cdot (CmA{b}_{vasc}^{Organ}-CmA{b}_{inter}^{Organ})\cdot \frac{P{e}_L}{e^{P{e}_L}-1}-S_{diff-conv}\cdot P{S}_S^{Organ}\cdot (CmA{b}_{vasc}^{Organ}-CmA{b}_{inter}^{Organ})\cdot \frac{P{e}_S}{e^{P{e}_S}-1}\\ & -S_{diff-conv}\cdot J_L^{Organ}\cdot (1-{\sigma }_L)\cdot CmA{b}_{vasc}^{Organ}-S_{diff-conv}\cdot J_S^{Organ}\cdot (1-{\sigma }_S)\cdot CmA{b}_{vasc}^{Organ}\end{array}$$ (2)

The symbols used to represent concentration variables and parameters involved in modeling the transport processes are provided in the Supplemental Material. The first line of Eq. (1) represents IgG transport via blood perfusion, the second line accounts for IgG exchange via pinocytosis and exocytosis (discussed below), while the last two lines represent IgG’s paracellular transport via diffusion and convection based on the two-pore model. A similar equation representing mAb exchange (Eq. (2)) includes scaling factors to represent antibody-specific differences in transport relative to IgG, including a scaling term for pinocytosis ($S_{pino}$) and a single term for diffusion and convection ($S_{diff-conv}$), following the approach reported by Glassman and Balthasar¹⁴ and used in our previous work. These two antibody-specific scaling factors were estimated as described below.

The corresponding mass balance for the concentrations of mAb and endogenous IgG in the interstitial space ($CmA{b}_{inter}^{Organ}$ and $CIg{G}_{inter}^{Organ}$) yields:

$$\begin{array}{rl}& V_{inter}^{Organ}\frac{dCIg{G}_{inter}^{Organ}}{dt}=(1-fIg{G}_{recyc})\cdot C{L}_{pino}^{Organ}\cdot CIgF{c}_{recyc}^{Organ}-C{L}_{pino}^{Organ}\cdot CIg{G}_{inter}^{Organ}-L^{Organ}\cdot CIg{G}_{inter}^{Organ}\\ & +P{S}_L^{Organ}\cdot (CIg{G}_{vasc}^{Organ}-CIg{G}_{inter}^{Organ})\cdot \frac{P{e}_L}{e^{P{e}_L}-1}+P{S}_S^{Organ}\cdot (CIg{G}_{vasc}^{Organ}-CIg{G}_{inter}^{Organ})\cdot \frac{P{e}_S}{e^{P{e}_S}-1}\\ & +J_L^{Organ}\cdot (1-{\sigma }_L)\cdot CIg{G}_{vasc}^{Organ}+J_S^{Organ}\cdot (1-{\sigma }_S)\cdot CIg{G}_{vasc}^{Organ}\end{array}$$ (3)

$$\begin{array}{rl}& V_{inter}^{Organ}\frac{dCmA{b}_{inter}^{Organ}}{dt}=S_{pino}\cdot (1-fIg{G}_{recyc})\cdot C{L}_{pino}^{Organ}\cdot CmAbF{c}_{recyc}^{Organ}-S_{pino}\cdot C{L}_{pino}^{Organ}\cdot CmA{b}_{inter}^{Organ}-L^{Organ}\cdot CmA{b}_{inter}^{Organ}\\ & +S_{diff-conv}\cdot P{S}_L^{Organ}\cdot (CmA{b}_{vasc}^{Organ}-CmA{b}_{inter}^{Organ})\cdot \frac{P{e}_L}{e^{P{e}_L}-1}+S_{diff-conv}\cdot P{S}_S^{Organ}\cdot (CmA{b}_{vasc}^{Organ}-CmA{b}_{inter}^{Organ})\cdot \frac{P{e}_S}{e^{P{e}_S}-1}\\ & +S_{diff-conv}\cdot J_L^{Organ}\cdot (1-{\sigma }_L)\cdot CmA{b}_{vasc}^{Organ}+S_{diff-conv}\cdot J_S^{Organ}\cdot (1-{\sigma }_S)\cdot CmA{b}_{vasc}^{Organ}\end{array}$$ (4)

See Supplemental Material for definition of all symbols.

The model used for endosomal transit and processing (Figure 1b and 1c) is an updated version of that used in our previous work and is based on further insight into the physiological processes governing IgG-FcRn interaction as reported by Ward and Ober.⁴⁷ Three endosomal compartments were used to represent separate stages of IgG endosomal transit (Figure 1b): early endosome (pH 7.4a), late endosome (pH 6.0) and cell membrane (pH 7.4b). Within each endosomal compartment, endogenous IgG or exogenous mAbs can interact with FcRn in a pH-dependent manner,¹⁵ via mass action association and dissociation rate constants, $k_{on}^{pHx}$ and $k_{off}^{pHx}$, as depicted in Figure 1c. Free IgG in the late endosome (pH 6.0) will be sorted to the lysosome for degradation (represented by “CL” term in Figure 1b), while FcRn-bound IgG is designated to the cell membrane compartment (pH 7.4b) for recycling or exocytosis. In the cell membrane compartment, a fraction of free IgG ($fIg{G}_{recyc}$) is recycled to the vascular space, while that bound to FcRn (FcRn-IgG complex) remains in the endosome (early endosome compartment). Free FcRn is assumed to move from the early endosome to subsequent compartments, with internalization from the last cell membrane compartment (pH 7.4b) to the first early endosome compartment (pH 7.4a). Based on these assumptions, the following equations describe the concentrations of the species in the early endosome compartment ($CIg{G}_{7.4a}^{Organ}$, $CIgF{c}_{7.4a}^{Organ}$, $CmA{b}_{7.4a}^{Organ}$, $CmAbF{c}_{7.4a}^{Organ}$ and $CFcR{n}_{pH7.4a}^{Organ}$):

$$\begin{array}{rl}& \frac{dCIg{G}_{7.4a}^{Organ}}{dt}=(C{L}_{pino}^{Organ}\cdot CIg{G}_{vasc}^{Organ}+C{L}_{pino}^{Organ}\cdot CIg{G}_{inter}^{Organ})/V_{endo,sub}^{Organ}\\ & +k_{off}^{7.4}\cdot CIgF{c}_{7.4a}^{Organ}-k_{on}^{7.4}\cdot CIg{G}_{7.4a}^{Organ}\cdot CFcR{n}_{7.4a}^{Organ}-\frac{1}{\tau }\cdot CIg{G}_{7.4a}^{Organ}\end{array}$$ (5)

$$\frac{dCIgF{c}_{7.4a}^{Organ}}{dt}=k_{on}^{7.4}\cdot CIg{G}_{7.4a}^{Organ}\cdot CFcR{n}_{7.4a}^{Organ}-k_{off}^{7.4}\cdot CIgF{c}_{7.4a}^{Organ}+\frac{1}{\tau }\cdot (CIgF{c}_{7.4b}^{Organ}-CIgF{c}_{7.4a}^{Organ})$$ (6)

$$\begin{array}{rl}& \frac{dCmA{b}_{7.4a}^{Organ}}{dt}=(S_{pino}\cdot C{L}_{pino}^{Organ}\cdot CmA{b}_{vasc}^{Organ}\\ & +S_{pino}\cdot C{L}_{pino}^{Organ}\cdot CmA{b}_{inter}^{Organ})/V_{endo,sub}^{Organ}\\ & +k_{off}^{7.4}\cdot CmAbF{c}_{7.4a}^{Organ}-k_{on}^{7.4}\cdot CmA{b}_{7.4a}^{Organ}\\ & \cdot CFcR{n}_{7.4a}^{Organ}-\frac{1}{\tau }\cdot CmA{b}_{7.4a}^{Organ}\end{array}$$ (7)

$$\frac{dCmAbF{c}_{7.4a}^{Organ}}{dt}=k_{on}^{7.4}\cdot CmA{b}_{7.4a}^{Organ}\cdot CFcR{n}_{7.4a}^{Organ}-k_{off}^{7.4}\cdot CmAbF{c}_{7.4a}^{Organ}+\frac{1}{\tau }\cdot (CmAbF{c}_{7.4b}^{Organ}-CmAbF{c}_{7.4a}^{Organ})$$ (8)

$$\begin{array}{rl}& \frac{dCFcR{n}_{pH7.4a}^{Organ}}{dt}=k_{off}^{7.4}\cdot CIgF{c}_{7.4a}^{Organ}-k_{on}^{7.4}\cdot CIg{G}_{7.4a}^{Organ}\\ & \cdot CFcR{n}_{7.4a}^{Organ}1mu1mu+k_{off}^{7.4}\cdot CmAbF{c}_{7.4a}^{Organ}\\ & -k_{on}^{7.4}\cdot CmA{b}_{7.4a}^{Organ}\cdot CFcR{n}_{7.4a}^{Organ}1mu\\ & +\frac{1}{\tau }\cdot (CFcR{n}_{pH7.4b}^{Organ}-CFcR{n}_{pH7.4a}^{Organ})\end{array}$$ (9)

The following equations describe the concentrations of the different species in the late endosome compartment (pH 6.0):

$$\frac{dCIg{G}_{6.0}^{Organ}}{dt}=k_{off}^{6.0}\cdot CIgF{c}_{6.0}^{Organ}-k_{on}^{6.0}\cdot CIg{G}_{6.0}^{Organ}\cdot CFcR{n}_{6.0}^{Organ}+\frac{1}{\tau }\cdot (CIg{G}_{7.4a}^{Organ}-CIg{G}_{6.0}^{Organ})$$ (10)

$$\frac{dCIgF{c}_{6.0}^{Organ}}{dt}=k_{on}^{6.0}\cdot CIg{G}_{6.0}^{Organ}\cdot CFcR{n}_{6.0}^{Organ}-k_{off}^{6.0}\cdot CIgF{c}_{6.0}^{Organ}+\frac{1}{\tau }\cdot (CIgF{c}_{7.4a}^{Organ}-CIgF{c}_{6.0}^{Organ})$$ (11)

$$\frac{dCmA{b}_{6.0}^{Organ}}{dt}=k_{off}^{6.0}\cdot CmAbF{c}_{6.0}^{Organ}-k_{on}^{6.0}\cdot CmA{b}_{6.0}^{Organ}\cdot CFcR{n}_{6.0}^{Organ}+\frac{1}{\tau }\cdot (CmA{b}_{7.4a}^{Organ}-CmA{b}_{6.0}^{Organ})$$ (12)

$$\frac{dCmAbF{c}_{6.0}^{Organ}}{dt}=k_{on}^{6.0}\cdot CmA{b}_{6.0}^{Organ}\cdot CFcR{n}_{6.0}^{Organ}-k_{off}^{6.0}\cdot CmAbF{c}_{6.0}^{Orgna}+\frac{1}{\tau }\cdot (CmAbF{c}_{7.4a}^{Organ}-CmAbF{c}_{6.0}^{Organ})$$ (13)

$$\begin{array}{rl}& \frac{dCFcR{n}_{pH6.0}^{Organ}}{dt}=k_{off}^{6.0}\cdot CIgF{c}_{6.0}^{Organ}-k_{on}^{6.0}\cdot CIg{G}_{6.0}^{Organ}\cdot CFcR{n}_{6.0}^{Organ}\\ & +k_{off}^{6.0}\cdot CmAbF{c}_{6.0}^{Organ}-k_{on}^{6.0}\cdot CmA{b}_{6.0}^{Organ}\cdot CFcR{n}_{6.0}^{Organ}\\ & +\frac{1}{\tau }\cdot (CFcR{n}_{pH7.4a}^{Organ}-CFcR{n}_{pH6.0}^{Organ})\end{array}$$ (14)

Similarly, the following equations apply to the cell membrane compartment (pH 7.4b):

$$\frac{dCIg{G}_{7.4b}^{Organ}}{dt}=k_{off}^{7.4}\cdot CIgF{c}_{7.4b}^{Organ}-k_{on}^{7.4}\cdot CIg{G}_{7.4b}^{Organ}\cdot CFcR{n}_{7.4b}^{Organ}-C{L}_{pino}^{Organ}\cdot CIg{G}_{7.4a}^{Organ}/V_{endo,sub}^{Organ}$$ (15)

$$\begin{array}{c}\frac{dCIgF{c}_{7.4b}^{Organ}}{dt}=k_{on}^{7.4}\cdot CIg{G}_{7.4b}^{Organ}\cdot CFcR{n}_{7.4b}^{Organ}-k_{off}^{7.4}\cdot CIgF{c}_{7.4b}^{Organ}+\frac{1}{\tau }\cdot (CIgF{c}_{6.0}^{Organ}-CIgF{c}_{7.4b}^{Organ})\\ \hspace{0.17em}\end{array}$$ (16)

$$\frac{dCmA{b}_{7.4b}^{Organ}}{dt}=k_{off}^{7.4}\cdot CmAbF{c}_{7.4b}^{Organ}-k_{on}^{7.4}\cdot CmA{b}_{7.4b}^{Organ}\cdot CFcR{n}_{7.4b}^{Organ}-S_{pino}\cdot C{L}_{pino}^{Organ}\cdot CmA{b}_{7.4a}^{Organ}/V_{endo,sub}^{Organ}$$ (17)

$$\frac{dCmAbF{c}_{7.4b}^{Organ}}{dt}=k_{on}^{7.4}\cdot CmA{b}_{7.4b}^{Organ}\cdot CFcR{n}_{7.4b}^{Organ}-k_{off}^{7.4}\cdot CmAbF{c}_{7.4b}^{Organ}+\frac{1}{\tau }\cdot (CmAbF{c}_{6.0}^{Organ}-CmAbF{c}_{7.4b}^{Organ})$$ (18)

$$\begin{array}{rl}& \frac{dCFcR{n}_{pH7.4b}^{Organ}}{dt}=k_{off}^{7.4}\cdot CIgF{c}_{7.4b}^{Organ}-k_{on}^{7.4}\cdot CIg{G}_{7.4b}^{Organ}\cdot CFcR{n}_{7.4b}^{Organ}\\ & +k_{off}^{7.4}\cdot CmAbF{c}_{7.4b}^{Organ}-k_{on}^{7.4}\cdot CmA{b}_{7.4b}^{Organ}\cdot CFcR{n}_{7.4b}^{Organ}\\ & +\frac{1}{\tau }\cdot (CFcR{n}_{pH6.0}^{Organ}-CFcR{n}_{pH7.4b}^{Organ})\end{array}$$ (19)

The lymph node compartment in Figure 1, representing all the body’s lymph nodes, collects the lymph drainage from all organs. The post-nodal lymph flow travels to a lumped lymphatic vessel (representing lymphatic trunk, thoracic duct and, cisterna chyli) before entering the central venous pool. The mass balance equations for the amounts and concentrations of endogenous IgG and exogenous mAbs in the lymph node and lymphatic vessel compartments are the same as our previous report.¹⁵

As reported in our previous modeling work,¹⁵ a sampling site compartment was included to better reflect the skin and muscle contributions to antibody concentrations at the peripheral sampling site, where $CmA{b}^{Peri}=0.7\cdot CmA{b}_{vasc}^{Skin}+0.3\cdot CmA{b}_{vasc}^{Muscle}$.

The complete set of equations and definition of all symbols used in the model, including all organs, is provided in the Supplemental Material.

Model parameter values – fixed

Individual organ/tissue values

Values for organ/tissue volumes (vascular, interstitial, and cell) were obtained by combining information from various sources.^12,48–51 The organ weights (without blood) for a representative 70-kg human were taken from the report by Sowby,⁴⁸ while reported⁵⁰ tissue densities were used to calculate organ volumes. Previously reported interstitial volume fractions¹² were adopted to calculate the interstitial volumes ($V_{inter}^{Organ}$) and cell volumes ($V_{cell}^{Organ}$) given in Table 3. Total plasma volume of 2906 ml was obtained assuming a blood mass of 5.6 kg, blood density of 1.06 g/ml, and hematocrit of 45%. Based on reported blood distribution in the vascular system,⁴⁸ total plasma volume was partitioned as follows: lung capillaries (2%), systemic organ/tissue capillaries (5%), central venous space (67%, including pulmonary artery, heart right chamber, large veins and organ veins), and arterial space (26%, including pulmonary vein, heart left chamber, large arteries, and organ arteries). The individual organ vascular volumes ($V_{vasc}^{Organ}$) listed in Table 3 were calculated by partitioning the total capillary volume using the blood volume distribution in adults reported by Sowby et al.⁴⁸

Table 3.

Values of the fixed physiological parameters of individual organs/tissues

Organ/tissue	Interstitial volume (ml)a$V_{inter}^{Organ}$	Cell volume (ml) a$V_{cell}^{Organ}$	Vascular volume (ml) a$V_{vasc}^{Organ}$	Plasma flow (ml/day)$Q^{Organ}$
Lung	151.2	325.0	58.11	5.148 × 106
Heart	47.67	272.7	2.571	2.059 × 105
Liver	382.5	1365	25.71	3.346 x 105
Spleen	32.59	110.3	3.600	1.544 × 105
GI Tract	335.1	1636	18.00	7.722 × 105
Kidney	46.85	248.4	5.143	9.781 × 105
Muscle	3702	24155	36.00	8.752 × 105
Skin	1099	2105	7.714	2.574 x 105
Other	4677	21479	46.54	1.570 × 106
Organ/tissue	Lymph flow (ml/day)b$L^{Organ}$	FcRn (nM)c$CFcRn$	Vascular IgG clearance via pinocytosis (ml/day)d$C{L}_{pino}^{Organ}$	Endosomal volume (ml)d$V_{endo}^{Organ}$
Lung	4.015 × 103	33000	1.083	8.120 × 10−3
Heart	1.606 × 102	20200	0.7286	5.460 × 10−3
Liver	2.610 × 102	33000	3.975	2.980 × 10−2
Spleen	1.205 × 102	33000	0.3249	2.430 × 10−3
GI Tract	6.023 × 102	4180	4.484	3.360 × 10−2
Kidney	7.629 × 102	33000	0.6714	5.036 × 10−3
Muscle	6.826 × 102	33000	63.36	4.751 × 10−1
Skin	2.008 × 102	33000	7.286	5.460 × 10−2
Other	1.225 × 103	33000	59.49	4.461 × 10−1

^aBased on previous literature, as detailed in text.

^bFixed to be 0.078% of organ plasma flow, with a total prenodal lymph flow ~ 8000 ml/day as reported.⁵²

^cFixed based on the FcRn concentration measured by Li et al.⁵³ or from Glassman et al.¹³

^dCalculated, as detailed in text.

The total cardiac output of plasma ($Q^{Total}$) was assumed to be 5.148 × 10⁶ ml/day, consistent with the values reported in different sources.^48–50 Based on reported⁴⁸ organ blood flow distribution values, the organ-specific plasma flow rates ($Q^{Organ}$) listed in Table 3 were calculated. The lymph flow of each organ ($L^{Organ}$) given in Table 3 was assumed to be 0.078% of the corresponding plasma flow, to yield a total prenodal lymph flow of approximately 8 L/day.⁵²

Assuming central venous and arterial plasma occupy 67% and 26% of the total plasma volume yields central venous and arterial volumes of 1947 and 755 ml, respectively. The values for the lymphatic system parameters, including volumes and flows were determined as described in our previous work.¹⁵ The Supplemental Material provides a complete list of all model parameters and their values.

Endosomal processing and antibody-specific values

The basal values of FcRn concentration for each organ, listed in Table 3, were based on measurements reported in Li et al.⁵³ or taken from Glassman et al.,¹³ as detailed in our previous work.¹⁵ Parameter values related to the two-pore transport model depend on molecular weights, or organ lymph flow, or both. Values for these parameters were calculated as described previously¹⁵ and are listed in Table 4 along with other two-pore transport model parameter values.

Table 4.

Parameters values related to endosomal processing and two-pore transport of mAbs

Parameter (unit)	Value	Description	Ref.
All organs, tissues, and mAbs
$\tau$ (day)	0.00375	Transit time of IgG between endosomal sub-compartments	13
$fIg{G}_{recyc}$	0.7150	IgG recycling fraction of IgG-FcRn complex back to vascular space	54
$k_{on}^{6.0}$ (nM−1day−1)	antibody-specific	Association rate constant between IgG and FcRn at pH = 6.0	13
$k_{off}^{6.0}$ (day−1)	573.1	Dissociation rate constant between IgG and FcRn at pH = 6.0	13
$k_{on}^{7.4}$ (nM−1 day−1)	0.06336	Association rate constant between IgG and FcRn at pH = 7.4	13
$k_{off}^{7.4}$ (day−1)	573.1	Dissociation rate constant between IgG and FcRn at pH = 7.4	13
$r_S$ (nm)	4.440	Small pore radius	46
$r_L$ (nm)	22.85	Large pore radius	46
${\alpha }_S$	0.9580	Fractional hydraulic conductance of small pores	46
${\alpha }_L$	0.04200	Fractional hydraulic conductance of large pores	46
Adjusted for mAb MW (150 kDa IgG as an example); All organs and tissues
$a_e$ (nm)	4.810	Stokes Einstein radius	46
${\sigma }_S$	0.9980	Small pore vascular reflection coefficient	46
${\sigma }_L$	0.1800	Large pore vascular reflection coefficient	46
$A/A{0}_S$	9.280 x 10–7	Fractional accessible pore size of small pore	46
$A/A{0}_L$	0.3490	Fractional accessible pore size of large pore	46
$P{e}_S$	9.820	Peclet number of small pores	46
$P{e}_L$	4.480	Peclet number of large pores	46
Adjusted for mAb MW and individual organs and tissues (150 kDa IgG in liver as an example)
$P{S}_S^{Liver}$ (ml/day)	0.03229	Permeability-surface area product of small pores	46
$P{S}_L^{Liver}$ (ml/day)	20.10	Permeability-surface area product of large pores	46
$J_{iso}^{Liver}$ (ml/day)	99.18	Circular isogravimetric flow	46
$J_S^{Liver}$ (ml/day)	150.8	Lymph flow through small pores	46
$J_L^{Liver}$ (ml/day)	110.1	Lymph flow through large pores	46

The binding affinity to FcRn at pH6.0 was assumed to be antibody-specific and was determined for each of the 22 antibodies in our study based on a relation derived between mAb equilibrium dissociation constant $K_d^{6.0}$ and hFcRn_RT. Using the $K_d^{6.0}$ and hFcRn_RT data from 37 mAbs as noted above, an exponential (decaying) relation was determined using the ID application (weighted least squares estimation) in the ADAPT software (version 5).⁵⁵ The resulting relationship was used to determine $K_d^{6.0}$ for each of the antibodies used in this study given their known measured hFcRn_RT. Assuming a value of $k_{off}^{6.0}$ of 573.1 day-1 for all antibodies,¹³ $k_{on}^{6.0}$ of each antibody was estimated as $k_{on}^{6.0}=k_{off}^{6.0}/K_d^{6.0}$.

Model parameter values – estimated

As indicated above, model equations describing endogenous IgG and its interactions with FcRn were included into the model. Assuming an endogenous IgG production rate ($IgG0$) of 1.540 × 10⁴ nmol/day as reported in the ref.,⁵⁶ the whole-body pinocytosis rate ($C{L}_{pino}^{Total}$) was then determined to achieve a steady state concentration of 12.1 mg/ml.⁵⁶ Individual organ pinocytosis rates were assumed to be in proportion to their individual total organ volumes and calculated as follows: $C{L}_{pino}^{Organ}=\left(V_{Total}^{Organ}/V_{\hspace{0.17em}}^{Total}\right)\cdot C{L}_{pino}^{Total}$ (Table 3). The endosomal volume of each organ was then calculated using $V_{endo}^{Organ}=2\cdot C{L}_{pino}^{Organ}\cdot \tau$⁵⁷ (Table 3).

For each antibody listed in Table 1, the two antibody-specific scaling factors,$S_{pino}$ and $S_{diff-conv}$, were estimated using on the plasma concentration time data described above (Table 2). The ADAPT software (version 5) was used for parameter estimation, with maximum likelihood estimation (additive plus proportional error variance model).⁵⁵ Model simulation was first conducted to reach the steady state of endogenous IgG within the system before antibody IV administration. The naïve pool data (NPD) application was used for antibodies that were administer at more than one dose, while the ID application was used for antibodies given at one dose amount.

Biophysical determinants of antibody-specific model parameters

Potential associations between the 14 assay readouts and each of estimated values of the two model parameters, $S_{pino}$ and $S_{diff-conv}$, were explored via linear regression analysis using the “lm” (linear model) function in the “stats” package as part of R.⁵⁸ The selection of significant biophysical assays was based on p values from the regression analysis.

Model-based prediction of antibody PK

As an illustration of the application of the developed PBPK model prediction framework, we incorporated the identified relationships between the two antibody-specific scale factors ($S_{pino}$ and $S_{diff-conv}$) and the physiochemical properties identified as significant into the PBPK model, to conduct model-based predictions of plasma PK for each of the 22 antibodies. For each antibody, a population simulation was also conducted (n = 1000) using the SIM application in ADAPT,⁵⁵ assuming a log-normal distribution of $S_{pino}$ and $S_{diff-conv}$. Mean values for the parameter distributions were determined as the predicted values of $S_{pino}$ and $S_{diff-conv}$ obtained from the identified relationship between these parameters and those physiochemical properties identified as significant. The standard errors of the linear regression model predictions were used as the standard deviation of $S_{pino}$ and $S_{diff-conv}$ in the population simulations.

Internal validation of model parameter-assay associations

As an internal validation of the identified model parameter-assay associations, we randomly selected 18 mAbs (approximately 80% of the total) and used these antibodies to determine new relationships between the model parameter scaling factors and the physiochemical properties determined to be significant as described above. This random selection was repeated (n = 100) and the resulting and p values were summarized.

Funding Statement

This work was supported by grants from National Institutes of Health/National Institute of Biomedical Imaging and Bioengineering (NIH/NIBIB) P41-EB001978 and the Alfred E. Mann Institute at USC (DD’A).

Disclosure statement

No potential conflict of interest was reported by the author(s).

Supplementary material

Supplemental data for this article can be accessed on the publisher’s website