Summary
Recent works have shown that SNP heritability—which is dominated by low-effect common variants—may not be the most relevant quantity for localizing high-effect/critical disease genes. Here, we introduce methods to estimate the proportion of phenotypic variance explained by a given assignment of SNPs to a single gene (“gene-level heritability”). We partition gene-level heritability by minor allele frequency (MAF) to find genes whose gene-level heritability is explained exclusively by “low-frequency/rare” variants (0.5% ≤ MAF < 1%). Applying our method to ∼16K protein-coding genes and 25 quantitative traits in the UK Biobank (N = 290K “White British”), we find that, on average across traits, ∼2.5% of nonzero-heritability genes have a rare-variant component and only ∼0.8% (327 gene-trait pairs) have heritability exclusively from rare variants. Of these 327 gene-trait pairs, 114 (35%) were not detected by existing gene-level association testing methods. The additional genes we identify are significantly enriched for known disease genes, and we find several examples of genes that have been previously implicated in phenotypically related Mendelian disorders. Notably, the rare-variant component of gene-level heritability exhibits trends different from those of common-variant gene-level heritability. For example, while total gene-level heritability increases with gene length, the rare-variant component is significantly larger among shorter genes; the cumulative distributions of gene-level heritability also vary across traits and reveal differences in the relative contributions of rare/common variants to overall gene-level polygenicity. While nonzero gene-level heritability does not imply causality, if interpreted in the correct context, gene-level heritability can reveal useful insights into complex-trait genetic architecture.
Keywords: gene-level heritability, fine-mapping, linkage disequilibrium, GWAS, posterior distribution
Introduction
It is well established that complex-trait SNP-heritability is enriched in regulatory regions.1, 2, 3 However, for most complex traits, fundamental characteristics of genetic architecture—for example, the number of variants/genes with nonzero effects (polygenicity), the number of genes regulated by local versus distal variants, and the relative contributions of rare versus common variants to gene expression and phenotype—remain actively debated.4, 5, 6, 7, 8, 9, 10, 11, 12
Because SNP-heritability is overwhelmingly driven by common variants of low effect—individual rare variants with large per-allele effects contribute very little to population-level phenotypic variance13,14—whether the largest heritability enrichments localize the most clinically relevant regions and/or genes for a trait is unclear. For example, a recent study found that most complex-trait SNP heritability mediated via the cis-genetic component of expression is explained by genes that individually have low cis-heritability of expression.15 Another study found that extreme complex-trait polygenicity may be explained in large part by negative/stabilizing selection, which by purging high-effect alleles from the population, “flattens” the distribution of SNP heritability across common variants genome wide.16,17 If the most critical genes for a trait are not necessarily localized by enrichments of total heritability,15,16,18,19 genes identified via heritability enrichments or overlaps between genome-wide association studies (GWASs) and expression quantitative trait loci20,21 become even more challenging to interpret. Gene-based association tests that aggregate signal from multiple rare variants—for example, burden tests and sequence-based association tests (SKATs)—can increase power under different genetic-architecture scenarios.22, 23, 24, 25, 26, 27, 28, 29, 30 However, such methods are generally designed to test for only rare-variant association or the combined effects of common and rare variants and thus are not ideal for parsing the relative contributions of rare/common variants to the heritability of a single gene.
Here, we define and aim to estimate a quantity we call “gene-level heritability” ()—the proportion of phenotypic variance explained by the additive effects of a given set of variants assigned to a gene of interest. The key challenge in estimating gene-level heritability lies in the uncertainty about which variants are causal and what their causal effect sizes are, both of which increase as the strength of linkage disequilibrium (LD) in the region increases and as GWAS sample size decreases.31 Consider a toy example in which a variant in the gene of interest is in perfect LD with a second variant adjacent to the gene and the observed data are GWAS marginal association statistics and LD (Figure 1A). Without additional information, it is impossible to elucidate the underlying causal configuration. Even if the LD is 0.9 instead of 1, if this GWAS has 90% power to identify the region, correctly rejecting the null hypothesis for the non-causal variant would require a sample size ≥ 4× that of the original GWAS.31 Because each causal configuration can yield a different gene-level heritability (with or without minor allele frequency [MAF] partitioning), randomly selecting one possible configuration (e.g., using variable selection methods such as the Lasso32) can yield inaccurate/misleading estimates. Estimators for the SNP heritability of a single region would most likely be inflated if applied as-is to genes because of LD between variants in the region of interest and the adjacent regions.18,33, 34, 35 Methods for partitioning genome-wide SNP heritability are also ill-suited to our goals, as they make distributional assumptions on the causal effects, which (1) limit power to detect enrichment in small categories of variants (<1% of the genome) and/or (2) may not apply equally to rare and common variants.3,36, 37, 38, 39, 40, 41
Figure 1.
Overview
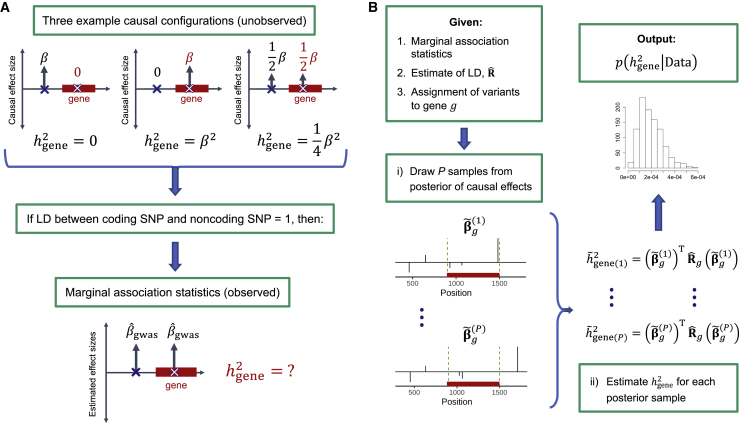
(A) Toy example with two variants, one of which is assigned to the gene of interest. The top row depicts three example causal configurations corresponding to three different gene-level heritabilities (0, , and ); for simplicity of presentation, we assume the genotypes are standardized to have variance 1 in the population (material and methods). All three causal configurations yield the same expected marginal association statistics.
(B) Given marginal association statistics, an estimate of LD, and an assignment of variants to the gene of interest, our method involves (1) sampling from the posterior of the causal effect sizes (assuming a sparse prior) to capture causal-effect uncertainty and then (2) estimating gene-level heritability for each posterior sample to approximate the posterior distribution of gene-level heritability.
We propose an approach to estimating that captures causal-effect uncertainty by sampling from the posterior distribution of the causal effect sizes within a probabilistic fine-mapping framework.42 We use the samples from the posterior of the causal effects to approximate the posterior distribution of (Figure 1B), from which one can compute various summary statistics of interest. For each gene, we report the posterior mean, denoted , and a -level credible interval, or -CI, defined as the central interval containing the true gene-level heritability with probability (material and methods). We confirm in simulations that accounting for uncertainty in the estimated causal effects significantly reduces the bias of and that both and -CIs are robust to causal effect sizes, gene length, allele frequencies of causal variants, and the strength of local LD. Under the (potentially strong) assumption that there is zero covariance between causal effects of different variants,43, 44, 45, 46 total gene-level heritability can be expressed as (material and methods), where the terms refer to the components of explained by rare (), low-frequency (, and common () variants, respectively. We apply the same approach to estimate the posterior distributions of , , and and observe similar trends and levels of accuracy. (While there are many definitions of “rare” in the literature, we use 0.5% ≤ MAF < 1% in the present work because we analyze imputed genotypes.)
Applying our approach to 15,770 protein-coding genes and 25 quantitative traits in the UK Biobank47 (N = 290K self-reported “White British,” MAF > 0.5%), we confirm that is indeed dominated by . On average across traits, among genes with 90%-CI > 0 (“nonzero-heritability genes”), 92% (SD 1%) have nonzero common-variant heritability, and 76% (SD 1%) have nonzero heritability exclusively from common variants (). In contrast, only 2.5% (SD 0.6%) of nonzero-heritability genes, averaged across traits, have nonzero rare-variant heritability, and a mere 0.8% (SD 0.4%) have nonzero heritability exclusively from rare variants (). The 2.5% of genes with 90%-CI > 0 is enriched for Mendelian-disorder genes and genes intolerant to loss of function (probability of loss-of-function [LoF] intolerance48,49 > 0.9), whereas the 0.8% of genes with (327 gene-trait pairs in total) is enriched only for LoF-intolerant genes. However, in both gene sets—genes with rare-variant heritability and genes with exclusively rare-variant heritability—the top genes (rank ordered by ) contain many examples of genes with known roles in phenotypically similar Mendelian disorders or other congenital growth and developmental disorders.
We emphasize that gene-level heritability is not an intrinsic property of a trait or gene but rather, like all “types” of heritability, a function of the environmental variance in the specific population being studied.50,51 Because allele frequencies are population specific, and causal alleles and their effect sizes can also differ across populations (e.g., due to population-specific environmental exposures),52,53 estimates of total and MAF-partitioned gene-level heritability—like all partitioned heritability estimates—are only meaningful when considered in the populations in which they were measured. The real-data results presented here are therefore specific to a population of “White British” individuals living in the UK. In addition, nonzero-heritability genes must not be interpreted as biologically causal without additional validation, as nonzero heritability indicates association not causality.51 Nevertheless, our results are consistent with the hypothesis that a sizable amount of complex-trait variation is driven by dysregulation of genes that—if completely disrupted—cause phenotypically similar monogenic disorders and/or systemic congenital and developmental disorders.54 Because genes can be disrupted/dysregulated by a combination of common and rare variants, should be considered alongside common-variant heritability enrichments if one is interested in identifying high-impact disease genes. While we restrict our analyses to genes (gene body ± 10-kb window), our method can be applied to any small annotation of interest (e.g., enhancers, a set of genes involved in a pathway). Similar approaches have also been applied for analysis of temporal trends in additive genetic variance (e.g., in livestock breeding programs).55,56
Material and Methods
Model and definitions of estimands
We model the phenotype of a given individual by using a standard linear model, , where is the vector of the individual’s genotypes at M variants, assumed to be standardized in the population such that and for ; is the vector of corresponding standardized causal effect sizes; and is environmental noise. The individual’s standardized genotype at the i-th variant is where is the number of copies of the effect allele carried by the individual at the i-th variant and is the allele frequency of the effect allele in the population. Under this model, LD between variants and is defined as and the full LD matrix for all M variants is . We assume that the phenotype is also standardized in the population such that , .
Let such that is the total number of causal variants. We assume the causal effect of the i-th variant is distributed with probability or with probability , where , total SNP heritability, is the proportion of phenotypic variance explained by all M variants. Using the law of total variance,
Let index a gene of interest. Given an assignment of variants to gene , let be the vector of genotypes at this set of variants and let be the genotypes of the remaining variants. We can rewrite the total SNP heritability of the trait in terms of gene as
where the fourth line follows from the law of total expectation. If we additionally assume that for all , then , which simplifies the above equation to
We refer to the first term, the component of heritability attributable to the causal effects in gene , as “total gene-level heritability”:
Using the same assumptions as above, we can partition the variants in gene by MAF such that
where , , and are the components of attributable to the causal effects of rare (MAF < 0.01), low-frequency (0.01 ≤ MAF < 0.05), and common (MAF ≥ 0.05) variants, respectively. The estimands of interest in this work are the four terms in .
Note on the impact of the assumption of zero covariance between causal effects at different loci
Although it is common for post-GWAS analysis methods to assume that for all to facilitate inference, this may in fact be a relatively strong assumption on the underlying genetic architecture.43, 44, 45, 46 If this assumption is unmet, the equation for total SNP heritability retains its covariance term, i.e.,
The interpretation of our definition of gene-level heritability, , can then be thought of as the component of heritability that is “uniquely assignable” to the gene of interest. See discussion for additional commentary on the impact of nonzero causal-effect covariance on estimates of gene-level heritability. We also note that alternative assumptions yield different models for analyses of genomic variance (e.g., models of temporal trends in additive genetic variance55,56).
Estimating the posterior distribution of gene-level heritability
Because we have neither the “true” causal effect sizes, , nor the population LD, , we must estimate both from data. We consider one approximately independent LD block at a time. Given a GWAS of N individuals, let be the matrix of standardized genotypes measured at M variants, let be an vector of phenotypes, and let be environmental noise.
It is often the case that individual-level genotype data are inaccessible for privacy or logistical reasons. However, GWAS summary statistics—estimates of the causal effects and their standard errors—are publicly available for thousands of traits. Ordinary least-squares (OLS) estimates of the causal effects are often provided, defined as
It follows that
In this scenario, the observed data, D, are not the individual-level genotypes and phenotypes (, but rather , where is an estimate of LD computed from either the genotypes of a set of individuals in the GWAS (“in-sample” LD) or from an external reference panel (e.g., 1000 Genomes57). By combining the prior on , ( represents the hyperparameters of the prior over ), and the likelihood of the observed data, , one can compute the posterior distribution of the causal effects, . The hyperparameters, and , can be estimated via empirical Bayes (e.g., as implemented in SuSiE42).
The posterior of , , is, in general, computationally intractable. However, approximate inference, e.g., Markov chain Monte Carlo (MCMC) or variational inference, can be used to approximate the posterior as . In this work, we use SuSiE,42 a variational inference-based implementation of linear regression that assumes a sparse prior, but in principle, it is straightforward to use any implementation of linear regression with a sparse prior. We draw P samples from the posterior of the causal effects, , and use these posterior samples to approximate the full posterior distribution of , i.e., . Given the approximate posterior of , one can compute any summary statistic of interest. Here, we report the estimated posterior mean,
and credible intervals, which are one possible metric of uncertainty (described below). The same procedure can be used to estimate the component of gene-level heritability explained by a subset of the SNPs assigned to the gene (such as a MAF-based annotation).
For computational efficiency, we partition the genome into approximately independent LD blocks58 and approximate the posterior distribution of separately for each LD block; the approximate independence of each LD block from the rest of the genome implies that the causal effects at SNPs outside of the LD block of interest are absorbed into the environmental noise term. Similarly, the hyperparameters are specific to and estimated independently for each LD block.
Quantifying uncertainty in gene-level heritability estimates
The posterior samples provide an approximation to the full posterior distribution of , thus capturing uncertainty in the causal effect sizes arising from two main sources: LD and finite GWAS sample size (Figure 1). By using the full posterior of to approximate the full posterior of , we propagate the uncertainty in the causal effects into our estimate of . (The noise in is also an important factor, but for simplicity, we investigate uncertainty in in simulations where .)
We summarize the uncertainty in by computing -level credible intervals (-CIs). For a given , -CI is defined as the central interval within which lies with probability . In other words, the upper and lower bounds of -CI are set to the empirical and quantiles of the posterior samples .
Implementation details
We partition the genome into approximately independent LD blocks58 and, for each gene of interest, we perform inference on the LD block containing the gene. For each LD block, we extract the marginal association statistics and estimate LD for all the variants in the LD block. We estimate the posterior distribution of effect sizes by using the function “susie_suff_stat” with default parameters, as implemented in SuSiE42 v0.8 (web resources). We use the function “susie_get_posterior_samples” to obtain 500 posterior samples.
Simulation framework
We simulate phenotypes from the real imputed genotypes of N = 290,273 “unrelated White British” individuals in the UK Biobank, obtained by extracting individuals with self-reported British ancestry who are greater than third-degree relatives (pairs of individuals with kinship coefficient < 1/2(9/2), as defined in Bycroft et al.47). Filtering on MAF > 0.5% leaves M = 200,235 variants on chromosome 1 from which to draw phenotypes.
The genotypes of the above individuals can be encoded as , the number of copies of the effect allele carried by individual at variant , for all and . We assume that the population and in-sample allele frequencies are the same, and we standardize the genotype vector at each variant to have mean 0 and variance 1 across individuals by computing . Importantly, this genotype standardization is equivalent to assuming that the variance of the per-allele causal effect at variant is proportional to — a relatively strong inverse coupling between allele frequency and allelic effect size.59
Given the standardized genotypes, we simulated phenotypes under a variety of genetic architectures by varying the number of causal genes and background polygenicity, . Total SNP heritability on chromosome 1 was fixed to and cumulative gene-level heritability was fixed to . First, we uniformly sample 3%, 8%, or 16% of the 1,083 genes on chromosome 1 (web resources) to be causal (). Second, for each causal gene, we draw causal variants uniformly from the set of variants in the gene body and within 10 kb upstream/downstream of the gene start/end positions; the causal variants in the window around the gene are intended to represent regulatory causal variants in transcription start sites (TSSs). The causal configuration is set to either (1) five causal variants in the gene body and three causal variants in TSS or (2) ten causal variants in the gene body and six causal variants in TSS. Third, for each variant not considered in the previous step (i.e., the variants that are not located within 10 kb upstream/downstream of any gene’s start/end positions), we draw its causal status as for .
Finally, for the variants with , we draw independent standardized causal effect sizes as , assuming for all . is set to 0 if . The value of is determined by whether the causal variant is located in a gene body, in a TSS, or elsewhere. Let , , and represent the total number of causal variants in gene bodies, TSSs, and the background, respectively. We assume that causal variants in gene bodies explain the same amount of cumulative gene-level heritability; thus, these variants have . Similarly, we assume that all causal variants in TSSs together have a heritability of 0.01, which corresponds to for these variants. The remaining 0.01 heritability is also assumed to be distributed evenly across the background causal variants, so these variants have . We note that the causal statuses and effect sizes for each variant are only drawn once; the environmental noise term is drawn 30 times independently to generate 30 simulation replicates.
Again, we emphasize that even though the standardized causal effects in gene bodies are drawn i.i.d. from regardless of allele frequency, the assumption of an inverse relationship between per-allele causal effects and allele frequency has already been baked into the simulation framework through the initial genotype standardization.
Evaluating and comparing gene-level heritability estimates in simulations
Recall that for a given gene , the causal effect sizes and LD of the variants assigned to the gene are denoted and , and ground-truth gene-level heritability is defined as . The posterior mean estimated for a single simulation replicate s is denoted . We estimate the bias of the estimator as ; the variance of the estimator as ; and the mean squared error as .
For each simulation replicate , we output -level credible intervals, defined as
where the and percentiles are estimated from posterior samples; we use instead of 0.95 to obtain more robust credible intervals from 500 posterior samples. To assess the accuracy of credible intervals, we calculate “empirical coverage” across simulation replicates, defined as the proportion of simulation replicates in which the -level credible interval covers the ground-truth gene-level heritability: .
Estimating the number of nonzero-heritability genes
We explore two metrics for quantifying polygenicity at the gene level that do not use 90%-CIs. First, for the k-th gene, we estimate the posterior probability that from posterior samples as
where is an indicator function that evaluates to 1 if and to 0 otherwise. The total number of nonzero-heritability genes is then estimated by summing the posterior probabilities across genes:
The second quantity we estimate is the number of genes that explain 50% of the cumulative gene-level heritability. This is done by rank ordering genes by their estimated posterior means, , and summing the posterior means across genes, starting with the largest estimate, until is reached.
Comparison to “naïve” gene-level heritability estimator
We compare our approach to an alternative “naïve” estimator of gene-level heritability that does not model LD between the gene and its adjacent regions and thus ignores causal-effect uncertainty. This estimator is similar to existing methods that are meant to be applied to approximately independent LD blocks.34,60 For each gene, we extract the marginal association statistics, , and the estimated LD, , for the variants assigned to the gene, and we compute the alternative estimator as , where and are the pseudo-inverse and rank of , respectively.34,60
Assessing robustness to LD panel sample size
To assess the robustness of our approach to the sample size of the LD panel used to estimate LD, we randomly draw a subset of N = {500, 1,000, 2,500, 5,000} individuals from the full 290,273 individuals. After extracting variants with MAF > 0.5%, genotypes are standardized to have mean 0 and variance 1, similar to the full-sample analysis. Because we are interested in assessing robustness to noisy estimates of LD, all analyses are performed with the same set of marginal association statistics used in the full-sample analysis, excluding the variants that were filtered from the LD panel based on MAF. The LD and marginal association statistics are fed into the “h2gene” software, similar to the full-sample analysis.
Analysis of 25 UK Biobank phenotypes
We analyzed 25 quantitative phenotypes in the self-reported “White British” cohort in the UK Biobank (web resources). Phenotypes and imputed genotypes were filtered according to the same procedures used in the simulation analyses, leaving N = 290,273 individuals and M = 5,650,812 variants with MAF > 0.5%. Quantitative phenotypes were quantile-normalized to a Gaussian distribution with mean 0 and variance 1. We then performed a GWAS for each trait using the “--assoc” option in PLINK (web resources) with age, sex, and the top ten genetic principal components (PCs) included as covariates. The genetic PCs were precomputed by the UK Biobank via fastPCA61 applied to genotypes measured at 147,606 SNPs (MAF > 1%) in 407,599 “unrelated” individuals.47
In-sample LD was computed for each approximately independent LD block.58 We downloaded gene names and coordinates (web resources) and, for each gene, we define the estimand of interest to be a function of the variants in the gene body and those located within 10 kb upstream/downstream of the gene start/end positions. Finally, given the in-sample LD and marginal association statistics, we infer the posterior distribution of the causal effect sizes one LD block at a time, and we estimate and partition gene-level heritability for all genes in each LD block, where we define the estimand of interest to be a function of the variants in the gene body and those located within 10 kb upstream/downstream of the gene start/end positions. MAGMA v1.09 was used for gene-level association testing with a 10-kb window around each gene. The same list of genes and the same set of imputed variants were used for the MAGMA analysis.
Additional quality control to mitigate rare-variant population stratification
Including the top 10–20 genome-wide PCs as covariates in a GWAS is a standard approach to controlling for population structure. However, because the PCs included in the UK Biobank data release were computed from common SNPs (MAF > 1%), our GWASs may be susceptible to false positives driven by population stratification among rare variants, which can exhibit stratification patterns quite different from those of common variants.62,63 If there is population structure of recent origin and the confounding environmental effects are smoothly distributed with respect to ancestry, PCs computed from rare variants may be able to correct for confounding resulting from this recent structure.64 However, because the distribution of confounding environmental effects is unknown a priori, we cannot tell whether a rare-variant PC correction would be sufficient for this analysis. Ideally, we would perform PCA on rare variants (MAF < 1%) and include the top PCs as covariates in the GWASs anyway, but this would require whole-genome sequencing data from the “unrelated White British” UK Biobank cohort, which are not readily available to us at this time.
While single rare-variant association tests are prone to false positives resulting from uncorrected recent and/or local population structure, aggregating evidence from multiple rare variants can make an association statistic more robust to such structure. This is because adding more rare variants to a single test statistic increases the recombination distance between the variants included in the test. Therefore, to try to reduce potential false positives from rare-variant stratification in the real-data analyses, we exclude genes in the bottom 5th percentile in terms of (1) the number of rare variants in the gene body ± 10 kb, which in this case corresponds to genes with <4 rare variants (Figure S19A), or (2) [number of rare variants in the gene body ± 10 kb] / [gene length], which in this case is <0.00021 (Figure S19B). This reduces the original set of 17,437 protein-coding genes to 15,770.
Results
Overview of the method
Given an assignment of variants to a gene of interest, total gene-level heritability is defined as , where is the vector of unknown causal effect sizes and is the LD for SNPs in the gene (material and methods). Our goal in this work is to estimate a “distribution” over that captures uncertainty in the causal effects that arises from LD and finite GWAS sample size (Figure 1A).
To this end, we adopt a probabilistic fine-mapping framework35,42 that assumes a sparse prior on the causal effect sizes in the LD block containing the gene and infers the posterior distribution of the causal effect sizes, , where is the vector of estimated marginal effects from GWAS and is an estimate of LD. By sampling from the posterior of , we generate an approximation to the posterior of (Figure 1B, material and methods). For each gene, we report the estimated posterior mean () and -level credible interval (-CI), defined as the central interval that contains the true gene-level heritability with probability . Whereas previous works applied similar approaches to generate credible sets of causal variants42 or to estimate regional SNP-heritability of LD blocks,35 our goal in this work is to estimate the heritability explained by any arbitrary (not necessarily contiguous) set of variants much smaller than an LD block.
Using the same approach, we estimate the components of gene-level heritability attributable to the rare (), low-frequency (), and common () variants assigned to the gene of interest; we denote these quantities , , and , respectively (material and methods). (We note that, while there are many definitions of “rare” in the literature, we threshold at MAF ≥ 0.5% to reduce potential noise from imputation; see discussion for details.)
Accuracy of gene-level heritability estimates in simulations
We perform simulations starting from real imputed genotypes of N = 290,273 “unrelated White British” individuals in the UK Biobank (chromosome 1, , M = 200,235 variants, 1,083 genes; material and methods). In all simulations, the estimand of interest (gene-level heritability, ) is the proportion of phenotypic variance explained by the variants in the gene body. We note that our choice of variant assignment is arbitrary; there are many ways to assign variants to a gene, but our goal in this section is to provide a proof of concept. In brief, our simulation framework consists of three steps. First, for a given total heritability (variance explained by all M variants) and cumulative gene-level heritability (variance explained by all genes), we randomly select 3%, 8%, or 16% of the genes to have . Second, for each gene with , we draw causal variants in the gene body and within 10 kb upstream/downstream of the gene start/end positions; the purpose of the latter is to create situations where the estimated effects of variants in the region of interest are inflated in part because they tag causal variants located adjacent to the region. Third, we sample noncoding “background” causal variants from the rest of the chromosome with frequency . Under this model, the majority of simulated gene-level heritabilities are on the order of to (Figure S1), similar to what we observe in real data in subsequent sections (e.g., Figure S20).
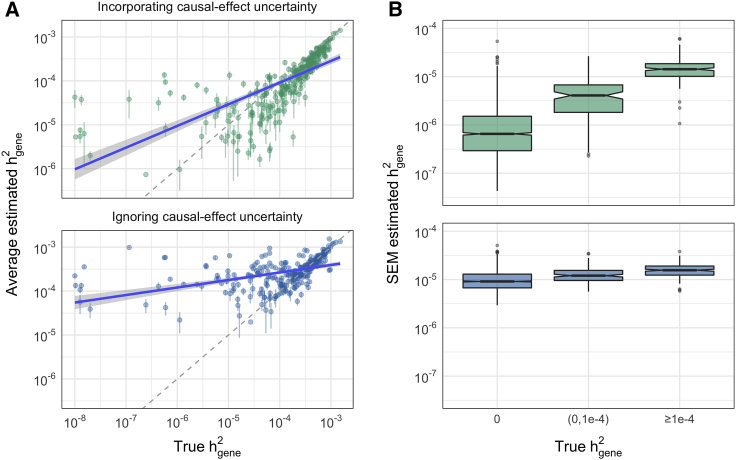
For each gene, we compute two metrics of accuracy from 30 simulation replicates: and (mean squared error) (material and methods). Overall, the estimated posterior means () are concordant with the true values of (Figure 2, Figure S2). For example, among just the causal genes () in the “most polygenic” simulations (where 16% of genes have nonzero heritability and per-causal-variant effect sizes are smallest), the estimator is slightly downward-biased for values and upward-biased for smaller value, but generally within the correct order of magnitude (Figure 2). To illustrate the impact of causal-effect uncertainty on gene-level heritability estimation, we compare to a naive estimator that ignores LD between the gene and its adjacent regions, thus ignoring causal-effect uncertainty (material and methods). As expected, the naive estimator is significantly more inflated (Figure 2); in particular, many zero-heritability genes have dramatically upward-biased estimates (Figure S3) due to LD between variants in the gene and nearby causal variants. As expected, increases with , the proportion of causal genes, and gene length (Figures S4–S6); average LD score and average MAF of variants in the gene have no discernible impact (Figures S5, S7, and S8).
Figure 2.
Impact of causal-effect uncertainty on gene-level heritability estimation in simulations
Chromosome 1, MAF > 0.5%, pcausal = 0.01, N = 290K individuals, and 1,038 genes, of which 16% have nonzero gene-level heritability.
(A) Average posterior mean of (±1.96 SEM) (green) and average “naïve” estimate (blue) for a given gene across 30 simulation replicates. To facilitate visualization, only genes with h2 > 10−8 are shown.
(B) SEM of (green) and of the naive estimator (blue) with respect to the underlying value of .
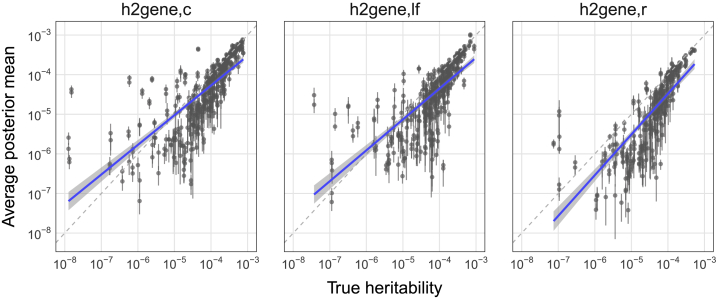
We also benchmark the estimators for , , and . Unlike , and , which display upward bias for values , is slightly downward-biased across all values of h2 (Figure 3). As with , increases with , , the proportion of causal genes, and gene length (Figures S4–S6) and does not noticeably vary with respect to average LD score or average MAF of variants in the gene (Figures S5, S7, and S8).
Figure 3.
Estimates of h2 contributions from common, low-frequency, and rare variants in simulations
Simulations were performed on chromosome 1 variants (MAF > 0.5%), with pcausal = 0.01, N = 290K individuals, and 1,083 genes, of which 16% have nonzero heritability. To facilitate visualization, and because all estimates in real traits were greater than 10−8, only genes with h2 > 10−8 are shown. Each point is the average posterior mean for one gene across 30 simulation replicates; error bars mark ± 1.96 x SEM.
Calibration of -credible intervals (-CIs)
Recall that -CI is defined as the central interval containing the true gene-level heritability with probability . We assessed calibration of -CIs by using “empirical coverage,” the proportion of simulation replicates in which -CI contains the true gene-level heritability (material and methods). Perfect calibration of -CI would manifest as empirical coverage equal to for all . In reality, we observe a downward bias in empirical coverage across all simulations that increases in magnitude as the proportion of causal genes increases (i.e., as per-variant causal effect sizes decrease); for example, at , empirical coverage ranges from approximately 0.75 when 3% of genes are causal to 0.65 when 16% are causal (Figure S9). While downward bias in empirical coverage could result from -CIs underestimating or overestimating , we find that, for true nonzero-heritability genes, the credible intervals at tend to underestimate . For example, at , as polygenicity increases from 3% to 16%, the average (and standard error of the mean [SEM]) proportion of genes with that are underestimated increases from approximately 14% (0.7%) to 29% (0.7%) while the average overestimated decreases from 6% (0.4%) to 3.5% (1.5%), respectively. The -CIs for are more conservative; for the same parameters, the proportion of genes that are underestimated increases from 38% (1%) to 45% (0.6%) while the proportion overestimated decreases from 1.5% (0.3%) to 0.7% (0.1%) (Table S2, Figure S10).
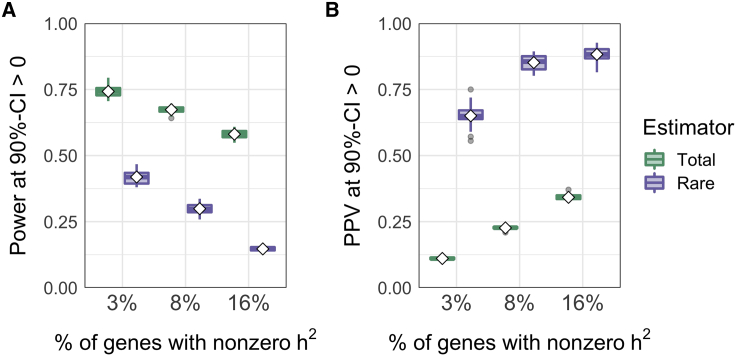
We estimate the power of -CI at as the proportion of nonzero-h2 genes correctly identified at the significance threshold 90%-CI > 0. As expected, power is higher in simulations where the average values of and are larger (i.e., when polygenicity is lower) and is higher overall for than for (Figure 4A). We also assess power with respect to the underlying value of or , estimated for each nonzero-h2 gene as the proportion of simulation replicates in which the gene correctly passes the threshold 90%-CI > 0. In the most polygenic simulations, power ranges from an average of 56% for genes in the lowest quartile () to 94% for the highest quartile () (Figure S11A). For , power is significantly lower, ranging from an average of 10% for genes with in the lower 50th percentile () to 72% for genes in the highest quartile () (Figure S11B).
Figure 4.
Power and PPV at 90%-CI > 0 in simulations
(A) Power is estimated per simulation replicate as the proportion of nonzero-h2 genes correctly identified at 90%-CI > 0 (green) or 90%-CI > 0 (purple).
(B) PPV is estimated per simulation replicate as the proportion of genes identified at 90%-CI > 0 that are, in fact, true positives. Each boxplot represents 30 simulation replicates; white diamonds mark the mean.
Since we are interested in using 90%-CIs to identify narrow sets of high-impact genes, it is also useful to assess the false positive rate (FPR) and positive predictive value (PPV). We estimate FPR as the proportion of zero-heritability genes that incorrectly pass the threshold 90%-CI > 0. For , FPR ranges from approximately 19% (SEM 0.2%) when 3% of genes are causal to 21% (0.2%) when 16% of genes are causal (Figure S12A). FPR is overall much smaller for and decreases as polygenicity increases, ranging from 0.2% (0.01%) when 16% of genes are causal to 0.5% (0.01%) when 3% of genes are causal (Figure S12B). Although the FPR for is relatively high, most genes passing the 90%-CI > 0 threshold that have > 10−4 are true positives (Figure S12C).
We estimate PPV as the proportion of genes with 90%-CI > 0 that are, in fact, true positives. Despite its relatively low power, 90%-CI > 0 has a dramatically higher PPV than does 90%-CI > 0 (Figure 4B). PPV increases as polygenicity increases (i.e., as causal effect sizes decrease), reaching an average of 35% (SEM 0.2%) for and 88% (0.5%) for . That is, in simulations where 16% of genes are causal, approximately 88% of genes identified at the significance threshold 90%-CI > 0 have , while only 35% of the genes identified at 90%-CI > 0 have . Moreover, the genes identified at 90%-CI > 0 are enriched for genes with of attributable to . In the same simulations, genes with comprise 24% of all genes with and 14% of all genes with ; PPV for identifying these genes at 90%-CI > 0 is 39% for and 4% for (Figure S13). In other words, approximately 39% of genes with 90%-CI > 0 have of explained by rare causal variants, whereas only 4% of genes with 90%-CI > 0 fall in this category. This corresponds to a 1.6× enrichment of genes with among those identified at the threshold 90%-CI > 0 and a depletion of these genes at 90%-CI > 0.
Quantification of polygenicity and related quantities in simulations
We explore different approaches for estimating the total number of nonzero-h2 genes. First, we estimate the expected number of nonzero-h2 genes by approximating, for each gene, the posterior probability that and summing the posterior probabilities across genes (material and methods). Unsurprisingly, because the method is not calibrated to be applied in this way, this approach produces highly inflated estimates (Figure S14A). The number of genes with 90%-CI > 0 is also a biased estimator; in lower-polygenicity settings (larger per-gene heritabilities), it overestimates the number of nonzero-h2 genes for both and , and in higher-polygenicity settings (smaller per-gene heritabilities), it underestimates for and (Figure S14B). However, across all simulation settings, we found that we obtain nearly unbiased estimates of the number of genes explaining 50% of the cumulative gene-level heritability by (1) rank ordering genes by and (2) summing across genes, from largest to smallest, until is reached (Figure S15). This metric captures the concentration or dispersion of heritability across genes—an important aspect of genetic architecture. Note that the estimated cumulative gene-level heritability, , is a sum across all genes, not just those that pass 90%-CI > 0. That we can accurately estimate the number of genes explaining is consistent with the trends we observe in bias[ (Figure 2A), i.e., the slight downward bias we observe in for larger values (e.g., ) and the upward bias we observe for smaller values (e.g., ).
Robustness to noise in estimates of LD
Finally, we assess whether is robust to the number of individuals used to estimate LD, i.e., the sample size of the “LD panel” (material and methods). Compared to in-sample LD computed from the full set of individuals in the GWAS (N = 290,273), using a random subset of N = {500, 1,000, 2,500, 5,000} individuals from the original GWAS does not significantly impact the MSE of or (Figure S16). Using 90%-CIs to identify nonzero-h2 genes, we find that the FPR (the proportion of zero-heritability genes incorrectly identified at 90%-CI > 0) is robust with respect to LD panel sample size for both and (Figure S17). Power (the proportion of true nonzero-h2 genes identified at 90%-CI > 0) is relatively robust to LD panel sample size in the most polygenic setting; however, in the least polygenic setting, power drops more significantly, from ∼73% at the full sample size to ∼47% at N = 500 (Figure S18A). We observe a similar drop in power for (Figure S18B). Thus, while using a smaller sample of individuals from the GWAS cohort does not significantly increase type I error, we recommend using the full GWAS cohort to compute in-sample LD in order to maximize power, especially for .
Gene-level heritability estimates for 25 quantitative traits in the UK Biobank
We estimate, and partition by MAF, the gene-level heritabilities of 15,770 protein-coding genes for 25 well-powered quantitative traits in the UK Biobank (N = 290,273 “unrelated White British” individuals,47 M = 5,650,812 with MAF > 0.5%, imputed data; material and methods). These 25 traits are a mix of serum and urine biomarker traits (many of which have known “causal” genes and biochemical pathways65, 66, 67, 68) and highly polygenic anthropometric traits (Table 1). Because our GWASs may contain uncorrected fine-scale population structure among rare variants (discussion), to reduce potential false positives, we exclude genes in the bottom 5th percentile in terms of (1) number of rare variants or (2) number of rare variants divided by gene length (Figure S19, material and methods). Unless otherwise stated, the estimands of interest are functions of the variants located in the gene body and the variants located within 10 kb upstream/downstream of the gene start/end positions. A gene is classified as having “nonzero heritability” if it meets two criteria: (1) 90%-CI > 0 and (2) 90%-CI > 0 for at least one MAF component (, , or ). Using this definition, the number of nonzero-h2 genes ranges from 1,103 (7%) for corneal hysteresis to 2,258 (14%) for height (Table 1). Most of the estimated posterior means for these genes lie between 10−6 and 10−4 (Figure S20). While the number of genes passing the 90%-CI > 0 threshold is a biased estimator of polygenicity (Figure S14B), we can relatively reliably estimate the number of genes that explain 50% of the trait’s cumulative gene-level heritability (Figure S15, material and methods). These estimates vary widely across traits, ranging from seven genes for hair color and sex hormone binding globulin concentration (SHBG) to 677 for BMI (Table 1).
Table 1.
Summary of estimates across 25 quantitative traits (N = 290K “White British,” UK Biobank)
| Trait | Num. genes w/90%-CI > 0 | Num. genes that explain | |||
|---|---|---|---|---|---|
| Alkaline phosphatase | 1,542 | 21 | 1,142 | 108 | 18 |
| Apolipoprotein A-I | 1,589 | 71 | 1,186 | 105 | 11 |
| Basal metabolic rate | 1,929 | 568 | 1,476 | 115 | 10 |
| BMD heel T-score | 1,297 | 251 | 1,006 | 76 | 3 |
| BMI | 1,722 | 677 | 1,312 | 98 | 6 |
| C-reactive protein | 1,561 | 9 | 1,187 | 88 | 6 |
| Corneal hysteresis | 1,103 | 321 | 833 | 74 | 3 |
| Cystatin C | 1,738 | 163 | 1,328 | 110 | 8 |
| Forced vital capacity | 1,748 | 565 | 1,337 | 108 | 5 |
| GGT | 1,650 | 166 | 1,256 | 101 | 12 |
| Hair color | 1,201 | 7 | 883 | 77 | 13 |
| HbA1c | 1,676 | 116 | 1,240 | 133 | 17 |
| HDL | 1,602 | 59 | 1,194 | 109 | 11 |
| Height | 2,258 | 445 | 1,713 | 152 | 27 |
| High light scatter reticulocyte count | 1,696 | 188 | 1,279 | 112 | 23 |
| IGF-1 | 1,691 | 270 | 1,265 | 116 | 10 |
| MCH | 1,557 | 109 | 1,151 | 122 | 15 |
| MSCV | 1,585 | 144 | 1,226 | 101 | 8 |
| Monocyte count | 1,601 | 144 | 1,219 | 100 | 9 |
| Mean platelet volume | 1,753 | 57 | 1,291 | 127 | 25 |
| Platelet count | 1,748 | 158 | 1,351 | 102 | 24 |
| Platelet distrib. width | 1,598 | 44 | 1,219 | 102 | 16 |
| RBC count | 1,752 | 310 | 1,341 | 122 | 18 |
| SHBG | 1,551 | 7 | 1,164 | 102 | 17 |
| Urate | 1,584 | 38 | 1,206 | 103 | 12 |
Column 2: number of genes (out of 15,770) with (1) 90%-CI > 0 and (2) 90%-CI > 0 for at least one MAF bin (rare, low-frequency, or common). Column 3: estimated number of genes that explain 50% of cumulative . Columns 4–6: numbers of 90%-CI > 0 genes with effects exclusively from common, low-frequency, or rare variants. (BMD, bone mineral density; MCH, mean corpuscular hemoglobin; MSCV, mean sphered corpuscular volume; RBC, red blood cell.)
We confirm that the approximation is largely satisfied in real data; the average Pearson correlation across traits between and is 0.97 (SD 0.05) (Figure S21). As expected, behaves similarly to . The average Pearson R2 of and across the 25 traits is 94% (SD 1%) (Figure S22). 92% (SD 1%) of nonzero-heritability genes have significant common-variant heritability; 76% (SD 1%) have significant causal effects exclusively from common variants (Table 1). On the other hand, is significantly less correlated with (average Pearson R2 = 30% [SD 21%] across traits) (Figure S22). Approximately 2.5% (SD 0.6%) of genes have significant rare-variant heritability (Table S3), and only 0.8% (SD 0.4%)—327 gene-trait pairs in total—have significant heritability exclusively from rare variants (Table 1, Table S4).
LoF-intolerant genes are strongly enriched among genes with only rare-variant heritability
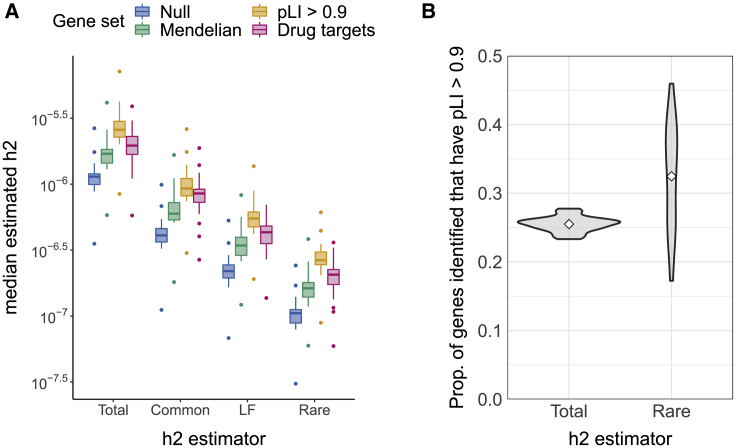
We estimate, and partition by MAF, the gene-level heritabilities of (1) known Mendelian-disorder genes from OMIM69 (n = 2,971), (2) loss-of-function (LoF)-intolerant genes (probability of LoF-intolerance [pLI] > 0.9)48 (n = 2,562), and (3) a set of FDA-approved drug targets for 30 immune-related traits70 (n = 176) (material and methods). Compared to a set of “null” genes (sampled from the set of genes not contained in any of the three gene sets), all three gene sets have significantly higher median estimates of total and MAF-partitioned gene-level heritability (Figure 5A).
Figure 5.
Genes of known biological importance have higher h2 estimates
(A) Distributions of h2 estimates for three gene sets: Mendelian-disorder genes (n = 2,971), LoF-intolerant genes (pLI > 0.9, n = 2,562), and immune-related drug targets (n = 176). Each point is the median posterior mean across genes for a given trait; each boxplot represents 25 traits.
(B) Proportion of nonzero-h2 genes identified at 90%-CI > 0 for and that are putatively LoF intolerant. Each violin plot is a distribution across 25 traits. For reference, genes with pLI > 0.9 comprise 16% of all genes in the analysis.
The Mendelian-disorder gene set comprises 19% of all genes and is enriched for genes with 90%-CI > 0 for at least one trait (Fisher’s exact test, OR and 95%-CI: 1.4 [1.1, 1.7], Table S3) but not for nonzero- genes (OR = 1.1 [1.0, 1.2]) or genes with exclusively rare-variant heritability (OR = 1.1 [0.8, 1.5], Table S4). In contrast, the LoF-intolerant genes comprise 16% of all genes and are enriched for nonzero- genes (OR and 95%-CI: 1.4 [1.3, 1.5]), nonzero- genes (OR = 1.5 [1.2, 1.8], Table S3), and genes with exclusively rare-variant heritability (OR = 1.6 [1.2, 2.2], Table S4). On average across traits, 26% (SD 1%) of the genes identified at 90%-CI > 0; 33% (SD 8%) of those with 90%-CI > 0; and 35% (SD 20%) of those with exclusively rare-variant heritability are also LoF-intolerant (Figure 5B).
Of the 327 gene-trait pairs with only rare-variant heritability (ranging from three genes for heel T-score and corneal hysteresis to 27 genes for height [Table 1, Table S4]), 213 gene-trait pairs are also identified by MAGMA71 (FDR < 0.05, material and methods). We observe a 1.6× enrichment of LoF-intolerant genes among the gene-trait pairs identified by both methods and a 2.3× enrichment among the gene-trait pairs identified by only our method, indicating that the genes identified by only our method are indeed capturing meaningful signal. The 114 additional gene-trait pairs found by our method (Table S5) include six unique genes (seven gene-trait pairs) with estimated posterior means > 10−4. Of these six genes, three are LoF-intolerant: DYNC1LI2, identified for MSCV ( 90%-CI = [2e−4, 4e−4], MAGMA Z score = 2.1, pLI = 1, recently implicated in cystinosis, a lysosomal storage disorder72); ARHGAP25, identified for monocyte count ( 90%-CI = [9e−5, 3e−4], MAGMA Z score = 2.1, pLI = 0.95, has known roles in phagocytosis73,74); and PHC3, identified for basal metabolic rate ( 90%-CI = [7e−5, 2e−4], MAGMA Z score = 1.9, pLI = 1, implicated in osteosarcoma75,76).
identifies genes that link complex traits to phenotypically related monogenic disorders
Among the 1,050 gene-trait pairs identified at 90%-CI > 0 (Table S3), 161 have 90%-CI > 10−4. Several of these genes with large rare-variant heritability are implicated in Mendelian disorders that are phenotypically related to the complex trait. For example, the gene with the largest rare-variant heritability we identify is MPDU1 for SHBG concentration, a liver-secreted glycoprotein77 ( 90%-CI = [0.020, 0.021]); certain mutations in MPDU1 are known to cause a congenital disorder of glycosylation,78,79 and there is evidence that MPDU1 interacts with SHBG.80 IL17RA, identified for monocyte count ( 90%-CI = [0.0040, 0.0048]), is involved in an autosomal recessive immunodeficiency disorder.81,82 GFI1B, identified for mean platelet volume ( 90%-CI = [0.0037, 0.0044]), is involved in platelet-type bleeding disorder-17, an autosomal dominant disorder characterized by increased bleeding due to abnormal platelet function.83
Although we did not find a statistically significant overlap between the Mendelian-disorder gene set and the set of genes with exclusively rare-variant heritability, the top genes (rank ordered by ) among the 114 gene-trait pairs identified by our method and not by MAGMA (FDR < 0.05, Table S5) also include examples of genes that may link complex traits to phenotypically related monogenic disorders. For example, we identify AKT2 for serum gamma-glutamyl transferase concentration (GGT) (90%-CI of = [3e−5, 1e−4]), which is used to test for the presence of liver disease; AKT2 is implicated in monogenic forms of type 2 diabetes84 and hypoinsulinemic hypoglycemia with hemihypertrophy.85 The AKT2 annotation used for this analysis contains 24 rare variants, of which, 1 is identified as causal. For serum apolipoprotein A1, we identify VPS13D ( 90%-CI = [4e−5, 2e−4]; annotation contains 119 are rare variants, of which ∼2 are identified as causal). Compound heterozygous mutations in VPS13D are known to cause an autosomal recessive ataxia characterized in part by abnormal mitochondrial morphology, reduced energy generation, and lipidosis,86,87 and VPS13D was recently shown to have direct involvement in trafficking fatty acids from lipid droplets to mitochondria.88
Our results are consistent with the hypothesis that complex-trait variation may be explained in part by dysregulation of genes that—if completely disrupted—cause phenotypically similar or related Mendelian disorders.54 We emphasize that, because heritability reflects genetic and phenotypic variation at the population level, if a common variant and rare variant explain the same heritability (i.e., have the same standardized causal effect size), the allelic effect—the expected change in phenotype per additional copy of the effect allele—is significantly larger for the rare variant.
MAF-partitioned gene-level heritability reveals unique insights into genetic architecture
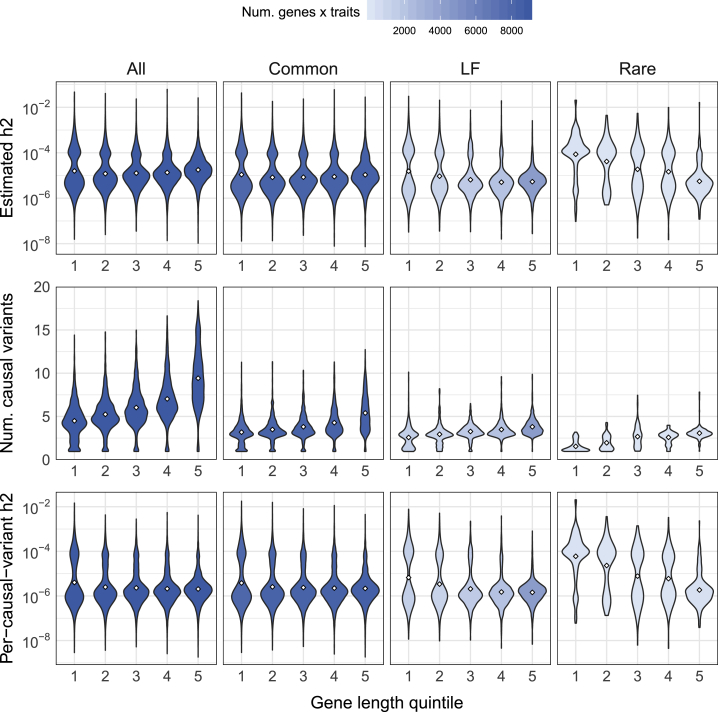
We investigated whether gene-level heritability estimates are correlated with gene length, average LD score of variants in the gene (a proxy for the strength of LD in the region), and average MAF of variants in the gene. (and, to a large extent, ) is distributed very similarly to with respect to these variables (Figure 6, Figure S23). However, the distribution of shows marked differences, particularly with respect to gene length. Specifically, we observe a higher average among shorter genes even though the number of causal variants per gene (across all allele frequencies) increases with gene length (Figure 6, Figure S24). The expected per-causal variant effect size per gene is invariant to gene length for common and low-frequency variants, but for rare variants, the average across gene-trait pairs is nearly 10−4 in the shortest quintile of genes versus 10−6 in the longest (Figure 6).
Figure 6.
Inverse relationship between rare-variant h2 estimates and gene length
Estimates of h2 (top), number of causal variants per gene (middle), and expected effect size per causal variant per gene (bottom) with respect to gene length (x axis) for 25 traits. Each violin plot is the distribution of posterior mean estimates for nonzero-heritability genes with 90%-CIs > 0 for each h2 quantity. Color gradient indicates the number of estimates in each violin plot (number of gene-trait pairs).
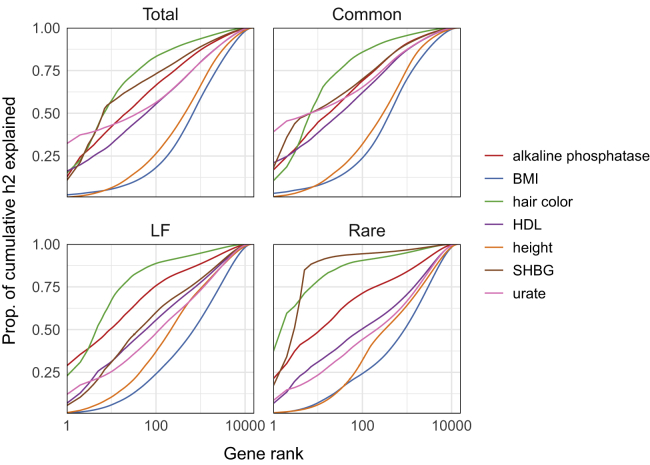
Using the empirical distributions of cumulative , , , and, we loosely quantify differences in polygenicity at the level of genes (with the caveat that, because there is a high degree of gene overlap in some regions, cumulative may be more informative for some traits over others). For example, if cumulative is divided equally across all genes, the empirical cumulative distribution function (CDF) for would be the line y = x, where the x axis is the rank ordering of genes from highest to lowest ; two traits with the same empirical CDF for can have different empirical CDFs for each MAF-partitioned component. Once again, we find that the empirical CDFs of are extremely similar to those of (Figure 7, Figure S25). Although the curves generally have similar shapes across traits (i.e., similar spread of heritability across genes), some traits have a notable amount of heritability concentrated in just the top gene, and many of these gene-trait pairs have been functionally validated in the literature. For example, for urate, SLC2A9—a known urate transporter89, 90, 91—is the single largest contributor to total, common-, and LF-variant gene-level heritability ( = 0.062, = 0.060, = 0.0034, = 0), accounting for 32%, 39%, and 12% of the cumulative heritability for each estimand, respectively (Figure 7). For alkaline phosphatase, we find that ALPL—which encodes the enzyme alkaline phosphatase—is the single largest contributor to total and LF-variant gene-level heritability ( = 0.041, = 0.018, = 0.021, = 0), explaining 13% and 29% of the respective cumulative heritability estimands (Figure 7).
Figure 7.
Gene-level heritability estimates capture differences in polygenicity across traits
Empirical distributions of cumulative heritability for seven example traits (clockwise from top left: total, common, rare, and low-frequency). Each curve can be read as, “the top X genes, rank ordered by estimated posterior mean, explain proportion Y of the cumulative gene-level heritability for a given trait” (Figure S25 shows all 25 traits).
Discussion
We propose a general approach for estimating the heritability explained by any set of variants much smaller than an LD block and assess its utility in estimating/partitioning gene-level heritability. In simulations, we confirm that incorporating uncertainty about which variants are causal and what their effect sizes are dramatically improves specificity over naive approaches that ignore uncertainty in the causal effects. For 25 complex traits and >15K genes, we estimate gene-level heritability—the heritability explained by variants in the gene body plus a 10-kb window upstream/downstream of the gene start/end positions—and partition by allele-frequency class to explore differences in genetic architecture across traits. As expected, most gene-level heritability is dominated by common variants, but we identify several genes per trait with nonzero heritability exclusively from rare or low-frequency variants. Notably, we find many genes with only rare-variant heritability that existing methods are underpowered to detect; these genes include LoF-intolerant genes and genes with known roles in Mendelian disorders that are phenotypically similar or related to the complex trait. Our results demonstrate that the rare-variant contribution to total gene-level heritability is a useful quantity that can be considered alongside common-variant heritability enrichments to obtain a more comprehensive understanding of genetic architecture.
We conclude by discussing the limitations of our approach. First, it is critical to remember that gene-level heritability is not an intrinsic property of a trait or gene. Like all “types” of heritability, estimates of total and MAF-partitioned gene-level heritability are only meaningful when considered in the populations in which they were measured.45,46 Our real-data results are therefore specific to the population from which the “White British” individuals in the UK Biobank are sampled. In addition, genes with credible intervals > 0 must not be interpreted as “causal” without additional functional validation, as nonzero gene-level heritability indicates association—not causality.51
Second, multiple lines of evidence suggest that rare and “ultra-rare” variants, which are not well tagged by variants on genotyping arrays, may explain much of the “missing heritability” not captured by genotyped or imputed variants.12,63,92 Because imputed genotypes are noisier for rarer variants and variants in lower LD regions, we analyze variants with MAF > 0.5%. Additional work is needed to assess the error incurred by using genotyped/imputed data in lieu of whole-genome sequencing (WGS) as well as the signal that is missed by excluding variants with MAF < 0.5%. While our estimator can be applied to whole-exome sequencing (WES) data, LD between coding and noncoding regions would significantly inflate gene-level heritability estimates; LD between exonic and intronic variants could also cloud interpretation, depending on the application. With multiple biobanks starting to sequence large numbers of individuals,93, 94, 95 we believe the availability of large-scale WGS data will gradually become less of an issue.
We corrected for population structure by using genome-wide PCs (precomputed and provided by the UK Biobank in their data release47) as covariates in each GWAS. This is a standard approach to correcting for population stratification, which typically reflects geographic separation, in estimates of genome-wide SNP-heritability and genome-wide functional enrichments, both of which are driven by common SNPs. However, rare variants generally have more complex spatial distributions and thus exhibit stratification patterns distinct from those of common SNPs.62,63 It is unclear whether methods that are effective for controlling stratification of common SNPs are applicable to rare variants.96 While we did perform additional quality control to reduce potential false positives due to uncorrected rare-variant population structure, we leave a thorough investigation of the impact of recent and/or fine-scale structure for future work.
Our approach requires OLS association statistics and LD computed from a subset of individuals in the GWAS. While estimates of gene-level heritability and the MAF-partitioned components are robust to sample sizes as low as 5,000, the individuals used to estimate LD must be a subset of the individuals in the GWAS. Although summary association statistics are publicly available for hundreds of large-scale GWASs, most of these studies are meta-analyses and therefore do not have in-sample LD available. Moreover, many publicly available summary statistics were computed from linear mixed models rather than OLS, which is used throughout our simulations and derivations. Additional work is needed to extend our approach to allow external reference panel LD (e.g., 1000 Genomes57) and/or mixed model association statistics. Biobanks can help to ameliorate potential issues stemming from noisy LD by releasing summary LD information alongside summary association statistics.97
Finally, gene-level heritabilities of different genes can have nonzero covariance due to physical overlap between genes and/or correlated causal effect sizes.98 In this work, we assume there is zero covariance between causal effects of different variants in order to facilitate inference. If, in fact, there is nonzero covariance between causal effects at different loci, total SNP-heritability would also include a nonzero covariance between the gene and its complement43, 44, 45, 46 (material and methods). Depending on whether the covariance is positive or negative, the gene-level heritability estimates from our method can be biased downward or upward. Thus, the heritability estimates for real traits reported in this work have additional sources of noise/uncertainty which were not directly modeled or accounted for. Since modeling correlation of causal effect sizes would make inference considerably more challenging, we leave this for future work.
Acknowledgments
We thank the UK Biobank Resource (application #33297) for making this work possible. We are also grateful to Alkes Price, Gregor Gorjanc, Harold Pimentel, Luke O’Connor, Nasa Sinnott-Armstrong, and Ruth Johnson for providing helpful comments and discussion. This work was funded in part by the National Institutes of Health under awards R01-HG009120 and R01-MH115676.
Declaration of interests
H.S. is now an employee of Genentech and holds stock in Roche.
Published: March 9, 2022
Footnotes
Supplemental information can be found online at https://doi.org/10.1016/j.ajhg.2022.02.012.
Contributor Information
Kathryn S. Burch, Email: kathrynburch@ucla.edu.
Bogdan Pasaniuc, Email: pasaniuc@ucla.edu.
Data and code availability
h2gene software and analysis scripts are available at https://github.com/bogdanlab/h2gene.
Web resources
LoF-intolerance metrics by gene, https://gnomad.broadinstitute.org/downloads
MAGMA software, https://ctg.cncr.nl/software/magma
OMIM gene list, https://github.com/bogdanlab/gene_sets/blob/master/mendelian_genes.bed
PLINK software, https://www.cog-genomics.org/plink2
Protein-coding gene list and coordinates, https://ctg.cncr.nl/software/magma
susieR software, https://github.com/stephenslab/susieR
UK Biobank Resource, https://www.ukbiobank.ac.uk/
Supplemental information
References
- 1.Maurano M.T., Humbert R., Rynes E., Thurman R.E., Haugen E., Wang H., Reynolds A.P., Sandstrom R., Qu H., Brody J., et al. Systematic localization of common disease-associated variation in regulatory DNA. Science. 2012;337:1190–1195. doi: 10.1126/science.1222794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pickrell J.K. Joint analysis of functional genomic data and genome-wide association studies of 18 human traits. Am. J. Hum. Genet. 2014;94:559–573. doi: 10.1016/j.ajhg.2014.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Finucane H.K., Bulik-Sullivan B., Gusev A., Trynka G., Reshef Y., Loh P.-R., Anttila V., Xu H., Zang C., Farh K., et al. Partitioning heritability by functional annotation using genome-wide association summary statistics. Nat. Genet. 2015;47:1228–1235. doi: 10.1038/ng.3404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wray N.R., Wijmenga C., Sullivan P.F., Yang J., Visscher P.M. Common disease is more complex than implied by the core gene omnigenic model. Cell. 2018;173:1573–1580. doi: 10.1016/j.cell.2018.05.051. [DOI] [PubMed] [Google Scholar]
- 5.Boyle E.A., Li Y.I., Pritchard J.K. An expanded view of complex traits: From polygenic to omnigenic. Cell. 2017;169:1177–1186. doi: 10.1016/j.cell.2017.05.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Liu X., Li Y.I., Pritchard J.K. Trans effects on gene expression can drive omnigenic inheritance. Cell. 2019;177:1022–1034.e6. doi: 10.1016/j.cell.2019.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bomba L., Walter K., Soranzo N. The impact of rare and low-frequency genetic variants in common disease. Genome Biol. 2017;18:77. doi: 10.1186/s13059-017-1212-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yao C., Joehanes R., Johnson A.D., Huan T., Liu C., Freedman J.E., Munson P.J., Hill D.E., Vidal M., Levy D. Dynamic role of trans regulation of gene expression in relation to complex traits. Am. J. Hum. Genet. 2017;100:985–986. doi: 10.1016/j.ajhg.2017.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Caballero A., Tenesa A., Keightley P.D. The nature of genetic variation for complex traits revealed by GWAS and regional heritability mapping analyses. Genetics. 2015;201:1601–1613. doi: 10.1534/genetics.115.177220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Golan D., Lander E.S., Rosset S. Measuring missing heritability: inferring the contribution of common variants. Proc. Natl. Acad. Sci. USA. 2014;111:E5272–E5281. doi: 10.1073/pnas.1419064111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Eyre-Walker A. Genetic architecture of a complex trait and its implications for fitness and genome-wide association studies. Proc. Natl. Acad. Sci. USA. 2010;107(Suppl 1):1752–1756. doi: 10.1073/pnas.0906182107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wainschtein P., Jain D., Zheng Z., Cupples L.A., Shadyab A.H., McKnight B., et al. Recovery of trait heritability from whole genome sequence data. Prepint at bioRxiv. 2021 doi: 10.1101/588020. [DOI] [Google Scholar]
- 13.Yang J., Benyamin B., McEvoy B.P., Gordon S., Henders A.K., Nyholt D.R., Madden P.A., Heath A.C., Martin N.G., Montgomery G.W., et al. Common SNPs explain a large proportion of the heritability for human height. Nat. Genet. 2010;42:565–569. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hunt K.A., Mistry V., Bockett N.A., Ahmad T., Ban M., Barker J.N., Barrett J.C., Blackburn H., Brand O., Burren O., et al. Negligible impact of rare autoimmune-locus coding-region variants on missing heritability. Nature. 2013;498:232–235. doi: 10.1038/nature12170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yao D.W., O’Connor L.J., Price A.L., Gusev A. Quantifying genetic effects on disease mediated by assayed gene expression levels. Nat. Genet. 2020;52:626–633. doi: 10.1038/s41588-020-0625-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.O’Connor L.J., Schoech A.P., Hormozdiari F., Gazal S., Patterson N., Price A.L. Extreme polygenicity of complex traits is explained by negative selection. Am. J. Hum. Genet. 2019;105:456–476. doi: 10.1016/j.ajhg.2019.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Simons Y.B., Bullaughey K., Hudson R.R., Sella G. A population genetic interpretation of GWAS findings for human quantitative traits. PLoS Biol. 2018;16:e2002985. doi: 10.1371/journal.pbio.2002985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gusev A., Bhatia G., Zaitlen N., Vilhjalmsson B.J., Diogo D., Stahl E.A., Gregersen P.K., Worthington J., Klareskog L., Raychaudhuri S., et al. Quantifying missing heritability at known GWAS loci. PLoS Genet. 2013;9:e1003993. doi: 10.1371/journal.pgen.1003993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Marouli E., Graff M., Medina-Gomez C., Lo K.S., Wood A.R., Kjaer T.R., Fine R.S., Lu Y., Schurmann C., Highland H.M., et al. Rare and low-frequency coding variants alter human adult height. Nature. 2017;542:186–190. doi: 10.1038/nature21039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gusev A., Ko A., Shi H., Bhatia G., Chung W., Penninx B.W.J.H., Jansen R., de Geus E.J.C., Boomsma D.I., Wright F.A., et al. Integrative approaches for large-scale transcriptome-wide association studies. Nat. Genet. 2016;48:245–252. doi: 10.1038/ng.3506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wainberg M., Sinnott-Armstrong N., Mancuso N., Barbeira A.N., Knowles D.A., Golan D., Ermel R., Ruusalepp A., Quertermous T., Hao K., et al. Opportunities and challenges for transcriptome-wide association studies. Nat. Genet. 2019;51:592–599. doi: 10.1038/s41588-019-0385-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ionita-Laza I., Lee S., Makarov V., Buxbaum J.D., Lin X. Sequence kernel association tests for the combined effect of rare and common variants. Am. J. Hum. Genet. 2013;92:841–853. doi: 10.1016/j.ajhg.2013.04.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wu M.C., Lee S., Cai T., Li Y., Boehnke M., Lin X. Rare-variant association testing for sequencing data with the sequence kernel association test. Am. J. Hum. Genet. 2011;89:82–93. doi: 10.1016/j.ajhg.2011.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Price A.L., Kryukov G.V., de Bakker P.I.W., Purcell S.M., Staples J., Wei L.-J., Sunyaev S.R. Pooled association tests for rare variants in exon-resequencing studies. Am. J. Hum. Genet. 2010;86:832–838. doi: 10.1016/j.ajhg.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zuk O., Schaffner S.F., Samocha K., Do R., Hechter E., Kathiresan S., Daly M.J., Neale B.M., Sunyaev S.R., Lander E.S. Searching for missing heritability: designing rare variant association studies. Proc. Natl. Acad. Sci. USA. 2014;111:E455–E464. doi: 10.1073/pnas.1322563111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Moutsianas L., Agarwala V., Fuchsberger C., Flannick J., Rivas M.A., Gaulton K.J., Albers P.K., McVean G., Boehnke M., Altshuler D., McCarthy M.I., GoT2D Consortium The power of gene-based rare variant methods to detect disease-associated variation and test hypotheses about complex disease. PLoS Genet. 2015;11:e1005165. doi: 10.1371/journal.pgen.1005165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Liu D.J., Peloso G.M., Zhan X., Holmen O.L., Zawistowski M., Feng S., Nikpay M., Auer P.L., Goel A., Zhang H., et al. Meta-analysis of gene-level tests for rare variant association. Nat. Genet. 2014;46:200–204. doi: 10.1038/ng.2852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lee S., Abecasis G.R., Boehnke M., Lin X. Rare-variant association analysis: study designs and statistical tests. Am. J. Hum. Genet. 2014;95:5–23. doi: 10.1016/j.ajhg.2014.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lee S., Emond M.J., Bamshad M.J., Barnes K.C., Rieder M.J., Nickerson D.A., Christiani D.C., Wurfel M.M., Lin X., NHLBI GO Exome Sequencing Project—ESP Lung Project Team Optimal unified approach for rare-variant association testing with application to small-sample case-control whole-exome sequencing studies. Am. J. Hum. Genet. 2012;91:224–237. doi: 10.1016/j.ajhg.2012.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lee S., Wu M.C., Lin X. Optimal tests for rare variant effects in sequencing association studies. Biostatistics. 2012;13:762–775. doi: 10.1093/biostatistics/kxs014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Udler M.S., Tyrer J., Easton D.F. Evaluating the power to discriminate between highly correlated SNPs in genetic association studies. Genet. Epidemiol. 2010;34:463–468. doi: 10.1002/gepi.20504. [DOI] [PubMed] [Google Scholar]
- 32.Tibshirani R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. 1996;58:267–288. [Google Scholar]
- 33.Gamazon E.R., Cox N.J., Davis L.K. Structural architecture of SNP effects on complex traits. Am. J. Hum. Genet. 2014;95:477–489. doi: 10.1016/j.ajhg.2014.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Shi H., Kichaev G., Pasaniuc B. Contrasting the genetic architecture of 30 complex traits from summary association data. Am. J. Hum. Genet. 2016;99:139–153. doi: 10.1016/j.ajhg.2016.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Benner C., Havulinna A.S., Salomaa V., Ripatti S., Pirinen M. Refining fine-mapping: effect sizes and regional heritability. Preprint at bioRxiv. 2018 doi: 10.1101/318618. [DOI] [Google Scholar]
- 36.Gusev A., Lee S.H., Trynka G., Finucane H., Vilhjálmsson B.J., Xu H., Zang C., Ripke S., Bulik-Sullivan B., Stahl E., et al. Partitioning heritability of regulatory and cell-type-specific variants across 11 common diseases. Am. J. Hum. Genet. 2014;95:535–552. doi: 10.1016/j.ajhg.2014.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Loh P.-R., Bhatia G., Gusev A., Finucane H.K., Bulik-Sullivan B.K., Pollack S.J., de Candia T.R., Lee S.H., Wray N.R., Kendler K.S., et al. Contrasting genetic architectures of schizophrenia and other complex diseases using fast variance-components analysis. Nat. Genet. 2015;47:1385–1392. doi: 10.1038/ng.3431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gazal S., Loh P.-R., Finucane H.K., Ganna A., Schoech A., Sunyaev S., Price A.L. Functional architecture of low-frequency variants highlights strength of negative selection across coding and non-coding annotations. Nat. Genet. 2018;50:1600–1607. doi: 10.1038/s41588-018-0231-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pazokitoroudi A., Wu Y., Burch K.S., Hou K., Zhou A., Pasaniuc B., Sankararaman S. Efficient variance components analysis across millions of genomes. Nat. Commun. 2020;11:4020. doi: 10.1038/s41467-020-17576-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Speed D., Balding D.J. SumHer better estimates the SNP heritability of complex traits from summary statistics. Nat. Genet. 2019;51:277–284. doi: 10.1038/s41588-018-0279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Yang J., Bakshi A., Zhu Z., Hemani G., Vinkhuyzen A.A.E., Lee S.H., Robinson M.R., Perry J.R.B., Nolte I.M., van Vliet-Ostaptchouk J.V., et al. Genetic variance estimation with imputed variants finds negligible missing heritability for human height and body mass index. Nat. Genet. 2015;47:1114–1120. doi: 10.1038/ng.3390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wang G., Sarkar A., Carbonetto P., Stephens M. A simple new approach to variable selection in regression, with application to genetic fine mapping. J. R. Stat. Soc. Series B Stat. Methodol. 2020;82:1273–1300. doi: 10.1111/rssb.12388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.de Los Campos G., Sorensen D., Gianola D. Genomic heritability: what is it? PLoS Genet. 2015;11:e1005048. doi: 10.1371/journal.pgen.1005048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gianola D., de los Campos G., Hill W.G., Manfredi E., Fernando R. Additive genetic variability and the Bayesian alphabet. Genetics. 2009;183:347–363. doi: 10.1534/genetics.109.103952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lehermeier C., de Los Campos G., Wimmer V., Schön C.-C. Genomic variance estimates: With or without disequilibrium covariances? J. Anim. Breed. Genet. 2017;134:232–241. doi: 10.1111/jbg.12268. [DOI] [PubMed] [Google Scholar]
- 46.Schreck N., Piepho H.-P., Schlather M. Best prediction of the additive genomic variance in random-effects models. Genetics. 2019;213:379–394. doi: 10.1534/genetics.119.302324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bycroft C., Freeman C., Petkova D., Band G., Elliott L.T., Sharp K., Motyer A., Vukcevic D., Delaneau O., O’Connell J., et al. The UK Biobank resource with deep phenotyping and genomic data. Nature. 2018;562:203–209. doi: 10.1038/s41586-018-0579-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lek M., Karczewski K.J., Minikel E.V., Samocha K.E., Banks E., Fennell T., O’Donnell-Luria A.H., Ware J.S., Hill A.J., Cummings B.B., et al. Analysis of protein-coding genetic variation in 60,706 humans. Nature. 2016;536:285–291. doi: 10.1038/nature19057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Karczewski K.J., Francioli L.C., Tiao G., Cummings B.B., Alföldi J., Wang Q., Collins R.L., Laricchia K.M., Ganna A., Birnbaum D.P., et al. The mutational constraint spectrum quantified from variation in 141,456 humans. Nature. 2020;581:434–443. doi: 10.1038/s41586-020-2308-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Feldman M.W., Lewontin R.C. The heritability hang-up. Science. 1975;190:1163–1168. doi: 10.1126/science.1198102. [DOI] [PubMed] [Google Scholar]
- 51.Lewontin R.C. Annotation: the analysis of variance and the analysis of causes. Am. J. Hum. Genet. 1974;26:400–411. [PMC free article] [PubMed] [Google Scholar]
- 52.Shi H., Burch K.S., Johnson R., Freund M.K., Kichaev G., Mancuso N., Manuel A.M., Dong N., Pasaniuc B. Localizing components of shared transethnic genetic architecture of complex traits from GWAS summary data. Am. J. Hum. Genet. 2020;106:805–817. doi: 10.1016/j.ajhg.2020.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Shi H., Gazal S., Kanai M., Koch E.M., Schoech A.P., Siewert K.M., Kim S.S., Luo Y., Amariuta T., Huang H., et al. Population-specific causal disease effect sizes in functionally important regions impacted by selection. Nat. Commun. 2021;12:1098. doi: 10.1038/s41467-021-21286-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Freund M.K., Burch K.S., Shi H., Mancuso N., Kichaev G., Garske K.M., Pan D.Z., Miao Z., Mohlke K.L., Laakso M., et al. Phenotype-specific enrichment of Mendelian disorder genes near GWAS regions across 62 complex traits. Am. J. Hum. Genet. 2018;103:535–552. doi: 10.1016/j.ajhg.2018.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Sorensen D., Fernando R., Gianola D. Inferring the trajectory of genetic variance in the course of artificial selection. Genet. Res. 2001;77:83–94. doi: 10.1017/s0016672300004845. [DOI] [PubMed] [Google Scholar]
- 56.Lara L.A.C., Pocrnic I., Oliveira T.P., Gaynor R.C., Gorjanc G. Temporal and genomic analysis of additive genetic variance in breeding programmes. Heredity. 2022;128:21–32. doi: 10.1038/s41437-021-00485-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Auton A., Brooks L.D., Durbin R.M., Garrison E.P., Kang H.M., Korbel J.O., Marchini J.L., McCarthy S., McVean G.A., Abecasis G.R., 1000 Genomes Project Consortium A global reference for human genetic variation. Nature. 2015;526:68–74. doi: 10.1038/nature15393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Berisa T., Pickrell J.K. Approximately independent linkage disequilibrium blocks in human populations. Bioinformatics. 2016;32:283–285. doi: 10.1093/bioinformatics/btv546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Speed D., Cai N., Johnson M.R., Nejentsev S., Balding D.J., UCLEB Consortium Reevaluation of SNP heritability in complex human traits. Nat. Genet. 2017;49:986–992. doi: 10.1038/ng.3865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Hou K., Burch K.S., Majumdar A., Shi H., Mancuso N., Wu Y., Sankararaman S., Pasaniuc B. Accurate estimation of SNP-heritability from biobank-scale data irrespective of genetic architecture. Nat. Genet. 2019;51:1244–1251. doi: 10.1038/s41588-019-0465-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Galinsky K.J., Bhatia G., Loh P.-R., Georgiev S., Mukherjee S., Patterson N.J., Price A.L. Fast principal-component analysis reveals convergent evolution of ADH1B in Europe and east Asia. Am. J. Hum. Genet. 2016;98:456–472. doi: 10.1016/j.ajhg.2015.12.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Mathieson I., McVean G. Differential confounding of rare and common variants in spatially structured populations. Nat. Genet. 2012;44:243–246. doi: 10.1038/ng.1074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Young A.I. Solving the missing heritability problem. PLoS Genet. 2019;15:e1008222. doi: 10.1371/journal.pgen.1008222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Zaidi A.A., Mathieson I. Demographic history mediates the effect of stratification on polygenic scores. eLife. 2020;9:e61548. doi: 10.7554/eLife.61548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Sinnott-Armstrong N., Tanigawa Y., Amar D., Mars N., Benner C., Aguirre M., Venkataraman G.R., Wainberg M., Ollila H.M., Kiiskinen T., et al. Genetics of 35 blood and urine biomarkers in the UK Biobank. Nat. Genet. 2021;53:185–194. doi: 10.1038/s41588-020-00757-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Lusis A.J., Fogelman A.M., Fonarow G.C. Genetic basis of atherosclerosis: part I: new genes and pathways. Circulation. 2004;110:1868–1873. doi: 10.1161/01.CIR.0000143041.58692.CC. [DOI] [PubMed] [Google Scholar]
- 67.Musunuru K., Strong A., Frank-Kamenetsky M., Lee N.E., Ahfeldt T., Sachs K.V., Li X., Li H., Kuperwasser N., Ruda V.M., et al. From noncoding variant to phenotype via SORT1 at the 1p13 cholesterol locus. Nature. 2010;466:714–719. doi: 10.1038/nature09266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Sharma U., Pal D., Prasad R. Alkaline phosphatase: an overview. Indian J. Clin. Biochem. 2014;29:269–278. doi: 10.1007/s12291-013-0408-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Amberger J.S., Bocchini C.A., Schiettecatte F., Scott A.F., Hamosh A. OMIM.org: Online Mendelian Inheritance in Man (OMIM®), an online catalog of human genes and genetic disorders. Nucleic Acids Res. 2015;43:D789–D798. doi: 10.1093/nar/gku1205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Fang H., De Wolf H., Knezevic B., Burnham K.L., Osgood J., Sanniti A., Lledó Lara A., Kasela S., De Cesco S., Wegner J.K., et al. A genetics-led approach defines the drug target landscape of 30 immune-related traits. Nat. Genet. 2019;51:1082–1091. doi: 10.1038/s41588-019-0456-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.de Leeuw C.A., Mooij J.M., Heskes T., Posthuma D. MAGMA: generalized gene-set analysis of GWAS data. PLoS Comput. Biol. 2015;11:e1004219. doi: 10.1371/journal.pcbi.1004219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Rahman F., Johnson J.L., Zhang J., He J., Pestonjamasp K., Cherqui S., Catz S.D. DYNC1LI2 regulates localization of the chaperone-mediated autophagy receptor LAMP2A and improves cellular homeostasis in cystinosis. Autophagy. 2021 doi: 10.1080/15548627.2021.1971937. Published online October 13, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Schlam D., Bagshaw R.D., Freeman S.A., Collins R.F., Pawson T., Fairn G.D., Grinstein S. Phosphoinositide 3-kinase enables phagocytosis of large particles by terminating actin assembly through Rac/Cdc42 GTPase-activating proteins. Nat. Commun. 2015;6:8623. doi: 10.1038/ncomms9623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Csépányi-Kömi R., Sirokmány G., Geiszt M., Ligeti E. ARHGAP25, a novel Rac GTPase-activating protein, regulates phagocytosis in human neutrophilic granulocytes. Blood. 2012;119:573–582. doi: 10.1182/blood-2010-12-324053. [DOI] [PubMed] [Google Scholar]
- 75.Iwata S., Takenobu H., Kageyama H., Koseki H., Ishii T., Nakazawa A., Tatezaki S., Nakagawara A., Kamijo T. Polycomb group molecule PHC3 regulates polycomb complex composition and prognosis of osteosarcoma. Cancer Sci. 2010;101:1646–1652. doi: 10.1111/j.1349-7006.2010.01586.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Sauvageau M., Sauvageau G. Polycomb group proteins: multi-faceted regulators of somatic stem cells and cancer. Cell Stem Cell. 2010;7:299–313. doi: 10.1016/j.stem.2010.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Thaler M.A., Seifert-Klauss V., Luppa P.B. The biomarker sex hormone-binding globulin - from established applications to emerging trends in clinical medicine. Best Pract. Res. Clin. Endocrinol. Metab. 2015;29:749–760. doi: 10.1016/j.beem.2015.06.005. [DOI] [PubMed] [Google Scholar]
- 78.Kranz C., Denecke J., Lehrman M.A., Ray S., Kienz P., Kreissel G., Sagi D., Peter-Katalinic J., Freeze H.H., Schmid T., et al. A mutation in the human MPDU1 gene causes congenital disorder of glycosylation type If (CDG-If) J. Clin. Invest. 2001;108:1613–1619. doi: 10.1172/JCI13635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Schenk B., Imbach T., Frank C.G., Grubenmann C.E., Raymond G.V., Hurvitz H., Korn-Lubetzki I., Revel-Vik S., Raas-Rotschild A., Luder A.S., et al. MPDU1 mutations underlie a novel human congenital disorder of glycosylation, designated type If. J. Clin. Invest. 2001;108:1687–1695. doi: 10.1172/JCI13419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Pope S.N., Lee I.R. Yeast two-hybrid identification of prostatic proteins interacting with human sex hormone-binding globulin. J. Steroid Biochem. Mol. Biol. 2005;94:203–208. doi: 10.1016/j.jsbmb.2005.01.007. [DOI] [PubMed] [Google Scholar]
- 81.Lévy R., Okada S., Béziat V., Moriya K., Liu C., Chai L.Y.A., Migaud M., Hauck F., Al Ali A., Cyrus C., et al. Genetic, immunological, and clinical features of patients with bacterial and fungal infections due to inherited IL-17RA deficiency. Proc. Natl. Acad. Sci. USA. 2016;113:E8277–E8285. doi: 10.1073/pnas.1618300114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Puel A., Cypowyj S., Bustamante J., Wright J.F., Liu L., Lim H.K., Migaud M., Israel L., Chrabieh M., Audry M., et al. Chronic mucocutaneous candidiasis in humans with inborn errors of interleukin-17 immunity. Science. 2011;332:65–68. doi: 10.1126/science.1200439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Monteferrario D., Bolar N.A., Marneth A.E., Hebeda K.M., Bergevoet S.M., Veenstra H., Laros-van Gorkom B.A.P., MacKenzie M.A., Khandanpour C., Botezatu L., et al. A dominant-negative GFI1B mutation in the gray platelet syndrome. N. Engl. J. Med. 2014;370:245–253. doi: 10.1056/NEJMoa1308130. [DOI] [PubMed] [Google Scholar]
- 84.George S., Rochford J.J., Wolfrum C., Gray S.L., Schinner S., Wilson J.C., Soos M.A., Murgatroyd P.R., Williams R.M., Acerini C.L., et al. A family with severe insulin resistance and diabetes due to a mutation in AKT2. Science. 2004;304:1325–1328. doi: 10.1126/science.1096706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Hussain K., Challis B., Rocha N., Payne F., Minic M., Thompson A., Daly A., Scott C., Harris J., Smillie B.J.L., et al. An activating mutation of AKT2 and human hypoglycemia. Science. 2011;334:474. doi: 10.1126/science.1210878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Seong E., Insolera R., Dulovic M., Kamsteeg E.-J., Trinh J., Brüggemann N., Sandford E., Li S., Ozel A.B., Li J.Z., et al. Mutations in VPS13D lead to a new recessive ataxia with spasticity and mitochondrial defects. Ann. Neurol. 2018;83:1075–1088. doi: 10.1002/ana.25220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Gauthier J., Meijer I.A., Lessel D., Mencacci N.E., Krainc D., Hempel M., Tsiakas K., Prokisch H., Rossignol E., Helm M.H., et al. Recessive mutations in VPS13D cause childhood onset movement disorders. Ann. Neurol. 2018;83:1089–1095. doi: 10.1002/ana.25204. [DOI] [PubMed] [Google Scholar]
- 88.Wang J., Fang N., Xiong J., Du Y., Cao Y., Ji W.-K. An ESCRT-dependent step in fatty acid transfer from lipid droplets to mitochondria through VPS13D-TSG101 interactions. Nat. Commun. 2021;12:1252. doi: 10.1038/s41467-021-21525-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Vitart V., Rudan I., Hayward C., Gray N.K., Floyd J., Palmer C.N.A., Knott S.A., Kolcic I., Polasek O., Graessler J., et al. SLC2A9 is a newly identified urate transporter influencing serum urate concentration, urate excretion and gout. Nat. Genet. 2008;40:437–442. doi: 10.1038/ng.106. [DOI] [PubMed] [Google Scholar]
- 90.Anzai N., Ichida K., Jutabha P., Kimura T., Babu E., Jin C.J., Srivastava S., Kitamura K., Hisatome I., Endou H., Sakurai H. Plasma urate level is directly regulated by a voltage-driven urate efflux transporter URATv1 (SLC2A9) in humans. J. Biol. Chem. 2008;283:26834–26838. doi: 10.1074/jbc.C800156200. [DOI] [PubMed] [Google Scholar]
- 91.Caulfield M.J., Munroe P.B., O’Neill D., Witkowska K., Charchar F.J., Doblado M., Evans S., Eyheramendy S., Onipinla A., Howard P., et al. SLC2A9 is a high-capacity urate transporter in humans. PLoS Med. 2008;5:e197. doi: 10.1371/journal.pmed.0050197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Mancuso N., Rohland N., Rand K.A., Tandon A., Allen A., Quinque D., Mallick S., Li H., Stram A., Sheng X., et al. The contribution of rare variation to prostate cancer heritability. Nat. Genet. 2016;48:30–35. doi: 10.1038/ng.3446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Younes N., Syed N., Yadav S.K., Haris M., Abdallah A.M., Abu-Madi M. A whole-genome sequencing association study of low bone mineral density identifies new susceptibility loci in the phase I Qatar Biobank cohort. J. Pers. Med. 2021;11:34. doi: 10.3390/jpm11010034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Taliun D., Harris D.N., Kessler M.D., Carlson J., Szpiech Z.A., Torres R., Taliun S.A.G., Corvelo A., Gogarten S.M., Kang H.M., et al. Sequencing of 53,831 diverse genomes from the NHLBI TOPMed Program. Nature. 2021;590:290–299. doi: 10.1038/s41586-021-03205-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Turro E., Astle W.J., Megy K., Gräf S., Greene D., Shamardina O., Allen H.L., Sanchis-Juan A., Frontini M., Thys C., et al. Whole-genome sequencing of patients with rare diseases in a national health system. Nature. 2020;583:96–102. doi: 10.1038/s41586-020-2434-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Bhatia G., Gusev A., Loh P.-R., Finucane H., Vilhjálmsson B.J., Ripke S., Purcell S., Stahl E., Daly M., de Candia T.R., et al. Subtle stratification confounds estimates of heritability from rare variants. Preprint at bioRxiv. 2016 doi: 10.1101/048181. [DOI] [Google Scholar]
- 97.Weissbrod O., Hormozdiari F., Benner C., Cui R., Ulirsch J., Gazal S., Schoech A.P., van de Geijn B., Reshef Y., Márquez-Luna C., et al. Functionally informed fine-mapping and polygenic localization of complex trait heritability. Nat. Genet. 2020;52:1355–1363. doi: 10.1038/s41588-020-00735-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Schoech A.P., Weissbrod O., O’Connor L.J., Patterson N., Shi H., Reshef Y., Price A.L. Negative short-range genomic autocorrelation of causal effects on human complex traits. Preprint at bioRxiv. 2020 doi: 10.1101/2020.09.23.310748. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
h2gene software and analysis scripts are available at https://github.com/bogdanlab/h2gene.