Global Sensitivity Analysis of Background Life Cycle Inventories

Abstract

In recent years many Life Cycle Assessment (LCA) studies have been conducted to quantify the environmental performance of products and services. Some of these studies propagated numerical uncertainties in underlying data to LCA results, and several applied Global Sensitivity Analysis (GSA) to some parts of the LCA model to determine its main uncertainty drivers. However, only a few studies have tackled the GSA of complete LCA models due to the high computational cost of such analysis and the lack of appropriate methods for very high-dimensional models. This study proposes a new GSA protocol suitable for large LCA problems that, unlike existing approaches, does not make assumptions on model linearity and complexity and includes extensive validation of GSA results. We illustrate the benefits of our protocol by comparing it with an existing method in terms of filtering of noninfluential and ranking of influential uncertainty drivers and include an application example of Swiss household food consumption. We note that our protocol obtains more accurate GSA results, which leads to better understanding of LCA models, and less data collection efforts to achieve more robust estimation of environmental impacts. Implementations supporting this work are available as free and open source Python packages.

Short abstract

This study proposes an operational protocol and open source software that enable accurate global sensitivity analysis of complete life cycle assessment models.

1. Introduction

Life Cycle Assessment (LCA) aims to quantify the environmental impacts of goods and services throughout their entire value chain.^1,2 LCA models cover complex material and energy requirements and their corresponding emissions to the natural world to estimate the impacts. These so-called inventories, collected along global supply chains, contain numerous sources of uncertainty and variability.^3,4 When propagated through LCA models, uncertain inventories can lead to broad numerical uncertainty distributions of the estimated impacts, rendering LCA results difficult to interpret and communicate.^5,6 One way of reducing this uncertainty is to first employ Global Sensitivity Analysis (GSA) to determine model inputs that contribute the most to the estimated uncertainty in an LCA model output and then improve their quality by improving the underlying data or refining the relevant process models.⁷ It is possible to locate unrealistically wide input distributions that need further investigation, as well as identify inputs with a strong model response even when the input uncertainty is narrow. The latter need particular attention because they are capable of making substantial differences in the interpretation of LCA results.

LCA model inputs can belong to three classes: (i) technosphere, which describes inputs and outputs of technological systems, such as energy and material consumption; (ii) biosphere, which gives interactions with the natural environment such as the consumption of natural resources or emissions to soil, water, or air; (iii) characterization factors, which link biosphere flows to concrete harms, such as climate change or health damage from air pollution.⁸ When conducting LCAs, researchers collect study-specific, so-called foreground data that contains processes under the control of decision-makers.⁹ Foreground data can be linked to comprehensive background databases with tens of thousands of technosphere and biosphere inputs. Examples of such databases include Ecoinvent,¹⁰ Exiobase,¹¹ and Eora.¹² Together, background and foreground systems constitute life cycle inventories. Inventories and characterization factors in Life Cycle Impact Assessment (LCIA) methods have quantitative uncertainties that can be derived in multiple ways, such as analytically, from measurements, or based on expert knowledge, assumptions, or existing literature.^3,13,14 The international standard for LCA ISO 14044 recommends analyzing these uncertainties and conducting Sensitivity Analysis (SA).¹

While some studies looked at GSA for the foreground uncertainties,¹⁵⁻²⁰ including the much larger background is still considered an unresolved problem. Analyzing the complete system would lead to more complete GSA of LCA results and comprehensive understanding of uncertainty drivers. Companies (and other actors) are increasingly forced to actively investigate their supply chains and ensure that environmental and social standards are met (see, e.g., the new European system of due diligence for supply chains²¹). Knowing about the influential processes will help to support supply chain management decisions, better understand environmental hotspots, and improve, or even correct, both foreground and background data and modeling of critical processes. This research gap appears due to the much larger number of inputs in background databases, and we lack systematic GSA protocols to tackle such high dimensionality reliably and with reasonable computational resources. Typical GSA is applied to hundreds of inputs²²⁻²⁴ because models similar to LCA in the number of independent inputs and execution times are rare in practice. To the extent of our knowledge only two works^25,26 addressed tens of thousands of inputs in LCA inventories. Subsequently, GSA is either excluded from LCAs, or only less than 0.1% of all uncertain inputs are considered.^4,27 The key question remains: how to accurately and efficiently conduct GSA for complete LCA models?

We address this important issue by developing a new multistep GSA protocol to conduct GSA for all LCA inputs. Our method is (i) applicable to model inputs with probability distribution functions or population sample data, (ii) flexible regarding model structure (no assumption made on model linearity), and (iii) extensively validated after each GSA step to ensure the correctness of intermediate and final results. To demonstrate the added value of our methodology, we compare an existing screening of lowly influential inputs based on contribution analysis²⁶ against our approach based on high-dimensional screening.²⁸ We illustrate the application of both methods to the LCA of Swiss household food consumption,²⁹ linked to Ecoinvent, with a climate change LCIA method including uncertain Global Warming Potential (GWP) values. We aim to demonstrate that complete GSA of LCA is computationally feasible and encourage research toward optimizing it to allow for wider usage while preserving the reliability and completeness of GSA.

2. Materials and Methods

2.1. Matrix-Based LCA

The matrix-based LCA with n unit processes, m environmental resources and emissions, and l impact categories is expressed as y = CBT^–1f.³⁰Unit processes are the smallest elements of life cycle inventories with quantified inputs and outputs. They are linked to each other by intermediate flows, whose amounts are elements in the technosphere matrix T ∈ R^n×n and to the environment by elementary flows in biosphere B ∈ R^m×n. Elements of matrix C ∈ R^l×m are characterization factors representing the relative importance of emissions for given impact categories.³ The functional unit vector f ∈ Rⁿ is the amount of each unit process output used in the given study. The estimated environmental impact, or LCIA score, is denoted as y ∈ R^l. For simplicity, we consider one impact category and rewrite y = cBT^–1f with characterization factors in vector c ∈ R^1×m. Our analysis, however, can be extended to any number of impact categories.

LCA models can also be expressed as y = g(x), where x ∈ R^k is a vector containing k = k_T + k_B + k_c uncertain inputs from T, B, and c, respectively. Or, in other words, each x_{j ∈ {1, ..., k}} is an uncertain model input. In a typical study, B and T would have hundreds of thousands of uncertain inputs, while c would only have tens or hundreds.

2.2. Global Sensitivity Analysis

The importance of model inputs on the uncertainty in the model output is estimated with sensitivity indices computed for each input with various GSA methods, such as variance-based Sobol,^31,32 delta moment-independent indices,³³ and regression and correlation coefficients.⁷ GSA can also be conducted using multistep protocols,^3,25,34 where the first k_∼inf lowly influential inputs are filtered out (“∼” stands for negation and “inf” for influential), and the remaining k_inf influential inputs are ranked according to their importance. Ranking hundreds of inputs is well-studied in general applications³⁵ and is often used in the GSA of LCA foreground systems;¹⁸ however, as backgrounds contain many more inputs, screening hundreds of thousands of non- and lowly influential inputs is much harder and rarely performed. We describe existing methods based on the traversal of the supply chain graph and contribution analysis in Section 2.3.1 and then propose a novel approach in Section 2.3.2 that leverages local SA and builds on our previous work on high-dimensional robust screening.²⁸ In both approaches we aim at filtering out k_∼inf inputs and then ranking the remaining influential inputs as explained in Section 2.4. The high-level GSA protocol is depicted in Figure S1 of the Supporting Information Section 1. Note that both methods are applicable to foreground and background systems (and their combination).

2.3. Screening Out Non- and Lowly Influential Inputs

2.3.1. Screening Based on Contributions to the LCIA Score

This approach has been proposed by Cucurachi et al.²⁶ and implemented in the Activity Browser software,³⁶ which provides a graphical user interface for LCA studies. It builds on the Brightway Python framework.³⁷ The main idea is to filter out inputs with contributions to y scores lower than a user-defined cutoff τ; here input uncertainty is not considered. Figure 1 depicts the procedure, which we describe below.

Figure 1.

Flowchart of screening based on contributions to the total LCIA score.²⁶ First, LCIA contributions of technosphere, biosphere, and characterization inputs are computed, and then k_inf inputs with contributions higher than τ are selected. Cutoff τ is a parameter chosen as a fraction of the total LCIA score. In the supply chain traversal (SCT) it also determines to which extent supply chains are traversed.

Step 1: The computation of technosphere contributions uses best-first graph traversal to identify intermediate flow elements in T whose contribution to the total LCIA score falls below the cutoff τ. Graph traversal can be performed on the directed adjacency matrix T. Each nonzero element f serves as a separate starting point, and separate LCA calculations are done for each input intermediate flow used by each starting point. This procedure is applied recursively in a best-first search algorithm.³⁸ Contribution scores of the same exchanges encountered multiple times are summed up (e.g., in cases where the same transport activities are used for different products). Nodes whose cumulative environmental impacts fall below the cutoff are considered noninfluential. Given the interconnected, cyclic nature of supply chains, the graph traversal is in principle infinite; it terminates when all branch nodes are below the cutoff or the threshold number of calculations has been performed. The complete and detailed supply chain traversal (SCT) algorithm was well-documented by Cardellini et al.³⁸ This step outputs a list T̃ of technosphere exchanges with scores above τ and their respective contributions to the total LCIA score.

Step 2: Computation of biosphere contributions requires rewriting the standard LCA formula:

1

where diag(·) converts vectors into diagonal matrices. The resulting B̃ ∈ R^m×n with elements b̃_s,t contains contributions of m elementary flows per n unit processes to the LCIA score, such that y = ∑_s=1^m∑_t=1b̃_s,t. By setting to 0 elements of the matrix B̃, where b̃_s,t < τ, we can filter out many biosphere exchanges with low scores. The resulting B̃ provides a list of biosphere exchanges and their contributions to the LCIA score that are greater than τ.

Step 3: Computation of characterization contributions is similar to the biosphere and is based on the following:

2

This is equivalent to computing contributions of the characterization as c̃_s = ∑_t=1ⁿb̃_s,t. The resulting c̃ ∈ R^m sums up to the LCIA score: y = ∑_s=1c̃_s. Similarly to the biosphere, elements c̃_s that are smaller than τ can be set to 0, such that we obtain a list of characterization factors with sufficiently high contribution scores.

Note that this step is not part of the original publication,²⁶ where all uncertain characterization inputs are considered. There it was appropriate because only a few methane elementary flow inputs had uncertainties. However, for the sake of consistency with Steps 1 and 2 above, we included explicit computation of characterization contributions. In Section 3.3 we will see that it achieves a better screening performance compared to the original paper and provides a fairer comparison with the new approach that we propose in Section 2.3.2.

Step 4: Remove k_∼inf noninfluential inputs with the lowest contributions among technosphere, biosphere, and characterization inputs using T̃, B̃, and c̃. The remaining k_inf exchanges are considered to be influential and need to be further ranked. Note that the τ parameter determines the maximum possible k_inf since its higher values would result in fewer inputs.

Since this approach is based on the deterministically computed LCIA scores, it considers contributions to scores as opposed to contributions to uncertainty of scores. Thus, inputs with low scores but high uncertainties might be filtered out, which could result in an incorrectly ranked list of inputs. Moreover, the SCT algorithm implies the construction of a strictly linear graph from the T matrix, which makes it nontrivial to include inputs from parametrized or other novel technosphere exchanges as inputs to GSA if they exhibit complex nonlinear relationships, including correlation across exchanges. On the other hand, this approach is worth analyzing as its computational gains allow complete screening within an hour. In the next section we propose a novel approach that does account for input uncertainty levels and is not restricted to a given model complexity.

2.3.2. Screening Based on Local SA

The flowchart of our screening approach that is based on local SA is presented in Figure 2. Below we elaborate on the flowchart steps.

Figure 2.

Flowchart of multistep screening based on local SA. In Steps 1–2 we remove inputs with zero influence on the LCIA score uncertainty, and then in Steps 3–4 we filter out k′_∼inf lowly influential inputs using local SA. The initial value for k′_∼inf is on the order of tens of thousands and is adjusted based on the validation of SA in Steps 5.1–5.3. In Step 6 we proceed by applying more refined high-dimensional screening²⁸ to further reduce inputs to the desired k_inf. This procedure determines model linearity first and then computes Spearman correlations for each input if the model is sufficiently linear and gradient boosting importance metrics otherwise.

Step 1: Remove noninfluential biosphere inputs by constructing B̃ (see eq 1) and choosing x_j that correspond to biosphere inputs with zero contributions, namely where b̃_s,t = 0.

Step 2: Remove noninfluential characterization inputs by constructing c̃ (see eq 2) and choosing x_j that correspond to characterization inputs with zero contributions, namely where c̃_s = 0.

Steps 3.1–3.3: Run local SA for P perturbations (changes) per input by varying each x_j (selected in the previous steps), while keeping all other inputs fixed to their deterministic values, namely those used in deterministic computations. For functional unit f, many inputs would have zero or low effect on the resulting score y_j ∈ R^P. If y_j has the same P values, all equal to the total deterministic LCIA score, then the input is noninfluential. If it contains very similar values, then the input is lowly influential and could be filtered out as described in the next step.

Step 4: Remove k′_∼inf inputs that induce the lowest uncertainty in y_j among technosphere, biosphere, and characterization inputs. The value of k′_∼inf < k is adjusted iteratively in validation Steps 5.1–5.3. The measure of uncertainty in y_j can be selected depending on the number of perturbations P. If P = 2, it can be chosen simply as the squared or absolute difference between LCIA scores. For P ⩾ 3, one can compute sum of absolute differences, variance Var[y_j], etc.

Steps 5.1–5.3: Validation of SA can be performed in multiple ways. The method we employ here can be used for validating both screening and ranking. It relies on two sets of model outputs obtained from N_v Monte Carlo (MC) simulations: (i) Y_all = g(X) with X ∈ R^N_v×k being random samples based on the underlying uncertainty distributions of model inputs, when all of them vary; and (ii) Y_inf = g(X|X_∼inf) where influential inputs vary consistently with the values they take in X, and noninfluential inputs are fixed to their deterministic values.²² In other words, sample values of a jth influential input would be the same in cases (i) and (ii).

If the correlation between Y_all and Y_inf is high, then the uncertainty is sufficiently captured, and k′_∼inf can be kept as is or even increased to save computational resources in the next step. Low correlations, on the other hand, indicate the need for reducing k′_∼inf and rerunning validation of the screening. Because this is only a preliminary screening, we recommend acceptable correlation values of 0.95 or higher. The number of MC samples has been chosen as N_v = 2 000.

Step 6: Run high-dimensional screening. The screening of clearly noninfluential inputs described in Steps 1–5 allows us to reduce the complexity of Step 6 by bringing the number of inputs from hundreds of thousands down to tens of thousands. Once those steps have been completed, we employ a more refined but also more computationally expensive analysis that was proposed by Kim et al.²⁸ First, that procedure runs N MC simulations on random samples X ∈ R^N×k_inf and generates Y = g(X) ∈ R^N model outputs. Using (X, Y) it performs linear regression and computes standardized regression coefficients for each model input. These coefficients allow us to assess how much of the model output variability is captured under the assumption of its linearity by computing the coefficient of determination.⁷ If the output variability is sufficiently reproduced with linear regression, the model is considered reasonably linear, and we compute Spearman correlations⁷ as sensitivity indices; otherwise, we calculate the feature importance values from the gradient-boosted tree method.^39,40 In both cases it is possible to reuse (X, Y) samples. The construction of this robust high-dimensional screening procedure was based on benchmarking multiple GSA methods for test models with an increasing number of inputs (1 000, 5 000, and 10 000), while analyzing the convergence and robustness of sensitivity indices, screening, and ranking.

2.4. Ranking of Influential Inputs

After filtering out lowly influential inputs with either of the screening procedures described in Section 2.3, we rank the remaining k_inf inputs to determine where to prioritize improved modeling or data quality. This task is computationally feasible for LCA models with k_inf on the order of hundreds. We employ Sobol total order indices,³² with details given in Supporting Information Section 2, but other methods can also be used.¹⁸ The high-level flowchart of the overall GSA protocol is in Supporting Information Section 1.

2.5. Case Study of Swiss Household Consumption

Household consumption is a major driver of the economy with housing, mobility, and food constituting the largest shares of environmental impacts.⁴¹ LCAs of consumption are aimed at tackling the challenge of sustainable consumption and identifying lifestyles with fewer impacts. Information on consumption patterns usually comes from consumer expenditure surveys. Several assessment methods compared by Nathani and Soceco⁴² based on input–output tables, process-based LCA models, or their hybrid combination have been performed to evaluate the impact of Swiss households with available breakdown per consumption categories. Here we follow the procedure implemented by Froemelt et al.,^29,43 which is in line with existing approaches.

2.5.1. Goal and Scope

The goal of this study is to propose and test a GSA methodology for background inventories. We test the performance of the described screening approaches on a case study of the climate change impact of average Swiss household food consumption.

2.5.2. LCA Modeling

The foreground system was originally built for the total consumption of Swiss households,²⁹ but for the present study, we will focus only on food and nonalcoholic beverages. The Swiss household budget survey (HBS) for 2015–2017 provides a basis for the foreground system and functional unit.⁴⁴ It contains consumption patterns of 9 955 households—their monetary expenses and purchased goods amounts—and encompasses 84 food items, excluding meals from restaurants and hotels and while traveling. The functional unit is one month of food, and the nonalcoholic beverage consumption is averaged among all households.

The background system contains process data from Ecoinvent (version 3.7.1, cutoff system model).¹⁰ The uncertainties for T and B come from Ecoinvent, where uncertainty distributions were derived using default basic uncertainty values. These default values were generated using expert judgment; new estimates of default uncertainty values based on empirical data have been published but are not yet used in Ecoinvent.⁴⁵ In principle, the variability of households’ consumption patterns could be added to the foreground, but in this particular case study it would result in much larger uncertainty in LCIA scores compared to considering only background uncertainty (see Figure S2 in the Supporting Information Section 3), removing the importance of background sensitivity analysis. This is not surprising, as there are substantial differences between the household profiles, including families with (many) kids, retired couples, single person households, etc. As our purpose here was the illustration of a method applied to large background databases and not a specific LCA study, we therefore do not include uncertainty in the foreground. However, the methods themselves are applicable to all uncertainties, as they would appear as part of T, B, and c matrices.

2.5.3. Life Cycle Impact Assessment

Environmental performance is assessed via the 100-year GWP values of elementary flows taken from the IPCC 2013 report⁴⁶ and provided together with the Ecoinvent database.⁴⁷ GWP values are expressed in kilograms of CO₂ equivalent (kg CO₂-eq). Uncertainties in GWP were computed for 90 greenhouse gases following methodology suggested in the IPCC report⁴⁸ that employs first-order Taylor expansion⁴⁹ (see Supporting Information Section 4 with GWP uncertainties depicted in Figure S3 and estimated uncertainty distributions given in Table S1).

2.5.4. Uncertainty Analysis and Propagation

The number of uncertain exchanges for Ecoinvent are k_T = 186 602 and k_B = 222 049, which in combination with k_c = 90 results in k = 408 741 model inputs. Uncertainty distributions are overwhelmingly log-normally distributed, with only 643 normally distributed inputs, 177 following triangular distribution, and 10 being uniform. This study only considers parameter uncertainty⁵⁰ that is propagated numerically with MC simulations. Following standard LCA practice and data availability, model inputs are sampled independently from each other, and input correlations are neither quantified in background databases nor taken into account in our analysis. For the ranking step, the Sobol method is used. This method does not correct for correlations and is therefore consistent with the given sampling.³² The limitations of this assumption of independence are addressed in the Outlook Section 4.

3. Results and Discussion

3.1. Software

The complete Swiss household consumption foreground inventory, compatible with Brightway database importers, and its contribution analysis for the average monthly food consumption are given in the Supporting Information Excel file. This database can be generated using the consumption_model GitHub repository,⁵¹ which links it to the Ecoinvent background. The code for generating a Brightway compatible LCIA method with uncertain GWP values is available as the Python package gwp_uncertainties.⁵² To perform SA we employed the gsa_framework Python package.⁵³ Note that the current implementation of GSA methods only allows sampling from distributions. All code developed in this study is open-source. The reader is referred to Supporting Information Section 5 for the detailed data and software description.

3.2. LCA of Swiss Household Food Consumption

We depict the distribution of LCIA scores obtained with 2 000 MC samples as a histogram in Figure 3. Its estimated mean ± standard deviation is given in black, where the red cross marks the deterministically computed LCIA score equal to 212 kg CO₂-eq per household per month (see the Supporting Information Excel file for contribution analysis). All k = 408 741 model inputs are sampled independently. The estimated mean is higher than the deterministic score due to numerous log-normally distributed inputs, whose values used for deterministic computations are set to their medians, which are always lower than the mean values. This skew becomes more pronounced with higher numbers of log-normally (or other asymmetrically) distributed inputs. As the interest of this study lies in the output distribution width, we do not focus on point values and merely acknowledge this issue, which might not be as clearly visible in models with fewer or less skewed asymmetric inputs, e.g., if only uncertainty in the foreground is considered. The reader is referred to Supporting Information Section 6, Figure S4 for more details.

Figure 3.

Histogram of uncertainty in LCIA scores when all model inputs vary. The high difference between the deterministic LCIA score and the distribution mean is due to many log-normally distributed inputs and their values in deterministic computations (see Supporting Information Section 6).

3.3. Screening Out Non- and Lowly Influential Inputs

The described screening approaches require LCA practitioners to specify the desired k_inf. By filtering out more inputs, we reduce the subsequent cost of ranking of the inputs; at the same time, k_inf should be conservative enough, such that no important inputs are filtered out. Then k_inf satisfying this trade-off can be found by performing validation of the SA procedure for multiple k_inf values (see Section 2.3.2). Here we assess the performance of the two screening approaches by running validation for 2 000 MC simulations and k_inf = [100, 200, 400, 800, 1 600]. As the screening based on contributions has a tuning parameter τ, we also investigate τ = [1e-2, 1e-3, 1e-4], i.e., one order of magnitude lower and higher than τ = 1e-3 from the original paper.²⁶

For the screening with local SA, we chose P = 3 for the technosphere inputs by setting them to their deterministic values, as well as 10 times lower and higher than the deterministic values. We also tested P = 10 because in principle model output is nonlinear with respect to technosphere (due to the inverse of T),⁵⁴ but our experiments showed that for the given LCA case study P = 3 and P = 10 yield the same screening results. For B and c, P = 2 is certainly sufficient due to model linearity in these inputs. This approach allows us to conduct local SA efficiently, independent of the input distributions, and reliably, because we validate results. The subsequent robust high-dimensional screening (see Step 6) revealed that the model is fairly linear and Spearman correlations were used as sensitivity indices.

Figure 4 shows two kinds of results for various levels of k_inf:

• (i)The first three columns consider different cutoffs τ. For each combination of k_inf and τ, we depict sets of influential inputs determined only by screening based on contributions (white bar) and then only by screening based on local SA (dark bar) and their intersection, or agreement, with each other (hatched bar). Filtering based on contributions does not always yield the desired number of influential inputs if the cutoff τ is chosen too high. This is the reason some subplots in the first column are missing.
• (ii)The last two columns show scatter plots for the validation of SA between the LCIA scores obtained when all inputs vary on the x-axes and when only influential inputs vary on the y-axes. Subplots are shown for τ = 1e-4 (the most conservative). Column 4 provides results for screening with contributions, whereas column 5 is for screening with local SA. Titles of the subplots print Spearman correlations ρ between Y_all and Y_inf. Higher Spearman values and visually narrower scatter plots indicate that more uncertainty is captured and a better screening outcome is achieved.

Figure 4.

Comparison between screening with contributions and local SA. For different k_inf in rows: (i) Columns 1–3 are for varying τ. Each subplot shows technosphere, biosphere, and characterization inputs classified as influential, respectively, identified by the two screening approaches. Areas of bars are proportional to the number of inputs within each subplot: only contributions approach is in white, only local SA is in dark, and their intersection is in hatched bars. Within each row, the area of dark plus hatched below the red line stays the same because local SA screening does not depend on τ. The actual number of inputs on which the methods agree is below the subplots for the three types of inputs. (ii) Columns 4–5 show validation of screening (for τ = 1e-4) as scatter plots between Y_all and Y_inf with their correlations given as subplot titles.

This figure enables a few insights about both screening approaches:

• 1.Scatter plots show that local SA screening yields better results since even 100 inputs capture more of the output uncertainty than 1 600 inputs obtained from screening with contributions.
• 2.Methods agree on a relatively low number of influential inputs, where even at τ = 1e-4 and k_inf = 1 600, only 310 inputs lie at the intersection. Ultimately, it shows that by only looking at input importance from contribution analysis, we fail to see the input’s uncertainty dimension, and hence our understanding cannot always be propagated to SA. Put simply, high contributions do not correspond to high importance for uncertainty in the LCIA score. Inputs with rather low contributions can become relevant if their uncertainty is large.

As mentioned in Step 3 of Section 2.3.1, contributions of the characterization factors have not been computed according to the original contributions-based method.²⁶Supporting Information Section 7 provides screening results without Step 3. We can see in Figure S5 (analogous to Figure 4) that the share of selected characterization inputs from contributions screening is much larger, but the agreement between the two methods is smaller, and ρ values in column 4 are also lower. We keep Step 3 as part of the contributions method in the following analysis since it yields better screening results.

3.4. Ranking of Influential Inputs

Based on the performed screening, we chose rather low k_inf = 200 that still results in high ρ > 0.85 for both approaches and the most conservative τ = 1e-4 that comprehensively traverses the supply chain. Experiments with lower cutoffs did not show substantial change in the selected inputs. We then conducted GSA for ranking with Sobol total order indices after both of the screening approaches. GSA results are given in the Supporting Information Section 8, and the Sobol indices estimates with confidence intervals are given in Figure S6. The convergence and robustness of sensitivity indices are depicted in Figure S7. To compare the two obtained rankings, we performed the same validation as in the previous section but by varying from 1 to 20 inputs starting with the most influential one and adding one input at a time. These results are depicted in Figure 5.

Figure 5.

Comparison between ranking after screening with contributions and local SA. The main correlation plot shows (i) on the left y-axis Spearman ρ between Y_all and Y_inf, where the latter is obtained for the number of varying inputs on the x-axis, and (ii) on the right y-axis the relative increase of ρ when each new input is added. Screening with contributions is in dashed lines, and with local SA in solid, with darker upper traces showing ρ and lower lighter traces showing increase in ρ. Green arrows for 2, 10, and 20 inputs lead to validation of screening with pairs of scatter plots between Y_all and Y_inf and their overlaying histograms.

The main plot in the top left corner shows ρ and relative increase in ρ versus the number of influential inputs included. We show scatter plots and histograms (i) for the two most influential inputs, as they are the same in both approaches; (ii) for 10 inputs, because this is the point where the relative increase in ρ is low; and (iii) for the maximum number of 20 influential inputs.

Ranking after screening with contributions gives reasonable results of ρ = 0.801 with only 10 inputs. Nevertheless, ranking after screening with local SA yields ρ = 0.926 at the same number of inputs, which is confidently higher than even ρ = 0.902 obtained from varying 1 600 inputs after screening with contributions (see last row of Figure 4). Some of the inputs filtered out with the contributions approach were in fact important for the uncertainty in the model output.

3.5. Ranked List of Exchanges

Table 1 and the Supporting Information Excel file contain lists of 20 and 200 exchanges, respectively, ranked with GSA after the two screening approaches. The lists contain information on the assigned ranks, exchange types, names, amounts, uncertainty information, and Sobol indices estimates. Both approaches agree on many inputs related to milk (ranks 1/1, 2/2, 4/6, 13/17, and 19/25 from screening with contributions and local SA, respectively) and beef (9/11) production. Among other exchanges related to milk and beef cattle supply chains are soybean (6/9, 10/13) and maize grain (7/10) feed production and their emissions (8/12), as well as transport (15/18, 18/21), housing (ranks 16/19, 20/26), and electricity (11/14). It is not surprising that these exchanges have high ranks because they are present in numerous household consumption categories, such as dairy, bakery, and meat products, and have high cumulative contribution scores. Less expected, given our focus on food, are biosphere emissions from heat production (5/7, 14/16), which appear in green salads, leafy, fruiting, and root vegetable food items. Similarly, hard coal mine operation in China (12/15) is part of cucumber, radish, and lettuce supply chains. Here is where the household food consumption modeling might not represent Swiss conditions due to the lack of Swiss-specific supply chain data.

Table 1. Ranked Lists of Influential Inputs Obtained after Screening with Contributions and with Local SA^a.

contributions rank	local SA rank	type	exchange		amount	distr.	σ	contributions ŜT	local SA ŜT
1	1	cf		methane, nonfossil	2.85e1 kg CO2e		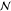6.749	0.457	0.352
2	2	tech	from	market for cow milk, GLO	6.75 kg	Log	0.214	0.192	0.145
			to	cheese production, soft, from cow milk, GLO
	3	bio	from	carbon dioxide, from soil or biomass stock	7.70e–5 kg		0.738		0.131
			to	onion seedling production, for planting, RoW
	4	bio	from	carbon dioxide, from soil or biomass stock	3.77e–2 kg		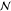0.738		0.073
			to	maize silage production, RoW
3	5	cf		dinitrogen monoxide	2.65e2 kg CO2e		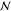46.8	0.073	0.056
4	6	bio	from	methane, nonfossil	1.84e–2 kg	Log	0.228	0.066	0.050
			to	milk production, from cow, RoW
5	7	bio	from	carbon monoxide, fossil	1.14e–2 kg	Log	0.833	0.037	0.030
			to	heat production, anthracite, at stove 5–15 kW, RoW
	8	bio	from	carbon dioxide, from soil or biomass stock	4.96e–3 kg		0.738		0.028
			to	orange production, fresh grade, RoW
6	9	tech	from	market for soybean, RoW	7.35e–1 kg	Log	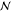0.245	0.033	0.025
			to	soybean, feed production, RoW
7	10	tech	from	market for maize grain, RoW	9.58e–1 kg	Log	0.245	0.012	0.009
			to	maize grain, feed production, RoW
9	11	bio	from	methane, nonfossil	4.22e–1 kg	Log	0.226	0.007	0.005
			to	intensive beef cattle production on pasture, RoW
8	12	bio	from	carbon dioxide, from soil or biomass stock	4.58 kg		0.738	0.007	0.005
			to	soybean production, RoW
10	13	tech	from	market for soybean, feed, GLO	9.78e–2 kg	Log	0.103	0.006	0.005
			to	milk production, from cow, RoW
11	14	tech	from	market for electricity, high voltage, CN-SGCC	1.01 kWh	Log	0.169	0.006	0.005
			to	el. voltage transformation from high to medium, CN-SGCC
12	15	bio	from	methane, nonfossil	1.31e–2 kg	Log	0.431	0.006	0.004
			to	hard coal mine operation and hard coal preparation, CN
14	16	bio	from	carbon dioxide, fossil	1.14e–1 kg	Log	0.207	0.005	0.004
			to	heat production, anthracite, at stove 5–15 kW, RoW
13	17	bio	from	dinitrogen monoxide	4.17e–4 kg	Log	0.295	0.005	0.004
			to	milk production, from cow, RoW
15	18	tech	from	market group for transport, freight, lorry, unspecified, GLO	4.63e–1 ton km	Log	0.452	0.004	0.003
			to	market for cow milk, GLO
16	19	tech	from	market for housing system, cattle, tied, per animal unit, GLO	2.00e–2 unit	Log	0.585	0.004	0.003
			to	operation, housing system, cattle, tied, RoW
17	20	cf		methane, fossil	2.97e1 kg CO2e		7.033	0.004	0.003
18	21	tech	from	market gr. for transp., freight, light commercial vehicle, GLO	2.95e–2 ton km	Log	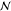0.452	0.004	0.003
			to	market for cow milk, GLO
19	25	tech	from	market for cow milk, GLO	5.06 kg	Log	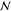0.214	0.003	0.002
			to	butter production, from cow milk, GLO
20	26	tech	from	market for housing system, pig, fully slatted floor, GLO	2.00e–2 unit	Log	0.585	0.002	0.002
			to	operation, housing system, pig, fully slatted floor, RoW

^aGLO, global region; RoW, rest of the world; , normal distribution; Log 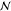, log-normal distribution; σ, standard deviation; Ŝ^T, Sobol total order index.

Notably, out of the first 20 exchanges, the two approaches agree on 17, and only three are identified differently. However, the three carbon dioxide flows from onion seedling (−/3), maize silage (−/4), and orange (−/8) production identified by screening with local SA are normally distributed with means close to zero but standard deviations of 0.738 for all of them. This distribution has both positive and negative values which implies that carbon can be not only emitted but also sequestered. While this could be possible in agriculture, further investigation is needed to determine whether the actual ranges of carbon amounts are reasonable. The contribution-based approach did not identify these biogenic carbon flows because they have very small median impact scores and have been filtered out at the screening step. By looking at the complete Ecoinvent biosphere, we found a total of 57 such normally distributed exchanges with the same standard deviation of 0.738 and varying mean values, all in agricultural processes and linked to the same carbon dioxide flow. Given that the standard deviation in normal distributions is scale dependent or depends on the unit of the input, it seems odd that the same value appears in the production of one onion seedling and a kilogram of soybean. Perhaps either the distribution type should be changed to log-normal, where the standard deviation is indeed unitless, or the values of standard deviation should be corrected. This finding reminds us that database users are not at the mercy of background providers; they can both report such inconsistencies and also amend or disaggregate them themselves.

Supporting Information Section 9 and Figure S8 show an example of how uncertainty in LCIA scores can be narrowed if we change distributions of biogenic carbon flows to log-normal and reduce uncertainty in the first 20 remaining inputs. Alternatively, if we convert all 57 carbon flows to log-normal distributions, then GSA results from contributions and local SA approaches would be very similar and exactly the same for the top 20 inputs. This specific result is a property of this LCA case study and would not hold for more complicated cases. We address this more in the Outlook section below.

4. Outlook

Despite recent advances in computational sciences and the need for more robust environmental impact assessments, uncertainty and sensitivity analyses remain challenging tasks and are rarely addressed in LCA. This is due to the lack of efficient software and suitable GSA methods, especially considering the high dimensionality of LCA models. One common misconception when tackling the GSA of LCA lies in equating it with contribution analysis. While our instinctual understanding that exchanges with high contributions are likely to have high influence on both the total LCIA scores and their uncertainty is reasonable, our results show that the true picture is more complex.

A clear advantage of the contributions-based approach lies in its computational performance, as it allows screening within 1 h on a local computer, whereas the local SA method would need a day of parallel computations or 5–6 h on a cluster. However, speed gains and simplicity come at a price of filtering out influential exchanges, especially if they are counterintuitive and cannot be anticipated from domain-specific knowledge. The approach we proposed in this paper is methodologically superior to the contributions method in a number of ways: (i) it is applicable to LCAs with parametrized exchanges and nonlinear or correlated relationships between parameters, whereas matrices are inherently linear structures, (ii) it explicitly incorporates uncertainties in model inputs, and (iii) it includes extensive validation of GSA. Among other properties, model inputs do not need to follow simple continuous probability density functions or a specific sampling design for MC simulations but can instead be based on real measurements or external models with their own logic.

Since the contributions approach does not account for variations in inputs, it cannot outperform more comprehensive GSA methods such as the one presented in this work. For the given case study, the first 20 most important inputs are similar because (i) inputs with high contributions happened to also display high uncertainties in the case investigated, and (ii) the given LCA model is rather linear. This would not necessarily be the same in other LCA studies. For the first 100 inputs, however, the two screening methods agree only on 63 inputs as depicted in Figure 4. Differences between the two approaches would be more prominent if lowly contributing inputs would have high uncertainties and if the LCA model contained more nonlinearity and correlations. Linearity plays a role because results of the contribution analysis would change if we vary inputs. Hence, as LCA models are becoming more complex and more nonlinear, contributions computed for one combination of input values would no longer generalize for other points in the input space.

One way forward would be to combine these two screening approaches. Since biosphere and characterization filtering is quick in both cases, the local SA approach should be employed for those inputs, and the main computational burden falls onto analyzing the technosphere. An easy improvement could be to modify the search algorithm in graph traversal such that nodes are visited based on not only their contributions to the total score but also their degree of uncertainty. We leave investigation of this exciting direction to future research.

One of the limitations of our work lies in independent sampling, where input correlations are not considered. In general, correlated sampling is rarely addressed in LCA studies, even though researchers recognize its importance.⁵⁵ While the proposed local SA screening can still be used for the correlated samples, the GSA method for the ranking step should be adjusted accordingly. There are a wide variety of ways to include correlations that remain to be investigated in future studies, including maintaining mass, energy, economic balances, parametrization of data sets, the use of correlated population data, and using process models in the sampling procedure.

Another limitation of our case study is the exclusion of foreground uncertainty—the different consumption patterns of the individual households—from the analysis. While our case study excluded this foreground uncertainty, the presented methodology can be applied to both foreground and background systems.

Irrespective of the GSA methodology employed, we are convinced that the validation of GSA results should be an essential component in the GSA of LCA, as it allows us to assess its quality and compare various sensitivity approaches. In particular, validated results of our protocol show that 99% of inputs can be fixed to their deterministic values, and varying as few as 20 most influential inputs almost entirely reproduces a complete uncertainty distribution of the estimated environmental impacts. Such validation will only become more important as LCA practice evolves to include larger databases and correlated, nonlinear inventory modeling.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.est.1c07438.

• GSA protocol flowchart; Sobol total order indices; background and foreground uncertainties; uncertainties in GWP values; software, data, and reproducibility of results; effect of asymmetrically distributed inputs on LCIA scores; input screening with the original contributions-based approach; GSA results; narrowing LCIA scores uncertainty (PDF)

• Excel sheets with (i) consumption model foreground compatible with Brightway import, (ii) contribution analysis for the household food consumption, and (iii) ranked list of 200 influential exchanges identified after screening with contributions and with local SA (XLSX)

The authors declare no competing financial interest.