Polyhedra and Honeycombs in a Coffered Ceiling in the Picasso Museum in Malaga

Abstract

This paper reflects upon the remarkable ceiling of the Picasso Museum in Malaga, an example of the wooden coffered ceilings built during the early Renaissance in Spain. The unusual design of the ceiling is based on octagons surrounded by four-pointed stars. This is used as the point of departure for a mathematical investigation of polyhedral forms. Two different polyhedra are constructed, conceived in such a way that the honeycombs generated by them, can be considered a polyhedral generalization of the planar pattern of regular octagons and four-pointed stars. Both are constructed by means of special truncations of a cube. The truncation procedure is extended to construct a polyhedral generalization of the planar pattern of four-pointed stars and 45° rhombuses; in this case, the polyhedron obtained is a variation of one of the star polyhedra drawn by Jamnitzer. The geometric honeycombs thus defined could be used as models for new designs.

Introduction

The Picasso Museum in Malaga is located in the sixteenth-century Buenavista Palace (Fig. 1b), which features interesting wooden ceilings of traditional Spanish structural carpentry (sometimes also called “Mudejar carpentry”). Some of these are original to the palace: the alfarjes de lazo (planar panels decorated by superimposed lacework) in the upper gallery around the courtyard (Fig. 1a); the exceptional replicas of the first floor; and the wooden frame shown in Fig. 1c, where the interlacing work appears to be integrated in the planes. Other ceilings are of the same age, but imported from demolished buildings (Nuere 2004).

Fig. 1.

a The ceiling of the upper gallery around the courtyard; b Buenavista Palace; c Wooden frame in the staircase to the first floor. Photos by the author

However, the most spectacular ceiling is the one in the small room at the right of the stairway of the entrance hall (Fig. 2).1 It differs from the other ceilings in design, colour and style. It is formed of twelve deep octagonal coffers of around 1 m. in diameter, devised from a pyramidal frustum and surrounded by stars. The main coffers are juxtaposed to squared central coffers, with triangular faces filling the gaps between the two. The decoration is plain, accomplished by means of simple mouldings. The octagonal coffers finish with carved vegetal motifs; the square ones present an intermediate row of small dentils and a carved central rosette. The centre of each star is decorated with a small pendant. The result is an elegant compound coffer that be seen as a material model of a three-dimensional generalization of the regular octagon.

Fig. 2.

The octagonal coffers and details before March 2020; see note 1. Photos by the author

From a geometrical point of view, this ceiling can be considered a three-dimensional expansion of a planar pattern formed by octagons and four-pointed stars (Fig. 3c), where each octagon is the base of a pyramidal frustum, visually approaching a layer of space-filling polyhedra. This configuration may be considered an attempt to fill space with three-dimensional stars and octagonal frustums. The aim of this paper is to try to fill space with convex polyhedra and star polyhedra such that the spatial pattern (or honeycomb) that it generates is a three-dimensional generalization of the initial planar pattern. In other words, the aim is to construct a geometric honeycomb that resembles the planar pattern of regular octagons and four-pointed stars.

Fig. 3.

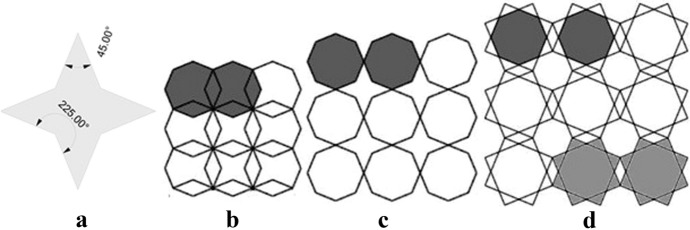
a Four-pointed star; b Pattern by stars and rhombuses; c Four-pointed stars and octagons with vertices in contact; d the result of {8/2} stars with points in contact

In architecture, the body of literature about coffered ceilings, also called polyhedral ceilings, is extensive and diverse, focusing on the history of the construction, structural aspects of the supporting frame, constructive materials, decorative elements, conservation and restauration, etc.2 There are also strictly geometric studies of coffered ceilings devoted to geometrical descriptions of the shapes and patterns.3 The geometry of the design is always studied by means of planar projections, where the coffers are recognized as pyramidal frustums, but with the sole geometric role of providing a decorative depth to a planar pattern. The main problem arises in the ceilings formed by the union of several planar panels, focusing the studies on how to fit a planar pattern in the sloped panels and the connexions among them.

The research presented in this paper is original and new since its purely mathematical approach, which considers the coffered ceiling as an inspiring three-dimensional material model, leads to new mathematical results in polyhedral geometry. It is a multidisciplinary contribution which clearly shows the nexus between architecture and mathematics.

The Building and the Ceiling

The Buenavista Palace (Fig. 1) is the most important example of civil architecture built in Malaga after the Reconquest from the Muslims in 1487. The original building, the home of a Muslim dignitary, was donated by the Catholic kingdom to the widow of the II Count of Cabra (1445–?). The Renaissance building we see today was built in the sixteenth century by Diego de Cazalla, a converted Jewish civil servant of the Crown. It belonged to the Buenavista counts until the nineteenth century. It was then used as a tenement house, school, carpenter’s workshop and hospital until 1938. Neglected by its owners, it was finally donated to the state in 1946, and became the home of the Fine Arts Museum inaugurated in 1961. The building was closed in 1997 for renovation, and opened again in 2003 as the Malaga Picasso Museum (Marías 2004).

The magnificent ceiling we are studying here was originally in the sixteenth-century palace of the Dukes of Mandas in Valencia, of the Maça de Liçana family. It was constructed in the transition from the Gothic to the Renaissance at an unknown date, but historical documentation says that the Mandas family was the owner of the palace in 1638; it later passed to the Casa de Dos Aguas. The palace was demolished in 1865, leaving behind only a portion of the façade with the entrance portal, today conserved in the Viveros Garden in Valencia, and our ceiling, which was dismantled and stored in the Palace of the Marques de Dos Aguas (Gómez Ferrer 2017: 26). Later, the ceiling was bought by the Valencian painter Antonio Muñoz Degrain (1840–1924), professor in the Fine Arts School of Malaga,4 and was transported to his studio there. After the death of Muñoz Degrain, the ceiling was donated by his family to the Fine Arts Museum. In 1961 this museum and the ceiling were moved to the Buenavista Palace.

An identical ceiling,5 also originally in the Palace of the Marques de Dos Aguas, was bought by a friend of Muñoz Degrain’s, the Valencian painter Bernardo Ferrándiz Bádenes (1835–1885), who transported it in 1867 to his home in Malaga, the estate Las Barcenillas. This ceiling has not survived, as it was destroyed by a fire in the early twentieth century, but it appears in one of the paintings by Ferrándiz, El Naturalista. A journal of the time shows an engraving of the painting.6

Our exemplar belongs to the genre of early wooden coffered ceilings built in the Valencia region, which integrated traditional carpentry techniques with the new ideas of the Renaissance. There are two important focuses of development of these wooden coffered ceilings in the early Renaissance in Spain. One is related to the works that the architect Alonso de Covarrubias (1488–1570) built for the Mendoza family; the other is centred in Zaragoza. The Valencia region is a third, insufficiently recognised, focus (Gómez Ferrer 2017: 17).

The link between the Crown of Aragon and Italy plays an important role here. The new Italian trends were shared and exchanged with Spain during the reigns of Alfonso the Magnanimus (Alfonso V of Aragón, 1396–1458, King of Aragón, Valencia, Mallorca, Sicilia, Cerdeña and Count of Barcelona, 1416–1458), who was also king of Naples (1442–1458). It is known that he sent carpenters from his kingdom in Spain to the works in Castel Nuovo in Naples. Upon his death, in 1458, they returned home, probably carrying the new ideas with them (Gómez Ferrer 2017: 16–17).

It is important to remark that the inspiring Renaissance treatises, mainly focused on recovering lost forms and proportions, presented few explanations on how the new ideas could be executed in reality. Consequently, in the early Spanish Renaissance, the works continued to be made by traditional carpenters (Nuere 2004: 88), who integrated their structural methods of woodworking to develop ceilings characterized by very deep coffers, in unpainted wood and with a total absence of polychromies.7

The Pattern

In geometry, a regular four-pointed star (Fig. 3a) is a concave octagon with eight equal sides that has the same symmetries as the regular octagon, with four vertices of angle α (where 0 < α < 90º) at the points of the star, alternating with four vertices of angle β = 270º − α (Grünbaum and Shephard 1987: 82). The Schläfli notations |p/q| and {p/q} commonly used to denote the star polygon with p points (Grünbaum and Shephard 1987: 83), is only applicable for p ≥ 5. The case of angles α = 45º and β = 225º together with the regular octagon generates the pattern shown in Fig. 3c.8

Figure 3 shows two more patterns involving the regular octagon and the four-pointed star. In Fig. 3b, the pattern uses four-pointed stars and rhombuses of angles 45º and 135º, which is determined by overlapping of regular octagons. In Fig. 3d, a variation of the one in Fig. 3c is shown, in which the use of octagons and interlocking four-pointed stars can be interpreted as a pattern by overlapping squares.

Patterns using regular octagons and squares, four-pointed stars or 45° rhombuses have been used extensively in the history of architecture. Well-known examples are the numerous and complex variations of mosaics in Ancient Greece and Rome, and the outstanding variations in Islamic decoration (Bonner 2016: 88–89; 2017: 254–260). During the Renaissance, patterns with octagons were used in the design of the ceilings in different materials. In the early Renaisance wooden ceilings, patterns based only on squares are frequent; two of the numerous examples are the ceiling of Santa Maria Maggiore in Rome and the ceiling of the Old Hall (Sala Vella) of Palacio de la Generalidad (c. 1481). However, thanks to the skill and geometric knowledges of traditional carpenters, the Spanish sixteenth-century ceilings soon developed more complex patterns with varied geometric shapes and combinations of them. Worthy of mention are the Montezumo Palace in Zaragoza, which features coffered ceilings imported from the demolished sixteenth-century Palacio Aytona, one of which is designed with elongated hexagons while another one presents an unusual design with parallel rows of symmetric rhombuses with alternating inclination.9 Parallel rows of regular hexagons alternating with pairs of equilateral triangles10 can be seen in the design of the ceiling of the Salon del Trono of Palacio Pastrana in Guadalajara. Hexagons surrounded by equilateral triangles11 are used in the Sala Norte of Palacio de Miguel Donlope in Zaragoza. The ceiling of the Paraninfo of the University of Alcalá (ca. 1516–1520) deserves a special mention. Designed with six-pointed stars surrounded by hexagonal coffers,12 it is considered one of the masterpieces of traditional Spanish carpentry.13 Also remarkable is the complex design of the Sala Honda of Cuenca Cathedral with rhombuses, triangles, hexagons and six-pointed stars.14

In Spain and throughout Europe, patterns with regular octagons with side in contact and squares15 are very frequent in sixteenth century wooden ceilings. Examples can be seen in the small Golden Hall (Sala Daurada Menuda) of Generalitat’s Palace in Valencia (c. 1519–1535) and in the late sixteenth century ceiling of Palazzo Raimondi in Cremona (Grimoldi and Landi 2015). However, the pattern using octagons with vertices in contact and four-pointed stars (Fig. 3c) is unusual.

Although the designers are unknown, the ceiling of the Palace of the Dukes of Mandas (Fig. 2) and that of the Palace of the Duke of Segorbe in Castellon16 (Fig. 4a) both belong to that period of the sixteenth century (Iborra 2012: 742; Gómez Ferrer 2017: 26) and both are based on patterns of octagons and four-pointed stars (see Fig. 3c–d). In Spain, outside of the Valencia region, in Castilla three known ceilings are based in the same pattern; these decorate buildings built under the patronage of the Mendoza family,17 all designed by the Spanish architect Alonso de Covarrubias (1488–1570). Covarrubias is considered to be one of the main architects who introduced the Renaissance in Spain. He designed the ceilings of the Ducal Palace of Pastrana in Guadalajara (1549–1550) (Fig. 4b), Castillo de La Calahorra in Granada (1509–1512) and the Archbishop’s Palace in Alcalá de Henares, Madrid (1524–1534), which was destroyed by the fire in 1939 (Fig. 4c).

Fig. 4.

a Palace of the Duke of Segorbe, Castellon (photo, author); b The Ducal Palace of Pastrana, Guadalajara (photo, author); c The lost ceiling of Alcala de Henares (Byne and Staplet 1920: 91)); d The dome of San Roman 's churche in Toledo (photo, David Utrilla)

Wooden coffered ceilings with this design are not found in other European regions. However, in Islamic decoration, the use of that pattern in wood, although not frequent, is found. Figure 5 shows two examples of Islamic work that predate the ceiling in the Picasso Museum: the vestibule of El Corral del Carbon in Granada (fourteenth century), originally a commercial warehouse (al-Funduq al-Jadida) (Fig. 5a), and the ceiling of the Mausoleum of Sultan Qalawun in the Qalawun complex at the Citadel in Cairo Egypt (thirteenth century) (Fig. 5b).

Fig. 5.

a El Corral del Carbón (photo, author); b The Qalawun complex (photo by Jorge Láscar from Melbourne, Australia, CC BY 2.0 via Wikimedia Commons, https://flickr.com/photos/8721758@N06/14795828135 (Accessed 05/04/2022)

Regarding the presence of the four-pointed star in Renaissance coffered ceilings in Spain, hypotheses can be made about the strong influence of the Islamic tradition leading to a taste for and familiarity with this kind of this pattern, but concerning their use by Alonso de Covarrubias, it is known (Marías 2008: 100–106; Santos Vaquero and Santos Martin 2022: 66–108) that he was greatly influenced by Books III and IV of architecture by Serlio. At that time, these were translated from the Tuscan into Spanish by Francisco de Villalpando (1510–1561) and published in Toledo in 1552 (Serlio 1552). Covarrubias’s designs for coffered ceilings were inspired by the drawings shown in Book IV in the section devoted to the planar ceilings and their ornaments (De i Cieli piani di legname, & de gli ornamenti suoi) (Serlio 1552: LXXIII-LXXVII). An example is shown in the decoration of the church of San Román in Toledo (Fig. 4d), where Covarrubias copies one of Serlio’s drawings of regular octagons surrounded by elongated hexagons and intersecting rectangles (Serlio 1552: LXXIV).18 It is noteworthy that the pattern using octagons and four-pointed stars does not appear in those plates; rhombuses and four-pointed stars (pattern in Fig. 3b) appear in his drawing of a mosaic in the Temple of Bacchus shown on page XIII of Book III.

In any case, the Spanish wooden ceilings and the ceiling of Qalawun complex (Fig. 5b), in spite of their common design, are structurally different. The ceiling of Qalawun complex is a decorative panel superimposed on the structure of the ceiling. The octagonal holes are determined by the crossing of the wooden ribs; in this case, it is a hemispheric variation of the polyhedral openings, characteristic of the interlacing Islamic frames. The ceiling in Alcazar de Sevilla is another example (Fig. 6a).

Fig. 6.

a Ceiling in Alcazar de Sevilla (photo, author); b The beams and an octagonal coffer in the Ducal Palace of Pastrana (drawing by Andrés Ramírez Santana)

In the Spanish ceilings, the role of the star is significant in the construction procedure since stars are included in the structure of the main parallel beams, by means of secondary beams that are fitted to cross each other, defining octagonal openings, in which the octagonal coffers are fitted. As result, very deep coffers can be designed, and the hardly noticeable distance between the beams is covered by the decoration, in this case, not necessarily complex. Figure 6b shows a simplified drawing of the structure of the ceiling of the Ducal Palace of the Pastrana Palace, made visible (Gonzalez Uriel et al. 2019: 67) during the works of restoration.

The Research

As said, the goal of this present research is to define the spatial version of this planar pattern of octagons and four-pointed stars using convex and concave polyhedra. In essence, we are facing two problems of generalization by means of similarity (in the general meaning of resemblance), so the concept of spatial version must be specified. More formally, both problems can be formulated in this way:

Define two polyhedra similar to the regular octagon and the four-pointed star, respectively

and

Define a spatial pattern (honeycomb) similar to the pattern by regular octagons and four-pointed stars.

Note that the two problems are related but not equivalent,19 because a possible solution of the first problem may not generate a solution of the second one (e.g., the small rhombicuboctahedron may be considered similar to the regular octagon, but it could never generate a honeycomb similar to the planar pattern shown in Fig. 3c).

According to George Polya, “Similar objects agree with each other in some respect, analogous objects agree in certain relations of their respective parts” (1945: 37). Thus, our two problems can be unified as follows:

Define two polyhedra analogous to the regular octagon and the four-pointed star, respectively

because in this way we are generalizing not only the shape of the polygons, but also the way in which they fill the plane, that is, the tessellation shown in Fig. 3c.

At the start, those polyhedra are unknown; the only characteristic required is the analogy between them and the considered polygons.

There is no known standard procedure to obtain a polyhedron analogous to a given polygon. However, the properties in the plane that characterize the elements of the polygons and the relations among them can be generalized. The polyhedra will then be determined by means of the geometric construction of a certain (still unknown) geometric object that satisfies those analogous properties in space. This procedure combines the analytic method in the plane, the synthetic method in space, and the generalization from the plane to space by means of analogy as a heuristic strategy20:

$$\text{Polygon}\stackrel{\mathit{Analysis}}{⟶}\text{Properties in the plane}\stackrel{\mathit{Analogy}}{⟶}\text{Properties in space}\stackrel{\mathit{Synthesis}}{⟶}\text{Polyhedron}$$

To define the analogous properties, we will translate them to space by replacing the elements with their corresponding analogous forms (e.g., circle → sphere; line bisector → plane bisector, etc.).

By nature of the concept of analogy, the goodness of the solving polyhedra cannot be verified; it can only be checked by means of the procedure of projection of the polyhedra and the honeycomb that is determined.

The concepts of spatial octagon and four-pointed stars must also be specified. In what follows, the terms “3D-octagon” and “3D-4star” will denote the polyhedra analogous to the octagon and the four-pointed star. Also, to unify the notation, the regular octagon and the four-pointed star will be called “2D-octagon” and “2D-4star”.

To guarantee a consistent construction that generalizes from the plane to space, the following conditions must be satisfied:

1. A 3D-octagon is a convex polyhedron with a circumscribed sphere.

2. The orthogonal projections of the maximal cross-sections of a 3D-octagon are 2D-octagons.

3. A 3D-4star is a concave polyhedron whose outermost points lie on a circumscribed sphere.

4. The orthogonal projections of three cross-sections of a 3D-4star are 2D-4stars.

5. The polyhedra defined in (1), (2), (3) and (4) are associated to fill space in such way that the three orthogonal projections of the honeycomb (spatial pattern) replicate the initial planar pattern of octagons and four-pointed stars.

The planar pattern in our study (Fig. 3c) is generated on a square grid (Fig. 7a) by the squared tile T2, but also by the elementary tile S2, which can in turn be dissected into a 2D-kite and a 2D-dart. Therefore, the 2D-octagon and the 2D-4star are the edge-to-edge union of four kites and four darts, respectively. Yet the 2D-4star can also be obtained by removing the four kites in the vertices of T₂. These properties are fundamental because they determine not only the construction of the polygons, but also the obtaining of the pattern.

Fig. 7.

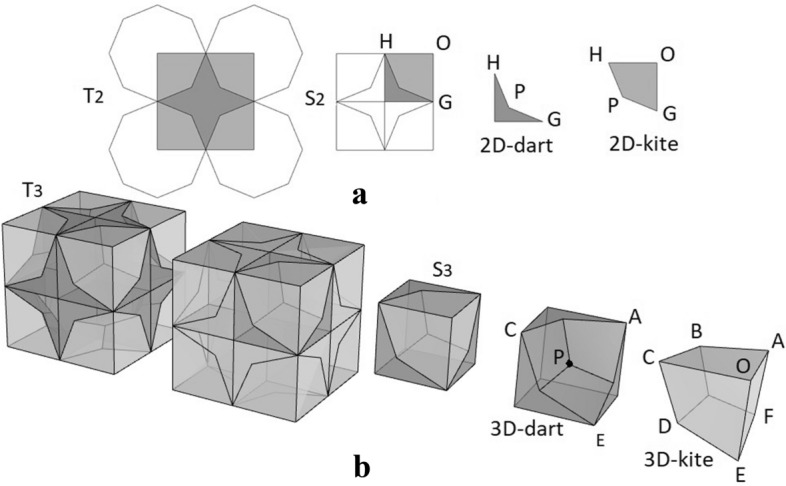
a Planar tiles; b Generalization to the polyhedral tiles

We generalize the procedure in a cubic grid (Fig. 7b) by defining the unit cube T3 as the union of eight elementary cubes S3, which we will dissect into certain 3D-kites and 3D-darts. In the spatial grid, eight 3D-kites meet in each vertex of the cube T3, and their face-to-face union determines a convex polyhedron, which will be the generalized 3D-octagon. The union of eight 3D-darts meeting in the centre of the unit cube T3 forms a concave polyhedron, which will be generalized 3D-4star. This 3D-4star could also be obtained directly by excavating the eight 3D-kites placed in the vertices of the cube T3.

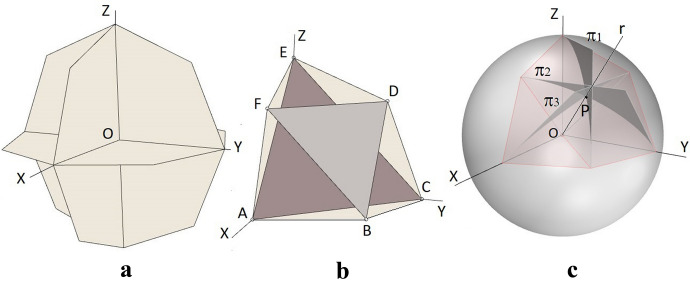
By means of this procedure, the three maximal cross-sections of the obtained 3D-octagons are 2D-octagons, and both polyhedra satisfy the conditions (3), (4) and (5) aforementioned. The three faces meeting in O (see Fig. 7b) are quarters of the regular octagon and mutually meet perpendicularly, so taking as unity the length of the edge of S3, we can use Cartesian coordinates. By considering the vertex O as the origin of the system (Fig. 8a), the vertices of the 3D-kite can then be given by A(1,0,0), B(√2/2,√2/2,0), C(0,1,0), D(0,√2/2,√2/2), E(0,0,1) and F(√2/2,0,√2/2).

Fig. 8.

a The three maximal cross-sections of the polyhedron in construction and the coordinate system; b The vertices of the 3D-kite in the first octant; c Determining the point P in Case I

Note that the key to dissecting S3 is to locate an occult point P (see Fig. 7b) to get a polyhedral kite with at least six faces, three of which are planar kites mutually meeting perpendicularly. The choice of that point is determined by the given conditions, as well as by the generalization to space of the metric properties of the regular octagon.

Figure 7a shows a planar kite OGPH. Observe that the vertex P belongs to the circle whose centre is O and whose radius is the side of the tile S2, OG. Also, P is equidistant from the vertices G and H, consequently P belongs to the bisector line of the right angle ∠HOG. Translating both properties to space for the 3D-kite ABCDEFPO (Fig. 7b), the hidden point P should belong to the sphere whose centre is O and whose radius is the edge of the tile S3, OA. Analogously, the point P should belong to a bisector plane of a right dihedral angle spanned by two coordinate planes; and P should be equidistant from the vertices A, B, C, D, E and F.

In the plane kite, the relationship between “be equidistant from” and “belong to the bisector line” is unequivocally determined. However, in space, we have three bisector planes, so the number of the involved planes could be one, two or three. In addition, in space, the condition of equidistance applied to P and a general set of six points is complex to state, because the possibility of the equality of distances depends on the position of the six points in space. In general, numerous possibilities for the coordinates of P should be considered, but in the particular case of the six vertices of the 3D-kite {A, B, C, D, E, F} the possibilities are reduced because the equilateral triangles ACE and BDF belong to parallel planes (Fig. 8b). In fact, the point P can only be equidistant from trios or pairs of vertices {A, B, C, D, E, F} and thus two possibilities must to be distinguished, Case I and Case II.

First solution

Considering the vertices grouped in triads, the only compatible equalities are given when we state: “P is equidistant from vertices A, C, E” and “P is equidistant from vertices B, D, F:

Case I: P(x,y,z) belongs to the sphere of center O(0,0,0) and radius 1. The point P is equidistant from the points A, C and E; and also from the points B, D and F. That is, d(P,A)=d(P,C)=d(P,E) and also d(P,B)=d(P,D)=d(P,F).

In this case, if the point P belong to the three bisector planes π₁, π₂ and π₃ (Fig. 8c) of the three right dihedral angles spanned by the three coordinate planes, then it also belongs to the right line r (Fig. 8c). Since the equilateral triangles ACE and BDF belong to parallel planes, only one point of the circumscribed sphere is simultaneously equidistant from the vertices of both triangles. Algebraically, this means that the coordinates of the point P are the solution of the equation system {$x=y=z$; $x^2+y^2+z^2=1$; $x>0$, $y>0$, $z>0$}. Thus, P = (√3/3, √3/3, √3/3). The 3D-kite placed in the first octant is first determined, then by its reflection with respect to the three coordinate planes, a 3D-octagon is determined with vertices (± 1,0,0), (0, ± 1, 0,), (0,0, ± 1), (± √3/3, ± √3/3, ± √3/3), (± √2/2, ± √2/2, 0), (± √2/2, 0, ± √2/2), (0, ± √2/2, ± √2/2).

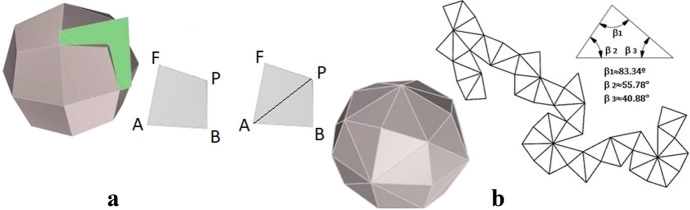
Consequently, in the vertex P three congruent planar kites meet. The 3D-octagon constructed appears similar to a deltoidal icositetrahedron, but it is distorted because a circumscribed sphere is mandatory (Fig. 9).

Fig. 9.

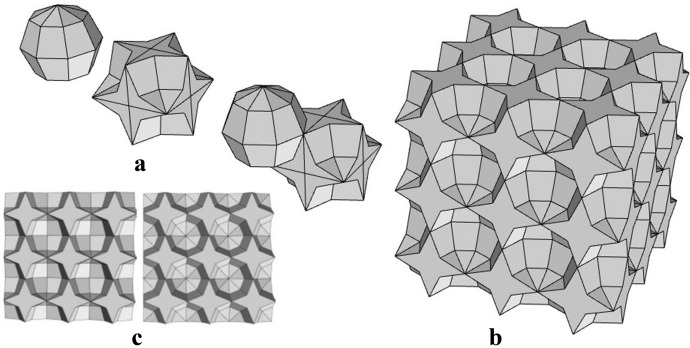
Case I (preliminary solution): a 3D-octagons and 3D-4stars; b The honeycomb and the orthogonal projections (three equal)

Although hardly noticeable, the four vertices of the kites are not coplanar (Fig. 10a) but we can obtain planar faces by replacing each curved face by two congruent scalene triangles, that is, we can replace the kite AFPB by AFP and APB (Fig. 10). Then the final solid has forty-eight triangular faces. It has octahedral symmetry, and it is similar to a disdyakis dodecahedron, with the same face configuration, V4,6,8, but the dihedral angles of the faces are α₁≈173.07º, α₂≈147.27º and α₃≈136.92º.

Fig. 10.

a The solution with non-planar faces; b The 3D-octagon with triangular faces and the net

Figure 11 shows the solid defined by the union of eight 3D-kites and its associated star The face-to-face arrangement in rows and columns of the stars creates the honeycomb. The orthogonal projections are shown in Fig. 11b.

Fig. 11.

First solution: a 3D-octagons and 3D-4stars; b The honeycomb and the orthogonal projections (three equal)

Second solution

When the points A, B, C, D, E and F are grouped in three pairs, only the groupings {{A,C}, {F,D}, {B,E}}, {{A,E}, {B,D}, {F,C}} and {{E,C}, {B,F}, {A,D}} make it possible for P to be equidistant from both points of each pair of the grouping.

By symmetry, the three different solutions of P provide the same final solid (Fig. 12a), so, without loss of generality, only one case will be considered here. For instance, P such that d(P,A) = d(P,C), d(P,F) = d(P,D) and d(P,B) = d(P,E) (Fig. 12a, top).

Fig. 12.

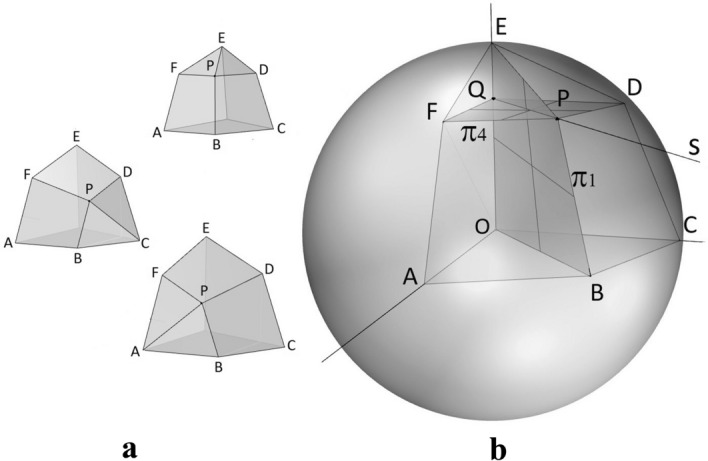
Case II: a Three possibilities of P being equidistant from pairs of the vertices ABCDEF; b Obtaining the point P for the first possibility

Consequently, we can formulate:

Case II: P(x,y,z) belongs to the sphere of center O(0,0,0) and radius 1. The point P is equidistant from the points A and C, from the points F and D, and from the points E and B.

Now, the point P belongs to the bisector plane π₁ and also to the bisector plane of the line segment BE, and its coordinates are the solution to the equation system {x = y; x + y − √2z = 0; x² + y² + z² = 1; x > 0, y > 0, z > 0}, that is, P = (1/2, 1/2, √2/2). The 3D-octagon is constructed again by reflections of the 3D-kite with respect to the coordinate planes.

Three points, P, D and F, determine a plane parallel to the xy-plane, π_4, which intersects the z-axis at the point Q (0, 0, √2/2) (see Fig. 12 b). The cross-section FPDQ is a quarter of the regular octagon. A 2D-kite, EOBP, is then determined, congruent to the mutually perpendicular faces of the 3D-kite.

In this case, the 3D-octagon constructed (Fig. 13) is a 32-faced polyhedron with sixteen isosceles trapezoids and sixteen isosceles triangles, simply a variation of the well-known 72-faced Campanus sphere, which Luca Pacioli called Septuaginta duarum basium in his Divina proportione (Pacioli 1509). The 32-faced polyhedron obtained is the union of an octagonal bifrustum and two octagonal pyramids. The trapezoidal faces have angles α≈81.6º and β≈98.4º and the sides in ratio √2, with three of them equal. The triangular faces also have sides in ratio √2, and angles γ≈69.3º and δ≈41.4º. The dihedral angles of the 32-octagon are β₁≈138.12º, β₂≈135.09º and β₃≈161.99º.

Fig. 13.

Second solution: a The 32-faced polyhedron and its 3D-4star; b The honeycomb; c The orthogonal projections (two equal to the one on the left)

A general construction of a 2n²-faced polyhedron of this kind, when n an even number, can be found in Cromwell (1997: 107). There, a polyhedral approximation of the sphere is given. Although the present goal and construction procedure are different, the 32-faced polyhedron (Fig. 13a) is the same polyhedron constructed by Cromwell when n = 4. This means our procedure is coherent because in fact, although not a close one, the octagon is an approximation of the circle in the plane; then by analogy, our 32-faced polyhedron is an approximation of the sphere.

Figure 13 shows the honeycomb and its orthogonal projections. Geometrically, the octagonal coffers of the ceiling studied here, are pyramidal frustums; note that the coffers correspond to the holes determined in between the stars of the honeycomb. Therefore, the honeycomb of case II could provide a model for the design of coffered ceiling with octagons and stars.

In both cases I and II, the honeycomb is derived from the cubic honeycomb, so, by construction, both couples of polyhedra fill the space. Observe that the 3D-4stars here constructed are excavated hexahedra but also excavated cuboctahedra (Fig. 14). On the other hand, the vertices (± 1,0,0), (0, ± 1,0,), (0,0, ± 1) of the 3D-kite determine an octahedron with the same center and edges √2. Thus, the process could also begin from the rectified cubic honeycomb (cuboctahedra and octahedra). Figure 14 shows the equivalence of both constructions.

Fig. 14.

The 3D-octagon and the 3D-4star from the octahedron and the cuboctahedron

Note. In Case I the point P belongs to the three bisector planes π₁, π₂ and π₃; in Case II P belongs to only one of the bisector planes; the possibility of P belonging to only two bisector planes is included in Case I, because π₁, π₂ and π₃ intersect each other at the right line r (Fig. 8c).

The preceding excavating procedure could be extended to the edges of the cube, so another generalization of the four-pointed star could be obtained, as shown in Case III.

Case III

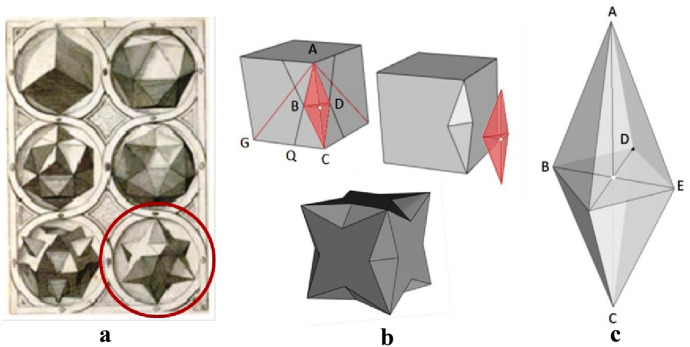
Wentzel Jamnitzer is famous for his outstanding drawings in his Perspectiva Corporum Regularum (1568). He presents imaginative variations of the Platonic solids without explanations, according to systematic constructions of increasing complexity by augmentation, addition, and truncation of the edges or the faces. He also makes notches or hollows out the volumes, to construct what he calls “transparent bodies”.

Jamnitzer’s plate C II is the third of those devoted to the hexahedron; it finishes with a simple star polyhedron (Fig. 15a). Most studies of Jamnitzer’s work focus on his most striking polyhedra, seldom considering that polyhedron. Surprisingly, we have discovered that it is related with the 3D-4stars constructed above. In fact, that polyhedron is also the result of excavation of the hexahedron, but along its edges. In fact, by removing a quarter of an appropriated square bipyramid (Fig. 15b) the resulting solid (Fig. 15b) could also be considered a 3D-4star. Figure 15 shows a unit cell of a cubic honeycomb, explaining the procedure.

Fig. 15.

a Jamnitzer’s star polyhedron (1568: Plate C II); b The excavation of the hexahedron and the obtained 3D-4star; c The bipyramid (union of four excavated pieces around the edge AC)

With reference to Fig. 15b, c, note that the height of the pyramid would be half of the removed edge AC, and that BD is the side of its squared base. The triangular face ABD is determined by a point Q (Fig. 15b) in the selected edge GC such that GQ + QC = GC and GQ/QC = √2. Then, AB/BD = √(2 + √2), the angle ∠QAC = 45º/2, and, consequently, in the bipyramid the angle ∠BAE = 45º is determined. The entire bipyramid is completed by the union of four excavated pieces, using four unit cubes meeting in each edge (e.g., AC) of the cubic grid (Fig. 15c).

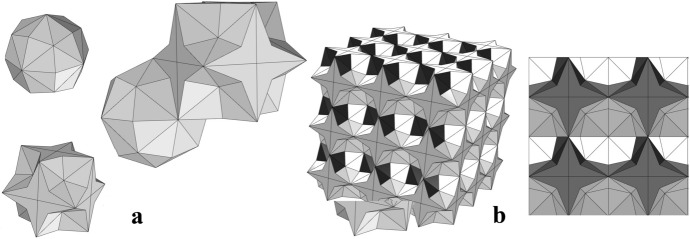
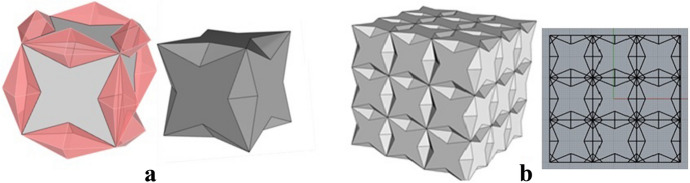
By construction, space can be filled by those stars and bipyramids, generating a three-dimensional pattern (Fig. 16b) that generalizes the planar pattern of four-pointed stars and rhombuses of 45º and 135º shown in Fig. 3b. This means the associated 3D-octagon to the 3D-4star would be formed by the union of the star and 12 bipyramids (Fig. 16a).

Fig. 16.

a 3D-octagon and D-star; b The honeycomb and its orthogonal projections

In this case, from the constructed 3D-4star (Fig. 16a) a generalized pattern is found (Fig. 16b) which generalizes a planar pattern (Fig. 3b); in contrast with the preceding heuristic procedure (Cases I and II), where from the considered planar pattern (Fig. 3c), the 3D-4star is constructed (Figs. 11a, 13a).

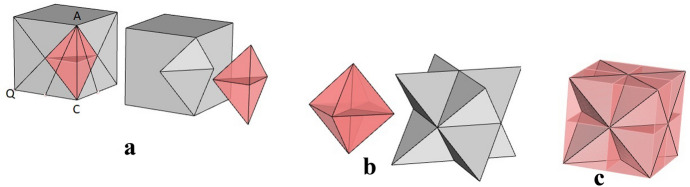
Observe that Jamnitzer’s star (Fig. 15a) and the third 3D-4star (Fig. 15b) are both variations of the stella octangula, where the octahedron is the excavated bipyramid (Fig. 17a, b). In fact, the constructed star depends on the depth of the excavated notch, which in turn depends on the position of the point Q in the edge GC. That is, it is determined by the ratio QC/GC. Thus, a set of eight-pointed stars is determined, depending on the ratio r = QC/GC, 0 ≤ r ≤ 1 (Fig. 15). The cube is the star with ratio 0, because no excavation is made, that is, QC = 0. In Fig. 15, the 3D-4star was constructed with GQ/QC = √2; it is therefore the star of ratio r = √2 − 1.

Fig. 17.

a Excavation of a quarter of octahedron (ratio 1); b The bipyramid (octahedron) and the 3D-4star (stella octangula); c The cube dissected into the star and 12 quarters of an octahedron

Looking at Jamnitzer’s star, the sharp points of the stellated face suggest that it might be a star of ratio √2 − 1 < r < 1. Finally, the maximum excavation is given when the ratio is 1, which happens when QC = GC, that is, when the constructed star is the well-known stella octangula (Fig. 17b).

Conclusions

We have seen that when the wooden coffers of the ceiling are seen as polyhedra, the ceiling can be seen as a three-dimensional version of the planar pattern by octagons and stars. The underlying geometry in the configuration of the ceiling is a perfect starting point for constructing different polyhedra analogous to the octagon and the four-pointed star, and thus generate several honeycombs that somehow resemble the ceiling. Reciprocally, the new honeycombs constructed with the procedures shown here could be used in the design of new ceilings.

The analysis presented here is not definitive, as there are numerous possibilities for polyhedra analogous to the regular octagon and the four-pointed star, and the generalization procedure could be applied to other patterns and other ceilings. This will be the focus of further research.

Antonia Redondo Buitrago

has a PhD in Functional Analysis (complex powers of operators). From 2001 to 2011 invited researcher in Department of Applied mathematics in Valencia University. She became interested in the field of continued fractions and geometry. She is specialized in the study of proportions (golden section, metallic means, cordovan proportion, plastic number), non-constructible polygons and Spanish historic carpentry. Her contributions are mainly focused on the interdisciplinary aspects in the domain of the art, design, architecture, and the relationship between them and mathematics.