Abstract
Ultrasmall metal nanoparticles (NPs) are next-generation nano-based platforms for in vivo disease diagnosis and treatment. Due to their small size below the kidney filtration threshold and marked resistance to nonspecific serum protein adsorption, ultrasmall NPs can be rapidly excreted through the kidneys and escape liver uptake. However, although ultrasmall particles may be deemed highly resistant to protein adsorption, the real extent of this resistance is not known. Here, a simple compartmental model simulation was therefore implemented to understand how NP behavior in vivo could be modulated by soft, transient NP–plasma protein interactions characterized by dissociation constants in the millimolar range. In Model 1, ultrasmall NPs functionalized with a targeting probe, plasma proteins and target receptors were assumed to co-exist within a single compartment. Simulations were performed to understand the synergistic effect of soft interactions, systemic clearance and NP size on receptor occupancy in the single compartment. The results revealed the existence of a narrow range of ultraweak affinities and optimal particle sizes leading to greater target occupancy. In Model 2, simulations were performed to understand the impact of soft interactions on NP accumulation into a peripheral (tumor) compartment. The results revealed that soft interactions – but not active targeting – enhanced tumor uptake levels when tumor accumulation was limited by ‘fast’ plasma clearance and ‘slow’ vascular extravasation. The simple model presented here provides a basic framework to quantitatively understand the blood and tumor pharmacokinetics of ultrasmall NPs under the influence of transient protein interactions.
A compartmental model simulation shows that the blood and tumor pharmacokinetics of ultrasmall metal nanoparticles can be modulated by soft interactions with plasma proteins.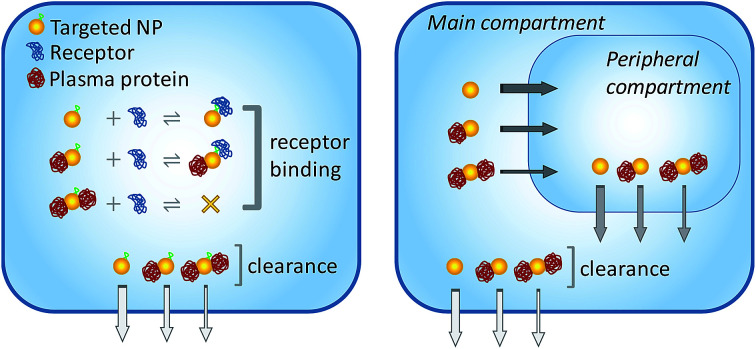
1. Introduction
To date, a myriad of noble metal nanoparticles (NPs) have been designed and tested in various biomedical applications. NPs can be utilized as theranostic platforms for cancer detection and treatment.1 They can be employed as delivery vehicles for traditional pharmaceutics in an effort to reduce side effects, increase therapeutic efficacy and improve pharmacokinetics.2
Nobel metal NPs can be broadly divided into two general categories concerning their size: (i) ultrasmall NPs of core diameters under ∼3 nm, and (ii) conventionally large NPs.3–5 The clinical translation of conventionally large particles has met with several challenges and limited success.6,7 For example, large NPs cannot be excreted in the urine because they have diameters greater than the kidney filtration threshold, which is around 8 nm.8,9 The lack of an efficient elimination route from circulation together with the chemical stability of the NPs contributes to their long-term accumulation in the body. In addition, large NPs generally end up accumulated in the liver and spleen by the phagocytic action of resident macrophages.10,11 PEGylation of the NP surface, a common method to minimize protein adsorption and opsonization, can delay macrophage uptake but not completely avoid it. Finally, serum protein adsorption can sterically shield targeting ligands attached onto the NP surface and hinder ligand–receptor interactions.10,12,13
Ultrasmall metal NPs and nanoclusters constitute an emerging class of nanomaterials for disease diagnosis and therapy.3,9,14–20 Due to their small size below the kidney filtration threshold, ultrasmall NPs can be rapidly excreted through the urine; e.g., clearances over 50% at 24 h p.i. have been routinely reported.21–26 The fast and efficient renal clearance, in turn, contributes to much lower levels of particle uptake by the reticuloendothelial system organs, avoids long-term accumulation in the organism, and minimizes toxicity. Remarkably, accumulation in the liver and spleen is typically 10- to 30-fold lower relative to conventional nonrenal clearable particles.16 It should be noted that the reduced size of ultrasmall NPs is a necessary but not sufficient condition for efficient renal clearance and reduced levels of uptake by the liver and spleen. Fundamentally, ultrasmall NPs must be highly resistant to serum protein binding, which can be generally accomplished by surface coating with hydrophilic peptides (e.g., glutathione), zwitterionic ligands or PEG.27–32 Ultrasmall NPs functionalized with targeting ligands have also shown promise in vivo.33–35
Paradoxically, the rapid renal clearance of ultrasmall NPs may limit their usage as cancer nanomedicines, since a fast drop in plasma concentration may hinder tumor uptake.36 Therefore, several strategies have been devised to prolong NP half-life in circulation and increase tumor accumulation levels.16,28,36–38 For example, it was found that PEGylation prolonged the plasma half-life of ultrasmall NPs relative to glutathione-coated particles, thus enhancing tumor uptake levels from 2.3 to 8.3% ID per g.28
Despite all the progress so far, fundamental issues concerning the biointeractions of ultrasmall NPs in complex biological fluid remain poorly understood. One interesting open question pertains to the extent to which ultrasmall NPs are able to avoid interactions with plasma proteins. In other words, although it may be taken for granted that ultrasmall NPs are highly resistant to protein binding, the real extent of this resistance is not known. Ultrasmall NPs coated with PEG may be especially prone to interacting with plasma proteins to some degree, as even free PEG molecules are known to bind weakly to proteins.39–41 Experiments performed so far to test the capability of ultrasmall particles to resist serum protein interactions have included, among others, gel electrophoresis and size-exclusion chromatography in combination with dynamic light scattering (DLS).32,42,43 However, none of these simple experimental methodologies are appropriate for the characterization of transient, ultraweak interactions characterized by very high dissociation constants and short residence times. Analytical ultracentrifugation constitutes a more robust and sensitive tool to investigate ultraweak biomolecular interactions,44–46 but this has yet to be explored in more detail in the study of NP interactions.31,47
While ultraweak interactions with dissociation constants in the millimolar (mM) range usually have no major impact on conventional biochemical assays performed in vitro under dilute solution conditions, they cannot be ignored in macromolecular crowded media.48 Blood plasma in particular contains high amounts of proteins in a total apparent concentration of ∼80 mg mL−1, and potentially reaching double this value inside capillaries.49 Serum albumin, the most abundant protein in plasma, is present at concentrations of 35–50 mg mL−1 (0.53–0.75 mM), while other major but less abundant proteins include the immunoglobulins, transferrin and fibrinogen.50 Assuming that the affinity of NP–protein interactions may be of the same order of magnitude as the overall concentration of proteins in blood raises the intriguing possibility that soft interactions may act in tandem with other molecular and physiological processes to modulate NP behavior in vivo.
Given the above considerations, here a simple compartmental model simulation was implemented to examine the hypothesis that soft interactions could modulate the blood and tumor pharmacokinetic properties of ultrasmall metal NPs (Fig. 1). The results revealed that the excretion, degree of receptor occupancy and tumor accumulation of the NPs could be modulated through transient interactions with plasma proteins. Controlling the nature and magnitude of these interactions could therefore provide new avenues to regulate ultrasmall NP behavior in vivo.
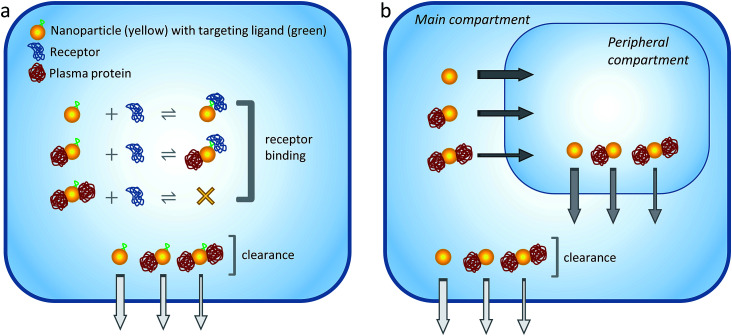
Fig. 1. Schematic illustration of the model. (a) Model 1: one-compartment model. Targeted NPs, plasma proteins and receptors co-exist within the single compartment. The plasma proteins interact nonspecifically to the NPs with ultraweak affinity. The maximum NP binding capacity is 2 proteins/NP (in the actual simulations the maximum binding capacities were 1, 6 and 10 proteins/NP for NPs of different radii). Binding of the first plasma protein does not interfere with NP-receptor complexation, whereas binding of the second protein shields the targeting moiety and prevents receptor complexation. The rate of systemic clearance from the compartment is size-dependent, being the fastest for free NPs and the slowest for NPs with 2 bound proteins (differences in clearance rates are represented with arrows of different widths). Simulations were performed to understand the cooperative action of ultraweak interactions, systemic clearance rate, and NP radius/binding capacity on the extent of receptor occupancy in the single compartment. (b) Model 2: two-compartment model. NPs are initially present in the main (‘plasma’) compartment but can reach a second, peripheral (‘tumor’) compartment. Proteins in both compartments interact nonspecifically to the NPs with ultraweak affinity. The rate of NP transfer between compartments is size-dependent, being the fastest for free NPs and the slowest for NPs with 2 bound proteins. NP clearance takes place through the main compartment as in Model 1. Simulations were performed to understand the cooperative action of ultraweak interactions, systemic clearance rate, inter-compartment transfer rates, and NP radius/binding capacity on the accumulation of NPs into the tumor compartment.
2. Model description
2.1. Model 1: impact of soft protein interactions on receptor occupancy
Model basics
Model 1 is illustrated schematically in Fig. 1a. It can be described by the following main features: (i) ultrasmall NPs, plasma proteins and target receptors are present within a single compartment; (ii) the NPs are assumed to be functionalized with a single targeting ligand for binding specifically to the receptors; (iii) the plasma proteins interact nonspecifically to the NPs with ultraweak affinity. A maximum of two individual proteins can bind to a single NP; (iv) it is assumed that binding of the first plasma protein does not interfere with NP-receptor complexation, whereas binding of the second protein shields the targeting moiety and prevents receptor interactions; (v) the NPs are removed from the compartment with time to simulate their clearance from the systemic circulation; (vi) the rate of systemic clearance is size-dependent, being the fastest for free NPs and the slowest for NPs with 2 bound proteins.
For the sake of clarity, the binding capacity of the NPs was restricted to two plasma proteins in the model depicted in Fig. 1. However, as discussed below, the actual simulations assumed NPs of different radii and binding capacities.
Reaction equations
The model depicted in Fig. 1a can be represented by the following set of biochemical equations:NP + P ⇆ NP·P1 KD,P1 = koff,P/2kon,PNP·P1 + P ⇆ NP·P2 KD,P2 = 2koff,P/kon,PNP + R ⇆ NP·R KD,R = koff,R/kon,RNP·P1 + R ⇆ NP·P1·R KD,R = koff,R/kon,RNP → NPout kclear0NP·P1 → NPout kclear1NP·P2 → NPout kclear2where NP, P and R refer to nanoparticles, plasma proteins and receptors, respectively; kon,P and koff,P are the intrinsic association and dissociation rate constants for NP–plasma protein binding; KD,P1 and KD,P2 are the macroscopic dissociation constants related to the successive binding of the two protein molecules to a single NP (where KD,P2 = 4KD,P1); kon,R and koff,R are the association and dissociation rate constants for NP-receptor binding; KD,R is the dissociation constant for NP-receptor binding; and kclear0, kclear1 and kclear2 are the first-order rates of systemic clearance for NPs with 0, 1 and 2 bound proteins, respectively.
The dynamics of the system is represented by a set of ordinary differential equations (ODEs), which are given in the ESI.† The differential equations can be easily modified to reflect the different NP–protein stoichiometries used in the actual simulations. The resulting ODEs are then solved numerically given the rate constants and initial boundary conditions as specified below under ‘Parameter values’. Numerical integration was performed with the program Polymath (http://www.polymath-software.com).
NP sizes and binding capacity
Owing to the small surface area of ultrasmall NPs, the binding capacity of the particles is restricted to a few proteins at most.47,51 In the limiting case where particle size ≪ protein size, only a single protein will bind the NPs. The simulations assumed NPs of three distinct hydrodynamic radii, namely 1, 3 and 4 nm, each able to accommodate, according to simple geometric considerations, a maximum of 1, 6 and 10 plasma proteins, respectively (these values were rounded from 0.6, 5.3 and 9.5). This was calculated according to the simple formula:
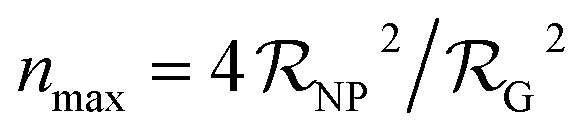 |
1 |
where nmax is the maximum binding capacity of the NPs for human serum albumin,  is the NP radius, and
is the NP radius, and 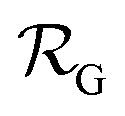 is the radius of gyration of albumin. Although it is only a rough approximation, eqn (1) nevertheless reflects the trend that more proteins can be accommodated around the surface of larger NPs. Alternatively to the use of eqn (1), the number of bound proteins as a function of NP radius could be estimated by computer simulations. For example, previous work indicated that, depending on the NP surface chemistry, up to 4 and 10 albumin proteins could bind around NPs of 3 and 6 nm in radius, respectively.52
is the radius of gyration of albumin. Although it is only a rough approximation, eqn (1) nevertheless reflects the trend that more proteins can be accommodated around the surface of larger NPs. Alternatively to the use of eqn (1), the number of bound proteins as a function of NP radius could be estimated by computer simulations. For example, previous work indicated that, depending on the NP surface chemistry, up to 4 and 10 albumin proteins could bind around NPs of 3 and 6 nm in radius, respectively.52
The apparent hydrodynamic radius for a NP–protein complex depends on the number n of bound proteins according to:53
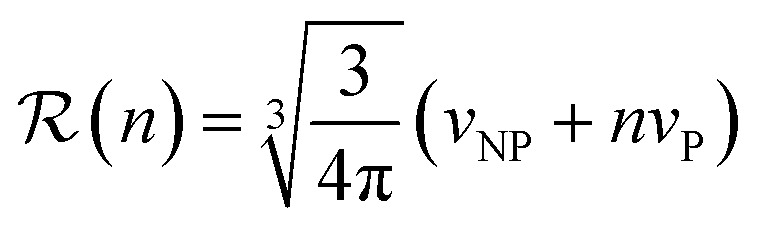 |
2 |
where the NP–protein complexes are treated as spherical; n is an integer from 0 to nmax (when n = 0, 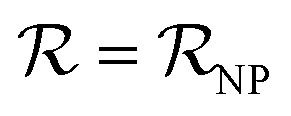 ); and vNP and vP are the volumes of the free NP and the individual protein (albumin).
); and vNP and vP are the volumes of the free NP and the individual protein (albumin).
Definition of partial and full protein coronas
The following definitions are adopted in this work to facilitate data interpretation and discussion. (i) NPfree refers to NPs without any bound protein; (ii) NPPC refers to NPs covered by a ‘partial’ protein corona. This includes NPs covered by 1, 2 or 3 proteins when 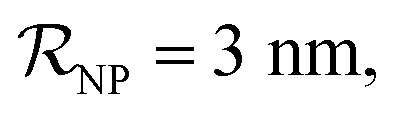 and NPs covered by 1, 2, 3, 4 or 5 proteins when
and NPs covered by 1, 2, 3, 4 or 5 proteins when 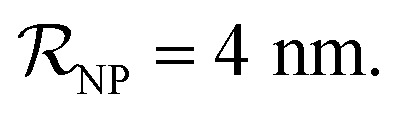 (iii) NPFC refers to NPs covered by a ‘full’ protein corona. This includes NPs covered by 1 protein when
(iii) NPFC refers to NPs covered by a ‘full’ protein corona. This includes NPs covered by 1 protein when 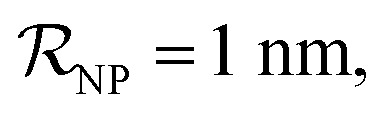 NPs covered by 4, 5 or 6 proteins when
NPs covered by 4, 5 or 6 proteins when 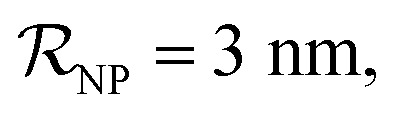 and NPs covered by 6, 7, 8, 9 or 10 proteins when
and NPs covered by 6, 7, 8, 9 or 10 proteins when 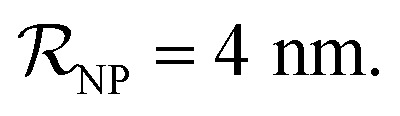
The model further assumes that the formation of a ‘partial’ protein corona around the NP surface does not interfere with receptor binding, whereas a ‘full’ corona sterically shields the functional ligand and prevents receptor binding (see also Fig. 1a). Of course, such simple general rule might not operate in practice, since it might be possible for even a single bound protein to hinder receptor interactions. Nevertheless, the simple assumption adopted here reflects the trend that the binding of fewer proteins around the NP surface has a lower probability of obstructing the targeting probe.
Rate of systemic clearance
Systemic clearance from plasma can be generally well described by a biexponential clearance model consisting of a distribution (alpha) and elimination (beta) phase. The distribution phase consists of the rapid partitioning of the compound out of the central plasma compartment into well-perfused tissues, whereas the elimination phase entails the actual elimination of the compound from the body.54 Mathematically, this can be expressed as:
| [C](t) = [C0](Ae−kαt + Be−kβt) | 3 |
where [C] is the plasma concentration of the compound at time t, [C0] is the initial plasma concentration, kα and kβ are the clearance rates for the alpha and beta phases in units of h−1, and A and B are the fractions of the alpha and beta phases in units of % ID per mL or % ID per g. The corresponding distribution and elimination half-lives can be calculated as t1/2α = ln(2)/kα and t1/2β = ln(2)/kβ, respectively.
Although not strictly accurate from a physiological standpoint, plasma clearance can nevertheless be reasonably approximated as a single exponential decay function, which is done to facilitate expressing systemic clearance as a function of compound size:55
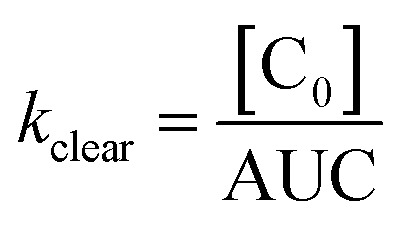 |
4 |
where AUC is the area under the plasma concentration vs. time curve (AUC = A/kα + B/kβ).
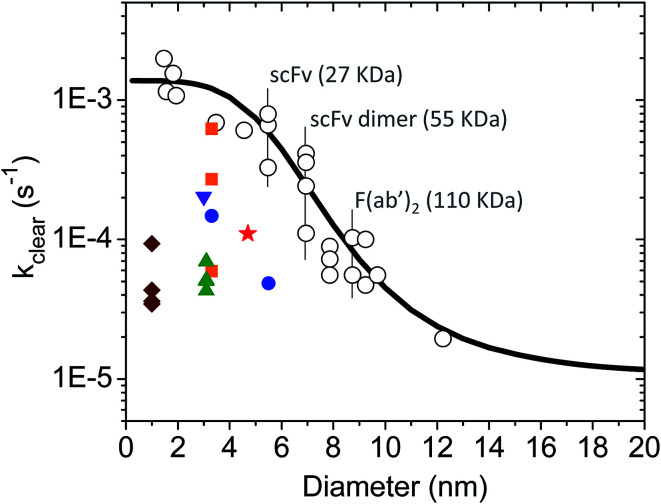
There is a large body of literature on the pharmacokinetics of hydrophilic compounds such as molecular tracers, antibody fragments and PEG of various sizes. Measurements of the plasma concentration in the mouse for such compounds were gathered by Wittrup et al.55 This data collection was analyzed according to eqn (3) and (4) to find the apparent kclear for each molecular species, and the results are plotted in Fig. 2 (open circles). Moreover, the following empirical formula was derived by Wittrup et al. to establish a direct relationship between systemic clearance rate and molecular size:56
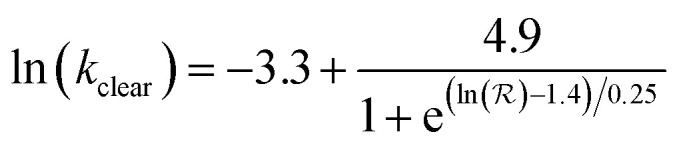 |
5 |
where 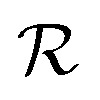 is hydrodynamic radius in nm and kclear is in units of h−1. The fit of this equation through the points in Fig. 2 is shown as a solid line.
is hydrodynamic radius in nm and kclear is in units of h−1. The fit of this equation through the points in Fig. 2 is shown as a solid line.
Fig. 2. Single exponential plasma clearance term, kclear, estimated for metal NPs, molecular tracers and protein drugs of different sizes. Open circles: kclear for molecular tracers and proteins; data obtained from ref. 55. The identity of some proteins is shown as example. Solid line calculated with eqn (5). Green triangles: glutathione-coated NPs of different core compositions (entries 1–4 in Table S1†). kclear was estimated as CL/Vd using pharmacokinetic data from ref. 38. Blue circles: glutathione- and PEG-coated gold NPs (entries 5–6 in Table S1†). kclear was estimated as [C0]/AUC using data from ref. 28. Brown diamonds: atomically precise glutathione-coated gold NPs (entries 7–10 in Table S1†). kclear was estimated as CL/Vd using data from ref. 42. Orange squares: glutathione-coated gold NPs administered under different doses (entries 14–16 in Table S1†). kclear was estimated as CL/Vd using data from ref. 18. Purple inverted triangle: glutathione-coated gold NPs (entry 17 in Table S1†). kclear was estimated as [C0]/AUC using data from ref. 57. Red star: PEG/MBA-coated gold NP. kclear was estimated as [C0]/AUC using data from ref. 58.
In this work the rates of systemic clearance (kclear0, kclear1, etc.) for the differently sized NPs and NP–protein complexes are calculated according to eqn (5), with the corresponding values of 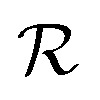 given by eqn (2). The results are presented graphically in Fig. S1a.† Implicit in the use of eqn (5) is that ultrasmall NPs display comparable plasma clearance rates as small protein drugs (see Discussion section). Simulations were also performed assuming that only NPfree was clearable, in which case kclear0 was the only biochemical reaction for clearance considered in the model.
given by eqn (2). The results are presented graphically in Fig. S1a.† Implicit in the use of eqn (5) is that ultrasmall NPs display comparable plasma clearance rates as small protein drugs (see Discussion section). Simulations were also performed assuming that only NPfree was clearable, in which case kclear0 was the only biochemical reaction for clearance considered in the model.
Receptor occupancy and area under the curve
The time-dependent receptor occupancy is defined as the concentration of NP-bound receptors, [Rb], over the total initial receptor concentration, [R0]:
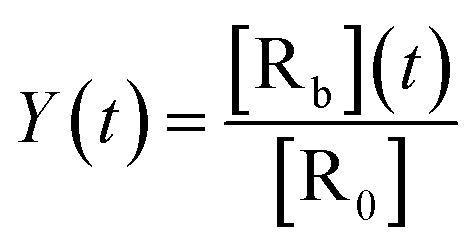 |
6 |
From this relation, the average area under the curve for receptor occupancy (AUCR) is calculated as:59
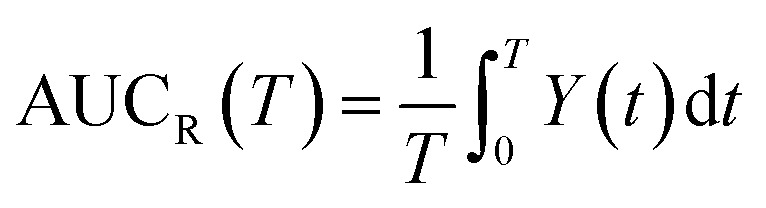 |
7 |
where T = 24 h is taken as a suitable time window. The average AUCR is used as a measure of nanodrug efficacy. It reaches the maximum value of 1 when all receptors remain in their bound state for 24 h.
Parameter values
Table 1 lists the unique values of NP radii, NP-receptor binding constants and clearance rates used in the simulations. In all simulations the kon,P was kept constant at 1 × 105 M−1 s−1 while the koff,P varied as 10, 50, 100, 200, 500, 1000 and 2000 s−1. The different pairs of kon,P and koff,P yielded the following values for the (microscopic) nonspecific binding affinity (KD,P): 0.1, 0.5, 1, 2, 5, 10 and 20 mM. Sim #3, #6 and #8 included the following lower values of KD,P as well: 5, 10, 20 and 50 μM. For all simulations, [R0] = 1 nM, [P0] = 1 mM and [NP0] = 1 μM, corresponding to the initial (t = 0 s) concentrations of receptor, plasma proteins and NPs, respectively. [P0] was set slightly higher to the maximum concentration of albumin in plasma (∼0.75 mM).
Unique simulation parameters for Model 1.
| Sim # | NP radius (nm) | k on,R (M−1 s−1) | k off,R (s−1) | K D,R (nM) | k clear0 a (s−1) | Clearanceb |
|---|---|---|---|---|---|---|
| 1 | 3 | 1 × 105 | 1 × 10−3 | 10 | 4.5 × 10−4 | All |
| 2 | 4 | 1 × 105 | 1 × 10−3 | 10 | 1.3 × 10−4 | All |
| 3 | 1 | 1 × 105 | 1 × 10−3 | 10 | 1.3 × 10−3 | All |
| 4 | 3 | 1 × 105 | 1 × 10−3 | 10 | 4.5 × 10−4 | NPfree |
| 5 | 4 | 1 × 105 | 1 × 10−3 | 10 | 1.3 × 10−4 | NPfree |
| 6 | 1 | 1 × 105 | 1 × 10−3 | 10 | 1.3 × 10−3 | NPfree |
| 7 | 3 | 1 × 105 | 1 × 10−1 | 1000 | 4.5 × 10−4 | NPfree |
| 8 | 1 | 1 × 103 | 1 × 10−5 | 10 | 1.3 × 10−3 | NPfree |
Systemic clearance rates (kclear0, kclear1, etc.) are calculated according to eqn (5). kclear0 is shown for reference.
Sim #1–3: NP clearance occurs through NPfree, NPPC and NPFC. Sim #4–8: NP clearance occurs through NPfree only.
2.2. Model 2: impact of soft protein interactions on NP tumor accumulation
Model basics
Model 2 is illustrated schematically in Fig. 1b. It can be described by the following main features: (i) ultrasmall NPs are initially present in the main (‘plasma’) compartment but can reach a second, peripheral (‘tumor’) compartment. (ii) Both compartments contain a high concentration of proteins interacting nonspecifically to the NPs with ultraweak affinity as described in Model 1. Although the chemical and physical state of blood differs from that of the tumor interstitium, the model assumes that soft interactions occur equally in both compartments; (iii) NP clearance takes place through the main compartment and is simulated as described in Model 1; (iv) the rate of NP transfer between compartments is size dependent and estimated as explained below. Furthermore, since the total protein concentrations in the plasma and tumor tissue are very high and similar to one another,60 the transport of proteins between compartments can be neglected in the model; (v) additional complexities such as the effect of tumor heterogeneity and NP diffusion are not incorporated in the model.
Reaction equations
NP transfer between compartments can be characterized by the following set of biochemical equations:NP ⇆ NPT kPT0, kTP0NP·P1 ⇆ NPT·PT1 kPT1, kTP1NP·P2 ⇆ NPT·PT2 kPT2, kTP2where kPT and kTP refer to the rates of transfer from the plasma to tumor compartment and from the tumor back into the plasma compartment, respectively; the superscript ‘T’ designates NP and protein species situated in the tumor compartment. The biochemical reactions for NP–protein binding and clearance are described similarly as in Model 1, and thus are not shown.
The dynamics of the system is characterized by a set of ordinary differential equations as shown in the ESI.† These ODEs can be easily modified to reflect the different NP–protein stoichiometries used in the actual simulations. The final ODEs are then solved numerically given the rate constants and initial boundary conditions as specified below under ‘Parameter values’. Numerical integration was performed with the software Polymath.
Extravasation and intravasation rate constants
The rate constant for the extravasation of NPs from leaky blood vessels and into the tumor interstitium can be defined as:
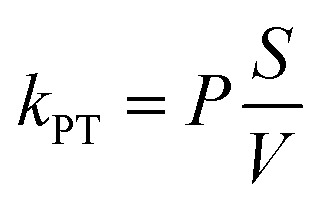 |
8 |
where P is the vascular permeability coefficient and S/V is the blood vessel surface area per unit volume of tissue.61–63
There is little quantitative knowledge on the kinetics of NP uptake in tumors.64 Thus, here the vascular permeability coefficient for ultrasmall NPs in the mouse is approximated to that of macromolecules, such as dextran, for which experimental data has been gathered.65 To a first approximation, the dependence of kPT on size can be estimated from the following empirical model based on experimental data, derived by Wittrup et al.:56
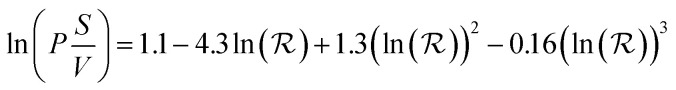 |
9 |
with the term between parenthesis on the left given in units of h−1.
The rates of extravasation (kPT0, kPT1, etc.) for the differently sized NPs and NP–protein complexes are calculated according to eqn (9), with the corresponding values of 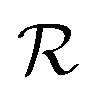 given by eqn (2). The results are presented graphically in Fig. S1b.† The effect of intravasation from the tumor site back into the main compartment is taken into account in the model by assuming either kTP = kPT or kTP = 0 (i.e., no intravasation).
given by eqn (2). The results are presented graphically in Fig. S1b.† The effect of intravasation from the tumor site back into the main compartment is taken into account in the model by assuming either kTP = kPT or kTP = 0 (i.e., no intravasation).
Percentage of injected dose (% ID)
The average % ID over 24 h is calculated as:
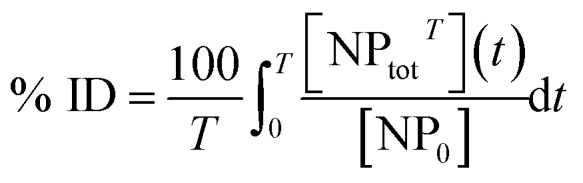 |
10 |
where [NPtotT] is the total concentration of NPs in the peripheral compartment as a function of time, and T = 24 h.
Parameter values
Table 2 lists the unique parameters used in the simulations. The remaining parameters were kept constant as such: kon,P and koff,P were given as in Model 1; [P0] = [P0T] = 1 mM; [NP0] = 1 μM; S/V = 2/mm.63
Unique simulation parameters for Model 2.
| Sim # | NP radius (nm) | k clear0 a (s−1) | k PT0 b (s−1) | k TP0 b (s−1) | Clearancec |
|---|---|---|---|---|---|
| 9 | 3 | 4.5 × 10−4 | 2.0 × 10−5 | 2.0 × 10−5 | All |
| 10 | 3 | 4.5 × 10−4 | 2.0 × 10−5 | 0 | All |
| 11 | 1 | 1.3 × 10−3 | 5.9 × 10−4 | 5.9 × 10−4 | All |
| 12 | 1 | 1.3 × 10−3 | 5.9 × 10−4 | 0 | All |
| 13 | 3 | 4.5 × 10−4 | 2.0 × 10−5 | 2.0 × 10−5 | NPfree |
| 14 | 3 | 4.5 × 10−4 | 2.0 × 10−5 | 0 | NPfree |
Systemic clearance rates (kclear0, kclear1, etc.) are calculated according to eqn (5). kclear0 is shown for reference.
Extravasation rate constants (kPT0, kPT1, etc.) are calculated according to eqn (9). Intravasation rate constants are defined as either kTP = 0 or kTP = kPT. kPT0 and kTP0 are shown for reference.
Sim #9–12: NP clearance occurs through NPfree, NPPC and NPFC. Sim #13–14: NP clearance occurs through NPfree only.
3. Results
3.1. Model 1: impact of soft protein interactions on receptor occupancy
Simulations #1, #2 and #3
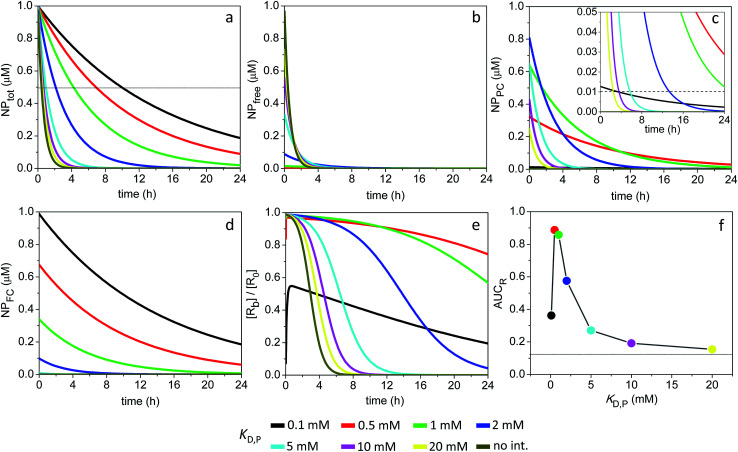
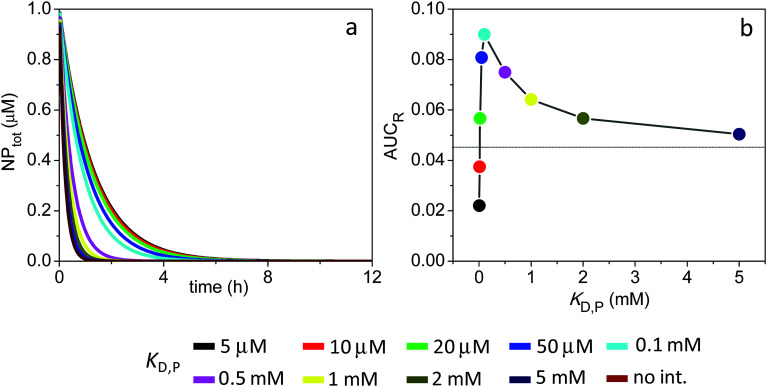
The time evolution of NPtot for different values of KD,P is shown in Fig. 3a for the 3 nm particles, where NPtot corresponds to the sum of all NP species in the compartment. The half-life for systemic clearance of NPtot for each value of KD,P can be found from the intercept of the corresponding decay curve with a horizontal line drawn at 0.5 μM. For example, in the absence of ultraweak interactions (figure legend = ‘no int.’), the NPtot half-life is 0.42 h, whereas this is extended to 4.2 and 9.9 h at a KD,P of 1 and 0.1 mM, respectively. More information about the dynamics of the system could be obtained by breaking down NPtot into three separate contributions: NPfree, NPPC and NPFC, where the time course of each species is depicted in Fig. 3b–d.
Fig. 3. Time course of NPtot, NPfree, NPPC and NPFC and extent of receptor occupancy assuming the model parameters in Sim #1. (a) Time course of NPtot. The apparent clearance half-life associated with each KD,P is given by the intercept of the thin line with each corresponding decay curve. (b) Time course of NPfree. (c) Time course of NPPC. Dashed line in the inset marks the point where [NPPC] = KD,R. For KD,P = 0.5 and 1.0 mM, [NPPC] > KD,R over the entire 24 h time window. (d) Time course of NPFC. (e) Receptor occupancy as a function of time. (f) Area under the curve for receptor occupancy as a function of KD,P; calculated from (e) with eqn (7). Thin line marks the calculated value of AUCR (0.12) in the absence of soft interactions.
The receptor occupancy (Y(t)) versus time profile is displayed in Fig. 3e. In the absence of ultraweak interactions, receptor occupancy is initially close to 1. However, this value drops quickly with time due to rapid compound elimination, and the corresponding average AUCR for receptor occupancy is low: AUCR = 0.12 (Fig. 3f). Toward the other extreme where the nonspecific binding affinity is strongest (KD,P = 0.1 mM), the AUCR is again very low since the NPs are mostly covered by a full corona and thus cannot bind to receptors (Fig. 3f). It then follows that there is an optimal range of KD,P around 0.5–1 mM for which the AUCR is maximized (AUCR = 0.86–0.89). This can be understood on the basis that, within this optimal range, the NPPC concentration is sustained above the KD,R (10 nM) for the entire 24 h time interval (Fig. 3c, inset). When considered in combination, Fig. 3a and f reveal an optimum KD,P of 1 mM for which the target occupancy is high (AUCR = 0.86; a 7.2-fold improvement over AUCR = 0.12) and the overall clearance is fast (t1/2 = 4.2 h for NPtot).
Fig. 4 shows the time evolution of NPtot and the average AUCR plot for the 4 nm particles (additional plots are shown in Fig. S2†). Relative to the 3 nm particles, the AUCR is now maximized over a broader range of nonspecific binding affinities: KD,P ∼ 0.5–5 mM. Together, Fig. 4a and b reveal an optimum KD,P of 2 mM for which the target occupancy is high (AUCR = 0.95) and the clearance is fast (t1/2 = 6.7 h for NPtot).
Fig. 4. Time course of NPtot and extent of receptor occupancy assuming the model parameters in Sim #2. (a) Time course of NPtot. The apparent clearance half-life associated with each KD,P is given by the intercept of the thin line with each corresponding decay curve. (b) Area under the curve for receptor occupancy as a function of KD,P; calculated from Fig. S2e† with eqn (7). Thin line marks the calculated value of AUCR (0.43) in the absence of soft interactions.
Fig. 5 shows the time evolution of NPtot and the average AUCR plot for the smaller 1 nm particles (additional plots are shown in Fig. S3†). Similarly to the larger particles discussed above, here the extent of receptor occupancy is also optimized within a narrow range of KD,P. However, the rapid drop in NPfree concentration with time, together with the inability of the protein-bound NPs (NPFC) to interact with receptors, yield very small average AUCR values (AUCR < 0.1) and an optimum KD,P that is outside the range of ultraweak interactions (KD,P = 100 μM).
Fig. 5. Time course of NPtot and extent of receptor occupancy assuming the model parameters in Sim #3. (a) Time course of NPtot. (b) Area under the curve for receptor occupancy as a function of KD,P; calculated from Fig. S3d† with eqn (7). Thin line marks the calculated value of AUCR (0.046) in the absence of soft interactions.
Simulations #4, #5 and #6
The calculations presented above assumed that all NP–protein species could be eliminated from the compartment following individual efflux rates (kclear0,kclear1,etc.) calculated according to eqn (5). However, this assumption is likely to overestimate the in vivo systemic clearance of the NPs leading to overly short half-lives. Therefore, here NP clearance is hypothesized to take place exclusively through the naked particle species (NPfree). Collective, Sim #1 through #6 therefore illustrate two limiting cases regarding NP clearance in systemic circulation.
The time evolution of the different NP species as well as the AUCR plots for the 1, 3 and 4 nm particles are shown in Fig. S4–S6.† Compared to Sim #1–3, the now much slower elimination rate of the NPs results in higher average AUCR values over 24 h. The AUCR plot for the 1 nm particles is particularly impacted: the average AUCR reaches a maximum of 0.4 at a KD,P of 20 μM (see Fig. 5vs. S6†).
Simulations #7
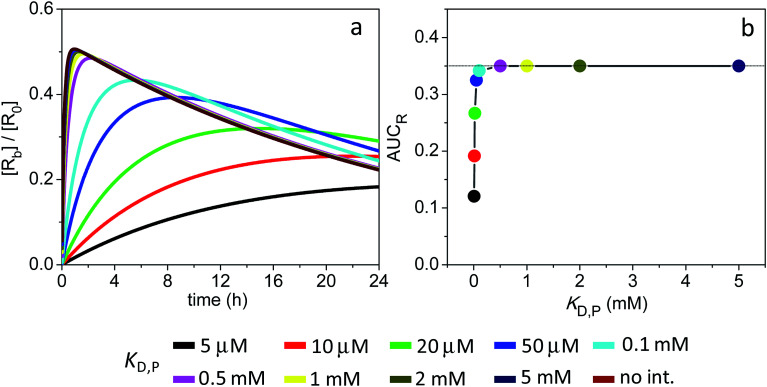
The simulations assumed to this point an intermediate value for the binding affinity between targeted NPs and receptors (KD,R = 10 nM). More likely, however, a typical targeting ligand such as a short peptide will bind its complementary receptor with high nanomolar to low micromolar dissociation constant.66 Additional simulations were therefore performed for the 3 nm particles assuming a KD,R of 1 μM. Here it should be noticed that, since KD,R = [NP0], no more than half the receptors can exist in the bound state, and thus the maximum possible AUCR is 0.5.
The calculated AUCR plot displays a maximum of 0.33 centered around a KD,P of 1 mM (Fig. S7†), which corresponds to a substantial ∼20-fold increase over the AUCR obtained in the absence of soft interactions (0.018). However, this high AUCR comes at the cost of a long clearance half-life for NPtot (t1/2 = 27 h) (Fig. S4a†).
Simulation #8
The relative magnitudes of kclear0 and koff,R define two characteristic regimes concerning receptor occupancy. On the one hand, for koff,R ≥ kclear0, target occupancy is driven by mass-balance effects, i.e., it is essentially governed by the interplay of compound concentration and binding affinity. All calculations so far have dealt with this particular kinetic regime. On the other hand, for koff,R < kclear0, the NPs are cleared from the compartment faster than they disengage from their bound receptor, and thus target occupancy over time is now majorly influenced by the NP-receptor residence time, tr, where tr = 1/koff,R. Additional information on the ‘residence-time concept’ as applied more broadly to the field of drug discovery can be found elsewhere.67,68
Here, additional simulations were implemented to illustrate the impact of nonspecific soft interactions on target occupancy for the particular kinetic regime where koff,R < kclear0. The calculations were performed for the 1 nm particles, for which kclear0 = 1.3 × 10−3 s−1. The association and dissociation rate constants for NP-receptor complexation were 103 M−1 s−1 and 10−5 s−1, respectively. Under these conditions, koff,R < kclear0 while KD,R is maintained at 10 nM as in the previous simulations.
The receptor occupancy versus time profile is displayed in Fig. 6a. In the absence of ultraweak interactions, target occupancy starts out low (Y ∼ 0.06 at t = 1 min) until it reaches a peak value of Y ∼ 0.5 at t ∼ 1 h. Fundamentally, this slow kinetics for receptor binding is a result of the small kon,R (103 M−1 s−1) adopted in the simulations. Nevertheless, Fig. 6b reveals that the degree of target occupancy is reasonably high (AUCR = 0.35) even in the absence of soft interactions and despite a sharp drop in the total NP concentration with time (cf. Fig. S6a†). In comparison, when target occupancy was limited by NP clearance as in Sim #6 (i.e., koff,R > kclear0), the calculated AUCR was only 0.046 (Fig. S6e†). Fig. 6b also shows that target occupancy is not affected by weak interactions having a KD,P > 0.1 mM.
Fig. 6. Extent of receptor occupancy assuming the model parameters in Sim #8. (a) Receptor occupancy as a function of time. (b) Area under the curve for receptor occupancy as a function of KD,P; calculated from (a) with eqn (7). Thin line marks the calculated value of AUCR (0.35) in the absence of soft interactions.
3.2. Model 2: impact of soft protein interactions on NP tumor accumulation
Simulations #9 and #10
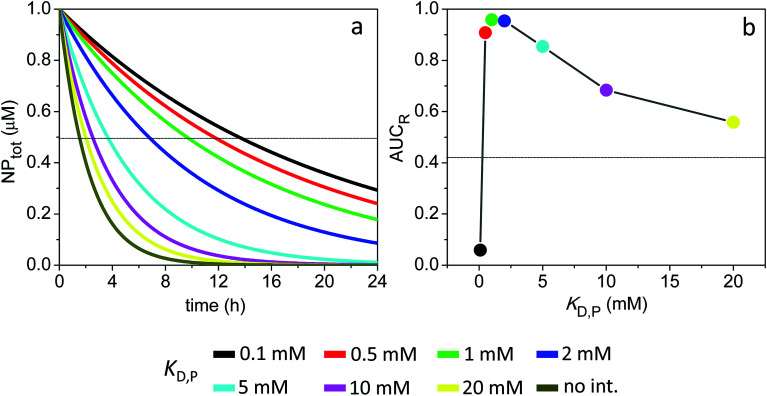
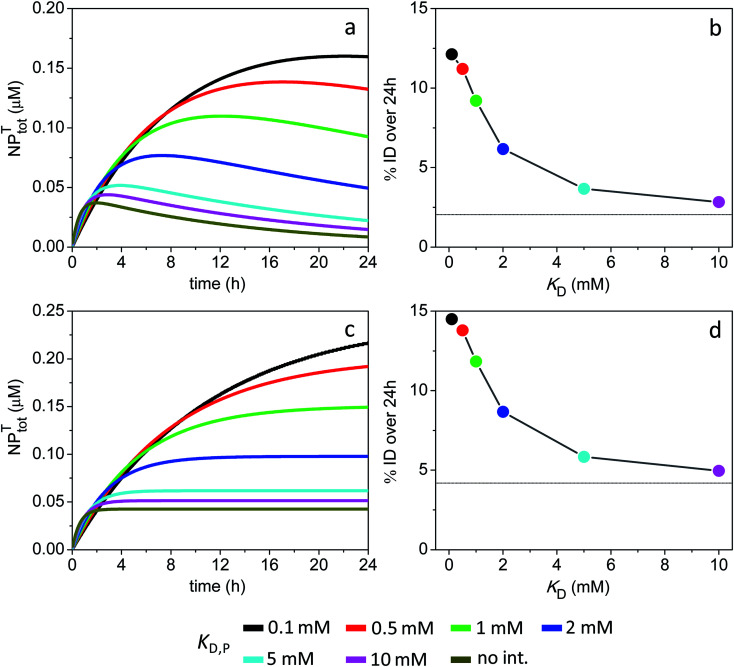
The time evolution of NPtotT for different values of KD,P is shown in Fig. 7a for the 3 nm particles and assuming equal rate constants of vascular extravasation and intravasation (kPT = kTP). Here, NPtotT corresponds to the sum of all NP species in the tumor compartment; the sum of all NP species in both compartments (NPtot) is displayed in Fig. S8.†Fig. 7a reveals that the time-dependent tumor accumulation of NPs increases for lower values of KD,P, which is consistent with soft interactions prolonging the half-life of particles in the main compartment (Fig. S8a†). The average % ID over 24 h, calculated from the data in Fig. 7a according to eqn (10), is shown in Fig. 7b. The % ID is found to be only 2% in the absence of ultraweak binding, whereas it reaches up to 9.2% at a KD,P of 1 mM.
Fig. 7. Time course of NPtotT in the peripheral compartment and % ID assuming the model parameters in Sim #9 and #10. (a) Time course of NPtotT and (b) % ID as a function of KD,P for Sim #9. (c) Time course of NPtotT and (d) % ID as a function of KD,P for Sim #10. Values of % ID were calculated from (a) and (c) with eqn (10). Thin lines in (b) and (d) mark the calculated values of % ID (2 and 4.2%) in the absence of soft interactions.
The simulations further reveal that a lack of NP intravasation back to the main compartment (kTP = 0) does not significantly affect tumor accumulation levels (Fig. 7c and d). This result reflects the fact that, under the given conditions, NP accumulation into the tumor site is essentially limited by a combination of ‘rapid’ systemic clearance with ‘slow’ vascular extravasation.
Simulations #11 and #12
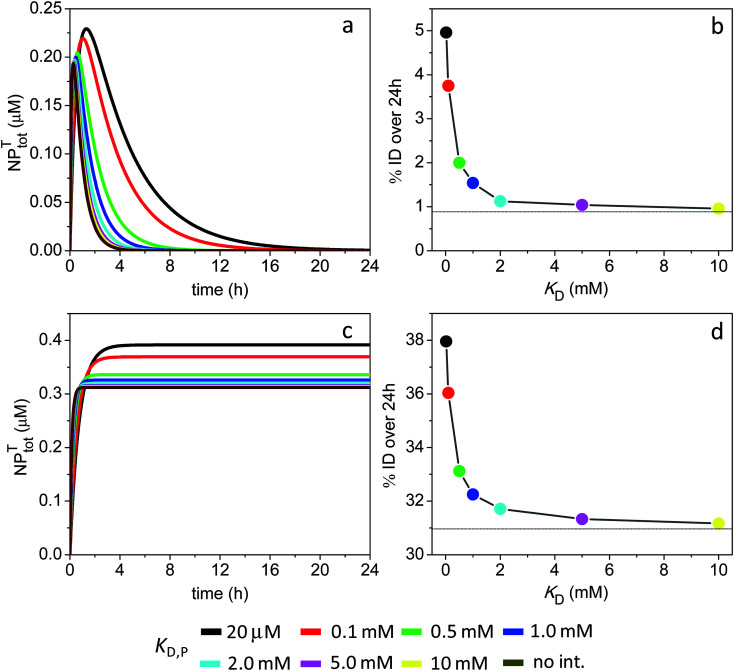
The time evolution of NPtotT for different values of KD,P is shown in Fig. 8a for the 1 nm particles and assuming kPT = kTP. In the absence of ultraweak binding, the NPtotT concentration increases sharply reaching 0.2 μM at short times. However, this high concentration is not sustained over time due to fast rates of systemic clearance and intravasation, and the resulting % ID falls under 1% (Fig. 8b). The results further reveal that ultraweak interactions with proteins do not slow down NP clearance and intravasation to a significant degree (Fig. S8c†), and therefore tumor accumulation is not improved; the % ID reaches only 1.5% at a KD,P of 1 mM.
Fig. 8. Time course of NPtotT in the peripheral compartment and % ID assuming the model parameters in Sim #11 and #12. (a) Time course of NPtotT and (b) % ID as a function of KD,P for Sim #11. (c) Time course of NPtotT and (d) % ID as a function of KD,P for Sim #12. Values of % ID were calculated from (a) and (c) with eqn (10). Thin lines in (b) and (d) mark the calculated values of % ID (0.88 and 31%) in the absence of soft interactions.
A different scenario arises assuming a lack of NP intravasation back into circulation. The NPs that have efficiently extravasated into the tumor site at short times now remain trapped inside, resulting in a high % ID of 31% in the absence of ultraweak binding (Fig. 8c and d). The data further shows that tumor accumulation is not significantly enhanced in the presence of soft interactions, with % ID = 32.3% at a KD,P of 1 mM.
Simulations #13 and #14
The current pair of simulations illustrate the impact of soft interactions on the tumor uptake of the 3 nm particles in the limiting case where systemic clearance occurs through NPfree only. The time evolution of NPtotT for different values of KD,P is shown in Fig. S9.† Relative to Sim #9–10, the slower elimination rate of the NPs in the presence of soft interactions results now in higher % ID values over 24 h. By comparing the time courses of NPtot and NPtotT in Fig. S9,† it is also clear that tumor accumulation is fundamentally limited by slow rates of extravasation when the KD,P falls in the range from ∼0.1 to 1 mM.
4. Discussion
Ultrasmall metal NPs are an emerging class of nanomaterials for cancer detection and treatment. In contrast to large inorganic NPs that cannot be directly excreted and therefore remain in the body for a long time, ultrasmall NPs are rapidly cleared from circulation through the kidneys and show reduced levels of uptake in the liver and spleen. Unfortunately, the efficient renal clearance has an associated drawback, in that it limits the tumor accumulation of the NPs. Of note, small protein drugs also usually exhibit rather short half-lives in circulation due to renal filtration and degradation.55,69,70 This puts a limit to their therapeutic efficacy in applications requiring long-lasting activity, such as in cancer treatment.
The current work introduces a hypothesis that, to the author's knowledge, has not been stated so far in an explicit manner. Accordingly, it is hypothesized that ultrasmall NPs could be engineered to undergo nonspecific ultraweak interactions with plasma proteins. Such ultraweak interactions could then modulate the pharmacokinetic and pharmacodynamic properties of NPs by essentially slowing down particle clearance through the kidneys. This proposed mechanism of half-life extension would be different than the corresponding strategies employed with protein therapeutics, some of which are based on increasing the hydrodynamic volume, e.g., by PEGylation.69,70
4.1. Ultraweak interactions
In this work, ultraweak interactions have by definition dissociation constants (KD,P) in the mM range. Ultraweak interactions might be modulated by numerous factors in the heterogeneous in vivo environment, such as shear forces and the local compositions and concentrations of proteins, lipids, metabolites, etc. Thus, KD,P must be strictly understood here as an apparent dissociation constant related to the in vivo conditions.
Ultraweak NP–protein interactions are unlikely to cause major particle toxicity or to elicit an immune response. This is because the interactions are, by definition, inherently transient, i.e., no given protein remains bound on the NP surface for too long; instead, the bound proteins are in fast and constant exchange with other proteins dispersed in solution. For example, ultraweak interactions are unlikely to cause meaningful alterations to protein structure and function, in marked contrast to the often substantial structural and functional changes resulting from the long-lived adsorption of proteins onto larger NPs. In addition, ultraweak interactions with opsonin proteins are unlikely to promote high levels of blood clearance by macrophages, since such transient interactions would not last sufficiently long to trigger phagocytosis.
Ultraweak interactions between two protein partners are prevalent in biology.48,71,72 They can have a profound effect on protein functionality in macromolecular crowded environments, such as the intracellular space. It has been suggested that transient protein–protein complexation takes place via short-range hydrophobic forces particularly if the protein partners display a small net charge to avoid strong electrostatic repulsions. The spatial distribution of hydrophobic residues (concentrated in patches vs. dispersed through the surface) and the conformational flexibility are additional factors that can influence the nature and magnitude of ultraweak interactions.71 Presumably, the current knowledge on the chemical and structural factors governing ultraweak interactions between proteins could be used as preliminary design rules for NPs. In addition, advanced computer simulations could be employed to understand or even predict the influence of NP characteristics such as size, curvature, surface chemistry, etc. on the magnitude of ultraweak interactions.
In closing this part, it is important to note that the term ‘soft corona’ has been usually employed in the nano literature to refer to the formation of a loose – as opposed to hard or permanent – adsorbed protein layer around large NPs.73–76 Due to its loose and transient nature, the soft corona is readily stripped off from the NP surface during most separation experiments such as centrifugation or gel filtration. The fact that the soft corona is not retained around the NP surface during separation experiments merely indicates that the residence time of the corona proteins is short owing to a fast dissociation rate constant. However, the binding affinity could be still quite strong given a sufficiently high association rate constant (kon).77 For example, assuming kon and koff constants of 108 M−1 s−1 and 10 s−1, respectively, would result in a binding affinity in the mid-nanomolar range (KD = 100 nM) but small residence time (∼0.1 s). In short, the common expression ‘soft corona’ found in the literature should not be mistaken for truly ultraweak interactions as defined here.
4.2. Compartmental model simulation
Here a simple compartmental model simulation was implemented to test the notion that soft interactions could modulate ultrasmall NP behavior in vivo. The model was designed as simple as possible to ease interpretations. Of course, minimal compartmental systems, as illustrated in Fig. 1, are only a crude approximation to in vivo physiology. Nevertheless, compartmental models have been widely used in pharmacology to provide quantitative insight into critical processes as drug distribution, elimination and binding.54,68,78 They have been also applied to understand the factors governing the tumor uptake of drugs and nanomedicines.64 Ultimately, classic compartmental models could help guide new experiments and be a starting point for the development of more accurate models.79–81
It should be pointed out that modeling the in vivo behavior of nonrenal clearable, conventionally large NPs could be significantly more challenging. For example, conventional NPs are cleared from systemic circulation by tissue uptake rather than kidney excretion.82 This process, in turn, may be strongly influenced by the nature of the protein corona formed around NPs and its associated interactions.82–86
4.3. Model 1: impact of soft protein interactions on receptor occupancy
In the absence of ultraweak interactions, the area under the curve for receptor occupancy (AUCR) over a given time window (here T = 24 h) would be close to the maximum value of 1 provided that [NPfree] ≫ KD,R > [R0]. In contrast, the AUCR would be low given a small value of the ratio [NPfree]/KD,R as a function of time. For example, for a 3 nm particle with kclear0 = 4.5 × 10−4 s−1 and KD,R = 10 nM, the calculated AUCR was only 0.12 (Fig. 3f). Assuming KD,R = 1 μM instead, the AUCR was reduced further to 0.018 (Fig. S7†). Therefore, soft interactions can be expected to significantly enhance target occupancy – relative to a situation where soft interactions are absent – when the NP clearance rate is high (leading to a rapid drop in [NPfree] with time) and/or when the NP-receptor binding affinity is weak (large KD,R). It should be recalled, however, that this generalization is only valid under the characteristic kinetic regime koff,R ≥ kclear0, under which target occupancy is driven by mass-balance effects.
The extent of receptor occupancy for the 3 nm particles was improved significantly at a KD,P around 0.5–1 mM (Fig. 3f, S4f and S7†). This occurred because, within this range of binding affinities, the concentration of NPs covered by a partial protein corona (NPPC) was sustained well above the KD,R over the entire 24 h time window. In the model, the factors governing the concentration of NPPC over time operated together in a synergistic way and included the initial NP and total plasma protein concentrations, the NP radius and binding capacity, rate of NP clearance, and magnitude of the nonspecific binding affinity. The results also revealed that the AUCR of the 4 nm particles was maximized over a wider range of affinities (KD,P = 0.5–5 mM) relative to the 3 nm particles (Fig. 4). This was mainly due to the greater binding capacity of the larger NPs such that, even at a relatively weak microscopic binding affinity of 5 mM, the overall NPPC concentration remained high enough to drive receptor complexation.
Although the simulations indicated a range of nonspecific binding affinities over which the AUCR was maximized, the effective elimination half-life of the NPs was different for each particular value of the affinity constant. This was especially evident when NPfree was assumed as the only clearable species. For example, the elimination half-life was exceedingly long (on the order of days) given a KD,P = 1 mM for the 4 nm particles (Fig. S5a†). This long half-life, in turn, could presumably result in higher levels of particle accumulation in off-target organs and greater toxicity. Therefore, the optimal value of binding affinity should result in a large AUCR together with a short half-life (e.g., KD,P = 5 mM, AUCR = 0.97 and t1/2 = 9.5 h as shown in Fig. S5†).
Receptor occupancy for the 1 nm particles was also modulated by interactions with plasma proteins. For example, Fig. S6e† showed that the AUCR was improved from 0.046 to 0.4 in the absence vs. presence of nonspecific interactions. However, the binding affinity that maximized the AUCR was KD,P = 20 μM, therefore falling well outside the range of ultraweak interactions. Conceivably, such binding affinity in the micromolar range could lead to greater NP toxicity. It can thus be concluded that ‘large’ NPs of higher binding capacity – as opposed to ‘very small’ particles that can only bind to a single plasma protein – may constitute a better choice to improve receptor occupancy in the plasma compartment via soft interactions. Fundamentally, this is because ultrasmall NPs must possess a minimum size to support the formation of a partial protein corona.
In closing this part, it is interesting to note that the extent of receptor occupancy by small molecule drugs is predicted to be modulated by drug interactions with plasma proteins in an similar way as shown here for NPs. Specifically, previous calculations have shown that drugs interacting either too weakly or too strongly with serum albumin do not bind efficiently to receptors since both situations lead to reduced free drug concentrations in plasma. As a result, an intermediate value of the plasma binding constant exists that maximizes the degree of target occupancy. However, there are important differences in the way that traditional drugs and NPs behave in vivo. For example, small-molecule drugs have much faster rates of systemic clearance and, as a consequence, target occupancy is maximized for drug-plasma protein binding affinities in the low micromolar range (∼1–10 μM).59
4.4. Model 2: impact of soft protein interactions on NP tumor accumulation
The simulations provided quantitative insight into the factors governing the tumor uptake of ultrasmall NPs. For the 3 nm particles and in the absence of soft interactions, tumor accumulation was limited by a ‘fast’ rate of clearance from the main compartment together with a ‘slow’ rate of extravasation into the tumor tissue. Nonspecific interactions with plasma proteins prolonged the elimination half-life of particles and increased their tumor uptake levels (Fig. 7).
A different picture emerged for the smaller 1 nm particles, in that their tumor accumulation was restricted by fast rates of both systemic clearance and intravasation (Fig. 8a and b). When no intravasation was assumed to take place in the model, the % ID increased all the way up to 31% (Fig. 8c and d). Tumor accumulation was not improved beyond this in the presence of ultraweak interactions, since the interactions could not significantly prolong NP half-life in the main compartment.
The above results illustrate how the enhanced permeation and retention (EPR) effect arises from the interplay of systemic clearance, vascular extravasation and intravasation. Intravasation, in particular, constitutes an important but often overlooked factor impacting the tumor uptake of drugs and NPs.64 For example, it has been argued that the slow rate of interstitial flow may prolong the residence time of NPs near an endothelial defect on the tumor side and lead to an increased probability of intravasation relative to extravasation.64,87 While the maximum rate constant of intravasation assumed in the model was kTP = kPT, the effect of kTP > kPT on tumor accumulation could be easily incorporated as well. It should be also noted that for the 3 nm particles the resulting % ID (from ∼1 to 15% depending on the KD,P) compares well to typical values of NP accumulation in xenograft mouse models.88 The great majority of experimental studies, however, lack detailed time-dependent measurements of NP concentrations in both the blood and tumor compartments, therefore precluding detailed quantitative comparisons with simulations.88
Setting the intravasation rate constant to zero in the simulations traps all extravasated NPs inside the tumor site. This, in turn, would be equivalent to a theoretically perfect active-targeting system resulting in complete NP binding to corresponding tumor cell receptors. Thus, it can be concluded that active targeting is not predicted to enhance tumor uptake levels when uptake is limited by rapid plasma clearance and slow extravasation in the first place (e.g., see Fig. 7). It is therefore interesting to note that, in such cases, ultraweak interactions with plasma proteins might prove a better strategy to improve the tumor localization of ultrasmall NPs. On the other hand, high-affinity active targeting is predicted to substantially enhance tumor uptake levels in the special case of very small NPs that show fast rates of vascular extravasation, but for which tumor accumulation might be limited by intravasation back into circulation. In a similar way, small high-affinity binding peptides are predicted to accumulate efficiently in tumors because of rapid uptake through capillary extravasation and effective retention by antigen binding.55,89
4.5. Plasma clearance of ultrasmall metal NPs
Ultrasmall NPs and small protein therapeutics have similar hydrodynamic sizes and hydrophilic surface chemistries and, in vivo, they both exhibit efficient renal elimination and two-compartment pharmacokinetics. Owing to these similarities, the calculations assumed that ultrasmall NPs displayed comparable rates of systemic clearance as small protein drugs. Here, the validity of this assumption is verified by comparing experimental clearance data for NPs and proteins.
Shown in Tables S1 and S2† is a short compilation of distribution and elimination plasma half-lives (t1/2α and t1/2β) for NPs and protein drugs. The NP data was obtained by Zheng and co-workers, and the reader is referred to their publications for additional information on other relevant pharmacokinetic parameters such as the plasma clearance (CL), volume of distribution (Vd) and AUC.23,28,36–38,42,43 The experimental data of Zheng were used to estimate a single-exponential plasma clearance term for the ultrasmall NPs according to either kclear = CL/Vd or kclear = [C0]/AUC (for the latter, AUC values were converted from % ID per g blood to % ID per mL plasma based on a hematocrit of 0.5, and [C0] was estimated as 50% ID per mL based on a mouse plasma volume of 2 mL – similarly to the [C0] estimation for the protein data included in Fig. 2). The results revealed a large scatter in the values of kclear for ultrasmall NPs of otherwise similar sizes (Fig. 2), which suggests, in turn, that the plasma clearance of the particles may be modulated by additional factors in vivo (see below). Nevertheless, it can be concluded that the overall clearance rates adopted in the simulations were within the range of experimentally estimated apparent plasma clearance values for ultrasmall metal NPs (Fig. S1a† and 2).
Finally, it can be noted that the experimentally estimated values of kclear varied from 6.1 × 10−4 s−1 to 3.5 × 10−5 s−1, this being 1.6 to 30-fold smaller than the predicted value of ∼1 × 10−3 s−1 for a protein drug of comparable size (Fig. 2). It is therefore instructive to consider some possible causes for this difference, as briefly discussed next. (i) Experimental uncertainties: while it may be useful to compare half-lives and clearance rates, these are time parameters that do not have a primary physiological basis.90 In fact, half-lives and rates are determined by other basic pharmacokinetic parameters such as the CL and Vd, which in turn are influenced by dose of administration as well as by physiological and pathological factors; (ii) NP size measurement: it is unclear whether typically quoted values of NP size are sufficiently accurate. This is because the core size and overall hydrodynamic diameter of ultrasmall NPs are frequently determined by a combination of standard bright-field transmission electron microscopy (TEM) and DLS. However, neither technique is ideally suited to achieve the necessary accuracy and precision in the characterization of ultrasmall NPs and nanoclusters, especially in the case of heterogeneous particle populations;31 (iii) size heterogeneity: NPs of different sizes in a given heterogeneous population might behave differently in vivo although they will be treated as a single entity in the application of pharmacokinetic analysis models; (iv) NP density: it has been proposed that high density gold NPs marginate faster to blood vessel walls than other nanostructures of similar size but lower density.38 Thus, in laminar blood flow, high density NPs would tend to circulate more slowly in blood vessels and display slower renal clearance rates; (v) NP retention in the glycocalyx: using atomically precise nanoclusters in the sub-nanometer size regime, Du et al. showed that the smallest of nanoclusters had surprisingly longer blood retention times and slower elimination rates.42 This behavior was proposed to originate from a more efficient physical retention of the smaller particles by the glomerular glycocalyx; (vi) nonrenal plasma clearance: although filtration through the kidneys is expected to dominate the plasma clearance of ultrasmall NPs and protein drugs, plasma clearance may be partly influenced by different routes of nonrenal elimination, such as the liver/spleen uptake of NPs and the proteolytic degradation of proteins; (vii) injection dose: Xu et al. showed that gold NPs were excreted more slowly when administered under lower doses, which was presumably related to dose-dependent margination effects in the blood vessels.18 The kclear was affected by a factor of as much as 10 depending on the injection dose (Fig. 2); (viii) protein interactions: last but not least, biomolecules in plasma may interact with ultrasmall NPs with ultraweak affinities and prolong blood half-lives as illustrated in this work.
5. Conclusions
Ultrasmall metal NPs are being developed as novel renal clearable formulations for disease diagnosis and treatment. In this work, ultrasmall NPs were hypothesized to interact nonspecifically and transiently with plasma proteins. A simple compartmental model simulation was then implemented to understand how such soft interactions could act in synergy with other molecular and physiological processes to impact NP receptor occupancy and tumor uptake levels. The results revealed that, given the proper conditions, soft interactions could increase receptor occupancy and enhance tumor accumulation via prolongation of blood circulation times.
The fundamental trends uncovered by the model could have important implications for NP design. Presumably, the nature and magnitude of transient interactions could be tailored through the surface engineering of ultrasmall NPs, therefore complementing the current array of strategies used to modulate NP behavior in vivo.
Finally, it is now clear that synthetic nanostructures may behave in novel and unpredictable ways in the complex in vivo environment. Thus, additional studies – covering a broader range of particle core types, sizes and surface coatings, as well as dose levels – will be required to understand the factors governing the pharmacokinetics of ultrasmall NPs in more detail. This added knowledge will be also essential toward the development of more comprehensive and accurate models.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
This work was supported by grant #2019/04372-6, São Paulo Research Foundation (FAPESP).
Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra04718b
References
- Chen H. Zhang W. Zhu G. Xie J. Chen X. Nat. Rev. Mater. 2017;2:17024. doi: 10.1038/natrevmats.2017.24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boisselier E. Astruc D. Chem. Soc. Rev. 2009;38:1759–1782. doi: 10.1039/B806051G. [DOI] [PubMed] [Google Scholar]
- Zarschler K. Rocks L. Licciardello N. Boselli L. Polo E. Garcia K. P. De Cola L. Stephan H. Dawson K. A. Nanomedicine. 2016;12:1663–1701. doi: 10.1016/j.nano.2016.02.019. [DOI] [PubMed] [Google Scholar]
- Kim B. H. Hackett M. J. Park J. Hyeon T. Chem. Mater. 2013;26:59–71. doi: 10.1021/cm402225z. [DOI] [Google Scholar]
- Kopp M. Kollenda S. Epple M. Acc. Chem. Res. 2017;50:1383–1390. doi: 10.1021/acs.accounts.7b00051. [DOI] [PubMed] [Google Scholar]
- Wilhelm S. Tavares A. J. Dai Q. Ohta S. Audet J. Dvorak H. F. Chan W. C. Nat. Rev. Mater. 2016;1:16014. doi: 10.1038/natrevmats.2016.14. [DOI] [Google Scholar]
- Venditto V. J. Szoka Jr F. C. Adv. Drug Delivery Rev. 2013;65:80–88. doi: 10.1016/j.addr.2012.09.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi H. S. Liu W. Misra P. Tanaka E. Zimmer J. P. Ipe B. I. Bawendi M. G. Frangioni J. V. Nat. Biotechnol. 2007;25:1165. doi: 10.1038/nbt1340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J. Peng C. Yu M. Zheng J. Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol. 2017;9:e1453. doi: 10.1002/wnan.1453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazarovits J. Chen Y. Y. Sykes E. A. Chan W. C. Chem. Commun. 2015;51:2756–2767. doi: 10.1039/C4CC07644C. [DOI] [PubMed] [Google Scholar]
- Zhang Y.-N. Poon W. Tavares A. J. McGilvray I. D. Chan W. C. J. Controlled Release. 2016;240:332–348. doi: 10.1016/j.jconrel.2016.01.020. [DOI] [PubMed] [Google Scholar]
- Dai Q. Bertleff-Zieschang N. Braunger J. A. Björnmalm M. Cortez-Jugo C. Caruso F. Adv. Healthcare Mater. 2018;7:1700575. doi: 10.1002/adhm.201700575. [DOI] [PubMed] [Google Scholar]
- Salvati A. Pitek A. S. Monopoli M. P. Prapainop K. Bombelli F. B. Hristov D. R. Kelly P. M. Åberg C. Mahon E. Dawson K. A. Nat. Nanotechnol. 2013;8:137. doi: 10.1038/nnano.2012.237. [DOI] [PubMed] [Google Scholar]
- Du B. Yu M. Zheng J. Nat. Rev. Mater. 2018;1:358–374. doi: 10.1038/s41578-018-0038-3. [DOI] [Google Scholar]
- Chen F. Ma K. Madajewski B. Zhuang L. Zhang L. Rickert K. Marelli M. Yoo B. Turker M. Z. Overholtzer M. Nat. Commun. 2018;9:4141. doi: 10.1038/s41467-018-06271-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu M. Zheng J. ACS Nano. 2015;9:6655–6674. doi: 10.1021/acsnano.5b01320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tao Y. Li M. Ren J. Qu X. Chem. Soc. Rev. 2015;44:8636–8663. doi: 10.1039/C5CS00607D. [DOI] [PubMed] [Google Scholar]
- Xu J. Yu M. Peng C. Carter P. Tian J. Ning X. Zhou Q. Tu Q. Zhang G. Dao A. Angew. Chem., Int. Ed. 2018;57:266–271. doi: 10.1002/anie.201710584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X. D. Chen J. Luo Z. Wu D. Shen X. Song S. S. Sun Y. M. Liu P. X. Zhao J. Huo S. Adv. Healthcare Mater. 2014;3:133–141. doi: 10.1002/adhm.201300189. [DOI] [PubMed] [Google Scholar]
- Zhang X. D. Luo Z. Chen J. Shen X. Song S. Sun Y. Fan S. Fan F. Leong D. T. Xie J. Adv. Mater. 2014;26:4565–4568. doi: 10.1002/adma.201400866. [DOI] [PubMed] [Google Scholar]
- Alric C. Miladi I. Kryza D. Taleb J. Lux F. Bazzi R. Billotey C. Janier M. Perriat P. Roux S. Nanoscale. 2013;5:5930–5939. doi: 10.1039/C3NR00012E. [DOI] [PubMed] [Google Scholar]
- Yu M. Xu J. Zheng J. Angew. Chem., Int. Ed. 2019;131:4156–4172. doi: 10.1002/ange.201807847. [DOI] [Google Scholar]
- Zhou C. Hao G. Thomas P. Liu J. Yu M. Sun S. Öz O. K. Sun X. Zheng J. Angew. Chem., Int. Ed. 2012;51:10118–10122. doi: 10.1002/anie.201203031. [DOI] [PubMed] [Google Scholar]
- Simpson C. A. Salleng K. J. Cliffel D. E. Feldheim D. L. Nanomedicine. 2013;9:257–263. doi: 10.1016/j.nano.2012.06.002. [DOI] [PubMed] [Google Scholar]
- Zhang X.-D. Luo Z. Chen J. Song S. Yuan X. Shen X. Wang H. Sun Y. Gao K. Zhang L. Sci. Rep. 2015;5:8669. doi: 10.1038/srep08669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong O. A. Hansen R. J. Ni T. W. Heinecke C. L. Compel W. S. Gustafson D. L. Ackerson C. J. Nanoscale. 2013;5:10525–10533. doi: 10.1039/C3NR03121G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García K. P. Zarschler K. Barbaro L. Barreto J. A. O'Malley W. Spiccia L. Stephan H. Graham B. Small. 2014;10:2516–2529. doi: 10.1002/smll.201303540. [DOI] [PubMed] [Google Scholar]
- Liu J. Yu M. Ning X. Zhou C. Yang S. Zheng J. Angew. Chem., Int. Ed. 2013;52:12572–12576. doi: 10.1002/anie.201304465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang S. Cao Z. Adv. Mater. 2010;22:920–932. doi: 10.1002/adma.200901407. [DOI] [PubMed] [Google Scholar]
- Knittel L. L. Schuck P. Ackerson C. J. Sousa A. A. RSC Adv. 2016;6:46350–46355. doi: 10.1039/C6RA07777C. [DOI] [Google Scholar]
- Sousa A. A. Hassan S. A. Knittel L. L. Balbo A. Aronova M. A. Brown P. H. Schuck P. Leapman R. D. Nanoscale. 2016;8:6577–6588. doi: 10.1039/C5NR07642K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boselli L. Polo E. Castagnola V. Dawson K. A. Angew. Chem., Int. Ed. 2017;56:4215–4218. doi: 10.1002/anie.201700343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinluan III R. D. Yu M. Gannaway M. Sullins J. Xu J. Zheng J. Bioconjugate Chem. 2015;26:2435–2441. doi: 10.1021/acs.bioconjchem.5b00490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X. He H. Wang Y. Wang J. Sun X. Xu H. Nau W. M. Zhang X. Huang F. Chem. Commun. 2016;52:9232–9235. doi: 10.1039/C6CC03814J. [DOI] [PubMed] [Google Scholar]
- Yin H.-Q. Bi F.-L. Gan F. Bioconjugate Chem. 2015;26:243–249. doi: 10.1021/bc500505c. [DOI] [PubMed] [Google Scholar]
- Liu J. Yu M. Zhou C. Yang S. Ning X. Zheng J. J. Am. Chem. Soc. 2013;135:4978–4981. doi: 10.1021/ja401612x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ning X. Peng C. Li E. S. Xu J. Vinluan III R. D. Yu M. Zheng J. APL Mater. 2017;5:053406. doi: 10.1063/1.4978381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang S. Peng C. Xu J. Du B. Wang Q. Vinluan III R. D. Yu M. Kim M. J. Zheng J. Angew. Chem., Int. Ed. 2016;128:16273–16277. doi: 10.1002/ange.201609043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J. Wang Z. Lin W. Chen S. Acta Biomater. 2013;9:6414–6420. doi: 10.1016/j.actbio.2013.01.006. [DOI] [PubMed] [Google Scholar]
- Wu J. Zhao C. Lin W. Hu R. Wang Q. Chen H. Li L. Chen S. Zheng J. J. Mater. Chem. B. 2014;2:2983–2992. doi: 10.1039/C4TB00253A. [DOI] [PubMed] [Google Scholar]
- Settanni G. Zhou J. Suo T. Schöttler S. Landfester K. Schmid F. Mailänder V. Nanoscale. 2017;9:2138–2144. doi: 10.1039/C6NR07022A. [DOI] [PubMed] [Google Scholar]
- Du B. Jiang X. Das A. Zhou Q. Yu M. Jin R. Zheng J. Nat. Nanotechnol. 2017;12:1096. doi: 10.1038/nnano.2017.170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou C. Long M. Qin Y. Sun X. Zheng J. Angew. Chem., Int. Ed. 2011;50:3168–3172. doi: 10.1002/anie.201007321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaturvedi D. S. K. Sagar V. Zhao H. Wistow G. Schuck P. J. Am. Chem. Soc. 2019;141:2990–2996. doi: 10.1021/jacs.8b11371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaturvedi S. K. Ma J. Brown P. H. Zhao H. Schuck P. Nat. Commun. 2018;9:4415. doi: 10.1038/s41467-018-06902-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rowe A. J. Methods. 2011;54:157–166. doi: 10.1016/j.ymeth.2011.02.006. [DOI] [PubMed] [Google Scholar]
- Bekdemir A. Stellacci F. Nat. Commun. 2016;7:13121. doi: 10.1038/ncomms13121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarkar M. Li C. Pielak G. J. Biophys. Rev. 2013;5:187–194. doi: 10.1007/s12551-013-0104-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klinger M. Protein Eng., Des. Sel. 2017;30:489–494. doi: 10.1093/protein/gzx035. [DOI] [PubMed] [Google Scholar]
- Peters Jr T., All about albumin: biochemistry, genetics, and medical applications, Academic Press, 1995 [Google Scholar]
- Sousa A. A. J. Fluoresc. 2015;25:1567–1575. doi: 10.1007/s10895-015-1665-3. [DOI] [PubMed] [Google Scholar]
- Ding H.-m. Ma Y.-q. Biomaterials. 2014;35:8703–8710. doi: 10.1016/j.biomaterials.2014.06.033. [DOI] [PubMed] [Google Scholar]
- Maffre P. Brandholt S. Nienhaus K. Shang L. Parak W. J. Nienhaus G. U. Beilstein J. Nanotechnol. 2014;5:2036–2047. doi: 10.3762/bjnano.5.212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J. Lannoy I. A. M. Biochem. Pharmacol. 2014;87:93–120. doi: 10.1016/j.bcp.2013.09.007. [DOI] [PubMed] [Google Scholar]
- Schmidt M. M. Wittrup K. D. Mol. Cancer Ther. 2009;8:2861–2871. doi: 10.1158/1535-7163.MCT-09-0195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wittrup K. D., Thurber G. M., Schmidt M. M. and Rhoden J. J., in Meth. Enzym., Elsevier, 2012, vol. 503, pp. 255–268 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng C. Gao X. Xu J. Du B. Ning X. Tang S. Bachoo R. M. Yu M. Ge W.-P. Zheng J. Nano Res. 2017;10:1366–1376. doi: 10.1007/s12274-017-1472-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng C. Xu J. Yu M. Ning X. Huang Y. Du B. Hernandez E. Kapur P. Hsieh J. T. Zheng J. Angew. Chem., Int. Ed. 2019;131:8567–8571. doi: 10.1002/anie.201903256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peletier L. A. Benson N. van der Graaf P. H. J. Theor. Biol. 2009;256:253–262. doi: 10.1016/j.jtbi.2008.09.014. [DOI] [PubMed] [Google Scholar]
- Wiig H. Tenstad O. Iversen P. O. Kalluri R. Bjerkvig R. Fibrog. Tissue Repair. 2010;3:12. doi: 10.1186/1755-1536-3-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reyes-Aldasoro C. C. Wilson I. Prise V. E. Barber P. R. Ameer-Beg M. Vojnovic B. Cunningham V. J. Tozer G. M. Microcirculation. 2008;15:65–79. doi: 10.1080/10739680701436350. [DOI] [PubMed] [Google Scholar]
- Yuan F. Leunig M. Huang S. K. Berk D. A. Papahadjopoulos D. Jain R. K. Cancer Res. 1994;54:3352–3356. [PubMed] [Google Scholar]
- Thurber G. M. Schmidt M. M. Wittrup K. D. Adv. Drug Delivery Rev. 2008;60:1421–1434. doi: 10.1016/j.addr.2008.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong A. D. Ye M. Ulmschneider M. B. Searson P. C. PLoS One. 2015;10:e0123461. doi: 10.1371/journal.pone.0123461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dreher M. R. Liu W. Michelich C. R. Dewhirst M. W. Yuan F. Chilkoti A. J. Natl. Cancer Inst. 2006;98:335–344. doi: 10.1093/jnci/djj070. [DOI] [PubMed] [Google Scholar]
- Ruoslahti E. Bhatia S. N. Sailor M. J. J. Cell Biol. 2010;188:759–768. doi: 10.1083/jcb.200910104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Copeland R. A. Nat. Rev. Drug Discovery. 2016;15:87. doi: 10.1038/nrd.2015.18. [DOI] [PubMed] [Google Scholar]
- Dahl G. Akerud T. Drug Discovery Today. 2013;18:697–707. doi: 10.1016/j.drudis.2013.02.010. [DOI] [PubMed] [Google Scholar]
- Kontermann R. E. BioDrugs. 2009;23:93–109. doi: 10.2165/00063030-200923020-00003. [DOI] [PubMed] [Google Scholar]
- Kontermann R. E. Curr. Opin. Biotechnol. 2011;22:868–876. doi: 10.1016/j.copbio.2011.06.012. [DOI] [PubMed] [Google Scholar]
- Wang Q. Zhuravleva A. Gierasch L. M. Biochemistry. 2011;50:9225–9236. doi: 10.1021/bi201287e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wirth A. J. Gruebele M. BioEssays. 2013;35:984–993. doi: 10.1002/bies.201300080. [DOI] [PubMed] [Google Scholar]
- Casals E. Puntes V. F. Nanomedicine. 2012;7:1917–1930. doi: 10.2217/nnm.12.169. [DOI] [PubMed] [Google Scholar]
- Milani S. Baldelli Bombelli F. Pitek A. S. Dawson K. A. Radler J. ACS Nano. 2012;6:2532–2541. doi: 10.1021/nn204951s. [DOI] [PubMed] [Google Scholar]
- Pederzoli F. Tosi G. Vandelli M. A. Belletti D. Forni F. Ruozi B. Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol. 2017;9:e1467. doi: 10.1002/wnan.1467. [DOI] [PubMed] [Google Scholar]
- Wang J. Jensen U. B. Jensen G. V. Shipovskov S. Balakrishnan V. S. Otzen D. Pedersen J. S. Besenbacher F. Sutherland D. S. Nano Lett. 2011;11:4985–4991. doi: 10.1021/nl202940k. [DOI] [PubMed] [Google Scholar]
- Lira A. L. Ferreira R. S. Torquato R. J. Zhao H. Oliva M. L. V. Hassan S. A. Schuck P. Sousa A. A. Nanoscale. 2018;10:3235–3244. doi: 10.1039/C7NR06810G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassingthwaighte J. B., Butterworth E., Jardine B. and Raymond G. M., in Comp. Toxicol., Springer, 2012, pp. 391–438 [Google Scholar]
- Danhof M. de Jongh J. De Lange E. C. Della Pasqua O. Ploeger B. A. Voskuyl R. A. Annu. Rev. Pharmacol. Toxicol. 2007;47:357–400. doi: 10.1146/annurev.pharmtox.47.120505.105154. [DOI] [PubMed] [Google Scholar]
- Moss D. M. Siccardi M. Br. J. Pharmacol. 2014;171:3963–3979. doi: 10.1111/bph.12604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M. Al-Jamal K. T. Kostarelos K. Reineke J. ACS Nano. 2010;4:6303–6317. doi: 10.1021/nn1018818. [DOI] [PubMed] [Google Scholar]
- Riviere J. E. Scoglio C. Sahneh F. D. Monteiro-Riviere N. A. Comput. Sci. Discovery. 2013;6:014005. doi: 10.1088/1749-4699/6/1/014005. [DOI] [Google Scholar]
- Lin Z. Monteiro-Riviere N. A. Riviere J. E. Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol. 2015;7:189–217. doi: 10.1002/wnan.1304. [DOI] [PubMed] [Google Scholar]
- Sahneh F. D. Scoglio C. Riviere J. PLoS One. 2013;8:e64690. doi: 10.1371/journal.pone.0064690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dell'Orco D. Lundqvist M. Cedervall T. Linse S. Nanomedicine. 2012;8:1271–1281. doi: 10.1016/j.nano.2012.02.006. [DOI] [PubMed] [Google Scholar]
- Dell'Orco D. Lundqvist M. Oslakovic C. Cedervall T. Linse S. PLoS One. 2010;5:e10949. doi: 10.1371/journal.pone.0010949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulmschneider M. B. Searson P. C. J. Controlled Release. 2015;212:78–84. doi: 10.1016/j.jconrel.2015.06.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawidczyk C. M. Russell L. M. Searson P. C. Front. Chem. 2014;2:69. doi: 10.3389/fchem.2014.00069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zahnd C. Kawe M. Stumpp M. T. de Pasquale C. Tamaskovic R. Nagy-Davidescu G. Dreier B. Schibli R. Binz H. K. Waibel R. Plückthun A. Cancer Res. 2010;70:1595–1605. doi: 10.1158/0008-5472.CAN-09-2724. [DOI] [PubMed] [Google Scholar]
- Toutain P.-L. Bousquet-Melou A. J. Vet. Pharmacol. Ther. 2004;27:427–439. doi: 10.1111/j.1365-2885.2004.00600.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.