A Satellite Account for Health in the United States

Abstract

This paper develops a satellite account for the US health sector and measures productivity growth in health care for the elderly population between 1999 and 2012. We measure the change in medical spending and health outcomes for a comprehensive set of 80 conditions. Medical care has positive productivity growth over the time period, with aggregate productivity growth of 1.5% per year. However, there is significant heterogeneity in productivity growth. Care for cardiovascular disease has had very high productivity growth. In contrast, care for people with musculoskeletal conditions has been costly but has not led to improved outcomes.

“The welfare of a nation can scarcely be inferred from a measure of national income.”

- Simon Kuznets (1934, p. 7)

Estimating medical care productivity growth is a central economic challenge. The National Income and Product Accounts (NIPAs) report that multi-factor productivity in the health care and social assistance sector declined by 0.4% annually between 1987 and 2018,¹ in contrast to the 0.9% increase in the economy as a whole. Given the size of health care in the economy, about 18% of GDP, low productivity growth in medical care influences aggregate productivity growth. Further, the low rate of measured productivity growth contributes to ongoing concerns about wasted resources in medicine (Chandra and Skinner, 2012).

However, official medical care productivity growth estimates suffer from a variety of problems (Advisory Commission to Study the Consumer Price Index, 1996; Berndt et al., 2001; Dunn, Rittmueller, and Whitmire, 2015). Quality adjustment is an often-noted issue. The primary output of medical care is improved health, yet health is not easily measured or attributed to medical interventions. Thus, health improvements are undercounted in official productivity growth estimates. This limitation was evident as far back as the 1930s, as the quotation from Simon Kuznets attests. In addition, the national accounts have difficulties when care from one type of provider substitutes for care from another. Each provider type is treated as a separate industry in the national accounts, for example pharmaceuticals, hospitals, and physicians. Thus, if a medication is developed which avoids the need for hospitalizations, the savings in hospital costs are not credited to the pharmaceutical industry. For each of these reasons, medical care productivity growth by sector may be significantly misstated.

To address these issues, proposals have periodically been made to establish a ‘satellite account’ for health. Such an account would measure health outcomes and medical inputs, and thus more accurately account for new goods and substitution of treatments (Schultze and Mackie, 2002; Abraham and Mackie, 2005; Rosen and Cutler, 2007; Rosen and Cutler, 2009; National Research Council, 2010).² The goal of this paper is to develop a satellite account for the US health sector and measure the change in the productivity of medical care over time.

The key design innovation in our accounts is to use medical conditions as the industries, not providers of care. For example, there is an industry for heart disease and a second one for lung cancer. Our accounts make no distinction based on the type of care provided; all that matters to people is how much they spend on care and their resulting health.³

The data needs for a satellite account are substantial, including measures of population health and medical spending matched to clinical characteristics and other sociodemographic factors. We benchmark medical spending and mortality to national data. Our empirical work adds measures of quality of life and allocates health and spending changes to conditions. The primary set we employ is the Medicare Current Beneficiary Survey (MCBS), an ongoing survey of the elderly population with data from 1999–2012. Thus, this initial satellite account is focused on the elderly, who account for one-third of total medical spending. We start by identifying a set of 80 conditions that are prevalent and severe enough to affect the elderly population. Of these conditions, 78 are clinical, for example heart attack and lung cancer. The remaining two are self-reported moderate and severe frailty (defined below). Frailty is not a disease that clinicians code, but we show that it is vital for both spending and health. We measure the prevalence of each condition using information from medical claims combined with imputations based on self-reports in the National Health and Nutrition Examination Survey (NHANES).

Aggregate medical spending is straightforward to measure. Real spending ($2010) on the elderly increased by roughly $5,000 per person over this time period. The change in health is more difficult to ascertain. The concept we wish to measure is quality-adjusted life expectancy (QALE), defined as the expected number of years a person will live, adjusted for the health-related quality of those years. To match our focus on the elderly, we measure QALE as of age 65. Life tables giving mortality by age are readily available from Vital Statistics. We develop an empirical measure of health-related quality of life based on survey data asking about difficulty with necessary physical activities, sensory impairments, and how much health interferes with social interactions. These domains capture many aspects of health, but not all; pain, cognition, and mental health symptoms are not asked about directly.⁴ We estimate that over the 1999–2012 time period, quality-adjusted life expectancy increased by about one year at age 65.

The bulk of our empirical analysis estimates how much of the change in spending and health outcomes result from medical treatment changes. The primary assumption we make in our analyses is that in most cases, medical care for a condition affects the health of people with that condition but not the prevalence of other conditions. That is, care for a heart attack influences the length and quality of life for people with a heart attack, but not whether the person develops cancer. The exceptions are medical risk factors such as hypertension and high cholesterol, where significant evidence shows an impact on downstream conditions. The assumption implies that the productivity of medical care can largely be determined by the health and spending trends for people once they have acquired conditions.

Empirical estimation of condition-specific health and spending trends is complex because of comorbidities. If a person has a heart attack and dies, how much of the death should be attributed to the heart attack, and how much to the mental illness which made taking preventive measures difficult? Our method to form condition-specific health and medical spending uses propensity score models to compare people with each condition to a similar group without the condition. The health and spending difference between these two groups is an estimate of the impact of that condition on the relevant outcome. We scale these estimates so that the total adds to national data on mortality and spending. We then transfer a portion of spending and health decrements from direct conditions to medical risk factors. The result is spending and health decrements for each condition in each year, which we use to form productivity growth at the condition level and, by adding up, for medical care as a whole.

Our analysis yields several conclusions. Over this time period we examine, productivity growth in medical care as a whole is relatively rapid: 1.5% annually. This is in contrast to official data, which show virtually no change in productivity over this interval. The high rate of productivity growth is a reflection of the large increase in QALE for the elderly population. As noted above, QALE at age 65 rose by 1 year. However, medical treatment changes accounted for an even greater increase, roughly 1.7 years, as overall QALE was held back by obesity and other non-medical factors. The value of health gains is large enough to outweigh the increase in lifetime medical spending.

Care for cardiovascular disease showed the largest productivity growth. Cardiovascular disease risk factors are better controlled than they were, and people who have had cardiovascular events live longer with fewer recurrent acute events than they did in the past. This survival gain has come at minimal cost increase, leading to large productivity growth. We validate our findings on cardiovascular disease by comparing our mortality trends to Vital Statistics tabulations and to epidemiological models of cardiovascular disease mortality. Our results match well those using other methodologies.

In contrast to the clear findings for cardiovascular disease, there is considerable heterogeneity in productivity change for other conditions. Musculoskeletal disease is a prototypical example; spending increased rapidly yet survival and quality of life for people with musculoskeletal disorders were barely affected. The same is true for mental illness, although this result is somewhat more tentative, as quality of life measurement for mental illness is less exact. Thus, musculoskeletal disorders and mental health are estimated to have low productivity growth. Overall, the heterogeneity in productivity growth across conditions suggests a significant opportunity for productivity-enhancing reforms in health care. The paper is structured as follows. The first section discusses the conceptual issues in health accounting. The second section describes our data. The third section details our methodology for estimating condition-specific spending growth and health improvement. The fourth and fifth sections estimate spending changes and health improvement by condition. The sixth section shows productivity growth. The last section concludes.

I. Accounting for Health

A. Current Treatment of Medical Care in NIPAs and Problems

The United States has two sets of medical spending accounts, one a part of the NIPAs and a second maintained by the Centers for Medicare and Medicaid Services (CMS). The two have many features in common (Sensenig and Wilcox, 2001). Both measure medical spending, not health outcomes. Both divide spending into industries based on the type of provider, not the disease. In the NIPAs, there are 13 industries relevant to health care, reflecting a mix of goods (prescription drugs, nonprescription drugs, and medical equipment) and services (e.g., hospital care and physician care).⁵

The Bureau of Labor Statistics (BLS) measures prices in each industry via surveys. Providers in the price surveys are asked to price the same bill over time, holding constant patient characteristics, payment source, and method of payment (for example, a hospitalization for a heart attack without significant comorbidities, covered by the Blue Cross-Blue Shield HMO plan). As in most industries, quality adjustment is designed to be incorporated at the price index stage. Real output is nominal spending deflated by quality-adjusted prices (BLS, 2007).

In practice, there are several difficulties with the national account treatment of health. We demonstrate these issues with an example consisting of a single condition, heart disease. The first problem is adjusting for changing quality. Imagine that a new surgical procedure is developed that allows people with heart disease to live longer. The impact of the new surgery on the medical price index will depend on how it is paid for. If the new service is placed in its own payment bucket, it will be linked into the existing price index and its introduction alone will not affect price trends. If the new surgery is placed in the same billing category as an older surgery or is put there by BLS,⁶ the price index will rise or fall depending on the relative reimbursement for the old and new surgery. However, neither of these methods has an explicit quality adjustment. BLS does not have a good quality adjustment in health care. Respondents to the BLS pricing surveys are asked to indicate if the good has changed materially, but few say so. And many changes in quality result from a series of small steps more than one large change. This is true in many industries, so other quality-adjustment techniques are standard. In many industries, quality adjustment is done through hedonic analysis (Groshen et al., 2017). For example, prices for each procedure or medication over time could be regressed on characteristics of the therapy, including outcomes and side effects (Cockburn and Anis, 2001; Comanor, Schweitzer, and Carter., 2005), with the non-quality component of a price change being the price index.

For several reasons, however, hedonic analysis is unlikely to work well in medical care (Berndt et al., 2000): consumers rarely pay the full cost of care they use, so marginal valuations are not equal to price; hedonics do not work well in life-or-death decisions; information asymmetries mean that consumers are unlikely to know the real value of services when they receive them; and health outcomes are difficult to parcel out to particular interventions, making it difficult for doctors and patients to know the consequences of what they are doing. As a result, hedonic analysis is not used in health care.

The impact of omitting quality change could be substantial. Life expectancy at birth increased 3.2 years between 1990 and 2017, at a time when medical care productivity was falling. If even a portion of the health improvement were due to medical care and this effect was captured, the overall evaluation of medical care productivity growth could change considerably.

A second problem with current methods is that they do not account for substitution across industries. Returning to the heart disease example, suppose that a new class of pharmaceuticals is developed which substitutes for surgery in people with heart disease. No lives are saved, but the new medication is sufficiently inexpensive that less is spent in total. Regardless of whether the new drug is linked into the existing pharmaceutical index or included in a basket with other medications, the national accounts will not show any productivity gain from reduced surgery. That is because pharmaceuticals and hospital care are different industries. In essence, the shift from surgery to medication will be attributed to consumer tastes, not to productivity growth.

To make progress on both of these issues, we need to partition medical care into more appropriate industries. The assumption we make is that the patient cares about their health and the total amount they spend on treatment, but not what treatment they receive. That is, pills and surgery differ only in their cost and whether their health outcomes. As a result, the relevant industries are not the providers of therapy but rather the conditions being treated.⁷

The Bureau of Economic Analysis has reached a similar conclusion and has recently started experimentally measuring medical spending on a condition basis (Dunn, Rittmueller, and Whitmire, 2015). However, the methods to do this are complex, as we explain below. And no attempt has been made to measure health outcomes systematically.

B. A Satellite Health Account

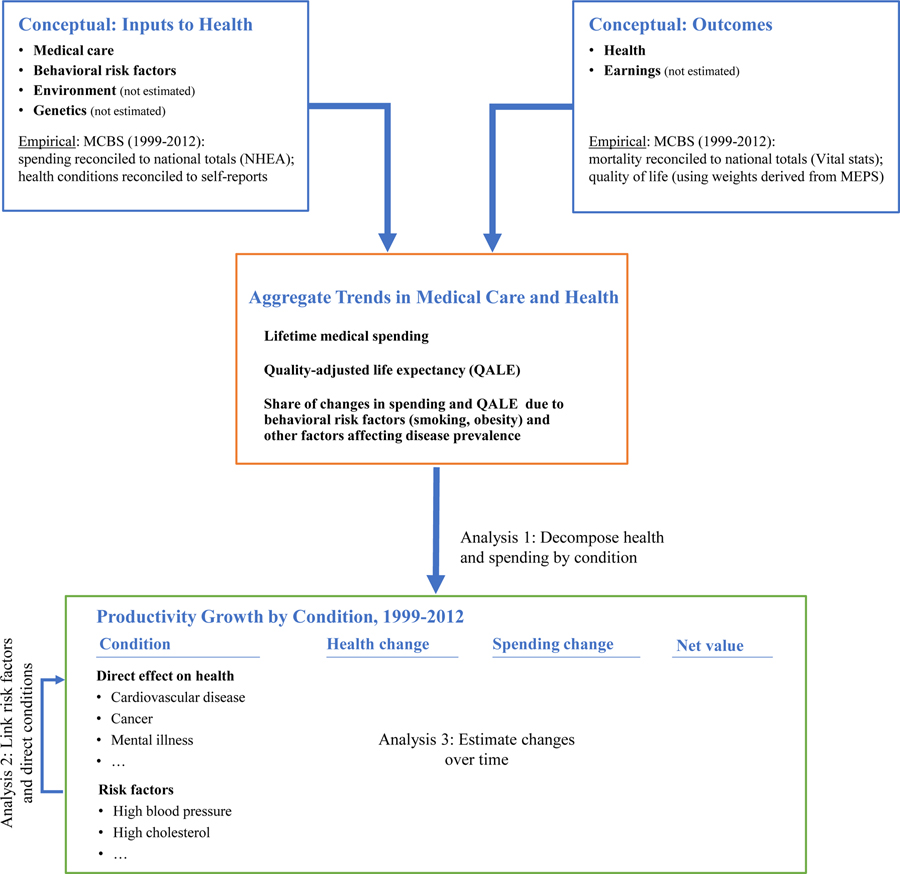
We start with a conceptual description of a satellite health account. The schematic for such an account is depicted in Figure 1. Health inputs include medical care, non-medical consumption and behaviors (e.g., cigarettes, physical activity, overall caloric intake), the environment, and genetics. We have data on the first two but leave aside environmental and genetic factors. The primary outcome of the health sector is the consumption value of better health. There is an investment value as well—higher earnings in the future—but this is not particularly important in the elderly population we analyze.

FIGURE 1. DEPICTION OF SATELLITE HEALTH ACCOUNT.

Notes: The top row shows the conceptual inputs to a satellite health account: the inputs and health outcomes. The middle row shows aggregate trends in medical care and health. The lower row shows the productivity analysis. Productivity growth is determined from changes in health and medical spending. MCBS=Medicare Current Beneficiary Survey, NHEA=National Health and Expenditure Accounts, Vital Stats=National Center for Health Statistics Mortality Data, MEPS=Medical Expenditure Panel Survey.

The middle part of Figure 1 shows the combination of these inputs and outcomes into population trends. Health has both a length-of-life and a quality dimension. We combine them into quality-adjusted life expectancy (QALE), the numbers of years a person can expect to live, adjusted for the quality of those years. Since our data is for the elderly population, we estimate QALE as of age 65. We summarize medical spending the same way, as expected spending from age 65 until death. Aggregate trends are informative about medical care productivity growth but not definitive. Both health and medical spending change over time for reasons beyond just changes in medical technology – most importantly prevalence changes.⁸ The third part of the analysis decomposes spending and health trends into the productivity of medical care. We do this by estimating the spending and outcomes associated with treating each condition. Before discussing the empirical implementation, we demonstrate the ideas theoretically. The framework follows other work on the productivity of medical care, for example Murphy and Topel (2006).

Individual behavior.—

Consider a population of ex-ante identical individuals who receive utility from two goods: health and non-medical consumption.⁹ Health is denoted H_t(a) for a person aged a in year t. We denominate health so that it ranges from 0 (death) to 1 (perfect health). In any period, utility is multiplicative in health and a concave function of non-medical consumption, x_t: U_t(a) = H_t(a) U(x_t), where U′>0 and U″<0. Thus, greater non-fatal health increases the value of all other consumption. Lifetime utility is the present value of flow utility for each year the person is alive. Denote S_t(a₀) as an indicator for whether the person is alive in year t conditional on being alive at age a₀ in t=0. ρ as the discount rate. Lifetime welfare is then given by:

$$\mathrm{W}\left({\mathrm{a}}_0\right)=\sum _{\mathrm{t}=0}^{\infty }{(1+\mathrm{\rho })}^{-\mathrm{t}}{\mathrm{S}}_{\mathrm{t}}\left({\mathrm{a}}_0\right){\mathrm{H}}_{\mathrm{t}}(\mathrm{a})\mathrm{U}\left({\mathrm{x}}_{\mathrm{t}}\right).$$ (1)

If people are fully insured or nearly so, medical spending in any period will be the average spending in the population, denoted m_ave,t.¹⁰ The budget constraint is that the present value of medical and non-medical consumption must be less than or equal to the present value of income plus initial assets (A₀). With perfect annuity markets, this will be an equality:

$$\sum _{\text{t}=0}^{\mathrm{\infty }}{(1+\mathrm{\rho })}^{-\mathrm{t}}{\mathrm{S}}_{\mathrm{t}}\left({\mathrm{a}}_0\right)\left({\mathrm{Y}}_{\mathrm{t}}-{\mathrm{x}}_{\mathrm{t}}-{\mathrm{m}}_{\mathrm{a}\mathrm{v}\mathrm{e},\mathrm{t}}\right)+{\mathrm{A}}_0=0.$$ (2)

For convenience, we assume the interest rate is equal to the discount rate, but this is not necessary if individuals can borrow and lend. Individuals maximize utility (1) subject to the budget constraint (2). The formulation of this problem is given in equation (3):

$$\text{W}\left({\text{a}}_0\right)=\sum _{\text{t}=0}^{\infty }{(1+\rho )}^{-\text{t}}\left\{{\text{S}}_{\text{t}}\left({\text{a}}_0\right){\text{H}}_{\text{t}}\text{U}\left({\text{x}}_{\text{t}}\right)+\mu {\text{S}}_{\text{t}}\left({\text{a}}_0\right)\left({\text{Y}}_{\text{t}}-{\text{x}}_{\text{t}}-{\text{m}}_{\text{ave},\text{t}}\right)\right\}+\mu {\text{A}}_0.$$ (3)

Equation (3) is denominated in utils. To translate this into dollars, we divide both sides by the marginal utility of wealth, μ.

There are two objects of choice in equation (3), medical spending and non-medical consumption. While medical care decisions are the outcome of some optimization problem, it is not clear that it is a rational decision. Our empirical work does not rely on the optimality of medical care decision-making. We assume only optimization of non-medical consumption. This implies that the marginal utility of non-medical consumption is the same in all periods;${\text{H}}_{\text{t}}{\text{U}}_{\text{t}}^{\text{'}}=\text{μ}$.

Health and Medical Treatments.—

We now provide more detail on the medical sector. People have one or more medical conditions, denoted by c. The prevalence of condition c at time t is prev_ct, and spending is m_ct. The vectors of condition prevalence and medical spending at time t are given by prev_t and m_t. Average medical spending is the inner product of these two vectors: m_ave,t = prev_t ∙ m_t.

Mortality for condition c denoted is γ_cat, and the vector of mortality rates is γ_at. This varies by age¹¹ and may change over time as medical treatments and other health inputs change. In our framework, as in our data analysis, we assume mortality rates for different conditions are independent—that is, γ_cat does not depend of other conditions the person has. This assumption is largely for data reasons; our data do not permit a richer mortality structure. Aggregate mortality is the prevalence-weighted average of the mortality rates for individual conditions: Γ_at = prev_at ∙ γ_at, and this, in turn, determines survival at each age up to a: ${\text{S}}_{\text{t}}\text{(a)}=\prod _{\tau =0}^{\text{t}-1}(1-{\mathrm{\Gamma }}_{\tilde{\text{a}}\text{τ}})$, for $\tilde{\text{a}}={\text{a}}_0+\tau$.

We model health-related quality of life as linear in the decrement associated with each condition. Let h_at denote the vector of health decrements associated with each condition, h_cat. Average quality of life is H_t(a) = 1 - prev_at ∙ h_at.

Now consider treatment changes for condition c. Differentiating equation (3) and considering a discrete change in medical care, Δm_c, the change in welfare associated with treatment change is given by:

$$\begin{array}{l}\frac{\mathrm{\Delta }\text{W}\left({\text{a}}_0\right)}{\mathrm{\mu }}=\sum _{\text{t}=0}^{\infty }{(1+\mathrm{\rho })}^{-\text{t}}\left\{\left(\frac{\text{dS}}{\text{d}{\mathrm{\gamma }}_{\text{c}}}\right)\left(\frac{\text{d}{\mathrm{\gamma }}_{\text{c}}}{{\text{dm}}_{\text{c}}}\right)\left(\frac{{\text{U}}_{\text{t}}}{{\text{U}}_{\text{t}}^{\prime }}+\left({\text{Y}}_{\text{t}}-{\text{x}}_{\text{t}}-{\text{m}}_{\text{ave},\text{t}}\right)\right)-{\text{S}}_{\text{t}}(\text{a})\frac{{\text{U}}_{\text{t}}}{{\text{H}}_{\text{t}}{\text{U}}_{\text{t}}^{\prime }}\left(\frac{{\text{dh}}_{\text{c}}}{{\text{dm}}_{\text{c}}}\right)\right\}{\text{prev}}_{\text{ct}}\mathrm{\Delta }{\text{m}}_{\text{c}}\\ +\sum _{\text{t}=0}^{\infty }{(1+\mathrm{\rho })}^{-\text{t}}\{\left(\frac{{\text{dS}}_{\text{t}}}{{\text{dprev}}_{\text{k}}}\right)\left(\frac{{\text{U}}_{\text{t}}}{{\text{U}}_{\text{t}}^{\prime }}+\left({\text{Y}}_{\text{t}}-{\text{x}}_{\text{t}}-{\text{m}}_{\text{ave},\text{t}}\right)\right)-{\text{S}}_{\text{t}}(\text{a})\frac{{\text{U}}_{\text{t}}}{{\text{H}}_{\text{t}}{\text{U}}_{\text{t}}^{\prime }}{\text{h}}_{\text{kat}})\left(\frac{{\text{dprev}}_{\text{k}}}{{\text{dm}}_{\text{c}}}\right)\mathrm{\Delta }{\text{m}}_{\text{c}}\\ -\sum _{\text{t}=0}^{\infty }{(1+\rho )}^{-\text{t}}{\text{S}}_{\text{t}}(\text{a}){\text{prev}}_{\text{ct}}\mathrm{\Delta }{\text{m}}_{\text{c}}\end{array}$$ (4)

The first row is the direct effect on health. It has two components. $\left(\frac{{\text{dS}}_{\text{t}}(\text{a})}{{\text{dγ}}_{\text{c}}}\right)\left(\frac{{\text{dγ}}_{\text{c}}}{{\text{dm}}_{\text{c}}}\right){\text{prev}}_{\text{ct}}{\text{Δm}}_{\text{c}}$ is the impact of medical care on survival to age a. The welfare value of this is found by multiplying the survival gain by $(\frac{{\text{U}}_{\text{t}}}{{\text{U}}_{\text{t}}^{\prime }}+({\text{Y}}_{\text{t}}-{\text{X}}_{\text{t}}-{\text{m}}_{\text{ave},\text{t}}))$, flow utility in year t plus the increment to future consumption. $\left(\frac{{\text{dh}}_{\text{c}}}{{\text{dm}}_{\text{c}}}\right){\text{prev}}_{\text{ct}}{\text{Δm}}_{\text{c}}$ is the impact of medical treatment changes on quality of life. The welfare value of this is found by multiplying by $-{\text{S}}_{\text{t}}\frac{{\text{U}}_{\text{t}}}{{\text{H}}_{\text{t}}{\text{U}}_{\text{t}}^{\prime }}$, the dollar value of improved health among those alive to experience it.

The second row involves clinical risk factors. It is operative when changes in medical care for one condition, c, affect the prevalence of another condition, k:$\left(\frac{{\text{dprev}}_{\mathrm{k}}}{{\mathrm{dm}}_{\mathrm{c}}}\right)$. The welfare impact of such a change is given by the health benefit associated with changes in the prevalence of k, the term in {.}. We term conditions that affect the prevalence of other conditions risk factors, and those with a direct impact on length or quality of life direct conditions.

The third row is the spending effect. The projected lifetime spending change due to a change in medical treatments is the present value of spending increases by people who are alive at each age.

Equation (4) is the multi-factor productivity (MFP) of medical treatment changes, or what Abraham and Mackie (2006) term ‘social profit.’ MFP can be positive or negative. We express MFP in dollars and as a growth rate, dividing by the net value of medical care in the base period.

Equations (3) and (4) are written from the perspective of the average person in society (a ‘per capita’ measure). An alternative is to estimate productivity growth for a person with a condition (a ‘per case’ measure). The per capita and per case measures are approximately related by the prevalence rate.¹² In evaluating each condition individually, we present the per case metric. That is, we ask the question: how is the welfare of people with condition c affected by treatment changes for that condition, assuming the person had the condition in the first and all subsequent years?¹³ We do this so that we can more easily compare across conditions. In contrast, when we evaluate medical care as a whole, we consider treatment changes per capita: what has been the impact on social welfare of all the medical care changes that have occurred, weighting each by the share of people affected by them?

The primary difficulty with estimating equation (4) empirically is isolating the impact of treatment changes from other factors influencing health and medical spending. We detail our approach to this issue after first describing the data we employ.

II. Data and Population Trends

The data needs for a satellite health account are shown in Figure 1. At the individual level, we need data on health status and medical spending for a representative share of the population. Information on other factors influencing health are needed to separate the role of medical advance from other factors that can drive outcomes.

Our primary dataset is the Medicare Current Beneficiary Survey (MCBS), an ongoing survey of the Medicare population (CMS, 199–2012). We use data from the population aged 65 and older, since Medicare is nearly universal in this age group. While data for the whole population would be preferred, data for the non-elderly population are less extensive, so we start with the elderly. This encompasses about one-third of national medical spending.¹⁴

The MCBS samples roughly 13,000 seniors annually. The survey gathers data on all use of medical care—both Medicare and non-Medicare. We modify MCBS data in two ways, discussed in more detail in Appendix A. First, Medicare claims data, and hence costs of care incurred, are only available for beneficiaries in traditional Medicare (i.e., not in Medicare Advantage HMO plans). To account for this, we reweight the population in traditional Medicare to reflect total Medicare enrollment, adjusting for the different demographics and health status of the two groups. Second, we adjust total spending in the MCBS by service category to match national estimates for the elderly (CMS, 2018). These adjustments are generally small and leave the trend in spending essentially unchanged (adjusted growth of 2.2% v. unadjusted growth of 2.1%). Figure 2 shows per capita spending for elderly Medicare beneficiaries, in real 2010 dollars (adjusted using the GDP deflator). Spending rose from $13,103 per capita in 1999 to $17,897 per capita in 2012, an increase of $4,794. There is a slowdown in spending growth around 2005, which has been examined (Cutler et al., 2019).

FIGURE 2. REAL, PER CAPITA MEDICAL SPENDING IN THE ELDERLY POPULATION, 1999–2012.

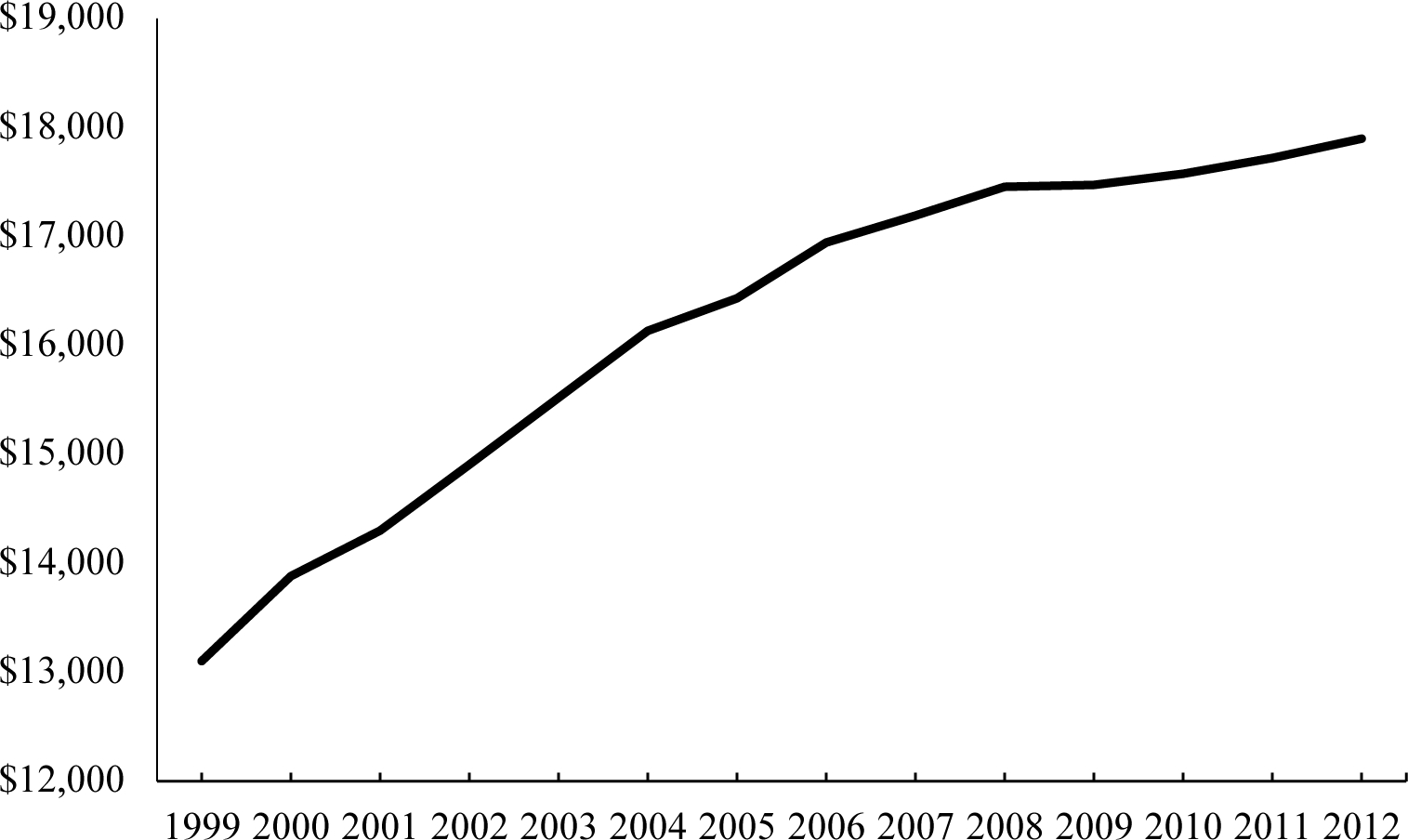
Notes: Spending is in real ($2010) dollars.

Source: MCBS data with totals matching estimated national spending on the elderly.

MCBS has a variety of sociodemographic and behavioral information, shown in Table 1. We present the means on these variables in five groups: sociodemographics (age, gender, race/ethnicity, marital status, poverty status, highest grade of education completed, and service in the armed forces), behavioral risk factors (smoking, body mass index [BMI]), self-reported health (one year prior and relative to others of the same age), mortality, and health impairments that we use to measure health-related quality of life, discussed in the next section.

Table 1:

Characteristics of the MCBS Sample, 2010–2012

Metric	Mean
Sociodemographics
Age	75.5
Male	44%
Race (white / black / other)	79%, 8%, 13%
Married	54%
Poverty category (1=worse, 5=best)	3.7
Education (<9 years, 9–11 years, HS/GED, some college, college grad)	10%, 13%, 28%, 27%, 23%
Veteran	24.1%
Behavioral risk factors
Smoking (never, current, former)	37%, 15%, 48%
BMI (underweight, normal, overweight, obese)	3%, 34%, 38%, 26%
Health Status
Self-reported health compared to one year previous (much/somewhat better, about the same, somewhat/much worse)	15%, 63%, 22%
Self-reported health compared to others of the same age (excellent, very good, good, fair, poor)	18%, 32%, 30%, 15%, 5%
Mortality rate (annual)	4.6%
Components of quality of life
Difficulty walking (1/4 mile/2–3 blocks; moderate, severe)	9%, 26%
Difficulty stooping/crouching/kneeling	47%
Difficulty lifting or carrying objects as heavy as 10 pounds	25%
Difficulty reaching or extending arms above shoulder level	17%
Difficulty writing or handling and grasping small objects	14%
Any ADL impairmenta	30%
Any IADL impairmenta	23%
Difficulty seeing (even with glasses)	33%
Difficulty hearing (even with hearing aid)	43%
Health limits social activities (moderate, severe)	7%, 5%

Notes: Means for sociodemographics, behavioral risk factors, health status, and mortality rate are from the MCBS FFS sample, weighted using sample weights adjusted to account for those omitted due to being in Medicare Advantage (HMO) plans. For components of quality of life, means are from the whole MCBS sample including Medicare advantage, and are weighted using survey weights. Survey questions for these impairments are shown in Appendix Table A5.

Source: Data are from those age 65 and older in the MCBS.

^aADL impairments include dressing, bathing/showing, or walking. IADL impairments include using the telephone, managing money, shopping, making meals, or doing light housework.

A. Population Health

Our primary measure of health is quality-adjusted life expectancy, or QALE. At age a₀, QALE is defined as:¹⁵

$$\text{QALE}\left({\text{a}}_0\right)=\sum _{\text{t}=0}^{\text{T}}{\text{S}}_{\text{t}}\left({\text{a}}_0\right)\cdot {\text{H}}_{\text{t}}(\text{a}).$$ (5)

As noted above, we take a₀ to be age 65.

Survival rates are straightforward to measure, as age-specific mortality is tracked in Vital Statistics data (Centers for Disease Control and Prevention, 2002–2016).¹⁶ Figure 3(a) shows a rapid decline in the age-adjusted mortality rate in the elderly population from 1999 to 2012, 1.5% annually.

FIGURE 3. MEASURES OF HEALTH IN THE ELDERLY POPULATION, 1999–2012.

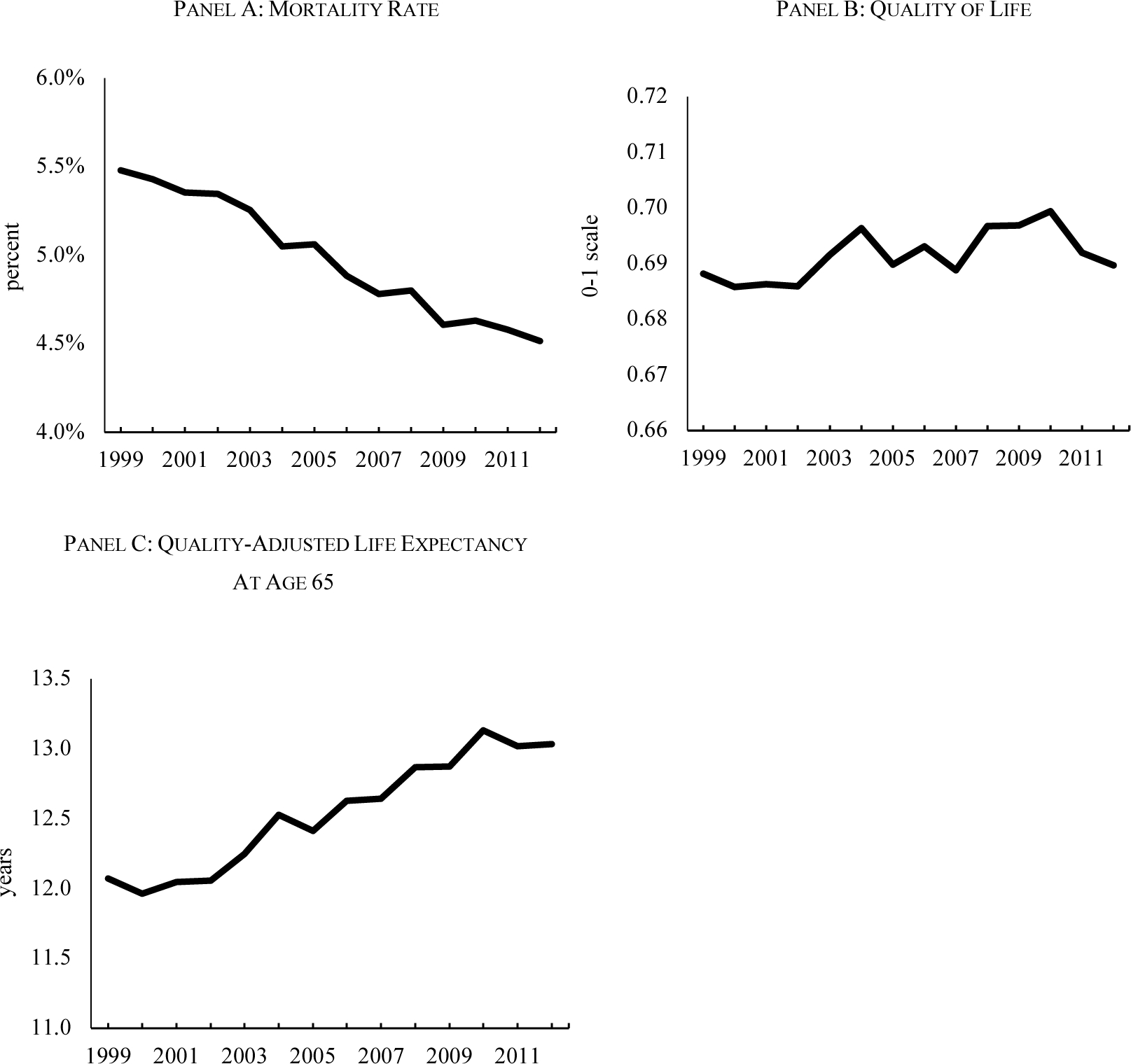
Notes: Mortality rates and quality of life in charts (a) and (b) are age-adjusted to the 2010 population, using data on population shares aged 65–74, 75–84, and 85+. Mortality rates are from Vital Statistics. Quality of life disutilities are based on a regression model relating self-rated health on a 0–100 scale in MEPS 2000–2002 to measures of ADL impairments, IADL impairments, functional limitations, sensory problems, and whether health limits social activities. These impairments are available in the MCBS each year from 1999–2012. Weights are assumed to be constant over time. Quality-adjusted life expectancy is the expectation of quality-adjusted years of life remaining, using age- and year-specific mortality and quality of life weights.

Source: MEPS and MCBS, with mortality rates matched to national totals.

There is no universally accepted metric of health-related quality of life. Typically, quality of life is measured in domains, including physical and mental functioning, role limitations, pain, and cognition (Ware and Sherbourne, 1992). We term these domains ‘symptoms and impairments’ and denote the vector of prevalence rates as si_t. h_si is the corresponding vector of health decrements. Quality of life is then expressed empirically as ${\text{H}}_{\text{t}}(\text{a})={\overline{\text{H}}}_{\text{t}}(\text{a})-\mathbf{s}{\mathbf{i}}_{\mathbf{t}}(\text{a})\cdot {\mathbf{h}}_{\text{si}}$, where ${\overline{\text{H}}}_{\text{t}}(\text{a})$ is the upper limit of health, which may be less than 1 because of symptoms and impairments that are not included in our data. Both as si_t and h_si may change over time, although for data reasons we hold the disutility of each symptom and impairment constant. Our choice of symptoms and impairments, along with the health decrement weights, are determined by data availability (Stewart et al., 2013). The symptoms and impairments in MCBS are presented in the lower part of Table 1. A first metric is functional limitations, including difficulty walking, stooping/crouching/kneeling, lifting or carrying heavy objects, reaching or extending arms, and writing or grasping small objects. A second is self-care: whether respondents have impairments in any of 3 Activities of Daily Living (ADLs: dressing, bathing/showering, or walking) or 6 Instrumental Activities of Daily Living (IADLs: using the telephone, managing money, shopping, making meals, or doing light housework). We also use respondents’ reports of whether they have difficulty seeing or hearing, even when wearing glasses or a hearing aid. Finally, we use a report of whether health limits respondents’ social interactions, such as visiting with friends or close relatives. Appendix Figure A3 shows the trend in each of these measures of health over time, age-adjusted to the 2010 population. The changes in each are very small.

While this is a rich set of metrics, it is worth noting that several domains of health are not asked about explicitly in MCBS, including pain, cognition, and mental health symptoms. Appendix Figure A4 shows trends in these three measures from the Health and Retirement Study (HRS, 2021; RAND, 2021), age-adjusted to the 2010 population. The prevalence of mild and moderate pain increased over this time period. Cognition was flat, and depression fell modestly. To examine the potential impact of not having information on these dimensions, Appendix Figure A5 shows how pain, cognition, and depression are related to ADL impairments, IADL impairments, and functional limitations, which we have in our data. Higher levels of pain, cognition, and depression are associated with much higher probabilities of ADL and IADL limitations and more functional limitations. Thus, while we are missing some quality of life domains, we suspect the impact on our overall quality of life metric is not major.

To estimate the h_si vector of health decrements for each symptom or impairment, we use data from the 2002 Medical Expenditure Panel Study (MEPS; AHRQ, 2002). This survey asks people questions about their health similar to the MCBS and also includes an overall health assessment on a scale from 0 (‘worse imaginable health state’) to 100 (‘best imaginable health state’).¹⁷ To form the disutility weight associated with each symptom and impairment, we regress the 100-point scale response on dummy variables for having each symptom or impairment.¹⁸ The results of the regression are shown in Appendix Table A5. The constant term, an estimate of $\overline{\text{H}}$, is 0.85, and is statistically different from 1. All of the coefficients for the symptoms and impairments are negative and statistically significant. The largest decrements are for health interfering with social interactions (−0.16 for moderate impairment and −0.20 for severe impairment) and for severe walking difficulty (−0.12).

We use these coefficients to calculate health-related quality of life for each person in each year of the MCBS.¹⁹ The minimum quality of life is 0.19; the average is 0.69. Figure 3(b) shows the trend in quality of life between 1999 and 2012. Consistent with the minor changes in the prevalence of symptoms and impairments over time, quality of life was generally unchanged, with a very modest increase. Put another way; survival has increased without creating a larger impaired population.

The combination of falling mortality and relatively constant quality of life implies that quality-adjusted life expectancy increased. This is shown in Figure 3(c), which plots QALE at age 65 over time. In 1999, the typical person aged 65 could expect to live 12.1 additional quality-adjusted years. In 2012, the value was 13.0 years, a 1-year increase in just over a decade.

As discussed below, our benchmark value of a year of quality-adjusted life is $100,000. Thus, the value of the QALE increase is roughly $100,000. The increase in real, per capita medical spending, added up over remaining life, is about $60,000 ($4,800 per year for ~13 years). Thus, if the only thing that changed over time were medical treatments, the spending would be worth it. Of course, other factors changed as well. The goal of our productivity analysis is to estimate the value of medical treatment changes. Still, the results of the detailed empirical work are consistent with this first impression.

B. Identifying Conditions

There is an enormous number of medical conditions; over 68,000 are noted in the latest International Classification of Diseases (ICD, version 10). This is far too many for our analysis. The Agency for Health Care Research and Quality has consolidated this list into 285 Clinical Conditions (termed CCS; Elixhauser, Steiner, and Palmer, 2014). However, even this condensed list is too granular for our purposes. For example, over 20 codes are for pregnancy and many others are for childhood conditions, each of which are uncommon in the elderly. In consultation with clinical experts, we reclassified the 285 CCS’s into 78 conditions (Raghunathan et al., 2020), shown in Appendix Table A6.²⁰ One way to characterize these 78 conditions is by chapters of the ICD manual: circulatory disease, respiratory disease, and so on. We delineate highly prevalent conditions within each chapter and generally create an ‘other’ category for the remainder. For example, our cardiovascular disease conditions include ischemic heart disease, congestive heart failure, stroke and cerebrovascular disease, and ‘other heart and vascular disease’—the latter of which is the residual. In some cases, there are no apparent subsets to pull out, and the entire chapter is left as one condition (as with gastrointestinal and liver disease). Some catchall categories are a bit broader. Two of our conditions are ‘after care’ (general sequelae to a hospitalization, for example physician visits for medication monitoring after surgery), and ‘signs and symptoms’ (adverse medical events of unknown origin, such as fainting or nausea). Seven of our categories are technically not conditions but preventive care: well care (such as medical checkups) immunization and screening for infectious disease, and cancer screening.

In addition to clinical conditions and preventive care, we create conditions for moderate and severe frailty. The frailty measures are based on self-reports of difficulty or inability to do 5 activities: walking 2–3 blocks, stooping/crouching/kneeling, lifting/carrying 10 lbs, reaching over one’s head, and writing or handling and grasping small objects. People with a lot of difficulty or an inability to do activities in 1–3 areas are classified as moderately frail, and people with difficulty in 4–5 areas are severely frail.

Most of the conditions that we measure have permanent impacts on health, for example heart disease and kidney failure.²¹ Thus, our measure of prevalence is whether the person ever had the condition. In principle, one might want to distinguish established cases from those that occurred more recently. However, the incidence of many conditions is too small to permit this.

Measuring condition prevalence accurately is important to our analysis. Given the observed improvement in aggregate health, increases in prevalence imply that the value of medical care is higher, since otherwise health would have fallen. To measure the prevalence of each condition, we start with diagnoses in the claims data in MCBS for all conditions except frailty, which is based on self-reports. Claims data are known to underreport prevalence, especially for less severe conditions. For example, 23% of people in the MCBS have a claim for arthritis in a year, but nearly half of the aged population in the National Health and Nutrition Examination Survey (NHANES) reports having been diagnosed with arthritis.

The underdiagnosis changes over time; our data show declines in undiagnosed hypertension and high cholesterol over time.

To estimate true prevalence, we impute ‘calibrated conditions’ using self-reports of ever having had a condition in NHANES (CDC, 1999–2012). The procedure is described in detail in Appendix A and in Raghunathan et al. (2020). When a disease that has a self-report question in NHANES matches one of our categories (e.g., ischemic heart disease), we impute prevalence in the MCBS to match the prevalence in NHANES, using demographic and health measures to match individuals across surveys. When there is not an exact self-report, we impute prevalence using conditions that have a similar overall prevalence rate to the relevant MCBS condition. In each case, we form five multiply-imputed datasets, each imputing different people to have each condition. Analyses using these data averages across the 5 data sets.

One important addition that comes from using the NHANES is that we can impute undiagnosed hypertension, high cholesterol, and diabetes, which are included in the NHANES from measurement and blood draws. As we show below, the treatment of cardiovascular risk factors is a significant part of health and spending changes for the elderly, so this imputation is quite valuable. Since the NHANES data are from 1999 onward, the beginning of our analysis period is limited to that year.

For presentation purposes, we generally aggregate the 80 conditions into 30 groups of relatively similar conditions. For example, acute myocardial infarction (heart attack) and coronary atherosclerosis (build-up of plaque in the coronary arteries) are grouped into ischemic heart disease. Within the 30 categories, trends tend to be relatively similar for the individual conditions. Appendix B shows all of our results for the 80 conditions.

The list of aggregated conditions, along with their prevalence in 2012, is shown in Figure 4. Cardiovascular risk factors are the most common condition; 86% of the elderly population has one or more. Other common conditions include musculoskeletal disorders (e.g., arthritis and back pain), eye and ear problems, respiratory problems, and uncategorized signs and symptoms. The presence of multiple chronic conditions is very common. The average elderly person has 13 conditions, and 95% of people have three or more conditions.

FIGURE 4. CONDITIONS AND PREVALENCE RATES, 2012.

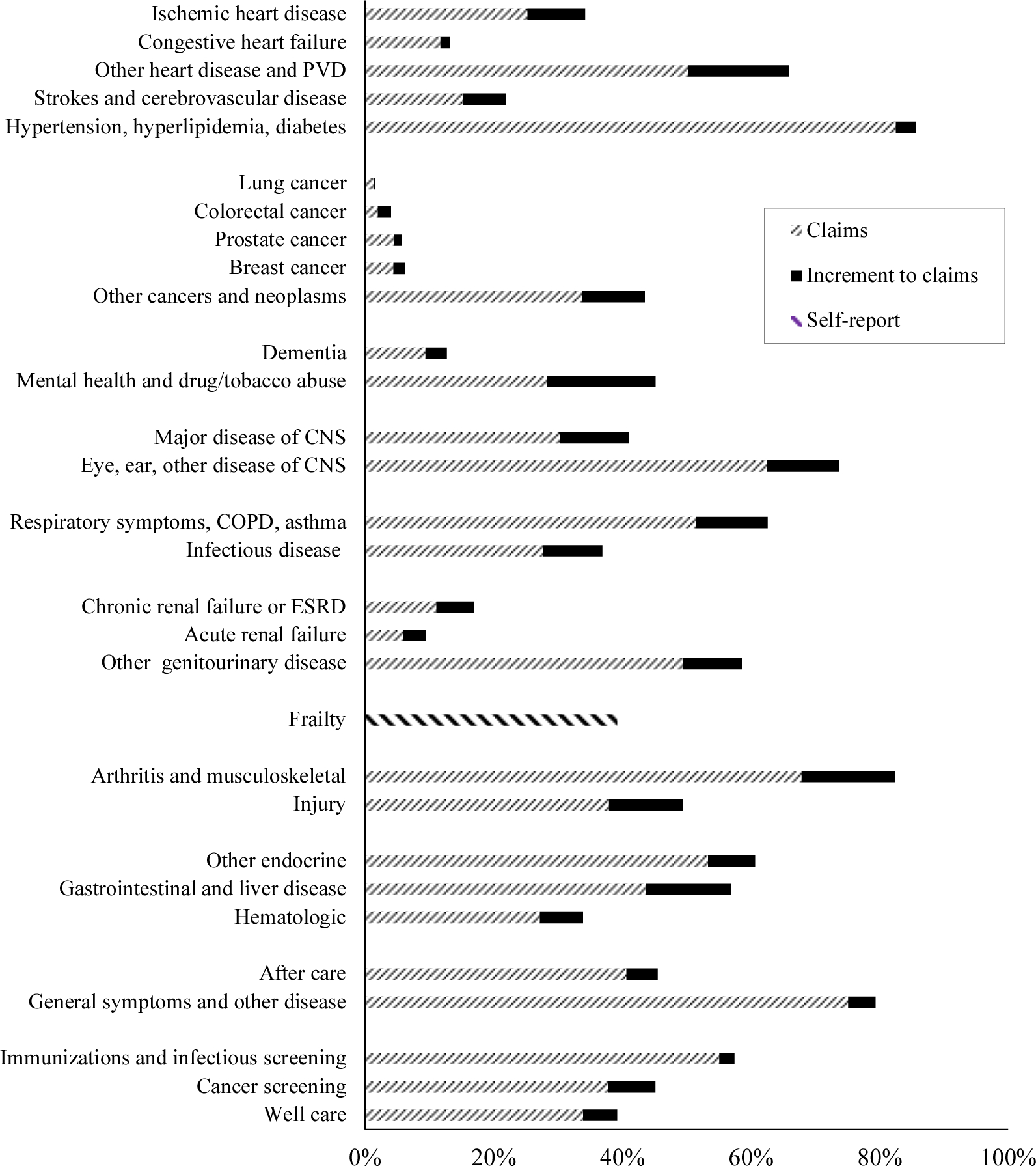
Notes: The figure shows the prevalence of different conditions in the elderly population in 2012. Except for frailty, each condition has two parts: the prevalence as measured by claims, and the additional prevalence added via calibration to prevalence in the NHANES. Frailty is based on self-reports of frailty in MCBS. Data are weighted using population weights. CNS = Central nervous system; COPD = Chronic obstructive pulmonary disease; ESRD = End-stage renal disease; ID = Infectious disease.

Sources: MCBS matched to NHANES prevalence.

The prevalence of most conditions is rising over time (Appendix Table A6). The largest increases are for cardiovascular risk factors, chronic renal failure, and musculoskeletal issues, all of which are related to obesity. We return to the role of obesity in section IV. The major exception to the trend of rising prevalence is frailty. Moderate frailty was constant over time, and severe frailty fell.

III. Methodology for Allocating Spending and Health to Medical Care

Having assembled the data on health and medical spending, we need to estimate the impact of medical treatment changes on each. Figure 1 shows the analytic steps involved in this. We start by estimating the direct effect of treatment changes on the health and medical spending of people with that condition. We then reallocate some spending and health outcomes from direct conditions to the exogenously identified medical risk factors. Finally, we estimate productivity change from trends in these estimates.

This analysis is particularly complex because there are many possible relationships across conditions. We need to pare this down to make progress. The primary assumption we make is that in most cases, medical care for a condition affects the health of people with that condition but not the prevalence of other conditions. That is, treatment changes for people with a heart attack influence the length and quality of life for people with a heart attack, but not whether the person develops cancer. The exception to this rule is conditions explicitly identified as risk factors, which we discuss below.

A. Estimating the Direct Effect of Each Condition

The first analytic step is to apportion total medical spending and health decrements to each condition. Recall from Section II that we have estimates of average medical spending (m_ave,t), mortality (Γ_t), and quality of life (H_t). These are the prevalence-weighted averages of the values for each condition:²² m_ave,t = prev_t ∙ m_t; Γ_t = prev_t ∙ γ_t; and ${\text{H}}_{\text{t}}={\overline{\text{H}}}_{\text{t}}-\mathbf{p}re{\mathbf{v}}_{\text{t}}\cdot {\mathbf{h}}_{\text{t}}$. The issue is to estimate m_t, γ_t, and h_t.

Aggregate medical spending for the elderly is estimated in the National Health Expenditure Accounts (CMS, 2021). Vital Statistics collects information on condition-specific mortality rates, for example death from ischemic heart disease (IHD) and lung cancer. These are per capita totals, i.e. prev_IHDt ∙ γ_IHDt. We could estimate the case fatality rate by dividing the per capita rate by prevalence. However, vital statistics reported underlying cause of death data are notoriously inaccurate. Vital Statistics attribute each death to one primary or underlying cause of death, but many deaths have multiple antecedents, as our example of mental illness suggests. The physician or coroner certifying death may not know about precursor events, and even if they do, they may not record them.²³ This is the analog to the issue of condition enumeration noted above; physicians tend to record the severe event but less commonly the comorbid conditions that contributed to it.

We develop a methodology to parcel overall health and medical spending to conditions that accounts for these issues (Ghosh et al., 2020, 2021). The methodology is described briefly here and in greater detail in Appendix B. The analysis relies on propensity score models. For each year, we estimate a logistic model for the probability of having each condition—80 regressions in total. The covariates include the other 79 conditions along with the demographic and behavioral risk factor variables shown in Table 1, including smoking status and obesity.²⁴

Based on the propensity scores, we stratify the population into quintiles, or quartiles/ terciles for conditions with relatively low prevalence.²⁵ The difference in the within-strata outcomes of people with and without the relevant condition, averaged across strata and across the five multiply-imputed datasets, is an estimate of relative mortality associated with each condition. Term this relative mortality ${\widehat{\mathrm{\theta }}}_{\mathrm{ct}}^{\text{γ}}$, where γ denotes mortality, c is the condition, and t is the year. The analogues for quality of life and medical spending are ${\widehat{\mathrm{\theta }}}_{\mathrm{ct}}^{\text{h}}$ and ${\widehat{\mathrm{\theta }}}_{\mathrm{ct}}^{\text{m}}$. The total mortality rate is allocated to conditions based on these relative mortality rates: ²⁶

$${\widehat{\mathrm{\gamma }}}_{\text{ct}}={\mathrm{\Gamma }}_{\mathrm{t}}\cdot \left(\frac{{\widehat{\mathrm{\theta }}}_{\text{ct}}^{\text{γ}}}{\sum _{\text{c}}{\widehat{\mathrm{\theta }}}_{\text{ct}}^{\text{γ}}}\right).$$ (6)

The analog of equation (6) for spending is somewhat more complex than for mortality because the distribution of spending is so skewed to high spenders. High spenders do not have different conditions than low or moderate spenders; rather, their high costs reflect common conditions whose course of therapy goes very poorly. As a result, when the condition-specific costs are then added up to the person level, they come nowhere close to reproducing the skewed distribution of individual spending (Appendix Figure B6). We thus concluded that a uniform adjustment to spending would not be appropriate.

To better capture the variability of spending, we use an alternative to equation (6). We relate the actual cost for each person, m_it, to the predicted cost based on summing the first stage estimates to the individual level, ${\widehat{\mathrm{\theta }}}_{\mathrm{i}\mathrm{t}}^{\text{m}}$, interacted with a series of variables capturing high use of services (X_it):

$${\text{m}}_{\text{it}}={\widehat{\mathrm{\theta }}}_{\text{it}}^{\text{m}}\cdot \left({\mathbf{X}}_{\mathbf{i}\text{t}}{\mathbf{\alpha }}_{\mathbf{t}}\right)+{\mathrm{\epsilon }}_{\text{it}}.$$ (7)

X_it includes the number of conditions and its square, an indicator for any hospitalization, the number of admissions, and the number of nights in the hospital, the number of days institutionalized, survival in the year, the number of months survived for those who are deceased, and the number of outpatient claims. We average the ${\mathbf{X}}_{\mathbf{i}\mathrm{t}}{\widehat{\mathbf{\alpha }}}_{\mathbf{t}}$ estimates across people with each condition to form a condition-specific correction factor, ${\widehat{\mathrm{\phi }}}_{\text{ct}}$, which is then multiplied by the first stage cost estimates:${\widehat{\text{m}}}_{\text{ct}}={\widehat{\mathrm{\theta }}}_{\text{ct}}^{\text{m}}\cdot {\widehat{\mathrm{\phi }}}_{\text{ct}}$. This effectively increments the spending of conditions where people have very extensive care utilization. Appendix Table B2 shows the estimates of equation (7) in 2009. The X variables lead to increased spending in the expected direction; for example, people who spend more time in a hospital or an institution cost more than people who do not.

Figure 5 shows an example of the resulting spending and health outcomes for coronary atherosclerosis and heart attack. Together, these make up the category of ischemic heart disease, which is among the categories where we find the highest productivity growth (as discussed below). While there are some outlier years, the trend is generally smooth, with declining mortality and relatively constant cost. The validity of the conditional unconfoundedness assumption cannot be tested completely. One empirical test is to examine covariate balance for people with and without each condition. Table 2 shows the cohort balance for coronary atherosclerosis and acute myocardial infarction in 1999. Panel A shows the balance for variables included in the model. The overall F-statistic fails to reject equality of the means between cases and controls, and only 2 of the 40 comparisons are statistically different. As shown in Appendix Figure B3, we fail to reject equality of the means between cases and controls for all conditions in all years (N=1120).

FIGURE 5. EXAMPLE OF COST AND HEALTH ESTIMATES FOR ISCHEMIC HEART DISEASE.

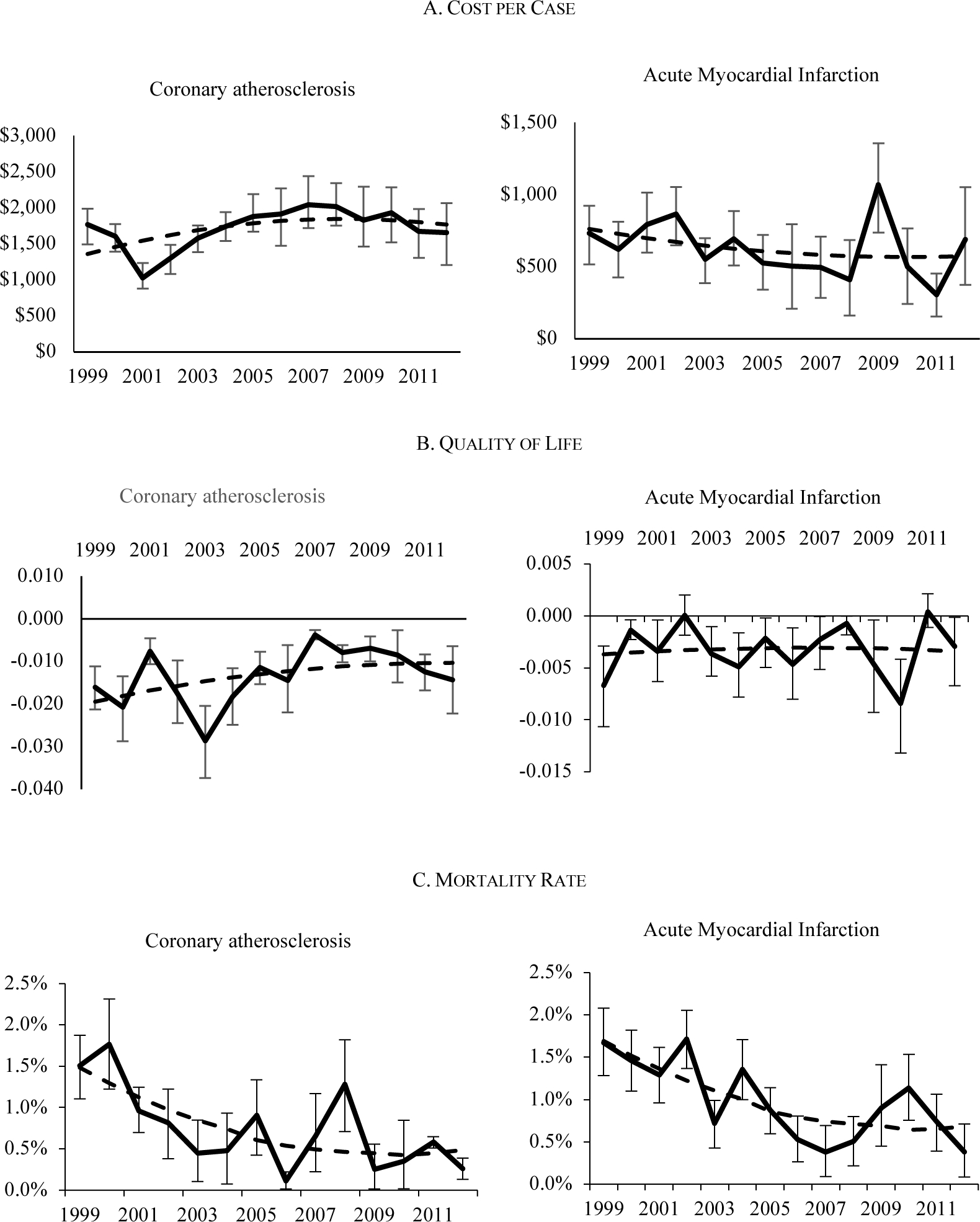
Notes: The outcomes are based on model estimates as described in the text. The solid line shows the estimates for each year, along with the 95% confidence intervals for the estimates. The dashed line shows the smoothed trend, fitted from a second order polynomial.

Source: Authors’ estimates from models described in text.

Table 2—

Cohort balance table for 1999: Ischemic Heart disease

	Acute Myocardial Infarction			Coronary Atherosclerosis
Variable	Yes	No	p-value	Yes	No	p-value
Variables Included in the Model
Age	77.5	77.4	0.37	77.0	77.1	0.71
Male	40.4%	40.3%	0.94	41.7%	41.6%	1.00
Education (9th–12th)	16.8%	17.1%	0.76	15.9%	17.0%	0.16
Education (High school)	28.4%	28.3%	0.90	29.6%	28.7%	0.35
Education (Assoc./some College)	19.9%	19.8%	0.92	22.0%	21.2%	0.40
Education (College and Above)	14.3%	14.3%	0.92	14.9%	15.6%	0.43
Military service	25.4%	25.8%	0.65	29.4%	28.1%	0.19
Smoke now	9.4%	9.9%	0.42	9.5%	10.1%	0.33
Ever smoke	54.2%	54.3%	0.93	58.4%	57.9%	0.68
Race (Black)	7.3%	7.9%	0.32	6.4%	7.0%	0.25
Race (Hispanic)	5.0%	5.3%	0.50	5.8%	6.3%	0.43
Race (Other)	2.8%	2.7%	0.77	4.6%	4.8%	0.64
Marital status (Widowed)	41.2%	40.9%	0.76	37.9%	37.0%	0.40
Marital status (Divorced/Separated)	6.4%	6.4%	0.94	7.1%	7.3%	0.73
Marital status (Never married)	4.5%	4.4%	0.77	4.8%	3.9%	0.06
Pneumonia shot	65.6%	64.7%	0.37	66.1%	65.3%	0.45
Flu shot	71.9%	71.4%	0.62	72.6%	71.3%	0.19
Hysterectomy	25.2%	25.1%	0.88	25.2%	26.0%	0.42
Income / FPL<1.5	9.9%	9.7%	0.86	9.5%	9.4%	0.86
Income / FPL<2.0	20.0%	20.2%	0.84	20.9%	21.2%	0.76
Income / FPL<4.0	27.7%	28.1%	0.73	29.9%	29.2%	0.44
Income / FPL<5.0	15.1%	15.1%	0.92	15.8%	16.1%	0.66
Other private insurance	74.2%	73.3%	0.31	76.0%	75.4%	0.51
Difficulty lifting (scale 1–4)	1.78	1.75	0.15	1.63	1.61	0.40
Difficulty stooping (scale 1–4)	2.11	2.09	0.39	1.99	1.96	0.19
Difficulty walking	44.1%	43.1%	0.34	39.5%	38.5%	0.35
Difficulty dressing	17.4%	16.1%	0.13	12.6%	12.5%	0.80
Difficulty eating	9.4%	8.6%	0.24	7.0%	6.4%	0.35
Health since last year – same	55.2%	56.1%	0.40	58.3%	59.2%	0.39
Health since last year – worse	22.4%	21.3%	0.22	21.6%	20.7%	0.30
General health status – very good	25.0%	25.4%	0.72	25.8%	27.2%	0.13
General health status – good	32.8%	33.0%	0.83	32.5%	32.9%	0.69
General health status – fair	20.4%	20.4%	0.98	19.8%	18.7%	0.22
General health status – poor	9.3%	8.4%	0.17	7.7%	7.1%	0.30
Hearing aid	12.4%	11.8%	0.34	10.7%	10.8%	0.91
Institutional days	32.7	31.2	0.48	23.1	20.7	0.18
Inpatient nights	3.0	2.6	0.01	2.6	2.1	0.00
Inpatient stays	0.5	0.4	0.00	0.5	0.4	0.00
Height	166.8	166.7	0.75	166.9	167	0.78
Weight(kg)	71.6	71.7	0.76	72.3	72.5	0.64
p-value for test of equality			0.628			0.929
Variables Excluded From the Model
Regular place of care (Doctor’s office)	84.7%	86.7%	0.09	85.6%	86.4%	0.32
Employer sponsored insurance (ESI)	39.6%	40.4%	0.48	40.9%	39.7%	0.27
Total out-of- pocket payments ($2010)	$2,679	$2,519	0.32	$2,903	$2,650	0.11
Total uncollected liability ($2010)	$142	$145	0.98	$156	$131	0.23
Medicaid drug coverage	7.4%	7.4%	1.00	8.2%	7.4%	0.16
Lives in metro region	70.9%	71.3%	0.69	71.6%	71.1%	0.61
p-value for test of equality			0.326			0.359

Notes: The last row in each panel reports the p-values for the joint F-test of equality between treatment and controls.

Source: Authors’ calculations as described in the text.

We also examined the balance of six covariates which were excluded from the model because they were judged not likely to be related to spending. These include whether care is regularly received in a doctor’s office or elsewhere, the source of Medicare supplemental insurance if any, out-of-pocket spending, uncollected liability, and residence in a rural location. Panel B of Table 2 shows no significant differences between cases and controls in these excluded variables. Appendix Figure B4 shows that we reject equality of the means between cases and controls for only 3% of the observations. Using data in 1999, Appendix Figure B5 shows that the standardized mean difference for each of the omitted conditions is very small. Thus, we do not find evidence of confounding from those variables we have chosen to omit.

Spending and health decrement can be read directly from the values for each year. However, because the sample sizes of people with each condition are not always large, each year is measured with some error. To minimize this error, we fit a second-order polynomial in year for each of the annual estimates of mortality, quality of life, and medical spending. The fitted values for the first and last year are then used to estimate productivity growth. The fitted values for heart disease are shown in Figure 5.

B. Accounting for Clinical Risk Factors

Our second analytic step is to reallocate some of the spending and health outcomes from direct conditions to clinical risk factors. Conceptually, the idea is that some of the direct effect estimated for conditions such as ischemic heart disease is better seen as attributable to hypertension or high cholesterol, which led to the heart disease in the first place.

To determine which conditions are risk factors and what direct conditions they contribute to, we consulted with a physician working group and examined published information. Figure 6 shows the resulting risk factors and their influenced direct conditions. The set of risk factors is reasonably conservative, to avoid inappropriately taking spending and health decrements away from direct conditions. Of our 80 conditions, four are classified as exclusively risk factors: high cholesterol, hypertension, eye and ear disorders, and infectious disease immunization (flu and pneumococcal vaccine). Two conditions, diabetes and mood disorders, are both direct conditions and risk factors for other diseases.²⁷ To determine the amounts to be reallocated, we estimate regression models relating each direct condition to its identified risk factors. The results of these regressions are shown in Appendix Table B5. A natural way to express the results is as relative risks—the probability of having the direct condition if one has the risk factor divided by the probability if one does not. Where possible, we compare our relative risks to those in the clinical literature; they match up reasonably well. To demonstrate the resulting adjustment, we use the example of hypertension leading to heart disease. Pooling 1999–2001, our regression estimate is that people with hypertension are 7.5 percentage points more likely to have heart disease than are people without high blood pressure. At that time, 57% of people had high blood pressure and 35% of people had ischemic heart disease. This implies that 12% of cases of ischemic heart disease are due to hypertension (7.5% × 57% / 35%). Thus, we reduce the prevalence of heart disease by 12%. We make an offsetting entry in the hypertension industry. People with heart disease spend on average $1,100 per person more than similar people without heart disease. We therefore transfer $1,100 per transferred case to the hypertension industry. This amounts to $47 per person with hypertension ($1,100 × 7.5% × 57%). This gets added to the direct spending on hypertension, estimated as above. Appendix Table B6 shows the full set of risk factor adjustments.

FIGURE 6. RELATIONSHIP BETWEEN RISK FACTORS ON DOWNSTREAM CONDITIONS.

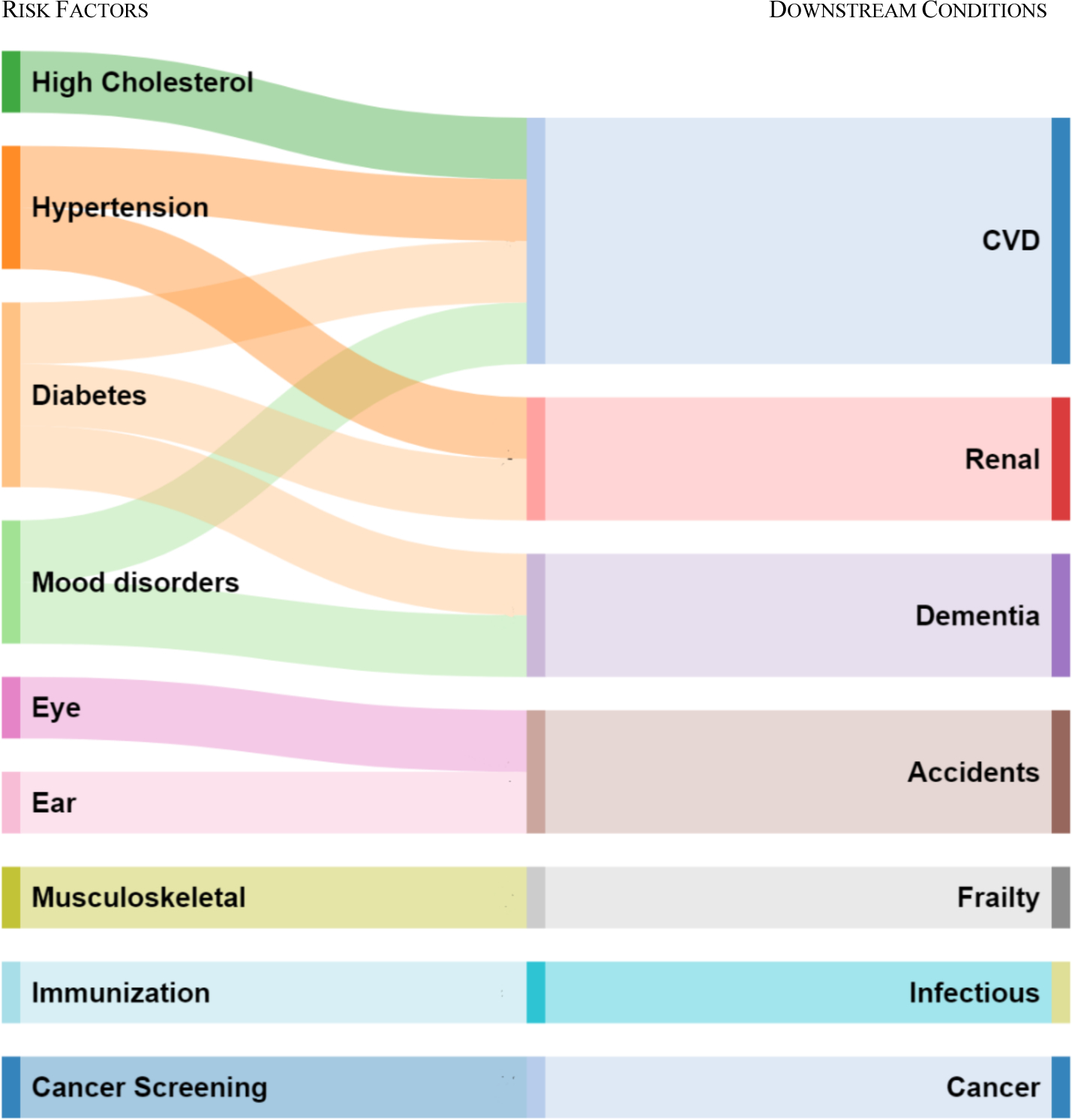
Notes: Each of the risk factors on the left is matched to downstream conditions on the right, based on studies in the clinical literature. Mood disorders include depression, bipolar disorder, and anxiety/post-traumatic stress disorder. CVD = cardiovascular disease and includes ischemic heart disease, congestive heart failure, other heart disease, and peripheral vascular disease, strokes, and cerebrovascular disease. Renal includes acute and chronic renal failure or end-stage renal disease. Eye and ear include disorders of the eye and ear. Accidents includes all injury: accidents, falls, poisoning. The full list of conditions in each category is shown in Appendix Table A6.

We make the same conceptual adjustment with mortality and quality of life, transferring decrements associated with direct conditions to risk factors. In this case, conditions that are purely risk factors are assumed to have no direct effect on death or quality of life, so the entirety of their impact on health is through the risk factor channel.

In addition to the risk factors, four of our conditions are cancer screening variables: breast, colorectal, prostate, and cervical cancer. Conceptually, these are closely related to risk factors, in that they influence health by affecting direct conditions. The difference is that cancer screening does not reduce the incidence of cancer in total. Rather, it reduces metastatic cancer, but increases local cancer. Indeed, the increase in local cancer is generally larger than the reduction in metastatic cancer, as some cases are detected that would never become metastatic (Welch and Brawley, 2018).²⁸

If we had data on cancer by stage, we could separately model the impact of cancer screening on local and metastatic disease. However, our data do not contain information on stage. As a result, we use impacts of cancer screening drawn from the clinical literature. As shown in Appendix Table B5, the clinical literature shows clear benefits of breast and colorectal screening in reducing mortality, but unclear benefits of cervical and prostate cancer screening, especially in the elderly. We thus model only mortality benefits from breast and colorectal cancer screening. We assume no impact of cancer screening on quality of life, since quality of life likely varies with treatment, and treated cases rise with screening. Because of these approximations, we note that the estimate of productivity growth estimate for cancer screening is subject to more uncertainty than are other conditions.

C. Productivity Growth Estimates

Our third analytic step is to estimate productivity growth, the net value of the change in QALE less the increase in medical spending (all in real 2010 dollars). The change in QALE is found by simulating the impact of changes in each condition individually on length and quality of life. These are then combined in equation (5). Spending is found by adding condition-specific spending in the relevant year over the remaining lifetime. To value QALE in dollars, we use a baseline value for a year of life in good health equal to $100,000 (Viscusi and Aldy, 2003). We conduct sensitivity analyses assuming the value is alternatively twice and half that amount. We use a baseline discount rate of 0% and perform sensitivity analyses using a rate of 3%.

To express productivity as a growth rate, we need to divide by the net value of medical care in the base year. As a rough estimate, we assume that half of QALE in 1999 is due to medical care (Cutler, Rosen, and Vijan, 2006).

D. Standard Errors

We use a bootstrap technique to calculate standard errors for the productivity growth estimates. We draw 1,000 simulated samples, taken from the actual MCBS population with replacement. We do this separately for each multiply-imputed dataset. For each draw, we repeat the three steps above. These estimates are used to calculate the empirical 95% confidence interval for the spending, health, and productivity growth impacts of each condition.

E. Model Uncertainty

In addition to classical uncertainty, it is worth noting that we do not have random variation in treatments with which to measure the impact of medical care changes. As a result, our evaluation of health and spending changes is a form of ‘residual analysis’—the difference for people with and without each condition after controlling for other factors that influence health.

To validate our most important results, we undertake several supplemental analyses, shown in Appendix C. These include examining how our results change if we use Vital Statistics estimates of changes in mortality by condition rather than our estimated rates; omitting quality of life; estimating condition-specific spending using different methodologies; and smoothing the time series in other ways. None of these changes has a large impact on our findings.

We also compare our findings about sources of health improvement to microsimulation estimates of the impact of treatment taken from validated and widely used clinical models. We focus particularly on cardiovascular disease and cancer, the source of our most important results. As we show below, our results match the clinical literature very closely.

IV. Change in Medical Spending by Condition

In this section, we present our estimates of spending by condition. The first two columns of Table 3 show spending per case for the 30 aggregated conditions in 1999 and 2012 (all in 2010 dollars). Appendix Table B4 shows direct spending for each of the 80 conditions. Almost all conditions are associated with higher spending. The major outlier to this is cancer screening, where the estimates suggest slightly lower spending for people who are screened relative to those who are not. It may be true that cancer screening saves money, though it is also possible that elderly people who are screened for cancer are healthier in ways that our model does not capture. In some studies (Trogdon, 2008), condition-specific spending is constrained to be non-negative. That may not be necessary for our application, however, as we are interested in the change in spending at the condition level. If the bias from unmeasured health status is constant over time, the change in spending will be accurate even if the level of spending is not. Thus, we do not constrain spending to be positive. That said, caution is warranted about the estimated cost changes for cancer screening.

Table 3—

Estimates of Spending and Health Decrements by Condition

	Spending per case		Mortality Rate		Quality of Life
Condition	1999	2012	1999	2012	1999	2012
Cardiovascular diseases
Ischemic heart disease	$1,300	$1,502	1.4%	0.5%	−0.011	−0.007
Congestive heart failure	$1,248	$2,049	1.5%	1.1%	−0.009	−0.010
Other heart and vascular disease	$2,264	$2,092	0.8%	0.4%	−0.007	−0.005
Strokes and cerebrovascular diseases	$1,432	$1,632	0.8%	0.4%	−0.011	−0.008
Cardiovascular risk factors	$1,212	$2,102	0.8%	0.5%	−0.014	−0.014
Cancers
Lung cancer	$2,948	$5,436	9.9%	9.9%	−0.034	−0.015
Colorectal cancer	$1,222	$1,042	1.3%	1.0%	−0.008	−0.008
Prostate cancer	$340	$873	0.4%	0.4%	0.005	0.000
Breast cancer	$285	$352	0.5%	0.2%	0.000	−0.004
Other cancers and neoplasm	$1,184	$1,005	0.6%	0.3%	−0.003	−0.002
Mental Health
Dementia	$2,132	$2,491	1.3%	1.1%	−0.023	−0.027
Mental health and tobacco/drug abuse	$1,740	$1,990	0.7%	0.7%	−0.026	−0.021
Central Nervous System
Major disease of the CNS	$1,224	$1,472	1.0%	0.9%	−0.013	−0.013
Eye, ear, other diseases of the CNS	$743	$827	0.0%	0.0%	0.000	0.000
Respiratory System
Respiratory symptoms, COPD, asthma	$2,177	$2,359	0.5%	0.4%	−0.007	−0.007
Infectious disease	$1,526	$1,605	0.6%	0.7%	−0.006	−0.008
Kidney Disease
Chronic renal failure or ESRD	$1,543	$1,484	1.1%	1.0%	−0.013	−0.012
Acute renal failure	$2,592	$3,260	3.2%	2.7%	−0.010	−0.008
Other genitourinary diseases	$563	$929	−0.1%	−0.1%	−0.004	−0.007
Frailty	$2,044	$2,249	1.3%	1.0%	−0.056	−0.055
Musculoskeletal
Arthritis and musculoskeletal	$1,190	$2,017	0.3%	0.2%	−0.023	−0.016
Injury	$1,743	$1,830	0.2%	0.2%	−0.007	−0.008
Endocrine, GI, Liver, Hematologic
Other endocrine	$1,071	$1,371	0.4%	0.2%	−0.006	−0.005
Gastrointestinal and liver disease	$934	$1,091	0.5%	0.4%	−0.004	−0.006
Hematologic	$1,645	$2,245	0.3%	0.3%	−0.008	−0.008
Miscellaneous
After care	$961	$1,807	0.4%	0.4%	−0.008	−0.006
General symptoms and other disease	$1,528	$1,770	0.0%	0.0%	−0.008	−0.009
Prevention and screening
Immunizations and infectious screening	$251	$243	0.0%	0.0%	0.000	0.000
Cancer screening	−$135	−$165	−0.1%	0.0%	0.000	0.000
Well Care	$680	$409	−0.4%	−0.4%	−0.001	0.001

Notes: The table shows the impact of each condition on medical spending, mortality, and quality of life. The year 1999 pools data from 1999–2001, and the year 2012 pools data from 2010–2012. PVD = Peripheral vascular disease. COPD = Chronic obstructive pulmonary disease. ID = Infectious disease. ESRD = End stage renal disease

Source: Authors’ calculations as described in the text.

The conditions for which per case spending is highest are generally the ones we would expect: heart disease, certain cancers (especially lung cancer), dementia, kidney failure, and frailty. The case-specific costs may seem low, but it is important to recall that these are the cost per prevalent case of disease, not per incident case. For example, spending on heart attacks is the average among everyone who ever had a heart attack, not new heart attack cases. Because past cases generally add a smaller increment to spending than new events, our estimates are smaller than are typically found in studies looking at acute disease onset.

Spending for most conditions rose over time. The largest increases were for lung cancer (a $2,500 per case increase) and arthritis and musculoskeletal problems (a $750 per case increase). Notably, the conditions that cost the most at a point in time are not always the ones for which spending rose the most. For example, spending for ischemic heart disease rose only modestly over the time period, despite starting at a high level.

Figure 7 shows the change in per capita spending—per case spending times the prevalence rate—accounted for by each of our 30 aggregated conditions. Acute cardiovascular diseases together account for 15% of spending in 1999, but only 0.05% of the spending increase. The largest contributors to increased spending are cardiovascular risk factor conditions, musculoskeletal diseases (which includes arthritis and back pain), and after care. Together, these three conditions account for 45% of the increase in spending.

FIGURE 7. CHANGE IN PER CAPITA MEDICAL SPENDING BY CONDITION, 1999–2012.

Notes: Per capita spending is spending per person with the disease multiplied by the disease prevalence rate. Spending is in real ($2010) dollars.

Source: Data are from the Medicare Current Beneficiary Survey, adjusted so that total spending matches national estimates of spending on the elderly.

Spending per capita can increase because the prevalence of disease increases or because each case costs more. The importance of each of these is shown in the first column of Table 4. Sixty percent of the increase in real spending is due to the greater cost per case; one-third is due to greater prevalence (the residual is the covariance term). Prevalence changes were particularly significant for cardiovascular risk factors, renal failure, and musculoskeletal problems. These three conditions are among those whose prevalence is most affected by obesity. To determine how much of the prevalence increase is due to obesity, we use the same methodology as for clinical risk factors. We estimate the impact of BMI and smoking on the prevalence of conditions that are listed in clinical reviews as resulting from these risk factors.²⁹ We then simulate the impact of changes in smoking and obesity on the prevalence of both direct conditions and risk factors. Table 4 shows the simulated impact of smoking and obesity changes on overall medical spending via their impact on disease prevalence. Increased obesity led to an increase in spending of $342 per person. Smoking declines were more modest, a reduction of $64 per capita. There is a sizeable residual increase in the prevalence of many conditions not associated with smoking or obesity changes, $1,382, shown in the last row of the table.³⁰

Table 4:

Factors Explaining Change in Medical Spending and Health, 1999–2012

	Change in
Measure	Annual Medical spending	Life Expectancy	QALE
Overall	$4,640	1.56	1.04
Treatment changes	$2,918	2.39	1.69
Prevalence changes	$1,661	−1.05	−0.86
Behavioral risk factors
Smoking	−$64	−0.02	−0.01
Obesity	$342	−0.17	−0.16
Other changes in prevalence	$1,382	−0.86	−0.69

Notes: The change in medical spending, life expectancy, and QALE are based on calculations described in the text. The components do not add to totals because of the covariance.

Source: Authors’ calculations as described in the text.

V. Change in Health by Condition

In this section, we decompose changes in health into the same conditions for which we estimate the change in spending. Estimates of mortality and quality of life impact for our 30 aggregated conditions are shown in the third–sixth columns of Table 3; results for all 80 conditions are in Appendix Tables B7 and B8. The direct conditions are almost all associated with higher mortality and lower quality of life than not having the condition. Further, the relative magnitude makes sense; people with lung cancer have an annual mortality rate 15% greater than comparable controls (this includes past as well as current cases of lung cancer); acute kidney failure adds a 3% increment to mortality.

The mortality and quality of life data allow us to estimate QALE for people with each condition in 1999 and 2012, and thus the change in QALE. These results are shown in Figure 8. The largest increase in QALE was for cardiovascular diseases—particularly ischemic heart disease but including other cardiovascular diseases as well. People with cardiovascular disease experienced an increase in QALE of 1 year over similar people without cardiovascular disease. Many other conditions had increases in QALE that were somewhat smaller than this but still substantial. For example, people with lung cancer, colorectal cancer, and acute kidney failure all experienced QALE increases of around 0.4 years. Frail people lived an additional 0.3 quality-adjusted years over the time period. Most of the increase was in life expectancy, but quality of life improved for people with cardiovascular disease and some other conditions.

FIGURE 8. CHANGE IN QALE BY CONDITION, 1999–2012.

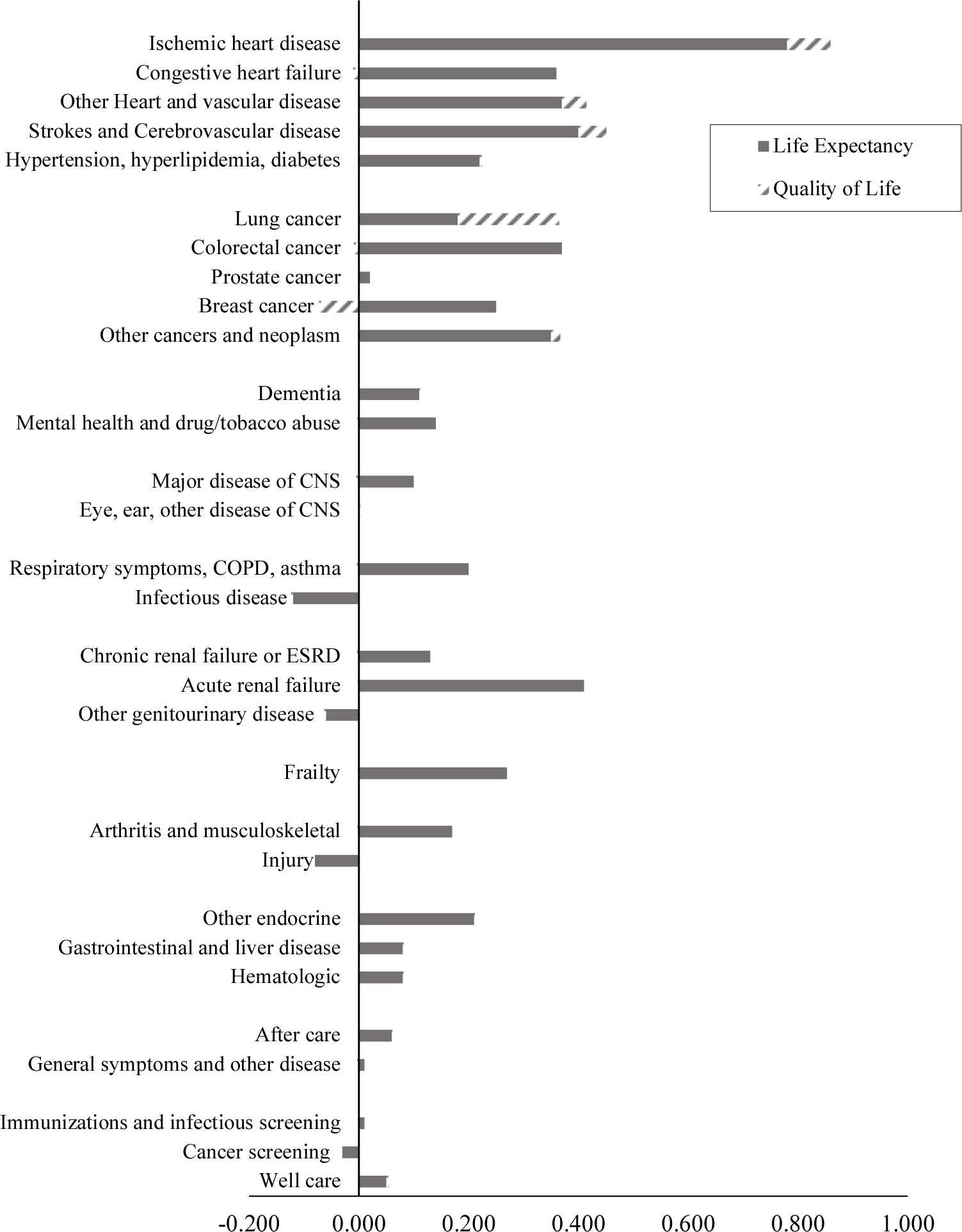
Notes: QALE is as of age 65. Mortality data are disaggregated from national totals to conditions. Quality of life is based on survey responses about symptoms and impairments. Disutility weights are based on analysis of the MEPS.

Sources: Authors’ calculations based on MCBS and MEPS.

Table 4 shows the combined impact of medical treatments and non-medical changes in prevalence on QALE at age 65. The overall increase in QALE noted above (1.04 years) is the net effect of two offsetting trends. Holding prevalence constant, QALE would have increased by 1.69 years. However, the rising prevalence of conditions reduced QALE by −0.86 years. Some of this reduction in QALE was a result of increasing obesity (−0.16 years). This effect, while only a portion of the prevalence increase, is quantitatively very large. For example, the negative impact of obesity on QALE is roughly equivalent to the entire QALE increase from improved care of musculoskeletal conditions and mental health conditions combined.

VI. Productivity Growth in Medical Care

Having estimated the cost and health consequences of changes in medical treatments, this section brings the two together to measure productivity growth. Figure 9 and Table 5 show the calculation of productivity change by condition and for the medical system as a whole.

FIGURE 9. NET VALUE OF MEDICAL SPENDING CHANGE BY CONDITION, 1999–2012.

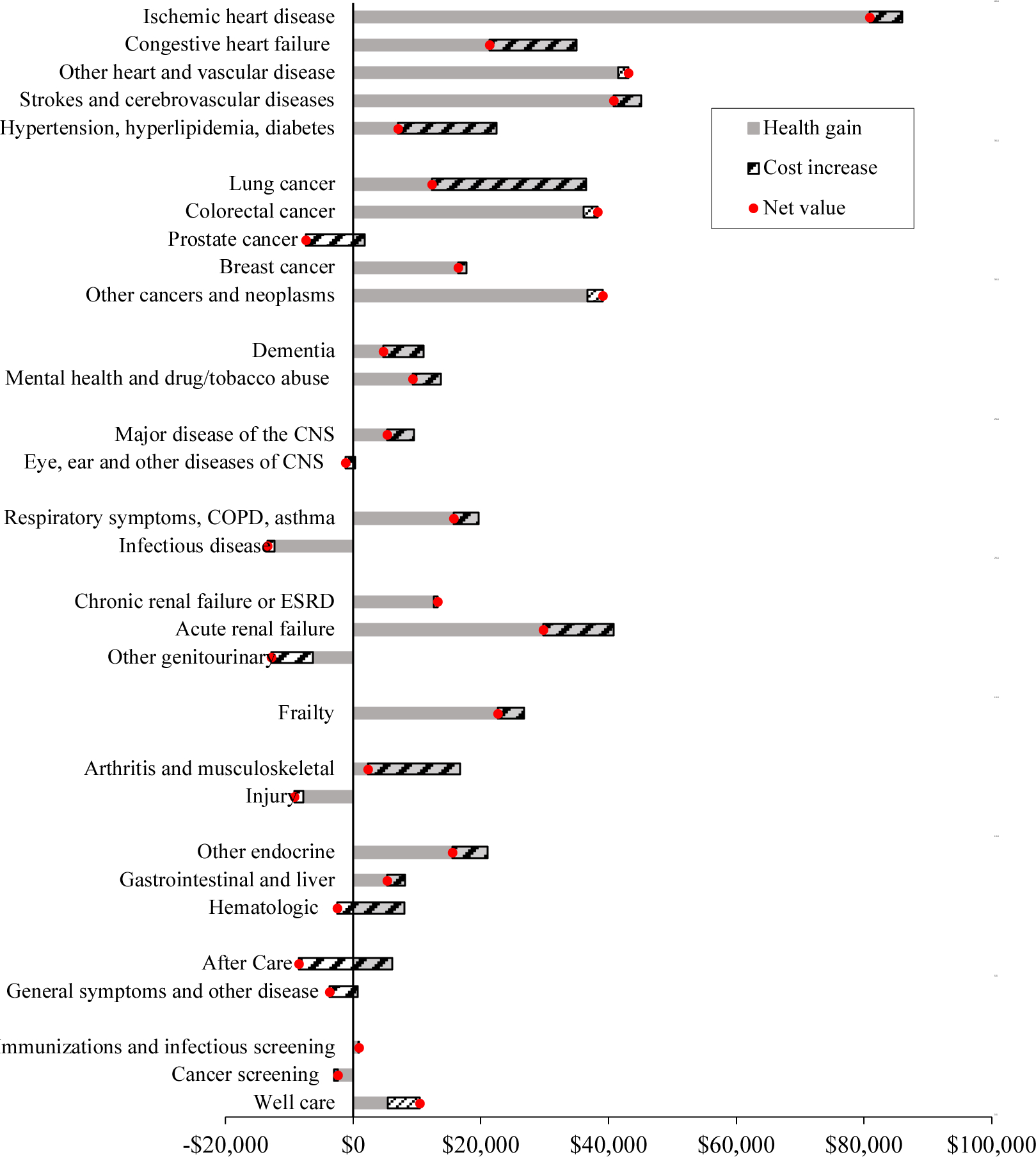
Notes: Spending is in real ($2010) dollars. The solid bar depicts improvement in health outcomes over the period, expressed in dollars. Health change is the change in QALE attributed to medical care and not changes in the prevalence of the condition. The hatched bar shows the change in medical spending. The dot shows the net change in productivity, defined as the dollar value of health improvement minus the increase in spending.

Source: MCBS data, with totals matching estimated national spending on the elderly.

Table 5:

Net Value of Medical Care, 1999–2012

	Spending Change	QALE Change	Value of a Year of Life			Discount rate
Condition			$100,000	$50,000	$200,000	(3%)
Overall (95% confidence interval, 000s)	$57,893 ($46–$69)	1.70 (0.7–2.5)	$112,575 ($14–$188)	$27,341 ($-18–$64)	$283,042 ($87–$440)	$66,220 ($0–$116)
Cardiovascular diseases	$5,157	0.94	$89,327	$42,085	$183,811	$56,731
Ischemic heart disease	$5,054	0.86	$80,888	$37,917	$166,830	$51,361
Congestive heart failure	$13,569	0.35	$21,395	$3,913	$56,358	$12,042
Other heart and vascular disease	−$1,573	0.41	$43,058	$22,316	$84,543	$27,848
Strokes and cerebrovascular disease	$4,354	0.45	$40,750	$18,198	$85,855	$25,588
Cardiovascular risk factors	$15,439	0.22	$6,995	−$4,222	$29,429	$2,289
Cancers	−$80	0.38	$37,987	$19,033	$75,895	$23,821
Lung cancer	$24,099	0.36	$12,384	−$5,857	$48,868	$8,994
Colorectal cancer	−$2,196	0.36	$38,275	$20,235	$74,353	$24,610
Prostate cancer	$9,211	0.02	−$7,374	−$8,292	−$5,537	−$6,918
Breast cancer	$1,272	0.18	$16,470	$7,599	$34,213	$9,041
Other cancers and neoplasm	−$2,423	0.37	$39,116	$20,770	$75,809	$24,909
Mental Health	$5,568	0.15	$4,397	−$493	$14,175	$3,126
Dementia	$6,355	0.11	$ 4,725	−$815	$15,805	$1,672
Mental health and tobacco/drug abuse	$4,343	0.14	$3,519	−$307	$11,170	$3,020
Central Nervous System (CNS)	$3,446	0.05	$1,591	−$927	$6,629	$729
Major disease of the CNS	$4,213	0.10	$5,305	$546	$14,822	$3,155
Eye, ear, other disease of the CNS	$1,484	0.00	−$1,197	−$1,341	−$911	−$955
Respiratory System	$3,815	0.10	$6,553	$1,369	$16,921	$3,535
Respiratory symptoms, COPD, asthma	$3,828	0.20	$15,789	$5,981	$35,406	$9,397
Infectious disease	$1,082	−0.12	−$13,404	−$7,243	−$25,726	−$8,687
Kidney Disease	$7,286	0.01	−$5,796	−$6,541	−$4,307	−$4,722
Chronic renal failure or ESRD	−$645	0.13	$13,281	$6,963	$25,917	$8,844
Acute renal failure	$11,009	0.41	$29,783	$9,387	$70,575	$19,183
Other genitourinary disease	$6,520	−0.06	−$12,826	−$9,673	−$19,132	−$9,386
Frailty	$4,168	0.27	$22,615	$9,224	$49,399	$14,458
Musculoskeletal	$14,172	0.11	−$2,792	−$8,482	$8,589	−$2,061
Arthritis and musculoskeletal	$14,416	0.17	$2,304	−$6,056	$19,024	$1,355
Injury	$1,375	−0.08	−$9,204	−$5,290	−$17,033	−$6,194
Endocrine, GI, Liver, Hematologic	$10,012	0.23	$13,146	$1,567	$36,304	$6,977
Other endocrine	$5,525	0.21	$15,553	$5,014	$36,631	$9,287
Gastrointestinal and liver disease	$2,836	0.08	$5,325	$1,245	$13,485	$2,767
Hematologic	$10,616	0.08	−$2,543	−$6,580	$5,531	−$2,963
Miscellaneous	$10,660	0.03	−$7,280	−$8,970	−$3,900	−$5,934
After care	$14,564	0.06	−$8,486	−$11,525	−$2,407	−$6,685
General symptoms and other disease	$4,365	0.01	−$3,680	−$4,023	−$2,994	−$3,110
Prevention and screening	−$2,557	0.02	$4,261	$3,409	$5,964	$3,024
Immunizations and infectious screening	−$134	0.01	$949	$541	$1,763	$580
Cancer screening	−$519	−0.03	−$2,437	−$959	−$5,393	−$1,369
Well care	−$4,975	0.05	$10,425	$7,700	$15,876	$7,188

Notes: In the first row, spending change uses the present value of expected lifetime costs for each disease per person in the population, and QALE change uses expected QALE at age 65 for each disease per person in the population. In subsequent rows, results are per person with the disease (or disease category). The discount rate is 0% in the columns varying the value of a year of life. The value of a year of life is $100,000 in the column varying the discount rate.

Source: Authors’ calculations as described in text.

The first column in Table 5 shows the increase in the present value of lifetime costs, the capitalized version of the changes in Table 3. The second column is the increase in QALE. The remaining columns show productivity growth estimates for different values of V (the value of a year of life) and ρ (the discount rate). Standard errors are presented in Table 5 for the overall productivity growth estimate and in Appendix Table B11 for each of the conditions.

Several results are apparent. The overall estimate of medical care productivity growth, shown in the first row of Table 5, is positive. On net, medical care increased in value by $113,000. This estimate is statistically significantly different from zero. The value of health improvement is roughly $170,000, offset by an increase in spending of $58,000. To express this as a growth rate, we need to divide by the net value of medical care in the base year. Assuming that half of QALE at age 65 in the base year is due to medical care, we estimate that medical care productivity growth was 21% in aggregate, or 1.5% per year.³¹

The high overall productivity growth estimate is a mix of heterogeneous estimates for different conditions, shown visually in Figure 9. Cardiovascular disease had the highest productivity growth rate. The net benefit from cardiovascular disease was $89,000 per case. Other conditions have more modest but still large increases in value-added. For example, the net benefit from treatment changes is $38,000 for people with colorectal cancer, $30,000 for people with acute kidney failure, and $22,000 for frail people.

Very few conditions have negative productivity growth, but many are near 0. For example, there was little productivity change for people with arthritis and musculoskeletal conditions (−$3,000 on net) or mental illness ($4,000 on net), even though treatment changed rapidly for both conditions. The declining productivity of treating musculoskeletal conditions likely reflects the increased use of opioids over this period. These drugs are expensive but do not appear to be very effective in reducing chronic pain (Phillips, Ford, and Bonnie, 2017). The low productivity change of mental illness is more difficult to understand. Despite a vast increase in the number of people treated with drugs for mental illness, life expectancy and quality of life among those with mental health diagnoses varied little. In interpreting both of these findings, it is worth reiterating that we do not have direct measures of pain and depressed mood in our data. Still, the measures we have are highly correlated with them.

Columns 4 and 5 of Table 5 show the impact of varying the value of a life-year, to $50,000 in column 4 and $200,000 in column 5. These changes affect the net value of medical care as one would expect. Medical care as a whole has a value of about $25,000 at the lower value, with a 95% confidence interval that includes 0. The higher value of life raises the net benefit to just above $280,000.

The final column of Table 5 shows the impact of using a 3% discount rate for both cost and utility discounting. The results show the same pattern, though the overall magnitude is somewhat smaller. The net benefit of medical care is $50,000 per person.

A. Sensitivity Analysis

We have explored the sensitivity of these results in several ways, detailed in Appendix C. First, we examined robustness to the measure of mortality change by condition. As expected, our methodology attributes far fewer deaths to heart disease in each year than does Vital Statistics—half as many to ischemic heart disease. However, our estimates of changes in death by cause are similar to Vital Statistics. Thus, productivity growth for cardiovascular disease is similar using the Vital Statistics data as our estimates: $77,000 using Vital Statistics data vs. $89,000 using the propensity score method.

Second, we consider productivity estimates using only length of life, since mortality is easier to measure than quality of life. As Appendix C shows, results using length of life only are very similar to those in Figure 9.

Third, we consider how our estimates of spending by condition compare to those using other methodologies. We examine two alternative methodologies: one that parcels out spending for each claim to conditions listed on that claim, and a second that uses a single regression model to parcel out total spending during the year to conditions coded during the year (see Appendix C for details). Using data from 2009, we show that spending by condition is reasonably highly correlated using the three methods: correlations are generally on the order of 0.7 to 0.8. Thus, while we have not estimated costs using these three methods in each year, we suspect that the impact of using alternative spending methodologies would be modest.

Finally, we compare results from our smoothed estimates of health and spending changes to estimates using averages of the first and last few years of the data. The change in health and medical spending is very similar using both methodologies.

B. Cardiovascular Disease

Because cardiovascular disease is so prominent as a cause of death, researchers have developed clinical models of cardiovascular disease mortality reductions to which we can compare our results. The most commonly referenced heart disease model is the IMPACT model (Ford et al., 2007; Ogata et al., 2019). The IMPACT model sorts people into cells based on the presence or absence of heart disease and uses clinical trial evidence on the impact of different treatments to simulate how treatment changes have affected mortality. For example, one cell of the model estimates the differential mortality rate for people with prior heart disease who are and are not taking antihypertensive medications. Using this coefficient and the share of people taking anti-hypertensive medications over time, the model estimates the change in mortality that is predicted to have occurred because of the expanded treatment of hypertension. We use the parameters of the IMPACT model to benchmark our findings.³²

In addition to looking at heart disease, we replicated the structure of the IMPACT model for congestive heart failure and cerebrovascular disease, the other major forms of cardiovascular disease. In some cases, the studies that provide the impact of treatments on mortality are the same as those for ischemic heart disease. In other cases, we find comparable meta-analyses.

Table 6 shows the comparison of our results to the IMPACT model. The first column shows national totals for cardiovascular disease mortality. Relative to a constant age and sex-specific death rate over time, cardiovascular disease mortality in the elderly declined by 300,000 deaths between 1999 and 2012. The results of the IMPACT model are shown in the second column. The model suggests there should be 219,000 fewer deaths resulting from medical treatments over the time period.

Table 6:

Comparison of Mortality Changes for Cardiovascular Diseases to Simulation Models, 1999–2012

Condition	Simulated total decline	IMPACT model Estimate	NHA - Treatment
Ischemic heart disease	−219,721	−129,568	−114,150
Congestive heart failure	−10,560	−41,901	−40,634
Cerebrovascular disease	−68,850	−47,488	−37,545
Cardiovascular risk factors	−2,496	—	−95,813
Total	−300,749	−218,957	−233,004

Notes: The simulated total decline in mortality is relative to a counterfactual where age-specific rates were assumed to be constant over time. Estimates from the IMPACT model are based on the most recent adaptation of the model (Ford et al., 2007; Ogata et al., 2019). The NHA estimate is from the analytic work underlying the national health accounts. It includes change in mortality attributed to medical care and not changes in the prevalence of the condition.

The estimates from our model, presented in the third column, are that medical care accounts for 233,000 fewer deaths over the time period. This is within 17% of the IMPACT model estimates. One would expect our results to be somewhat greater than the IMPACT model since we allow for all effects of cardiovascular risk factors, which include non-cardiovascular complications such as kidney disease. Thus, the estimates are very close.

In addition to matching model totals, our results add richness to them. In the national data, very few deaths are attributable to cardiovascular risk factors, and in the IMPACT model, deaths due to risk factor management are not separated out. Our data shows that a good deal of the improvement in cardiovascular disease mortality comes from better control of risk factor conditions. That is, the prevention industry is important alongside the treatment industry.

C. Cancer

We can also compare our results for certain cancers to those in the clinical literature. Table 5 shows large productivity gains in lung, colorectal, and ‘other’ cancers (most commonly skin and cervical cancer). QALE for each of these conditions increased about 0.4 years. We use data from the National Cancer Institute’s Surveillance, Epidemiology, and End Results (SEER) program (NCI, 1999–2012) to benchmark the lung and colorectal cancer results.³³

The trend in mortality that we attribute to lung cancer matches well with national data. SEER data indicate that mortality per case fell 10% between 1999 and 2012; our estimate is a reduction of 8%. For colorectal cancer, there is a larger discrepancy: an 8% reduction in per case mortality in SEER, compared to 35% in our data. It is not clear what explains this difference, but it suggests that our estimate of productivity growth in colorectal cancer may be too high.

The clinical literature helps evaluate whether the survival gains for these conditions are likely due to medical treatment advances. The major alternative explanation for improved survival is that survival gains are an artifact of detecting smaller cancers that would never become fatal or detecting cancers earlier in the process, so that survival appears to improve.³⁴ Bias from increased diagnosis is unlikely to be an issue in lung cancer, where screening was minimal over the time period and most tumors grow rapidly (Noone et al., 2017). Further, treatments have improved over time. Lung surgery is generally less invasive, and chemotherapy is more common, as are biomarker-targeted therapies. Van der Drift et al. (2012) and Gunn et al. (2018) argue that these treatment changes have improved lung cancer survival in the Netherlands and Finland.

Screening for colorectal cancer grew over the time period, therefore diagnosis changes could be an explanation for improved survival. However, other evidence suggests that medical technology changes have materially improved survival for colorectal cancer. Treatment changes include greater use of pre-surgical radiation, increased use of adjuvant chemotherapy, new medications for metastatic disease, and development of new targeted biologic agents. Colorectal cancer models suggest that greater use of therapies known about in 2000 could lead to reduced mortality on the order of what occurred (Vogelaar et al., 2006). Lemmens et al. (2010) and Brouwer et al. (2018) argue that these treatment changes can explain the improvement in case-specific colorectal cancer survival that was observed in the Netherlands. However, there is no definitive evidence for the United States as yet.

VII. Conclusion

Measuring productivity growth in medical care is a central policy concern. In this paper, we model the productivity of the medical sector as a whole along with specific conditions. We do so in the context of a satellite health account, an account designed to complement current accounts, which focuses largely on medical spending.

Our analysis is detailed, but the facts underlying the conclusions are straightforward. First, there has been a large increase in survival for the elderly. The survival increase occurred despite a rise in obesity and thus condition prevalence. Using conventional estimates of the value of life, the gain in QALE attributable to treatment changes is valued much more than the increase in spending. The net is a productivity increase of 21% in total, or 1.5% annually. Second, the most important contributor to rising productivity is cardiovascular disease. Cardiovascular risk factors are better controlled over time, and interventions for acute disease have improved survival. The improved health we find for people with cardiovascular disease is also found in aggregate evidence and is consistent with clinical trial data on the impact of particular therapies. These gains have been achieved at very modest cost increase, leading to very high productivity growth.

Third, medical spending increases were spread across many conditions, including many with little health improvement. The prototypical example is musculoskeletal disease, where pharmaceutical use and surgical interventions grew rapidly but overall health was unchanged. The same is true for mental health, though this is subject to more uncertainty. As a result, musculoskeletal and mental health conditions are estimated to have low productivity growth.

There are several estimates of health care productivity in the economic literature (Sheiner and Malinovskaya, 2018). However, comparing our estimates with others is difficult. Conceptually, some studies look at changes in the average cost of a year of life over time (e.g., Romley et al., 2015, 2020). An increased average cost per year of QALE is judged to reflect declining productivity. In contrast, we look at the marginal value of health changes relative to their marginal cost. The idea that increasing average cost reflects low productivity growth is true only if one could have bought additional years of quality-adjusted life at the same price in the base year. In that case, spending more per QALY over time is a productivity reduction. If technical constraints prohibited buying more health in the base period, however, an increasing average cost of QALE improvement is not a sign of declining productivity. Rather, one needs to evaluate the marginal cost and benefit of treatment changes. Comparing across studies is also difficult because different studies use different measures of quality. Quality metrics in past studies include clinical estimates of the value of innovation (Lakdawalla et al., 2015), predicted survival based on biomarkers (Eggleston et al., 2011), and expert opinion about the value of treatment changes (Berndt et al., 2002). It is unclear how these relate to actual changes in outcomes. Even studies that look at health outcomes (Romley et al., 2015, 2020) do so over different time horizons.

The most comparable papers to ours are Cutler et al. (1998) and Dauda, Dunn, and Hall (2019). Cutler et al. estimate price reductions of 14% annually for elderly heart attack sufferers. Dauda, Dunn, and Hall estimate price reductions of 7% annually for elderly people hospitalized with heart attack, heart failure, or pneumonia conditions. The price reductions in both of these studies are larger than we estimate for the average elderly person, reflecting the very high benefits of treatment change for acute cardiovascular events.

Our analysis has several limitations, which would be valuable to address in future research. We have estimated the value of medical care for the elderly. However, Case and Deaton (2017) show different trends in mortality in the adult non-elderly populations. Similarly, our findings do not provide guidance on which types of care have been most and least valuable over this time period. Expanding the health account to cover such topics is a worthy area for future research.