Abstract
Global supply chains are increasingly becoming complex by having numerous suppliers around the world. To manage this complexity, organizations must identify the optimum number of suppliers. There have been many examples in the literature that used different approaches to solve this problem. Despite the importance of this issue, less attention has been paid to it and managers of the companies do not know how, and based on which approach and criteria, they should determine the optimal number of suppliers which leads to lower cost and higher reliability of the production line. Therefore, in this study, a hybrid methodology is proposed to expose the process of this problem which helps managers to learn how they can determine the optimal number of suppliers. We address this gap by developing an integrated approach based on multi-criteria decision-making (MCDM) comprising best-worst method (BWM), simple additive weighting (SAW), and technique for order preference by similarity to ideal solution (TOPSIS), and simulation to determine the optimal number of suppliers. This study utilizes a comprehensive approach based on leagile and environmentally sustainable criteria to determine the optimal number of suppliers. To examine the efficiency of the proposed approach, an empirical case study is conducted in an Iranian oil company. The final results represent that the scenario with a 1-1-1 arrangement (one supplier for each type of equipment) is the best possible scenario to determine the optimal number of leagile-sustainable suppliers. To examine the reliability and robustness of the obtained results, a sensitivity analysis based on the three most important criteria is conducted. Finally, discussions on the findings as well as theoretical and managerial implications are presented.
Keywords: Supply chain management, Optimal number of suppliers, Leagile-sustainable suppliers, BWM, SAW, TOPSIS
Introduction
According to the growing customer awareness and ecological pressures from different stakeholders, companies have been forced to consider environmental issues in all parts of their supply chain (Gaziulusoy 2015; Heydari et al. 2021; Wang et al. 2018). The incorporation of environmental issues in companies’ strategic tasks can increase their competitive advantage and lead to sustainable development (Govindan et al. 2013; Grimm et al. 2014; Tsai et al. 2021; Vandchali et al. 2021a; Vandchali et al. 2021b). Suppliers as the first element of supply chains have a crucial role in achieving a sustainable supply chain. Therefore, companies should include the environmental criteria in the supplier evaluation metrics (Çalık 2021; Chang et al. 2019; Vörösmarty and Dobos 2020). In addition, customers are always looking for diverse products and tend to receive them as fast as possible (Carlson and Yao 2008). To follow their needs, companies should apply adaptive strategies which can help them to survive in the long term. Lean paradigm is one of the solutions that help companies to improve the process and operational efficiency, service quality, organizational culture, staff, and administrative efficiencies, standardizing and streamlining the process, delays and operational time, and eliminate waste and non-value-adding tasks (Antony et al. 2019). However, previous works indicated that using only the lean paradigm cannot guarantee survival in today’s constantly changing environments (Abdollahi et al. 2015; Sharma et al. 2021). The environment is changing, customer demands are fluctuating, and they need a variety of products that a lean-based company cannot meet the customers’ expectations. To respond to the customers’ fluctuation demands, the agile paradigm has been introduced to companies as it can help them to overcome unexpected challenges to face unprecedented workplace threats and to take advantage of changes as opportunities. Agility can be defined as the close alignment of an organization with the varied needs of the business to achieve a competitive advantage (Eltawy and Gallear 2017). The recent COVID-19 crisis has highlighted agility as one of the most important and prominent competitive tools that ensure the success of companies in complex and dynamic environments (Al-Omoush et al. 2020; Wanasida et al. 2021). Therefore, having lean, agile, and sustainable paradigm at the same time can benefit companies to apply in their supply chains. Zara the Spanish fashion company provides a good example of a lean, agile, and sustainable supply chain strategy (Christopher 2000; Nayak et al. 2020; Ciccullo et al. 2018).
Purchasing function plays a critical role in the companies’ supply chains (Wisner and Tan 2000). As the products or services procured by this function can cover up to 80 % of final product prices which highlights the importance of continuous improvements in the procurement department (Luzzini and Ronchi 2011). By opening the door to new opportunities, applying lean and agile criteria in purchasing can help supply chains to react to sudden changes in demand, which can be considered as a characteristic of successful purchasing departments because companies with high-performing purchasing functions outperform their competitors (El Mokadem 2017). Lean paradigm focuses on higher quality through the elimination of non-added value things (Nawanir et al. 2020), while the agile paradigm emphasizes adaptability in meeting needs, sustainability focuses on minimizing the adverse impacts of fulfilling those needs (Singh and Vinodh 2017). Implementing the lean, agile, and environmental approach can help to purchase to cope with uncertainties in a volatile environment by monitoring the key metrics that measure suppliers’ health (Agarwal et al. 2006).
Most previous studies have used criteria such as low cost and high quality (Barla 2003) or speed, flexibility, and quality (Luo et al. 2009; Alimardani et al. 2013) or environmental friendly criteria (Segura et al. 2020) in supplier evaluation. In addition, the problem of the optimal number of suppliers has received less attention (Ruiz-Torres and Mahmoodi 2007). Optimizing the number of suppliers not only improves the reliability of the production line and sustainability, but also can minimize the costs of the number of suppliers (Berger et al. 2004). Improving reliability and continuity in companies’ activities without interruption by increasing the number of suppliers has always led to increasing the companies’ costs (Carbone 2003). In other words, there are different approaches to the number of suppliers. For example, the lean paradigm proposed to work with a few suppliers under a long-term contract and the agile paradigm proposed to work with a lot of suppliers under a short-term contract. This problem has forced companies to balance supply chain reliability and companies’ resources. Therefore, creating a trade-off between reliability and costs of the company by determining the optimal number of suppliers considering sustainability criteria is an important issue that has received less attention. On the other hand, determining the optimal number of suppliers is a way to manage risks and mitigate supply disruption. There are different approaches in the literature to address this issue and determine the optimal number of suppliers. For example, some studies utilized the decision tree approach to calculate the optimal number of suppliers (Berger et al. 2004; Ruiz-Torres and Mahmoodi 2007). In this study, we treat this issue as an optimization problem and develop an optimization-simulation-based approach. This paper aims to fill these gaps by developing an integrated approach to find the optimal number of lean, agile, and environmentally sustainable suppliers with the following contributions:
-
I.
Most of the previous studies on optimizing the number of suppliers have considered a limited number of criteria (e.g., Berger et al. (2004); Ruiz-Torres and Mahmoodi (2007)), while this study tries to enrich the literature by incorporating lean, agile, and environmental sustainability criteria simultaneously,
-
II.
Incorporating lean approach-working with a few suppliers under a long-term contract- and agile approach- working with a lot of suppliers under a short-term contract- in determining the optimal number of suppliers to improve the reliability of the production line and minimize the total cost,
-
III.
To the best of our knowledge, there is no study on optimizing the number of suppliers using an integrated framework of MCDM and simulation in the literature. Due to the practical complexity of the problem, this integrated methodology can cope with complex decision-making processes more efficiently, and consequently, leads to valid and reliable results. Therefore, the proposed methodology contributes to the literature by taking advantage of BWM, SAW, TOPSIS, Taguchi-based design of experiments (DOE), and simulation methods to find the optimal number of suppliers.
-
IV.
Utilizing the BWM technique due to its unique characteristics comparing other similar pairwise comparison-based techniques such as AHP in determining the weights of criteria/objectives which leads to more reliable results.
-
V.
Applying Taguchi-based DOE as a structured approach in defining a number of suppliers for the first time.
-
VI.
Conducting a sensitivity analysis based on three most important criteria to demonstrate the robustness and reliability of the proposed methodology.
The rest of this study is organized as follows: In Section 2, an in-depth review of the literature is conducted to analyze different criteria and methods for supplier evaluation. In Section 3, a novel approach based on simulation and MCDM methods to optimize the number of leagile-sustainable suppliers is described. In Section 4, the suggested methodology is illustrated to determine the optimal number of leagile-sustainable suppliers of a real case study. Section 5 concludes the research in terms of main findings. In Section 6, the discussion and the main theoretical and managerial implications are presented. Finally, concluding remarks, limitations, and future research directions are discussed in Section 7.
Literature review
There are several factors influencing disruptions in the supply chain. One of the most important factors that can disrupt supply chain activities is a supplier’s failure to supply in time (Berger et al. 2004). Therefore, suppliers as the first element of supply chains have a prominent role in the regular flow of supply chain activities. In this regard, identifying and evaluating the suppliers has been considered by both academicians and practitioners. On the other hand, determining the optimal number of suppliers is an important decision for any company to manage risks and mitigate supply disruption which has attracted less attention by researchers. Therefore, in this section, we first discuss supplier identification and evaluation, and the related criteria and methods. Then, a review on the problem background is conducted to find the gaps.
Supplier evaluation criteria and methods
There have been many studies in the literature that used different criteria and methods to solve supplier selection and evaluation problems. Ghodsypour and O’brien (2001) introduced net price, storage, transportation and ordering costs as the most important criteria in evaluating suppliers. They applied a mixed-integer non-linear programming (MINLP) model to solve sourcing problem. Kahraman et al. (2003) applied a fuzzy analytical hierarchy process (AHP) to evaluate and rank three Turkish white goods manufacturers based on four categories of criteria including supplier-related criteria (such as financial strength, management stability, technical capability to provide high-quality product and service, quality systems that improve delivery performance, and quality), product performance criteria (such as quality, reliability, durability tolerance, functionality, compatibility, maintainability, and environmentally friendly criteria), service performance criteria (such as accessibility, reliability, and responsiveness), and cost criteria (such as purchase price, transportation cost, and taxes). Chang et al. (2011) used the fuzzy decision-making trial and evaluation laboratory (DEMATEL) method for developing the top 10 important criteria for supplier evaluation including product quality, stable delivery of goods, reaction to demand change in time, service, product price, delivery performance, technology capability, production capability, financial situation, and lead time. Setak et al. (2012) conducted an extensive review of supplier selection literature and introduced three criteria of price, quality and timely delivery as the most common criteria utilized in supplier evaluation. Abdollahi et al. (2015) applied an integrated approach based on fuzzy DEMATEL, analytical network process (ANP), and data envelopment analysis (DEA) methods to evaluate suppliers based on lean (cost, quality, and timely delivery) and agile (human resources capabilities, technological capabilities, management system capabilities, and cultural capabilities) criteria. Bai et al. (2017) evaluated and segmented the suppliers of a chemical company using rough sets theory, fuzzy VlseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) and C-means (FCM) hybrid methodology based on their capabilities and willingness regarding environmental criteria. Zhou and Xu (2018) used the BWM technique, Shannon entropy, and multi-objective optimization model under fuzzy environment to solve the problem of green supplier selection. Parkouhi et al. (2019) applied grey DEMATEL and SAW techniques to the resilient supplier selection. Watróbski et al. (2017) proposed several approaches to compare various most commonly used methods for supplier evaluation. Recently, an integrated MCDM was developed by Tirkolaee et al. (2021) to address green supplier selection in an agri-food supply chain. The proposed approach was based on AHP and fuzzy technique for order of preference by similarity to ideal solution (TOPSIS) and robust goal programming model. Finally, they introduced and discussed the threshold of robustness worthiness (TRW) by analyzing various budgets of uncertainty for the case study problem. Haseli et al. (2021) introduced a novel group decision-making based on the BWM (G-BWM) to investigate a green supplier selection problem as well as supplier development/segmentation problem. It was revealed that their suggested approach is capable of handling a large number of decision-makers (DMs) efficiently.
Many other studies utilized the power of different statistical and operational research methods in a hybrid way to get more reliable results (e.g., Nguyen et al. (2021, 2021)). As can be seen, most of the previous studies have applied classical or single methods such as AHP Kahraman et al. (2003) and ANP Abdollahi et al. (2015) in order to address supplier evaluation criteria. These methods require a high cognitive effort from decision-makers (DMs), and therefore, there might be some ineffective pairwise comparisons (in terms of inconsistency) and application. Hence, we employed a hybrid MCDM–simulation approach to treat the problem. Accordingly, BWM technique is selected to address the research criteria since it is more efficient than the other similar pairwise comparison-based techniques such as AHP and is capable of handling a large number of DMs efficiently Haseli et al. (2021). If n is the number of criteria and we aim to calculate the weights of criteria using the AHP technique, we need to make pairwise comparisons that are very more than pairwise comparisons that need in the BWM technique. On the other hand, statistical analysis indicated that BWM leads to more reliable results than the AHP. Furthermore, to rank the scenarios, two most commonly used outranking techniques; i.e., SAW and TOPSIS are employed. Although SAW is one of the primary, most widely known, and practically used methods, there is no certain pattern to choose a more appropriate method to rank scenarios in this study (Hwang and Yoon 1981; Ginevičius et al. 2008; Ginevičius and Ginevičiene 2009; Zavadskas et al. 2007; Jakimavičius and Burinskiene 2009; Podvezko 2011). Therefore, both SAW and TOPSIS techniques are utilized to calculate the final scores of scenarios in this study, and then a sensitivity analysis is conducted to compare the results obtained from each technique.
As mentioned above, previous works have employed different criteria such as leanness (price, quality and timely delivery) (Ghodsypour and O’brien C 2001; Kahraman et al. 2003; Chang et al. 2011; Setak et al. 2012), agility (human resources capabilities, technological capabilities, management system capabilities, and cultural capabilities) (Kizielewicz et al. 2021) and environment (Bai et al. 2017; Parkouhi et al. 2019) or evaluating suppliers, and fewer studies have simultaneously addressed lean, agile and environmental criteria in supplier evaluation. In their works, the supplier evaluation process was mostly based on cost-related criteria with a high weight. However, the problem of supplier evaluation and selection problem is a multi-criteria decision-making (MCDM) problem, including tangible, intangible, quantitative, and qualitative criteria (Abdollahi et al. 2015). Companies need to be flexible and fast to respond to the constantly changing needs of the market and customers. Also, companies should focus on eliminating waste and non-value added activities to maintain their competitiveness and provide customer satisfaction by increasing efficiency. In addition, due to the increased importance of environmental issues to achieve sustainable development, companies should consider environmental sustainability criteria in the process of supplier evaluation.
The lean paradigm emphasizes the mass production of high-quality and low diversity products in a predictable environment, while the agile paradigm emphasizes the production of varied products in a constantly changing and unpredictable environment (Christopher 2000). A lean supply chain cannot respond quickly to customer demands within the environment associated with high uncertainty and variety in customer needs. Reducing the number of suppliers make it simpler to preserve repeated relationships with the remaining suppliers (Aral et al. 2018). In addition, the use of agility tools to meet the diverse needs of the markets requires spending more resources and costs that result in raising the price of the final products which in the lean paradigm, it can be considered as a type of waste (Krishnamurthy and Yauch 2007). On the other hand, incorporating environmental criteria in evaluating the suppliers can lead companies to sustainable development. Therefore, forming a leagile-sustainable supply chain not only can bring the benefits of both lean and agile paradigms and avoid their weaknesses (Zhang et al. 2012) but also can lead to a sustainable supply chain. In such a supply chain, companies are constantly communicating with their supply chain partners to be able to offer their environmentally friendly products at the right time at a competitive price to the market and customers. Therefore, this study takes the lean, agile, and environmental criteria in the evaluation of suppliers into account, simultaneously.
Optimizing the number of suppliers
Although researchers have been using different approaches for supplier evaluation, there are a few studies that addressed optimizing the number of suppliers. Bakos and Brynjolfsson (1993) focused on the relationship between information technology and the number of suppliers. They argued that although information technology reduces coordination costs, the need to provide incentives for quality may lead companies to work with a limited number of suppliers. Guo and Ganeshan (1995) investigated how the number of suppliers can change the mean and variance of the lead time. They propose a simple decision rule to determine the optimal number of suppliers when lead times are normally, uniformly and exponentially distributed. Berger et al. (2004) and Ruiz-Torres and Mahmoodi (2007) utilized the decision tree approach to calculate the optimal number of suppliers. Nam et al. (2011) proposed a model for determining the constant optimal number of suppliers under the given level of coordination. Their proposed model by considering flexibility and supply costs can lead focal companies to more robust supply management. Babich et al. (2012) investigated the impact of the economic environment on the number of suppliers. They gathered data from companies in both developed and developing countries and found out that supply risk, fixed costs of working with suppliers, and access to financing can influence the optimal number of suppliers. Kumar et al. (2018) modified the presented model by Berger et al. (2004) to calculate the optimal number of suppliers to mitigate supply disruption in an Indian locomotive manufacturer. Aral et al. (2018) developed an integrated multi-period model to determine the optimal number of suppliers in the information technology industry. The proposed model was examined with the large volume of data gathered from 1355 IT firms of 12 countries.
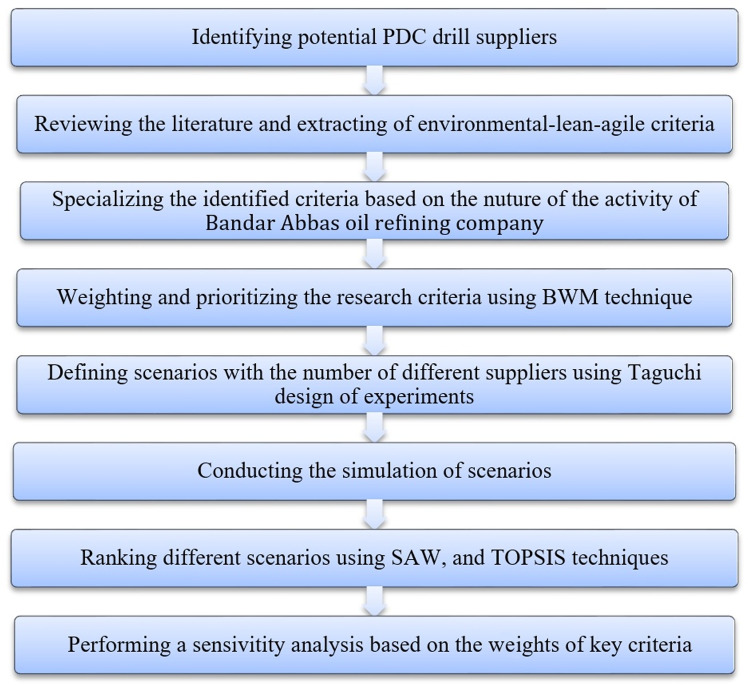
Table 1 provides some evidence of the complexity of the supplier evaluation problem and the inadequacy of mathematical methods in solving this problem. According to the information given in Table 1, it can be deduced that the supplier evaluation can be seen as a mathematical optimization problem with computational complexity (Tan and Alp 2016). As shown in Table 1, the left column indicates four features of a complex and unstructured problem and the right column provides some evidence from the literature that confirms that the supplier evaluation is an NP-Hard problem. Hence, the use of a combination of optimization and simulation techniques is the best approach for facing and solving such problems. This study aims to fill this gap by using the simulation technique in designing the proposed model. As it is clear, most of the mentioned studies have addressed the supplier evaluation problem, while this paper not only provides a comprehensive approach based on leagility-sustainability criteria for supplier evaluation but also the main contribution of this study is to develop a new hybrid methodology to determine the optimal number of suppliers. A schematic diagram of the research implementation process is represented in Fig. 1.
Table 1.
Features of the complex and unstructured problem and the characteristics of supplier evaluation
| Features of a complex and unstructured problem | Characteristics of the supplier selection |
|---|---|
| The existence of different and sometimes conflicting views among DMs with various goals (Munro and Mingers 2002; Checkland and Poulter 2006). | Managers and researchers often had different and conflicting approaches for supplier evaluation. Some have an economic approach, some have an environmental approach, and some others applied a resiliency approach to supplier evaluation (Parkouhi et al. 2019). |
| The nature of the problem is vague and unclear (Munro and Mingers 2002; Heyer 2014; Checkland and Poulter 2006). | The large variety of supplier evaluation methods indicates the complexity of the supplier evaluation and selection process (Chai et al. 2013; Govindan et al. 2015). |
| It is not easily possible to determine the important criteria affecting the problem (Munro and Mingers 2002). | Researchers have proposed different and sometimes conflict criteria (such as profit and risk, cost, quality, etc.) depending on their knowledge, experience, and organization, to supplier evaluation. This suggests that there are different views on the issue of supplier evaluation problem (Rezaei and Ortt 2012). |
| The inefficiency of quantitative and mathematical methods (Wilson 2001; Munro and Mingers 2002; Heyer 2014). | Different methods have been employed for suppliers’ evaluation and selection, such as elimination methods, probabilistic methods, optimization methods and also quantitative and analytical methods, but these methods are unable to provide reliable solutions that can be implemented in practice. These methods neglect the human and social factors affecting the problem situations (Hanafizadeh and Zadeh 2015). |
Fig. 1.
Framework and steps of research implementation
Proposed methodology
The proposed methodology not only makes a more reliable supply chain at the minimum possible amount of the cost but also leads to a sustainable supply chain considering lean, agile, and environmental criteria in determining the best number of suppliers. In this section, the proposed approach is introduced step by step to determine the optimal number of suppliers in a real-world case study. First, the case study problem and experts who participated in this research are introduced.
Sampling and real-world problem description
In this study, Bandar Abbas oil refining company is selected as a real case study which is one of the biggest Iranian oil and gas companies in the south of Iran. The required data were collected through a panel of experts with at least 15 years of experience in the oil industry. Due to the limited number of qualified experts with mentioned characteristics, no sampling was conducted and all experts participated in the study. The required data to determine weights of criteria were collected through a pairwise comparison questionnaire from a panel of experts including the head of the sourcing department, procurement manager, and head of standard engineering department of the company under study by at least master degree, and a minimum of 15 years work experience in sourcing, and foreign goods and equipment ordering. Recently, severe economic sanctions have created many restrictions for managers of the Bandar Abbas oil refining company which limited their decision-making process regarding the supplier selection and evaluation process. Many foreign suppliers terminated the relationship with the Bandar Abbas oil refining company to follow the global sanctions imposed on Iranian companies which result in reducing the supply base. In this situation, optimizing the number of suppliers based on the environmental, lean, and agile criteria was considered as the vital option for the sustainable performance of the Bandar Abbas oil refining company. This is important as paying no attention to this matter not only transfers Iran’s market share to other Middle East countries, such as Saudi Arabia and Qatar, but also there would be a possibility of bankruptcy of many Iranian companies operating in the oil and gas industry. The main finding of this research, considering the current situation of Iranian companies operating in the oil and gas industry, can help them manage their supply side of the supply chain and mitigate the disruptions in the supply chain. As mentioned earlier, increasing reliability and improving the quality and environmental sustainability of the supply chain can increase costs. Therefore, it is necessary to determine the optimal number of suppliers to strike a balance between the reliability, environmental sustainability, and the costs of the number of suppliers in each scenario.
Figure 2 illustrates the problem schematically. Here, suppliers are identified as potential suppliers of different types of polycrystalline diamond compact (PDC) drills.
Fig. 2.

Diagram of the problem to optimize the number of suppliers
The decision variable is the number of leagile-sustainable suppliers of each kind of PDC drill, so while satisfying different and sometimes conflicting objectives of the model, it also applies to the constraints of the problem. The assumptions and parameters and the mathematical programming model of the problem are presented as follows:
- The problem assumptions:
- Each supplier has a specific supply cost
- Failure rate is constant and has a normal distribution.
- Failure rate of each supplier is independent. In other words, the delay in the timely delivery of goods by a supplier does not have a relation with other suppliers.
- Notations of the model are defined as follows:
- i : Set of all PDC drills of the line
- Number of suppliers of PDC drill
- Supply cost of PDC drill
- Total cost of supplying all types of PDC drill
- Total number of PDC drill supplier
- MTTFD: Mean of time until the first delay in the delivery of the drill (a delay of more than a day in drill delivery is considered as delay)
- Var(TTFD): The variance of the time until the first delay in the delivery of the drill
Considering the research background and the structure of the problem, besides lean and agile criteria, the following criteria have also been considered as research criteria/objectives:
Maximizing mean of time until the first delay (MTTFD)
Minimizing variance of time to the first delay (Var(TTFD))
Minimizing total cost (TC)
The cost of suppliers for type one, two, and three PDC drills was considered as 80, 90, and 60 monetary units, respectively, and also the total cost of supply was considered equivalent to 600 monetary units. The maximum number of suppliers for each type of drill was equivalent to 4 suppliers. Therefore, the problem of this study is a multi-objective problem with two constraints as described in Model (1):
| 1 |
Proposed methodology to find the optimal number of suppliers
The suggested approach of the present research to solve the supplier selection problem consists of the following seven steps:
Step 1: Identifying potential suppliers
In this step, the DMs of Bandar Abbas oil refining company identified and listed all potential PDC drill suppliers that had the capability and willingness to supply PDC drill. There is no evaluation in this step.
Steps 2 and 3: Identifying and extracting leagility-sustainability criteria and then adjusting and specializing them with the industry
After an extensive review of the literature, the leagile-sustainable criteria used in supplier selection were identified and extracted. The three criteria of the meantime to first delay (MTTFD), the variance of time to first delay (Var(TTFD)), and total cost (TC) of the number of suppliers in the different scenarios were added to the list of criteria to balance the supply chain reliability and total cost. The results of these two steps are presented in Table 2.
Table 2.
Supplier evaluation criteria
| Component | Criterion | Symbol | References |
|---|---|---|---|
| Environmental | Ability and willingness to meet the environmental standards (e.g., ISO 14001 standard) | C1 | (Mohammed et al. 2019; Yu et al. 2019; Jain and Singh 2020; Zhou and Xu 2018; Arabsheybani et al. 2018; Sen et al. 2018; Luthra et al. 2017). |
| Ability and willingness to invest in specific tech | C2 | (Büyüközkan and Çifçi 2011; Luthra et al. 2017; Sen et al. 2018; Jain and Singh 2020). | |
| Commitment to greening | C3 | (Fu et al. 2012; Luthra et al. 2017; Ecer and Pamucar 2020). | |
| Lean | Waiting time to complete an order | C4 | (Chang et al. 2011; Choy et al. 2003; Punniyamoorthy et al. 2011). |
| Warranty policies | C5 | (Dickson 1966; Guo et al. 2009; Kuo et al. 2010). | |
| Effort in eliminating waste | C6 | (Huang and Keskar 2007; Punniyamoorthy et al. 2011; Takeishi 2001). | |
| Product life time | C7 | (Chen 2011; Kuo et al. 2010). | |
| Timely delivery | C8 | (Chen 2011; Vinodh et al. 2011; Xia and Wu 2007). | |
| Agile | Long term relationship | C9 | (Luo et al. 2009; Punniyamoorthy et al. 2011; Sarkar and Mohapatra 2006). |
| Team structures | C10 | (Croom 2001; Krishnan and Ulrich 2001; Yauch 2007). | |
| Communication and e-commerce system | C11 | (Guo et al. 2009; Katsikeas et al. 2004). | |
| Innovative and R&D capabilities | C12 | (Chen 2011; Katsikeas et al. 2004). | |
| Equipment and production capacity | C13 | (Dickson 1966; Punniyamoorthy et al. 2011; Weber et al. 1991). | |
| Quality systems | C14 | (Choi and Hartley 1996; Dulmin and Mininno 2003; Hsu and Hu 2009). | |
| Financial capabilities | C15 | (Choi and Hartley 1996; Punniyamoorthy et al. 2011; Vinodh et al. 2011). | |
| Information sharing level | C16 | (Hajji et al. 2011; Krause et al. 2007; Luo et al. 2009). | |
| Mutual trust | C17 | (Amin et al. 2011; Punniyamoorthy et al. 2011; Zhang et al. 2011). | |
| MTTFDs | Mean time to the first delay | C18 | (Yalaoui et al. 2005). |
| Var(TTFDs) | Variance of the time to first delay | C19 | (Yalaoui et al. 2005). |
| TC | Supply cost based on the number of suppliers in different scenarios | C20 | (Mettas 2000). |
Step 4: Weighing criteria using BWM technique
BWM was offered by Rezaei (2015) as one of the most efficient MCDM approaches based on pairwise comparisons. This technique requires less pairwise comparisons and access to more consistent comparisons, and in comparison to other similar methods, such as AHP, it leads to more efficient and reliable results (Rezaei 2015). The proposed model used in this study is a linear version of the initial model introduced by (Rezaei 2016) that gives a unique and global solution. The main steps of BWM are as follows:
-
i.
Defining a set of decision criteria;
-
ii.
Identifying the most important and least important criteria;
-
iii.
Finding the preference degree of the most important criteria over the other criteria within the 1–9 scale. The preference vector of the most important criterion compared to other criteria is denoted by . Here, stands for the preference degree of the most important criterion (B) over criterion j. It is obvious that ;
-
iv.
Finding the preference degree of the other criteria over the least important criterion within the 1–9 scale. The preference vector of the other criteria over the least important criterion is denoted by . Here, stands for the preference degree of j criterion over the least important criterion (W). It is obvious that ;
-
v.
Determining the final weights of the criteria : to determine the optimal weight for each of the criteria, for every couple of and should be satisfied and for all j. Hence, a solution should be provided where the maximum absolute value differences and minimize for all j. Due to the non-negative weight of each criterion and the constraint that satisfies the sum of weights , the optimization model is formulated as Model (2). Now, the optimal weights of all criteria and value are obtained by solving this model.
| 2 |
where and represents the weight of the most important criterion, weight of the least important criterion, and weight of criterion j. Furthermore, and stands for the preference degree of the most important criterion over criterion j and preference degree of criterion j over the least important criterion. To compute the inconsistency ratio (IR), the value found in the previous step and consistency index (CI) reported for various values of are employed (see Table 3 and Eq. 3).
| 3 |
Table 3.
Specific consistency index (CI) of BWM
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| CI | 0 | 0.44 | 1 | 1.63 | 2.3 | 3 | 3.73 | 4.47 | 5.23 |
Step 5: Scenario determination using DOE
In cases where there is insufficient knowledge about the relationship between input and output of a process, DOE is a good way to select several scenarios from existing scenarios (Freddi and Salmon 2019). In this study, DOE is utilized to determine scenarios.
Step 6: Simulation and replication of scenarios to determine MTTFD and Var(TTFD)
Simulation is one of the most useful techniques to overcome planning uncertainties in any organization. Simulation is the science and art of building a model of a process, to evaluate and test different scenarios. Simulation can be applied as a way of knowing the results of proposed ideas before they are implemented. Therefore, in this research, the simulation approach is used to evaluate different scenarios and determine the optimal number of suppliers to supply each of the required types of PDC drill of the Iranian South Oil Company.
Step 7: Ranking different scenarios using SAW technique
The SAW technique was proposed by Hwang and Yoon (1981). The steps of these two techniques are given below.
7-1. SAW technique
-
i.
Creating the decision matrix of scenarios and criteria: Values 1 to 9 are employed to determine each scenario’s score over each of the criteria as described in Table 4.
- ii.
-
iii.
Determining the weight vector of the criteria using BWM techniques
-
iv.Computing the final score of each option using Eq. 6:
6
Table 4.
Linguistic variable and corresponding numeric equivalents
| Linguistic variable | Corresponding number |
|---|---|
| Extremely poor | 1 |
| Very poor | 2 |
| Poor | 3 |
| Almost poor | 4 |
| Medium | 5 |
| Almost strong | 6 |
| Strong | 7 |
| Very strong | 8 |
| Excellent | 9 |
7-2. TOPSIS technique
-
i.
Creating the decision matrix of scenarios and criteria: Values 1 to 9 are used to determine each scenario’s score over each of the criteria as described in Table 4.
-
ii.Normalization of decision matrix using Eq. 7.
7 -
iii.
Determining the weight vector of the criteria using BWM techniques.
-
iv.Constructing the normalize weighted matrix using Eq. 8:
8 - v.
- vi.
-
vii.Calculating the final score of each scenario using Eq. 13:
13
Results
In this section, the proposed approach is implemented step by step to demonstrate how it can be utilized in practice. The first step involved identifying potential suppliers by DMs and seven potential suppliers were identified. The second and third steps are related to identifying, extracting, adjusting, and specializing leagility and sustainability criteria for the industry under study. The second and third steps of the proposed approach resulted in the 20 criteria listed in Table 2. Implementation of the fourth to seventh steps of the proposed approach is discussed in the following. In Step 4, the local weight of each of the criteria/objectives was calculated using the BWM method. To show how to calculate the weights of the components using the BWM technique, the degree of importance of the six main research components is calculated based on the data gathered from the panel of experts.
- Step 4. Weighting the criteria using BWM technique
- Step 4.1. Determining a set of decision components: The six main components of the research are included (i) Environmental, (ii) Lean, (iii) Agile, (iv) MTTFDs, (v) Var(TTFDs), (vi) TC.
- Step 4.2. Determining the most important and least important components: According to the DMs’ opinions, the most and the least important components are environmental and Var(TTFDs), respectively.
- Step 4.3. Determining the degree of preference of the most important component over the other components: Table 5 shows the degree of preference of the most important component (environmental component) over the other components according to DMs. As seen in Table 5, the degree of preference of the most important component over the first component (environmental) is equal to 1 . It is obvious that the degree of preference of the most important component over the second component (lean) is equal to 3 . The degree of preference of the most important component over the third component (agile) is equal to 3 . The degree of preference of the most important component over the fourth component (MTTFDs) is equal to 2 . The degree of preference of the most important component over the fifth component (Var(TTFDs)) which is the least important component is equal to 6 . And finally, the degree of preference of the most important component over the sixth component (TC) is equal to 2 .
- Step 4.4. Determining the degree of preference of the other components over the least important component: Table 6 represents the degree of preference of the other components over the least important component according to DMs. As seen in Table 6, the degree of preference of the first component (environmental) over the least important component (Var(TTFDs)) is equal to 6 . The degree of preference of the second component (lean) over the least important component is equal to 2 . The degree of preference of the third component (agile) over the least important component is equal to 2 . The degree of preference of the fourth component (lean) over the least important component is equal to 3 . It is obvious that the degree of preference of the fifth component over the least important component is equal to 1 . And finally, the degree of preference of the sixth component (TC) over the least important component is equal to 3 .
- Step 4.5. Determining the final weights of the components: In order to calculate the weights of each of the research components, it is sufficient to formulate and solve the linear programming model presented below using the represented data in Tables 5 and 6. This issue is discussed as follows.
minimize Output: subject to , , , , , , , , Consistent. ,
Table 5.
The degree of preference of the most important component over the other components
| Components | Environmental | Lean | Agile | MTTFDs | Var(TTFDs) | TC |
|---|---|---|---|---|---|---|
| The most important component: Environmental | 1 | 3 | 3 | 2 | 6 | 2 |
Table 6.
The degree of preference of the other components over the least important component
| Components | The least important component: Var(TTFDs) |
|---|---|
| Environmental | 6 |
| Lean | 2 |
| Agile | 2 |
| MTTFDs | 3 |
| Var(TTFDs) | 1 |
| TC | 3 |
By solving the above linear programming model, the weights of the main components are obtained. As can be seen, according to DMs’ opinions, the degree of importance of the environmental, lean, agile, MTTFDs, Var(TTFDs), and TC are equal to 0.359, 0.117, 0.117, 0.176, 0.058, and 0.176, respectively. The inconsistency rate is calculated using Eq. 3. As it is clear, the inconsistency rate is equal to 0.000 and it indicates that the comparisons are fully consistent. The weights of the components were calculated according to the DMs.
The weights of other criteria were calculated similarly and are presented in Table 7. The final weight of each criterion is obtained by multiplying the local weight of that criterion in the local weight of the corresponding component. Table 5 displays the meeting environmental standards (e.g., ISO 14001 standard) with the weight of 0.201563 is located in the first priority. Also, the meantime to first delay (MTTFD), and supply cost (TC) based on the number of suppliers in different scenarios with the weight of 0.176 were jointly located in the second priority.
Table 7.
Weight and final importance of each criteria
| Component | Weight | Criterion | Weight | Final weight |
|---|---|---|---|---|
| Environmental | 0.353 | C1 | 0.571 | 0.201563 |
| C2 | 0.285 | 0.100605 | ||
| C3 | 0.142 | 0.050126 | ||
| Lean | 0.117 | C4 | 0.214 | 0.025038 |
| C5 | 0.142 | 0.016614 | ||
| C6 | 0.071 | 0.008307 | ||
| C7 | 0.142 | 0.016614 | ||
| C8 | 0.428 | 0.050076 | ||
| Agile | 0.117 | C9 | 0.154 | 0.018018 |
| C10 | 0.075 | 0.008775 | ||
| C11 | 0.105 | 0.012285 | ||
| C12 | 0.309 | 0.036153 | ||
| C13 | 0.158 | 0.018486 | ||
| C14 | 0.105 | 0.012285 | ||
| C15 | 0.309 | 0.036153 | ||
| C16 | 0.079 | 0.009243 | ||
| C17 | 0.037 | 0.004329 | ||
| MTTFDs | 0.176 | C18 | 0.176 | 0.176 |
| Var(TTFDs) | 0.059 | C19 | 0.059 | 0.059 |
| TC | 0.176 | C20 | 0.176 | 0.176 |
Step 5: Scenario determination using DOE
After weighing the research criteria, it is time to determine scenarios. In this step, different scenarios are developed by considering different statuses and using the Taguchi orthogonal array L8. These scenarios were created in each subsystem by considering a number of surplus suppliers for each group of PDC drills. Table 8 illustrates the different scenarios of the Taguchi orthogonal array L8. In each of the scenarios, the number of suppliers of each type of PDC drill is different.
Table 8.
Different scenarios of the Taguchi-based DOE
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | |
|---|---|---|---|---|---|---|---|---|
| PDC1 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 |
| PDC2 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| PDC3 | 1 | 2 | 1 | 2 | 2 | 1 | 2 | 1 |
| Total cost | 230 | 370 | 320 | 460 | 470 | 490 | 560 | 580 |
Step 6: Simulation and replication of scenarios to determine MTTFD and Var (TTFD)
After defining the scenarios, it is time to simulate each of the scenarios. In this step, using the simulation technique, the decision matrix is completed. For this purpose, each of the eight scenarios presented in Table 8, which also satisfies the model constraints, was simulated using the ED software. Each scenario was run 20 times and the results are presented in Table 9. For example, number 191 (row 1: column A1) denotes the time of the first delay in supplying the PDC drill and stops the system, which is obtained as a result of employing one supplier for each type of drill. The MTTFDs denote the meantime to the first delay in each scenario and Var(TTFDs) in the last row denotes the variance of the time to the first delay.
Table 9.
MTTFD in supply of PDC drill based on different scenario
| Replication | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 191 | 169 | 476 | 379 | 478 | 371 | 496 | 92 |
| 2 | 125 | 178 | 145 | 369 | 541 | 135 | 183 | 292 |
| 3 | 127 | 511 | 305 | 400 | 501 | 197 | 114 | 417 |
| 4 | 559 | 552 | 308 | 292 | 153 | 542 | 493 | 333 |
| 5 | 363 | 179 | 465 | 587 | 518 | 262 | 225 | 360 |
| 6 | 430 | 172 | 555 | 328 | 163 | 474 | 368 | 291 |
| 7 | 138 | 135 | 173 | 506 | 510 | 176 | 241 | 523 |
| 8 | 337 | 564 | 424 | 444 | 245 | 320 | 490 | 180 |
| 9 | 533 | 385 | 324 | 351 | 246 | 297 | 346 | 407 |
| 10 | 460 | 166 | 146 | 379 | 154 | 103 | 305 | 591 |
| 11 | 459 | 297 | 498 | 247 | 371 | 522 | 537 | 250 |
| 12 | 116 | 250 | 192 | 468 | 291 | 312 | 123 | 472 |
| 13 | 293 | 453 | 547 | 568 | 425 | 95 | 179 | 333 |
| 14 | 371 | 149 | 324 | 437 | 245 | 175 | 163 | 498 |
| 15 | 405 | 416 | 156 | 212 | 441 | 477 | 107 | 277 |
| 16 | 536 | 118 | 163 | 223 | 381 | 532 | 109 | 334 |
| 17 | 209 | 579 | 431 | 494 | 495 | 563 | 143 | 380 |
| 18 | 269 | 129 | 278 | 303 | 375 | 582 | 190 | 482 |
| 19 | 262 | 441 | 397 | 364 | 263 | 575 | 175 | 409 |
| 20 | 150 | 183 | 206 | 475 | 301 | 243 | 226 | 562 |
| MTTFD | 374.15 | 260.65 | 347.65 | 354.85 | 391.3 | 325.65 | 301.3 | 316.65 |
| Var(TTFD) | 16115.39 | 20917.92 | 29586.34 | 17078.34 | 11430.74 | 19885.60 | 27848.11 | 22446.13 |
Step 7: Ranking different scenarios using SAW and TOPSIS technique
By adding the outputs of the simulation of phase to the decision matrix, we can start to rank the scenarios using the SAW technique. Table 10 represents the decision matrix of scenarios and criteria.
Table 10.
Decision matrix of scenarios and criteria
| Scenarios Criteria | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 |
|---|---|---|---|---|---|---|---|---|
| 8 | 6 | 7 | 5 | 4 | 5 | 5 | 4 | |
| 7 | 6 | 7 | 8 | 8 | 7 | 7 | 6 | |
| 9 | 7 | 8 | 6 | 5 | 6 | 5 | 5 | |
| 4 | 6 | 5 | 7 | 7 | 7 | 8 | 8 | |
| 9 | 6 | 8 | 7 | 7 | 7 | 6 | 6 | |
| 8 | 6 | 7 | 5 | 5 | 5 | 4 | 4 | |
| 4 | 6 | 5 | 7 | 7 | 7 | 8 | 8 | |
| 4 | 6 | 5 | 7 | 6 | 5 | 9 | 8 | |
| 9 | 7 | 8 | 6 | 6 | 6 | 5 | 5 | |
| 7 | 6 | 7 | 6 | 5 | 5 | 4 | 4 | |
| 7 | 5 | 6 | 4 | 4 | 4 | 4 | 4 | |
| 4 | 4 | 4 | 6 | 6 | 6 | 7 | 7 | |
| 3 | 4 | 3 | 5 | 5 | 5 | 6 | 6 | |
| 8 | 6 | 7 | 6 | 6 | 6 | 5 | 5 | |
| 3 | 5 | 4 | 5 | 5 | 5 | 6 | 6 | |
| 8 | 6 | 7 | 5 | 5 | 5 | 4 | 4 | |
| 8 | 6 | 7 | 5 | 5 | 5 | 4 | 4 | |
| 374.15 | 260.65 | 347.65 | 354.85 | 391.3 | 325.65 | 301.3 | 316.65 | |
| 16115 | 20917 | 29586 | 17078 | 11430 | 19885 | 27848 | 22446 | |
| 230 | 370 | 320 | 460 | 470 | 490 | 560 | 580 |
After constructing the decision matrix, we should normalize the decision matrix and compute the weight of the criteria and the final score for each scenario. Already, the weight of each criterion/objective was computed using the BWM technique. The final score for each scenario has also been calculated using SAW technique and is reported in the last row of Table 11.
Table 11.
Normal decision matrix of scenarios and criteria (SAW)
| Scenarios Criteria | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 |
|---|---|---|---|---|---|---|---|---|
| 1.000 | 0.750 | 0.875 | 0.625 | 0.50 | 0.625 | 0.625 | 0.50 | |
| 0.875 | 0.750 | 0.875 | 1.000 | 1.000 | 0.875 | 0.875 | 0.750 | |
| 1.000 | 0.778 | 0.889 | 0.667 | 0.556 | 0.667 | 0.556 | 0.556 | |
| 0.500 | 0.750 | 0.625 | 0.875 | 0.875 | 0.875 | 1.000 | 1.000 | |
| 1.000 | 0.667 | 0.889 | 0.778 | 0.778 | 0.778 | 0.667 | 0.667 | |
| 1.000 | 0.750 | 0.875 | 0.625 | 0.625 | 0.625 | 0.500 | 0.500 | |
| 0.500 | 0.750 | 0.625 | 0.875 | 0.875 | 0.875 | 1.000 | 1.000 | |
| 0.444 | 0.667 | 0.556 | 0.778 | 0.667 | 0.556 | 1.000 | 0.889 | |
| 1.000 | 0.778 | 0.889 | 0.667 | 0.667 | 0.667 | 0.556 | 0.556 | |
| 1.000 | 0.857 | 1.000 | 0.857 | 0.714 | 0.714 | 0.571 | 0.571 | |
| 1.000 | 0.714 | 0.857 | 0.571 | 0.571 | 0.571 | 0.571 | 0.571 | |
| 0.571 | 0.571 | 0.571 | 0.857 | 0.857 | 0.857 | 1.000 | 1.000 | |
| 0.500 | 0.667 | 0.500 | 0.833 | 0.833 | 0.833 | 1.000 | 1.000 | |
| 1.000 | 0.750 | 0.875 | 0.750 | 0.750 | 0.750 | 0.625 | 0.625 | |
| 0.500 | 0.833 | 0.667 | 0.833 | 0.833 | 0.833 | 1.000 | 1.000 | |
| 1.000 | 0.750 | 0.875 | 0.625 | 0.625 | 0.625 | 0.500 | 0.500 | |
| 1.000 | 0.750 | 0.875 | 0.625 | 0.625 | 0.625 | 0.500 | 0.500 | |
| 0.811 | 0.770 | 0.834 | 1.000 | 0.908 | 0.890 | 0.668 | 0.957 | |
| 0.510 | 0.410 | 0.510 | 1.000 | 0.670 | 0.386 | 0.546 | 0.708 | |
| 1.000 | 0.622 | 0.719 | 0.500 | 0.489 | 0.469 | 0.411 | 0.397 | |
| 0.869 | 0.729 | 0.800 | 0.797 | 0.722 | 0.711 | 0.698 | 0.713 | |
| Final rank | 1 | 4 | 2 | 3 | 5 | 7 | 8 | 6 |
As it can be seen from Table 11, Scenario A1 with a score equivalent to 0.869 was identified as the best scenario in determining the optimal number of suppliers. In other words, according to the experts’ opinions and output of the SAW technique, selecting one supplier for each type of the PDC drill is the best possible status. Then, Scenario A3 with a score of 0.800 took the second place by arranging 1, 2, and 1 (1 supplier for PDC1, 2 suppliers for PDC2, and 1 supplier for PDC3). Scenario A7 with a score equivalent to 0.698 was identified as the worst scenario with seven suppliers and arranged 1, 4, 2 (1 supplier for PDC1, 4 suppliers for PDC2, and 2 suppliers for PDC3). To reach more reliable results and to compare the outputs of SAW and TOPSIS techniques, the rank of each scenario was calculated using the TOPSIS technique. Table 12 indicates the normal decision matrix obtained through Eq. 7.
Table 12.
Normal decision matrix of scenarios and criteria (TOPSIS)
| Scenarios Criteria | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 |
|---|---|---|---|---|---|---|---|---|
| 0.500 | 0.375 | 0.438 | 0.313 | 0.250 | 0.313 | 0.313 | 0.250 | |
| 0.352 | 0.302 | 0.352 | 0.402 | 0.402 | 0.352 | 0.352 | 0.302 | |
| 0.487 | 0.379 | 0.433 | 0.325 | 0.271 | 0.325 | 0.271 | 0.271 | |
| 0.213 | 0.320 | 0.267 | 0.373 | 0.373 | 0.373 | 0.426 | 0.426 | |
| 0.450 | 0.300 | 0.400 | 0.350 | 0.350 | 0.350 | 0.300 | 0.300 | |
| 0.500 | 0.375 | 0.438 | 0.313 | 0.313 | 0.313 | 0.250 | 0.250 | |
| 0.213 | 0.320 | 0.267 | 0.373 | 0.373 | 0.373 | 0.426 | 0.426 | |
| 0.220 | 0.329 | 0.274 | 0.384 | 0.329 | 0.274 | 0.494 | 0.439 | |
| 0.480 | 0.373 | 0.426 | 0.320 | 0.320 | 0.320 | 0.267 | 0.267 | |
| 0.441 | 0.378 | 0.441 | 0.378 | 0.315 | 0.315 | 0.252 | 0.252 | |
| 0.508 | 0.363 | 0.435 | 0.290 | 0.290 | 0.290 | 0.290 | 0.290 | |
| 0.251 | 0.251 | 0.251 | 0.376 | 0.376 | 0.376 | 0.439 | 0.439 | |
| 0.223 | 0.297 | 0.223 | 0.372 | 0.372 | 0.372 | 0.446 | 0.446 | |
| 0.457 | 0.342 | 0.400 | 0.342 | 0.342 | 0.342 | 0.285 | 0.285 | |
| 0.214 | 0.356 | 0.285 | 0.356 | 0.356 | 0.356 | 0.427 | 0.427 | |
| 0.500 | 0.375 | 0.438 | 0.313 | 0.313 | 0.313 | 0.250 | 0.250 | |
| 0.500 | 0.375 | 0.438 | 0.313 | 0.313 | 0.313 | 0.250 | 0.250 | |
| 0.333 | 0.316 | 0.343 | 0.411 | 0.373 | 0.366 | 0.274 | 0.393 | |
| 0.365 | 0.453 | 0.365 | 0.186 | 0.278 | 0.481 | 0.340 | 0.263 | |
| 0.181 | 0.291 | 0.252 | 0.362 | 0.370 | 0.386 | 0.441 | 0.456 |
The normal and weighted decision matrix, the positive ideal scenario , the negative ideal scenario , the distance between each scenario and and , and the final score of each scenario are presented in Table 13.
Table 13.
Weighted decision matrix and final scores of the scenarios (TOPSIS)
| Scenarios Criteria | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1008 | 0.0756 | 0.0882 | 0.063 | 0.0504 | 0.063 | 0.063 | 0.0504 | 0.101 | 0.05 | |
| 0.0354 | 0.0303 | 0.0354 | 0.0404 | 0.0404 | 0.0354 | 0.0354 | 0.0303 | 0.04 | 0.03 | |
| 0.0244 | 0.019 | 0.0217 | 0.0163 | 0.0136 | 0.0163 | 0.0136 | 0.0136 | 0.024 | 0.014 | |
| 0.0053 | 0.008 | 0.0067 | 0.0093 | 0.0093 | 0.0093 | 0.0107 | 0.0107 | 0.011 | 0.005 | |
| 0.0075 | 0.005 | 0.0066 | 0.0058 | 0.0058 | 0.0058 | 0.005 | 0.005 | 0.007 | 0.005 | |
| 0.0042 | 0.0031 | 0.0036 | 0.0026 | 0.0026 | 0.0026 | 0.0021 | 0.0021 | 0.004 | 0.002 | |
| 0.0035 | 0.0053 | 0.0044 | 0.0062 | 0.0062 | 0.0062 | 0.0071 | 0.0071 | 0.007 | 0.004 | |
| 0.011 | 0.0165 | 0.0137 | 0.0192 | 0.0165 | 0.0137 | 0.0247 | 0.022 | 0.025 | 0.011 | |
| 0.0086 | 0.0067 | 0.0077 | 0.0058 | 0.0058 | 0.0058 | 0.0048 | 0.0048 | 0.009 | 0.005 | |
| 0.0039 | 0.0033 | 0.0039 | 0.0033 | 0.0028 | 0.0028 | 0.0022 | 0.0022 | 0.004 | 0.002 | |
| 0.0062 | 0.0045 | 0.0053 | 0.0036 | 0.0036 | 0.0036 | 0.0036 | 0.0036 | 0.006 | 0.004 | |
| 0.0091 | 0.0091 | 0.0091 | 0.0136 | 0.0136 | 0.0136 | 0.0159 | 0.0159 | 0.016 | 0.009 | |
| 0.0041 | 0.0055 | 0.0041 | 0.0069 | 0.0069 | 0.0069 | 0.0082 | 0.0082 | 0.008 | 0.004 | |
| 0.0056 | 0.0042 | 0.0049 | 0.0042 | 0.0042 | 0.0042 | 0.0035 | 0.0035 | 0.006 | 0.004 | |
| 0.0077 | 0.0129 | 0.0103 | 0.0129 | 0.0129 | 0.0129 | 0.0155 | 0.0155 | 0.015 | 0.008 | |
| 0.0046 | 0.0035 | 0.004 | 0.0029 | 0.0029 | 0.0029 | 0.0023 | 0.0023 | 0.005 | 0.002 | |
| 0.0022 | 0.0016 | 0.0019 | 0.0014 | 0.0014 | 0.0014 | 0.0011 | 0.0011 | 0.002 | 0.001 | |
| 0.0586 | 0.0557 | 0.0603 | 0.0723 | 0.0657 | 0.0644 | 0.0483 | 0.0692 | 0.072 | 0.048 | |
| 0.0215 | 0.0267 | 0.0215 | 0.011 | 0.0164 | 0.0284 | 0.0201 | 0.0155 | 0.028 | 0.011 | |
| 0.0319 | 0.0512 | 0.0443 | 0.0637 | 0.0651 | 0.0679 | 0.0776 | 0.0803 | 0.08 | 0.032 | |
| 0.0544 | 0.0453 | 0.0438 | 0.0463 | 0.0565 | 0.0436 | 0.0477 | 0.0547 | |||
| 0.0543 | 0.0377 | 0.0444 | 0.0448 | 0.0406 | 0.0463 | 0.052 | 0.0556 | |||
| 0.4993 | 0.4544 | 0.5036 | 0.4918 | 0.4183 | 0.5146 | 0.5219 | 0.5042 | |||
| Final rank | 5 | 7 | 4 | 6 | 8 | 2 | 1 | 3 |
There is a doubt that the results of which method can exactly capture the DM’s point of view. This problem becomes more complicated when the number of criteria, alternatives and DMs increases. On the other hand, the issue of validity becomes more important when different methods obtain different results. According to Table 14, there is a negative correlation (-0.548) between the final ranks of SAW and TOPSIS. Hence, the authors employed these two popular outranking methods with different assumptions to provide more options for DMs.
Table 14.
Spearman’s correlation between the results of SAW and TOPSIS
| SAW | TOPSIS | |||
|---|---|---|---|---|
| Spearman’s | SAW | Correlation Coefficient | 1.000 | -.548 |
| N | 8 | 8 | ||
| TOPSIS | Correlation Coefficient | -.548 | 1.000 | |
| N | 8 | 8 |
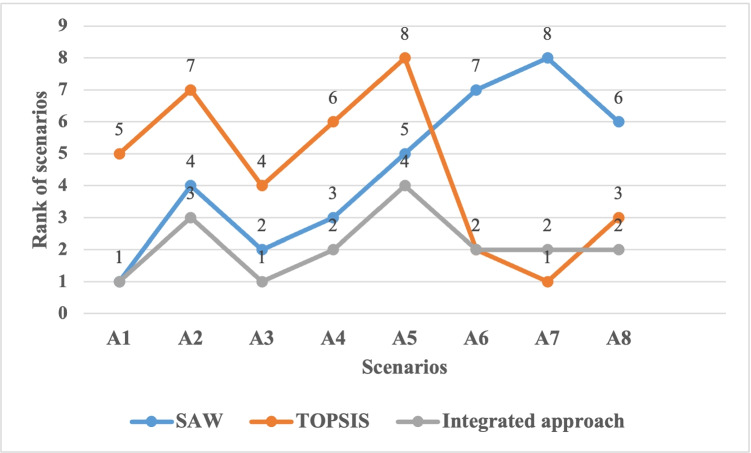
According to Table 13, Scenario A7 with a score equivalent to 0.5219 by arranging 1, 4, and 2 was identified as the best scenario in determining the optimal number of suppliers. In other words, according to experts’ opinions and outputs of the TOPSIS technique, selecting 1 supplier for PDC1, 4 suppliers for PDC2, and 2 suppliers for PDC3 is the best possible status. As it is clear, there are many differences between the final rank of scenarios obtained from SAW and TOPSIS techniques. In such a situation, DMs get confused when they want to decide to choose the best number of suppliers. One of the proposed solutions to make a more reliable decision is to integrate the outputs of different techniques. In this study, the average of ranks obtained from SAW and TOPSIS was calculated to integrate the outputs of the two techniques. As shown in Table 15, based on integrating the outputs of the two mentioned techniques, scenario A3 by arranging 1, 2, and 1 (1 supplier for PDC1, 2 suppliers for PDC2, and 1 supplier for PDC3) is the best scenario, and scenario A1 by arranging 1, 1 and 1 is located in the second priority. Figure 3 represents the different ranks of each scenario based on SAW, TOPSIS, and integrated techniques.
Table 15.
Final ranking of scenarios
| Techniques Criteria | Integrated approach | |||
|---|---|---|---|---|
| A1 | 1 | 5 | 3 | 1 |
| A2 | 4 | 7 | 5.5 | 3 |
| A3 | 2 | 4 | 3 | 1 |
| A4 | 3 | 6 | 4.5 | 2 |
| A5 | 5 | 8 | 6.5 | 4 |
| A6 | 7 | 2 | 4.5 | 2 |
| A7 | 8 | 1 | 4.5 | 2 |
| A8 | 6 | 3 | 4.5 | 2 |
Fig. 3.
Ranking of scenarios based on SAW, TOPSIS, and integrated approach
Sensitivity analysis
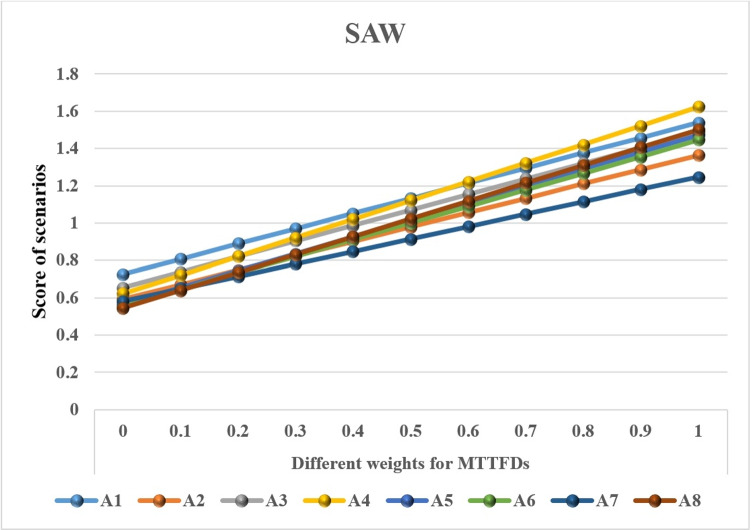
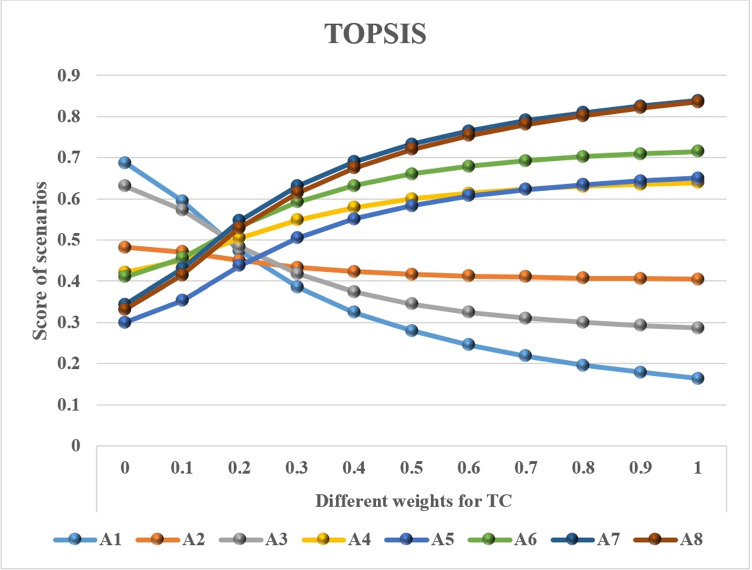
Another way to compare the reliability of the outputs of different techniques is to evaluate the robustness of each technique concerning changing the weights of the criteria. To evaluate the robustness of the final results of each technique a sensitivity analysis based on the three most important criteria is conducted. Figures 4 and 5 indicate the priority of the scenarios obtained from SAW and TOPSIS considering the changing weight of ability and willingness to meet the environmental standards; Figs. 6 and 7 indicate the priority of the scenarios obtained from SAW and TOPSIS considering the changing weight of MTTFDs, and Figs. 8 and 9 indicate the priority of the scenarios obtained from SAW and TOPSIS considering the changing weight of TC. As it is clear, the status of the scenario priorities given in Figs. 4, 6, and 8 are more stable than the status of the scenario priority given in Figs. 5, 7, and 9 with the increase in the weight of the three most important criteria from 0 to 1. Therefore, it can be argued that the outputs of the ranking of the scenarios by the SAW technique are more robust than the outputs of the ranking of the scenarios by the TOPSIS technique. According to Fig. 4, the scenarios priority is stable with the increase in weight of ability and willingness to meet the environmental standards from 0.1 to 1, and Scenario A1 is the best scenario. According to Fig. 6, the scenarios priority is stable with the increase in the weight of MTTFDs from 0.1 to 0.5, and Scenario A1 is still the best scenario. With increasing the weight of MTTFDs from 0.6 to 1, the priority of Scenario A1 is replaced with Scenario A4. It indicates that if the DMs of the Bandar Abbas oil refining company want to increase the weight of MTTFDs by more than 0.6, the best scenario is Scenario A4. Finally, according to Fig. 8, the scenarios priority is stable with the increase in the weight of TC from 0.1 to 1, and Scenario A1 is the best scenario.
Fig. 4.
Sensitivity analysis based on the ability and willingness to meet the environmental standards (SAW)
Fig. 5.
Sensitivity analysis based on the ability and willingness to meet the environmental standards (TOPSIS)
Fig. 6.
Sensitivity analysis based on the MTTFDs (SAW)
Fig. 7.
Sensitivity analysis based on the MTTFDs (TOPSIS)
Fig. 8.
Sensitivity analysis based on the TC (SAW)
Fig. 9.
Sensitivity analysis based on the TC (TOPSIS)
Discussion, theoretical and managerial implications
The originality of this paper lies in providing an MCDM and simulation hybrid approach to determine the optimal number of leagile-sustainable suppliers. To this end, first, an in-depth literature review is conducted and lean and agile criteria were identified. Then, using the BWM technique, the weights of lean and agile criteria were calculated according to the experts’ opinion of the oil industry. After that, eight scenarios for a number of suppliers were defined using the DOE technique. Finally, the rank of each scenario was determined using the SAW, TOPSIS, and integrated techniques. According to the sensitivity analysis, the results obtained from SAW technique are more robust than the results obtained from TOPSIS technique. Scenario ranking results obtained from SAW technique indicated that the first scenario with a 1-1-1 arrangement (one supplier for each type of PDC drill) is the best possible scenario to determine the optimal number of leagile-sustainable suppliers.
As mentioned in Section 2, Bakos and Brynjolfsson (1993) revealed that although information technology reduces coordination costs, it may lead companies to work with a limited number of suppliers. They focused on just two factors in determining the optimal number of suppliers including coordination costs and the need to provide incentives for quality by suppliers. Guo and Ganeshan (1995) investigated how the number of suppliers can change the mean and variance of the lead time. Nam et al. (2011) focused on flexibility and supply costs to find the optimal number of suppliers. Babich et al. (2012) just focused on economic criteria to determine the optimal number of suppliers. As can be seen, different studies have focused on the different and limited number of factors in determining the number of suppliers and have neglected many other criteria that can affect the optimal number of suppliers. In the present study, we provide a comprehensive list of 20 criteria including the lean, agile, and environmental sustainability components that involve most of the used criteria in the previous studies. This study by linking and adopting the supplier evaluation criteria with the criteria used in determining the optimal number of suppliers provided a comprehensive list of criteria that may lead to more reliable results. Berger et al. (2004); Ruiz-Torres and Mahmoodi (2007); Nam et al. (2011); Babich et al. (2012); Kumar et al. (2018), and Bakos and Brynjolfsson (1993) have used different methods to find the optimal number of suppliers. Berger et al. (2004), and Ruiz-Torres and Mahmoodi (2007) used the decision tree method to determine the optimal number of suppliers considering the different scenarios developed based on events (super-events and unique events) which may influence all/many or one of the suppliers. Nam et al. (2011); Babich et al. (2012); Kumar et al. (2018), and Bakos and Brynjolfsson (1993) have used statistical-based approaches to find the optimal number of suppliers. In our research, a novel hybrid technique based on MCDM and simulation method was implemented to determine the optimal number of suppliers. In this study, simulation data and expert-driven data simultaneously were used to reach more reliable results. In this regard, after identifying the research criteria, we utilized the power of BWM technique to calculate the importance of the criteria based on data gathered from oil and gas industry experts. We used the data generated through the simulation to construct the decision matrix of evaluating scenarios based on criteria. Finally, SAW and TOPSIS techniques were employed to rank the different scenarios for a number of suppliers.
In todays’ competitive world, most companies do not perform all of the activities by themselves. They usually outsource non-strategic activities to the suppliers and take more attention to the strategic activities. One of the challenges that has received a great deal of attention from researchers and purchasing or supplier relationship managers is the optimal number of suppliers in order to increase the mean time to the first delay as well as reduce delays and interruptions. There are two different strategies about the number of suppliers based on lean and agile concepts. According to the lean paradigm establishing a few suppliers with the long-term contract and according to the agile paradigm establishing a large number of suppliers with the short-term contract is the best strategy. It is obvious that both strategies have advantages and disadvantages. Establishing many suppliers can increase the reliability of the company’s activities and maximize the mean time to the first delay, but it leads to more supply costs. In contrast, establishing a few suppliers can reduce supply costs, but it may cause more interruptions in the company’s activities. Therefore, purchasing managers are dealing with a great challenge about the optimal number of suppliers to satisfy the reliability of the company’s activities and supply costs.
Aside from the theoretical contribution, this research resolves the existing conflict in the research literature about large or a few suppliers by proposing a hybrid technique based on MCDM and simulation methods to determine the optimal number of leagile-sustainable suppliers. The suggested methodology can help to purchase managers to find the optimal number of suppliers by creating a trade-off between lean, agile, and environmental criteria through the following steps:
Identify lean, agile, and environmental criteria and specialize them according to the company’s activities;
Calculate the weights of lean, agile, and environmental criteria using the BWM technique;
Define some scenarios for a number of suppliers using DOE technique;
Simulate and repeat each of the scenarios to calculate MTTF, Var(MTTF), and total costs of implementing each scenario;
Construct the decision matrix indicating criteria in rows and scenarios in columns;
Rank the scenarios using the SAW and TOPSIS techniques and determine the optimal number of suppliers
Examine the robustness of the final results using a sensitivity analysis based on the three most important criteria
Conclusion, limitations and future directions
To gain a competitive advantage and survive in today’s ever-changing markets, companies focus solely on their strategic activities and outsource their other activities. Suppliers are companies that specialize in performing a specific activity or preparing a specific type of material or equipment and can enhance the company’s competitive advantage. Lean, agile, and environmentally friendly suppliers who can provide high-quality products to the company in the shortest possible time and at the lowest cost can lead the companies to achieve sustainable development. On the one hand, more suppliers lead to fewer interruptions in the company’s activities. On the other hand, increasing the number of suppliers will increase the cost of supply. Therefore, determining the optimal number of suppliers so that the average time to the first delay is maximized as well as the total costs are minimized is one of the challenges for managers to reach sustainable development.
Despite addressing the main aim of the study and developing an effective hybrid approach, there are some limitations. For example, due to the lack of opportunity to reach real data for calculating MTTF, the needed data were generated through the simulation. Accordingly, the MTTF can be calculated based on real historical data to determine the optimal number of suppliers in future research. In this study, the crisp version of BWM, SAW, and TOPSIS techniques have been employed. Due to existing vagueness and uncertainty in DMs’ judgments, future studies can use the fuzzy version of mentioned techniques to increase the validity and reliability of the results. In this research, data were collected from an oil company, and may not be possible to generalize the results of this study to other industries. Future studies can use the proposed methodology to find the optimal number of suppliers in different industries, to increase the generalization of the proposed methodology. Also, it suggests extending the proposed methodology to the project management scope and applying it to determine the optimal number of contractors/sub-contractors. Since all of the model parameters and data were assumed to be deterministic, fuzzy programming or robust optimization approach can be employed to calculate the optimal number of suppliers under uncertain conditions. As mentioned earlier, there is no standard to determine the best MCDM method; thus, employing the other MCDM methods such as VIKOR and preference ranking organization method for enrichment evaluation (PROMETHEE) can be also taken into account to rank the scenarios and be compared with the current results.
Acknowledgements
The research was partially supported by the Faculty of Informatics and Management UHK specific research project 2107 Integration of Departmental Research Activities and Students’ Research Activities Support II. We’d also like to thank S. Krizkova, a student, for the topic contributing.
Author contributions
S.S. and F.M.M.: conceptualization, methodology, project administration, writing—original draft, investigation; F.M.M. and H.R.V.: formal analysis, software; H.R.V. and E.B.T.: writing—review and editing, validation; H.T.: investigation, visualization, validation; E.B.T. and H.T.: data curation, supervision, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Data availability
Not applicable
Code availability
Not applicable
Declarations
Ethics approval
Not applicable
Consent to participate
Not applicable
Consent for publication
Not applicable
Conflict of interest
The authors declare no competing interests.
Contributor Information
Saeid Sadeghi Darvazeh, Email: sadeghi.management@gmail.com.
Farzaneh Mansoori Mooseloo, Email: farzanmansoori7@gmail.com.
Hadi Rezaei Vandchali, Email: hadi.rezaei@utas.edu.au.
Hana Tomaskova, Email: hana.tomaskova@uhk.cz.
Erfan Babaee Tirkolaee, Email: erfan.babaee@istinye.edu.tr.
References
- Abdollahi M, Arvan M, Razmi J. An integrated approach for supplier portfolio selection: lean or agile? Expert Syst Appl. 2015;42(1):679–690. doi: 10.1016/j.eswa.2014.08.019. [DOI] [Google Scholar]
- Agarwal A, Shankar R, Tiwari M. Modeling the metrics of lean, agile and leagile supply chain: An ANP-based approach. Eur J Oper Res. 2006;173(1):211–225. doi: 10.1016/j.ejor.2004.12.005. [DOI] [Google Scholar]
- Al-Omoush KS, Simón-Moya V, Sendra-García J. The impact of social capital and collaborative knowledge creation on e-business proactiveness and organizational agility in responding to the COVID-19 crisis. Journal of Innovation & Knowledge. 2020;5(4):279–288. doi: 10.1016/j.jik.2020.10.002. [DOI] [Google Scholar]
- Alimardani M, Hashemkhani Zolfani S, Aghdaie MH, Tamošaitienė J. A novel hybrid SWARA and VIKOR methodology for supplier selection in an agile environment. Technol Econ Dev Econ. 2013;19(3):533–548. doi: 10.3846/20294913.2013.814606. [DOI] [Google Scholar]
- Amin SH, Razmi J, Zhang G. Supplier selection and order allocation based on fuzzy swot analysis and fuzzy linear programming. Expert Syst Appl. 2011;38(1):334–342. doi: 10.1016/j.eswa.2010.06.071. [DOI] [Google Scholar]
- Antony J, Sreedharan R, Chakraborty A, Gunasekaran A et al (2019) A systematic review of lean in healthcare: a global prospective. Int J Qual Reliab Manag
- Arabsheybani A, Paydar MM, Safaei AS. An integrated fuzzy MOORA method and FMEA technique for sustainable supplier selection considering quantity discounts and supplier’s risk. J Clean Prod. 2018;190:577–591. doi: 10.1016/j.jclepro.2018.04.167. [DOI] [Google Scholar]
- Aral S, Bakos Y, Brynjolfsson E. Information technology, repeated contracts, and the number of suppliers. Manage Sci. 2018;64(2):592–612. doi: 10.1287/mnsc.2016.2631. [DOI] [Google Scholar]
- Babich V, Aydın G, Brunet PY, Keppo J, Saigal R (2012) Risk, financing and the optimal number of suppliers. In: Supply chain disruptions. Springer, pp 195–240
- Bai C, Rezaei J, Sarkis J. Multicriteria green supplier segmentation. IEEE Trans Eng Manage. 2017;64(4):515–528. doi: 10.1109/TEM.2017.2723639. [DOI] [Google Scholar]
- Bakos JY, Brynjolfsson E (1993) Why information technology hasn’t increased the optimal number of suppliers. In: [1993] Proceedings of the Twenty-sixth Hawaii International Conference on System Sciences, IEEE, pp 799–808
- Barla SB (2003) A case study of supplier selection for lean supply by using a mathematical model. Log Inf Manag
- Berger PD, Gerstenfeld A, Zeng AZ. How many suppliers are best? a decision-analysis approach. Omega. 2004;32(1):9–15. doi: 10.1016/j.omega.2003.09.001. [DOI] [Google Scholar]
- Büyüközkan G, Çifçi G. A novel fuzzy multi-criteria decision framework for sustainable supplier selection with incomplete information. Comput Ind. 2011;62(2):164–174. doi: 10.1016/j.compind.2010.10.009. [DOI] [Google Scholar]
- Çalık A. A novel Pythagorean fuzzy AHP and fuzzy TOPSIS methodology for green supplier selection in the industry 4.0 era. Soft Comput. 2021;25(3):2253–2265. doi: 10.1007/s00500-020-05294-9. [DOI] [Google Scholar]
- Carbone J. Delphi demands lowest total cost from suppliers. Purchasing. 2003;132(14):15–17. [Google Scholar]
- Carlson JG, Yao AC. Simulating an agile, synchronized manufacturing system. Int J Prod Econ. 2008;112(2):714–722. doi: 10.1016/j.ijpe.2007.06.008. [DOI] [Google Scholar]
- Chai J, Liu JN, Ngai EW. Application of decision-making techniques in supplier selection: A systematic review of literature. Expert Syst Appl. 2013;40(10):3872–3885. doi: 10.1016/j.eswa.2012.12.040. [DOI] [Google Scholar]
- Chang B, Chang CW, Wu CH. Fuzzy dematel method for developing supplier selection criteria. Expert Syst Appl. 2011;38(3):1850–1858. doi: 10.1016/j.eswa.2010.07.114. [DOI] [Google Scholar]
- Chang HH, Tsai SH, Huang CC. Sustainable development: The effects of environmental policy disclosure in advertising. Bus Strateg Environ. 2019;28(8):1497–1506. doi: 10.1002/bse.2325. [DOI] [Google Scholar]
- Checkland P, Poulter J. Learning for action: a short definitive account of soft systems methodology and its use for practitioner, teachers, and students. Chichester: Wiley; 2006. [Google Scholar]
- Chen YJ. Structured methodology for supplier selection and evaluation in a supply chain. Inf Sci. 2011;181(9):1651–1670. doi: 10.1016/j.ins.2010.07.026. [DOI] [Google Scholar]
- Choi TY, Hartley JL. An exploration of supplier selection practices across the supply chain. J Oper Manag. 1996;14(4):333–343. doi: 10.1016/S0272-6963(96)00091-5. [DOI] [Google Scholar]
- Choy KL, Lee WB, Lo V. Design of a case based intelligent supplier relationship management system-the integration of supplier rating system and product coding system. Expert Syst Appl. 2003;25(1):87–100. doi: 10.1016/S0957-4174(03)00009-5. [DOI] [Google Scholar]
- Christopher M. The agile supply chain: competing in volatile markets. Ind Mark Manage. 2000;29(1):37–44. doi: 10.1016/S0019-8501(99)00110-8. [DOI] [Google Scholar]
- Ciccullo F, Pero M, Caridi M, Gosling J, Purvis L. Integrating the environmental and social sustainability pillars into the lean and agile supply chain management paradigms: A literature review and future research directions. J Clean Prod. 2018;172:2336–2350. doi: 10.1016/j.jclepro.2017.11.176. [DOI] [Google Scholar]
- Croom SR. The dyadic capabilities concept: examining the processes of key supplier involvement in collaborative product development. European Journal of Purchasing & Supply Management. 2001;7(1):29–37. doi: 10.1016/S0969-7012(00)00019-8. [DOI] [Google Scholar]
- Dickson GW. An analysis of vendor selection systems and decisions. Journal of purchasing. 1966;2(1):5–17. doi: 10.1111/j.1745-493X.1966.tb00818.x. [DOI] [Google Scholar]
- Dulmin R, Mininno V. Supplier selection using a multi-criteria decision aid method. J Purch Supply Manag. 2003;9(4):177–187. doi: 10.1016/S1478-4092(03)00032-3. [DOI] [Google Scholar]
- Ecer F, Pamucar D. Sustainable supplier selection: A novel integrated fuzzy best worst method (F-BWM) and fuzzy CoCoSo with Bonferroni (CoCoSo’B) multi-criteria model. J Clean Prod. 2020;266(121):981. [Google Scholar]
- El Mokadem M (2017) The classification of supplier selection criteria with respect to lean or agile manufacturing strategies. Journal of Manufacturing Technology Management
- Eltawy N, Gallear D (2017) Leanness and agility: a comparative theoretical view. Ind Manag Data Syst
- Freddi A, Salmon M. Design principles and methodologies. Cham: Springer; 2019. Introduction to the Taguchi method; pp. 159–180. [Google Scholar]
- Fu X, Zhu Q, Sarkis J. Evaluating green supplier development programs at a telecommunications systems provider. Int J Prod Econ. 2012;140(1):357–367. doi: 10.1016/j.ijpe.2011.08.030. [DOI] [Google Scholar]
- Gaziulusoy AI. A critical review of approaches available for design and innovation teams through the perspective of sustainability science and system innovation theories. J Clean Prod. 2015;107:366–377. doi: 10.1016/j.jclepro.2015.01.012. [DOI] [Google Scholar]
- Ghodsypour SH, O’brien C. The total cost of logistics in supplier selection, under conditions of multiple sourcing, multiple criteria and capacity constraint. Int J Prod Econ. 2001;73(1):15–27. doi: 10.1016/S0925-5273(01)00093-7. [DOI] [Google Scholar]
- Ginevičius R, Ginevičiene VB. The compliance of master’s degree studies with the economic needs of the country. Technol Econ Dev Econ. 2009;15(1):136–153. doi: 10.3846/1392-8619.2009.15.136-153. [DOI] [Google Scholar]
- Ginevičius R, Podvezko V, Raslanas S. Evaluating the alternative solutions of wall insulation by multicriteria methods. J Civ Eng Manag. 2008;14(4):217–226. doi: 10.3846/1392-3730.2008.14.20. [DOI] [Google Scholar]
- Govindan K, Khodaverdi R, Jafarian A. A fuzzy multi criteria approach for measuring sustainability performance of a supplier based on triple bottom line approach. J Clean Prod. 2013;47:345–354. doi: 10.1016/j.jclepro.2012.04.014. [DOI] [Google Scholar]
- Govindan K, Rajendran S, Sarkis J, Murugesan P. Multi criteria decision making approaches for green supplier evaluation and selection: a literature review. J Clean Prod. 2015;98:66–83. doi: 10.1016/j.jclepro.2013.06.046. [DOI] [Google Scholar]
- Grimm JH, Hofstetter JS, Sarkis J. Critical factors for sub-supplier management: A sustainable food supply chains perspective. Int J Prod Econ. 2014;152:159–173. doi: 10.1016/j.ijpe.2013.12.011. [DOI] [Google Scholar]
- Guo X, Yuan Z, Tian B. Supplier selection based on hierarchical potential support vector machine. Expert Syst Appl. 2009;36(3):6978–6985. doi: 10.1016/j.eswa.2008.08.074. [DOI] [Google Scholar]
- Guo Y, Ganeshan R (1995) Are more suppliers better? J Oper Res Soc 892–895
- Hajji A, Gharbi A, Kenne JP, Pellerin R. Production control and replenishment strategy with multiple suppliers. Eur J Oper Res. 2011;208(1):67–74. doi: 10.1016/j.ejor.2010.08.010. [DOI] [Google Scholar]
- Hanafizadeh P, Zadeh RV. Vendor selection using soft thinking approach: A case study of National Iranian South Oil Company. Systemic Practice and Action Research. 2015;28(4):355–381. doi: 10.1007/s11213-014-9334-z. [DOI] [Google Scholar]
- Haseli G, Sheikh R, Wang J, Tomaskova H, Tirkolaee EB. A novel approach for group decision making based on the best-worst method (G-bwm): application to supply chain management. Mathematics. 2021;9(16):1881. doi: 10.3390/math9161881. [DOI] [Google Scholar]
- Heydari J, Govindan K, Basiri Z. Balancing price and green quality in presence of consumer environmental awareness: a green supply chain coordination approach. Int J Prod Res. 2021;59(7):1957–1975. doi: 10.1080/00207543.2020.1771457. [DOI] [Google Scholar]
- Heyer R (2014) Understanding soft operations research: The methods, their application and its future in the defence setting. command and control division information science laboratory, defence science and technology organization, Australian government, Edinburg, Australia. Tech. rep., Report No. DSTO-GD-0411. http://dspace.dsto.defence.gov.au/dspace/handle, Edinburg, Australia
- Hsu CW, Hu AH. Applying hazardous substance management to supplier selection using analytic network process. J Clean Prod. 2009;17(2):255–264. doi: 10.1016/j.jclepro.2008.05.004. [DOI] [Google Scholar]
- Huang SH, Keskar H. Comprehensive and configurable metrics for supplier selection. Int J Prod Econ. 2007;105(2):510–523. doi: 10.1016/j.ijpe.2006.04.020. [DOI] [Google Scholar]
- Hwang CL, Yoon K. Multiple attribute decision making. Cham: Springer; 1981. Methods for multiple attribute decision making; pp. 58–191. [Google Scholar]
- Jain N, Singh A. Sustainable supplier selection under must-be criteria through fuzzy inference system. J Clean Prod. 2020;248(119):275. [Google Scholar]
- Jakimavičius M, Burinskiene M. A GIS and multi-criteria-based analysis and ranking of transportation zones of Vilnius city. Technol Econ Dev Econ. 2009;15(1):39–48. doi: 10.3846/1392-8619.2009.15.39-48. [DOI] [Google Scholar]
- Kahraman C, Cebeci U, Ulukan Z (2003) Multi-criteria supplier selection using fuzzy AHP. Logist Inf Manag
- Katsikeas CS, Paparoidamis NG, Katsikea E. Supply source selection criteria: The impact of supplier performance on distributor performance. Ind Mark Manage. 2004;33(8):755–764. doi: 10.1016/j.indmarman.2004.01.002. [DOI] [Google Scholar]
- Kizielewicz B, Wieckowski J, Shekhovtsov A, Watróbski J, Depczyński R, Sałabun W. Study towards the time-based MCDA ranking analysis-a supplier selection case study. Mechanical Engineering: Facta Universitatis, Series; 2021. [Google Scholar]
- Krause DR, Handfield RB, Tyler BB. The relationships between supplier development, commitment, social capital accumulation and performance improvement. J Oper Manag. 2007;25(2):528–545. doi: 10.1016/j.jom.2006.05.007. [DOI] [Google Scholar]
- Krishnamurthy R, Yauch CA (2007) Leagile manufacturing: a proposed corporate infrastructure. Int J Oper Prod Manag
- Krishnan V, Ulrich KT. Product development decisions: A review of the literature. Manage Sci. 2001;47(1):1–21. doi: 10.1287/mnsc.47.1.1.10668. [DOI] [Google Scholar]
- Kumar R, Padhi SS, Sarkar A. Optimal number of suppliers to mitigate supply disruption: a case of Indian locomotive manufacturer. International Journal of Logistics Systems and Management. 2018;31(1):132–149. [Google Scholar]
- Kuo RJ, Wang YC, Tien FC. Integration of artificial neural network and MADA methods for green supplier selection. J Clean Prod. 2010;18(12):1161–1170. doi: 10.1016/j.jclepro.2010.03.020. [DOI] [Google Scholar]
- Luo X, Wu C, Rosenberg D, Barnes D. Supplier selection in agile supply chains: An information-processing model and an illustration. J Purch Supply Manag. 2009;15(4):249–262. doi: 10.1016/j.pursup.2009.05.004. [DOI] [Google Scholar]
- Luthra S, Govindan K, Kannan D, Mangla SK, Garg CP. An integrated framework for sustainable supplier selection and evaluation in supply chains. J Clean Prod. 2017;140:1686–1698. doi: 10.1016/j.jclepro.2016.09.078. [DOI] [Google Scholar]
- Luzzini D, Ronchi S. Organizing the purchasing department for innovation. Oper Manag Res. 2011;4(1):14–27. doi: 10.1007/s12063-010-0042-2. [DOI] [Google Scholar]
- Mettas A (2000) Reliability allocation and optimization for complex systems. In: Annual Reliability and Maintainability Symposium. 2000 Proceedings. International Symposium on Product Quality and Integrity (Cat. No. 00CH37055). pp 216–221
- Mohammed A, Harris I, Govindan K. A hybrid MCDM-FMOO approach for sustainable supplier selection and order allocation. Int J Prod Econ. 2019;217:171–184. doi: 10.1016/j.ijpe.2019.02.003. [DOI] [Google Scholar]
- Munro I, Mingers J. The use of multimethodology in practice-results of a survey of practitioners. J Oper Res Soc. 2002;53(4):369–378. doi: 10.1057/palgrave.jors.2601331. [DOI] [Google Scholar]
- Nam SH, Vitton J, Kurata H. Robust supply base management: Determining the optimal number of suppliers utilized by contractors. Int J Prod Econ. 2011;134(2):333–343. doi: 10.1016/j.ijpe.2009.11.010. [DOI] [Google Scholar]
- Nawanir G, Lim KT, Lee KL, Moshood TD, Ahmad ANA, et al. Less for more: the structural effects of lean manufacturing practices on sustainability of manufacturing SMES in Malaysia. International Journal of Supply Chain Management. 2020;2(2):961–975. [Google Scholar]
- Nayak R, Nguyen LT, Panwar T, Ulhaq I, George M (2020) Standards, organizations and lean concept in managing sustainable fashion supply chains. Supply Chain Management and Logistics in the Global Fashion Sector 183–215
- Nguyen PH, Tsai JF, Dang TT, Lin MH, Pham HA, Nguyen KA. A hybrid spherical fuzzy MCDM approach to prioritize governmental intervention strategies against the COVID-19 pandemic: A case study from Vietnam. Mathematics. 2021;9(20):2626. doi: 10.3390/math9202626. [DOI] [Google Scholar]
- Nguyen PH, Tsai JF, Lin MH, Hu YC (2021) A hybrid model with spherical Fuzzy-AHP, PLS-SEM and ANN to predict vaccination intention against COVID-19. Math 9(23):3075
- Parkouhi SV, Ghadikolaei AS, Lajimi HF. Resilient supplier selection and segmentation in Grey environment. J Clean Prod. 2019;207:1123–1137. doi: 10.1016/j.jclepro.2018.10.007. [DOI] [Google Scholar]
- Podvezko V. The comparative analysis of MCDA methods SAW and COPRAS. Eng Econ. 2011;22(2):134–146. doi: 10.5755/j01.ee.22.2.310. [DOI] [Google Scholar]
- Punniyamoorthy M, Mathiyalagan P, Parthiban P. A strategic model using structural equation modeling and fuzzy logic in supplier selection. Expert Syst Appl. 2011;38(1):458–474. doi: 10.1016/j.eswa.2010.06.086. [DOI] [Google Scholar]
- Rezaei J. Best-worst multi-criteria decision-making method. Omega. 2015;53:49–57. doi: 10.1016/j.omega.2014.11.009. [DOI] [Google Scholar]
- Rezaei J. Best-worst multi-criteria decision-making method: Some properties and a linear model. Omega. 2016;64:126–130. doi: 10.1016/j.omega.2015.12.001. [DOI] [Google Scholar]
- Rezaei J, Ortt R. A multi-variable approach to supplier segmentation. Int J Prod Res. 2012;50(16):4593–4611. doi: 10.1080/00207543.2011.615352. [DOI] [Google Scholar]
- Ruiz-Torres AJ, Mahmoodi F. The optimal number of suppliers considering the costs of individual supplier failures. Omega. 2007;35(1):104–115. doi: 10.1016/j.omega.2005.04.005. [DOI] [Google Scholar]
- Sarkar A, Mohapatra PK. Evaluation of supplier capability and performance: A method for supply base reduction. J Purch Supply Manag. 2006;12(3):148–163. doi: 10.1016/j.pursup.2006.08.003. [DOI] [Google Scholar]
- Segura M, Maroto C, Segura B, et al. (2020) Improving food supply chain management by a sustainable approach to supplier evaluation. Mathematics 8(11):1952
- Sen DK, Datta S, Mahapatra S (2018) Sustainable supplier selection in intuitionistic fuzzy environment: a decision-making perspective. Int J
- Setak M, Sharifi S, Alimohammadian A. Supplier selection and order allocation models in supply chain management: a review. World Appl Sci J. 2012;18(1):55–72. [Google Scholar]
- Sharma V, Raut RD, Mangla SK, Narkhede BE, Luthra S, Gokhale R. A systematic literature review to integrate lean, agile, resilient, green and sustainable paradigms in the supply chain management. Bus Strateg Environ. 2021;30(2):1191–1212. doi: 10.1002/bse.2679. [DOI] [Google Scholar]
- Singh AK, Vinodh S (2017) Modeling and performance evaluation of agility coupled with sustainability for business planning. J Manag Dev
- Takeishi A. Bridging inter-and intra-firm boundaries: management of supplier involvement in automobile product development. Strateg Manag J. 2001;22(5):403–433. doi: 10.1002/smj.164. [DOI] [Google Scholar]
- Tan T, Alp O. Optimal sourcing from alternative capacitated suppliers with general cost structures. Omega. 2016;58:26–32. doi: 10.1016/j.omega.2015.03.011. [DOI] [Google Scholar]
- Tirkolaee EB, Dashtian Z, Weber GW, Tomaskova H, Soltani M, Mousavi NS. An integrated decision-making approach for green supplier selection in an agri-food supply chain: threshold of robustness worthiness. Mathematics. 2021;9(11):1304. doi: 10.3390/math9111304. [DOI] [Google Scholar]
- Tsai JF, Wang CP, Lin MH, Huang SW. Analysis of key factors for supplier selection in Taiwan’s thin-film transistor liquid-crystal displays industry. Mathematics. 2021;9(4):396. doi: 10.3390/math9040396. [DOI] [Google Scholar]
- Vandchali HR, Cahoon S, Chen SL (2021) The impact of power on the depth of sustainability collaboration in the supply chain network for Australian food retailers. Int J Proj Manag 14(2):165–184
- Vandchali HR, Cahoon S, Chen SL (2021b) The impact of supply chain network structure on relationship management strategies: An empirical investigation of sustainability practices in retailers. Sustain Prod Consump 28:281–299
- Vinodh S, Ramiya RA, Gautham S. Application of fuzzy analytic network process for supplier selection in a manufacturing organisation. Expert Syst Appl. 2011;38(1):272–280. doi: 10.1016/j.eswa.2010.06.057. [DOI] [Google Scholar]
- Vörösmarty G, Dobos I. A literature review of sustainable supplier evaluation with data envelopment analysis. J Clean Prod. 2020;264(121):672. [Google Scholar]
- Wanasida AS, Bernarto I, Sudibjo N, Purwanto A. The role of business capabilities in supporting organization agility and performance during the COVID-19 pandemic: An empirical study in Indonesia. The Journal of Asian Finance, Economics and Business. 2021;8(5):897–911. [Google Scholar]
- Wang CN, Nguyen VT, Thai HTN, Tran NN, Tran TLA, et al. Sustainable supplier selection process in edible oil production by a hybrid fuzzy analytical hierarchy process and green data envelopment analysis for the SMES food processing industry. Mathematics. 2018;6(12):302. doi: 10.3390/math6120302. [DOI] [Google Scholar]
- Watróbski J, Sałabun W, Ladorucki G (2017) The temporal supplier evaluation model based on multicriteria decision analysis methods. In: Asian Conference on Intelligent Information and Database Systems, Springer, pp 432–442
- Weber CA, Current JR, Benton W. Vendor selection criteria and methods. Eur J Oper Res. 1991;50(1):2–18. doi: 10.1016/0377-2217(91)90033-R. [DOI] [Google Scholar]
- Wilson B (2001) Soft systems methodology conceptual model building and its contribution, 2001. Tech. rep., Wiley, 111 River Street Hoboken, NJ 07030 USA
- Wisner JD, Tan KC. Supply chain management and its impact on purchasing. J Supply Chain Manag. 2000;36(3):33–42. doi: 10.1111/j.1745-493X.2000.tb00084.x. [DOI] [Google Scholar]
- Xia W, Wu Z. Supplier selection with multiple criteria in volume discount environments. Omega. 2007;35(5):494–504. doi: 10.1016/j.omega.2005.09.002. [DOI] [Google Scholar]
- Yalaoui A, Chu C, Chatelet E. Reliability allocation problem in a series-parallel system. Reliability engineering & system safety. 2005;90(1):55–61. doi: 10.1016/j.ress.2004.10.007. [DOI] [Google Scholar]
- Yauch CA. Team-based work and work system balance in the context of agile manufacturing. Appl Ergon. 2007;38(1):19–27. doi: 10.1016/j.apergo.2006.02.002. [DOI] [PubMed] [Google Scholar]
- Yu C, Shao Y, Wang K, Zhang L. A group decision making sustainable supplier selection approach using extended TOPSIS under interval-valued Pythagorean fuzzy environment. Exp Syst Appl. 2019;121:1–17. doi: 10.1016/j.eswa.2018.12.010. [DOI] [Google Scholar]
- Zavadskas EK, Turskis Z, Dejus T, Viteikiene M. Sensitivity analysis of a simple additive weight method. Int J Manag Decis Mak. 2007;8(5–6):555–574. [Google Scholar]
- Zhang C, Viswanathan S, Henke JW., Jr The boundary spanning capabilities of purchasing agents in buyer-supplier trust development. J Oper Manag. 2011;29(4):318–328. doi: 10.1016/j.jom.2010.07.001. [DOI] [Google Scholar]
- Zhang Q, Irfan M, Khattak MAO, Abbas J, Zhu X, Shah MS. Critical success factors for successful lean six sigma implementation in Pakistan. Interdiscip J Contemp Res Bus. 2012;4(1):117–124. [Google Scholar]
- Zhou X, Xu Z. An integrated sustainable supplier selection approach based on hybrid information aggregation. Sustainability. 2018;10(7):2543. doi: 10.3390/su10072543. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Not applicable
Not applicable