Designing an integrated responsive-green-cold vaccine supply chain network using Internet-of-Things: artificial intelligence-based solutions

Abstract

In this paper, a new responsive-green-cold vaccine supply chain network during the COVID-19 pandemic is developed for the first time. According to the proposed network, a new multi-objective, multi-period, multi-echelon mathematical model for the distribution-allocation-location problem is designed. Another important novelty in this paper is that it considers an Internet-of-Things application in the COVID-19 condition in the suggested model to enhance the accuracy, speed, and justice of vaccine injection with existing priorities. Waste management, environmental effects, coverage demand, and delivery time of COVID-19 vaccine simultaneously are therefore considered for the first time. The LP-metric method and meta-heuristic algorithms called Gray Wolf Optimization (GWO), and Variable Neighborhood Search (VNS) algorithms are then used to solve the developed model. The other significant contribution, based on two presented meta-heuristic algorithms, is a new heuristic method called modified GWO (MGWO), and is developed for the first time to solve the model. Therefore, a set of test problems in different sizes is provided. Hence, to evaluate the proposed algorithms, assessment metrics including (1) percentage of domination, (2) the number of Pareto solutions, (3) data envelopment analysis, and (4) diversification metrics and the performance of the convergence are considered. Moreover, the Taguchi method is used to tune the algorithm’s parameters. Accordingly, to illustrate the efficiency of the model developed, a real case study in Iran is suggested. Finally, the results of this research show MGO offers higher quality and better performance than other proposed algorithms based on assessment metrics, computational time, and convergence.

Introduction

COVID-19 is an unprecedented respiratory disease discovered on December 31, 2019, in Wuhan (Sohrabi et al., 2020). COVID-19 is caused by the severe acute respiratory syndrome coronavirus 2 (SARSCoV2). SARS-CoV-2 is transmitted rapidly, mainly through close contact between people and through small droplets produced when sneezing and coughing (Chen, Xiong, et al., 2020). However, in some cases the patient’s symptoms may be exacerbated by pneumonia and acute respiratory distress syndrome (ARDS) (Chen, Zhou, et al., 2020). Epidemic mortality rates range from 1.2 to 3.7 percent worldwide (Baud et al., 2020; Carvalho et al., 2021) depending upon the COVID-19 variant. The number of infected and recovered people and the number of deaths are reported in Table 1. To date, no effective medicine for treating COVID-19 has been conclusively discovered. However, new vaccines have been developed that effectively increase population protection and reduce virus transmission (Lipsitch & Dean, 2020).

Table 1.

The number of infected and recovered cases with total death (7/20/2021) (https://www.worldometers.info/coronavirus/)

Countries	Total confirmed cases	Total deaths	Total recovered
USA	35,018,600	624,983	29,406,202
India	31,174,322	414,513	30,353,710
Brazil	19,391,845	542,877	18,067,080
France	5,871,881	111,492	5,661,352
Turkey	5,537,386	50,604	5,390,739
Iran	3,576,148	87,624	3,168,834

From the beginning of the COVID-19 pandemic to the present day, harmful economic and social consequences have affected various communities. Most countries’ gross domestic product (GDP) declined in 2020, and many businesses closed, leaving a large number of people unemployed (Wang & Su, 2020). Moreover, increasing consumption of plastic and medical products in hospitals and homes has resulted in a significant increase in the amount of plastic and infectious waste produced. Lack of proper management of health waste can cause irreparable damage to the environment and people’s lives (Klemes et al., 2020).

According to epidemiologists and the researchers’ results, the only way to definitively break the coronavirus chain is through general vaccination, and means such as global quarantine or the use of masks offer only temporary protection. Pfizer Pharmaceuticals succeeded in developing the first vaccine against COVID-19 and it was approved by the Food and Drug Administration (FDA). Since then, several other vaccines have been produced and are being used in various countries after obtaining a license. Modern vaccines include Oxford–AstraZeneca, Sputnik V, Janssen, Pfizer–BioNTech, Sinopharm, and Moderna. Unfortunately, a few rich countries have bought larger amounts of the available vaccine, which can cause significant problems in poorer and developing countries and create injustices. Figure 1 shows the rate of vaccinated people in some countries; the existing figures are related to people who have received at least one dose of the vaccine.

Fig. 1.

The total Number of people who received at least one dose of the vaccine to May 30, 2021

The vaccine supply chain entails four main issues, involving (1) How many vaccines do we need? (2) How many vaccines should we produce? (3) How should we allocate vaccines? and (4) How to distribute the vaccines? (Duijzer et al., 2018). The vaccine supply chain is one of the most essential and sensitive supply chains. This is because it usually has special conditions for holding and transporting through the cold chain. For example, the Pfizer COVID-19 vaccine must be held in a cold chain at − 70 °C and it lasts less than a few hours at ambient temperature. According to the World Health Organization, due to poor logistical conditions, approximately half of vaccine doses are wasted before use in some developing countries (Sadjadi et al., 2019). As a result, specific and complete equipment is needed to provide a supply chain that can meet the required demand without quality being compromised.

According to the IoT, sensors and actuators are connected to transmit data through an integrated framework to enable heuristic applications. In supply chain management, IoTs are used in the fields of logistics, manufacturing, quality control, inventory management, and real-time decision-making (Ben-Daya et al., 2019). In recent years, IoT-based technologies have been widely used in health-related fields because they play a pivotal role in monitoring patients, diagnosis, and disease prevention (Tekeste Habte et al., 2019). The application of the IoT in healthcare, advanced technology for detecting cases of infection, allocating ambulances to patients, monitoring the general condition of patients in hospitals, disinfecting infected places, informing people of important announcements, monitoring people in quarantine, and data collection from people for vaccination in the outbreak of COVID-19 are used. During the COVID-19 epidemic, robots, drones, smartphones with web applications, wearables, and thermal sensors, all enriched with artificial intelligence, could reduce the adverse effects of COVID-19 (Kumar, Kumar, et al., 2020; Kumar et al., 2020; Nasajpour et al., 2020).

Therefore, in this paper, a new Green-Cold Vaccine Supply Chain Network (GCVSCN) in the COVID-19 condition is set out. In this regard, based on the proposed network, a new multi-objective, multi-echelon, multi-period mathematical model for the distribution-allocation-location problem during the COVID-19 pandemic is designed for the first time. The IoT application in the GCVSCN model is thus used to enhance the justice of COVID-19 vaccine injection with existing priorities. Priorities are divided into seven groups, including (1) the elderly aged 65 + with their care workers, (2) all people aged 16 + with a severe medical problem, (3) all people aged 50 + , (4) all people aged between 16 and 50 whose job involves being in public and crowded places, (5) all people aged between 30 and 50, (6) all people aged between 16 and 30, and (7) all people aged under 16. In the model developed, waste management, environmental effects, demand coverage, and delivery time for transporting the COVID-19 vaccine are considered simultaneously. Moreover, the LP-metric method is used to solve the GCVSCN model for small-sized problems. Furthermore, meta-heuristic algorithms called GWO and VNS algorithms are suggested, and a new heuristic method called modified GWO (MGWO) algorithm is developed to find Pareto solutions and near-optimal solutions for the first time in this paper. Then, to tune and control the algorithm’s parameters, the Taguchi approach is used. And, to compare algorithms, the performance of the convergence and assessment metrics containing Percentage of Domination (POD), Number of Pareto Solutions (NPS), Data Envelopment Analysis (DEA), and Diversification Metric (DM) are used. Managerial insights related to the GCVSCN considering IoT in the COVID-19 epidemic are discussed. Finally, a real case study in Iran is suggested, and a set of sensitivity analyses are performed to validate the model set out.

The rest of the paper is organized as follows. In Sect. 2, the literature review, the gaps, and the contribution of this paper are investigated. Problem description and mathematical modeling are discussed in Sect. 3. The solution methods are explained in Sect. 4. The computational results, Taguchi method, assessment metrics, the convergence of the proposed meta-heuristic algorithms, case study, sensitivity analysis, and managerial insights are stated in Sect. 5. The conclusion and future work are discussed in the last section.

Literature review

In this section, the vaccine supply chain network, COVID-19’s effects on the supply chain, and waste management fields are examined. Also, the details of the examined papers are shown in Table 2. Moreover, the existing gaps and contributions are elaborated on the following.

Table 2.

The details of the literature review

Author/year	Model type	Coverage demand	Prioritization	Environmental effects	Time minimization	IoT	Product type	Waste management	Cold supply chain network	COVID-19 condition	Solution methodology	Case study
Govindan et al. (2016)	MILP	–	–	*	–	–	–	*	–	–	MOGA, MOPSO, Epsilon constraint	–
Sadjadi et al. (2019)	MILP	–	–	–	–	–	vaccine	*	–	–	Branch and cut	*
Saeidi-Mobarakeh et al. (2020)	MILP	–	*	–	–	–	–	*	–	–	Robust optimization method	*
Kargar et al. (2020)	MILP	–	–	–	–	–	–	*	–	*	Goal Programming	*
Yang et al. (2020)	MILP	–	–	–	–	–	vaccine	–	–	–	Disaggregation-and-merging algorithm	–
Lin et al. (2020)	LP	*	–	–	–	–	vaccine	–	*	–	Exact method	–
Yu et al. (2020)	MILP	–	–	–	–	–	–	*		*	Interactive fuzzy approach + GAMS	*
Wang et al. (2020)	–	–	–	–	–	–	–	*	–	–	–	–
Zambrano et al. (2020)	–	–	–	*	–	–	–	*	–	*	–	–
Neumeyer et al. (2020)	–	–	–	–	–	–	–	*	–	*	–	–
Klemes et al. (2020)	–	–	–	*	–	–	–	*	–	*	–	–
Tirkolaee et al. (2021)	MILP	–	–	–	*	–	–	*	–	*	Weighted goal programming	*
Babaee Tirkolaee & Aydın (2021)	MILP	–	–	*	–	–	–	*	–	*	Meta-goal programming approach	*
Goodarzian, Taleizadeh, et al. (2021)	MILP	*	–	–	–	–	medicine	–	–	*	ACO, FSA, VNS, FA	*
Sazvar et al. (2021)	MILP	–	–	*	–	–	pharmaceutical	*	–	–	Hybrid method, LP-metric	*
Nagurney (2021)	–	–	–	–	–	–	–	–	–	*	–	–
Singh et al. (2021)	Simulation	–	–	–	–	–	–	–	–	*	–	–
This paper	MINLP	*	*	*	*	*	Vaccine	*	*	*	LP-metric, VNS, GWO, Modified GWO	*

Govindan et al. (2016) presented a fuzzy multi-objective mathematical model for a sustainable reverse logistics network. Thus, they considered the management and recycling of medical syringe waste, which identifies the best technology for waste treatment. Eco-indicator 99 was also used to minimize pollution. They used the epsilon-constraint method, multi-objective genetic algorithm (MOGA), and multi-objective particle swarm optimization (MOPSO) to solve their model.

Torabi (2018) developed an option contract to prevent the required dose of vaccine. They designed a model with the aim of minimizing purchasing and social costs, which had two suppliers (main and backup). Also, the buyer had two choices: the original supplier, which was cheaper but less reliable, and the backup supplier, which was more expensive but much more reliable and responsive. Their proposed model was made using the SIR epidemic model. To solve their model, they presented a solution method combining optimal control theory, Stackelberg game, and nonlinear programming approaches. Ng et al. (2018) formulated a multi-criteria mathematical model to provide an optimal structure for vaccination planning, evaluation, and analysis. Reducing costs, increasing vaccination efficiency, and increasing social benefit indicators were the objectives of their proposed model. Finally, they concluded that an integrated vaccination strategy, in the form of mass, non-discriminatory general vaccination, and targeted vaccination is better than other strategies.

Sadjadi et al. (2019) set out a robust network for vaccine supply chain management. A model for determining supply chain strategies and tactical decisions was presented according to the priority of demand and the perishability of vaccines. They used the robust counterpart model to deal with the uncertainty of the parameters. Eventually, using a real case study, they examined both the deterministic model and the robust model and concluded that the robust model was more efficient.

Saeidi-Mobarakeh et al. (2020) developed a bi-level MILP model considering waste management. A multi-part solution methodology combining the robust optimization method and a feasibility repairing mechanism was then used to solve their model. Finally, a real case study was considered with a real-life hazardous medical waste management scenario. A vaccine supply chain network consisting of a distributor and a retailer was therefore designed by Lin et al. (2020). The distributor had the right to use the cold or non-cold transmission chain. Then, the retailer can inspect them in two common ways (single-stage and two-stage) when receiving vaccines. Finally, after examining both methods, they concluded that single-stage inspection is more effective than two-stage inspection. Zambrano et al. (2020) examined the indirect effects of the COVID-19 virus on the environment. They summarized their studies on the effects of the COVID-19 virus in six cases, divided into three positive and three adverse effects. Increased organic and inorganic waste, disruption of the waste recycling cycle, and some specific adverse effects, such as contamination of sewage systems due to the use of disinfectants to prevent the spread of the COVID-19 virus in some countries, such as China, were among the negative effects of the coronavirus. They also claimed that COVID-19 caused a reduction in air pollution and the emission of gases such as nitrogen dioxide, besides helping to clean up beaches and reduce harmful noise in the environment. However, they eventually concluded that some of the positive effects of the COVID-19 virus do not appear to be lasting and that serious and intelligent management will be required to deal with its negative effects in the long term. Kargar et al. (2020) considered all the producers of medical waste, and their main goal was to minimize the maximum amount of collected waste from these centers. Due to the unknown behavior of the coronavirus, fuzzy programming was used to uncertain the demand parameters. Then, Wang et al. (2020) categorized the types of medical waste and proposed the most appropriate technology for each category. Yu et al. (2020) considered a mathematical model for locating temporary treatment waste treatment plants. Minimizing the risk of spreading the coronavirus around temporary facilities was the main contribution of their paper. Finally, their proposed model was implemented in Wuhan, China. Klemes et al. (2020) investigated the effects of the COVID-19 pandemic on the amount of plastic waste and its effects on the environment and energy. A perspective to better understand the role that entrepreneurs play in resource management and waste management during the COVID-19 outbreak was presented by Neumeyer et al. (2020) and explored the challenges and opportunities in this area.

Yang et al. (2021) designed a Mixed-Integer Linear Programming (MILP) model for a vaccine distribution network. They developed a new algorithm to solve large-sized problems. The results were then used to validate their model in four countries in South Africa. Singh et al. (2021) examined a simulation model of a network public distribution system with three different scenarios to demonstrate disruptions in the supply chain under COVID-19 conditions. They placed great emphasis on a resilient supply chain during the pandemic. They also claimed that their proposed simulation model could create a resilient and responsive supply chain network. Nagurney (2021) proposed an optimization model for a supply chain in a COVID-19 pandemic situation and considered the workforce to be an important element in linking the economic activities of the supply chain network and its related capacities. Their chain provided includes medical and protective equipment and some special food items. Additionally, due to the lack of mathematical models in the field of sustainable pharmaceutical industry during the COVID-19 pandemic, Goodarzian, Taleizadeh, et al. (2021) designed a comprehensive pharmaceutical supply chain network for production, distribution, inventory control, allocation, and location problems. Moreover, a new multi-objective, multi-product, and multi-echelon MILP model was formulated. They developed three new hybrid meta-heuristic algorithms called ant colony optimization algorithm, fish swarm algorithm, and firefly algorithm, along with variable neighborhood search. The response surface method was used to tune the algorithm’s parameters. Finally, they suggested a real case study in Iran and concluded from numerical results that the hybrid fish swarm algorithm with a variable neighborhood search algorithm was more efficient than the other algorithms. In the field of waste management during the COVID-19 epidemic, Tirkolaee et al. (2021) presented a location-routing model with the aim of minimizing the time of waste collection and transportation to reduce risk. The developed location-routing model proposed by Tirkolaee and Aydın (2021) addressed the problem of infectious medical wastes amid the COVID-19 pandemic by minimizing the exposure risk and reducing the total costs. One of the principles of building a smart city is to use IoT-based infrastructure and blockchain. Medical waste control is one of the main targets of smart cities. Torkayesh et al. (2021) conducted the research to find the contributing factors of failure in the utilization of IoT-based systems in the medical waste area. Sazvar et al. (2021) designed a sustainable pharmaceutical supply chain network under uncertainty considering waste management. They considered a scenario-based multi-objective MILP model. To cope with uncertain parameters, a new scenario-based game theory model was provided. Hence, a hybrid solution method was developed by hybridizing the LP-metrics approach with a heuristic method. Finally, a real case study was suggested to assess the performance of their model.

Vaccination, the vaccine production chain, and the distribution of vaccines have always been among the most critical issues worldwide, especially in low-income and developing countries. Since the outbreak of COVID-19, the importance of this issue has become even more apparent, and the need for governments and communities to address the obstacles to establishing a coherent and comprehensive vaccination program has increased. In green-cold vaccine supply chain management, little research has been performed on mathematical modeling, and no research has been done on green-cold vaccine supply chain management during the COVID-19 pandemic. Moreover, the issue of the impact of IoT on the green-cold vaccine supply chain network in the COVID-19 condition, bearing in mind demand coverage, waste management, and environmental effects, has not been used in any of the papers examined.

In this paper, to fill gaps available in the literature review, the contributions of the proposed research are explained thoroughly, as follows:

• It designs a new multi-objective multi-echelon responsive-green-cold vaccine supply chain during the COVID-19 pandemic for the first time,

• It considers waste management and environmental effects in the proposed model,

• It provides an IoT application in the GCVSCN model in the COVID-19 outbreak to increase the accuracy, speed, and justice of vaccine injection with existing priorities for the first time,

• It uses demand coverage and COVID-19 vaccine delivery time simultaneously in the proposed model,

• It develops a novel meta-heuristic algorithm based on VNS and GWO algorithms called modified GWO (MGWO) to solve the proposed model.

Description of the problem

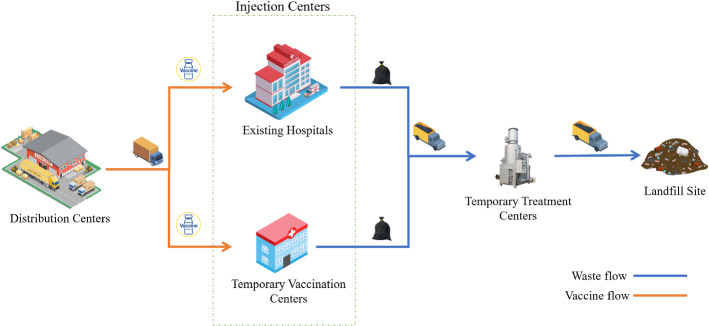
In this paper, a new Green-Cold Vaccine Supply Chain Network (GCVSCN) using the Internet-of-Things (IoT) during the COVID-19 pandemic is developed for the first time. Additionally, a new multi-period multi-echelon MILNP model for a distribution-location-allocation problem considering waste management has been developed for the first time. The considered echelon is divided into four levels, including Distribution Centers (DCs), Injection Centers (ICs), Temporary Treatment Centers (TTCs), and Landfill Sites (LSs). Injection centers are then divided into two categories containing ($i$) hospitals and ($\mathit{ii}$) Temporary Vaccination Centers (TVCs). The main aims of the proposed problem include decreasing total costs, demand coverage, total time, and environmental effects. Considering demand coverage and environmental effects simultaneously using IoT concepts is a significant novelty in this paper. In this regard, the echelon considered in the GCVSCN is shown in Fig. 2.

Fig. 2.

The structure of the GCVSCN

To vaccinate individuals effectively against COVID-19, grouping people living in a region and prioritizing vulnerable tiers is paramount in the immunization program. At this vital stage, collecting accurate and reliable data leads to effective widespread vaccination as well as the lowest shortage of vaccines and maximum peoples’ satisfaction. Hence, using state-of-the-art systems, for example, IoT-based applications, can be considered a viable solution to gather data and process it. To fill in this gap, the IoT-based application is presented in this paper for the first time and is considered a significant contribution. Therefore, in this paper, the IoT application classifies people into various groups, including ages, jobs, and underlying medical problems. Underlying medical problems are divided into four groups: cardiovascular disease, respiratory disease, diabetes, and cancer. Age is one of the critical factors for vaccination prioritization because elderly people have higher mortality rates. Thus, there is a sequence of how people should be vaccinated according to their age group. This sequence is broken down as follows:

• The elderly aged 65+ with their care workers.

• All people aged 16+ with a severe medical problem

• All people aged 50+ 

• All people aged between 16 and 50 that have a job in public and crowded places

• All people aged between 30 and 50

• All people aged between 16 and 30

• All people aged under 16

The general citizen vaccination program prioritizes people to receive vaccines. According to the prioritization established by the experts, seven groups are selected for this purpose, as stated above. The groups set out are vaccinated in order and separately; that is, until the vaccination of the first group is performed, the vaccination of the second group does not start and also continues until the seventh group. The population of each group is obtained through IoT-based data. The allocated time for the vaccination of each group is a specific time and should not exceed the set time. Since the unit of index $t$ in our model is daily, we can obtain the daily demand in each of the seven age groups. Thus, the parameter $D_t$ is obtained through Eq. (1).

$$Theamountofdailydemandforeachgroup=\frac{populationofeachgroup}{Thelimitedtimeframeforeachgroup}.$$ 1

According to the abovementioned explanation related to the range of people’s ages at vaccination based on the IoT-based application, vaccines must be transported from DCs to ICs. Based on vaccines provided, vaccines are distributed between DCs based on the needs of the ICs. In this paper, to find the optimal locations for TVCs between the potential locations based on the decreasing shortage and cost, and fair distribution is addressed for the first time. Moreover, another significant contribution, cooling infrastructures for vaccine transportation, is used for the first time, whereby the distance between DCs and ICs as well as delivery times are the main criteria for locating TVCs because the longer distance leads to vaccine perishability. Thereafter, the Hazardous Medical Wastes (HMWs) generated through ICs are inevitable problems that jeopardize people’s lives unless they manage them swiftly. Thus, TTCs aimed at decreasing the influx volume of HMWs are set out for the first time in this paper. It is clear that the significant proportion of HMWs in ICs consists of vials and syringes that are classified as glass and sharp waste, respectively. Moreover, the suggested technology for treating these types of HMWs during the COVID-19 pandemic is incinerators. The waste from treated HMWs is then transported to an LFs for safe disposal.

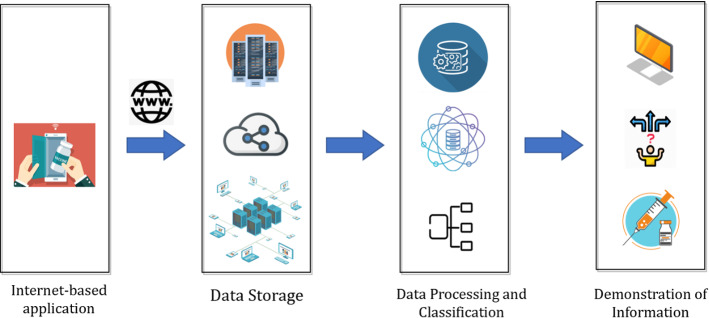
The IoT-based application is presented in this paper for the first time as a means of gathering data. Thus, the collected data is transmitted to data clouds via the internet network. After that, the data, including date of birth, employment, and underlying medical problems, are processed in data centers. The sophisticated tools, for example, Data Science and Machine Learning, can cope with the massive quantity of data to group people. In the final stage, the demand for each tier is calculated and shown on the monitor. The data gathering procedure is depicted in Fig. 3.

Fig. 3.

The procedure for data gathering based on the IoT

The main assumptions of the proposed problem are explained as follows:

• The locations of DCs, hospitals, and LSs are pre-determined.

• The locations of TVCs and TTCs are unknown and must be selected.

• The capacity of DCs, TVCs, hospitals, and TTCs is limited.

• The distances between DCs, ICs, TTCs, and LSs are known.

• The vaccination is performed according to the priority of each group.

• Each group of patients must be vaccinated in a specific timeframe defined by the Ministry of Health.

• The vehicle, along with cooling infrastructure, is considered to transport vaccines from DCs and ICs.

• HMWs are transferred by special trucks from ICs to LSs.

In the following, the notations, parameters, decision variables, the mathematical modeling of the proposed problem are stated and formulated.

Notations:

Sets
$i$	Set of distribution centers
$k$	Set of temporary vaccination centers
$h$	Set of hospitals
$j$	Set of temporary treatment centers
$v$	Set of vaccines
$t$	Set of time periods
Parameters
${\mathit{IN}}_{\mathit{ivt}}$	The inventory of DC $i$ for vaccine type $v$ at period $t$
$C_{\mathit{kvt}}$	The capacity of TVC $k$ vaccine type $v$ at period $t$
$C_{\mathit{hvt}}$	The capacity of hospital $h$ vaccine type $v$ at period $t$
$D_{\mathit{vt}}$	The demand of vaccine $v$ at period $t$
$\mathit{TC}$	The transportation cost for vehicle per kilometer
${\mathit{DS}}_{\mathit{ik}}$	The distance between DC $i$ and TVC $k$
${\mathit{DS}}_{\mathit{ih}}$	The distance between DC $i$ and hospital $h$
${\mathit{DS}}_{\mathit{kj}}$	The distance between TVC $k$ and TTC $j$
${\mathit{DS}}_{\mathit{hj}}$	The distance between hospital $h$ and TTC $j$
${\mathit{SC}}_{\mathit{vkt}}$	The surplus cost of vaccine type $v$ in TVC $k$ at period $t$
${\mathit{SC}}_{\mathit{vht}}$	The surplus cost of vaccine type $v$ in hospital $h$ at period $t$
${\mathit{SCH}}_{\mathit{vkt}}$	The shortage cost of vaccine $v$ in TVC $k$ at period $t$
${\mathit{SCH}}_{\mathit{vht}}$	The shortage cost of vaccine $v$ in hospital $h$ at period $t$
${\mathit{FC}}_k$	The fixed cost of establishing the TVC $k$
${\mathit{FC}}_j$	The fixed cost of establishing the TTC $j$
$\mathit{AVG}$	Average vehicle speed
$\mathit{OC}$	The incinerator’s operating costs
$\mathit{CC}$	The capacity of the vehicle
$F$	vehicle fuel consumption per kilometer (l/km)
$\mathit{FP}$	The cost of fuel consumption of each vehicle dollar/litre
$\mathit{CR}$	The amount of carbon emission by vehicles gram/kilometer
$\mathit{EI}$	The rate of environmental impact for establishing temporary centers
$\mathit{CE}$	The rate of environmental impact for burning in waste incinerator
Decision variables
$Y_k$	If TVC $k$ is established:1; otherwise 0
$Y_j$	If TTC $j$ is established:1; otherwise 0
$Q_{\mathit{ivkt}}$	The amount of vaccine type $v$ that is transported from the DC $i$ to the TVC $k$ at period $t$
$Q_{\mathit{ivht}}$	The amount of vaccine type $v$ that is transported from the DC $i$ to the hospital $h$ at period $t$
$W_{\mathit{kjt}}$	The amount of waste, including used syringes and vials, transported from TVC $K$ to the TTC $j$ at period $t$
$W_{\mathit{hjt}}$	The amount of waste, including used syringe and vials, transported from hospital $h$ to the TTC $j$ at period $t$
$A_{\mathit{kit}}$	If TVC $k$ allocated to DC $i$ at period $t$ is equal to 1; otherwise 0
$A_{\mathit{hit}}$	If hospital $h$ allocated to DC $i$ at period $t$ is equal to 1; otherwise 0
$A_{\mathit{jkt}}$	If TTC $j$ allocated to TVC $k$ at period $t$ is equal to 1; otherwise 0
$A_{\mathit{jht}}$	If TTC $j$ allocated to hospital $h$ at period $t$ is equal to 1; otherwise 0
${\mathit{QS}}_t$	The amount of surplus at period $t$
${\mathit{QSH}}_t$	The amount of shortage at period $t$
$N_{\mathit{ikt}}$	The number of vehicles needed for use at period $t$ from DC $i$ to TVC $k$
$N_{\mathit{iht}}$	The number of vehicles needed for use at period $t$ from DC $i$ to hospital $h$
$N_{\mathit{kjt}}$	The number of vehicles needed for use at period $t$ from TVC $K$ to TTC $k$
$N_{\mathit{hjt}}$	The number of vehicles needed for use at period $t$ from hospital $h$ to TTC $j$
${\mathit{DT}}_{\mathit{ik}}$	The delivery time from DC $i$ to the vaccination center $k$
${\mathit{DT}}_{\mathit{ih}}$	The delivery time from DC $i$ to hospital $h$
${\mathit{DT}}_{\mathit{kj}}$	The delivery time from vaccination center $k$ to treatment center $j$
${\mathit{DT}}_{\mathit{hj}}$	The delivery time from hospital $h$ to treatment center $j$

Mathematical modeling

Minimum total cost

$$\begin{array}{cc}\hfill Min{Z}_1& =\sum _k{Y}_k\times F{C}_k+\sum _j{Y}_j\times F{C}_j+\sum _i\sum _k\sum _t{N}_{\mathit{ikt}}\times D{S}_{\mathit{ik}}\times TC+\hfill \\ \hfill & +\sum _k\sum _j\sum _t{N}_{\mathit{kjt}}\times D{S}_{\mathit{kj}}\times TC+\sum _h\sum _j\sum _t{N}_{\mathit{hjt}}\times D{S}_{\mathit{hj}}\times TC+\sum _{t}Q{S}_t\times S{C}_t\hfill \\ \hfill & +\sum _{t}QS{H}_t\times SC{H}_t+\sum _k\sum _j\sum _t{W}_{\mathit{kjt}}\times OC+\sum _h\sum _j\sum _t{W}_{\mathit{hjt}}\times OC\hfill \\ \hfill & +F\times FP\left[\sum _i,\sum _k,\sum _t,N_{\mathit{ikt}},\times ,D,S_{\mathit{ik}},+,\sum _i,\sum _h,\sum _t,N_{\mathit{iht}},\times ,D,S_{\mathit{ih}}\right)\hfill \\ \hfill & \left(+\sum _k\sum _j\sum _t{N}_{\mathit{kjt}}\times D{S}_{\mathit{kj}}+\sum _h\sum _j\sum _t{N}_{\mathit{hjt}}\times D{S}_{\mathit{hj}}\right]\hfill \\ \hfill \end{array}$$ 2

The objective function (2) shows how to minimize total costs, including established distribution and vaccination center costs, transportation cost from distribution center to vaccination center, from distribution center to hospital, from vaccination center to treatment center, and from hospital to treatment center, shortage and surplus costs in vaccination centers and hospitals, the operational cost of burning the syringes, and fuel consumption cost between all echelons.

Minimum unmet demand

$$Min{Z}_2=\mathrm{Max}\left[\sum _t,\left(D_t,-,\left[\sum _i,\sum _v,\sum _k,Q_{\mathit{ivkt}},+,\sum _i,\sum _v,\sum _h,Q_{\mathit{ivht}}\right]\right)\right]$$ 3

The objective function (3) indicates minimizing the maximum unmet demand by determining an upper bound for the total unmet demand during the planning horizon.

Minimum delivery time

$$\begin{array}{cc}\hfill Min{Z}_3& =\sum _i\sum _k\sum _t{N}_{\mathit{ikt}}\times D{T}_{\mathit{ik}}+\sum _i\sum _h\sum _t{N}_{\mathit{iht}}\times D{T}_{\mathit{ih}}+\sum _k\sum _j\sum _t{N}_{\mathit{kjt}}\hfill \\ \hfill & \times D{T}_{\mathit{kj}}+\sum _h\sum _j\sum _t{N}_{\mathit{hjt}}\times D{T}_{\mathit{hj}}\hfill \end{array}$$ 4

The objective function (4) seeks to minimize the delivery time of vaccines from the distribution center to the vaccination center, from the distribution center to the hospital, from the vaccination center to the waste management center, and from the hospital to the waste management center.

Minimum environmental impacts

$$\begin{array}{cc}\hfill Min{Z}_4& =CR\times \left[\sum _i\sum _k\sum _t{N}_{\mathit{ikt}}\times D{S}_{\mathit{ik}}+\sum _i\sum _h\sum _t{N}_{\mathit{iht}}\times D{S}_{\mathit{ih}}+\sum _k\sum _j\sum _t{N}_{\mathit{kjt}}\right)\hfill \\ \hfill & \left(\times D{S}_{\mathit{kj}}+\sum _h\sum _j\sum _t{N}_{\mathit{hjt}}\times D{S}_{\mathit{hj}}\right]+EI\times \left[\sum _k{Y}_k+\sum _j{Y}_j\right]+CE\hfill \\ \hfill & \times \left[\sum _k\sum _j\sum _t{W}_{\mathit{kjt}}+\sum _h\sum _j\sum _t{W}_{\mathit{hjt}}\right]\hfill \end{array}$$ 5

Objective function (5) shows the environmental impacts of transportation of the products between levels of the supply chain by vehicles, establishing VCs and TTCs, and burning the syringes in the waste management phase.

Constraints

$$Q_{\mathit{ivkt}}\le M\times Y_k\forall i,v,k,t$$ 6

$$W_{\mathit{kjt}}\le M\times Y_k\forall k,j,t$$ 7

$$W_{\mathit{kjt}}\le M\times Y_j\forall k,j,t$$ 8

$$W_{\mathit{hjt}}\le M\times Y_j\forall h,j,t$$ 9

$$\sum _i{A}_{\mathit{kit}}\le 1\forall k,t$$ 10

$$\sum _i{A}_{\mathit{hit}}\le 1\forall h,t$$ 11

$$\sum _k{A}_{\mathit{jkt}}\le 1\forall j,t$$ 12

$$\sum _h{A}_{\mathit{jht}}\le 1\forall j,t$$ 13

$$A_{\mathit{kit}}\le Y_K\forall i,k,t$$ 14

$$A_{\mathit{jkt}}\le \frac{Y_K+Y_j}{2}\forall j,k,t$$ 15

$$A_{\mathit{jht}}\le Y_j\forall j,h,t$$ 16

$$N_{\mathit{ikt}}\times CC\ge \sum _v{Q}_{\mathit{ivkt}}\forall i,k,t$$ 17

$$N_{\mathit{iht}}\times CC\ge \sum _v{Q}_{\mathit{ivht}}\forall i,h,t$$ 18

$$N_{\mathit{kjt}}\times CC\ge W_{\mathit{kjt}}\forall k,j,t$$ 19

$$N_{\mathit{hjt}}\times CC\ge W_{\mathit{hjt}}\forall h,j,t$$ 20

$$\sum _k{Q}_{\mathit{ivkt}}+\sum _h{Q}_{\mathit{ivht}}\le I{N}_{\mathit{ivt}}\forall i,v,t$$ 21

$$\sum _i{Q}_{\mathit{ivkt}}\le C_{\mathit{vkt}}\times A_{\mathit{kit}}\forall v,k,t$$ 22

$$\sum _i{Q}_{\mathit{ivht}}\le C_{\mathit{vht}}\times A_{\mathit{hit}}\forall h,v,t$$ 23

$$Q{S}_t\ge \sum _i\sum _v\sum _k{Q}_{\mathit{ivkt}}+\sum _i\sum _v\sum _h{Q}_{\mathit{ivht}}-D_t\forall t$$ 24

$$QS{H}_t\ge D_t-\left[\sum _i\sum _v\sum _k{Q}_{\mathit{ivkt}}+\sum _i\sum _v\sum _h{Q}_{\mathit{ivht}}\right]\forall t$$ 25

$$\left[\sum _i\sum _v\sum _k{Q}_{\mathit{ivkt}}+\sum _i\sum _v\sum _h{Q}_{\mathit{ivht}}\right]-D_t=Q{S}_t-QS{H}_t\forall t$$ 26

$$D{T}_{\mathit{ik}}\ge \frac{D{S}_{\mathit{ik}}}{\mathit{AVG}}-M\times \left(1-A_{\mathit{kit}}\right)\forall i,k,t$$ 27

$$D{T}_{\mathit{ih}}\ge \frac{D{S}_{\mathit{ih}}}{\mathit{AVG}}-M\times \left(1-A_{\mathit{hit}}\right)\forall i,h,t$$ 28

$$D{T}_{\mathit{kj}}\ge \frac{D{S}_{\mathit{kj}}}{\mathit{AVG}}-M\times \left(1-A_{\mathit{jkt}}\right)\forall j,k,t$$ 29

$$D{T}_{\mathit{hj}}\ge \frac{D{S}_{\mathit{hj}}}{\mathit{AVG}}-M\times \left(1-A_{\mathit{jht}}\right)\forall j,h,t$$ 30

$$Q_{\mathit{ivkt}},Q_{\mathit{ivht}},W_{\mathit{kjt}},W_{\mathit{hjt}},Q{S}_t,QS{H}_t,N_{\mathit{ikt}},N_{\mathit{iht}},\forall i,j,v,k,h,t$$ 31

$$N_{\mathit{kjt}},N_{\mathit{hjt}}\ge 0$$

$$Y_k,Y_j,A_{\mathit{kit}},A_{\mathit{hit}},A_{\mathit{jkt}},A_{\mathit{jht}}\in \left\{0,1\right\}$$

Constraints (6) and (7) state that the vaccine is transported from the DCs to TVCs and from the TVCs to TTCs if the TVCs are established. Constraints (8) and (9) show that the used syringe is transported from hospitals and TVCs to TTCs if the TTCs are established. Constraints (10)—(13) ensure that at each time period, each vaccine center is assigned to a maximum of one distribution center, each hospital is allocated to a maximum of one distribution center, and each waste center is assigned to a maximum of one vaccine center. Eventually, each waste center is assigned to a hospital. Constraints (14)–(16) show the relationship between location and allocation variables. Constraints (17)–(20) specify the number of vehicles required in each period between distribution centers and vaccination centers, distribution centers and hospitals, vaccination centers, and waste centers, and between hospitals and waste centers. Constraints (21)–(23) specify the inventory of distribution centers, vaccination centers’ capacity, and hospitals’ capacity in each period. Constraints (24) and (25) determine a lower bound for the surplus rate and a higher bound for the shortage rate in each period. Constraint (26) shows the balance between shortage and surplus in each period. Constraints (27)–(30) determine the delivery time from the distribution center to the vaccination center, from the distribution center to the hospital, from the vaccination center to the waste center, and from the hospital to the waste center. Constraint (31) defines the type of decision variables.

Methodology solutions

This section explains approaches to the solution. Firstly, the LP-metric method is proposed for how to tackle the multi-objective technique. The LP-metric method seeks a solution that is nearest to the optimal values of the objectives. Using meta-heuristic methods to solve NP-hard problems, despite being approximate, seems to be the most appropriate solution (Goodarzian et al., 2020). Meta-heuristic algorithms including GWO and VNS are then presented, and anew meta-heuristic algorithm called MGWO is developed for the first time to address how to deal with the complexity of the problem.

The reason for using the proposed algorithms is that calculation in the proposed algorithms is simple, and implementation is straightforward. Also, both of them are useful in engineering and scientific research and capable of performing both global and local searches. Moreover, GWO and VNS can be used to address an enormous number of multi-objective problems, and they are flexible. The suggested algorithms need few parameters, are very robust to solve the supply chain models, and converge more quickly (Lejeune, 2006; Lo et al., 2021; Şenel et al., 2019). These can be combined with other algorithms or improved based on other algorithms. The limitations of the proposed algorithms are as follows: 1. Meta-heuristic algorithms are not able to calculate the global optimum and calculate the local optimum. 2. The final solution in GWO, VNS, and MGWO algorithms depends on the coder’s skill in defining chromosomes and the initial value of its parameters. 3. The proposed meta-heuristic algorithms also require access to a computer system equipped with features such as a large RAM and CPU. The description of the suggested approaches is discussed in the following sub-sections.

LP-metric method (multi-objective technique)

A multi-objective decision model involves decision variables, objective functions, and constraints, as well as the decision-maker’s aim is to maximize or minimize objective functions. Since these problems rarely have a unique solution, the decision-maker chooses a solution from a set of efficient solutions. This method minimizes the sum of the relative deviations of the objectives from their optimum values and combines multiple objective functions into a single objective. This approach has been used for two reasons: ($I$) requiring less information than decision-makers and ($\mathit{II}$) being easy to use in practice. The proposed method is used to measure the proximity of an ideal solution. This measure of deviation will be as follows. Since the objective functions are the form of minimum used in this paper, the minimum f is formulated in Eq. (32).

$$minf=\sum _{j=1}^m{\omega }_j\times {\left(\frac{f_j^{\ast }-f_j}{f_j^{\ast }}\right)}^p$$ 32

where $\omega$ shows the significance (weight) of the objective. To eliminate the problem of differences in objective scales, we divide the deviation of the ideal solution of the $j$ ^th objective by $f_j^{\ast }$. It determines the degree of emphasis on deviations, so that the larger this value, the greater the emphasis on the largest deviation. The overall objective function of the LP-metric method should also be minimized to minimize deviations from the ideal.

In this method, we optimize the objective functions by considering all the constraints of the problem and considering the optimal solutions obtained from each objective function as $f_j^{\ast }$. Therefore, the LP-metric method is defined as follows:

$$minf=\sum _{j=1}^m{\omega }_j\times {\left(\frac{f_j^{\ast }-f_j}{f_j^{\ast }}\right)}^p$$ 33

$$k_j\left(Y_j,Y_2,\dots ,Y_m\right)\le a_{j}j=1,2,\dots m$$ 34

$$f_j=z_j\left(Y_1,Y_2,\dots ,Y_m\right)$$ 35

$$Y_j\ge 0j=1,2,\dots m$$ 36

Solution representation

In this sub-section, the Random-Key method is applied to encode as well as to analyze initial solutions (Goodarzian et al., 2020). Then, the sub-solutions are divided into two sorts in the suggested model. The encoding scheme is explained below.

• (I)To assess the open vaccination and treatment centers, sub-solution is used as follows. Accordingly, firstly, a matrix with $\left|N\right|$ elements is generated with a uniform distribution $U$ (0,1). Hence, the first $N_{\mathit{max}}$ units are chosen with the most values as open centers. Therefore, one example is depicted in Fig. 4.
• (II)To allocate a hospital to DC, an allocation sub-solution is used. For instance, five hospitals and three DCs are considered. An array with a length of $H$ is created with a uniform distribution: $U$ (0, $H$). Then, according to Fig. 5, the allocated hospitals to DCs are indicated. It is clear that in Fig. 5, the third DC is allocated to hospital $h1$, the second DC is allocated to hospitals $h2$, $h3$, and $h5$, and the first DC is allocated to hospital $h4$.

Fig. 4.

The producer used to evaluate the opened centers

Fig. 5.

The producer used to allocate the hospitals to DCs

Gray wolf optimization

The GWO algorithm is a meta-heuristic algorithm inspired by the hierarchical structure and social behavior of gray wolves while hunting. The GWO algorithm was first introduced by Mirjalili et al. (2016). This algorithm is population-based, it has a simple process, and it can be easily generalized to large-scale problems. Gray wolves are thought of as apex predators; that is, they are at the top of the food chain. Gray wolves prefer to live in a pack, and each pack has an average of 5–12 members. All members of this pack have a very precise hierarchy of social domination and have specific tasks. In each wolfpack, there are four degrees to hunt, including alpha, beta, delta, and omega. This algorithm is therefore divided into three main steps: containing tracking and approaching, pursing and encircling, and attacking.

In GWO, the most appropriate solution is considered alpha, and the second and third appropriate solutions are called beta and delta, respectively. The rest of the solutions are considered omega. In the GWO algorithm, hunting is driven by alpha, beta, and delta. The omega solution follows these three wolves. When the hunt is surrounded by wolves and stops moving, the attack starts on the alpha leader of the wolves. This algorithm requires all wolves to update their position according to the position of alpha, beta, and delta wolves.

During the hunt, gray wolves surround the prey. The siege behavior is presented in Eqs. (34) and (35). Where $m$ shows the current iteration,$B$ and $D$ indicate coefficient vectors, $Y_z$ represents the position vector of the prey, and $Y$ displays the position vector of the gray wolf.

$$\overrightarrow{B}=2\overrightarrow{b}.\overrightarrow{n_1}-\overrightarrow{b}$$ 37

$$\overrightarrow{D}=\overrightarrow{n_2}$$ 38

Vectors B and D are calculated in Eqs. (37) and (38). In Eqs. (39) and (40), the variable $b$ decreases linearly from 2 to 0 during the iterations. Thus,$n_1$ and $n_2$ are random vectors in the range [0, 1].

$$\overrightarrow{W}=\left|\overrightarrow{D}.\overrightarrow{Y_z}\left(m\right)-\overrightarrow{Y}\left(m\right)\right|$$ 39

$$\overrightarrow{Y}\left(m+1\right)=\overrightarrow{Y_z}\left(m\right)-\overrightarrow{B}.\overrightarrow{W}$$ 40

Hunting operations are usually conducted by alpha. Beta and delta wolves may occasionally participate in the hunting. In the gray wolf hunting behavior, we assumed that alpha, beta, and delta had better knowledge of the potential prey’s position. The first three solutions are best stored, and the other agent is required to update their positions according to the position of the best search agents according to Eqs. (41), (42), and (43).

$$\overrightarrow{W_{\alpha }}=\left|\overrightarrow{D_1}.\overrightarrow{Y_{\alpha }}-\overrightarrow{Y}\right|,\overrightarrow{W_{\beta }}=\left|\overrightarrow{D_2}.\overrightarrow{Y_{\beta }}-\overrightarrow{Y}\right|,\overrightarrow{W_{\delta }}=\left|\overrightarrow{D_3}.\overrightarrow{Y_{\delta }}-\overrightarrow{Y}\right|$$ 41

$$\overrightarrow{Y_1}=\overrightarrow{Y_{\alpha }}-\overrightarrow{B_1}.\left(\overrightarrow{W_{\alpha }}\right),\overrightarrow{Y_2}=\overrightarrow{Y_{\beta }}-\overrightarrow{B_2}.\left(\overrightarrow{W_{\beta }}\right),\overrightarrow{Y_3}=\overrightarrow{Y_{\delta }}-\overrightarrow{B_3}.\left(\overrightarrow{W_{\delta }}\right)$$ 42

$$\overrightarrow{Y}\left(m+1\right)=\frac{\overrightarrow{Y_1}+\overrightarrow{Y_2}+\overrightarrow{Y_3}}{3}$$ 43

The pseudo-code of the GWO is shown in Fig. 6.

Fig. 6.

The pseudo-code of the GWO

Variable neighborhood search

The VNS algorithm was first proposed by Mladenovic and Hansen (1997). The main idea of this algorithm is to systematically change the neighborhood structure during the search to prevent falling into the local optimal. The simplicity of implementation and the quality of the solutions obtained from the VNS algorithm quickly made this algorithm a good means to solve optimization problems. The VNS algorithm begins by generating the initial answer, defining the neighborhood structures, and using a method to search the neighborhood.

Neighbor structures the $k=\left\{1,2,\dots ,k_{\mathit{max}}\right\}$ algorithm are $M_k$, in which $M_k$ is the $k$th neighborhood structure. After determining the possible neighborhood structures, their sequence is determined. The two significant points here are selecting the appropriate neighborhood structures and determining the appropriate sequence (for instance, the sequence based on the size of the neighborhood structures). Generating initial quality solutions, defining neighborhood structures, determining their sequence, and using the appropriate method for a local search are the factors that determine the quality of the solutions obtained from the algorithm. The algorithm begins using the generated initial solution $\left(I_0\right)$ and repeats the main loop of the algorithm until the termination criterion is established. The main loop of the VNS algorithm consists of two main phases of shocking and local search.

In the shocking phase, the algorithm moves from the current solution to the neighbor solution ($I^{\prime }$) using the $k$ ^th neighborhood structure. In the local search phase, the search is performed on the solution ($I^{\prime }$) using local search methods to reach the local optimization ($I^{{}^{\prime }\ast }$). Now, in the move or not move sections, if the local optimization obtained was better than the current solution $I$, it will be replaced, and the search will return to $M_1$, otherwise, the $\left(M_{k+1}\right)$ neighborhood structure is used to continue the search. This search dimension continues as long as it is $k\le k_{\mathit{max}}$. Figure 7 shows the pseudo-code of the VNS algorithm.

Fig. 7.

The pseudo-code of the VNS

Modified Gray wolf optimization

In this sub-section, a new modified meta-heuristic algorithm called MGWO is developed to obtain the best GCVSCN design. We have therefore developed a modified meta-heuristic method to solve the problem set out. The GWO algorithm is modified based on the VNS algorithm as a local search. The GWO is a new approach used to solve different problems, including allocation, location, routing, distribution, supply chain network, inventory management, production, etc. (Makhadmeh et al., 2021; Qu et al., 2020). The process of the GWO and VNS algorithms is then explained in Sects. 4.3 and 4.4, respectively. Accordingly, VNS is applied as a local search approach in the modified GWO on the best solution obtained from the main loop in each iteration. There are differences between our proposed algorithm and in some references. For example, Nadimi-Shahraki et al., (2021) used a new search strategy called dimension learning-based hunting to improve the GWO algorithm, Guo et al., (2020) improved the GWO algorithm based on seeking mode and tracking and seeking mode, but our proposed algorithm improves using the VNS algorithm as a local search in this paper. The pseudo-code steps of the MGWO algorithm are shown in Fig. 8.

Fig. 8.

The pseudo-code of the MGWO

Computational results

In this section, the data generated is first provided to investigate the efficiency of the proposed algorithms. In this regard, the Taguchi method is presented to tune and control the parameters of the algorithm developed. Thereafter, assessment metrics and the convergence of the proposed algorithms to evaluate the performance of the developed algorithms are addressed. Moreover, to validate the GCVSCN model, a real case study during the COVID-19 pandemic is presented. Finally, a set of sensitivity analyses are performed. To run the LP-metric method, GAMS Software is used and the meta-heuristic algorithm is implemented by MATLAB 2020b.

Data generation

According to the novelty of the presented GCVSCN model, there is no paper related to or similar to our model in the papers examined. Thus, the benchmarks related to the model developed do not exist in the literature reviewed. In this paper, we need to provide experimental problems. Ten experimental problems are designed; they are divided into three categories, containing small- and medium-sized problems for the test problems and large-sized problems for the case study. The size of the problems designed is illustrated in Table 3. The values of the presented parameters are then shown in Table 4.

Table 3.

The size of the experimental problems

Categories	Sample	$\mathit{i}$	$\mathit{j}$	$\mathit{k}$	$\mathit{h}$	$\mathit{v}$	$\mathit{t}$(daily)
Small	S1	1	2	1	1	1	10
	S2	1	2	2	1	2	15
	S3	2	2	2	2	2	20
	S4	2	3	2	2	2	25
	S5	3	3	2	3	3	30
Medium	M1	3	4	3	3	3	50
	M2	4	4	3	4	3	80
	M3	4	6	4	4	3	90
	M4	5	6	5	5	4	110
	M5	6	6	6	5	5	120

Table 4.

The range of the presented parameters of the GCSCN

Parameter	Value	Parameter	Value
${\mathit{C}}_{\mathit{ivt}}$	$u\sim$(500, 2500)	${\mathit{SC}}_{\mathit{vkt}}$	$u\sim$(5, 25) $
${\mathit{C}}_{\mathit{kvt}}$	$u\sim$(400, 2000)	${\mathit{SC}}_{\mathit{vht}}$	$u\sim$(4, 20) $
${\mathit{C}}_{\mathit{hvt}}$	$u\sim$(350, 2000)	${\mathit{SCH}}_{\mathit{vkt}}$	$u\sim$(3, 18) $
${\mathit{D}}_{\mathit{t}}$	$u\sim$(300, 1500)	${\mathit{SCH}}_{\mathit{vht}}$	$u\sim$(4, 15) $
$\mathit{TC}$	$u\sim$(30, 80) $	${\mathit{FC}}_{\mathit{k}}$	$u\sim$(15, 45) $
${\mathit{DS}}_{\mathit{ik}}$	$u\sim$(15, 1000) Km	${\mathit{FC}}_{\mathit{j}}$	$u\sim$(20, 65) $
${\mathit{DS}}_{\mathit{ih}}$	$u\sim$(20, 500) Km	$\mathit{AVG}$	$u\sim$(60, 80)
${\mathit{DS}}_{\mathit{kj}}$	$u\sim$(15, 500) Km	$\mathit{OC}$	$u\sim$(20, 65) $
${\mathit{DS}}_{\mathit{hj}}$	$u\sim$(15, 100) Km	$\mathit{FP}$	$u\sim$(5, 25) $/ L
$\mathit{CR}$	$u\sim$(5, 30) g/ KM	$\mathit{CE}$	$u\sim$(5, 25)
$\mathit{EI}$	$u\sim$(0.2, 0.45)	$\mathit{F}$	$u\sim$(5, 25) L/KM

Taguchi method

This sub-section sets out an, experimental design for controlling and tuning the algorithm’s parameters. In this paper, the Taguchi approach is used to tune the parameters of the algorithms set out. For more details about this method, interested researchers can examine a few papers related to the Taguchi method, such as Rezaei et al. (2020), Janatyan et al. (2021), etc.

The Signal-to-Noise ratio (S/N) is used to analyze the experiment. The S/N value expresses the degree of scatter around a certain value or, in other words, how our solutions have changed across several experiments. To obtain the S/N value, there are three equations, each of which applies to specific conditions.

$$SB=\frac{1}{n}\sum {\left(y_i\right)}^2$$ 44

$$LB=\frac{1}{n}\sum {\left(\frac{1}{y_i}\right)}^2$$ 45

$$NB=\frac{1}{n}\sum {\left(y_i-y_0\right)}^2$$ 46

Moreover, the Taguchi approach mechanism focuses on the sort of solution. Therefore, the solution obtained that is relevant to three Eqs. (44)-(46) of this method is divided into three groups including the smaller is better (see Eq. (47)), larger is better (see Eq. (44), and the nominal is better (see Eq. (47)). In the proposed model, objective functions are a type of minimization, to control the parameters of the algorithm set out, the smaller the better is used. Thus, Eq. (47) shows the S/N ratio value set out in this paper.

$$\frac{S}{N}=-10\times log\left(\frac{{\sum }_{i=1}^n{Y}_i^2}{n}\right)$$ 47

where $n$ shows the orthogonal array as well as $y_i$ represents the value of the solution for the orthogonal array.

Since the scale of objective functions in each example is various, they could not be used directly. Accordingly, the Relative Percent Deviation (RPD) is used for each example to solve this problem. The RPD value for the data is obtained using Eq. (48).

$$RPD=\frac{Al{g}_{\mathit{sol}}-Mi{n}_{\mathit{sol}}}{Mi{n}_{\mathit{sol}}}\times 100$$ 48

where $Mi{n}_{\mathit{sol}}$ and $Al{g}_{\mathit{sol}}$ show the achieved best solution and the values of the achieved objective for each iteration of the experiment in a provided example, respectively. Therefore, the mean RPD is computed for each experiment after transforming the values of the objective to RPDs.

The provided levels with the factors (the algorithm’s parameters) are reported in Table 5, which for algorithm’s factors, three levels are provided. It should be noted that the Taguchi approach reduces the total number of tests by presenting a set of orthogonal arrays to control the proposed algorithms in a reasonable time. This approach suggests L9 for three VNS, GWO, and MGWO (see Table 6) obtained by Minitab Software.

Table 5.

The levels and factors of the algorithm’s parameters to tune the algorithms set out

Algorithm	Factor	Level
GWO, MGWO	Maximum Iteration ($Maxit)$	A = 200, B = 400, C = 600
	Number of search agents ($N$)	A = 20, B = 60, C = 100
	Initial population of wolves $\left(\mathit{nPop}\right)$	A = 50, B = 100, C = 150
VNS	Maximum Iteration ($Maxit)$	A = 200, B = 400, C = 600
	Number of neighborhood ($nn)$	A = 20, B = 30, C = 20
	Population size $\left(\mathit{nPop}\right)$	A = 50, B = 100, C = 150

Table 6.

The orthogonal array L9 for VNS, GWO, and MGWO

L9	A	B	C
1	1	1	1
2	1	2	2
3	1	3	3
4	2	1	2
5	2	2	3
6	2	3	1
7	3	1	3
8	3	2	1
9	3	3	2

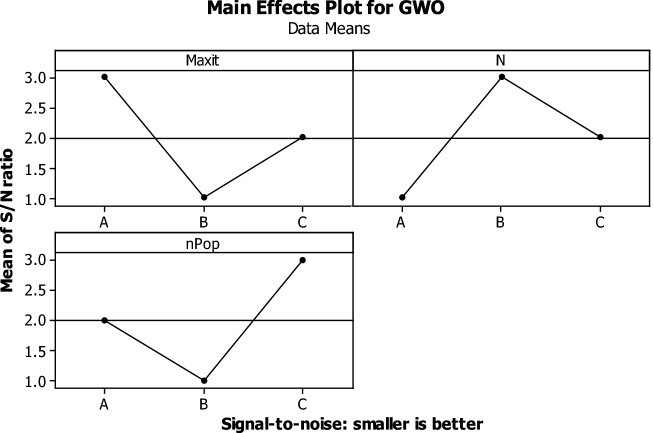
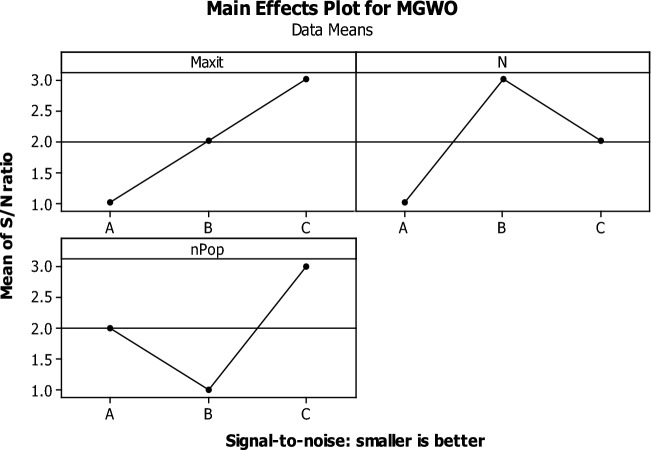
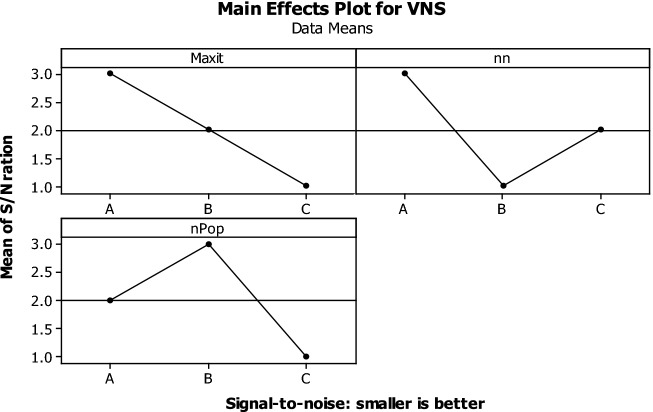
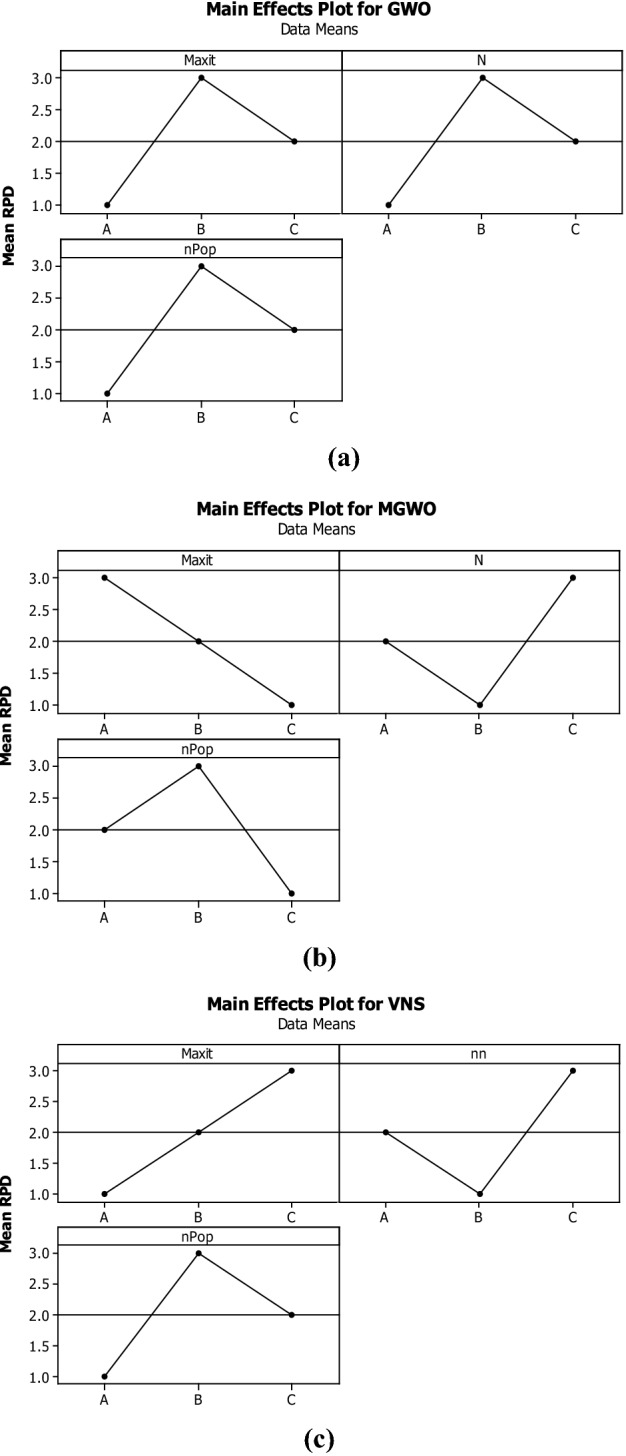
Therefore, the output of the S/N ratio should be analyzed by Minitab Software to detect the best levels for each algorithm (see Figs. 9, 10, 11). Where the S/N index has reached its minimum, the levels can be selected as the optimal levels.

Fig. 9.

Minitab Software output for the Taguchi method of the GWO algorithm

Fig. 10.

Minitab Software output for the Taguchi method of the MGWO algorithm

Fig. 11.

Minitab Software output for the Taguchi method of the VNS algorithm

The RPD is also used to confirm the selected best factors based on S/N ratios. Figure 9 shows the outcomes of RPD for each parameter level. It is clear that in Fig. 12, the RPD shows the best factors, which confirm the same outcomes as S/N ratios.

Fig. 12.

Mean RPD plot for each level of the factors

The LP-metric method and three meta-heuristics (GWO, VNS, and MGWO) are therefore provided to solve the experimental problems. Table 7 illustrates the results of the objective functions and computational (CPU) time. Figure 13 shows the behavior of CPU time of the proposed methods in small- and medium-sized problems.

Table 7.

The average results of objective functions and CPU times (based on seconds) of the method developed

Problem size	Objective function	LP-metric	CPU	GWO	CPU	MGWO	CPU	VNS	CPU
S1	$Z_1$ $Z_2$ $Z_3$ $Z_4$	374,125.4 1035 58.73 237.05	6	374,125.4 1035 58.73 237.05	6	374,125.4 1035 58.73 237.05	6	374,125.4 1035 58.73 237.05	7
S2	$Z_1$ $Z_2$ $Z_3$ $Z_4$	389,209.3 1108 84.52 318.47	159	389,238.9 1123 85.29 320.98	11	389,233.3 1114 84.86 319.73	11	389,245.7 1127 85.33 322.15	13
S3	$Z_1$ $Z_2$ $Z_3$ $Z_4$	467,910.2 1433 127.94 485.34	479	467,978.7 1439 128.89 487.30	54	467,965.0 1436 128.23 486.46	38	467,989.4 1442 129.32 489.19	66
S4	$Z_1$ $Z_2$ $Z_3$ $Z_4$	609,198.5 2674 177.84 539.47	703	609,209.4 2682 183.93 545.48	68	609,203.7 2678 179.23 542.40	49	609,211.0 2688 186.09 549.08	74
S5	$Z_1$ $Z_2$ $Z_3$ $Z_4$	769,428.6 3002 298.67 723.31	1454	769,444.7 3015 303.25 735.39	78	769,435.3 3009 300.44 728.14	55	769,449.1 3021 311.69 738.08	83
M1	$Z_1$ $Z_2$ $Z_3$ $Z_4$	– – – –	–	1,012,524.0 3877 411.5 816.32	99	1,012,508.3 3875 408.9 811.56	68	1,012,538.3 3881 417.2 821.55	103
M2	$Z_1$ $Z_2$ $Z_3$ $Z_4$	– – – –	–	1,014,025.3 3909 463.5 871.19	110	1,013,988.0 3901 459.1 866.04	82	1,014,036.4 3914 468.9 880.25	122
M3	$Z_1$ $Z_2$ $Z_3$ $Z_4$	– – – –	–	1,015,589.6 3998 504.4 940.10	135	1,015,573.6 3995 499.3 931.11	98	1,015,573.6 4006 514.4 949.68	151
M4	$Z_1$ $Z_2$ $Z_3$ $Z_4$	– – – –	–	1,222,556.4 4219 562.6 1035.08	149	1,222,539.5 4210 557.2 1026.75	115	1,222,566.2 4222 565.3 1042.61	179
M5	$Z_1$ $Z_2$ $Z_3$ $Z_4$	– – – –	–	1,319,439.1 4435 5816.9 1267.03	173	1,319,428.4 4426 5810.3 1256.08	144	1,319,445.9 4441 5826.6 1274.11	188

Fig. 13.

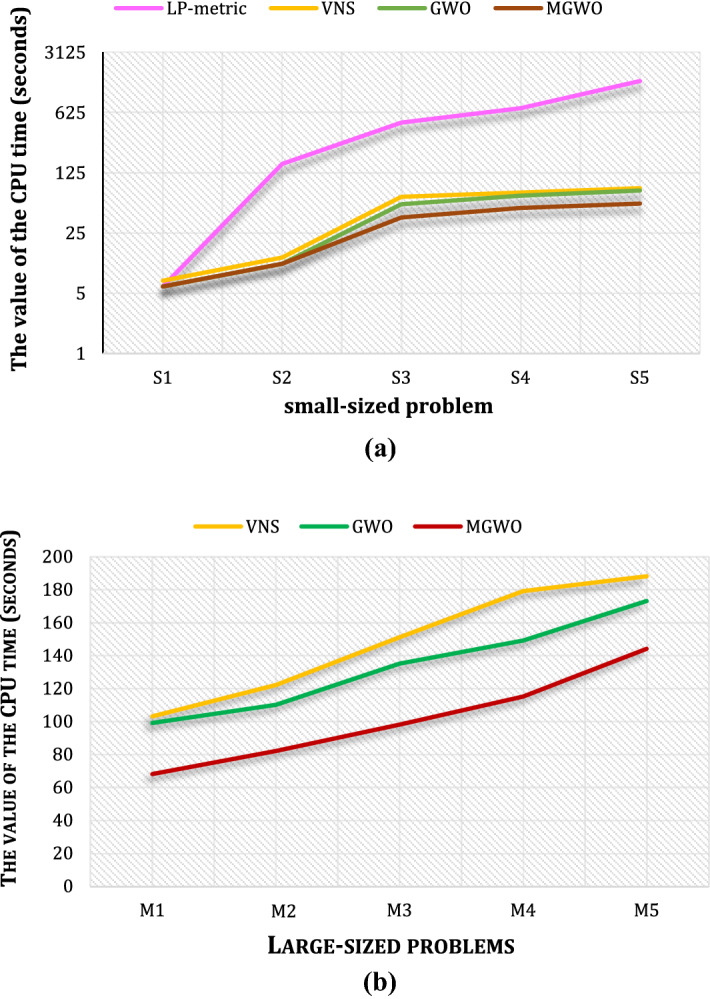
The behavior of CPU time of the proposed methods in small- and medium-sized

Assessment metrics

In this sub-section, various efficiency evaluation metrics are suggested to compare the quality of the non-dominated solutions obtained for the proposed meta-heuristic methods. Therefore, four assessment metrics are used to evaluate the algorithms. They work as follows:

• Percentage of Domination (POD): This metric assesses the ability of an algorithm to dominate the solutions of other algorithms (Govindan et al., 2015).

  $$POD\left(X^{\prime },X^{″},\dots ,X^{″\prime }\right)=\frac{\left|\left\{x_{\mathit{ki}}{X}_i\right\}\left|x_{\mathit{kj}}{X}_j,ij:x_{\mathit{ki}}\le x_{\mathit{kj}}\right)\right|}{\left|X_j\right|}\times 100$$ 49

  where $X_i$ and $X_j$ show non-dominated solutions of the proposed algorithms. One Pareto set $X^{″}$ is covered by another solution set $X^{\prime }$ by comparing the number of solutions in $X^{″}$ covered by solutions in $X^{\prime }$. In this regard, if the number of algorithms is more than two, all pair combinations should be analyzed. To calculate the POD, all the non-dominated solutions acquired by algorithms are combined into one Pareto set, and the percentage of solutions belonging to each algorithm is then calculated.

• The Number of Pareto Solutions (NPS): NPS computes all the non-dominated solutions obtained by an algorithm (Goodarzian, Taleizadeh, et al., 2021 and b)

• Data Envelopment Analysis (DEA): This metric specifies the performance of the algorithm versus other algorithms (Yu et al., 2021). One of the best-known criteria in the field of multi-criteria decision-making is DEA. This criterion is used for the assessment of the efficiency of choice with some attributes compared to each other. In this paper, this criterion is used to determine the performance of non-dominated solutions achieved by each algorithm. To compute this assessment metric, all non-dominated solutions achieved by the algorithms are combined, and the performance of these points is computed by the DEA model, which was introduced by Amin (2009).

• Diversification Metric (DM): DM counts the spread of the non-dominated solution set (Nemati-Lafmejani et al., 2019). It is calculated using Eq. (50).

  $$DM=\sqrt{{\left(max{f}_{1i}-min{f}_{1i}\right)}^2+{\left(max{f}_{12i}-min{f}_{2i}\right)}^2}$$ 50

In this paper, four assessment metrics are suggested to evaluate the performance of the proposed meta-heuristic algorithms. Hence, according to obtained Pareto front, the assessment metrics are counted to evaluate the proposed algorithms’ performance, as shown in Table 8. According to Table 8, MGWO shows high performance and efficiency over VNA and GWO algorithms as four assessment metrics have a high value (more is better for four assessment metrics), but VNS has the worst performance than the other algorithms in terms of the four assessment metrics.

Table 8.

The results of the assessment metrics for the algorithms set out

Sample	POD			NPS			DEA			DM
	VNS (%)	GWO (%)	MGWO (%)	VNS	GWO	MGWO	GWO	GWO	MGWO	VNS	GWO	MGWO
S1	22	31	38	4	7	10	0.22	0.27	0.31	12	11	17
S2	25	34	40	3	5	9	0.25	0.32	0.34	9	10	16
S3	27	38	44	5	8	12	0.18	0.21	0.28	10	13	18
S4	29	39	48	3	6	8	0.28	0.31	0.34	7	6	10
S5	32	35	42	6	9	10	0.17	0.23	0.28	8	10	12
M1	23	27	32	4	8	11	0.23	0.31	0.42	11	9	14
M2	25	29	35	5	7	9	0.19	0.26	0.31	6	8	10
M3	24	28	33	3	7	10	0.21	0.31	0.42	15	17	21
M4	28	32	37	7	10	12	0.16	0.21	0.29	11	9	16
M5	31	34	38	6	9	10	0.24	0.29	0.33	13	8	16

In this regard, an example of non-dominated solutions of suggested algorithms in an experimental problem (M1) is displayed in Fig. 14. It is clear that MGWO indicates the best efficiency, and VNS shows the worst proficiency.

Fig. 14.

The trend of the non-dominated solutions for the proposed algorithms in M1

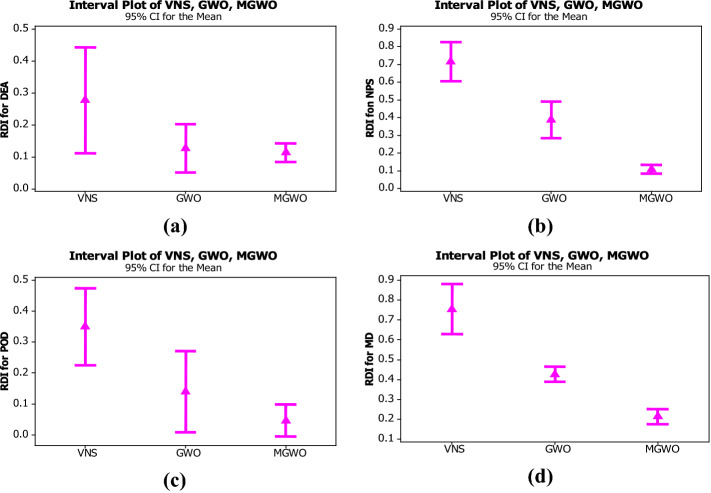
Moreover, a set of statistical comparisons between the proposed meta-heuristic algorithms according to the assessment metrics are performed to realize which the presented meta-heuristic is the best. Furthermore, the attained outputs of the suggested problems are transformed to Relative Deviation Index (RDI) that is calculated based on Eq. (51):

$$RDI=\frac{\left|Al{g}_{\mathit{sol}}-Bes{t}_{\mathit{sol}}\right|}{Ma{x}_{\mathit{sol}}-Mi{n}_{\mathit{sol}}}\times 100$$ 51

where $Bes{t}_{\mathit{sol}}$ shows the best solution between the algorithms. $Al{g}_{\mathit{sol}}$ indicates the value of the objective function. $Mi{n}_{\mathit{sol}}$ and $Ma{x}_{\mathit{sol}}$ illustrate the minimum and maximum values of the proposed assessment metrics. Accordingly, the confidence interval of 95% for the assessment metrics in the algorithms set out is conducted to analyze the efficiency of the presented meta-heuristics statistically. Figure 15 depicts the Mean plots and LSD intervals for the proposed meta-heuristics.

Fig. 15.

The means plot and LSD intervals for the suggested algorithms

It should be noted that the lower the value of RDI, the better. In Fig. 15, in terms of the MD, POD, DEA, and NPS metrics, the value of the RDI for MGWO is lower than the GWO and VNS algorithms and indicates that MGWO has the best statistical performance, but VNS has the highest value of the RDI and shows the worst performance.

Convergence of the proposed meta-heuristic algorithms

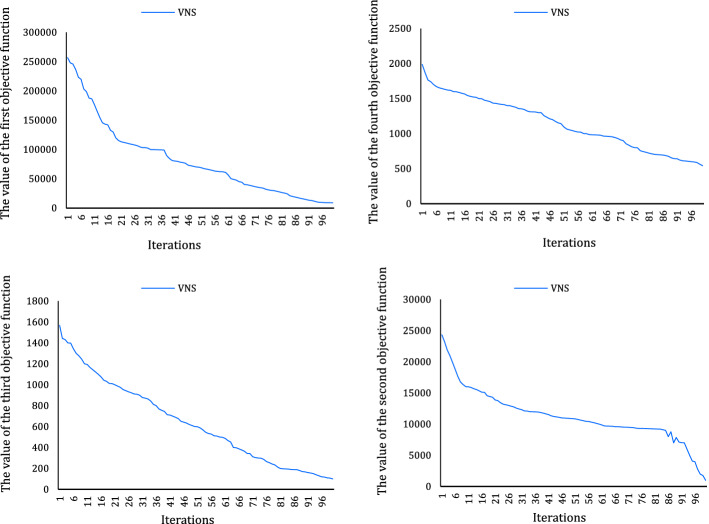
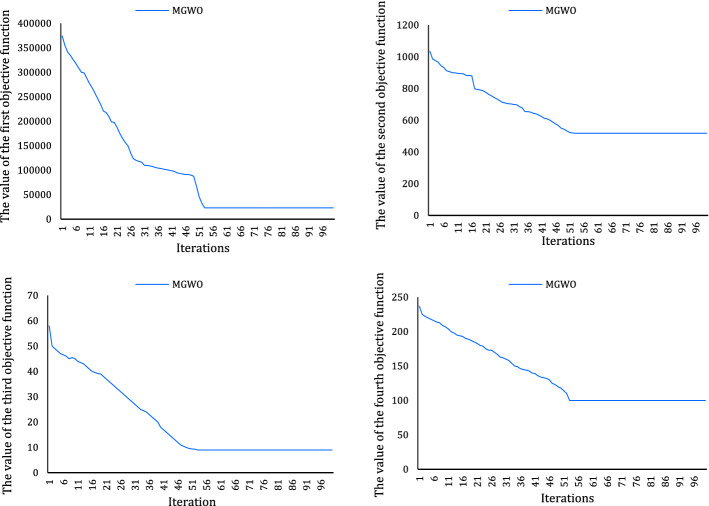
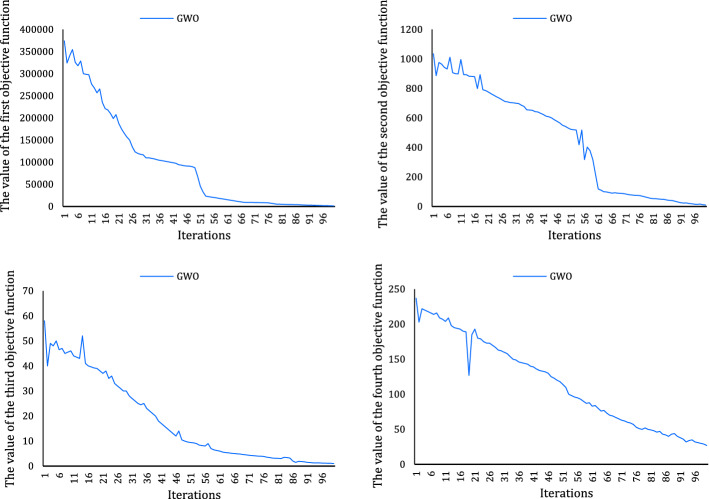
The efficiency of the algorithms set out as regards their convergence is surveyed by the plots of the convergence. Thus, the plots of the convergence for three proposed algorithms (VNS, GWO, and MGWO), respectively, based on the objective functions, are shown in Figs. 16, 17, 18. It is evident that MGWO is fixed after 54 iterations with a steady line. But the GWO and VNS algorithms are converging after 100 iterations. As a result, the MGWO has the best quality, and performance, and high convergence compared to VNS and GWO algorithms.

Fig. 16.

Convergence of VNS

Fig. 17.

Convergence of MGWO

Fig. 18.

Convergence of GWO

Case study

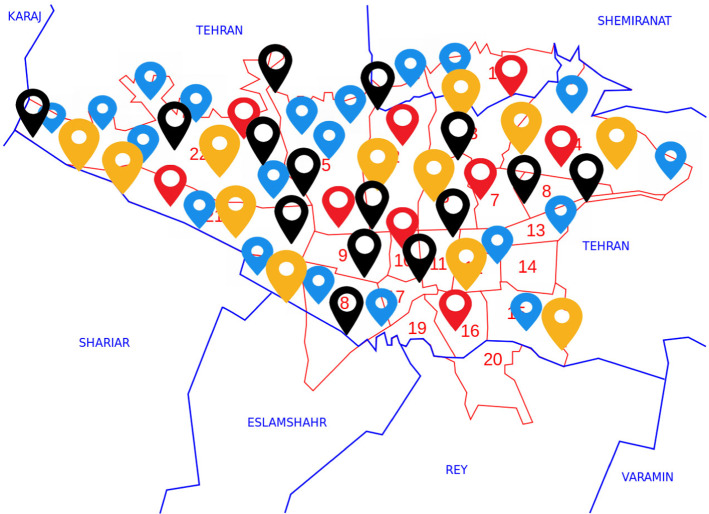
The city of Tehran is the capital of Iran that is one of the most populous cities in Asia. As of 01.07.2021, 3,218,860 people had COVID-19, and 84,389 people had died. The Ministry of Health has announced that the number of hospitalizations is increasing due to the start of the fifth COVID-19 wave. The time period considered in the case study is the first 6 months of 2021. Decision-makers’ main purpose in the case study is to minimize costs, delivery time, environmental costs, and demand coverage. In the case study, 9 distribution centers, 20 temporary vaccination centers, 12 hospitals, and 15 temporary treatment centers are considered. Decision-makers’ main concern is the location of temporary vaccination and treatment centers. Also, allocating vaccination centers and hospitals to temporary treatment centers is one of the main decisions addressed in this research. Finally, the number of vaccines sent from suppliers to other centers, the number of cars required to transport the vaccines, and the delivery time of the vaccines are among the items examined in the case study. It should be noted that due to the prevalence of two types of vaccines, $\mathit{Barekat}$ and $Sputnik,$ in Iran, these two types of vaccines have been considered in this study. Figure 19 shows a case study map. As it makes clear, distribution centers are marked in red, temporary vaccination centers are marked in blue, hospitals are marked in yellow, and temporary treatment centers are marked black.

Fig. 19.

Case study map

Table 9 shows the distance between hospitals and temporary treatment centers in kilometers. Moreover, Table 10 details the capacity of temporary vaccination centers by vaccine dose.

Table 9.

The distance between hospitals and temporary treatment centers

J/H	H1	H2	H3	H4	H5	H6	H7	H8	H9	H10	H11	H12
J1	6	37	5	18	20	34	40	45	51	50	43	31
J2	39	32	27	33	48	6	47	29	29	19	47	11
J3	35	41	41	51	45	45	8	55	17	50	48	16
J4	35	45	54	37	16	18	23	45	23	38	28	15
J5	7	5	23	50	22	27	54	55	29	24	16	5
J6	19	11	32	27	39	32	47	29	19	39	18	22
J7	37	19	30	46	7	52	37	38	37	18	47	41
J8	45	31	37	41	23	8	33	37	27	51	10	22
J9	13	28	14	28	44	28	23	49	40	48	20	48
J10	38	28	49	6	9	36	6	15	35	49	43	28
J11	29	52	34	53	18	6	7	37	55	33	52	40
J12	50	39	5	30	5	27	6	18	45	13	10	26
J13	44	41	41	15	53	12	19	53	34	7	36	33
J14	53	51	54	42	47	18	39	53	9	55	6	5
J15	21	29	51	46	52	18	19	29	41	27	19	37

Table 10.

The capacity of TVC $k$ vaccine type $v$

TVC	TVC1	TVC2	TVC3	TVC4	TVC5	TVC6	TVC7	TVC8	TVC9	TVC10
CAP V1	20,000	15,000	10,000	20,000	20,000	15,000	25,000	10,000	25,000	20,000
CAPV2	20,000	10,000	10,000	20,000	15,000	15,000	25,000	10,000	10,000	10,000
TVC	TVC11	TVC12	TVC13	TVC14	TVC15	TVC16	TVC17	TVC18	TVC19	TVC20
CAP V1	20,000	20,000	20,000	15,000	15,000	10,000	15,000	25,000	25,000	20,000
CAPV2	15,000	10,000	15,000	15,000	10,000	10,000	15,000	20,000	20,000	15,000

The results of the case study

The results of the case study are investigated in this sub-section. Accordingly, Table 11 shows the Pareto points resulting from the case study solution. This table shows 10 different Pareto points with their CPU time. Due to the importance of the third objective function (minimizing delivery time) compared to other objective functions, in the case study, the Pareto point with the shortest delivery time is selected to report the results.

Table 11.

The results of the Pareto points from the case study solution

	${\mathit{F}}_1$	${\mathit{F}}_2$	${\mathit{F}}_3$	${\mathit{F}}_4$	Time(s)
1	1,724,319	5293	6609	1673.2	173
2	1,724,786	5325	6647	1694.1	182
3	1,725,085	5367	6684	1716.6	186
4	1,725,335	5405	6700	1755.4	192
5	1,725,443	5454	6748	1781.9	199
6	1,725,611	5479	6778	1802.3	211
7	1,725,698	5539	6815	1823.5	213
8	1,725,884	5597	6838	1846.9	225
9	1,726,232	5671	6877	1892.0	229
10	1,726,609	5709	6910	1925.6	236

Table 12 shows the TVCs and TTCs established. As is known, 17 centers will be established, and centers 3, 8, and 12 will not be established. Also, in the case study, 14 TTCs were established, and only TTC Center No. 2 was not established.

Table 12.

The location of the established TVCs and TTCs

TVC	TVC1	TVC2	TVC3	TVC4	TVC5	TVC6	TVC7	TVC8	TVC9	TVC10
Establish	1	1	0	1	1	1	1	0	1	1
TVC	TVC11	TVC12	TVC13	TVC14	TVC15	TVC16	TVC17	TVC18	TVC19	TVC20
Establish	1	0	1	1	1	1	1	1	1	1
TTC	TTC1	TTC2	TTC3	TTC4	TTC5	TTC6	TTC7	TTC8	TTC9	TTC10
Establish	1	0	1	1	1	1	1	1	1	1
TTC	TTC11	TTC12	TTC13	TTC14	TTC15
Establish	1	1	1	1	1

Table 13 displays the allocation of TTCs to hospitals. For example, it is clear that TTC 1 is assigned to hospitals 2, 3, 4, 6, 8, 11, and 12. Also, TTC 9 is assigned to 3, 6, and 8 hospitals.

Table 13.

Allocation of TTCs to hospitals

J/H	H1	H2	H3	H4	H5	H6	H7	H8	H9	H10	H11	H12
J1	1	1	1	1	0	1	0	1	0	0	1	1
J2	0	1	0	0	1	1	1	1	1	1	1	0
J3	1	0	0	0	1	1	0	1	0	1	0	1
J4	0	1	0	1	0	0	0	1	1	1	1	1
J5	0	1	1	1	0	0	0	1	1	1	0	1
J6	0	0	0	1	1	0	0	1	1	1	1	0
J7	0	0	1	0	1	0	1	0	1	0	0	0
J8	0	0	1	0	0	0	0	0	0	1	1	1
J9	0	0	1	0	0	1	0	1	0	0	0	0
J10	1	0	1	0	0	1	0	0	1	0	1	1
J11	1	0	0	0	0	0	1	1	1	0	1	1
J12	0	0	0	1	1	0	0	1	0	0	0	0
J13	0	1	1	1	1	0	0	1	1	0	1	0
J14	0	0	0	1	0	0	1	0	0	0	1	1
J15	1	0	1	1	0	0	1	0	1	1	0	1

Thus, Table 14 represents the quantity of delivered vaccine from DCs to the hospital by dose. For instance, supplier 1 sent 3952, 1612, 1807, 2189, 3089, 2785, 2022, and 1788 vaccine doses to hospitals 1, 3, 4, 5, 6, 7, 11, and 12, respectively.

Table 14.

The amount of vaccine that is transported from the DC to the hospital

I/H	H1	H2	H3	H4	H5	H6	H7	H8	H9	H10	H11	H12
I1	3952	0	1612	1807	2189	3089	2785	0	0	0	2022	1788
I2	0	1694	2318	0	2003	2862	0	1191	3597	1693	0	2926
I3	2110	1092	3017	3387	0	2251	1501	0	2769	2349	0	1618
I4	0	1620	1122	1276	0	2128	1475	2443	3614	2495	1301	2423
I5	1749	0	2789	3126	2824	0	1084	0	1992	2678	3366	0
I6	3192	2926	2796	0	2258	0	1533	2931	1217	2284	1264	0
I7	0	2997	2793	1498	0	0	0	1246	3260	3758	0	1058
I8	1390	1589	2856	3855	2985	3761	3154	0	0	1464	2742	3984
I9	1069	0	1921	0	1483	2729	1481	0	2732	3795	3775	0

Sensitivity analysis

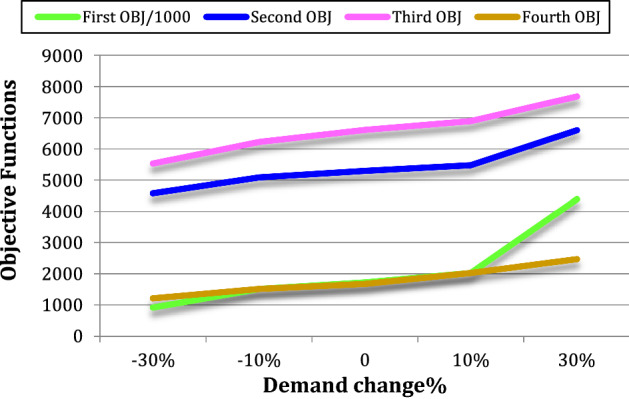
Here, a set of sensitivity analyses on important parameters are performed. In this regard, Fig. 20 shows the changes in objective functions in terms of demand change. As can be seen, with increasing demand, supply chain costs (OBJ1) increase sharply. The reason for this is the increase in the number of transportation times and the increase in transportation costs. For example, with a 30% increase in demand, costs increase to 4,389,918 units, and with a 30% decrease in demand, costs fall to 914,125 units.

Fig. 20.

The trend of the changes in objective functions in terms of demand change

Also, as demand increases, the amount of demand coverage (OBJ2) increases. For example, given a 10% increase in demand, unsatisfied demand increases to 5476 units, and if there is a 10% decrease in demand, unsatisfied demand decreases to 5085 units. Then, as demand increases, delivery time also increases. The reason for this is the increase in the number of transportation times. Finally, with increasing demand, the environmental impact also increases. For instance, given a 30% increase in demand, environmental costs increase to 2469.9 units, and given a 30% decrease in demand, environmental costs decrease to 1210.9 units.

Figure 21 shows the changes in the number of established centers as demand increases. It is clear that with the increase in demand, the number of established TVC and TTC increases. Accordingly, given a 10% increase in demand, 17 TTCs and 24 TVCs were established. Additionally, given a 30% increase in demand, 23 TTCs and 31 TVCs were established. Finally, given a 30% drop in demand, 9 TTCs and 10 TVCs were established.

Fig. 21.

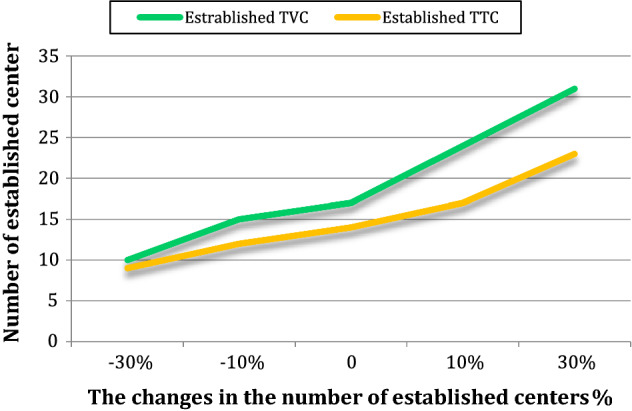
The trend of the changes in the number of established centers as demand increases

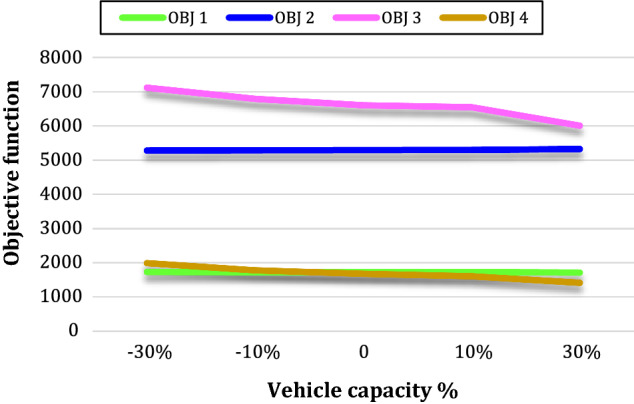
In the following, Fig. 22 depicts the effect of vehicle capacity changes on objective functions. As can be seen, supply chain costs decrease as vehicle capacity increases. The reason for this is to reduce the number of transportation times and minimize transportation costs. The second objective function remains almost constant as vehicle capacity increases and decreases.

Fig. 22.

The behavior of the effect of vehicle capacity changes on objective functions

Delivery time decreases as vehicle capacity increases. For instance, given a 30% increase in vehicle capacity, the delivery time will decrease by 6009 units, and if there is a 30% decrease in vehicle capacity, the delivery time will increase to 7123 units. The reason for this is the reduction in the number of transportation times and of course faster service.

Environmental costs are reduced by increasing the capacity of vehicles due to the reduction in the number of times of transportation. For example, if there is a 10 percent increase in vehicle capacity, costs are reduced to 1602.7 units, and with a 10 percent increase in vehicle capacity, costs are reduced to 1411.3 units.

Figure 23 shows the changes in the fixed cost of establishing the TVCs as demand increases. It is clear that as the fixed cost of establishing TVCs increases, the total cost of the supply chain, delivery time, and the amount of unmet demand also increase. Also, with an increase in the fixed cost of establishing TVC, the environmental impacts decrease. There is a 30% increase in the fixed cost of setting up TVC, which makes it more expensive to set up the supply chain. The total cost rises to 3983.3, the unmet demand rises to 6756 units, the delivery time rises to 7378 s, and the environmental impacts fall to 1186.4 units.

Fig. 23.

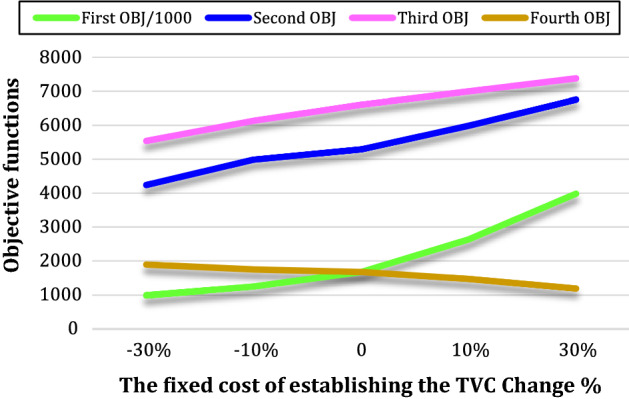
The behaviour of the effect of the fixed cost of establishing the TVC on objective functions

Managerial insights

Air pollution is the fourth leading cause of premature death globally after hypertension, smoking, and malnutrition, and the second leading cause of death from non-communicable diseases after smoking. Thus, increasing the number of airborne particles can increase the transmission of coronavirus and respiratory infections. Air pollution increases the risk of respiratory diseases. COVID-19 is essentially a respiratory disease, which is why people living in polluted areas are more vulnerable to the COVID-19. Managers, on the other hand, are told to use more hybrid cars to cut down on air pollution.

As the capacity of vehicles increases, it can reduce supply chain costs and environmental impacts. Therefore, it is recommended that managers increase the vaccine capacity of vehicles. It also minimizes vaccine delivery time.

Based on the results of this research, the IoT-based infrastructure can be widely deployed to combat pandemics. Regarding the weird behavior of COVID-19, new variants, e.g. Delta and Lambda mutations, have emerged over time. Based on daily COVID-19 active cases, vaccines should be injected periodically to protect people against the incapacitating virus. Therefore, healthcare managers can use the specific mobile application for booking vaccination appointments, prioritizing people for receiving vaccines, and assessing people’s wellbeing before and after vaccination. The more IoT-based devices are used, the less inequality there is, shortages are eased, and vaccine distribution accelerates. It should be noted that finding the exact quantity of demand for each priority is impactful on the reduction of a vaccine shortage.

Also, determining the optimal location of vaccination and medical centers reduces costs and minimizes vaccine delivery times and unsatisfied demand, thus fulfilling more requests for vaccine injections. As a result, the results of this research may be useful to organizations such as the Crisis Relief Organization, hospitals, the Ministry of Health, vaccination centers, municipalities, and vaccine transportation companies, among others.

Conclusion and future work

In this study, a four-echelon, multi-objective model for the green-cold vaccine supply chain network during the COVID-19 pandemic is developed for the first time. In this regard, minimizing supply chain costs, demand coverage, delivery time, and adverse environmental effects are the most important aims of this study. Moreover, considering the use of IoT to manage the supply chain of the COVID-19 vaccine with a simultaneous focus on distribution-location-allocation decisions in the proposed network is one of the novelties of this study. Therefore, to solve the proposed problem, GWO and VNS algorithms are suggested, and a new heuristic method called modified GWO (MGWO) is developed for the first time. Additionally, a real case study is considered in the proposed network for distributing the COVID-19 vaccines in Tehran/Iran.

The results of model solving indicate that the MGWO algorithm performed better than other proposed algorithms as regards CPU time and convergence as well as in terms of assessment metrics. The results of a case study show that 17 temporary vaccination centers and 14 temporary treatment centers have been established. As can be seen, supply chain costs increase sharply as demand increases. The reason for this is the increase in total transportation time and the increase in transportation costs. Also, increasing demand increases delivery time, environmental effects, and the number of established centers. Additionally, as vehicle capacity increases, supply chain costs, delivery times, and environmental impacts decrease. The reason for this is to reduce the number of transportation times and minimize transportation costs.

The following matters are suggested for future work:

• Considering demand forecasting approaches such as neural network and a fuzzy inference system to predict the required vaccine demand

• Presenting the cooperative game and cooperation of different organizations to minimize the delivery time of vaccines to vaccination centers

• Using scenario uncertainty and solve the mathematical model by the robust optimization approach

• Other decisions such as routing vaccine vehicles or other objectives such as maximizing justice in vaccine distribution