Abstract
Recently, lineage tracing technology using CRISPR/Cas9 genome editing has enabled simultaneous readouts of gene expressions and lineage barcodes, which allows for the reconstruction of the cell division tree and makes it possible to reconstruct ancestral cell types and trace the origin of each cell type. Meanwhile, trajectory inference methods are widely used to infer cell trajectories and pseudotime in a dynamic process using gene expression data of present-day cells. Here, we present TedSim (single-cell temporal dynamics simulator), which simulates the cell division events from the root cell to present-day cells, simultaneously generating two data modalities for each single cell: the lineage barcode and gene expression data. TedSim is a framework that connects the two problems: lineage tracing and trajectory inference. Using TedSim, we conducted analysis to show that (i) TedSim generates realistic gene expression and barcode data, as well as realistic relationships between these two data modalities; (ii) trajectory inference methods can recover the underlying cell state transition mechanism with balanced cell type compositions; and (iii) integrating gene expression and barcode data can provide more insights into the temporal dynamics in cell differentiation compared to using only one type of data, but better integration methods need to be developed.
INTRODUCTION
Understanding how single cells divide and differentiate into different cell types in developed organs is one of the major tasks of developmental biology. The temporal dynamics of cells are being studied by various approaches from different aspects. First, trajectory inference (TI) methods (1–5) are developed to infer the trajectories of cells from single-cell gene expression data, typically obtained from single-cell RNA sequencing (scRNA-seq) experiments. TI methods make the assumption that although the cells sequenced together are collected at the same time, they represent different stages of the temporal dynamics process in the cell populations. Prevalent TI methods aim to find the trajectory backbone that represents the major cell states and the dynamic paths between the states, and then ‘sort’ the cells onto the backbone structure. These methods have assisted biological discoveries in various biological systems (6–9); however, it is not clear whether using only the scRNA-seq data of present-day cells can always reconstruct the cell trajectories, as some information may have been lost during the developmental processes and not captured in the scRNA-seq data (10–12).
Second, lineage tracing technologies using CRISPR/Cas9 genome editing technology blaze a new trail to study the cell developmental mechanisms. A barcode is inserted into the genome that accumulates CRISPR-induced mutations during the process of the cell divisions, and the mutated barcode can be read out together with the gene expression profile in a cell through scRNA-seq (10,13–15). This barcode will be referred to as lineage barcode in this paper. Thus, the output of these lineage tracing experiments is composed of two types of data: the single-cell gene expression and the lineage barcode of each cell. Computational tools to reconstruct the cell division history of single cells from the lineage barcodes are widely explored (16,17). In an ideal scenario, the reconstructed cell division tree along with the gene expression profiles of present-day cells can provide insights into how different cell types originate from progenitor cells, and allow us to draw the cell fate map at an unprecedented high resolution. However, the missing data in the lineage barcodes and the large number of cells pose challenges for cell lineage tree reconstruction methods, resulting in low-resolution, inaccurate reconstructed trees.
With simultaneously profiled single-cell gene expression data and lineage barcodes, methods that integrate the two modalities started to emerge, aiming to achieve better results than the unimodal methods in terms of inferring cell lineage and developmental trajectories. However, only a few methods have been developed to date and their performances are unclear (17–19).
Previously, computational tools to simulate either single-cell gene expression data (20–22) or lineage barcode data (23) were proposed. Due to the lack of ground truth information in biology, simulation tools have been used to provide quantitative evaluations of existing computational methods and set baselines for the development of new methods. Existing simulators for single-cell gene expression data mostly sample gene expression levels of single cells from probability distributions of the data under certain statistical assumptions (20–22). The synthetic expression levels can maintain transcriptome similarity between cells but do not maintain the actual lineage relationships between single cells. On the other hand, Salvador-Martínez et al. developed a simulator to generate the lineage barcode information by simulating the cell division processes but not the gene expression data (23).
The joint profiling of single-cell gene expression and the lineage tracing barcode data allows for the analysis of the origin of various cell types. Previously, the lineage barcodes and the gene expression data, respectively, were utilized to reconstruct the lineage tree and identify the cell types separately (10,13–15,24). Recently, hybrid methods that attempt to use both types of information are being designed to either use the gene expression information to obtain better lineage trees (17), to reconstruct transcriptome and cell states of ancestral cells (19), or use the lineage information to improve the ancestor–descendant relationship inferred from gene expression data (18). To study the relationship between gene expression and lineage origins and to evaluate the hybrid methods, we need to generate both single-cell gene expression and lineage barcode information simultaneously along the cell division processes with ground truth information on the cell division history and cell state transition.
In this paper, we present TedSim (single-cell temporal dynamics simulator), the first simulator that outputs combined readouts of single-cell gene expression and lineage barcode data. Unlike existing simulators for scRNA-seq data (20,22,25), TedSim simulates the actual cell division events and obtains cells of different cell types at different stages of the developmental trajectories, alongside with lineage barcodes through genetic scarring during cell divisions.
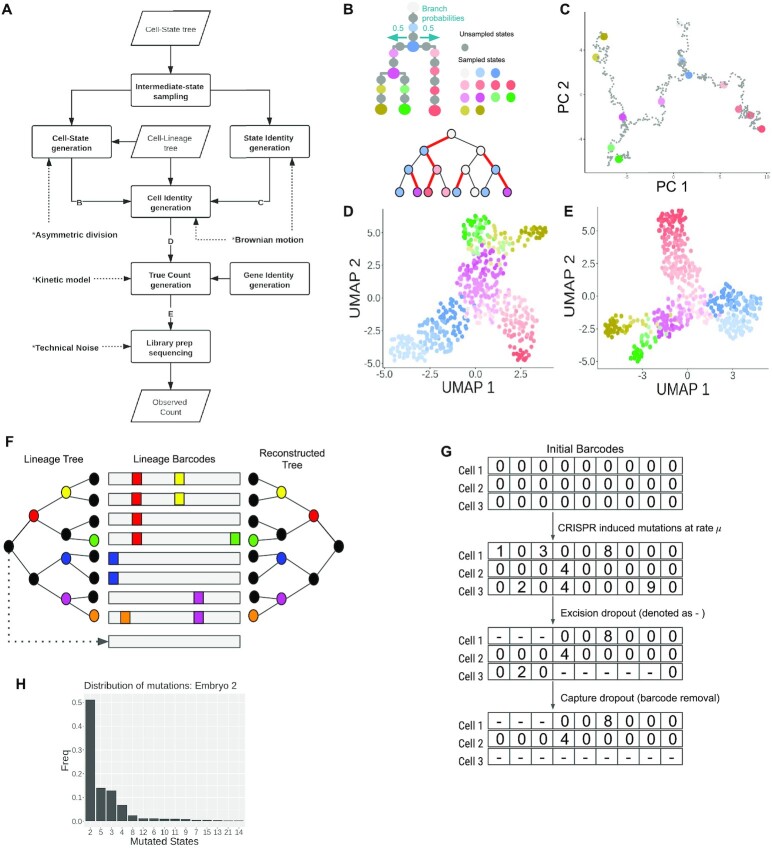
One key feature of TedSim that distinguishes it from existing scRNA-seq simulators is that it generates observed scRNA-seq data through cell division events, which is closer to what happens in biology. How to obtain various cell types through cell divisions is a challenge for TedSim. We present a simple model that utilizes asymmetric cell divisions (26–28) to assign cell types on the cell division tree. We consider an underlying cell state tree, which represents the developmental paths of cell states, as the input to TedSim. The cell state tree helps to determine the states of the cells on the cell division tree (Figure 1). The state shifts of cells during cell divisions are achieved by asymmetric cell divisions, and at the same time genetic scarring events can happen in the lineage barcodes and be inherited by the daughter cells.
Figure 1.
TedSim workflow. The cell state tree models the true trajectories of cell differentiation and the cell division tree represents the true lineage. When traversing the cell division tree from root to leaves, the cell states are determined based on the state tree and the asymmetric division events (denoted by red edges in the cell division tree). TedSim simultaneously simulates gene expressions and lineage barcodes of all the cells, while the state and lineage relationships of the cells are maintained. The simulated data can be used to test not only TI or tree reconstruction methods, but also hybrid methods that use both gene expression and lineage barcode data.
We show that TedSim can generate both discrete and continuous cell populations, lineage barcode data with similar mutation distribution as observed in real data, and, in particular, realistic ‘relationship’ between the lineage barcode and gene expression data (Figure 1). By ‘relationship’ we particularly look into the following question: do cells from the same cell types (defined by their gene expression profiles) necessarily originate from the same clone? We show that similar to that in real data, in our simulated data, each clone can have multiple cell types and one cell type can spread over multiple clones.
We demonstrate the application of TedSim in evaluating the following computational methods (Figure 1): (i) with synthetic lineage barcodes of single cells, we can evaluate lineage tree reconstruction methods; (ii) with simulated scRNA-seq data, we can apply the TI methods and test whether using only the present-day cells can recover the underlying cell state tree; and (iii) with both lineage barcode and scRNA-seq data, we can benchmark methods that combine gene expression and lineage barcodes. In particular, we discuss the limitations of current methods that integrate the two types of data. TedSim is available at https://github.com/Galaxeee/TedSim.
MATERIALS AND METHODS
Generating single-cell gene expression data with TedSim
Cell divisions are the events through which cells form populations and various cell types. By simulating cell divisions, TedSim directly models the temporal dynamics of single cells and thus can be used to analyse the underlying relationships of lineage and gene expressions. TedSim can naturally generate discrete or continuous populations in the present-day cells, with the same underlying cell state transition mechanisms.
In order to obtain cells with diverse cell types through cell divisions, we adopt the fundamental concept of asymmetric divisions. In biology, stem cells are characterized by their ability to self-renew and produce differentiated phylogeny, which is achieved through controlled asymmetric divisions (26–28). Asymmetric division is a key process for a cell to divide into two cells with different cellular fates, where one cell remains at the same state as the parent and the other shifts to the future state that will eventually develop into fully differentiated cells. TedSim utilizes a cell state tree that models the cell differentiation process to determine the future state when a cell divides asymmetrically. Starting from the root of the cell lineage tree, a cell can divide either symmetrically into two cells of the same state as their parent or asymmetrically as described earlier. By incorporating the parent cell’s identity when generating the identity of the daughter cells, we are able to combine heterogeneities from both its cell state and lineage path. Transcriptomic data simulated by TedSim can reflect the true trajectory as demonstrated in the cell state tree while being compounded by lineage relationships between cells, which reflects the scenario in reality (29).
The process of how TedSim simulates scRNA-seq data is shown in Figure 2A. The cell state tree and cell lineage tree (Figure 2B) provide two different sources of heterogeneities in the gene expression profiles of cells, where the former represents the underlying programmed cell fate decision mechanism and the latter represents effects from clonal origins of cells. At each branching point of the cell state tree, by default each branch is taken with equal probability, but unequal branch probabilities can be used to represent different probabilities of cells going to different cell fates. Users can define the desired structure of the cell state tree using Newick format in a text file.
Figure 2.
Simulation of scRNA-seq data and lineage barcode in TedSim. (A) Flowchart of generating observed gene expression counts. Parallelogram represents input/output and rectangle represents process. ‘B’, ‘C’, ‘D’ and ‘E’ in the flowchart represent key intermediate data that are visualized in panels (B)–(E) with an example. (B) Cell state tree and cell lineage tree where each cell is coloured with its state. At an asymmetric division, a state shift happens to one of the daughter cells (the edge between this daughter cell and its parent is coloured red). (C) 2D PCA visualization of simulated state identity vectors (SIVs) along the cell state tree. The length of the SIVs is 30 (20 diff-SIVs and 10 non-diff-SIVs). (D) 2D UMAP visualization of cell identity vectors (CIVs) of 2048 cells. A CIV has the same length as a SIV. (E) 2D UMAP visualization of true counts of 2048 cells and 500 genes. (F) Reconstructing cell lineage using simulated lineage barcodes. During the cell division process, mutation events can randomly happen (different non-black colours represent different mutations and the black colour means no mutation event) and cause insertion/deletion on the lineage barcode (middle); a coloured box represents an insertion/deletion and is termed a mutated state (non-zero characters in the character vectors). Given the mutated barcodes of the present-day cells (leaf nodes of the lineage tree), tree reconstruction algorithms can be applied to infer the lineage tree (right). (G) Simulating dropouts of lineage barcodes. When two or more mutations happen at one division, the excision dropout will randomly drop characters between two mutated sites; after library preparation steps, the capture dropout will completely drop the barcode if the associated gene is not captured. (H) Distribution of mutated states (only the top 15 most frequent mutations are shown) observed in lineage barcodes of the embryo2 from Chan et al. (14). The frequencies are used to generate synthetic mutations in TedSim in the ‘biased’ mode.
We assume that cell states change gradually along the given cell state tree, and each state is represented by a SIV that can be considered as the latent representation of the state. Suppose a SIV is of length 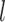 . Considering that the differences between cell states originate from only a subset of factors in the SIV, we assign
. Considering that the differences between cell states originate from only a subset of factors in the SIV, we assign 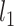 factors as differential factors that change along the cell state tree, and the rest of the
factors as differential factors that change along the cell state tree, and the rest of the 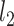 factors are sampled from the same Gaussian distribution
factors are sampled from the same Gaussian distribution 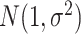 . We generate the differential SIVs along the cell state tree from the root using the Brownian motion model that was used to model the evolution of genetic traits (30). The changes of trait values of the Brownian motion are drawn from a normal distribution. That is, for each differential factor in SIVs, one starts with a given value at the root (default is 1), and for each cell state
. We generate the differential SIVs along the cell state tree from the root using the Brownian motion model that was used to model the evolution of genetic traits (30). The changes of trait values of the Brownian motion are drawn from a normal distribution. That is, for each differential factor in SIVs, one starts with a given value at the root (default is 1), and for each cell state 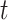 , its SIV value for this differential factor
, its SIV value for this differential factor  is calculated as
is calculated as 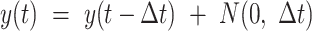 , where
, where 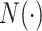 represents a Gaussian function and
represents a Gaussian function and  is the distance between state
is the distance between state 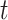 and state
and state 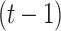 on the tree, which can also be considered as the step size of a random walk. In this manner, the covariance matrix of the generated trait values corresponds to the given tree structure (Supplementary Section S1).
on the tree, which can also be considered as the step size of a random walk. In this manner, the covariance matrix of the generated trait values corresponds to the given tree structure (Supplementary Section S1).
Figure 2C shows the 2D PCA visualization of the SIVs generated along the cell state tree in Figure 2B. To obtain a desired number of cell types in simulated data, we sample states from the cell state tree by taking the SIVs at both ends of each edge and some intermediate positions of each edge where each sampled state corresponds to a cell type. For example, in the cell state tree shown in Figure 1, we take states S0, S1, …, S12 as the sampled states to guide the state transitions in the cell division tree. These states are sampled from all states such that the distance between two adjacent sampled states on the cell state tree is the same. This distance, denoted as step_size, is a user-defined parameter used in the simulation and we will investigate the resulting cell populations with various step_size values.
Based on the cell state tree and the sampled states, we can simulate the cell divisions and the two types of information of each cell: the lineage barcode and the gene expression data. Each cell’s gene expression data are associated with a cell state sampled from the state tree and its lineage. The procedure of generating the gene expression data of a cell is illustrated in Figure 2A. Starting from the root of the cell division tree, the root cell’s state is the root state on the cell state tree. Recursively, we determine the states of the children based on the state of their parent cell, with either symmetric division or asymmetric division. At each cell division event, we first probabilistically decide whether this is a symmetric division or asymmetric division according to parameter pa, which is the asymmetric division rate. pa influences how fast the cells can get to the terminal cell states (Supplementary Section S2). Denote the cell state of the parent cell by 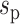 and the states of the two daughter cells by
and the states of the two daughter cells by  and
and 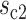 . Now we consider two cases: (i) In the case of symmetric division, the two daughter cells inherit the same cell state as their parent, that is
. Now we consider two cases: (i) In the case of symmetric division, the two daughter cells inherit the same cell state as their parent, that is 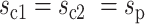 . (ii) In the case of asymmetric division, one daughter cell inherits the cell state of the parent cell, whereas the other daughter cell shifts to a future state on the cell state tree. To account for varying differentiation speeds, when a cell is moving to a future state, we allow the daughter cell’s new state to be nstep
. (ii) In the case of asymmetric division, one daughter cell inherits the cell state of the parent cell, whereas the other daughter cell shifts to a future state on the cell state tree. To account for varying differentiation speeds, when a cell is moving to a future state, we allow the daughter cell’s new state to be nstep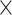 step_size after that of the parent cell, and nstep is sampled from a discrete distribution Pjump with nstep values ranging from 1 to max_step, where a larger probability is assigned to the case nstep = 1. A larger nstep value indicates that the cell differentiates faster and arrives at a state that is further away from the parent’s state on the cell state tree. When there is a split of branches on the state tree, the state shift will select an edge to follow according to the branch probabilities.
step_size after that of the parent cell, and nstep is sampled from a discrete distribution Pjump with nstep values ranging from 1 to max_step, where a larger probability is assigned to the case nstep = 1. A larger nstep value indicates that the cell differentiates faster and arrives at a state that is further away from the parent’s state on the cell state tree. When there is a split of branches on the state tree, the state shift will select an edge to follow according to the branch probabilities.
For each new cell, we generate its CIV based on the CIV of its parent and the SIV of its cell state. A CIV’s length is the same as that of the SIVs. For the daughter cells with the state as the parent cell, each value in the CIV of a daughter cell is produced by adding the CIV of its parent with a random walk distance sampled from a Gaussian distribution, that is 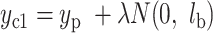 , where
, where  is the daughter cell,
is the daughter cell, 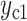 and
and  , respectively, are the CIVs of the daughter and the parent cell, and
, respectively, are the CIVs of the daughter and the parent cell, and  is the branch length in the cell division tree. If the state of the daughter cell is different from that of the parent cell (suppose this daughter cell is
is the branch length in the cell division tree. If the state of the daughter cell is different from that of the parent cell (suppose this daughter cell is 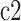 ), then
), then 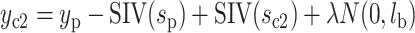 (
(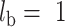 in our tests since we consider the branch lengths on the cell division to be 1), where
in our tests since we consider the branch lengths on the cell division to be 1), where 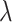 is the weight for the additional random walk distance on the cell lineage tree and it tends to be a very small value (
is the weight for the additional random walk distance on the cell lineage tree and it tends to be a very small value (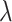 = 1/9 in the results shown in the paper) in order to ensure that the cells do not deviate too much from their state means (Supplementary Section S3). We also provide the option for users to provide a range of the start and end values for
= 1/9 in the results shown in the paper) in order to ensure that the cells do not deviate too much from their state means (Supplementary Section S3). We also provide the option for users to provide a range of the start and end values for 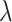 , and the
, and the  value will change for different generations of cell divisions.
value will change for different generations of cell divisions.
The CIV of each cell models the combined heterogeneities of lineage and cell type of the cell and it can be considered as the cell’s latent space representation (Figure 2D). It is then used to generate the gene expression data of the cell (Figure 2E). In Figure 2E, UMAP (31) was used to create the visualization of the gene expression data. In Supplementary Figure S1A–C, we show that t-SNE (32) and diffusion map (33) give similar visualization; thus, using UMAP for visualization of single-cell gene expression data is sufficient.
The advantages of introducing low-dimensional vectors to represent cell identities over manipulating gene expression counts directly are as follows: (i) the CIVs, as the way they are calculated, are able to characterize the biological dependences of single cells during cell divisions, which are consistent with the true trajectories provided by the cell state tree and the cell lineage tree; and (ii) performing low-dimensional random walks is informative enough to capture the variances in the transcriptomic data while at the same time making the simulation computationally efficient. The pseudocode for generating CIVs is provided in Supplementary Section S4. The values of parameters 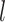 ,
,  ,
,  and
and  used in this paper are listed in Supplementary Section S5.
used in this paper are listed in Supplementary Section S5.
Apart from each cell’s CIV, we also generate a gene identity vector (GIV) for each gene following the procedure used in SymSim (22) (where the GIVs are termed as gene effect vectors). The GIV of a gene represents how much the gene is affected by each factor in the CIV. The GIVs can then be considered as the weights on the CIVs, which together decide the expression pattern of a given gene in a given cell. The details of generating GIVs are provided in Supplementary Section S6. The SIVs, CIVs and GIVs all have the same length 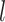 .
.
Now with the CIV of a cell and the GIV of a gene, we can generate the true mRNA counts of this gene in this cell through a two-state kinetic model (22,34), where the parameters of the kinetic model are calculated from the CIV and GIV. This step follows a similar process in SymSim (22) and is described in Supplementary Section S6. After generating the true mRNA counts of genes in cells, we follow the steps used in SymSim (22) to add technical noise to the data by simulating the major steps in scRNA-seq experiments to get realistic observed gene expression counts (Supplementary Section S6).
Generating heritable lineage barcode data with TedSim
TedSim simulates the cell lineage tree, which is a binary tree that models the cell division events (Figure 2F). Starting from the root cell, we simulate the accumulation of CRISPR/Cas9-induced scars along the paths from the root to all the leaf cells. In practice, the barcodes with accumulated scars in present-day cells can be measured using scRNA-seq and used to reconstruct the cell lineage tree (Figure 2F).
The lineage barcodes of a cell can be represented by a character vector. Each character represents a target site where a CRISPR-induced mutation can possibly happen (14,23) (Figure 2G). The root cell in the cell division tree has its default barcode with all states unmutated (an unmutated state is denoted as ‘0’). When it divides, mutations happen at a mutation rate 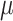 that randomly select certain target sites and change them to mutated states (denoted as non-‘0’ integers) in the daughter cells, and the mutations will be carried on to further descendants (Figure 2G). We keep the mutation rate
that randomly select certain target sites and change them to mutated states (denoted as non-‘0’ integers) in the daughter cells, and the mutations will be carried on to further descendants (Figure 2G). We keep the mutation rate 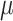 constant across all target sites and all cell divisions, and then after a number of generations, the probability of a particular target site being mutated follows a geometric distribution. We assume that the mutation is irreversible so that a mutated state will not go back to the unmutated state. And once a target site is mutated, it stays at that state and does not change into other mutated states.
constant across all target sites and all cell divisions, and then after a number of generations, the probability of a particular target site being mutated follows a geometric distribution. We assume that the mutation is irreversible so that a mutated state will not go back to the unmutated state. And once a target site is mutated, it stays at that state and does not change into other mutated states.
When an unmutated state decides to mutate (according to the mutation rate  ), it needs to choose a mutated state (a non-‘0’ integer in Figure 2G) from a set of predefined mutated states. We consider two modes regarding the transition probabilities from the unmutated state to mutated states. One is the ‘equal chance’ mode, and the other is the ‘biased’ mode. With the equal chance mode, the probability of an unmutated state changing into any possible mutated state is equal. However, it is observed in real data that different mutated states do not occur with equal frequencies, but rather show significant biases towards certain mutated states and the frequencies of the mutated states follow an exponential curve (14,23) (Figure 2H). In TedSim, we simulate this bias by sampling the mutation events from such a distribution obtained from an experimental dataset in (14). That is, given the character matrix (where each row corresponds to a cell and each column corresponds to a target site in the barcodes) of a real dataset, we first calculate the frequencies of each occurred mutation, and then take the top
), it needs to choose a mutated state (a non-‘0’ integer in Figure 2G) from a set of predefined mutated states. We consider two modes regarding the transition probabilities from the unmutated state to mutated states. One is the ‘equal chance’ mode, and the other is the ‘biased’ mode. With the equal chance mode, the probability of an unmutated state changing into any possible mutated state is equal. However, it is observed in real data that different mutated states do not occur with equal frequencies, but rather show significant biases towards certain mutated states and the frequencies of the mutated states follow an exponential curve (14,23) (Figure 2H). In TedSim, we simulate this bias by sampling the mutation events from such a distribution obtained from an experimental dataset in (14). That is, given the character matrix (where each row corresponds to a cell and each column corresponds to a target site in the barcodes) of a real dataset, we first calculate the frequencies of each occurred mutation, and then take the top  most frequent mutation states (
most frequent mutation states (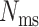 is a user-defined parameter and is set to 100 in our results). The resulting frequencies are normalized into probabilities and used in TedSim ‘biased’ mode (Figure 2H). In TedSim, we have implemented both modes. Later in this paper, we will show that the differences between the two modes of transition probabilities between mutation states can influence the performances of tree reconstruction algorithms.
is a user-defined parameter and is set to 100 in our results). The resulting frequencies are normalized into probabilities and used in TedSim ‘biased’ mode (Figure 2H). In TedSim, we have implemented both modes. Later in this paper, we will show that the differences between the two modes of transition probabilities between mutation states can influence the performances of tree reconstruction algorithms.
The problem of dropouts in the lineage barcodes is one of the main challenges towards reconstructing the cell division tree using computational algorithms. Following Salvador-Martínez et al. (23), TedSim models two types of dropouts widely occurring in wet-lab experiments (Figure 2G): ‘capture dropout’ that refers to experimental dropouts due to low capture efficiency, and ‘collapse dropout’ or ‘excision dropout’ means inter-target deletions when two or more sites are cut at the same time (35). Both dropouts are denoted as ‘-’ in the character vectors. According to experimental protocols where the barcode is inserted to a specific endogenous site (a real or an artificial gene) in the genome (36), we associate the capture dropout of the lineage barcode in each cell with the expression level of the gene in the cell. If the gene is not captured in the simulated observed counts, the capture dropout to the lineage barcode is applied. Simulating gene expression profiles together with lineage barcodes allows TedSim to generate more realistic dropout events compared to randomly removing barcodes. Due to dropouts, a number of mutation events cannot be observed, which limits the accuracy of cell division tree reconstruction. In TedSim, users can choose whether or not to generate dropouts in the simulation using a Boolean parameter pd. The pseudocode for generating lineage barcodes simultaneously with CIVs can be found in Supplementary Section S4.
Fitting simulated gene expression data to real datasets
By tuning the parameters in TedSim, we are able to generate gene expression datasets of different levels of continuity and balance the number of cells for each cell state (Figure 3A–D). Moreover, we demonstrate that TedSim can generate realistic gene expression data that share cell-type-specific properties with real datasets where there are multiple cell types. We use a zebrafish larvae dataset at 5 days post-fertilization (dpf) as the reference dataset (24) (Figure 3E). We removed undifferentiated cell types and selected 10 cell types with 9393 cells as terminal cell states (Supplementary Section S5.1). We then generate simulated data with TedSim that resemble the properties of the real data in terms of variation between cell types and gene expression distribution within each cell type, using the following procedure.
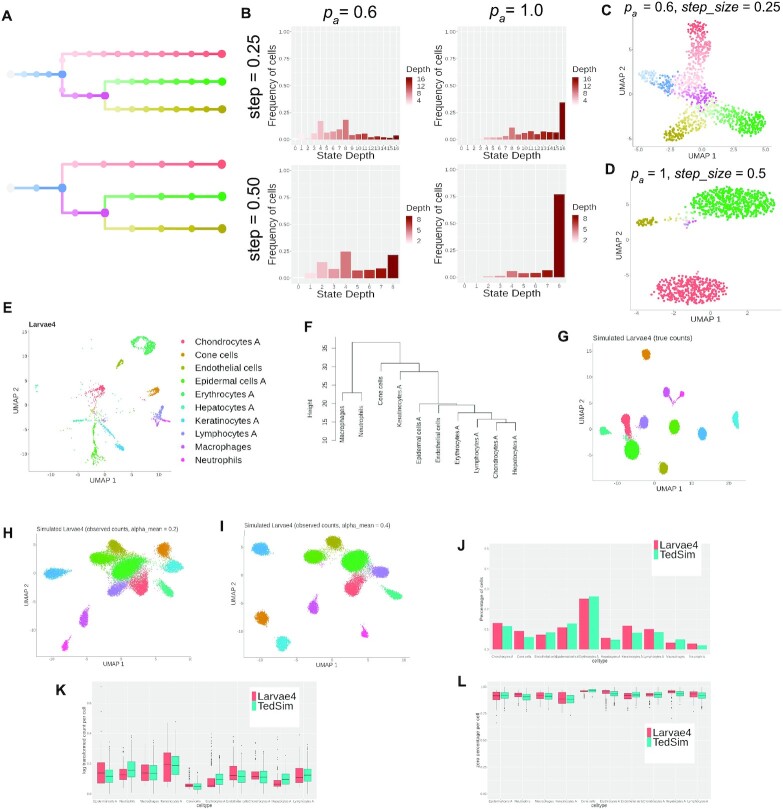
Figure 3.
TedSim simulates both continuous and discrete populations and can generate datasets with multiple cell types that resemble real datasets. (A) Cell state trees sampled with two different step_size =0.25 and 0.5; colours represent cell states in panels (C) and (D). (B) The frequency of cells belonging to each cell state in the simulated dataset, stratified by the depth of the corresponding state in the cell state tree. (C) 2D UMAP visualization of a continuous population of cells where pa and step_size are small, and the trajectory of the states can be observed. (D) 2D UMAP visualization of a discrete population of cells where pa and step_size are large, and the cells are separated into discrete clusters. (E) UMAP visualization of 5-dpf zebrafish larvae cells from (24). Nine thousand three hundred ninety-three cells of 10 cell types are sampled from the original dataset. (F) Cell state tree estimated from the real dataset. Hierarchical clustering is applied to the pairwise distances of the average expressions of the 10 cell types. (G–I) UMAP visualization of simulated zebrafish larvae cells. Twenty simulations each with 1024 cells are generated with selected parameters to fit the dataset to the referred real dataset. (G) True counts without technical noise. (H and I) Observed counts with different capture efficiency values. (J) Comparison of cell type compositions between simulated data and real data. (K and L) Statistical comparison between cell types of simulated data and the real data. Both metrics are calculated based on observed counts with capture efficiency alpha_mean = 0.1. Each box corresponds to a cell type. Red boxes represent real data and green boxes represent TedSim simulated data. (K) Average expression per cell. (L) Average zero percentages per cell.
First, we applied Ward’s agglomerative clustering method (implemented in ‘The R Stats Package’) on the real dataset to obtain the cell state tree (Figure 3F). The edge lengths of the state tree are rounded up to the nearest integer. With the inferred state tree, in order to maintain the relative size of each cell type (i.e. the proportion of cells in each cell type), at each branching node in the cell state tree, we calculate branch probabilities according to the total number of cells in the respective subtree (see pseudocode in Supplementary Section S4). We ran the TedSim simulation 20 times, each with a single root and 1024 leaf cells, using the same cell state tree and branch probabilities. We then combine the cells from the 20 runs and obtain the final dataset. The asymmetric division rate pa and step_size used in the simulations are set to maximize the numbers of cells in the terminal cell types (pa = 1, step_size = 1) (Figure 3G–I). Other parameters in TedSim that are fitted to simulate a dataset that resembles the real data are (i) scale_s: a parameter in the kinetic model adjusting for the difference in cell size of different cell types; and (ii) alpha_mean: the capture efficiency during library preparation in scRNA-seq experiments. The detailed information about the parameters used for the simulations can be found in Supplementary Section S5.1. Figure 3J–L and Supplementary Figure S2A and B show statistical comparisons between the simulated data and real data.
Evaluation of TI methods
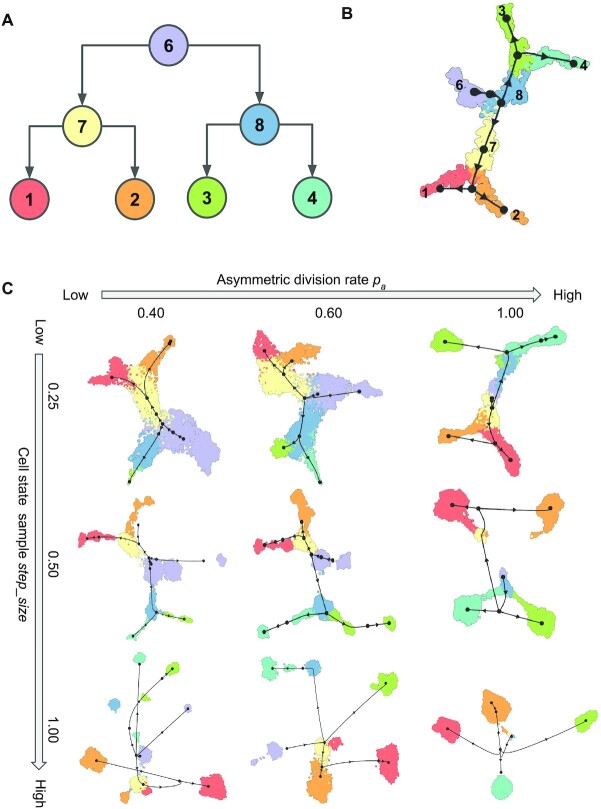
The cell state tree used in TedSim is the ground truth cell trajectory for TI methods (Figure 4A). To evaluate TI methods, we generate datasets where cell populations have different differentiation speeds by tuning the parameters pa and step_size (see Figure 4B and C for PAGA-Tree and Supplementary Figure S3 for Slingshot). For each parameter configuration, we simulate 8192 cells with the same bifurcating lineage (Figure 4A) and run the simulation 10 times to calculate the average performance. Values of other parameters used to generate the datasets can be found in Supplementary Section S5.2.
Figure 4.
Running TI methods on TedSim datasets. (A) The structure of the cell state tree used for the simulation in this figure. Number of intermediate states on each edge varies with step_size. (B) UMAP visualization of inferred trajectories by PAGA-Tree, on a dataset with 1024 cells and 500 genes. pa = 0.85 and step_size =0.25; these parameters are set to obtain continuous populations of cells. (C) UMAP visualization of inferred trajectories by PAGA-Tree with varying pa and step_size. The black network corresponds to ‘milestone network’, which is obtained by post-processing the output of the methods into a common probabilistic trajectory model to make different methods comparable, as implemented in the ‘dynwrap’ package.
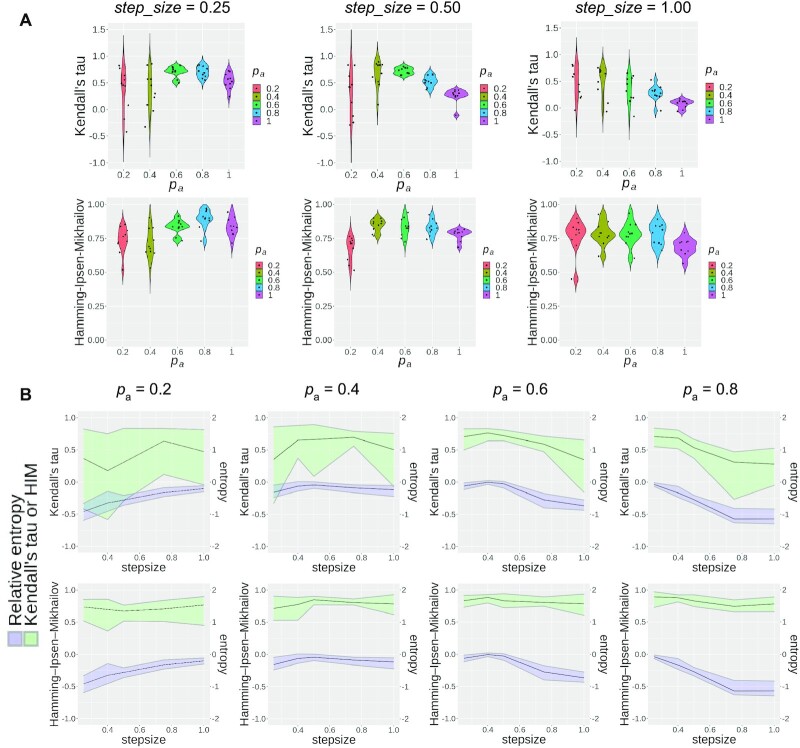
With a simulated dataset, we first apply PCA and select the first 50 PCs as input to UMAP for visualization in 2D (min_dist = 0.3 for UMAP). We use the R packages dynwrap and dynmethods to run the two best TI methods, found by the built-in TI method browser dynguidelines: PAGA-Tree (version 2.0.0) and Slingshot (version 2.0.1). All methods were run with default parameters and both methods take prior information of ground truth cluster (cell type) information and root cell information. The dynwrap, dynmethods and dynguidelines are part of the collection of R package dynverse used in the paper by Saelens et al. (1). Websites of the packages used are included in the ‘Data Availability’ section. We evaluate the performances of the TI methods using two metrics, Kendall’s  and Hamming–Ipsen–Mikhailov (HIM) score (41) (Figure 5A and B, and Supplementary Figure S4).
and Hamming–Ipsen–Mikhailov (HIM) score (41) (Figure 5A and B, and Supplementary Figure S4).
Figure 5.
Statistical results of TI methods. (A and B) Evaluating PAGA-Tree results with varying parameters pa and step_size. Ten datasets are simulated for each parameter configuration to generate the violin plot. (A) Pseudotime inference performances with the same step_size and varying pa. The ground truth for pseudotime rank is obtained from the depth of the cells’ states on the state tree, and the HIM score is calculated between the state tree topology and the milestone network (1) inferred by the TI method. (B) Pseudotime inference performances of PAGA-Tree and relative entropy of the dataset with varying step_size parameters. The black curve represents the average score of 10 runs and the upper and lower bounds of the ribbon represent maximum and minimum scores.
We designed a measure, relative entropy, to calculate how good the dataset is in terms of balancing the number of cells across all the cell states so that the underlined state tree is better preserved (Figure 5B). Given a distribution of the states 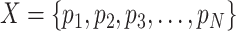 , the relative entropy is calculated as follows:
, the relative entropy is calculated as follows:
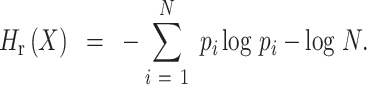 |
Here,  , where
, where 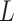 denotes the height of the cell state tree, and
denotes the height of the cell state tree, and 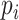 represents the frequency of the states at depth i on the state tree. The relative entropy subtracts the entropy of the uniform distribution of the same length (the length is
represents the frequency of the states at depth i on the state tree. The relative entropy subtracts the entropy of the uniform distribution of the same length (the length is 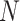 ) so that the bias introduced by different step_size is removed. In other words, the relative entropy of a distribution is equal to the relative entropy of a piecewise constant interpolation of the distribution (Supplementary Section S7).
) so that the bias introduced by different step_size is removed. In other words, the relative entropy of a distribution is equal to the relative entropy of a piecewise constant interpolation of the distribution (Supplementary Section S7).
When relative entropy is high, it means different cell types in the dataset have similar number of cells, which is an easy case for TI methods; when relative entropy is low, it means some cell types have very small number of cells, which poses challenges for TI methods. Different combinations of parameters pa and step_size can give rise to different levels of relative entropy. In Supplementary Figure S5, we use a simple trajectory as an example to show how relative entropy changes with pa and step_size. This figure can also serve as a guide for users to choose pa and step_size parameters given how balanced they want the cell types to be. We recommend pa > 0.5 as small pa requires a large number of generations to obtain cells at the terminal state.
Evaluation of lineage tree reconstruction methods
TedSim is able to generate lineage barcode data and gene expression data for present-day cells (leaf cells in the cell division tree). Using these datasets, we compare the performances of lineage reconstruction methods: Cassiopeia and DCLEAR, which use only the lineage barcodes, and LinTIMaT, which also incorporates the gene expressions to refine cell lineage trees. We ran and compared two modes of Cassiopeia (Cassiopeia-greedy and Cassiopeia-hybrid), two modes of DCLEAR (DCLEAR-NJ and DCLEAR-FM) and LinTIMaT. The detailed parameter settings to run the algorithms are provided in Supplementary Section S5.3.
The datasets used to evaluate the lineage reconstruction methods have different numbers of cells (512 and 8192 cells) and vary in their mutation rate 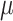 = (0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4). The default mutation rate is 0.15, and users can also use the method provided in Supplementary Section S8 to estimate the mutation rate from a real dataset. We also compare their performances with and without lineage barcode dropouts and under two different modes of mutation state distribution: the ‘equal chance’ mode and the ‘biased’ mode where a distribution obtained from real datasets is used. Here, we used the embryo2 from (14) to obtain the mutation state distribution.
= (0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4). The default mutation rate is 0.15, and users can also use the method provided in Supplementary Section S8 to estimate the mutation rate from a real dataset. We also compare their performances with and without lineage barcode dropouts and under two different modes of mutation state distribution: the ‘equal chance’ mode and the ‘biased’ mode where a distribution obtained from real datasets is used. Here, we used the embryo2 from (14) to obtain the mutation state distribution.
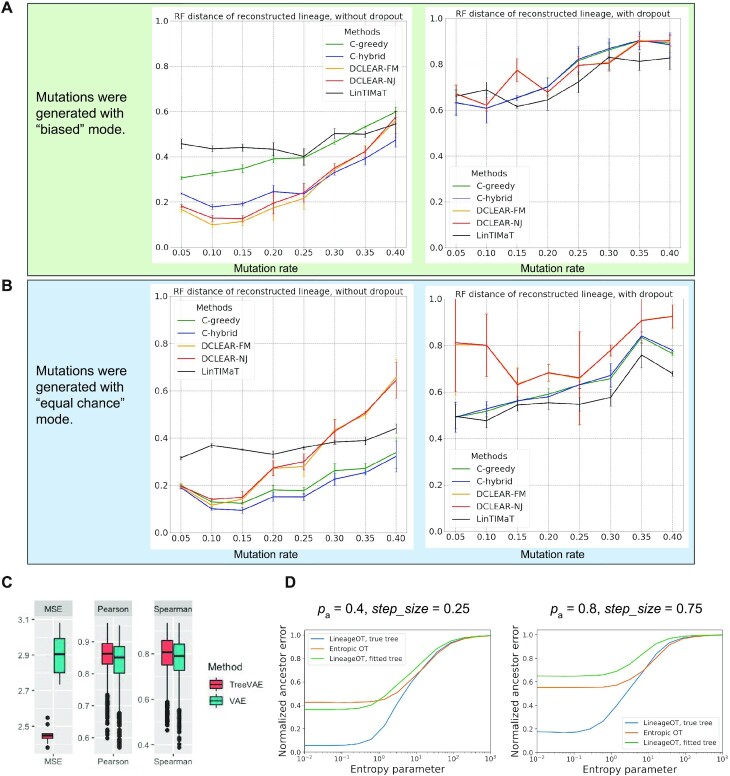
The reconstructed trees are compared to the same ground truth using two metrics: (i) the Robinson–Foulds (RF) distance (37) that quantifies the symmetric difference in splits between the reconstructed tree and the ground truth, which reflects the accuracy of the overall topology of the tree (Figure 6A and B); and (ii) triplets’ correct rate that calculates the percentage of correctly located triplets of cells on the cell lineage, which reflects the accuracy of inferring local lineages of single cells (Supplementary Figure S6A and B). For the RF distance, we use the API from the ete3 toolkit (38). For the triplet score, we randomly select 10 000 triplets and calculate the percentage of triplets that have the same structure in the reconstructed tree and the ground truth. To account for randomness in our simulation, we run the simulation 10 times with each combination of parameters and calculate the mean and standard deviation of the metrics.
Figure 6.
Statistical results of lineage reconstruction methods and other hybrid methods. (A and B) Testing five tree reconstruction methods on synthetic lineage barcodes using the RF distance. Lower RF distance indicates higher reconstruction accuracy. The mutation states are sampled from a fitted distribution of real mutations of embryo2 from (14) (A) or a uniform distribution of synthetic mutations (B). Parameters used to simulate the datasets can be found in Supplementary Section S5.3. For each configuration (mutation rate and dropout), 10 simulations are run and used to test the methods. Each simulated dataset has 512 cells. (C) Testing ancestral gene expression inference accuracy of TreeVAE. The correlation and distance metrics are calculated between the inferred gene expression of ancestor cells and the true counts of the same cells given by TedSim. (D) Testing ancestor–descendant inference accuracy of LineageOT. The normalized ancestor error is calculated as the marginal of the mean squared optimal transport distance between inferred ancestors and ground truth (18).
Evaluation of ancestral gene expression inference methods
Using the simulated gene expression and lineage barcode data from the root to the leaf cells, we evaluate the accuracy of ancestral gene expression inference, performed by TreeVAE (19). TreeVAE takes as input a cell lineage tree and the gene expression data of leaf cells. We compare TreeVAE with a naive VAE-based baseline method. To take into account the accuracy of the input cell lineage tree, we test TreeVAE with two tree inputs: (i) the tree reconstructed by Cassiopeia (16) with the lineage barcodes of the leaf cells and (ii) the true cell lineage tree.
We used TedSim to generate 10 datasets with 128 leaf cells and 126 internal cells. The gene expressions of the leaf cells are used as input data for the algorithm and the gene expressions of the internal cells serve as the ground truth. We quantify the performances of TreeVAE and the baseline method using the following comparisons between the inferred ancestral gene expression and the ground truth (Figure 6C and Supplementary Figure S6C and D): (i) cell to cell correlation (Spearman’s and Pearson’s correlations) and MSE (mean squared error), using the true lineage; and (ii) correlation and MSE of the average expression over all ancestral cells, using the reconstructed lineage and the true lineage.
Evaluation of hybrid lineage inference methods on time-course data
We can obtain time-course scRNA-seq and lineage barcode data from TedSim by selecting cells at different depths of the lineage tree. Methods including LineageOT (18) and EntropicOT (8) were developed to infer the cell lineage relationships using time-course single-cell gene expression data. LineageOT also uses the cell lineage tree reconstructed from lineage tracing barcodes to improve their inference; thus, it is one of the ‘hybrid’ methods we evaluate in this paper. We perform LineageOT in two different modes: either using the reconstructed cell lineage tree or using the true tree. The algorithms are tested on both continuous and discrete populations obtained by varying the values of step_size and pa (Figure 6D).
We generated the dataset with a binary cell division tree of 512 leaves, and selected two generations of cells to obtain time-course data: the 512 descendant cells and 64 ancestor cells at the same depth. The ground truth of ancestor–descendant relationships is directly obtained from the cell division tree. We vary pa and step_size to get both discrete and continuous trajectories: pa = 0.4 and step_size = 0.25 for the continuous dataset; and pa = 0.8 and step_size = 0.75 for the discrete dataset. We evaluate the accuracy of the lineage inference using ‘ancestor prediction error’ from the paper (18), which calculates the mean squared optimal transport distance between the inferred coupling matrix and the ground truth (Figure 6D).
RESULTS
TedSim generates realistic single-cell gene expression and barcode data
TedSim generates both continuous and discrete populations through cell divisions
In some real scRNA-seq datasets, cells form discrete clusters and in some other datasets cells form continuous trajectories. Biological factors that cause these different patterns can include the following: (i) cell differentiation speed: cells with high differentiation speed can reach terminal cell states fast and we tend to observe terminal cell types that are often discrete; and (ii) whether there exist intermediate cell types when cells transit from one cell type to another. TedSim models the first factor through the parameter pa (asymmetric division rate) and the distribution Pjump (probability of jumping beyond the immediate next cell state at one cell division), and models the second factor through step_size (determines how dense cell states are sampled from the original cell state tree).
We show that by varying pa and step_size TedSim can generate scRNA-seq data with different compositions and patterns of cell types. Given the same number of cell divisions, larger pa and larger step_size values result in more cells at the terminal states (Figure 3A–D). The states sampled using step_size = 0.25 and step_size = 0.5, respectively, are shown in Figure 3A. In order to show the effect of these two parameters, we take all the cells at the leaves of the cell lineage tree, and classify them by the depth of their corresponding states in the cell state tree. In Figure 3B, we show the frequency of cells belonging to states at different depths in the cell state tree. With larger pa and step_size, most cells’ states are the terminal states with the largest depth (bottom right plot of Figure 3B). In Figure 3C and D, we show the UMAP visualization of the present-day cells using two combinations of pa and step_size values, where one leads to continuous populations and the other leads to discrete populations. TedSim is able to naturally simulate continuous or discrete population of cells or a mixture of the two using the same model with different parameters.
TedSim is able to generate scRNA-seq data with multiple cell types that mimic real datasets in multiple aspects. Existing simulators compare various statistical properties of simulated and real data, including the distribution of mean expression and the percentage of zeros in each cell (20,22,25). However, these publications use only statistical properties within one cell type or averaged over all cell types of real datasets to perform the comparison. We show that data simulated by TedSim can preserve the statistical properties of every cell type individually. Moreover, TedSim simulated data also maintains the cross-cell-type relationships as in the real data.
To demonstrate this, we use TedSim to generate an scRNA-seq dataset close to the gene expression data of 10 selected cell types of zebrafish larvae at 5 dpf from (24) (Figure 3E) (Supplementary Section S5.1). First, we learn a cell state tree from the real data, in order to preserve the cross-cell-type relationship. We calculate the pairwise Euclidean distances between the mean expressions of the cell types, and then run hierarchical clustering to get the cell state tree (Figure 3F) (see the ‘Materials and Methods’ section). Second, in order to maintain the relative numbers of cells in each cell type, we assign probabilities for the choice of each branch at each branching point in the cell state tree. With the state tree and branch probabilities, TedSim is able to generate data that have similar cell type composition and relative locations of clusters (Figure 3G–I). Figure 3J shows that the proportion of cells in each cell type matches between real and simulated data. We can match the statistical properties of the simulated data to a given dataset with selected simulation parameters (see the ‘Materials and Methods’ section). Figure 3J–L shows, respectively, the comparison between simulated and real data in terms of mean gene expression and percentage of zeros per cell in each cell grouped by cell type, and the gene-wise comparison results are provided in Supplementary Figure S2.
TedSim generates realistic lineage barcode data
The CRISPR/Cas9-induced lineage barcodes contain various mutations that occurred during cell divisions. These mutations, however, tend to be not evenly distributed, and some mutations would appear more frequently than other mutations. During the simulation of cell divisions in TedSim, we sample the mutations from a fitted distribution of a real dataset (14) (see the ‘Materials and Methods’ section). Therefore, we are able to generate simulated lineage barcodes that have a similar pattern of mutation distribution as the real dataset (Figures 2H and 7A). In comparison to (23), which simulates lineage barcode data, TedSim has the following new features: (i) TedSim simulates lineage barcodes simultaneously with gene expression data (CIVs) while traversing the cell lineage tree; and (ii) the simulated lineage barcodes can be connected to a gene and the capture dropout can happen based on the observed gene expression of the gene.
Figure 7.
Simulation of lineage barcodes and inconsistency between cell lineage and cell state. (A) Mutated state distribution (top 15 frequent mutations are shown) in simulated lineage barcodes by TedSim. Mutation rate  = 0.1. No dropouts are introduced. One can observe that this distribution is similar to the one shown in Figure 2H. (B) Cell type visualization in the true lineage tree shows inconsistency between states and lineage barcodes. Different colours represent different cell types. (C) Cell type composition in subtrees with roots at the same depth (the fifth generation from the root) in panel (B). Sixteen subtrees are shown. Each colour represents a cell type and the height of each colour bar represents the percentage of cells in that cell type in the corresponding subtree.
= 0.1. No dropouts are introduced. One can observe that this distribution is similar to the one shown in Figure 2H. (B) Cell type visualization in the true lineage tree shows inconsistency between states and lineage barcodes. Different colours represent different cell types. (C) Cell type composition in subtrees with roots at the same depth (the fifth generation from the root) in panel (B). Sixteen subtrees are shown. Each colour represents a cell type and the height of each colour bar represents the percentage of cells in that cell type in the corresponding subtree.
TedSim generates the inconsistency between transcriptome similarity and barcode similarity observed in real data
One important question in developmental biology is how cell types are related to cell lineages. With the development of CRISPR/Cas9 lineage barcoding alongside scRNA-seq technologies, researchers aim to uncover the mechanisms of how single totipotent cells give rise to complex multicellular organisms. For example, we can examine the cell type composition within subtrees at different levels of the cell lineage. Data from recent papers that jointly profile lineage barcodes and gene expression data show that while some subtrees in the cell lineage tree have dominating cell types, there are a considerable number of cells of the same type located in different subtrees, and in the same subtree there can be multiple cell types (13,14,24,39). We call this the inconsistency between transcriptome similarity and lineage barcode similarity. Various scenarios that cause this inconsistency are discussed in (10).
The model we use in TedSim combining an underlying cell state tree with asymmetric cell divisions can generate such inconsistency between transcriptome similarity and barcode similarity of cells. The given cell state tree and the asymmetric cell division events modelled in TedSim allow both the scenario of the same clone to be dominated by one cell type and the scenario where different clones generate the same cell types. Therefore, TedSim can generate realistic cell type composition within subtrees of the lineage tree (Figure 7B and C). Chan et al. presented the cell type composition under various progenitors (Figure 6a in their paper) (14) in a similar form to Figure 7C, from which we see that the simulated dataset shows similar heterogeneity in cell types in each subtree/progenitor, including a mix of multiple cell types as well as biases towards some cell types.
The connections between lineage and transcriptomic data can also be dynamic and transient (29). By default in TedSim, we assume that the state of the cell has a bigger impact on the gene expression than the lineage of the cell, but we can also increase the impact of cell lineage information by tuning the weight of the SIVs in the CIVs (see the ‘Materials and Methods’ section and Supplementary Section S3). With future research uncovering how the correlation between cell lineage and cell state changes over time, we can easily generalize the current model to dynamically adjust the balance between the impact of parent state and the assigned state by the cell state tree on a daughter cell based on the current developmental stages.
Evaluating TI methods
ScRNA-seq data provide transcriptome information of every single cell, but as a cell can be sequenced only once and in most of the experiments all cells are sequenced at the same time, scRNA-seq data do not provide data of the cells in the past for researchers to study developmental processes. TI methods were developed to infer the cell trajectories using only data from present-day cells, assuming that there are cells in the dataset that represent cell states at various stages of the developmental process.
Various TI methods have been tested in multiple publications using simulated data (1,22), but the data simulation procedures used in these publications align with the assumption that the data cover the entirety of the continuous manifolds that the transcriptomic data live in. However, in practice, some experiments may capture only the terminal cell states, or part of the intermediate states. These scenarios can be generated by TedSim. Therefore, the TedSim simulated data can reflect the realistic challenges for the TI methods. In particular, in previous sections we showed that the cell type composition in the present-day cells can be different depending on various factors (Figure 2A–C), and how balanced the cell state composition is in the data can be important for the performance of TI methods. Therefore, instead of comparing different TI methods, we will focus on investigating the performances of the top TI algorithms on datasets with different compositions of cell states, controlled by TedSim parameters.
When applying a TI method to data generated by TedSim, the input to the TI method is the scRNA-seq data from TedSim, and the cell state tree used in TedSim serves as ground truth to evaluate the TI method (Figure 4A). We apply two state-of-the-art TI methods, Slingshot (2) and PAGA-Tree (3), as benchmarked by (1). For both TI methods, we provide the ground truth root cell in the trajectory. Figure 4B shows the inferred trajectory by Slingshot on one of our simulated datasets generated by TedSim that covers most of the cell states in the data, and the TI methods are able to infer the correct state tree shown in Figure 4A. We then focus on testing TI methods under various compositions of cell types in the present-day cells, which can be controlled by parameters pa and step_size. We vary parameters pa and step_size when generating and applying PAGA-Tree on the resulting simulated scRNA-seq datasets. Figure 4C shows the UMAP visualization of the simulated data and inferred trajectories. In Figure 5B and C, the black coloured network is the ‘milestone network’, which is a common trajectory model used in dynwrap to align the outputs of different methods and make them comparable (1). Each black dot is a ‘milestone’. A milestone may or may not correspond to a cell type. Consistent with Figure 3C and D, high pa and step_size result in more discrete populations of cells, mainly belonging to the terminal states in the cell state tree. Lower pa and step_size values, on the other hand, lead to more cells at non-terminal cell states. TI methods work better when the present-day cells cover as many cell states (both terminal and non-terminal) as possible. For example, PAGA-Tree infers the correct trajectory when pa = 0.6 and step_size = 0.25, while when pa = 1 and step_size = 1, it is very difficult for the TI method to find the correct trajectory. The results of Slingshot on the same datasets are shown in Supplementary Figure S3.
We propose a measure relative entropy (see the ‘Materials and Methods’ section and Supplementary Section S7) to quantify whether a dataset has a balanced composition of all cell types. Higher relative entropy corresponds to more balanced populations. We also quantitatively evaluate the performance of the TI methods under different pa and step_size values. We calculated the HIM score (40) for the difference between the topology of inferred and true trajectories as used in (1). The HIM score was calculated between the milestone networks of inferred and true trajectories, and a higher score means better results. To measure whether cells are correctly ordered on the topology, we calculated Kendall’s 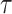 (41) correlation between the inferred pseudotime and true pseudotime of cells. Figure 5A shows that when step_size is relatively small (step_size = 0.25 or step_size = 0.5), both the HIM score and Kendall’s
(41) correlation between the inferred pseudotime and true pseudotime of cells. Figure 5A shows that when step_size is relatively small (step_size = 0.25 or step_size = 0.5), both the HIM score and Kendall’s 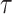 first increase and then decrease. These scores are relatively low with small pa because small pa and step_size together lead to a small number of cells in states towards the terminal states. This is also reflected in the relative entropy levels shown in Figure 5B (e.g. the relative entropy is low when step_size
first increase and then decrease. These scores are relatively low with small pa because small pa and step_size together lead to a small number of cells in states towards the terminal states. This is also reflected in the relative entropy levels shown in Figure 5B (e.g. the relative entropy is low when step_size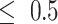 and pa = 0.2 or pa = 0.4). In Figure 5A, we also observe that both HIM score and Kendall’s
and pa = 0.2 or pa = 0.4). In Figure 5A, we also observe that both HIM score and Kendall’s  decrease when pa = 1. This is because in this case the numbers of cells in ancestral states are small, which also leads to lower relative entropy levels and makes it harder for TI methods to infer the correct cell state tree.
decrease when pa = 1. This is because in this case the numbers of cells in ancestral states are small, which also leads to lower relative entropy levels and makes it harder for TI methods to infer the correct cell state tree.
We plot the relative entropy of the datasets along with the Kendall’s 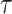 and HIM score of trajectories inferred by PAGA-Tree in Figure 5B. We observe that Kendall’s
and HIM score of trajectories inferred by PAGA-Tree in Figure 5B. We observe that Kendall’s 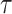 changes in consistence with the trend of the relative entropy, where for smaller pa such as pa = 0.2, the relative entropy increases with step_size since it requires larger step_size in order to capture the whole developmental trajectory; on the contrary, when pa gets closer to 1 and cells get to the terminal states fast, the relative entropy declines with step_size. In Figure 5B, while the HIM score also follows the trend of relative entropy when fixing pa and changing step_size, the HIM score changes within a small range and remains at a relatively high level (>0.5 most of the time), which indicates that with a given root cell of the trajectory, PAGA-Tree can infer the topology of the ground truth state tree reasonably well when the relative entropy fluctuates. Slingshot, on the other hand, overall has lower HIM scores, although Kendall’s
changes in consistence with the trend of the relative entropy, where for smaller pa such as pa = 0.2, the relative entropy increases with step_size since it requires larger step_size in order to capture the whole developmental trajectory; on the contrary, when pa gets closer to 1 and cells get to the terminal states fast, the relative entropy declines with step_size. In Figure 5B, while the HIM score also follows the trend of relative entropy when fixing pa and changing step_size, the HIM score changes within a small range and remains at a relatively high level (>0.5 most of the time), which indicates that with a given root cell of the trajectory, PAGA-Tree can infer the topology of the ground truth state tree reasonably well when the relative entropy fluctuates. Slingshot, on the other hand, overall has lower HIM scores, although Kendall’s 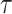 values of the two methods are comparable (Supplementary Figure S4).
values of the two methods are comparable (Supplementary Figure S4).
These results suggest that top TI methods are likely to find the correct or near-correct underlying trajectory that represents cell state transition if the dataset covers most states on the state tree and forms continuous populations (Figure 4A–C). Therefore, when applying TI methods, it is important to be aware that the composition of cell types in the dataset is a key factor to determine the reliability of the results.
TedSim has the potential to suggest the time to harvest cells for the most comprehensive cell type compositions. For example, given a hypothesized asymmetric cell division rate and cell state tree, running TedSim allows for the estimation of the number of divisions needed to obtain cells with comprehensive cell type compositions.
Evaluating lineage reconstruction algorithms
Given the lineage barcodes of present-day cells, reconstructing the lineage tree is an NP-hard problem (42,43). A few computational methods have been developed to reconstruct the cell lineage tree from the lineage barcodes of the present-day cells (16,23). However, it is very challenging to obtain a cell lineage tree with high accuracy due to various reasons, including the large number of cells, the limitation of target sites and missing data in the barcodes (23). To improve the accuracy of reconstructed trees, hybrid methods that use both the scRNA-seq and lineage barcode data are emerging, with LinTIMaT (17) as a representative. Since TedSim generates both scRNA-seq and the lineage barcode data simultaneously, it can be used to benchmark not only tree reconstruction methods that use only lineage barcode data, but also those that use both gene expression and barcode data. In particular, we would like to find out whether the performances of lineage reconstruction are improved by integrating gene expressions with the lineage barcodes. We compare the performance of LinTIMaT (17) against DCLEAR (44) and Cassiopeia (16), which are the best-performing algorithms in the recent Allen Institute Cell Lineage Reconstruction DREAM Challenge (44) that use only the CRISPR/Cas9-induced lineage barcodes.
We set up the simulation of TedSim as follows: for each cell, the lineage barcode contains 32 target sites, and each target site, if mutated, can be sampled from 100 possible mutated states. Simulations are run with varying mutation rate 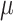 , dropout setting (on/off) and mutation state distributions (equal chance or biased). The parameters for simulating gene expression values are included in Supplementary Section S5.3. We used medium-sized datasets (with 512 cells) to test all methods and used large datasets (with 8192 cells) to run a subset of methods that can scale. The RF distance and triplet scores are used to evaluate performances of the methods.
, dropout setting (on/off) and mutation state distributions (equal chance or biased). The parameters for simulating gene expression values are included in Supplementary Section S5.3. We used medium-sized datasets (with 512 cells) to test all methods and used large datasets (with 8192 cells) to run a subset of methods that can scale. The RF distance and triplet scores are used to evaluate performances of the methods.
From the results with 512 cells (Figure 6A and B), we observe that the RF distance metric for all methods shows consistent dependence on the mutation rate 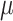 , and the trend is consistent with that is shown in (23) although Salvador-Martinez et al. used different lineage tree reconstruction methods. The triplet score results are much less affected by
, and the trend is consistent with that is shown in (23) although Salvador-Martinez et al. used different lineage tree reconstruction methods. The triplet score results are much less affected by 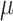 (Supplementary Figure S6A and B). Cassiopeia-hybrid has the best triplet score overall, outperforming all other methods by a large margin under the condition of high mutation rate without dropout, possibly due to the advantage of using an ILP formulation. With dropout, Cassiopeia-greedy outperforms Cassiopeia-hybrid slightly, but both are still better than the two DCLEAR modes and LinTIMaT. The results of the RF distance show similar trends for all selected methods, and we find that the best mutation rate is around 0.1–0.15 for both conditions: with and without dropouts, and excessively high mutation rate does not result in higher tree reconstruction accuracy as people may intuitively think so. In Figure 6B, we show the same comparison of tree reconstruction methods using simulated data where the mutations occur uniformly on the barcode (the ‘equal chance’ mode). Comparing Figure 6A and B, we see that the tree reconstruction methods generally perform better with the data where mutation states are selected with equal probabilities, suggesting that the bias in mutation distribution on the barcode should be modelled when developing tree reconstruction methods in the future.
(Supplementary Figure S6A and B). Cassiopeia-hybrid has the best triplet score overall, outperforming all other methods by a large margin under the condition of high mutation rate without dropout, possibly due to the advantage of using an ILP formulation. With dropout, Cassiopeia-greedy outperforms Cassiopeia-hybrid slightly, but both are still better than the two DCLEAR modes and LinTIMaT. The results of the RF distance show similar trends for all selected methods, and we find that the best mutation rate is around 0.1–0.15 for both conditions: with and without dropouts, and excessively high mutation rate does not result in higher tree reconstruction accuracy as people may intuitively think so. In Figure 6B, we show the same comparison of tree reconstruction methods using simulated data where the mutations occur uniformly on the barcode (the ‘equal chance’ mode). Comparing Figure 6A and B, we see that the tree reconstruction methods generally perform better with the data where mutation states are selected with equal probabilities, suggesting that the bias in mutation distribution on the barcode should be modelled when developing tree reconstruction methods in the future.
Interestingly, we see that LinTIMaT does not perform well for lower mutation rates but its performances decline much slower with the increase of mutation rate. The reasons that LinTIMaT does not overperform other methods, as we interpret, are 2-fold: (i) the initial tree obtained by LinTIMaT before it is refined using gene expression data is of low quality, which can be due to bad initialization, and this affects the accuracy of the final output tree; and (ii) LinTIMaT relies on the assumption that cells with similar gene expression profiles should be located closely in the cell lineage tree, which is not always true. On the other hand, LinTIMaT’s performance does not deteriorate as much as other methods when the mutation rate increases because the incorporation of gene expressions helps to maintain relatively good results when the barcodes are not very informative.
On the datasets with 8192 cells, we tested Cassiopeia-greedy, DCLEAR-NJ and DCLEAR-FM as Cassiopeia-hybrid and LinTIMaT do not scale to this size of datasets (Supplementary Figure S7). We can see that the two DCLEAR methods have similar performances (and the two curves largely overlap) and outperform other methods in the majority of cases, which is consistent with the results on datasets with 512 cells. When there are dropouts, DCLEAR methods do not outperform Cassiopeia-greedy.
We also tested lineage reconstruction methods on the real barcode data of the zebrafish dataset from (24). As there does not exist a ground truth cell division tree for these cells, we compared the trees inferred from various methods with each other (using the RF distance) and presented characteristics of the trees: maximum depth and number of internal nodes (Supplementary Figure S8). From the pairwise RF distance between the reconstructed trees, we can see that the DCLEAR tree is significantly less similar to the other two trees. This can be caused by the design of the neighbour joining algorithm to randomly merge nodes that have the same barcodes to enforce binary structure, whereas the other two methods assign all nodes with the same barcode under the same subtree. That is also why the DCLEAR tree has more internal nodes and higher maximum depth in comparison to the other two.
Evaluating hybrid methods of various inference tasks
With the development of technologies that jointly profile lineage barcodes and scRNA-seq data, hybrid computational methods are emerging to integrate these data for various purposes. Three hybrid methods, LineageOT (18), TreeVAE (19) and LinTIMaT (17), are tested in this paper, where the first two are evaluated in this section.
Given time-course scRNA-seq data, researchers try to infer the relationships (the ancestor–descendent correspondence) between cells at different timestamps (8). Forrow and Schiebinger proposed LineageOT (18), which aims to incorporate the cell lineage tree reconstructed from the lineage barcodes to improve the accuracy of ancestor–descendant inference when the lineage barcode data are available. Here, we use the data simulated by TedSim to evaluate this method (see the ‘Materials and Methods’ section). As performed in (18), we compare their proposed method LineageOT with EntropicOT (8), which uses only gene expression data. From the results, we can see that by using good lineage information (LineageOT, true tree), the normalized ancestor error can be largely improved (Figure 6D). By varying the parameters that affect the continuity of populations and cell type compositions pa and step_size, we can see all methods perform worse when pa and step_size are increased, considering the fact that larger parameters result in more discrete populations (Figure 6D). In this case, the cells of two different generations are more likely to have the same cell state, making it harder to infer the ancestor–descendant relationships. While LineageOT with true lineage tree is still able to maintain decent ancestor error, LineageOT with fitted tree falls behind even compared with EntropicOT. How to better reconstruct the lineage tree from the barcodes will be the key to infer the developmental trajectory more accurately.
Another computational problem using both the scRNA-seq and the lineage tracing barcode data is to reconstruct the gene expression profiles of ancestral cells on the cell division tree. Ouardini et al. developed TreeVAE, which utilizes paired single-cell lineage tracing and transcriptomic data (19). Here, we test the accuracy of the reconstructed gene expressions of ancestor cells using the known ancestral data in TedSim. The method is compared with a VAE (variational auto-encoder)-based baseline method, which first runs on leaf nodes and then calculates the gene expressions of an internal node by averaging the latent space for leaves below the node and decodes them using the trained decoder (19). With the ground truth of the ancestor cells’ gene expression, we evaluate the inferred expression of all ancestor cells by calculating the Pearson’s correlation, Spearman’s correlation and MSE scores (Figure 6C). From the results, we can see that TreeVAE outperforms the baseline method in all three metrics. Besides, we also compare the inferred expressions for individual genes using either the true lineage or reconstructed lineage from the simulated lineage barcodes. From the results, we can see that the correlation scores of TreeVAE still consistently outperform the baseline method no matter which tree is used (Supplementary Figure S6C and D).
DISCUSSION
We presented TedSim, a simulator that generates both scRNA-seq data and lineage barcodes simultaneously through simulating the cell division events. Compared to existing simulators of scRNA-seq or CRISPR lineage recorders, TedSim has the following novel features: (i) TedSim models the underlying temporal dynamics of the development of cells by simulating the processes of cell division and differentiation to get both gene expressions and lineage barcode data simultaneously. (ii) TedSim is able to simulate both discrete and continuous gene expressions of single cells under the same framework by adjusting the cell differentiation speed and the continuity of cell states. (iii) Given simultaneously simulated gene expression and lineage barcode data, TedSim can evaluate hybrid methods that use both types of data. (iv) The simulated data show realistic inconsistency between transcriptome similarity and lineage barcode similarity of cells, which cause the heterogeneity of cell types in a lineage subtree, and meanwhile the subtree can have a dominant cell type.
By applying state-of-the-art TI methods to scRNA-seq data simulated by TedSim, we have gained insights towards experimental design for studying cell trajectories: it is important to maintain cells from ancestral states in the cell state tree and the cell type composition in a dataset is crucial for the TI methods to return meaningful inference. One may consider sequencing cells at multiple time points in order to capture early cell states. Overall, we found that the TI methods, although using scRNA-seq data of present-day cells, can recover the underlying state tree that guides the cell division and differentiation events reasonably well, as long as the dataset has a good coverage of both terminal and non-terminal cell states.
As more datasets that profile both the CRISPR/Cas9-induced scars and single-cell gene expression data become available, hybrid algorithms that integrate both types of data to learn cell dynamics are needed. Current hybrid methods (e.g. LinTIMaT), as we tested with TedSim, have not provided satisfactory results. Future methods may benefit from better modelling the relationship between the two types of data, possibly using the asymmetric cell division model we propose in TedSim.
DATA AVAILABILITY
TedSim is available at https://github.com/Galaxeee/TedSim.
Dynverse is an open set of packages to benchmark, construct and interpret single-cell trajectories available at https://github.com/dynverse.
Cassiopeia is an end-to-end pipeline for single-cell lineage tracing experiments available at https://github.com/YosefLab/Cassiopeia.
DCLEAR is an R package for distance-based cell lineage reconstruction available at https://github.com/ikwak2/DCLEAR.
LinTIMaT is a statistical method for reconstructing lineages from joint CRISPR–Cas9 mutations and single-cell transcriptomic data available at https://github.com/jessica1338/LinTIMaT.
LineageOT is a unified framework for lineage tracing and trajectory inference available at https://github.com/aforr/LineageOT.
The reference dataset used in Figure 2H is available in the Gene Expression Omnibus database under accession number GSE117542.
Supplementary Material
Contributor Information
Xinhai Pan, School of Computational Science and Engineering, College of Computing, Georgia Institute of Technology, Atlanta, GA 30332, USA.
Hechen Li, School of Computational Science and Engineering, College of Computing, Georgia Institute of Technology, Atlanta, GA 30332, USA.
Xiuwei Zhang, School of Computational Science and Engineering, College of Computing, Georgia Institute of Technology, Atlanta, GA 30332, USA.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
National Science Foundation [DBI-2019771]; National Institute of General Medical Sciences [R35GM143070]. Funding for open access charge: National Institute of General Medical Sciences [R35GM143070].
Conflict of interest statement. None declared.
REFERENCES
- 1. Saelens W., Cannoodt R., Todorov H., Saeys Y.. A comparison of single-cell trajectory inference methods. Nat. Biotechnol. 2019; 37:547–554. [DOI] [PubMed] [Google Scholar]
- 2. Street K., Risso D., Fletcher R.B., Das D., Ngai J., Yosef N., Purdom E., Dudoit S.. Slingshot: cell lineage and pseudotime inference for single-cell transcriptomics. BMC Genomics. 2018; 19:477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Wolf F.A., Hamey F.K., Plass M., Solana J., Dahlin J.S., Göttgens B., Rajewsky N., Simon L., Theis F.J.. PAGA: graph abstraction reconciles clustering with trajectory inference through a topology preserving map of single cells. Genome Biol. 2019; 20:59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Qiu X., Mao Q., Tang Y., Wang L., Chawla R., Pliner H.A., Trapnell C.. Reversed graph embedding resolves complex single-cell trajectories. Nat. Methods. 2017; 14:979–982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Luecken M.D., Theis F.J.. Current best practices in single-cell RNA-seq analysis: a tutorial. Mol. Syst. Biol. 2019; 15:e8746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Trapnell C., Cacchiarelli D., Grimsby J., Pokharel P., Li S., Morse M., Lennon N.J., Livak K.J., Mikkelsen T.S., Rinn J.L.. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol. 2014; 32:381–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Farrell J.A., Wang Y., Riesenfeld S.J., Shekhar K., Regev A., Schier A.F.. Single-cell reconstruction of developmental trajectories during zebrafish embryogenesis. Science. 2018; 360:eaar3131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Schiebinger G., Shu J., Tabaka M., Cleary B., Subramanian V., Solomon A., Gould J., Liu S., Lin S., Berube P.et al.. Optimal-transport analysis of single-cell gene expression identifies developmental trajectories in reprogramming. Cell. 2019; 176:928.e22–943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Cao J., Spielmann M., Qiu X., Huang X., Ibrahim D.M., Hill A.J., Zhang F., Mundlos S., Christiansen L., Steemers F.J.et al.. The single-cell transcriptional landscape of mammalian organogenesis. Nature. 2019; 566:496–502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Wagner D.E., Klein A.M.. Lineage tracing meets single-cell omics: opportunities and challenges. Nat. Rev. Genet. 2020; 21:410–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Tritschler S., Büttner M., Fischer D.S., Lange M., Bergen V., Lickert H., Theis F.J.. Concepts and limitations for learning developmental trajectories from single cell genomics. Development. 2019; 146:dev170506. [DOI] [PubMed] [Google Scholar]
- 12. Kester L., van Oudenaarden A.. Single-cell transcriptomics meets lineage tracing. Cell Stem Cell. 2018; 23:166–179. [DOI] [PubMed] [Google Scholar]
- 13. Raj B., Wagner D.E., McKenna A., Pandey S., Klein A.M., Shendure J., Gagnon J.A., Schier A.F.. Simultaneous single-cell profiling of lineages and cell types in the vertebrate brain. Nat. Biotechnol. 2018; 36:442–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Chan M.M., Smith Z.D., Grosswendt S., Kretzmer H., Norman T.M., Adamson B., Jost M., Quinn J.J., Yang D., Jones M.G.et al.. Molecular recording of mammalian embryogenesis. Nature. 2019; 570:77–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. McKenna A., Gagnon J.A.. Recording development with single cell dynamic lineage tracing. Development. 2019; 146:dev169730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Jones M.G., Khodaverdian A., Quinn J.J., Chan M.M., Hussmann J.A., Wang R., Xu C., Weissman J.S., Yosef N.. Inference of single-cell phylogenies from lineage tracing data using Cassiopeia. Genome Biol. 2020; 21:92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Zafar H., Lin C., Bar-Joseph Z.. Single-cell lineage tracing by integrating CRISPR–Cas9 mutations with transcriptomic data. Nat. Commun. 2020; 11:3055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Forrow A., Schiebinger G.. LineageOT is a unified framework for lineage tracing and trajectory inference. Nat. Commun. 2021; 12:4940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Ouardini K., Lopez R., Jones M.G., Prillo S., Zhang R., Jordan M.I., Yosef N.. Reconstructing unobserved cellular states from paired single-cell lineage tracing and transcriptomics data. 2021; bioRxiv doi:30 May 2021, preprint: not peer reviewed 10.1101/2021.05.28.446021. [DOI]
- 20. Zappia L., Phipson B., Oshlack A.. Splatter: simulation of single-cell RNA sequencing data. Genome Biol. 2017; 18:174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Vieth B., Ziegenhain C., Parekh S., Enard W., Hellmann I.. powsimR: power analysis for bulk and single cell RNA-seq experiments. Bioinformatics. 2017; 33:3486–3488. [DOI] [PubMed] [Google Scholar]
- 22. Zhang X., Xu C., Yosef N.. Simulating multiple faceted variability in single cell RNA sequencing. Nat. Commun. 2019; 10:2611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Salvador-Martínez I., Grillo M., Averof M., Telford M.J.. Is it possible to reconstruct an accurate cell lineage using CRISPR recorders?. eLife. 2019; 8:e40292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Spanjaard B., Hu B., Mitic N., Olivares-Chauvet P., Janjuha S., Ninov N., Junker J.P.. Simultaneous lineage tracing and cell-type identification using CRISPR–Cas9-induced genetic scars. Nat. Biotechnol. 2018; 36:469–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Dibaeinia P., Sinha S.. SERGIO: a single-cell expression simulator guided by gene regulatory networks. Cell Syst. 2020; 11:252–271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Lin H., Schagat T.. Neuroblasts: a model for the asymmetric division of stem cells. Trends Genet. 1997; 13:33–39. [DOI] [PubMed] [Google Scholar]
- 27. Morrison S.J., Kimble J.. Asymmetric and symmetric stem-cell divisions in development and cancer. Nature. 2006; 441:1068–1074. [DOI] [PubMed] [Google Scholar]
- 28. Knoblich J.A. Mechanisms of asymmetric stem cell division. Cell. 2008; 132:583–597. [DOI] [PubMed] [Google Scholar]
- 29. Packer J.S., Zhu Q., Huynh C., Sivaramakrishnan P., Preston E., Dueck H., Stefanik D., Tan K., Trapnell C., Kim J.et al.. A lineage-resolved molecular atlas of C. elegans embryogenesis at single-cell resolution. Science. 2019; 365:eaax1971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Felsenstein J. Inferring Phylogenies. 2004; Sunderland, MA: Sinauer Associates. [Google Scholar]
- 31. McInnes L., Healy J., Melville J.. UMAP: uniform manifold approximation and projection for dimension reduction. 2018; arXiv doi:18 September 2020, preprint: not peer reviewedhttps://arxiv.org/abs/1802.03426.
- 32. van der Maaten L., Hinton G.. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008; 9:2579–2605. [Google Scholar]
- 33. Angerer P., Haghverdi L., Büttner M., Theis F.J., Marr C., Buettner F.. destiny: diffusion maps for large-scale single-cell data in R. Bioinformatics. 2016; 32:1241–1243. [DOI] [PubMed] [Google Scholar]
- 34. Munsky B., Neuert G., van Oudenaarden A.. Using gene expression noise to understand gene regulation. Science. 2012; 336:183–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Espinosa-Medina I., Garcia-Marques J., Cepko C., Lee T.. High-throughput dense reconstruction of cell lineages. Open Biol. 2019; 9:190229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Ye C., Chen Z., Liu Z., Wang F., He X.. Defining endogenous barcoding sites for CRISPR/Cas9-based cell lineage tracing in zebrafish. J. Genet. Genomics. 2020; 47:85–91. [DOI] [PubMed] [Google Scholar]
- 37. Robinson D.F., Foulds L.R.. Comparison of phylogenetic trees. Math. Biosci. 1981; 53:131–147. [Google Scholar]
- 38. Huerta-Cepas J., Serra F., Bork P.. ETE 3: reconstruction, analysis, and visualization of phylogenomic data. Mol. Biol. Evol. 2016; 33:1635–1638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Zhang S., Cui Y., Ma X., Yong J., Yan L., Yang M., Ren J., Tang F., Wen L., Qiao J.. Single-cell transcriptomics identifies divergent developmental lineage trajectories during human pituitary development. Nat. Commun. 2020; 11:5275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Jurman G., Visintainer R., Filosi M., Riccadonna S., Furlanello C.. The HIM glocal metric and kernel for network comparison and classification. Proceedings of the 2015 IEEE International Conference on Data Science and Advanced Analytics (DSAA). 2015; 1–10. [Google Scholar]
- 41. Kendall M.G. A new measure of rank correlation. Biometrika. 1938; 30:81–93. [Google Scholar]
- 42. Bodlaender H.L., Fellows M.R., Warnow T.J.. Two strikes against perfect phylogeny. Automata, Languages and Programming. 1992; Berlin: Springer; 273–283. [Google Scholar]
- 43. Steel M. The complexity of reconstructing trees from qualitative characters and subtrees. J. Classif. 1992; 9:91–116. [Google Scholar]
- 44. Gong W., Granados A.A., Hu J., Jones M.G., Raz O., Salvador-Martínez I., Zhang H., Chow K.-H.K., Kwak I.-Y., Retkute R.et al.. Benchmarked approaches for reconstruction of in vitro cell lineages and in silico models of C. elegans and M.musculus developmental trees. Cell Syst. 2021; 12:810–826. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
TedSim is available at https://github.com/Galaxeee/TedSim.
Dynverse is an open set of packages to benchmark, construct and interpret single-cell trajectories available at https://github.com/dynverse.
Cassiopeia is an end-to-end pipeline for single-cell lineage tracing experiments available at https://github.com/YosefLab/Cassiopeia.
DCLEAR is an R package for distance-based cell lineage reconstruction available at https://github.com/ikwak2/DCLEAR.
LinTIMaT is a statistical method for reconstructing lineages from joint CRISPR–Cas9 mutations and single-cell transcriptomic data available at https://github.com/jessica1338/LinTIMaT.
LineageOT is a unified framework for lineage tracing and trajectory inference available at https://github.com/aforr/LineageOT.
The reference dataset used in Figure 2H is available in the Gene Expression Omnibus database under accession number GSE117542.