Abstract
Omics-based biomedical learning frequently relies on data of high-dimensions (up to thousands) and low-sample sizes (dozens to hundreds), which challenges efficient deep learning (DL) algorithms, particularly for low-sample omics investigations. Here, an unsupervised novel feature aggregation tool AggMap was developed to Aggregate and Map omics features into multi-channel 2D spatial-correlated image-like feature maps (Fmaps) based on their intrinsic correlations. AggMap exhibits strong feature reconstruction capabilities on a randomized benchmark dataset, outperforming existing methods. With AggMap multi-channel Fmaps as inputs, newly-developed multi-channel DL AggMapNet models outperformed the state-of-the-art machine learning models on 18 low-sample omics benchmark tasks. AggMapNet exhibited better robustness in learning noisy data and disease classification. The AggMapNet explainable module Simply-explainer identified key metabolites and proteins for COVID-19 detections and severity predictions. The unsupervised AggMap algorithm of good feature restructuring abilities combined with supervised explainable AggMapNet architecture establish a pipeline for enhanced learning and interpretability of low-sample omics data.
INTRODUCTION
Biomedical investigations frequently rely on the high-dimensional, unordered feature, low-sample size, and multi-platform (BioHULM) data derived from omics (transcriptomics, proteomics, metabolomics) (1–3) analysis. Individual investigations have primarily focused on dozens to hundreds of samples. The derived omics data contains hundreds-to-thousands of unordered features (in the order of appearance). Although deep learning (DL) is superior in learning complex data, conventional machine learning (ML) methods are the primary tools for the recent BioHULM-based biomedical investigations (1–3), such as nonlinear SVM or ensemble tree-based random forest in combination with various feature selection techniques (1,2). There are two obstacles hindering the direct DL of BioHULM data. First, DL trained by BioHULM data tends to overfit with numerous hyperparameters (4). A comprehensive study has revealed that ML models outperform deep representation learning models trained by the same low-sample transcriptomic data (5). Secondly, the DL outcomes are more difficult to explain than some ML algorithms (6). Explainability is essential in biomedical investigations (7,8), particularly for informed decisions, mechanism investigations, biomarker discoveries, and model assessments (9,10).
High performance and explainable DL algorithms are needed for BioHULM tasks (11). To adequately alleviate the “curse of dimensionality” problem in BioHULM learning, recent studies have focused on converting the 1D unordered data into 2D spatially-correlated image-liked feature maps (Fmaps) based on genetic locations (12,13), data neighborhoods (14) or functional relationships (15). Although this conversion enables efficient deep learning with convolutional neural networks (CNNs), they lack rich channel information about the cluster groups of the input feature points. Because multi-channel networks are helpful for learning complex data by separately learning feature subsets (16), their representational richness often allows capturing nonlinear dependencies at multiple scales (17). The localized stationarity and compositionality of data can be efficiently extracted by CNNs (18), the success of CNN hinges on its ability to leverage the compositional hierarchies (19) and intrinsic data structures (18).
In this work, to enhance efficient CNN-based learning of the low sample omics data, we developed a novel unsupervised feature aggregation tool AggMap for aggregating and mapping individual unordered BioHULM feature points (FPs) into spatial-correlated multi-channel 2D Fmaps (Figure 1A). AggMap feature restructuring focuses on the spatial and channel dimension of the Fmaps. With unsupervised AggMap, FPs are embedded in a 2D space using the manifold learning method Uniform Manifold Approximation and Projection (UMAP) (20) based on their pairwise correlation distances. Meanwhile, the FPs are agglomerated into multiple feature clusters (feat-clusters) using the agglomerative hierarchical clustering method (21). FPs are aggregated into 2D grids by linear assignment algorithm LAPJV (22) based on the embedding coordinates to form spatially-correlated Fmaps, and the feat-clusters guide feature assignment into split channels. The proposed AggMap is defined as a jigsaw puzzle solver (23) because it solves jigsaw puzzles of unordered FPs based on their intrinsic similarities and topological structures. We also constructed a new multi-channel CNN architecture AggMapNet (Figure 1B) with two explainable modules (Shapley-explainer and Simply-explainer) for enhanced and explainable learning of BioHULM from AggMap Fmaps. AggMap/AggMapNet open-source codes are at https://github.com/shenwanxiang/bidd-aggmap.
Figure 1.
AggMap/AggMapNet pipeline and key applications. (A) Unsupervised AggMap flowchart of feature mapping and aggregation into ordered (spatially-correlated) channel-split feature maps (Fmaps). (B) CNN-based AggMapNet architecture for Fmaps learning. The unsupervised AggMap converts unordered vectors into spatially correlated multi-channel Fmaps (3D data), which are the inputs of AggMapNet. (C) proof-of-concept illustration of AggMap restructuring of unordered data (randomized MNIST) into clustered channel-split Fmaps (reconstructed MNIST) for CNN-based learning and important feature analysis. (D) typical biomedical application pipelines of transferable AggMap in restructuring omics data into channel-split Fmaps for multi-channel CNN-based AggMapNet diagnosis and biomarker discovery (explanation global important features from saliency-map).
The feature restructuring capability of AggMap was evaluated by a proof-of-concept (POC) experiment on MNIST (24). Interestingly, AggMap could almost completely reconstruct the original images from the random permutations based on their intrinsic correlations (Figure 1C), and the reconstruction ability of AggMap can be enhanced if it were fitted by higher-sample size randomized data. AggMap's good ability to rearrange FPs improves the learning of random data. The usefulness of AggMap for learning BioHULM data was evaluated by several tests. First, AggMap multi-channel Fmaps show notable improvements and better robustness than single-channel Fmaps on the learning of several datasets by AggMapNet. Secondly, AggMap outperforms the existing 2D feature engineering methods such as Lyu-reshape (12) and Bazgir-REFINED (14) on a multi-task of RNA-seq based pan-cancer classification. In a cell-cycle dataset, AggMap can pick up the stage-specific genes easily by aggregating and grouping the FPs. Thirdly, multi-channel AggMapNet outperformed six ML models that are k-nearest neighbors (kNN), L2-regularized multinomial Logistic Regression (LGR), Random Forest (RF), Rotation Forest (RotF), Xgboost (XGB) and LightGBM (GBM) in most of the 18 low-sample transcriptomic benchmark datasets. Lastly, based on the developed Simply-explainer in AggMapNet, we further explored the important biomarkers for COVID-19 detection and severity predictions. Those identified COVID-19 relevant biomarkers are highly consistent with literature-reported findings or biological mechanisms. These results demonstrate that the feature representation ability in CNN models can be enhanced by unsupervised feature aggregation and multi-channel operations in AggMap, and the developed AggMap/AggMapNet pipeline is superior for DL of BioHULM data and key biomarker discovery (Figure 1D).
MATERIALS AND METHODS
Motivations of AggMap feature restructuring
Humans are capable of logical restoration of broken fragmented objects, such as solving jigsaw puzzles or restoration of cultural property as illustrated in Figure 2A. This ability arises from pre-learned prior knowledge to connect and combine the fragments based on their correlations and edge connections. This knowledge is learned through various fragmentation-restoration processes. However, we are unable to reconstruct an image with its pixels randomly permuted (e.g. from image “a” to image “b” in Figure 2B) despite our ability to restore the image from larger fragments (Figure 2A). This is because the original information of the image from “b” to “a” has been lost completely. Nevertheless, we may restructure the image from “a” to “c” based on the similarities of the pixels (feature points, FPs) in “a”. The new image “c” is much more structured than image “a”, or even with fragments very close to those of the original image for various patterns such as flowers, trunks, and leaves. The proposed AggMap was designed to Aggregate and Map the unordered FPs into structured feature maps (Fmaps) by imitating the assembly ability of humans (solving the jigsaw puzzles) in a self-supervised way. This restructuring process enables the mapping of unordered FPs into structured patterns for more effective deep learning (DL).
Figure 2.

Illustration of the restoring and restructuring process. (A) Restoring of the broken fragments to object with specific patterns. (B) Restructure and restore a randomly permuted image to structured and original image, respectively.
Theoretical basis of unsupervised AggMap
To restructure the unordered FPs into structured Fmaps, self-supervised AggMap needs a metric to measure the similarities between the FPs, an approach to embed the FPs, and an algorithm to assign the embedded FPs to the regular grid (i.e. the position map of the FPs). In AggMap , these tasks were performed by the correlation metric, the manifold-based UMAP (20,25) approach and linear assignment Jonker–Volgenant (J–V) (22) algorithm, respectively. UMAP was initially developed for dimensionality reduction by embedding the samples in low-dimensional space. It can effectively aggregate similar FPs while preserving their relative proximities for both local and global data structure (20,25), leading to SOTA performance for dimensionality reduction in real world data (20,25). UMAP was employed in AggMap by default for embedding FPs instead of samples into 2D space.
There are nine steps in the fitting of AggMap, as indicated by a flowchart (Figure 3) using the restructuring of the randomized MNIST FPs (pixels are randomly permuted MNIST) as an example. In Step 1, given an input tabular data A with a shape of  , where
, where 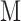 and
and 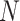 are the number of the samples and features, respectively, AggMap measures the pairwise distance of FPs by the correlation distance to generate the distance matrixB(
are the number of the samples and features, respectively, AggMap measures the pairwise distance of FPs by the correlation distance to generate the distance matrixB(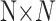 ). AggMap then uses the UMAP (20) algorithm to embed the FPs to 2D space in Step 3–Step 7 based on the calculated B. For the pixel randomly permuted MNIST training data,
). AggMap then uses the UMAP (20) algorithm to embed the FPs to 2D space in Step 3–Step 7 based on the calculated B. For the pixel randomly permuted MNIST training data, 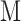 is 60 000 and
is 60 000 and  is 784 (28 × 28), where the
is 784 (28 × 28), where the  pixels are in arbitrary order. The pairwise correlation distance is defined by
pixels are in arbitrary order. The pairwise correlation distance is defined by 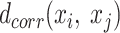 :
:
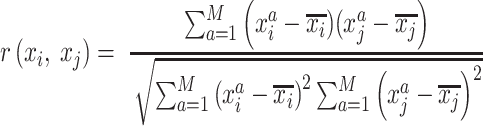 |
(1) |
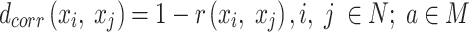 |
(2) |
where 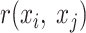 is the Pearson's r for the given FPs of
is the Pearson's r for the given FPs of  .
.
Figure 3.
Flowchart the of self-supervised AggMap fitting process, the dynamic process of MNIST restructuring from randomly permuted images with 500 epochs is available in Video_MNIST.mp4. The Input is the M× N matrix, where M is number of the samples, and N is number of the FPs with arbitrary order, i.e. the randomly permuted MNIST pixels across all training set of MNIST data (M = 60 000, N = 784). Step 1 to Step 9 are the steps in the fitting stages and Step 10 is the transform stage. The Step 3 to Step 7 are the basic ideas of UMAP 2D embedding. One sample, the handwritten number “9”, is used as a tracker to illustrate how it will be restructured. The blank dots in the object E, D, F, F’, G, H and Iare the pixels value of the number “9”. The colors in the object G’, H’ and I’are the same five colors (clusters) as shown in object C, and the five colors stand for five clusters in hierarchical clustering C. The outputs are the single-channel or multi-channel Fmaps.
Step 2 is to conduct hierarchical clustering of the FPs to generate clusters C based on the calculated B, where complete linkage was used and the default number of clusters is 5. This clustering operation splits the FPs into different groups (clusters), more clusters produce more fine-grained separations. Each cluster is separately embedded into an individual Fmap channel for feature group-specific or feature-selective learning by a CNN classifier. Because multi-channel colour images contain more information than grayscale images, multi-channel AggMap Fmaps are with more enriched and distinguished patterns. To visualize the multi-channel Fmaps in AggMap tool, the FPs of each channel were coloured in different colour, and the brightness of the colour corresponds to the FP value. The optimal number of clusters of FPs is a hyperparameter (described in the AggMap Hyperparameters section).
Step 3 is the first phase of UMAP graph construction (25), but different from default UMAP in building the weighted topological k-neighbour graph using Euclidean distance, AggMap builds the weighted graph D by exponential probability distribution using correlation distance B:
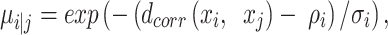 |
(3) |
where  is the weighted adjacency matrix of graph D,
is the weighted adjacency matrix of graph D, 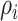 represents the distance from
represents the distance from 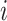 th FP to its first nearest neighbor; this ensures the local connectivity of the manifold.
th FP to its first nearest neighbor; this ensures the local connectivity of the manifold. 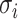 is a (smoothed) normalization factor for the metric
is a (smoothed) normalization factor for the metric 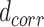 local to the point
local to the point 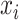 . In UMAP Algorithm 3 (25), distance
. In UMAP Algorithm 3 (25), distance  can be estimated by binary search using the given hyperparameter k number of nearest neighbors (i.e. n_ neighbors). The adjacency matrix
can be estimated by binary search using the given hyperparameter k number of nearest neighbors (i.e. n_ neighbors). The adjacency matrix 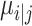 has to satisfy the symmetry condition according to the UMAP algorithm (25):
has to satisfy the symmetry condition according to the UMAP algorithm (25):
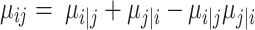 |
(4) |
The graph D is thus an undirected weighted graph whose adjacency matrix is given by  , this construction provides an appropriate fuzzy topological representation of the data (20).
, this construction provides an appropriate fuzzy topological representation of the data (20).
Step 4 and Step 5 are to construct a weighted graph Fin low-dimensional space (i.e. the 2D embedding space). To initialize the 2D coordinates of the FPs in Step 4, AggMap uses the spectral layout to initialize the embedding E. The randomized initialization is unsuitable for preserving global data structure in both t-SNE and UMAP (26). Therefore, AggMap uses the default spectral layout to initialize the embedding for faster convergence and greater stability within the algorithm (25). Specifically, AggMap utilizes the correlation distance B to initialize the embedding E. To ensure a more uniform initialization embedding, AggMap first converts this distance matrix 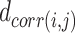 of Binto an exponential affinity matrix
of Binto an exponential affinity matrix  :
:
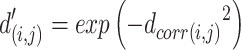 |
(5) |
Subsequently, the matrix  is used for the spectral embedding by the Laplacian Eigenmaps (LE) algorithm. LE finds a low dimensional representation of the data using a spectral decomposition of the graph Laplacian (UMAP algorithm 4 (25,27)):
is used for the spectral embedding by the Laplacian Eigenmaps (LE) algorithm. LE finds a low dimensional representation of the data using a spectral decomposition of the graph Laplacian (UMAP algorithm 4 (25,27)):
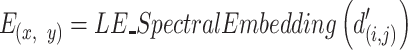 |
(6) |
 |
(7) |
where  is the 2D embedding results inE, and
is the 2D embedding results inE, and 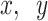 are the coordinates for the
are the coordinates for the 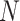 feature points. The pairwise Euclidean distance
feature points. The pairwise Euclidean distance 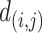 of the FPs is calculated from the 2D coordinates in E. The weighted graph Fin low-dimension space is constructed based on
of the FPs is calculated from the 2D coordinates in E. The weighted graph Fin low-dimension space is constructed based on  according to the UMAP definition (25):
according to the UMAP definition (25):
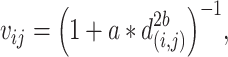 |
(8) |
where  is the weight matrix of the low-dimensional neighbour graph F, and
is the weight matrix of the low-dimensional neighbour graph F, and  and
and  are the parameters estimated from non-linear least-square fitting to the piecewise function with the min_dist hyperparameter.
are the parameters estimated from non-linear least-square fitting to the piecewise function with the min_dist hyperparameter.
Step 6 is the graph layout optimization of F. Since there are two weighted graph D and F, AggMap optimizes the layout of graph F to F’ by minimizing the error between the two topological representations D and F. The graph layout for F(F’) is force-directed, the forces are derived from gradients optimizing the edge-wise cross-entropy in formula (9) between the weighted graph  (i.e. the D) and an equivalent weighted graph
(i.e. the D) and an equivalent weighted graph 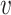 (i.e. the F) constructed from low-dimension space:
(i.e. the F) constructed from low-dimension space:
 |
(9) |
where 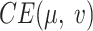 is the total cross entropy loss over all the edge existence probabilities between weighted graphs
is the total cross entropy loss over all the edge existence probabilities between weighted graphs 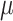 and
and 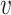 . Minimization of
. Minimization of 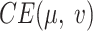 will let the low dimensional representation settle into a state that relatively accurately represents the overall topology of the source data. During the optimization, the similarities between the Dand Fcan also be measured by metric
will let the low dimensional representation settle into a state that relatively accurately represents the overall topology of the source data. During the optimization, the similarities between the Dand Fcan also be measured by metric 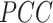 :
:
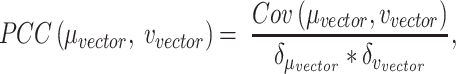 |
(10) |
where the  and
and are the vector-form of the weighted graph
are the vector-form of the weighted graph 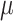 and
and 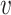 , respectively.
, respectively. 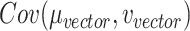 is the covariance of
is the covariance of  and
and 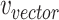 , and the terms
, and the terms 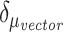 and
and  are the standard deviations of the two weighted graphs. To minimize
are the standard deviations of the two weighted graphs. To minimize 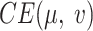 , the derivative of the
, the derivative of the 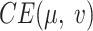 is used to update the coordination of the low-dimensional data points to optimize the projection space until the convergence:
is used to update the coordination of the low-dimensional data points to optimize the projection space until the convergence:
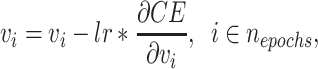 |
(11) |
where 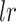 is the learning rate, the term
is the learning rate, the term 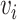 is the weight matrix of topological graph F, and will be updated after each
is the weight matrix of topological graph F, and will be updated after each 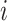 th epoch. The stochastic gradient descent (SGD) algorithm is used due to its faster convergence and lower memory consumption since we compute the gradients for a subset of the data set. Optimized weighted graph F’ is generated upon the convergence of the loss.
th epoch. The stochastic gradient descent (SGD) algorithm is used due to its faster convergence and lower memory consumption since we compute the gradients for a subset of the data set. Optimized weighted graph F’ is generated upon the convergence of the loss.
Step 7 is to generate the 2D embedding resultsG by the graph F’with optimized layout. Meanwhile, Step 8 groups Ginto G’by the groups defined in Step 2. Each colour in G’is one cluster group as shown in C. Once AggMap has generated the G(G’), it will assign the 2D embedded FPs into the 2D regular grid H(H’) by linear assignment algorithm in Step 9. The J–V algorithm (22) is used for the assignment, which preserves the 2D embedded neighbourhood relationships while the FPs are assigned into the grid points. Specifically, AggMap calculates the pairwise squared Euclidean distance as the cost matrix (CM) between two FPs from the 2D embedding and 2D regular mesh grid:
 |
(12) |
where  is the 2D coordinates of the
is the 2D coordinates of the 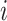 th FP,
th FP, 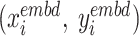 is the 2D coordinates of
is the 2D coordinates of 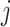 th FP in the mesh grid. The squared Euclidean distance matrix is the
th FP in the mesh grid. The squared Euclidean distance matrix is the 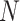 x
x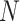 size matrix (
size matrix (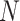 is the number of the FPs), which further serves as the cost matrix (CM) to solve the linear assignment problem (LAP) by J–V algorithm. The J–V algorithm finds an optimal solution to the global nearest neighbour assignment problem by finding the set of assignments that minimize the total cost (i.e. the CM) of the assignments. The regular grid H(H’) is the assignment result, in 2D grid, each FP has an optimized location and its neighbours are the highly correlated FPs. Based on the regular grid H(H’), the input
is the number of the FPs), which further serves as the cost matrix (CM) to solve the linear assignment problem (LAP) by J–V algorithm. The J–V algorithm finds an optimal solution to the global nearest neighbour assignment problem by finding the set of assignments that minimize the total cost (i.e. the CM) of the assignments. The regular grid H(H’) is the assignment result, in 2D grid, each FP has an optimized location and its neighbours are the highly correlated FPs. Based on the regular grid H(H’), the input 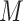 x
x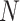 FPs can be transformed into standard 4D tensor with a shape of (
FPs can be transformed into standard 4D tensor with a shape of (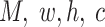 ), where
), where 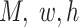 and
and 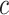 are the number of the input samples, the width, the height and the channels of the Fmaps, respectively. The minimum value (or zero) of FPs is used to mend the Fmaps if in the case of
are the number of the input samples, the width, the height and the channels of the Fmaps, respectively. The minimum value (or zero) of FPs is used to mend the Fmaps if in the case of 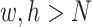 . The output of a multi-channel Fmap for one sample is shown in I’, each channel contains one group cluster in C.
. The output of a multi-channel Fmap for one sample is shown in I’, each channel contains one group cluster in C.
AggMap is an unsupervised learning method because no label is required during feature restructuring. AggMap can be considered as a Fmap jigsaw puzzle solver (23) because it solves jigsaw puzzles of unordered FPs based on their intrinsic similarities and topological structures. It can also be regarded as a representation learning tool because it presents a 1D vector into an image-liked 3D tensor by self-supervised learning. It employs UMAP to restructure unordered FPs by learning their intrinsic structures. The proxy task is to minimize the differences between the two weighted topological graphs built in the input data space and embedding 2D space. Thus, AggMap can expose the overall topology of the FPs to generate structured Fmaps based on the intrinsic structure of FPs.
AggMap hyperparameters
AggMap is divided into three stages of initialization, fitting, and transformation, which is useful for learning low-sample labeled data because higher-sample unlabeled data may be used for training AggMap. The intrinsic relationship between FPs may be better exposed by higher-sample data. The hyperparameters in each stage of AggMap is provided in Supplementary Table S1. In the initialization stage, the pairwise distance matrix of FPs was typically computed by the higher-sample unlabeled data (28). The fitting stage controls how AggMap rearranges the FPs. The hyperparameters in this stage are very important, which include non-UMAP-mediated and UMAP-mediated parameters. For the non-UMAP-mediated parameters, “cluster_channels” is the number of clusters of the multi-channel Fmaps (greater number of clusters leads to finer separation of FPs), “var_thr” is the threshold for filtering out lower variance FPs (default is –1, i.e. no FPs are filtered out). For the UMAP-mediated parameters, “n_neighbors” is the k number of nearest neighbours for estimating the manifold structure of the data (Equation 3), “min_dist” is the minimum distance between two FPs that can be explicitly separated and shown in the low dimensional representation (Equation 8), the number of the epochs (“n_epochs”) and learning rate (“lr”) are to minimize the CE loss (Equation 9) to optimize the layout of the low-dimension graph. In the transformation stage, the inputs are 1D vectors while the outputs are the structured 3D tensor. The important parameter is the data scaling method. AggMap supports two kinds of data scaling methods: the “minmax” and the “standard” scaling. In minmax scaling, the data is transformed into 0-1 range based on the minimal and maximal value of data. In standard scaling (also called z-score normalization), the feature is standardized by removing the mean and scaling to unit variance.
AggMapNet architecture, hyperparameters and training
We specifically developed a simple yet efficient CNN, AggMapNet (Figure 1B) dedicated for learning the structured AggMap Fmaps. The multi-channel Fmaps (each in unstacked format of the single-channel Fmap), have two major advantages for omics data learning. Firstly, the separation of the FPs into several groups (channels) enables feature group-specific or feature-selective learning. Division of mages into multiple patches also benefits the vision transformer (ViT) model in image recognition tasks (29). Secondly, multi-channel Fmaps provide more enriched information and more distinguished patterns than single-channel Fmaps. However, AggMap multi-channel Fmaps may potentially break the local coherence and connectivity among the boundary FPs between two clusters, leading to information loss at the boundary. To overcome this potential problem, AggMapNet uses the 1 × 1 convolutional kernel in inception layers for cross-channel learning, which creates a projection of a stack of multi-channel Fmaps for avoiding the information loss from local boundary-breaking of the Fmaps.
AggMapNet consists of three parts, the input of AggMap Fmaps, the CNN-based feature extraction layers, and pyramid fully connected (FC) layers (Supplementary Figure S1). The first convolutional layer has a larger kernel number for increased data dimension. The max-pooling layer (kernel size=3) has a stride size 2 for more aggressive reduction of the spatial resolution and thus lowering the computational cost. Choosing the right kernel size for the convolution operation is difficult because different tasks may favor different kernel sizes. For performance improvement, AggMapNet adopts the naïve inception layer of GooLeNet (30) (a top-performer of the ILSVRC-2014 classification task). The inception layer in AggMapNet consists of three small parallel kernels (sizes of 1 × 1, 3 × 3 and 5 × 5) for enhanced local perception. The 1 × 1 convolution is for cross-channel learning. Subsequently, a global max-pooling (GMP) layer is introduced before a dense layer instead of a flatten layer, which significantly decrease the number of parameters, followed by dense layers for improved nonlinear transformation capability. Overall, AggMapNet has a relatively small number of trainable parameters (∼0.3 million) but has a complex topological structure of two inception blocks.
The hyperparameters (HPs) and their default setting are in Supplementary Table S2, which include the network architecture parameters (NAPs) and the training-control parameters (TCPs). The NAPs are the kernel size of the first convolutional layer (conv1_kernel_size), the number of dense layers and corresponding units (dense_layers), dropout rate in the dense layers (dropout), number of the inception layers (n_inception), and batch normalization after convolution layers. AggMapNet uses a larger kernel size for the first convolutional layer for enabling more expressive power and a global perception (28,31). To decrease the trainable parameter, default AggMapNet adopts 2 inception layers and 1 dense layer, and no dropout is used for the dense layer. The TCPs include the number of epochs, learning rate (lr), and batch size. The cross-entropy loss was used for both multi-task and binary tasks. During the training, AggMapNet has two important parameters (the monitor and patience) for early stopping. The monitor is the metric performance of the validation set, and the patience parameter is the number of epochs with no improvement on the monitor after which training will be stopped.
In this study, the AggMap feature restructuring object was pre-fit by the its default parameters, but different channel setup in AggMap was explored for enhanced AggMapNet performance. The optimized HPs of AggMap and AggMapNet for each dataset are in Supplementary Table S3. The model parameters were determined by the first inner fold of the nested cross-validations and then used for all the outer folds. The early-stopping method was used to avoid overfitting during the nested validations. To prevent the variability of the models of low-sample data, cross-validations were conducted for at least 5 times by different random seeds.
AggMapNet model interpretation and feature importance saliency-map
Interpretability of DL and ML models is important for informed decisions, mechanism investigations, biomarker discoveries, and model assessments (9,10). However, it is challenging to identify important features effectively and reproducibly based on low-sample BioHULM data. The perturbation-based model interpretation is an established post hoc feature attribution method for interpreting black box models (7,32), which interprets predictions by altering or removing parts of input features to assess its influence on the prediction. Kernel Shapley Additive exPlanations (SHAP) is such kind of the model interpretation method, which can be used for any black-box model explanation (33). Kernel SHAP requires a background data set for training, and feature absence is simulated by substituting feature values with prevalent values of training data. The feature importance in kernel Shapley value is measured by comparing the prediction value obtained with the feature and without it (33).
AggMapNet integrated the kernel SHAP method (i.e. the Shapley-explainer) as one of the model explainers in AggMapNet. However, AggMapNet also complement a new model explainer, i.e. the Simply-explainer. Kernel Shapley method is based on a solid theoretical foundation in game theory and is a popular explainer in local model explanation by calculating the magnitude of feature attributions. Nonetheless, it has several problems in the measurement of feature importance (34). One problem is that it suffers from the computational complexity in the global explanation for the many samples (34). Moreover, since kernel SHAP method considers the amount of contribution each feature makes to the model prediction value instead of the true value, thus it may not able to fully explore the global relationship between the features and the true outcomes (35). The Simply-explainer was developed for providing additional means for AggMapNet model explanation. The Simply-explainer aims to be faster for calculating the global feature importance of the high-dimensional omics features and to consider the relationship of the features with the true labels.
The perturbation-based interpretation method Simply-explainer can be used for both local (individual sample) and global (all samples of a dataset) (8) interpretation tasks. The feature importance (FI) score 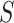 in Simply-explainer is straightforwardly determined by replacing each FP with a background value, without retraining the model:
in Simply-explainer is straightforwardly determined by replacing each FP with a background value, without retraining the model:
Input: Trained model 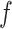 , feature matrix , feature matrix 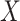 , target true label vector , target true label vector 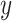 , error measure , error measure  To estimate this error To estimate this error 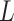 , the log loss(cross-entropy) is used for the classification model and the mse loss is used for the regression model: , the log loss(cross-entropy) is used for the classification model and the mse loss is used for the regression model: |
a) Estimate the original model error 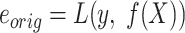
|
b) For each feature 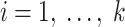 do: do: |
Generate feature matrix  by replacing feature by replacing feature 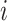 with the minimal value (background value) in the data with the minimal value (background value) in the data 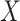 . This breaks the association between feature . This breaks the association between feature 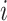 and true outcome and true outcome  . . |
Estimate error 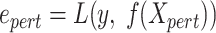 based on the predictions of the perturbed data. based on the predictions of the perturbed data. |
Calculate perturbation feature importance score: 
|
c) Sort features by descending feature importance score  . . |
d) Optional corrections: applying a standard scaling or logarithm transformation on 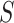
|
The AggMapNet inputs are 4D tensor (batch size, width, height, channels) data in multiple channels. The perturbation only occurs on these meaningful FPs, and the perturbation value is a background value (e.g. zero value for blank pixel) of the input Fmaps. Noted that for the local FI, the model error 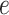 is calculated by the log loss of the individual sample prediction values versus true labels across the labels (classes). However, for the global FI, the model error
is calculated by the log loss of the individual sample prediction values versus true labels across the labels (classes). However, for the global FI, the model error  is calculated by the log loss of the prediction values versus true labels for one class by many samples. That is, in multi-tasks, the Simply-explainer can calculate FI for each class. The global FI based on all samples of a dataset provides a highly compressed, global insight into the behaviours between the feature and true outcomes for the whole dataset in Simply-explainer. In contrast, the local FI reveals the FI that is important to individual sample (8). The correction of the FI of Simply-explainer includes the logarithm transformation and standard scaling of the FI values to reveal the important FPs. After scaling, those FPs with FI score Fl > 0 are considered notable FPs in a saliency-map for the proposed Simply-explainer. The local or global feature importance (FI) is of a Fmap can be presented as a 2D saliency-map for revealing the important features (Figure 1C).
is calculated by the log loss of the prediction values versus true labels for one class by many samples. That is, in multi-tasks, the Simply-explainer can calculate FI for each class. The global FI based on all samples of a dataset provides a highly compressed, global insight into the behaviours between the feature and true outcomes for the whole dataset in Simply-explainer. In contrast, the local FI reveals the FI that is important to individual sample (8). The correction of the FI of Simply-explainer includes the logarithm transformation and standard scaling of the FI values to reveal the important FPs. After scaling, those FPs with FI score Fl > 0 are considered notable FPs in a saliency-map for the proposed Simply-explainer. The local or global feature importance (FI) is of a Fmap can be presented as a 2D saliency-map for revealing the important features (Figure 1C).
In this study, the revealed important features can be presented by a saliency-map (36). The Pearson's correlation coefficient (PCC) and structure similarity index (SSIM) (37) were used to measure the performances of two explainers on the local explanation of the same MNIST recognition models. The PCC and SSIM were calculated based on the original images and the explanations saliency-maps. The full code for AggMap feature restructuring, AggMapNet model learning, and AggMapNet model explanations with both Shapley-explainer and Simply-explainer are in Supplementary Figure S2; AggMap/AggMapNet was coded by Python 3+, and the AggMapNet was built by TensorFlow 2.x framework.
Datasets and evaluation metrics
The datasets used in this study are listed in Table 1. Proof-of-concept (POC) MNIST and F-MNIST benchmark datasets are 28x28 grayscale images, with a training and a test set of 60,000 and 10,000 image respectively (24,38). An original image in MNIST or F-MNIST is named as Org1, where “1” refers to the number of channels being 1 (the grayscale image). To randomize Org1, it was first flattened into a vector of 684 feature points (FPs), then shuffled with a random seed (randomly permuted), followed by the re-folding back into a newly-shuffled 28 × 28 image, which is named as OrgRP1. AggMap restructuring was conducted on the shuffled FPs. The image reconstruction capability of AggMap was tested by the criterion that the reconstructed image patterns is independent of how FPs are shuffled. The reconstructed images are named as RPAgg1 and RPAgg5 for 1-channel and 5-channel AggMap Fmap, respectively. The structure similarity index (SSIM) (37) for an original image and restructured image was used to measure the feature restructuring ability of AggMap on MINST and F-MNIST. The average accuracy was used to measure the performances of the AggMapNet models that were trained on the multi-task MNIST and F-MNIST.
Table 1.
Summary of the datasets in this study
| Project | Datatype | Dataset | Num. of samples | Num. of features |
|---|---|---|---|---|
| Proof-of-Concept | Image data | MNIST (24): handwritten digits. | 70K images including 10 classes: 60K training set, 10K test set. | 28×28 grayscale images, 684 pixels. |
| Image data | Fashion-MNIST (38): Zalando's article images. | 70K images including 10 classes: 60K training set, 10K test set. | 28×28 grayscale images, 684 pixels. | |
| Cell-cycle | Transcriptomics | CCTD-U (39): cell-cycle transcriptome data of U2OS cells | 5 different phases of cell cycle (G1, G1/S, S, G2, M) in biological replicates | 5162 RNA-seq genes expression of U2OS cells during cell-cycle progression |
| Pan-Cancer | Transcriptomics | TCGA-T (12): The Cancer Genome Atlas (TCGA) of 33 cancer types. | 10446 samples, including 33 cancer types from Pan-Cancer Atlas, the number of samples for each class is ranged from 45 to 1212, with an average of 317. The sample sizes for 15 tumor types are less than 200. | 10 381 normalized-level3 RNA-Seq gene expression data. |
| TCGA-S (5): TCGA cancer in different stages. | TCGA cancer stage (10 datasets), 249-554 patients in each of 9 datasets, 1,134 in 1 dataset. | 17 970 “O” genes with Z-score transformed RNA-Seq gene expression data. | ||
| TCGA-G (5): TCGA cancer in different grades. | TCGA cancer grade (8 datasets), 179-554 patients in each of 8 datasets. | |||
| COVID-19 | Proteomics | COV-D (1): Proteomic MALDI-MS data of COVID-19 nasal swabs | 363 samples, 211 SARS-CoV-2 positives, and 151 negatives that are from 3 different labs. | 88 nasal swabs MALDI-MS signal peaks. |
| Proteomics & Metabolomics | COV-S (2): Multi-omics data of COVID-19 sera. | 41 patients, including 31 in the training set (18 non-severe and 13 severe) and an independent cohort of 10 patients (6 non-severe and 4 severe). | 1486 markers from the sera samples, including 649 proteins and 847 metabolites. |
The CCTD-U (39) dataset is a cell-cycle transcriptome data of U2OS cells, consisting of the expression levels of 5162 genes at 5 different cell cycle stages (G1, G1/S, S, G2, M). This dataset was transformed using z-score standard scaling. The multi-task pan-cancer transcriptomic benchmark dataset TCGA-T of 33 cancers is from normalized-level3 RNA-Seq expression studies of normal and tumor conditions, which is compiled by Lyu and Haque (12). TCGA-T consists of 10446 samples (45-1212 samples each cancer type, average: 317). We used the same data and pre-processing method as provided by these studies (https://github.com/HHHit/DL-based-Tumor-Classification). Each sample contains 10,381 normalized gene expression read count data, which was transformed using y = log2(x + 1) (12). For training and testing on TCGA-T, the same stratified 10-fold cross-validation metrics of Lyu and Haque (12) were used. The overall average accuracy and average accuracy of each class were calculated based on the test et performances using the scikit-learn (40) package, where the weighted average was used for the average performance calculation.
Two groups of low-sample binary task cancer transcriptomic benchmark datasets TCGA-S and TCGA-G include 10 cancer stage and 8 cancer grade datasets, which are from reproducible RNA-seq analysis and compiled by Smith et al. (5). Each TCGA-S and TCGA-G consists of 249–1154, 179–554 samples; each sample contains 17 970 “O” (in GO under the “biological process” or “molecular function” categories) genes with Z-score standardization (5). For training and testing on TCGA-S and TCGA-G, the same 5-fold nested cross-validation ROC-AUC metrics of Smith et al. (5) were used for rigorously assessing the out-of-sample performance of the models.
Two COVID-19 proteomic/metabolomic datasets COV-D and COV-S, are from COVID-19 detection (1) and severity determination (2) investigations, respectively. COV-D includes 363 samples (211 Covid-positives and 151 negatives by RT-PCR) from 3 labs, and each sample contains 88 nasal swabs matrix-assisted laser desorption/ionization mass spectrometry (MALDI-MS) signal peaks (1). To make a fair comparison with original ML models (1), the performance of AggMapNet was also evaluated by the overall accuracy, sensitivity, and specificity of the test fold in 4-fold cross-validation with 5 times repeat (using different split seeds for each repeat). COV-S includes 41 COVID-19 patients, split into 31 for training (18 non-severe and 13 severe) and 10 patients for testing (6 non-severe and 4 severe), the features are the 1486 integrated signatures from the sera samples (649 proteins and 847 metabolites) analyzed by untargeted metabolomics approach using the ultra-performance liquid chromatography/tandem mass spectrometry (UPLC-MS/MS) (2).
Generation of the noisy test set for MNIST/F-MNIST and TCGA-T
The noisy test set for the four Fmaps of Org1, OrgRP1, RPAgg1 and RPAgg5 on MNIST were generated by following steps: First, Gaussian noises of varying levels (standard deviation 0.00 to 0.72 with a step of 0.12) were added to the MNIST/F-MNIST test set images (images of higher noise levels become harder to recognize Supplementary Figure S3), i.e. the noise was added to Org1 tests only (The Fmap values are divided by 255 to scale into 0–1), leading to a noise-added dataset Org1-N set, then Org1-N Fmaps were further randomly permuted into OrgRP1-N using the same random seed as the OrgRP1 generation. Subsequently, the OrgRP1-N Fmaps were transformed into the noisy set of RPAgg1-N and RPAgg5-N by the pre-fit AggMap (Supplementary Figure S4). AggMapNet models trained on the Org1, OrgRP1, RPAgg1 and RPAgg5 Fmaps were evaluated on the derived noisy test Fmaps of Org1-N, OrgRP1-N, RPAgg1-N and RPAgg5-N, respectively. On the multi-task TCGA-T dataset, noises were added to the test set of each fold in the 10-fold cross-validation for testing AggMapNet model performance. Specifically, various levels of Gaussian noise (standard deviation 0.00–0.48 with a step of 0.08, Supplementary Figure S5) were added to the test set of each fold in the TCGA-T dataset (scaled to 0–1), then the unstructured noise-added data was transformed into 1-channel and 5-channel noise-added but structured Fmaps by pre-fitting AggMap.
Benchmarking of ML models and AggMapNet on 18 transcriptomic benchmark datasets
We compared AggMapNet with several ML models on 18 transcriptomic datasets (10 TCGA-S and 8 TCGA-G, all binary tasks). Although Smith et al. (5) have benchmarked the performances of three standard ML models (RF, LGR, and kNN)) with or without feature embedding on these datasets, more advanced and efficient tree-based ensemble ML models such as RotF (41), XGB (42), and LGB (43) have not been evaluated. To compare AggMapNet with ML models, we also evaluated the performance of RotF, XGB and LGB with or without subset feature selection (FS). These 18 datasets provide expression levels of 17970 genes, thus Smith et al.(5) used PCA and deep representation methods to convert the original high dimensional data into 512 bits vectors as the inputs for the three standard ML models of RF, LGR and kNN. In this study, we also tried the FS method for the three tree-based ML models of RotF, XGB and LGB to reduce the number of the features. We selected the subset features in the training set by the median-based generalized absolute fold change (FC) (44) among the two classes (binary labels) using the optimized cut-offs (for example, at least a 0.5× fold change across any two conditions). The cut-offs of FC were determined by the performance of the nested 5-fold cross-validations. Therefore, the number of the selected features are different in the each of the outer fold of the five-fold cross-validations.
All these ML models were evaluated by the average performance of the outer 5-fold cross-validation. The exhausted grid-search strategy was used to find the best in the inner 5-fold cross validation. Specifically, for each fold of the outer folds, a nested inner 5-fold cross-validation was used to select optimal hyperparameters, and then the optimal hyperparameters were used to build the model for the outer fold. We optimized the important HPs such as “n_estimators”, “num_leaves”, “max_depth” for the tree-based models by scikit-learn package the “GridSearchCV” module (40). Nested cross validation is resistant to hyperparameter overfitting, as the model is evaluated on data completely held out from the process of selecting the optimal hyperparameter (5).
To make fair comparisons, AggMapNet models were evaluated by the same data split random seeds, data scaling methods, and model evaluation metric as published ML models. To make AggMapNet more user-friendly, in the nested cross-validations, only one hyperparameter (i.e. the number of epochs) in AggMapNet was optimized while all other HPs of AggMap and AggMapNet were kept as default. AggMap was pre-fit by the unlabeled gene expression data of all 18 datasets and multi-channel Fmaps were generated by the default parameters (C = 5).
RESULTS AND DISCUSSIONS
Good feature restructuring capability of AggMap
To explore the restructuring ability of AggMap in exposing the unordered data, we randomly permuted the MNIST (24) data by shuffling the orders of pixels (Figure 4A). Randomly permuted MNIST represents the unordered data with prior intrinsic patterns. We evaluated the extent to which AggMap Fmaps reconstruct MNIST from randomly permuted data (OrgRP1). We pre-fit AggMap using fractions (full, 1/2, 1/5, 1/10, 1/100 and 1/1000) of an OrgRP1-tr (60K randomly permuted MNIST training set) and employed it to transform the Fmaps of the OrgRP1-tr and OrgRP1-ts (10K randomly permuted MNIST/F-MNIST test-set). We found that AggMap can reconstruct the randomly permuted MNIST data to the original data, and its reconstruction ability depends on the sample to perform the pre-fitting. Pre-fitting with the full MNIST OrgRP1-tr, AggMap well-restored MNIST, down to local patches. Pre-fitting with 1/2, 1/5 or 1/10 MNIST OrgRP1-tr, AggMap roughly restores MNIST at an increasing level of deformation, tilt or flip when trained with decreasing fractions of training sets (Figure 4B). Pre-fitting with 1/100 or 1/1000 F-MNIST OrgRP1-tr, AggMap cannot restore F-MNIST but still generate distorted curve-shaped patterns (Supplementary Figure S6A). Pre-fitting with the full F-MNIST OrgRP1-tr, AggMap cannot restore the original F-MNIST but aggregates together the original local patches (Supplementary Figure S6 B).
Figure 4.
Proof-of-concept experiments on MNIST benchmark set. (A) the example of AggMap fit and transform to generate the Org1, OrgRP1, RPAgg1 and RPAgg5 Fmaps as the inputs of AggMapNet. In the training set, the 28x28 pixels were reshaped into 684 feature points (FPs) and randomly permuted into 684 unordered FPs (unordered image data). Then they were reshaped into the shuffled 28x28 images (namely the OrgRP1 images). The random permuted images OrgRP1 have destroyed the spatial correlation of the original images (Org1) completely. The AggMap was fit on the unordered image data and transformed the OrgRP1 images into RPAgg1 (channel = 1). The split-channel operations help transform the greyscale images into multi-channel images based on the clustered groups (RPAgg5, channel = 5). (B) AggMap pre-fit with a different number of random permuted images to reconstruct the MINST images (RPAgg1). The all (60K), 1/2, 1/5, 1/10, 1/100 and 1/1000 of the randomly permuted MNIST training set OrgRP1 were used for pre-fitting by AggMap, which was used for the reconstruction of the randomized MNIST test set. (C) the original, randomized, and restructured MNIST data. RPAgg5-tkb: the original images with the pixels divided into five groups according to the 5-channels of RPAgg5 and colored in the same way as RPAgg5. (D) the historical validation accuracies of AggMapNet training on the four Fmaps. To perform the training on the four Fmaps (Org1, OrgRP1, RPAgg1, RPAgg5), we stratified sampled 10% data from the training set (60K samples) as the validate set, leading to 54 000 training samples and 6000 validate samples; the degree of the validation loss and accuracy is monitored during the training, and the early stopping strategy was used to prevent from overfitting (store the model only that has the best performance on the validation set). (E) the accuracies of the final four models on the test set with noise-free and varying degrees of noise. The performance of the model deteriorates as the noise increases (standard deviation of Gaussian white noise from 0.0–0.72)
The dynamic processes of AggMap restructuring of the randomized MNIST and F-MNIST FPs are in Video_MNIST.mp4 and Video_F-MNIST.mp4, respectively, which showed that the restoration abilities of AggMap are linked to the reduction of the cross-entropy loss defined in Equation 9. With increasing number of iterations (epochs), the generated Fmaps become more structured and eventually form stable patterns when the loss reaches convergence. AggMap can roughly restore the randomized MNIST FPs into original images, but not the randomized F-MNIST. MNIST is curve-shaped data and the correlation between FPs is not discrete but more uniformly distributed, which conforms to the UMAP assumption of data uniform distribution (25). We compared the CE loss and PCC of MNIST with those of F-MNIST during the graph layout optimization stage of AggMap feature restructuring (Supplementary Figure S7A). MNIST has a lower loss and higher PCC value, indicating that the 2D embedded distribution in MNIST more resembles the topological structure of the original data. The final 2D embedding of MNIST FPs is also more uniformly distributed than that of F-MNIST FPs (Supplementary Figure S7B). Therefore, AggMap can reconstruct randomized MNIST partly because the manifold structure of the FPs is not totally changed despite the MNIST FPs being randomly permuted, and the manifold structure can be approximated by the weighted graph in low-dimension. The randomized F-MNIST was restructured into more compact patterns with some local patches restored to the original patches. Therefore, AggMap can restructure randomized F-MNIST into highly structured form even though it cannot fully restore the original image.
The split-channel operations based on the cluster groups enable the greyscale images to be presented as multi-channel-colored images (Figure 4C, RPAgg5, each color represents one channel), the further tracking of these colorful channels into the original MNIST images showed that they are in the same relative positions (Figure 4C, RPAgg5-tkb), indicating that the reconstruction is able to maintain the same local structure with original images. Thus, AggMap feature restructuring can expose the curve-shaped intrinsic patterns (i.e., the MNIST restructuring example) and the local patches (i.e. the F-MNIST restructuring example) of the packed intrinsic patterns. AggMap's ability in exposing local intrinsic patterns is largely useful for CNN-based learning because the CNN classifier has been proved to rely on local texture cues strongly (45).
Enhanced learning of randomized data by AggMap feature restructuring
We evaluated to what extent does AggMap feature restructuring improves AggMapNet classification of randomized MNIST, which sheds light on the ability to learn unordered data. AggMapNet was trained by the training set of the four Fmaps separately (Org1, OrgRP1, RPAgg1 and RPAgg5, Figure 4A, C), validated on their corresponding validation set, and tested on their corresponding test set (10K). The results show that AggMap (RPAgg1,5) transformation improved MNIST classification performance of AggMapNet from 96.7% (without AggMap, OrgRP1 Fmaps) to 99.1–99.2%, close to the performance of the model (99.5%) that was trained on the original images (Figure 4D, E). Therefore, the AggMap feature restructuring enhanced DL of randomized (unordered) data. The results show that the high performance of CNNs in image-related tasks critically lies in its architecture that takes advantage of the local order of images, and AggMap is a useful tool to restructure the unordered data into locally-ordered data.
AggMap multi-channel Fmaps and their notable contributions to the improved performance of AggMapNet
AggMap multi-channel Fmaps have an obvious advantage over single-channel Fmaps. Visualization of AggMap multi-channel Fmaps of the cell-cycle CCTD-U (39) dataset at different cell replication phases indicated that multi-channel Fmaps can easily select stage-specific genes (Figure 5). The stage -specific genes in the five cell-cycle phases can be easily aggregated into hot-zones in the single-channel Fmaps based on their correlations, while the multi-channel Fmaps further separate the phase-specific genes into different channels. Therefore, the multi-channel Fmaps facilitate group-specific feature learning or feature selective learning by AggMapNet. By the hierarchical clustering-guided channel splits, each cluster (group) of FPs may be separately embedded into a different Fmap channel. More clusters enable more fine-grained separations of FPs into groups. However, AggMap multi-channel Fmaps may potentially break the local coherence and connectivity among the boundary FPs between two clusters (e.g. Figure 4C, RPAgg5), leading to information loss at the boundary. To overcome this potential problem, AggMapNet uses the 1 × 1 convolutional kernel in inception layers for cross-channel learning, which creates a projection of a stack of multi-channel Fmaps for avoiding the information loss from local boundary-breakage of the Fmaps.
Figure 5.
The performance of AggMap on the restructuring of the cell-cycle dataset of CCTD-U (39). (A) the hierarchical clustering of the 5162 genes in AggMap (number of the clusters C = 6). (B) the 2D embedding of the 5162 genes by UMAP-mediated AggMap, the clusters are from (A). (C) the 2D regular grid of the 5162 genes which are assigned by AggMap linear assignment algorithm. (D) the AggMap transformed multi-channel Fmaps of the cell-cycle five stages. (E) the AggMap transformed single-channel Fmaps of the cell-cycle five stages, the hot-zone indicates the stage-specific genes, these genes are highly expressed in a specific cell stage. (F) the five phases of cell-cycle: G1, G1/S, S, G2 and M
We tested the effects of channel number on the four representative datasets of MNIST, TCGA-S COAD, TCGA-G HNSC and COV-S (Figure 6). The performance of AggMapNet can be improved with the increasing the number of channels, because more channels generate more fine-grained separations of the FP groups. However, if the number of channels increases to a certain extent, the performance of the model in some dataset can be decreased. This is because the greater number of channels in the Fmaps, the more trainable parameters of the model, which can lead to the overfitting problem. Overall, the multi-channel Fmaps are helpful for CNN-based model to learn complex data by separately learning feature subsets. Their representational richness often allows the capturing of nonlinear dependencies at multiple scales (17). Thus, multi-channel Fmaps notably improve the performance of AggMapNet, where the channel number is a hyperparameter that need be optimized.
Figure 6.
The five-fold cross-validation average performance of AggMapNet using different number of channels on the four datasets. (A) the average accuracy performance of the 5-fold cross-validation on multi-task MNIST dataset. (B) the average ROC-AUC performance of the 5-fold cross-validation on binary task transcriptomic dataset of TCGA-S COAD (stage II- versus III+). (C) the average ROC–AUC performance of the five-fold cross-validation on binary task transcriptomic dataset of TCGA-G HNSC (grade II- versus III+). (D) the average ROC–AUC performance of the five-fold cross-validation on binary task proteomic dataset of COV-S (COVID-19 positive vs. negative). For the low-sample size datasets of TCGA-S COAD, TCGA-G HNSC and COV-S, we repeated five rounds using different random seeds (total 25 training times), their average performances of the validation set were reported.
AggMap Multi-channel Fmaps enhance robustness of AggMapNet models on noisy test data
The CNN models have been proved very vulnerable to attacks in the form of subtle perturbations to inputs that lead a model to predict incorrect outputs (46,47), and although CNNs perform better than or on par with humans on good quality images, CNN performance is still much lower than human performance on distorted noise images (48). We, therefore, examined whether the AggMapNet models trained on AggMap multi-channel Fmaps show better robustness on noisy test data. These models were trained on the noise-free Org1, OrgRP1, RPAgg1 and RPAgg5 Fmaps and then evaluated on the corresponding noisy test set (Org1-N, OrgRP1-N, RPAgg1-N, RPAgg5-N, Supplementary Figure S4) with different noise levels. As the noise level increases, the performances of all models showed varying degrees of deterioration. Nevertheless, the models trained by AggMap-transformed multi-channel Fmaps (RPAgg5) in both MNIST and F-MNIST showed better robustness to noise (Table 2, Supplementary Figure S8). For example, on the noise level of 0.36 in the MNIST test set, the classification accuracy of RPAgg5 can still be maintained at 90%, but the corresponding accuracy performances for single-channel Fmaps of Org1, OrgRP1 and RPAgg1 are 77%, 56% and 0.75% respectively. We performed the same experiments on the multi-task pan-cancer transcriptomic dataset TCGA-T (12), it classified the noise-added pan-cancer transcriptomic test set with 95.1% and 13.2% accuracy at zero and 0.48 noise levels, respectively (Table 2). While after the pre-fit AggMap transforming the data into 5-channel Fmaps, it classified the noise-added pan-cancer transcriptomic test set with 96.4% and 53.6% accuracy at zero and 0.48 noise levels, respectively. These results demonstrated that the multi-channels Fmaps enhanced AggMapNet learning of noisy/unordered data, the cluster-based channel-split feature in AggMap transformation is crucial.
Table 2.
Proof-of-concept evaluation of the contribution of AggMap feature restructuring to the robustness of AggMapNet classification of the original and noise-added randomized data. AggMapNet was trained with noise-free training-sets and tested by noise-added test-sets with original or randomized data as direct input or with AggMap Fmaps as input
| AggMapNet classification performance | |||||
|---|---|---|---|---|---|
| Without AggMap transform | With AggMap transform | ||||
| Data set | Gaussian noise level (standard deviation) | Original: Org1 | Randomly permuted: OrgRP1 | Randomly permuted then restructured: RPAgg1 (C = 1) | Randomly permuted then restructured: RPAgg5 (C = 5) |
| MNIST test-set (noise-added) | 0.00 (noise-free) | 99.5% | 96.7% | 99.2% | 99.1% |
| 0.12 | 99.4% | 95.4% | 99.1% | 99.1% | |
| 0.24 | 97.5% | 82.5% | 96.4% | 97.9% | |
| 0.36 | 76.9% | 56.0% | 75.1% | 90.0% | |
| 0.48 | 45.6% | 37.5% | 47.4% | 67.9% | |
| 0.60 | 25.0% | 26.0% | 27.1% | 42.0% | |
| 0.72 | 15.4% | 20.4% | 18.1% | 26.6% | |
| F-MNIST test-set (noise-added) | 0.00 (noise-free) | 92.5% | 88.8% | 90.7% | 91.1% |
| 0.12 | 83.6% | 81.6% | 82.8% | 86.9% | |
| 0.24 | 58.7% | 61.7% | 61.2% | 71.1% | |
| 0.36 | 32.7% | 41.7% | 43.4% | 47.4% | |
| 0.48 | 19.4% | 28.6% | 30.2% | 31.3% | |
| 0.60 | 14.5% | 21.8% | 21.1% | 23.6% | |
| 0.72 | 12.7% | 18.5% | 16.0% | 20.9% | |
| TCGA-T (10-fold cross validation, average performance) | 0.00 (noise-free) | 95.1% | NA | 95.5% | 96.4% |
| 0.08 | 94.0% | NA | 94.7% | 96.0% | |
| 0.16 | 86.4% | NA | 92.1% | 94.2% | |
| 0.24 | 62.7% | NA | 84.8% | 89.9% | |
| 0.32 | 36.4% | NA | 71.7% | 81.3% | |
| 0.40 | 20.9% | NA | 55.4% | 68.4% | |
| 0.48 | 13.2% | NA | 41.3% | 53.5% | |
Unsupervised transferable AggMap boosts the classification accuracy of AggMapNet
Unsupervised AggMap operates in separate fitting and transformation stages for enabling transfer learning (Figure 7A). The fitting operation can be trained on higher-sample data and subsequently used for transforming low-sample data. In the fitting stage, AggMap inputs are tabular data matrix of size (n, p) to calculate the correlation distance of feature points (FPs) for performing manifold 2D embedding and clustering, where n and p are the number of samples and FPs, respectively. In the transformation phase, 1D unorder FPs are input to AggMap for transforming into Fmaps, and a scaling method such as minmax or standard scaling was used for scaling the FPs. This setup is useful for learning low-sample data because a larger amount of unlabeled data could be used for fitting and generating AggMap objects to transform low-sample 1D unordered data into structured Fmaps. The intrinsic relationship between FPs could be more accurate if it were determined by higher-sample data and exposed by manifold-based learning. We fit AggMap by using different numbers of MNIST training samples (full, 1/2, 1/5, 1/10, 1/100 and 1/1000 of 60K), which showed that the AggMap Fmaps pre-fitted by a larger dataset has a better local and global reconstruction ability (Figure 4B). The same behavior was found on the multi-task omics TCGA-T dataset (Figure 7B). Pre-fitting AggMap with a very low sample subset of TCGA-T, the generated Fmap is closer to the randomized result because subset data alone cannot properly measure the intrinsic correlation similarities of the pairwise FPs. Pre-fitting AggMap with a larger sample size leads to more locally structured TCGA-T Fmaps (Figure 7B) and consequently, achieve a relatively higher classification accuracy (Figure 7C). The average 10-fold cross-validation accuracies for the five lower-performing tasks of the multi-task TCGA-T (the five cancer types: READ, CHOL, UCS, KICH and ESCA) have boosted from 44%, 62%, 79%, 84%, and 85% to 47%, 71%, 82%, 91% and 87%, respectively. Thus, the unsupervised transferable AggMap could boost the classification accuracy of AggMapNet if it were pre-fitted on higher sample unlabeled data.
Figure 7.
The performances of AggMap and AggMapNet learning model on transcriptomic data TCGA-T, TCGA-S and TCGA-G. (A) the fit and transform operations in the AggMap tool enable the Fmaps transfer learning in TCGA-T data: the pre-fit AggMap based on unlabeled high-data can be used for low-data feature maps transformation. (B) the pre-fit sample size effects on the TCGA-T Fmaps: feature maps transformed by AggMap objects that are pre-fitted (pre-learned) by different numbers of samples in TCGA-T dataset (The sample size of 45 is the smallest sample size of the class (the CHOL type) in the dataset, the sample size of 317 is the average sample size among all the classes in TCGA-T dataset, the sample size of 10446 is the total number of the samples). Using a very small sample size in TCGA-T for pre-learning (pre-fitting) in AggMap, the closer the Fmap is to the randomized result. The larger the sample size for pre-fitting (pre-learning), the more structured TCGA-T Fmaps will be generated. (C) the pre-fit sample size effects on learning accuracies, the average 10-fold cross-validation performances for the 5 cancer types (READ, CHOL, UCS, KICH, ESCA) on the four Fmaps that are pre-fitted by different numbers of the samples. Larger samples to perform the pre-fitting in AggMap can achieve relatively better classification accuracy. (D) a comparison of four Fmaps that are generated by Lyu's reshaping (based on genetic locations) (12), Bazgir-REFINED (based on data neighbors by MDS) (14), single-channel AggMap (C = 1) and multi-channel AggMap (C = 5) on the five lower-performing cancer tasks of the TCGA-T dataset. (E) the ten-fold cross-validation average loss performances of AggMapNet models trained on the four different Fmaps. (F) the nested five-fold cross-validation average ROC-AUC performance of AggMapNet versus the six ML models LGR, kNN, RF, RotF, XGB and LGB (with or without PCA embedding and feature selection) on the 10 TCGA-S (cancer stage) and 8 TCGA-G (cancer grade) datasets. The performance of three ML models of LGR, kNN and RF with or without PCA dimensionality reduction were benchmarked by xx. The three ML models of RotF, XGB and LGB with or without absolute fold change (FC) based feature selection were evaluated by this paper. LGR: L2-regularized multinomial Logistic Regression, RF: Random Forest, kNN: k Nearest Neighbor, RotF: Rotation Forest, XGB: Xgboost, LGB: Lightgbm, PCA: principal component analysis, FS: feature selection.
Multi-channel AggMap versus existing feature restructuring methods
We compared the DL performance of AggMap with existing 2D Fmap generation methods Lyu's reshaping (12) and Bazgir-REFINED (14) based on AggMapNet learning of the TCGA-T dataset. Lyu's reshaping method straightforwardly converts 1D vector into 2D image by directly reshaping the vector (12). Bazgir-REFINED method projects 1D vector into 2D image according to their neighborhood dependencies by means of the linear multidimensional scaling (MDS) method (14). AggMap Fmaps exhibited more structured local textures than those of the two existing methods (Figure 7A, Supplementary Figure S9). Based on the 10-fold cross-validation performance of these Fmaps on AggMapNet learning of the TCGA-T dataset (Figure 7B), the models of AggMap Fmaps scored lower loss values than the two existing methods, while AggMap 5-channel Fmaps achieved the lowest loss values. The accuracies of the AggMapNet models of these Fmaps for the 33 cancers of the multi-task TCGA-T dataset are in Supplementary Table S4. For all 33 cancer tasks, the use of multi-channel AggMap Fmaps substantially improved the average accuracy over existing methods from 92% to 94%. In particular, AggMap Fmaps boosted the accuracies (ACCs) of the cancer classes of lower performances. For instance, the models of Lyu-reshaping (12), scored <90% ACCs for five cancers (CHOL, ESCA, GBM, READ and KICH). Multi-channel AggMapNet improved the accuracies from 35% to 47%, 56% to 71%, 77% to 87%, 81% to 82% and 87% to 91%, respectively. Therefore, AggMap feature restructuring method outperformed the existing methods Lyu's reshaping and Bazgir-REFINED. The advantage of AggMap arises from two reasons: Firstly, the UMAP-mediated AggMap nonlinear mapping tends to generate more structured and local texture, while the local texture and local connectivity are crucial to the accuracy and robustness of CNN model (45). Secondly, the multi-channel Fmaps are helpful for CNN-based models to learn complex data by separately learning feature subsets (16), and their representational richness often allows CNN models to capture nonlinear dependencies at multiple scales (17).
Multi-channel AggMapNet versus ML models on the 18 transcriptomic benchmark datasets
ML methods, combined with feature dimensionality reduction (DR) or feature selection (FS) techniques, have been commonly used for learning BioHULM data (1,5). AggMapNet models were thus compared with six ML models on 18 low-sample (179–554 patients) and high-dimension (17970 genes) transcriptomic datasets. These datasets are TCGA cancer stage (TCGA-S, 10 datasets) and grade (TCGA-G, 8 datasets) (5). Three standard ML models RF, LGR and kNN with or without DR (PCA or deep representation method, which reduced the dimensionality to 512) have been developed and benchmarked by Smith et al. (5). They found no consistent improvements of ML models with DR (5). We compared AggMapNet with these three ML models with or without PCA. We additionally benchmarked three efficient tree-based models of RotF, XGB and LGB. These three models with or without FC-based FS were also compared with AggMapNet. The comparison was measured by the nested five-fold cross-validation ROC-AUC performances of AggMapNet and six ML models with or without DR or FC. AggMapNet outperformed all six ML models with or without DR or FS (Figure 7C). Specifically, it outperformed the three standard ML models LGR, RF and kNN on 12, 17 and 18 of the 18 benchmark datasets (Supplementary Table S5), and these three ML models with PCA on 18, 15, and 18 of the 18 benchmark datasets (Supplementary Table S6). AggMapNet outperformed the three tree-based ML models RotF, XGB, and RF on 18, 18 and 15 of the 18 benchmark datasets (Supplementary Table S7), and these three ML models with FS on 18, 16 and 16 of the 18 benchmark datasets (Supplementary Table S8). AggMapNet can achieve higher performance if a proper AggMap channels number is selected (Figure 6). Therefore, AggMapNet coupled with AggMap is a highly completive learning method for DL of BioHULM and other low-sample size and high-dimension data.
Interpreting AggMapNet models by Simply-explainer and Shapley-explainer
AggMapNet provides two perturbation-based interpretation methods for revealing important features of AggMapNet models (i. e. the Simply-explainer and Shapley-explainer), which facilitates biomarker discovery from BioHULM data. The Shapley-explainer is based on the kernel SHAP values, which considers the amount of contribution each FP makes to the model prediction value (33). AggMapNet also provides a simple interpretation tool that select important features simply by the loss changes between the outcomes and the true labels before and after each feature alteration. We first compared the Simply-explainer and Shapley-explainer on the local explanation of the same MNIST recognition model. The PCC and SSIM between the original image and the explanation saliency-map were used for measuring the explanation performances. Simply-explainer tends to score better explanation performance with higher PCC and SSIM values than the Shapley-explainer on both explanations of noise-free and noisy test images (Supplementary Figures S10 and S11). Noticeably, Simply-explainer focuses on the relationships between the outcomes with the true labels instead of the changes in prediction values, which might be advantageous for better explanation performance.
We also compared the two explainers on the global explanations of the breast cancer diagnostic model trained on the WDBC dataset (569 samples, 30 features) (49). The feature importance (FI) score of the two explanations is highly-correlated (Persons’ r = 0.866) to each other (Supplementary Figure S12A). However, the FI scores in Simply-explainer tends to be more discrete than Shapley-explainer, suggesting that Simply-explainer can be a competitive method for biomarker identifications. The computational complexity for the Simply-explainer is O(n), which is much faster than the kernel Shapley-explainer (The complexity in kernel Shapley-explainer is O(m*l*(2n + 2048)), where l is the number of background samples, n is number of features and m is number of samples (33)) (Supplementary Figure S12B). These results indicate that Simply-explainer is robust, highly discriminative and fast for the selection of important features, even with noisy data, which is particularly suitable for discovering the key biomarkers in BioHULM data.
Applications of multi-channel AggMapNet in the COVID-19 detection on mass spectrometry data
We further tested AggMapNet on COVID-19 detections from a real-world spectra data of proteome COV-D. COV-D has been derived from the nasal swabs of 363 COVID-19 patients/controls using clinically-available MALDI-MS equipment (1). MALDI-MS assays exploit reference spectra for disease diagnosis through proteomic profiling. Six MLs and two feature selection methods have been exploited in previous study (1) for COVID-19 diagnosis and spectra marker identification, where Support Vector Machines with a Radial kernel (SVM-R) achieved SOTA performance in the detections, the average accuracy by the nested 4-fold cross-validation (4-FCV) with optimized SVM-R is 93.9% (1), however AggMapNet with multi-channel Fmaps inputs has achieved 94.5% detection accuracy based on the same data split method and evaluation metric (Figure 8C). By converting 1D spectral data into 2D multi-channel Fmaps, AggMap boosted the detection accuracy, because multi-channel Fmaps are easier to distinguish the positive cases from controls (Figure 8A), and their representational richness allows the capturing of nonlinear dependencies at multiple scales, thus have improved the detection accuracies notably compared with single-channel Fmaps (Figure 8B).
Figure 8.
AggMapNet in COVID-19 detections based on COV-D spectra dataset from the nasal swabs. (A) an illustration of AggMap transforming MALDI-MS signal peaks from the six positive cases and six negative controls into structured multi-channel Fmaps, the orange peaks are the COVID-19 positives, the inter-correlated peaks have been aggregated into neighbor pixels in the Fmaps. (B) the five-fold cross-validation average performances of AggMapNet models that are trained on AggMap Fmaps with different numbers of channels (1, 3 and 5). (C) a comparison of the four-fold cross-validation performances for the SVM-R models with or without feature selection methods (1) and multi-channel AggMapNet model on COVID-19 detections. CFS: correlation-based feature selection, IGFS: information-gain based feature selection. (D) the global feature importance (FI) correlations among the 4-fold of AggMapNet detection models. (E) the overlap peaks of top10/30 important peaks in AggMapNet with the 39 statistically significant (P < 0.05) peaks of the previous MALDI-MS study (1). (F) The Top 10 important peaks in AggMapNet and the two-tailed Wilcoxon rank-sum test (with Bonferroni correction) results for peaks intensities between COVID-19 and control samples, the significant level ****P ≤ 0.0001, ***0.0001 < P ≤ 0.001, **: 0.001 < P ≤ 0.01, *: 0.01 < P ≤ 0.05, not significant (ns): 0.05 < P ≤ 1.
Examination of AggMapNet-revealed important features showed that, the global feature importance (FI) scores calculated by Simply-explainer for COV-D peaks in different folds of 4-FCV are highly correlated (the pairwise fold Pearson's r = 0.71–0.91) (Figure 8D). Notably, 7 of the top-10 and 18 of the top-30 important peaks are among the 39 statistically significant (p<0.05) COVID-19-correlated peaks of the previous MALDI-MS study (1) (Figure 8D, E), where the most correlated peak (p-7612) of that study ranked fifth by AggMapNet. Moreover, the first ranked peak p-7654 by AggMapNet is highly correlated with p-7612, the relative average intensities of both p-7612 and p-7654 for the COVID-19 positives are lower than the healthy controls (Figure 8F).
Applications of AggMapNet in the severity prediction and key biomarkers identification of COVID-19 on low-sample size multi-omics data
AggMapNet was also applied to classify the severe and non-severe COVID-19 patients and identify key proteomic and metabolomic biomarkers. The sera multi-omics (proteomic and metabolomic) dataset of COV-S with 49 COVID-19 patients has been used for ML-facilitated determination of COVID-19 severity and sera protein/metabolite changes(potential biomarkers) (2). The random forest (RF) model scored 70% accuracy in classifying the severe cases from non-severe cases in the independent test cohort in COV-S (2), while AggMapNet with multi-channel Fmaps (Figure 9A, B) inputs can improve the accuracy to 80%. A non-severe patient XG45 misclassified by RF but correctly classified by AggMapNet reportedly received traditional Chinese medicines for >20 days before admission (2). The 43-year-old male non-severe case XG25 was incorrectly classified as severe by both RF and AggMapNet model for reasons unclear, another non-severe patient XG22 misclassified by both RF and AggMapNet had chronic hepatitis B virus infection, diabetes, and long hospitalization (2) (Supplementary Figure S13).
Figure 9.
The Multi-channel Fmaps and important FPs in distinguishing COVID-19 severe and non-severe cases by AggMapNet classification of the multi-omics COV-S dataset. (A) the regular grid positions for the 1486 multi-omics feature points (649 proteins and 847 metabolites) to form the multi-channel Fmaps, the size of the grid is 39x39, each different color in the grid stands for one cluster group or one channel in the Fmaps. Cluster 1 and 2 are major proteins, and Clusters 3, 4 and 5 are major metabolites. (B) the transformed multi-channel Fmaps for the six non-severe and six severe cases, the XG43–XG46 and XG20–XG25 are the four severe six non-severe cases in the independent test cohort, respectively. (C) the top-50 feature points (39 metabolites and 11 proteins) were embedded based on the correlation distance using UMAP, they can be grouped into six groups, G1–G5 are the metabolites (except for the Q9NPH3 in G2), and G6 is the proteins (except for the Genistein sulfate), their scatter size stands for the importance score. Metabolites in G1 are the sphingomyelins (SMs), in G2 are the phospholipid metabolites, including glycerophosphatidylcholines (GPCs), glycerophosphatidylinositols (GPIs), glycerophosphatidylethanolamines (GPEs). (D) the list card for the top-10 ranked feature points with their importance scores, and the two-sided Wilcoxon rank-sum test (with Bonferroni correction) P-value is used for the significant test among the severe and non-severe patients. (E) the detail information card for the proteins in G6.
We analyzed the global feature importance (GFI) on AggMapNet severity prediction model, the top-50 important FPs including 39 metabolites and 11 proteins, are clustered into six major groups (G1–G6) by 2D embedding of UMAP (Figure 9C). Few of the 39 metabolites and 11 proteins are among the important signatures of the previous study (2), partly because of high variations of merely 41 samples. G1–G5 are the metabolites (except for the Q9NPH3 in G2), and G6 is the proteins (except for the Genistein sulfate). Metabolites in G1 are the sphingomyelins (SMs), G2 are the phospholipid metabolites, G3 are the derivates of amino acids such as tryptophan and thyroxine, G4 and G5 are major the amino acids and their metabolites.
AggMapNet-selected important metabolites sphingomyelins, phospholipids and ergothioneine (Figure 9D) are consistent with literature reports. Sphingomyelins (SMs) in group G1 show the most important contributes to the model (Ranks 1 and 3 in top-10). Plasma SMs have been proved that is a useful biomarker for distinguishing between COVID-19 patients and healthy subjects (50), and more importantly, the serum level of the metabolites of SMs, sphingosine-1-phosphate (S1P), have been reported as a novel circulating biomarker negatively associated with COVID-19 severity and morbidity (51). Those phospholipid metabolites in G2 group including glycerophosphatidylcholines (GPCs), glycerophosphatidylinositols (GPIs), glycerophosphatidylethanolamines (GPEs) are also reported as important phospholipidome signatures for Ebola virus disease (EVD) fatal outcomes (52) and associated with severity of COVID-19 (50). Other most important biomarker is ergothioneine in G5, which ranked 2 among all the FPs. It can modulate inflammation and has been proposed as a therapeutic to reduce the severity and mortality of COVID-19, especially in the elderly and those with underlying health conditions (53).
Among the 11 AggMapNet-selected important proteins (Figure 9E), three proteins (Immunoglobulin kappa 1D-13 and 2D-30, Semaphorin-4B) are immune-related (54), 1 protein (Vasorin) modulates arterial response to injury (55) and six proteins (NOTCH2, MMP2, SELENOP, GPX3, IL1RAP and SOD3) are related to COVID-19 severity (Supplementary Table S9). Overall, AggMapNet has achieved SOTA performances in COVID-19 detections or severity predictions and may potentially facilitate biomarker discovery. These important biomarkers are discovered only based on 31 patients (18 non-severe and 13 severe, many of the signatures by the Wilcoxon rank-sum test is not statistic significant in the distinguish of severe and non-severe (P value < 0.05) due to limited number of samples, but AggMapNet model explanation is still able to identify these important biomarkers, suggesting the practicality and effectiveness of the method in the case of low-data samples with high-dimension.
CONCLUSION
Robust learning of Biomedical data is vital for disease diagnosis, biomarker discovery, and biological mechanism investigations (1,56). The relevant learning tasks are hindered by the high dimensional, variational (biological and technical), and unordered nature of BioHULM data (57). Another obstacle is the low-sample sizes of typical biomedical investigations and the corresponding learning tasks (1). These problems confound the process of statistical inference and subject learning outcomes to random chances (58), which may lead to false model explanations, false discoveries and mask the identification of genuine biological variations (58). Interpretable DL algorithms provide additional means for assessing learning outcomes and support informed clinical decisions and biomarker discoveries (9,10). The new self-supervised AggMap algorithm restructures and aggregates unordered data into structured multi-channel Fmaps to expose the intrinsic data clusters, enabling enhanced DL by multi-channel CNNs. Together with unsupervised AggMap, the multi-channel CNN-based AggMapNet models showed enhanced and robust ability in learning both low-sample and higher-sample omics data, which outperformed the SOTA ML models in most of 18 low-sample omics benchmark tasks, suggesting that AggMapNet is a valuable complement of ML methods for omics-based learning. The use of perturbation-based interpretation algorithm facilitates the assessment of important features of AggMapNet learning. The revealed important features are highly consistent with the literature-reported disease-related markers. Unsupervised AggMap and supervised AggMapNet, together with other emerging DL methods, collectively facilitate enhanced and robust learning of complex omics data for clinical diagnosis and biomedical investigations.
DATA AVAILABILITY
The MNIST/F-MNIST datasets are available in the Open Machine Learning repository (OpenML, https://www.openml.org/). Other all datasets in this study are released in the Zenodo repository (https://doi.org/10.5281/zenodo.3999156).
The source code of the manifold-guided AggMap framework is freely available at GitHub (https://github.com/shenwanxiang/bidd-aggmap) to allow replication of the results, and the “paper” folder in this repository contains all codes and results in this study. The example code of AggMap on the reconstruction of MNIST from a random permutation is in MNIST_reconstruction_code.pdf.
Supplementary Material
ACKNOWLEDGEMENTS
We would also like to thank the anonymous reviewers for their constructive suggestions on this article.
Author contributions: Wan Xiang Shen and Yu Zong Chen conceptualized and developed AggMap and AggMapNet model. Wan Xiang Shen and Yu Zong Chen designed the study and wrote the manuscript. Yu Liu provided the computational strategies and analyzed the results of the COVID-19 modeling. Yan Chen, Xian Zeng, Ying Tan, Yu Yang Jiang and Yu Zong Chen provided platforms and suggestions. All authors read and approved the manuscript.
Contributor Information
Wan Xiang Shen, The State Key Laboratory of Chemical Oncogenomics, Key Laboratory of Chemical Biology, Tsinghua Shenzhen International Graduate School, Tsinghua University, Shenzhen 518055, P.R. China; Bioinformatics and Drug Design Group, Department of Pharmacy, and Center for Computational Science and Engineering, National University of Singapore 117543, Singapore.
Yu Liu, Institute for Health Innovation & Technology, National University of Singapore 117543, Singapore; Department of Biomedical Engineering, Faculty of Engineering, National University of Singapore 117543, Singapore.
Yan Chen, The State Key Laboratory of Chemical Oncogenomics, Key Laboratory of Chemical Biology, Tsinghua Shenzhen International Graduate School, Tsinghua University, Shenzhen 518055, P.R. China.
Xian Zeng, Department of Biological Medicines & Shanghai Engineering Research Center of Immunotherapeutics, School of Pharmacy, Fudan University, Shanghai 201203, P.R. China.
Ying Tan, The State Key Laboratory of Chemical Oncogenomics, Key Laboratory of Chemical Biology, Tsinghua Shenzhen International Graduate School, Tsinghua University, Shenzhen 518055, P.R. China; Shenzhen Kivita Innovative Drug Discovery Institute, Shenzhen 518110, P.R. China.
Yu Yang Jiang, The State Key Laboratory of Chemical Oncogenomics, Key Laboratory of Chemical Biology, Tsinghua Shenzhen International Graduate School, Tsinghua University, Shenzhen 518055, P.R. China; Institute of Biomedical Health Technology and Engineering, Shenzhen Bay Laboratory, Shenzhen 518132, P.R. China.
Yu Zong Chen, The State Key Laboratory of Chemical Oncogenomics, Key Laboratory of Chemical Biology, Tsinghua Shenzhen International Graduate School, Tsinghua University, Shenzhen 518055, P.R. China; Institute of Biomedical Health Technology and Engineering, Shenzhen Bay Laboratory, Shenzhen 518132, P.R. China.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
National Key R&D Program of China, Synthetic Biology Research [2019YFA0905900]; Shenzhen Municipal Government [2019156, JCYJ20170413113448742, 201901]; Department of Science and Technology of Guangdong Province [2017B030314083]; Singapore Academic Funds [R-148-000-273-114]; NUS Research Scholarships. Funding for open access charge: Shenzhen Municipal Government [2019156, JCYJ20170413113448742, NO.201901].
Conflict of interests statement. None declared.
REFERENCES
- 1. Nachtigall F.M., Pereira A., Trofymchuk O.S., Santos L.S.. Detection of SARS-CoV-2 in nasal swabs using MALDI-MS. Nat. Biotechnol. 2020; 38:1168–1173. [DOI] [PubMed] [Google Scholar]
- 2. Shen B., Yi X., Sun Y., Bi X., Du J., Zhang C., Quan S., Zhang F., Sun R., Qian L.. Proteomic and metabolomic characterization of COVID-19 patient sera. Cell. 2020; 182:59–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Yachida S., Mizutani S., Shiroma H., Shiba S., Nakajima T., Sakamoto T., Watanabe H., Masuda K., Nishimoto Y., Kubo M.. Metagenomic and metabolomic analyses reveal distinct stage-specific phenotypes of the gut microbiota in colorectal cancer. Nat. Med. 2019; 25:968–976. [DOI] [PubMed] [Google Scholar]
- 4. Liu B., Wei Y., Zhang Y., Yang Q.. Deep Neural Networks for High Dimension, Low Sample Size Data. International Joint Conference on Artificial Intelligence (IJCAI). 2017; 2287–2293. [Google Scholar]
- 5. Smith A.M., Walsh J.R., Long J., Davis C.B., Henstock P., Hodge M.R., Maciejewski M., Mu X.J., Ra S., Zhao S.. Standard machine learning approaches outperform deep representation learning on phenotype prediction from transcriptomics data. BMC Bioinform. 2020; 21:119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Chen D., Liu S., Kingsbury P., Sohn S., Storlie C.B., Habermann E.B., Naessens J.M., Larson D.W., Liu H.. Deep learning and alternative learning strategies for retrospective real-world clinical data. NPJ Digit. Med. 2019; 2:43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Jiménez-Luna J., Grisoni F., Schneider G.. Drug discovery with explainable artificial intelligence. Nat. Mach. Intell. 2020; 2:573–584. [Google Scholar]
- 8. Lundberg S.M., Erion G., Chen H., DeGrave A., Prutkin J.M., Nair B., Katz R., Himmelfarb J., Bansal N., Lee S.-I.. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020; 2:2522–5839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Lee H., Yune S., Mansouri M., Kim M., Tajmir S.H., Guerrier C.E., Ebert S.A., Pomerantz S.R., Romero J.M., Kamalian S.. An explainable deep-learning algorithm for the detection of acute intracranial haemorrhage from small datasets. Nat. Biomed. Eng. 2019; 3:173–182. [DOI] [PubMed] [Google Scholar]
- 10. Samek W., Wiegand T., Müller K.-R.. Explainable artificial intelligence: Understanding, visualizing and interpreting deep learning models. 2017; arXiv doi:28 Aug 2017, preprint: not peer reviewedhttps://arxiv.org/abs/1708.08296.
- 11. Eraslan G., Avsec Ž., Gagneur J., Theis F.J.. Deep learning: new computational modelling techniques for genomics. Nat. Rev. Genet. 2019; 20:389–403. [DOI] [PubMed] [Google Scholar]
- 12. Lyu B., Haque A.. Deep learning based tumor type classification using gene expression data. Proceedings of the 2018 ACM international conference on bioinformatics, computational biology, and health informatics (ACM-BCB). 2018; 89–96. [Google Scholar]
- 13. Chen X., Chen D.G., Zhao Z., Zhan J., Ji C., Chen J.. Artificial image objects for classification of schizophrenia with GWAS-selected SNVs and convolutional neural network. Patterns. 2021; 2:100303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Bazgir O., Zhang R., Dhruba S.R., Rahman R., Ghosh S., Pal R.. Representation of features as images with neighborhood dependencies for compatibility with convolutional neural networks. Nat. Commun. 2020; 11:4391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Ma S., Zhang Z.. OmicsMapNet: transforming omics data to take advantage of deep convolutional neural network for discovery. 2018; arXiv doi:23 may 2019, preprint: not peer reviewedhttps://arxiv.org/abs/1804.05283.
- 16. Cheng D., Gong Y., Zhou S., Wang J., Zheng N.. Person re-identification by multi-channel parts-based cnn with improved triplet loss function. Proceedings of the iEEE Conference on Computer Vision and Pattern Recognition (CVPR). 2016; 1335–1344. [Google Scholar]
- 17. Wainberg M., Merico D., Delong A., Frey B.J.. Deep learning in biomedicine. Nat. Biotechnol. 2018; 36:829–838. [DOI] [PubMed] [Google Scholar]
- 18. Bronstein M.M., Bruna J., LeCun Y., Szlam A., Vandergheynst P.. Geometric deep learning: going beyond euclidean data. IEEE Signal Process. Mag. 2017; 34:18–42. [Google Scholar]
- 19. LeCun Y., Bengio Y., Hinton G.. Deep learning. Nature. 2015; 521:436–444. [DOI] [PubMed] [Google Scholar]
- 20. Becht E., McInnes L., Healy J., Dutertre C.-A., Kwok I.W., Ng L.G., Ginhoux F., Newell E.W.. Dimensionality reduction for visualizing single-cell data using UMAP. Nat. Biotechnol. 2019; 37:38–44. [DOI] [PubMed] [Google Scholar]
- 21. Müllner D. fastcluster: Fast hierarchical, agglomerative clustering routines for R and Python. J. Stat. Softw. 2013; 53:1–18. [Google Scholar]
- 22. Jonker R., Volgenant A.. A shortest augmenting path algorithm for dense and sparse linear assignment problems. Computing. 1987; 38:325–340. [Google Scholar]
- 23. Noroozi M., Favaro P.. Unsupervised learning of visual representations by solving jigsaw puzzles. Eur. Conf. Comput. Vis. 2016; 69–84. [Google Scholar]
- 24. LeCun Y. The MNIST database of handwritten digits. 1998; [Google Scholar]
- 25. McInnes L., Healy J., Melville J.. Umap: uniform manifold approximation and projection for dimension reduction. 2018; arXiv doi:18 September 2020, preprint: not peer reviewedhttps://arxiv.org/abs/1802.03426.
- 26. Kobak D., Linderman G.C.. Initialization is critical for preserving global data structure in both t-SNE and UMAP. Nat. Biotechnol. 2021; 39:156–157. [DOI] [PubMed] [Google Scholar]
- 27. Belkin M., Niyogi P.. Laplacian eigenmaps and spectral techniques for embedding and clustering. Nips. 2001; 14:585–591. [Google Scholar]
- 28. Shen W.X., Zeng X., Zhu F., li Wang Y., Qin C., Tan Y., Jiang Y.Y., Chen Y.Z.. Out-of-the-box deep learning prediction of pharmaceutical properties by broadly learned knowledge-based molecular representations. Nat. Mach. Intell. 2021; 3:334–334. [Google Scholar]
- 29. Dosovitskiy A., Beyer L., Kolesnikov A., Weissenborn D., Zhai X., Unterthiner T., Dehghani M., Minderer M., Heigold G., Gelly S.. An image is worth 16x16 words: Transformers for image recognition at scale. 2020; arXiv doi:03 June 2021, preprint: not peer reviewedhttps://arxiv.org/abs/2010.11929.
- 30. Szegedy C., Liu W., Jia Y., Sermanet P., Reed S., Anguelov D., Erhan D., Vanhoucke V., Rabinovich A.. Going deeper with convolutions. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 2015; 1–9. [Google Scholar]
- 31. Peng C., Zhang X., Yu G., Luo G., Sun J.. Large kernel matters–improve semantic segmentation by global convolutional network. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 2017; 4353–4361. [Google Scholar]
- 32. Ribeiro M.T., Singh S., Guestrin C.. “Why should i trust you?" Explaining the predictions of any classifier. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2016; 1135–1144. [Google Scholar]
- 33. Lundberg S.M., Lee S.-I.. A unified approach to interpreting model predictions. Proceedings of the 31st International Conference on Neural Information Processing Systems. 2017; 4768–4777. [Google Scholar]
- 34. Kumar I.E., Venkatasubramanian S., Scheidegger C., Friedler S.. Problems with Shapley-value-based explanations as feature importance measures. Proceedings of the 37th International Conference on Machine Learning (PMLR). 2020; 5491–5500. [Google Scholar]
- 35. Fryer D.V., Strümke I., Nguyen H.. Explaining the data or explaining a model? Shapley values that uncover non-linear dependencies. 2020; arXiv doi:06 march 2021, preprint: not peer reviewedhttps://arxiv.org/abs/2007.06011. [DOI] [PMC free article] [PubMed]
- 36. Simonyan K., Vedaldi A., Zisserman A.. Deep inside convolutional networks: visualising image classification models and saliency maps. 2013; arXiv doi:19 April 2014, preprint: not peer reviewedhttps://arxiv.org/abs/1312.6034.
- 37. Wang Z., Bovik A.C., Sheikh H.R., Simoncelli E.P.. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004; 13:600–612. [DOI] [PubMed] [Google Scholar]
- 38. Xiao H., Rasul K., Vollgraf R.. Fashion-mnist: a novel image dataset for benchmarking machine learning algorithms. 2017; arXiv doi:15 September 2017, preprint: not peer reviewedhttps://arxiv.org/abs/1708.07747.
- 39. Hao Q., Zong X., Sun Q., Lin Y.-C., Song Y.J., Hashemikhabir S., Hsu R.Y., Kamran M., Chaudhary R., Tripathi V.. The S-phase-induced lncRNA SUNO1 promotes cell proliferation by controlling YAP1/Hippo signaling pathway. Elife. 2020; 9:e55102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V.. Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 2011; 12:2825–2830. [Google Scholar]
- 41. Rodriguez J.J., Kuncheva L.I., Alonso C.J.. Rotation forest: a new classifier ensemble method. IEEE Trans. Pattern Anal. Mach. Intell. 2006; 28:1619–1630. [DOI] [PubMed] [Google Scholar]
- 42. Chen T., Guestrin C.. Xgboost: A scalable tree boosting system. Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining. 2016; 785–794. [Google Scholar]
- 43. Ke G., Meng Q., Finley T., Wang T., Chen W., Ma W., Ye Q., Liu T.-Y.. Lightgbm: a highly efficient gradient boosting decision tree. Adv. Neural Inform. Process. Syst. 2017; 30:3146–3154. [Google Scholar]
- 44. Feng J., Meyer C.A., Wang Q., Liu J.S., Shirley Liu X., Zhang Y.. GFOLD: a generalized fold change for ranking differentially expressed genes from RNA-seq data. Bioinformatics. 2012; 28:2782–2788. [DOI] [PubMed] [Google Scholar]
- 45. Geirhos R., Rubisch P., Michaelis C., Bethge M., Wichmann F.A., Brendel W.. ImageNet-trained CNNs are biased towards texture; increasing shape bias improves accuracy and robustness. 2018; arXiv doi:14 Jan 2019, preprint: not peer reviewedhttps://arxiv.org/abs/1811.12231.
- 46. Akhtar N., Mian A.. Threat of adversarial attacks on deep learning in computer vision: a survey. IEEE Access. 2018; 6:14410–14430. [Google Scholar]
- 47. Ford N., Gilmer J., Carlini N., Cubuk D. Adversarial examples are a natural consequence of test error in noise. 2019; arXiv doi:29 January 2019, preprint: not peer reviewedhttps://arxiv.org/abs/1901.10513.
- 48. Dodge S., Karam L.. A study and comparison of human and deep learning recognition performance under visual distortions. 2017 26th International Conference on Computer Communication and Networks (ICCCN). 2017; 1–7. [Google Scholar]
- 49. Dua D., Graff C.. UCI machine learning repository, Wisconsin Diagnostic Breast Cancer (WDBC) Data Set. 2019; 37:https://archive.ics.uci.edu/ml/datasets/breast+cancer+wisconsin+(diagnostic). [Google Scholar]
- 50. Song J.-W., Lam S.M., Fan X., Cao W.-J., Wang S.-Y., Tian H., Chua G.H., Zhang C., Meng F.-P., Xu Z.. Omics-driven systems interrogation of metabolic dysregulation in COVID-19 pathogenesis. Cell Metab. 2020; 32:188–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Marfia G., Navone S., Guarnaccia L., Campanella R., Mondoni M., Locatelli M., Barassi A., Fontana L., Palumbo F., Garzia E.. Decreased serum level of sphingosine-1-phosphate: a novel predictor of clinical severity in COVID-19. EMBO Mol. Med. 2021; 13:e13424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Kyle J.E., Burnum-Johnson K.E., Wendler J., Eisfeld A., Halfmann P.J., Watanabe T., Sahr F., Smith R., Kawaoka Y., Waters K.. Plasma lipidome reveals critical illness and recovery from human Ebola virus disease. Proc. Natl. Acad. Sci. U.S.A. 2019; 116:3919–3928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Cheah I.K., Halliwell B.. Could ergothioneine aid in the treatment of coronavirus patients. Antioxidants. 2020; 9:595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Nishide M., Kumanogoh A.. The role of semaphorins in immune responses and autoimmune rheumatic diseases. Nat. Rev. Rheumatol. 2018; 14:19. [DOI] [PubMed] [Google Scholar]
- 55. Ikeda Y., Imai Y., Kumagai H., Nosaka T., Morikawa Y., Hisaoka T., Manabe I., Maemura K., Nakaoka T., Imamura T.. Vasorin, a transforming growth factor β-binding protein expressed in vascular smooth muscle cells, modulates the arterial response to injury in vivo. Proc. Natl. Acad. Sci. U.S.A. 2004; 101:10732–10737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Yu K.-H., Beam A.L., Kohane I.S.. Artificial intelligence in healthcare. Nat. Biomed. Eng. 2018; 2:719–731. [DOI] [PubMed] [Google Scholar]
- 57. McIntyre L.M., Lopiano K.K., Morse A.M., Amin V., Oberg A.L., Young L.J., Nuzhdin S.V.. RNA-seq: technical variability and sampling. BMC Genomics. 2011; 12:293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Teschendorff A.E. Avoiding common pitfalls in machine learning omic data science. Nat. Mater. 2019; 18:422–427. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The MNIST/F-MNIST datasets are available in the Open Machine Learning repository (OpenML, https://www.openml.org/). Other all datasets in this study are released in the Zenodo repository (https://doi.org/10.5281/zenodo.3999156).
The source code of the manifold-guided AggMap framework is freely available at GitHub (https://github.com/shenwanxiang/bidd-aggmap) to allow replication of the results, and the “paper” folder in this repository contains all codes and results in this study. The example code of AggMap on the reconstruction of MNIST from a random permutation is in MNIST_reconstruction_code.pdf.










