Abstract
Comparative effectiveness research using network meta-analysis can present a hierarchy of competing treatments, from the most to the least preferable option. However, in published reviews, the research question associated with the hierarchy of multiple interventions is typically not clearly defined. Here we introduce the novel notion of a treatment hierarchy question that describes the criterion for choosing a specific treatment over one or more competing alternatives. For example, stakeholders might ask which treatment is most likely to improve mean survival by at least 2 years, or which treatment is associated with the longest mean survival. We discuss the most commonly used ranking metrics (quantities that compare the estimated treatment-specific effects), how the ranking metrics produce a treatment hierarchy, and the type of treatment hierarchy question that each ranking metric can answer. We show that the ranking metrics encompass the uncertainty in the estimation of the treatment effects in different ways, which results in different treatment hierarchies. When using network meta-analyses that aim to rank treatments, investigators should state the treatment hierarchy question they aim to address and employ the appropriate ranking metric to answer it. Following this new proposal will avoid some controversies that have arisen in comparative effectiveness research.
Keywords: multiple treatments, network meta-analysis, probability, ranking, surface under the cumulative ranking curve, treatment hierarchy
Abbreviations
- BV
best value
- NMA
network meta-analysis
- LDL-C
low-density lipoprotein cholesterol
- SD
standard deviation
- SUCRA
surface under the cumulative ranking curve
In comparative effectiveness research, the ranking of multiple competing treatments is a potentially important advantage of network meta-analysis (NMA) over pairwise meta-analysis (1–3). Different methods have been proposed in the literature, including estimation of the probability of each treatment assuming each rank, the median and mean rank of each treatment, and the surface under the cumulative ranking curve (SUCRA) for each treatment. The SUCRA is a (Bayesian) summary of the rank distribution which can be interpreted as the estimated proportion of treatments worse than the treatment of interest. It can be approximated by a frequentist analog, the P-score (2, 4).
Several tutorials correctly point out that while ranking metrics may be useful, the relative treatment effects and their uncertainty are the most clinically relevant output from NMA (5–7). Criticism of the use of ranking metrics is abundant in the literature. For example, Kibret et al. performed a simulation study and concluded that “decisions should not be made based on rank probabilities[,] especially when treatments are not directly compared… as they may be ill-informed” (8, p. 459). Mills et al. concluded that “interpretability [of treatment ranks] is limited by the fact that they are driven predominantly by the estimated effect sizes, and that standard errors play an unduly small role in determining their position” (9, p. 3). Veroniki et al. (10, p. 127) and Trinquart et al. (11, p. 671) examined several published networks and concluded that the ranking statistic values “may be unstable.” Wang and Carter stated that “SUCRA findings can be misleading and should be interpreted with caution” (12, p. 843).
These concerns have raised awareness of what ranking can and cannot do and have drawn attention to the dangers of oversimplification and reliance on treatment hierarchy alone. However, some of the criticisms inappropriately attribute the problem to the ranking metrics per se. In this article, we argue that ranking metrics are not misleading. Rather, the confusion in the literature is due to the fact that different ranking metrics aim to answer different questions about treatment hierarchy and that researchers do not clearly define what they mean by “the best treatment” in a given setting. In a collection of 232 NMAs, we did not find any review that reported the definition of the preferable treatment or anything that could be interpreted as what we define below as a “treatment hierarchy question” (13). We show that this confusion is specific to networks and does not arise in comparisons of 2 treatments. We also suggest that any comparison of the treatment hierarchies obtained by different ranking metrics should acknowledge that they provide answers to different treatment hierarchy questions.
We first introduce the notion of the treatment hierarchy question and argue that the question addressed by an NMA should determine the quantities used to answer this question (i.e., the ranking metrics used to obtain the treatment hierarchy). We then present the properties of the commonly used ranking metrics and discuss the questions they address. We use theoretical examples to show that each ranking metric encompasses the uncertainty in the estimation of the relative treatment effects in a different way, and this can lead to different treatment hierarchies. We conclude with recommendations and a discussion about possible future extensions of the existing ranking metrics, which can answer more complex treatment hierarchy questions.
All results, figures, and tables presented in this article were produced using R software and are reproducible with the scripts shown in our GitHub repository (14).
WHAT ARE TREATMENT HIERARCHY QUESTIONS AND RANKING METRICS?
Defining a treatment hierarchy question
A treatment hierarchy question is a question that determines when a treatment is preferred over another or several competing treatments. It involves considerations about the chosen health-related endpoint (e.g., low-density lipoprotein cholesterol (LDL-C) concentration), the summary of the endpoint within each treatment arm (e.g., the mean LDL-C concentration), the effect measure between treatment arms (e.g., mean difference), and the criterion according to which a treatment will be preferred over another. Preference for a treatment in the treatment hierarchy question is phrased according to the maximization of a statistic; the latter we term the ranking metric and discuss it in more detail in the next section.
Careful and clear framing of the research question before starting any systematic review is good practice, to which most published NMAs adhere. In a recent bibliographical study, investigators in all published NMAs clearly stated the efficacy and safety outcomes and the effect measure(s) used to compare each pair of competing interventions (15). The focus of evidence synthesis in comparative effectiveness research is the relative treatment effect—for example, the difference in the mean value of a quantitative outcome between treatments. The clinical trials literature now calls this quantity the estimand: the quantity that is to be estimated (16). In this paper, we consider absolute estimands, such as the treatment-specific mean, as well as relative estimands, which are comparisons of absolute estimands. In the case where 2 treatments are compared, if we knew the true value of the relative treatment effect, this would automatically define which treatment is preferable; in practice, the relative treatment effect is estimated with error, but its value still shows which treatment appears preferable.
Similar attention to a clear definition of the research question has not been paid when several treatments are compared. Authors typically do not report a clear definition of what they mean by the “best” or “preferable” treatment. In NMA, we have several relative treatment effects. If they were known without error, then the treatment hierarchy would be clear. When the relative treatment effects are estimated with error, however, they cannot easily be translated into a treatment hierarchy. As we discuss below, the crucial difficulty arises when we have to deal with uncertainty around multiple relative treatment effects.
The treatment hierarchy question must be answerable from the available data and must relate to the selected estimand. We take the example of treatments for lowering LDL-C. “Which is the best treatment?” is not an appropriate treatment hierarchy question, because it cannot be answered from data. Instead, we can answer the question, “Which treatment is most likely to be the best treatment?” by using data to make probability statements about the treatment effects. Next, the term “best” needs to be defined by linking it to an estimand. Such refinement of the question might, for example, lead to the clear question, “Which treatment is most likely to produce a mean LDL-C level of <2.5 mmol/L?”. In this case, we will need to use our data to calculate the probability of the mean LDL-C level’s not exceeding 2.5 mmol/L for each treatment and then order the treatments according to those probabilities.
Defining a ranking metric
A treatment hierarchy question defines, among others, the criterion used to identify the best treatment. This is the maximization of a summary statistic of the (beneficial) impact of the treatment on one or more health outcomes. Ranking metrics are such treatment-specific statistics and are used to answer treatment hierarchy questions. More formally, we define a ranking metric as a treatment-specific summary of the joint distribution of the absolute estimands or the relative treatment effects.
In the question above, the relevant ranking metric is the probability that the mean LDL-C concentration is less than 2.5 mmol/L. Then the answer to the treatment hierarchy question is given by maximizing this probability across all treatment options; we call this the preferable treatment. Further examples of commonly used ranking metrics are discussed below.
Setting and notation
Consider several medications denoted by i (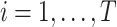 ) and a single harmful outcome of interest, where the estimands are the (absolute) true means of the outcome
) and a single harmful outcome of interest, where the estimands are the (absolute) true means of the outcome 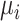 or their relative treatment effects
or their relative treatment effects 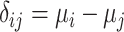 . For ease of interpretation, we take a Bayesian approach to the estimation, where treatment effects are estimated with uncertainty conveyed by their joint posterior distribution; we will subsequently refer to this as “the distribution.” Consequently, any subsequent reference to the estimation of
. For ease of interpretation, we take a Bayesian approach to the estimation, where treatment effects are estimated with uncertainty conveyed by their joint posterior distribution; we will subsequently refer to this as “the distribution.” Consequently, any subsequent reference to the estimation of 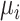 or
or 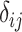 will involve a whole distribution of possible values, and ranking metrics will describe features of these joint distributions (one for each i). A popular way to communicate the uncertainty is to present a range of plausible values for each estimand separately, such as a 95% credible interval. At the center of the distribution that estimates
will involve a whole distribution of possible values, and ranking metrics will describe features of these joint distributions (one for each i). A popular way to communicate the uncertainty is to present a range of plausible values for each estimand separately, such as a 95% credible interval. At the center of the distribution that estimates 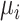 is the point estimate
is the point estimate 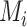 (the posterior mean), our “most likely” estimate of the true mean outcome with treatment i.
(the posterior mean), our “most likely” estimate of the true mean outcome with treatment i.  is a single known value (unlike the unknown
is a single known value (unlike the unknown 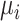 ), and it is one of the many possible ranking metrics discussed below. Similarly, the point estimate of the relative treatment effect
), and it is one of the many possible ranking metrics discussed below. Similarly, the point estimate of the relative treatment effect 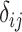 is
is 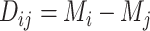 . We consider that a treatment i “beats” treatment
. We consider that a treatment i “beats” treatment 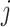 when
when 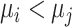 , but we do not know from data whether this is true; however, we can use the data distribution that estimates
, but we do not know from data whether this is true; however, we can use the data distribution that estimates 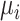 and
and 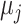 to estimate the probability that treatment i beats treatment
to estimate the probability that treatment i beats treatment 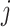 . A summary of the notation is presented in Table 1.
. A summary of the notation is presented in Table 1.
Table 1.
Notation Used for the Observed and Unobserved Quantities in a Network Meta-Analysis Comparing T Competing Treatments
| Term | Unobserved Quantity (to Be Estimated) | Observed Quantity (Estimate) |
|---|---|---|
| Mean | Parameters 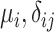
|
Summaries 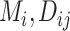
|
| Treatment comparison | Treatment 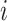 beats treatment beats treatment 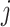 , , 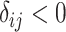
|
Probability that treatment 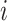 beats treatment beats treatment 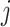 , , 
|
| Treatment ranking | Treatment 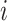 is the best, is the best, 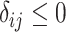 for all for all 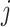
|
Probability that treatment 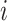 is the best, is the best, 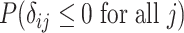
|
| Ranking metric | Any summary of the estimates above or probabilities |
Example: formulating treatment hierarchy questions for interventions to reduce LDL-C levels
Consider the fictional example of 3 treatments (A, B, and C) aiming to lower LDL-C levels in patients at high risk of cardiovascular disease, plus a placebo (P). Suppose for a moment that only LDL-C levels determine the preferable treatment, though in reality we should also consider high-density lipoprotein cholesterol levels, cardiovascular events, and mortality, as well as cost and convenience. After synthesis of randomized trials that compare pairs of cholesterol-lowering treatments in participants with baseline LDL-C levels between 2.60 mmol/L and 5.10 mmol/L, suppose that our knowledge about the true population mean posttreatment levels 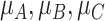 is shown in the distributions of Figure 1. These distributions are characterized by the 3 centers (or point estimates)
is shown in the distributions of Figure 1. These distributions are characterized by the 3 centers (or point estimates) 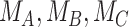 and uncertainty that depends on the amount of information available for each treatment, with treatment C having the most information and treatment B the least.
and uncertainty that depends on the amount of information available for each treatment, with treatment C having the most information and treatment B the least.
Figure 1.
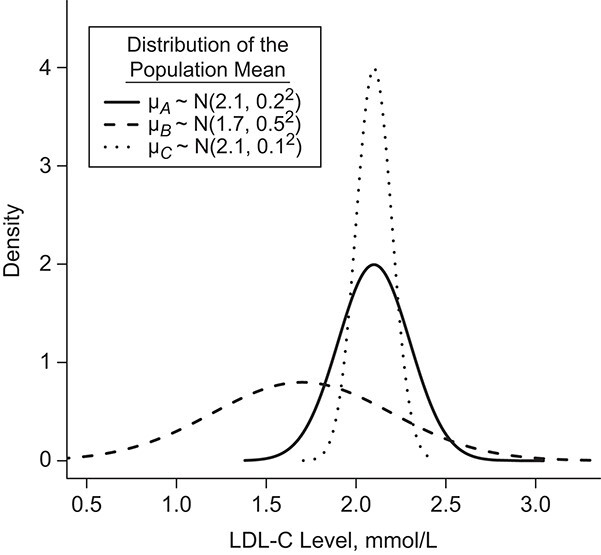
Hypothetical example of 3 interventions (A, B, and C) aiming to reduce low-density lipoprotein cholesterol (LDL-C) levels. The distributions refer to the true population mean 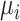 for posttreatment LDL-C levels and is the result of the synthesis of randomized trials that compare pairs of treatments.
for posttreatment LDL-C levels and is the result of the synthesis of randomized trials that compare pairs of treatments.
There are several treatment hierarchy questions one can ask, and the order of the treatments depends on that question. One possible question is, “Which treatment has the smallest estimated mean posttreatment LDL-C level?” (treatment hierarchy question 1). This orders the treatments according to 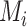 and indicates B as the preferable treatment.
and indicates B as the preferable treatment.
Alternatively, we can heuristically interpret the European guidelines, which recommend that treatment should halve LDL-C levels, to obtain another treatment hierarchy question (17). In a population with an average LDL-C level of 5 mmol/L, we can set the goal to have a posttreatment mean value 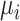 below 2.5 mmol/L; a possible question is then, “Which treatment maximizes the probability
below 2.5 mmol/L; a possible question is then, “Which treatment maximizes the probability 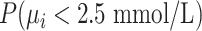 ?” (treatment hierarchy question 2). This orders the treatments according to their areas below 2.5 mmol/L in Figure 1 and indicates C as the preferable treatment.
?” (treatment hierarchy question 2). This orders the treatments according to their areas below 2.5 mmol/L in Figure 1 and indicates C as the preferable treatment.
Note that treatment hierarchy questions can be expressed using absolute estimands or relative treatment effects. In Web Appendix 1 (available at https://doi.org/10.1093/aje/kwab278), we explain why this choice is important when more than 2 treatments are to be compared.
RANKING METRICS AND THEIR PROPERTIES
All ranking metrics summarize the distribution of 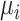 or
or 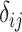 estimated in NMA and transform them into a set of numbers, one number (metric) for each treatment. Ranking metrics mostly differ in the way they combine the mean and uncertainty in the estimated
estimated in NMA and transform them into a set of numbers, one number (metric) for each treatment. Ranking metrics mostly differ in the way they combine the mean and uncertainty in the estimated 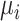 or
or 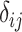 . The most commonly used ranking metrics are discussed below and are summarized in Table 2.
. The most commonly used ranking metrics are discussed below and are summarized in Table 2.
Table 2.
Ranking Metrics Used to Obtain a Treatment Hierarchy in Network Meta-Analysis, Their Formulas, and the Treatment Hierarchy Questions They Can Answer
| Ranking Metric | Method of Calculation | Treatment Hierarchy Question(s) |
|---|---|---|
Point estimate of the mean absolute estimand or relative treatment effect (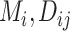 ) ) |
The center of the distribution of the absolute estimand or relative treatment effect | Which treatment has the smallest estimated mean value on the studied outcome? Which treatment has the largest estimated mean advantage compared with all other competitors? |
Probability of a treatment’s having the best mean outcome value (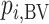 ) ) |
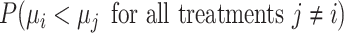
|
Which treatment is most likely to have the best (most desirable) mean value on the studied outcome? |
SUCRA for treatment i (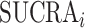 ) ) |
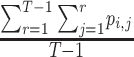 a
a
|
Which treatment has the largest fraction of competitors that it beats?b |
Mean rank (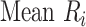 ) ) |
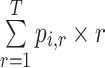 c
c
|
In the distribution of treatment effect ranks, which treatment has the largest mean rank? |
Median rank (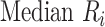 ) ) |
The value satisfying 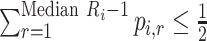 and and 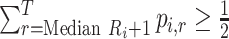
|
In the distribution of treatment effect ranks, which treatment has the largest median rank? |
Abbreviations: BV, best value; SUCRA, surface under the cumulative ranking curve.
a 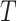 represents the number of competing treatments.
represents the number of competing treatments.
b Assuming a harmful outcome, we consider that a treatment 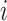 “beats” treatment
“beats” treatment 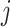 when the true mean values of the outcome fulfill
when the true mean values of the outcome fulfill 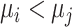 .
.
c 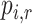 represents the probability that treatment i will produce the rth most favorable value (or will “beat” exactly r treatments).
represents the probability that treatment i will produce the rth most favorable value (or will “beat” exactly r treatments).
The role of precision in the estimation of 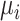 or
or 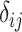 when calculating ranking metrics is responsible for the disagreement in the resulting hierarchies. In Web Appendix 2, we outline the factors that control the precision in the estimation of
when calculating ranking metrics is responsible for the disagreement in the resulting hierarchies. In Web Appendix 2, we outline the factors that control the precision in the estimation of 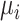 or
or 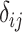 . To explore these further, we compare the hierarchy of treatments whose effects are estimated with different levels of precision in the following hypothetical example.
. To explore these further, we compare the hierarchy of treatments whose effects are estimated with different levels of precision in the following hypothetical example.
Hypothetical example
In Figure 2, we present 2 possible scenarios for the estimates of the absolute estimands 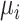 , where we have 4 treatments named P (placebo), A, B, and C. Clearly, the active treatments (A, B, and C) are better than P, and we now want to create a hierarchy between the active treatments.
, where we have 4 treatments named P (placebo), A, B, and C. Clearly, the active treatments (A, B, and C) are better than P, and we now want to create a hierarchy between the active treatments.
Figure 2.
Distributions of the absolute estimands ( ) of 3 active treatments (A, B, and C) and a placebo (P) with means
) of 3 active treatments (A, B, and C) and a placebo (P) with means 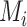 and standard deviations SDi in a hypothetical example. A) Scenario 1; B) scenario 2.
and standard deviations SDi in a hypothetical example. A) Scenario 1; B) scenario 2.
Hierarchy based on the point estimates
In many applications, it is implicit that the treatment hierarchy question relates to the center of the distribution 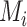 (or
(or 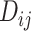 ). Ranking treatments according to
). Ranking treatments according to 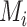 answers the question, “Which treatment is associated with the smallest estimated mean value on the studied outcome?”. Similarly, ranking according to
answers the question, “Which treatment is associated with the smallest estimated mean value on the studied outcome?”. Similarly, ranking according to 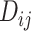 answers the equivalent question, “Which treatment is associated with the largest estimated mean advantage compared with all other competitors?”.
answers the equivalent question, “Which treatment is associated with the largest estimated mean advantage compared with all other competitors?”.
This approach considers only the point estimate 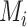 in each distribution and incorporates uncertainty in the estimation only to the degree that this contributes to the calculation of
in each distribution and incorporates uncertainty in the estimation only to the degree that this contributes to the calculation of 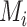 . This can be justified from decision theory (18). In scenario 1 in Figure 2, the treatment hierarchy is A, B, and then C, while in scenario 2 all 3 active treatments are equivalent.
. This can be justified from decision theory (18). In scenario 1 in Figure 2, the treatment hierarchy is A, B, and then C, while in scenario 2 all 3 active treatments are equivalent.
Hierarchy based on the probability of a treatment’s producing the best mean outcome value
The probability 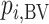 that treatment
that treatment 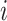 has the best value (BV) for a mean outcome at the population level (the smallest value for a harmful outcome or the largest value for a beneficial outcome) is misinterpreted in many reports of NMAs, as the probability of a treatment’s being overall the best option (and often denoted as “P(best)”). Note again the distinction between a treatment’s having the best mean outcome at the population level (which is not directly observed) and a treatment’s being the best treatment option (which is a clinical decision based on observed data). In the context of our example of Figure 2,
has the best value (BV) for a mean outcome at the population level (the smallest value for a harmful outcome or the largest value for a beneficial outcome) is misinterpreted in many reports of NMAs, as the probability of a treatment’s being overall the best option (and often denoted as “P(best)”). Note again the distinction between a treatment’s having the best mean outcome at the population level (which is not directly observed) and a treatment’s being the best treatment option (which is a clinical decision based on observed data). In the context of our example of Figure 2, 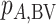 is the probability that the mean outcome
is the probability that the mean outcome 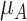 with treatment A is more favorable than the mean outcome with either treatment B, treatment C, or placebo. The probability
with treatment A is more favorable than the mean outcome with either treatment B, treatment C, or placebo. The probability 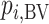 is defined as the probability that i “beats” all other competing treatments and can be directly estimated in a Bayesian setting or in a frequentist setting using resampling.
is defined as the probability that i “beats” all other competing treatments and can be directly estimated in a Bayesian setting or in a frequentist setting using resampling.
Ranking based on 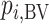 answers the question, “Which treatment is most likely to have the best (most desirable) mean value on the studied outcome?”. Then the hierarchy will be obtained using
answers the question, “Which treatment is most likely to have the best (most desirable) mean value on the studied outcome?”. Then the hierarchy will be obtained using 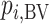 , with larger values corresponding to more preferable treatments. However, a high
, with larger values corresponding to more preferable treatments. However, a high 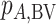 value does not suggest that treatment A is preferable under any treatment hierarchy question. In particular, there might be a large probability that A also produces the worst mean outcome among all competitors.
value does not suggest that treatment A is preferable under any treatment hierarchy question. In particular, there might be a large probability that A also produces the worst mean outcome among all competitors.
In scenario 1 in Figure 2, the hierarchy using 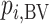 agrees with that obtained from ranking
agrees with that obtained from ranking 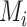 . In scenario 2,
. In scenario 2, 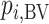 gives the hierarchy C, B, and A: This differs from the hierarchy when ranking
gives the hierarchy C, B, and A: This differs from the hierarchy when ranking 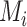 because it reflects differences in the precision with which
because it reflects differences in the precision with which 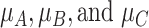 are estimated. However, it cannot be described as a “wrong” or “misleading” treatment hierarchy.
are estimated. However, it cannot be described as a “wrong” or “misleading” treatment hierarchy.
Rankograms and cumulative ranking plots
An extension to 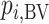 considers both tails of the distributions of
considers both tails of the distributions of 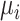 , by calculating the probability that a treatment is the best, the worst, and all positions in between. The probability
, by calculating the probability that a treatment is the best, the worst, and all positions in between. The probability 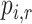 is the probability that treatment i will “beat” exactly
is the probability that treatment i will “beat” exactly 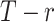 treatments;
treatments; 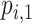 is the same as
is the same as 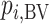 . The cumulative probability
. The cumulative probability 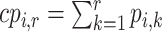 is the probability that treatment i “beats” at least
is the probability that treatment i “beats” at least 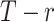 treatments or, equivalently, the probability that i is one of the top
treatments or, equivalently, the probability that i is one of the top 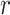 treatments. The plots of
treatments. The plots of 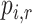 and
and 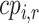 (presented in Table 3 for the scenarios in Figure 2) are termed rankograms and cumulative ranking plots.
(presented in Table 3 for the scenarios in Figure 2) are termed rankograms and cumulative ranking plots.
Table 3.
| Ranking Metric | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
Scenario and
Treatment |
Mi b | pi ,BV , % c | cpi ,2 , % d | cpi ,3 , % d | cpi ,4 , % d | SUCRA, % | P-Score | MeanRank | MedianRank |
| Scenario 1 | |||||||||
| P | 10 | 0.2 | 1.4 | 8.0 | 100 | 3.2 | 3.2 | 3.9 | 4 |
| A | 1 | 48.0 | 79.2 | 98.8 | 100 | 75.2 | 75.2 | 1.8 | 2 |
| B | 2 | 31.7 | 67.7 | 97.5 | 100 | 65.6 | 65.6 | 2.0 | 2 |
| C | 3 | 20.1 | 51.7 | 95.7 | 100 | 56.0 | 56.0 | 2.3 | 2 |
| Scenario 2 | |||||||||
| P | 10 | 0.1 | 0.6 | 7.4 | 100 | 2.6 | 2.6 | 3.9 | 4 |
| A | 1 | 26.1 | 73.9 | 99.9 | 100 | 66.6 | 66.6 | 2.0 | 2 |
| B | 1 | 33.1 | 66.6 | 98.6 | 100 | 66.1 | 66.1 | 2.0 | 2 |
| C | 1 | 40.7 | 58.9 | 94.1 | 100 | 64.7 | 64.7 | 2.1 | 2 |
Abbreviations: BV, best value; SUCRA, surface under the cumulative ranking curve.
a All probabilities are converted to percentages in the table.
b 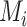 is the mean of the distribution of the absolute estimand i.
is the mean of the distribution of the absolute estimand i.
c The probability 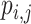 is the probability that treatment i has the rth-best mean value,
is the probability that treatment i has the rth-best mean value, 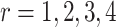 (e.g., the best value, the second-best value, etc.) on the studied outcome.
(e.g., the best value, the second-best value, etc.) on the studied outcome.
d 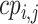 are the cumulative ranking probabilities.
are the cumulative ranking probabilities.
A rankogram is a distribution of the treatment ranks, and it is not to be confused with the notion of a ranking metric. In contrast to the ranking metrics, rankograms do not necessarily imply a treatment hierarchy or answer a specific treatment hierarchy question. A summary measure of a rankogram is, however, a ranking metric; several possible options are presented below.
Hierarchy based on the SUCRA
A numerical summary of the rankograms is provided by the SUCRA (2). The SUCRA is calculated as the sum of all cumulative rank probabilities up to 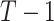 divided by
divided by 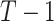 (Table 1). For a treatment i,
(Table 1). For a treatment i, 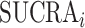 measures the extent of certainty that a treatment beats all other competing treatments. It can therefore answer the question, “Which treatment has the largest estimated fraction of competitors that it beats?”.
measures the extent of certainty that a treatment beats all other competing treatments. It can therefore answer the question, “Which treatment has the largest estimated fraction of competitors that it beats?”.
The SUCRA synthesizes all ranking probabilities in a single number and reflects the overlap between the treatment effect distributions; the larger the overlap, the more similar are the 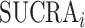 values. If all treatments have the same
values. If all treatments have the same 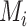 but various degrees of uncertainty, then they all have
but various degrees of uncertainty, then they all have 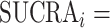 50%. Rücker and Schwarzer (4) suggested a transformation of the 1-sided P values that test the differences between the means of the distributions as another way to calculate the SUCRA, termed the P-score.
50%. Rücker and Schwarzer (4) suggested a transformation of the 1-sided P values that test the differences between the means of the distributions as another way to calculate the SUCRA, termed the P-score.
Table 3 shows SUCRA values for the 2 scenarios in Figure 2. The hierarchy obtained by the SUCRA in scenario 1 is in agreement with the hierarchy obtained with 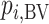 . In scenario 2, SUCRA values are very close together for the 3 active interventions.
. In scenario 2, SUCRA values are very close together for the 3 active interventions.
Hierarchy based on mean or median rank
To rank treatments, the mean or median rank for treatment i (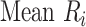 and
and 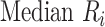 ) can also be used. Mean ranks are transformations of SUCRAs (
) can also be used. Mean ranks are transformations of SUCRAs (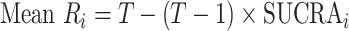 ) and can be estimated via P-scores. Consequently,
) and can be estimated via P-scores. Consequently, 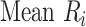 answers the same question as the SUCRA. However, mean and median ranks are more intuitively associated with the question, “In the distribution of treatment effect ranks, which treatment has the largest mean (or median) rank?”. Because of their mathematical relationship, mean ranks always result in the same treatment hierarchy as the SUCRA. Median ranks might be easier to gauge, as they are integers, but the presence of many ties might conceal small differences between treatments.
answers the same question as the SUCRA. However, mean and median ranks are more intuitively associated with the question, “In the distribution of treatment effect ranks, which treatment has the largest mean (or median) rank?”. Because of their mathematical relationship, mean ranks always result in the same treatment hierarchy as the SUCRA. Median ranks might be easier to gauge, as they are integers, but the presence of many ties might conceal small differences between treatments.
IMPACT OF IMPRECISELY ESTIMATED TREATMENT EFFECTS ON THE TREATMENT HIERARCHY
As discussed above, the various ranking metrics differ in the way they incorporate uncertainty in the estimation of 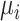 . Below we explore further the level of agreement between the ranking metrics
. Below we explore further the level of agreement between the ranking metrics 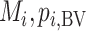 , and SUCRA. We assume that the distributions of
, and SUCRA. We assume that the distributions of 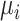 are normal.
are normal.
Impact of uncertainty on hierarchies obtained by estimated mean 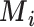 and SUCRA
and SUCRA
When the differences in precision across estimates of 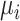 are extreme, the hierarchy obtained with the SUCRA can differ from that obtained with
are extreme, the hierarchy obtained with the SUCRA can differ from that obtained with 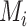 . Consider the example in Figure 2, scenario 1. According to
. Consider the example in Figure 2, scenario 1. According to 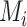 , the hierarchy is treatment A, then B, and finally C. We gradually increase the uncertainty around the estimation of
, the hierarchy is treatment A, then B, and finally C. We gradually increase the uncertainty around the estimation of 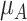 as shown in the first column of Table 4. In the extreme scenario where the variance of
as shown in the first column of Table 4. In the extreme scenario where the variance of 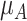 is 20, the hierarchy obtained with SUCRAs is B, C, A.
is 20, the hierarchy obtained with SUCRAs is B, C, A.
Table 4.
Example Showing the Impact of Increased Imprecision Associated With the Estimation of the Mean Outcome With Intervention A
| SUCRA, % | ||||
|---|---|---|---|---|
| Absolute Treatment Effect μ A | Placebo | Treatment A | Treatment B | Treatment C |
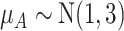
|
3.2 | 75.3 | 65.6 | 55.9 |
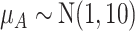
|
9.1 | 63.9 | 67.5 | 59.5 |
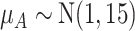
|
11.9 | 59.9 | 67.9 | 60.3 |
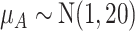
|
13.6 | 57.7 | 68.1 | 60.6 |
Abbreviation: SUCRA, surface under the cumulative ranking curve.
a The first column shows the outcome distribution of 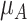 as a normal (N) distribution with mean 1 and a standard deviation that ranges from 3 to 20. The distributions for the other interventions are
as a normal (N) distribution with mean 1 and a standard deviation that ranges from 3 to 20. The distributions for the other interventions are 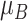 ~ N(2, 3),
~ N(2, 3), 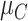 ~ N(3), and
~ N(3), and 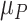 ~ N(3, 10), as shown in Figure 2, scenario 1.
~ N(3, 10), as shown in Figure 2, scenario 1.
Increased uncertainty in the estimation of 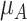 results in wider overlap with its competitors. When these competitors have point estimates worse than A (as is the case here), then lower precision in
results in wider overlap with its competitors. When these competitors have point estimates worse than A (as is the case here), then lower precision in 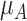 leads to lower ranks for A. If the competitors P, B, and C had point estimates superior to A, then lower precision in
leads to lower ranks for A. If the competitors P, B, and C had point estimates superior to A, then lower precision in 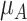 would lead to higher ranks for A. In general, when the competitors of a random treatment
would lead to higher ranks for A. In general, when the competitors of a random treatment 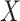 have
have 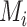 worse than
worse than 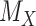 , then larger imprecision in
, then larger imprecision in 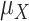 leads to lower ranks for
leads to lower ranks for 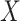 . The opposite occurs when the competitors of X have more favorable point estimates than
. The opposite occurs when the competitors of X have more favorable point estimates than 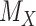 , as will be shown in the next section and Figure 3.
, as will be shown in the next section and Figure 3.
Figure 3.
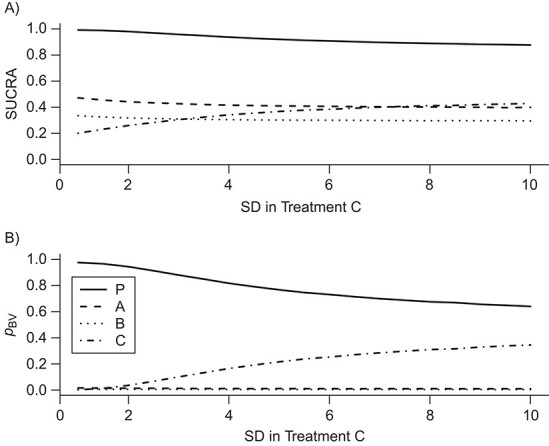
Differences in treatment hierarchy obtained from the surface under the cumulative ranking curve (SUCRA) (panel A) and from the probability of a treatment’s having the best mean outcome value  (panel B) when the standard deviation (SD) for the absolute estimand of treatment C,
(panel B) when the standard deviation (SD) for the absolute estimand of treatment C,  , increases from 1 to 10. The other effects are
, increases from 1 to 10. The other effects are  = 2,
= 2, 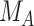 = 1,
= 1, 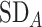 = 1,
= 1, 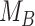 = 1.5,
= 1.5, 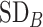 = 1,
= 1, 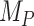 =
=  2, and
2, and 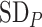 = 1. BV, best value.
= 1. BV, best value.
As we explained above, this disagreement occurs because SUCRAs (and other probabilistic metrics) incorporate the uncertainty in the estimates, while the point estimates of the mean effects 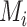 do not.
do not.
Impact of uncertainty on the hierarchies obtained by pi,BV and SUCRA
To study further the impact of uncertainty on the differences in hierarchy between 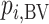 and SUCRA, we now assume placebo to have the lowest mean value
and SUCRA, we now assume placebo to have the lowest mean value 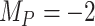 and the other treatments A, B, and C to have the values
and the other treatments A, B, and C to have the values 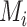 = 1, 1.5, and 2, respectively. We start with all standard deviations (SDs) of the estimated distributions set equal to 1; then we gradually increase the SD of C,
= 1, 1.5, and 2, respectively. We start with all standard deviations (SDs) of the estimated distributions set equal to 1; then we gradually increase the SD of C, 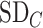 , up to 10. Increased uncertainty in C produces more overlap between the distributions of
, up to 10. Increased uncertainty in C produces more overlap between the distributions of  and
and 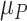 ; because placebo is the most preferable treatment, C “moves up” in the hierarchy. With
; because placebo is the most preferable treatment, C “moves up” in the hierarchy. With 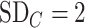 ,
, 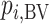 suggests that treatment C is higher in the hierarchy than treatment A, while it needs an
suggests that treatment C is higher in the hierarchy than treatment A, while it needs an 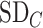 as large as 7.5 for the SUCRA to indicate that C is higher in the hierarchy than A (Figure 3).
as large as 7.5 for the SUCRA to indicate that C is higher in the hierarchy than A (Figure 3).
DISCUSSION
In this article, we introduced the idea of a treatment hierarchy question, and we suggested that the clinical decision-making problem should be clearly defined at the beginning of every comparative effectiveness review. We discussed the most commonly used ranking metrics, which are either the mean of each treatment-specific distribution or a more general summary of the joint distribution (such as SUCRA and 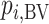 ). We showed that each ranking metric could, in principle, answer a specific treatment hierarchy question, and when used in this context, every ranking metric provides a valid treatment hierarchy for the corresponding question.
). We showed that each ranking metric could, in principle, answer a specific treatment hierarchy question, and when used in this context, every ranking metric provides a valid treatment hierarchy for the corresponding question.
Several authors have criticized the use of ranking metrics in published NMAs. Their criticism is misplaced, because there is no universally accepted “gold standard” treatment hierarchy against which the hierarchy obtained by the various ranking metrics is to be evaluated. All apparent limitations of the ranking metrics result from the fact that they transform a complex set of information (e.g., distributions for the mean treatment effect with location and dispersion) into a set of (univariate) numbers. Our theoretical examples suggested that, when the treatment-specific outcome distributions are estimated with different degrees of precision, the hierarchy based on the mean estimate may disagree with that obtained by more general summaries of the distribution. We also observed that:
1. SUCRA values depend on the precision of estimation of treatment effects, but they do not consistently under- or overestimate the rank of the treatments whose effects are imprecise; instead, changes in hierarchy very much depend on the rankings of the other treatments.
2. 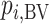 is more sensitive to differences in precision across treatment effect estimates than the SUCRA. Among treatments with the same point estimate,
is more sensitive to differences in precision across treatment effect estimates than the SUCRA. Among treatments with the same point estimate, 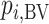 ranks first the treatment with the most imprecise effect, because it ignores the equally high probability of the treatment’s being worst.
ranks first the treatment with the most imprecise effect, because it ignores the equally high probability of the treatment’s being worst.
Setting up the treatment hierarchy question is not trivial, and further research is needed to define the spectrum of questions that an NMA can answer. Part of the difficulty in specifying a treatment hierarchy question is in clear use of language. In this article, we offer some ideas about what the question could be, but some stakeholders may be interested in questions that cannot be answered by any of the described approaches. Decision-making is a complex process that considers several efficacy and safety or tolerability outcomes, clinically important differences in the relative treatment effects, the utilities associated with each outcome value, and predictions in real-world conditions. These considerations motivate extensions of the existing ranking metrics or formal decision analysis (19–21). Additionally, in the current work, we discuss the ranking metrics as summary statistics. Many ranking metrics are also interpretable as parameter estimates, however, and for these it is reasonable to report a measure of uncertainty provided that the change of perspective is made clear. For example, the 95% credible interval for the mean rank describes our uncertainty about the true rank of that treatment compared with its comparators.
Without loss of generality, we assumed that the outcome of interest is continuous. It is possible to have dichotomous or dichotomized continuous outcomes, depending on the research question of interest. For example, the outcome might be whether each individual within a trial has an LDL-C level less than 2.5 mmol/L or not. In this case, the estimand 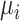 would be a probability and, as with a continuous outcome, the ranking metrics would summarize the treatment-specific joint distribution of
would be a probability and, as with a continuous outcome, the ranking metrics would summarize the treatment-specific joint distribution of 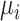 ’s. Finally, we assumed that the distributions of the estimands
’s. Finally, we assumed that the distributions of the estimands 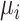 are normal. Although nonnormal distributions can occur, extreme skewness that affects the agreement between ranking metrics was empirically assessed to occur infrequently (13).
are normal. Although nonnormal distributions can occur, extreme skewness that affects the agreement between ranking metrics was empirically assessed to occur infrequently (13).
Treatment rankings have also been criticized for not including assessments of the quality of evidence (22); this applies equally to relative treatment effects. In a pairwise meta-analysis, interventions with large and precise effects are not necessarily preferable if the evidence is of low quality. Similarly, the treatments at the top of the hierarchy should not be blindly recommended without first scrutinizing the confidence in the results. The risk of bias in the included studies, the amount of heterogeneity, the plausibility of the consistency assumption, and the threat of publication bias could all limit the credibility of a treatment hierarchy, just as for effect sizes in pairwise meta-analysis. An attempt to produce statements about the credibility of ranking can be found in Salanti et al. (23) and is subject to ongoing research extending the Confidence in Network Meta-Analysis (CINeMA) framework (24). Systematic reviewers should consider the quality of the evidence when translating numerical results (effect sizes or rankings) into recommendations, and failure to do so should not be perceived as a shortcoming of the ranking metrics employed.
The main challenge that analysts face is to be aware of the advantages and disadvantages of rankings and to be transparent about the methods used. Even when a treatment hierarchy question is clearly defined and the appropriate ranking metric is used, the importance of ranking interventions is not to provide a “cookbook” for health-care decision-making. Interpretation of a treatment hierarchy must ideally extend beyond inspection of the values from ranking measures and draw on the totality of the evidence synthesis results. In this spirit, we recommend that every systematic review explicitly define in its protocol the treatment hierarchy question it aims to answer, choose an appropriate ranking metric for that question, and interpret the obtained hierarchy after considering the uncertainty in the treatment effects and the quality of the evidence.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Institute of Social and Preventive Medicine, University of Bern, Bern, Switzerland (Georgia Salanti, Adriani Nikolakopoulou, Orestis Efthimiou, Matthias Egger); Institute of Medical Biometry and Statistics, Faculty of Medicine, University of Freiburg and Medical Center–University of Freiburg, Freiburg, Germany (Adriani Nikolakopoulou); Department of Psychiatry, Medical Sciences Division, University of Oxford, Oxford, United Kingdom (Orestis Efthimiou); Department of Primary Education, School of Education Sciences, University of Ioannina, Ioannina, Greece (Dimitris Mavridis); Population Health Sciences, Bristol Medical School, University of Bristol, Bristol, United Kingdom (Matthias Egger); and MRC Clinical Trials Unit at UCL, University College London, London, United Kingdom (Ian R. White).
This work was funded by the Swiss National Science Foundation (grant 179158). I.R.W. was supported by the Medical Research Council (Programme Grant MC_UU_12023/21). O.E. was supported by the Swiss National Science Foundation (grant 180083). D.M. was supported by the European Union’s Horizon 2020 COMPAR-EU Project (grant 754936).
Conflict of interest: none declared.
REFERENCES
- 1. Caldwell DM, Ades AE, Higgins JP. Simultaneous comparison of multiple treatments: combining direct and indirect evidence. BMJ. 2005;331(7521):897–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Salanti G, Ades AE, Ioannidis JP. Graphical methods and numerical summaries for presenting results from multiple-treatment meta-analysis: an overview and tutorial. J Clin Epidemiol. 2011;64(2):163–171. [DOI] [PubMed] [Google Scholar]
- 3. Lu G, Ades AE. Combination of direct and indirect evidence in mixed treatment comparisons. Stat Med. 2004;23(20):3105–3124. [DOI] [PubMed] [Google Scholar]
- 4. Rücker G, Schwarzer G. Ranking treatments in frequentist network meta-analysis works without resampling methods. BMC Med Res Methodol. 2015;15(1):58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Salanti G. Indirect and mixed-treatment comparison, network, or multiple-treatments meta-analysis: many names, many benefits, many concerns for the next generation evidence synthesis tool. Res Synth Methods. 2012;3(2):80–97. [DOI] [PubMed] [Google Scholar]
- 6. Cipriani A, Higgins JPT, Geddes JR, et al. Conceptual and technical challenges in network meta-analysis. Ann Intern Med. 2013;159(2):130–137. [DOI] [PubMed] [Google Scholar]
- 7. Hutton B, Salanti G, Caldwell DM, et al. The PRISMA extension statement for reporting of systematic reviews incorporating network meta-analyses of health care interventions: checklist and explanations. Ann Intern Med. 2015;162(11):777–784. [DOI] [PubMed] [Google Scholar]
- 8. Kibret T, Richer D, Beyene J. Bias in identification of the best treatment in a Bayesian network meta-analysis for binary outcome: a simulation study. Clin Epidemiol. 2014;6:451–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Mills EJ, Kanters S, Thorlund K, et al. The effects of excluding treatments from network meta-analyses: survey. BMJ. 2013;347:f5195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Veroniki AA, Straus SE, Rücker G, et al. Is providing uncertainty intervals in treatment ranking helpful in a network meta-analysis. J Clin Epidemiol. 2018;100:122–129. [DOI] [PubMed] [Google Scholar]
- 11. Trinquart L, Attiche N, Bafeta A, et al. Uncertainty in treatment rankings: reanalysis of network meta-analyses of randomized trials. Ann Intern Med. 2016;164(10):666–673. [DOI] [PubMed] [Google Scholar]
- 12. Wang Z, Carter RE. Ranking of the most effective treatments for cardiovascular disease using SUCRA: is it as sweet as it appears? [editorial]. Eur J Prev Cardiol. 2018;25(8):842–843. [DOI] [PubMed] [Google Scholar]
- 13. Chiocchia V, Nikolakopoulou A, Papakonstantinou T, et al. Agreement between ranking metrics in network meta-analysis: an empirical study. BMJ Open. 2020;10(8):e037744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Salanti G. esm-ispm-unibe-ch-REPRODUCIBLE/RankingPaper. https://github.com/esm-ispm-unibe-ch-REPRODUCIBLE/RankingPaper. Published April 29, 2021. Accessed April 29, 2021.
- 15. Zarin W, Veroniki AA, Nincic V, et al. Characteristics and knowledge synthesis approach for 456 network meta-analyses: a scoping review. BMC Med. 2017;15(1):3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Committee for Medicinal Products for Human Use, European Medicines Agency . ICH E9 (R1) Addendum on Estimands and Sensitivity Analysis in Clinical Trials to the Guideline on Statistical Principles for Clinical Trials. Amsterdam, the Netherlands: European Medicines Agency; 2020. https://www.ema.europa.eu/en/documents/scientific-guideline/ich-e9-r1-addendum-estimands-sensitivity-analysis-clinical-trials-guideline-statistical-principles_en.pdf. Accessed August 15, 2021. [Google Scholar]
- 17. Piepoli MF, Hoes AW, Agewall S, et al. 2016 European Guidelines on Cardiovascular Disease Prevention in Clinical Practice: The Sixth Joint Task Force of the European Society of Cardiology and Other Societies on Cardiovascular Disease Prevention in Clinical Practice (constituted by representatives of 10 societies and by invited experts). Eur J Prev Cardiol. 2016;23(11):NP1–NP96. [DOI] [PubMed] [Google Scholar]
- 18. Berger JO. Statistical Decision Theory and Bayesian Analysis. 2nd ed. New York, NY: Springer-Verlag New York; 1985. [Google Scholar]
- 19. Brignardello-Petersen R, Johnston BC, Jadad AR, et al. Using decision thresholds for ranking treatments in network meta-analysis results in more informative rankings. J Clin Epidemiol. 2018;98:62–69. [DOI] [PubMed] [Google Scholar]
- 20. Tervonen T, Naci H, van Valkenhoef G, et al. Applying multiple criteria decision analysis to comparative benefit-risk assessment: choosing among statins in primary prevention. Med Decis Making. 2015;35(7):859–871. [DOI] [PubMed] [Google Scholar]
- 21. Mavridis D, Porcher R, Nikolakopoulou A, et al. Extensions of the probabilistic ranking metrics of competing treatments in network meta-analysis to reflect clinically important relative differences on many outcomes. Biom J. 2020;62(2):375–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Mbuagbaw L, Rochwerg B, Jaeschke R, et al. Approaches to interpreting and choosing the best treatments in network meta-analyses. Syst Rev. 2017;6(1):79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Salanti G, Del Giovane C, Chaimani A, et al. Evaluating the quality of evidence from a network meta-analysis. PLoS One. 2014;9(7):e99682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Nikolakopoulou A, Higgins JPT, Papakonstantinou T, et al. CINeMA: an approach for assessing confidence in the results of a network meta-analysis. PLoS Med. 2020;17(4):e1003082. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


