Inertial artifact in viscoelastic measurements of striated muscle: Modeling and experimental results

Abstract

Viscoelastic properties of striated muscle are often measured using length perturbation analysis and quantified as a complex modulus, whose elastic and viscous components reflect the energy-storage and energy-absorbing properties of the tissue, respectively. The energy stored as inertia is commonly ignored due to the small size of samples examined, typically <1 mm. Considering recent advances in tissue engineering to generate muscle tissues of larger sizes, we questioned whether ignoring the inertial artifact was still reasonable in these samples. To answer this question, we derived and solved the one-dimensional wave equation that describes the propagation of strain along the length of a sample. The inertial artifact was predicted to contaminate the elastic modulus with (2πf)²L₀²ρ/6, where f is perturbation frequency, L₀ is muscle length, and ρ is muscle density. We then measured viscoelastic properties up to 500 Hz in mouse skeletal muscle fibers at long (4.8 mm) and short (<1 mm) lengths and up to 100 Hz in rat cardiac slices at long (10–12 mm) and short (<2 mm) lengths. We found the elastic modulus of long preparations was elevated as frequency increased and was about half the magnitude of that predicted by the model. While the prediction tended to overestimate the measured inertial artifact, these results provided some validity to the model. We used the predicted artifact as an overly conservative estimate of error that might arise in a mechanics assay of mammalian striated muscle, whose nominal resting stiffness is on the order 100 kN m⁻². We found that muscle lengths of <1 mm resulted in negligible inertial artifact (<0.5% error) for perturbation frequencies under 250 Hz. Muscle samples longer than 5 mm, on the other hand, would result in >5% error at frequencies of 200 Hz and higher.

Significance

This study demonstrates that measurements of stiffness in muscle samples can, under certain conditions, be contaminated by the effects of sample inertia, which could confound interpretation of the data. The degree of contamination is dependent on the sample length and the frequency with which the sample length is perturbed during the measurement. We report that measures of viscoelasticity are not contaminated with this artifact when samples are short (<1 mm), but in larger samples, such as those exemplified by engineered muscle tissue and myocardial slices, the inertial artifact in the elastic modulus is not negligible. We provide here a guideline that would be useful to assure conditions that reduce and minimize inertial artifact.

Introduction

Sound preclinical experimental models are critical for inferring how striated muscle mechanics measured in the laboratory would be expected to scale up to higher anatomical levels (e.g., whole heart or whole skeletal muscle). One measure often used to characterize striated muscle is its viscoelasticity, which describes an energy-storing property, also called the elastic or storage modulus, and an energy-absorbing property, also called the viscous or loss modulus. These moduli and their frequency dependence can be used to probe myosin kinetics (1, 2, 3, 4, 5), calcium-independent thin filament activation (5), and chord stiffness (6) as might underlie physiological and pathophysiological states of muscle function.

The examination of viscoelasticity in striated muscle was first described over 70 years ago (7). For at least 50 years since then, single-fiber preparations have been the model system of choice. Engineered tissue and myocardial slices are relatively recent and novel model systems for understanding striated muscle function (8,9). Although there are numerous approaches to studying muscle function in vitro, myocardial slices in particular offer notable advantages, including maintenance of the native myofiber architecture and unique electrophysiological properties. While permeabilized fibers and myocardial slices both represent viable preclinical models for studying striated muscle function, there are notable differences in their experimental preparation that warrant consideration. For example, in contrast to single skeletal muscle fibers, which are often 50–100 μm in width and ∼1 mm in length, myocardial slices are typically at least twice as thick (200–300 μm) and 5- to 10-fold wider and longer (10,11).

Differences in sample preparation size are not expected to affect the resulting measure of viscoelasticity due to the normalization factors of length and cross-sectional area used to define strain and stress, respectively, from which the elastic and viscous moduli are calculated. In the simplest terms, the elastic modulus refers to the capacity of the tissue to store mechanical energy in its deformation akin to energy stored in the extension or compression of a spring. Mechanical energy can also be stored as inertia due to tissue mass in motion, which obviously occurs when length perturbations are applied to measure viscoelasticity. Inertia is usually assumed negligible and ignored due to the small size of muscle samples historically used in the laboratory. While it is tempting to continue to ignore inertia in these larger samples, the validity of that assumption is not immediately obvious. A quantitative rationale for ignoring the consequences of inertia when examining muscle viscoelasticity would be useful.

In this study, we asked how and under what conditions the energy-storing property of inertia arises in the measurement of viscoelastic characteristics of striated muscle. We present in this paper a quantitative analysis of the extent to which linear viscoelastic measurements of striated muscle are contaminated with inertial artifact. We start with basic definitions of linear stiffness and viscoelasticity, derive the wave equation that describes the influence of inertia in a linear preparation of muscle, and examine the solution of the wave equation to quantify the inertial artifact carried in the observed elastic modulus. Finally, we compare the mathematical computations to experimental results and provide guidance of the experimental conditions under which inertia can be validly ignored.

Measuring macroscopic viscoelasticity

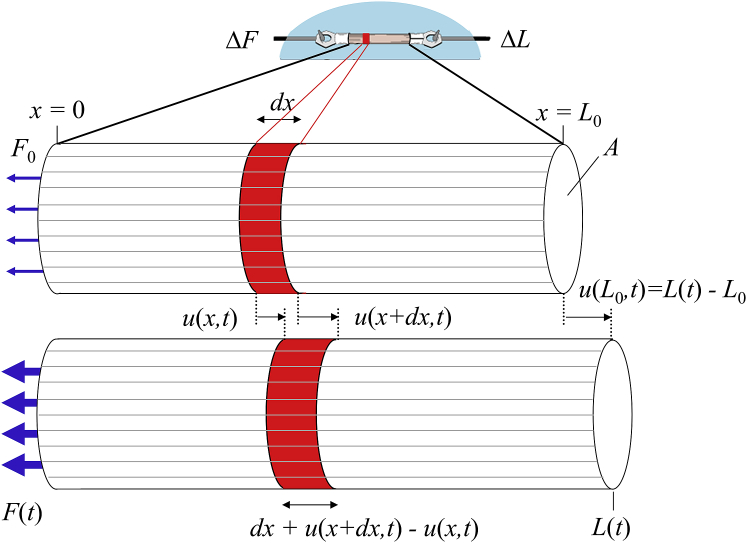
Striated muscle commonly offers a clear longitudinal orientation that allows for one-dimensional analysis of stiffness and viscoelasticity. Once orientation has been established, a length change can be applied to one end of the muscle sample and a force response is measured at the other end. The smallest functional unit of striated muscle is the half sarcomere, which has a very small length (∼1 μm) compared with that of the whole sample (∼1 mm) (Fig. 1). Typically, the experimentalist would like to have a measure of the viscoelastic characteristics of the half sarcomere but will take the viscoelasticity of the whole sample as a proxy for that of the half sarcomere. One goal in this study is to demonstrate the extent to which that assumption is valid. Much of the development and definitions presented here can be found in textbooks like that of Y.C. Fung (12).

Figure 1.

Mechanics assay of a muscle sample. In a mechanics assay of this type, striated muscle length is often on the order of 1 mm or less. The length of the half sarcomere, which is the smallest complete contractile unit, is on the order of 1 μm. When the muscle is lengthened, each half sarcomere is also lengthened. Values of length change, ΔL, normalized to muscle length, L₀, and force change, ΔF, normalized to cross-sectional area, A, are normally used to characterize whole muscle viscoelasticity and used as a proxy for that of the half sarcomere. To see this figure in color, go online.

The simplest example of relating force and length would be a steady-state proportionality constant indicating stiffness bearing no consideration of dynamics that arise from viscous or inertial effects. The relationship between a change in force and a change in length is simply a constant, E:

$$\frac{F-F_{\text{0}}}{A}=E\frac{L-L_0}{L_0},$$ (1)

where F is the measured force, A is the cross-sectional area, and L is the imposed muscle length. The stiffness constant E is also termed the chord stiffness and corresponds to the elastic or Young’s modulus characterizing the longitudinal stiffness of the muscle per cross-sectional area. The subscript 0 refers to initial conditions of the sample preparation. Therefore, F−F₀ refers to the change in force, ΔF, and L−L₀ refers to the change in length, ΔL. We can now define tensile stress, σ = ΔF/A, and strain, ε = ΔL/L₀, which provide terms that apply equally for the entire muscle sample as well as for the half sarcomere. Likewise, the stiffness, E, measured at the whole muscle level is a valid representation of stiffness of the half sarcomere. We have used Eq. 1 in the past to demonstrate that the passive stiffness of cardiac muscle in diastolic heart failure is due primarily to enhanced stiffness in titin and collagen (6).

A more generalized linear mechanical transfer function allows for use of an imposed time-varying strain as well as a combination of elastic and viscous behavior. The recorded stress response would then be represented in a mechanical transfer function, $Y_{L_0}\left(t\right)$, convolved with the imposed strain:

$${\sigma }_r\left(t\right)=\underset{-\infty }{\overset{t}{\int }}{Y}_{L_0}\left(t-\tau \right){\epsilon }_r\left(\tau \right)d\tau ,$$ (2)

where σ_r(t) is the recorded stress transient and ε_r(t) is the recorded strain transient imposed on the muscle. The subscript L₀ seen in term $Y_{L_0}\left(t\right)$ indicates that this mechanical transfer function relates to the entire length of the muscle sample. Equation 2 can also be written as:

$${\sigma }_r\left(t\right)=Y_{L_0}\ast {\epsilon }_r\left(t\right),$$ (3)

where the symbol ^∗ represents the convolution operation.

A step length change, like that shown in Fig. 2 A, applied to relaxed striated muscle results in a force response exemplified in Fig. 2 B. If our muscle represents a linear mechanical system, which is valid for small length perturbations, then mechanical transfer function, $Y_{L_0}\left(t\right)$, can be calculated as the time derivative of the step response (Fig. 2 C). The transfer function represents the force response to an infinitely short duration length change called an impulse. We could theoretically use the mechanical transfer function to calculate the force response to any imagined length change. This transfer function, however, is not generally used, in part because calculation of the transfer function in the time domain in practice is difficult. The complex modulus in the frequency domain, on the other hand, is much more easily calculated and generally more useful, thus we work in the frequency domain for the remainder of this study.

Figure 2.

Viscoelastic characteristics represented as mechanical step response, impulse response, and complex modulus. (A) A step length change applied to a muscle sample can be used to characterize viscoelasticity. The recorded change in length, ΔL, normalized to original length, L₀, represents the strain, ε_r(t), imposed on the sample and is usually very small <1%. (B) The recorded change in force, ΔF, normalized to cross-sectional area, A, represents the stress, σ_r(t), propagated along the length of the sample due to the strain. This example step response of the stress exemplifies the fractional derivative stress release (log plot in inset shows a straight line indicative of a fractional derivative) often exhibited by biological samples (11). (C) The impulse response, $Y_{L_0}\left(t\right)$, is calculated as the time derivative of the step response, but is not generally used to characterize viscoelasticity. (D) A sinusoidal strain applied over several frequencies can also be used to characterize viscoelasticity. (E) The stress response will also be sinusoidal, but usually out of phase with the sinusoidal strain. The magnitude of the stress that is in-phase with the strain, σ_E, divided by the magnitude of strain, ε, defines the elastic modulus. The magnitude of the stress 90 degrees out-of-phase, σ_V, divided by ε defines the viscous modulus. (F) The frequency domain representation of viscoelasticity is provided by the complex modulus, which consists of the elastic modulus (i.e., real part of the complex modulus) and viscous modulus (imaginary part) across the range of perturbation frequencies applied in the assay.

Within the bounds of linear systems analysis, linear operators, such as the Fourier transform (FT), can be applied to the time domain description of viscoelasticity, such as Eq. 3. The frequency domain representation of the relationship among stress, strain and complex modulus is then:

$$\stackrel{\sim }{{\sigma }_r}\left(\omega \right)=\stackrel{\sim }{Y_{L_0}}\left(\omega \right)\stackrel{\sim }{{\epsilon }_r}\left(\omega \right),$$ (4)

where ω is angular frequency related to frequency, f, as ω = 2πf, and ${\tilde{Y}}_{L_0}\left(\omega \right)$ = complex modulus for length L₀ defined as the FT of the $Y_{L_0}\left(t\right)$. In practice the complex modulus ${\tilde{Y}}_{L_0}\left(\omega \right)$ is calculated from experimental measures as the FT of recorded stress, ${\tilde{\sigma }}_r\left(\omega \right)$, divided by the FT of recorded strain, ${\tilde{\epsilon }}_r\left(\omega \right)$ (Fig. 2, D and E). The real part of $Y_{L_0}\left(t\right)$ is the elastic modulus and the imaginary part is the viscous modulus. An example complex modulus measured in relaxed striated muscle is shown in Fig. 2 F.

The complex modulus utilized in Eq. 4 represents the elastic and viscous characteristics of the full length of the sample. As we are interested in the complex modulus of the half sarcomere, we would have to apply (1), (2), (3), (4) to a half sarcomere within a muscle sample. Fig. 3 illustrates a cylindrical muscle sample with an initial length L₀ and tensile force F₀. Recognizing that we will later develop the wave equation (13), we will call the length of this half sarcomere, dx. If we let u(x,t) represent the time-varying displacement of the half sarcomere at position x, then u(x + dx,t) is the time-varying displacement at position x + dx.

Figure 3.

The one-dimensional longitudinal wave equation is used to model the influence of inertia on the complex modulus. The time-varying displacement of any part of the sample along its length, x, is represented here by the function u(x,t). Muscle length is perturbed at x = L₀, and the displacement is represented by u(L₀,t), which when normalized to L₀ is the recorded strain, ε_r(t). The displacement of the muscle at x = 0 is held constant, u(0,t) = 0. The tensile force required to maintain that boundary condition at x = 0 is measured with a force transducer. The recorded force normalized to cross-sectional area A provides the recorded stress, σ_r(t). An infinitesimally small length, dx, would be elongated and displaced relative to its original length and position. This length dx is analogous to the half sarcomere within the muscle. Elongation of dx described in terms of displacements of its boundaries, u(x + dx,t) − u(x,t), is useful in the derivation of the one-dimensional longitudinal wave equation. To see this figure in color, go online.

The change in length of the half sarcomere is therefore u(x + dx,t) − u(x,t) (Fig. 3). We have assumed here a negligible radial compression with longitudinal expansion, i.e., Poisson ratio = 0, for very small perturbations that allows linear analysis. Referring to Eqs. 1 and 3 for whole muscle length, we produce an analogous relationship between stress and strain for the half sarcomere of length dx and the local microscopic transfer function over dx, i.e., ${\tilde{Y}}_{dx}\left(t\right)$:

$$\frac{F\left(x,t\right)-F_0\left(x\right)}{A}=Y_{dx}\left(t\right)\ast \left(\frac{\left[dx+u\left(x+dx,t\right)-u\left(x,t\right)\right]-dx}{dx}\right)$$ (5)

Equation 5 is the starting point for deriving and solving the wave equation, which will relate the complex modulus of the whole sample with that of the half sarcomere and account for the effects of mass. Please refer to the Appendix for the derivation and solution.

The solution suggests that the complex modulus measured at the macroscopic level, ${\tilde{Y}}_{L_0}\left(\omega \right)$, is related to the complex modulus present at the microscopic level, ${\tilde{Y}}_{dx}\left(\omega \right)$, as follows:

$$\stackrel{\sim }{Y_{L_0}}\left(\omega \right)=\stackrel{\sim }{Y_{dx}}\left(\omega \right)\frac{\theta }{\sin \left(\theta \right)},$$ (6)

where θ = $\frac{\omega L_0}{\sqrt{({\tilde{Y}}_{dx}\left(\omega \right)/\rho )}}$, and ρ = tissue density. The term θ/sin(θ) on the right-hand side of Eq. 6 is recognizable as the reciprocal of a sinc function, sin(θ)/θ, which has a unity value at θ = 0. However, while the value of θ may be small, it cannot be 0 due to non-zero values for ω, L₀, ${\tilde{Y}}_{dx}\left(\omega \right)$, and ρ that define θ. We quantify in the next section the inertial artifact introduced into ${\tilde{Y}}_{L_0}\left(\omega \right)$ due to θ/sin(θ).

Quantifying the inertial artifact

A series expansion of the θ/sin(θ) term of Eq. 6, also given in the Appendix, is useful to estimate the inertial artifact. The first-order approximation is (14):

$${\stackrel{\sim }{Y}}_{L_0}\left(\omega \right)\cong \stackrel{\sim }{Y_{dx}}\left(\omega \right)+\frac{1}{6}{\omega }^2{L}_0^2\rho$$ (7)

This result suggests that the real part of the macroscopic complex modulus, i.e., the elastic modulus, would be observed higher than that of the microscopic mass-independent complex modulus due to the addition of an inertial artifact approximated as

$$\text{Artifact}\cong \frac{1}{6}{\omega }^2{L}_0^2\rho .$$ (8)

It is worth noting that units of the complex moduli are N m⁻² or kg m⁻¹ s⁻², which matches that of the artifact term when using units of s⁻¹ for angular frequency, m for length, and kg m⁻³ for density.

We can make a cursory estimate of the magnitude of this artifact based on reasonable values for ω, L₀, and ρ. A reasonable angular frequency to consider would be ω = 10 s⁻¹, which corresponds to 1.6 Hz and falls within the normal range of frequencies for human resting heart rate (0.8–2.8 Hz) and walking stride (1.41–2.13 Hz) (15,16). For assays depicted in Fig. 1, a reasonable value for L₀ = 1 mm or 1 × 10⁻³ m. Mammalian striated muscle density is accepted as ρ = 1.06 kg per liter or 1,060 kg m⁻³ (17). Applying these values to Eq. 8, the inertial artifact would have a value of 17.7 × 10⁻³ N m⁻². Values for the elastic modulus of relaxed muscle under the conditions noted above are on the order of 100 × 10³ N m⁻² (1,2,18). Therefore, the inertial artifact associated with the above-specified conditions is more than 6 orders of magnitude smaller than the expected mass-independent complex modulus ${\tilde{Y}}_{dx}\left(\omega \right)$ at 1.6 Hz and would contribute only ∼0.00017% error. However, if the length of the muscle sample is on the order of 5 mm and the measured complex modulus includes ω = 1256.6 s⁻¹, corresponding to 200 Hz, the inertial artifact at that frequency would be on the order of 6.97 × 10³ N m⁻², which is greater than 5% of the nominal 100 × 10³ N m⁻² and would not be considered negligible. The wide range of values for the inertial artifact results from its dependence upon the squared values of both frequency and muscle length, which can vary over multiple orders of magnitude.

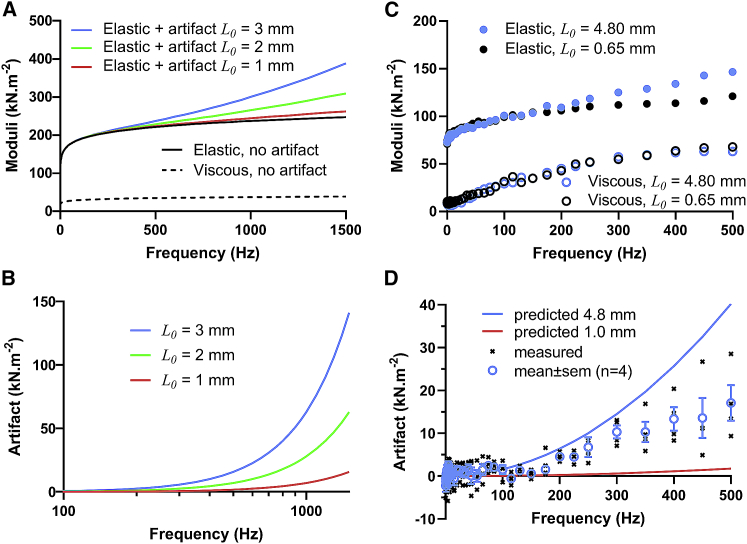
To illustrate how inertial artifact might be observed in practice, we modeled the elastic and viscous moduli that would result from Eq. 7 using reasonable values for ${\tilde{Y}}_{dx}\left(\omega \right)$. This mass-independent complex modulus was modeled as a fractional derivative viscoelasticity common for biological tissues. We used values for the stiffness (100 × 10³ N m⁻²) and the fractional derivative coefficient (0.1) common for relaxed mammalian striated muscle ${\tilde{Y}}_{dx}\left(\omega \right)$ = 100 × 10³ (iω)^0.1 N m⁻² (2,18,19). Fig. 4 A illustrates the modeled elastic and viscous moduli with the inertial artifact over a frequency range up to 1,500 Hz for muscle lengths of 1, 2, and 3 mm. Fig. 4, A and B demonstrate that, if the wave equation model is applicable, the inertial artifact would be noticeable at frequencies above ∼200–500 Hz and more so noticeable as frequencies increased and muscle samples became longer.

Figure 4.

Inertial artifact expected (A and B) and measured (C and D) in permeabilized skeletal muscle samples. (A) Based on the results of the wave equation, an inertial artifact is expected to arise in relatively long muscle samples and at relatively high perturbation frequencies. The elastic and viscous moduli without an artifact were generated using the fractional derivative representation of the complex modulus common for muscle at rest: 100 × 10³ (iω)^0.1 N m⁻². Muscle density was assumed to be 1060 kg m⁻³. The expected inertial artifact was then calculated for L₀ = 1, 2, and 3 mm samples. (B) The inertial artifact can be substantial as frequency rises and, in this example, introduces more than 5 × 10³ N m⁻², thus adding ∼5% error, at frequencies greater than 1400, 650, and 450 Hz for L₀ = 1, 2, and 3 mm samples, respectively. (C) Elastic and viscous moduli were measured in long (4.8 mm) and short (0.65 mm) preparations of the same mouse EDL muscle fiber, and therefore were expected to possess similar viscoelastic qualities. The elastic modulus of the longer sample appears to include an inertial artifact compared with that of the shorter sample. (D) Using the difference of the elastic moduli of long and short samples, the inertial artifact was estimated and plotted against the predicted inertial artifact based on a sample length of 4.8 mm. The mean measured artifact was about half that predicted. Symbols indicate mean ± SE.

To illustrate the point with recorded data, we measured the complex modulus of a skeletal muscle fiber isolated from a mouse extensor digitorum longus. Euthanasia and animal use were undertaken in accordance with and approved by the IACUC of the University of Massachusetts at Amherst. Details of the methods used to prepare the sample have been described elsewhere (3). The same fiber was clipped at two different lengths, long ∼3–4 mm and short ∼400 μm, and bathed in relaxing solution containing 40 mM BDM. The long sample was examined first and prestretched to 4.8 mm, the longest possible for the apparatus, which corresponded to sarcomere lengths 2.8–3.4 μm. Sinusoidal length perturbations were applied at 0.1% muscle length, and the complex modulus was recorded up to 500 Hz. The short sample was stretched to match the sarcomere length of the longer sample, and then fine adjusted to match stiffness of the longer sample at <10 Hz.

Example elastic and viscous moduli of the two sample lengths are superimposed in Fig. 4 C, where the elastic modulus of the longer sample appears elevated at higher frequencies. If we assume that no inertial artifact impacted the moduli of both samples at frequencies <10 Hz and of the shorter sample at all frequencies, the difference in elastic moduli between the long and short samples should reflect the inertial artifact. Fig. 4 D illustrates that the measured inertial artifact resembled that predicted by Eq. 8 and would not obviously be considered negligible, although the predicted artifact appears to have overestimated the actual artifact by a factor of 2. Nevertheless, we would conclude that the inertial artifact can arise under assay conditions that include high frequencies of length perturbation applied to relatively long muscle samples.

We also measured the complex modulus of a myocardial slice prepared from rat heart. Euthanasia and animal use were approved by the IACUC of the University of Vermont. Sample preparation followed methods described by Pitoulis et al. (10). The same slice was clipped at two different lengths, long ∼8–10 mm and short ∼1 mm, and bathed in a Tyrode’s solution containing 30 mM BDM. The long sample was examined first and prestretched to 10–12 mm, which resulted in sarcomere lengths 2.2–2.4 μm. Sinusoidal length perturbations were applied at 0.25% muscle length, and the complex modulus was recorded up to 100 Hz. Again, the short sample was stretched to match stiffness of the longer sample at <10 Hz.

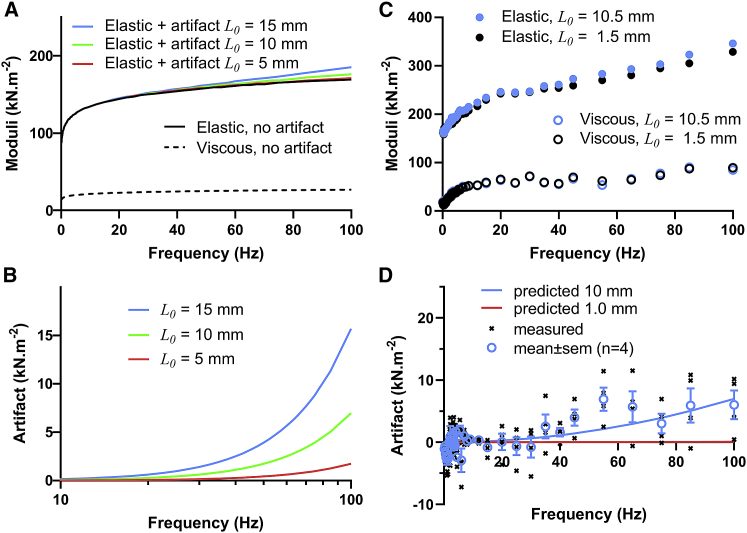
Fig. 5, A and B, present the expected inertial artifact over a frequency range up to 100 Hz for slice lengths of 5, 10, and 15 mm. An example pair of elastic and viscous moduli for two sample lengths examined are superimposed in Fig. 5 C. As observed in the skeletal muscle, the elastic modulus of the longer myocardial slice sample is elevated at higher frequencies. Fig. 5 D compares the mean observed inertial artifact and that predicted. Again, the inertial artifact appears to play some role in the measure of the elastic modulus.

Figure 5.

Inertial artifact expected (A and B) and measured (C and D) in cardiac slices. (A) Some inertial artifact is expected to arise in relatively long samples and with perturbation frequencies as low as 100 Hz. The expected inertial artifact was calculated for L₀ = 5, 10, and 15 mm, which would be relevant for cardiac slices and other engineered tissue samples. (B) The inertial artifact could add as much as 2, 6, and 10% error at 100 Hz for L₀ = 5, 10, and 15 mm, respectively. (C) Elastic and viscous moduli were measured in long (10.5 mm) and short (1.5 mm) preparations of the same cardiac slice. The elastic modulus of the longer sample appears to include an inertial artifact. (D) The mean of the artifacts observed in long samples. Symbols indicate mean ± SE.

Conditions for negligible inertial artifact

Here, we provide a quantitative estimate of errors due to an inertial artifact that would be expected in assays of viscoelasticity. We first note that the density of striated muscle does not differ much from sample to sample, and we assume a value of 1060 kg m⁻³ for the remainder of our analyses. The angular frequency and sample length, on the other hand, can vary widely depending on the assay and muscle type. The angular frequency, for example, can get at least as high as 1,250 s⁻¹, which corresponds to a low wing beat frequency of a fruit fly at ∼200 Hz (20). It is also often advantageous to acquire data at much higher frequencies, e.g., greater than 10× the normal physiological frequency, to detect the viscoelastic consequences of myosin-actin interactions (1, 2, 3, 4). The angular frequencies we might apply to fruit fly flight muscle could therefore be on the order of 12,500 s⁻¹ or ∼2,000 Hz.

It would be useful then to evaluate the percent error that would arise in measurements of viscoelasticity over a wide range of frequencies, up to 10 kHz, and preparation lengths, up to 100 mm. We assumed an elastic modulus of 100 kN m⁻² or 10⁵ N m⁻² (1,5), which reasonably reflects the stiffness of relaxed mammalian striated muscle and, because it is a low stiffness, represents a worst case scenario for evaluating error caused by artifact relative to actual stiffness. The expected error as a fraction of 10⁵ N m⁻² attributable to inertial artifact is then:

$$error\times {10}^5=\frac{1}{6}{\omega }^2{L}_0^2\rho$$ (9)

If we recognize the angular frequency ω = 2πf, the perturbation frequency (f) versus length (L₀) relationship is given as

$$f=\frac{1}{2\pi L_0}\sqrt{\left(error\times {10}^5\right)\times \frac{6}{\rho }}$$ (10)

Fig. 6A illustrates the f versus L₀ relationship for five error levels, 0.5, 1, 2, 5, and 10% error, compared with relaxed conditions with an elastic modulus of 100 kN m⁻². At long lengths and high frequencies (upper right-hand part of Fig. 6 A), the error associated with measures of viscoelasticity is above 10%. At short lengths and low frequencies (lower left-hand side), the error is below 0.5%. Fig. 6 B illustrates the f versus L₀ relationship for the five error levels under activated conditions, which result in an elastic modulus on the order of 500 kN m⁻² (1, 2, 3). The value 10⁵ N m⁻² in Eq. 10 is replaced by 5 × 10⁵ N m⁻², and the frequencies in Fig. 6 B are raised by √5 compared with Fig. 6 A.

Figure 6.

The frequency-length relationship was calculated for errors corresponding to 10, 5, 2, 1, and 0.5% error of a nominal 100 × 10³ N m⁻² elastic modulus (A) and 500 × 10³ N m⁻² elastic modulus (B), which are values relevant for relaxed and activated mammalian striated muscle, respectively. Low inertial artifact and low errors occur with short samples and low frequencies. High inertial artifact and high errors occur with long samples and high frequencies. Examples of a single cardiac myocyte (120 μm long) and a typical skeletal muscle sample (1 mm long) would not likely be subject to inertial artifact unless perturbation frequencies were exceptionally high, e.g., >2,000 and >500 Hz, respectively. Relatively long muscle samples of 5 and 10 mm would be subject to some degree of inertial artifact at 200 and 100 Hz, respectively, which are not uncommon frequencies for characterizing viscoelasticity.

We have noted in Fig. 6, A and B the placement of four example muscle samples. A single mammalian cardiac myocyte is about 120 μm long and would normally operate near a physiological range of 10 Hz for a mouse. Any inertial artifact associated with a measure of elastic modulus in this muscle would be less than 0.5% error up to at least 2000 Hz. A skeletal muscle strip 1 mm long could likewise be examined up to at least 250 Hz with less than 0.5% error. However, a skeletal muscle fiber taken from a rodent limb, for example, may be as long as 5 or 10 mm, and any measure of the elastic modulus over ∼200 and ∼100 Hz, respectively, may carry an artifact over 5% error under relaxed conditions (Fig. 6 A), but not more than 2% under activated conditions (Fig. 6 B).

Discussion

In this study, we demonstrated that the inertial artifact may contaminate measurements of the elastic modulus during measures of tissue viscoelasticity under certain conditions. Using a one-dimensional wave equation, we predicted the inertial artifact in terms of perturbation frequency, muscle length, and muscle density (see Eq. 8). Accordingly, the inertial artifact is not dependent upon muscle fiber type, temperature, or perturbation amplitude when experimental conditions allow for linear systems analysis.

Our model suggests that, under those conditions that generate artifact, the observed elastic modulus will overestimate the actual elastic modulus, and that this overestimate will increase with higher perturbation frequencies and longer preparations. With the growing use of engineered tissues and cardiac slices (8, 9, 10, 11), which are generally larger than single muscle fiber preparations, the inertial artifact may need to be anticipated when examining viscoelastic characteristics of muscle samples. For example, samples as long as 10 mm could demonstrate an artifact that adds 6% error for frequencies up to 100 Hz, which for many purposes could distort the physiological interpretation of viscoelasticity. The issue would be worse for faster muscle types. For example, insect flight muscle bears important viscoelastic information at 200 Hz and higher (7), although it is not possible to prepare native flight muscle longer than 1 mm. Nevertheless, if myosin of insect flight muscle were to be engineered into a muscle tissue of larger scale, the impact of an inertial artifact may need to be addressed.

We demonstrated that the inertial artifact measured in long muscle preparations (5–10 mm) matched the predicted artifact within a factor of 2, thus giving some validity to the model. The discrepancy must be due to factors that play some role in defining the inertial artifact but were not accounted for in our model. Those factors could include series compliance between the sample and the measurement apparatus or viscous load due to bathing medium. It is also worth questioning whether the clips used to attach the muscle sample to the apparatus may have contributed inertia. The clip attached to the force transducer does not move and therefore would not be affected by inertia. The clip attached to the length motor certainly moves and experiences inertia. In both cases illustrated in this study, either aluminum T-clips used to attach the skeletal muscle or acrylic triangles used to attach the myocardial slice, the material is so much stiffer than the muscle that the wave equation model would not need to take these components into account. Furthermore, at least in the case of the acrylic clips, these clips become an extension of the apparatus. For the clip on the force transducer, the resonant frequency may be reduced, but there is no effect of the clip attached on the length motor.

We would define a reasonably negligible artifact as contributing less than 0.5% error. With this definition, as illustrated in Fig. 6, A and B, the degree of contamination due to inertia is reasonably negligible for samples under ∼1 mm in length examined with perturbation frequencies under 250 Hz. Those conditions are usually met when studying amphibian and mammalian striated muscle, and the interpretation of previous studies need not be reexamined. Nevertheless, if perturbation analysis requires frequencies higher than 250 Hz or samples longer than 1 mm, it may be necessary to characterize and correct for an inertial artifact to avoid spurious interpretations of the measured elastic modulus. Other investigators using other muscles that are especially fast, e.g., those of insect, fish, or bird muscle, that require a high frequency range of length perturbation may need to reevaluate whether experimental conditions result in a negligible inertial artifact or warrant correction.

Appendix

In this Appendix, we derive and solve the one-dimensional wave equation, which will be used to model the effects of inertia on macroscopic measures of viscoelasticity.

Derivation of the wave equation

The one-dimensional longitudinal wave equation describes the time-varying displacement u(x,t) of a material at any position x along its length (13). A cartoon depiction of a cylindrical muscle sample with an initial length L₀ and tensile force F₀ is provided in Fig. 3. The derivation starts with consideration of an infinitesimally small length, dx, within the muscle sample analogous to the single half sarcomere in Fig. 1. Upon application of a time-varying displacement at L₀, u(L₀,t), the total sample length expands (and/or contracts), and the length enclosed within dx likewise expands (and/or contracts) according to the relative displacements on either end of dx. We recognize that u(x,t) is the time-varying displacement at position x, and u(x + dx,t) is the time-varying displacement at position x + dx. The change in length of the infinitesimally small length dx is therefore u(x + dx,t) − u(x,t) (Fig. 3). We have assumed here a negligible radial compression with longitudinal expansion, i.e., Poisson ratio = 0, for very small perturbations that allows linear analysis.

Referring to Eqs. 1 and 3 for whole muscle length, we produce an analogous relationship for stress and strain experienced by the infinitesimally small length dx and the local microscopic transfer function over dx, i.e., ${\tilde{Y}}_{dx}\left(t\right)$:

$$\frac{F(x,t)-F_0\left(x\right)}{A}=Y_{dx}\left(t\right)\ast \left(\frac{\left[dx+u(x+dx,t)-u(x,t)\right]-dx}{dx}\right)$$ (A1)

We can replace the left-hand side of Eq. A1 as the transient stress at point x, $\sigma (x,t)$. After canceling the dx terms in the numerator of the right-hand side, we can further recognize the first derivative of local displacement with respect to the x dimension. Equation A1 can then be rewritten

$$\sigma (x,t)=Y_{dx}\left(t\right)\ast \left(\frac{u(x+dx,t)-u(x,t)}{dx}\right)=Y_{dx}\left(t\right)\ast \frac{\partial u(x,t)}{\partial x}$$ (A2)

Equation A2 will be useful after we have developed the equation of motion for the length dx.

The equation of motion refers to the application of Newton’s second law of motion for the length dx, i.e., force = mass × acceleration. The net force on length dx is given as $A\left(\sigma (x+dx,t)-\sigma (x,t)\right)$, where Aσ(x + dx,t) = tensile force applied to length dx at x + dx, and Aσ(x,t) = tensile force applied to length dx at x. Given a tissue density of ρ, the mass contained within length dx is ρAdx. We can now write the equation of motion, force = mass × acceleration, for the length dx as follows:

$$A\left(\sigma (x+dx,t)-\sigma (x,t)\right)=\rho Adx\frac{{\partial }^{2}u(x,t)}{\partial t^2},$$ (A3)

where $\frac{{\partial }^{2}u(x,t)}{\partial t^2}$ is the acceleration of the length dx. The force term in this equation of motion can now be rewritten using the expression for stress due to strain provided in Eq. A2:

$$A\left[Y_{dx}\left(t\right)\ast \frac{\partial u(x+dx,t)}{\partial x}-Y_{dx}\left(t\right)\ast \frac{\partial u(x,t)}{\partial x}\right]=\rho Adx\frac{{\partial }^{2}u(x,t)}{\partial t^2}$$ (A4)

Next, we divide each side of Eq. A4 by ρ, and allow dx/dx to be multiplied to the left-hand side of Eq. A4.

$$\frac{A}{\rho }\frac{dx}{dx}\left[Y_{dx}\left(t\right)\ast \frac{\partial u(x+dx,t)}{\partial x}-Y_{dx}\left(t\right)\ast \frac{\partial u(x,t)}{\partial x}\right]=Adx\frac{{\partial }^{2}u(x,t)}{\partial t^2}$$ (A5)

The infinitesimal volume Adx can now be removed from each side. As long as $Y_{dx}\left(t\right)$ is not a function of position x, it can be moved out of the brackets.

$$\frac{Y_{dx}\left(t\right)}{\rho dx}\ast \left[\frac{\partial u(x+dx,t)}{\partial x}-\frac{\partial u(x,t)}{\partial x}\right]=\frac{{\partial }^{2}u(x,t)}{\partial t^2}$$ (A6)

The left-hand side of Eq. A6 is recognized as bearing the second-derivative of the displacement u(x,t) with respect to position x, or

$$\frac{Y_{dx}\left(t\right)}{\rho }\ast \frac{{\partial }^{2}u(x,t)}{\partial x^2}=\frac{{\partial }^{2}u(x,t)}{\partial t^2}$$ (A7)

Equation A7 is the longitudinal wave equation in one dimension.

Solution to the wave equation

Upon applying the FT, Eq. A7 is transformed from a partial differential equation into an ordinary differential equation in frequency space for the function $\tilde{U}(x,\omega )$, which is the FT of u(x,t):

$$\left(\frac{{\tilde{Y}}_{dx}\left(\omega \right)}{\rho }\right)\frac{{\partial }^2\tilde{U}(x,\omega )}{\partial x^2}=-{\omega }^2\tilde{U}(x,\omega ).$$ (A8)

Notably, Eq. A8 is written as though the sample is at rest before time zero (pictured in Fig. 1 A), thus the displacement and velocity, u(x,t) and du(x,t)/dt, are zero valued.

The general solution to a second-order ordinary differential equation, like Eq. A8, can be found in several textbooks including Berg and McGregor (13) and is:

$$\tilde{U}(x,\omega )=\tilde{V}\left(\omega \right)\exp \left[\frac{i\omega x}{\sqrt{({\tilde{Y}}_{dx}\left(\omega \right)/\rho )}}\right]+\tilde{W}\left(\omega \right)\exp \left[\frac{-i\omega x}{\sqrt{({\tilde{Y}}_{dx}\left(\omega \right)/\rho )}}\right]$$ (A9)

where $\tilde{V}(x,\omega )$ and $\tilde{W}(x,\omega )$ are arbitrary functions of frequency to be determined by boundary conditions (3), and exp[ ] = e^{[ ]}. The boundary conditions refer to stipulations applied to the ends of the sample. As illustrated in Fig. 3, the boundary conditions would be:

$$\tilde{U}(0,\omega )=0$$ (A10a)

$$\tilde{U}(L_0,\omega )=\Delta \tilde{L}\left(\omega \right),$$ (A10b)

where L₀ is the original length of sample being assayed, $\Delta \tilde{L}\left(\omega \right)$ is FT of the imposed displacement at x = L₀, namely u(L₀,t) = L(t) − L₀. Upon applying the boundary condition stipulated by Eq. A10a to Eq. A9, we find $\tilde{V}(x,\omega )=-\tilde{W}(x,\omega )$. Using Euler’s identity for the sine function, i.e., 2isin(θ) = exp(iθ) – exp(-iθ), the solution for $\tilde{U}(x,\omega )$ in Eq. A9 becomes:

$$\tilde{U}(x,\omega )=\tilde{V}\left(\omega \right)2i\sin \left(\frac{\omega x}{\sqrt{({\tilde{Y}}_{dx}\left(\omega \right)/\rho )}}\right).$$ (A11)

Applying the boundary condition stipulated by Eq. A10b, $\tilde{V}(x,\omega )$ must be:

$$\tilde{V}\left(\omega \right)=\frac{\text{Δ}\tilde{L}\left(\omega \right)}{2i\sin \left(\frac{\omega L_0}{\sqrt{\left({\tilde{Y}}_{dx}\left(\omega \right)/\rho \right)}}\right)}$$ (A12)

Therefore, the solution for the frequency domain displacement at any point x along the length of the muscle is then:

$$\tilde{U}(x,\omega )=\frac{\sin \left(\frac{\omega x}{\sqrt{({\tilde{Y}}_{dx}\left(\omega \right)/\rho )}}\right)}{\sin \left(\frac{\omega L_0}{\sqrt{({\tilde{Y}}_{dx}\left(\omega \right)/\rho )}}\right)}\Delta \tilde{L}\left(\omega \right).$$ (A13)

We now use this solution to relate the macroscopic complex modulus, ${\tilde{Y}}_{L_0}\left(\omega \right)$, which bears inertial artifact, to the microscopic complex modulus, ${\tilde{Y}}_{dx}\left(\omega \right)$, which is independent of mass and sample length.

Relating macroscopic and microscopic complex moduli

As mentioned earlier, in practice, the macroscopic complex modulus ${\tilde{Y}}_{L_0}\left(\omega \right)$ is calculated from experimental measures as the FT of recorded stress, ${\tilde{\sigma }}_r\left(\omega \right)$, divided by the FT of recorded strain, ${\tilde{\epsilon }}_r\left(\omega \right)$. Here, we use Eqs. A1 and A13 to provide the expected FT of the recorded stress, ${\tilde{\sigma }}_r\left(\omega \right)$. The recorded stress at x = 0 in the frequency domain is given by the FT of Eq. 6 evaluated at x = 0:

$${\tilde{\sigma }}_r\left(\omega \right)={\tilde{Y}}_{dx}\left(\omega \right){\frac{\partial \tilde{U}(x,\omega )}{\partial x}|}_{x=0}.$$ (A14)

Using the solution of Eq. A13 and carrying out the differentiation:

$${\tilde{\sigma }}_r\left(\omega \right)={\tilde{Y}}_{dx}\left(\omega \right){\frac{\left(\frac{\omega }{\sqrt{({\tilde{Y}}_{dx}\left(\omega \right)/\rho )}}\right)\cos \left(\frac{\omega x}{\sqrt{({\tilde{Y}}_{dx}\left(\omega \right)/\rho )}}\right)}{\sin \left(\frac{\omega L_0}{\sqrt{({\tilde{Y}}_{dx}\left(\omega \right)/\rho )}}\right)}\Delta \tilde{L}\left(\omega \right)|}_{x=0}.$$ (A15)

Evaluating at x = 0 gives:

$${\tilde{\sigma }}_r\left(\omega \right)={\tilde{Y}}_{dx}\left(\omega \right)\frac{\left(\frac{\omega }{\sqrt{\left({\tilde{Y}}_{dx}\left(\omega \right)/\rho \right)}}\right)}{\sin \left(\frac{\omega L_0}{\sqrt{\left({\tilde{Y}}_{dx}\left(\omega \right)/\rho \right)}}\right)}\text{Δ}\tilde{L}\left(\omega \right).$$ (A16)

We multiply the right-hand side by L₀/L₀, and use the definition of recorded strain for muscle sample, ${\tilde{\epsilon }}_r\left(\omega \right)=\Delta \tilde{L}\left(\omega \right)/L_0$. The ratio of stress recorded at x = 0 to strain recorded at x = L₀ is then:

$$\frac{{\tilde{\sigma }}_r\left(\omega \right)}{{\tilde{\epsilon }}_r\left(\omega \right)}={\tilde{Y}}_{dx}\left(\omega \right)\frac{\left(\frac{\omega L_0}{\sqrt{({\tilde{Y}}_{dx}\left(\omega \right)/\rho )}}\right)}{\sin \left(\frac{\omega L_0}{\sqrt{({\tilde{Y}}_{dx}\left(\omega \right)/\rho )}}\right)}.$$ (A17)

Equation A17 represents the measured complex modulus of a muscle preparation of length L₀ and density ρ and bearing a microscopic complex modulus ${\tilde{Y}}_{dx}\left(\omega \right)$. Compare Eq. A17 with Eq. 4, and the complex modulus measured at the macroscopic level, ${\tilde{Y}}_{L_0}\left(\omega \right)$, is related to the complex modulus present at the microscopic level, ${\tilde{Y}}_{dx}\left(\omega \right)$, as follows:

$${\tilde{Y}}_{L_0}\left(\omega \right)={\tilde{Y}}_{dx}\left(\omega \right)\frac{\left(\frac{\omega L_0}{\sqrt{({\tilde{Y}}_{dx}\left(\omega \right)/\rho )}}\right)}{\sin \left(\frac{\omega L_0}{\sqrt{({\tilde{Y}}_{dx}\left(\omega \right)/\rho )}}\right)}.$$ (A18)

If we use θ =$\left(\frac{\omega L_0}{\sqrt{({\tilde{Y}}_{dx}\left(\omega \right)/\rho )}}\right)$, the term θ/sin(θ) on the right-hand side of Eq. A18 is recognizable as the reciprocal of a sinc function, sin(θ)/θ, which has a unity value at θ = 0. However, while the value of θ may be small, it cannot be 0 due to non-zero values for ω, L₀, ${\tilde{Y}}_{dx}\left(\omega \right)$, and ρ that define θ. We quantify in the next section the inertial artifact introduced into ${\tilde{Y}}_{L_0}\left(\omega \right)$ due to θ/sin(θ).

Series expansion approximation

A series expansion of the θ/sin(θ) term of Eq. A18 is useful to estimate the inertial artifact:

$${\tilde{Y}}_{L_0}\left(\omega \right)={\tilde{Y}}_{dx}\left(\omega \right)\left[1+\frac{{\omega }^2{L}_0^2}{6\left({\tilde{Y}}_{dx}\left(\omega \right)/\rho \right)}+\frac{7{\omega }^4{L}_0^4}{360{\left({\tilde{Y}}_{dx}\left(\omega \right)/\rho \right)}^2}+\cdots +\sum _{n=0}^{\infty }\frac{2\left(2^{2n-1}-1\right)\left|B_{2n}\right|}{\left(2n\right)!}{\left(\frac{\omega L_0}{\sqrt{\left({\tilde{Y}}_{dx}\left(\omega \right)/\rho \right)}}\right)}^{2n}\right],$$ (A19)

where B_n is Bernoulli number (14). The first-order approximation is:

$${\tilde{Y}}_{L_0}\left(\omega \right)\cong {\tilde{Y}}_{dx}\left(\omega \right)+\frac{1}{6}{\omega }^2{L}_0^2\rho .$$ (A20)

Author contributions

M.S.M. and B.M.P. designed the research. C.R.S. and B.M.P. performed the experiments. B.M.P. analyzed the data. B.M.P. developed the model. M.S.M., C.R.S., and B.M.P. wrote the manuscript.

Editor: Steven Rosenfeld.