Abstract
ATP-sensitive K+ (K(ATP)) channels were first reported in the β-cells of pancreatic islets in 1984, and it was soon established that they are the primary means by which the blood glucose level is transduced to cellular electrical activity and consequently insulin secretion. However, the role that the K(ATP) channels play in driving the bursting electrical activity of islet β-cells, which drives pulsatile insulin secretion, remains unclear. One difficulty is that bursting is abolished when several different ion channel types are blocked pharmacologically or genetically, making it challenging to distinguish causation from correlation. Here, we demonstrate a means for determining whether activity-dependent oscillations in K(ATP) conductance play the primary role in driving electrical bursting in β-cells. We use mathematical models to predict that if K(ATP) is the driver, then contrary to intuition, the mean, peak, and nadir levels of ATP/ADP should be invariant to changes in glucose within the concentration range that supports bursting. We test this in islets using Perceval-HR to image oscillations in ATP/ADP. We find that mean, peak, and nadir levels are indeed approximately invariant, supporting the hypothesis that oscillations in K(ATP) conductance are the main drivers of the slow bursting oscillations typically seen at stimulatory glucose levels in mouse islets. In conclusion, we provide, for the first time to our knowledge, causal evidence for the role of K(ATP) channels not only as the primary target for glucose regulation but also for their role in driving bursting electrical activity and pulsatile insulin secretion.
Significance
Pancreatic β-cells regulate blood glucose by secreting insulin in accordance with the glucose concentration. This metabolic sensing depends critically on ATP-dependent potassium channels, which link β-cell fuel metabolism to the membrane potential. A key feature of this mechanism is the slow, 5-min oscillations observed in electrical activity, calcium, and metabolism. Mathematical models variously propose that oscillations in ATP/ADP either cause these oscillations or are just a consequence, as calcium influences both the production and consumption of ATP. We propose a novel way to test which is the case and confirm experimentally that ATP/ADP is the driver of β-cell oscillations. Other proposed oscillation mechanisms in contrast may mediate the faster oscillations that are also seen in β-cells.
Introduction
Pancreatic β-cells are clustered together with other endocrine cells in the pancreatic islets of Langerhans and are the sole insulin-secreting cells of the body. When blood glucose is low, β-cells are mostly inactive, but as glucose is increased, so too is the cells’ activity level (1). As a result, the rate of release of insulin from β-cells increases in response to increases in the blood glucose level. This is accomplished in two ways. In the first, primary pathway, β-cell electrical activity is increased at higher glucose levels, resulting in higher mean intracellular Ca2+ levels and, subsequently, increased insulin secretion. A glucose amplification pathway builds on this primary or “triggering” pathway and acts downstream of Ca2+ entry (2). The increased electrical activity associated with increases in glucose is due to an increase in the ratio of ATP to ADP that is the direct result of glucose uptake and metabolism (1). ATP-sensitive K+ (K(ATP)) channels in the plasma membrane are closed by ATP and opened by ADP, so the increase in ATP/ADP that results from glucose metabolism decreases the hyperpolarizing K(ATP) current (IK(ATP)) thereby depolarizing the cell (3, 4, 5).
In mouse islets, β-cells exhibit a robust bursting pattern over most of the stimulatory range of glucose, characterized by an active phase of electrical impulse generation followed by a silent period during which the cell membrane is hyperpolarized. Sustained electrical oscillations in turn result in oscillations in intracellular Ca2+ concentration: Ca2+ concentration is high during the burst active phase when Ca2+ channels are open and while the cell is spiking and low during silent phases when they are closed and spiking is suppressed (6). Since insulin exocytosis is driven by elevations in intracellular Ca2+ concentration, the oscillations in Ca2+ concentration produce concomitant pulses of insulin secretion (7). A range of bursting patterns have been reported, including slow bursting with periods of around 5 min, consistent with periods reported for pulsatile insulin release, as well as fast bursting with periods of around 30 s or less.
What drives the slow bursting activity of β-cells? One hypothesis is that it results from oscillations in the open/closed state of K(ATP) channels (8, 9, 10, 11). In the simplest form of this hypothesis, reduced K(ATP) conductance causes cells to depolarize and begins the active spiking phase of a burst. The spikes bring in Ca2+, which activates Ca2+ pumps (12). The pumps consume ATP (11), which allows some K(ATP) channels to reopen, terminating the spiking. Intracellular Ca2+ also increases dehydrogenase activity, increasing the production rate of ATP (13). The oscillations in ATP/ADP that have been observed in MIN6 β-cells (14) and in β-cells in intact islets are indeed consistent with this model (14,15). (For a discussion of how oscillations in individual β-cells are coordinated by gap junctions see (16, 17, 18, 19, 20).)
However, even if bursting is driven by other mechanisms, changes in intracellular Ca2+ would affect ATP hydrolysis and dehydrogenase activity so still produce oscillations in ATP/ADP. It is therefore hard to differentiate between cause and effect. Other mechanisms for electrical bursting have also been proposed, including cyclic activation of Ca2+-activated K+ (K(Ca)) channels (21), current due to the activity of electrogenic ion pumps in the plasma membrane (22,23), or a combination of various channels, pumps, and transporters (24). See (25) for a review of models for bursting in β-cells. The difficulty of identifying the key mechanism underlying bursting is that all of these and other factors are known to oscillate in β-cells and may therefore be correlated with bursting activity.
In principle, one could block one of these potential mediators, such as the K(ATP) channels, to determine if this interferes with the bursting rhythm. However, this may yield a misleading result due to the complexity of the system. For example, although blocking K(ATP) channels is known to reliably terminate the bursting pattern, blocking these channels removes most of the hyperpolarizing current of the cell, putting the cell into a highly active state. Therefore, the bursting might stop not because K(ATP) channel activity is no longer oscillatory, but because the depolarization that results from channel blockade overwhelms the effects on membrane potential of the true oscillatory mechanism.
We reasoned that what is needed is an approach that does not require artificial manipulation of any of the potential rhythmogenic factors. In this report, we demonstrate using mathematical modeling that monitoring changes in cytosolic ATP/ADP in response to changing glucose can determine whether K(ATP) channel activity drives bursting in β-cells. Specifically, we demonstrate that if oscillations in K(ATP) conductance are responsible for starting and stopping bursts of electrical activity, then increases in glucose should have little or no effect on the mean, peaks, or nadirs of ATP/ADP oscillations, provided that the cell is bursting. On the other hand, if another mechanism drives bursting, such as K(Ca) channel current, then we predict that the mean, peaks, and nadirs of ATP/ADP will increase with glucose rather than staying constant.
To experimentally test this hypothesis, we monitored the β-cell ATP/ADP ratio using the fluorescent biosensor Perceval-HR (26) over a range of glucose concentrations where bursting oscillations are observed. We also used the biosensor to examine the impact of interventions that separately increase ATP consumption or production, since ATP/ADP reflects both processes. Overall, we show that, contrary to intuition, mean, peak, and nadir ATP/ADP levels are nearly constant over the range of glucose where islet β-cells exhibit bursting. With the aid of mathematical modeling, we interpret this as direct evidence that slow bursting electrical oscillations in mouse islet β-cells are driven by activity-dependent oscillations in the open/closed state of K(ATP) channels.
Materials and methods
Mathematical model
The invariance of ATP/ADP peak, nadir, and mean values with changes in the stimulatory glucose concentration is, as we demonstrate later, a property of a system in which the bursting electrical activity requires oscillations in K(ATP) current that are driven by electrical activity-dependent changes in ATP/ADP, i.e., changes in the current that are due to the intracellular Ca2+ level, which is high when the cell is in a burst active phase and low when in a silent phase. To demonstrate this, we use two mathematical models: a simple mathematical model called the phantom bursting model (PBM) (27), which contains a variable for the nucleotide ratio and a K(ATP) current, among other currents, and a more complex one called the integrated oscillator model (IOM) that is described in detail in (28) and in the Supporting material. This model has similar electrical and Ca2+ components, but more realistic K(ATP) current and a more detailed description of the ATP dynamics that allows for intrinsic glycolytic oscillations.
Here we give a brief description of the elements of the PBM, which is employed in the geometric demonstration for the mechanism underlying the ATP/ADP invariance phenomenon. Fig. 1 provides a visualization of the PBM. The β-cell membrane potential is described by
| (1) |
where is an inward Ca2+ current, is a delayed rectifying outward K+ current, is a Ca2+-activated K+ current, is an ATP-sensitive K+ current, and is the membrane capacitance. Activation of the Ca2+ current is assumed to be instantaneous with changes in voltage . The activation variable for the delayed rectifier, , is described by the first-order rate equation
| (2) |
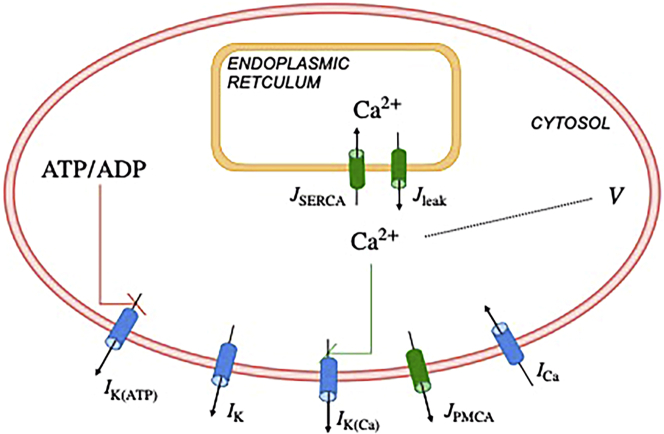
Figure 1.
Illustration of the phantom bursting model (PBM). The model contains modules for electrical activity and Ca2+ dynamics, and a variable for the nucleotide ratio ATP/ADP. : currents, : fluxes. K(ATP): ATP-sensitive K+ channels. K: delayed rectifier K+ channels. K(Ca): Ca2+-activated K+ channels. PMCA: plasma membrane Ca2+ ATPase. Ca: V-dependent Ca2+ current. SERCA: sarcoplasmic endoplasmic reticulum Ca2+ pumps. The red and green lines represent negative and positive feedback, respectively. To see this figure in color, go online.
The steady-state activation functions for the Ca2+ and delayed rectifier K+ channels, respectively, are
| (3) |
| (4) |
The K(Ca) channels are gated by the free cytosolic Ca2+, with concentration . This concentration is increased by Ca2+ entering the cell through Ca2+ channels, and by Ca2+ entering the cytosol from the endoplasmic reticulum (ER). The concentration is decreased by Ca2+ extrusion from the cell by plasma membrane Ca2+ ATPase pumps (PMCA) and transported into the ER by sarcoplasmic endoplasmic reticulum Ca2+ pumps. Thus, the cytosolic Ca2+ changes in time according to
| (5) |
where is the fraction of cytosolic Ca2+ that is free, and the membrane and ER Ca2+ fluxes are
| (6) |
| (7) |
where is a parameter, the flux of Ca2+ through the PMCA pumps () is
| (8) |
with parameter , and the leak of Ca2+ out of the ER () and pumping of Ca2+ into the ER through sarcoplasmic endoplasmic reticulum Ca2+ pumps () are
| (9) |
| (10) |
where and are parameters. The free Ca2+ concentration in the ER, , changes in time according to
| (11) |
where is the fraction of free Ca2+ in the ER, and are the volumes of the cytosol and ER, respectively.
The K(ATP) conductance is assumed to be increased in proportion to the ratio of the nucleotides ADP and ATP, a simplifying assumption but adequate for our purposes. In the model, the ratio changes in time according to
| (12) |
where the steady-state function is an increasing sigmoid function of ,
| (13) |
with parameters and sa. We interpret this equation as representing the increase of ATP hydrolysis with calcium. The function r depends on the blood glucose concentration, G:
| (14) |
In figures, we typically plot the ratio .
Finally, the ionic currents are as follows:
| (15) |
| (16) |
| (17) |
| (18) |
with . The values used for the conductance parameters, and all other parameters, are given in Table 1. The full set of equations for the IOM is given in the Supporting material. Computer codes for both the PBM and the IOM are available for free download from www.math.fsu.edu/∼bertram/software/islet.
Table 1.
Parameter values used in the model
| pS | pS | pS | pS |
|---|---|---|---|
| mV | mV | fF | fA−1 μM ms−1 |
| ms | ms−1 | ||
| μM | mV | mV | mV |
| mV | ms−1 | ms−1 | ms−1 |
| μM | ms | ||
Experimental methods
Pancreatic islet isolation
Male Swiss-Webster mice (25–30 g) were euthanized in accord with the policies of the University of Michigan Institutional Animal Care and Use Committee. The pancreatic bile duct was cannulated, allowing the pancreas to be inflated using a solution containing collagenase P (Roche Diagnostics, Indianapolis, IN). The pancreas was then isolated from the animal and digested further, allowing the islets to be freed from acinar tissue pancreas and hand-picked, as described in (15). Individual islets were then transferred into RPMI1640 culture media supplemented with fetal bovine serum (10%), glutamine, and penicillin/streptomycin. Islets were kept in culture in an air/CO2 incubator at 37°C for 3 days (15).
Heterologous expression of the ATP/ADP reporter gene Perceval-HR and live cell imaging
A replication-deficient adenovirus was used to express the Perceval-HR biosensor into pancreatic islet β-cells under the control of the rat insulin promoter to limit expression to β-cells (15). Islets were placed in a glass-bottomed chamber (54 μL volume) (Warner Instruments/Harvard Bioscience, Holliston, MA) on an Olympus IX71 inverted microscope equipped with a 20X/0.8 N.A. objective (Olympus, Melville, NY). The chamber was perifused at 0.3 mL/min and temperature was maintained at 33°C using an inline solution and chamber heaters (Warner Instruments/Harvard Bioscience, Holliston, MA). Excitation light was provided by a TILL Polychrome V monochromator (F.E.I., Munich, Germany). Excitation (x) or emission (m) filters (Chroma Technology Corporation, Bellows Falls, VT) were used in combination with a 510lpxrxt dichroic mirror as follows: 400/20x, 490/20x, and 535/30m. Fluorescence emission was collected using a QuantEM:512SC camera (PhotoMetrics, Tucson, AZ), and excitation light was repeated every 6 s. A single region of interest was used to quantify the average response of the β-cells using MetaFluor software (Molecular Devices, San Jose, CA).
Analysis of imaging data obtained using Perceval-HR
Statistical analysis was done using MATLAB. A linear mixed-effects model was fit using the MATLAB command fitlme to assess the dependence of the Perceval-HR fluorescence ratio on Time and Experiment. The model formula is as follows: Ratio (493/403) ∼ Time ∗ Experiment + (1|Islet) + (1|Mouse), where the predictor Experiment corresponds to the different experimental protocols as described in Results. A further linear mixed-effects analysis was done to assess the dependence of the mean, amplitude, peak, and nadir values of Perceval-HR oscillations on Glucose in the case of bursting islets. The model formula is Ratio (493/403) ∼ Glucose + (1|Islet) + (1|Mouse). Details of the results obtained are given in the Supporting material.
Results
Mean ATP/ADP increases steadily with glucose concentration in models in which K(ATP) channels are not the primary oscillatory mechanism
It has long been debated whether bursting electrical activity is driven by oscillations in K(ATP) channel activity, or by another mechanism, with K(ATP) current simply setting the threshold for the production of oscillations once the channels are closed by increased ATP/ADP. Ideally, these two mechanisms could be distinguished by clamping K(ATP) conductance to its mean value. If the oscillations in the K(ATP) conductance drive bursting, then clamping the K(ATP) conductance should stop them. On the other hand, if other mechanisms mediate bursting, then preventing oscillations in K(ATP) conductance should not prevent oscillations in Ca2+ or electrical bursting.
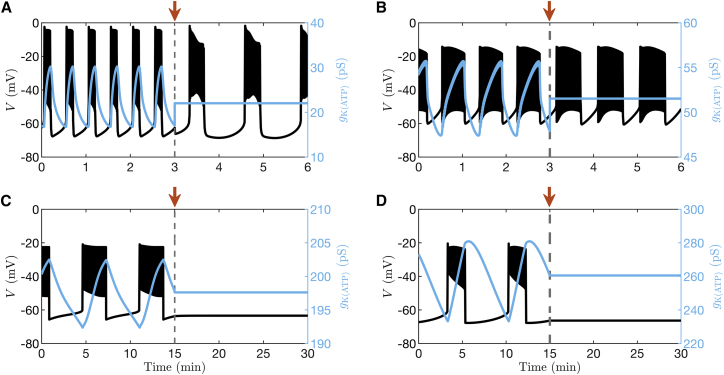
Two recent mathematical models of β-cell electrical activity are examples where bursting occurs because of the combined activity of ion pumps, transporters, and ion channels rather than due to K(ATP) conductance oscillations (24,29). We illustrate in Fig. 2 A and B the predictions of the models of Cha et al. (24) and Fridlyand et al. (29) and demonstrate how electrical oscillations respond to clamping K(ATP) conductance to a fixed level at 3 min (as indicated by the arrow in the figure) for these cases. In both models, bursting electrical activity can be seen to persist even if oscillations in K(ATP) current are halted, highlighting the fact that these oscillations are not essential to bursting; the mean contribution of K(ATP) current to the depolarization observed is sufficient.
Figure 2.
Model simulations in which the K(ATP) conductance is clamped at the arrow. The time courses are generated with (A) the Cha et al. model (24), (B) Fridlyand et al. model (29), (C) the IOM (28), and (D) the PBM (27). The clamped level of K(ATP) conductance is equal to the mean value of the preceding oscillations. To see this figure in color, go online.
In contrast, as shown by the simulations depicted in Fig. 2 C and D using the IOM or the PBM in (27), respectively, bursting is abolished by clamping the K(ATP) conductance at 15 min (indicated by the arrow), demonstrating that in these models oscillations in K(ATP) are essential to the production of bursting.
Although this intervention is straightforward to perform mathematically using a model, it is considerably more difficult to do experimentally in islets. Therefore, we directed our attention to developing a simpler approach that does not rely on invasive interventions. Motivated by the importance of K(ATP) conductance oscillations described above, we instead focus on experimentally monitoring changes in nucleotide concentrations that occur in response to the application of a range of concentrations of glucose to isolated mouse islets.
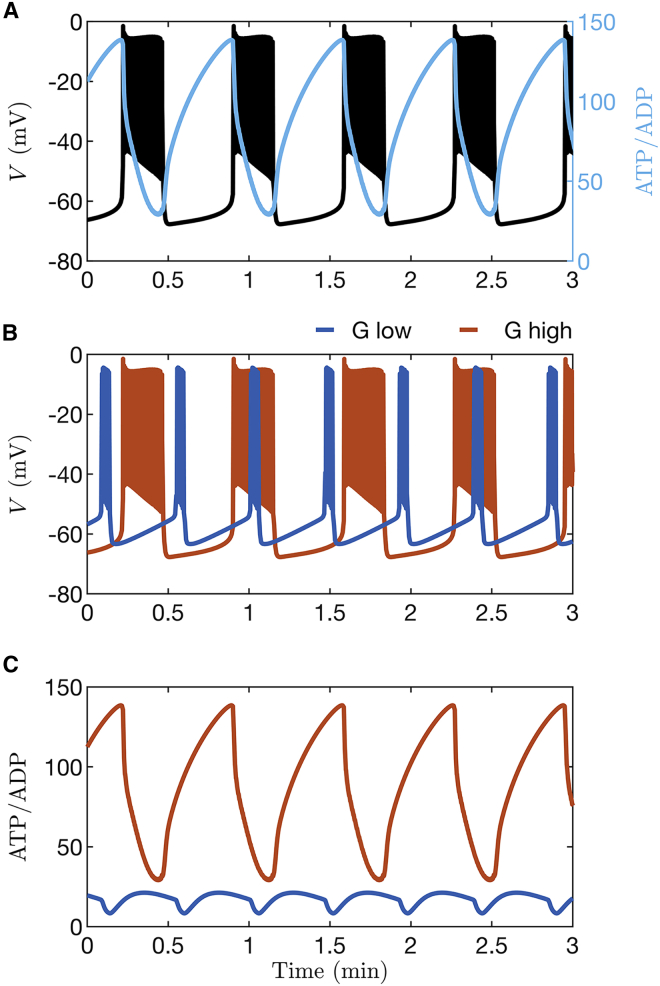
As Cha et al. showed using their model (24), ATP increases and ADP decreases as glucose concentration is increased. To demonstrate what happens when oscillations in K(ATP) channel activity do not drive bursting, we used the Cha model to simulate the responses expected for two different glucose concentrations, both of which result in electrical bursting. Fig. 3 A shows simulated oscillations in membrane potential () with the corresponding time course of ATP/ADP superimposed. ATP/ADP can be observed to oscillate, declining during the burst active phase and rising during its silent phase, as has been observed experimentally (14,15). Fig. 3 B and C show instead membrane potential and ATP/ADP oscillations obtained with two levels of glucose, with only traces shown (3 B) or ATP/ADP (3 C). Fig. 3 B shows that the duty cycle (the ratio of the active phase duration to the sum of the active and silent phase durations) is increased at the higher glucose concentration relative to the lower one, in agreement with experimental studies (30). Further, the ATP/ADP ratio is demonstrably larger at the higher versus the lower glucose concentration, with peak, nadir, and mean levels all increasing with increased glucose (Fig. 3 C).
Figure 3.
Time courses generated with the β-cell model from Cha et al. (24). (A) Bursting electrical activity with the ATP/ADP ratio superimposed. (B) Comparison of bursting at a lower glucose level (blue) and a higher level (orange). (C) The ratio of ATP to ADP increases when the glucose concentration is increased. For all panels, and 11 for low and high stimulatory glucose, respectively. To see this figure in color, go online.
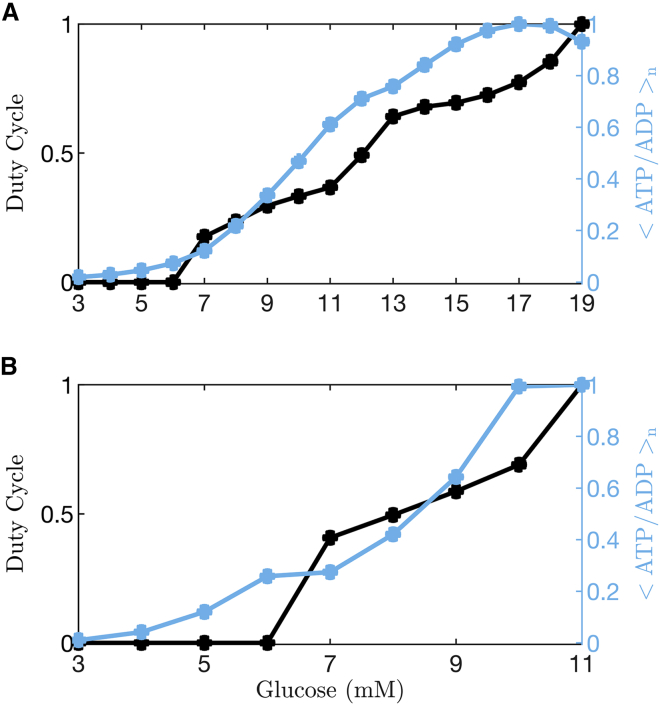
The responses to glucose concentration as simulated using the Cha et al. (24) and Fridlyand et al. (29) models are summarized in Fig. 4. Here, both the duty cycle and the mean ATP/ADP ratio normalized to its largest value (<ATP/ADP > n) are shown for glucose levels where the model cell is either silent (the lowest levels), bursting, or spiking tonically (the highest level). A duty cycle of 0 indicates that the model cell is silent, whereas a value of 1 means that it is tonically spiking. Values between 0 and 1 are obtained when the cell is bursting. In the case of bursting, mean ATP/ADP is computed over an entire burst period (the active plus silent phases).
Figure 4.
Quantification of duty cycle and normalized free ATP/ADP over a range of glucose levels. When the model cell is bursting, the mean value of ATP/ADP, <ATP/ADP>, is determined over one entire burst period (active phase plus silent phase). The normalization is performed by dividing <ATP/ADP > by its maximum over the full range of glucose concentrations. (A) Data from simulations of the Cha et al. model (24) show a monotonic increase in the normalized mean ATP/ADP level, <ATP/ADP > n, as the glucose level is increased, with a dip to a slightly lower level at the last data point at which the cell enters a tonic spiking state. (B) Data from simulations of the Fridlyand et al. model (29) show a similar increase in <ATP/ADP > n as the glucose concentration is increased and the cell is bursting, with a slight drop when the cell enters a tonic spiking state. To see this figure in color, go online.
In simulations performed using either model, <ATP/ADP > n increases at substimulatory glucose levels, when the model cell is silent, as has been shown experimentally (31). The rate of increase in ATP/ADP is accelerated when the model cell enters the bursting state (e.g., duty cycle >0), and <ATP/ADP > n continues to increase with glucose concentration at levels where the cell is bursting. Only at the highest glucose level, when the model cell enters a tonic spiking state, does < ATP/ADP > n decline slightly, due to the increased ATP hydrolysis that drives Ca2+ pumping. Overall, simulations carried out using either of these models predict a nearly monotonic increase in <ATP/ADP > n should be observed as glucose is increased, and the model cell transitions from a quiescent electrical state to bursting states with progressively increasing duty cycle. This behavior is predicted for bursting that is predominantly driven by processes other than oscillations in K(ATP) current (e.g., models where bursting persists despite clamping K(ATP) conductance to a constant value, as in Fig. 2 A and B).
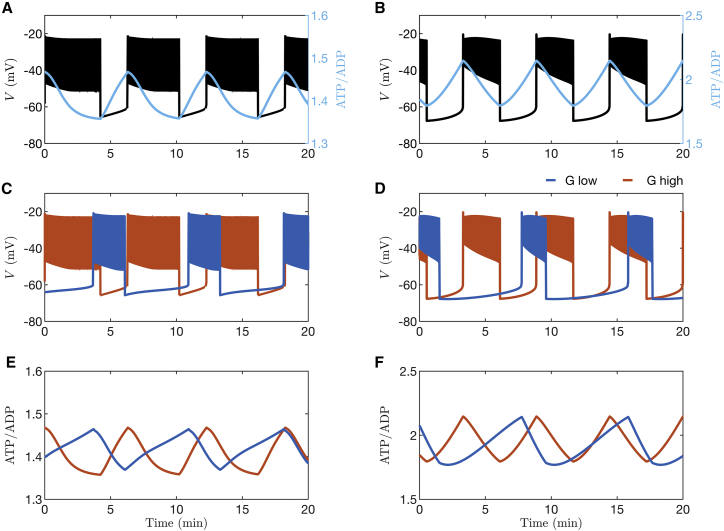
Invariance in mean ATP/ADP ratio when oscillations in K(ATP) current drive bursting
We next wished to determine how ATP/ADP varies with glucose when oscillations in K(ATP) conductance drive islet bursting. To do so, we examined responses to changing glucose concentration using two mathematical models in which oscillations in K(ATP) conductance mechanistically drive bursting. Fig. 5 shows the counterpart of Fig. 3 for the IOM (left panels) and for the PBM (right panels). In both models, the peak in ATP/ADP occurs at the beginning of the active phase, and its nadir occurs at the end of the active phase (Fig. 5 A and B), as is also seen using the model of Cha et al. The middle panels of the figure show the bursting patterns ( is depicted) produced in response to two levels of glucose. The burst properties change as glucose is raised; the active phases become longer, and the silent phase shorter, resulting in a larger duty cycle at higher glucose. Also, the ATP/ADP ratio rises faster in the silent phase and declines more slowly in the active phase when the glucose level is higher. This is a necessary consequence of the increase in plateau fraction, provided that the peak ATP/ADP value occurs at the start of the active phase and the nadir occurs at or near the end. That is the prediction of the IOM and the PBM (Fig. 5), but not consistently of the model of Cha et al. (Fig. 3), and is also in agreement with experimental data (14,15). Yet, despite these changes, the peak and nadir levels of ATP/ADP are the same at both glucose levels (Fig. 5 E and F), as is mean ATP/ADP averaged over a burst period. This “ATP/ADP invariance” is in striking contrast with the predictions of the other models, where ATP/ADP rises steadily as glucose concentration is increased (Figs. 3 and 4). In contrast, other aspects of the observed time course do change with glucose, such as the rate of rise and fall of ATP/ADP (Fig. 5 E). The reason for this invariance will be discussed later. The response of the IOM and the PBM models to a range of glucose levels is quantified in Fig. 6. In both these cases, at substimulatory levels of glucose (indicated by the 0 duty cycle), normalized ATP/ADP increases as glucose concentration is increased, as we saw for the other mathematical models (Fig. 4). However, unlike those models, normalized mean ATP/ADP is nearly flat over the range of glucose concentration where the model cell exhibits bursting. When the cell enters a tonic spiking state (duty cycle = 1), <ATP/ADP > n declines, as was seen with the other models. The flat region shows the ATP/ADP invariance property that was illustrated in Fig. 5. The lack of a rise in ATP/ADP when glucose increases may seem counter to expectations, but it results from the fact that in the model, increased production of ATP is balanced by increased consumption over the course of each burst. This is discussed in more detail in a later section.
Figure 5.
Simulations performed with the integrated oscillator model (left panels) and the phantom bursting model (right panels). (A and B) Bursting electrical activity with the ATP/ADP ratio superimposed. (C and D) Comparison of bursting at a lower glucose level (blue) and a higher level (orange). (E and F) Demonstration of invariance in the ATP/ADP peak, nadir, and mean at the two glucose levels. For both left and right panels, and 13 for low and high stimulatory glucose, respectively. To see this figure in color, go online.
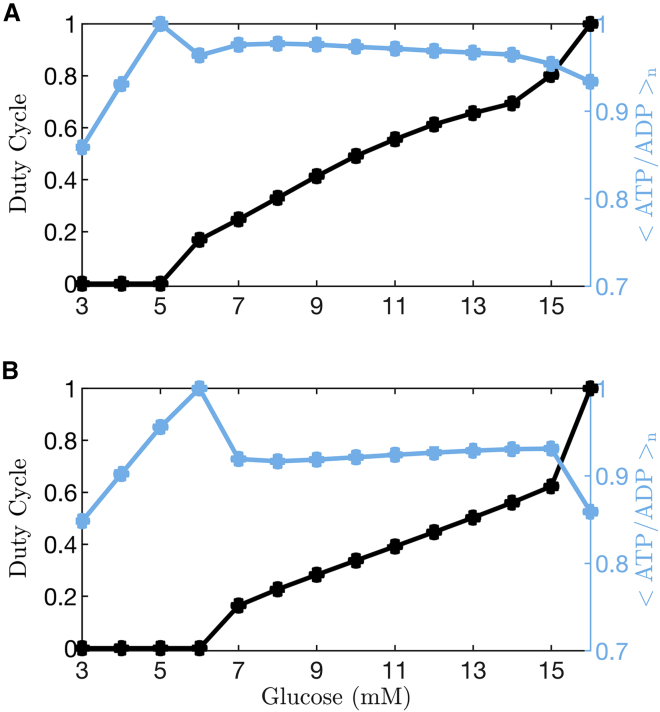
Figure 6.
Quantification of duty cycle and ATP/ADP normalized over the range of values of glucose for the integrated oscillator model (A) and the phantom bursting model (B). The normalized ATP/ADP value < ATP/ADP > n increases with increases in glucose concentration while the model cell is quiescent, but once the cell is busting, < ATP/ADP > n is invariant to changes in glucose concentration. When the cell enters a tonic spiking state, there is a small decline in <ATP/ADP > n due to ATP hydrolysis by Ca2+ pumps. To see this figure in color, go online.
Experimental measurements using a fluorescent biosensor show the ATP/ADP invariance predicted by the models
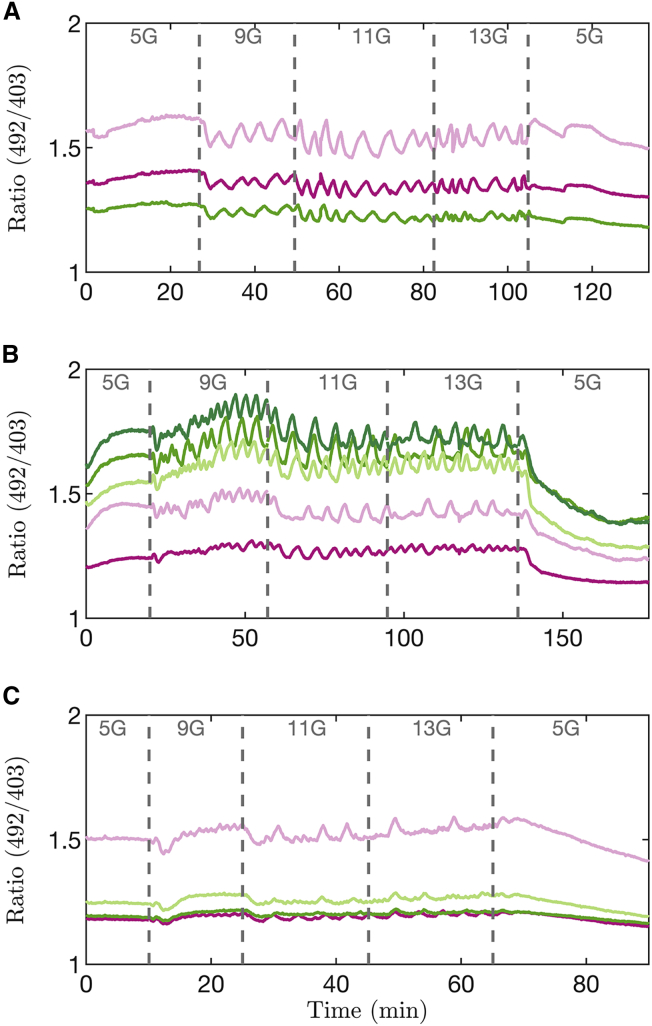
The model simulations shown thus far predict that if bursting is driven by oscillations in K(ATP) current, then the peak, nadir, and mean values of ATP/ADP should be invariant over the range of glucose where bursting occurs. Alternatively, if bursting is driven by another mechanism, then we predict that invariance should not be observed. To test this prediction experimentally, we utilized the fluorescent biosensor Perceval-HR, which reports the ATP/ADP ratio selectively in islet β-cells (26). Islets were incubated in 5 mM glucose before increasing the concentration of glucose in steps, from 5, to 9, 11, 13, and finally back to 5 mM. In Fig. 7, the three panels shown depict Perceval-HR ratio measurements taken from islets of three different mice.
Figure 7.
Measurements of Perceval-HR fluorescence ratio from 12 islets exposed to different glucose concentrations. Each panel corresponds to a different experiment from a Swiss-Webster mouse, and each trace to a different islet in which oscillations were present. For times when islets were bursting (9–13G) we observed no significant deviation of ratio as a function of Time (slope = –5e-5 min−1, p-value = 0.6; see Supporting material). To see this figure in color, go online.
In response to increasing the concentration of glucose from 5 to 9 mM, most islets exhibited an immediate drop of their fluorescence ratio (Fig. 7 A and C). This same drop was observed with the model, as shown in Fig. 6. Our model suggests that this reflects an increase in ATP hydrolysis by the Ca2+ pumps of the plasma and ER membranes. At 5 mM glucose the islet is at rest and Ca2+ influx across the plasma membrane is consequently small. At 9 mM glucose, where islet β-cells are bursting, each burst brings Ca2+ into the cell, which must in turn be pumped out. As a result, the Ca2+ pumps are more activated, and more ATP is correspondingly consumed.
For the three glucose levels where islets are bursting, we observed sawtooth-shaped oscillations in the ATP/ADP ratio. We observed small oscillation-to-oscillation variations in the patterns but not any systematic increase in ATP/ADP as glucose was increased (Experiment [1] in the statistical analysis in Supporting material; slope = –5e-5 min−1; p-value = 0.6). Indeed, the peak, nadir, and mean levels we observed did not significantly increase over the range of glucose levels where bursting is seen, as predicted by models where K(ATP) conductance oscillations drive bursting (change in peak Perceval-HR ratio per mM glucose: −0.00322 mM−1, p-value = 0.0044; nadir: −0.00158 mM−1, p-value = 0.219; mean: −0.00339 mM−1, p-value = 0.055; see Supporting material for details). The amplitude of oscillations also did not change significantly (−0.00164 mM−1, p-value = 0.086). The data were therefore not compatible with the progressive increase in ATP/ADP predicted by the alternative models where bursting is driven by a different mechanism not involving K(ATP) oscillations, such as cyclic activation of K(Ca) channels or oscillatory ion pump activity (Figs. 3 and 4). This agreement with our model prediction supports the hypothesis that the bursting oscillations of mouse islets are driven by oscillations in K(ATP) conductance, and again, our model suggests that increased ATP consumption during bursts prevents ATP/ADP from increasing despite the increase in glucose.
When the glucose level was returned to 5 mM, all islets exhibited a decrease in fluorescence, sometimes following a transient increase (as in Fig. 7 C). In all cases, the fluorescence level was observed to be lower in 5 mM at the end of the protocol than at the beginning. Although more work is required to pin down the specific reason for this, our working hypothesis is that at higher glucose levels, the ER Ca2+ of bursting islets progressively increases due to increased cytosolic Ca2+ concentration driving ER Ca2+ loading. Once glucose is returned to 5 mM, however, Ca2+ drains from the ER into the cytosol, where it is pumped out of the cell by plasma membrane ATPases. This extra pumping action, not present initially when ATP/ADP was low, consumes more ATP, thereby reducing ATP/ADP, and in turn reducing Perceval-HR fluorescence.
ATP/ADP invariance is lost when β-cells are prevented from bursting
In the data shown in Fig. 7 and the simulations produced using models of bursting driven by K(ATP) oscillations (Figs. 5 and 6), invariance in mean ATP/ADP occurs only at glucose concentrations where bursting is occurring. To further test this association, we examined how ATP/ADP changed with glucose over the same concentration range but under conditions that prevented bursting. Thus, we repeated the experimental protocol shown in Fig. 7, but now in the presence of the K(ATP) channel activator diazoxide (Dz, 200 M) and elevated extracellular KCl concentration (30 mM), a procedure widely used to clamp Ca2+ and voltage in β-cells (32). Dz was used to eliminate bursting at stimulatory glucose levels by pharmacologically opening K(ATP) channels, and KCl was used to clamp the Ca2+ concentration to a level comparable to that observed in control islets exposed to stimulatory glucose. With Dz and KCl present at these levels, bursting did not occur.
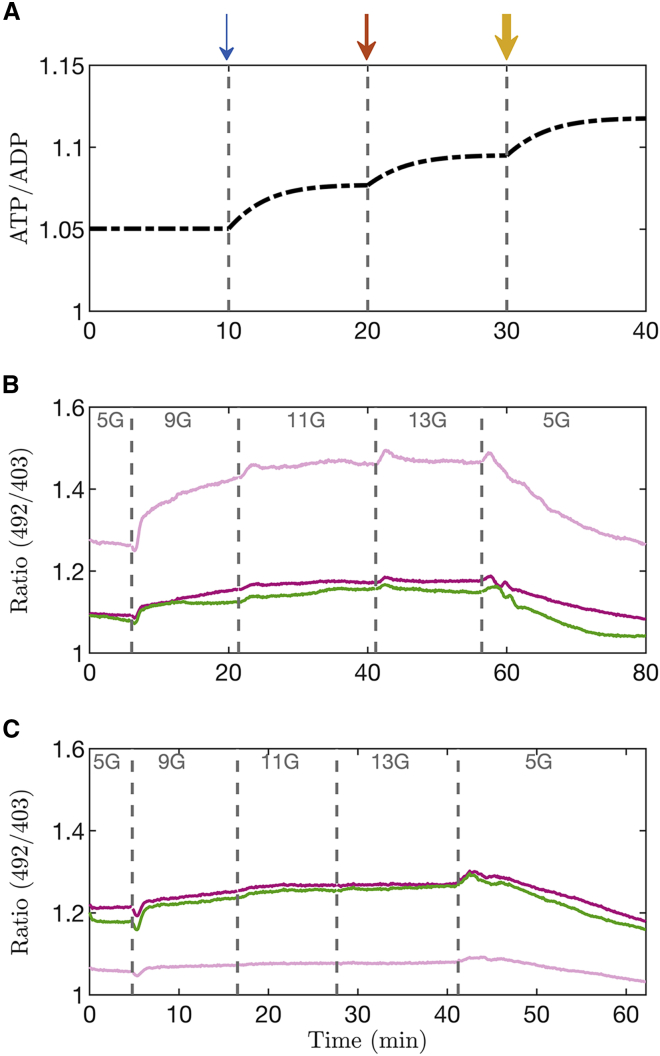
Fig. 8A shows a simulation of this experiment carried out using the PBM. With each increase in glucose concentration (shown by the arrows), ATP/ADP is predicted to increase. This is because whereas ATP production increases with glucose, the presence of Dz and KCl clamp Ca2+ to a fixed level, preventing a countervailing increase in ATP consumption due to bursting and allowing production to dominate.
Figure 8.
(A) Model simulation in which the membrane potential is clamped with diazoxide (Dz) and elevated KCl. Glucose concentration is increased at the arrows, from to 9 , from 9 to 11 , and finally to 13 . The width of each arrow indicates the size of the glucose concentration. (B and C) Two experiments in which islets were exposed to Dz (200 μM) and KCl (30 mM) and in which glucose was increased from 5 mM to higher levels, as indicated, before being returned to 5 mM. Each trace corresponds to an islet and is representative of the protocol applied to 21 islets isolated from two different Swiss-Webster mice from six different sets of recording sessions. During the time interval where glucose concentrations were increased, we observed a significant positive slope in ratio versus time (slope = 0.0021 min−1; p-value < 0.001). To see this figure in color, go online.
This was tested experimentally using Perceval-HR to measure ATP/ADP (Fig. 8 B and C). When the glucose concentration was increased from 5 to 9 mM in the presence of 200 M Dz, the large drop of the florescence ratio typically seen (see Fig. 7) was no longer present. Instead, the ratio can be seen to rise in this case. As the glucose level was increased further, the ratio continued to increase (Experiment [2] in the statistical analysis in Supporting material; slope = 0.0021 min−1; p-value < 0.001). This monotonic increase confirmed the prediction of the model. Our interpretation is that the increase in ATP production was not offset by an increase in ATP consumption (as when islets are bursting) due to the clamping of cytosolic Ca2+ and thus a constant level of ATP consumption.
ATP/ADP declines when ATP consumption is increased
To test whether increasing ATP consumption while keeping production constant causes ATP/ADP to decrease, Dz was again used to inhibit electrical bursting, but this time the glucose level was kept constant (5 mM), and we sequentially increased the extracellular KCl concentration instead to stimulate Ca2+ entry. A model simulation of this experiment is shown in Fig. 9 A, where the K+ Nernst potential was increased at the time points denoted by the arrows, simulating the effects of stepwise increases in KCl concentration. The result of increasing is to depolarize the cell membrane, opening Ca2+ channels and bringing more Ca2+ into the cell. This Ca2+ must then be pumped out, and the increased hydrolysis of ATP needed to power the Ca2+ pumps to do this results in a decline in ATP/ADP.
Figure 9.
(A) Model simulation in which the membrane potential is clamped with diazoxide (Dz) and low glucose , and application of KCl was simulated by changing the K+ Nernst potential. At the first arrow , at the second , and at the third . (B) Experiment in which islets were exposed to Dz (200 M) and 5 mM glucose, and in which the KCl concentration was increased in steps, as indicated, before being returned to 5 mM. Each trace corresponds to an islet and is representative of the protocol applied to 22 islets isolated from four different Swiss-Webster mice from six different sets of recording sessions. During the time interval where KCl concentrations were increased, we observed a significant positive slope in Ratio versus Time (slope = −0.0033 min−1; p-value < 0.001). To see this figure in color, go online.
To test this prediction experimentally, islets were exposed to Dz and to increasing levels of KCl, with glucose held constant at 5 mM (Fig. 9 B). In each of the islets, an increase in KCl concentration resulted in a corresponding drop in Perceval-HR fluorescence. Thus, depolarizing the cell and increasing Ca2+ influx resulted in a net drop in ATP/ADP (Experiment [3] in the statistical analysis in Supporting material; slope = −0.0033 min−1; p-value < 0.001), as predicted by the model. Our interpretation here is that increased ATP hydrolysis is necessary to power Ca2+ pumping due to the presence of KCl (11), increasing ATP demand.
A mechanism for the ATP/ADP invariance seen when bursting is driven by K(ATP) conductance
Why is the mean ATP/ADP level invariant over the range of glucose levels at which the cell is bursting when the bursting is driven by K(ATP) current oscillations? The previous section suggests that this happens because the production and consumption of ATP by the cell are balanced during each oscillation cycle, but not when oscillations are absent.
To understand this in greater depth, we used a mathematical approach called fast-slow analysis, applied to the PBM used to demonstrate invariance in Figs. 5 B and 6 B. In fast-slow analysis, first introduced to the analysis of β-cell bursting by Rinzel (33,34), model variables are partitioned into those that change rapidly and those that change slowly during bursting. The subsystem of fast variables is then analyzed while treating the slow variables as slowly varying parameters. In our case, membrane potential (), the activation of delayed rectifier K+ channels (), and free cytosolic Ca2+ concentration () are all fast variables. The Ca2+ concentration of the ER () and the ATP/ADP ratio () are slow variables. The long-term behavior of the three-dimensional fast subsystem is characterized as a bifurcation diagram, as shown in Fig. 10. Here, the slow variable is fixed at the value it takes on at the beginning of a burst active phase to focus on the more important changes in ATP/ADP. At each value of ATP/ADP the long-term behavior of the fast subsystem is shown, using as a readout.
Figure 10.
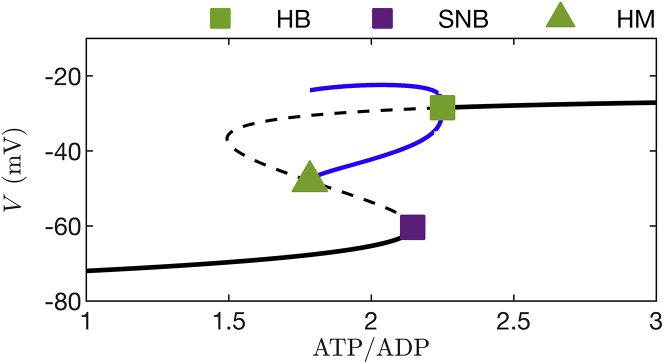
Bifurcation diagram of the fast subsystem (, , and ) of the model used in Figs. 5B and 6B. The slow variable is held fixed at the value it takes on at the beginning of a burst active phase, μM. The maximal K(Ca) conductance parameter is 10 pS. The black curves represent resting or stationary solutions, solid portions represent stable solutions, and dashed portions represent unstable solutions. The two blue curves represent periodic tonic spiking solutions, points on the bottom curve are spike minima, and points on the top curve are spike maxima. There are three bifurcation points: HB = Hopf bifurcation from which the periodic branch emerges, SNB = saddle-node bifurcation where stable and unstable stationary solutions coalesce, and HM = homoclinic bifurcation. To see this figure in color, go online.
At low values of ATP/ADP, K(ATP) channels are largely activated, providing hyperpolarizing current that pins the cell to a negative resting state, near −70 mV. This is illustrated by the left portion of Fig. 10; each point on the solid black curve represents the resting value at the corresponding value of ATP/ADP. At the other extreme, when ATP/ADP is large, the K(ATP) channels are mostly closed, which greatly reduces the magnitude of the hyperpolarizing current.
This puts the model cell into another resting state, but this time at a voltage near −30 mV. This is the case shown in the right portion of Fig. 10, where again the solid black curve is a curve of resting or “stationary” states. Between these extremes, the fast subsystem has two co-existing stable behaviors. One is a hyperpolarized steady state (points on the bottom solid black curve), and the other is a periodic solution that corresponds to the spikes during a burst. This periodic solution reflects spiking, with the minimum voltage of the action potential shown as a point on the bottom blue curve in Fig. 10, and the maximum voltage shown as a point in the top blue curve.
Thus, for any fixed value of ATP/ADP between the green triangle (a homoclinic bifurcation, HM) and the green square markers (a Hopf bifurcation, HB), the fast subsystem can produce spiking. However, between the green triangle and the purple square (a saddle-node bifurcation, SNB), the fast subsystem can also be quiescent. The system is therefore bistable over this parameter interval. The dashed curves in the figure represent unstable equilibria, where the system cannot rest but that influence its behavior.
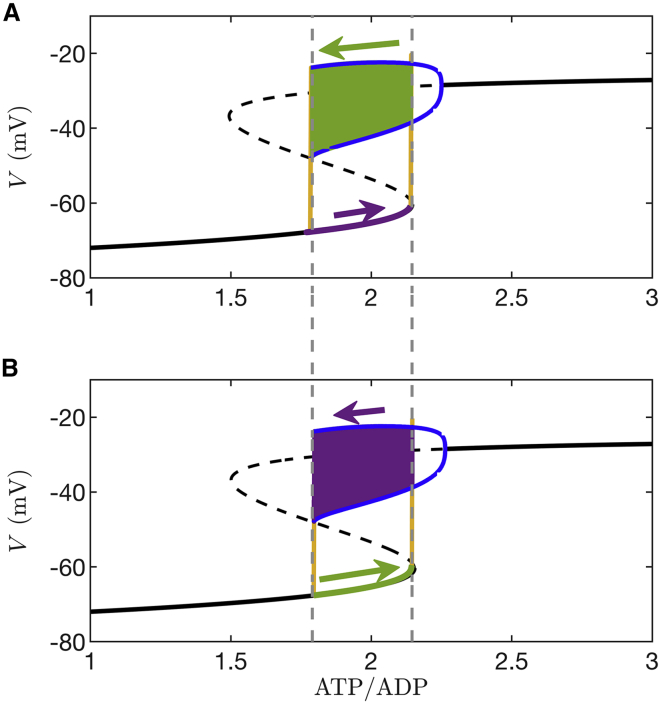
The next step in the fast-slow analysis is to superimpose the bursting trajectory onto the fast subsystem bifurcation diagram, as is shown in Fig. 11. During the start of the silent phase (Fig. 11 A), the system trajectory (purple) moves from left to right along the bottom stationary branch. The left-to-right motion occurs because the Ca2+ concentration is low, and little ATP hydrolysis is needed to power the Ca2+ pumps, so ATP/ADP increases due to glucose metabolism (this is also observed in Fig. 5 A). Once the trajectory reaches the rightmost dashed vertical line, which indicates the end of the lower stationary branch, it rapidly moves to the spiking branch, starting a burst active phase (green). The subsequent spiking that ensues brings Ca2+ into the cell, and ATP is consumed as Ca2+ pumps work to remove it. As a result, ATP/ADP declines and the trajectory moves leftward along the periodic branch until its termination point (the leftmost dashed vertical line). From here the trajectory returns to the bottom stationary branch, ending the active phase and starting the next silent phase.
Figure 11.
ATP/ADP invariance explained through a fast-slow analysis. The arrows indicate direction and relative magnitude of motion. (A) The burst trajectory is projected into the plane of the ATP/ADP and variables. The silent-to-active transition (rightmost dashed vertical line) occurs at the knee of the s-shaped bifurcation diagram (the saddle-node bifurcation), whereas the active-to-silent transition (leftmost dashed vertical line) occurs at the termination of the periodic spiking branch (the homoclinic bifurcation). The glucose concentration is . The color coding is purple = slow motion, green = fast motion, and yellow = very fast motion. (B) When the glucose level is increased to the burst trajectory covers the same path along the fast subsystem bifurcation diagram. For this reason, the peak, nadir, and mean values of ATP/ADP are the same at both glucose levels. The only difference is the speed at which the trajectory moves through the silent phase and the active phase of the burst. In both (A) and (B), pS. To see this figure in color, go online.
The peak ATP/ADP during bursting is the value at the silent-to-active phase transition (the rightmost dashed curve). Here, the conductance of K(ATP) current (; Eq. 18) is sufficiently small that the cell escapes from the resting state and begins spiking. The nadir of ATP/ADP is the value at which the active-to-silent transition occurs (the leftmost dashed curve). Here, is so large that the hyperpolarizing K(ATP) current stops the cell from spiking. These critical values are the same for any glucose level for which the cell bursts because it always takes the same amount of K(ATP) conductance to start or stop a burst active phase. The only thing that changes when the glucose level is changed is the rate at which ATP/ADP changes, i.e., the rate at which the trajectory travels rightward along the lower stationary branch (due to net ATP production) or leftward along the upper spiking branch (due to net ATP utilization). At lower glucose levels with lower ATP synthesis, the trajectory moves slowly (color coded as purple with short purple arrow) along the bottom stationary branch and rapidly (color coded as green with long arrow) along the spiking branch, so the duty cycle is near 0. At higher glucose levels with greater ATP synthesis, the trajectory moves rapidly along the stationary branch and slowly along the spiking branch, so the duty cycle is near 1. However, the peak and nadir levels of ATP/ADP, as well as mean ATP/ADP, are all invariant since the amount of K(ATP) conductance needed to start or stop the burst active phase is always the same (assuming that glucose has no direct effect on ion channels). This is demonstrated in Fig. 11 B, which shows the fast subsystem bifurcation diagram and the superimposed burst trajectory at a higher glucose level. This panel looks similar to panel A. All that has changed is how rapidly the trajectory moves along portions of the bifurcation diagram. Motion during the silent phase is fast (green with long arrow), whereas motion during the active phase is slow (purple with short arrow). In this model, as long as the cell is bursting, changes in glucose will have no effect on the ATP/ADP peak, nadir, or mean values. This is the basis for the ATP/ADP invariance property observed in Figs. 5 and 6, and our experimental findings support this mechanism for invariance of mean, peak, and nadir ATP/ADP with changes in the glucose concentration.
ATP/ADP invariance is lost when other currents contribute to drive the bursting
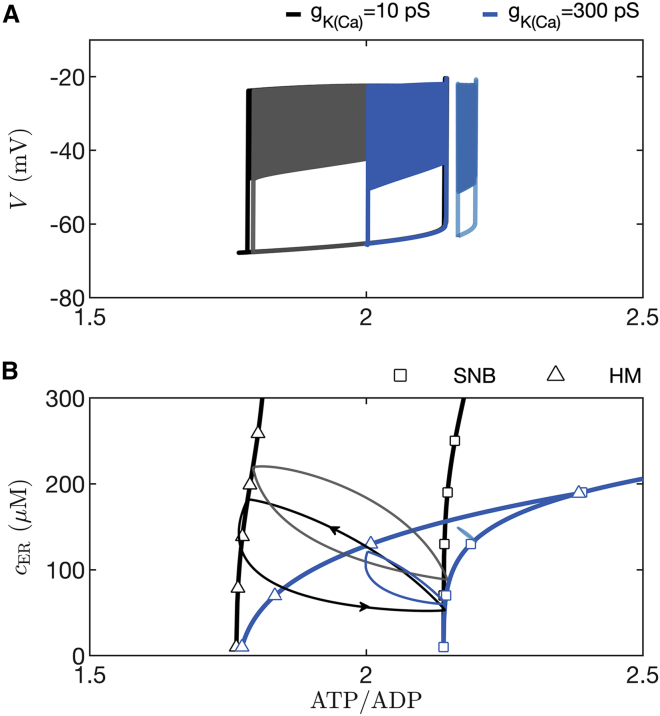
We now consider the case where oscillations in K(ATP) current are not the prime driver of bursting. This is the case in fast bursting, where variations in K(Ca) conductance or some other process initiate and terminate bursts of β-cell spikes (24,27,35,36). In Fig. 4 we showed that in such a case the invariance we observed for the ATP/ADP nadir, peak, and mean values is lost. In Fig. 12 we demonstrate why this is the case. The figure was made using the PBM, which produces slow bursting driven almost entirely by variation in K(ATP) current when the K(Ca) conductance is low, and faster bursting driven primarily by variation in K(Ca) current when its conductance is high (27). The bursting is shown projected into two different planes, both with ATP/ADP on the x axis. In the versus ATP/ADP plane (Fig. 12 A), with a small K(Ca) conductance ( pS), the slow bursting trajectory is almost the same when mM (black curve) and when mM (gray), for the reasons described earlier and in Fig. 11. That is, the SNB and HM bifurcations that start and stop each burst active phase are nearly the same at both glucose levels, so the nadir, peak, and mean ATP/ADP values are invariant to changes in glucose. With the faster bursting (period ∼2 min when mM) produced with a larger K(Ca) conductance ( pS), the projected burst trajectory is very different at the two different glucose concentrations. When the glucose concentration is increased from 8 mM (blue curve) to 13 mM (cyan curve), the burst trajectory is shifted rightward. This rightward shift results in an increase in the nadir, peak, and mean ATP/ADP levels. In this case, the SNB and HM bifurcations that start and stop each burst are right shifted.
Figure 12.
In simulations with the PBM, ATP/ADP invariance to changes in glucose is lost when is increased from 10 pS, which yields slow bursting (period ∼6 min) driven by K(ATP) current, to 300 pS, which yields faster bursting driven mainly by K(Ca) current (period ∼2 min). (A) Simulated slow bursting trajectory with mM (black) and mM (gray) glucose projected into the versus ATP/ADP plane. The projections are nearly identical, in contrast to the case with faster bursting, where the trajectory corresponding to mM (blue) is to the left of that corresponding to mM (cyan). (B) Curves of saddle-node bifurcations (SNB) and homoclinic bifurcations (HM) in the cER versus ATP/ADP plane are identified using squares and triangles, respectively. The black curves correspond to slow bursting, and the blue correspond to faster bursting. Also shown are projections of slow bursting at 8 mM and 13 mM glucose (black and gray loops, respectively) and of the faster bursting at 8 mM and 13 mM glucose (blue and cyan loops, respectively). To see this figure in color, go online.
What is responsible for these differences between the low and high values of ? As described in the previous section, in the case of low , the primary intracellular variable controlling the transitions between active and silent phases is ATP/ADP. However, still contributes but to a very small degree; even large, burst-driven changes in intracellular Ca2+ activate only a small K(Ca) current. On the other hand, when is larger, the K(Ca) current can contribute significantly to burst initiation and termination, with Ca2+ entry and movement in and out of the ER taking on a more central role. The slow filling of the ER slows the rise of during the active phase, and the slow emptying of the ER slows the fall of during the silent phase (27).
The shift in the two bifurcations can be viewed in the plane of cER and the ATP/ADP concentration (Fig. 12 B), as was done in an earlier analysis (37). This plane is used to illustrate the shift in bifurcations because the range of cER values covered during bursting is different for fast and slow bursting, and for different glucose levels. For each value of and the trajectory of cER and ATP/ADP forms a closed loop.
The active phase starts when the trajectory reaches the curve of SNB bifurcations (black squares) and ends when it reaches the curve of HM bifurcations (black triangles). Both bifurcation curves are nearly vertical, indicating that their ATP/ADP values do not vary much with changes in the glucose level. Indeed, at higher glucose levels the burst trajectory is shifted upward (gray loop), but the ATP/ADP values that bound it on the left and right change little. In contrast, during fast bursting, both the HM and SNB curves bend dramatically rightward (blue curves with blue triangles and squares), becoming nearly horizontal. This indicates that an increase in the glucose level dramatically shifts the ATP/ADP levels at which burst active phases start and stop. Indeed, the projected fast burst trajectory is far to the right at a high glucose concentration (cyan curve, mM) compared with the case of a lower glucose concentration (blue curve, mM).
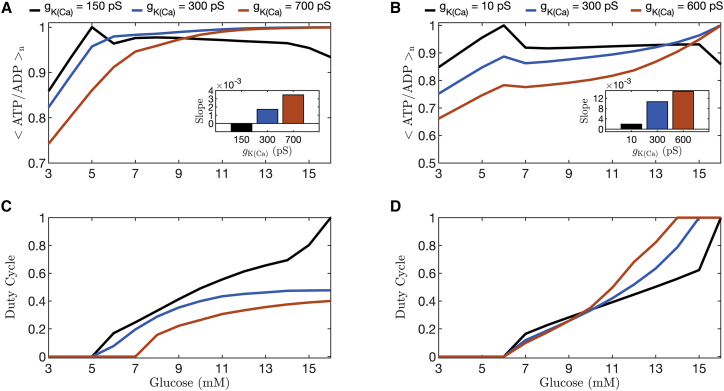
We quantify the progressive loss of invariance that occurs as control of bursting is shifted from K(ATP) current to K(Ca) current in Fig. 13, using the PBM as well as the more complex IOM model. In both models, fast bursting is produced by increasing the value of the K(Ca) conductance (). Fig. 13 shows the duty cycle and <ATP/ADP > n over a range of values of glucose for three values of for the IOM (left panels) and the PBM (right panels). The black curves represent the slow bursting (period ∼6 min) analyzed in Fig. 6, and the orange curves illustrate the results obtained for fast bursting (period 20 s). For each curve, the slope averaged over the range of glucose values that produced bursting was calculated by fitting straight lines using least squares and is plotted as a bar graph in the inset. The slope of the normalized ATP/ADP curves increases with higher values of for both the IOM (panel A) and the PBM (panel B). That is, the invariance in the mean ATP/ADP value with changes in glucose is progressively lost as the role of K(Ca) current in driving bursting is increased.
Figure 13.
Quantification of the mean normalized ATP/ADP ratio (A and B) and duty cycle (C and D) over the range of values of glucose for three different values of (color coded). The curves were generated with the integrated oscillator model (left column) and the phantom bursting model (right column). The black curve shows the results for slow bursting (as in Fig. 6). At 11 mM glucose, the bursting simulated with the IOM (A and C) has a period of ∼6 min for (black curves), min for pS (blue curves), and ∼9 s for (orange curves). The PBM (B and D) has a period of min for (black curves), ∼2 min for (blue curves), and sec for (orange curves). For each curve, the slope averaged over the range of glucose values that produced bursting was calculated using linear least squares fitting and is plotted as a bar graph in the insets to the top panels. To see this figure in color, go online.
Discussion
We have proposed a novel approach for determining whether bursting electrical activity in pancreatic β-cells is driven by activity-dependent oscillations in K(ATP) current. This method requires only that ATP/ADP be monitored in the islet at different glucose concentrations for which the islet cells are bursting. If there is invariance in the peak, nadir, and mean of ATP/ADP during the oscillations, then K(ATP) channels drive bursting. If there is no invariance, then K(ATP) channels alone do not drive bursting but would still help to set the level of depolarization of the membrane and the threshold where oscillations begin. We demonstrated these points using mathematical models (Figs. 3, 4, 5, 6), and verified ATP invariance using the fluorescent probe Perceval-HR to monitor the ATP/ADP level of single islets (Fig. 7). Such invariance does not occur at subthreshold glucose concentrations (14,31) or at stimulatory glucose levels when bursting is prevented by activating K(ATP) channels pharmacologically with diazoxide. Indeed, experiments where we blocked bursting demonstrated that increasing ATP production by increasing the glucose concentration resulted in an increase in the ATP/ADP ratio (Fig. 8), whereas increasing ATP utilization by depolarizing the cell and raising the intracellular Ca2+ level resulted in a decrease in the ATP/ADP ratio (Fig. 9). These data match predictions generated by the PBM and the IOM, but also match predictions from other β-cell models that differ from ours primarily in the mechanism for bursting (22,24).
Although the ATP/ADP invariance property may seem counterintuitive, it has appeared in two previous studies, but its significance and implications for the mechanism of bursting were not explored (Fig. 3 of (14), Fig. 3 of (38)). In (14), the submembrane ATP/ADP level was measured with Perceval fluorescence, and in one islet recording it appears that the mean level was invariant over a glucose range of 9–20 mM (the regions where oscillations were evident). The invariance of peak and nadir values is not as evident, and it appears that the amplitude of the oscillations may grow with the glucose level. However, this was not quantified, and there appears to be significant burst-to-burst heterogeneity in oscillation amplitude for a single glucose level.
It is natural to assume that ATP/ADP should increase when glucose is raised from one level to a higher level, as suggested in a recent review (1), since ATP production increases with glucose. Indeed, several studies showed an increase in islet ATP content or ATP/ADP ratio at higher glucose levels. However, in these studies no comparison was made between ATP/ADP at different glucose levels at which the islet was bursting. For example, in one study most of the data points were obtained at basal glucose (Fig. 3 of (31)) and only one data point (at 10 mM glucose) likely corresponded to a bursting islet. At the basal levels, the ATP concentration increased with the glucose concentration, as predicted in our model simulations with the IOM and the PBM (Fig. 6). In another study, comparison was made at a very low glucose level (3 mM) when the β-cells would be electrically silent and at a very high glucose level (17 mM) when they would most likely be continuously spiking (39). In two other studies, batches of islets were averaged, and it was not determined whether they were silent, bursting, or continuously spiking (Fig. 2 of (11), Fig. 5 of (40)).
During bursting, the Ca2+ level is increased during each active phase, and the increased level results in increased ATP consumption to power Ca2+ pumps (11). With the longer duty cycles associated with higher glucose levels, this consumption is greater, so even though ATP production is higher, so is ATP consumption. When an islet is bursting, these two effects exactly balance over the course of a complete active/silent cycle. We illustrated this using fast-slow analysis (Figs. 10 and 11), where the essence of the argument is that if activity-dependent oscillations in K(ATP) channels alone drive bursting, then a burst active phase starts when ATP/ADP is sufficiently high (so the K(ATP) conductance is sufficiently low) and stops when ATP/ADP is sufficiently low (so the K(ATP) conductance is sufficiently high). The glucose level only determines how fast ATP/ADP rises and falls, which determines the duty cycle, but does not change the ATP/ADP or levels required to start/stop burst active phases.
It is often the case that the details of a mathematical model, such as specific values of parameters chosen, have a large effect on the behavior of the model. Fortunately, that is not the case with the invariance in mean ATP/ADP. Any β-cell model in which the bursting is driven by oscillations in the K(ATP) current would exhibit invariance in the ATP/ADP peaks, nadir, and mean. We demonstrated this using two different models in Figs. 5, 6. Indeed, this universality (illustrated in the fast-slow analysis of Figs. 11 and 12) is precisely why ATP/ADP invariance implies that oscillations in K(ATP) current drives the bursting. In contrast, invariance in the mean ATP/ADP level would not be expected if bursting was driven by a mechanism other than oscillations in K(ATP) conductance (Figs. 3 and 4). In this case, the initiation and termination points of a burst active phase are set largely by conductances that do not depend on ATP/ADP, so no constraint is imposed on the level of K(ATP) conductance, nor consequently the peaks and nadirs of the oscillating ATP/ADP levels.
If a different channel other than K(ATP) drives bursting, and the activation/inactivation variable for that current were a target of glucose, then that variable would exhibit invariance, rather than ATP/ADP. As a demonstration of this, and that history indeed seems to repeat itself, this invariance argument was used by Himmel et al. in 1987 as evidence against Ca2+-activated K+ current (K(Ca) current) as being the mechanism for bursting in β-cells (41). It had been proposed earlier by Chay and Keizer that K(Ca) channels drive bursting and that glucose acts by increasing the Ca2+ pump rate (21,42). That model predicted that cytosolic Ca2+ would rise and fall during bursting in a sawtooth manner, as for the ATP/ADP ratio used here (Fig. 5). Increasing the pump rate indeed increased the duty cycle in the original Chay-Keizer model, as desired, but as pointed out in (41), it had no effect on the mean intracellular Ca2+ concentration. Since an increase in mean intracellular Ca2+ is one factor responsible for triggering glucose-dependent insulin secretion, the Ca2+ invariance clearly conflicted with the data and therefore argued against the assumption that K(Ca) current drives bursting or that the Ca2+ pump rate is glucose-dependent, or both. Both assumptions turned out to be incorrect.
Throughout the article, our main focus has been on “slow bursting”, which is bursting that exhibits a period of several minutes. However, mouse islets also exhibit a faster form of bursting having a period of 30 s or less (43). It is almost certain that the mechanism for this “fast bursting” is different from that of slow bursting, and it is likely driven at least in part by K(Ca) conductance, as originally proposed (21,42). For this fast bursting, then, we showed that increasing glucose from one stimulatory level to another would increase ATP/ADP (Fig. 13). More generally, the models (27,44) predict that as burst period varies from slow to fast, K(Ca) channels would play an increasingly large role, whereas K(ATP) channels become progressively less important. We have found in model simulations that the slope of the ATP/ADP ratio versus glucose curve within the burst increases continuously from 0 as the burst period decreases. Thus, others trying to replicate our findings may obtain a range of possible results, depending on the period of the oscillations in their islet preparations. Similarly, the invariance property would not hold if multiple currents work together to drive bursting if K(ATP) channels play only a minor role, as in (24,29), as we demonstrated in Figs. 3 and 4. Therefore, the ATP/ADP invariance is quite unusual, but also very informative, since it indicates both that for the slowest range of burst periods, K(ATP) current drives bursting and that the target of glucose is the nucleotide ratio.
Conclusion
We used mathematical models to predict that if oscillations in K(ATP) channel conductance drive the slow Ca2+ oscillations of pancreatic β-cells, then ATP/ADP should exhibit invariance over glucose concentrations that support bursting. Our confirmation of this prediction supports the conclusion that K(ATP) channels are the primary drivers of slow Ca2+ oscillations and not merely passive followers of Ca2+-mediated changes in metabolism. The model indicates that this is the case because during oscillations, glucose-induced increases in mean Ca2+ due to increased ATP production are balanced by increased ATP consumption to pump Ca2+. We supported this interpretation experimentally by showing that when glucose is increased but Ca2+ is clamped, ATP/ADP rises, whereas if glucose is fixed and Ca2+ is increased, ATP/ADP falls.
Author contributions
All authors contributed to the conceptualization of the project, the experimental design, and the writing and editing of the manuscript. I.M. performed mathematical simulations and analysis and the statistical analysis, B.M.T. and V.P. carried out experiments, L.G.-G., A.S.S., L.S.S., and R.B. provided resources and supervision, P.A.F., A.S.S., and R.B. provided conceptual advice on the model and experiments and helped with the statistical analysis.
Acknowledgments
The authors acknowledge the excellent technical services of the University of Michigan Vector Core and Advanced Genomics Core. Both were supported by P30DK020572 (MDRC) from the National Institute of Diabetes and Digestive and Kidney Diseases. R.B. was partially supported by NSF grant number DMS 1853342. L.S.S. was partially supported by NIH grant number RO1 DK46409. V.P. was supported by an Upjohn Fellowship. P.F. and A.S. were supported by the Intramural Research Program of the National Institutes of Health (NIDDK). Part of this research was performed when I.M. and L.G.G. were with BCAM, the Basque Center for Applied Mathematics, Bilbao, Spain. I.M. and L.G.G. acknowledge the support of the Basque Government through the BERC 2018-2021 program, and of the Spanish State Research Agency through the BCAM Severo Ochoa excellence accreditation SEV-2017-0718, and grant RTI2018-093416-B-I00 MULTIQUANT. L.G.G. is partially supported by the State of Upper Austria. I.M. acknowledges financial support from the University of Birmingham Dynamic Investment Fund.
Editor: Mark Alber.
Footnotes
Isabella Marinelli and Benjamin M. Thompson contributed equally
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2022.03.015.
Supporting material
References
- 1.Rorsman P., Ashcroft F.M. Pancreatic β-cell electrical activity and insulin secretion: of mice and men. Physiol. Rev. 2018;98:117–214. doi: 10.1152/physrev.00008.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Henquin J.C. Triggering and amplifying pathways of regulation of insulin secretion by glucose. Diabetes. 2000;49:1751–1760. doi: 10.2337/diabetes.49.11.1751. [DOI] [PubMed] [Google Scholar]
- 3.Henquin J.C. ATP-sensitive K+ channels may control glucose-induced electrical activity in pancreatic B-cells. Biochem. Biophys. Res. Commun. 1988;156:769–775. doi: 10.1016/s0006-291x(88)80910-0. [DOI] [PubMed] [Google Scholar]
- 4.Ashcroft F.M., Harrison D.E., Ashcroft S.J.H. Glucose induces closure of single potassium channels in isolated rat pancreatic β-cells. Nature. 1984;312:446–448. doi: 10.1038/312446a0. [DOI] [PubMed] [Google Scholar]
- 5.Cook D.L., Hales N. Intracellular ATP directly blocks K+ channels in pancreatic B-cells. Nature. 1984;311:271–273. doi: 10.1038/311271a0. [DOI] [PubMed] [Google Scholar]
- 6.Nunemaker C.S., Satin L.S. Episodic hormone secretion: a comparison of the basis of pulsatile secretion of insulin and GnRH. Endocrine. 2014;47:49–63. doi: 10.1007/s12020-014-0212-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Satin L.S., Butler P.C., et al. Sherman A.S. Pulsatile insulin secretion, impaired glucose tolerance and type 2 diabetes. Mol. Aspects Med. 2015;42:61–77. doi: 10.1016/j.mam.2015.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bertram R., Satin L.S., Sherman A.S. Closing in on the mechanisms of pulsatile insulin secretion. Diabetes. 2018;67:351–359. doi: 10.2337/dbi17-0004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Keizer J., Magnus G. ATP-sensitive potassium channel and bursting in the pancreatic β cell. Biophys. J. 1989;56:229–242. doi: 10.1016/S0006-3495(89)82669-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Magnus G., Keizer J. Model of β-cell mitochondrial calcium handling and electrical activity. I. Cytoplasmic variables. Am. J. Physiol. 1998;274:C1158–C1173. doi: 10.1152/ajpcell.1998.274.4.C1158. [DOI] [PubMed] [Google Scholar]
- 11.Detimary P., Gilon P., Henquin J.C. Interplay between cytoplasmic Ca2+ and the ATP/ADP ratio: a feedback control mechanism in mouse pancreatic islets. Biochem. J. 1998;333:269–274. doi: 10.1042/bj3330269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chen L., Duk-Su K., Hille B. Dynamics of calcium clearance in mouse pancreatic β-cells. Diabetes. 2003;52:1723–1731. doi: 10.2337/diabetes.52.7.1723. [DOI] [PubMed] [Google Scholar]
- 13.Denton R.M. Regulation of mitochondrial dehydrogenases by calcium ions. Biochim. Biophys. Acta. 2009;1787:1309–1316. doi: 10.1016/j.bbabio.2009.01.005. [DOI] [PubMed] [Google Scholar]
- 14.Li J., Shuai H.Y., et al. Tengholm A. Oscillations of sub-membrane ATP in glucose-stimulated beta cells depend on negative feedback from Ca2+ Diabetologia. 2013;56:1577–1586. doi: 10.1007/s00125-013-2894-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Merrins M.J., Poudel C., et al. Satin L.S. Phase analysis of metabolic oscillations and membrane potential in pancreatic islet β cells. Biophys. J. 2016;110:691–699. doi: 10.1016/j.bpj.2015.12.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tsaneva-Atanasova K., Zimliki C.L., et al. Sherman A. Diffusion of calcium and metabolites in pancreatic islets: killing oscillations with a pitchfork. Biophys. J. 2006;90:3434–3446. doi: 10.1529/biophysj.105.078360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ren J., Sherman A., et al. Satin L.S. Slow oscillations of KATP conductance in mouse pancreatic islets provide support for electrical bursting driven by metabolic oscillations. Am. J. Physiol. 2013;305:E805–E817. doi: 10.1152/ajpendo.00046.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pedersen M.G., Bertram R., Sherman A. Intra- and inter-islet synchronization of metabolically driven insulin secretion. Biophys. J. 2005;89:107–119. doi: 10.1529/biophysj.104.055681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sherman A., Rinzel J., Keizer J. Emergence of organized bursting in clusters of pancreatic β-cells by channel sharing. Biophys. J. 1988;54:411–425. doi: 10.1016/S0006-3495(88)82975-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Benninger R.K.P., Hodson D.J. New understanding of β-cell heterogeneity and in situ islet function. Diabetes. 2018;67:537–547. doi: 10.2337/dbi17-0040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chay T.R., Keizer J. Minimal model for membrane oscillations in the pancreatic β-cell. Biophys. J. 1983;42:181–190. doi: 10.1016/S0006-3495(83)84384-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fridlyand L.E., Tamarina N., Philipson L.H. Modeling of Ca2+ flux in pancreatic β-cells: role of the plasma membrane and intracellular stores. Am. J. Physiol. 2003;285:E138–E154. doi: 10.1152/ajpendo.00194.2002. [DOI] [PubMed] [Google Scholar]
- 23.Fridlyand L.E., Jacobson D.A., et al. Philipson L.H. A model of action potentials and fast Ca2+ dynamics in pancreatic β-cells. Biophys. J. 2009;96:3126–3139. doi: 10.1016/j.bpj.2009.01.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cha C.Y., Nakamura Y., et al. Noma A. Ionic mechanisms and Ca2+ dynamics underlying the glucose response of pancreatic β cells: a simulation study. J. Gen. Physiol. 2011;138:21–37. doi: 10.1085/jgp.201110611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Félix-Martínez G.J., Godínez-Fernández J.R. Mathematical models of electrical activity of the pancreatic β-cell: a physiological review. Islets. 2014;6:e949195. doi: 10.4161/19382014.2014.949195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tantama M., Martínez-François J.R., et al. Yellen G. Imaging energy status in live cells with a fluorescent biosensor of the intracellular ATP-to-ADP ratio. Nat. Commun. 2013;4:2550. doi: 10.1038/ncomms3550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bertram R., Sherman A. A calcium-based phantom bursting model for pancreatic islets. Bull. Math. Biol. 2004;66:1313–1344. doi: 10.1016/j.bulm.2003.12.005. [DOI] [PubMed] [Google Scholar]
- 28.Marinelli I., Parekh V., et al. Satin L.S. Slow oscillations persist in pancreatic beta cells lacking phosphofructokinase M. Biophys. J. 2022;121:692–704. doi: 10.1016/j.bpj.2022.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fridlyand L.E., Ma L., Philipson L.H. Adenine nucleotide regulation in pancreatic β-cells: modeling of ATP/ADP-Ca2+ interactions. Am. J. Physiol. 2005;289:E839–E848. doi: 10.1152/ajpendo.00595.2004. [DOI] [PubMed] [Google Scholar]
- 30.Nunemaker C.S., Bertram R., et al. Satin L.S. Glucose modulates [Ca2+]i oscillations in pancreatic islets via ionic and glycolytic mechanisms. Biophys. J. 2006;91:2082–2096. doi: 10.1529/biophysj.106.087296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ashcroft S.J.H., Weerasinghe L.C.C., Randle P.J. Interrelationship of islet metabolism, adenosine triphosphate content and insulin release. Biochem. J. 1973;132:223–231. doi: 10.1042/bj1320223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gembal M., Gilon P., Henquin J.C. Evidence that glucose can control insulin release independently from its action on ATP-sensitive K+ channels in mouse β cells. J. Clin. Invest. 1992;89:1288–1295. doi: 10.1172/JCI115714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Rinzel J., Lee Y.S. Dissection of a model for neuronal parabolic bursting. J. Math. Biol. 1987;25:653–675. doi: 10.1007/BF00275501. [DOI] [PubMed] [Google Scholar]
- 34.Rinzel J., Ermentrout G.B. In: Methods in Neuronal Modeling: From Synapse to Networks. Koch C., Segev I., editors. MIT Press; 1998. Analysis of neural excitability and oscillations. [Google Scholar]
- 35.Fridlyand L.E., Tamarina N., Philipson L.H. Bursting and calcium oscillations in pancreatic beta-cells: specific pacemakers for specific mechanisms. Am. J. Physiol. 2010;299:E517–E532. doi: 10.1152/ajpendo.00177.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Göpel S.O., Kanno T., et al. Rorsman P. Activation of Ca2+-dependent K+ channels contributes to rhythmic firing of action potentials in mouse pancreatic β cell. J. Gen. Physiol. 1999;114:759–769. doi: 10.1085/jgp.114.6.759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Goel P., Sherman A. The geometry of bursting in the dual oscillator model of pancreatic β-cells. SIAM J. Appl. Dyn. Syst. 2009;8:1664–1693. [Google Scholar]
- 38.Lewandowski S.L., Cardone R.L., et al. Merrins M.J. Pyruvate kinase controls signal strength in the insulin secretory pathway. Cell Metab. 2020;32:736–750. doi: 10.1016/j.cmet.2020.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tarasov A.I., Semplici F., et al. Rutter G.A. The mitochondrial Ca2+ uniporter MCU is essential for glucose-induced ATP increases in pancreatic β-cells. PLoS One. 2012;7:e39722. doi: 10.1371/journal.pone.0039722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Haythorne E., Rohm M., et al. Ashcroft F.M. Diabetes causes marked inhibition of mitochondrial metabolism in pancreatic β-cells. Nat. Comm. 2019;10:2474. doi: 10.1038/s41467-019-10189-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Himmel D.M., Chay T.R. Theoretical studies on the electrical activity of pancreatic β-cells as a function of glucose. Biophys. J. 1987;51:89–107. doi: 10.1016/S0006-3495(87)83314-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Atwater I., Dawson C.M., et al. Rojas E. Biochemistry, Biophysics of the Pancreatic β-Cell. Verlag; 1980. The nature of the oscillatory behaviour in electrical activity for pancreatic β-cell; pp. 100–107. [PubMed] [Google Scholar]
- 43.Nunemaker C.S., Zhang M., et al. Satin L.S. Individual mice can be distinguished by the period of their islet calcium oscillations. Diabetes. 2005;54:3517–3522. doi: 10.2337/diabetes.54.12.3517. [DOI] [PubMed] [Google Scholar]
- 44.McKenna J.P., Bertram R. Fast-slow analysis of the integrated oscillator model for pancreatic β-cells. J. Theor. Biol. 2018;457:1520162. doi: 10.1016/j.jtbi.2018.08.029. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.