Interacting-heads motif explains the X-ray diffraction pattern of relaxed vertebrate skeletal muscle

Abstract

Electron microscopy (EM) shows that myosin heads in thick filaments isolated from striated muscles interact with each other and with the myosin tail under relaxing conditions. This “interacting-heads motif” (IHM) is highly conserved across the animal kingdom and is thought to be the basis of the super-relaxed state. However, a recent X-ray modeling study concludes, contrary to expectation, that the IHM is not present in relaxed intact muscle. We propose that this conclusion results from modeling with a thick filament 3D reconstruction in which the myosin heads have radially collapsed onto the thick filament backbone, not from absence of the IHM. Such radial collapse, by about 3–4 nm, is well established in EM studies of negatively stained myosin filaments, on which the reconstruction was based. We have tested this idea by carrying out similar X-ray modeling and determining the effect of the radial position of the heads on the goodness of fit to the X-ray pattern. We find that, when the IHM is modeled into a thick filament at a radius 3–4 nm greater than that modeled in the recent study, there is good agreement with the X-ray pattern. When the original (collapsed) radial position is used, the fit is poor, in agreement with that study. We show that modeling of the low-angle region of the X-ray pattern is relatively insensitive to the conformation of the myosin heads but very sensitive to their radial distance from the filament axis. We conclude that the IHM is sufficient to explain the X-ray diffraction pattern of intact muscle when placed at the appropriate radius.

Significance

Electron microscopy shows that myosin heads in thick filaments of muscle interact with each other under relaxing conditions. This “interacting-heads motif” (IHM) is conserved across the animal kingdom. However, a recent X-ray modeling study concludes that the IHM is not present in intact muscle. We propose that this results from modeling with a thick filament in which the heads are too close to the filament backbone, not from absence of the IHM. We tested this by carrying out similar X-ray modeling. When the IHM is at a radius 3–4 nm greater than in the recent study, there is good agreement with the X-ray pattern. Thus, the IHM explains the X-ray pattern of muscle when placed at an appropriate radius.

Introduction

The interacting-heads motif (IHM) is a configuration of myosin heads in thick filaments of relaxed muscle (1). It was first discovered by cryoelectron microscopy (cryo-EM) of 2D crystals of myosin molecules in the switched-off state (2,3), and later demonstrated to be present in native thick filaments by cryo-EM of filaments isolated from relaxed tarantula muscle (4,5). The IHM is characterized by the asymmetric interaction of myosin’s two heads with each other and with the myosin tail, switching off the activity of each head. The motif is highly conserved in thick filaments across the animal kingdom (4,6, 7, 8, 9, 10, 11, 12, 13). Similar broad conservation of the IHM, from the earliest animals (sponges) to humans, is also evident in single myosin molecules (14, 15, 16, 17). The high level of conservation of the IHM implies that it plays a key role in muscle physiology. Multiple studies suggest that the inhibition of head activity in the IHM is intimately connected to the super-relaxed state (SRX) of thick filaments (18, 19, 20). Like the IHM, SRX is also widely distributed, being found in smooth, cardiac, and fast and slow skeletal muscles, and in vertebrates as well as invertebrates (19,21, 22, 23, 24, 25). SRX is thought to play a critical role in energy conservation in animals.

Despite the ubiquity of the IHM in isolated thick filaments and molecules demonstrated by electron microscopy (EM), its presence in intact relaxed muscle has recently been questioned (26). Low-angle X-ray diffraction patterns of live or chemically demembranated striated muscle fibers show a series of myosin layer lines, revealing helical organization of the myosin heads in the relaxed state (27, 28, 29, 30, 31, 32). Knupp et al. (26) modeled the X-ray pattern of intact, relaxed bony fish muscle with different thick-filament models, based on previous X-ray (33) and EM (9) studies, to determine which one best explained the X-ray patterns. Fish muscle was chosen because it has a “simple” filament lattice, in which all thick filaments are in rotational register (34). This lattice samples the myosin layer lines, producing peaks whose intensities and positions can be compared with the predictions of different models, generating an overall R-factor (residual factor, a measure of how well model predictions match observed X-ray intensities (29); see section “materials and methods”). Knupp et al. found that a 3D reconstruction based on EM of isolated native vertebrate thick filaments, showing heads in the IHM configuration (9), gave a poor fit to the X-ray pattern (i.e., a high R-factor, 0.54). In contrast, an earlier, X-ray based model, in which there are no head interactions but the heads project to much higher radius (33), fitted much better (R-factor 0.079). The EM reconstruction used in the modeling was based on negatively stained filaments (EMD-2240; (9)), in which the myosin heads are centered at a radius of ∼9.2 nm from the filament axis (see supporting material (1) and Fig. S1). The center of mass (COM) of the heads in the X-ray-based, non-IHM model that gave the better fit (33) was at a radius that we estimate to be ∼13.5 nm (based on Fig. 3 of Knupp et al.). This therefore raises the question: could the difference of fit be related to the different radius of the heads from the filament axis in the two structures rather than to differences in their conformation, as concluded by Knupp et al.? This is important to establish because negative staining is known to cause radial collapse (≥3 nm) of heads onto the surface of thick filaments when compared with unstained cryo-EM reconstructions (8,35). It is therefore likely to give a substantial underestimate of the true radius in situ.

We have carried out an X-ray modeling study to test this possibility, assessing the R-factor of models in which a constant IHM structure is placed at varying radii. We find a similar poor fit to that of Knupp et al. (R-factor 0.59) when using the same IHM reconstruction used by them (9). However, when the IHMs are moved to higher radius to simulate the more likely in situ value, the R-factor drops to ∼0.13, reflecting a relatively good fit of the model to the X-ray data. We conclude that the IHM structure, when placed at a realistic radius, accounts reasonably well for the X-ray diffraction pattern. When we include partial disordering of IHMs at every third crown in the thick filament perturbed zone (6,9) and of heads in the ideal zones, the R-factor improves to 0.047. We have also modeled the X-ray pattern using thick filaments in which the IHMs are represented simply as spheres. These models give good agreement with the X-ray data on the first myosin layer line (M1) when the spheres are placed at an appropriate COM radius of ∼13.5 nm, although the higher-order layer lines are not so well reproduced. We conclude that the IHM is most likely the conformation of the majority of heads in thick filaments in intact, relaxed muscle: it is consistent with the numerous EM studies showing the IHM in thick filaments and myosin molecules across the animal kingdom; it also fits the X-ray data from intact muscle. There is no need to invoke a different structure. We also conclude that, while the observed layer lines are sensitive to head radius, they are relatively insensitive to head configuration and cannot be used to distinguish detailed head arrangements at the relatively low resolution of most X-ray data.

Materials and methods

Muscle sample

Single fibers or bundles of two or three fibers were dissected from the dorsal side of the fin muscle of plaice (Pleuronectes platessa) in relaxing solution and permeabilized as described (36). The relaxing solution contained 100 mM 3-[N-morpholino]-propanesulfonic acid (MOPS), 5 mM ethylene glycol bis-(β-aminoethyl ether) N,N,N′,N′ tetraacetic acid (EGTA), 5 mM MgATP, 2 mM MgCl₂, 80 mM potassium propionate, and 5 mM dithiothreitol (DTT); the ionic strength was 150 mM, pH 7.1, at 20°C (36).

X-ray diffraction

Central segments 3–3.7 mm long of the fibers or bundles were mounted horizontally in the X-ray setup at sarcomere length ∼2.2 μm, controlled by diffraction of light from a He-Ne laser, and kept in the relaxing solution at 0°C–2°C. Just before a 50-ms X-ray exposure, the muscle sample was suspended in an empty, cold, wet, windowless trough at 4°C–5°C and returned to the relaxing solution trough just after the exposure. The use of the windowless trough increased the signal-to-noise ratio by reducing X-ray scattering by windows and solution. Between subsequent exposures, the setup was moved horizontally by 0.2-mm steps to spread radiation damage along the sample. The total sample exposure was up to 0.2 s.

Data (Fig. 1) were collected at ID02 station at European Synchrotron Radiation Facility (ESRF; Grenoble, France), wavelength 0.0995 nm, flux 10¹³ photons/s, using a FReLoN CCD detector operating in 1024 × 1024-pixel mode with a sample-to-detector distance of 2.4 m; the pixel size corresponded to 6.94 × 10⁻⁴ nm⁻¹ in reciprocal space. The beam size on the sample was 240 μm vertically and 400 μm horizontally (full width at half-maximal intensity). The beam stop was placed slightly off the center of the beam so that the sampling of the 10 equatorial reflections on the first myosin layer line was seen on one side of the X-ray diffraction pattern. In addition to the beam stop, a long and narrow attenuator was placed along the equator to absorb some of the brightest diffracted X-rays to avoid detector saturation.

Figure 1.

X-ray diffraction pattern of relaxed, permeabilized plaice muscle. Half-mirrored pattern shows equator (Eq), meridian (Mer), and main myosin layer lines (M1–M6). Numerals 10, 11, 20, and 21 indicate sampling of M1 by equatorial reflections 10, 11, 20, and 21. Beam stop is shifted slightly off center to expose sampling of 10 reflection on right side of M1 layer line.

Data analysis

Diffraction patterns collected from each X-ray exposure were corrected for dark current and spatial distortion of the detector (including a flat-field correction) using software provided by ESRF, then added together and half-mirrored to improve the signal-to-noise ratio using bs freeware written by N.K. (http://muscle.imec.msu.ru/club_eng.htm). The distribution of X-ray intensity along the myosin layer lines was obtained using bs software as described (37). X-ray scattering from the edge of the attenuator that covered the equator caused artificial peaks in the background between the equator and the M1 myosin layer line at the radial positions of the equatorial reflections (Fig. 1). These background peaks were removed during background subtraction to provide an accurate measure of the M1 intensity.

X-ray modeling

The general approach was similar to that described in (37): a 3D atomic model of a thick filament was constructed using the minimal required number of parameters. A 42.9-nm-long repeat of the filament included three crowns of myosin heads, modeled as IHMs using the PDB structure PDB: 3jbh, based on cryo-EM of tarantula filaments (38); other IHM models have essentially the same structure and could also have been used: PDB: 3dtp (an earlier version of PDB: 3jbh, used by Knupp et al.) and PDB: 5tby (a vertebrate cardiac homology model of PDB: 3jbh). In each crown, three IHMs were azimuthally separated from each other by 120° (i.e., the filament had 3-fold rotational symmetry). In an ideal repeat, assumed to occur in the P and D zones (39), IHMs were positioned in a three-stranded, right-handed helix with an axial separation of 14.3 nm and angular shift of 40° between crowns. A perturbed repeat, corresponding to the C zone, was constructed according to the 3D reconstruction of Al-Khayat et al. (9) (see also (6)), where the distances between the crowns were 14.9, 14.8, and 13.2 nm, and the angular shifts were 25°, 35°, and 60°. The atomic model of one unit (three crowns) of perturbed heads was repeated in the axial direction to generate a full-length C zone and then extended beyond that at each end with unperturbed head repeats to produce a P zone and D zone (39). As every third crown of myosin heads in the EM density map of the C zone is thought to be partially disordered (6,9), we also calculated myosin layer line intensities for a structure where two crowns of IHMs are in their known positions in the EM map (9), and the disordered head pairs in the third crown are represented by spheres of 5-nm radius attached at the head-tail junction of PDB: 3jbh. The structure was split at residue 843; the S2 portion remained at atomic resolution, while the COM of the sphere was placed at the same point as the COM of the head pair. The 5-nm radius produces a volume of ∼500 nm³, about double the volume of two myosin heads. The spheres had uniform electron density and the same total scattering power as the pair of heads in PDB: 3jbh; they thus approximate delocalization (disorder) of the head pairs within this volume. For some simulations, instead of using the IHM, all motifs (two heads plus S2) were considered as spheres of radius 5 nm. The COM of each sphere was placed at the same position as that of the corresponding IHM in the perturbed and ideal zones.

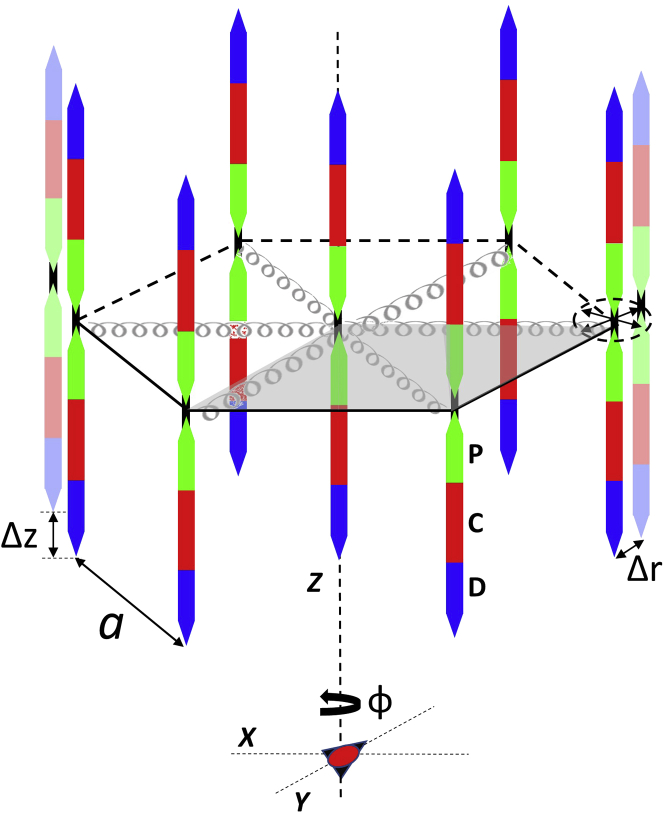
The intensities of myosin layer lines M1–M4 were calculated from the different thick-filament models and compared with those observed experimentally. The Fourier transform F of the heads in a filament is the sum of the Fourier transforms of the P, C, and D zones. If 0 ≤ f ≤ 1 (where f is the fractional length of the perturbed zone), then F = f × F_p + (1 − f) × F_i, where F_p, and F_i are Fourier transforms of a perturbed and an ideal repeat unit, respectively. f was varied in the simulations to determine its impact on the diffraction pattern. The intensity of each layer line was calculated as the azimuthally averaged square of the summed Fourier transforms, F. To calculate the Fourier transform of such a thick filament when placed in the simple filament lattice, the single-filament transform was multiplied by the transform of the lattice, with all filaments assumed to have the same orientation about their long axis (34) (Fig. 2). Five parameters characterized the unit cell: R, the radial position of the COM of an IHM from the myosin filament axis (the same for all IHMs in a crown); a, the length of the side of the unit cell (estimated to be 48.8 nm, based on the spacing of the equatorial X-ray reflections; Fig. 2); φ, the angle of rotation of the filament (Fig. 2), which we define as the angle between the vector from the center of the myosin filament to the COM of an IHM in the first crown and the lattice translation vector from the center of the same thick filament toward the center of a nearest neighbor thick filament; and Δ_r and Δ_z, the radial (in plane) and axial (along the filament axis) disorder of the second kind (40) of the myosin filament lattice, described by standard deviations from the ideal lattice positions of neighboring unit cells in the lattice (Fig. 2). For a single filament, Δ_r and Δ_z were set to infinity.

Figure 2.

Myosin filament lattice in fish muscle (perspective view). Myosin filaments show P, C, and D zones (green, red, and blue, respectively) (39). One unit cell of hexagonal lattice (side a) is shaded in gray. φ is angle of rotation of filament within unit cell; all filaments in simple lattice have same rotation. Springs represent inter-filament connections formed by M-line proteins at center of sarcomere. The deviation of the center of a filament from its ideal position in the lattice is controlled by the stiffness of these connections, causing disorder of the second kind (40), characterized by the standard deviations of the neighboring filaments in a plane perpendicular to, or along, the filament axis (Δr, Δz, respectively); dotted ellipse indicates that Δr can be in any radial direction. To see this figure in color, go online.

Having established the most appropriate values for f, Δ_r, _and Δ_z, an R-factor (a measure of the goodness of fit of the calculated X-ray diffraction pattern to the observed pattern) was calculated, while varying R and φ, according to Equation 2 of Knupp et al. (26,29):

$$R_f=\frac{\sum {\left(I_{obs}-\lambda I_{calc}\right)}^2}{\sum {\left(I_{obs}\right)}^2}$$

where I_obs and I_calc are the observed and calculated X-ray intensities, λ is a scaling factor, and summation is along the off-meridional parts of the M1–M4 myosin layer lines from 0.02 nm⁻¹ to 0.08 nm⁻¹ for M1 and from 0.01 nm⁻¹ to 0.08 nm⁻¹ for M2–M4. We excluded meridional intensities from the fit as they are sensitive to axial disorder and are thought to contain significant contributions from structures other than the myosin heads (41), including MyBP-C (42,43) and possibly titin and the myosin tails; these contributions cannot be disentangled from those of the myosin heads, making these meridional reflections inappropriate for modeling the heads.

Results

X-ray diffraction pattern used for modeling

An X-ray diffraction pattern was obtained from chemically permeabilized plaice (P. platessa) fin muscle in relaxing solution (Fig. 1; section “materials and methods”). The pattern shows myosin layer lines (M1–M6) out to the sixth order based on the 42.9-nm pseudo-helical repeat of the thick filament (27). The majority of the off-meridional intensity (apart from the equator) is on the first layer line (M1), with weaker intensity visible out to the fourth layer line (M4). Due to the “simple” thick filament lattice present in fish muscle, M1 and the other layer lines are sampled at positions corresponding to the 10, 11, 20, and 21 lattice planes of the hexagonal filament lattice (34). The intensity distribution along the layer lines was compared with the intensities calculated for different filament models to determine the effect of changing various parameters of thick filament structure and positioning in the filament lattice (Fig. 2). Following optimization of these parameters (Figs. 3, 4, 5, 6, and 7), the R-factor was calculated as a function of filament rotation and IHM radius, to provide a measure of the goodness of fit, and thus the likely correctness of the final model.

Figure 3.

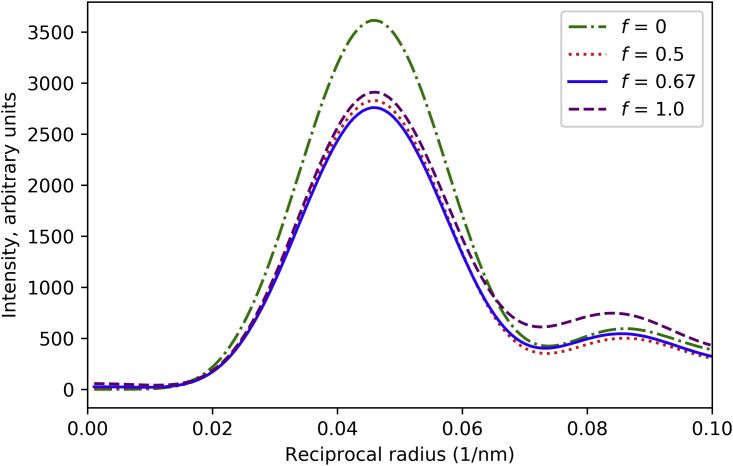
Effect of the fraction of helically perturbed myosin heads on the M1 intensity from a myosin filament. Intensity is strongest with no perturbation (f = 0; all myosin heads organized in ideal helix). With varying numbers of heads lying on a perturbed helix (the arrangement found in the C zone) (6,9), intensities are weaker but similar, and remain in the same position radially. Thus, the perturbation has only a minor effect on the modeling. We used f = 0.67, for subsequent modeling. See also Fig. S2. To see this figure in color, go online.

Figure 4.

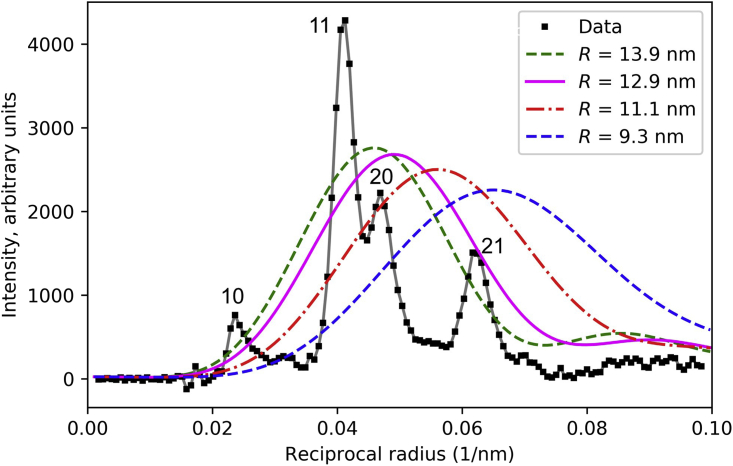
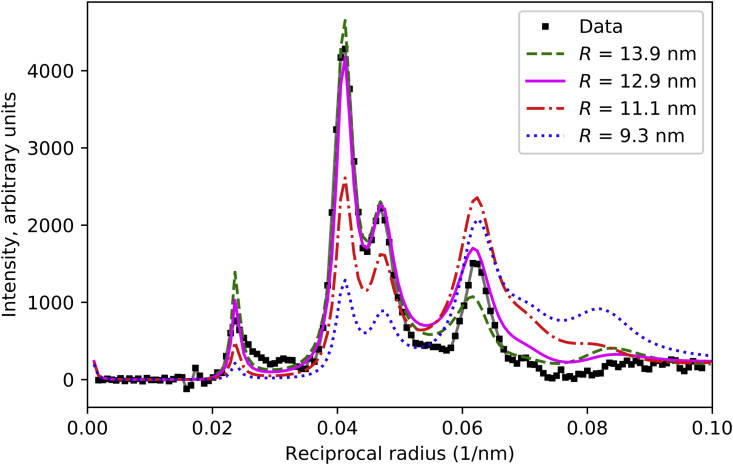
Effect of radial position of myosin heads on M1 intensity. Calculation of diffraction from a single myosin filament (f = 0.67) shows that radial distance of COM of IHMs from filament axis dramatically affects the radial position (i.e., along x axis) of diffracted intensity. When the COM of the IHM (PDB: 3jbh) is at R = 13.9 nm (green), intensity occurs roughly over observed intensity in the X-ray pattern (black squares; cf. M1 of Fig. 1). At lower radii (11.3 nm and 9.3 nm) the observed intensity is not well accounted for. The best match appears to be in the range 13–14 nm. Calculated intensities were scaled by the same factor compared with the observed data. Numerals 10, 11, 20, and 21 indicate indices of sampled reflections in X-ray data. See also Fig. S3. To see this figure in color, go online.

Figure 5.

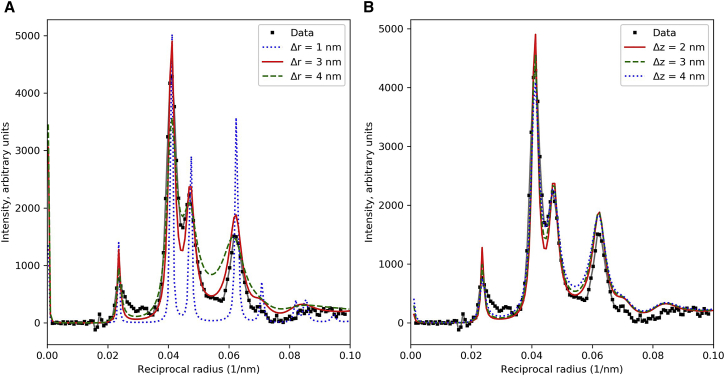
Effects of radial (A) and axial (B) disorder on calculated M1 intensity. (A) Radial disorder (Δr) affects primarily the sharpness and separation of the sampled peaks on M1. (B) Axial disorder (Δz) has little effect on M1, but affects meridional intensity on M3 and M6 (Fig. S4). Other parameters: f = 0.67; R = 12.9 nm, φ = 37°. In (A) Δz = 2 nm; M1 R-factors were 0.521, 0.053, and 0.064 for Δr = 1 nm, 3 nm, and 4 nm respectively. In (B) Δr = 3 nm; M1 R-factors were 0.053, 0.040 and 0.039 for Δz = 2 nm, 3 nm, and 4 nm respectively. See also Fig. S4. To see this figure in color, go online.

Figure 6.

Effect of radial position of myosin heads on M1 intensity in sampled diffraction pattern. Same models as in Fig. 4, but here placed in filament lattice, giving rise to diffraction peaks due to sampling of single-filament transforms by the lattice. Best match is for R ∼13.5 nm. For this simulation, f = 0.67, Δr = 3.5 nm, Δz = 2.5 nm, and φ = 37°. R-factors for M1 were 0.023, 0.042, 0.268, and 0.551 in order of descending R. See also Fig. S5. To see this figure in color, go online.

Figure 7.

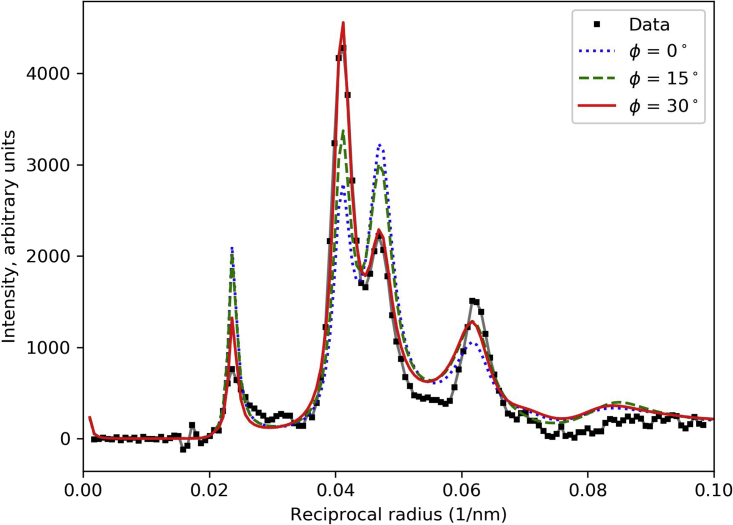
Effect of myosin filament rotation about long axis, φ, on M1 intensity. f = 0.67; R = 13.5 nm. Δr = 3.5 nm, Δz = 2.5 nm. R-factors were 0.164 (φ = 0°), 0.098 (φ = 15°), and 0.022 (φ = 30°). Thus, the best match to the data was obtained with a rotation of ∼30°. See also Fig. S6. To see this figure in color, go online.

Starting thick-filament model

Our starting thick filament structure for fitting to the X-ray data was an atomic model of a vertebrate thick filament constructed as described in section “materials and methods”. The bipolar filament has 3-fold (C3) rotational symmetry, and is divided into regions containing myosin-binding protein C (MyBP-C; the C zone) and lacking MyBP-C (the P and D zones; Fig. 2) (39). An IHM, based on the tarantula thick filament cryo-EM structure (PDB: 3jbh) (38), comprising the two interacting heads and ∼18 nm of S2, was placed in regular helical positions in the P and D zones and the known perturbed positions for the C zone (6,9) (section “materials and methods”). The orientation of the IHM and the starting radial position of its COM were the same as those in the tarantula filament (R = 13.9 nm).

Modeling parameters

Using this starting model, filament parameters were varied to determine their individual impact on the diffraction pattern. The parameters tested were the fractional length of the perturbed zone (see section “X-ray modeling” in “materials and methods”), f; radial (Δ_r) and axial (Δ_z) disordering of myosin filaments within the lattice; rotation φ of filaments about their longitudinal axes (all rotations are the same in the simple lattice); and distance R of the COM of the IHMs from the thick filament longitudinal axis. The effects of varying these parameters were sometimes best understood in terms of single-filament diffraction (seen as a continuous Fourier transform) and at other times by placing the filaments in the hexagonal lattice, producing discrete peaks in the transform due to lattice sampling. The single-filament plot was useful for showing how R and other parameters affect the radial position (position along the equatorial direction, or x axis) of the reflection. The lattice plot, produced by multiplying the single-filament transform by the lattice transform, showed how well the actual predicted intensities matched the observed reflections. The results presented below describe the fitting to the first myosin layer line (M1), the strongest layer line, and the one with the greatest effect on the R-factor (Figs. 3, 4, 5, 6, and 7). Results for the higher (weaker) layer lines are shown in Figs. S2–S6.

Varying the fraction of filament with a perturbed myosin helix

Vertebrate thick filaments contain MyBP-C, titin, and other proteins, in addition to myosin, dividing the filament into different zones: the P, C, and D zones (39). Myosin heads in the C zone lie on a perturbed helix (i.e., they are pseudo-helically organized), with small variations in axial rise and rotation of crowns within the 43-nm repeat unit compared with the ideal helix (6,9). Head organization in the P and D zones is unknown, possibly being disordered (44), or ordered on a regular (unperturbed) helix. Knupp et al. (26) assumed that the entire filament was pseudo-helical. We tested the effect of varying the fraction f of filament with pseudo-helically ordered heads, assuming that the rest of the heads are helically ordered (Figs. 3 and S2). Intensity on M1 was strongest with no perturbation (f = 0). With varying numbers of heads lying on a perturbed helix, intensities were weaker but very similar to each other, from 50% perturbed heads (f = 0.5) to all perturbed heads (f = 1.0, equivalent to the situation where all heads outside the perturbed region are completely disordered). The main diffraction peak remained in the same position radially for all f values: the perturbation will therefore have minimal effect on the relative intensities of the sampled reflections. For the remaining calculations, we used f = 0.67, roughly the fraction of myosin heads in the C zone (42).

Varying the radial position of the IHM COM

With our starting COM radius (13.9 nm, the radius in tarantula filaments), the thick filament transform lay roughly over the main intensity peaks on M1 (Figs. 4 and S3), suggesting that this radius was approximately correct. As R decreased, diffraction intensity shifted outward along M1, away from those peaks, implying a poor fit for the smallest radii (Fig. 4). The position of peak intensity for the radius derived from the negative stain reconstruction of Al-Khayat et al. (9) (∼9.2 nm)—the model used in the analysis of Knupp et al.—was a poor match to the measured intensity, which presumably accounts for the large R-factor obtained with this model (26). A simple visual analysis of Fig. 4 suggests that an IHM radial position of ∼13–14 nm is likely to give the best match to the experimental data.

Radial disordering of filaments

Varying the dispersion of the separation of neighboring filaments within the hexagonal lattice (radial disordering, Δ_r; Fig. 2) was carried out in the range 1.0–4.0 nm, representing lateral movement of the filaments by up to a quarter of their backbone diameter (i.e., relatively small excursions from their ideal positions). This is disordering of the second kind, namely local, neighbor-to-neighbor variations in lateral positioning of the filaments (40), and causes broadening of the X-ray reflections at higher angles, as observed in the patterns (Fig. 5 A; see also Fig. S4) (37)). Such local variations are consistent with axial and radial positioning of the filaments in the hexagonal lattice through their connections at the M-line, but with some variation due to flexibility in the connections. The value of Δ_r giving the best agreement with the experimental data was ∼3.0 nm, a plausible number considering reasonable flexibility of the M-line bridges (45) and flexural rigidity of the filaments (46).

Axial disordering of filaments

Varying the relative axial alignment of adjacent thick filaments by movement of neighbors along their longitudinal (z) axis was also carried out. This affected primarily the M3 meridional reflection (Fig. S4; also the M6, not shown), but also had a small impact on the width of the reflections at higher reciprocal radii (Fig. 5 B). Axial disorder (Δ_z) of 2.0–2.5 nm gave the best agreement with the X-ray patterns. As with the radial disordering, this value appears to be quite plausible in terms of the flexible/elastic structure of the M-line proteins connecting the thick filaments (45), and consistent with the high degree of axial alignment of thick filaments seen in EM sections of muscle (47).

Effect of varying radial position of the IHM on the sampled diffraction pattern

Using the above-optimized parameters, we calculated the sampled diffraction pattern of thick filaments placed in the simple filament lattice, with varying radial positions of the IHMs. Fig. 6 shows the best agreement with the M1 intensity distribution when R is between 12.9 and 13.9 nm. The smaller radii (9.3 and 11.1 nm) gave a poor fit. These results agree with our preliminary interpretation based on single-filament transforms (Fig. 4, discussed above), and confirm that the 9.2 nm radial position of the IHM derived from the negative stain reconstruction (9), like the model used in the calculations of Knupp et al. (26), is too small. In particular, modeling shows that low-radius heads generate strong diffraction intensity at higher angles that is notably absent in the observed X-ray pattern (Figs. 4 and 6). Fig. 6 shows that a 4-nm increase in the radial position leads to a model with an excellent fit to the experimental data.

Rotational angle of thick filaments in hexagonal lattice

Because the thick filaments lie in a regular hexagonal lattice, rotation about their longitudinal axes can dramatically affect the intensities of the lattice reflections in the pattern. If the head densities lie along a lattice plane, the corresponding reflection will be strong, and, if between the lattice planes, it will be weak. To determine the rotation that best fitted the observed diffraction pattern, we rotated filaments from φ = 0 to 60° in steps of 2° and calculated the corresponding layer line pattern (the calculated pattern repeats every 60°; Fig. 8 A). The variation of φ mainly affected the intensity ratio of the 11 and 20 sampling peaks on M1 (Fig. 7). The best fit was obtained for a rotation of ∼30°; i.e., when the vector directed from the thick filament axis toward the COM of an IHM in the first crown of heads in a unit cell was aligned with an 11 plane. Smaller angles produced a 20 peak on the M1 layer line that was equal to or higher than the 11 peak, contrary to the observed M1 intensity (Fig. 7).

Figure 8.

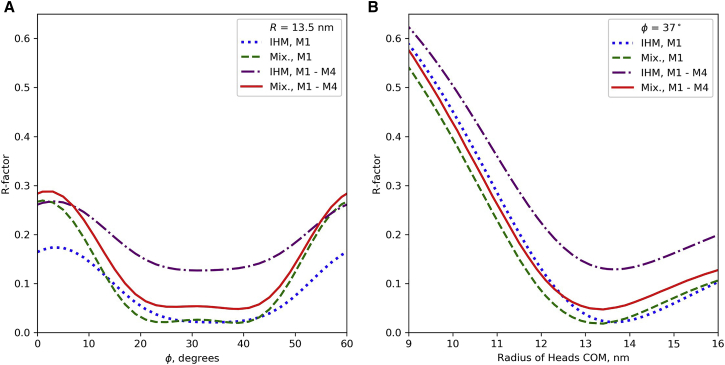
R-factor calculated for best model, with Δr = 3.5 nm, Δz = 2.5 nm, and f = 0.67. (A) R is set to 13.5 nm and rotation angle φ is varied. Best R-factor obtained for φ = 37° (see Fig. 7). (B) φ set to 37°, and IHM COM varied. Best R-factor obtained for R ∼13.5 nm. Traces are shown for M1 alone (the strongest layer line, blue) and for the first four layer lines together (purple). Traces are also shown for the same model but where disorder in crown 2 and the ideal regions has been simulated by replacing the head pairs with 5-nm radius spheres (see text), improving the R-factor (Mix = mixed model; green and red traces; see also Fig. 9). To see this figure in color, go online.

Calculation of R-factor to determine best overall fit

Using the insights gained above from visually comparing calculated and observed X-ray intensities, we determined the best overall fit for different COM radii of the IHMs and different filament rotations, by calculating an R-factor, for either M1 alone or all four myosin layer lines (M1–M4; Fig. 8; see section “materials and methods”). Varying the angle produced a curve similar in shape to that of Knupp et al. and confirmed that the optimum rotation angle was centered on ∼30° (minimum at 37°) (Fig. 8 A). Varying R showed that the best radial positioning of the IHM COM was ∼13.5 nm (Fig. 8 B). These parameters gave an R-factor of 0.13 when all four layer lines were included and 0.02 with only M1. Thus the IHM gives a good fit to the measured X-ray diffraction pattern when placed at an appropriate radius (∼4 nm greater than that used by Knupp et al.).

Calculation of R-factor with partial disordering of heads

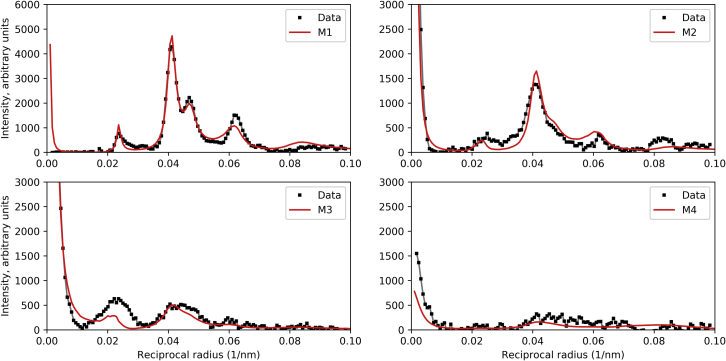
The 3D reconstructions of vertebrate thick filaments suggest that the heads in every third crown in the C zone are more mobile (i.e., dynamically disordered) than in the other crowns (6,9). We modeled the effect of disordering of this crown (crown 2 of Al-Khayat et al., 2013) by spreading the diffracting power of the two heads of a molecule uniformly within a sphere of 5-nm radius (having roughly twice the volume of a head pair), while the S2 portion of the atomic structure remained unaltered. The COM of the spheres was assumed to be at the same radial and axial position as in the IHM model. The same assumption was applied to all crowns in the ideal zones to simulate similar local mobility of heads in these regions (44). With the heads partially disordered in this way, we built a mixed model, which generated an improved fit, with an R-factor of 0.047 for all four layer lines and 0.018 for M1 alone (Figs. 8 B and 9), significantly better than the model where all IHMs are ordered.

Figure 9.

Effect of partial disordering of crown 2 and ideal region head pairs on myosin layer line intensities M1–M4. Compare with Figs. S5 and S6. Disordering has little effect on the fitting of M1 but substantially improves the fit to the off-meridional portions of M2 and M3, reflected in the improved R-factor seen in Fig. 8. Data: squares, black lines; calculation with f = 0.67; R = 13.4 nm. Δr = 3.5 nm, Δz = 2.5 nm, and φ = 37° (red lines). Disordered pairs of myosin heads in crown 2 and in the ideal zone were modeled by spheres of 5-nm radius with centers at the same radial and axial positions as the COM of the heads in the IHM. The R-factor for M1 = 0.018 and for M1–M4, 0.047 (Fig. 8B). To see this figure in color, go online.

Calculation of R-factor with “sphere” model

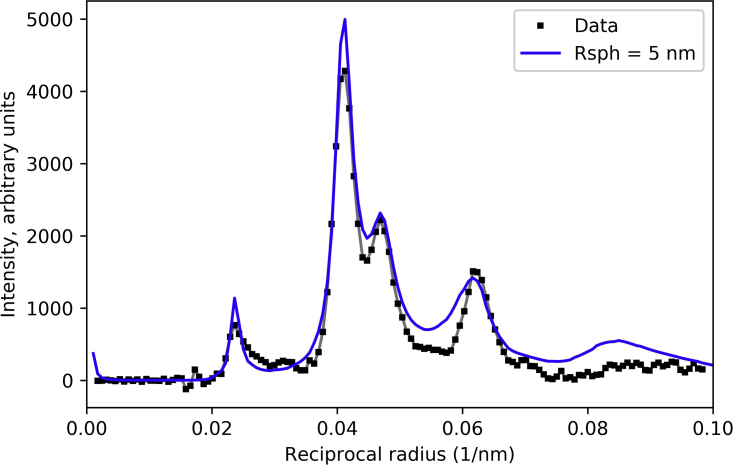
To evaluate the effect of the shape of the myosin heads on the calculated intensities, we performed a simulation in which all IHMs in the structure were represented as uniform spheres of 5-nm radius. The R-factor calculated for M1 was 0.020 (Fig. 10), a low value, similar to that for the IHM, showing that head shape is not important for modeling a layer line reflecting the relatively long repeat of ∼43 nm: when the object is several times smaller in size than the repeat, its shape is not important. For the second and higher-order layer lines, the shape had a significant impact. The 5-nm sphere model overestimated the intensities on the M2 and M3 layer lines (Fig. S7 B, C, and F), while the IHM model underestimated them (Fig. S5 B and C). The lowest R-factor for M1–M4 with the spheres model was ∼0.16 (Fig. 7 F, purple line). However, we found that varying the size of the sphere used to represent the IHM also had an impact on the fitting. While the best R-factor for M1 (0.018) was obtained with a sphere of radius 5.5-nm, and remained good (0.033) at the 4- and 7-nm limits of our tests, the best R-factor for all four layer lines (0.094) was obtained with a 7-nm radius sphere, declining to 0.28 for 4-nm radius (data not shown).

Figure 10.

Effect of replacing IHMs with spheres on calculated M1 intensity. A thick-filament model was constructed where spheres of 5-nm radius replaced the IHMs, to determine whether diffraction was sensitive to the shape of the diffracting unit. Here, R = 13.6 nm, Δr = 3.5 nm, Δz = 2.5 nm, f = 0.67, φ = 37°, and sphere radius (Rsph) = 5 nm. The R-factor for this model was 0.020 for M1. See also Fig. S7. To see this figure in color, go online.

Discussion

The IHM is highly conserved across species in both single myosin II molecules and isolated thick filaments (13,15, 16, 17); it is therefore widely believed to characterize the structure of the thick filament in resting striated muscle. Numerous studies suggest that the motif is the structural basis of SRX, an equally ubiquitous biochemical state of the thick filament, in which myosin ATPase activity is strongly inhibited, conserving energy (18, 19, 20,22,23). However, despite the widespread occurrence of the IHM in isolated thick filaments, and its intimate connection with the ubiquitous SRX state, Knupp et al. have questioned its existence in intact muscle (26), based on simulation of the X-ray diffraction pattern of resting skeletal muscle using IHM and non-IHM thick-filament models.

Placing IHMs at the appropriate radius and rotational angle provides good agreement with the X-ray pattern

We have shown that Knupp et al.’s conclusion arises because they did not consider the effect of the different radial positions of the heads in their models. The IHM model used by Knupp et al. has heads at low radius (COM ∼9.2 nm), while the non-IHM model has heads at high radius (we estimate ∼13.5 nm). Therefore, the different R-factors obtained could in principle result from different COM radii rather than from the different configurations (IHM or non-IHM) of the heads. We find that when heads in the IHM configuration are placed at a radius similar to the ∼13.5 nm favored by Knupp et al., the match to the diffraction pattern is very good (R-factor ∼0.12; Fig. 8), and that it declines dramatically (R-factor ∼0.60) with the low R used by Knupp. Thus, it is not necessary to invoke the IHM configuration of heads as the cause of the high R-factor: it results mainly from the low radius of the COM. As with R, the rotation of the thick filaments within the filament lattice is also important to fit the observed M1 intensity, by optimizing the ratio of the 11 and 20 sampling peaks (Fig. 7). The broad R-factor minimum occurred with a rotation of ∼30° (Fig. 8 A), so that an IHM in the first crown of heads in a unit cell was located approximately in the 11 plane of the filament lattice.

Our conclusion that a different configuration of heads is not required to explain the X-ray data is supported by our modeling using simple spheres to replace the IHMs. The R-factor calculated for M1–M4 and 5-nm radius spheres is not much greater than that using the IHM (0.16 cf. 0.12; Fig. S7 F cf. Fig. 8 B), and changes in a similar way with R. With spheres of radius 7 nm, the R-factor is in fact slightly better than for the IHM model (0.095 cf. 0.12). Thus, the M1–M4 X-ray data, which only provide relatively low-resolution information, are not very sensitive to the precise conformation of the heads and cannot be used to distinguish detailed head arrangements; however, they are highly sensitive to R. Other X-ray studies have been interpreted in terms of a variety of head configurations in relaxed muscle (48, 49, 50). These varying results could arise from the relative insensitivity of the observed myosin layer lines to configuration of the heads, and it is possible that the canonical IHM may also explain these studies.

R-factor is improved by modeling disordered heads at every third level in C zone

Although placing the IHMs at an appropriate radius from the filament axis, choosing reasonable axial and radial disorder parameters, and an appropriate rotation for the filaments provided a good fit of the M1 intensity (Figs. 6 and 8 B), the overall fit of the M1–M4 layer lines was not perfect (R-factor 0.12; Fig. 8 B, purple line), due to underestimation of the off-meridional intensities of M2 and M3 (Figs. S5 and S6). This was substantially improved by simulating partial disordering of the heads at every third level in the perturbed region (C zone; Fig. 9). Such disordering is suggested by much weaker density at every third level of heads in the EM reconstructions (crown 2 (9), equivalent to crown 3 in (6)). When simulated, it produced an R-factor of only 0.047 for M1–M4 at a COM radius of ∼13.3 nm (Fig. 8 B, red line). The only significant remaining discrepancy between the observed and calculated off-meridional intensities was underestimation of the 10 peak on the M3 layer line (Fig. 9). Possibly MyBP-C, which has the same axial repeat as myosin, and has regions lying at a significant distance from the filament axis (51,52), contributes to low radius intensity in reciprocal space, as seen in the X-ray pattern. Its low mass and stoichiometry in relation to myosin heads would make its contribution small, and close to meridional (43,53); MyBP-C was therefore not included in our modeling (see section “materials and methods”).

The improved agreement with the observed diffraction pattern using this more realistic filament model provides additional support for disordering of every third level of heads in the native filament environment. Such dynamically disordered heads (6,9) have been suggested as potential “sentinels” in relaxed muscle that can interact transiently with and thus detect thin filament activation, while the other heads of the C zone remain in their IHM configurations, in a super-relaxed state, sequestered from actin interaction (54, 55, 56).

EM supports X-ray modeling after correction for radial collapse of heads

Is the 13.3–13.5-nm radial position for the COM of the IHMs implied by our X-ray modeling consistent with other structural data? At first, the answer would appear to be no. As discussed, the negative-stain EM reconstruction used in the Knupp et al. modeling places the head COM at lower radius (∼9.2 nm), with a concomitant poor fit to the experimental data of the M1 reflections derived from low-angle X-ray diffraction of intact muscle. However, negative staining involves drying of the specimen before examination in the EM, and this can lead to substantial shrinkage (57,58). In the case of thick filaments, we have previously documented severe collapse of heads onto the filament backbone in negatively stained specimens. This is based on reconstructions of two species of thick filament—tarantula and scallop (8,35)—where negatively stained and frozen-hydrated filaments were compared, allowing head collapse to be directly determined. In both cases, the backbone diameter was hardly affected, while the heads collapsed radially on to the backbone by ∼3.5 nm in the case of tarantula and more for scallop (supporting material (2); Fig. S8). Based on these comparisons, a similar radial collapse of the heads seems likely in vertebrates, and an appropriate correction must be made to obtain a realistic value of the COM. Assuming a head collapse of 3.5 nm, this would imply an actual COM radius of approximately 9.2 + 3.5 = 12.7 nm. An additional correction may also be appropriate. We obtained the starting COM estimate of 9.2 nm by fitting IHMs to the negative stain reconstruction, first manually and then refining, using the Fit in map tool of Chimera. This automated fitting always pulled the IHMs to slightly lower radius (away from the outer contour) compared with our preliminary manual fitting, possibly because negative stain does not reveal actual protein density, but only the outer envelope of the structure; we found that applying a correction of ∼0.5 nm for this effect brings the IHMs back close to the outer contour, as appropriate given the mechanism of staining. Taking both corrections into account, a realistic estimate of the COM of the IHMs in a native vertebrate thick filament, based on negative stain EM, is 9.2 + 0.5 + 3.5 = 13.2 nm, close to the estimate based on X-ray modeling. There are clearly uncertainties in this estimate, and it can only be regarded as an approximation. Nevertheless, we consider it to be the best EM estimate available for vertebrate thick filaments (and clearly different from the 9.2-nm value of Knupp et al.), as no cryo-EM reconstruction of frozen-hydrated vertebrate filaments has been reported. This corrected EM estimate therefore provides good support for the X-ray modeling. Approximations of R from modeling X-ray data of muscles with the more common super-lattice organization (frog skeletal (27,48,49), mammalian skeletal and cardiac (59, 60, 61)) is probably less precise, due to the influence of the more complex super-lattice sampling of the M1 layer line. Nevertheless, estimates based on the overall peak position in diffraction patterns where sampling is relatively weak suggest a head COM of 12.5–14.5 nm, encompassing the value determined by our detailed modeling of the simple lattice and excluding the IHM radial position of Knupp et al.

Is this model consistent with other thick filament parameters? We estimate that the diameter of the backbone of the vertebrate thick filament is ∼16.5 nm (radius ∼8.3 nm; see supporting material (3)). This would place the IHM COM about 13.2–8.5 = 4.7 nm above the filament backbone. This lies within the 3.8–6.0 nm range defined by the cryo-EM studies of tarantula and scallop, supporting the plausibility of the vertebrate model; in this position, the IHMs would just contact or lie slightly above the filament surface, again, similar to the known organization in scallop and tarantula (Fig. S9). We conclude that 13.2 nm is a plausible estimate of the COM radius of the IHM in vertebrate thick filaments.

Conclusions

The apparent ubiquity of the IHM suggests that it is a common feature of most relaxed muscles. Our results show that there is no reason to question its existence in intact vertebrate muscle: X-ray diffraction of muscle and EM of isolated filaments, where the IHM has been directly demonstrated, are consistent with each other. This is supported by previous modeling of the X-ray diffraction pattern of live, relaxed tarantula muscle (62), which is well accounted for (R-factor 0.04) by the IHM thick-filament model demonstrated by cryo-EM (4,5).

Our modeling supports previous studies showing IHMs in striated muscle thick filaments and single myosin molecules of a variety of animal species under relaxing conditions and removes the puzzling inconsistency suggested by Knupp et al. Our analysis also provides consistency with the apparent ubiquity of the SRX state of thick filaments in relaxed muscle. Given that SRX is thought to be based largely on the interactions of the IHM, it is not apparent how SRX would be present without the IHM. Our findings are also consistent with studies of intact muscle using an entirely different approach (fluorescence polarization), which suggest a high level of IHM (54), and with the low-resolution appearance in electron tomograms of relaxed muscle (51), where the heads appear to lie flat on the filament, rather than projecting out as in the model favored by Knupp et al. (26,33). We conclude that the IHM satisfactorily explains the X-ray diffraction pattern of resting vertebrate striated muscle and provides an explanation for the different result presented by Knupp et al. We hope that, by resolving the controversy regarding the in vivo existence of the IHM, the field can now address critical remaining questions, including the significance and structure of the thick-filament P, C and D zones (44,63), the role of MyBP-C in stabilizing the IHM and SRX (25,63, 64, 65), and how sentinel (constitutively on) myosin heads are able to rapidly interact with actin to initiate contraction (55,56,66).

Author contributions

N.K. and A.T. designed and performed research and analyzed data. S.B. and M.F. collected data. R.P. conceived research and analyzed data. R.C. conceived research, analyzed data, and wrote the paper, with input from all co-authors.

Editor: Kathleen Trybus.

Supporting citations

References (67, 68, 69, 70, 71, 72, 73) appear in the supporting material.