Distinct timing of neutrophil spreading and stiffening during phagocytosis

Abstract

Phagocytic cells form the first line of defense in an organism, engulfing microbial pathogens. Phagocytosis involves cell mechanical changes that are not yet well understood. Understanding these mechanical modifications promises to shed light on the immune processes that trigger pathological complications. Previous studies showed that phagocytes undergo a sequence of spreading events around their target followed by an increase in cell tension. Seemingly in contradiction, other studies observed an increase in cell tension concomitant with membrane expansion. Even though phagocytes are viscoelastic, few studies have quantified viscous changes during phagocytosis. It is also unclear whether cell lines behave mechanically similarly to primary neutrophils. We addressed the question of simultaneous versus sequential spreading and mechanical changes during phagocytosis by using immunoglobulin-G-coated 8- and 20-μm-diameter beads as targets. We used a micropipette-based single-cell rheometer to monitor viscoelastic properties during phagocytosis by both neutrophil-like PLB cells and primary human neutrophils. We show that the faster expansion of PLB cells on larger beads is a geometrical effect reflecting a constant advancing speed of the phagocytic cup. Cells become stiffer on 20- than on 8-μm beads, and the relative timing of spreading and stiffening of PLB cells depends on target size: on larger beads, stiffening starts before maximal spreading area is reached but ends after reaching maximal area. On smaller beads, the stiffness begins to increase after cells have engulfed the bead. Similar to PLB cells, primary cells become stiffer on larger beads but start spreading and stiffen faster, and the stiffening begins before the end of spreading on both bead sizes. Our results show that mechanical changes in phagocytes are not a direct consequence of cell spreading and that models of phagocytosis should be amended to account for causes of cell stiffening other than membrane expansion.

Significance

Some specialized immune cells form the first line of defense of an organism by engulfing microbial pathogens, a process termed phagocytosis. During this process, immune cells become stiffer, but we do not well understand the function and how these mechanical changes depend on their target. Quantifying these mechanical events is important for understanding how elimination of microbes works. It also represents opportunities for developing new diagnostic tools based on mechanical states of leukocytes. We asked how human phagocytes adapt to the size of their target by feeding them antibody-coated microbeads and quantifying cell mechanical changes during phagocytosis. Our results enhance our understanding of this complex defense mechanism.

Introduction

Neutrophils are leukocytes of the innate immune system that are often first arrivers at a site of infection. Neutrophils engulf microbial pathogens by performing phagocytosis, which is triggered through the engagement of specific receptors present at the neutrophil surface (1,2). A cell that performs phagocytosis (called a phagocyte) contacts, spreads, engulfs, and destroys its target inside a phagosome, a specialized and transient organelle in which the target is attacked by reactive oxygen species produced by NADPH oxidase (Nox) and aggressive biochemical agents delivered through granule fusion (3). Abundant literature describes the biochemical reactions and signaling pathways involved during phagocytosis (2,4, 5, 6), dissects the role of receptor engagement (7), and details the formation of the phagosome and Nox assembly (8, 9, 10). Conversely, literature on the mechanical events that occur during phagocytosis is scarcer, in part due to the difficulty of quantifying mechanical properties in live leukocytes at the single-cell level during processes that last only a few minutes. Quantifying these mechanical events is necessary to fully understand the cellular process of phagocytosis and why it is sometimes less efficient, leading to evasion of the immune system by some pathogens. More broadly, human neutrophil mechanical properties are thought to play an important role in a number of pathological settings including acute respiratory distress syndrome (11), during which neutrophils stiffen and become trapped in the lung microvasculature. Improved understanding of leukocyte mechanical properties also provides an opportunity to develop new diagnostic tools based on mechanical states of leukocytes (12, 13, 14, 15). Finally, understanding the mechanics of phagocytosis is required for elucidating how a phagocyte reacts to its mechanical environment and how it adapts to the shape and stiffness of its target (16, 17, 18, 19) and to external forces (20), thereby using the mechanical input to identify its target (21).

Micromanipulation techniques such as micropipettes, magnetic and optical tweezers, and atomic force microscopy have been used to quantify mechanical properties of phagocytes in a resting state or during phagocytosis (22, 23, 24, 25, 26, 27, 28, 29). More than 20 years ago, Evans et al. (30) showed that phagocytes stiffen during phagocytosis of opsonized yeast. A series of studies by Herant et al. (31,32) represented a significant milestone in quantitative measurements and modeling of phagocytosis, confirming that phagocytes stiffen during phagocytosis. They described an increase in cortical tension induced by expansion of the membrane beyond a threshold of initially available membrane. During expansion, the tension would progressively build up in proportion to the rate of membrane expansion. Following this model, one would expect that once engulfment is complete, tension would drop or at least not increase further, which is difficult to reconcile with Evans’s finding of a rising cell tension after spreading. Kovari et al. (33) used traction force microscopy to measure contraction forces during spreading of macrophages on planar surfaces that were too large to be engulfed, leading to so-called frustrated phagocytosis. They observed that upon reaching the maximal spreading area, phagocytes contracted, exerting major stresses on their substrate. Using optical tweezers, Masters et al. (34) showed that a peak in membrane tension signaled the transition from spreading to contraction during frustrated phagocytosis, which appears to be consistent with a sequence of spreading followed by contraction. However, Masters et al. measured the membrane tension, as opposed to the cell tension, including contributions of membrane, cortex, and membrane-cortex adhesion (35), thereby making it difficult to compare with other studies. In light of the above, it remains unclear why cell expansion and stiffening seems to be simultaneous is some studies and sequential in others.

Cell stiffening was measured in several studies, but leukocytes are viscoelastic, and few studies have quantified both elastic and viscous changes in phagocytes. Herant et al. (31) made the most refined, albeit indirect, measurements of viscous effects. We have recently shown that activation of a variety of types of leukocytes (T cells, B cells, and neutrophil-like PLB cells) induced a large increase in both cell stiffness and viscosity and that the viscous properties of leukocytes were intrinsically linked to their elastic properties (29). Following our previous results, an increase in stiffness during leukocyte activation occurs simultaneously with an increase in viscosity, with a modulation in the ratio of elastic-to-viscous properties that evolves over time and is a signature of leukocyte type (29).

In this study, we address the question of simultaneity or sequential occurrence of spreading and mechanical changes in a phagocyte during the course of phagocytosis. We asked if the viscous properties of both primary cells and cell lines evolve simultaneously with elastic properties during phagocytosis and confronted this with the established model of Herant et al. To address these questions, we used a single-cell rheometer (29) that allowed us to monitor both elastic and viscous properties with a high temporal resolution together with the monitoring of cell morphology using high-magnification transmitted-light microscopy.

Materials and methods

Cells and reagents

PLB cells and reagents

Cells of the human acute myeloid leukemia cell line PLB-985 (henceforth referred to as PLB cells) were cultured in RPMI 1640 1X GlutaMax (Gibco, Waltham, MA) supplemented with 10% heat-inactivated fetal bovine serum (FBS) and 1% penicillin/streptomycin. Cells were passaged twice a week and differentiated into a neutrophil-like phenotype by adding 1.25% (v/v) dimethyl sulfoxide (Sigma-Aldrich, St. Louis, MO) to the cell suspension the first day after passage and, in a second time, 3 days later when changing the culture media (36). 24 h before experiments, 2000 U/mL of interferon- γ (Immuno Tools, Friesoythe, Germany) was added to the cell-culture flask (37), and cells were centrifuged for 3 min at 300 x g and resuspended in complete HEPES medium (140 mM NaCl, 5 mM KCl, 1 mM MgCl₂, 2 mM CaCl₂, 10 mM HEPES pH 7.4, 1.8 mg/mL glucose, and 1% heat-inactivated FBS). All solutions in contact with cells were filtered using 0.22-μm-diameter pore filters (Merck Millipore, Burlington, MA).

Primary human neutrophils and reagents

Human blood samples were taken with the understanding and written consent of each volunteer by the “Etablissement Français du Sang, Cabanel, Paris” (the French blood transfusion service and national blood bank: https://www.ints.fr/). An agreement (N°11/Necker/103) allowing us to use blood samples from volunteers for research purposes was signed between this organization and the Institut de Chimie Physique. Neutrophils were isolated from healthy donor whole blood by means of dextran sedimentation and Ficoll centrifugation, as previously described (38). Briefly, after sedimentation for 30 min in 2% Dextran 50 G (Sigma-Aldrich, ref. 31392) in physiologic serum (0.9% NaCl in purified water), the leukocyte-rich yellow part of the liquid was centrifuged for 8 min at 400 x g, then the supernatant was discarded, and leukocytes were resuspended in Dulbecco’s phosphate buffer saline (DPBS; Gibco). The leukocytes were then isolated with density separation in 15 mL Ficoll (Ficollpaque-plus GE-Healthcare, ref. GE17-144002, Sigma-Aldrich). Cells were counted, and before the experiment, cells were centrifuged for 3 min at 300 x g at room temperature and resuspended in the same volume of complete HEPES medium. Between experiments, the batch of tested primary neutrophils was maintained at 4°C.

Opsonization of beads and flat surfaces

20-μm beads

20-μm-diameter polystyrene microbeads at 10⁶ beads/mL (ref. 74491-5ML-F, Sigma-Aldrich) were washed three times by centrifugation at 16,000 x g for 3 min and resuspended in DPBS. Beads were then incubated overnight at room temperature with a 5% (w/v) solution of bovine serum albumin (BSA; Sigma-Aldrich) in DPBS. The beads were washed again three times by centrifugation at 16,000 x g for 3 min, resuspended in DPBS, and incubated with 1:500 anti-BSA rabbit antibody (Sigma-Aldrich, ref. B1520) in DPBS for 1 h at room temperature. Microbeads were again washed three times (16,000 x g for 3 min in DPBS), stored at 4°C, and resuspended in DPBS at 10⁶ beads/mL before use.

8-μm beads

8-μm-diameter polystyrene BSA-covered microbeads (ref. BP-60-5, Spherotech, Lake Forest, IL) were opsonized with the same anti-BSA rabbit antibodies used for 20-μm beads. Control microbeads were non-opsonized BSA microbeads and were washed three times and resuspended in DPBS at the same concentration as the opsonized microbeads. In the absence of the anti-BSA antibodies on beads, cells never spread around the bead as clearly as in the presence of antibodies.

Flat surfaces

Glass-bottom Petri dishes (Fluorodish, WPI, Sarasota, FL) were washed three times with DPBS and incubated overnight at room temperature with 1 mL of 5% (w/v) BSA (Sigma-Aldrich) in DPBS, after which they were washed three times with DPBS. Dishes were then incubated with 1:500 anti-BSA rabbit antibody (ref. B1520, Sigma-Aldrich) in DPBS for 1 h at room temperature. The Petri dishes were finally washed three times with 1 mL of complete HEPES medium (140 mM NaCl, 5 mM KCl, 1 mM MgCl2, 2 mM CaCl2, 10 mM HEPES 448 pH 7.4, 1.8 mg/mL glucose, and 1% heat-inactivated FBS). Control surfaces were made on glass-bottom Petri dishes coated with BSA only. We never observed any cell spreading on these surfaces, while in the presence of these anti-BSA antibodies, every cell eventually spread on the surface.

Micropipette preparation

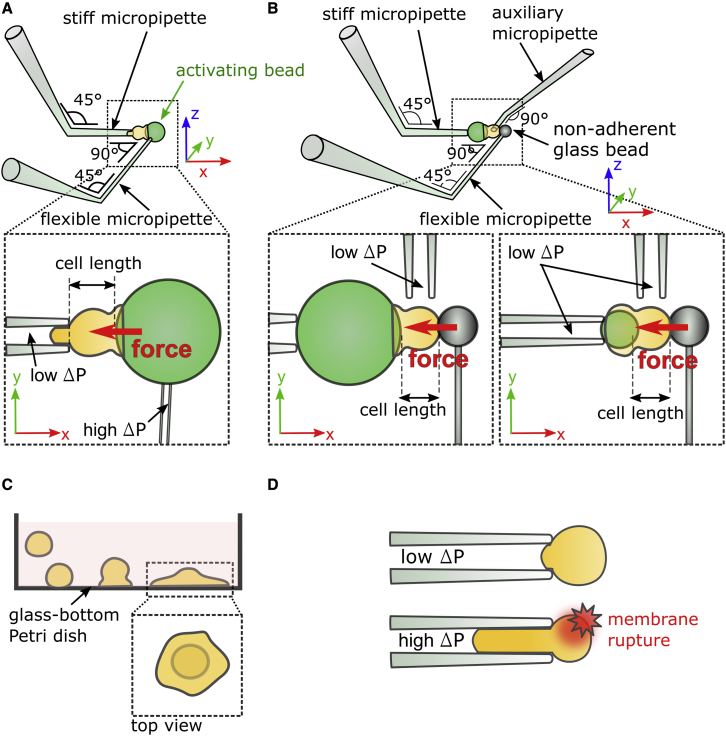
Stiff micropipettes were prepared as described previously (39, 40, 41, 42) by pulling borosilicate glass capillaries (Harvard Apparatus, Holliston, MA) with a P-97 micropipette puller (Sutter Instruments, Novato, CA) and cutting them with an MF-200 microforge (World Precision Instruments, Sarasota, FL) to get an inner diameter of 3 μm at the tip of the micropipette. This micropipette was then bent at a 45° angle with an MF-900 microforge (Narishige, Tokyo, Japan).

Flexible micropipettes were either connected to a pneumatic microinjector (IM-11-2, Narishige, Amityville, NY) used to strongly hold a polystyrene bead with an aspiration pressure on the order of 1 kPa when used to indent phagocytes in the front (see below), or their extremity was melted to form a (non-adherent) glass bead, when used to indent phagocytes in the back. The bending stiffness of these flexible micropipettes was calibrated as previously described (40) by pressing them against standard microindenters of known stiffness and by measuring the resulting bending of both micropipettes. The stiffness of the standard microindenters was calibrated using a commercial force probe (model 406A with a force range of 0–500 nN; Aurora Scientific, Aurora, Ontario, Canada). In the present study, flexible micropipettes had a typical bending stiffness of 0.1–0.2 nN/μm.

Single-cell rheometer

The rheometer was developed based on our microindentation setups (40,41) and as described in (29). The principle of the rheometer is to apply a controlled force to a cell and to record the resulting cell deformation during phagocytosis. To do so, we use an inverted microscope (Ti2, Nikon Instruments, Tokyo, Japan) equipped with a SPARK camera (Hamamatsu Photonics, Hamamatsu City, Japan) and a 100x oil immersion 1.3 numerical aperture objective (Nikon Instruments) placed on an air suspension table (Newport, Irvine, CA). The microscope is equipped with 2 or 3 micropipettes whose tips are plunged into a glass-bottom Petri dish (Fluorodish, WPI) placed on the microscope stage. The force is applied to the cell by compressing it with a flexible micropipette of known bending stiffness. This flexible micropipette is linked to a manual micropositioner (Thorlabs, Newton, NJ) placed on top of a single-axis translation stage controlled with a piezo actuator (TPZ001; Thorlabs). The force is applied to the cell via a bead located at the tip of this flexible micropipette. When used for both activating and probing the cell, this microbead is opsonized and maintained by a strong aspiration pressure provided by the flexible micropipette. When used only for probing the cell, the bead is made of glass and fused with the flexible micropipette.

By translating the piezo stage, the bead (activating bead or the bare glass bead) at the tip of a flexible micropipette is pushed against the cell that is gently held by a stiff micropipette, which is linked to a motorized micromanipulator (MP-285; Sutter Instruments). To control the force toward the cell, a live feedback loop detects the position of the bead (at a rate of 400–500 Hz) by analyzing a portion of each image acquired by the microscope camera, which is controlled by the Micromanager software (43). The latter is controlled by a Matlab (MathWorks, Portola Valley, CA) custom code. The force applied by the bead on the cell is the product of the deflection and the bending stiffness of the flexible micropipette. The deflection is obtained as the difference between the position of the bead and the position of the piezo stage. The feedback loop adapts the position of the base of the flexible micropipette in order to set a desired micropipette deflection, hence a desired force applied to the cell. The cell deformation is determined by the position of the bead.

During each experiment, a first mechanical measurement is performed when the initial contact is made between the bead and the cell, which is obtained by translating the base of the flexible micropipette at a constant velocity of 1 μm/s until an initial compressive force F₀ = 180 pN is attained. This level of force was chosen to obtain an indentation that was not too large at early times (less than 1 μm), when cells were soft, but not too small (more than 0.1 μm) when cell became stiffer. We analyze the resulting force-indentation curve, where the indentation is obtained by analyzing the position of the tip of the indenting bead, x_tip(t), from which the position of the contact point is subtracted. We use the Hertz model (44,45) to extract the cell’s Young’s modulus from the force-indentation curve (29). We did not correct for finite thickness of the cell, but we estimated that although it would modulate the quantitative values of the Young’s modulus, the trends would be unaffected (an increase in Young’s modulus during activation). Once the 180-pN threshold F₀ is reached, the setup automatically switches to a regime during which an oscillatory force F(t) is applied to the cell: $F\left(t\right)=⟨F⟩+\Delta F\mathit{cos}\left(\omega t\right)$, where the average of the force $⟨F⟩$ = F₀ = 180 pN, the amplitude of the oscillations $\Delta F$ = 50 pN, and $\omega =2\pi f$ is the angular frequency of the oscillations at a frequency f = 1Hz. The amplitude $\Delta F$ was chosen to be large enough so that the induced modulation in indentation would be detectable but small enough so that it could be considered a small perturbation. The 1-Hz frequency was sufficiently faster than the timescale associated with the spreading process, but it also had to be low enough to consider that measurements performed at this frequency would be close to the zero-frequency values. As a result of this oscillatory force, the cell deforms in a sinusoidal manner, as reported by the position of the tip of the flexible micropipette, $x_{tip}\left(t\right)=⟨x_{tip}⟩+\Delta x_{tip}cos\left(\omega t-\phi \right)$, where $⟨x_{tip}⟩$ is the average of $x_{tip}\left(t\right)$, $\Delta x_{tip}$ the amplitude of the oscillations (typically 100 nm, with a few-nanometer accuracy), and $\phi$ is a phase lag due to the cell’s viscous properties (an applied force leads to a delayed deformation) (Fig. S1). Note that the relative variation of $x_{tip}\left(t\right)$ is a measure of the relative variations of the cell length. As usually done in rheological studies (27), we consider a complex number formalism where the complex force is $F^{\ast }\left(t\right)=⟨F⟩+\Delta F{e}^{i\omega t}$ and the corresponding complex tip position is $x_{tip}^{\ast }\left(t\right)=⟨x_{tip}⟩+\Delta x_{tip}{e}^{i\left(\omega t-\phi \right)}$. We define the complex stiffness of the cell $K^{\ast }$ by writing $F^{\ast }\left(t\right)-⟨F⟩=K^{\ast }\left(x_{tip}^{\ast }\left(t\right)-⟨x_{tip}⟩\right)$. The complex cell stiffness $K^{\ast }=K^{\prime }+i{K}^{″}$ has a real part K′ characterizing the elastic properties of the cell and an imaginary part K″ characterizing its viscous properties. Henceforth, for simplicity, we call K′ the cell stiffness, but we refer to our previous study where we addressed in detail why K′ can be considered to reflect changes in intrinsic elastic modulus of the cell, not only a change in cell geometry (29). Note that this stiffness is an effective parameter that does not allow identifying a specific contribution of different compartments of the cell. K′ and K″ are deduced from experimental measurements through the relationship $K^{\prime }=\frac{\Delta F}{\Delta x_{tip}}\cos \phi$ and $K^{″}=\frac{\Delta F}{\Delta x_{tip}}\sin \phi$, respectively (29). It is also relevant to monitor the ratio of $K^{″}$ and $K^{\prime }$, which is called the loss tangent $\eta$. From the above relationships, $\eta$ is solely related to the phase lag $\phi$ by the relationship $\eta =\tan \phi$. Experiments were performed at room temperature to avoid thermal drift. On top of the live detection of the flexible micropipette tip, one image of a region of interest showing the pipettes, cell, and bead was recorded every second.

Setup configuration to indent the cell in the front or in the back

The automation of the setup was used in three different ways in order to indent activating leukocytes: in the “front,” in the “back,” and in the “back” but by cyclically retracting the indenter and forming a new contact at the beginning of each ∼30-s cycle. Micropipette positioning and shape were adapted accordingly (see below, Fig. 1, and Video S1).

Figure 1.

Experimental techniques. (A) Setup to indent cells at the “front.” Left inset: a compressive force (red arrow) is exerted against the cell while it is phagocyting a 20-μm activating bead (represented in green) tightly held by a flexible micropipette. The cell length is recorded during the experiments. (B) Setup to indent cells at the “back.” Left inset: a 20-μm activating microbead is held by a stiff micropipette. A compressive force is exerted at the back of the cell with a non-adherent glass bead located at the tip of a flexible micropipette. Right inset: an 8-μm activating microbead is held by a stiff micropipette with a low aspiration pressure ΔP ∼20 Pa. With this setup and bead size, cells can perform complete phagocytosis. (C) Frustrated phagocytosis on IgG-coated flat surfaces seen from the side. Inset: top view of a cell during frustrated phagocytosis. (D) Passive aspiration of a neutrophil into a stiff micropipette. A cell is first gently held (with a low aspiration pressure ΔP ∼20 Pa) and then aspirated under high aspiration pressure (ΔP ∼ 500 Pa) until the cell membrane breaks as reported by an increase in fluorescence level of propidium iodide (red star). To see this figure in color, go online.

Video S1. Activation of PLB cells using different beads and indentation modes

Time is in minutes:seconds. Top row/ left: 20-μm bead and indentation in the front; right: control non-activating 20-μm bead and indentation in the front. Middle row/ left: 20-μm bead and indentation in the back; right: 8-μm bead and indentation in the back. Bottom row/ left: 20-μm bead and cyclic indentation in the back; right; 8-μm bead and cyclic indentation in the back.

Indentation in the front of the cell

To indent the cell in the front, a stiff micropipette holds the cell gently, and the flexible micropipette holds an activating bead with a strong aspiration (Video S1). Before testing a new cell, a new activating microbead is picked up from the bottom of the Petri dish and aspirated by the flexible micropipette. A cell is then also picked up from the bottom of the dish by micromanipulation of the stiff micropipette.

Indentation in the back of the cell

Indenting the cell in the front allows monitoring only frustrated phagocytosis due to the high aspiration pressure (several kPa) used to aspirate the activating microbead at the tip of the flexible micropipette. The seal between the pipette and the bead surface is not perfect (probably due to nanometer-scale imperfections), so cell membrane can get aspirated by the flexible micropipette if it reaches its tip, thus making the phagocytic cup closure impossible. In order to study complete phagocytosis, we developed a more complex setup using three micropipettes: a stiff pipette that holds an activating bead, with a low (∼20 Pa) aspiration, while the cell is gently positioned on the other side of the bead (Fig. 1 B) using an auxiliary micropipette holding the cell also with a low aspiration (∼20 Pa). The auxiliary pipette is withdrawn once the cell adheres to the activating bead. To indent the cell, a flexible micropipette is used as in the case of front indentation, but this flexible micropipette now has a glass bead fixed (through melting the pipette tip) at its extremity. This glass bead can indent the cell on its back, while it is phagocyting the bead on its front (Video S1). In the presence of serum, we very rarely saw any clear adhesion between the glass bead and the cell within the timescale of an experiment. The principle used to measure the viscoelastic properties of the cell during phagocytosis remains the same as for front indentation. Representative examples for 8- and 20-μm bead phagocytosis are shown in Video S1.

Cyclic indentation in the back of the cell

During the indentation in the back described above, the microindenter (the flexible micropipette with a fused bead at its tip) stays in contact with the cell throughout phagocytosis. In a previous study, we addressed the question of whether the changes in K′ and K’’ reflected intrinsic changes in cell stiffness and viscosity, respectively (29). This requires measuring the Young’s modulus of the cell over time in order to correlate it with K’. To do so, the setup is the same as for indentation in the back, but the automation is changed. The microindenter follows a sequence of repeated operations (called cycles) during which it 1) is brought into contact with the cell as done at the beginning of experiments when indenting in the front or in the back, 2) applies an oscillatory force to the cell following the preceding compressive phase, and 3) is retracted away from the cell, which ends one cycle (Video S1). Fifteen cycles are repeated consecutively, allowing fifteen consecutive measurements of the Young’s modulus of each cell, assuming a Poisson’s ratio of the cell equal to 0.5 (29). We took into account the cell curvature that we updated over time while the cell was spreading over the bead, based on video images. A complete cyclic indentation for a cell lasts ∼7.5 min (Fig. S1).

Measuring curvilinear abscissa

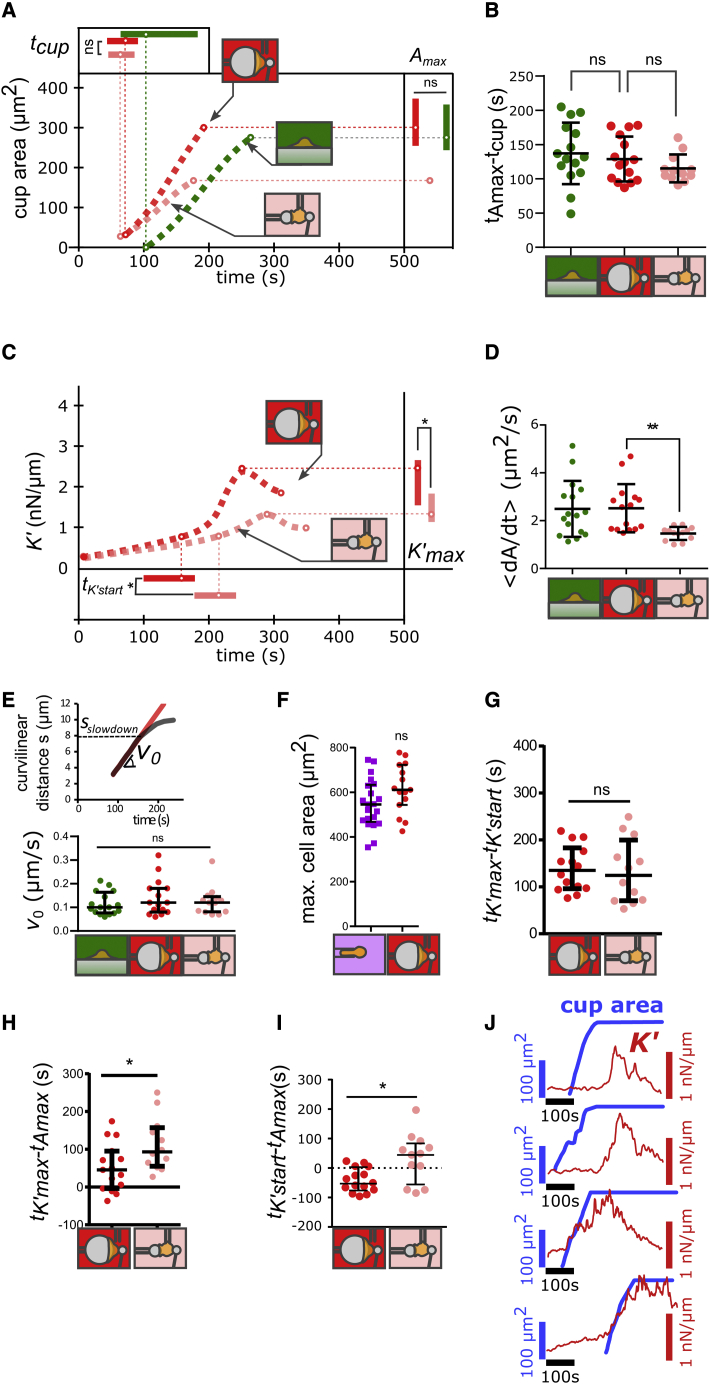
The curvilinear abscissa of the cup front position was measured using a kymograph (Fig. S2). To determine when the spreading slowed down and transitioned from linear to slower spreading, a linear trend was fitted over the first 5 μm of the curvilinear abscissa s, which led to a measurement of v₀ = ds/dt. Departure from this linear trend was defined as the time at which s was more than 0.5 μm away from the linear trend (Figs. 2 E and S2). The maximum of s, s_max, was also determined based on the kymograph.

Figure 2.

Spreading and stiffening of PLB cells during phagocytosis. (A) Phagocytic cup area as a function of time following cell-substrate contact for PLB cells. Dotted lines are a guide to the eye, but circles on the lines are median values, and error bars on top and right are interquartile ranges. Raw data are shown in Figs. S6–S11. Each condition is represented by a drawing: back indentation of PLB cells during phagocytosis of 20-μm beads (red; N = 3, n = 15 cells) and 8-μm beads (pink, N = 3, n = 12 cells), and frustrated phagocytosis on flat surfaces (green; N = 3, n = 16 cells, a condition where K′ was not quantified). Inset on the right: maximal phagocytic cup area A_max. Inset on top: time t_cup (relative to cell-substrate contact) when cells start forming a phagocytic cup. (B) Delay between the beginning of the cup formation (t_cup) and the time at which the phagocytic cup reaches its maximal area (t_Amax). (C) Cell stiffness K′ as a function of time following cell-substrate contact for PLB cells. Curves are a guide to the eye, but dots on the curves are median values. Each condition is represented by a drawing: back indentation of PLB cells during phagocytosis of 20-μm beads (red; N = 3, n = 15 cells) and 8-μm beads (pink, N = 3, n = 12 cells). Inset on the right: maximal value of K′, K’_max. Inset at the bottom: time t_K’start (relative to cell-substrate contact) when K′ starts increasing faster. (D) Average spreading rate of the phagocytic cup $⟨\frac{dA}{dt}⟩=\frac{A_{max}-A_{init}}{t_{Amax}-t_{cup}}$, where $A_{init}$ is the initial area of the phagocytic cup. (E) Initial speed $v_0=\frac{ds}{dt}$ of the cup front during spreading. Inset on top: example of time evolution of the curvilinear abscissa s of the front of a PLB cell during the phagocytosis of a 20-μm bead. During indentation in the back of the cell, s slows down when reaching a level s = s_slowdown. (F) Maximal total cell area as measured using micropipette aspiration (purple squares) and during frustrated phagocytosis on 20-μm beads during back indentation (red squares), both for PLB cells. (G) Duration of cell stiffening, t_K’max- t_K’start. (H) Difference between t_K’max and t_Amax. This difference is positive if K′ reaches its maximum after the phagocytic cup had already reached its maximal area. (I) Difference between t_K’start and t_Amax. This difference is positive if K′ starts increasing after the phagocytic cup had already reached its maximal area. (J) Examples of different relative time of cell spreading (phagocytic cup area in thick blue line) and stiffening (cell stiffness K′ in red thin line) during phagocytosis (indentation in the back of PLB cells phagocyting 8-μm beads). In (A)–(I), lines are median values, and error bars are interquartile ranges. Statistical tests in (A) and (F): Kolmogorov-Smirnov test (^∗p < 0.05, ^∗∗p < 0.01). Statistical tests in (B)–(E) and (G)–(I): two-tailed Mann-Whitney (^∗p < 0.05, ^∗∗p < 0.01). To see this figure in color, go online.

Measuring total cell surface area

When indenting PLB cells in the back while they phagocyte 20-μm beads, we also estimated the total cell surface area when the phagocytic cup attained its maximal area. To do so, we modeled the outer cell area as a spherical cap whose height was measured directly on video for each cell, and we added to the surface area of this spherical cap the surface area of another spherical cap defined by the curvature of the 20-μm bead.

Frustrated phagocytosis on flat surfaces

A glass-bottom Petri dish (Fluorodish, WPI) was placed in the focal plane of an inverted microscope under bright-field or differential interference contrast illumination (TiE or Ti2, Nikon Instruments) equipped with a 40X or a 60X objective (Nikon Instruments) and a CMOS camera (Flash 4.0 or SPARK, Hamamatsu Photonics, Hamamatsu City, Japan). A few thousands cells were then injected into the Petri dish. Time-lapse recordings were acquired at the rate of one image per second. The focus was adjusted manually, and experiments were performed at room temperature (Video S3). The spreading dynamics were assessed using a kymograph based on a line oriented radially across the cell (Fig. S2). The radius of the cell’s phagocytic cup was analyzed the same way as the curvilinear abscissa s on beads in order to measure the velocity of the cell’s front during spreading, v₀, and the value of the radius r = s_slowdown (r = s on a flat surface) at which the spreading began to slow down, as well as the maximum value of r, s_max.

Micropipette aspiration to determine maximal cell surface area

A glass bottom Petri dish (Fluorodish, WPI) was placed on a TE300 inverted microscope (TE300, Nikon Instruments, Tokyo, Japan) placed on an air suspension table (CVI Melles Griot, Netherlands). The microscope was equipped with a 100× oil immersion objective (Nikon Instruments) and a Flash 4.0 CMOS camera (Hamamatsu). Epifluorescence illumination using a mercury lamp (Intensilight, Nikon Instruments) was used simultaneously with a faint bright-field illumination provided by a light-emitting diode placed on a custom-made holder. Exposure time was typically set to 80 ms, and a neutral density filter 4 or 8 in the fluorescence illumination path was used. The fluorescence aperture diaphragm was adjusted to limit exposure in the field of view. The Petri dish was filled with complete HEPES medium supplemented with 160 μg/mL of propidium iodide (Sigma-Aldrich). A stiff micropipette filled with HEPES medium at its tip (the rest being filled with distilled water) was connected to a water-filled glass tube, whose height was adjusted to control hydrostatic pressure inside the micropipette. The reservoir level was set at 2 mm below zero-pressure level, at which the flow through the tip of the micropipette vanishes, leading to an aspiration pressure in the micropipette of approximately 20 Pa. Once a cell was picked up at the bottom of the Petri dish and aspirated for a few seconds, we shifted the aspiration level from the previous -2 mm to a high aspiration level of -50 mm (i.e., about 500 Pa). Time-lapse image series were acquired at one image per second using Micromanager software (43). Cell-area measurements during passive aspiration were made by approximating cell shape with simple geometrical shapes, as described previously (41). Briefly, the cell body inside the micropipette was modeled as a cylinder, while the part of the cell at the tip inside the micropipette and out of the micropipette was modeled as a spherical cap.

Quantifying cell spreading and stiffening

To quantify changes in cell shape and mechanics during phagocytosis, we defined a set of parameters to be monitored over time.

Quantifying cell spreading

Following the contact between the cell and the activating surface (bead or plane) at a time taken as t = 0, the phagocytic cup starts spreading at time t = t_cup determined by visual inspection of the movies. Spreading stops at time t = t_Amax, when the phagocytic cup reaches its maximal area A_max, either because the phagocytosis is frustrated or because the bead has been engulfed. The duration of cup spreading is the difference t_Amax - t_cup. The average rate of spreading is $⟨\frac{dA}{dt}⟩=\frac{A_{max}-A_{init}}{t_{Amax}-t_{cup}}$, where A_init is the cup area when its formation is detected (A_init is non-zero as the initial contact zone hides the cup at its very early moments), and A_max - A_init is its area expansion.

Quantifying cell stiffening

The cell stiffness is characterized by the elastic part K′ of the complex stiffness K^∗ (see Single-cell rheometer in Materials and methods). After cell-bead contact, K′ remains close to its initial value K’_init, until it starts increasing quickly at t = t_K’start. To set t_K’start systematically, we defined it as the time at which K′ overtakes K’_init by 0.5 nN/μm. Following this time point, K′ increases until it peaks at a value K’ = K’_max at time t = t_K’max, after which K′ decreases (Fig. S3). We also measured an average rate of increase of K′, $\frac{d{K}^{\prime }}{dt}=\frac{K_{max}^{\prime }-K_{start}^{\prime }}{t_{K^{\prime }max}-t_{K^{\prime }start}}$ (Fig. S4).

Influence of setup configuration on these parameters

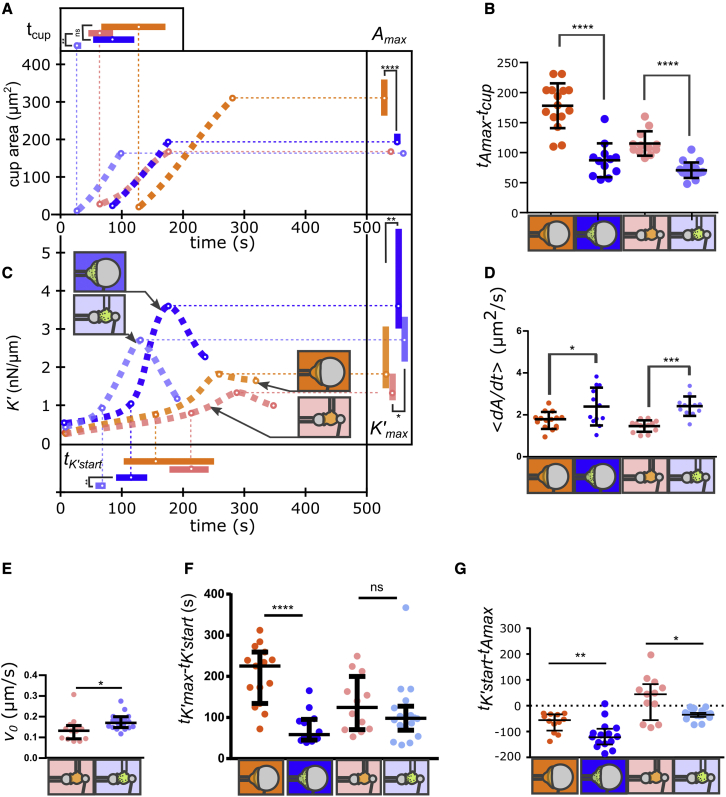
The protocol used to probe cell stiffness did influence cell behavior: front indentation led to a delayed onset of cup formation (t_cup = 128 s versus 72 s on 20-μm beads, median values, p < 0.05, two-tailed Mann Whitney test; Figs. 2 A and 3 A, inset on top), a longer spreading time (t_Amax - t_cup, about 3 instead of 2 min; Fig. 3 B). However, some parameters were independent of the protocol: back and front indentation led to the same maximal cup area (A_max; Figs. 2 A and 3 A, inset on right) and t_K’start (Figs. 2 A and 3 A, inset below). Being aware of this influence of the protocol, we compared dynamics on 8- and 20-μm beads using the same protocol.

Figure 3.

Comparison of PLB cells and primary neutrophils. (A) Phagocytic cup area as a function of time following cell-substrate contact. Dotted lines are a guide to the eye, but circles on the lines are median values, and error bars on top and right are interquartile ranges. Added data for primary neutrophils (blue) are back indentation during phagocytosis of 20-μm beads (dark blue in A–G; N = 2, n = 15 cells) and 8-μm beads (light blue in A–G; N = 2, n = 13 cells). Inset on the right: maximal phagocytic cup area A_max. Inset on top: time t_cup (relative to cell-substrate contact) at which cells start forming a phagocytic cup. Raw data are shown in Figs. S6–S11. (B) Delay t_Amax- t_cup between the beginning of the cup formation (t_cup) and the time at which the phagocytic cup reaches its maximal area (t_Amax). (C) Cell stiffness K′ as a function of time following cell-substrate contact. Curves are a guide to the eye, but dots on the curves are median values. Each condition is represented by a drawing: back indentation of 20- and 8-μm beads for PLB cells and primary neutrophils. Inset on the right: maximal value of K′, K’_max. Inset at the bottom: time t_K’start (relative to cell-substrate contact) when K′ starts increasing faster. (D) Average spreading rate of the phagocytic cup $⟨\frac{dA}{dt}⟩=\frac{A_{max}-A_{init}}{t_{Amax}-t_{cup}}$, where $A_{init}$ is the initial area of the phagocytic cup. (E) Initial speed $v_0=\frac{ds}{dt}$ of the cup front during spreading. (F) Duration of cell stiffening, t_K’max- t_K’start. (G) Difference between t_K’start and t_Amax. This difference is positive if K′ starts increasing after the phagocytic cup had already reached its maximal area. In (A)–(G), median values are shown with interquartile ranges. Statistical tests in (A) and (C): Kolmogorov-Smirnov test (^∗p < 0.05). Statistical tests in (B) and (D)–(G): two-tailed Mann-Whitney (^∗p < 0.05, ^∗∗p < 0.01, ^∗∗∗p < 0.001, ^∗∗∗∗p < 0.0001). To see this figure in color, go online.

Results

The rate of membrane expansion is larger on 20-μm beads due to a constant velocity of the front of the spreading lamellum

Back indentation on phagocytes fed with 8- and 20-μm beads and flat surfaces led to the same delay t_cup to start forming the phagocytic cup (Fig. 2 A). The spreading duration t_Amax - t_cup was also the same for 8- and 20-μm beads with back indentation and on flat surfaces (t_Amax - t_cup ∼ 2 min; Fig. 2 B).

One notable difference among the targets of different sizes was the average spreading rate <dA/dt>. It was significantly larger on 20- than on 8-μm beads (Fig. 2 D). To test if this difference was a sign of adaptation by the cell to the size of the bead, we measured the advancing speed of the cell front on beads and flat surfaces by quantifying the curvilinear abscissa s of the cell front over time (see Materials and methods). This curvilinear abscissa s first increased linearly with time, meaning that the speed v₀ = $\frac{ds}{dt}$ was constant over time (v₀ ≈ 0.1 μm/s; Fig. 2 E). After this first constant-speed spreading phase, the abscissa s reached a value s_slowdown above which its increase slowed down (Fig. 2 E, inset above), until reaching a local maximum. Afterward, it usually exhibited oscillatory movement of small amplitude, similar to that observed in macrophages on flat substrates (33). Given a constant v₀, one can follow purely geometrical considerations to quantitatively predict a rate of increase of the phagocytic cup area that depends on the bead radius (Material S1). For a v₀ independent of bead size, one predicts that the larger the bead, the larger the spreading rate dA/dt. Our predictions of the ratio of average rates <dA/dt> on large and small beads are consistent with our experimental observation (Material S1), suggesting that instead of an adaptation to curvature, the observed increasing spreading rate (in surface area per unit time) is a direct consequence of a conserved velocity of the advancing front of the cell lamellum during phagocytosis.

The surface area deployed during frustrated phagocytosis is the same as that deployed by micropipette aspiration

The maximal surface area reached by the phagocytic cup of PLB cells during frustrated phagocytosis was the same on 20-μm beads as on planar surfaces (A_max∼300 μm²; Fig. 2 A, inset on right). On 8-μm beads, this maximum area was set by the bead surface area (A_max∼200 μm²). Phagocytosis, frustrated or not, requires the deployment of membrane stores such as those present in surface folds and microvilli (31,46). To test if the maximal cup area reached during frustrated phagocytosis corresponded to the mobilization of these membrane stores, we aspirated PLB cells in a micropipette until their membrane broke (see Materials and methods). This micropipette aspiration assay led to the same measured area as the one reached during spreading on 20-μm beads (Fig. 2 F).

Cells become stiffer during frustrated phagocytosis on 20-μm beads than during complete phagocytosis of 8-μm beads

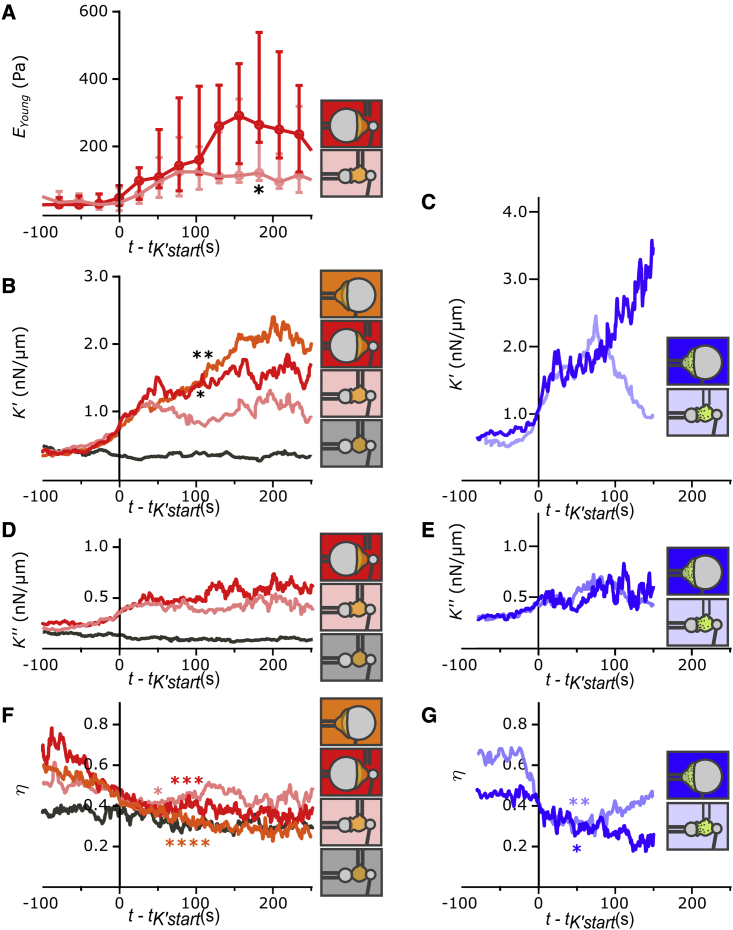
The delay between the onset of increase in K′ and the time when K′ attains its maximum value, t_K’max - t_K’start, was the same on 8- and 20-μm beads, but the peak value of K′, K’_max, was larger on 20- than on 8-μm beads (Fig. 2 C and G). The stiffness depends on the geometry of the cell: for a given cell’s Young’s modulus, which is the intrinsic elasticity of the cell material, a thinner cell will have a larger K'. To exclude a potential geometrical contribution to the measured differences in K′, we proceeded as in our previous study (29) and measured the effective cell’s Young’s modulus E_Young using cyclic indentation in the back on the cell (see Materials and methods). Confirming the trend in K′, E_Young was significantly higher during back indentation on 20-μm than on 8-μm beads (Fig. 4 A).

Figure 4.

Viscoelastic behavior during both complete and frustrated phagocytosis when indenting PLB cells (A, B, D, and F) and primary neutrophils (C, E, and G). Indentation in the front, back, and on 20- or 8-μm beads is indicated with schematics of the protocol used. In (B)–(G), for each individual curve, time was shifted so that time origin corresponds to the moment at which K′ reaches a level of 0.5 nN/μm above the initial level (t = t_K’start). (A) Young’s modulus E_Young of PLB cells measured by cyclic indentation in the back (see Materials and methods and Fig. S1). E_Young is significantly higher during back indentation on 20- than on 8-μm beads at t = 178 s (^∗). Median values (dots) and interquartile ranges (error bars) are shown. (B and C) Median cell stiffness K′ over time. In (B), at t = 78 s, K′ is larger during indentation of 20- than 8-μm beads (^∗ and ^∗∗, Mann). (D and E) Median K″ over time. (F and G) Bottom: loss tangent $\eta =\frac{K^{″}}{K^{\prime }}$ over time. Different experimental conditions are shown: PLB cells with 20-μm (red; N = 3, n = 15 cells) and 8-μm beads (pink; N = 3 experiments; n = 12 cells); control condition with non-opsonized 8-μm beads with back indentation of PLB cells (black, N = 3 experiments, n = 17 cells), and human primary neutrophils with 20-μm (dark blue; N = 2 experiments, n = 12 cells) and 8-μm (light blue; N = 2 experiments, n = 18 cells) beads. Each solid line represents the median value; for readability, the interquartile range is not shown. $\eta$ decreases during phagocytosis (comparing t - t_K’start = -100 s with t - t_K’start = 50 or 80 s in (F) and comparing t - t_K’start = -60 s with t - t_K’start = 50 s in (G), star symbols, two-tailed Mann-Whitney test). Raw data are shown in Figs. S6–S11. To see this figure in color, go online.

Cell stiffness reaches its maximum after spreading has ended, and in some cells stiffening starts after total engulfment of 8-μm beads

In some cells, stiffening starts after total engulfment of 8-μm beads. During most cases (73%) of frustrated phagocytosis of 20-μm beads by PLB cells, K′ reached its maximum after spreading had stopped (i.e., t_K’max - t_Amax > 0; Fig. 2 H): stiffness continued increasing even after completion of cell spreading. With some 20-μm beads (23% of cases) and more often with 8-μm beads (75% of cases), K′ started increasing after spreading had already stopped (Fig. 2 I and J; t_K’start - t_Amax > 0), meaning that K′ rose after any new mobilization of membrane was needed. Later, we discuss that this would not be predicted to happen by the model of Heinrich et al. but appears to be consistent with the older observations by Evans et al. (30) mentioned earlier.

Primary neutrophils spread faster and become stiffer than PLB cells during phagocytosis

Primary neutrophils (see examples in Video S2) formed their phagocytic cup quicker than PLB cells on 8-μm beads (shorter t_cup delay; Fig. 3 A). Primary neutrophils were quicker to reach their maximal cup area on both 20- and 8-μm beads (Fig. 3 B). The spreading rate $⟨\frac{dA}{dt}⟩$ was larger for primary neutrophils than for PLB cells on 8-μm beads (Fig. 3 D), which was a direct consequence of the fact that primary neutrophils spread with a front speed v₀ that was larger than the front speed of PLB cells on 8-μm beads (Fig. 3 E). The maximal cup area of primary cells was significantly smaller than that of PLB cells, which might only be coincidental based on the fact that resting primary neutrophils are smaller in radius than resting PLB cells (Fig. S5). This maximal cup area of about 200 μm² is comparable with the one obtained by Herant et al. for primary neutrophils (32). Primary neutrophils became stiffer than PLB cells (larger K’_max; Fig. 3 C), and on 20-μm beads, this stiffening occurred faster for primary neutrophils (Fig. 3 F). The average stiffening rate of primary neutrophils was larger than that of PLB cells (front/back indentation; Fig. S4). To sum up, primary cells exhibited “exacerbated” and faster reactions, leading to more pronounced mechanical changes.

Video S2. Activation of primary human neutrophils

Left: 20-μm bead, front indentation. Center: 8-μm bead, indentation in the back. Right: control non-activating 20-μm bead, indentation in the front.

Video S3. Frustrated phagocytosis of PLB cells on a flat surface

Left: large field of view. Right: zoom on the cell located in the upper right part in the large field of view. This cell was also shown as example in Suppl. Fig. S2. Time is in minutes:seconds.

For primary neutrophils, stiffness started increasing before maximal area was reached

As opposed to the case of PLB cells, even on 8-μm beads, primary neutrophils started stiffening before reaching their maximum area (Fig. 3 G).

During phagocytosis by both PLB cells and primary neutrophils, elastic and viscous properties increase, and the ratio of viscous to elastic properties decreases

For each cell, our rheometer allows quantifying the cell stiffness K′, the viscous part of the complex stiffness K’’ (which reports viscous properties of the cell), and the loss tangent $\eta =\frac{K^{″}}{K^{\prime }}$ (see Materials and methods). Given that t_K’start varied considerably among cells, we synchronized K′ curves before averaging them by using t = t_K’start as the time origin for each curve; we used this same time origin to average K’’ and $\eta$ (Fig. 4). We had shown previously that elastic and viscous properties of leukocytes follow parallel evolutions during activation (29) and that the loss tangent $\eta$ characterizes the type of leukocyte during its activation. Here, besides confirming that $\eta$ decreases during activation of PLB cells, i.e., that cell stiffness increases faster than cell viscous properties, we report the same behavior for primary neutrophils, at least at early times (see in Fig. 4 G: $\eta$ increases again ∼90 s after t = t_K’start for back indentation and 8-μm beads). K′, K’’, and $\eta$ follow a remarkably similar evolution for PLB cells in front and back indentations on small and large beads during the first ∼50 s following t = t_K’start (Fig. 4 B, D, and F). Our measurements show that primary neutrophils and PLB cells have a similar mechanical signature during activation that consists of a decrease in $\eta$ at early times.

Discussion

Phagocytes generate force during phagocytosis, change their mechanical properties, and adapt to the shape and stiffness of their target (16, 17, 18, 19,47). However, the mechanical aspects of phagocytosis are not fully understood (21,48, 49, 50). To better characterize these aspects, we used a micropipette-based single-cell rheometer to monitor the elastic and viscous properties and morphology of neutrophils and PLB cells during the phagocytosis of immunoglobulin G (IgG)-coated microbeads. We compared dynamics in spreading and mechanical changes, depending on target size, and we used micropipette aspiration to quantify the area of membrane stores available in microvilli and ruffles at the surface of resting PLB cells. We were able to show that bead size does not have a significant impact on the response time of PLB cells but leads to a rate of area expansion that increases with bead size. We have shown that this is a geometrical effect due to the fact that the advancing speed of the phagocytic cup is independent of the target size.

In a previous study, we used scanning electron microscopy to estimate the microscopic area contained in microvilli and folds present on the surface of Jurkat cells, primary human CD4 T lymphocytes, and human lymphoblasts (41). We showed that this surface microscopic area closely matched the membrane area obtained using the same micropipette aspiration experiment assay as used here on PLB cells. This suggested that passive extension of membrane is an effective readout of membrane-surface reservoirs. Assuming that this is also true for PLB cells, our micropipette-aspiration experiments show that their total surface area is about 1.8-fold larger than their apparent surface area (547 versus 309 μm², respectively; Figs. 2 F and S5). As we obtained a maximal surface area during frustrated phagocytosis that is consistent with this total area (Fig. 2 F), we speculate that frustrated phagocytosis does not require the mobilization of large inner membrane stores but mainly of membrane reservoirs present at the surface of PLB cells. Note that a small amount of inner-membrane recruitment is not excluded and may occur even during micropipette aspiration, as it has been shown that other means of passive extension of the cell membrane area such as osmotic swelling can provoke some exocytosis in human cells over a timescale of seconds to tens of seconds (51).

Cells became stiffer on 20- versus 8-μm beads over similar timescales. The relative timing of spreading and stiffening of PLB cells depended on target size: on larger beads, stiffening started before the maximal spreading area was reached. However, stiffening ended after this maximal area was reached. On 8-μm beads, this trend was more pronounced as in some PLB cells, stiffening started even after they had already engulfed the bead. In primary neutrophils, we did not observe this sequence, as stiffening started before the end of spreading even on smaller beads. Primary cells responded and stiffened faster but behaved similar to PLB cells by also becoming stiffer on larger beads.

Herant et al. characterized the tension of neutrophils as a function of the total apparent surface area A of the cell (31). Following their model, once a certain amount of membrane slack has been extended, the tension can be written as the sum of two terms that increase linearly with $\frac{A-A_0}{A_0}$ and $\frac{dA}{dt}$, respectively, where $A_0$ is the apparent surface area of the resting spherical neutrophil. This model allowed understanding of why phagocytosis of beads of 2-μm diameter did not evoke any increase in tension (expanded surface area was lower than the slack), while larger beads led to an increase in tension that increased with the size of the target. In the present study, during back indentation of PLB cells on 20-μm beads, in most cases, we observed that the phagocytic cup started spreading and cell stiffness K′ started increasing at a similar moment, consistent with the observations and model of Herant et al. However, we also observed that K′ reached its maximum after the maximum area A_max was reached. Once A_max is reached, $\frac{dA}{dt}$ vanishes, so following Herant’s model, K′ is not expected to evolve any further if cortical tension is the only contributor to K’. Even more puzzling, we observed that on 20-μm beads, a minority of cells reached their maximum cup area before K′ started increasing. These cases of late increase in K′ occurred more often when cells phagocyted 8-μm beads. In the latter cases, again, Herant’s model cannot account for the increase in K′, as the cell’s apparent area is constant, and its derivative is null. Our observation is consistent with earlier observation by Evans et al. of a sequence of spreading followed by an increase in tension in primary granulocytes phagocyting yeast (30). However, it is not clear why Evans et al. seem to have only seen spreading preceding an increase in stiffness. The different nature (opsonized yeast) might be a reason, as Lee et al. later showed that the mechanical response of phagocytes is different on zymosan versus antibody-coated targets (52).

An alternative to Herant’s model is keeping the concept of membrane slack to deploy before inducing a signal leading to an increase in K′ but with a time delay between reaching the threshold in membrane expansion and triggering the increase in stiffness. K′ starts increasing earlier on larger beads on which the membrane expands faster, supporting this idea of a threshold reached earlier. As K′ takes the same amount of time to reach its maximum on both large and small beads, we shall consider a constant delay independent of target size, which would reflect an inner timescale to turn on cell contractility. As a consequence of a delayed increase in stiffness, the evolution of K′ would not be directly linked to spreading through a term proportional to either A or dA/dt. Another alternative to amend the Herant model would be to consider that during phagocytosis, an important contribution to effective cell stiffness comes not from an increase in cell tension due to membrane expansion but rather from an increased active cell contraction not directly correlated to cell surface area. To account for the fact that the maximum in stiffness K′ is higher when a larger surface area has been deployed by a PLB cell, we speculate that the rate of increase of K′ scales with the total amount of mobilized surface-membrane stores. Irmscher et al. (28) measured a stiffening in phagocytic cups of THP-1 macrophages phagocyting 4.5-μm IgG-coated magnetic particles. The stiffness reached its maximum during particle engulfment. Interestingly, some phagocytoses that were interrupted led to a larger increase in stiffness, supporting the idea that stiffening is not only a function of membrane expansion. Other studies suggested that membrane tension instead of global cell tension is the signal triggering cell contraction via myosins (34). Cell tension is a compound parameter that encompasses membrane tension, actomyosin cortex tension, and energetic contributions from membrane-cortex adhesion (35). In unperturbed cells, Masters et al. measured a peak in tension at the onset of cell contraction after spreading, but this peak in tension was typically ∼10% in magnitude (34). Based on measurements of cell tension in the literature and on our measurements of cell stiffness, it appears that long before reaching its maximum area, the cell builds up a massive increase in stiffness or (cell) tension that can be of up to ∼1000% (29,31). This buildup might well end with a small peak in membrane tension, but it is hard envisioning that this massive increase in stiffness does not also play a role per se in the regulation of cell spreading. Further work should investigate how both cell and membrane tension regulate the dynamics of cells during phagocytosis.

In this study, we measured no difference in the time to start forming the phagocytic cup on 8- and 20-μm beads (using back indentation) and on planar surfaces; the maximal phagocytic cup surface area was also the same on 20-μm beads and on planar surfaces, suggesting that for targets of more than 8 μm, PLB cells are not sensitive to target size or curvature (we restricted our study to beads, and we could not vary curvature and size independently). It is not clear why others observed that phagocytes respond faster on larger targets (31,32), although comparison is not straightforward when the effect of target was explored on targets smaller than our 8-μm beads and kinetics of the onset of phagocytic cups were not systematically studied (53,54). Other studies suggest that phagocytes might sense the two local main curvatures (19), reacting differently to elongated ellipsoids versus flat prolate ellipsoids (16). For beads, sensitivity to the target remains seemingly controversial. Montel et al. (55) obtained results with fluid droplets that are consistent with the prediction of Simon and Schmid-Schöenbein (22) that the critical parameter is the surface-area reservoir of the cell and not the target size per se. In our study, phagocytes do not seem to adapt to target size. We saw a conserved spreading velocity of the phagocytic cup front v₀ of about 0.1 μm/s, comparable to velocities measured during phagocytosis of yeasts by granulocytes (30), to the spreading velocity of macrophages (33), and to the faster internalization velocity of IgG-opsonized particles by macrophages (16). This velocity is also compatible with polymerization velocity of actin filaments by the Brownian ratchet model (56). Interestingly, Champion et al. (57) reported no difference in the average speed of cup progression in macrophages, which was about 4 μm/min (i.e., about 0.07 μm/s), again consistent with our measured speed v₀ of about 0.1 μm/s. Champion et al. used beads of diameters ranging from 3 to 9 μm, suggesting that the v₀ that we measured could be constant even for targets as small as 3 μm. Jaumouillé et al. also measured cup-protrusion speeds of 0.1 μm/s, in RAW 264.7 macrophages (49). This constant front velocity v₀ raises the possibility of considering a mechanism for “feeling” the local curvature of a target because, at constant velocity, the rate of increase in surface area $\frac{dA}{dt}$ scales with the radius of the target. Furthermore, at a constant ligand density on the target surface, $\frac{dA}{dt}$ is proportional to $\frac{dN}{dt}$, where N is the number of ligated receptors on the phagocyte surface. Thus, a phagocyte could “measure” the local curvature of its target by “sensing” the rate of receptor engagement. However, this model remains insufficient because $\frac{dA}{dt}$ would also depend on the ligand being homogeneously distributed, as well as its average density: the phagocyte could not decipher a difference in curvature and in ligand density, although Kovari et al. showed that this density did not influence spreading dynamics once cells were committed to phagocytosis (33).

When compared with indentation in the back of PLB cells, indentation in the front led to a delayed onset of cup formation and a longer spreading time, although the same maximal phagocytic cup area was reached (Fig. 2). Thus, the front-indentation protocol can be interpreted as perturbing the cells. One possibility is that during front indentation, the cell has to be held in the pipette with some aspiration during the entire experiment (although experiments usually end with the cell extracting itself from the pipette because of its increased tension), which might perturb the cell. Future studies will require careful control of the influence of the protocol with the single-cell rheometer and possibly favor the more challenging but less perturbing back indentation of the phagocyte.

Our technique allows direct quantification of viscous effects through the measurement of K″, the imaginary part of the complex stiffness K^∗, which is intimately linked to cell stiffness K’. An increase in cell phagocyte stiffness is paralleled by an increase in phagocyte viscosity. This is difficult to account for by a model where viscous effects emanate mainly from surface expansion during phagocyte spreading because in cases when K′ increased only after an 8-μm bead had been engulfed, there was no additional membrane expansion. Heinrich et al. provided a clear explanation (58) of how the ratio of the leukocyte tension $\gamma$ to its effective viscosity $\nu$ (different from the surface viscosity introduced by Herant et al. mentioned above), i.e., the capillary velocity $v_c=\frac{\gamma }{\nu }$, is the relevant scale for the cell-deformation speed. Heinrich et al. argued that comparing the capillary velocity $v_c$ with the spreading velocity v₀ during phagocytosis allows understanding of why a phagocyte rounds up after spreading a thin lamellum around its target. It is worth noting that the loss tangent that we measured here, $\eta =\frac{K^{\prime }}{K^{″}}$ (29), scales as $\frac{1}{v_c}$ following dimensional analysis, so that our experiments allow us to estimate $v_c$ with high temporal resolution. We have shown that $\eta$ decreases during phagocytosis (Fig. 4); hence, $v_c$ increases, consistent with the fact that rounding up of the phagocyte requires a higher value of $v_c$ than during spreading (58). Further work should make more systematic use of this high-temporal resolution measurement of the loss tangent in order to better understand the physical determinants of cell geometrical changes during activation.

As our observations suggest that an increase in cell stiffness during phagocytosis is not a direct consequence of surface expansion, we shall speculate on the origin and role of these mechanical changes. The fact that on smaller beads cell stiffness increased after cup closure suggests that the stiffening that we measure is not directly due to myosin-II-generated contractile force considered to be at play during cup closure (33,48). The role of myosins during phagocytosis is debated (48), and myosin II could have a role in disassembling F-actin rather than only in exerting contractile forces (50). It is possible that the recently described myosin-dependent “teeth” that indent a phagocytic target are part of actin-recruiting machinery that leads to cell-scale stiffening (50). The formation of the phagosome might also explain cell stiffening, since it requires actin polymerization (3), and a larger target requiring a larger phagosome might thus explain a larger increase in K’. A transient accumulation of F-actin on phagosomes has been observed during phagocytosis of bacteria and IgG-opsonized particles. In a recent study, Poirier et al. study these so-called “F-actin flashes” in macrophages. The flashes appear on phagosomes shortly after internalization and coincide with deformation of phagocyted red blood cells (59). F-actin flashes recruit myosin II, whose activity leads to phagosome-content deformation. Interestingly, the rigidity of the phagosome contents influenced F-actin flashing dynamics, suggesting that this “chewing” might help probe the target mechanical properties. This process might also help severing a target into two subtargets, as has been observed in Dictyostelium discoideum (19) and occasionally in macrophages (59). We speculate that increasing tension around the phagosome could also decrease the phagosomal volume and thus increase local concentration of aggressive species aimed at attacking a phagocyted target. Poirier et al.’s observations of deformed phagosomes occurring during F-actin flashes are consistent with observations by Vorselen et al. that macrophages induce a large reduction in soft gel particles after complete internalization (50). It would be very interesting to directly correlate potential F-actin flashes in neutrophils and direct measurements of cell stiffness.

We showed that understanding mechanical aspects of phagocytosis can benefit from a direct measurement of viscoelastic properties of cells with a high temporal resolution and simultaneous monitoring of cell morphology with high spatial resolution. We have shown that not all mechanical changes can be considered direct consequences of cell spreading. Further work is required to understand the function of these mechanical changes. One possible direction is to slow phagocytosis dynamics and better separate the timescales of spreading and stiffening by performing experiments at a temperature lower than room temperature (30).

Author contributions

J.H. designed experiments; A.Z. and J.H. performed experiments; A.Z., S.D.-C., E.H., O.N., and J.H. analyzed the data; A.B., S.D.-C., E.H., A.I.B., and O.N. contributed material; A.Z. and J.H. wrote the manuscript with helpful critical reading from the other authors.

Editor: Kinneret Keren.