Skip to main content
PMC home page
RSC Advances logoLink to RSC Advances
. 2019 Oct 8;9(55):31999–32009. doi: 10.1039/c9ra06291b

Materials with the CrVO4 structure type as candidate superprotonic conductors†

Pandu Wisesa 1, Chenyang Li 1, Chuhong Wang 1, Tim Mueller 1,✉
PMCID: PMC9072970  PMID: 35530777

Abstract

Proton conducting oxides have the potential to improve the efficiency of solid oxide fuel cells and electrolyzers, yet many oxide structures remain relatively unexplored for the ability to conduct protons. To accelerate the search for novel proton-conducting oxides, we have performed a computational screen of the proton migration energy in 41 different commonly-occurring oxide structure types. The results of this screen, which are supported by a comprehensive set of density functional theory calculations, indicate that known materials with the CrVO4 structure type have an average migration energy for proton diffusion of less than 0.2 eV, with several known materials having calculated migration energies below 0.1 eV. These results indicate that materials with the CrVO4 structure type, which to our knowledge have not been previously explored as candidate proton conductors, may exhibit very high proton conductivity that surpasses that of leading proton-conducting oxides. We present the results of our screen as well as diffusion dimensionality analysis and thermodynamic stability analysis for materials with the CrVO4 structure.

A computational screen reveals that materials with the CrVO4 structure type may have very low migration barriers for proton conduction.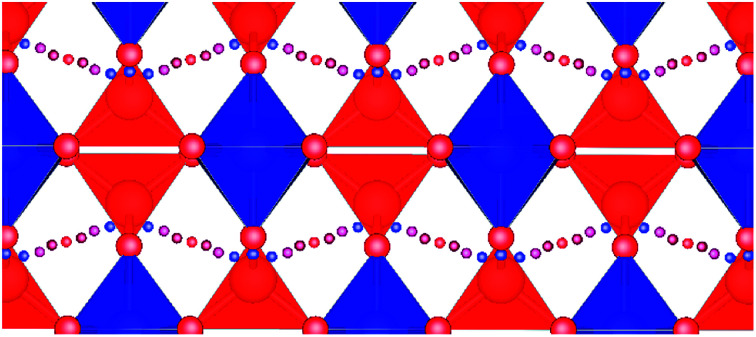graphic file with name c9ra06291b-ga.jpg

1. Introduction

Proton-conducting solids are used in a variety of applications, including as hydrogen separation membranes in chemical processing1–11 and in electrodes or electrolytes in solid oxide fuel cells12–21 and electrolyzers.22–26 There is particular interest in using proton-conducting oxides as electrolytes and electrode materials in fuel cells, where an electrolyte must be electronically insulating but an electrode material may be a mixed ionic-electronic conductor. A widely-used fuel cell technology, proton exchange membrane (PEM) fuel cells, uses polymer electrolytes that operate in an aqueous environment, so their operating temperatures are typically below 100 °C.27,28 At such low operating temperatures PEM cells require the use of expensive catalysts to achieve sufficiently high rates.28 An alternative is to use a solid oxide that conducts oxygen ions for the electrolyte (and ideally the electrode as well), but to achieve sufficiently high rates such fuel cells typically need to be operated at temperatures above about 600 °C.18,29 There is increasing interest in developing fuel cells that can operate at intermediate temperature ranges, which could lower the cost of the fuel cells, reduce start-up times, improve efficiency, and improve long-term durability.22,29–32 As protons are smaller than oxygen ions and carry half the electronic charge, they tend to diffuse more readily than oxygen ions; thus a promising route to improving the rate capability (and lowering the operating temperature) of solid oxide fuel cells is to use proton-conducting oxides as electrolytes and electrode materials.12–21 Fuel cells with proton-conducting electrolytes have additional advantages in that the reaction products are produced at the cathode, rather than the anode, so they are kept separate from the fuel, which can result in gains in efficiency.13,14 For fuel cells that use ammonia as a fuel, the use of proton-conducting electrolytes prevents the formation of NO, an unwanted byproduct.17 Despite their advantages, fuel cells that use proton-conducting oxides are limited by a number of factors including poor proton transport through grain boundaries and poor stability in fuel cell operating conditions.20,33–36 To address these issues, there is a need to develop new proton-conducting oxides that are stable in fuel cell operating conditions and have high proton conductivity.

The most widely-studied class of proton-conducting oxides contains materials with the perovskite structure or closely related structures.20,34–42 A perovskite-structured material, SrCeO3, was one of the first proton-conducting oxides with high proton conductivity,43 and two of the current leading families of proton conducting oxides, based on BaZrO3 and BaCeO3, have the perovskite structure.20,34,36 Perovskite-structured oxides can accommodate a wide variety of cations in different stoichiometries,44 providing researchers great flexibility in tailoring their properties. Many perovskite-structured oxides can also accommodate high concentrations of oxygen vacancies and allow for relatively facile diffusion of oxygen ions, providing a mechanism to introduce protons into the host material through a reaction with water. Importantly, the arrangement of oxygen ions in the perovskite structure provides a continuous three-dimensional network for protons to migrate via the Grotthuss mechanism,45 in which they rotate around oxygen ions and then hop between them. In the search for new proton-conducting oxides, researchers have increasingly been exploring materials that do not have the perovskite structure. These efforts have revealed proton conductivity in materials such as solid acids,21,46–48 ortho-niobates,33 ortho-tantalates,33,49 orthophosphates,50,51 pyrochlores,52 sesquioxides,53 (oxy)sulfides,54 nitrides,55 tungstates,56 tungsten oxide, where the Grotthuss mechanism was not observed,57 and recently Li13.9Sr0.1Zn(GeO4)4 (LSZG).58

There are a number of criteria that must be met for a proton conductor to work in a fuel cell, electrolysis cell, or related technology. Among these, the material must be stable at operating temperatures, resistant to poisoning, and selective. It must also have sufficiently high proton solubility. It is important to consider the electronic conductivity when assessing whether the material would be suitable for use as an electrolyte, membrane, or electrode material. However in all applications, it is necessary that the bulk mobility of protons through the material is high. There are on the order of 100 000 known inorganic materials,59 but the bulk proton mobility is unknown for most materials, making it possible that there are entire classes of known materials that are good proton conductors but are currently being overlooked.

In this work we perform a high-throughput computational search to identify structure types that are likely to have high proton mobility. We focus on structure types rather than individual compounds as the ionic conductivity of a material is determined to a large extent by whether arrangement of cations and anions in the material is conducive to creating a potential energy surface with a low activation energy for ionic migration.36,60–62 Once a structure type conducive to proton mobility is identified, materials with that structure type and different chemical compositions can be designed and/or synthesized to try to find a material with high stability and proton solubility while maintaining a relatively high probability of having high proton mobility.

2. Methodology

We searched for promising structure types for proton conducting oxides using a multi-level screening approach. We first identified over 37 000 unique oxide materials with fully occupied sites from the Inorganic Crystal Structure Database (ICSD).59 The structures were grouped by their structure types using an algorithm developed by our group to compare crystalline structures, resulting in 3663 different oxide structure types. As we are most interested in structure types that can accommodate a variety of different elements, we selected from these the structure types for which the ICSD contained at least 20 unique materials, resulting in a data set of 41 structure types and 1946 structures in total.

We use the classical activation energy for proton migration (within the Born–Oppenheimer approximation) as our primary descriptor for proton mobility. We will refer to this value as the “migration energy”. As the contribution to the material energy from the zero-point vibrational energy of protons can be large (∼100–200 meV),63,64 there is likely a significant quantum contribution to proton mobility that is not captured by classical transition state theory. However even if quantum corrections are taken to account, it can be expected that materials with a lower classical activation energies will generally have faster proton migration.65–67 Thus for the purposes of screening for promising proton conductors it is sufficient to use the classical migration energy.

The 1946 different oxide materials we consider contain 75 different elements. To calculate activation energies for proton migration in all 1946 materials it is necessary to use an energy model that works for most of the periodic table. As the use of first-principles methods such as density functional theory (DFT)68,69 for all materials in our data set would have been prohibitively expensive, we developed a simpler model based on the bond valence method,70–74 which has been parameterized for nearly all elements.75 In the bond valence model, the bond valence between two neighboring atoms is given by

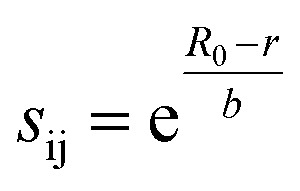2. 1

where sij is the bond valence, r is the bond length, and R0 and b are parameters of the model. The valence of an atom is then given by the sum of the bond valences for bonds containing that atom. Here we have used the parameterization of Brese and O'Keefe,75 in which b = 0.37 and R0 can be calculated for nearly any pair of elements in the periodic table.

The bond valence method relates the valence of a bond to the equilibrium bond length, but it cannot be used directly to calculate energies.74,76 However there is a natural relationship between the bond valence approach and electrostatic interactions77 that makes it possible to construct a simple pairwise interatomic potential that is largely consistent with the bond valence model. Adams and Rao have developed a method for using the bond-valence method to construct a pairwise interatomic potential by combining a Morse-type term with a repulsive electrostatic term,78 and they have used their approach to study lithium ion diffusion in battery materials.79–81 Here we use a similar approach. The main difference between our approach and that of Adams and Rao is that the repulsive part of our potential is exponential, and attraction is represented by a screened Coulomb potential rather than a Morse potential. All electrostatic interactions, both attractive and repulsive, are thus combined in a single term:

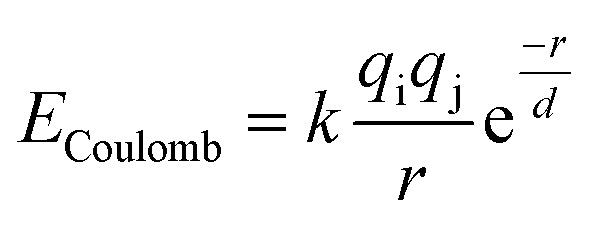2. 2

where k is the Coulomb constant, qi and qj are the electrostatic charges of the two atoms, r is the distance between the two atoms, and d is the screening radius. Here we approximate the electrostatic charges to be proportional to the valence of the atoms as determine by the bond valence model, where the coefficient of proportionality and screening radius are determined by fitting to DFT data.

The repulsive part of the potential is given by:

Eexp = A e−rC 3

where r is the distance between two neighboring atoms, and A and C are constants for specific element pairs. The combined potential is then

Epair = Eexp + ECoulomb 4

To determine approximate values for A and C in eqn (3), we use the fact that for a given set of atomic valences, the equilibrium bond length in eqn (4) should match the bond length used to generate those valences in eqn (1). For a given value of R0, we find the values for A and C that minimize the mean squared difference between the equilibrium bond length and the value of r in eqn (1) over seven different binary crystal structures: rhenium trioxide, cristabolite, cuprite, wurtzite (hexagonal), rutile, fluorite, rock salt, and cesium chloride. The values of A and C were then further refined by linearly scaling them using universal scale factors fit to DFT data. To account for atomic relaxations from ideal crystalline sites in the presence of a proton, we connected each atom to its ideal site through a virtual spring, where the spring constant was a linear function of absolute value of the atomic charge. The parameters of this function were also fit to DFT data. Additional details about our approach, including the parameters used for our calculations, are provide in the ESI.†

We used the above energy model to construct the potential energy surface for a single proton in the different oxide materials studied. We used a combination of a grid search, gradient descent, and structural symmetry to find saddle points, local minima, and diffusion pathways through each material. Starting from the proton site with the lowest potential energy, all possible diffusion pathways that fully crossed a unit cell were evaluated, and the pathway with the lowest maximum potential energy was selected as the most likely diffusion path. The migration energy for proton diffusion through the material was then calculated as the difference between the maximum and minimum potential energies along the most likely diffusion path.

2.1. Density functional theory calculations

All DFT calculations were done using the Vienna Ab initio Simulation Package (VASP)82–86 versions 5.3 and 5.4 using “accurate” precision. The electronic minimization was done using a combination of blocked Davidson iteration scheme and RMM-DIIS.87,88 Perdew–Burke–Ernzerhof (PBE)89 projector augmented wave (PAW)90 potentials were used for all calculations. To take into account of possible spin polarization in the material, all calculations are set to be spin polarized. The electronic self-consistency cutoff was set to 10−5 eV and the relaxation cutoff was set to 10−3 eV. The relaxation was done using the RMM-DIIS algorithm. The k-point grid was generated using the k-point grid server91 with a minimum periodic distance of 28.1 Å. For thermodynamic stability calculations, we used the GGA + U approach of Dudarev.92 We used a U-J value of 3.25 eV for vanadium, as determined by the Materials Project by fitting to the experimental formation energies of different vanadium oxides.93 For cerium we used a value of 4.5 eV, which was determined self-consistently for Ce2O3 by Fabris et al.94 and is close to the value of 5 eV determined empirically for BaCeO3 by Shishkin and Ziegler.95

2.2. Nudged elastic band calculations

We used the climbing image nudged elastic band (CI-NEB) method as implemented in VASP by the Henkelman group.96–100 The spring constant used for the elastic band was 5 eV Å−2 and atomic relaxation was performed using damped molecular dynamics with scaling constant (POTIM) of 0.01. The energy model described above was run using experimental lattice parameters and atomic positions, as these are the values available from the ICSD. As the equilibrium structure in DFT calculations is typically slightly different from the experimentally-determined structure, we relaxed the volume of all structures using DFT prior to running NEB calculations. By relaxing the volume while leaving the fractional atomic coordinates unchanged, we ensured that it was straightforward to use the diffusion paths discovered using our energy model to initialize NEB calculations while avoiding spurious relaxations in DFT due to large stresses on the unit cell.

All NEB calculations were run in supercells of the relaxed unit cells that ensured there were at least 8 Å between periodic images. All NEB calculations were run at fixed volume and atomic positions were allowed to relax to create realistic models of proton diffusion in the dilute limit.35,101 For each diffusive hop, the NEB images were initialized by placing hydrogen atoms along the path of the hop with no more than 0.5625 Å between successive hydrogen locations. The end points of the NEB calculation had their lattice vector frozen and atomic positions relaxed.

Oxides are typically doped with an electron acceptor to incorporate protons into the lattice. As this would break symmetry and significantly increase the computational expense of our calculations, we generated training data for our energy model using a perfect (undoped) crystal in which a single electron was removed per diffusing hydrogen atom in the NEB calculations. To minimize discontinuities due to spin flips during the NEB calculations, the magnetic moments on all atoms in each image were fixed to the values of the relaxed, empty (without hydrogen) structure. The conjugate gradient algorithm was used for atomic relaxation in all NEB runs. The relaxation was stopped when forces converged within 0.05 eV Å−1. All other parameters were the same as those listed in the above section on density functional theory calculations.

2.3. Stability of doped phases

We used PyMatGen102 to identify the likely decomposition products of the doped compositions from the Materials Project database, and we calculated the energies of the doped phases and possible decomposition products using DFT as described above. For the DFT calculations we assume the dopants are distributed in a way that maximizes the distance between dopant atoms in the resulting materials, and we use our energy model to calculate the likely position of H in the doped material.

3. Results

3.1. Migration energies of the training data

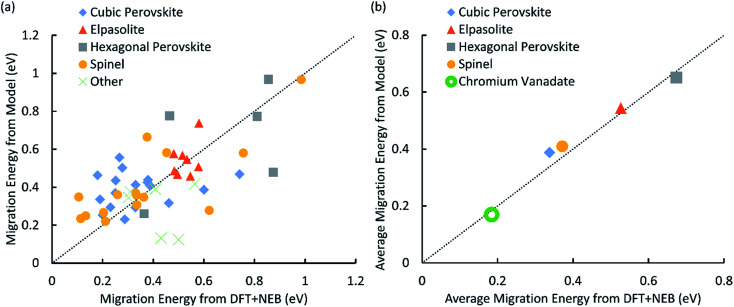
The parameterized potential model was able to predict the migration barriers energies of the 52 structures in our training set (Table 3-S in the ESI†) with a mean absolute error of 0.126 eV (Fig. 1) relative to DFT. Within the set of 52 training structures, there are four structure types that are represented by at least five structures: cubic perovskite, hexagonal perovskite, elpasolite, and spinel. Much of the noise in the fit disappears when we evaluate the average activation energies for each of these structure types (Fig. 1b), and the mean absolute error between the potential model and DFT decreases to 0.032 eV. This reduction in error can be understood by considering a simple model in which the migration energy can be expressed as the sum of two components: the average migration energy for materials with that structure type, and the deviation from this average due to the chemical composition of the material. The total prediction error (Fig. 1a) will be a sum of the errors for each of these components. If the parameter fitting produces a model for which the mean error in the chemical composition component is nearly zero, then even if the variance of this error is large its contribution to the overall error can be greatly reduced by averaging over different chemical compositions.

Fig. 1. (a) A plot of activation energy for proton migration calculated by DFT + NEB vs. predicted by the energy model. Structure types with less than 5 members in the dataset are put together and represented by the green cross. (b) A plot of average migration energy by structure type calculated by DFT + NEB vs. predicted by the energy model. The filled shapes correspond to the training data in part (a), and the empty green circle represents the CrVO4 structure type discovered by our screen, with the DFT activation energy averaged over all 29 structures in Table 2. In both (a) and (b) the diagonal dotted line represents perfect agreement.

Fig. 1

Open in a new tab

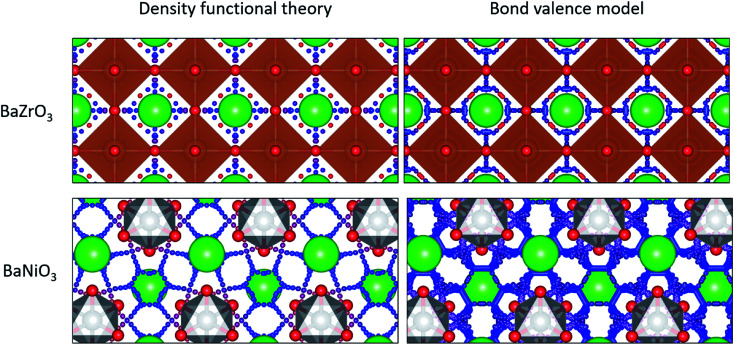
As expected, our calculations show that the average migration energy for cubic perovskites, the most studied class of proton conductors, is relatively low. Our DFT-calculated activation energies are consistent with those reported by Bork et al.103 A typical diffusion pathway in a cubic perovskite, BaZrO3, is shown in Fig. 2. The pathway predicted by the energy model, including the locations of the end points and saddle points, corresponds well to DFT + NEB pathways. Diffusion occurs via a Grotthuss-type mechanism, where the proton rotates around the oxygen atom before hopping to the next oxygen atom. Protons also diffuse through hexagonal perovskites via a Grotthuss-type mechanism (Fig. 2), but the hexagonal perovskites in our training data have nearly twice the average activation energies of cubic perovskites even though they share the same composition of ABX3, providing an indication of the importance of structure type in determining activation energies.

Fig. 2. Ab initio (left) and model-predicted (right) diffusion pathways in a cubic perovskite (top) and hexagonal perovskite (bottom). Large green spheres represent barium atoms, orange polyhedra contain zirconium, and grey polyhedra contain nickel. Small spheres represent the possible diffusion pathways with warm (more red) colors representing high energy sites and cool (more blue) colors representing low energy sites.

Fig. 2

Open in a new tab

3.2. Screening structure types

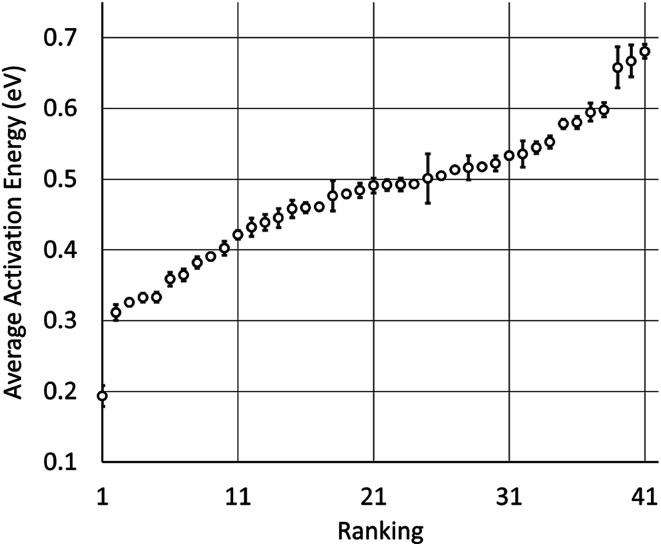
We used our model to predict the activation energies for proton diffusion in all 1946 test structures, representing 41 different structure types with at least 20 oxide materials per type. On average, predicting the average migration energy for a structure type took around 20 minutes on a single core, which is a small fraction of the cost of DFT + NEB calculations. The average activation energies per by structure type are provide in Table 1 and Fig. 3. We note that the average activation energies for cubic perovskite, hexagonal perovskite, spinel, and elpasolite are different than the averages shown in Fig. 1, as these averages were taken over all oxide structures in the ICSD rather than just those in our training set.

A ranking of 41 oxide structure types screened by the model based on their average migration energy.

Rank Average migration energy (eV) Sample standard deviation (eV) Structure type name Number of materials Space group
1 0.193 0.105 CrVO4 29 Cmcm
2 0.312 0.099 Calcite 20 R3̄c
3 0.326 0.084 Zircon 64 I41/amd
4 0.332 0.067 NaMn7O12 30 Im3̄
5 0.333 0.074 Fergusonite 27 C2/c
6 0.359 0.154 Spinel–Al2MgO4 64 Fd3̄m
7 0.364 0.105 Rutile 41 P42/mnm
8 0.382 0.089 LiYb(WO4)2 30 P2/n
9 0.391 0.100 Pyrochlore 91 Fd3̄m
10 0.402 0.129 Scheelite 43 I41/a
11 0.421 0.093 ZrCuSiAs–CuHfSi2 57 P4/nmm
12 0.432 0.241 Cubic perovskite 88 Pm3̄m
13 0.439 0.107 Barite–BaSO4 23 Pnma
14 0.445 0.129 Sc2Si2O7 23 C2/m
15 0.458 0.121 Th2TeN2 24 I4/mmm
16 0.460 0.094 Olivine 44 Pnma
17 0.461 0.101 Tilted perovskite 161 Pnma
18 0.477 0.231 PbClF 29 P4/nmm
19 0.479 0.067 Quaternary double perovskite 47 P21/n
20 0.484 0.118 Pyroxene–CaMg(SiO3)2 35 C2/c
21 0.491 0.093 Monazite 20 P21/n
22 0.492 0.085 CaFe2O4 30 Pnma
23 0.492 0.091 BaCuY2O5 26 Pnma
24 0.493 0.068 Double perovskite 96 P21/n
25 0.501 0.271 Fluorite–CaF2 15 Fm3̄m
26 0.505 0.064 Bi2ErO4I 38 P4/mmm
27 0.513 0.052 Sr2NiWO6 34 I4/m
28 0.516 0.181 Rocksalt 28 Fm3̄m
29 0.517 0.079 Elpasolite 121 Fm3̄m
30 0.522 0.133 La2O3 40 P3̄m1
31 0.533 0.035 Apatite 17 P63/m
32 0.536 0.231 K2MgF4 39 I4/mmm
33 0.545 0.075 La3NbO7(OS) 21 Cmcm
34 0.553 0.131 K4CdCl6 56 R3̄c
35 0.578 0.081 Melilite 39 P4̄21m
36 0.580 0.108 K2SO4 41 Pnma
37 0.595 0.170 Delafossite 45 R3̄m
38 0.598 0.088 Bixbyite–Mn2O3 19 Ia3̄
39 0.658 0.296 Delafossite–NaCrS2 26 R3̄m
40 0.667 0.169 CuFeO2 14 P63/mmc
41 0.681 0.124 Hexagonal perovskite 40 P63/mmc
Open in a new tab

Fig. 3. Plot of the ranking shown in Table 1, along with calculated standard errors of the averages. CrVO4 is represented by the dot near 0.2 on the left.

Fig. 3

Open in a new tab

The structure types with the highest predicted average activation energies are elpasolite, hexagonal perovskite, CuFeO2, delafossite–NaCrS2, and Sr2NiWO6. The average activation energies for proton diffusion in these structure types is about 200 meV higher than the average for cubic spinel, which at 600 °C would correspond to a more than 10-fold decrease in proton mobility assuming an Arrhenius-type dependence on migration energy. However within these structure types there can be significant variation in activation energies among individual materials (Table 1), leaving open the possibility that some materials with these structure types may be competitive as proton conductors.

There are 11 oxide structure types for which the predicted average activation energies are below that of cubic perovskite, and nearly 20 more with average activation energies within 100 meV. This suggests that materials with a variety of different structure types could have proton mobilities competitive with cubic perovskites. The fifth-best structure type, a monoclinic fergusonite, has been experimentally investigated for proton conductivity. Several rare-earth niobates and tantalates with this structure type have demonstrated proton conductivity on the order of 10−4 to 10−3 S cm−1 at about 700 °C, making them among the best known proton conductors outside the Ba- and Sr-based cubic perovskites.33 Many materials of this class transform to a high-temperature scheelite phase (#10 on our list) that has similar proton conductivity.33,104 The ninth-best structure type, pyrochlore, has also been investigated for proton conductivity.52,105 Materials of this type have demonstrated proton conductivity on the order of 10−4 to 10−3 S cm−1 at about 800 °C.105

The four structure types with the lowest average activation energies are CrVO4, calcite, zircon, and NaMn7O12. NaMn7O12 is a cubic double-perovskite structure closely related to the cubic perovskites.106 To our knowledge, the remaining three structure types have never been studied for proton conductivity. Of these, the CrVO4 structure type is an outlier in our analysis (Fig. 3), with a predicted average migration energy more than 0.1 eV below that of the next-best structure type, suggesting exceptionally high proton mobility. We have investigated the prediction of our model by using DFT to calculate the activation energies for proton migration in all 29 materials with this structure type in the ICSD (Table 2). We have used both DFT and DFT + U to calculate proton migration barriers (Section 4 in the ESI†) and found that the mean absolute difference is only 34 meV and the mean difference is only 2 meV, suggesting low sensitivity of these results to the U values. The average DFT-calculated migration energy, 184 meV, is in excellent agreement with the model prediction (Fig. 1). These low activation energies for diffusion suggest that some materials with the CrVO4 structure type may be superprotonic conductors.

Calculated properties for the 29 known CrVO4-structured oxides in the ICSD.

ICSD ID Composition Energy above hull (eV per atom) Predicted activation migration energy for 1D diffusion (eV) Predicted activation migration energy for 2D diffusion (eV) Predicted activation migration energy for 3D diffusion (eV) DFT calculated migration energy (eV)
16618 InPO4 0.000 0.084 0.427 0.870 0.340
16619 TlPO4 0.000 0.159 0.473 0.841 0.270
16741 NiSO4 0.000 0.067 0.389 0.865 0.161
16759 MgSO4 0.000 0.048 0.433 0.959 0.234
18117 MgCrO4 0.000 0.259 0.430 0.775 0.094
18118 CdCrO4 0.000 0.212 0.518 0.620 0.056
23492 CoCrO4 0.000 0.232 0.414 0.873 0.094
23493 NiCrO4 0.000 0.228 0.306 0.875 0.053
25700 NiSeO4 0.000 0.219 0.421 0.906 0.249
31231 MnSO4 0.000 0.386 0.386 0.669 0.217
60571 CdSO4 0.000 0.135 0.470 0.924 0.177
82286 VPO4 0.000 0.070 0.367 0.810 0.196
155162 InVO4 0.000 0.246 0.494 0.881 0.054
416147 HgCrO4 0.000 0.270 0.551 0.943 0.085
23507 FeSO4 0.001 0.075 0.437 0.725 0.159
33736 CoSO4 0.002 0.048 0.437 0.752 0.229
109070 MgSeO4 0.002 0.140 0.447 0.935 0.282
109071 MnSeO4 0.002 0.133 0.465 0.923 0.165
109072 CoSeO4 0.005 0.158 0.444 0.918 0.256
36244 CrVO4 0.007 0.275 0.338 0.881 0.172
109073 CuSeO4 0.007 0.128 0.462 0.898 0.295
82161 FeVO4 0.015 0.214 0.459 0.897 0.262
62159 CrPO4 0.018 0.048 0.366 0.848 0.242
155065 FePO4 0.021 0.037 0.428 0.862 0.195
183216 CuCrO4 0.031 0.152 0.383 0.853 0.154
82282 TiPO4 0.074 0.167 0.311 0.627 0.321
159272a AlPO4 0.106 0.091 0.218 0.846 0.161
89505 LiMnO4 0.143 0.242 0.444 0.831 0.086
166436b TiSiO4 0.156 0.054 0.437 0.695 0.091
Open in a new tab
a

The CrVO4 structure type has been identified as that of the high-pressure phase.107

b

The CrVO4 structure type was computationally determined to be the lowest-energy polymorph,108 but to our knowledge it has never been synthesized.

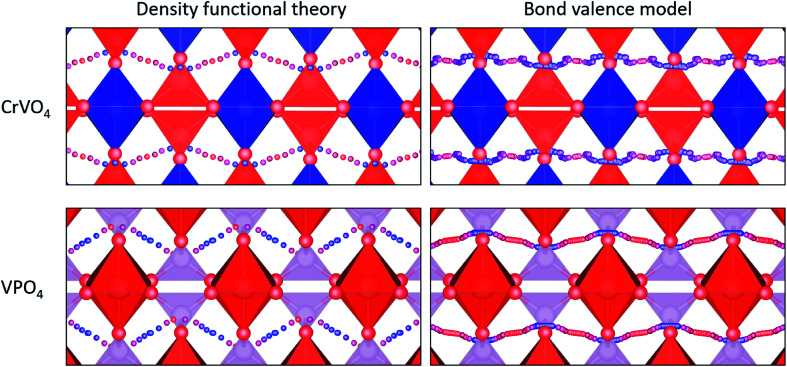
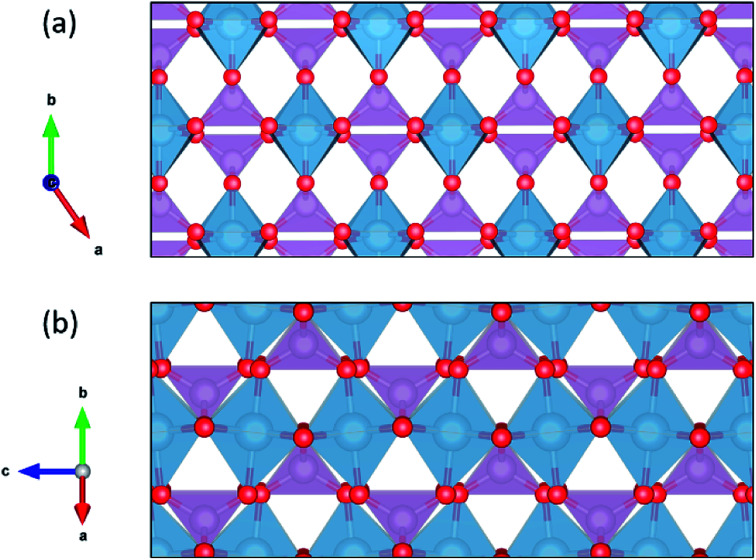
CrVO4 has an orthorhombic lattice, with one-dimensional columns of CrO6 octahedra linked together by sharing common oxygen atoms with VO4 tetrahedra. It is generally the stable structure for compositions in which the crystal radius of the octahedrally-coordinated ion is between 0.75 and 1.1 Å, and the crystal radius of the tetrahedrally-coordinated ion is between 0.25 and 0.5 Å.109 Proton diffusion is predicted to preferentially occur along a one-dimensional path through the lattice perpendicular to the columns of CrO6 octahedra (Fig. 4). As with most oxides, proton conduction is predicted to occur via a Grotthuss-type mechanism where the proton rotates around on oxygen ion and then jumps to another. Large rotations of the tetrahedra, as observed in CsH2(PO4),110 are not required for proton migration. Because the potential energy surface along the diffusion path is fairly flat, the local minimum varies from material to material, and the jump between the oxygen ions sometimes represents the local minimum along the diffusion path (Fig. 4). As our energy model sometimes identifies the wrong local minimum along this path due the small energy differences between the local minima and the transition states (Fig. 4), we manually evaluated different possible local minima for many of the DFT nudged-elastic-band calculations.

Fig. 4. Fastest diffusion paths for VPO4 and CrVO4, which are the representatives of the CrVO4 structure type. Red tetrahedra represent the bonds between vanadium and oxygen blue tetrahedra represent the bonds between chromium and oxygen, and purple tetrahedra represent PO4−3. Small blue and red spheres represent the diffusion pathway, with blue indicating low energy sites and red indicating high energy sites.

Fig. 4

Open in a new tab

Ionic conductivity in one dimension presents practical challenges, as defects that block the diffusion channel could significantly inhibit diffusivity.111 For this reason it is important to assess the ability of protons to migrate around defects by diffusing in a second dimension. We have used our model to calculate the minimum migrations energies required for one-, two-, and three-dimensional diffusion in each of the 29 materials with the CrVO4 structure type (Table 2). As we ran some of these calculations with denser grids to ensure convergence in all three dimensions, the average migration energy in one dimension is slightly below that reported in Table 1. The directions through the crystal along which one-, two-, and three-dimensional diffusion are predicted to occur most readily are shown in Fig. 5. The average migration energy required for diffusion in two dimensions is 419 meV, which is approximately the calculated average migration energy for diffusion in cubic perovskites. This suggests that in many of these materials there will likely be an acceptably fast path around any defects that block the fastest diffusion channels. Diffusion in three dimensions has an average predicted migration energy of 838 meV, indicating that diffusion at competitive rates will likely be limited to two dimensions in these materials. In practice, the degree to which the single dimensionality of the highly conductive channel limits ionic conductivity will vary by material based on both the two-dimensional migration energy in that material and the defect density.

Fig. 5. The structure of CrVO4 family represented by AlPO4. Blue spheres in the tetrahedra represent aluminum, and purple tetrahedra represents PO4−3 ions. The fastest diffusion path is left-to-right in (a), and the second-fasted diffusion path is left-to-right (along the c axis) in (b).

Fig. 5

Open in a new tab

Proton conduction depends on both proton mobility and proton concentration in the material. As none of the known CrVO4-structured materials intrinsically contain hydrogen atoms, it would be necessary to introduce protons into these materials. In some materials this might be accomplished through redox reactions with transition metals or by hydrating intrinsic oxygen vacancies. However in many cases it will likely be necessary to introduce protons by doping the materials with electron acceptors, as is commonly done in proton-conducting oxides.12 The conductivity of the doped materials will depend on the concentration of protons (and dopants) that can be introduced without sacrificing stability.

To assess the stability of the doped and undoped materials, we use a DFT-calculated convex hull of stable phases, which provides the energy of the thermodynamically stable phase or combination of phases as a function of composition.112–114 The 0 K DFT-calculated energy relative to the convex hull has been shown to be a useful descriptor for stability and synthesizability.115 This value is an estimate of the thermodynamic driving force for decomposition, with a value of 0 indicating a stable material. Most known oxides have energies within about 15 meV per atom of the convex hull, and 90% of known oxides have energies within about 62 meV per atom of the convex hull.115 The energies above the convex hull for the 29 known CrVO4-structured materials, calculated using data from the Materials Project, are provided in Table 2. Fourteen of the twenty-nine materials are on the DFT-calculated convex hull, and another eleven are within 35 meV per atom of the hull. Of the remaining four, one (AlPO4) is a high-pressure phase, and another (TiSiO4) has never been synthesized to our knowledge. The CrVO4 structure type is predicted to be the lowest-energy polymorph of TiSiO4,108 but as it is calculated to be 156 meV per atom above the convex hull we believe TiSiO4 is unlikely to exist in a form stable enough for practical use.

We assess the thermodynamic stability of the doped phases in a similar way. The widely-studied proton conducting oxides BaZrO3 and BaCeO3 are typically doped with about 10% (mole fraction) Y,12 resulting in nominal compositions of H0.1Y0.1BaZr0.9O3 and H0.1Y0.1BaCe0.9O3. We predict these materials to be 19 meV per atom and 36 meV per atom above the convex hull, respectively. For comparison, we have performed similar calculations on two promising CrVO4-structured materials, VPO4 and InVO4, doped with 10% Mg. The doped materials, with nominal compositions of H0.1Mg0.1V0.9PO4 and H0.1Mg0.1In0.9VO4, have DFT-calculated energies that are 5 meV per atom and 18 meV per atom above the hull, respectively. These results indicate that doping is likely to be a viable strategy for incorporating practically high concentrations of protons into materials with the CrVO4 structure type.

Materials with the CrVO4 structure type are generally composed of common, non-precious elements (Table 2). Our calculations indicate that most of them are electronically insulating, with a band gap of greater than 1 eV as calculated using GGA/GGA + U (Section 4 in the ESI†). They have been studied for their magnetic properties116,117 and as possible battery electrodes.118–120 However although all of the known CrVO4-structured materials are predicted to have low migration barriers for protons, with DFT-calculated values ranging from 53 to 340 meV, to our knowledge no materials in this class have been investigated as possible proton conductors. Of particular note is InVO4, a compound with high chemical stability and a melting point of 1134 °C,109 that has been extensively studied as a photocatalyst for H2 production.121–123 It has recently been shown that thin, single crystals of InVO4 also serve as efficient catalysts for CO2 photoreduction in the presence of water vapor.121 The DFT-calculated proton migration barrier in InVO4 is only 54 meV, and its ability to rapidly transport protons may play a role in its catalytic properties for reactions involving protons.

4. Conclusions

A high-throughput computational screen has identified materials with the CrVO4 structure type as likely to have very low migration energies for the one-dimensional diffusion of protons, and this prediction is supported by density functional theory calculations on known CrVO4-structured materials. In practice proton conduction may be limited by the one-dimensional nature of the path for rapid migration; the average migration energy for two-dimensional diffusion is predicted to be comparable to that of leading structure types for proton conduction. A thermodynamic assessment of acceptor-doped CrVO4-structured materials indicates that this structure type is capable of hosting competitively high concentrations of protons without creating an unacceptably large thermodynamic driving force for decomposition. Known materials with this structure type are typically composed of common, non-precious elements, providing flexibility to chemically tailor their properties materials and investigate different strategies for proton incorporation. These results indicate that CrVO4-structured materials are a promising new area for exploration in the search for new proton-conducting oxides.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

RA-009-C9RA06291B-s001

Acknowledgments

This project was funded by ONR Grant N00014-15-1-2494 and supported by XSEDE Grant DMR-140068. All 3D models were generated using VESTA.124

†

Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra06291b

References

  1. Bredesen R. Jordal K. Bolland O. Chem. Eng. Process. 2004;43:1129–1158. doi: 10.1016/j.cep.2003.11.011. [DOI] [Google Scholar]
  2. Baker R. W. Ind. Eng. Chem. Res. 2002;41:1393–1411. doi: 10.1021/ie0108088. [DOI] [Google Scholar]
  3. Phair J. W. Badwal S. P. S. Sci. Technol. Adv. Mater. 2006;7:792–805. doi: 10.1016/j.stam.2006.11.005. [DOI] [Google Scholar]
  4. Phair J. W. Badwal S. P. S. Ionics. 2006;12:103–115. doi: 10.1007/s11581-006-0016-4. [DOI] [Google Scholar]
  5. P. o. S. T. f. I. Reuse, Recycling, C. o. I. T. Assessments, C. o. Engineering, T. Systems and N. R. Council, Separation Technologies for the Industries of the Future, The National Academies Press, 1998 [Google Scholar]
  6. M. T. a. R. Inc., Case Study: Hydrogen Separations in Syngas Processes, http://www.mtrinc.com/case_study/h2_co_ratio_adjustment_in_syngas_production.html, 2014
  7. Tosti S. Basile A. Chiappetta G. Rizzello C. Violante V. Chem. Eng. J. 2003;93:23–30. doi: 10.1016/S1385-8947(02)00113-4. [DOI] [Google Scholar]
  8. Barbieri G. Brunetti A. Caravella A. Drioli E. RSC Adv. 2011;1:651–661. doi: 10.1039/C1RA00375E. [DOI] [Google Scholar]
  9. Uemiya S. Sato N. Ando H. Kikuchi E. Ind. Eng. Chem. Res. 1991;30:585–589. doi: 10.1021/ie00051a022. [DOI] [Google Scholar]
  10. Malerød-Fjeld H. Clark D. Yuste-Tirados I. Zanón R. Catalán-Martinez D. Beeaff D. Morejudo S. H. Vestre P. K. Norby T. Haugsrud R. Serra J. M. Kjølseth C. Nat. Energy. 2017;2:923–931. doi: 10.1038/s41560-017-0029-4. [DOI] [Google Scholar]
  11. Morejudo S. H. Zanón R. Escolástico S. Yuste-Tirados I. Malerød-Fjeld H. Vestre P. K. Coors W. G. Martínez A. Norby T. Serra J. M. Kjølseth C. Science. 2016;353:563–566. doi: 10.1126/science.aag0274. [DOI] [PubMed] [Google Scholar]
  12. Fabbri E. Pergolesi D. Traversa E. Chem. Soc. Rev. 2010;39:4355–4369. doi: 10.1039/B902343G. [DOI] [PubMed] [Google Scholar]
  13. Demin A. Tsiakaras P. Int. J. Hydrogen Energy. 2001;26:1103–1108. doi: 10.1016/S0360-3199(01)00043-X. [DOI] [Google Scholar]
  14. Coors W. G. J. Power Sources. 2003;118:150–156. doi: 10.1016/S0378-7753(03)00072-7. [DOI] [Google Scholar]
  15. Jamsak W. Assabumrungrat S. Douglas P. L. Laosiripojana N. Suwanwarangkul R. Charojrochkul S. Croiset E. Chem. Eng. J. 2007;133:187–194. doi: 10.1016/j.cej.2007.03.003. [DOI] [Google Scholar]
  16. Ni M. Leung D. Y. C. Leung M. K. H. J. Power Sources. 2008;183:133–142. doi: 10.1016/j.jpowsour.2008.04.073. [DOI] [Google Scholar]
  17. Ma Q. Peng R. Lin Y. Gao J. Meng G. J. Power Sources. 2006;161:95–98. doi: 10.1016/j.jpowsour.2006.04.099. [DOI] [Google Scholar]
  18. Duan C. Tong J. Shang M. Nikodemski S. Sanders M. Ricote S. Almansoori A. O'Hayre R. Science. 2015;349:1321–1326. doi: 10.1126/science.aab3987. [DOI] [PubMed] [Google Scholar]
  19. Taillades J. R. G., Dailly J., Fukatsu N., and Magrasó R. H. A., and Slater P. R., in Proton-Conducting Electrolytes for Solid Oxide Fuel Cell Applications, ed. M. Marrony, 2016, ch. 2, pp. 73–146, 10.1007/978-3-319-46146-5_3 [DOI] [Google Scholar]
  20. Kochetova N. Animitsa I. Medvedev D. Demin A. Tsiakaras P. RSC Adv. 2016;6:73222–73268. doi: 10.1039/C6RA13347A. [DOI] [Google Scholar]
  21. Haile S. M. Boysen D. A. Chisholm C. R. I. Merle R. B. Nature. 2001;410:910–913. doi: 10.1038/35073536. [DOI] [PubMed] [Google Scholar]
  22. Bi L. Boulfrad S. Traversa E. Chem. Soc. Rev. 2014;43:8255–8270. doi: 10.1039/C4CS00194J. [DOI] [PubMed] [Google Scholar]
  23. Laguna-Bercero M. A. J. Power Sources. 2012;203:4–16. doi: 10.1016/j.jpowsour.2011.12.019. [DOI] [Google Scholar]
  24. Giddey S. Badwal S. P. S. Kulkarni A. Int. J. Hydrogen Energy. 2013;38:14576–14594. doi: 10.1016/j.ijhydene.2013.09.054. [DOI] [Google Scholar]
  25. Garagounis I. Kyriakou V. Skodra A. Vasileiou E. Stoukides M. Frontiers in Energy Research. 2014;2:1–10. doi: 10.3389/fenrg.2014.00001. [DOI] [Google Scholar]
  26. Vøllestad E. Strandbakke R. Tarach M. Catalán-Martínez D. Fontaine M.-L. Beeaff D. Clark D. R. Serra J. M. Norby T. Nat. Mater. 2019;18:752–759. doi: 10.1038/s41563-019-0388-2. [DOI] [PubMed] [Google Scholar]
  27. Carter D. and Wing J., The Fuel Cell Industry Review 2013, 2013 [Google Scholar]
  28. Hauch A. Ebbesen S. D. Jensen S. H. Mogensen M. J. Mater. Chem. 2008;18:2331–2340. doi: 10.1039/B718822F. [DOI] [Google Scholar]
  29. Gao Z. Mogni L. V. Miller E. C. Railsback J. G. Barnett S. A. Energy Environ. Sci. 2016;9:1602–1644. doi: 10.1039/C5EE03858H. [DOI] [Google Scholar]
  30. Brett D. J. L. Atkinson A. Brandon N. P. Skinner S. J. Chem. Soc. Rev. 2008;37:1568–1578. doi: 10.1039/B612060C. [DOI] [PubMed] [Google Scholar]
  31. Wachsman E. D. Lee K. T. Science. 2011;334:935–939. doi: 10.1126/science.1204090. [DOI] [PubMed] [Google Scholar]
  32. Kilner J. A. Burriel M. Annu. Rev. Mater. Res. 2014;44:365–393. doi: 10.1146/annurev-matsci-070813-113426. [DOI] [Google Scholar]
  33. Haugsrud R. Norby T. Nat. Mater. 2006;5:193–196. doi: 10.1038/nmat1591. [DOI] [Google Scholar]
  34. Marrony M. and Pan Stanford P., Proton-conducting ceramics from fundamentals to applied research, Pan Stanford Publishing, Singapore, 2016 [Google Scholar]
  35. Munch W. Kreuer K. D. Seifert G. Maier J. Solid State Ionics. 2000;136:183–189. doi: 10.1016/S0167-2738(00)00304-0. [DOI] [Google Scholar]
  36. Kreuer K. D. Annu. Rev. Mater. Res. 2003;33:333–359. doi: 10.1146/annurev.matsci.33.022802.091825. [DOI] [Google Scholar]
  37. Zhang Q. Wahnstrom G. Bjorketun M. E. Gao S. Wang E. Phys. Rev. Lett. 2008;101:215902. doi: 10.1103/PhysRevLett.101.215902. [DOI] [PubMed] [Google Scholar]
  38. Gomez M. A. Liu F. J. Solid State Ionics. 2013;252:40–47. doi: 10.1016/j.ssi.2013.05.014. [DOI] [Google Scholar]
  39. Dawson J. A. Tanaka I. J. Mater. Chem. A. 2015;3:10045–10051. doi: 10.1039/C5TA01450F. [DOI] [Google Scholar]
  40. Kreuer K. D. Solid State Ionics. 1997;97:1–15. doi: 10.1016/S0167-2738(97)00082-9. [DOI] [Google Scholar]
  41. Shimojo F. Solid State Ionics. 1998;113–115:319–323. doi: 10.1016/S0167-2738(98)00296-3. [DOI] [Google Scholar]
  42. Matsushita E. Sasaki T. Solid State Ionics. 1999;125:31–37. doi: 10.1016/S0167-2738(99)00155-1. [DOI] [Google Scholar]
  43. Iwahara H. Esaka T. Uchida H. Maeda N. Solid State Ionics. 1981;3–4:359–363. doi: 10.1016/0167-2738(81)90113-2. [DOI] [Google Scholar]
  44. Peña M. A. Fierro J. L. G. Chem. Rev. 2001;101:1981–2018. doi: 10.1021/cr980129f. [DOI] [PubMed] [Google Scholar]
  45. de Grotthuss C. J. T., Mémoire sur la décomposition de l'eau: et des corps qu' elle tient en dissolution à l'aide de l'électricité galvanique, 1805 [Google Scholar]
  46. Chisholm C. R. I. Jang Y. H. Haile S. M. Goddard W. A. Phys. Rev. B: Condens. Matter Mater. Phys. 2005:72. [Google Scholar]
  47. Wood B. C. Marzari N. Phys. Rev. B: Condens. Matter Mater. Phys. 2007;76:134301. doi: 10.1103/PhysRevB.76.134301. [DOI] [Google Scholar]
  48. Barron O. Su H. N. Linkov V. Pollet B. G. Pasupathi S. J. Appl. Electrochem. 2014;44:1037–1045. doi: 10.1007/s10800-014-0715-x. [DOI] [Google Scholar]
  49. Haugsrud R. Norby T. J. Am. Ceram. Soc. 2007;90:1116–1121. doi: 10.1111/j.1551-2916.2007.01621.x. [DOI] [Google Scholar]
  50. Amezawa K. Tomii Y. Yamamoto N. Solid State Ionics. 2003;162:175–180. doi: 10.1016/S0167-2738(03)00223-6. [DOI] [Google Scholar]
  51. Hatada N. Toyoura K. Onishi T. Adachi Y. Uda T. J. Phys. Chem. C. 2014;118:29629–29635. doi: 10.1021/jp5105642. [DOI] [Google Scholar]
  52. Toyoura K. Nakamura A. Matsunaga K. J. Phys. Chem. C. 2015;119:8480–8487. doi: 10.1021/acs.jpcc.5b00573. [DOI] [Google Scholar]
  53. Norby T. Dyrlie O. Kofstad P. J. Am. Ceram. Soc. 1992;75:1176–1181. doi: 10.1111/j.1151-2916.1992.tb05556.x. [DOI] [Google Scholar]
  54. Polfus J. M. Norby T. Bredesen R. J. Phys. Chem. C. 2015;119:23875–23882. doi: 10.1021/acs.jpcc.5b08278. [DOI] [Google Scholar]
  55. Polfus J. M. Haugsrud R. Solid State Commun. 2012;152:1921–1923. doi: 10.1016/j.ssc.2012.07.010. [DOI] [Google Scholar]
  56. Haugsrud R. Solid State Ionics. 2007;178:555–560. doi: 10.1016/j.ssi.2007.01.004. [DOI] [Google Scholar]
  57. Lin H. Zhou F. Liu C. P. Ozolins V. J. Mater. Chem. A. 2014;2:12280–12288. doi: 10.1039/C4TA02465F. [DOI] [Google Scholar]
  58. Wei T. Zhang L. A. Chen Y. Yang P. Liu M. L. Chem. Mater. 2017;29:1490–1495. doi: 10.1021/acs.chemmater.6b03471. [DOI] [Google Scholar]
  59. Inorganic Crystal Structure Database, Fiz Karlsruhe, http://www.fiz-karlsruhe.de/icsd.html [Google Scholar]
  60. Wang Y. Richards W. D. Ong S. P. Miara L. J. Kim J. C. Mo Y. Ceder G. Nat. Mater. 2015;14:1026–1031. doi: 10.1038/nmat4369. [DOI] [PubMed] [Google Scholar]
  61. Kreuer K.-D. Chem. Mater. 1996;8:610–641. doi: 10.1021/cm950192a. [DOI] [Google Scholar]
  62. Van der Ven A. Bhattacharya J. Belak A. A. Acc. Chem. Res. 2013;46:1216–1225. doi: 10.1021/ar200329r. [DOI] [PubMed] [Google Scholar]
  63. Wolverton C. Ozoliņš V. Asta M. Phys. Rev. B: Condens. Matter Mater. Phys. 2004;69:144109. doi: 10.1103/PhysRevB.69.144109. [DOI] [Google Scholar]
  64. Jiang D. E. Carter E. A. Phys. Rev. B: Condens. Matter Mater. Phys. 2004;70:064102. doi: 10.1103/PhysRevB.70.064102. [DOI] [Google Scholar]
  65. Henkelman G. Arnaldsson A. Jonsson H. J. Chem. Phys. 2006;124:044706–044709. doi: 10.1063/1.2161193. [DOI] [PubMed] [Google Scholar]
  66. Garrett B. C. Truhlar D. G. J. Phys. Chem. 1979;83:200–203. doi: 10.1021/j100464a026. [DOI] [Google Scholar]
  67. Wigner E. Trans. Faraday Soc. 1938;34:29–41. doi: 10.1039/TF9383400029. [DOI] [Google Scholar]
  68. Hohenberg P. Kohn W. Phys. Rev. B. 1964;136:B864–B871. doi: 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
  69. Kohn W. Sham L. J. Phys. Rev. 1965;140:A1133–A1138. doi: 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
  70. Pauling L. J. Am. Chem. Soc. 1929;51:1010–1026. doi: 10.1021/ja01379a006. [DOI] [Google Scholar]
  71. Brown I. D. Shannon R. D. Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr. 1973;29:266–282. doi: 10.1107/S0567739473000689. [DOI] [Google Scholar]
  72. Altermatt D. Brown I. D. Acta Crystallogr., Sect. B: Struct. Sci. 1985;41:240–244. doi: 10.1107/S0108768185002051. [DOI] [Google Scholar]
  73. Bragg W. L., 1930, 74, 237 [Google Scholar]
  74. Brown I. D. Chem. Rev. 2009;109:6858–6919. doi: 10.1021/cr900053k. [DOI] [PMC free article] [PubMed] [Google Scholar]
  75. O'Keefe M. Brese N. E. J. Am. Chem. Soc. 1991;113:3226–3229. doi: 10.1021/ja00009a002. [DOI] [Google Scholar]
  76. Adams S. Swenson J. Phys. Rev. B: Condens. Matter Mater. Phys. 2000;63:054201. doi: 10.1103/PhysRevB.63.054201. [DOI] [Google Scholar]
  77. Preiser C. Losel J. Brown I. D. Kunz M. Skowron A. Acta Crystallogr., Sect. B: Struct. Sci. 1999;55:698–711. doi: 10.1107/S0108768199003961. [DOI] [PubMed] [Google Scholar]
  78. Adams S. Rao R. P. Phys. Chem. Chem. Phys. 2009;11:3210–3216. doi: 10.1039/B901753D. [DOI] [PubMed] [Google Scholar]
  79. Adams S. Rao R. P. J. Mater. Chem. 2012;22:1426–1434. doi: 10.1039/C1JM14588F. [DOI] [Google Scholar]
  80. Adams S. Rao R. P. Solid State Ionics. 2011;184:57–61. doi: 10.1016/j.ssi.2010.09.011. [DOI] [Google Scholar]
  81. Adams S. Rao R. P. Phys. Status Solidi A. 2011;208:1746–1753. doi: 10.1002/pssa.201001116. [DOI] [Google Scholar]
  82. Kresse G. Hafner J. Phys. Rev. B: Condens. Matter Mater. Phys. 1993;47:558–561. doi: 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  83. Kresse G. Hafner J. Phys. Rev. B: Condens. Matter Mater. Phys. 1994;49:14251–14269. doi: 10.1103/PhysRevB.49.14251. [DOI] [PubMed] [Google Scholar]
  84. Kresse G. Furthmuller J. Phys. Rev. B: Condens. Matter Mater. Phys. 1996;54:11169–11186. doi: 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  85. Kresse G. Furthmuller J. Comput. Mater. Sci. 1996;6:15–50. doi: 10.1016/0927-0256(96)00008-0. [DOI] [Google Scholar]
  86. Kresse G. Joubert D. Phys. Rev. B: Condens. Matter Mater. Phys. 1999;59:1758–1775. doi: 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  87. Wood D. M. Zunger A. J. Phys. A: Math. Gen. 1985;18:1343–1359. doi: 10.1088/0305-4470/18/9/018. [DOI] [Google Scholar]
  88. Pulay P. Chem. Phys. Lett. 1980;73:393–398. doi: 10.1016/0009-2614(80)80396-4. [DOI] [Google Scholar]
  89. Perdew J. P. Burke K. Ernzerhof M. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  90. Blochl P. E. Phys. Rev. B: Condens. Matter Mater. Phys. 1994;50:17953–17979. doi: 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  91. Wisesa P. McGill K. A. Mueller T. Phys. Rev. B. 2016;93:155109. doi: 10.1103/PhysRevB.93.155109. [DOI] [Google Scholar]
  92. Dudarev S. L. Botton G. A. Savrasov S. Y. Humphreys C. J. Sutton A. P. Phys. Rev. B: Condens. Matter Mater. Phys. 1998;57:1505–1509. doi: 10.1103/PhysRevB.57.1505. [DOI] [Google Scholar]
  93. Jain A. Ong S. P. Hautier G. Chen W. Richards W. D. Dacek S. Cholia S. Gunter D. Skinner D. Ceder G. Persson K. A. APL Mater. 2013;1:011002. doi: 10.1063/1.4812323. [DOI] [Google Scholar]
  94. Fabris S. Vicario G. Balducci G. de Gironcoli S. Baroni S. J. Phys. Chem. B. 2005;109:22860–22867. doi: 10.1021/jp0511698. [DOI] [PubMed] [Google Scholar]
  95. Shishkin M. Ziegler T. Surf. Sci. 2012;606:1078–1087. doi: 10.1016/j.susc.2012.03.003. [DOI] [Google Scholar]
  96. Henkelman G. Uberuaga B. P. Jonsson H. J. Chem. Phys. 2000;113:9901–9904. doi: 10.1063/1.1329672. [DOI] [Google Scholar]
  97. Henkelman G. Jonsson H. J. Chem. Phys. 2000;113:9978–9985. doi: 10.1063/1.1323224. [DOI] [Google Scholar]
  98. Sheppard D. Terrell R. Henkelman G. J. Chem. Phys. 2008;128:134106. doi: 10.1063/1.2841941. [DOI] [PubMed] [Google Scholar]
  99. Sheppard D. Henkelman G. J. Comput. Chem. 2011;32:1769–1771. doi: 10.1002/jcc.21748. [DOI] [PubMed] [Google Scholar]; , author reply 1772-1763
  100. Sheppard D. Xiao P. Chemelewski W. Johnson D. D. Henkelman G. J. Chem. Phys. 2012;136:074103. doi: 10.1063/1.3684549. [DOI] [PubMed] [Google Scholar]
  101. Sundell P. G. Björketun M. E. Wahnström G. Phys. Rev. B: Condens. Matter Mater. Phys. 2007;76:094301. doi: 10.1103/PhysRevB.76.094301. [DOI] [Google Scholar]
  102. Ong S. P. Richards W. D. Jain A. Hautier G. Kocher M. Cholia S. Gunter D. Chevrier V. L. Persson K. A. Ceder G. Comput. Mater. Sci. 2013;68:314–319. doi: 10.1016/j.commatsci.2012.10.028. [DOI] [Google Scholar]
  103. Bork N. Bonanos N. Rossmeisl J. Vegge T. Phys. Rev. B: Condens. Matter Mater. Phys. 2010;82:014103. doi: 10.1103/PhysRevB.82.014103. [DOI] [Google Scholar]
  104. Haugsrud R. Norby T. Solid State Ionics. 2006;177:1129–1135. doi: 10.1016/j.ssi.2006.05.011. [DOI] [Google Scholar]
  105. Omata T. Otsuka-Yao-Matsuo S. J. Electrochem. Soc. 2001;148:E252–E261. doi: 10.1149/1.1369370. [DOI] [Google Scholar]
  106. Marezio M. Dernier P. D. Chenavas J. Joubert J. C. J. Solid State Chem. 1973;6:16–20. doi: 10.1016/0022-4596(73)90200-4. [DOI] [Google Scholar]
  107. Pellicer-Porres J. Saitta A. M. Polian A. Itié J. P. Hanfland M. Nat. Mater. 2007;6:698. doi: 10.1038/nmat1966. [DOI] [PubMed] [Google Scholar]
  108. Gracia L. Beltrán A. Errandonea D. Phys. Rev. B: Condens. Matter Mater. Phys. 2009;80:094105. doi: 10.1103/PhysRevB.80.094105. [DOI] [Google Scholar]
  109. Baran E. J. J. Mater. Sci. 1998;33:2479–2497. doi: 10.1023/A:1004380530309. [DOI] [Google Scholar]
  110. Kim G. Griffin J. M. Blanc F. Haile S. M. Grey C. P. J. Am. Chem. Soc. 2015;137:3867–3876. doi: 10.1021/jacs.5b00280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  111. Malik R. Burch D. Bazant M. Ceder G. Nano Lett. 2010;10:4123–4127. doi: 10.1021/nl1023595. [DOI] [PubMed] [Google Scholar]
  112. Emery A. A. Wolverton C. Sci. Data. 2017;4:170153. doi: 10.1038/sdata.2017.153. [DOI] [PMC free article] [PubMed] [Google Scholar]
  113. Curtarolo S. Morgan D. Ceder G. Calphad. 2005;29:163–211. doi: 10.1016/j.calphad.2005.01.002. [DOI] [Google Scholar]
  114. Hildebrandt D. Glasser D. Chem. Eng. J. Biochem. Eng. J. 1994;54:187–197. doi: 10.1016/0923-0467(94)00202-9. [DOI] [Google Scholar]
  115. Sun W. Dacek S. T. Ong S. P. Hautier G. Jain A. Richards W. D. Gamst A. C. Persson K. A. Ceder G. Sci. Adv. 2016;2:e1600225. doi: 10.1126/sciadv.1600225. [DOI] [PMC free article] [PubMed] [Google Scholar]
  116. Frazer B. C. Brown P. J. Phys. Rev. 1962;125:1283–1291. doi: 10.1103/PhysRev.125.1283. [DOI] [Google Scholar]
  117. Isasi M. J. Saezpuche R. Veiga M. L. Pico C. Jerez A. Mater. Res. Bull. 1988;23:595–601. doi: 10.1016/0025-5408(88)90168-7. [DOI] [Google Scholar]
  118. Arroyo-de Dompablo M. E. Gallardo-Amores J. M. Azcondo M. T. García-Alvarado F. Amador U. J. Phys. Chem. Solids. 2006;67:1243–1247. doi: 10.1016/j.jpcs.2006.01.053. [DOI] [Google Scholar]
  119. Liang X. Ou X. Dai H. Zheng F. Pan Q. Liu P. Xiong X. Liu M. Yang C. Chem. Commun. 2017;53:12696–12699. doi: 10.1039/C7CC07566A. [DOI] [PubMed] [Google Scholar]
  120. Denis S. Baudrin E. Touboul M. Tarascon J. M. J. Electrochem. Soc. 1997;144:4099–4109. doi: 10.1149/1.1838150. [DOI] [Google Scholar]
  121. Han Q. Bai X. Man Z. He H. Li L. Hu J. Alsaedi A. Hayat T. Yu Z. Zhang W. Wang J. Zhou Y. Zou Z. J. Am. Chem. Soc. 2019;141:4209–4213. doi: 10.1021/jacs.8b13673. [DOI] [PubMed] [Google Scholar]
  122. Ye J. Zou Z. Oshikiri M. Matsushita A. Shimoda M. Imai M. Shishido T. Chem. Phys. Lett. 2002;356:221–226. doi: 10.1016/S0009-2614(02)00254-3. [DOI] [Google Scholar]
  123. Krol R. V. d. Ségalini J. Enache C. S. J. Photonics Energy. 2011;1:1–11. [Google Scholar]
  124. Momma K. Izumi F. J. Appl. Crystallogr. 2011;44:1272–1276. doi: 10.1107/S0021889811038970. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

RA-009-C9RA06291B-s001
RA-009-C9RA06291B-s001.pdf (355.3KB, pdf)

Articles from RSC Advances are provided here courtesy of Royal Society of Chemistry

RESOURCES