Abstract
The current status of electrochemical impedance spectroscopy (EIS) and related analysis on perovskite solar cells (PSC) is still unsatisfactory. The provided models are still vague and not really helpful for guiding the efforts to develop more efficient and stable devices. Due to the slow and complex dynamics of these devices, the obtained spectra need to be validated, which is hardly ever done. This study may be the first to provide fully validated impedance spectra and presents reproducible EIS time series at open circuit voltage (VOC) for more than 20 hours, with a total of 140 analysed spectra. We conclude that the observed changes stem from a temporary reduction of the electronically active area of the devices, as can be deduced from the inverse behaviour of resistance and capacitance. The changes in these values are almost 100% reversible if the devices are kept in the dark for only one day, while the time constant of the high-frequency process remains unchanged throughout the whole characterization procedure. The tested devices are full PSC devices that have proven to be stable over more than 500 hours, and the non-steady impedance measurements shine a critical light on previously published EIS data. With the results of this study, it can be rationalized that the high-frequency semicircle can serve as a good indicator for ionic migration by monitoring its consequences. The results presented here are helpful to quantify ionic migration on the device level in order to derive new stability criteria and countermeasures against degradation.
Reversible changes in perovskite solar cells (PSC) are detected and analysed by electrochemical impedance spectroscopy (EIS).
Introduction
Electrochemical impedance spectroscopy (EIS) is a powerful tool to characterize (photo-) electrochemical systems. In the past, EIS analysis has not been a very vibrant topic in solar cell research – the relevant parameters for silicon based solar cells have been traditionally determined by admittance spectroscopy1,2 plus photocurrent spectroscopy (also called incident photon to current efficiency (IPCE) measurements) and the impedance response of dye-sensitized solar cells shows a very straightforward pattern that leaves almost no open questions.3 That has changed with the emergence of perovskite solar cells (PSC) which have gained a lot of attention recently throughout all fields of materials characterization. The major driving force to employ EIS for PSCs is the lack of knowledge about the details of the reversible and irreversible, the beneficial and detrimental processes that occur in PSCs with respect to operating conditions and material compositions.4–8 Conveniently, the features to be identified by EIS are in the practical frequency range for ordinary EIS (1 MHz to ∼50 mHz). However, the limited stability of PSC has hampered a consistent analysis and the establishment of a physically based equivalent circuit model (ECM) so far.9 The phenomenon referred to as the hysteresis as part of the dynamic response has also long been a major concern10 and gives an idea of the complicated electronic behaviour of PSCs.11 Especially for the assessment of such complicated behaviour and interplay of electronic and ionic charge transport phenomena, EIS should be the most appropriate technique on the device level.
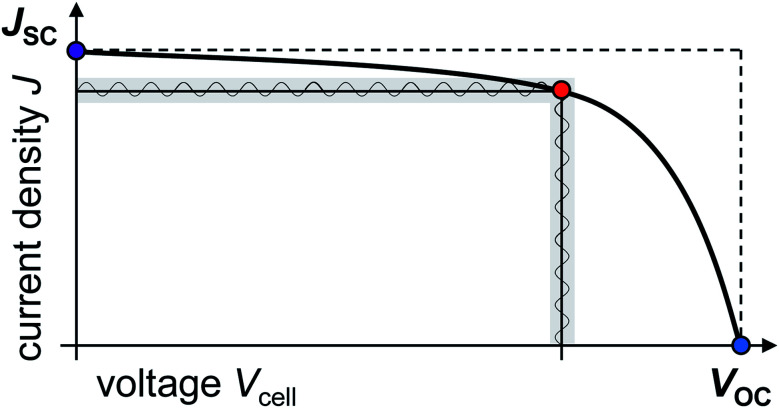
As introduced by Pitarch-Tena et al.,8 measuring EIS at different (forward) bias voltages is helpful for characterizing the evolution of the processes, which indicated the losses or performance limits depend on the operating voltage. In basic electrochemistry, any (positive) contribution to the impedance is a loss, dissipated as heat. Hence, the smaller in magnitude of the impedance the better the device. For solar cells, this is not so easy because their current density–voltage (J–V) characteristics show different regimes, as shown in Fig. 1. The impedance Z at ω = 0 (in the following referred to as ZDC with ZDC = dV/dJ) also indicates the inverse of the slope in a J–V curve. In solar cells, however, the aim is to reach a fill factor (FF) close to 1 and the ideal behaviour is shown by the dashed rectangular in Fig. 1. The J–V curve should exhibit a small slope close to 0 around short circuit conditions (V = 0, with JSC being the short circuit current density), which corresponds to a large impedance (ZDC → ∞). In contrast, the slope at the open circuit voltage, VOC, should be as large as possible and in the ideal case, it is ZDC = 0. Such ideality is of course not realistic, due to contact resistances and other non-ideal behaviour in the several components of the device and the current collectors. However, PSC usually exhibit a clear trend that ZDC becomes very large for operating points close to JSC and quite small close to VOC.4
Fig. 1. Schematic of a J–V curve for PSC (straight line). An ideal J–V curve is indicated by the dashed line. Exemplary signals for an EIS measurement at an arbitrary operating point (red dot) are given by the sine waves in the grey bars.
The EIS of PSC shows two main semicircles or arcs, one at high frequencies >10 kHz and one at low frequencies <100 Hz, plus potential additional features such as a mid-frequency semicircle or negative hooks or loops.4,6,7,12–21 There is no general agreement on the interpretation of the two main features but there is a certain tendency towards a common explanation. Summarized in short, most researchers agree that the capacitive component of the high-frequency semicircle is provided by the geometrical capacitance.6,14 The resistance could be transport or recombination resistance – that is still under debate. However, both these terms describe the same physical scenario where the current density is limited by transport or recombination: charges have to be transported through the device and the conductivity is essentially decreased if charge carriers are lost through recombination. More speculative are the interpretations of the second semicircle and any of the additional contributions. It has been remarked – and it is seen as one complication to unambiguously identify the physical origin exactly – that both these semicircles often change uniformly for a change in operating conditions such as light intensity or voltage variation.4,12,22 Another problem is the stability of the cells during measurements.9 It is rarely considered or checked whether the cell was stable (time invariant) during the impedance measurement, and to the best of our knowledge, no time dependent EIS measurements have been reported so far. It has been argued that measurements under reduced light intensity are beneficial, because these indeed improve the stability or, in other words, provide a more stable or less fast evolving operating point and impedance result. Yet, all features present at 1 sun should also be present at reduced light intensity. However, the measurements under reduced light intensity are difficult to compare with measurements conducted under 1 sun, because the magnitudes of all essential quantities including voltage drop over the device, VOC (and therefore internal electric field), current density and charge carrier distribution differ in a non-trivial way and an extrapolation to 1 sun has not been successfully implemented yet. Pockett et al. have used impedance measurements at VOC under 1 sun illumination and also compared them to other measurement techniques,6 which resulted in a comprehensive picture about the small-signal (linear) behaviour and large-signal (nonlinear) behaviour.
Recently, fundamental processes, effects and basic reaction mechanisms of PSCs have been investigated and there has been a lot of discussion about ionic migration in halide perovskites23–27 and its consequences.18,21,28–31 On model cells, a lot of the effects have been detected, visualized and explained,32–36 There are only very few studies that investigated and discussed the impact of ionic migration for technically relevant device architectures – by measuring and modelling the hysteresis,28 by transient optoelectronic measurements combined with device simulations20 and investigating the reversibility of ionic migration during day/night-cycles.21 It has also been argued that the ionic migration should be almost instantaneous due to the short diffusion path and the high mobility.37 In conclusion, a study that clearly relates the ionic migration to electrically measurable quantities is still missing and one of the most urgent questions remains unanswered: how do these effects show up, affect or influence a PSC on the device level during operation?
EIS is supposed to be a very helpful tool in that sense, as it can be used for model systems in very controlled and simplified conditions (“simplified” can signify well-defined geometry and microstructure, single crystal materials, inert contacting materials such as noble metals, and controlled temperature and atmosphere) as well as in operando on the device level. In other words, EIS is applicable to characterize full solar cells while they are being operated under technically relevant operating conditions.
It is unlikely that the ionic migration of PSCs within its ∼500 nm thick layer of the perovskite layer is in an easily detectable order of magnitude. What is of relevant magnitude though are the consequences of ionic migration.28 Possibilities for such consequences are: (local) change in conductivity, change in recombination characteristics and material decomposition and thereby influencing VOC, JSC and the hysteresis (or the dynamic behaviour in general). The latter three quantities show complicated relationships between each other and with respect to other characteristics of the device. Directly relating a certain behaviour to ionic migration has not been achieved yet. Another important aspect is to find out whether these changes are reversible or irreversible,20 beneficial33 or detrimental38 for the device performance and if that can be generalized as there are a lot of material compositions being considered at the moment.
With this study, we demonstrate that polarization and therefore ionic migration can be detected by a change in the impedance of the PSC over time. Only focussing on the evolution of the high-frequency behaviour of PSC over time, we will also show that our results are applicable to explain other commonly observed phenomena, such as the special relationship between high-frequency and low-frequency semicircle. We are aware that by neglecting the low-frequency part of the impedance, this study seems incomplete. However, with the systematic analysis of the high-frequency semicircle, we present an important step towards a full understanding of the impedance response of PSC. In fact, if the observed change is due to a temporary loss of active area, as proposed here, this has direct consequences for the low-frequency impedance of PSC as well. It might even indicate the necessity of reconsidering previous analyses, which is beyond the scope of this study. Our goal is rather to sensitize researchers to reversible and irreversible changes in PSC and how they can be analysed by EIS. Time-evolving EIS spectra are rarely shown in the literature but they are an important indicator of the stability or the evolution of parameters over time. Without demonstrating the time invariance of the system under test, it is not clear whether the reported EIS spectra obtained by a single experiment are consistent and representative for the device behaviour at all. We confirm the validity of the measured spectra by repeated measurements as well as by the Kramers–Kronig test.39,40 That is an important precondition for any impedance analysis.
Experimental
The measured devices for this impedance analysis have been characterized in a separate study by Tumen-Ulzii et al.41 The state-of-the-art perovskite films (mixed cation and anion perovskite, Cs0.05(FA0.85MA0.15)0.95Pb(I0.85Br0.15)3, abbreviated as CsFAMA)42–46 fabricated from solutions with differing concentrations of lead iodide (PbI2) such as 1.12 M, 1.15 M and 1.18 M (labelled S-1, S-2 and S-3, respectively), while the concentrations of caesium iodide (CsI), formamidinium iodide (FAI), methylammonium bromide (MABr), and lead bromide (PbBr2) were kept constant as 0.08 M, 1.10 M, 0.20 M, and 0.20 M, respectively. The composition of 1.18 M provides a stoichiometric balance. The electron transport layer (ETL) is made of tin oxide (SnO2) and spiro-OMeTAD serves as hole transport layer (HTL). Mainly, we show the EIS results of the device S-2, which exhibits the best long-term stability and less than 1% degradation of its initial power conversion efficiency (PCE) after continuous illumination for 520 hours.
All EIS measurements are performed at VOC. That is different from the conditions for stability testing, which is usually done at the maximum power point (MPP) or with a load resistance. It has to be considered that the devices possibly show different long-term stability at VOC. The VOC was chosen as measurement condition because it represents a well-defined operating point and can easily be monitored.5,6 Prior to the EIS measurements the devices were kept under white LED light with an intensity of 1.5G (1 sun) until the VOC stabilized after several minutes, as described previously by Ebadi et al.18 The measured VOC was then chosen as output voltage of the impedance analyser (Solartron 1260) and four successive spectra were measured, each of which takes around 12 minutes (1 MHz to 70 mHz). After that, the VOC was measured again and readjusted if necessary, and the series measurement was repeated three times as a standard (4 + 4 + 4 + 4 spectra). After leaving the device at VOC under light for about 12 hours, the measurements were repeated in the same way two times (4 + 4 spectra). Measurements were conducted on fresh devices S-1, S-2 and S-3, and after recovery (see below), plus on an additional device of type S-2, which had been aged for 500 hours under 1 sun illumination. A total of 140 spectra was analysed. All EIS measurement are sectioned into two parts, high-frequency and low-frequency part, because a high pass filter was applied for high-frequencies that suppresses the VOC bias and allows for a better resolution and therefore better accuracy. One drawback is a possible gap between high-frequency and low-frequency data if the system is changing during the measurement or if the measurement ranges of the impedance analyser are not perfectly calibrated and synchronized. Here, we will only focus on the high-frequency part of the impedance as its identification and the full understanding of its evolution over time are preconditions for any detailed study trying to elucidate the low frequency part.
Results and discussion
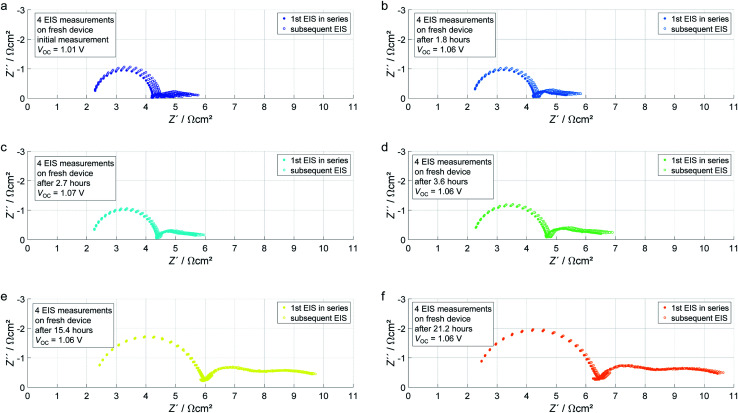
The 24 spectra obtained for sample S-2 are shown in Fig. 2. Each series of four successive measurements shows a continuous increase from the first to the last measurement in the individual diagrams. Furthermore, each series shows larger values than the precedent one. The only exception is the second series that is comparable with the first one but here it is suspected that the adjustment of the VOC plays a role that increased from 1.01 V to 1.06 V. From then on, the VOC was stable ±1 mV. After 21.2 hours all contributions apart from the series resistance seem to have doubled in magnitude as compared to the initial measurement. The time elapsed after the initial measurement and the measured and adjusted VOC are indicated in each diagram.
Fig. 2. EIS series measured on a fresh device (S-2, 1.15 M PbI2). Each colour indicates a measurement series of four successive measurements. The first spectrum of each series is plotted as filled circles, the subsequent three measurements are indicated by open symbols of the same colour.
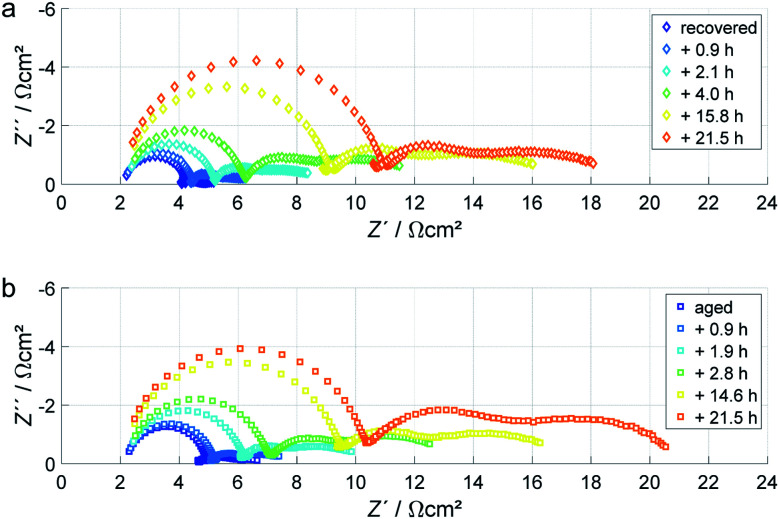
The measurement was then repeated after keeping the sample disconnected in the dark for about 24 hours (the corresponding device will be referred to as “recovered” in the following). Surprisingly, the initial impedance spectrum of the repeat series is almost equivalent to the initial measurement of the fresh device as shown in Fig. 3a. Ohmic resistance and polarization resistance of the high-frequency semicircle are about 2 Ω cm2 each in the first measurement. Fig. 3a only shows the first measurement of each series, but the trend was similar to the measurements on the fresh sample and the impedance increased monotonically within each of the series. There is a similar increase with time as in the measurements on the fresh device, which is happening at a higher rate and larger magnitude than for the fresh device. Fig. 3b shows the same measurement procedure as Fig. 3a but is performed on another device of the same material that was aged for 500 hours under 1 sun illumination. The values for the impedance and the evolution (increase) is very similar for the fresh, the recovered and the aged device, only the initial diameter of the high-frequency semicircle is about 20% larger for the aged device.
Fig. 3. EIS series measured on a (a) recovered device (kept disconnected in the dark for one day) and (b) aged device (aged for 500 hours). Both devices are of the type S-2 with 1.15 M PbI2 in the precursor. Each colour indicates a measurement series of four successive measurements, while in contrast to Fig. 2, only the first measurement of each series is shown.
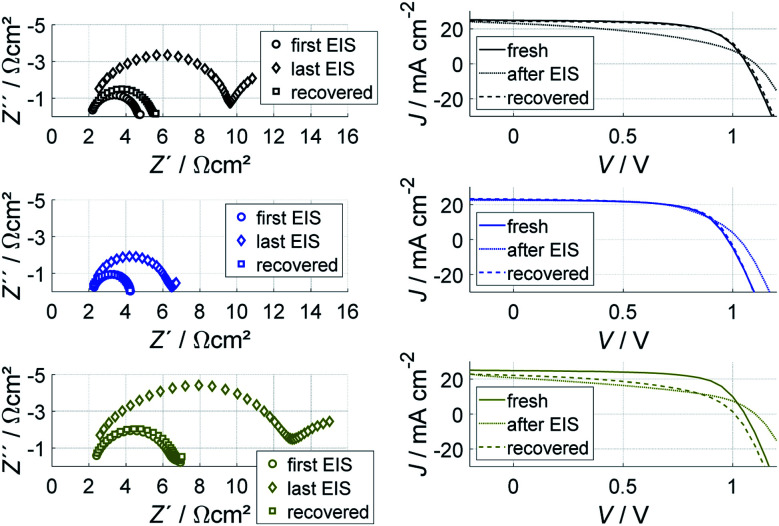
These measurements suggest that we are observing a reversible effect here and it is apparently not related to the long-term experiment over 500 hours. Another proof for the reversibility is given in Fig. 4, where the high-frequency semicircle is shown for three devices with different stoichiometries in the perovskite layer (S-1, S-2 and S-3 with 1.12 M, 1.15 M and 1.18 M of PbI2 in the precursor, respectively). The measurement procedure was the same for all three devices:
Fig. 4. . Left: First and last high frequency part of the EIS spectrum for a fresh device (S-1: black; S-2: blue; S-3: brown) and first measurement after recovery for one day, respectively. Right: respective J–V curves measured at 200 mV s−1 sweep rate. Note that the first EIS and the recovered one overlap and are not to distinguish for S-2.
1. A J–V curve was recorded (labelled “fresh” on the right side).
2. An EIS series was recorded as described above that lasted approximately one day (the first and last spectrum are shown and labelled as “first EIS” and “last EIS”, respectively, in the Nyquist plots on the left).
3. Right after the EIS series another J–V curve was recorded that is labelled “after EIS”.
4. The devices were disconnected and kept in the dark for at least a day and another J–V curve was recorded (labelled “recovered”).
5. Another EIS series was measured but only the first spectrum is shown on the left labelled “recovered”.
The trend is the same for all three samples: the fresh initial measurement and the first measurement after recovery even coincide for device S-2 and are not distinguishable in Fig. 4. These measurements are exactly the same as the initial ones shown in Fig. 2 and 3a, where the similarity is shown with better resolution.
The J–V curves show a similar trend and for devices S-1 and S-2, the fresh and recovered devices show tiny differences. Only device S-3 does not fully recover. That is mostly due to the initial fast degradation that was investigated in detail in ref. 41, where it could be attributed to PbI2 precipitation. The EIS spectra of S-3 after recovery show an additional mid-frequency semicircle of considerable size as shown in Fig. S1 (ESI†).
It should be noted the zero crossings in the J–V curves shown in Fig. 4 do not represent the VOC that was measured after relaxation under open circuit conditions for several minutes (before starting the EIS measurements). The latter did not change significantly during the EIS series and among the different devices and lay within the interval of 0.97 V to 1.07 V. The VOC is a complex characteristic that depends on the energy band structure, the injection barriers and charge carrier recombination. We are not able to correlate the small changes in the VOC with the reversible changes of R and C yet, and we also cannot exclude secondary effects.
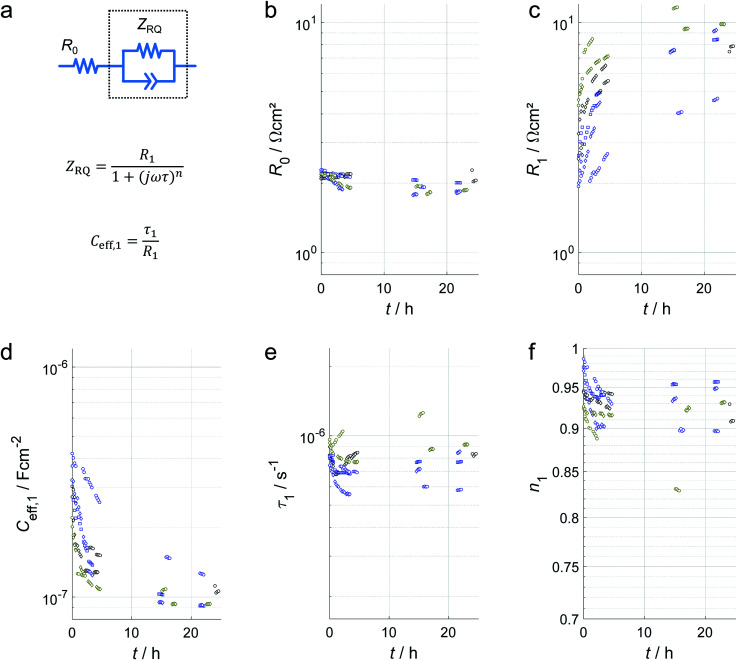
In order to quantify the EIS results, the high-frequency semicircles of all measurements were fitted to a simple process-oriented equivalent circuit model (ECM),19,47 consisting of a series resistor and an RQ element (resistor and constant phase element in parallel). The fits, the residuals of the fits and the Kramers–Kronig residuals of the measurements are shown in Fig. S2–S7 (ESI†), respectively.
Fig. 5 shows the relevant parameters for all fits: the series resistance R0, the resistance of the high-frequency semicircle R1, the effective capacity Ceff,1 (calculation see equation in Fig. 5a) and the time constant τ1. Please note that all logarithmic diagrams span an interval of the same magnitude on the y-axis in order to provide a good comparison of the relative changes.
Fig. 5. (a) Fit model for the high frequency part of the EIS spectra, highlighting the RQ circuit (dashed box), and applied equation for the RQ circuit and for the calculation of the effective capacity, Ceff,1. Fitting result: (b) ohmic resistance, R0; (c) resistance of the RQ circuit, R1; (d) effective capacity of the RQ circuit, Ceff,1; (e) time constant of the RQ circuit, τ1; (f) exponent of the RQ circuit, n1. A total of 140 spectra have been analysed and the obtained parameters are shown in this figure.
R 0 does not show any clear trend which is also expected because it is mostly caused by the in-plane resistance of the current collectors. However, the small spread in R0 is also an indicator that the high-frequency semicircle was fitted consistently.
R 1 is increasing steadily for all measurement series and increases by about half an order of magnitude within 24 hours.
C eff,1 interestingly shows a trend of about the same order of magnitude, but towards smaller values.
τ 1, consequently, does not show any clear trend and all obtained values gather around one value ±25%.
It should be considered that the changes in R and C are rather fast and a delay of the initial impedance measurement or a potential difference in settling time for VOC could have a significant influence on the first values obtained for these parameters. Similarly related trends were previously reported for a change in voltage and/or light intensity in ref. 4 and 12. There, it was concluded that the elements R and C are somehow “connected”. In the following, we want to derive a physical explanation for (1) the related behaviour of R and C and (2) the reversibility of the changes in the impedance. After that, we will summarize (3) the consequences of these results for impedance analysis on PSC and finally explain how (4) the high-frequency impedance of PSC can be used for the detection of ion migration.
Relationship between the evolution of R and C
Usually, an increase in resistance goes along with an increase in the time constant according to τ = RC, if the capacity is fixed, which is expected as we assume C1 to be a geometrical capacitance. In our opinion it is not a coincidence that τ1 remains almost unchanged. We think it is rather a fundamental characteristic of the effect that is responsible for the observed evolution of R1 and C1. Our hypothesis for the observed behaviour is a temporary reduction of electronically active area. That means that parts of the device are not active anymore. That results in larger resistance (R ∝ 1/A, with A being the geometrical area) and smaller capacity (C ∝ A), while the time constant τ is not affected: τ = RC. A loss of half the active area will result in a doubling of the resistance and a halving of the capacitance, while the time constant will remain the same, as we have roughly observed in all the experiments presented above.
The hypothesis of the loss in active area is confirmed by the following considerations:
1. There is a consensus about the high-frequency capacity originating from the geometrical capacity, C1 = ε0εrA/d. The change in capacity observed here is around half an order of magnitude or even more and cannot be explained by a material change – even if 100% if the material was changed, the new εr would need to be half an order of magnitude smaller than before, which is unlikely given that the change is reversible in the given case. Also, a change in thickness, due to lattice expansion through more interstitials is not supposed to happen on the observed scales.
2. In the past, it has been difficult to attribute the two main semicircles to solely one dominating physical origin, respectively, because they both show dependencies on several changes of the device structure (thickness of the perovskite layer and ETL composition, for example).14 A temporary loss in active area results in a proportionate scaling of the semicircles, as already mentioned has been observed previously,12 and would provide a sensible explanation for the observed behaviour. In fact, the temporary loss in active area could be the missing link to deconvolute the physical origin of the impedance features in PSC.
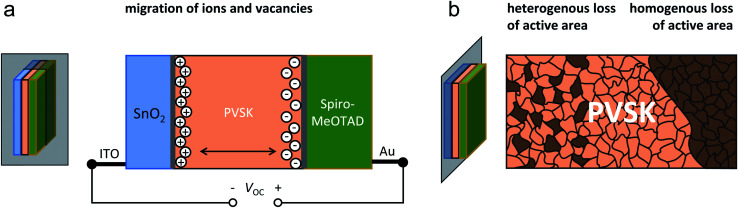
Phenomenologically, the loss in active area can be caused by several effects. An insulating layer is the simplest explanation, while this suggest a severe change in the perovskite material or the characteristics of the interface, which seems unlikely to be reversible. Also, a thin insulating layer will not change the capacitance towards smaller values as observed – it rather creates a more ideal capacitor. It is more likely that the loss in active area occurs because the probability for charge carriers to recombine supersedes the probability of being injected at the contacts. That can be regarded as an increased injection barrier and decreased injection efficiency. However, charges do not accumulate at the contacts but recombine instantaneously – at least faster than can be observed via EIS. Otherwise, the capacity would not drop but rather increase. The injection efficiency still shows a strong voltage dependency as JSC is constant for S-1 and S-2 and only decreases slightly for S-3 as shown in Fig. 4. If single grains of the perovskite layer are temporarily altered by ionic migration and act as recombination centres where essentially all arriving charge carriers recombine, parts of the area can become inactive. An accumulation of positively charged ions or vacancies are supposed to act as such recombination centres at the interface with the ETL (left side in Fig. 6a).48 But also negatively charged ions or vacancies can act as recombination centres (right side in Fig. 6a)37,48,49 that essentially inhibit any charge carrier to be injected into the respective transport layers and can therefore not be measured externally by an electrical measurement. The major part of the perovskite absorber might still be active in creating charge carriers, but this activity is screened by the recombination centres and the behaviour of the whole device mimics a smaller device. As mentioned above, it is not likely that the ionic migration takes tens of hours to occur in the thin perovskite layer.37 However, it is reasonable that the establishment of a complete equilibrium of all defects (mobile ions, vacancies and interstitials) takes much longer than that and happens at the actual timescales that we observe here, given that neutral interstitials can only move through chemical diffusion, which is expected to be much slower. Also, the polarization voltage is quite small, assuming that ionic migration does not happen during the stability test as will be addressed in point (3).
Fig. 6. Schematic of the consequence of ionic migration. (a) Cross-sectional image showing the positively charged ions or vacancies in the perovskite layer (PVSK) at the interface to the ETL and the negatively charged ions at the interface to the HTL. (b) Plan view of the interface with a loss of active area as indicated by the dark brown colour for the case of heterogeneous (left) and homogenous (right) loss of active area.
From the impedance measurements, little can be deduced about the geometrical characteristics of the loss in active area. Fig. 6b is a schematic that shows how a heterogenous (single grains, left) and a homogenous loss in active area (continuous layer, right) are supposed to look like.
When regarding the exponent n1 of the RQ element in Fig. 5f, it can clearly be seen that n1 changes only slightly but is systematically decreasing. The parameter n1 can be viewed as an ideality indicator (this is not strictly correct from a mathematical point of view but describes the characteristics of n1 well enough for the argument here) and decreases significantly for longer polarization. Such behaviour is not expected if a large area becomes inactive and the rest of the device remains unchanged. It is rather indicating that the remaining active area has become inhomogeneous, for example due to a spread in conduction pathway lengths or local current constrictions. That is not sufficient evidence that single grains instead of a large area becomes inactive but the evolution of n1 strongly suggests it.
Reversibility of the changes in the impedance
Based on the presented results it is not deniable that the changes in the impedance in Fig. 2–4 are reversible. That is already a strong indication that the changes are caused by a temporary polarization effect.
Polarization effects are a complicated issue in PSC because charge carriers, cations, anions and interstitials have been shown to be mobile to a certain extent. A lot of studies have recently focused on the polarization and ionic migration under illumination and in the dark, as introduced above. However, little is known about the processes that happen on the device level and how detrimental effects of this migration can be avoided.
We here suggest that whole grains of the perovskite material change their properties and characteristics due to a temporary change in stoichiometry (ionic migration) or a change in crystal structure (formation of interstitials), such that single grains become inactive and act as recombination centres.
We are positive that we have identified the impact of the ionic migration in PSC by EIS in operando. Yet the quantification of conductivity or velocity is rather difficult because the deactivation (as consequence) will probably have a threshold beyond which the grain is deactivated, but that is yet unknown for the constellation in a device architecture. Therefore, we cannot directly give a quantification of the ionic migration. However, this study motivates further investigations on model cells with well-defined grain sizes where the passivation could be confirmed and monitored in a more precise and controlled manner.
One of the open questions is why the polarization takes place at different speeds even for samples that have proven to reverse back to the initial state after polarization.
General consequences for impedance studies on PSC
The effects analysed in this study also motivate revised guidelines for impedance measurements on PSC. Generally, a waiting time should be inserted such that the system under test is in equilibrium before measuring an EIS spectrum. We have shown that this is almost impossible for the case of VOC as bias voltage, whereas it is likely that any other operating point shows similar polarization behaviour that will also change the impedance response over time. It is important to note here that this phenomenon is not a particularity for the here tested device type but is expected for any PSC where ionic migration plays a role. Measurements at lower light intensity could be a solution because the polarization effects will occur at much slower timescales. However, the interpretation remains a challenge as has been discussed above.
We suggest recording and showing at least two spectra for every operating point and situation tested, as it is the easiest and most straightforward way to demonstrate the stability during the measurement period. This study has demonstrated the crucial factor of the polarization as it affects the impedance and the performance in a reversible way. We did not show the relationship with the hysteresis. In order to make a consistent comparison between the results of the two methods, reliable impedance measurements over the whole voltage range from JSC to VOC and a host of examples including regular and inverted hysteresis are required. For now, we can confidently state that the VOC is not a stable operating point for PSC – even for a device, of which another sample has proven 500 hours of operation with only 1% PCE degradation. The stability measurements were performed in the same setup with the same light source but with a 1 kΩ resistor in parallel to the device such that the voltage ranged between MPP and VOC (0.9 V < V < 0.95 V), which represents standard testing conditions. It is worth mentioning that those voltages are less than 100 mV smaller than the VOC values we have found here, which could explain the long timescales at which the polarization effects are occurring. During the only 24 hours of testing under VOC, the temporary degradation was much larger in the 500 hours stability test and it is comparable with the temporary degradation shown by Domanski et al.21 Unfortunately, a direct comparison is not possible.
In order to prove that the temporary degradation was not caused by the EIS measurement but the operating point only, we performed a series of EIS measurements for about 5 hours at the exact voltage that resulted when the device was connected to the 1 kΩ resistor. As shown in Fig. S8 (ESI†), the high-frequency impedance is stable over this period and even slightly decreasing in the high-frequency part, while the low frequency part is increasing. The latter behaviour is not understood yet, but J–V curves in Fig. S9 (ESI†) recorded before and after the EIS measurements show that there was no degradation due to the measurements. So in fact, the EIS measurement itself is not responsible for the temporary degradation but the operating point.
Apart from this, VOC is a very reasonable well-defined operating point for an EIS study of PSCs. The other well-defined operating point would be a voltage of 0 V (JSC). However, the impedance at 0 V is not very useful because it increases to very large magnitudes and the time constants are much larger, which means that the measurement time increases to impractical timescales and the whole spectrum can hardly be measured accurately as demonstrated by Pitarch-Tena et al.8 A consistent measurement procedure that provides both consistent EIS and performance in one simple measurement routine is yet to be proposed.
Detection of ionic migration through EIS
With all the difficulties about EIS measurements on PSC that have been pointed out in this study, there are important new findings regarding ionic migration, its detection and its impact on the device level. Not only was the ionic migration held responsible for the temporary reversible loss of active area by deactivating single grains of the perovskite material. Also, it was shown that the evolution of those consequences related to ionic migration was accelerated in the second cycle after the recovery step and after the degradation test (compare Fig. 2 and 3). With the help of the three impedance series at VOC, we can state that the evolution of the measured impedance took place at shorter timescales after the first series. It must be considered that it is not clear whether the velocity of the changes is limited by ionic migration, chemical diffusion of interstitials or the material changes at the interfaces. However, as the effects we observe here are reversible, there are no structural material changes expected, such that we are likely to have found a way to quantify (at least qualitatively) the velocity of ionic migration in a full device by EIS. That means we can monitor the ionic migration by the evolution of the high-frequency semicircle of the EIS. Since the time constant of this semicircle is usually (for all spectra shown on similar devices in the literature) smaller than 2 μs, it is well-separated from the mid-frequency and low-frequency features in PSC, and an in operando detection through this technique is feasible. An EIS measurement can be performed from 1 MHz to 10 kHz (which is feasible in less than 1 min) and this will give an idea of the current state of the PSC. Subsequent measurements can show the evolution of the polarization.
Conclusions
The high-frequency impedance of very stable perovskite solar cells (PSC) changes significantly over time due to continuous polarization at VOC under 1 sun. We propose a temporary loss of electronically active area as the main effect on the device level. Series of EIS measurements on fresh, recovered and aged devices provide clear indications that the increase in resistance and the decrease in capacitance, while the time constant of the respective semicircle remained almost unchanged, is caused by a temporary loss in active area. This effect is reversed to almost 100% after keeping the device in the dark for one day.
From this analysis, it is inferred that ionic migration results in decreased injection and increased recombination at the contacts of PSC such that single grains of the perovskite are essentially deactivated. Ions, vacancies and interstitials accumulate at the interfaces to the electron and hole transport layers acting as recombination centres and increasing the transport resistance. In effect, none of the incoming charge carriers are injected, which leads to an electrical response mimicking a device of much smaller area.
We further show that the VOC is not a stable operating point for the tested devices that have confirmed their stability over more than 500 hours in a separate long-term stability test. These volatile results at VOC suggest that other operating points show similar fluctuations in the impedance. That should be considered during impedance analysis on PSC in general and it shines a critical light on the results that are already published.
Finally, we see such an impedance series focussed on the high-frequency semicircle as valuable tool to monitor (the impact of) ionic migration in lead halide perovskites embedded in a technically relevant device architecture.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
This work was supported by the Japan Science and Technology Agency (JST), ERATO, Adachi Molecular Exciton Engineering Project (JST ERATO Grant Number JPMJER1305), by the International Institute for Carbon-Neutral Energy Research (WPI-I2CNER) sponsored by the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan, by JSPS KAKENHI (grant numbers JP18K13993, JP15K14149 and JP16H04192), and by The Canon Foundation.
Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra07048f
References
- Mora-Seró I. Garcia-Belmonte G. Boix P. P. Vázquez M. A. Bisquert J. Energy Environ. Sci. 2009;2(6):678. doi: 10.1039/B812468J. [DOI] [Google Scholar]
- Peter L., “Studying Solar Cells with the ModuLab XM PhotoEchem Optical and Electrical Measurement System” Ametek Application Note SA 105, 2016, www.solartronanalytical.com, accessed July 23rd, 2019
- Fabregat-Santiago F. Bisquert J. Garcia-Belmonte G. Boschloo G. Hagfeldt A. Sol. Energy Mater. Sol. Cells. 2005;87(1–4):117. doi: 10.1016/j.solmat.2004.07.017. [DOI] [Google Scholar]
- Contreras-Bernal L. Ramos-Terrón S. Riquelme A. Boix P. P. Idígoras J. Mora-Seró I. Anta J. A. J. Mater. Chem. A. 2019;7(19):12191. doi: 10.1039/C9TA02808K. [DOI] [Google Scholar]
- Pockett A. Eperon G. E. Peltola T. Snaith H. J. Walker A. Peter L. M. Cameron P. J. J. Phys. Chem. C. 2015;119(7):3456. doi: 10.1021/jp510837q. [DOI] [Google Scholar]
- Pockett A. Eperon G. E. Sakai N. Snaith H. J. Peter L. M. Cameron P. J. Phys. Chem. Chem. Phys. 2017;19(8):5959. doi: 10.1039/C6CP08424A. [DOI] [PubMed] [Google Scholar]
- Todinova A. Contreras-Bernal L. Salado M. Ahmad S. Morillo N. Idígoras J. Anta J. A. ChemElectroChem. 2017;4(11):2891. doi: 10.1002/celc.201700498. [DOI] [Google Scholar]
- Pitarch-Tena D. Ngo T. T. Vallés-Pelarda M. Pauporté T. Mora-Seró I. ACS Energy Lett. 2018;3(4):1044. doi: 10.1021/acsenergylett.8b00465. [DOI] [Google Scholar]
- Raga S. R. Qi Y. J. Phys. Chem. C. 2016;120(50):28519. doi: 10.1021/acs.jpcc.6b11584. [DOI] [Google Scholar]
- Tress W. Marinova N. Moehl T. Zakeeruddin S. M. Nazeeruddin M. K. Grätzel M. Energy Environ. Sci. 2015;8(3):995. doi: 10.1039/C4EE03664F. [DOI] [Google Scholar]
- Moia D. Gelmetti I. Calado P. Fisher W. Stringer M. Game O. Hu Y. Docampo P. Lidzey D. Palomares E. Nelson J. Barnes P. R. F. Energy Environ. Sci. 2019;12(4):1296. doi: 10.1039/C8EE02362J. [DOI] [Google Scholar]
- Zarazua I. Han G. Boix P. P. Mhaisalkar S. Fabregat-Santiago F. Mora-Seró I. Bisquert J. Garcia-Belmonte G. J. Phys. Chem. Lett. 2016;7(24):5105. doi: 10.1021/acs.jpclett.6b02193. [DOI] [PubMed] [Google Scholar]
- Zarazúa I. Sidhik S. Lopéz-Luke T. Esparza D. de La Rosa E. Reyes-Gomez J. Mora-Seró I. Garcia-Belmonte G. J. Phys. Chem. Lett. 2017;8(24):6073. doi: 10.1021/acs.jpclett.7b02848. [DOI] [PubMed] [Google Scholar]
- Guerrero A. Garcia-Belmonte G. Mora-Sero I. Bisquert J. Kang Y. S. Jacobsson T. J. Correa-Baena J.-P. Hagfeldt A. J. Phys. Chem. C. 2016;120(15):8023. doi: 10.1021/acs.jpcc.6b01728. [DOI] [Google Scholar]
- Ghahremanirad E. Bou A. Olyaee S. Bisquert J. J. Phys. Chem. Lett. 2017;8(7):1402. doi: 10.1021/acs.jpclett.7b00415. [DOI] [PubMed] [Google Scholar]
- Bag M. Renna L. A. Adhikari R. Y. Karak S. Liu F. Lahti P. M. Russell T. P. Tuominen M. T. Venkataraman D. J. Am. Chem. Soc. 2015;137(40):13130. doi: 10.1021/jacs.5b08535. [DOI] [PubMed] [Google Scholar]
- Gonzalez-Pedro V. Juarez-Perez E. J. Arsyad W.-S. Barea E. M. Fabregat-Santiago F. Mora-Sero I. Bisquert J. Nano Lett. 2014;14(2):888. doi: 10.1021/nl404252e. [DOI] [PubMed] [Google Scholar]
- Ebadi F. Taghavinia N. Mohammadpour R. Hagfeldt A. Tress W. Nat. Commun. 2019;10(1):1574. doi: 10.1038/s41467-019-09079-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klotz D. Electrochem. Commun. 2019;98:58. doi: 10.1016/j.elecom.2018.11.017. [DOI] [Google Scholar]
- Calado P. Telford A. M. Bryant D. Li X. Nelson J. O'Regan B. C. Barnes P. R. F. Nat. Commun. 2016;7:13831. doi: 10.1038/ncomms13831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domanski K. Roose B. Matsui T. Saliba M. Turren-Cruz S.-H. Correa-Baena J.-P. Carmona C. R. Richardson G. Foster J. M. de Angelis F. Ball J. M. Petrozza A. Mine N. Nazeeruddin M. K. Tress W. Grätzel M. Steiner U. Hagfeldt A. Abate A. Energy Environ. Sci. 2017;10(2):604. doi: 10.1039/C6EE03352K. [DOI] [Google Scholar]
- Wang H. Guerrero A. Bou A. Al-Mayouf A. M. Bisquert J. Energy Environ. Sci. 2019;33:1443. [Google Scholar]
- Kim G. Y. Senocrate A. Yang T.-Y. Gregori G. Grätzel M. Maier J. Nat. Mater. 2018;17(5):445. doi: 10.1038/s41563-018-0038-0. [DOI] [PubMed] [Google Scholar]
- Azpiroz J. M. Mosconi E. Bisquert J. de Angelis F. Energy Environ. Sci. 2015;8(7):2118. doi: 10.1039/C5EE01265A. [DOI] [Google Scholar]
- Senocrate A. Moudrakovski I. Kim G. Y. Yang T.-Y. Gregori G. Grätzel M. Maier J. Angew. Chem., Int. Ed. 2017;56(27):7755. doi: 10.1002/anie.201701724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y.-C. Zhou W.-K. Zhou X. Liu K.-H. Yu D.-P. Zhao Q. Light: Sci. Appl. 2017;6(5):e16243. doi: 10.1038/lsa.2016.243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barboni D. de Souza R. A. Energy Environ. Sci. 2018;11(11):3266. doi: 10.1039/C8EE01697F. [DOI] [Google Scholar]
- Jacobs D. A. Wu Y. Shen H. Barugkin C. Beck F. J. White T. P. Weber K. Catchpole K. R. Phys. Chem. Chem. Phys. 2017;19(4):3094. doi: 10.1039/C6CP06989D. [DOI] [PubMed] [Google Scholar]
- Carrillo J. Guerrero A. Rahimnejad S. Almora O. Zarazua I. Mas-Marza E. Bisquert J. Garcia-Belmonte G. Adv. Energy Mater. 2016;6(9):1502246. doi: 10.1002/aenm.201502246. [DOI] [Google Scholar]
- Correa-Baena J.-P. Turren-Cruz S.-H. Tress W. Hagfeldt A. Aranda C. Shooshtari L. Bisquert J. Guerrero A. ACS Energy Lett. 2017;2(3):681. doi: 10.1021/acsenergylett.7b00059. [DOI] [Google Scholar]
- Elumalai N. K. Uddin A. Sol. Energy Mater. Sol. Cells. 2016;157:476. doi: 10.1016/j.solmat.2016.06.025. [DOI] [Google Scholar]
- deQuilettes D. W. Zhang W. Burlakov V. M. Graham D. J. Leijtens T. Osherov A. Bulović V. Snaith H. J. Ginger D. S. Stranks S. D. Nat. Commun. 2016;7:11683. doi: 10.1038/ncomms11683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hentz O. Rekemeyer P. Gradečak S. Adv. Energy Mater. 2018;8(18):1701378. doi: 10.1002/aenm.201701378. [DOI] [Google Scholar]
- Hentz O. Zhao Z. Gradečak S. Nano Lett. 2016;16(2):1485. doi: 10.1021/acs.nanolett.5b05181. [DOI] [PubMed] [Google Scholar]
- Li W. Liu J. Bai F.-Q. Zhang H.-X. Prezhdo O. V. ACS Energy Lett. 2017;2(6):1270. doi: 10.1021/acsenergylett.7b00183. [DOI] [Google Scholar]
- Zohar A. Levine I. Gupta S. Davidson O. Azulay D. Millo O. Balberg I. Hodes G. Cahen D. ACS Energy Lett. 2017;2(10):2408. doi: 10.1021/acsenergylett.7b00698. [DOI] [Google Scholar]
- Li C. Guerrero A. Huettner S. Bisquert J. Nat. Commun. 2018;9(1):5113. doi: 10.1038/s41467-018-07571-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birkhold S. T. Precht J. T. Liu H. Giridharagopal R. Eperon G. E. Schmidt-Mende L. Li X. Ginger D. S. ACS Energy Lett. 2018;3(6):1279. doi: 10.1021/acsenergylett.8b00505. [DOI] [Google Scholar]
- Boukamp B. A. J. Electrochem. Soc. 1995;142(6):1885. doi: 10.1149/1.2044210. [DOI] [Google Scholar]
- Schönleber M. Klotz D. Ivers-Tiffée E. Electrochim. Acta. 2014;131:20. doi: 10.1016/j.electacta.2014.01.034. [DOI] [Google Scholar]
- Tumen-Ulzii G. Qin C. Klotz D. Leyden M. Wang P. Auffrey M. Fujihara T. Matsushima T. Lee J.-W. Lee S.-J. Yang Y. Adachi C. Adv. Mater. 2019 doi: 10.1002/adma.201905035. [DOI] [PubMed] [Google Scholar]; , submitted
- Saliba M. Matsui T. Seo J.-Y. Domanski K. Correa-Baena J.-P. Nazeeruddin M. K. Zakeeruddin S. M. Tress W. Abate A. Hagfeldt A. Grätzel M. Energy Environ. Sci. 2016;9(6):1989. doi: 10.1039/C5EE03874J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deepa M. Salado M. Calio L. Kazim S. Shivaprasad S. M. Ahmad S. Phys. Chem. Chem. Phys. 2017;19(5):4069. doi: 10.1039/C6CP08022G. [DOI] [PubMed] [Google Scholar]
- Hu Y. Hutter E. M. Rieder P. Grill I. Hanisch J. Aygüler M. F. Hufnagel A. G. Handloser M. Bein T. Hartschuh A. Tvingstedt K. Dyakonov V. Baumann A. Savenije T. J. Petrus M. L. Docampo P. Adv. Energy Mater. 2018;8(16):1703057. doi: 10.1002/aenm.201703057. [DOI] [Google Scholar]
- Seo J.-Y. Kim H.-S. Akin S. Stojanovic M. Simon E. Fleischer M. Hagfeldt A. Zakeeruddin S. M. Grätzel M. Energy Environ. Sci. 2018;11(10):2985. doi: 10.1039/C8EE01500G. [DOI] [Google Scholar]
- Bu T. Li J. Zheng F. Chen W. Wen X. Ku Z. Peng Y. Zhong J. Cheng Y.-B. Huang F. Nat. Commun. 2018;9(1):4609. doi: 10.1038/s41467-018-07099-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klotz D. Ellis D. S. Dotan H. Rothschild A. Phys. Chem. Chem. Phys. 2016;18(34):23438. doi: 10.1039/C6CP04683E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu F. Bahrami B. Chen K. Mabrouk S. Pathak R. Tong Y. Li X. Zhang T. Jian R. Qiao Q. ACS Appl. Mater. Interfaces. 2018;10(30):25604. doi: 10.1021/acsami.8b07298. [DOI] [PubMed] [Google Scholar]
- Wei L.-y. Ma W. Lian C. Meng S. J. Phys. Chem. C. 2017;121(11):5905. doi: 10.1021/acs.jpcc.6b12583. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.