Genomic Data Sharing under Dependent Local Differential Privacy

Abstract

Privacy-preserving genomic data sharing is prominent to increase the pace of genomic research, and hence to pave the way towards personalized genomic medicine. In this paper, we introduce (ϵ, T)-dependent local differential privacy (LDP) for privacy-preserving sharing of correlated data and propose a genomic data sharing mechanism under this privacy definition. We first show that the original definition of LDP is not suitable for genomic data sharing, and then we propose a new mechanism to share genomic data. The proposed mechanism considers the correlations in data during data sharing, eliminates statistically unlikely data values beforehand, and adjusts the probability distributions for each shared data point accordingly. By doing so, we show that we can avoid an attacker from inferring the correct values of the shared data points by utilizing the correlations in the data. By adjusting the probability distributions of the shared states of each data point, we also improve the utility of shared data for the data collector. Furthermore, we develop a greedy algorithm that strategically identifies the processing order of the shared data points with the aim of maximizing the utility of the shared data. Our evaluation results on a real-life genomic dataset show the superiority of the proposed mechanism compared to the randomized response mechanism (a widely used technique to achieve LDP).

1. INTRODUCTION

Recent advances in genome sequencing technologies have enabled individuals to access their genome sequences easily, resulting in massive amounts of genomic data. On one hand, sharing this massive amount of data is important for the progress of genomics research. Genomic data collected by research laboratories or published in public repositories leads to significant breakthroughs in medicine, including discovery of associations between mutations and diseases. On the other hand, since genomic data contains sensitive information about individuals, such as predisposition to diseases and family relationships, individuals are generally hesitant to share their genomic data. Therefore, how to facilitate genomic data sharing in a privacy-preserving way is a crucial problem.

One way to preserve privacy in genomic data sharing and analysis is to utilize cryptographic techniques. However, encrypted data can only be used for a limited number of operations and high computation costs decrease the applicability of these techniques for large scale datasets. Local differential privacy (LDP) is a state-of-the-art definition to preserve the privacy of the individuals in data sharing with an untrusted data collector, and hence it is a promising technology for privacy-preserving sharing of genomic data. Perturbing data before sharing provides plausible deniability for the individuals. However, the original LDP definition does not consider the data correlations. Hence, applying existing LDP-based data sharing mechanisms directly on genomic data makes perturbed data vulnerable to attacks utilizing correlations in the data.

In this work, our goal is to provide privacy guarantees for the shared genomic sequence of a data owner against inference attacks that utilize correlations in the data while providing high data utility for the data collector. For that, we develop a new genomic data sharing mechanism by defining a variant of LDP under correlations, named (ϵ, T)-dependent LDP. We use randomized response (RR) mechanism as a baseline since the total number of states for each genomic data point is 3 and the RR provides the best utility for such a small number of states [30]. Moreover, RR uses the same set of inputs and outputs without an encoding, which allows the data collector to use perturbed data directly. We first show how correlations in genomic data can be used by an attacker to infer the original values of perturbed data points when RR mechanism is directly used. We describe a correlation attack and show how estimation error of the attacker (a commonly used metric to quantify genomic privacy) decreases due to the direct use of RR.

In the correlation attack, the attacker detects (and eliminates) the data values that are not consistent with the other shared values based on correlations. Thus, in the proposed data sharing scheme, we consider such an attack by-design and do not share the values of the shared data points which are inconsistent with the previously shared data points. During sharing of each data point (single nucleotide polymorphism - SNP) with the data collector, the proposed algorithm eliminates a particular value of a shared SNP if the corresponding value of the SNP occurs with negligible probability considering its correlations with the other shared SNPs (to prevent an attacker utilize such statistically unlikely values to infer the actual values of the SNPs). Then, the algorithm adjusts the sharing probabilities for the non-eliminated values of the SNP by normalizing them and making sure that the attacker’s distinguishability between each possible values of the SNP is bounded by e^ϵ, which achieves (ϵ, T)-dependent LDP.

To improve utility, we introduce new probability distributions (for the shared states of each SNP), such that, for each shared SNP, the probability of deviating significantly from its “useful values” is small. Useful values of a SNP depend on how the data collector intends to use the collected SNPs. For this, we focus on genomic data sharing beacons (a system constructed with the aim of providing a secure and systematic way of sharing genomic data) and show how to determine probability distributions for different states of each shared SNP with the aim of maximizing the utility of the collected data (this can easily be extended for other uses of genomic data, such as in statistical databases). In the proposed mechanism, SNPs of a genome donor are processed sequentially. Although the proposed (ϵ, T)-dependent LDP definition is satisfied in any order, the number of eliminated states for each SNP can be different based on the order of processing. Hence, we also show how to determine an optimal order of processing (which provides the highest utility) via Markov decision process (MDP) and provide a value iteration-based algorithm to optimize the utility of shared data. Furthermore, due to complexity of the optimal algorithm, we propose an efficient greedy algorithm to determine the processing order of the SNPs in the proposed data sharing mechanism.

We conduct experiments with a real-life genomic dataset to show the utility and privacy provided by the proposed scheme. Our experimental results show that the proposed scheme provides better privacy and utility than the original randomized response mechanism. We also show that using the proposed greedy algorithm for the order of processing, we improve the utility compared to randomly selecting the order of processed SNPs.

The rest of the paper is organized as follows. We review the related work in Section 2 and provide the technical preliminaries in Section 3. We present the proposed framework in Section 4. We propose an algorithm for optimal data processing order in Section 5. We evaluate the proposed scheme via experiments in Section 6. Finally, we conclude the paper in Section 7.

2. RELATED WORK

In this section, we discuss relevant existing works.

2.1. Genomic Privacy

Genomic privacy topic has been recently explored by many researchers [22]. Several works have studied various inference attacks against genomic data including membership inference [24, 29] and attribute inference [2, 11, 17]. To mitigate these threats, some researchers proposed using cryptographic techniques for privacy-preserving processing of genomic data [1, 3, 36]. The differential privacy (DP) concept [13] has also been used to release summary statistics about genomic data in a privacy-preserving way (to mitigate membership inference attacks) [19, 35]. Unlike the existing DP-based approaches, our goal is to share the genomic sequence of an individual, not summary statistics. To share genomic sequences in a privacy-preserving way, techniques to selectively share (or hide) data points (SNPs) have been proposed [18, 33]. However, they do not provide formal privacy guarantees. For the first time, we study the applicability of LDP for genomic data sharing and develop a variant of LDP for correlated data.

2.2. Local Differential Privacy

Differential privacy (DP) [13] is a concept to preserve the privacy of records in statistical databases while publishing statistical information about the database. Although DP provides strong guarantees for individual privacy, there may be privacy risks for individuals when data is correlated. Several approaches have been proposed [7, 20, 26] in order to protect the privacy of individuals under correlations. Since these works focus on privacy of aggregate data release (e.g., summary statistics about data), they are not suitable for individual data sharing. Local differential privacy (LDP) is a state-of-the-art definition to preserve the privacy of the individuals in data sharing with an untrusted data collector. However, a very limited number of tasks, such as frequency estimation [30], heavy hitters [4], frequent itemset mining [31], and marginal release [9] have been demonstrated under LDP and the accuracy of these tasks are much lower than performing the same task under the central model of differential privacy. Collecting perturbed data from more individuals decreases the accuracy loss due to randomization. Hence, practical usage of LDP-based techniques needs a high number of individuals (data owners), which limits the practicality of LDP-based techniques. To overcome the accuracy loss due to LDP, a shuffling technique [14] has recently been proposed. The main idea of shuffling is to utilize a trusted shuffler which receives the perturbed data from individuals and permutes them before sending to data collector. However, requiring a trusted shuffler also restricts the practical usage of this method.

Another approach to improve utility of LDP is providing different privacy protection for different inputs. In the original definition of LDP, indistinguishability needs to be provided for all inputs. Murakami et al. divided the inputs into two groups as sensitive and non-sensitive ones [21]. They introduced the notion of utility-optimized LDP, which provides privacy guarantees for only sensitive inputs. Gu et al. [15] proposed input-discriminative LDP, which provides distinct protection for each input. However, grouping inputs based on their sensitivity is not realistic in practice due to the subjectivity of sensitivity. In this work, we discriminate the inputs based on their likelihood instead of their sensitivity. We focus on how correlations can be used by an attacker to degrade privacy and how we mitigate such degradation. Hence, we provide indistinguishability between possible states by eliminating the states that are rarely seen in the population using correlations. By doing so, we aim to decrease the information gain of an attacker that uses correlations for inference attacks. Furthermore, both of these works [15, 21] aim to improve utility by providing less indistinguishability for non-sensitive data and providing more accurate estimations. In our work, the accuracy does not rely on estimations. Instead, we provide high accuracy by eliminating rare values from both input and output sets. We also improve the utility by increasing the probability of “useful values” considering the intended use of the shared data.

3. TECHNICAL PRELIMINARIES

In this section, we give brief backgrounds about genomics and LDP.

3.1. Genomics Background

The human genome contains approximately 3 billion pairs of nucleotides (A, T, C, or G). Approximately 99.9% of these pairs are identical in all people. When more than 0.5% of the population does not carry the same nucleotide at a specific position in the genome, this variation is considered as single-nucleotide polymorphism (SNP). More than 100 million SNPs have been identified in humans. For a SNP, the nucleotide which is observed in the majority of the population is called the major allele and the nucleotide which is observed in the minority of the population is called the minor allele. Each person has two alleles for each SNP position, and each of these alleles are inherited from a parent of the individual. Hence, each SNP can be represented by the number of its minor alleles, which can be 0, 1, or 2. In this work, we study the problem of sharing the values of SNPs in a privacy-preserving way. It is shown that SNPs may have pairwise correlations between each other (e.g., linkage disequilibrium [25]). Since an attacker can use such correlations to infer the original values of the shared SNPs, privacy of the family members should also be considered in genomic data sharing.

3.2. Definition of Local Differential Privacy

Local differential privacy (LDP) is a variant of differential privacy that allows to share data with an untrusted party. In LDP settings, each individual shares her data with the data collector after perturbation (randomization). Then, the data collector uses all collected perturbed data to estimate statistics about the population. During data perturbation, the privacy of the individuals are protected by achieving indistinguishability.

In this work, we adopt the general definition of LDP [12], which is expressed as follows:

Definition 1 (Local Differential Privacy [12]). A randomized mechanism A satisfies ϵ-local differential privacy if

$$\underset{y\in \sigma (\mathcal{Y}),d_{\alpha },d_{\beta }\in \mathcal{X}}{\text{sup}}\frac{\text{Pr}\left(y\mid A\left(x=d_{\alpha }\right)\right)}{\text{Pr}\left(y\mid A\left(x=d_{\beta }\right)\right)}\le e^{ϵ},$$

where d_α and d_β are two possible values of an element x, y is the output value, $\mathcal{Y}$ is the collection of all possible output values of x, and $\sigma \left(\mathcal{Y}\right)$ denotes an appropriate σ-filed on $\mathcal{Y}$.

Definition 1 captures a type of plausible-deniability, i.e., no matter what input value of x is released, it is nearly equally as likely to have come from any of its possible values. The parameter ϵ is the privacy budget, which controls the level of privacy. Randomized response (RR) [32] is a mechanism for collecting sensitive information from individuals by providing plausible deniability. We use the general definition of LDP (i.e., Definition 1), instead of the commonly used one, i.e., Pr (A(x) ∈ Range(A))/Pr (A(x′) ∈ Range(A)) ≤ e^ϵ (x and x′ are a pair of user’s possible private data element, and Range(A) is the range of the mechanism A) [4, 31], because the general definition explicitly considers the possible (statistical likely) input and output values of each data point by using σ-algebra, which is more convenient for us to incorporate correlation models and develop dependent LDP (Section 4.3). Although RR is originally defined for two possible inputs (e.g., yes/no), this mechanism can also be generalized. In generalized RR [31], the correct value is shared with probability p = e^ϵ/(e^ϵ+m−1) and each incorrect value is shared with probability q = 1/(e^ϵ+m−1) to achieve ϵ-LDP, where m is the number of states.

4. PROPOSED FRAMEWORK

In this section, we first introduce the problem and explain genomic data sharing with an untrusted data collector by directly applying RR mechanism. We then present a correlation attack that utilizes correlations between SNPs and show the significant decrease in privacy after the attack. We also show how to simultaneously improve privacy against the correlation attacks and improve utility for genomic analysis. Finally, we present our proposed genomic data sharing mechanism.

4.1. Problem Statement

System Model.

Figure 1 shows the overview of the system model and the steps of the proposed framework. We focus on a problem, where genome donors share their genomic data in a privacy-preserving way with a data collector who will use collected data to answer queries about the population. In genomic data sharing scenario, there are n individuals (I₁, …, I_n) as genome donors. A genome donor I_j has a sequence of SNPs denoted by ${\mathcal{X}}^j=\left[x_1^j,\dots ,x_l^j\right]$. Since each SNP is represented by the number of minor alleles it carries, each $x_i^j$ has a value from the set {0, 1, 2}. Today, individuals can obtain their genomic sequences via various online service providers, such as 23andMe, and they also share their sequences with other service providers or online repositories (e.g., for research purposes). Hence, the proposed system model has real-world applications, where individuals want to preserve privacy of their genomic data when they share their genomic sequences.

Figure 1:

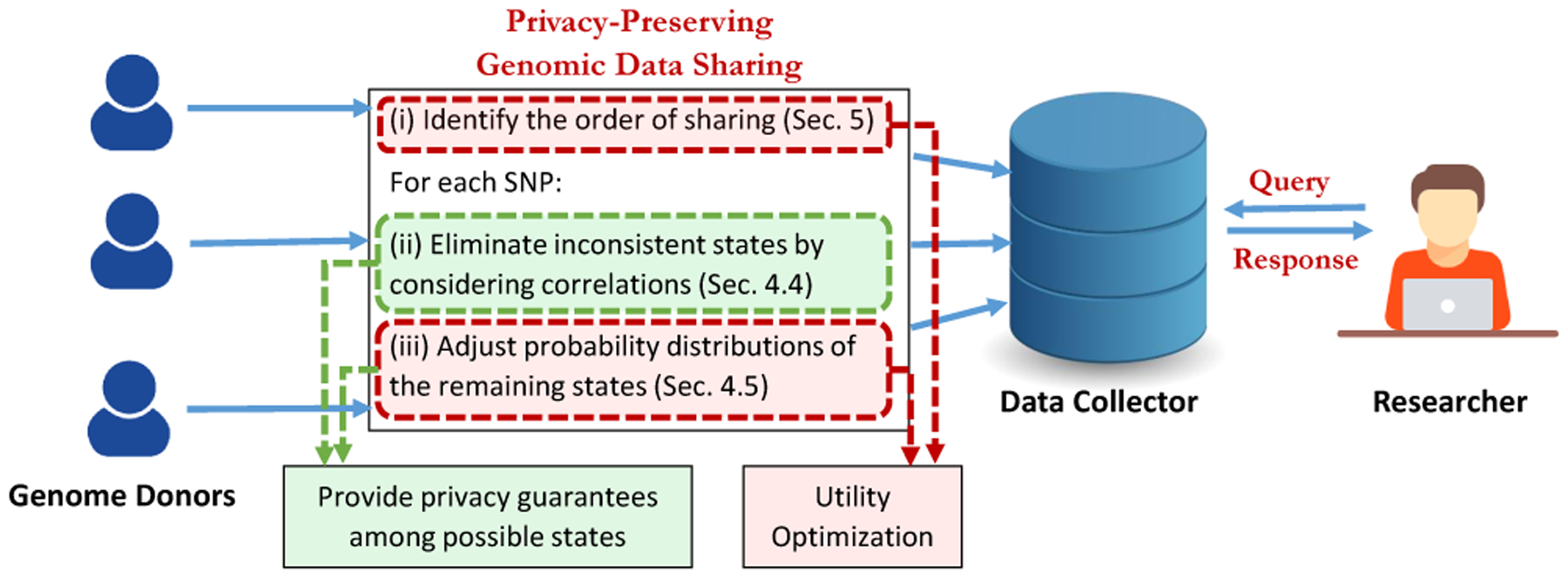
System Model.

Threat Model.

The data collector is considered as untrusted. It can share the data directly with another party or use it to answer queries. Hence, we assume the attacker has data shared by all genome donors with the data collector, however, it does not know the original values of any SNPs. In addition, we assume that the attacker knows the pairwise correlations between SNPs (which can be computed using public datasets), the perturbation method, and the privacy budget ϵ. Thus, the attacker can infer whether the shared value of a SNP is equal to its original value using correlations.

Data Utility.

The data collector uses data collected from genome donors to answer queries. Therefore, we define the utility as the accuracy of data collector to answer such queries. For genomic data, typically, the utility of each value of a SNP is different and the utility of a SNP may change depending on the purpose of data collection (e.g., statistical genomic databases, genomic data sharing beacons, or haploinsufficiency studies). Thus, one of our aims is to improve the utility of LDP-based data collection mechanism by considering data utility as a part of the data sharing mechanism.

Genomic Data Sharing Under Local Differential Privacy.

In [30], several approaches have been explained for estimating frequency of inputs under LDP such as direct encoding, histogram encoding, and unary encoding. As shown in [30], when the size of input set is less than 3e^ϵ +2, direct encoding is the best among these approaches. Since the size of input set for genomic data is 3, we also use direct encoding approach for genomic data sharing. In direct encoding approach, no specific encoding technique is applied to inputs before perturbation and randomized response (RR) mechanism (introduced in Section 3.2) is used for perturbing inputs. To apply RR mechanism and achieve ϵ-LDP for genomic data, the value of a SNP is shared correctly with probability p = e^ϵ /(e^ϵ + 2) and each incorrect value is shared with probability q = 1/(e^ϵ+ 2). After receiving perturbed values from n individuals, the data collector estimates the frequency of each input in the population as $\frac{c_i-n\cdot q}{p-q}$, where c_i is the number of individuals who shared i ∈ {0, 1, 2}.

4.2. Correlation Attack Against LDP-Based Genomic Data Sharing

When multiple data points are shared with the RR mechanism, ϵ-LDP is still guaranteed if the data points are independent. However, it is known that SNPs have pairwise correlations between each other (e.g., linkage disequilibrium [25]). An attacker can use the correlations between SNPs to infer incorrectly or correctly shared SNPs as a result of the RR mechanism.

To show this privacy risk, we consider a correlation attack that can be performed by an attacker in the following. We represent a SNP i as SNP_i and we represent the value of SNP_i for individual I_j as $x_i^j$. We assume that all pairwise correlations between SNPs are publicly known. Hence, Pr(SNP_i = d_α | SNP_k = d_β) is known by the attacker for any i, k ∈ {1,…, l} and d_α, d_β ∈ {0, 1, 2}. Let ${\mathcal{Y}}^j=\left[y_1^j,\dots ,y_l^j\right]$ be the perturbed data that is shared by I_j with the data collector (potential attacker whose goal is to infer the actual SNP values). Without using the correlations, the attacker’s only knowledge about any $x_i^j$ is the probability distribution of RR mechanism. However, using the correlations, the attacker can enhance its knowledge about the probability distribution of $x_i^j$ by eliminating the values that are not likely to be observed (i.e., that have low correlation with the other received data points).

To achieve this, for each SNP_i of I_j, using all other received data points $\left[y_1^j,\dots ,y_l^j\right]$ (except for $y_i^j$), the attacker counts the number of inconsistent instances in terms of correlations between different values of SNP_i and all other received data points (i.e., having correlation less than a threshold). Let τ be the correlation threshold of the attacker. The attacker keeps a count for the number of instances for each SNP_k (k ∈ {1, …, l},k ≠ i) having $\text{Pr}\left(x_i^j=0\mid x_k^j=y_k^j\right)<\tau ,\text{\hspace{0.17em}Pr}\left(x_i^j=1\mid x_k^j=y_k^j\right)<\tau$, and $\text{Pr}\left(x_i^j=2\mid x_k^j=y_k^j\right)<\tau$ as $c_{i,0}^j$, $c_{i,1}^j$, and $c_{i,2}^j$, respectively. If any of these values is greater than or equal to γ · l (where γ is an attack parameter for the number of inconsistent data points), the attacker eliminates that value in the probability distribution of $x_i^j$ and considers the remaining values for its inference about the correct value of $x_i^j$.

To show the effect of this correlation attack on privacy, we implemented the RR mechanism for genomic data and computed the attacker’s estimation error, a metric used in genomic privacy, to quantify the distance of the attacker’s inferred values from the original data, before and after the attack. Our results (in Figure 5, Section 6.1) clearly show the vulnerability of directly using RR in genomic data sharing. For instance, when ϵ = 1, the attacker’s estimation error decreases from 0.8 to 0.4 after the correlation attack. In general, we observed that the attacker’s estimation error decreases approximately 50% by using this attack strategy.

Figure 5:

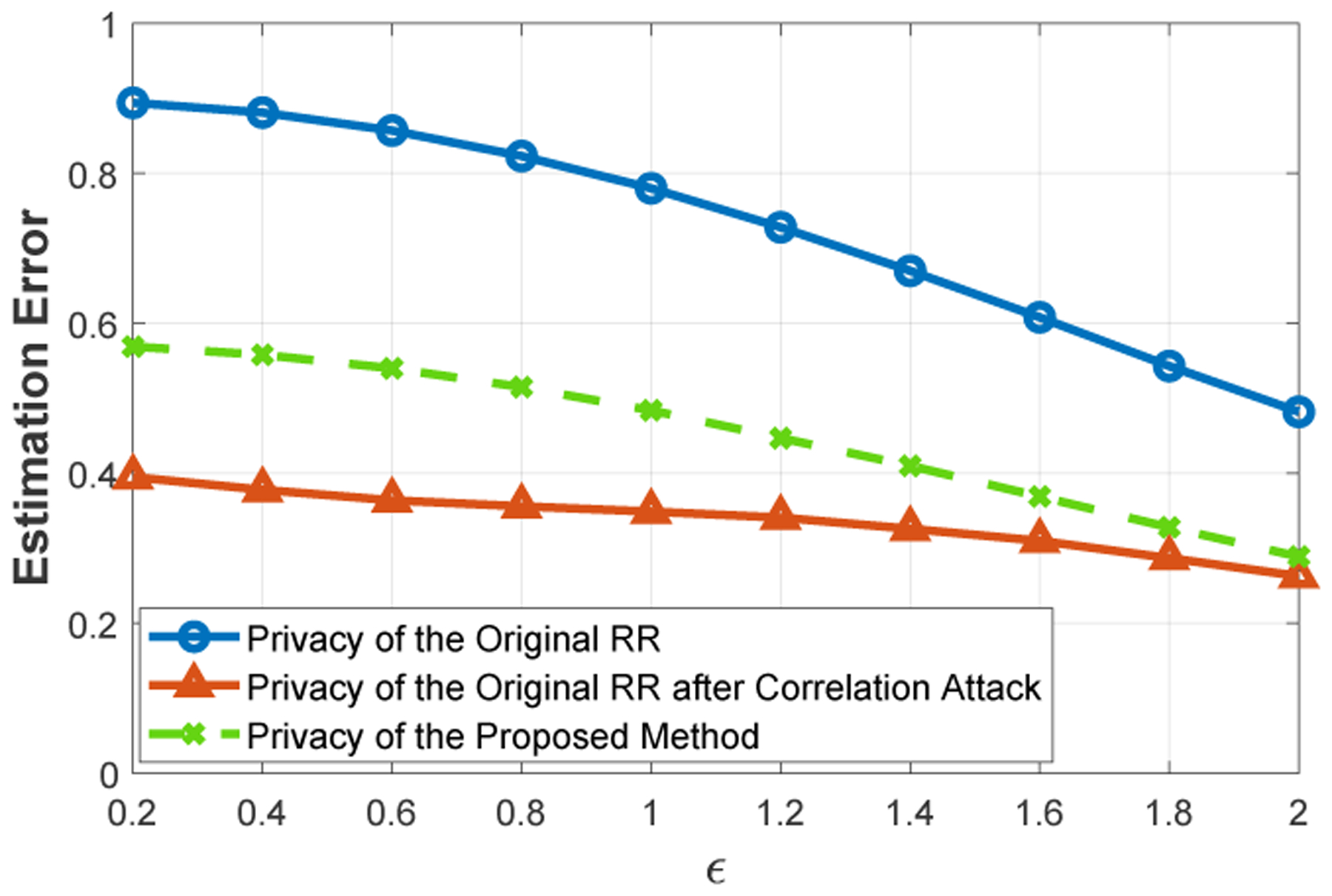
Comparison of the proposed method with original RR mechanism in terms of attacker’s estimation error.

4.3. (ϵ, T)-dependent Local Differential Privacy

To handle data dependency in privacy-preserving data sharing, some works, such as [7, 20] extend the definition of traditional differential privacy by considering the correlation between elements in the dataset. However, there is a lack of such variants for local differential privacy models, which hinders the application of LDP-based solutions for privacy-preserving genomic data sharing. In this paper, inspired by [20], which handles data dependency by considering the number of elements that can potentially be affected by a single element, we propose the following definition.

Definition 2. An element x in a dataset $\mathcal{X}$ is said to be T-dependent under a correlation model (denoted as Corr) if its released value y depends on at most other T elements in $\mathcal{X}$. The dependency is measured in terms of the conditional probability of x taking value y given the knowledge on the value of another element in $\mathcal{X}$.

Furthermore, let ${\mathcal{Q}}_i$ be the set of elements on which a T-dependent element $x_i\in \mathcal{X}$ is dependent (through model Corr_i) $\left(\left|{\mathcal{Q}}_i\right|\le T\right)$, $A\left({\mathcal{Q}}_i\right)$ be the set of released values of elements in ${\mathcal{Q}}_i$, and $d_{\alpha \mid A\left({\mathcal{Q}}_i\right),{\text{corr}}_i}$ represent the possible value(s) of x_i that can be released due to the releasing of $A\left({\mathcal{Q}}_i\right)$ and model Corr_i. Note that it is possible for some elements to have only one possible value to be shared under a specific correlation model. If the only possible value happens to be the true value of that element, we call these elements ineliminable elements, whose privacy will be inevitably compromised for the sake of the utility improvement of the entire shared elements (we formally investigate this issue in Section 5). Thus, we propose the following definition.

Definition 3 (Dependent Local Differential Privacy). A randomized mechanism A is said to be (ϵ, T)-dependent local deferentially private for an element that is not ineliminable if

$$\underset{y\in \sigma (\mathcal{Y}),d_{\alpha \mid A\left({\mathcal{Q}}_i\right),\text{Cor}{\text{r}}_i},d_{\beta \mid A\left({\mathcal{Q}}_i\right),{\text{Corr}}_i}}{\text{sup}}\frac{\text{Pr}\left(y\mid A\left(x_i=d_{\alpha \mid A\left({\mathcal{Q}}_i\right),{\text{Corr}}_i}\right)\right)}{\text{Pr}\left(y\mid A\left(x_i=d_{\beta \mid A\left({\mathcal{Q}}_i\right),{\text{Corr}}_i}\right)\right)}\le e^{ϵ}.$$

Definition 3 can be considered as a specialization of the general LDP definition (Definition 1) by having $d_{\alpha }=d_{\alpha \mid A}\left({\mathcal{Q}}_i\right),{\text{Corr}}_i$ and $d_{\beta }=d_{\beta \mid A\left({\mathcal{Q}}_i\right),{\text{Corr}}_i}$. Essentially, Definition 3 means that any output of a T-dependent element x is nearly equally as likely to have come from any of its possible input values given other already shared elements (i.e., $A\left({\mathcal{Q}}_i\right)$ and a correlation model Corr_i). In other words, a specific element x_i, taking value of $d_{\alpha \mid A\left({\mathcal{Q}}_i\right),{\text{Corr}}_i}$ or $d_{\beta \mid A\left({\mathcal{Q}}_i\right),{\text{Corr}}_i}$, will be almost equally perturbed as $y\in \sigma (\mathcal{Y})$ by the randomized mechanism A.

Remark. It is noteworthy that our definition of dependent local differential privacy does not compromise the privacy guarantee of the conventional LDP, because if we assume no correlation model, i.e., Corr_i = ∅, ∀i, then dependent LDP reduces to the conventional LDP. By incorporating the correlation model, given the same privacy guarantee with conventional LDP, our proposed dependent LDP can achieve higher data utility by eliminating statistically unlikely values.

4.4. Achieving (ϵ, T)-dependent LDP in Genomic Data Sharing

Our experimental results show the vulnerability of directly applying RR mechanism for genomic data sharing.

Thus, here, our goal is to come up with a genomic data sharing approach achieving (ϵ, T)-dependent LDP that is robust against the correlation attack. The definition of LDP states that given any output, the distinguishability between any two possible inputs needs to be bounded by e^ϵ. In Section 4.2, all values in set {0, 1, 2} are considered as possible inputs for all SNPs during data sharing. However, we know that the attacker can eliminate some input states using correlations. Hence, for the rest of the paper, we consider the possible input states as the ones that are not eliminated by using correlations. In other words, we provide indistinguishability between the values that are statistically possible.

In the correlation attack described in Section 4.2, the attacker uses two threshold values. The correlation values less than τ are considered as low correlation. In addition, if the fraction of SNPs having low correlation with a state of a particular SNP is more than γ, such state of the SNP is eliminated by the attacker. In the data sharing scheme, we also use these two parameters to eliminate states. However, the parameters used by the algorithm may not be same with the ones used by the attacker. Hence, to distinguish the parameters used by the algorithm and the attacker, we represent the parameters used in the algorithm as $\widehat{\tau }$ and $\widehat{\gamma }$ (which are the design parameters of the proposed data sharing algorithm). We describe this algorithm for a donor I_j as follows.

In each step of the proposed algorithm, one SNP $x_i^j$ is processed. The algorithm first determines the states to be eliminated by considering previously processed SNPs. Then, the algorithm selects the value to be shared $\left(y_i^j\right)$ by limiting the distinguishability of non-eliminated states by e^ϵ. Hence, the order of processing may change the number of eliminated states for a SNP, which may also change the utility of the shared data. For instance, when a SNP is processed as the first SNP, all its three states are possible (for sharing) since there is no previously shared SNP. However, processing the same SNP as the last SNP may end up eliminating one or more of its states (due to their correlations with previously shared SNPs). We propose an algorithm to select the optimal processing order (considering utility of shared data) in Section 5. In the following, we assume that a processing order is provided by the algorithm in Section 5 and SNPs are processed one by one following this order.

For $x_i^j$, the algorithm considers the previously processed data points and identifies the states which will be eliminated. As explained in the correlation attack, the algorithm counts the number of previously processed SNPs which have low correlation with states 0, 1, and 2 of $x_i^j$.

Thus, the algorithm keeps counts for the previously processed SNPs (SNP^k) having $\text{Pr}\left(x_i^j=0\mid x_k^j=y_k^j\right)<\widehat{\tau }$, $\text{Pr}\left(x_i^j=1\mid x_k^j=y_k^j\right)<\widehat{\tau }$, $\text{Pr}\left(x_i^j=2\mid x_k^j=y_k^j\right)<\widehat{\tau }$ as $c_{i,0}^{\widehat{j}}$, $c_{i,1}^{\widehat{j}}$, and $c_{i,2}^{\widehat{j}}$, respectively. If any of these values is greater than or equal to $\widehat{\gamma }\cdot i$, the algorithm eliminates such value from the possible outputs of $x_i^j$. Let p = e^ϵ/(e^ϵ + 2) and q = 1/(e^ϵ + 2), and the value of $x_i^j$ be 0. Then, the algorithm assigns the probabilities of non-eliminated states as follows:

• If there are three possible outputs (i.e., no eliminated state), the algorithm uses the same probability distribution with the RR mechanism as (p, q, q). Thus, $\text{Pr}\left(y_i^j=0\right)=p$ and $\text{Pr}\left(y_i^j=1\right)=\text{Pr}\left(y_i^j=2\right)=q$.

• If there are two possible outputs (i.e., one eliminated state) and $x_i^j$ (state 0) is not eliminated, the algorithm uses an adjusted probability distribution as (p/(p + q), q/(p + q), 0) (or (p/(p + q), 0, q/(p + q)), depending on which state is eliminated).

• If there are two possible outputs (i.e., one eliminated state) and $x_i^j$ is eliminated, the algorithm uses an adjusted probability distribution as (0, 0.5, 0.5).

• If there is one possible output (i.e., two eliminated states), the corresponding state is selected as the output.

• If there is no possible output (i.e., three eliminated states), the algorithm uses the same probability distribution as the RR mechanism.

For other values of $x_i^j$, the algorithm also works in a similar way. The probability distributions for sharing a data point are also shown in Figure 2. Based on these probabilities, the algorithm selects the value of $y_i^j$. If the attacker knows $\widehat{\tau }$ and $\widehat{\gamma }$ used in the algorithm, it can compute the possible values for each SNP using perturbed data ${\mathcal{Y}}^j=\left[y_1^j,\dots ,y_l^j\right]$, $\widehat{\tau }$, $\widehat{\gamma }$ and the correlations between the SNPs. Since e^ϵ ratio is preserved in each case, the attacker can only distinguish the possible inputs with e^ϵ difference.

Figure 2:

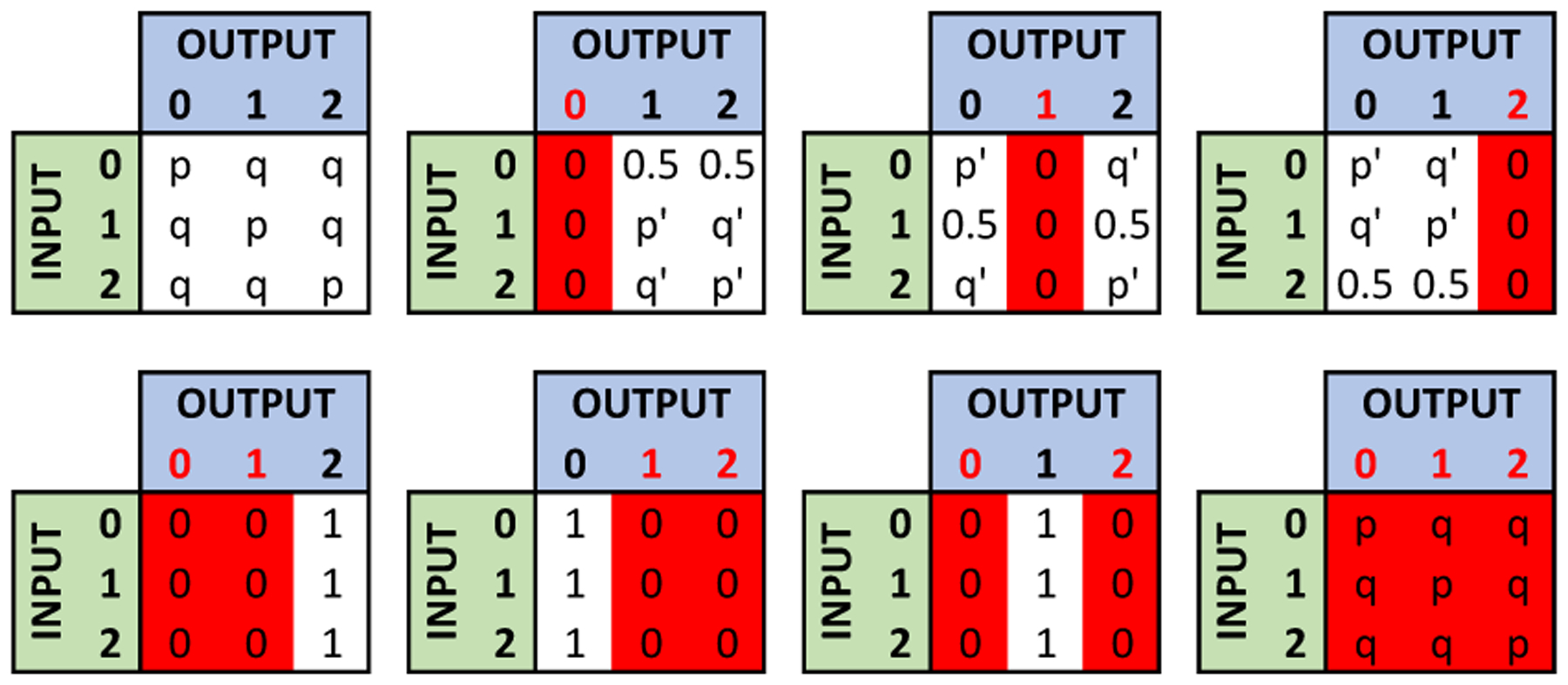
Probability distribution used by the data sharing mechanism after eliminating states using correlations as described in Section 4.4. p = e^ϵ /(e^ϵ + 2), q = 1/(e^ϵ+ 2), p′ = p/(p + q), and q^′ = q/(p + q). Red columns represent the eliminated states.

4.5. Improving Utility by Adjusting Probability Distributions

In Section 4.4, we proposed a data sharing mechanism to improve the privacy of RR mechanism against the correlation attack. The mechanism guarantees that the perturbed data ${\mathcal{Y}}^j=\left[y_1^j,\dots ,y_l^j\right]$ belonging to I_j does not include any value that have low correlation with other SNPs. However, consistent with existing LDP-based mechanisms, the algorithm assigns equal sharing probabilities for each incorrect value of a SNP i. However, this may cause significant utility loss since the accuracy of genomic analysis may significantly decrease as the values of shared SNPs deviate more from their original values (e.g., in genomic data sharing beacons or when studying haploinsufficiency). For genomic data, typically, the utility of each value of a SNP is different and the utility of a SNP may change depending on the purpose of data collection. Here, our goal is to improve the utility of shared data by modifying the probability distributions without violating (ϵ, T)-dependent LDP.

To improve utility, we introduce new probability distributions, such that, for each shared SNP, the probability of deviating high from its “useful values” is small. Useful values of a SNP depend on how the data collector intends to use the collected SNPs. For instance, for genomic data sharing beacons, changing the value of a shared SNP with value 2 to 1 does not decrease the utility, but sharing it as 0 may cause a significant utility loss. Similarly, while studying haploinsufficiency, obfuscating a SNP with value 2 results in a significant utility loss while changing a 0 to 1 (or 1 to 0) does not cause a high utility loss. Here, to show how the proposed data sharing mechanism improves the utility, we focus on genomic data sharing beacons without loss of generality (similar analysis can be done for other uses of genomic data as well).

Genomic data sharing beacons allow users (researchers) to learn whether individuals with specific alleles (nucleotides) of interest are present in their dataset. A user can submit a query, asking whether a genome exists in the beacon with a certain nucleotide at a certain position, and the beacon answers as “yes” or “no”. Since having at least one minor allele is enough for a “yes” answer, having one minor allele (a SNP value of 1) or two minor alleles (a SNP value of 2) at a certain position is equivalent in terms of the utility of beacon’s response. Therefore, if the correct value of a SNP is 1 or 2, sharing the incorrect value as 2 or 1 will have higher utility than sharing it as 0. Considering this, we change the probability distributions of the data sharing mechanism (given in Section 4.4) as shown in Figure 3) to improve the utility. As in Section 4.4, p = e^ϵ/(e^ϵ + 2) and q = 1/(e^ϵ + 2). These probability distributions still preserve the e^ϵ ratio between states. Note that for eliminating the states, the same process is used as described in Section 4.4. To determine the processing order of the SNPs, the algorithm in Section 5 is used.

Figure 3:

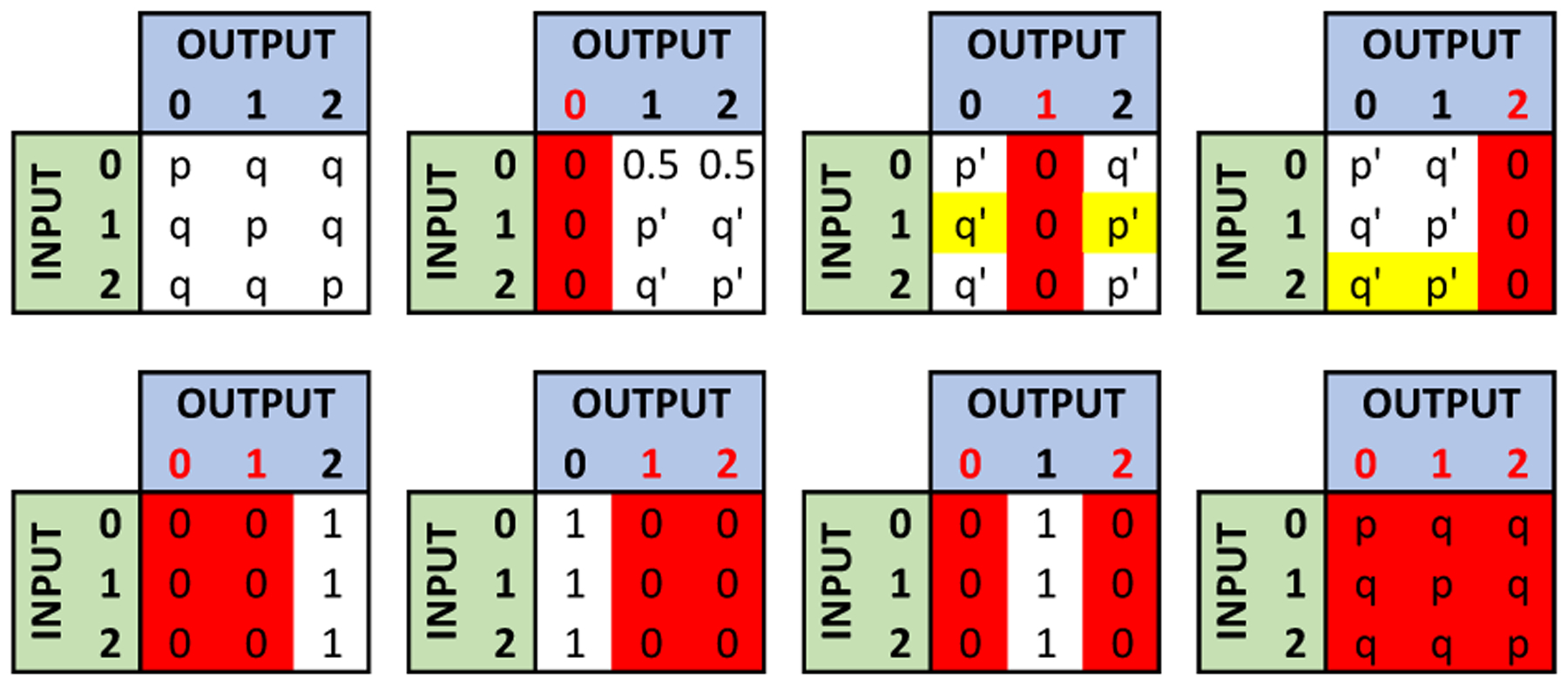
Probability distribution used by the data sharing mechanism to improve utility of beacon queries (in genomic data sharing beacons). p = e^ϵ/(e^ϵ +2),q = 1/(e^ϵ +2), p′ = p/(p + q), and q′ = q/(p + q). Red columns represent the eliminated states. The differences with Figure 2 are highlighted with yellow.

4.6. Proposed Data Sharing Algorithm

In Section 4.4, we described how to improve privacy by eliminating statistically unlikely values for each SNP. In Section 4.5, we explained how to modify probability distributions to improve utility of shared data for genomic data sharing beacons. Using these two ideas, we describe our proposed genomic data sharing algorithm in the following and provide the details for an individual I_j in Algorithm 4.1. The algorithm processes all SNPs one by one and in each iteration, it computes a value to share for the SNP being processed (eventually, all SNPs are processed and they are shared at the same time with the data collector). The algorithm first eliminates the states having low correlations with the previously processed SNPs, as described in Section 4.4. Two thresholds $\widehat{\tau }$ and $\widehat{\gamma }$ are used to determine the eliminated states. We evaluate the effect of these threshold values on utility and privacy in Section 6.2. Then, the algorithm decides the shared value of the SNP using the probability distribution in Figure 3. This process is repeated for all SNPs and the SNP sequence to be shared (i.e., output) is determined. Since we consider all pairwise correlations, changing the order may change the utility of the proposed scheme by eliminating different states. We discuss the optimal selection of this order (in terms of utility) in Section 5 and Algorithm 5.1 outputs the optimal order for each individual I_j (i.e., ${\pi }^{j^{*}}$). Due to the computational complexity of Algorithm 5.1, we also propose a greedy algorithm in Section 5.2. Thus, either the output of the optimal or the greedy algorithm is used as the input for the proposed data sharing algorithm.

Lemma 4.1. Given a processing order, Algorithm 4.1 achieves (ϵ, l − 1)-dependent local differential privacy for each genomic data point that is not ineliminable.

Proof. The proof directly follows from the reallocation of probability mass used in the RR mechanism. Since Corr_i is the pairwise correlation between SNPs, we have T = l −1. Besides, the e^ϵ ratio is preserved in the modified RR mechanism, and hence the condition in Definition 3 can always hold for ineliminable SNPs. □

5. OPTIMAL DATA PROCESSING ORDER FOR THE PROPOSED GENOMIC DATA SHARING MECHANISM

Algorithm 4.1 considers/processes one SNP at a time and as discussed, different processing orders may cause elimination of different states of a SNP, which, in turn, may change the utility of the shared data. Assuming there are totally l SNPs in ${\mathcal{X}}^j$ of an individual I_j, Algorithm 4.1 can process them in l! different orders. As a result, determining an optimal order of processing to maximize the utility of the shared sequence of SNPs is a critical and challenging problem. In this section, we formulate the problem of determining the optimal order of processing as a Markov Decision Processes (MDP) [27], which can be solved by value iteration using dynamic programming. Note that the algorithm locally processes all SNPs, and then perturbed data is shared all at once. Hence, the data collector does not see or observe the order of processing.

Since we consider genomic data sharing beacons to study the utility of shared data (as in Section 4.5) and the proposed sharing scheme is non-deterministic, we aim at achieving the maximum expected utility for the beacon responses using the shared SNPs. Note that similar analysis can be done for other uses of genomic data as well. Beacon utility is typically measured over a population of individuals, however, in this work, we consider an optimal processing order, which maximizes the expected beacon utility for each individual. The reason is twofold: (i) an individual does not have access to other individuals’ SNPs and (ii) a population’s maximum expected beacon utility can be achieved if all individuals’ maximum expected beacon utility are obtained due to the following Lemma, whose proof is given in [34].

Lemma 5.1. Maximizing the expectation of individuals’ beacon utility is a sufficient condition for maximizing the expectation of a population’s beacon utility.

The sufficient condition in Lemma 5.1 can easily be extended to other genomic data sharing scenarios as long as the individuals share their SNPs independently from each other.

5.1. Determining the Optimal Processing Order via Markov Decision Processes (MDP)

Here, we proceed with obtaining the optimal order of processing which maximizes individuals’ expected beacon utility. First, we model the SNP state elimination and processing order as an agent-environment interaction framework, where the agent is a specific individual (donor), the environment is the proposed SNP sharing scheme considering correlations (in Algorithm 4.1), and the interaction between the agent and environment follows a MDP.

For instance, consider the individual (donor) I_j in the population. Then, her MDP interaction with the environment is characterized as a tuple $\left\{{\mathcal{S}}^j,s_1^j,{\mathcal{A}}^j,{\text{Pr}}^j(\cdot ),{\mathcal{R}}^j,H^j\right\}$, where ${\mathcal{S}}^j$ is the set of all MDP states of individual I_j, $s_1^j$ is her initial MDP state, ${\mathcal{A}}^j$ is her action set, Pr^j(·) is the transition probability between two MDP states of I_j, ${\mathcal{R}}^j$ is her set of rewards, and H^j is the horizon of the MDP (i.e., number of rounds in discrete time). In our case, H = l (number of SNPs to be processed), and $s_1^j=\varnothing$. At each time step i ∈ {1, 2, ⋯, H} (i.e., when individual I_j processes her ith SNP), the agent chooses an action $a_i^j$ from her action pool ${\mathcal{A}}_i^j\subset {\mathcal{A}}^j$ (i.e., selects a specific SNP from her remaining unprocessed SNPs), where ${\mathcal{A}}_i^j$ is the set of remaining unprocessed SNPs and ${\mathcal{A}}^j$ is the set of all SNPs of individual I_j. Then, the environment provides the agent with a MDP state $s_i^j$ and a reward $r_i^j$. In particular, $s_i^j=\left\{y_1^j,y_2^j,\cdots ,y_i^j\right\}$ (i.e., the list recording all observations of previously processed SNPs of individual I_j) and $r_i^j$ is the utility of the beacon response on $y_i^j$, and hence, we have $r_i^j\in {\mathcal{R}}^j=\left\{0,1\right\}$.

After observing $s_i^j$ and receiving $r_i^j$, the agent takes the next action $a_{i+1}^j\in {\mathcal{A}}_{i+1}^j$, which causes $s_i^j$ to transit to $s_{i+1}^j$ via the transition probability $\text{Pr}\left(s_{i+1}^j\mid s_i^j,a_i^j,s_{i-1}^j,a_{i-1}^j,\cdots ,s_1^j,a_1^j\right)=\text{Pr}\left(s_{i+1}^j\mid s_i^j,a_i^j\right)$. Here, the equality holds due to the Markov property [27] and $\text{Pr}\left(s_{i+1}^j\mid s_i^j,a_i^j\right)$ is determined by the probability distribution with improved utility in Figure 3. An illustration of the MDP interaction between the agent (individual I_j) and the environment (Algorithm 4.1) at time step i (processing the ith SNP) is shown in Figure 4.

Figure 4:

The interaction between the agent (individual I_j) and the environment (Algorithm 4.1) at time step i, i.e., when processing the ith SNP ($x_i^j$) of individual I_j.

Since the optimal order can be predetermined and should be invariant in time, we model the agent’s (individual I_j) decision policy at time step i as a deterministic mapping as ${\pi }_i^j:{\mathcal{S}}^j\to {\mathcal{A}}_i^j$, i.e., $a_i^j={\pi }_i^j\left(s_i\right)$, ∀i ∈ {1, 2, ⋯, l}. Let ${\pi }^j=\left\{{\pi }_1^j,{\pi }_2^j,\cdots ,{\pi }_l^j\right\}$ be the sequence of decision policies of the agent. Due to the nondeterministic behavior of Algorithm 4.1, we characterize the environment’s behavior on individual I_j as a probabilistic mapping as $p:{\mathcal{S}}^j\times {\mathcal{A}}_i^j\to {\mathcal{S}}^j\times {\mathcal{R}}^j$ (i.e., $\text{Pr}\left(s_{i+1}^j\mid s_i^j,a_i^j\right)$). Furthermore, we define the future cumulative return for individual I_j starting from MDP state $s_i^j$ as $R_i^j={\sum }_{\eta =i}^{\eta =l}{r}_{\eta }^j$ and the state-value function of MDP state $s_i^j$ under policy ${\pi }_i^j$ as $v^{{\pi }_i^j}\left(s_i\right)={\mathbb{U}}_p\left[R_{i+1}^j\mid s_i^j\right]$ (${\mathbb{U}}_p[\cdot ]$ indicates that utility is considered in an expected manner with respect to the environment’s probabilistic mapping p). Then, to maximize an individual’s expected beacon utility at time step i, the agent takes the optimal decision ${\pi }_i^{j^{*}}\in {\text{argmax}}_{{\pi }_i^j}{v}_i^{{\pi }_i^j}\left(s_i\right),\forall s_i^j\in {\mathcal{S}}^j$ and ∈ suggests that ${\pi }_i^{j^{*}}$ may not be unique.

Thus, we have formulated the optimal order of processing problem as a finite-horizon MDP problem, whose state, action, and reward sets are all finite and dynamics are characterized by a finite set of probabilities (i.e., $\text{Pr}\left(s_i^j\mid s_{i-1}^j,a_{i-1}^j\right)$). The finite-horizon MDP problem is P-complete, as it can be reduced from the circuit value problem, which is a well-known P-complete problem [23]. In the literature, exact optimal solution of finite-horizon MDP problem can be obtained by quite a few methods, for example value iteration, policy iteration, or linear programming [5]. In Algorithm 5.1, we provide a value iteration [27] based approach to determine the optimal order of processing for an individual.

Algorithm 5.1 is implemented using dynamic programming starting from the last time step, and it has a computational complexity of $\mathcal{O}\left({\left|{\mathcal{S}}^j\right|}^2\left|{\mathcal{A}}^j\right|\right)$ for individual I_j [27]. For finite-horizon MDP, the number of MDP states grows exponentially with the number of variables, which is known as the curse of dimensionality. For example, in our case, at time step i, Algorithm 5.1 needs to calculate the state-value function for 3ⁱ states. In the literature, many approaches have been proposed to address this issue, such as state reduction [10] and logical representations [6], which, however are outside the scope of this paper. Therefore, Algorithm 5.1 may be computationally expensive to process large amount of data, and hence in the following section, we also propose a heuristic approach to process long sequence of SNPs.

5.2. A Heuristic Approach

In this work, we consider sharing thousands of SNPs of individuals in a population. As a consequence, it is computationally prohibitive to obtain the exact optimal order of processing for each individual. We propose the following heuristic approach for an individual I_j to process her SNPs in a local greedy manner. Specifically, at each time step i, the algorithm selects the SNP with the maximum expected beacon utility, i.e., $a_i^j={\text{argmax}}_{a^j\in {\mathcal{A}}_i^j}{\mathbb{U}}_{a^j}$, where ${\mathcal{A}}_i^j$ is the set of remaining SNPs of individual I_j, and ${\mathbb{U}}_{a^j}$ denotes the expected immediate utility if individual I_j selects SNP a^j and it can be determined by the adjusted state distribution in Figure 3. After evaluating the state elimination condition using a specific SNP, we greedily choose one SNP to share. For example, without loss of generality, assume that at time step l – 1, SNPs $x_i^j$ and $x_k^j$ are left in ${\mathcal{A}}_{l-1}^j$, after the elimination check, $x_i^j$ has state distribution $\left(0,\frac{p}{p+q},\frac{q}{p+q}\right)$ withU = 1, and $x_k^j$ has state distribution $\left(\frac{q}{p+q},0,\frac{q}{p+q}\right)$ with $U=\frac{q}{p+q}$. Then, the heuristic algorithm selects SNP $x_i^j$ to process at time step l − 1. If there is a tie between two SNPs, we randomly choose one. As a result, the computational complexity of the heuristic approach is $\mathcal{O}\left({\left|{\mathcal{A}}^j\right|}^2\right)$. The difference between the heuristic approach and Algorithm 5.1 is that Line 7 in Algorithm 5.1 is replaced with the maximizer of ${\mathbb{U}}_{a^j}$. For finite-horizon MDP problem, the gap between the optimal and heuristic solution can be established by exploring the asynchronous value iteration that updates a subset of the states of an MDP at each iteration [16], which, however, is outside the scope of this work. We will compare the heuristic approach with the optimal algorithm (in Algorithm 5.1) experimentally in Section 6.3.

6. EVALUATION

We implemented the proposed data sharing scheme in Section 4.6 and used a real genomic dataset containing the genomes of the Utah residents with Northern and Western European ancestry (CEU) population of the HapMap project [8] for evaluation. We used 1000 SNPs of 156 individuals from this dataset for our evaluations. Using this dataset, we computed all pairwise correlations between SNPs. For each 1 million (1000 × 1000) SNP pairs, we computed 9 (3 × 3) conditional probabilities. Hence, we totally computed 9 million conditional probabilities (for all pairwise correlations between all SNPs). Note that, to quantify the privacy of the proposed scheme against the strongest attacks, we used the same dataset to compute the attacker’s background knowledge. However, in practice, the attacker may use different datasets to compute such correlations and its attacks may become less successful when less accurate statistics are used. We also assumed that each donor has the same privacy budget (ϵ). To quantify privacy, we used the attacker’s estimation error. Estimation error is a commonly used metric to quantify genomic privacy [28], which quantifies the average distance of the attacker’s inferred SNP values from the original data $\left({\mathcal{X}}^j\right)$ as

$$E=\left(\sum _{v\in \left\{0,1,2\right\};k\in \left\{1,\dots ,l\right\}}\text{Pr}\left(x_k^j=v\right)\Vert x_k^j-v\Vert \right)/l,$$

where $\text{Pr}\left(x_k^j=v\right)$ is the attacker’s inference probability for $x_k^j$ being υ. We assume the attacker’s only knowledge is p and q initially, which are computed based on ϵ. Then, using the correlations, the attacker improves its knowledge by eliminating the statistically less likely values. For the eliminated states, attacker sets the corresponding probability to 0. Since $\Vert x_k^j-v\Vert$ can be at most 2 for genomic data, E is always in the range [0, 2], where higher E indicates better privacy. Thus, when the attacker’s estimation error decreases, the inference error of the attacker (e.g., to infer the predisposition of a target individual to a disease) decreases accordingly. To quantify the utility, we used the accuracy of beacon responses. For each SNP, we first run the beacon queries using the original values and then run the same queries with the perturbed values. Let the number of beacon responses (SNPs) for which we obtain the same answer for both original data and perturbed data be n_s. We computed the accuracy as A = n_s/l (l is the total number of beacon queries), which is always in the range [0, 1].

In the following, we first compare the proposed algorithm with the original RR mechanism in terms of privacy and utility. Then, we evaluate the effect of the design parameters on privacy and utility. Finally, we show the effect of the order of processing on utility.

6.1. Comparison with the Original Randomized Response Mechanism

As we discussed in Section 4.2, the original randomized response (RR) mechanism is vulnerable to correlation attacks because when a given state of a SNP is loosely correlated with at least γ · l other SNPs, the attacker can eliminate that state, and hence improve its inference power for the correct value of the SNP. In Figure 5, we show this vulnerability in terms of attacker’s estimation error (blue and red curves in the figure). We observed that attacker’s estimation error is the smallest (i.e., its inference power is the strongest) when the correlation threshold of the attacker (τ) is 0.02 and inconsistency threshold of the attacker (γ) is 0.03, and hence we used these parameters for the attack.

Under the same settings, we also computed the estimation error provided by the proposed algorithm when $\widehat{\tau }=0.02$ and $\widehat{\gamma }=0.03$. Therefore, during data sharing, we eliminated states of the SNPs having correlation less than $\widehat{\tau }=0.02$ (the correlation threshold of the algorithm) with at least $\widehat{\gamma }=0.03$ of the previously shared SNPs (in Section 6.2, we also evaluate the effect of these parameters on privacy and utility). We also let the attacker conduct the same attack in Section 4.2 with the same attack parameters as before. Figure 5 shows the comparison of the proposed scheme with original RR mechanism (green curve in the figure is the privacy provided by the proposed scheme). The results clearly show that the proposed method improves the privacy provided by RR after correlation attack. For instance, for ϵ = 1, the proposed scheme provides approximately 25% improvement in privacy compared to the RR mechanism. Note that the privacy of RR before the attack (blue curve in the figure) is computed by assuming the attacker does not use correlations. Hence, when the attacker uses correlations, it is not possible to reach that level of privacy with any data sharing mechanism and the privacy inevitably decreases. With the proposed scheme, we reduce this decrease in the privacy. To observe the limits of the proposed approach, we performed the correlation attack by assuming the attacker has 0 value for all SNPs (which is the mostly observed value in genomic data) and we observed the attacker’s estimation error as 0.66 (under the same experimental settings) after the correlation attack. Hence, with any mechanism it is not possible to exceed 0.66 after correlation attack and the privacy provided by the proposed scheme is remarkable.

Focusing on genomic data sharing beacons, we also compared the utility of shared data using the proposed scheme with the original RR mechanism in terms of accuracy of beacon answers (using the accuracy metric introduced before). We randomly selected 60 people from the population and used their 1000 SNPs to respond to the beacon queries. For 257 SNPs there was no minor allele, and hence the original response of the beacon query was “no”. There was at least one minor allele in 60 people for the remaining 743 SNPs (and hence, the original response of the beacon query was “yes”).

For the original RR mechanism, we shared 1000 SNPs of 60 individuals after perturbation. In the RR mechanism, the data collector eliminates the noise by estimating the frequency of each value using the sharing probabilities as described in Section 4.1. Hence, if 60 · p or more individuals report 0 for the value of a SNP (after perturbation), we considered the answer of beacon as “no”. For the proposed data sharing scheme, we did not apply such an estimation since in the proposed scheme, the sharing probabilities of the states are different for each SNP. Figure 6 shows the accuracy of the beacon for 1000 queries. We observed that our proposed scheme provides approximately 95% accuracy even for small values of ϵ, while the accuracy of the RR mechanism is less than 70% for small ϵ values and it only reaches to 85% when ϵ increases. We provide the accuracy evaluation for the “yes” and “no” responses separately in [34]. Note that we do not quantify the utility over the probability of correctly reporting a point. We quantify the utility over the accuracy of beacon answers. When the answer of the beacon query is “yes”, the original response of the beacon is mostly preserved after perturbation in both the original RR and the proposed mechanism (while the proposed mechanism still outperforms the RR mechanism, especially for smaller ϵ values). On the other hand, when the original answer of a beacon query is “no”, all individuals must report 0 for that SNP (to preserve the accuracy of the response). In this case, applying the original RR cannot provide high accuracy when ϵ is small, because with high probability, at least one individual reports its SNP value as 1 or 2 (i.e., incorrectly). Hence, our proposed approach significantly outperforms the RR mechanism in terms of the accuracy of the “no” responses. We conclude that the proposed scheme provides significantly better utility than the original RR mechanism.

Figure 6:

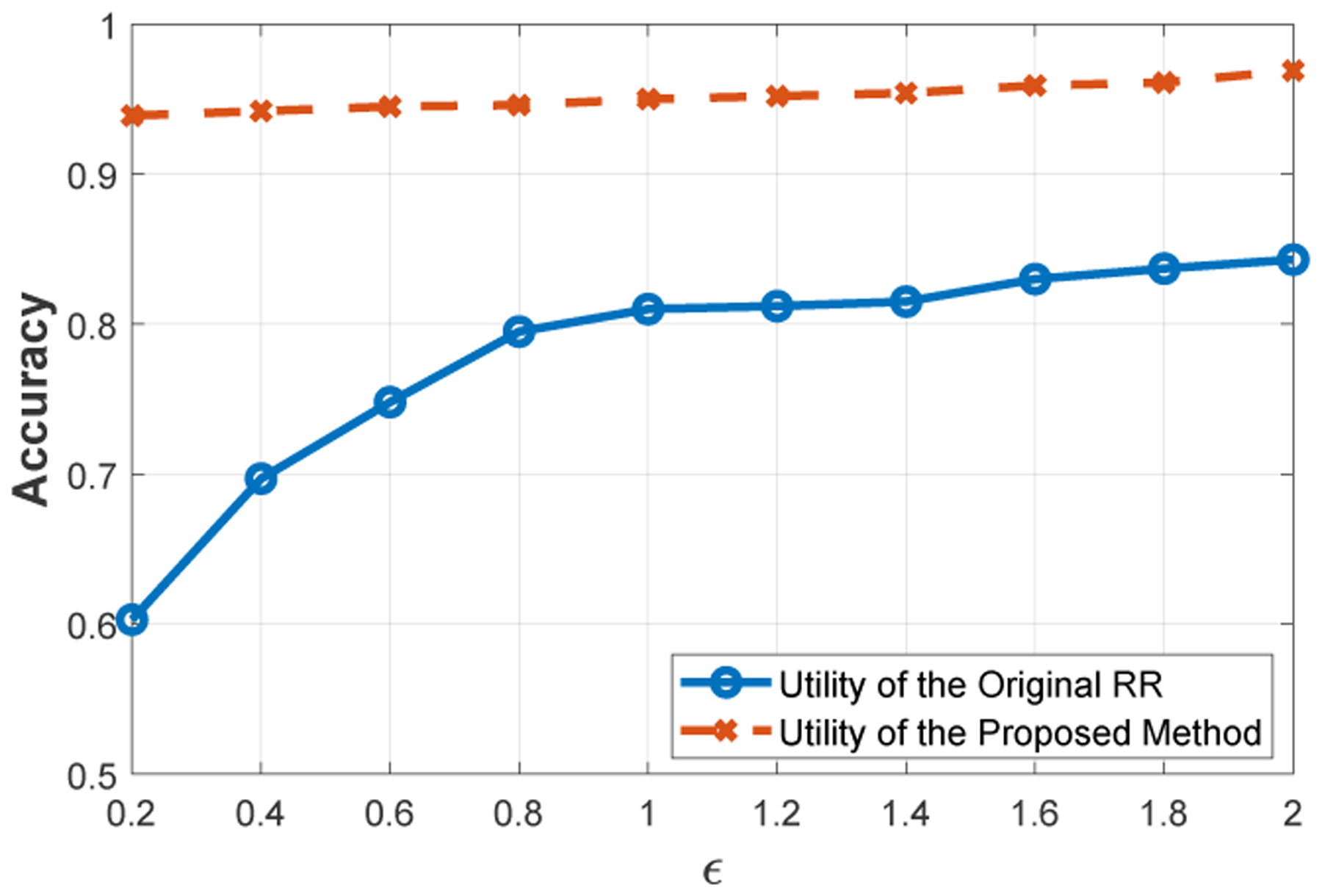
Comparison of the proposed method with RR mechanism in terms of utility, which is measured as the accuracy of responses provided from a genomic beacon.

Although here we evaluated utility for genomic data sharing beacons, similar utility analyses can be done for other applications as well. Since the proposed scheme eliminates statistically unlikely values, the proposed scheme will still outperform the original RR mechanism under similar settings. Since the proposed data sharing mechanism considers the correlations with the previously shared data points (as in Algorithm 4.1) its computational complexity is $\mathcal{O}\left(l^2\right)$, where l is the number of shared SNPs of a donor.

One alternative approach to improve privacy in the original RR mechanism can be adding a post-processing step that includes identifying the SNPs having low correlations with the other SNPs and replacing them with the values that have high correlations. Such an approach can be useful to prevent correlation attacks due to eliminating less likely values. However, this approach provides much lower utility compared to the proposed mechanism since the proposed mechanism improves utility by adjusting probability distributions and optimizing the order of processing. We also implemented this alternative post-processing approach and compared with the proposed mechanism. We observed similar estimation error with the proposed mechanism, which shows that this approach can also prevent correlation attacks. However, as shown in Table 1, post-processing approach provides even lower utility than the original RR mechanism without post-processing, because it becomes harder to do efficient estimation after the post-processing. Hence, the proposed mechanism outperforms the original RR mechanism even if post-processing is applied.

Table 1:

Comparison of the proposed method with original RR mechanism (with and without post-processing) in terms of utility (accuracy of responses provided from a genomic data sharing beacon).

ϵ	0.4	0.8	1.2	1.6	2
RR without post-processing	0.697	0.791	0.808	0.831	0.849
RR with post-processing	0.667	0.715	0.734	0.765	0.788
Proposed method	0.934	0.941	0.945	0.952	0.961

6.2. The Effect of Parameters on Utility and Privacy

In Section 6.1, we used the correlation threshold of the attacker (τ) as 0.02 and inconsistency threshold of the attacker (γ) as 0.03 in its correlation attack. In our experiments, these parameters provided the strongest attack against the original RR mechanism. In Table 2, we show how the estimation error of the attacker changes for different values of γ when ϵ = 1 and τ = 0.02. When ϵ = 1 in the original RR mechanism, we computed the estimation error before the attack as 0.78. Increasing γ results in eliminating less states by the attacker. For instance, if attacker selects γ = 0.5, it cannot eliminate any states and the estimation is still 0.78. As γ decreases, more states are eliminated and the estimation error keeps decreasing up to a point (up to γ = 0.03 in our experiments, which provides the smallest estimation error). As we further decreased γ beyond this point, we observed higher estimation error values, since as γ approaches to 0, all 3 states are eliminated for more SNPs. Also, when γ = 0, we computed the estimation error as 0.78 as well. We also observed similar results for different values of ϵ. Similarly, when γ = 0.03, we obtained the smallest estimation error for the attacker (and hence the strongest attack) when τ = 0.02.

Table 2:

Privacy (in terms of estimation error) of the original randomized response mechanism after the correlation attack for different values of γ (inconsistency threshold of the attacker) when τ = 0.02 and ϵ = 1.

γ	0.01	0.02	0.03	0.04	0.05
Estimation error (E)	0.491	0.380	0.348	0.368	0.415

Since the attack against the original RR mechanism is the strongest when τ = 0.02 and γ = 0.03, we set the correlation parameters of the proposed data sharing algorithm the same as the attack parameters (i.e., $\widehat{\tau }=0.02$ and $\widehat{\gamma }=0.03$) in Section 6.1. Here, we study the effect of changing these parameters on the performance of the proposed mechanism. We assume that the attacker does not know the parameters ($\widehat{\tau }$ and $\widehat{\gamma }$) used in the algorithm and uses the parameters providing the strongest attack (τ = 0.02 and γ = 0.03) against the original RR mechanism. First, we evaluated the effect of correlation threshold $\widehat{\tau }$ on privacy and utility (all correlations that are smaller than $\widehat{\tau }$ are considered as low by the algorithm). Our results are shown in Table 3. We observed that increasing $\widehat{\tau }$ increases the attacker’s estimation error since we assume the attacker does not know $\widehat{\tau }$ and uses τ = 0.02 in its attack. However, using $\widehat{\tau }=0.02$ provided the best utility for the proposed algorithm. Since there is no correlation (conditional probability) that is less than 0.02 in our dataset, the minimum possible value that we can use for $\widehat{\tau }$ in the algorithm is 0.02. We also show the privacy and utility of the proposed scheme for different values of $\widehat{\gamma }$ in Table 4. We observed that increasing $\widehat{\gamma }$ slightly increases utility, however, the privacy also decreases at the same time.

Table 3:

Privacy (in terms of estimation error) and utility (in terms of accuracy of beacon responses) of the proposed scheme for different values of $\widehat{\tau }$ (correlation threshold) when $\widehat{\gamma }=0.03$.and ϵ = 1. Estimation error is computed by assuming the attacker uses τ = 0.02 and γ = 0.03.

$\widehat{\tau }$	0.02	0.04	0.06	0.08	0.1
Estimation Error (E)	0.483	0.486	0.492	0.499	0.503
Accuracy (A)	0.950	0.942	0.918	0.892	0.865

Table 4:

Privacy (in terms of estimation error) and utility (in terms of accuracy of beacon responses) of the proposed scheme for different values of $\widehat{\gamma }$ (inconsistency threshold) when $\widehat{\tau }=0.02$ and ϵ = 1. Estimation error is computed by assuming the attacker uses τ = 0.02 and γ = 0.03.

$\widehat{\gamma }$	0.01	0.02	0.03	0.04	0.05
Estimation Error (E)	0.490	0.487	0.483	0.479	0.476
Accuracy (A)	0.932	0.940	0.950	0.954	0.959

In the previous experiments (Table 3 and 4), we assumed that the attacker does not know the parameters used in the experiments and uses τ = 0.02 and γ = 0.03. However, the attacker can perform stronger attacks if it knows the design parameters ($\widehat{\tau }$ and $\widehat{\gamma }$) of the algorithm. Thus, we also computed the attacker’s estimation error by assuming it knows the parameters used in the algorithm ($\widehat{\tau }=0.02$ and $\widehat{\gamma }=0.03$)). Estimation error of the attacker for different values of τ and γ are shown in Table 5. When we increased τ up to 0.1, we observed a slight decrease in the estimation error. For instance, when τ = 0.1 and $\widehat{\tau }=0.02$, we observed the estimation error of the attacker as 0.42. Similarly, the attacker can decrease the estimation error to 0.434 by knowing the value of $\widehat{\gamma }$ and selecting γ = 0.01. We also observed that for τ values greater than 0.1 and γ values less than 0.01, the decrease in attacker’s estimation error converged. Overall, we conclude that the attacker can slightly reduce its estimation error by knowing the design parameters of the proposed mechanism, however, the gain of the attacker (in terms of reduced estimation error) is negligible (at most 0.07). Furthermore, the proposed scheme still preserves its advantage over the original RR mechanism in all considered scenarios. These results show that varying design parameters only slightly affect the performance of the proposed scheme.

Table 5:

Privacy (in terms of estimation error) of the proposed scheme for different values of τ (correlation threshold of the attacker) and γ (inconsistency threshold of the attacker) when ϵ = 1. The parameters used in the data sharing algorithm are $\widehat{\tau }=0.02$ and $\widehat{\gamma }=0.03$.

τ (γ = 0.03)	0.02	0.04	0.06	0.08	0.10
Estimation Error (E)	0.483	0.478	0.462	0.446	0.420
γ (τ = 0.02)	0.01	0.02	0.03	0.04	0.05
Estimation Error (E)	0.434	0.468	0.483	0.497	0.508

In our experiments, we assume that the attacker has the same background knowledge (i.e., correlations between SNPs) as the data owner. If the attacker’s knowledge is weaker than this assumption (e.g., if the computed correlations on the attacker’s side are not accurate), then its estimation error will be higher than the one we computed in our experiments. On the other hand, if the attacker’s knowledge about the correlations in the data is stronger than the data owner, it can perform more successful attacks. To validate this, we added Gaussian noise to the correlations computed by the data owner and observed that the attacker’s estimation error decreases when the amount of noise increases. For instance, when ϵ = 1, the mean is equal to 0 and standard deviation is 0.1 in Gaussian distribution, estimation error decreases from 0.491 to 0.451. In the worst case scenario, when the data owner does not know (or use) the correlations in the data, the estimation error of the attacker becomes equal to its estimation error when it performs the attack to the original RR mechanism (i.e., solid line marked with triangles in Figure 5). In [34], we discuss more how attacker’s background knowledge affects the privacy guarantees.

6.3. The Effect of the Processing Order on Utility

In this section, we show the effect of different order of processing on the utility of the beacon responses. For all experiments, we set the parameters the same as in Section 6.1 (i.e., $\widehat{\tau }=0.02$ and $\widehat{\gamma }=0.03$) and we also quantified the accuracy in terms of the fraction of correct beacon responses for a population. We reported the results averaged over 100 trials.

To demonstrate that the greedy order of processing (in Section 5.2) outperforms the random order and provides an accuracy that is close to the optimal order (in Algorithm 5.1), we first compared them using a small dataset of 10 SNPs of 10 individuals (obtained from the same HapMap dataset [8] introduced before). When processing the SNPs of an individual I_j using the random order, we randomly permuted the order of her SNP sequence and then fed it into Algorithm 4.1. Assuming each donor has the same privacy budget (ϵ) and varying the privacy budget from 0.2 to 2, we show the results in Figure 7. We observed that for all the privacy budgets, the accuracy obtained by the greedy order is close to that obtained by the optimal order (when ϵ ≥ 1, the accuracy provided by both orders differ only by less than 2%). Whereas, the accuracy achieved by the random order is the lowest for all the privacy budgets because the random order does not try to maximize individuals’ expected beacon utility. These results show that greedy order of processing (in Section 5.2) performs comparably to the optimal algorithm (in Algorithm 5.1), and hence we use the greedy algorithm for our evaluations with larger datasets.

Figure 7:

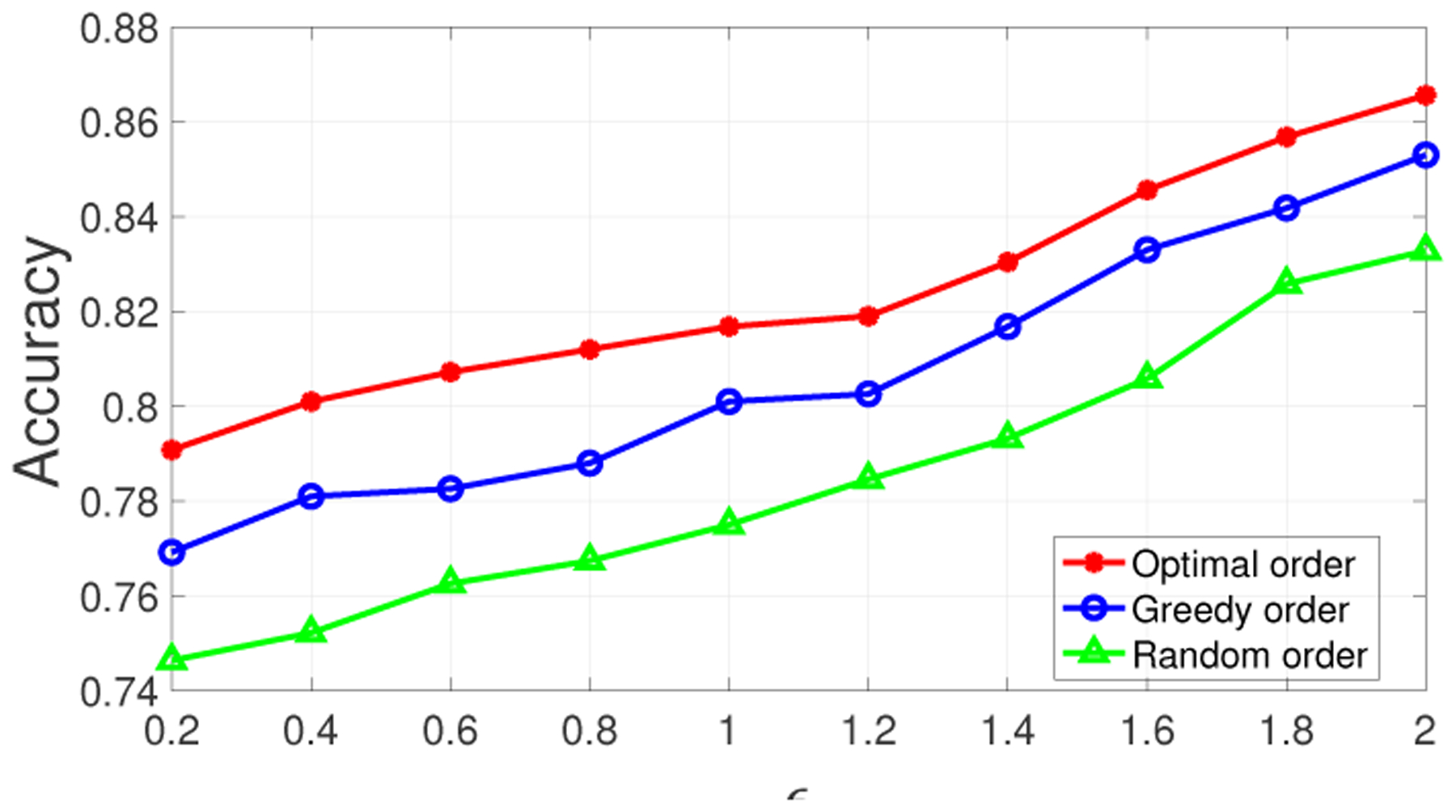
Accuracy of beacon responses on 10 SNPs from 10 individuals using optimal (Algorithm 5.1), greedy (Section 5.2), and random orders of processing.

Next, we compared the accuracy achieved by the greedy and random orders on the original dataset (i.e., 1000 SNPs of 156 individuals). The experiment results are shown in Figure 8. We observed that compared to the small dataset, the accuracy is improved significantly. For example, even under very limited privacy budgets (e.g., ϵ ≤ 0.4), both orders can achieve an accuracy over 93% since large dataset contains stronger (and more) correlations among SNPs. Correlations in the data is critical for the utility of the proposed data sharing mechanism, since when data is correlated, the proposed algorithm eliminates statistically unlikely states and adjusts the probability distributions of the remaining states in such a way that deviating highly from the “useful values” of the shared SNPs is small (as discussed in Section 4.5). From Figure 8, we also observed that the accuracy achieved by the greedy order consistently outperforms that obtained by the random processing order. This suggests that the utility varies under different processing orders and we can improve the utility of shared data points (SNPs) in a strategic way (e.g., by selecting them in a greedy manner). This outcome can also be generalized when sharing other types of correlated data. Another advantage of determining the processing order using the greedy algorithm is its computational complexity $(\mathcal{O}\left(l^2\right)$, where l is the number of shared SNPs of a donor), whereas the computational complexity of the optimal algorithm (in Algorithm 5.1) is $\mathcal{O}\left(3^l\right)$.

Figure 8:

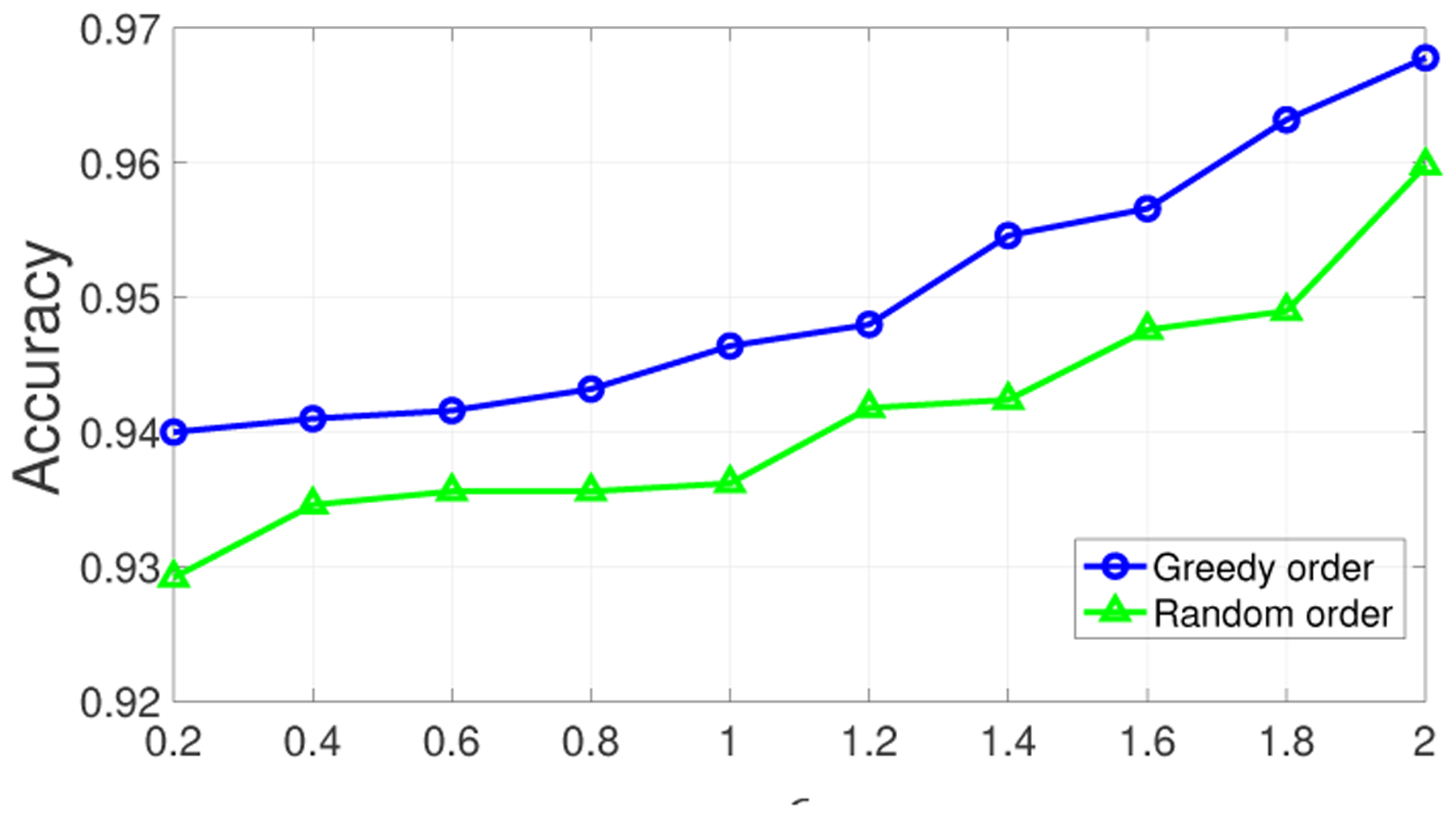
Accuracy of beacon responses on the original dataset using greedy and random orders of processing.

7. CONCLUSION

In this paper, we have introduced (ϵ, T)-dependent LDP and proposed a data sharing scheme for genomic data sharing achieving (ϵ, T)-dependent LDP. We have first described a correlation attack to show that directly applying the randomized response mechanism to correlated data causes vulnerabilities. To improve privacy against the correlation attacks, we have proposed a scheme that eliminates certain states of a SNP (and does not use such states during data sharing) which are loosely correlated with the previously shared SNPs. The proposed scheme decides a value to share among the non-eliminated states by providing formal privacy guarantees. To improve the utility of the shared data, we have shown how to adjust probability distributions for the non-eliminated states of the SNPs while still guaranteeing (ϵ, T)-dependent LDP. We have also proposed an optimal algorithm and a greedy algorithm to determine the processing order of SNPs in the proposed data sharing algorithm to optimize utility. We have implemented the proposed scheme and evaluated its privacy and utility via experiments on a real-life genomic dataset. The proposed data sharing mechanism can also be utilized for sharing of similar sensitive information that includes correlations (e.g., location patterns). In future work, we will evaluate the proposed mechanism considering different application of the data collector. We will also study how to compute the data sharing probabilities for different values of the SNP as a donor shares data with more data collectors.

CCS CONCEPTS.

• Security and privacy → Privacy-preserving protocols; • Applied computing → Genomics.