A facile and concise route to (hydroxybenzoyl)pyrido[2,3-d]pyrimidine heterocycle derivatives: synthesis, and structural, spectral and computational exploration

Abstract

In this work, we report the efficient synthesis of novel (hydroxybenzoyl)pyrido[2,3-d]pyrimidine heterocycle derivatives: 6-(2-hydroxy-5-methylbenzoyl)-1-methylpyrido[2,3-d]pyrimidine-2,4(1H,3H)-dione (6a), 6-(5-fluoro-2-hydroxybenzoyl)-1-methylpyrido[2,3-d]pyrimidine-2,4(1H,3H)-dione (6b), 6-(5-ethyl-2-hydroxybenzoyl)-1-methylpyrido[2,3-d]pyrimidine-2,4(1H,3H)-dione (6c) and 6-(2-hydroxy-5-isopropylbenzoyl)-1-methylpyrido[2,3-d]pyrimidine-2,4(1H,3H)-dione (6d). The chemical structures of the title compounds were ascertained by spectral techniques including ¹H, ¹³C NMR, UV-visible and FT-IR spectroscopy as well as single-crystal X-ray diffraction analysis. Additionally, density functional theory (DFT) and time-dependent (TD-DFT) computation were adopted to analyze the electronic structures of 6a–d. Compounds 6a–d were computed in the ground state for FT-IR spectroscopic and natural bond orbital (NBO) analysis by DFT/B3LYP with the 6-311+G(d,p) basis set. UV-vis spectroscopic and HOMO and LUMO energy values for 6a–d were determined via TD-DFT/B3LYP with the 6-311+G(d,p) basis set. The optimized geometric parameters, UV-vis findings, and vibrational frequencies indicate good consistency with the experimental data. NBO analysis was conducted to explore the interactions and charge transfer among different orbitals in the title compounds. The HOMO and LUMO band gap (ΔE) values for 6a–d were found to be 3.93, 3.91, 4.10 and 3.91 eV, respectively. Molecular electrostatic potential (MEP) analysis explored the reactivity of the title compounds by predicting their nucleophilic as well as electrophilic sites.

The chemical structures of the title compounds were ascertained by spectral techniques including ¹H, ¹³C NMR, UV-vis and FT-IR spectroscopy as well as single-crystal X-ray diffraction, and DFT computation adopted to analyze the electronic structure.

Introduction

Among the synthetic heterocyclic compounds, N-heterocycles have received widespread consideration from researchers in pharmaceutics and drug discovery. Pyridines as common six-membered heterocycles are important building blocks of biologically active and naturally occurring compounds.¹ Pyridopyrimidines represent a wide-ranging class of annulated uracils, which have gained substantial attention over the last few decades owing to the presence of the pyrimidine nucleus, which occurs frequently in nature in nucleic acids, coffee, nucleotides, cocoa, alkaloids from tea and uric acid. Xanthene was the first pyrimidine nucleus-containing compound discovered in bladder stones by Marget in 1817.² Owing to the position of the nitrogen atom in the pyridine moiety, there are four possible isomers of pyrido[d]pyrimidines.³ Among these isomers, pyrido[2,3-d]pyrimidines are the most abundant as potent inhibitors of adenosine kinase,⁴ tyrosine kinase,⁵ dihydrofolate reductase 1,⁶ and cyclin-dependent kinase (4) 2.⁷ Moreover, pyrido[2,3-d]pyrimidines are molluscicidal, anti-inflammatory and analgesic,⁸ anticancer,^9–11 antitumor,^12,13 anti-diarrhea 3,¹⁴ calcium channel antagonist, and anti-leishmanial agents¹⁵ (Fig. 1).

Fig. 1. Some drugs with a pyridopyrimidine skeleton.

Owing to their biological prominence, substantial effort has been focused towards synthetic strategies for pharmacologically active pyrido[2,3-d] pyrimidines, though there remain many challenges for the synthesis of naturally occurring complex molecules.²

In continuation of our research work,^16–20 we have synthesized some bioactive nitrogen- and oxygen-containing (hydroxybenzoyl)pyrido[2,3-d]pyrimidine heterocycles. Quantum chemical approaches provided promising insights regarding the chemical and biological systems that often found good agreement with the experimental results. Nowadays, the term “quantum chemical approaches” is used almost synonymously with density functional theory (DFT). DFT calculations provide a reasonable compromise between cost and accuracy. Many scientific publications have revealed that the DFT findings have been in line with experiments.²¹ Moreover, DFT-based findings have been recognized as being better than the findings obtained from ab initio methods.²² This might be one of the reasons behind the acceptance of DFT and it is extensively used in different fields of chemistry. Many DFT-based studies have addressed the various structural and mechanistic aspects of chemical systems.²³ In this context, we performed DFT calculations for the molecular geometry to understand the structural parameters, vibrational spectroscopy, NBO analysis for intermolecular interactions and MEP for chemical reactivity surfaces, HOMO–LUMO and nonlinear optics (NLO) analysis for the electronic properties of (hydroxybenzoyl)pyrido[2,3-d]pyrimidine heterocycle derivatives.

Experimental

Materials and methods

IR spectra were recorded using a Bruker Alpha FT-IR spectrometer. Melting points were recorded using a Fisher-John melting point apparatus and were uncorrected. UV-visible spectra were recorded using a Shimadzu UV-1800. Proton NMR spectra were recorded using a Bruker (Rheinstetten-Forchheim, Germany) AM 300 MHz spectrometer and ¹³C NMR spectra were recorded using a Bruker spectrometer at 75 MHz with TMS as the internal standard. Mass spectra were obtained using a Thermo Scientific LTQ-XL system with an electrospray ionization (ESI) source, a JEOL 600 MSRoute, and a JEOL Hx110 mass spectrometer (EI-HR).

General procedure

Synthesis of 6-(2-hydroxybenzoyl)-1-methylpyrido[2,3-d]pyrimidine-2,4(1H,3H)-dione (6a–d)

A solution of substituted 3-formylchromone (2 mmol), 6-amino-1-methyluracil (2 mmol) and a catalytic amount of p-toluenesulfonic acid in 15 mL of THF was stirred under reflux for an appropriate time at 60 °C. The completion of the reaction was examined by TLC. The yellow solid formed was filtered under hot conditions and washed with hot ethanol to afford the pure product (Scheme 1).

Scheme 1. The synthesis of the pyrido[2,3-d]pyrimidine derivatives 6a–d.

Characterization

6-(2-Hydroxy-5-methylbenzoyl)-1-methylpyrido[2,3-d]pyrimidine-2,4(1H,3H)-dione (6a)

Light yellow; yield: 92%; mp: 256–258 °C; ¹H NMR (DMSO-d6, 300 MHz): δ = 2.52 (s, 3H, C–CH₃), 3.53 (s, 3H, N–CH₃), 6.90 (d, J = 8.4 Hz, 1H, benzyl C₃–H), 7.21 (s, 1H, benzyl C₆–H), 7.29 (dd, J = 8.4 Hz, 2.1 Hz, 1H, benzyl C₄–H), 8.42 (d, J = 1.8 Hz, 1H, pyridyl C₅–H), 8.97 (d, J = 1.8 Hz, 1H, pyridyl C₇–H), 10.13 (s, 1H, OH), 11.93 (s, 1H, NH) ppm; ¹³C NMR (DMSO-d6, 75 MHz) δ = 20.3, 29.1, 111.0, 117.1, 124.6, 128.3, 128.7, 130.7, 134.9, 138.0, 151.0, 154.5, 154.6, 155.0, 161.4, 194.0 ppm; MS: m/z 310.17 [M − H]⁻; anal. calcd for C₁₆H₁₃N₃O₄: C, 61.73; H, 4.21; N, 13.50%; found: C, 61.78; H, 4.24; N, 13.48%.

6-(5-Fluoro-2-hydroxybenzoyl)-1-methylpyrido[2,3-d]pyrimidine-2,4(1H,3H)-dione (6b)

Yellow; yield: 77%; mp 214–216 °C; ¹H NMR (DMSO-d6, 300 MHz): δ = 3.53 (s, 3H, N–CH₃), 7.00 (dd, J = 9.0 Hz, 4.5 Hz, 1H, benzyl C₃–H), 7.24 (dd, J = 8.7 Hz, 3.3 Hz, 1H, benzyl C₆–H), 7.33 (td, J = 8.7 Hz, 3.3 Hz, 1H, benzyl C₄–H), 8.43 (d, J = 2.4 Hz, 1H, pyridyl C₅–H), 8.99 (d, J = 2.4 Hz, 1H, pyridyl C₇–H), 10.26 (s, 1H, OH), 11.95 (s, 1H, NH) ppm; MS: m/z 314.17 [M − H]⁻; anal. calcd for C₁₅H₁₀FN₃O₄: C, 57.15; H, 3.20; N, 13.33%; found: C, 57.20; H, 3.17; N, 13.29%.

6-(5-Ethyl-2-hydroxybenzoyl)-1-methylpyrido[2,3-d]pyrimidine-2,4(1H,3H)-dione (6c)

Yellow; yield: 88%; mp: 270–272 °C; ¹H NMR (DMSO-d6, 300 MHz): δ = 1.16 (t, J = 7.8 Hz, 3H, ethyl CH₃), 2.57 (q, J = 7.5 Hz, 2H, benzyl CH₂), 3.53 (s, 3H, N–CH₃), 6.93 (d, J = 8.4 Hz, 1H, benzyl C₃–H), 7.24 (d, J = 2.1 Hz 1H, benzyl C₆–H), 7.33 (dd, J = 8.4 Hz, 2.4 Hz, 1H, benzyl C₄–H), 8.43 (d, J = 2.4 Hz, 1H, pyridyl C₅–H), 8.98 (d, J = 2.1 Hz, 1H, pyridyl C₇–H), 10.15 (s, 1H, OH), 11.92 (s, 1H, NH); ¹³C NMR (DMSO-d6, 75 MHz) δ = 16.1, 27.5, 29.1, 111.0, 117.2, 124.6, 128.3, 129.6, 133.8, 135.2, 138.0, 151.0, 154.5, 154.8, 155.0, 161.4, 194.0 ppm; MS: m/z 326.25 [M + H]⁺; anal. calcd for C₁₇H₁₅N₃O₄: C, 62.76; H, 4.65; N, 12.92%; found: C, 62.80; H, 4.63; N, 12.90%.

6-(2-Hydroxy-5-isopropylbenzoyl)-1-methylpyrido[2,3-d]pyrimidine-2,4(1H,3H)-dione (6d)

Orange red; yield: 89%; mp 220–222 °C; ¹H NMR (DMSO-d6, 300 MHz): δ = 1.19 (d, J = 6.9 Hz, 6H, isopropyl CH₃), 2.57 (sept, J = 6.9 Hz, 1H, benzyl CH), 3.53 (s, 3H, N–CH₃), 6.94 (d, J = 8.4 Hz, 1H, benzyl C₃–H), 7.26 (d, J = 2.1 Hz 1H, benzyl C₆–H), 7.33 (dd, J = 8.4 Hz, 2.4 Hz, 1H, benzyl C₄–H), 8.43 (d, J = 2.4 Hz, 1H, pyridyl C₅–H), 8.98 (d, J = 2.4 Hz, 1H, pyridyl C₇–H), 10.17 (s, 1H, OH), 11.93 (s, 1H, NH); ¹³C NMR (DMSO-d6, 75 MHz) δ = 24.4, 29.1, 32.9, 111.0, 117.2, 124.5, 126.0, 128.2, 128.3, 128.5, 132.3, 138.1, 139.8, 151.0, 154.5, 154.9, 155.0, 161.4, 194.0 ppm; MS: m/z 340.25 [M + H]⁺; anal. calcd for C₁₈H₁₇N₃O₄: C, 63.71; H, 5.05; N, 12.38%; found: C, 63.66; H, 4.98; N, 12.36%.

Computational procedures

The Gaussian 09 program package²⁴ was used for all the theoretical calculations by employing DFT.²⁵ The initial geometry was retrieved by using the single-crystal structures of compounds 6a–d. The geometry of 6a–d was optimized in the gas phase without following any symmetry restrictions by employing the B3LYP level of theory and the 6-311+G(d,p) basis set. Frequency analysis was used to confirm the ground state structures. No imaginary frequency was there in all cases. Hence, the stability of the optimized structures was ascertained by all the calculated vibrational frequencies. The B3LYP/6-311+G(d,p) level of theory was employed for frontier molecular orbitals (FMOs), NBO, FT-IR and NLO calculations. UV-vis spectra were computed by employing time-dependent density functional theory (TD-DFT) with the B3LYP level and the 6-311+G(d,p) basis set. GaussView 5.0 (ref. 26) was used to organize the input files. The molecular visualization programs Avogadro,²⁷ Chem Craft²⁸ and GaussView 5.0 were used to interpret the output file results.

Results and discussion

Chemistry

A series of substituted (2-hydroxybenzoyl)pyridopyrimidines, diverse heterocyclic compounds exhibiting biological importance, have been prepared by reacting substituted 3-formylchromone, 6-amino-1-methyluracil and a catalytic amount of p-toluenesulfonic acid in THF under reflux for an appropriate time at 60 °C. The corresponding (2-hydroxybenzoyl)pyrido[2,3-d]pyrimidines were obtained as yellow-orange red solids in yields of 77–92%. The reaction was started by the protonation of the formyl group with p-toluenesulfonic acid followed by the addition of 6-amino-1-methyluracil to obtain the targeted (2-hydroxybenzoyl)pyridopyrimidine 6a. The structure of the synthesized compounds was established by spectroscopic data, i.e. FT-IR, ¹H and ¹³C NMR. The FT-IR spectra of (2-hydroxybenzoyl)pyridopyrimidines 6a–d showed characteristic OH and NH stretching frequencies at 3212–3026 cm⁻¹ and the C O stretching was observed in the 1721–1571 cm⁻¹ region. The ¹H NMR spectra showed two separate singlets at 10.13–10.26 for OH and 11.92–11.95 for NH protons while N–CH₃ protons resonate at 3.52–3.53 ppm. The ¹³C NMR data for compounds 6a–d also support the IR and ¹H NMR data. The plausible mechanism of the reaction is outlined in Scheme S1.†

Crystallographic data collection and structural refinement

Crystals of compounds 6a–d suitable for X-ray analysis (Table 1) were obtained by slow evaporation of their solutions in THF and MeOH solvent under ambient conditions and were found to have a monoclinic crystal lattice with the P2₁/n space group, a monoclinic crystal lattice with the P2₁/c space group, a triclinic crystal lattice with the P1̄ space group and a monoclinic crystal lattice with the C2/c space group, respectively (Table 1).

X-ray crystallographic data for 6a–d.

Crystal data	6a	6b	6c	6d
CCDC	1909617	1909620	1909619	1909618
Chemical formula	C16H13N3O4	C15H10FN3O4	C17H15N3O4	C18H17N3O4
M r	311.29	315.26	325.32	339.34
Crystal system, space group	Monoclinic, P21/n	Monoclinic, C2/c	Monoclinic, P21/c	Triclinic, P1̄
Temperature (K)	296	296	296	296
a, b, c (Å)	8.1712 (11), 13.873 (2), 12.3934 (17)	23.336 (3), 6.9240 (6), 17.2853 (18)	11.7250 (5), 13.3565 (6), 10.1992 (4)	8.4030 (4), 9.6898 (4), 10.9110 (7)
α, β, γ (°)	92.098 (6)	108.798 (3)	114.332 (2)	105.870 (2), 98.586 (2), 102.351 (4)
V (Å3)	1403.9 (3)	2643.9 (5)	1455.37 (11)	814.10 (7)
Z	4	8	4	2
Radiation type	Mo Kα	Mo Kα	Mo Kα	Mo Kα
μ (mm−1)	0.11	0.13	0.11	0.10
Crystal size (mm)	0.44 × 0.30 × 0.28	0.44 × 0.38 × 0.30	0.44 × 0.38 × 0.36	0.41 × 0.30 × 0.27
Data collection
T min, Tmax	0.940, 0.980	0.930, 0.970	0.930, 0.975	0.940, 0.985
No. of measured, independent and observed [I > 2σ(I)] reflections	9802, 3315, 2477	8315, 3120, 2521	8838, 3413, 2687	8321, 3154, 2336
R int	0.057	0.031	0.035	0.032
(sin θ/λ)max (Å−1)	0.659	0.658	0.659	0.617
Refinement
R[F2 > 2σ(F2)], wR(F2), S	0.055, 0.172, 1.04	0.043, 0.123, 1.04	0.046, 0.133, 1.05	0.048, 0.156, 1.04
Δ〉max, Δ〉min (e Å−3)	0.38, −0.28	0.26, −0.19	0.29, −0.20	0.23, −0.23

The information regarding the type of diffractometer, absorption correction and H-atom treatment can be seen in Table S17.† The molecular structures of 6-(2-hydroxybenzoyl)-1-methylpyrido[2,3-d]pyrimidine-2,4-diones 6a–d along with the crystallographic numbering schemes are shown in Fig. 2. As shown in Fig. 2, the benzoyl moiety present at the 6-position of 1-methylpyrido[2,3-d]pyrimidine-2,4-dione is tilted from the methylpyrido[2,3-d]pyrimidine-2,4-dione plane in 6a–d with dihedral angles of C(6)–C(8)–C(9)–C(13) = 49.40(2)° in 6a, C(6)–C(9)–C(10)–C(11) = 30.1(2)° in 6c, C(1)–C(10)–C(11)–C(15) = −150.19(16)° in 6d and C(6)–C(7)–C(8)–C(12) = 146.45(14)° in 6b. In all four compounds, the sigma bond on one side of the central carbonyl that is acting as a bridge between the phenyl and the 1-methylpyrido[2,3-d]pyrimidine-2,4-dione rings has frozen rotation owing to the presence of strong intramolecular hydrogen bonds [O(1)–H(1)⋯O(2), 1.79(3) Å in 6a; O(1)–H(1)⋯O(2), 1.89 Å in 6c; O(1)–H(1)⋯O(2), 1.89 Å in 6d; and [O(1)–H(1)⋯O(2), 1.83 Å in 6b], whereas the sigma bond on the other side can freely rotate. Owing to this rotation, the substituents present on the hydroxybenzoyl can adopt two arrangements, i.e. cis or trans to the methyl group present on the pyrido[2,3-d]pyrimidine-2,4-dione. In both 6a and 6c where the substituents are methyl and ethyl, respectively, on the hydroxybenzoyl moiety, this arrangement is cis while it is trans in 6d and 6b where the substituents are isopropyl and fluorine, respectively, on the hydroxybenzoyl moiety.

Fig. 2. The molecular structures (ORTEP diagram) of 6-(2-hydroxybenzoyl)-1-methylpyridopyrimidine-2,4-diones 6a–d. Displacement ellipsoids are drawn at the 50% probability level.

An interesting feature of compounds 6a–d is their molecular packing in the solid state owing to the presence of various hydrogen bond donor and acceptor sites (Fig. 2 and 3). Interestingly, in compound 6a the amide moiety in pyrido[2,3-d]pyrimidinedione interacts with the hydroxybenzyl moiety through hydrogen bonding [N(2)–H(2A)⋯O(2), 2.00 Å; O(1)–H(1)⋯O(3), 2.42(2) Å] providing a ten-membered ring rather than forming the centrosymmetric R₂²(8) {⋯H–N–C O}₂ synthon, resulting in 1D zig-zag supramolecular chains. However, this centrosymmetric R₂²(8) {⋯H–N–C O}₂ synthon is observed in both 6c [N(2)–H(2A)⋯O(3), 2.02 Å] and 6b [N(3)–H(3A)⋯O(4), 1.98 Å]. Interestingly, none of the arrangement observed in 6a, 6c and 6b is present in the solid-state structure of 6d, most probably owing to the presence of a bulky isopropyl group. The packing of compound 6d is mainly driven by N–H⋯O [N(2)–H(2)⋯O(1), 2.16 Å] and C–H⋯O [C(6)–H(6)⋯O(4), 2.496 Å] hydrogen bonds (Fig. 4).

Fig. 3. The hydrogen bond-driven supramolecular chains in 6a–d.

Fig. 4. 3D packing of (a) 6a along the c-axis; (b) 6c along the b-axis; (c) 6d along the a-axis; and (d) 6b along the b-axis in the solid state.

Molecular geometry

The structural parameters of 6a–d were calculated at the B3LYP level with the 6-311+G(d,p) basis set. The structural parameters resulting from DFT calculations were compared with the subsequent crystal structural values obtained from XRD analysis. For 6a, the experimentally determined values for the N1–C13, N2–C14, N2–C15, N3–C12, N3–C15 and N3–C16 bond lengths were 1.334(2), 1.372(2), 1.383(2), 1.385(2), 1.386(2) and 1.464(2) Å, respectively. The DFT values for the aforementioned bond lengths were found to be 1.336, 1.332, 1.391, 1.393, 1.387, 1.395 and 1.470 Å, respectively. The experimentally determined values for the O1–C1, O2–C8, O3–C14 and O4–C15 bond lengths were 1.352(2), 1.235(2), 1.222(2), and 1.209(2) Å, respectively, whereas, the DFT values were calculated to be 1.340, 1.239, 1.214 and 1.213 Å, respectively (Table S1†). The experimentally observed bond angles for O1–C1–C2, O2–C8–C9, O3–C14–N2, C12–N3–C15, O4–C15–N2 and C6–C8–C9 were 117.5(15), 117.2(14), 121.3(15), 122.0(14), 121.3(16) and 121.9(14)°, while the DFT values were found to be 117.8, 122.9, 121.7, 118.0, 121.2 and 121.6°, respectively (Table S1†).

For 6b, the experimentally determined values of the C–N bond lengths for N1–C11, N1–C12, N2–C11, N2–C14 and N3–C15 were 1.336(18), 1.324(19), 1.384(17), 1.367(19), and 1.378(18) Å, respectively. However, the DFT values of the C–N bond lengths were found to be 1.339, 1.327, 1.386, 1.396 and 1.390 Å, respectively (Table S2†). Further, the experimentally determined values for the O1–C1, O2–C7, O3–C14 and O4–C14 bond lengths were 1.351(18), 1.242(16), 1.212(17) and 1.222(17) Å, respectively, whereas the DFT values of these C–O bond lengths were found to be 1.340, 1.239, 1.215 and 1.212 Å, respectively (Table S2†). The experimentally determined bond angles values for F1–C4–C3, O2–C7–C6, O3–C15–N3, N1–C11–N2, C13–N2–C14 and N3–C15–C10 were 118.2(13), 120.8(12), 121.2(12), 116.7(11), 117.8(12) and 113.9(11)°, while the DFT values for the same angles are 118.8, 120.7, 121.8, 116.8, 118.2 and 113.0°, respectively (Table S2†).

For 6c, the experimentally determined values for the N1–C11, N1–C12, N2–C15, N2–C16, N3–C12, N3–C16 and N3–C17 bond lengths were 1.332(19), 1.336(17), 1.391(19), 1.393(19), 1.387(18), 1.395(18) and 1.470(18) Å, respectively. The DFT values of the above-mentioned bond lengths were found to be 1.333, 1.337, 1.371, 1.380, 1.383, 1.380 and 1.468 Å, respectively. The experimentally determined values for the O1–C1, O2–C9, O3–C15 and O4–C16 bond lengths were 1.340(2), 1.239(18), 1.214(17) and 1.213(18) Å, respectively. The DFT-based values of the above-mentioned bond lengths (C–O) were 1.349, 1.228, 1.220 and 1.210 Å, respectively (Table S3†). The experimentally determined bond angles observed for O1–C1–C2, O2–C9–C6, O3–C15–C13, O4–C16–N3, N1–C11–C10, N2–C16–N3 and C3–C4–C5 were 117.8(14), 121.1(13), 125.4(13), 123.6(14), 124.3(12), 115.2(13) and 117.5(14)° while their DFT values were found to be 117.9, 120.8, 124.1, 122.8, 124.7, 116.2 and 117.1°, respectively (Table S3†).

Furthermore, for 6d, the experimentally determined values of the N1–C14, N1–C15, N2–C16, N2–C17, N3–C14, N3–C17 and N3–C18 bond lengths were 1.332(2), 1.323(2), 1.368(2), 1.376(2), 1.384 (2), 1.377(2) and 1.462(2) Å, respectively and the DFT values were 1.339, 1.328, 1.390, 1.394, 1.387, 1.395 and 1.471 Å, respectively (Table S4†). The experimentally obtained C–O bond lengths for O1–C2, O2–C10, O3–C16 and O4–C17 were 1.352(2), 1.232(2), 1.210(2) and 1.205(2) Å, respectively, while the DFT values were observed to be 1.341, 1.240, 1.215 and 1.213 Å, respectively (Table S4†). The experimentally determined bond angles for O1–C2–C3, O2–C10–C1, O3–C16–N2, N1–C14–N3, N1–C14–C13 and C2–C3–C4 were 118.3(16), 121.6(16), 121.5(17), 116.7(15), 123.2(16) and 120.7(18)° while the DFT values were 117.8, 121.2, 121.1, 116.8, 122.5 and 120.5°, respectively. The comparative analysis reveals that the experimentally determined bond lengths and bond angles are slightly lower than the calculated parameters, as can be seen in Tables S1–S4.† The observed difference between the DFT and experimental findings might be because of the medium effect. Overall, the obtained structural results for 6a–d from the DFT and XRD studies show good agreement, as can be seen in Tables S1–S4,† respectively.

FT-IR analysis

The experimental FT-IR absorption spectroscopic studies^29,30 were performed for the vibrational modes of compounds 6a–d. Further, FT-IR absorption spectroscopic studies based on DFT analysis were also conducted to understand the vibrational modes of compounds 6a–d using the B3LYP/6-311+G(d,p) level of theory in the gas phase. The vibrational modes were assigned by employing the animation option available in GaussView software. Both the calculated and experimental frequencies are given in Tables S5–S8† for compounds 6a–d, respectively.

N–H vibrations

The wavenumbers for the nitrogen–hydrogen (N–H) vibrations were located at 3092, 3119–3026, 3131–3045 and 3051 cm⁻¹ for 6a–d, respectively, in experimental FT-IR spectrum which are in agreement with the calculated modes of 3594–3592 cm⁻¹ (see Tables S5–S8†).

O–H vibrations

The experimentally determined wavenumbers for the hydroxy (O–H) groups were 3217, 3163, 3168, and 3168 cm⁻¹ for 6a–d, respectively (Fig. S1–S4†); these lower frequencies might be due to intramolecular hydrogen bonding. The simulated bands of the former group were at 3382, 3395, 3385, and 3391 cm⁻¹ for 6a–d, respectively.

C O vibrations

A strong C O stretching vibration is found at 1850–1550 cm⁻¹, which is a characteristic carbonyl group peak.³¹ The carbonyl (C O) group bands were located at 1717–1625, 1721–1589, 1685–1628 and 1717–1571 cm⁻¹ for 6a–d, respectively (in the experimental spectra), and 1778–1629, 1780–1768, 1779–1770 and 1778–1632 cm⁻¹ for 6a–d, respectively (in the DFT spectra). Good agreement was observed between the experimental and DFT-based wavenumbers (see Tables S5–S8†).

Natural bond orbital (NBO) analysis

NBO analysis is a significant method for examining intra- and inter-molecular bonding, especially in terms of conjugative and charge transfer interactions between the electron donor and acceptor.^32–39 NBO analysis is helpful in the transmission of electron density from a filled electron orbital to an unoccupied orbital.⁴⁰ The stabilization energy can be calculated using eqn (1) with the second-order perturbation approach.

1

where E⁽²⁾ is the stabilization energy, q_i is the donor orbital occupancy, F_(i,j) is the diagonal and ε_j and ε_i are the off-diagonal NBO Fock matrix elements.⁴¹

The value of the perturbation stabilization energy [E⁽²⁾] depicts the level of conjugation in the whole system. The data for the NBO study regarding molecules 6a–d was obtained using the B3LYP/6-311+G(d,P) level of theory, as tabulated in Tables S9–S12.† The highest transitions (π → π*) take place as π(N6–C28) → π*(C24–C29) with 43.15 kcal mol⁻¹, π(C11–C19) → π*(C12–C14) with kcal mol⁻¹, π(C6–C30) → π*(C27–C28) with kcal mol⁻¹ and π(C10–C11) → π*(C12–C14) with 170.92 kcal mol⁻¹ for 6a–d, respectively. These are the largest values among the stabilization energies given in Tables S9–S12.† The stabilization energy value of 6b is higher than those for the other compounds 6a, 6c and 6d owing to the stronger intramolecular hyper conjugative interactions, which might be due to the fluoro group. Transitions σ(O1–H2) → σ*(C10–C12), σ(O5–C33) → σ*(C24–C33), σ(C36–H39) → σ*(C36–H39) and σ(C39–H42) → σ*(C39–H42) shown stabilization energy values of 6.07, 65.09, 53.30 and 51.83 kcal mol⁻¹ for 6a–d, respectively. These are the highest σ → σ* stabilization energies in the studied compounds, which result in a strong interaction between the donor (σ) and the acceptor (σ*). In the case of the resonance, the transitions LP(N9) → σ*(O5–C32), LP(N9) → π*(C35–C37), LP(N9) → σ*(C35–C37) and LP(N7) → π*(O4–C37) exhibit stabilization energy values of 70.30, 51.05, 78.19 and 52.43 kcal mol⁻¹ for 6a–d, respectively, as the largest energy values (see Tables S9–S12†). The lowest values of 5.53, 5.88, 5.45 and 7.05 kcal mol⁻¹ were exhibited by LP(N6) → σ*(N9–C28), LP(F1) → σ*(C16–C17), LP(N6) → σ*(N9–C30) and LP(N9) → σ*(C39–C40) in 6a–d, respectively (see Tables S9–S12†). Subsequently, on the basis of the NBO analysis, it can be concluded that the increased stability in these systems (6a–d) is mainly contributed by strong intramolecular hyper conjugative interactions.

Frontier molecular orbital analysis

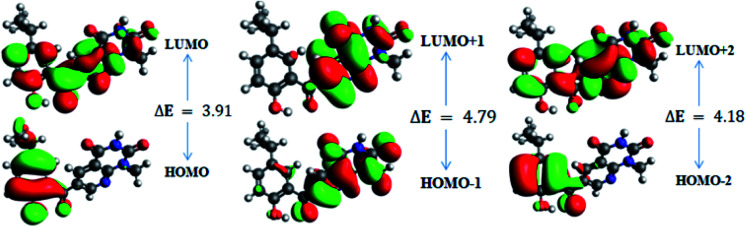
In order to gain an understanding of the optical properties shown by these compounds, TD-DFT calculations for 6a–d were carried out at the TD-B3LYP/6-311G+(d,p) level after optimization of their molecular structures for stable spatial conformation. It was realized from SC-XRD findings that the molecular structure of the benzoyl moiety present at position 6 of 1-methylpyridopyrimidine-2,4-dione is tilted from the methylpyridopyrimidine-2,4-dione plane in 6a–d with the dihedral angles C(6)–C(8)–C(9)–C(13) = 49.40° in 6a, C(1)–C(10)–C(11)–C(15) = −150.17° in 6b, C(6)–C(9)–C(10)–C(11) = 30.11° in 6c, and C(6)–C(7)–C(8)–C(12) = 146.45° in 6d, which provides some obstruction for the intramolecular charge transfer (ICT) process within 6a–d. The TD-DFT calculations anticipated that the S0 → S1 transitions are governed through a one-electron transformation from the HOMO to the LUMO. Additionally, according to the TD-B3LYP calculations, the preeminent contributions for the frontier molecular orbitals (FMOs) to the leading transitions in the investigated compounds are shown in Table S13.† The major contribution of the molecular orbitals to the leading transitions is HOMO → LUMO+1 (99%) and HOMO → LUMO (97%) for 6a. Similarly, the major contribution of the molecular orbitals to the leading transitions is HOMO → LUMO+1 (98%) and HOMO → LUMO (97%) for 6b. Moreover, the major contribution of the molecular orbitals to the leading transitions is HOMO → LUMO+1 (99%) and HOMO → LUMO (97%) for 6c and HOMO → LUMO+1 (98%) and HOMO → LUMO (96%) for 6d (see Table S13†). The FMO diagrams can be seen in Fig. 5–8, which show the electron distribution of the HOMO−2, HOMO−1 and HOMO as well as the LUMO, LUMO+1 and LUMO+2 of molecules 6a–d. We can see that the electron distribution of the HOMOs of compound 6a is mainly dispersed over methyl benzoyl moiety, while the LUMO electron distribution is mainly localized over the compound with the exception of the methyl group of the benzoyl moiety and the pyridopyrimidine-2,4-dione moiety (Fig. 5).

Fig. 5. Frontier molecular orbitals of 6a.

Fig. 6. Frontier molecular orbitals of 6b.

Fig. 7. Frontier molecular orbitals of 6c.

Fig. 8. Frontier molecular orbitals of 6d.

For 6b, the electron distribution of the HOMOs is also mainly dispersed over methyl benzoyl moiety, while the LUMO electron distribution is mainly localized over the whole compound with the exception of the methyl group and the C–N bond of the pyridopyrimidine-2,4-dione moiety as well as only a bit extended on the carbonyl functional group of the pyridopyrimidine-2,4-dione moiety (see Fig. 6).

For 6c, the electron distribution of the HOMOs is mainly dispersed over the pyridopyrimidine-2,4-dione moiety, while the LUMO electron distribution is are mainly localized on over the pyridopyrimidine-2,4-dione moiety as well as only a bit extended on the carbonyl functional group of the benzoyl moiety (see Fig. 7).

Further, for 6d, the electron distribution of the HOMOs is mainly dispersed over the methyl benzoyl moiety, while the LUMO electron distribution is mainly localized over the compound with the exception of the methyl group of the benzoyl moiety (see Fig. 8).

Subsequently, this mechanism reveals the existence of ICT character from HOMO to LUMO orbitals.

In addition, the calculated energy values for the HOMO–LUMO and energy gap (E_gap) for these compounds are tabulated in Table 2. Subsequently, the energy band gaps (E_gap) of the HOMO–LUMO levels for compounds 6a–d are 3.93 eV, 3.91 eV, 4.1 eV and 3.91 eV, respectively.

Computed energies (E) for compounds 6a–d^a.

6a			6b			6c			6d
MO	Energy	ΔE	MO	Energy	ΔE	MO	Energy	ΔE	MO	Energy	ΔE
HOMO	−6.6	3.93	HOMO	−6.8	3.91	HOMO	−10.6	4.10	HOMO	−6.5	3.91
LUMO	−2.6		LUMO	−2.9		LUMO	−6.5		LUMO	−2.6
HOMO−1	−7.2	4.8	HOMO−1	−7.3	4.7	HOMO−1	−10.7	5.10	HOMO−1	−7.2	4.78
LUMO+1	−2.4		LUMO+1	−2.5		LUMO+1	−5.6		LUMO+1	−2.4
HOMO−2	−7.7	6.23	HOMO−2	−7.9	6.24	HOMO−2	−11.2	6.10	HOMO−2	−7.6	6.291
LUMO+2	−1.5		LUMO+2	−1.7		LUMO+2	−5.2		LUMO+2	−1.4

^a E = energy; ΔE (eV) = E_LUMO − E_HOMO; HOMO, highest occupied molecular orbital; LUMO, lowest unoccupied molecular orbital; MO, molecular orbital.

The energy gaps of the studied compounds decrease in the following order:6c > 6a > 6b = 6d

The computing calculations show that the electronic properties of the four derivatives might be affected through by the electron donating capability of the substituents, which might effectively tune their optical characteristics and the lower E_gap explains that the aforesaid derivatives would contain strong electron transfer ability and larger second-order NLO properties.^42,43

Moreover, the calculated energy values for the FMOs are used for calculating the values of the global reactivity descriptors.^44–47

The electronic affinity (A) and ionization potential (I) have been calculated in a vertical manner using eqn (2) and (3).

I = E_c^N−1 − E_o^N 2

A = E_o^N − E_A^N+1 3

where I = ionization potential; A = electron affinity; E_c^N−1 = cation (energy after losing one electron); E_o^N = basal state energy (neutral); and E_A^N+1 = anion (energy after gaining one electron).

Hardness and electronegativity values have been calculated using eqn (4) and (5).

4

5

Electrophilicity calculations were performed to establish the charge transfer process. This describes the relationship between energy variation and the maximum electrons transferred.

6

The ability of a chemical species to donate or accept an electron can be explained with the help of two descriptors. eqn (7) and (8) were used to calculate the donating and accepting ability of 6a–d, respectively.

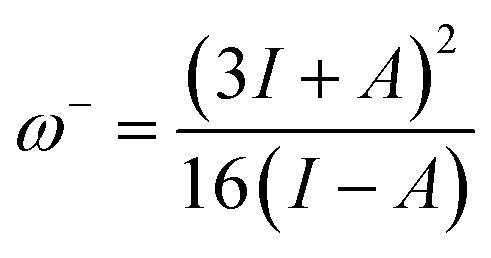7

8

where, ω⁻ = electron donating capability; and ω⁺ = electron accepting capability.

Eqn (9) was used to calculate the softness value.

9

The results obtained from eqn (2)–(9) are summarized in Table 3.

Ionization potential (I), electron affinity (A), electronegativity (X), global hardness (η), chemical potential (μ), global electrophilicity (ω), electron donor capability (ω⁻), electron acceptor capability (ω⁺) and global softness (σ) values of 6a–d (units in eV).

Com	I	A	X	η	μ	ω	ω −	ω +	σ
6a	4.80	4.43	4.62	0.18	−4.62	57.42	59.75	55.13	2.69
6b	5.46	4.63	5.04	0.41	−5.04	30.79	33.36	28.32	1.21
6c	5.20	4.43	4.81	0.38	−4.81	30.09	32.55	27.73	1.30
6d	5.14	4.43	4.78	0.35	−4.78	32.16	34.59	29.81	1.41

The highest ionization potential was calculated to be 5.46 eV for 6b, while the lowest ionization potential was observed for 6a with a value of 5.19 eV. The ionization potential decreases in the following order: 6b > 6c > 6d > 6a. The highest electron affinity value was found to be 4.63 eV for 6b, while the other three derivatives have the same electron affinity of 1.43 eV. The ionization potential and electron affinity can be used to describe the electron releasing and accepting capabilities of the investigated molecules, which are directly related to the energy of the HOMOs and LUMOs. Overall, the ionization potential values are observed to be larger than the electron affinity values, highlighting the better electron donating capability of the investigated molecules (6a–d). Usually, a molecule with a high energy gap can be considered as a hard, non-reactive, stable species, and vice versa. The global hardness values of our studied systems were found to descend in the following order; 6b > 6c > 6d > 6a (Table 3). A similar trend is observed for the electronegativity values of the studied compounds (6a–d) (Table 3). The chemical potential value of any system can be used to describe its reactivity and stability. Molecules with greater chemical potential values could be considered as less reactive and more stable, and vice versa. In decreasing order, the chemical potential values for the studied compounds are: [6b (μ = −5.04 eV)] > [6c (μ = −4.81 eV)] > [6d (μ = −4.78 eV)] > [6a (μ = −4.62 eV)].

The global softness values were found to be 2.69, 1.21, 1.30 and 1.41 eV for 6a–d, respectively. These values have a greater magnitude as compared to their global hardness values. The global electrophilicity (ω) decreases in the following order: 6a (57.42 eV) > 6d (32.16 eV) > 6b (30.79 eV) > 6c (30.09 eV). In decreasing order, the electron donor capability (ω⁻) values are: 6a (59.75 eV) > 6d (34.59 eV) > 6b (33.36 eV) > 6c (32.55 eV) and the electron acceptor capability (ω⁺) values are: 6a (55.13 eV) > 6d (29.81 eV) > 6b (28.32 eV) > 6c (27.73 eV).

Overall, the electron donating capability (ω⁻) values were found to be higher than the electron accepting (ω⁺) capability values. The ionization energy and electron affinity values represent the ability of an atom to donate and accept electrons, respectively. In our compounds, the ionization energies were much higher than the electron affinity values, which supports the finding that the electron donating ability (ω⁻) of the investigated compounds is higher than their electron accepting ability (ω⁺). The aforementioned results show that all investigated molecules have good kinetic stability and electron donating capability.

UV-visible study

The UV-vis absorption spectra of the derivatives (6a–d) in acetone, dimethyl sulfoxide (DMSO) and 1, 4-dioxane were recorded at room temperature. DT-DFT UV-vis absorption data were calculated in the gas phase. The UV-visible results for 6a–d are presented in Table 4.

Wavelengths, excitation energies, and oscillator strengths for 6a–d^a.

Com	Exp λ (nm)	DFT λ (nm)	E (cm−1)	f	MO contributions
6a		364	27 437	0.1408	H → L (97%)
	332b	342	29 193	0.0017	H → L+1 (99%)
		327	30 522	0.0131	H-4 → L (27%), H-3 → L (29%), H-2 → L (15%), H-1 → L (23%)
	305c	302	33 156	0.2089	H-1 → L (52%), H-1 → L+1 (27%), H-4 → L (4%), H-3 → L (3%), H-3 → L+1 (3%), H-2 → L (6%)
	300d	294	34 030	0.0761	H-4 → L+1 (10%), H-3 → L+1 (33%), H-1 → L (13%), H-1 → L+1 (24%), H-3 → LUMO (4%), H-2 → L (9%), H-2 → L+1 (2%)
		292	34 260	0.0399	H-4 → L+1 (10%), H-3 → L+1 (29%), H-1 → L+1 (39%), H-4 → L (4%), H-2 → L (4%), H-1 → L (6%)
6b	377b	367	27 245	0.1553	H → L (97%)
	373d	336	29 736	0.002	H → L+1 (98%)
	300c	330	30 331	0.0282	H-4 → L (25%), H-3 → L (20%), H-2 → L (15%), H-1 → L (33%), H-6 → L (2%)
		307	32 606	0.1772	H-3 → L (14%), H-2 → L (18%), H-1 → L (60%), H-4 → L (5%)
		298	33 599	0.0738	H-1 → L+1 (93%) H-8 → L (2%)
		293	34 114	0.0043	H-2 → L+1 (85%) H-3 → L+1 (3%)
6c	332b	367	27 347	0.1357	H → L (97%)
	311c	343	29 155	0.0018	H → L+1 (99%)
	305d	328	30 511	0.0131	H-4 → L (26%), H-3 → L (33%), H-2 → L (13%), H-1 → L (22%)
6d	372d	368.198	27 159	0.120	H → L (96%)
	365b	350.274	28 549	0.002	H → L+1 (98%)
	313c	327.391	30 544	0.019	H-4 → L (20%), H-3 → L (38%), H-1 → L (28%), H-2 → L (8%)
		298.863	33 460	0.125	H-3 → L (10%), H-1 → L (45%), H-1 → L+1 (35%), H-2 → L (4%)
		298.517	33 499	0.195	H-2 → L (12%), H-1 → L (20%), H-1 → L+1 (55%), H-3 → L (7%)
		292.103	34 234	0.008	H-4 → L+1 (25%), H-3 → L+1 (61%), H-4 → L (3%)

^aCom = compounds; Exp = experimental; E = Excitation energy; λ = wavelength; f = oscillator strength; MO = molecular orbitals; H = HOMO; L = LUMO; λ (nm).

^bAcetone.

^cDMSO.

^d1,4-Dioxane.

The experimental absorption maxima of 6a were found to be 332 (acetone), 305 (DMSO) and 300 (1,4-dioxane), while the TD-DFT absorption maxima were found to be 364, 342, 327 and 302 nm in the gas phase with major molecular orbital contributions HOMO → LUMO (97%), HOMO → LUMO+1 (99%), HOMO+4 → LUMO (27%) and HOMO → LUMO+1 (52%), respectively (Table 4). For 6b, the experimental absorption maxima were found to be 377 (acetone), 300 (DMSO) and 373 nm (1,4-dioxane), while the TD-DFT absorption maxima were found to be 367, 336, 329 and 307 nm in the gas phase with major molecular orbital contributions HOMO → LUMO (97%), HOMO → LUMO+1 (98%), HOMO+4 → LUMO (25%) and HOMO−1 → LUMO (60%), respectively (Table 4). Similarly, for 6c, the experimental absorption maxima were found to be 332 (acetone), 311 (DMSO) and 305 nm (1,4-dioxane), while the TD-DFT absorption maxima were found to be 367, 343 and 328 nm in the gas phase with major molecular orbital contributions HOMO → LUMO (97%), HOMO → LUMO+1 (98%) and HOMO+4 → LUMO (26%), respectively (Table 4). Further, for 6d, the experimental absorption maxima were found to be 365 (acetone), 313 (DMSO) and 372 nm (1,4-dioxane), while the TD-DFT absorption maxima were found to be 368, 350 and 327 nm in the gas phase with major molecular orbital contributions HOMO → LUMO (96%), HOMO → LUMO+1 (98%) and HOMO−1 → LUMO (28%), respectively (Table 4). The maximum absorption bands of the investigated derivatives (6a–d) are visibly redshifted, which could be because of the conjugated fused ring system and the influence of the substituents. The bands at the maximum wavelengths might be assigned to the nπ* transitions of the C C, C N and C O bonds of the investigated derivatives (6a–d) while the bands at lower wavelengths (∼290 nm) might be assigned to the π–π* transitions of the benzene and pyridine rings (Table 4). The UV-visible data reveal good agreement between the experimental and TD-DFT findings.

Nonlinear optical (NLO) properties

Nonlinear optical (NLO) organic molecules have attracted great industrial, current research and academic interest because of their potential applications in the field of optoelectronic technologies.⁴⁸ The organic second-order nonlinear optical materials have promising applications in the field of nonlinear optics (NLO) owing to their chemical tunability and choice of synthetic strategies.⁴⁹ The sketch of dynamic organic compounds for utilization in NLO response is established on the basis of asymmetric (neocentromeric) polarization. The NLO efficiency could be enhanced by increasing the electron donating and withdrawing groups attached to the π-conjugated system. Therefore, we also studied NLO parameters of the π-conjugated systems at the molecular level (6a–d) using the B3LYP level of theory with the 6-311+G(d,p) basis set. In the finite field (FF) method, when a species is placed in a static field (F), the resulting energy (E) is represented by eqn (10):

10

where E₀ stands for the molecular energy in the absence of an electronic field. α represents polarizability, β_tot is the first hyperpolarizability, and γ stands for the second hyperpolarizability, which are calculated by eqn (11)–(13) from the tensors in the x, y and z directions.

α = 1/3(α_xx + α_yy + α_zz) 11

β_tot = (β_x² + β_y² + β_z²)^1/2 12

β_tot = [(β_xxx + β_xyy + β_xzz)² + (β_yyy + β_yzz + β_yxx)² + (β_zzz + β_zxx + β_xyz)²]^1/2 13

The first order and the second-order hyperpolarizability for 6a–d, as well as their component values, are summarized in Tables S15 and S16.†

The first order polarizability along the x direction was found to be 346, 331, 355 and 354 a.u. for 6a–d, respectively. The first order polarizability along the x direction is larger than along the y and z directions (positive directions) for all compounds, which indicates the non-uniform distribution of the charges on the molecules. The total dipole polarizability (α_total) was found to be 238, 223, 251 and 261 a.u. for 6a–d, respectively (Table S15†). The dipole polarizability magnitudes of 6c and 6d are approximately the same but greater than those for 6a and 6b. The first order hyperpolarizability was found to be 1144.46, 1468.42, 1103.06 and 1095.34 a.u. for 6a–d, respectively (Table S16†). The first order hyperpolarizability of 6b is higher than those for 6a, 6c and 6d, which might be due to the electron withdrawing ability because of the more electronegative fluoro group. Moreover, we compared our obtained parameters for 6a–d with urea because it is frequently used as a reference molecule for comparative NLO analysis. The first order hyperpolarizability for 6a–d is remarkably greater than the value for urea (β = 43 a.u.),⁵⁰ which is due to the effect of the extended conjugation in said compounds (Table S16†).

MEP analysis

The reactive sites of molecules 6a–d have been determined by MEP descriptor. The MEP descriptor is more frequently utilized for the affirmation of the molecular domains that are most suitable susceptible towards nucleophilic and electrophilic attacks.⁵¹ The MEP descriptor is mostly visualized by mapping values on the electron density surface, which is the procedure adopted in our study. MEP surfaces have been displaced in Figure S5.† With respect to the displayed MEP surface of molecules 6a–d, the fluoro, oxygen and nitrogen atoms are considered as sensitive to electrophilic attacks because the MEP surface has the maximal electron density values at these areas. Lower MEP electron density values are situated in the near vicinities of hydrogen atoms and carbon atoms, designating these areas as possibly most sensitive for nucleophilic attacks.

Conclusions

In summary, we synthesized four novel (hydroxybenzoyl)pyrido[2,3-d]pyrimidine heterocycle derivatives 6a–d with the chemical formulas of C₁₆H₁₃N₃O₄, C₁₇H₁₅N₃O₄, C₁₈H₁₇N₃O₄ and C₁₅H₁₀FN₃O₄ and good yields of 92%, 77%, 88%, and 89%, respectively. Their chemical structures have been characterized using experimental and sophisticated computational methods. The experimental techniques of ¹H NMR, ¹³C NMR, UV-vis and FT-IR, as well as SC-XRD, were performed to characterize the synthesized derivatives. SC-XRD analysis revealed that 6a–c crystallized in the monoclinic crystal lattice with the P2₁/n, C2/c and P2₁/c space groups, respectively, but 6d crystallized in a triclinic crystal lattice with the P1̄ space group. Spectroscopic findings were found to be quite in line with the SC-XRD data. Further, the quantum chemical-based UV-vis absorption and FT-IR spectra were also found to be quite in line with the SC-XRD and experimental spectroscopic findings. FMO analysis indicated that the studied derivatives are kinetically stable hard compounds with small electron accepting and greater electron donating capabilities. NBO analysis revealed that the increased stability in 6a–d is mainly contributed to by strong intramolecular hyper-conjugative interactions. Comparative analysis of the NLO properties revealed that 6a–d have higher NLO values than urea, making them brilliant candidates for hi-tech applications associated with NLO properties. The MEP surfaces of molecules 6a–d revealed that the fluoro, oxygen and nitrogen atoms are considered sensitive to electrophilic attacks.

Conflicts of interest

The authors declare that they have no conflicts of interest.