Stepped Wedge Cluster Randomized Trials: A Methodological Overview

Abstract

BACKGROUND:

Stepped wedge cluster randomized trials enable rigorous evaluations of health intervention programs in pragmatic settings. The current study aims to update neurosurgeon scientists on the design of stepped wedge randomized trials.

METHODS:

An overview of recent methodological developments for stepped wedge designs is presented. An update on newer associated methodological tools is included to aid with future study designs.

RESULTS:

The stepped wedge trial design is defined. Indications for the design are reviewed in depth. Key considerations are discussed including mainstream methods of analysis and sample size determination.

COINCLUSIONS:

Stepped wedge designs can be attractive to study intervention programs aiming to improve the delivery of patient care, especially when examining a small number of heterogeneous clusters.

INTRODUCTION

Cluster randomized designs are commonly used in pragmatic trial research evaluating the effect of healthcare interventions that are delivered to clinics, hospitals, or nursing homes.^1,2 A key feature of these designs is that intact clusters are randomized to each arm, and outcome measurements are typically taken from each participant, just like individual randomized designs. Statistical methods for cluster randomized trials (CRTs) have been extensively studied for decades and have been made accessible in published methodological reviews.^3,4 A recent variant of CRTs, called the stepped wedge cluster randomized trials (SW-CRTs), are gaining traction, from just a few published studies two decades ago to more than 40 protocols per year nowadays.^5–7 In an SW-CRT, the implementation of intervention is staggered over time such that each cluster is randomized to a time point when the intervention starts to roll out. A typical feature of SW-CRTs is that all clusters will eventually be exposed to the intervention during the study period. Figure 1 provided an illustration of a SW-CRT with the Early Recognition and Response to Increases in Surgical Site Infection (Early 2RIS) Trial.⁸ Thirteen surgical procedures were classified into six types (e.g., cardiac, spine, etc). Clusters, constructed at each of the 29 study hospitals based on the type of surgical procedure performed, were the units for randomization and analysis. The study randomized 105 clusters over 14 periods to assess the effectiveness of surveillance using optimized statistical process control methods and feedback on rates of surgical site infections compared to traditional infection surveillance methods. In Figure 1, there are 12 randomization sequences; each randomization sequence is determined by the first period a group of clusters crossover from control to intervention. This is in comparison to parallel-arm designs, where usually half of clusters are simultaneously randomized to either intervention or control at baseline.

Figure 1.

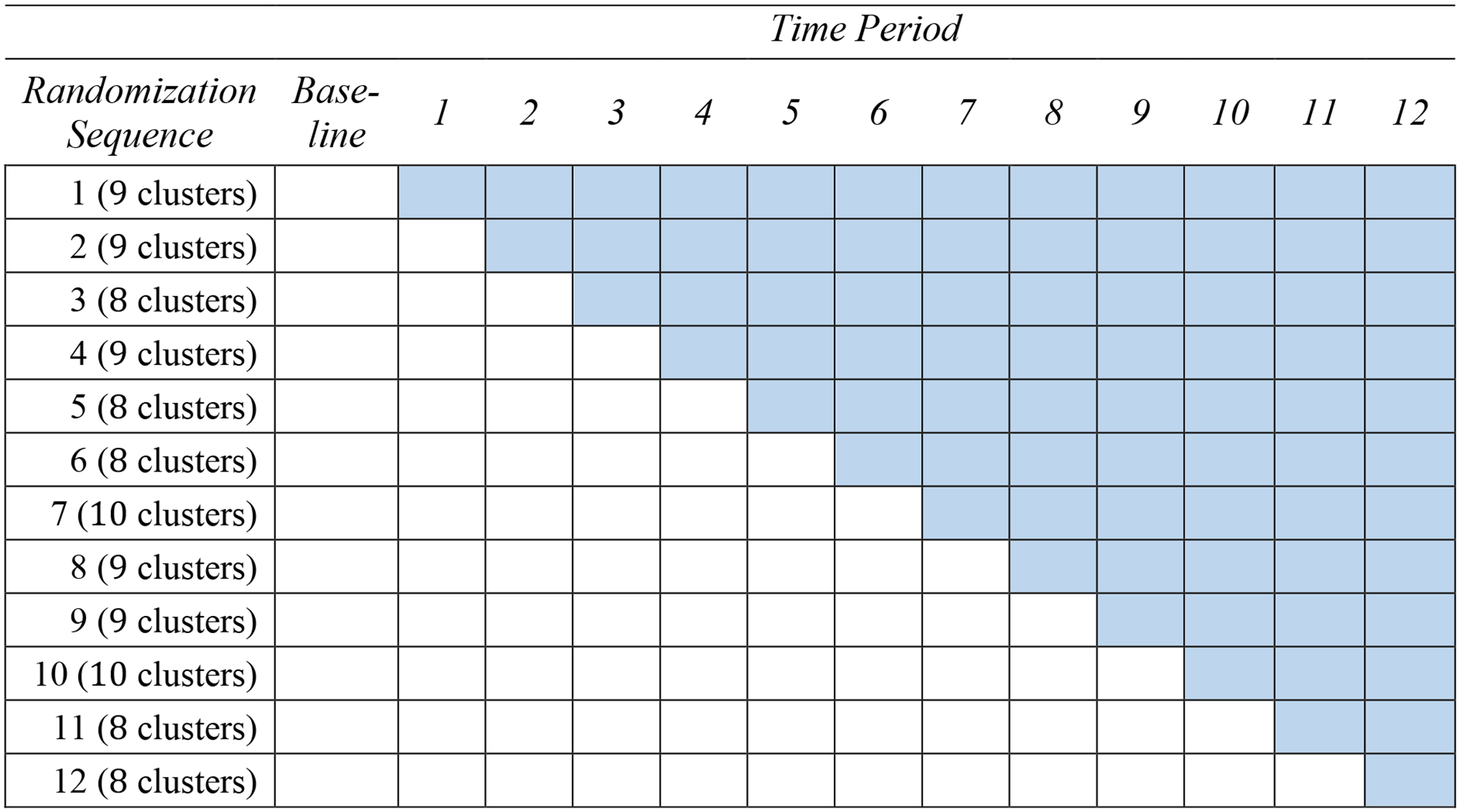
A schematic of stepped wedge design for the Early Recognition and Response to Increases in Surgical Site Infection (Early 2RIS) Trial. The shaded cell indicates treatment status, and a white cell indicates control status. There are 12 randomization sequences (defined by the first time period during which each group of clusters crossover to intervention). There are in total 105 clusters and 13 time periods. In the Early 2RIS trial, the baseline period is one year, and each subsequent period is 3 months.

Compared to parallel CRTs, SW-CRTs require more sophisticated statistical considerations for design and analysis. For example, the staggered treatment initiation induces confounding by time and unbiased estimation of intervention effect requires statistical adjustment for secular trend; repeated outcome assessment from each cluster also necessitates considerations for complex correlation structures among outcomes.^6,9–11 While SW-CRTs have been successfully deployed in many previous trials, with interventions for infectious disease prevention,¹² diagnostic imaging,¹³ geriatric care,¹⁴ among others, few neurosurgical studies have adopted the stepped wedge design. In this review, we explore current state of methodological developments for stepped wedge designs and reflect upon potential opportunities for their adoption in neurosurgery trials.

STEPPED WEDGE DESIGNS—DEFINED

Design Variants

In a stepped wedge design, each cluster initially starts from the control period where baseline outcome measures are collected. In each subsequent period, a random selected group of clusters will cross over from control to intervention and the outcome data are collected from each cluster. Depending on how outcomes from participants are collected from each cluster, broadly there are three design variants.¹⁵ A cross-sectional design enrolls new participants from each cluster during each period, whereas a closed-cohort design identifies a cohort of participants at the beginning of the study and schedules repeated follow-up outcome assessments for the same cohort over time. An open-cohort design, however, allows the attrition of members and the addition of new members to the existing cohort identified at baseline in each cluster. The choice of design variant is often based on the research question and practical considerations. For example, a closed-cohort design necessitates a longer follow-up time for each participant and can run the risk of informative drop-out, while a cross-sectional design often involves continuous recruitment and only retain each participant for a single period for a short exposure.¹⁵

When is a Stepped Wedge Design Appropriate?

The decision to adopt a SW-CRT are based on several considerations.⁷ First, the successive rollout of intervention to clusters in a SW-CRT ensures all health care units receive intervention before the end of study, and can facilitate cluster recruitment when the intervention is perceived to be effective with minimal harm to providers and patients.^16,17 This contrasts with a parallel design, which only allows a subset of the health care units to receive the intervention during the study. Second, the logistical resources and efforts may be less demanding in a SW-CRT if the intervention is rolled out according to a staggered schedule.^16,17 Third, a SW-CRT collects outcome data from multiple time periods, and offers the advantage of having each cluster contribute observations under both the intervention and control conditions. As a result, while the treatment effect estimation based on the parallel design only makes use of information from between-cluster comparisons, the stepped wedge design pools information from both within-cluster comparisons and between-cluster comparisons,^18,19 and can require fewer clusters to achieve the same amount of statistical power.¹⁰ This is especially the case when the intraclass correlation coefficient (ICC) is high or the cluster sizes are large.⁷

On the other hand, there are also limitations associated with SW-CRTs. For example, SW-CRT involves repeated data collection and can often give rise to a study with a longer duration. There may also be potential for biases due to insufficient control of secular trends (defined as the outcome trajectory in the absence of intervention) affected by a concurrent external intervention program, or unexpected disruption from a pandemic. The decision to adopt a SW-CRT, therefore, should deserve a comprehensive evaluation by weighing the associated strengths against limitations in specific trial contexts.

STATISTICAL CONSIDERATIONS FOR STEPPED WEDGE DESIGNS

Method of Analysis—Conditional Models

To account for clustering between data observations, two mainstream regression models for analyzing SW-CRTs are the conditional (cluster-specific) models and marginal (population-averaged) models. The conditional models refer to the class of mixed-effects models, which specify fixed effects for the secular trend and the intervention effect, and random effects to characterize the correlation among observations collected from the same cluster.¹¹ The widely-used linear mixed model, originally proposed in Hussey and Hughes,¹⁸ includes a categorical fixed effect for the secular trend, a common intervention effect and a single cluster-level random intercept. The random intercept implies a common ICC both within the same time period and across any two different time periods. However, this can be a rather strong assumption, especially for trials with a longer duration.^20,21

Model extensions have been developed to represent the outcome trajectories and correlations in SW-CRTs in a more flexible fashion. For example, under a cross-sectional design, including a random cluster-by-time interaction accounts for unobserved time-varying factors within each cluster, and differentiates between the so-called within-period and between-period ICCs.^22–24 Alternatively, Kasza et al.²¹ developed the exponential decay model which allows the between-period ICC to decay at an exponential rate over each discrete time period. This model has been generalized to allow for continuous-time correlation decay.²⁵ Besides random deviations across time-periods, model extensions can further accommodate a random-intervention effect to address treatment effect heterogeneity by clusters.^26,27 This may be particularly relevant if a study recruits heterogeneous clusters, such as neurosurgeons from multiple hospitals or intensive care units across multiple healthcare systems with diverse health care practice. Under a closed-cohort design, an additional participant-level random effect should be included to adjust for the serial correlation between repeated measurements.^22,28 Regardless of design variants, while the most common practice is to assume a categorical secular trend and a common fixed-effect to describe the intervention effect, linear mixed models can be modified with a smooth parametric secular trend (e.g., a linear trend) and delayed intervention effect, which are more appropriate when an intervention requires additional time to become fully embedded and influence the study endpoint.^11,26,29

Conditional models have been most frequently used for SW-CRTs, according to recent systematic reviews of published trials.³⁰ They allow flexible specification of complex random effect structures, and have the ability to directly quantify between-cluster heterogeneity through variance component parameters.¹¹ Model parameters are estimated by maximum likelihood or restricted maximum likelihood methods (the latter produces more accurate estimates for the random-effects variance parameters), which now becomes standard in statistical software such as SAS and R.³¹ Table 1 provides a select summary of model variants and associated software for model fitting. Limitations of the mixed-effects models include that the interpretation of the treatment effect parameter can depend on the specification of random-effects structure.^32,33 The validity of hypothesis testing and confidence interval estimation for the treatment effect also critically depends on correct modeling assumptions in these models including the random-effects structure.³⁴

Table 1.

Select summary of conditional and marginal model variants and associated statistical software for estimating model parameters.

CONDITIONAL MODELS
Model (random-effects structure)	Feature	SAS and R Software Package	Reference
Random intercept model	One common ICC	PROC MIXED (SAS) PROC GLIMMIX (SAS) nlme (R) lme4 (R)	Hussey and Hughes18
Random cluster-by-time interaction model	Allows for different within-period and between-period ICCs	PROC MIXED (SAS) PROC GLIMMIX (SAS) nlme (R) lme4 (R)	Hooper et al.22 Girling and Hemming24
Random cluster-by-time interaction model (cohort designs)	Allows for different within-period, between-period and repeated measures ICCs	PROC MIXED (SAS) PROC GLIMMIX (SAS) nlme (R) lme4 (R)	Hooper et al.22 Girling and Hemming24
Exponential decay model	Between-period ICC decays exponentially over time	PROC MIXED (SAS) PROC HPMIXED (SAS)	Kasza et al.21 Kasza and Forbes73
Random intervention model	Allows for heterogeneous treatment effect by clusters	PROC MIXED (SAS) PROC GLIMMIX (SAS) nlme (R) lme4 (R)	Hughes et al.26 Hemming et al.27
MARGINAL MODELS
Model (working correlation structure)	Feature	SAS and R Software Package	Reference
Simple exchangeable structure	One common ICC	PROC GEE (SAS) PROC GLIMMIX (SAS) gee (R) geepack (R) geesmv (R)	Hussey and Hughes18 Thompson et al.46 Ford and Westgate47
Nested exchangeable structure	Allows for within-period and between-period ICCs	%GEECORR (SAS macro) geepack (R) geeCRT (R)	Li et al.36,37
Block exchangeable structure (cohort designs)	Allows for within-period, between-period and repeated measures ICCs	%GEECORR (SAS macro) geepack (R) geeCRT (R)	Li et al.36,37
Exponential decay structure	Between-period ICC decays exponentially over time	geeCRT (R)	Li et al.37
Proportional decay structure (cohort designs)	Both the between-period ICC and the repeated measured ICC decay exponentially over time	Available on GitHub and Journal Website	Li41

^aThe code for implementing the proportional decay GEE model is available at https://github.com/lifanfrank/Li_Quasi-least-squares_SWD and https://onlinelibrary.wiley.com/doi/10.1002/sim.8415.

Method of Analysis—Marginal Models

Marginal models fitted with the generalized estimating equations (GEE)³⁵ provide a natural approach to analyze SW-CRTs because the population-averaged treatment effect is typically of primary interest. This approach requires the specification of a marginal mean model and a working correlation structure. For SW-CRTs, marginal models are considered more robust because the interpretation of the treatment effect parameter does not depend on the correlation model specification, and that valid estimation and inference of treatment effect does not require the correlation structure to be correctly specified.^36,37 This suggests the use of the independence working correlation model coupled with a sandwich standard error as a simple way to analyze SW-CRTs. However, the working independence assumption can lead to loss of statistical power in SW-CRTs, and should be used with caution.^34,37–39

In SW-CRTs, the marginal mean model includes a population-averaged secular trend and treatment effect parameter. Because careful modeling of the correlation structure can lead to a more efficient treatment effect estimator, a suitable correlation model often directly describes the within-time and between-time ICC parameters on the natural scale of the outcome measurements.⁴⁰ Parallel to the development of conditional models, the development of marginal models for SW-CRTs have also investigated different parameterizations of the correlation models, given a categorical secular trend and an average intervention effect parameter. Under a cross-sectional design, Hussey and Hughes¹⁸ described the simple exchangeable correlation model, mimicking the linear mixed model with a single cluster-level random intercept. To differentiate the within-period and between-period ICCs, Li et al.³⁶ considered the nested exchangeable correlation structure, which resembles the mixed-effects model with an additional random cluster-by-time interaction. An exponential decay correlation structure has also been studied in the marginal model context with an exponential family type outcome.³⁷ Under a closed-cohort design, the block exchangeable correlation structure and the proportional decay structure have been proposed to accommodate correlation for repeated outcome measurements taken from the same participant.^36,41

Compared to mixed-effects models, a caveat of marginal models is that the robust standard errors may exhibit negative bias with a limited number of clusters (often not exceeding 30). In a recent systematic review of SW-CRTs, Grayling et al.⁵ reported that the median number of clusters in published SW-CRTs is below 25, and small-sample corrections of the sandwich standard error becomes particularly important for marginal model inference in SW-CRTs.^42–44 Several simulation studies have reported the performance of small-sample corrections for GEE robust standard errors, and recommended the Kauermann and Carroll, or the Fay and Graubard standard errors for SW-CRTs.^{36,41,45–47} Finally, while the general method of GEE have been developed decades ago, software that permits the simultaneous estimation of treatment effect and multiple ICC parameters for SW-CRT applications are relatively limited (Table 1). Computational challenges in GEE methods for CRTs with large cluster sizes have also been investigated in Chen et al.⁴⁸ with a stochastic GEE and Li et al.³⁷ with an efficient cluster-period GEE method.

Method of Analysis—Randomization-Based Inference

Randomization-based inference provides a flexible alternative to analyze SW-CRTs. In this approach, the outcome data in an SW-CRT are first analyzed based on the actual randomized allocation. Then the observed statistics is referenced against the exact randomization distribution obtained by permuting the time points clusters crossover to intervention status.⁴⁹ Under the strong null hypothesis, the randomization test can preserve the type I error rate without requiring a correctly-specified correlation structure in a linear mixed model.^50,51 Thompson et al.⁵² and Kennedy-Shaffer et al.⁵³ developed test statistics that are more robust to modeling assumptions on secular trend by leveraging the between-cluster contrasts in outcomes. To alleviate the computational burden associated with enumerating all possible randomized allocations, Hughes et al.⁵⁴ derived the closed-form permutation variances of the test statistic and showed that the resulting randomization test preserved the valid type I error even when both the mean and covariance structures are incorrectly specified. Beyond testing, Rabideau and Wang^55,56 developed a computationally efficient method to estimate randomization-based confidence intervals for the treatment effect in SW-CRTs.

Sample Size Determination

For a continuous outcome, the required number of clusters in an SW-CRT for a desired level of power depends on the number of time periods, number of participants per period, effect size and ICC parameters.^9,10,18,57 An analytical sample size formula was developed in Hussey and Hughes for the random intercept model,¹⁸ and has been extended by a number of authors to address more complex random-effects structures.^{11,21,22,25,58} Table 2 provides a select summary of sample size procedures and the associated statistical software. A tutorial and R Shiny App can be found in Hemming et al.⁵⁹ In the design stage, sample size estimates can be sensitive to the choice of random-effect structure. While historical or routinely collected data can be useful for drawing assumptions on the random-effects or correlation structures, in the absence of such information, sensitivity analysis is recommended to obtain more robust sample size estimates.²¹ In simple cases, the relationship between sample size and ICC parameters have been studied, which facilitates the choice of design parameters. For example, under the cross-sectional design, the required sample size increases with larger within-period ICC but decreases with larger between-period ICC, suggesting that a conservative between-period ICC value is unlikely to result in an underpowered study.³⁶ Table 2 also reveals that there are relatively more methods devoted to estimating the sample size in SW-CRTs with a continuous outcome, whereas software for binary and count outcomes (except for those based on linear mixed model approximation) is limited, even though they are common especially for patient-reported outcomes in clinical research. Zhou et al.⁶⁰ developed a maximum likelihood procedure to obtain the sample size for cross-sectional SW-CRTs with a binary outcome, and found inadequacy from the conventional linear mixed model approximation.¹⁸ Li et al.³⁶ developed a GEE approach to obtain the sample size with binary outcomes. These sample size methods for binary outcomes have been implemented in an R package swdpwr.⁶¹

Table 2.

Select summary of sample size methods for stepped wedge cluster randomized trials and related software.

Outcome Type	Design	Analysis	Software	Reference
Continuous	Cross-sectional	Linear mixed model (random intercept)	swCRTdesign (R) 74 swdpwr (R) 61 SWSamp (R) 75 SteppedPower (R) * %swdpwr (SAS macro) 61 steppedwedge (Stata) 76 Shiny CRT Calculator (Web-based) 59	Hussey and Hughes18
		Linear mixed model (random cluster-by-time interaction)	swCRTdesign (R) 74 swdpwr (R) 61 SteppedPower (R) * %swdpwr (SAS macro) 61 Shiny CRT Calculator (Web-based) 59	Hooper et al.22
		Linear mixed model (exponential decay)	Shiny CRT Calculator (Web-based) 59	Kasza et al.21
		Linear mixed model (random intervention)	swCRTdesign (R) 74	Hughes et al.26 Hemming et al.27
		GEE (nested exchangeable correlation structure)	swdpwr (R) 61 %swdpwr (SAS macro) 61	Li et al.36
	Closed-cohort	Linear mixed model (random cluster-by-time interaction)	swdpwr (R) 61 %swdpwr (SAS macro) 61 Shiny CRT Calculator (Web-based) 59	Hooper et al.22
		GEE (block exchangeable correlation structure)	swdpwr (R) 61 %swdpwr (SAS macro) 61	Li et al.36
		GEE (proportional decay correlation structure)	SteppedPower (R) *	Li41
	Open-cohort	Linear mixed model (random cluster-by-time interaction or exponential decay)	SteppedPower (R) *	Kasza et al.58
Binary	Cross-sectional	Linear mixed model approximation	swCRTdesign (R) 74 SWSamp (R) 75 steppedwedge (Stata) 76 Shiny CRT Calculator (Web-based) 59	Hussey and Hughes18
		Linear probability mixed model (random intercept)	swdpwr (R) 61 %swdpwr (SAS macro) 61	Zhou et al.60
		GEE (nested exchangeable correlation structure)	swdpwr (R) 61 %swdpwr (SAS macro) 61	Li et al.36
		GEE (exponential decay correlation structure)	Available on GitHub or Journal website †	Harrison and Wang38 Tian et al.39
	Closed-cohort	GEE (block exchangeable correlation structure)	swdpwr (R) 61 %swdpwr (SAS macro) 61	Li et al.36

^*The SteppedPower R package is available on The Comprehensive R Archive Network (CRAN) at https://cran.r-project.org/web/packages/SteppedPower/index.html

^†The code for sample size estimation with exponential decay correlation structure can be found in https://github.com/lindajaneharrison/SW-CRTs/releases/tag/v2.0 for Harrison and Wang³⁸, and in https://github.com/Zebedial/SWD-variable-cluster-sizes or https://onlinelibrary.wiley.com/doi/full/10.1002/bimj.202100112 for Tian et al.³⁹

A typical assumption made in many sample size formulas is that the same number of participants are recruited in each cluster per period. This assumption, while convenient for deriving sample size formulas, is often violated, for example, when each intensive care unit in a SW-CRT has different patient volumes or each surgeon corresponds to a different patient panel size.⁶² Martin et al.⁶³ studied the implication of unequal cluster sizes in SW-CRTs and conclude that the average power is less affected in SW-CRTs compared to a parallel design. Girling⁶⁴ suggested variance inflation expressions between unequal versus equal cluster sizes assuming a linear mixed model analysis of SW-CRTs. Harrison et al.⁶⁵ provided a set of sample size expressions which specifically includes the coefficient of variation of cluster sizes. Methods for addressing unequal cluster sizes were also extended to accommodate SW-CRTs with a binary outcome.^38,39

OPPORTUNITIES FOR CONSIDERING STEPPED WEDGE DESIGNS IN FUTURE NEUROSURGERY TRIALS

Stepped wedge designs are relatively uncommon in existing neurosurgical trials, but they can provide a robust design option for future studies. Besides the Early 2RIS trial (Figure 1), we identified four additional SW-CRT examples related to neurosurgery^66–69 and summarized them in Table 3. In these trials, a neurosurgeon or a service unit performing neurosurgical operations was the unit of randomization, and the study intervention program often aimed at improving surgery-related patient care. Furthermore, the advantage of rolling out the intervention to all clusters and logistical convenience in staggered implementation were the primary reasons for choosing a stepped wedge design. Following these published trials, when limited resource or capacity is available to simultaneously roll out the program in a future neurosurgery trial, a SW-CRT may be considered as a robust design to effectively study intervention programs. In addition, three trials in Table 3 included fewer than 10 clusters, in which case a stepped wedge design can be more powerful than the parallel-arm design by leveraging both within-cluster and between-cluster comparisons. Finally, three out of four SW-CRTs in Table 3 adopted the linear or generalized linear mixed models for the design and analysis, whereas our methodological review suggests that marginal models are viable alternatives for designing and analyzing SW-CRTs. Application of marginal models to future neurosurgical SW-CRTs can be based on software tools listed in Table 1 and 2.

Table 3.

Examples of stepped wedge cluster randomized trials related to neurosurgery.

Publication	Description	Reasons for SW-CRT	Relevance
Palmay et al.66	Rolling out an intensive care unit (ICU) audit-and-feedback program to 6 non-ICU services, and evaluating targeted antimicrobial utilization. Location: Toronto, Canada.	1. All participating clusters receive the intervention during the study. 2. Overcomes the financial or workload difficulties in concurrent roll-out.	One of the inpatient services receiving intervention is a neurosurgery unit.
Haugen et al.67	Rolling out the WHO Surgical Safety Checklist intervention to 5 surgical specialties (clusters), and evaluating outcomes including morbidity, mortality and length of hospital stay. Location: Norway	1. Unethical not to deliver or retract intervention with perceived benefit. 2. Logistical and financial reasons to stagger the intervention delivery	One of the surgical specialties is neurosurgery.
Schwarze et al.68	Rolling out the question prompt list intervention to 40 surgeons and assessing its effectiveness on patient engagement and well-being among patients considering major surgery. Location: United States.	1. Allows all surgeons to have access to the intervention during the study, and avoided contamination between study participants.	The participating surgeons include neurosurgeons performing high-risk neurosurgical operations.
Malone et al.69	Assessing the impact of two de-implementation strategies, order set change and facilitation training, across 9 Children’s Hospitals. Location: United States	1. Allows for phased implementation of intervention with logistical convenience. 2. Permits all clusters to receive intervention and therefore increases participation.	The intervention aims to reduce unnecessary post-operative antibiotics in surgical procedures performed by surgeons, including neurosurgeons.

CONCLUSION

The review in this article provides an accessible entry point to the recent developments in methods for SW-CRTs, particularly on available tools to assist design and analysis. A critical consideration in using existing tools for sample size calculation is the assumptions on unknown ICCs. It has been encouraged in the CRT and SW-CRT literature^{70 71} to report ICCs to facilitate the design of future trials with similar endpoints. Beyond reporting ICCs, a high-quality SW-CRT should also clearly describe the modeling assumptions for secular trend, and the random-effects or correlation structures to ensure reproducible sample size calculation.¹¹ The CONSORT extension to SW-CRTs⁷² is devoted to developing the recommended practices for conduct and reporting, which serve as a principal guidance for researchers working with SW-CRTs. By providing key conceptual and analytical considerations, we aspire to encourage researchers to evaluate the potential for adopting a stepped wedge design in their study and thereby help with generating high-quality treatment effect evidence for patient care.

Abbreviations and Acronyms:

CRT

cluster randomized trial

ICC

intraclass correlation coefficient

SW-CRT

stepped wedge cluster randomized trials