Abstract
The transport coefficients, in particular the transference number, of electrolyte solutions are important design parameters for electrochemical energy storage devices. The recent observation of negative transference numbers in PEO–LiTFSI under certain conditions has generated much discussion about its molecular origins, by both experimental and theoretical means. However, one overlooked factor in these efforts is the importance of the reference frame (RF). This creates a non-negligible gap when comparing experiment and simulation because the fluxes in the experimental measurements of transport coefficients and in the linear response theory used in the molecular dynamics simulation are defined in different RFs. In this work, we show that, by applying a proper RF transformation, a much improved agreement between experimental and simulation results can be achieved. Moreover, it is revealed that the anion mass and the anion–anion correlation, rather than ion aggregates, play a crucial role for the reported negative transference numbers.
One factor that limits the fast charging and discharging of lithium and lithium-ion batteries is the buildup of a salt concentration gradient in the cell during operation,1,2 since the anion flux due to migration must be countered by that of diffusion at steady state. It is therefore desirable for the electrolyte material to carry a greater fraction of cations for migration to minimize the concentration gradient. This fraction, known as the cation transference number, is thus of vital importance in the search for novel electrolyte materials. It is therefore problematic that conventional liquid electrolytes display rather low such numbers and even more troublesome that they are even lower for solid-state polymer electrolytes based on polyethers.
While the condition of a uniform concentration when measuring the transference number can be achieved in typical aqueous electrolytes, its experimental determination in polymer electrolytes is much more challenging due to the continuous growth of the diffusion layer.3 At low concentrations, the effect of the concentration gradient may be estimated by assuming an ideal solution without ion–ion interactions, as is done in the Bruce–Vincent method.4 At higher concentrations, its effect on the transference number can be taken into account by the concentrated solution theory developed by Newman and can be obtained through a combination of experimental measurements.5
The cation transference
number 
measured in these experiments is defined
typically in the solvent-fixed reference frame (RF), denoted by the
superscript 0 here.6 However, the transference
number 
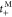as computed in molecular dynamics (MD)
simulation based on the linear response theory7 is instead related to the velocity correlation functions under the
barycentric RF (denoted by the superscript M). This difference creates
a conceptual gap when comparing experiments and simulations and interpreting
results measured in different types of experiments, when seeking the
molecular origin behind the observed phenomenon.
To illustrate
this point, we here study a typical polymer electrolyte
system: PEO–LiTFSI. For this, a negati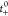ve 
has been reported with Newman’s
approach,8,9 which has rendered much discussion in the
literature.10−12 While the formation of ion aggregates has often been
suggested to cause such negative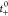 
,11 only marginally
negative values were observed in MD simulations,13 even when the correlation due to charged ion clusters was
considered explicitly.
To reconcile these observations, we will
first investigate how
the choice of RF affects the transference number. In fact, it is possible
to relate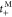 
to 
via a simple transformation rule, as shown
by Woolf and Harris:14
 |
1 |
where the mass fraction
of species i is denoted as ωi. According
to eq 1, the relation
between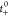 
and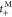 
depends only on the composition, specifically
the mass fractions, of the electrolyte.
While the two transference
numbers are equivalent at the limit
of infinite dilution (ω0 → 1), they become
distinctly different at higher concentrations. As shown in Figure 1, at the concentration
where negative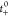 
is observed, 
is still positive.
Moreover, t+ generally shifts downward
in the solvent-fixed RF as
the concentration increases, as seen in Figure 1. This trend can be expected, since at the
other limit (ω0 → 0), 
must converge to the ω– in order to satisfy eq 1. This suggests that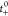 
will become increasingly sensitive at higher
concentrations since its value will be determined by the motion of
a small fraction of solvent molecules. The distinction between 
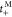and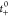 
may already explain why a negative transference
number is seldom observed in MD simulations where the barycentric
RF is the default setting. However, more importantly, the strong dependence
of t+ on the RF suggests that the intuitive
explanation of the observed negative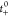 
being due to the population of ion aggregates
is not necessarily the case. Instead, as pointed out in recent studies,15−19 the explicit consideration of ion–ion correlations is essential
to understand ion transport in polymer electrolytes.
Figure 1.
Transference number under
(a) barycentric RF and (b) solvent-fixed
RF in PEO–LiTFSI for different concentrations r [Li/EO] (the ratio of Li to ether oxygen). The conversion rule of t+ as determined by eq 1 is shown by projecting the grid of part a
to part b. The experimental data and fitting of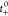 
are reproduced from ref (8). The transfer numbers in
MD simulations are computed from the corresponding Onsager coefficients
using eq 3; see the Supporting Information for simulation details.
In the following, we will show how the ion–ion
correlations
contribute to the negative transference number in light of the RF.
In the Onsager phenomenological equations,20 the flux 
of species under a
reference frame S can
be considered as the linear response of the external driving forces Xj acting on any species j:
 |
2 |
where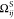 
are the Onsager coefficients. For the index j, here we denote the solvent as 0, the cation as +, and
the anion as −. In addition, the fluxes satisfy the following
RF condition: 
, where 
are the proper weighing factors, i.e., 
for the barycentric RF
and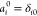 
for the solvent-fixed
RF.21 Then, a unique set of the Onsager
coefficients can be determined
by applying the Onsager reciprocal relation,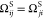 
, and the RF constraint, 
.
Knowing these Onsager coefficients, one can express the transport properties of interest here, i.e., the transference number and the ionic conductivity, as
 |
3 |
 |
4 |
where qi is the formal charge of species i and NA is the Avogadro constant. It is worth noting that, unlike the transference number, the ionic conductivity is RF-independent because of the charge neutrality condition.
While the transformation
of t+ from
the solvent-fixed RF to the barycentric RF can follow the straightforward
rule of eq 1, the corresponding
RF transformation of Ωij is not
trivial. This is illustrated by a simplified example shown in Figure 2, where the driving
force acting on the cation is assumed to be zero. In the barycentric
RF, both driving forces X0 acting on the solvent
and X– acting on the anion will contribute
to the anion flux 
.
When transforming the Onsager coefficients
to the solvent-fixed RF, only the driving force X– contributes to the anion flux 
, as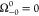 
by construction.
Figure 2.
An illustration of the
transformation procedure when converting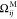 
to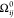 
for the case where
the driving force acting
on the cation is zero. The dashed lines indicate relevant parts related
to the solvent.
Nevertheless, the general transformation rule can be derived using the independent fluxes and driving forces,21 which is consistent with the above constructions. Following the notation of Miller,22 one can consider only the n – 1 independent fluxes and driving forces in an n component system, where the flux of the solvent J0 is treated as a redundant variable. This leads to the following set of rules for the RF transformation:
 |
5 |
 |
6 |
 |
7 |
where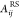 
is the matrix that converts the independent
fluxes from the reference frame S to R, and ci is the molar concentration of species i. The coefficients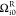 
may then be fixed according to the RF constraint.
The specific transformation equations for the barycentric and solvent-fixed
RFs are provided in the Supporting Information.
This transformation provides the connection between 
measured experimentally
and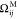 
derived
from MD simulations. Thus, one
can compare Onsager coefficients under a common RF to see whether
the simulation describes the same transport mechanism as in experiment
or not. Here, we computed Onsager coefficients following Miller’s
derivation6 with experimental measurements
by Villaluenga et al.8 MD simulations were
performed using GROMACS23 and the General
AMBER Force Field,24 from which Onsager
coefficients were derived with in-house analysis software. Details
of the conversion and simulation procedure can be found in the Supporting Information. In addition, we shall
note here that an alternative set of transport coefficients, i.e.,
the Maxwell–Stefan diffusion coefficients, were originally
reported from experiment,8 and they are
consistent with the present framework (see the Supporting Information for the interconversion). In addition,
the Onsager phenomenological equations may also be written in terms
of the resistance coefficients,25 which
closely resemble the Maxwell–Stefan equations. However, the
Onsager coefficients are favored here because they are well-behaved
at any given concentration and therefore helpful to understand the
RF dependency of the ion–ion correlations.
As shown in Figure 3, the conductivity
and Onsager coefficients obtained from MD simulations
generally match the experimental values. In particular,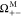 
is negative in the entire concentration
range, and this indicates an anticorrelation between cations and anions.
Furthermore, we see that the experimentally observed negative transference
number at r = 0.15 is reproduced in the MD simulation,
with consistent features of Ωij,
namely, 
and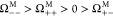 
. These results
demonstrate that the experimentally
observed negative transference number in PEO-LiTFSI systems is captured
with the present force field parametrization used in the MD simulations.
Figure 3.
Ionic conductivity and Onsager coefficients under the barycentric and solvent-fixed RF derived from (a–c) experimental measurements and (d–f) MD simulations. The experimental measurements (▲) and fittings (curved lines) are converted from ref (8). The MD simulation results are computed by fitting the mean cross displacements, as detailed in the Supporting Information.
Looking at the effects of RF, we see that Ω–– and Ω+– changes more significant upon RF
transformation as compared to Ω++. In particular,
at r = 0.15,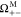 
is negative while 
is positive. This
means that the driving
force applied to the cations correlates to a codirectional anion flux
in the solvent-fixed RF but that an opposite anion flux is found in
the barycentric RF. This, together with the observations made above,
cannot be explained by any distribution of ideal charge carrying clusters.
To better understand the underlying physical account, we can look
into the Onsager coefficients from a microscopic point of view, as
they are related to the correlation functions of the fluxes. From
the equations shown below, it is clear that the RF transformation
is equivalent to transforming either the current-correlation function
shown in eq 8 or, equivalently, the displacements
of ions shown in eq 9. Thus, this result (eq 10) is consistent with eq 7 and the Wheeler−Newman expression
for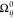 
.26
 |
where β = 1/(kBT) is the inverse temperature, and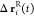 
is the total displacement of species i over a time interval t.
Based on this result, the conversion of Onsager coefficients upon an RF transformation can be visualized as an affine transformation of ion displacement, as shown in Figure 4. At r = 0.15, the displacement of cations and anions is apparently anticorrelated in the barycentric RF, while the correlation becomes positive in the solvent-fixed RF. This can be rationalized, since the motion of anions in the barycentric RF entails the motion of solvent in the opposite direction, giving rise to the enhanced anion motion and the positive cation–anion correlation in the solvent-fixed RF. On the other hand, the motion of cations induces a much less significant effect, as signified by the small distortion along the x-axis. This indicates that anions play a significant role for the transference number of Li+, not only by its relative motion to the cation.
Figure 4.
Transformation of the normalized displacement correlations upon a change of reference frame. ΔrM/nion is the total displacement ΔrM (of cations “+” or anions “–”) normalized by the number of ions nion. The correlation is obtained from a 400 ns MD trajectory, where the correlation between mean displacements of cations and anions over Δt = 10 ns is plotted in (a) the barycentric RF and (b) the solvent-fixed RF. The RF transformation according to eq 7 is visualized as the projection of grid lines from part a to b.
Indeed, the sign of the experimentally measured 
depends not only on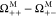 
, but also on the 
and the anion mass fraction. The importance
of the anion–anion correlation and the anion mass is demonstrated
in Figure 5, where
the partial derivative of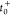 
shows its strong dependency on the anion
mass and Onsager coefficients. An increase of the anion mass introduces
an even stronger reduction of the transference number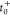 
, and therefore, 
is more likely to be negative. The same
effect occurs when the anion–anion correlation becomes stronger,
and 
becomes larger. This suggests a direct
connection between the observed negative 
and a strong anion–anion correlation
found at higher concentrations. The latter effect was also indicated
in a recent X-ray scattering study of PEO–LiTFSI systems.12
Figure 5.
Sensitivity analysis
of transference number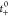 
in solvent-fixed RF to the variations in
the anion molecular weight MTFSI and different
Onsager coefficients 
in the barycentric RF. The analysis is
performed by evaluating the partial derivative of 
to the logarithm of MTFSI or 
, with
data derived from experimental measurements
in ref (8). Note that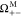 
is mostly negative as shown in Figure 3, while the other
variables are positive.
In summary, our present analysis reveals a strong RF dependency of the transference number and the Onsager coefficients in the PEO–LiTFSI system. With a proper transformation, the Onsager coefficients can be used as a rigorous test to compare the transport properties from experimental measurements and MD simulations, as shown here. This will provide new ground to refine force field parametrization, for example, by including the subtle effects of electronic polarization,27 although we found that the standard force field already captures the main features observed in experiments.
Not only do our results demonstrate that the experimentally observed
negative 
can be reproduced with MD simulations,
but they also show that cations and anions are mostly anticorrelated
in the barycentric RF (
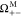< 0) throughout the entire concentration
range in both experiment and simulation. While this does not rule
out the possibility of short-lived ion aggregates, neither does it
support a transport mechanism based on negatively charged ion clusters.
Instead, we show that a large anion mass and strong anion–anion
correlations can be responsible for a negative transference number
of 
.
Furthermore, the RF dependence of ion–ion correlations suggests that any discussions about ion–ion correlations need to be had within the same RF. This may shed light on why a different observation was made regarding the sign of t+ with alternative experimental approaches such as electrophoretic NMR (eNMR).10
Although we do not expect that all discrepancies in transport properties between different experimental approaches and between experiment and simulation can be resolved by the present analysis, insights regarding the RF dependency of ion–ion correlations and a direct comparison of the complete set of Onsager coefficients between experiment and simulation as demonstrated in this work would be essential to elucidate the ion transport mechanism in polymer electrolytes and concentrated electrolyte systems alike.
Acknowledgments
This work has been supported by the European Research Council (ERC), grant 771777 “FUN POLYSTORE” and the Swedish Research Council (VR), grant 2019-05012. The authors are thankful for the funding from the Swedish National Strategic e-Science program eSSENCE, STandUP for Energy and BASE (Batteries Sweden). The simulations were performed using resources provided by the Swedish National Infrastructure for Computing (SNIC) at PDC.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.2c02389.
Details of MD simulations and force field parameters; computation and conversion of Onsager coefficients in different RFs; conversion between different sets of transport equations; and a list of symbols (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Mindemark J.; Lacey M. J.; Bowden T.; Brandell D. Beyond PEO—Alternative Host Materials for Li+-Conducting Solid Polymer Electrolytes. Prog. Polym. Sci. 2018, 81, 114–143. 10.1016/j.progpolymsci.2017.12.004. [DOI] [Google Scholar]
- Choo Y.; Halat D. M.; Villaluenga I.; Timachova K.; Balsara N. P. Diffusion and Migration in Polymer Electrolytes. Prog. Polym. Sci. 2020, 103, 101220. 10.1016/j.progpolymsci.2020.101220. [DOI] [Google Scholar]
- Evans J.; Vincent C. A.; Bruce P. G. Electrochemical Measurement of Transference Numbers in Polymer Electrolytes. Polymer 1987, 28, 2324–2328. 10.1016/0032-3861(87)90394-6. [DOI] [Google Scholar]
- Bruce P. G.; Vincent C. A. Steady State Current Flow in Solid Binary Electrolyte Cells. J. Electroanal. Chem. Interfacial Electrochem. 1987, 225, 1–17. 10.1016/0022-0728(87)80001-3. [DOI] [Google Scholar]
- Newman J.; Balsara N. P.. Transport Properties. In Electrochemical Systems; John Wiley & Sons, 2021; pp 283–300. [Google Scholar]
- Miller D. G. Application of Irreversible Thermodynamics to Electrolyte Solutions. I. Determination of Ionic Transport Coefficients lij for Isothermal Vector Transport Processes in Binary Electrolyte Systems. J. Phys. Chem. 1966, 70, 2639–2659. 10.1021/j100880a033. [DOI] [Google Scholar]
- Zwanzig R. Time-Correlation Functions and Transport Coefficients in Statistical Mechanics. Annu. Rev. Phys. Chem. 1965, 16, 67–102. 10.1146/annurev.pc.16.100165.000435. [DOI] [Google Scholar]
- Villaluenga I.; Pesko D. M.; Timachova K.; Feng Z.; Newman J.; Srinivasan V.; Balsara N. P. Negative Stefan-Maxwell Diffusion Coefficients and Complete Electrochemical Transport Characterization of Homopolymer and Block Copolymer Electrolytes. J. Electrochem. Soc. 2018, 165, A2766–A2773. 10.1149/2.0641811jes. [DOI] [Google Scholar]
- Hoffman Z. J.; Shah D. B.; Balsara N. P. Temperature and Concentration Dependence of the Ionic transport Properties of Poly(ethylene Oxide) Electrolytes. Solid State Ion. 2021, 370, 115751. 10.1016/j.ssi.2021.115751. [DOI] [Google Scholar]
- Rosenwinkel M. P.; Schönhoff M. Lithium Transference Numbers in PEO/LiTFSA Electrolytes Determined by Electrophoretic NMR. J. Electrochem. Soc. 2019, 166, A1977–A1983. 10.1149/2.0831910jes. [DOI] [Google Scholar]
- Molinari N.; Mailoa J. P.; Kozinsky B. Effect of Salt Concentration on Ion Clustering and Transport in Polymer Solid Electrolytes: A Molecular Dynamics Study of PEO–LiTFSI. Chem. Mater. 2018, 30, 6298–6306. 10.1021/acs.chemmater.8b01955. [DOI] [Google Scholar]
- Loo W. S.; Fang C.; Balsara N. P.; Wang R. Uncovering Local Correlations in Polymer Electrolytes by X-ray Scattering and Molecular Dynamics Simulations. Macromolecules 2021, 54, 6639–6648. 10.1021/acs.macromol.1c00995. [DOI] [Google Scholar]
- France-Lanord A.; Grossman J. C. Correlations from Ion Pairing and the Nernst-Einstein Equation. Phys. Rev. Lett. 2019, 122, 136001. 10.1103/PhysRevLett.122.136001. [DOI] [PubMed] [Google Scholar]
- Woolf L. A.; Harris K. R. Velocity Correlation Coefficients as an Expression of Particle–Particle Interactions in (Electrolyte) Solutions. J. Chem. Soc., Faraday Trans. 1 1978, 74, 933–947. 10.1039/f19787400933. [DOI] [Google Scholar]
- Vargas-Barbosa N. M.; Roling B. Dynamic Ion Correlations in Solid and Liquid Electrolytes: How Do They Affect Charge and Mass Transport?. ChemElectroChem. 2020, 7, 367–385. 10.1002/celc.201901627. [DOI] [Google Scholar]
- Zhang Z.; Wheatle B. K.; Krajniak J.; Keith J. R.; Ganesan V. Ion Mobilities, Transference Numbers, and Inverse Haven Ratios of Polymeric Ionic Liquids. ACS Macro Lett. 2020, 9, 84–89. 10.1021/acsmacrolett.9b00908. [DOI] [PubMed] [Google Scholar]
- Pfeifer S.; Ackermann F.; Sälzer F.; Schönhoff M.; Roling B. Quantification of Cation–Cation, Anion–Anion and Cation–Anion Correlations in Li Salt/Glyme Mixtures by Combining Very-Low-Frequency Impedance Spectroscopy with Diffusion and Electrophoretic NMR. Phys. Chem. Chem. Phys. 2021, 23, 628–640. 10.1039/D0CP06147F. [DOI] [PubMed] [Google Scholar]
- Fong K. D.; Self J.; McCloskey B. D.; Persson K. A. Ion Correlations and Their Impact on Transport in Polymer-Based Electrolytes. Macromolecules 2021, 54, 2575–2591. 10.1021/acs.macromol.0c02545. [DOI] [Google Scholar]
- Gudla H.; Shao Y.; Phunnarungsi S.; Brandell D.; Zhang C. Importance of the Ion-Pair Lifetime in Polymer Electrolytes. J. Phys. Chem. Lett. 2021, 12, 8460–8464. 10.1021/acs.jpclett.1c02474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onsager L. Theories and Problems of Liquid Diffusion. Ann. N.Y. Acad. Sci. 1945, 46, 241–265. 10.1111/j.1749-6632.1945.tb36170.x. [DOI] [PubMed] [Google Scholar]
- Kirkwood J. G.; Baldwin R. L.; Dunlop P. J.; Gosting L. J.; Kegeles G. Flow Equations and Frames of Reference for Isothermal Diffusion in Liquids. J. Chem. Phys. 1960, 33, 1505–1513. 10.1063/1.1731433. [DOI] [Google Scholar]
- Miller D. G. Some Comments on Multicomponent Diffusion: Negative Main Term Diffusion Coefficients, Second Law Constraints, Solvent Choices, and Reference Frame Transformations. J. Phys. Chem. 1986, 90, 1509–1519. 10.1021/j100399a010. [DOI] [Google Scholar]
- Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Tyrrell H. J. V.; Harris K. R.. Principles of Non-Equilibrium Thermodynamics. In Diffusion in Liquids: A Theoretical and Experimental Study; Butterworth-Heinemann, 1984; pp 21–55. [Google Scholar]
- Wheeler D. R.; Newman J. Molecular Dynamics Simulations of Multicomponent Diffusion. 1. Equilibrium Method. J. Phys. Chem. B 2004, 108, 18353–18361. 10.1021/jp047850b. [DOI] [Google Scholar]
- Borodin O. Polarizable Force Field Development and Molecular Dynamics Simulations of Ionic Liquids. J. Phys. Chem. B 2009, 113, 11463–11478. 10.1021/jp905220k. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.