Abstract
The water sorption of proton-exchange membranes (PEMs) was measured in situ using high-resolution neutron imaging in small-scale fuel cell test sections. A detailed characterization of the measurement uncertainties and corrections associated with the technique is presented. An image-processing procedure resolved a previously reported discrepancy between the measured and predicted membrane water content. With high-resolution neutron-imaging detectors, the water distributions across N1140 and N117 Nafion membranes are resolved in vapor-sorption experiments and during fuel cell and hydrogen-pump operation. The measured in situ water content of a restricted membrane at 80 °C is shown to agree with ex situ gravimetric measurements of free-swelling membranes over a water activity range of 0.5 to 1.0 including at liquid equilibration. Schroeder’s paradox was verified by in situ water-content measurements which go from a high value at supersaturated or liquid conditions to a lower one with fully saturated vapor. At open circuit and during fuel cell operation, the measured water content indicates that the membrane is operating between the vapor- and liquid-equilibrated states.
I. INTRODUCTION
Sufficient ionomer hydration is required for high performance operation of proton exchange membrane fuel cells (PEMFCs). Hydration of the electrolyte membrane and catalyst-layer ionomer is necessary for adequate ionic conductivity. From this constraint along with the need to prevent water from blocking oxygen access to the reaction sites stems the issue of water management in PEMFCs, one of the critical topics in optimizing cell performance. Furthermore, the hydration state of the membrane affects the water transport within the cell, as both the diffusion and electro-osmotic coefficients depend on water content.1 The water uptake of a membrane is conventionally measured ex situ by weighing free-swelling samples equilibrated at controlled water activity and in PEM is measured as a ratio, λ, of moles of water per moles of sulfonic acid site.2–4
Neutron imaging has been used extensively in water-management studies due to its ability to measure water content in an operating fuel cell. The spatial resolution of this technique has been improved by a factor of 20 over the past four years, thus enabling the resolution of the water distribution along the critical through-plane direction.5,6 This also provides important model validation data. One of the earliest efforts at comparing a through-plane simulation to neutron-radiography data revealed that the presence of a thermal gradient transported significant amounts of water through the cathode gas-diffusion layer (GDL), which was termed phase-change-induced flow.7 While the focus of that paper was on qualitatively matching the shape of the water content in the GDL, there was a discrepancy in the membrane water content of about a factor of 4 between the model prediction and the neutron-imaging measurement. A recent modeling effort has addressed this discrepancy by introducing a scaling parameter to match the data.8 However, there are several systematic effects in the neutron-radiography experiment that were not fully understood at the time of publication,5,7 which affect the quantification of the membrane water content. It should be emphasized that the qualitative trends that were examined in Weber and Hickner7 are not impacted by these systematic effects in the membrane.
To determine the source of this discrepancy, a number of calibration and water-sorption measurements have been carried out at the National Institute of Standards and Technology (NIST) neutron-imaging facility and improved image-analysis methods have been developed. In the remainder of this article, a brief overview of the NIST neutron-imaging facility and a discussion of measuring water content of a PEM and the associated uncertainties is given in Sec. II. These water quantification methods are applied to the water sorption of 178 μm thick Nafion9 membrane (N117) under a range of humidity conditions in Sec. III. In Sec. IV, the water content measured during fuel cell and hydrogen-pump operation of a test section with a catalyzed ~1000 μm thick Nafion membrane (N1140) is compared to a one-dimensional model of the through-plane water content that is similar to the one presented in Weber and Hickner.7
II. METHODS
A. NIST Neutron radiography facility
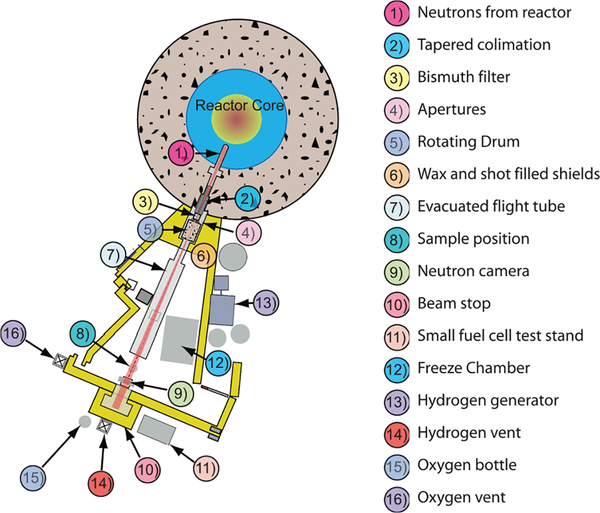
The neutron source at the NIST is a 20 MW heavy-water fission reactor operated at 37 °C with a split-core design to reduce fast neutron and gamma-ray backgrounds. The NIST neutron-imaging facility views the center of the reactor on beam tube 2 (BT2), and a schematic layout of the facility is shown in Figure 1. There are two main considerations for a neutron imaging facility: the geometric blur and the neutron fluence rate. The fluence rate determines the exposure time to reach a given measurement uncertainty due to Poisson counting statistics as discussed in Sec. II D 1 below. The geometric blur can limit the image spatial resolution and is described by a full-width at half max given by
where z is the separation between the detector and the object, L is the distance between the detector and the beam-defining aperture, and D is the size of the beam-defining aperture. In practice, there is always a separation between the object and the detector, and λg can limit the image resolution; thus it might be necessary to decrease the ratio D/L to achieve a given image spatial resolution. However, since the fluence rate scales as (D/L)2, decreasing D to improve λg increases image acquisition time; a factor of 2 improvement in λg results in a factor of 4 increase in the image exposure time required to obtain the same water-measurement uncertainty. For high-resolution imaging of the through-plane water content in PEMFCs, the optimal aperture geometry is a slit, with the narrow dimension of the slit parallel to the fuel cell through-plane direction.10 The apertures currently available at the NIST neutron-imaging-facility, and the beam properties for these are given in Table I.
FIG. 1.
Schematic layout of the NIST BT2 neutron imaging facility.
TABLE I.
Apertures and beam properties available at the NIST neutron imaging facility. Apertures with only one dimension listed are circular and the dimension is the diameter; the apertures with two dimensions listed are slits.
| Aperture dimension | ≈ L/D (x,y) | Fluence Rate (cm−2 s−1) |
|---|---|---|
|
| ||
| 20 mm | 300 | 3.3 × 107 |
| 15 mm | 450 | 1.4 × 107 |
| 10 mm | 600 | 5.0 × 106 |
| 3 mm | 2000 | 5.2 × 105 |
| 10 mm × 1 mm | 600, 6000 | 7.5 × 105 |
| 1 mm × 10 mm | 6000, 600 | 8.0 × 105 |
| 20 mm × 2 mm | 300, 3000 | 3.2 × 106 |
| 2 mm × 20 mm | 3000, 300 | 3.4 × 106 |
B. Neutron-imaging detectors and spatial resolution
Since the neutron is a neutral particle, neutron detection is a multi-step process: (i) absorption of a neutron; (ii) the release of charged particles as a byproduct of the neutron absorption; (iii) interaction of the charged particle with a second medium, which produces either scintillation light or a charge avalanche; and (iv) detection of the scintillation light or charge. There are a few isotopes that have a large neutron absorption cross-section; those most often employed in neutron-imaging detectors are 6Li, 10B, and natGd. In the case of neutron capture by 6Li, the emitted charged particles are 3H and 4He with a total energy of about 4.8 MeV. In the case of Gd, a simple description of the neutron capture is that the decay of the excited nucleus results in the emission of gamma rays (with up to 7 MeV in energy) and electrons, which produce additional conversion electrons through the Auger process with an average energy of about 50 keV. When these isotopes are incorporated into a scintillator, the energetic charged particles induce scintillation light; this light is then imaged by a camera, such as a charge-coupled device (CCD). Using modern CCDs with thin (~10 μm) scintillators has enabled researchers to achieve image spatial resolutions of order 10 μm.10,11
At the NIST neutron-imaging facility, high-resolution detectors based on microchannel plates (MCPs) have been employed.12–15 Two advantages of MCPs over CCDs include the following. First, there is no read noise so that the uncertainty is dominated by neutron-counting statistics. Second, one can cover a large field of view while maintaining high spatial resolution, as opposed to a changing field of view with spatial resolution with conventional CCDs coupled with a camera lens. The MCP glass can contain either Gd or 10B. On neutron capture, charged particles are released that have a range of approximately 5 μm in the MCP glass. When a charged particle enters a pore, electrons are stripped from the surface. A high electric field (3 kV to 5 kV) accelerates the electrons down the channel; subsequent wall collisions result in more electrons being stripped; thus with a sufficiently long channel, the initial charge is amplified by a factor of 106 to 107. The centroid of the charge cloud is determined with a two-dimensional (2D) position-sensitive anode. Since the detection is event based, there is a limit to the global count rate before events are lost due to event overlap. The number of lost events is characterized by the deadtime, which is the percentage of events lost at a given input rate. In practice, 10% deadtime loss is typically the maximum acceptable. In the work presented here, two generations of MCP detectors have been used. The first used a cross-delay-line anode (XDL), which had a field of view of 25 mm in diameter, a spatial resolution of about 30 μm, pixel pitch of 16 μm, and a 10% deadtime at an event rate of 200 kHz.6 The second generation MCP had a cross-strip anode (XS), enabling a 10% deadtime at a 1 MHz event rate, 40 mm diameter field of view, a pixel pitch of 5 μm, and a nominal 10 μm spatial resolution as shown in Figure 2. The deadtime limits the field of view of the cross-strip detector to a maximum area of about 3 cm2. As an aside, the pixel pitch is the spatial sampling period of the real, analog image; the spatial resolution of a neutron-imaging detector is at least larger than the pixel pitch.
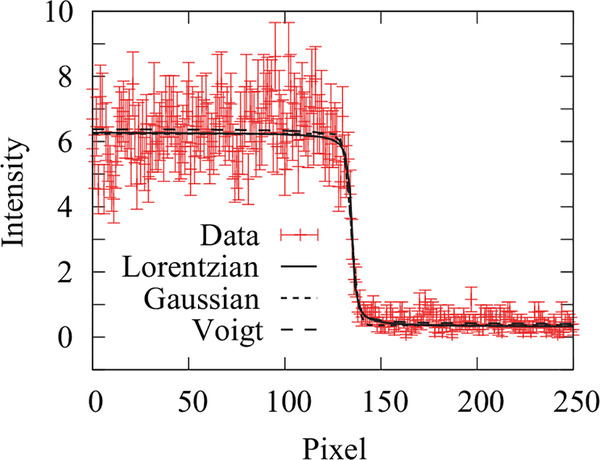
FIG. 2.
(a) The line profile across a sharp Gd edge. Three system PSFs (a Lorentzian, a Gaussian, and a Voigt profile) are used to model the measured line profile, and all three models result in a reduced χ2 ≈ 1. In the case of the Lorentzian model, the obtained half width at half maximum is γ = (6.0 ± 1.5) μm, corresponding to a resolution of 8.2 μm with a reduced χ2 = 0.94. In the case of the Gaussian model, the obtained σ = (14.9 ± 2.1) μm, corresponding to a resolution of 21.8 μm with a reduced χ2 = 0.98. In the case of the Voigt model, the obtained σ = (9.0 ± 0.4) μm and γ = (4.0 ± 0.4) μm, corresponding to a resolution of 21.8 μm with a reduced χ2 = 1.02. The uncertainty in the neutron counts is assumed to be from random noise, reduced by averaging over 8 pixels.
The spatial resolution of a detector is typically determined by measuring the width of a sharp edge. This edge-spread function (ESF) in spatial coordinates is the basis for deriving the point-spread function (PSF) and the modulation transfer function (MTF), which is the Fourier transform of the PSF. The quoted detector spatial resolution corresponds to the frequency at which the MTF reaches 10% of its maximum value. There are a number of functions that are used to model a detector-system’s PSF; considered here are a Gaussian, a Lorentzian, and a Voigt Profile (convolution of a Gaussian with a Lorentzian). The resolution for each of these three PSFs, characterized by a standard deviation, σ, or half width at half maximum, γ, is, respectively
| (2) |
The corresponding ESF is given by
| (3) |
and for a Gaussian (Lorentzian) PSF, the ESF is an error function (arctangent); there is no simple closed form ESF for a Voigt Profile PSF. As shown in Figure 2, the three PSF models generate reasonable fits to the measured ESF in the vicinity of the edge, in particular, the Lorentzian model gives δLorentz = (8.2 ± 1.5) μm. However, the decay of the PSF can introduce a systematic measurement uncertainty, which depends on many factors, including the field of view illuminated by neutrons.16 The overall image resolution is a combination of the geometric unsharpness and the PSF of the detector. If one approximates both as independent Gaussian functions, the estimate for the overall resolution is the sum in quadrature of δ and λg. The impact of the detector PSF on the measured water content is discussed in more detail in Sec. II D.
C. Water content measured by neutron radiography
In the case of transmission neutron radiography, the overall interaction of a neutron with a material can be described with a collision cross-sectional area referred to as the total scattering cross section, σT,
| (4) |
where σa is the absorption cross section and σs is the scattering cross section, which is the sum of the coherent cross section, σc, and the incoherent scattering cross section, σi. In radiography, the local transmission T(x,y) of the neutron beam is measured. The transmission is given by the Lambert-Beer law of attenuation
| (5) |
where I(x,y) is the background-corrected intensity in the object state of interest (operating fuel cell), I0(x,y) is the background-corrected intensity of the reference state (incident beam or image of a dry fuel cell), N is the material number density, t is the material thickness through which the neutron beam passes, NσTt(x, y) is the local optical density (OD), and the total macroscopic scattering cross section, Σ, is given by
| (6) |
where the sum is over all species that compose the material. (Some reports use the attenuation coefficient, μ, equivalently for Σ; for consistency within this article, we use Σ.) In general, σT can depend on neutron energy, due to absorption and Bragg scattering. In some molecular species, such as water, σT depends on the rotational and vibrational excitation modes; thus Σ is not always given by Eq. (6), rather a more complicated model is required17 or calibration measurements using well-characterized stepped wedges (Figure 3(a)) need to be performed.18 As a final note, the contrast in a neutron image is determined by the Σ of the materials present; for neutrons with a wavelength of 0.18 nm, the total macroscopic scattering cross section for water, aluminum, and carbon for material density at room temperature and atmospheric pressure are approximately 0.37 mm−1, 0.009 mm−1, and 0.055 mm−1, respectively; thus water is a factor ~10 more apparent in an image than either carbon or aluminum.
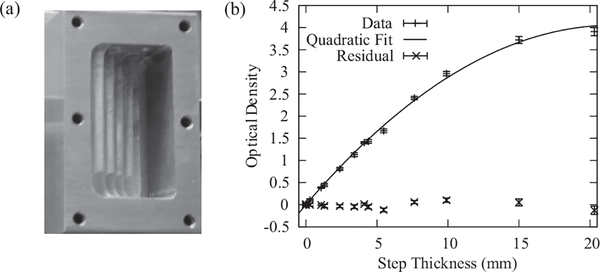
FIG. 3.
(a) Aluminum cuvette used to measure the attenuation of neutrons by water. A lid is secured to provide a leak tight fit. The step depths are measured optically with an accuracy of ±1 μm. (b) The measured optical density as a function of step thickness. The fit parameters are Σw = (0.38483 ± 0.00025) mm−1 and βw = (−0.00947 ± 0.00015) mm−2 with a reduced χ2 = 1.3.
The neutron transmission through water (or through other strong neutron absorbers) for a polychromatic beam that is employed in high-resolution imaging is slightly more complicated than Eq. (5). Since the total scattering cross-section is neutron-energy dependent, σT increases with decreasing neutron energy. This means that the neutron beam that emerges from a section of water has a more energetic spectrum than the incident beam and is more penetrating. The result is that the optical density, −ln(T), is nonlinear in the water thickness, tw, an effect known as beam hardening, and is an effect frequently encountered in x-ray imaging.19 It should be noted that while the physical processes involved in the attenuation of a neutron beam vs. an x-ray beam are different, the fact that the cross-section increases with decreasing wavelength gives rise to a more penetrating beam of radiation, but the corrections developed for x-rays may not be applicable to the neutron case. In order to obtain analytical expressions for the effect of beam hardening, the deviation from the linear relationship is modeled with a quadratic term as shown in Figure 3 where the optical density as a function of water thickness is modeled as
| (7) |
Σw and βw are obtained from a non-linear least squares fit: Σw = (0.38483 ± 0.00025) mm−1, βw = (−0.00947 ± 0.00015) mm−2 with a reduced χ2 = 1.3. The water thickness is then obtained from the transmission image via
| (8) |
While the water content is accurately obtained, beam hardening limits the maximum thickness of water that can be measured. The quadratic approximation is valid for water thickness much less than
| (9) |
For the NIST high-resolution MCP detector, twmax = 20.3 mm; for a fuel cell design commonly used for high-resolution imaging at NIST, with 1 cm wide active area (along the beam direction) and liquid saturated, free-swelling Nafion membrane, the maximum water thickness is about 6 mm (see Sec. II D 6), which is well within the range of validity of Eq. (8). The neutron scattering from typical materials used to fabricate the fuel cell test section (Al, C, and F) is dominated by coherent scattering, which does not contribute to beam hardening; thus, only beam hardening due to water must be considered in neutron imaging of PEMFCs.
D. Water-content-measurement uncertainty and corrections
There are several sources of uncertainty in the measurement of membrane water content with neutron radiography. These include neutron counting statistics, image registration errors, detector resolution, membrane water content in the dry image, in-plane membrane water diffusion, and membrane swelling. These sources of uncertainty are discussed in depth below, and where possible are quantified in Table II.
TABLE II.
Percent relative error due to isolated systematic effects. In all cases, the systematic effect results in observing less water than is actually present.
1. Counting statistics
The fundamental limit to the water-content-measurement uncertainty is from Poisson counting statistics. For tw < 6 mm, the one-sigma uncertainty in the water content can be approximated by the counting statistics due to the operating image of the fuel cell
| (10) |
where I0 is the incident neutron fluence rate, A is the area over which the water content is measured, T is the image exposure time, and η is the detector efficiency (nominally 20% for the MCP detectors). As shown in Hussey et al.,18 for a fixed neutron fluence rate, the uncertainty improves with longer exposure times or larger integration areas, with water-mass-measurement sensitivities of <100 ng possible. Since the beam-defining aperture is typically a slit in high-resolution imaging of fuel cells, it is natural to integrate the images along the in-plane direction, so as to maintain reasonable exposure times. For the data presented below, T = 30 min, A = 7.5 × 10−4 cm2, and ηI0 = 105 cm−2 s−1, so that δtw ~ 10 μm.
2. Image registration errors due to changes in the optical axis
To obtain the water content, one must compare the dry image to the wet image. If there is a shift in the position of one image relative to the other, this registration error will result in artifacts in the obtained water content. Unfortunately, these shifts occur on occasion due to the operation of the NIST reactor.20 To address this systematic error when it occurs, the dry and wet images are normalized by the flat field (neutron image of an empty beam) and then shifted using linear interpolation for sub-pixel motion until the registration errors are minimized. In addition, multiple reference images can be obtained to provide better registration and remove the need for and uncertainty associated with image shifting.
3. Residual membrane water content
One of the somewhat surprising effects of beam hardening is that water present in the reference image changes the conversion of optical density to water thickness, as shown in Figure 4(a). This situation occurs in neutron imaging of fuel cells as it is impractical to completely dry the membrane. Hence, the residual membrane water content in a “dry” reference image needs to be quantified and accounted for to evaluate accurately the water content from the “wet” image. Specifically, the change in the measured optical density due to a residual water thickness, tr, is included in Eq. (5) as follows:
| (11) |
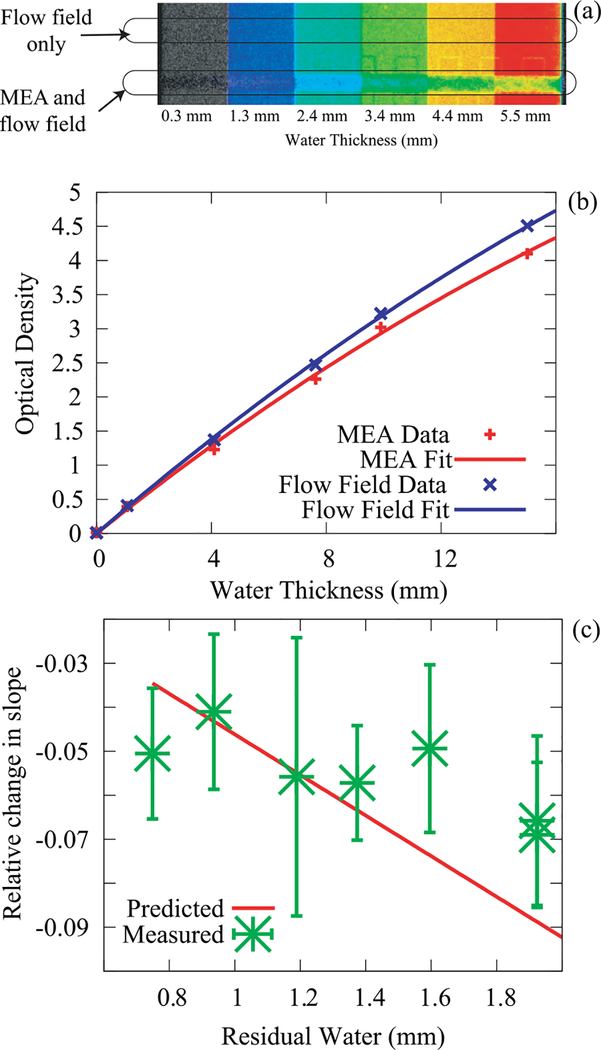
FIG. 4.
Effect of residual water in the membrane on measuring the water content. (a) Colorized image of the cuvette with a PEMFC test section in front showing the shift in observed optical density due to the water content of the in the MEA. (b) The change in the observed optical density due to beam hardening is a change in the linear term converting optical density to water thickness. (c) This effect was measured for various membrane water contents and compared to the prediction using Eq. (11) with no free parameters. The reasonably good agreement between the data and the prediction indicate that the residual water effect on the effective water calibration has been adequately modeled.
To quantify the effect, the calibration measurement carried out in Sec. II C (Figure 3(b)) was repeated by placing a membrane directly in front of the cuvette and flowing humidified gases on either side of the membrane. By varying the relative humidity and the membrane width (i.e., thickness in the beam direction), a range of induced residual membrane water contents was obtained. Shown in Figure 4(c) is the measured and predicted change in slope of the optical density curve showing reasonable agreement between the two. To obtain the membrane water content during in-situ fuel cell operation, one must account for the residual water both in the effect of the slope change as well as the base water content of the membrane.
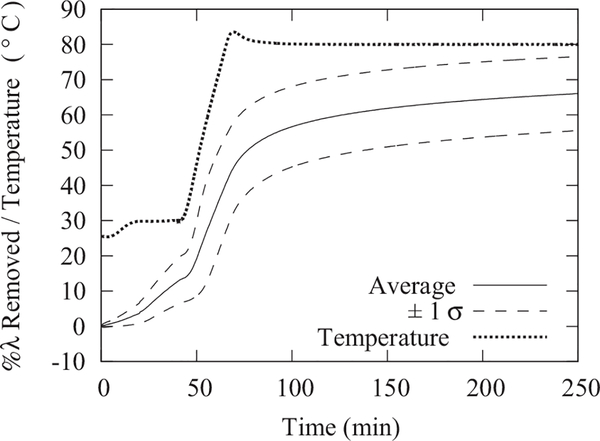
To measure this residual water, an extensive set of ex-situ thermogravimetric analyses (TGAs) were performed on bare Nafion membranes in conditions that mimicked the conditions used to obtain the neutron images of the dry cell (dry nitrogen flow at 80 °C). Shown in Figure 5 is a summary of the water removed as a function of drying time. A Netzsch STA-409PC TGA instrument using dry, ultra-high purity N2 as the sample purge and balance protective gas was used to dry membrane samples with precisely determined water contents. The balance was tared in a static nitrogen atmosphere at ambient pressure (approximately 78 kPa at 2195 m elevation) and at room temperature (27 °C). The final sample weights after sample drying were recorded under identical conditions and balance drift was less than 0.2 mg or 0.1%. The drying protocol included a 5 h isothermal step at 80 °C, which served to evaluate the drying rates at conditions used to acquire the reference “dry” image. The dry weight was determined by subsequently drying the samples at 105 °C under vacuum (70 kPa) for 40 h. The water content of the membrane under equilibration with ambient air varied with environmental temperature (25 °C to 30 °C) and humidity (RH ranged from 20% to 30%), but was on average λ = (3.64 ± 0.27) mol H2O/mol SO3H. Due to the residual water content at ambient conditions, the uncertainty in the drying λ typically dominates the absolute measurement uncertainty of the membrane water content since the typical random uncertainty is less than 1% (see Sec. II D 1). Under typical drying conditions during neutron-imaging experiments, the water content is reduced by 60% of the initial water content. As the initial water content can vary due to environmental variation, one must determine the water content in the active and gasket regions in the dry image. The region of the membrane surrounding the active area (Fig. 6) is not directly exposed to the gas flow, as it is compressed between the polytetraflouroethylene (PTFE) gaskets and the metal plates. During the drying of the membrane (before recording dry images), water is removed from the gasket region via in-plane diffusion. In a dry image of the cell, the membrane in the gasket region directly adjacent to the active area will have a similar residual lambda to the active area. Residual water content under the gasket will increase away from the active area and will remain unchanged in areas close to the outer edges of the compression plates (Fig. 6).
FIG. 5.
The average water content removed in 8 repeat measurements from Nafion membranes during a thermogravimetric analysis simulating the drying conditions with a dry nitrogen purge used in typical neutron imaging experiments. The 1 σ uncertainty is calculated from the standard deviation of the 8 measurements. To determine the dry weight of the Nafion, the chamber was subsequently evacuated (70 kPa vacuum pressure) and the temperature was elevated to 105 °C for 40 h. The initial water content varied with environmental temperature and humidity, but was on average λ = (3.64 ± 0.27) mol H2O/mol .
FIG. 6.
Photograph of the fuel cell hardware for measuring water sorption in Nafion at the NIST neutron imaging facility. Active area (i.e., the membrane region exposed to the humidified gas flow in sorption experiments), denoted by the GDL, is 2.5 cm2, with the width of 12 mm (in the beam direction). The membrane extends across the entire face of the plate and is compressed by the gaskets outside of the active area.
To confirm that all the (physically bound) water had been removed during the drying protocol, an additional TGA experiment was performed using a Netzsch STA-449 thermogravimetric analyzer with a Netzsch Aeolus QMS-403C quadrupole mass spectrometer (QMS) sampling the evolved gas from the TGA instrument through a heated capillary transfer line (250 °C) and heated TGA furnace head assembly (150 °C). The TGA-MS experiment was performed for selected dried samples as follows: the dry samples were heated to 150 °C at 10 °C/min and held isothermal for 7.5 h while the TGA exhaust (purge and balance protective gas UHP N2, ca. 100 ml/min flow rate) of the instrument was sampled by the QMS. The recorded sample weight remained constant during the isothermal segment while the ion-current for water (17 amu and 18 amu) was zero. The sample temperature was ramped to 300 °C at 10 °C/min at the end of the 7.5 h isotherm. No mass change was observed until the membrane started decomposing at a temperature of 220 °C. Commensurate with the weight loss due to membrane decomposition, an increase of water, fluorine, and sulfur dioxide ion currents was recorded by the QMS. While all the physically bound water had been removed prior to the decomposition of the membrane, some portion of the water ion current after the decomposition started may be due to chemically bound water in the dry membrane (corresponding to λ of ~1 mol H2O / mol SO3H).
4. Membrane swelling
As shown by Weber and coworkers, under normal fuel cell assembly, a non-reinforced membrane will be in a mostly free-swelling state in the through-plane direction, and thus one must account for swelling when analyzing the neutron radiographs of the membrane.21,22 There are two artifacts due to membrane swelling. First, the attenuation due to just the “dry” membrane is less when the membrane has absorbed water, thus one would infer less water when the membrane has absorbed water. Second, the membrane protrudes into the GDL, compressing the GDL and so one would infer that this region would have more water than is actually present, as well as reducing the GDL pore volume. The water-sorption measurements discussed below focus solely on the membrane water content and ignore the issue of changes at the membrane/GDL interface. To analyze the impact of swelling, the image of the dry membrane is given by
| (12) |
where ΣPEM = NPEM σPEM is the total macroscopic scattering cross section of the dry membrane; tPEM is the entire thickness of the membrane through which the neutron beam passes; Σw and βw are coefficients to convert the water thickness to OD as discussed in Sec. II C; and tr is the residual water content of the membrane discussed above. The image of the wet membrane is given by
| (13) |
where a “~” superscript indicates dry properties of the swollen Nafion membrane and tw is the additional water thickness that is being measured. The change in neutron attenuation of Nafion due to swelling is only a change in number density. Inside the fuel cell, it is assumed that the in-plane dimensions are fixed, so that the swelling only occurs along the through-plane direction (i.e., the membrane thickness). This is a valid assumption if the membrane is supported (constrained) by the GDLs in the active area and by the gaskets outside of the active area and is not able to wrinkle. To calculate the effect of swelling, we assume that the swelling is linearly proportional to the water content,23 dw/w = η λ. λ is related to the water thickness in the active area via
| (14) |
| (15) |
where and are the partial molar volumes of dry membrane (550 cm3/mol) and water (18 cm3/mol), respectively, and the degree of constraint, χ, is used as in Weber and Newman22 with χ = 0 indicating a free-swelling membrane and χ = 1 indicating a fully constrained membrane (with respect to the dry volume). Equation (15) is a first-order approximation of Eq. (14), which enables obtaining a closed-form expression for the effect of swelling. The accuracy of this polynomial approximation over the range 0 mol H2O / mol SO3H < λ < 26 mol H2O / mol SO3H is improved to ±5% by including a scaling of the second order term, C ≈ 1.6 as opposed to a maximum error of about 20% for λ = 25 mol H2O / mol SO3H without this ad hoc parameter. Using Eq. (15) to write the change in attenuation with respect to the dry state to second order in tw gives
| (16) |
One can estimate the value for η by taking the maximum expansion to be 0.125 under liquid saturation conditions.21 Thus, the effect of membrane swelling is to introduce both a second source of slope change and a change in the quadratic term in the conversion between tw and optical density, so that the linear term is given by
| (17) |
| (18) |
and the water content in the center of the membrane can be obtained by extending the correction due to the residual water, so that
| (19) |
5. Finite resolution
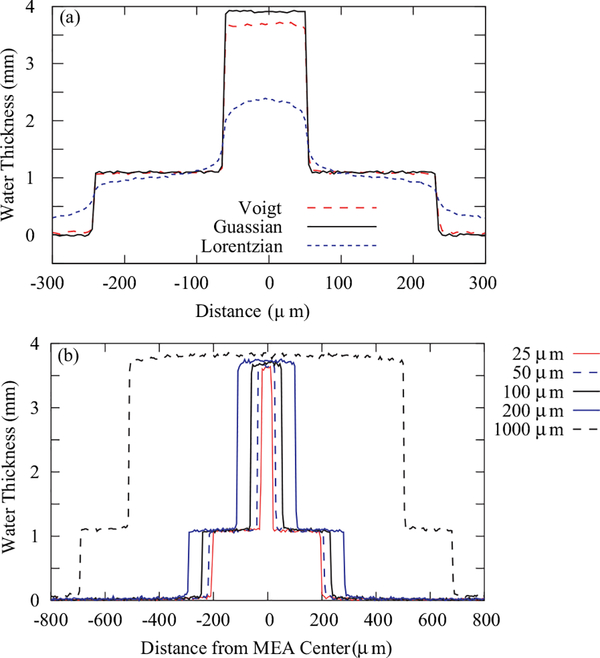
As discussed above, a large source of systematic uncertainty in measuring the through-plane water content is due to the finite image resolution. Further, as shown in Figure 7(a), having the correct PSF model is important to interpret correctly the obtained water content. The main difference is the decay of each PSF; since a Lorentzian decays much more slowly, the inferred water content shows a systematic effect even for very thick membranes; the Gaussian decays rapidly with little effect on the measured membrane water content for a membrane thickness of 10 μm, while the Voigt profile is intermediate. Thus, the PSF impacts the measurement of the water content in two ways. The first effect is that the measured water profile will not contain discontinuous jumps or step-like image features, for instance at the boundary of the catalyst layer and microporous layer (MPL). Rather, an image of a step change will be described as an error function, with the width determined by δi. At the edges of the transition, the neutron transmission significantly deviates from that of the sharp profile. The second effect is lower observed water content in the water profile in the through-plane direction. The size of the deviation depends on the PSF, the thickness of the water along the beam path and the membrane width (shown in Figure 7(b)), as well as the illuminated field of view.16 In determining the water sorption (Sec. III A), only the center section of the image of a thick membrane has been used, so that resolution effects are negligible. In simulating images from model predictions of the water content in Sec. III B, a Voigt profile has been used to model the point spread function of both generations of MCP detectors, the XDL and XS.
FIG. 7.
(a) Effect of the PSF on the measured through-plane water distribution for three PSF models: a Voigt profile, a Lorentzian distribution, and a Gaussian distribution, for the same spatial resolution of 10 μm, as defined by Eq. (1) and including a λg = 3.3 μm. (b) Effect of membrane thickness on the inferred water content due to spatial blurring with a Voigt profile; for a membrane with a thickness comparable to the spatial resolution, there is about a 6% reduction in the water content.
6. In-plane water diffusion
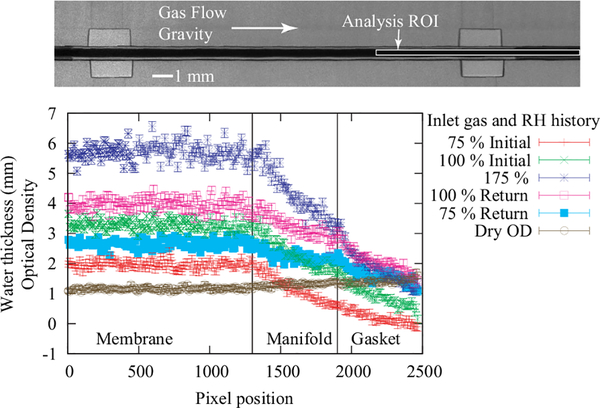
The membrane extended across the entire plate area (Figure 6) for sealing purposes and to help retain the membrane shape (i.e., prevent wrinkling), but this introduced additional consideration in image processing due to in-plane diffusion of water into (or from) the portion of the membrane under the gaskets. Since there is in-plane water diffusion, there is a slow increase in the water content under the gasket regions when the RH increased;24 thus, one infers higher water content from a later image. An order of magnitude estimate for the amount of water that will diffuse under the gaskets can be made by assuming that the water transport is driven by Fickian diffusion. Using Fick’s second law, taking the diffusion coefficient to be Dw = 1.2 × 10−6 cm2 s−1 at λ = 3 mol H2O / mol SO3H,4 a gasket λ = 2 mol H2O / mol SO3H, and an active area λ = 22 mol H2O / mol SO3H, there will be an average increase in the gasket region λ of about 1 mol H2O / mol SO3H (1 mm of water thickness) over the course of 1 h. This is close to what is observed in the change from 100% RH to liquid saturation in the bottom of Figure 8. Rather than relying on a calculated estimate, the water content under the gasket region (as shown in the top of Figure 8) can be measured and the active area water content can be corrected for this increase. Further, at lower humidities, this water flux will be lower; one would also expect to observe a hysteresis and possibly a reversal in the water flux as one lowers the inlet gas humidity, and both of these trends are observed in Figure 8. The gradient due to in-plane water diffusion was also observed in the images of the dry membrane, as the active area (under the GDL) was exposed to the dry nitrogen stream, in contrast to the region under the gaskets. These effects of in-plane diffusion either due to drying or wetting the membrane were evaluated directly from the images and were accounted for when quantifying the water content in the data below.
FIG. 8.
Top, raw image of the test section for a free-swelling membrane, showing the direction of the gas flow and gravity, as well as indicating the region of the membrane used to generate the water profiles shown below. Bottom, membrane water content at 80 °C under a compression pressure of 1.4 MPa compression in a test section composed of metal foam flow fields and the optical density of the dry image from the flat field normalization. The region over which the membrane water content and the gasket water content were measured are indicated (see also Figure 6). During the measurement, the water content increases under the gasket region due to in-plane water diffusion; this must be accounted for when calculating the water content in the active area of the flow field.
7. Neutron scattering and refraction
Since the attenuation of a neutron beam by water is primarily through incoherent scattering rather than absorption, the sample represents a secondary neutron source. The neutrons emanating from the sample radiate in all directions, and the intensity of the beam is reduced as the square of the distance from the sample. As shown in Kim et al.,25 the intensity of this scattered beam from a section of water similar in size to that in a high resolution PEMFC imaging is one to two orders of magnitude smaller than the variation due to Poisson counting statistics and in general correcting the image PSF is a larger correction.16 As a result, no correction for scattering is required for membrane or PEMFC through-plane water-content measurements. In addition, neutron refraction has been reported in cold neutron imaging which can be a source of image artifacts, however it has not been observed in high resolution images acquired at NIST. Refraction increases with neutron wavelength, and thus for a thermal source will be a factor several less than at a cold beam. As well, the PEMFC test sections frequently imaged at the NIST facility are gold coated, and gold has a 98 b absorption cross-section, which further reduces the size of refractive effects. As such, correction for refraction is not considered here.
E. Test sections
To overcome the systematic uncertainty due to spatial resolution, test sections were fabricated using thick Nafion membranes (Ion Power), with nominal thicknesses of 178 μm (N117) and 203 μm (N1110) for the water sorption measurements and 1000 μm (N1140) for the fuel cell and hydrogen-pump experiments. In both test sections, the image of the membrane was confirmed to have a flat region in the center of the dry membrane indicating the spatial resolution was not affecting the measurement. The fuel cell flow field (Figure 6) consisted of parallel channels (0.635 mm by 0.635 mm), with 0.635 mm wide lands machined into Al blocks. After machining, the Al blocks were gold coated to prevent corrosion. The width of the Al block in the beam direction was 27 mm (12 mm active area width and 7.5 mm gasket width on either side of the active area). Sorption experiments employed similar hardware, but with a porous metal foam as a flow field instead of parallel channels. Both designs had the same active area of about 2.5 cm2, where the neutron beam traversed through the 12 mm length (as indicated in Figure 6). The gaskets were a combination of PTFE films and PTFE-coated fiber glass films. In both sets of experiments, GDLs were placed between the flow field and the membrane on either side. The GDL material in all tests was SGL24AA. This GDL is a single layer of carbon fiber and does not contain any PTFE, nor a microporous layer.
The water-sorption measurements were performed with 200 sccm (800 sccm) N2 flow on either side of the test cell for the N117 (N1100) case. Humidity of the gas streams was controlled by the temperature of bubbler-type humidifiers (dew point temperature), and independently monitored and verified by humidity measurement with Vaisala HMT338 RH sensors placed at the cell outlets. For the fuel cell and hydrogen-pump experiments, the MEA was fabricated by painting the Pt-black catalysts (using Nafion binder) onto the N1140 membrane with a Pt areal density of 6 mg/cm2 on both the cathode and anode. The thicker membrane for the operating cell was required for the coarser detector spatial resolution of 30 μm. The operating conditions for the fuel cell tests were 80 °C, 300 sccm H2, 200 sccm O2, inlet-gas relative humidity was 100%, and 71 kPa backpressure on both sides. For the hydrogen-pump tests, the 300 sccm H2 was split and fed to both sides and was over-humidified to 175% relative humidity and the backpressure was again 71 kPa.
III. RESULTS AND DISCUSSION
Corrections for the above systematic measurement uncertainties were not included in early high-resolution neutron-imaging work, likely resulting in underestimates of the membrane water content; in Hickner et al., this is especially important considering that the test section used a 50 μm thick membrane, which was strongly blurred by the image spatial resolution of about 30 μm.5 Two sets of measurements were undertaken: (i) water-sorption measurements to ensure that water-content measurements made via neutron radiography were consistent with gravimetric measurements and (ii) the water profiles measured during fuel cell and hydrogen-pump operation. These data were then analyzed according to the following 10-step procedure:
Background subtract flatfield, dry, and wet images.
Average data along the in-plane direction to yield neutron intensity along the through-plane direction, this reduces the bias due to low count data and produces line profiles.
Form dry optical density by taking the natural logarithm of Eq. (5) with the flatfield as the reference image (I0).
Use the dry optical density to estimate the attenuation of the dry polymer in the gasket region, ΣPEM tPEM.
Form wet OD by taking the natural logarithm of Eq. (5) with the flatfield as the reference image (I0).
Estimate the residual water content in the gasket away from the active area assuming a λres corresponding to ambient temperature and humidity.
Estimate total water content in the gasket region across the entire cell width using Eq. (19) with the parameters specified in Eqs. (17) and (18).
Estimate the residual water content in the active area assuming a λres corresponding to ambient temperature and humidity and reduced by the time dried at 80 °C to estimate the residual water in the membrane using the data in Figure 5.
Estimate total water content in the active area including the surrounding gaskets using Eq. (19) with the parameters specified in Eqs. (17) and (18).
Calculate the absolute water content in the active area only by subtracting the gasket water (step 7, scaled to the width of gaskets adjacent to the active area) from the water content calculated in step 9.
A. In-situ water-sorption measurements
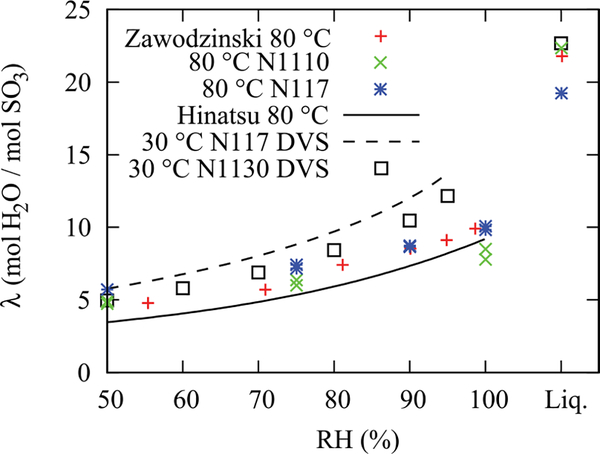
To ensure accurate correlations of the fuel cell data, the water uptake of the thick membranes was also measured using a dynamic-vapor-sorption (DVS) apparatus (SMS, Ltd) at room temperature. The relative humidity was adjusted from dry to wet conditions in 10% steps with 2 h hold times between steps, at which point the change in mass was comparable to the quoted mass sensitivity. To obtain the dry weight, the membrane was dried at 80 °C, and the data were corrected for the residual water content using the results of Figure 5. The membranes were boiled and cleaned before testing. The results are shown in Figure 9 for a 700 μm to 720 μm thick Nafion 1130 membrane (Ion Power), which is similar to the fuel cell tested 1140 membrane. The water uptake is shown to be similar to traditional 1100 equivalent weight Nafion membranes.
FIG. 9.
Water-sorption data for N1110 and N117 restricted membranes at 80 °C compared with historical data (Zawodzinski, et al.1 and Hinatsu et al.24 at 80 °C) and measurements made with DVS at 30 °C using N117 and N1130 membranes. Repeat measurements were performed after liquid equilibration. There is an uncertainty of ±1 λ (mol H2O/mol SO3) due to the applied corrections for residual water content in the active area and under the fuel cell gaskets as well as in-plane water diffusion to under the gasket region.
The in situ water sorption was measured via neutron radiography using the nominal 10 μm spatial resolution MCP detector. To improve neutron-counting statistics, images with a 120 s exposure time were acquired over a period of at least 30 min at each test condition; by acquiring multiple frames, one has the ability to investigate the stability of the test section, and the image download time was small so that additional dead-time losses were minimal. Dry images were acquired initially for a period of 1 h; if image registration artifacts were visible, a dry image was taken at the end of the tests. As well, flatfield images were acquired so that any registration errors due to the change in the optical axis could be corrected through image shifting; a flat field is required since the MCP detector response is not spatially uniform. On average, about 1.5 neutrons were detected per pixel per minute in the flatfield; the transmission through the dry (wet) membrane was about 0.22 (0.11). The membrane water-content profiles shown in Figure 8 were taken over a height of about 3000 pixels, so that the nominal one-sigma Poisson counting statistics relative uncertainty in the dry (fully saturated) images of the membrane was 0.41% (0.58%), corresponding to a water-thickness uncertainty of δtw ~ 10 μm.
To estimate the water content in the membrane, the procedure described in Sec. III was applied to the raw neutron images for all water-sorption data sets shown in Figure 9 with the following specific parameters for these sorption measurements. The gamma-ray background of the detector (dark image) was subtracted from the flatfield, dry, and wet images. The image of the dry membrane was normalized by the flatfield to determine if there was a variation in the membrane water content between the active area and the region under the gasket; a difference of about Dλ ≈ 2 mol H2O / mol SO3H was observed between the exposed membrane region and the region under the gasket far away from the active area. The wet membrane images were then normalized by the dry image, and the neutron attenuation along the in-plane direction was obtained over a region within the membrane that showed a nearly constant through-plane direction attenuation profile. The water content in the gasket region above and below the active area was then obtained by applying Eq. (17) with the assumption of an average residual water content under the gaskets of λ = 2.6 mol H2O / mol SO3H as determined by the ex situ TGA analysis and the transmission profiles of dry images. This water content was then scaled for the length of the gasket region in front of and behind the active area and added to the residual water in the active area of λ = 1.4 molH2O / mol SO3H. The water thickness in the membrane after these corrections is plotted in Figure 8. From the average water thickness, the water content λ is then determined by Eq. (14), with the assumption that the membrane is free-swelling, i.e., χ = 0. To correct for swelling of the membrane in Eqs. (15) and (16), the attenuation of the dry membrane was ΣPEM tPEM = 1.03 ± 0.01.
Shown in Figure 9 are the in situ measurements of the water sorption of a Nafion 117 membrane and a Nafion 1110 membrane restricted by metal-foam flow fields and the GDLs at a temperature of 80 °C. Water values were obtained by averaging the water content in the flat region of the profile and by applying the procedure and corrections described above. As shown in Figure 9, the water content of the restricted membrane at 80 °C matches reasonably well with gravimetric data at 80 °C of Zawodzinski et al.2 and Hinatsu et al.26 The neutron data for a restricted membrane at 40 °C (not shown) also reasonably matched the ex-situ DVS data at 25 °C, where the mass increase of the membrane is measured during 10% relative-humidity steps, which is then normalized to the dry mass and converted to a λ value
| (20) |
where is the dry weight of the ionomer, EW is the equivalent weight of the ionomer (1100 g/mol), and is the molar weight of water (18 g/mol). The primary source of uncertainty is the residual water content under the gaskets and in the active area in the dry image; from the TGA analysis, the estimated one sigma uncertainty in the derived λ is δλ ~ ±1 mol H2O / mol SO3H.
In addition to assuring that the neutron-radiography water-content measurement is in agreement with historic ex situ data, there are two additional observations. The first is that, as expected from calculations in Kusoglu et al.,21 the compression pressure applied in the restricted construction is not sufficient to change the swelling properties of the membrane in the thickness direction. Pressure exerted onto the membrane under compression from the GDLs and the fuel cell hardware was less than 480 kPa, measured by a pressure-indicating film. The second is the observation of Schroeder’s paradox for each temperature, as there are repeat measurements at 100% relative humidity before and after over-humidification. Schroeder’s paradox is the observation that the membrane water content differs at unit activity depending on whether the boundary layer is liquid water or saturated vapor.27 There are multiple reports of observing Schroeder’s paradox in Nafion26,28–30 although there is some current question over the source of these observations.29,31,32 The data in Figure 9 show that the in situ water content indeed goes from a high value at supersaturated or liquid conditions to a lower one with fully saturated vapor; thus it is a positive indication of Schroeder’s paradox. In fact, the values of λ that can be calculated from the data at 80 °C (Eqs. (19) and (20)), demonstrate that one moves from about λ = 10 mol H2O/mol SO3H to 22mol H2O/mol SO3H to 14 mol H2O/mol SO3H during the experiment. This is not surprising since the paradox is linked to the interfacial morphology that is different between liquid and vapor boundaries.33–35
B. Analysis of membrane water profiles during fuel cell and hydrogen-pump operation
Since neutron radiography accurately measures the membrane water sorption, one can have confidence that under fuel cell operation accurate membrane water contents will be obtained by following the above image-analysis procedure. As a demonstration, we examined the through-plane membrane water content under several conditions to build an understanding of water-transport phenomena in the membrane in an operating fuel cell environment. The exact water profile in the membrane under operation remains unknown, requiring the use of models to predict the profile shape; shapes ranging from linear, to sharp transitions, to entirely flat have been used in the literature.28,36–39 In this section, water-content profiles under both fuel cell and hydrogen-pump conditions are analyzed, including comparison to relatively simple models.
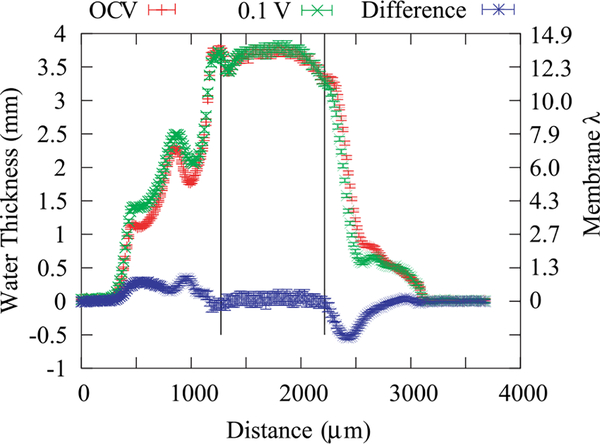
Figure 10 shows the corrected, measured water profiles for the fuel cell at open circuit voltage (OCV) and during operation (0.135 A/cm2). The membrane is thick enough that a clear, flat region is obtained in the center of the membrane. The water content in both cases is calculated to be around a value of λ = 13.7 mol H2O / mol SO3H using Eq. (19) (λ = 9.5 mol H2O / mol SO3H if the membrane were actually fully compressed). This result indicates that the membrane is operating where it is a mixture of liquid and vapor equilibrated. Assuming λ = 22 molH2O / mol SO3H for full liquid equilibration and λ = 11 mol H2O / mol SO3H for vapor at 80 °C (see Figure 9), the membrane is around 35% liquid equilibrated on average along the beam path length. This volume fraction makes sense if the boundary phase controls this behavior,35,40 especially as it is similar to the Nafion volume fraction in the catalyst layers. The observation of such a high λ at OCV also suggests that liquid water condenses in the catalyst-layer ionomer as perhaps a liquid film, even though the feed conditions are only 100% relatively humidity. Even without water production, the membrane exhibits some liquid-equilibrated character, which is not unexpected (see for example, Adachi et al.41), but has not been shown previously in situ. Under fuel cell operation, where water production does occur, the water profile in the membrane remains essentially identical; this is especially apparent when examining the differential plotted in Figure 10. Of course, the current density is low, but the electroosmotic flux and water production change the water levels in the catalyst layers and GDLs, with more water in the cathode and less in the anode. This change in water thickness is in agreement with expected changes in saturation due to the changes in the liquid (and hence capillary) pressure caused mainly by electroosmosis and water production.42 Note that these results are averages and include averaging over both land and channel regions along the through-plane direction.
FIG. 10.
Water content and water-content difference along the through-plane direction of a fuel cell with a Nafion 1140 membrane during OCV and operating at a current density of 0.135 A/cm2 and 0.1V with H2 and O2 gases humidified at 100% RH. The vertical lines denote the boundary between the MEA and the GDLs; the cathode channel and GDL regions range between 500 μm to 1250 μm, the anode channel and GDL regions range between 2250 μm and 3000 μm.
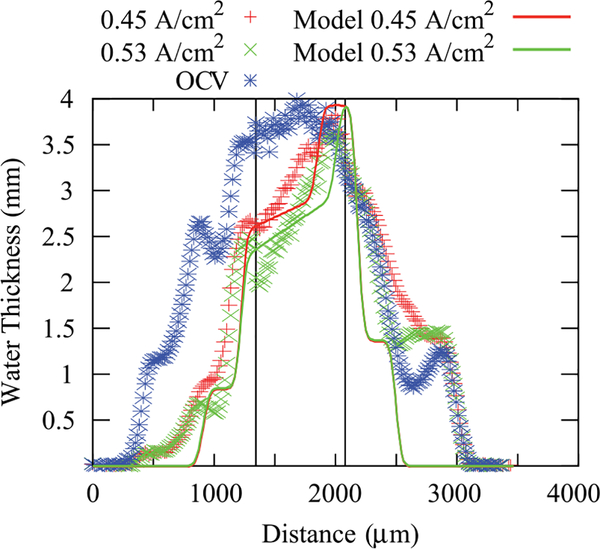
To enable quantification and comparisons of the determined in situ water content, it is more convenient to deal with a simpler system than an operating fuel cell. For this reason, hydrogen-pump experiments, where one can avoid water production and the sluggish oxygen-reduction reaction, were undertaken. The results are shown in Figure 11 for OCV and two different current densities. In Figure 11, the protons are moving from left to right, and thus there is a dehydration of the anode side of the membrane due to electroosmotic flow toward the cathode. The hydrogen pump shows a similar water-content value at OCV as in the fuel cell-model data (Figure 10) even though the feeds are much more humidified. Thus, the extra humidification is not necessarily getting to the membrane and is probably condensing more in the channels, which agrees with the neutron–imaging results. A comparison to Figure 8 also shows that the GDL seems to inhibit this extra water from reaching the membrane, unlike the porous metal foam which is probably more hydrophilic. As current flows, there is a small plateau in the water content and then a linear decrease in the water thickness or volume fraction. The electroosmotic flow is enough to lower the anode GDL saturation under full humidification to levels similar to those observed with sub-saturated gas flows. This is also apparent as the water content in the anode GDL is approaching its residual saturation or percolation threshold.
FIG. 11.
Comparison of the through-plane water content in hydrogen pump mode between model and data at three operating current densities. The model computes only the membrane water content; the measured saturation in the GDL region is included, so that the image simulation yields a more realistic transition between the GDL and the membrane. The vertical lines denote the boundary between the MEA and the GDLs; the anode GDL and channel region ranges from 320 μm to 1360 μm the cathode GDL and channel region ranges from 2240 μm to 3040 μm.
To analyze the above curves, the approach of Weber and coworkers can be followed as discussed in the Appendix,7,28,43 where for the membrane, the maximum amount of liquid-equilibrated mode is scaled using the 0.35 value mentioned above due to interface-in-contact approach. The model is run in a 1-D macrohomogeneous approach such that the effects of the land and channel are averaged, similar to the data collection, and uses measured properties for Nafion 1100 equivalent weight membranes,28 however, as discussed below, the value of the net transport coefficient is altered to fit the data better. The results of the model are compared to the neutron-imaging data in Figure 11. The agreement is reasonable and demonstrates that model and data are converging. For instance, as opposed to the findings in Weber and Hickner where there was a factor of 4 difference between model and data,7 the difference in the maximum membrane water content using the above image analysis is now about 10%. The model contains a transition point that agrees with the flat water profile near the cathode, where more liquid-equilibrated-type conditions occur. The transition between modes is dependent on the current density. In addition, the transition will naturally be sharper in the model than in the data due to blurring as discussed above in the resolution discussion. One might expect the measured data to look more like the model results, although it seems that the transition region within the model is too sharp, and the model has not correctly predicted the slope after the transition region, which is dependent on the balance between the electroosmotic and water-transport coefficients. Therefore, some model refinement is required. The data and the model are consistent in terms of maximum water content, but they do not validate each other. In particular, one might use a linear water-content gradient to fit the data, although this has some issues due to the need for the correct water content and partial pressure at the membrane/anode interface, which is dependent on the nonlinear water-uptake isotherm (Figure 9).
Due to limitations of beam-time availability and small active area, water-balance data were not obtained during the imaging experiment, which limits the quantitative assessment possibilities of the curves. As seen in the Appendix, the water flux is determined to be a balance between back diffusion and electro-osmosis, and only with water balance or similar data can they be decoupled and determined separately. As noted above, the net water transport coefficient, β, is used to describe the balance between the electroosmotic and water-transport fluxes
| (21) |
where Nw is the water flux, i is the current, and F is Faraday’s constant. For both current densities, the curves shown in Figure 11 correspond to β values of about 1.5. As a point of comparison, using traditional Nafion 1100 values, the β value would be closer to 1.2, and the slope after the transition in Figure 11 would be much shallower. Due to the thickness of the membrane, electro-osmosis is more dominant than the water-transport flux (from the simulations above, the water-transport flux results in about 25% change of the net flux). However, the above results are also dependent on the partial pressure of water assumed from the modeling analysis in the anode channel (100% relative humidity is used) as it impacts the dry out of the anode.
Some simple estimates can also be made for the electroosmotic coefficient. Assuming the water transport coefficient is a = 10−9 mol2 J−1 cm−1 s−1, then the curves in Figure 11 would correspond to an electro-osmotic coefficient of 2, instead of the often-used value of 1, which is not too far off considering that the value of the transport coefficient for this membrane is also not known definitively. To determine the limiting case or maximum value that could be obtained from the data, one can ignore the back water transport and then assume that all oversaturated water is consumed in order to reduce the water content at the anode to the vapor-saturated value as the data suggests. Doing this calculation results in a value of ξ = 3.6, which is similar to a fully liquid-equilibrated N117 membrane value at 80 °C (ξ = 3.3).28
IV. CONCLUSIONS
Neutron imaging is an invaluable tool for investigating water transport in operating PEMFCs due to its ability to measure quantitatively the water content and distribution in situ. While low-resolution neutron imaging is useful for cell-level studies such as flow-field optimization and manifold design, fundamental understanding of the through-plane water transport phenomena in the membrane requires well-characterized, high-spatial-resolution measurements. However, there are issues with analyzing such data, and this article discussed the comprehensive characterization of systematic effects and uncertainties associated with high-spatial-resolution neutron imaging. Through proper accounting of systematic measurement effects in the image processing and analysis procedure, neutron radiography yields accurate in situ water-content values of proton-exchange membranes. The approach presented here was verified by investigating water-sorption isotherms, which are in agreement with literature and our own ex situ measurements.
The in situ water-sorption measurements also demonstrated that the measured water content of a restricted membrane at 80 °C matches reasonably well with data previously measured ex situ with free-swelling membranes. Schroeder’s paradox was also verified to exist by in situ water-content measurements which cycled from fully humidified to supersaturated (liquid) and back, where the data exhibted the previously measured, nearly doubling of the water content.
Additional studies of operating cells with thick (180 to 1000 μm) membranes in fuel cell and hydrogen-pump modes were investigated. Comparison of the results to a 1D macrohomogeneous water-transport model demonstrated that we have resolved a previously reported discrepancy between the measured and predicted membrane water content. The 10 μm resolution neutron-imaging detector at NIST provides a means to measure the water uptake of fuel cell membranes in situ and, when combined with water-balance measurements, the membrane’s transport properties during operation. While this work emphasized characterizing the measurement technique and developing the image-processing procedure for accurate water measurement with neutron imaging, a future publication will focus on particular aspects of membrane’s water uptake, such as the influence of compression and thermal history.
ACKNOWLEDGMENTS
The authors would like to thank Mr. Kyle Clark and Dr. Ahmet Kusoglu for their help in providing the water-uptake isotherms. They also would like to thank Dr. Stephen Grot of Ion Power for generating the extra-thick Nafion membranes and Mr. Eli Baltic of NIST for assistance with performing the neutron-imaging experiments. We thank Nuvera Fuel Cells for providing the metal-foam flow fields used in the sorption measurements. The Los Alamos team gratefully acknowledges the support of the technology development manager Nancy Garland, and funding from the US Department of Energy, the Office of Energy Efficiency and Renewable Energy, Office of Fuel Cell Technologies. D. S. Hussey and D. L. Jacobson acknowledge support from the U.S. Department of Commerce, the NIST Ionizing Radiation Division, the Director’s office of NIST, the NIST Center for Neutron Research, and the Department of Energy interagency Agreement No. DE_AI01-01EE50660. A. Z. Weber acknowledges support from EERE OFCT under Contract DE-AC02-05CH11231.
APPENDIX: 1-D MODEL DESCRIPTION
For modeling the water profiles, a simple 1D approach is taken. The governing transport equation of water in the membrane is
| (A1) |
where Nw is the flux of water, ξ is the electroosmotic coefficient, F is Faraday’s constant, i is the current density, α is the water transport coefficient, and μw is the water chemical potential. Since there is no water production in the cell for the hydrogen pump,
| (A2) |
for all layers. The transport equations for the water in the gas and liquid phases in the other layers are Stefan-Maxwell diffusion and Darcy’s law, respectively. For the two-phase-flow effects, the contact-angle-distribution approach is used with measured capillary pressure—saturation relationships.44 To convert the water saturations in the model to water thickness in the membrane, the equations discussed in Weber and Hickner7 are used, where the total water-volume fractions are multiplied by the active width of the cell along the beam direction (12.2 mm) to convert them into water thicknesses.
The boundary condition used is a Dankwertz-Wehner-Wilhelm, which is essentially a mass balance for water and hydrogen,
| (A3) |
| (A4) |
respectively, where the superscripts denote water in the gas and liquid phases and into and out of the cell. Similar equations can be written for the cathode gas channel. With the above mass balances, the water partial pressure can be calculated in each element and each gas channel by
| (A5) |
This equation can return values of the water partial pressure that are above the vapor pressure of water due to the presence of liquid water, and thus the results of the equation have to be bounded such that if it returns a value greater than the vapor pressure, the value of the vapor pressure is used. However, it must be noted that for the oversaturated conditions, the exact water partial pressure to be used is somewhat ill-defined and this makes quantitative analysis of the results challenging. It may be that a relative humidity around 100% should be used, especially considering that the hydrogen-pump and fuel cell-mode water profiles at OCV are similar.
References
- 1.Zawodzinski TA, Davey J, Valerio J, and Gottesfeld S, Electrochim. Acta 40(3), 297–302 (1995). [Google Scholar]
- 2.Zawodzinski TA, Springer TE, Uribe F, and Gottesfeld S, Solid State Ion. 60(1–3), 199–211 (1993). [Google Scholar]
- 3.Springer TE, Zawodzinski TA, and Gottesfeld S, J. Electrochem. Soc 138(8), 2334–2342 (1991). [Google Scholar]
- 4.Zawodzinski TA, Neeman M, Sillerud LO, and Gottesfeld S, J. Phys. Chem 95(15), 6040–6044 (1991). [Google Scholar]
- 5.Hickner MA, Siegel NP, Chen KS, Hussey DS, Jacobson DL and Arif M, J. Electrochem. Soc 155(4), B427–B434 (2008). [Google Scholar]
- 6.Hussey DS, Jacobson DL, Arif M, Owejan JP, Gagliardo JJ, and Trabold TA, J. Power Sources 172, 225–228 (2007). [Google Scholar]
- 7.Weber AZ and Hickner MA, Electrochim. Acta 53(26), 7668–7674 (2008). [Google Scholar]
- 8.Yun W and Chen KS, J. Electrochem. Soc 157(12), B1878–B1886 (2010). [Google Scholar]
- 9.Certain trade names and company products are mentioned in the text or identified in an illustration in order to adequately specify the experimental procedure and equipment used. In no case does such identification imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the products are necessarily the best available for the purpose.
- 10.Boillat P, Frei G, Lehmann EH, Scherer GG, and Wokaun A, Electrochem. Solid State Lett 13(3), B25–B27 (2010). [Google Scholar]
- 11.Kardjilov N, Hilger A, Manke I, Strobl M, Dawson M, Williams S, and Banhart J, Nucl. Instrum. Methods in Phys. Res. A 651(1), 47–52 (2011). [Google Scholar]
- 12.Vallerga J, Raffanti R, Tremsin A, Siegmund O, McPhate J, and Varner G, Proc. SPIE 7732, 773203 (2010). [Google Scholar]
- 13.Siegmund OHW, Vallerga JV, Tremsin AS, and Feller WB, IEEE Trans. Nucl. Sci 56(3), 1203–1209 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Siegmund OHW, Vallerga JV, Martin A, Feller B, Arif M, Hussey DS, and Jacobson DL, Nucl. Instrum. Methods Phys. Res. A 579(1), 188–191 (2007). [Google Scholar]
- 15.Siegmund OH, Vallerga JV, Tremsin AS, McPhate J, and Feller B, Nucl. Instrum. Methods Phys. Res. A 576(1), 178–182 (2007). [Google Scholar]
- 16.Hussey DS, Baltic E, Coakley KJ, and Jacobson DL, “Improving quantitative neutron radiography through image restoration,” Nucl. Instrum. Methods Phy. Res. A (submitted). [Google Scholar]
- 17.Edura Y and Morishima N, Nucl. Instrum. Methods Phys. Res. A 534(3), 531–543 (2004). [Google Scholar]
- 18.Hussey DS, Jacobson DL, Arif M, Coakley KJ, and Vecchia DF, J. Fuel Cell Sci. Technol 7(2), 021024–1–021024–6 (2010). [Google Scholar]
- 19.Barrett HH and Swindell W, Radiological imaging. The Theory of Image Formation, Detection and Processing (1981), Vol. 2, pp. 370–377. [Google Scholar]
- 20.Hussey DS, Jacobson DL, and Baltic E, Nucl. Instrum. Methods Phys. Res. A 651, 73–76 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kusoglu A, Kienitz BL and Weber AZ, J. Electrochem. Soc 158(12), B1504–B1514 (2011). [Google Scholar]
- 22.Weber AZ and Newman J, AIChE J. 50(12), 3215–3226 (2004). [Google Scholar]
- 23.Termonia Y, Polymer 48(5), 1435–1440 (2007). [Google Scholar]
- 24.Ludlow DJ, Calebrese CM, Yu SH, Dannehy CS, Jacobson DL, Hussey DS, Arif M, Jensen MK, and Eisman GA, J. Power Sources 162(1), 271–278 (2006). [Google Scholar]
- 25.Kim F, Penumadu D, and Hussey DS, J. Geotech. Geoenviron. Eng 138, 147–154 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hinatsu JT, Mizuhata M, and Takenaka H, J. Electrochem. Soc 141(6), 1493–1498 (1994). [Google Scholar]
- 27.von Schroeder P, Z. Phys. Chem 45(1), 75–117 (1903). [Google Scholar]
- 28.Weber AZ and Newman J, J. Electrochem. Soc 151(2), 311–325 (2004). [Google Scholar]
- 29.Onishi LM, Prausnitz JM, and Newman J, J. Phys. Chem. B 111, 10166–10173 (2007). [DOI] [PubMed] [Google Scholar]
- 30.Choi P and Datta R, J. Electrochem. Soc 150(12), E601–E607 (2003). [Google Scholar]
- 31.Cornet N, Gebel G, and de Geyer A, J. Phys IV 8(P5), 63–68 (1998). [Google Scholar]
- 32.Jeck S, Scharfer P, and Kind M, J. Membr. Sci 337(1–2), 291–296 (2009). [Google Scholar]
- 33.Freger V, J. Phys. Chem. B 113(1), 24–36 (2009). [DOI] [PubMed] [Google Scholar]
- 34.Bass M, Berman A, Singh A, Konovalov O, and Freger V, J. Phys. Chem. B 114(11), 3784–3790 (2010). [DOI] [PubMed] [Google Scholar]
- 35.Kusoglu A, Modestino MA, Hexemer A, Segalman RA, and Weber AZ, ACS Macro Lett. 1(1), 33–36 (2012). [DOI] [PubMed] [Google Scholar]
- 36.Weber AZ and Newman J, in Advances in Fuel Cells, edited by Kreuer K-D and Nguyen TV (2007), Vol. 1. [Google Scholar]
- 37.Wang CY, Chem. Rev 104(10), 4727–4765 (2004). [DOI] [PubMed] [Google Scholar]
- 38.Zhao Q, Majsztrik P, and Benziger J, J. Phys. Chem. B 115(12), 2717–2727 (2011). [DOI] [PubMed] [Google Scholar]
- 39.Weber AZ and Newman J, Chem. Rev 104(10), 4679–4726 (2004). [DOI] [PubMed] [Google Scholar]
- 40.Bass M, Berman A, Singh A, Konovalov O, and Freger V, Macromolecules 44(8), 2893–2899 (2011). [Google Scholar]
- 41.Adachi M, Navessin T, Xie Z, Frisken B, and Holdcroft S, J. Electrochem. Soc 156(6), B782–B790 (2009). [Google Scholar]
- 42.Gostick JT, Ioannidis MA, Fowler MW, and Pritzker MD, in Modern Aspects of Electrochemistry, edited by Pasaogullari U and Wang CY (Springer, New York, 2009), Vol. 45, pp. 225–254. [Google Scholar]
- 43.Weber AZ and Newman J, J. Electrochem. Soc 151(2), A326–A339 (2004). [Google Scholar]
- 44.Weber AZ, J. Power Sources 195, 5292–5304 (2010). [Google Scholar]