Continuous real-time prediction of surgical case duration using a modular artificial neural network

Abstract

Background

Real-time prediction of surgical duration can inform perioperative decisions and reduce surgical costs. We developed a machine learning approach that continuously incorporates preoperative and intraoperative information for forecasting surgical duration.

Methods

Preoperative (e.g. procedure name) and intraoperative (e.g. medications and vital signs) variables were retrieved from anaesthetic records of surgeries performed between March 1, 2019 and October 31, 2019. A modular artificial neural network was developed and compared with a Bayesian approach and the scheduled surgical duration. Continuous ranked probability score (CRPS) was used as a measure of time error to assess model accuracy. For evaluating clinical performance, accuracy for each approach was assessed in identifying cases that ran beyond 15:00 (commonly scheduled end of shift), thus identifying opportunities to avoid overtime labour costs.

Results

The analysis included 70 826 cases performed at eight hospitals. The modular artificial neural network had the lowest time error (CRPS: mean=13.8; standard deviation=35.4 min), which was significantly better (mean difference=6.4 min [95% confidence interval: 6.3–6.5]; P<0.001) than the Bayesian approach. The modular artificial neural network also had the highest accuracy in identifying operating theatres that would overrun 15:00 (accuracy at 1 h prior=89%) compared with the Bayesian approach (80%) and a naïve approach using the scheduled duration (78%).

Conclusions

A real-time neural network model using preoperative and intraoperative data had significantly better performance than a Bayesian approach or scheduled duration, offering opportunities to avoid overtime labour costs and reduce the cost of surgery by providing superior real-time information for perioperative decision support.

Editor's key points.

• •Methods to predict procedure duration could inform perioperative decisions, increase operating efficiency, and reduce staffing costs.
• •The authors developed a machine learning approach that continuously incorporates preoperative and intraoperative information to forecast surgical duration.
• •Using data from 70 826 cases from eight hospitals, a modular artificial neural network outperformed a Bayesian approach and the scheduled duration in predicting surgical end time.
• •A real-time neural network model using preoperative and intraoperative data for real-time perioperative decision support may help to avoid overtime labour costs and reduce costs of surgery.

Staffing and utilising operating theatres (OTs) incur considerable costs, and stakeholders are invested in maximising efficient use of perioperative resources.1, 2, 3 Preoperative planning is frequently complicated by uncertainty in surgical case duration.^4,5 Similarly, operational decisions on the day of surgery are often guided by subjective perceptions regarding the remaining duration of an ongoing surgery. For example, an OT manager may estimate the remaining time on a case in the early afternoon to make decisions regarding the assignment of on-call staff,^6,7 scheduling an add-on case,⁸ or opening an additional OT.⁹ Typical approaches, such as calling into the OT and reviewing the intraoperative record, are confounded by bias^10,11 and distract from clinical responsibilities. Inaccurate prediction of surgical case duration contributes to increased costs of surgery,^1,4 longer working hours leading to staff dissatisfaction and attrition,¹² fatigue and medical errors,^13,14 and increased patient wait times.⁴ These challenges underscore a need for improved methods of predicting surgical duration in real time.

Machine learning (ML) is a promising strategy for addressing this problem. ML techniques and other advanced statistical techniques have been used successfully to predict surgical case duration in various settings.15, 16, 17, 18, 19 However, previous studies have exclusively relied on preoperative variables and have not incorporated intraoperative data, such as the timing of critical events or medications. As such, previous models are of limited value for day-of-surgery operational decision-making, when decisions are typically required after a procedure has already started. Furthermore, most ML studies were based on single academic hospitals, without validation in alternate datasets, such as community hospitals with low operative volume.

We present a novel approach for real-time prediction of surgical case duration by continuously incorporating preoperative and intraoperative characteristics, including vital signs, medications, and intraoperative events. We had the following three research objectives: (i) develop and validate a real-time surgical case duration algorithm using global measures of accuracy, (ii) evaluate the feasibility of the model for informing operational decisions, and (iii) evaluate the transferability of the model in an external dataset.

Methods

Study setting and data sources

Data for this study included anaesthesia records from eight hospitals within the BJC HealthCare System (St Louis, MO, USA). This data set incorporates a heterogeneous surgical population, including urban and rural hospitals, academic and community centres, and various surgical specialties.

The institutional review board (IRB) of Washington University (St Louis, MO, USA) approved this study with a waiver of patient consent (IRB #201910015). The model development adhered to the Transparent Reporting of a Multivariable Prediction Model for Individual Prognosis or Diagnosis guidelines.²⁰

Variable definitions and feature extraction

Anaesthesia records stored in the Epic (Verona, WI, USA) electronic health record of eight hospitals between March 1, 2019 and October 31, 2019 were extracted. The target outcome variable was total anaesthesia time, defined as the difference between anaesthesia start and stop times. Surgeries were scheduled with a specified case start and end time. The difference between these times (hereafter ‘scheduled duration’) was extracted as a continuous variable. All extracted anaesthesia records were included in this study, except those with missing scheduled duration. Other missing variables were imputed as described in the following sections.

Several categorical predictor variables were extracted: surgeon name, anaesthesiologist name, procedure location, procedure urgency, and whether a case was the last elective case for its respective surgeon (hereafter ‘last case’). Procedure location referred to the specific anaesthetising location (e.g. ‘hospital A main OT’). The scheduled procedure(s) (hereafter ‘procedure name’) was/were extracted as free text.

Each intraoperative feature in this study was extracted with both the time of occurrence and the time of documentation. Expired sevoflurane/desflurane/nitrous oxide concentrations, inspired oxygen concentration, bispectral index, and HR were extracted as continuous variables. All intraoperative events (e.g. ‘induction’ and ‘tourniquet up’) were extracted as categorical variables. Medication name and actions (e.g. ‘given’ and ‘rate change’) were extracted as categorical variables.

Variable transformation and imputation

Scheduled duration and actual duration were normalised to have a standard deviation (sd) of 1. Continuous intraoperative data were normalised to have an sd of 1. Missing continuous intraoperative data were encoded as –1 to allow models to distinguish between missing values and those with measured values of 0. Missing categorical variables were assigned as ‘unknown’. Missing procedure names were imputed with an empty string.

Model development

Cases from March 1, 2019 to September 30, 2019 were used to train all models (hereafter ‘training data set’); cases from October 1, 2019 to October 31, 2019 were used to evaluate model efficacy (hereafter ‘test data set’). Cases from one community hospital were sequestered and used as a holdout data set (hereafter ‘holdout training’ and ‘holdout test data sets’) to evaluate model transferability.

To simulate intraoperative predictions, an elapsed time was chosen between anaesthesia start and stop times. All data that were documented after the elapsed time were masked from the models during training and testing.

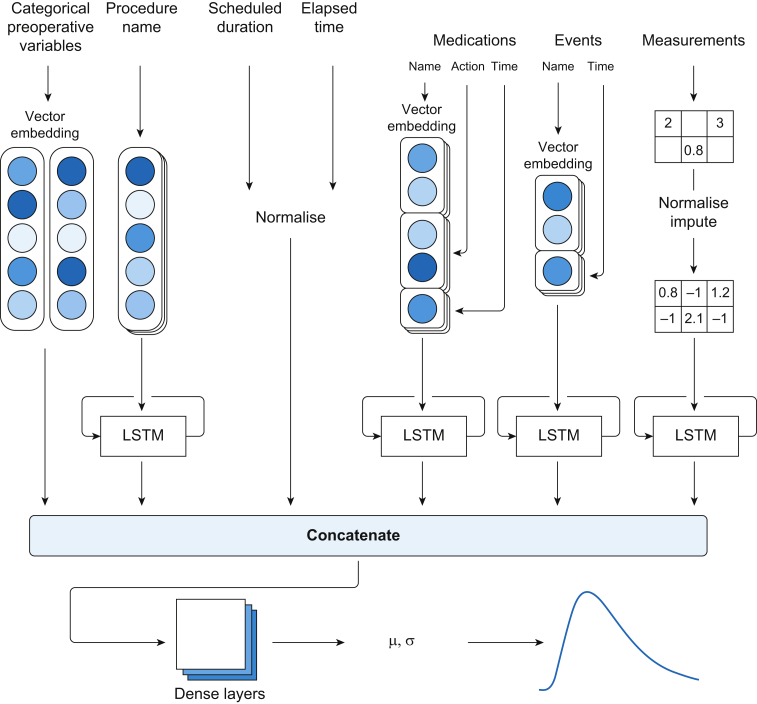
A modular artificial neural network (MANN) architecture was developed to account for preoperative and intraoperative variables (Fig. 1). A vector embedding layer was used for all categorical variables. Time series features were treated with long short-term memory units and then concatenated with static features before being treated with a dense multilayer perceptron. The model outputs were parameters of a log-normal distribution, with negative log likelihood of the actual duration as loss function. Models were trained by repeated random sampling of training case and elapsed time.

Fig 1.

Architecture of modular artificial neural network. LSTM, long-short term memory.

As a baseline, we implemented a previously described statistical method that used Bayes theorem to make updated intraoperative predictions conditional on elapsed time^19,21 (hereafter ‘Bayesian approach’). This approach produces probability distributions of surgical duration from a weighted combination of historical data and scheduled duration. In the originally described method, further information was retrieved from OT providers regarding their expectations of remaining time for an ongoing surgery, to update predictions. This aspect of ‘direct’ information from OTs could not be replicated because of the retrospective nature of this study. However, as a surrogate measure, the Bayesian approach was modified to update its expected remaining time after the following two intraoperative events: (i) reversal of neuromuscular block and (ii) procedure completion (see additional details in Supplementary Appendix A).

Model accuracy

The global accuracy of each technique was quantified using continuous ranked probabilistic score (CRPS), a generalised form of absolute error for probabilistic forecasts of deterministic outcomes.²² We have previously used CRPS to measure performance in prediction of surgical case duration.¹⁶ Continuous ranked probabilistic score has two qualities that make it an intuitive measure of ‘time error’. First, it is measured in units of minutes and has a minimum (i.e. optimal) score of 0. Second, it can be measured for any forecast with a known cumulative probability distribution, including deterministic predictions, for which it simplifies to absolute error. This allows direct comparison of the probabilistic approaches developed in this study with the scheduled duration. Continuous ranked probabilistic score was calculated at each fifth percentage (e.g. 5%, 10%, and 15%) of total anaesthesia time for each case in the test data set and is reported with a mean and sd (see additional details in Supplementary Appendix B). A paired t-test was used to compare the performance of MANN and the Bayesian approach.

Identification of impending staff overtime

We also evaluated the performance of MANN in a clinical scenario to ascertain its viability for predicting impending staff overtime. Perioperative departments commonly employ contractual workers, such as certified registered nurse anaesthetists (CRNAs) who incur additional productivity costs when working beyond a predetermined time (CRNA shifts commonly end at 15:00 or 17:00). Frequently, attempts are made to identify rooms likely to overrun a scheduled shift end time, so alternative staff can be identified to relieve them, thus improving CRNA satisfaction and avoiding overtime costs.

In this scenario, we compared three approaches to discern whether an ongoing case would continue beyond 15:00 (i.e. the contractual end time), using data available at 11:00, 12:00, 13:00, and 14:00 (i.e. the various decision times). For MANN and the Bayesian approach, which output a probability distribution, the time represented by the 50% cumulative distribution function was used to predict whether the case would exceed the contractual end time. We devised a naïve approach to approximate staff management in the considered OTs, without advanced decision support. In this approach, scheduled stop time (actual start time+scheduled duration) was used to make predictions, until neuromuscular block or the ‘procedure finish’ event occurred. After these events, the case was predicted to end before the contractual end time, irrespective of the scheduled duration.

The sensitivity and specificity of each approach are reported along with their 95% confidence intervals (CIs). This analysis was repeated with a contractual end time of 17:00 for sensitivity analysis. A post hoc analysis was also performed to assess potential cost savings.

Model transferability to an external data set

A holdout data set was created and comprised cases from the main OT of a community hospital, which was chosen because of its relatively low case volume and physical distance (∼25 miles) from the primary academic centre. The holdout training dataset was used to (i) retrain select layers of MANN (hereafter ‘transfer-MANN’) and (ii) train a new MANN with the same model architecture (hereafter ‘isolated-MANN’). We refer to the MANN trained in the previous section as the ‘base-MANN’. Details of the transfer learning process can be found in Supplementary Appendix A. The Bayesian approach used in this section utilised data from both the main training data set and holdout training data set. Continuous ranked probability score was calculated for the three ML models and the Bayesian approach. This evaluation was repeated at two different community hospitals for sensitivity analysis.

Results

General characteristics

A total of 79 752 anaesthesia records were retrieved. Scheduled duration was missing in 8926 cases, and these were excluded. Of these excluded cases, 2683 (30%) were labour epidurals. The remaining 6243 (70%) were anaesthetics performed for non-surgical procedures (e.g. electroconvulsive therapy). The primary training dataset consisted of 59 926 cases, whilst the holdout training data set consisted of 1554 cases. The primary test data set consisted of 9092 cases, whilst the holdout test data set consisted of 254 cases. The test dataset contained 4751 procedures that were not performed in the training data set. A summary of patient and surgical characteristics can be found in Table 1 (see Supplementary Appendix D for common procedure names).

Table 1.

Patient and surgery characteristics.

	Main training data set	Main test data set	Holdout train	Holdout test
Number of cases	59 926	9092	1554	254
Mean scheduled duration (min)	125.64	128.06	90.79	89.49
Mean actual duration (min)	119.53	121.65	82.21	80.31
Unique procedure names	30 624	5655	1072	214
Number of procedures performed only once	27 410	5058	978	201
Unique surgeons	803	536	72	48
Unique anaesthetising locations	37	32	1	1
Elective cases (%)	54 914 (92)	7991 (88)	1306 (84)	218 (86)
Last cases (%)	38 079 (64)	5801 (64)	843 (54)	134 (53)
Service
Gastroenterology	16 075	2424	1	0
Orthopaedic surgery	9886	1514	648	106
Ophthalmology	4649	715	0	0
General surgery	4355	678	351	56
Otolaryngology	4082	579	0	0
Urology	3289	496	115	17
Obstetrics/gynaecology	3107	476	344	53
Cardiothoracic surgery	2651	383	0	0
Neurosurgery	2123	360	0	0
Plastic surgery	2068	306	21	1
Vascular surgery	1340	204	1	0
Trauma surgery	1104	180	0	0
Transplant surgery	558	95	0	0
Other	4639	682	73	21

Model accuracy

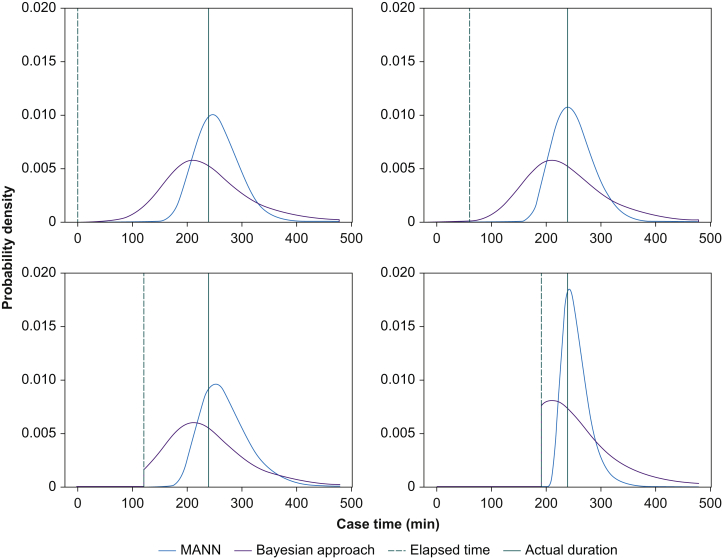
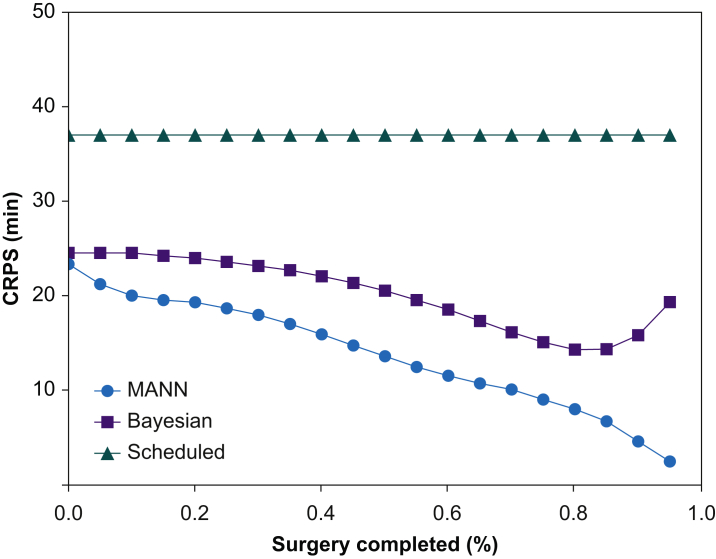
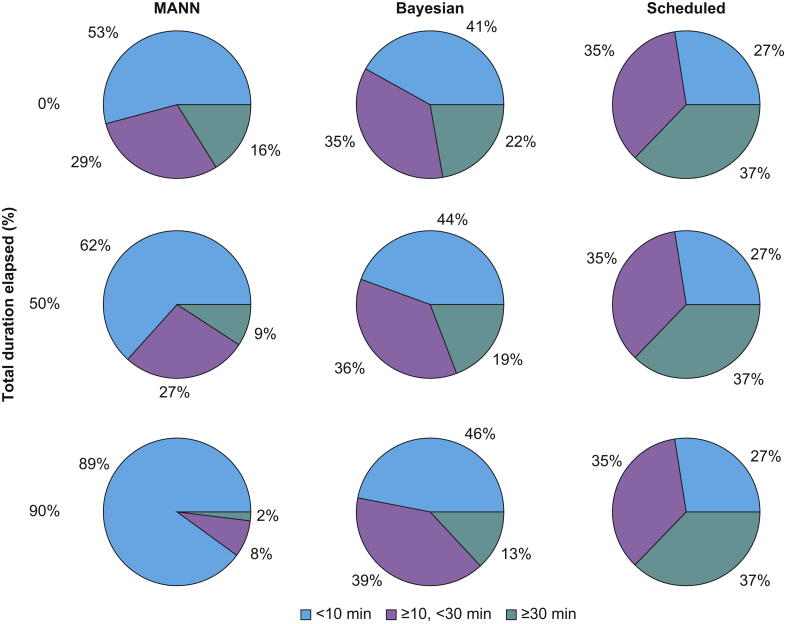
Sample model outputs are shown in Figure 2. MANN had the lowest mean (sd) CRPS across all time points at 13.8 (35.4) min. The Bayesian approach and the scheduled duration had a mean CRPS of 20.3 (40.3) min and 37.0 (77.3) min, respectively. MANN outperformed the Bayesian approach on average by 6.4 min (95% CI [6.3–6.5]; P<0.001) (Fig. 3). The mean CRPS at the beginning of surgery was 23.6 (72.3) min for the MANN vs 24.6 (64.5) min for the Bayesian approach (mean difference [MD]=1.23 min; 95% CI: 0.7–1.8; P<0.001). At the midpoint of surgery, mean CRPS was 13.6 (25.0) min for MANN and 20.5 (29.4) min for the Bayesian approach (MD=6.9 min; 95% CI: 6.5–7.3; P<0.001). After 90% of the surgery had elapsed, the CRPS was 4.63 (11.4) min for MANN and 15.8 (22.8) min for the Bayesian approach (MD=11.2 min; 95% CI: 10.8–11.5; P<0.001). The majority of the predictions of MANN had CRPS <10 min (Fig. 4).

Fig 2.

Sample model outputs. Procedure name: ‘INSERTION BILATERAL TISSUE EXPANDER AND PLACEMENT OF BILATERAL ALLODERM (Bilateral); BILATERAL MASTECTOMY SIMPLE SKIN NIPPLE SPARING W/ RECON (PROPHYLACTIC) (Bilateral Breast)’. MANN, modular artificial neural network.

Fig 3.

Time error of different approaches to predicting surgical duration. CRPS, continuous ranked probability score; MANN, modular artificial neural network.

Fig 4.

Performance of predictive models binned by time error (continuous ranked probability score) and percentage of total surgical duration elapsed. Number of cases in each bin is expressed as a percentage of the total 9092 cases in the test data set. MANN, modular artificial neural network.

Identification of impending staff overtime

MANN was the best-performing approach for all decision times (Table 2). At a decision time of 11:00 (4 h from contractual end time), MANN had a marginal advantage (93% accuracy) over the Bayesian approach (91%) and naïve approach (91%). This advantage increased as the decision time neared the contractual end time (15:00). At a decision time of 14:00, MANN had a considerable advantage in terms of accuracy (89%) over the Bayesian (80%) and naïve (78%) approaches. At this decision time, MANN had a sensitivity of 88.8% (95% CI: 86.7–90.8%) and a specificity of 89.8% (95% CI: 87.5–91.8%), the Bayesian approach had a sensitivity of 87.5% (95% CI: 85.2–89.5%) and a specificity of 69.9% (95% CI: 66.5–73.1%), and the naïve approach had a sensitivity of 77.4% (95% CI: 74.6–80.0%) and a specificity of 79.5% (95% CI: 76.5–82.3%). Repeating the analysis for a contractual end time of 17:00 yielded similar results (see Supplementary Appendix C).

Table 2.

Accuracy at identifying whether ongoing cases will finish by 15:00. MANN, modular artificial neural network.

Model	True positive	True negative	False positive	False negative	Sensitivity (%)	Specificity (%)	Precision (%)	Accuracy (%)
Prediction time: 11:00
MANN	156	1711	25	114	57.78	98.56	86.19	93.07
Bayesian	140	1682	54	130	51.85	96.89	72.16	90.83
Naïve	152	1672	64	118	56.30	96.31	70.37	90.93
Prediction time: 12:00
MANN	250	1464	48	121	67.39	96.83	83.89	91.02
Bayesian	216	1427	85	155	58.22	94.38	71.76	87.25
naïve	225	1404	108	146	60.65	92.86	67.57	86.51
Prediction time: 13:00
MANN	447	1126	71	147	75.25	94.07	86.29	87.83
Bayesian	422	1062	135	172	71.04	88.72	75.76	82.86
naïve	413	1037	160	181	69.53	86.63	72.08	80.96
Prediction time: 14:00
MANN	853	698	79	107	88.85	89.83	91.52	89.29
Bayesian	840	543	234	120	87.50	69.88	78.21	79.62
naïve	743	618	159	217	77.40	79.54	82.37	78.35

Cost analysis

A post hoc analysis was performed to estimate potential cost savings. In the test data set, 1709 cases were running at 14:00 and 960 cases ran past 15:00. MANN correctly identified 110 more cases that would run past the contractual end time (true positives) than the naïve approach; these cases, on average, ran 154 (sd 298) min past 15:00. For accurate predictions to result in cost savings, a clinician assigned to a case must be at risk to accrue overtime costs by the contractual end time, and an alternate clinician with a later contractual end time or with a lower cost must be available. These conditions will only be true in a fraction of the cases, and circumstances of these cases will vary across institutions.

If 10% of additional true positives lead to an intraoperative provider handoff that avoids overtime pay, then overtime pay will be avoided in 11 cases. If an additional assumption is made that the original clinician will finish the case if not relieved, then 28.2 h of overtime pay will have been avoided. Repeating this analysis for the Bayesian method yields 24.9 h of overtime avoided. Additionally, the Bayesian approach produced 155 additional false positives in the test data set compared with MANN, which may motivate many unnecessary handoffs.

Model transferability to external data set

The transfer-MANN had the lowest time error in the first quartile (CRPS 10.4 min) and last quartile of surgery (CRPS 2.8 min). The isolated-MANN had poor performance in the first quartile (CRPS 13.5 min) and excellent performance in the last quartile (3.2 min). Compared with MANN, the Bayesian approach had modest performance in the first quartile of surgery (CRPS 12.8 min) and poor performance in the last quartile (CRPS 13.1 min). Overall, the transfer-MANN had a CRPS 1.8 min lower than the isolated-MANN (95% CI: 1.6–2.0; P<0.001). The performance benefit was statistically significant for all four quartiles of surgery. Repeating this analysis with two alternate community hospitals yielded similar results (Supplementary Appendix C).

Discussion

We developed a ML-based MANN model that incorporated preoperative and intraoperative data to provide real-time predictions regarding remaining surgical duration. MANN performed significantly better than the Bayesian model on all considered evaluation metrics. This advantage was modest at the beginning of surgery, consistent throughout surgery, and increased dramatically during the last quartile of surgery time. This is likely because of the preponderance of data in the intraoperative anaesthesia record that signal the impending conclusion of a procedure, such as administration of reversal medications, emergence events (e.g. extubation), and changes in vital signs. Conversely, in many surgeries, there is a dearth of information in the anaesthesia record that encodes progress during surgery, which may explain why the advantage of MANN over the Bayesian approach remains roughly constant between 25% and 75% of the total surgery duration.

The performance of MANN was also better than that of the Bayesian approach in a simulated clinical scenario directly related to operational decision-making. Because of the heterogeneity of the data set, there were a high number of cases with no historical data. This may explain the marginal improvement of the Bayesian method over the naïve method, as both methods relied on scheduled duration in the absence of historical data. Furthermore, traditional statistical techniques are frequently limited by their inability to incorporate complex and often incomplete data, such as intraoperative time series variables. MANN, by leveraging the strengths of ML, could simultaneously account for all intraoperative events, medications, and vital signs, resulting in superior accuracy.

Improved accuracy also has cost implications. A post hoc analysis showed that MANN would avoid more overtime pay than the Bayesian method, whilst correspondingly requiring fewer unnecessary intraoperative handoffs, a patient safety risk.²³ This analysis does not include potential savings from other common decision times, such as 17:00, and many other potential use cases, such as efficient allocation of add-on cases to OTs or efficient assignment of on-call staff.

We also demonstrated the generalisability and transferability of the MANN methodology. The isolated-MANN had excellent performance at the end of surgery, but it had poor performance at the beginning. This is likely because of insufficient data to learn uncommon and rare procedure types but sufficient examples of common events that signal the end of surgery. Further tuning the base-MANN on the holdout training dataset produced the best results at all time points during surgery, suggesting that hospitals with operative volume too low to train an accurate MANN can still benefit from ML-driven surgical duration prediction by fine tuning a model trained predominantly at large nearby healthcare systems.

This study had several limitations. This was a retrospective study, and continued innovation and exploration will be required to transition to a prospective model that can be implemented in a real-world environment. There are other non-ML statistical approaches for predicting surgical duration with potentially better performance. Our post hoc analysis greatly simplified the process of operationalising this technology and made assumptions that may not apply to other medical centres. It also does not address the potential downsides of additional patient handoffs.

These limitations highlight the need for subsequent work. Many technical challenges must be addressed to implement the proposed ML model, including establishing a real-time data pipeline and designing a rational platform on which clinicians can view the results of the model and consider suggested actions. In addition, our results suggest the lack of meaningful information in the anaesthesia record between 25% and 75% of the total duration of surgery. Strategies to bridge this gap include developing more sophisticated ML techniques and acquiring new sources of information, such as cameras inside of OTs.

In conclusion, these findings suggest a role for ML models to inform operational decisions on the day of surgery. The model developed in this work was superior to a traditional statistical alternative, and its advantage dramatically increased as surgery progressed. This achievement builds upon previous efforts to predict surgical duration and represents important progress towards the goal of leveraging ML to reduce the high costs of surgery.

Authors' contributions

Study conceptualisation: YJ

Model design: YJ, BX, CL

Model testing: YJ

Model implementation: YJ, BX

Data curation: TK

Critical discussion of findings: CL, MSA, TK

Drafting of paper: YJ

Review of paper: CL, MSA, TK

Editing of paper: YJ, CL, MSA, TK

Handling editor: Hugh C Hemmings Jr

Declarations of interest

MSA is an editor of the British Journal of Anaesthesia. The other authors have no competing interests to declare.

Funding

Division of Clinical and Translational Research of the Department of Anesthesiology at Washington University School of Medicine in St Louis.

Appendix A. Supplementary data

The following is the Supplementary data to this article: