Glassy phases in organic semiconductors

Abstract

Organic semiconductors may be processed from fluids using graphical arts printing and patterning techniques to create complex circuitry. Because organic semiconductors are weak van der Waals solids, the creation of glassy phases during processing is quite common. Because structural disorder leads to electronic disorder, it is necessary to understand these phases to optimize and control the electronic properties of these materials. Here we review the significance of glassy phases in organic semiconductors. We examine challenges in the measurement of the glass transition temperature and the accurate classification of phases in these relatively rigid materials. Device implications of glassy phases are discussed. Processing schemes that are grounded in the principles of glass physics and sound glass transition temperature measurement will more quickly achieve desired structure and electronic characteristics, accelerating the exciting progress of organic semiconductor technology development.

1. Introduction

Organic semiconductors have been pursued with great interest and substantial investment over the last several years because they are elementally abundant, they enable new processing approaches and product form factors, and their properties can be tuned using synthetic chemistry. Intramolecular transport in these materials occurs through delocalized valence orbitals that are realized via extensive conjugation. Steady advances in synthetic chemistry, materials characterization, and device physics over the last several decades have led to a mature understanding of how to control important aspects of organic semiconductors, such as the highest occupied molecular orbital (HOMO) level (analogous to valence band), lowest unoccupied molecular orbital (LUMO) level (analogous to conduction band), and bandgap. A large materials library is now accessible commercially, and new materials with superior properties are frequently announced.

One of the key advantages of organic semiconductors is that they are readily dissolved and processed as solutions or via low-temperature vapor deposition. Such approaches are possible because these materials form weak van der Waals solids rather than covalent crystals. These characteristics enable additive manufacturing approaches such as inkjet printing, screen printing, and slot-die coating. The flexible and conformable form factors enabled by organic semiconductors may also open new applications that are inaccessible to more traditional inorganic semiconductor technologies.

With a few notable exceptions, optimal electrical transport is achieved in highly-ordered, crystalline material; however, most polymeric or even small molecule organic semiconductors, when processed as thin films, exhibit polycrystalline or paracrystalline structure. Most polymeric semiconductor films are semicrystalline or glassy, and in many cases the crystals themselves contain significant packing defects or dynamic disorder. The amount of order within the films is expected to affect their semiconducting properties. Specifically, there is a connection between structural disorder and “electronic disorder,” where the latter refers to a distribution of HOMO/LUMO levels resulting in a complex density of states for charge carriers. From a molecular charge transport perspective, there are two types of energetic disorder. In diagonal disorder, the local intramolecular HOMO level and LUMO level of a material will vary spatially at the nanoscale [1]. The most common origin of diagonal disorder is conformal freedom - rotation about sp² bonds in a conjugated molecule to form different conformers, which may be planar or nonplanar. In off-diagonal disorder, variations in the regular intermolecular spacing or orientation lead to a distribution of different electronic couplings between molecules [1]. This type of disorder occurs in glassy phases and also to various extents within defective crystals. Several approaches have been developed to evaluate the impact of energetic disorder on the device physics of organic electronics devices, such as transistors, with significant connections to the thermally-activated charge transport that is typically observed in such systems [2]. Molecular dynamics simulations reveal strong impacts of molecular conformation on hole transport rates [3]. For these reasons, there has been a significant investment in developing and adapting materials structure measurements that can be applied to organic semiconductors [4–7].

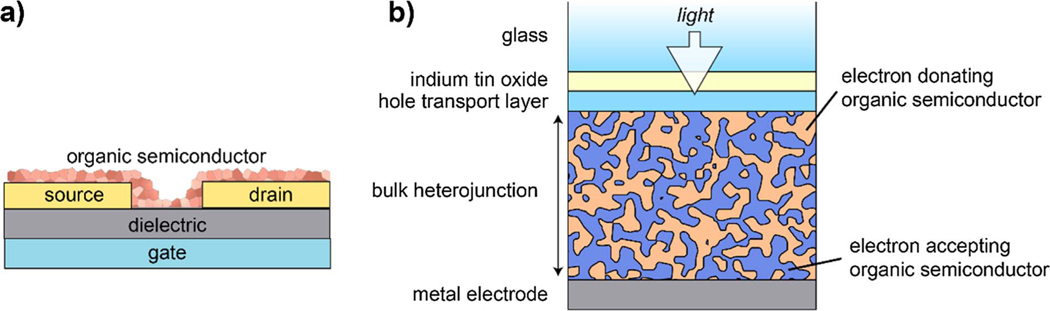
In this perspective, we will examine some connections between glassy phases and the processing, structure, and device considerations of organic semiconductors. We believe that understanding the physics of glassy materials can accelerate the development of organic semiconducting materials with superior properties, and it is essential for the optimization of organic semiconductor processing. We will primarily focus on organic thin film transistor (OTFT) and organic photovoltaic (OPV) devices (see Fig. 1). Although it is true that in organic light emitting devices (OLEDs) [8] the behavior of glassy phases is of paramount importance, it is most relevant in OLEDs to long-term device stability. This is because OLED devices are generally processed to ensure that the materials remain homogeneous glasses, as aggregates will induce quenching that dramatically degrades device performance [9]. Contrarily, in OTFT and OPV applications some extent of crystallinity is thought to be advantageous, so controlling glassy phases and understanding their interactions with more ordered phases becomes more important. The focus of this perspective is on the broad category of organic semiconductors, which includes both small molecule and polymeric semiconductors. However, because of the unique aspects of polymeric materials, such as chain entanglement, additional emphasis will be placed on semiconducting polymers.

Fig. 1.

Schematic of (a) a bottom-gate/bottom-contact organic thin-film transistor (OTFT) and (b) a bulk heterojunction (BHJ) organic photovoltaic (OPV) device in what is called the “conventional” geometry (contrasted by a now-common “inverted” geometry with electron extraction on the glass side).

First, in this perspective, we will begin by considering the different types of glassy states that can exist in materials and their respective levels of order, the challenges associated with discerning between these different types of glassy states due to semiconductor backbone rigidity, and the connection between types of order and charge carrier mobility. Secondly, the added complications that arise in multicomponent systems, either during processing from solution or in mixed-glass phases such as in a BHJ, and the effect of phase purity on charge transport in BHJ’s will be discussed. Thirdly, the impact of confinement and interfaces on ordering/vitrification and the resultant effect on charge transport will be examined. Finally, we will explore the challenges associated with measuring the glass transition temperature of organic semiconductors.

2. Glassiness and charge transport

Before discussing the connections between glassy phases and other aspects of organic semiconductors, we feel it necessary to define what we mean by a glassy phase. At its simplest, a glassy phase forms by a transformation from a state with molecular mobility to an immobilized state, relative to the experimental timescale, with the same or similar structure due to, for example, a decrease in temperature or removal of solvent [10]. Because this transition into a glass occurs when large-scale cooperative molecular or segmental rearrangements (dynamics) are arrested [11], it is not limited to a transition from an amorphous state, i.e., amorphous melt, but also includes transitions of mesophases (such as liquid crystals, plastic crystals, and conformationally disordered (CONDIS) crystals, as well as possibly in fully crystalline materials) into their associated glassy phase, such as a liquid crystalline glass [12]. For example, at temperatures significantly below the glass transition temperatures (T_g) of their mesophases, a nematic liquid crystalline (LC) glass will no longer have translational motion and a plastic crystal glass will no longer have rotational motion [13]. Therefore, as we continue our discussion into the glassy phase of organic semiconductors, there will always be two underlying concerns related to the device performance: (1) the nature and composition of the glassy phase, which govern its underlying order, and (2) the underlying molecular dynamics related to where the system is relative to its T_g, which will influence what phases can form in both neat and blended systems as well as the thermal stability of the nanostructures and the mechanical properties of the device [14].

One metric for determining the nature of glassy state present in the system, i.e., amorphous or mesophase, is through Hosemann’s paracrystalline disorder parameter g [15,16]. At the simplest level, the parameter is a measure of the relative cumulative statistical fluctuations across all crystallographic planes, with the higher g values pointing to higher levels of disorder. Rivnay and coworkers discussed methods for accurately determining g for semiconducting polymers; however, it is often challenging due to the frequently limited number of crystalline reflections in organic semiconductors [5]. g values have been attributed to various phases and mesophases with extreme limits of g = 0 for a perfect crystal and g = 100% for a Boltzmann gas. Real materials fall more broadly into the following ranges for g: < 1% for highly crystalline samples, ≈(10–15)% for amorphous materials, and therefore ≈(1–10)% for the remaining imperfect crystals and mesophases [5,16,17]. Using this range to strictly identify mesophases in polymers can be problematic, however, because it has been shown, in some cases, that as the degree of crystallinity of a polymer increases, g decreases [16]. Thus, it can be challenging to discriminate between a low crystallinity, nearly amorphous material and a 100% liquid crystalline material [13,18]. As pointed out elsewhere [19], this difference makes a huge impact on semiconducting polymer post-processing and annealing schemes, and this will be one of the challenges we return to repeatedly throughout this perspective. With effort, however, the thermodynamics and kinetics of the phase transitions of these systems can be used to properly classify these two separate cases, but a discussion of those methods is beyond the scope of this perspective [19].

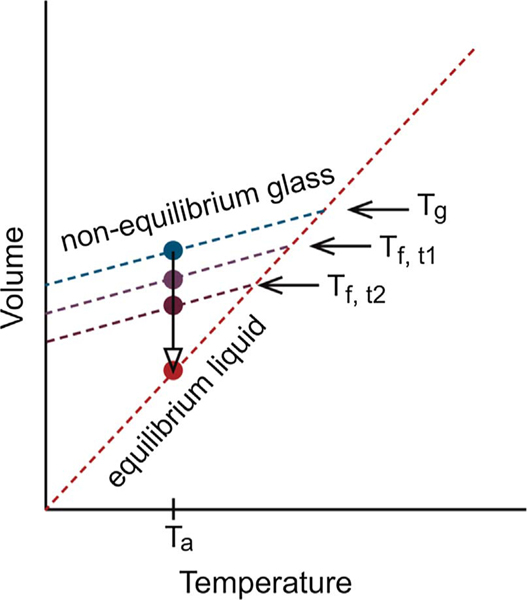
If we, for the moment, limit ourselves to amorphous glasses, it must be emphasized that not all amorphous glasses are the same because their thermal processing history determines their packing (volume). Subsequent aging below their T_g can, through structural recovery, help them approach their equilibrium state (as shown in Fig. 2). With increased aging time, the observed T_g on heating (known as the fictive temperature) decreases as the packing density increases. However, the lower the annealing temperature, the exponentially longer it will take to reach the equilibrium line [20]. This packing density will influence the “structure” of the underlying semiconducting organic glass and likely the charge transport. For example, studies on poly(ethylene terephthalate) (PET) have shown that the path taken to the glassy state results in changes in the rate of cold crystallization, suggesting that density fluctuations and ordering in the glassy state occur that are precursors to crystallization but that are not identifiable as either liquid crystals or small crystals. Furthermore, it has been shown that melt drawing of amorphous PET allows a continuous transformation of the paracrystallinity from amorphous to nematic hexagonal packing to a smectic packing and finally to the triclinic crystalline form [21].

Fig. 2.

Schematic of the volume evolution towards equilibrium of a glass with an observed glass transition T_g as characterized by the intersection of the non-equilibrium glass and equilibrium liquid lines, after annealing at T_a for various times (t1, t2, etc.). The fictive temperatures T_f,t1 and T_f,t2 are the glass transition temperatures that would be measured on heating for the glasses aged at T_a for times t1 and t2, respectively.

Most recently, glasses with far closer to equilibrium structures, known as “stable glasses,” have been produced through vapor deposition [22]. The glasses have densities and kinetic stabilities that theoretically would have required aging on the order of (10²–10⁵) years. More specifically, for organic semiconductors deposited as stable glasses by vapor deposition, it has been shown that stable glasses can be formed with varying levels of anisotropy [23], smectic-like structures for systems with no known liquid-crystalline phases [24], and highly-ordered columnar liquid crystalline structures [25]. This recent work on stable organic semiconductors also highlights some of the challenges in determining the difference between an anisotropic amorphous glass and a liquid-crystalline glass.

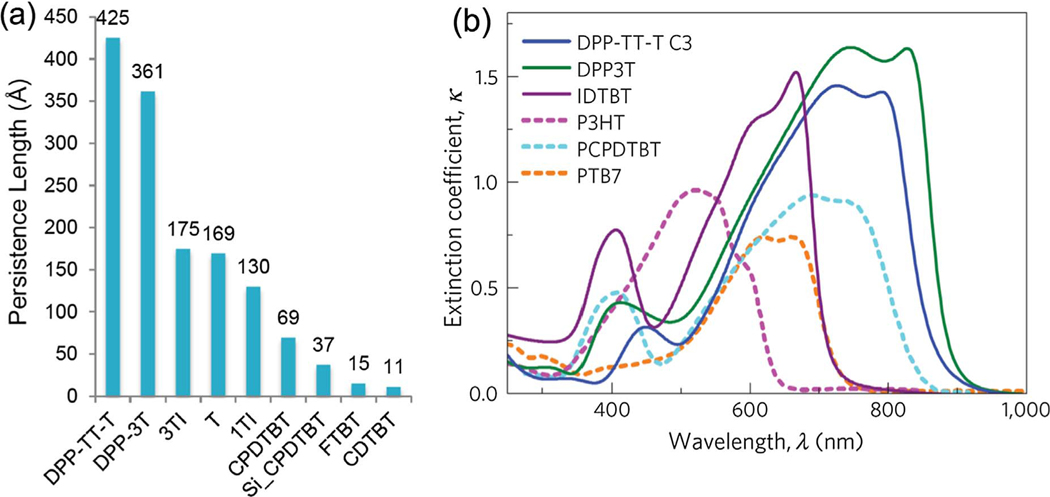
Beyond the challenges described above, one of the reasons why it is even more difficult to discern between anisotropic amorphous and liquid crystalline semiconducting polymeric glasses is that many recently synthesized molecules with high mobilities are not just rigid, but they also tend to be straight and coplanar (e.g., having low diagonal disorder, from our discussion of energetic disorder above [1]). This rigidity is often characterized by the chain’s persistence length, which, with some oversimplification, describes the length-scale above which a polymer chain’s conformations mimic a random walk. (See Fig. 3(a) for persistence lengths for a number of semiconducting polymers.) The persistence length has been linked to the presence of liquid crystalline phases [17], and for semiconducting polymers, high persistence length has been tied to high optical absorption (see Fig. 3(b)) [26]. For straight (rectilinear) chains, paracrystalline disorder in two dimensions normal to the chain axis (e.g., off-diagonal disorder) can lead to a number of possible types of liquid crystals depending upon whether there are rotational correlations and/or longitudinal registry between the chains [17]. These correlations could have a strong impact on the charge carrier mobility of the semiconducting polymer but would not necessarily be reflected in the paracrystallinity disorder parameter.

Fig. 3.

(a) Calculated persistence lengths for a number of semiconducting polymers. (b) Extinction coeffcient of polymers with high (solid lines) and low (dashed lines) theoretical persistence length. Reprinted by permission from Springer Nature: Nature Materials. M.S. Vezie, et al., Nature Materials 15 (2016) 746–753. Copyright (2016).

Below, we will show the challenges in identifying the nature of the glass as well as demonstrate that while rigidity may be necessary for LC formation, it is not a sufficient condition by comparing two polymeric semiconductors. The first polymer, poly[N-9′-heptadecanyl-2,7-carba-zole-alt-5,5-(4′,7′-di-2-thienyl-2′,1′,3′-benzothiadiazole)] (PCDTBT), is considered “largely amorphous” with primarily order only in the π-stacking direction. However, it is known to display an LC phase at high temperatures and based on the thermal behavior of the transition into this LC phase it is also believed to be in a mesophase at lower temperatures [27]; therefore, it is likely an LC glass versus an amorphous glass below its T_g of ≈130 °C [28]. This statement can be further justified by using the single-peak paracrystalline-disorder parameter approximation rewritten in terms of the coherence length (L_hkl) [5,29]:

$$g_{hkl}\cong \frac{1}{\sqrt{L_{hkl}{q}_0}}$$ (1)

where q₀ is the magnitude of the scattering vector corresponding to the diffraction peak center. Using the π-stacking coherence length data of Wang and coworkers [30] and Eq. (1), it can be determined that the π-stacking paracrystallinity is ≈6.2% after annealing at ≈70 °C. This can be compared to the known liquid crystalline polymer poly(2,5-bis(3,6-tetra-decylthiophen-2-yl)thieno[3,2-b]thiophene) (PBTTT-C₁₄) [19] with a π-stacking paracrystallinity of ≈8.1% (obtained from Eq. (1) and literature data on its coherence length [5]). However, as hinted at above, not all high performing “largely amorphous” organic semiconductors are LC glasses, because a similar analysis on the high-performing, rigid-backboned polymer indacenodithiophene–benzothiadiazole (IDTBT-C₁₆) [31] results in a π-stacking paracrystallinity of ≈13.6% - well within the amorphous range.

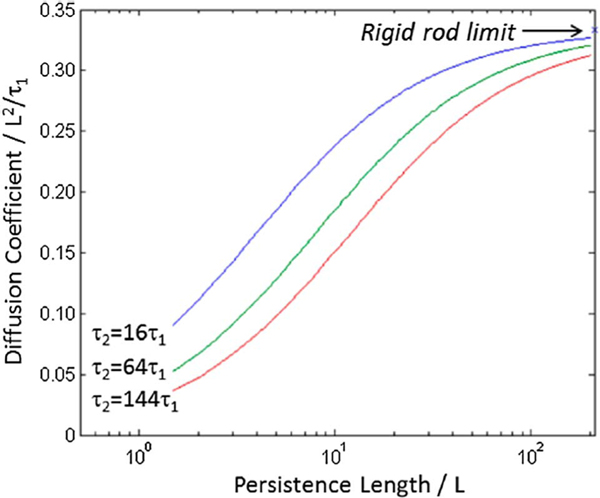
So, we ask, if the chains are straight enough and coplanar enough, what is the minimum amount of order that is necessary for efficient chain transport? It has been shown that the higher the persistence length the higher the macroscopic charge diffusion coefficient for given intra- and inter-chain charge hopping times [32]. While the chain backbone direction is the fastest direction for chain transport, at some point transport will have to occur between chains (see Fig. 4), such as at the chain ends at the very least. In a liquid crystalline glass, there would be a large number of opportunities for transport in the π-stacking direction with high backbone orientation in one direction, likely reducing the interchain hopping times. However, g likely does not provide the full picture into a material’s order, as small paracrystals have been detected in amorphous glassy materials such as SiO₂ with a g ≈ 12% [15], and the studies, discussed earlier in this perspective, on PET’s cold crystallization behavior support this as well. This is further substantiated by recent simulations of an apparently amorphous system (with a liquid-like structure factor) that found that almost all the molecules were in locally crystalline regions, and the study pointed out that such regions of medium range order would be undetectable by X-ray diffraction [33]. Thus, the presence of small paracrystalline aggregates throughout a nominally amorphous organic semiconductor cannot be ruled out and hence could help create the necessary percolation network for effcient charge transport. The question then remains, for an amorphous glass, whether the interchain hopping would likely be governed by this medium-range order that would not be captured by X-ray diffraction measurements?

Fig. 4.

Theoretical macroscopic charge diffusion coeffcient in the bulk as a function of semiconducting polymer persistence length for varying relative hopping times (τ₁ is for hopping along a given chain and τ₂ is for interchain hopping). Reprinted with permission from P. Carbone, A. Troisi, J. Phys. Chem. Lett. 5 (2014) 2637–2641. Copyright 2014 American Chemical Society [32].

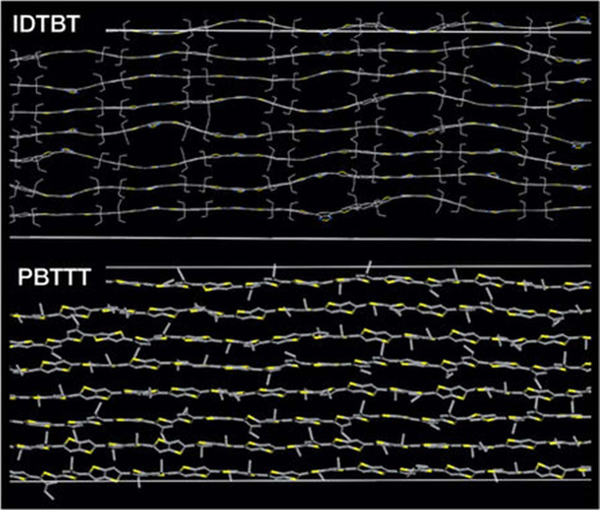
The issue of whether long-range order detected by X-ray diffraction strength should be the ultimate predictor of good charge transport is further challenged by emergent results on new materials that question whether chain rigidity is as important as the elimination of torsional defects. Simulated IDTBT structures, as shown in Fig. 5, top panel, show a long axis contour that is not particularly linear, but having conjugated units that are remarkably co-planar [34]. The PBTTT structure, in contrast, shows a more linear chain that is achieved by torsional rotations that break conjugation (see Fig. 5, bottom panel). It seems possible that for organic semiconductors the conformations sought for high levels of crystallinity may not always be the conformations that result in the lowest (diagonal) energetic disorder given the collections of bond angles employed in their synthesis and considering the packing constraints imposed by the covalent attachment of side groups to these molecules and the necessity to pack them into the same lattice. These results raise the intriguing possibility that high crystallinity may only be one approach among many to achieve high charge carrier mobility in organic semiconductors. If high charge carrier mobility were possible for amorphous systems, that could mitigate one of the most significant disadvantages of highly crystalline organic semiconductors: their brittleness. PBTTT, a material renowned for its high levels of crystalline order and excellent charge transport, has been shown to exhibit crack onset at strains lower than 2.5% [35]. Without better plastic (or elastic) properties, organic semiconductors will not be able to deliver the flexible form factor that is often invoked as a key advantage over incumbent technologies.

Fig. 5.

Simulations of the backbone conformation of IDTBT and PBTTT in side-chain-disordered and non-interdigitated structures. The side chains and hydrogen atoms are omitted for clarity. Yellow, sulfur atoms; blue, nitrogen atoms. Reprinted by permission from Springer Nature: Nature. D. Venkateshvaran, et al., Nature 515 (2014) 384–388. Copyright (2014) [34].

3. Multicomponent systems

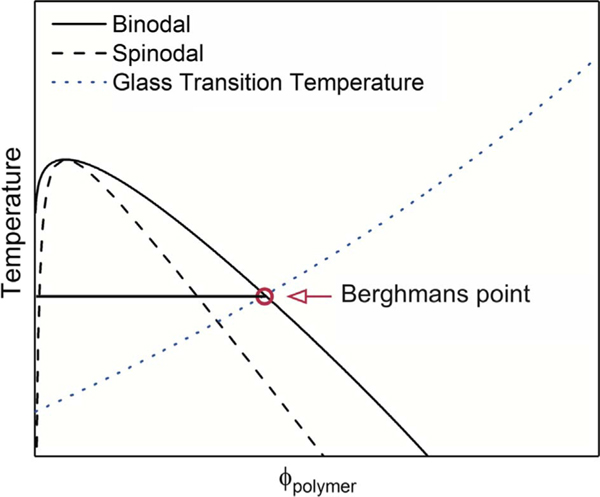
To this point, we have discussed mostly single component glasses. However, organic semiconductors are often deposited from solution, creating a minimum two-component system, and the real systems are typically far more complicated. For example, to achieve optimal device performance, many organic semiconductors are deposited from either mixed solvent systems or systems with small quantities of additives, such as diiodooctane or chloronaphthalene; and for organic photovoltaic devices, the system is typically composed of two organic semiconductors (with one potentially being a fullerene derivative) plus the solvent system from which they are deposited. Considering the simplest system first, in Fig. 6 is shown a phase diagram for a polymer in solution. The key point, relevant to the current discussion, is understood by following the glass transition line for the polymer. As expected, the presence of solvent depresses T_g of the polymer; however, at a certain concentration the glass transition line intersects the binodal. At this point (Berghmans point), further phase separation stops because vitrification locks in the structure, causing gelation [36].

Fig. 6.

Schematic phase diagram for a polymer solution with upper critical solution behavior derived from the Flory-Huggins lattice theory [37]. The interception of the binodal with the glass transition line is shown, indicating frustration of the phase separation due to vitrification at Berghmans point [36].

In a polymer-fullerene bulk heterojunction (BHJ) film, the glass transition of the mixed BHJ as well as the influence of solvent on either component must also be considered. One of the earliest P3HT/PCBM BHJ processing approaches demonstrated a significant increase in power conversion effciency when the film was heated to temperatures of ≈110 °C [38]. P3HT’s anomalously low T_g among polymer semiconductors allowed that approach to work, but it proved ineffective for the vast majority of later donor–acceptor polymers paired with PCBM, presumably because their glass transitions were at a higher temperature.

Because the glass transition temperatures of many fullerene derivatives are well above room temperature, e.g., PCBM-71 with T_g ≈ 163 °C, the influence of vitrification on the phase behavior must always be considered [39]. The general impact of vitrification on low- T_g polymers is that solidification processes generally result in a greater amount of glass when fullerene is present than might otherwise be produced if it were not [40]. It has been shown that T_g can be accurately predicted in these blends using the Fox equation [39,40]; but it can be challenging to quantify the amounts of each amorphous component, and the miscibility of the amorphous components may also affect the composition of the mixed glass and the T_g that it ultimately exhibits. Even cutting-edge, high power conversion efficiency OPV materials, such as PCE11 [41], appear to exhibit a clear vitrification effect with fullerenes, as the blend results in more glassy phase than the neat polymer processed the same way [40].

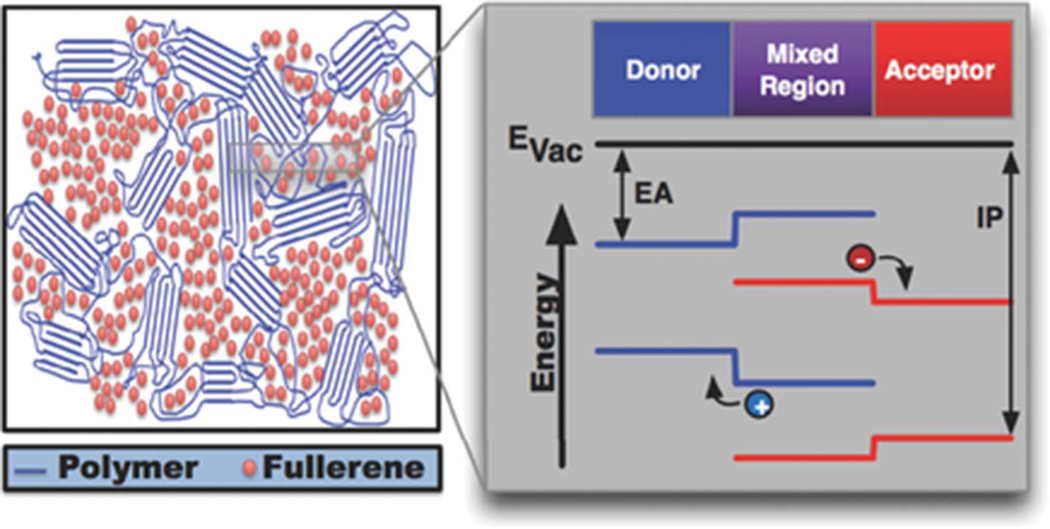
Apart from their influence on processing choices, the importance of glassy phases to charge separation and charge transport in polymer-fullerene BHJ OPV cells has been a topic of much interest. Several models suggest that glassy phases containing one or both organic semiconductors in the BHJ are essential to charge separation. In most polymer-fullerene OPV cells, the polymer and fullerene are found in a mixed glass phase. The polymer in this region is more disordered than it is in the crystal. The increased amount of disorder is expected to widen the bandgap of the polymer, specifically decreasing its HOMO level [42]. Similarly, dispersion of the fullerene appears to raise its LUMO level [43]. This variation may create an electronic landscape that facilitates charge separation [44,45]. A hole that is moving away from a charge transfer state will encounter an increasing HOMO level as it moves away from the glassy region (where the fullerene and the separated electron reside) and into the crystalline region of the polymer, which is spatially separated from the fullerene. This “energy cascade,” as shown in Fig. 7, may also prevent charges from returning to the amorphous region and recombining. McGehee and co-workers showed that such a mechanism would require mobilities higher than are typically measured in whole-device mobility measurements [45]. The precise values for mobility, energy level shift, and interfacial region thickness that are required would depend greatly on the identity of the BHJ components. High mobilities may be possible on a local molecular length scale, a hypothesis that is supported by terahertz measurements.

Fig. 7.

Schematic of a BHJ solar cell including the mixed region. Potential shifts in the local energetic landscape at the border between the donor, mixed and acceptor phases are shown in detail. EA is the electron affnity, IP is the ionization potential. From T.M. Burke, M.D. McGehee, Advanced Materials 26 (2014) 1923–1928. Copyright © 2014 by John Wiley & Sons, Inc. Reprinted by permission of John Wiley & Sons, Inc.

A further critical question about glassy phases in BHJ OPVs relates to whether they should be mixed or of high purity. The development of new techniques to monitor composition in non-crystalline phases based on Resonant Soft X-ray Scattering (RSoXS) and energy-filtered transmission electron microscopy (EF-TEM) has revealed that there are variations in relative phase purity between various OPV systems [46]. Higher phase purity is generally associated with higher power conversion efficiency [41,47,48]. This trend was supported by simulations that indicated that simple mixed phases without an “energy cascade” would be detrimental to device performance [49]. In contrast, other work has suggested that having glassy phases that are too pure in one component may prevent charge percolation; well-mixed phases ensure charge transport paths for both components [50]. An important facet of this discussion relates to the general finding that well-performing BHJ OPV systems exhibit bimolecular recombination rates that are orders of magnitude slower than predicted from Langevin theory [51]. And yet there is little consensus on what aspects of morphology influence the amount of recombination suppression [52]. The “energy cascade” and energetic disorder resulting from glassy phases are likely implicated in this phenomenon [53]. The issue of glassy phase purity and how it interacts with order and morphology variations in BHJ OPVs remains an active area of inquiry. As an unsolved fundamental issue, it must be better understood to enable the rational design of OPV systems.

4. Confinement and interface effects

The complicated structures of OTFTs and OPVs described above lead to one additional concern for polymeric semiconductors, which is the effect of confinement and interface interactions on T_g. A full discussion of the challenges associated with measuring and understanding T_g of polymers at interfaces and under confinement is well beyond the scope of this work, but it has been covered extensively in the literature [54]. However, some key points can be made that are particularly relevant to multilayered or multicomponent devices. Thin polymer films on a substrate can often be treated as a trilayer structure composed of a substrate-interface region, an interior bulk-like region, and a free surface region [55]. For substrates that have strong interactions with the polymer, the chain dynamics near the interface is suppressed, increasing the local T_g. The reverse is true for free surfaces or weakly interacting substrates, where a liquid-like layer is present and the local T_g is lower. Finally, the presence of bulky side groups, as are frequently found in organic semiconductors, change these effects by reducing the amount by which T_g is increased near strongly interacting substrates, increasing the bulk T_g, and decreasing the free surface T_g more strongly than when they were not present [55].

One way to think about the impact of altered dynamics for an organic electronic device is by considering the OTFT structure. For a bottom gate OTFT device (see Fig. 1(a)), there are a number of different interfaces, including at the dielectric layer and with the source and drain electrodes. Depending upon where the bulk T_g is relative to the usage temperature a number of different things could happen. For a truly amorphous organic semiconductor, increased molecular mobility would increase the dynamic disorder at the interfaces, which could (1) potentially reduce the charge mobility at the interface or (2) enable passage of the mobile amorphous structure into a structure with a less-favored paracrystalline structure. For example, it has been understood for some time that field effect mobility of organic semiconductors in OTFT structures exhibits thermally activated (“hopping”) behavior due to energetic disorder at the gate dielectric interface [2]. For evaporated electrode deposition, a mobile surface layer would also result in a deeper metal interdiffusion into the active semiconductor layer [56]. Alternately, for an LC or crystalline structure a reduction in mobility near a strongly interacting interface could result in a disordered quenched glassy state at the interface relative to the highly ordered bulk, which would degrade device performance but would likely not be detected by normal scattering techniques. Finally, it should be apparent for an OPV device with a BHJ structure (see Fig. 1(b)) that the dynamics are even more complicated, because there are even more complex shaped interfaces and, due to the exciton diffusion length, the desired domain size is ≈10 nm, which is similar to the order of the size scale of the interfacial layers [57].

5. Challenges associated with measuring the glass transition

It should be clear that characterization of the glass transition(s) of the semiconducting materials and devices is critical in understanding their performance and thermal stability. Methods for characterization of T_g fall into two broad categories: (1) “static” measurements that characterize the T_g of a material corresponding to an underlying relaxation time of ≈100 s [10], such as standard differential scanning calorimetry (DSC) at a heating rate of 10 K/min or dilatometric measurements (e.g., ellipsometry, X-ray reflectivity, or capacitance dilatometry) and (2) dynamic measurements that characterize signatures of the segmental relaxations as a function of frequency such as modulated DSC (MDSC), dielectric relaxation spectroscopy (DRS), or rheological/(dynamic mechanical) measurements. All of the dynamic measurements are normally performed at temperatures in excess of T_g measured via “static” measurements due to instrument frequency limitations or the much longer measurement times necessary to access the characteristic timescales at lower temperatures. For comparison with other measurements, the dynamic measurements are typically extrapolated to a characteristic relaxation time of 100 s so as to better approximate the “static” measurements. This extrapolation is also necessary for the more recently employed fast scanning DSC techniques, as they are effectively characterizing T_g at shorter characteristic relaxation times [20,58]. One additional item to be kept in mind is that the “static” measurements discussed above are more likely to be affected by the surface or interface layers than dynamic measurements, because, as stated previously, the dynamic measurements are nearly always performed at temperatures in excess of the bulk T_g.

Due to ease of access and use, DSC is typically the first method employed to try to characterize T_g for organic semiconductors. In DSC, T_g is characterized by a change in heat capacity ΔC_p during the transformation from the glassy to mobile states. However, ΔC_p is not always easy to capture, particularly for organic semiconductors [58]. A number of possible reasons for this exist. For LC glasses, only some of the modes for molecular motion become available on changing from the LC glass to the LC melt versus the transformation from the amorphous glass to the amorphous melt resulting in a concomitant reduction in ΔC_p at T_g [59,60]. Furthermore, if side chains typically added for solubility only add to the heat capacity of the glassy state then the measured increment in heat capacity at T_g would be reduced, i.e., if they are already mobile they likely would not add additional heat capacity to the backbone’s liquid state [61]. (See also supporting information to Ref. [39].) Finally, for semicrystalline polymers ΔC_p,sc will be

$$\text{Δ}{C}_{p,sc}⩽\left(1-x_c\right)\text{Δ}{C}_p$$ (2)

where x_c is the mass fraction crystallinity and the inequality can take place if a rigid amorphous phase is present in addition to the crystalline and mobile amorphous phases [62]. Variations on Eq. (2), where ΔC_p,sc is replaced by some other relevant property, will apply to all of the static or dynamic measurements as it reflects the signal generated by the mobile or active material.

Many of the dynamic measurements such as DRS or dynamic mechanical measurements are limited to larger sample sizes (> 100 mg), and DRS is further complicated by both the semiconducting properties of the samples as well as the effect of oxygen doping [14,58]. However, recently Xie and coworkers have demonstrated the capability of oscillatory shear rheometry to characterize T_g of semiconducting polymers using only 10 mg of material [58]. However, among all the measurements, excluding perhaps ultrafast DSC which uses ng quantities of material [63], dilatometric measurements require the least amount of material. Variable temperature spectroscopic ellipsometry (SE) has been used extensively with semiconducting polymers to characterize T_g [28,64], to perform temperature dependent diffusivity studies [39], and to characterize the depth dependence of thermal transitions by employing the added information obtained from the wavelength dependent absorption of the polymers [65]. However, it is important to realize that dilatometric measurements on thin polymer films are influenced not just by the interaction of the polymer with the substrate, as discussed previously, but also by the mismatch in the coefficients of thermal expansion between the film and substrate and the thermal history of the system [66]. It is also necessary to be cautious to understand whether the glass transition process being measured corresponds to the backbone motion or the side chains, because each will have different influences on the device. If samples of the same polymer with varying molar masses are available and, as expected for lower molar masses [67], the measured T_g varies with polymer molar mass, then the measured T_g corresponds to the backbone T_g [58].

6. Closing remarks

In closing, we hope that we have shown that the glassy phases of organic semiconductors are critical to semiconductor device performance. While it is often difficult to measure the glass transition temperature of these materials, it is crucial to do so to enable understanding of the behavior of these materials in the bulk, at interfaces, in solutions, and in blends. This information in turn can help to optimize the semiconductor devices with respect to material dissolution, deposition, drying, annealing, layer and electrode deposition, and device post-processing. This information will also provide insight into the ultimate device stability. The nature of the glass (amorphous or mesophases), the local conformations, and the medium range order are also key to modeling the electron and hole transport processes in devices made from these materials; modeling and new measurement methods will continue to expand our understanding of these features. Finally, because many of the parameters listed above are tunable through changes in chemistry of the material, the processing solvent, and the materials with which the organic semiconductors are blended, the possibilities are boundless.