A collection of forcefield precursors for metal–organic frameworks

Abstract

A host of important performance properties for metal–organic frameworks (MOFs) and other complex materials can be calculated by modeling statistical ensembles. The principle challenge is to develop accurate and computationally efficient interaction models for these simulations. Two major approaches are (i) ab initio molecular dynamics in which the interaction model is provided by an exchange–correlation theory (e.g., DFT + dispersion functional) and (ii) molecular mechanics in which the interaction model is a parameterized classical force field. The first approach requires further development to improve computational speed. The second approach requires further development to automate accurate forcefield parameterization. Because of the extreme chemical diversity across thousands of MOF structures, this problem is still mostly unsolved today. For example, here we show structures in the 2014 CoRE MOF database contain more than 8 thousand different atom types based on first and second neighbors. Our results showed that atom types based on both first and second neighbors adequately capture the chemical environment, but atom types based on only first neighbors do not. For 3056 MOFs, we used density functional theory (DFT) followed by DDEC6 atomic population analysis to extract a host of important forcefield precursors: partial atomic charges; atom-in-material (AIM) C₆, C₈, and C₁₀ dispersion coefficients; AIM dipole and quadrupole moments; various AIM polarizabilities; quantum Drude oscillator parameters; AIM electron cloud parameters; etc. Electrostatic parameters were validated through comparisons to the DFT-computed electrostatic potential. These forcefield precursors should find widespread applications to developing MOF force fields.

Atom-in-material (AIM) partial charges, dipoles and quadrupoles, dispersion coefficients (C₆, C₈, C₁₀), polarizabilities, electron cloud parameters, radial moments, and atom types were extracted from quantum chemistry calculations for >3000 MOFs.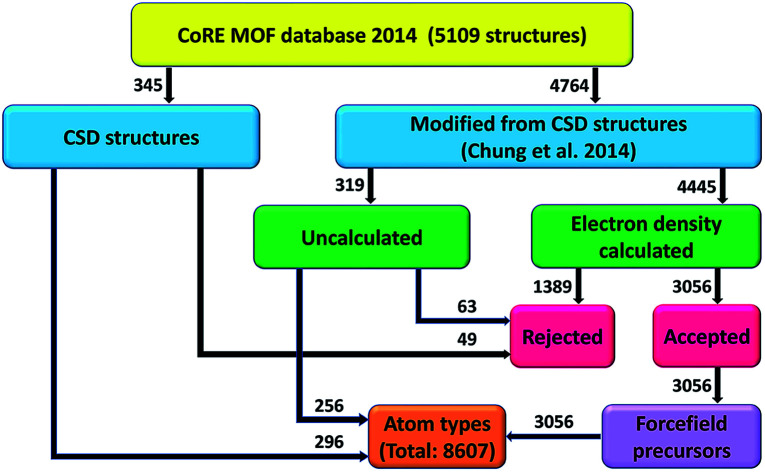

1. Introduction

Metal–organic frameworks (MOFs) are a kind of coordination network comprised of metal atoms connected by organic linkers.¹ In this work, we are interested in MOFs that are porous crystals. Because of their nanoporous structures, these materials attract much interest for gas storage, gas separation, catalysis, and other applications.^2–6 Many thousands of MOF crystal structures have been deposited in the Cambridge Structural Database (CSD).^{1,7,8,115–117} Most often, these crystal structures were measured using X-ray diffraction crystallography (XRDC). Since hydrogen atoms contain no core electrons, they diffract X-rays extremely weakly.⁹ This makes it much harder to refine hydrogen atom positions than positions for heavier atoms.^9–11 Consequently, hydrogen atom positions may be unresolved in some of the reported crystal structures. Other complications include the presence of disordered atoms, solvent molecules, and/or free ions in some of the reported MOF crystal structures.

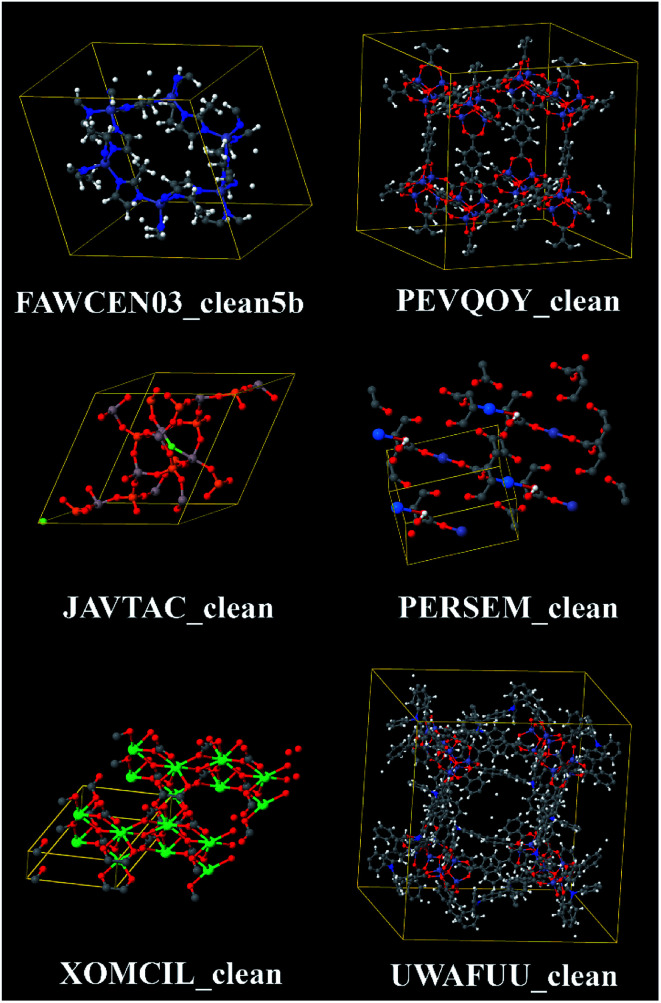
In 2014, Chung et al. reported a Computation Ready Experimental (CoRE) MOF database that was constructed by first searching the CSD to identify MOFs and then partially cleaning these structures.⁷ The searching step was designed to identify structures containing metal atoms bonded to non-metal atoms that form 3-dimensional networks. The cleaning process was intended to fix or discard structures containing disordered atoms and partial occupancies. The cleaning process was also intended to remove solvent molecules and other small adsorbates in the MOF's pores but to retain charge-balancing ions. Finally, missing hydrogen atoms were added to some of the structures. However, this cleaning process was imperfect resulting in some structures with errors.^12,13,115 This 2014 CoRE MOF database was the starting point for our study. It contains a total of 5109 structures, of which 4764 structures were modified during the cleaning process and 345 retained their original CSD structures.⁷Fig. 1 illustrates some of the chemical diversity within this database. Since organic compounds contain carbon, porous metal-linker networks that do not contain any carbon atoms are called metal–inorganic frameworks (MIFs).^14,15 The 2014 CoRE database contains some structures that are MIFs.¹³

Fig. 1. Example structures from the 2014 CoRE MOF database. Top left: ZIF-8 is a zeolitic imidazolate framework containing zinc atoms and imidazolate linkers. Top right: IRMOF-3-AM4XL is an isoreticular metal–organic framework (IRMOF) containing interligand crosslinks.⁵¹ Middle left: example metal–inorganic framework (MIF) containing no carbon or hydrogen atoms. Middle right: example MOF containing an actinide element (uranium). Bottom left: example MOF having a small unit cell, containing a lanthanide element (erbium), with no hydrogen atoms. Bottom right: example MOF having a large unit cell (1160 atoms).

Several follow-ups were subsequently made to the CoRE MOF database. In 2016, Nazarian et al. reported DDEC net atomic charges (NACs) for 2932 structures.¹⁶ In 2017, Nazarian et al. reported DFT-optimized geometries for 838 structures including 502 with computed DDEC NACs.¹⁷ Soon, a major revision of the CoRE MOF database will be published that expands the number of structures to approximately 15 thousand (Yongchul G. Chung, Emmanuel Haldoupis, Benjamin J. Bucior, Maciej Haranczyk, Seulchan Lee, Hongda Zhang, Konstantinos D. Vogiatzis, Marija Milisavljevic, Sanliang Ling, Jeff S. Camp, Ben Slater, J. Ilja Siepmann, David S. Sholl, Randall Q. Snurr, in revision). Altintas et al.¹¹⁵ reported a comparative analysis between the 2014 CoRE MOF database and the CSD-derived MOF database of Moghadam et al.¹¹⁶

Although many thousands of MOFs have been synthesized to date, this is only a tiny fraction of the number of MOFs that could potentially be made.¹ Owing to the large number of different metal atoms and organic linkers that could be combined in various ways, there is a nearly infinite number of potentially synthesizable MOFs.^1,18–20 Computational chemistry can be an efficient way to search this vast chemical space to help identify the most promising materials to later synthesize and experimentally test.²¹ This will avoid unnecessary efforts to synthesize a large number of materials that do not perform well for the desired applications.

A host of important performance properties for MOFs and other complex materials can be calculated by modeling statistical ensembles (e.g., constant NVE, NVT, NPT, μVT, μPT, NPH, etc.). Here, the properties can be roughly divided into thermodynamic properties that occur at equilibrium and dynamic properties that describe transient system response to non-equilibrium. Gas adsorption isotherms are often computed in the grand canonical (μVT) or Gibbs ensembles.^22,23 Gas diffusion constants are often computed in the canonical (NVT) or microcanonical (NVE) ensembles using equilibrium molecular dynamics.^24,25 System behaviors under extreme conditions, such as high pressures, low or high temperatures, applied electromagnetic fields, irradiation, high stresses, and corrosive conditions are of emerging interest.

When modeling statistical ensembles, an interaction model is required to compute the system's energy as a function of chemical configuration. Several different types of interaction models exist depending on the length scale at which the system is modeled. The smallest length scale considers individual electrons using an exchange–correlation theory (e.g., DFT + dispersion functional^26,27) to solve the Schrodinger equation for the material's electron distribution (i.e., quantum chemistry). A somewhat larger length scale considers individual atoms interacting via a classical force field in atomistic simulations.^21,28,29 Coarse-grained and continuum models treat even larger length scales.^30,31

Quantum chemistry using an exchange–correlation theory has different advantages and limitations compared to classical atomistic simulations using a force field. An exact exchange–correlation theory (e.g., full configuration interaction) would describe all material types but is extremely computationally expensive. In practice, approximate exchange–correlation theories are used that describe an extremely broad range of different material types with acceptable accuracy and computational efficiency. Because exchange–correlation theories are not material specific, they should not have to be reparameterized for a new material type. In contrast, classical force fields have to be extensively parameterized for individual atoms or atom types.^29,32 Because computing the system's energy is usually much faster using a classical force field than an exchange–correlation theory, classical atomistic simulations can usually be performed faster and over larger length and time scales than quantum chemistry calculations.

Classical force fields typically contain bonded and non-bonded terms. Bonded terms describe flexibility (bond stretching, angle bending, torsion, and/or out-of-plane parameters) and have been incorporated into many flexible force fields for MOFs.^33–38 Non-bonded terms describe electrostatic interactions (NACs, atomic multipoles, charge penetration, polarizability^39–43), London dispersion interactions, and/or short-range exchange-repulsion.^44,45 When optimizing the bonded parameter values, it is orders of magnitude more efficient to fit them to atom-in-material forces across multiple geometries than to only fit them to the system's total energy across multiple geometries.^46,47 Because each geometry yields many atom-in-material forces but only one total energy, fewer geometries are needed to fit the bonded parameter values to forces than to energies.

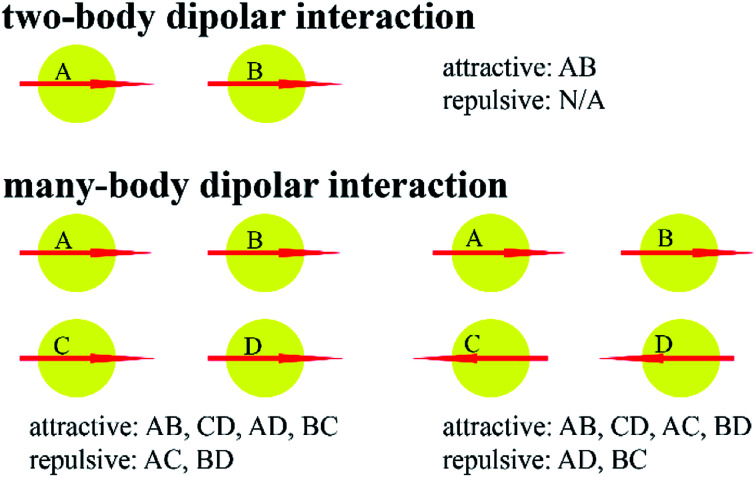
A classical force field must contain many-body dispersion and/or many-body polarization to accurately describe system properties over a wide range of conditions.⁴⁸ As shown in Fig. 2, dipolar interactions between two particles can be purely attractive, but dipolar interactions between many non-collinear particles are partly attractive and partly repulsive. Consequently, fitting two-body potentials (e.g., Lennard-Jones) to two-particle interaction curves gives force fields that often overestimate liquid-phase densities.⁴⁹ If the parameters of the two-body potential are adjusted to yield correct liquid-phase densities, then the two-particle interaction curve will be incorrectly described.⁴⁵ This problem can be fixed by explicitly including many-body dispersion and/or many-body polarization in the force field. For example, Kiss and Baranyai showed polarizability must be included in a force field to describe liquid water accurately over a wide range of conditions.⁵⁰

Fig. 2. Two-body (top) versus many-body (bottom) dipolar interactions. Two-body dipolar interactions can be purely attractive. As shown in the bottom left and bottom right, many-body dipolar interactions often contain a mixture of attractive and repulsive contributions.

Currently, there is a bottleneck to effectively model statistical ensembles: the quantum chemistry calculations are computationally expensive while the classical force fields are tedious to accurately parameterize. To resolve this bottleneck, either the quantum chemistry calculations should be sped up by orders of magnitude or classical force field parameterization should be made orders of magnitude easier. Some progress was made, but much more work remains to be done. Car-Parrinello molecular dynamics (CPMD) is a quantum chemistry method in which the wavefunction does not have to be self-consistently solved at each time step, because it evolves via an effective Lagrangian. CPMD improves the computational efficiency of ab initio molecular dynamics, but CPMD is limited to materials containing a band gap (i.e., insulators and semi-conductors).^52–54 VASP can perform ab initio molecular dynamics even for metals, but this requires computing self-consistent orbitals at each time step.^54,55 Recently, many studies focused on first-principles derived classical force fields whose parameters are extracted from quantum chemistry calculations.^{22,35,40,44,45,49,56,57} Other studies parameterized force fields by fitting to experimental data^36,58 or using machine learning (ref. 59–62).

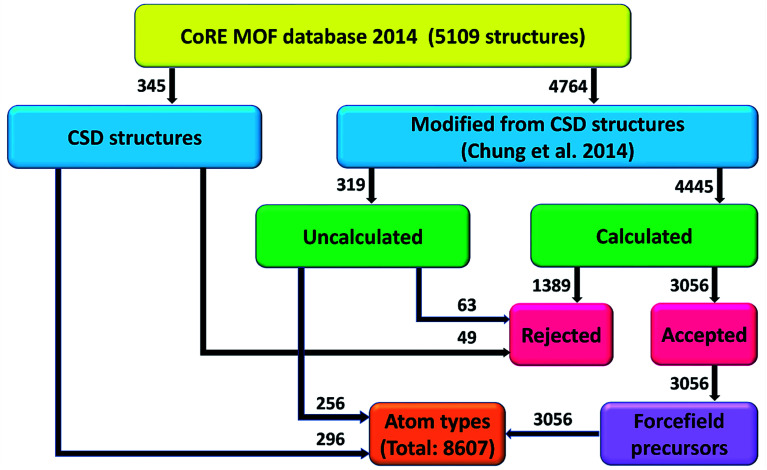
This work is a large-scale computation of atom types and non-bonded parameters for MOFs. Fig. 3 summarizes our project workflow. The 5109 structures from the 2014 CoRE MOF database included 345 structures directly from CSD plus 4764 structures modified by Chung et al.⁷ We attempted DFT calculations on all of the modified structures except the largest ones containing >∼1700 atoms; however, some DFT calculations did not converge. DFT calculations converged for 4445 structures that formed the calculated group, while the unconverged and large structures comprised 319 uncalculated structures. The acceptance or rejection criteria described in Section 2.4 were then applied to the CSD, calculated, and uncalculated structures. Atom typing was then applied to all of the accepted structures. A total of 8607 different atom types were identified. Various forcefield precursors were computed and reported in the ESI† for 3056 accepted calculated structures.

Fig. 3. Project flow diagram. Number of structures labeled next to each arrow.

2. Methods

2.1. Electron density calculation

The periodic quantum chemistry calculations of MOFs were performed using the PBE⁶³ exchange–correlation functional and the VASP^64,65 software. Frozen-core all-electron calculations were performed using the projector augmented wave^66,67 (PAW) method that uses a scalar-relativistic treatment of relaxed valence electrons and high-level relativistic treatment of frozen-core electrons.⁶⁸ The PAW potentials recommended on the VASP website were used for all these calculations. The planewave energy cutoff was 400 eV. Following prior recommendation,⁶⁹ the number of k-points along each lattice vector times the lattice vector length was ≥16 Å. If the k-points mesh was 1 × 1 × 1 then the Gamma point was used, otherwise we used Monkhorst–Pack⁷⁰k-point grids. Real-space grids were chosen to avoid aliasing errors (i.e., PREC = accurate).⁶⁹ The magnetic alignment of unpaired electron spins was optimized starting from the VASP default guess (which corresponds to a ferromagnetic alignment).

Calculations for the small organic molecules in Section 3.3 were performed using Gaussian16 (ref. 71) with the B3LYP^72,73 functional and def2QZVPPDD^74,75 basis set. Geometries of these molecules were optimized at this level of theory.

2.2. Computing forcefield precursors via atoms-in-material partitioning

Table 1 lists the computed forcefield precursors. The net atomic charge, atomic dipole, atomic quadrupole, electron cloud parameters, 〈r³〉 and 〈r⁴〉 radial moments, and atomic spin moment were computed in the Chargemol program using DDEC6 partitioning.^69,76,77

List of computed forcefield precursors.

Forcefield precursor	Method reference
Net atomic charge	69 and 76
Atomic dipole and quadrupole	76
Electron cloud parameters	This work
〈r3〉 and 〈r4〉 radial moments	69
Atomic spin moment	69 and 77
C6, C8, C10 dispersion coefficients	74
QDO parameters	74
Forcefield, fluctuating, and static polarizability scalars	74
Static polarizability tensor	74

The electron cloud parameters fit the electron density tail of each atom in the material to an exponential decay function. Specifically, the logarithm of the spherically averaged electron density assigned to atom A was fit to a straight line

ln(ρ^avg_A(r_A)) ≈ a − br_A 1

using least squares regression over the r_A values for which 10⁻⁴ ≤ ρ^avg_A(r_A) ≤ 10⁻² e bohr⁻³. r_A is the distance from position r⃑ to atom A's nuclear position. The fitted intercept a, slope b, and squared correlation coefficient R² are reported. The R² values were nearly always > 0.99 indicating nearly perfect linearity. These electron cloud parameters have several uses in molecular mechanics force fields. First, they are useful to describe charge penetration (also called cloud penetration).⁷⁶ Second, they are useful to describe short-range exchange-repulsion.⁴⁴ van Vleet et al. showed the Born-Mayer exponential term describing short-range exchange-repulsion has an effective exponent of ∼0.84 × b.⁴⁴ Although their results were derived for iterated stockholder atom⁷⁸ (ISA) partitioning,⁴⁴ we expect the same relation to hold for DDEC6 partitioning. Third, these electron cloud parameters are useful to parameterize dispersion damping functions (e.g., Tang–Toennies^79,80) that keep the dispersion energy finite as the distance between two atoms approaches zero.^44,45

The polarizabilities, dispersion coefficients, and quantum Drude oscillator (QDO) parameters were computed using the MCLF method⁷⁴ and software (ref. 81). The MCLF method yields several different types of polarizabilities and dispersion coefficients. The forcefield polarizability is a non-directionally screened polarizability that is suitable for use as an input parameter in polarizable force fields.⁷⁴ This avoids double counting the directional screening, because directional screening naturally arises during the classical atomistic simulation when the force field is used.⁷⁴ The fluctuating polarizability is the polarizability associated with the fluctuating dipoles of the London dispersion interaction.⁷⁴ The static polarizability and static polarizability tensor quantify the system's response to an externally applied constant electric field.⁷⁴ Various dispersion coefficients are associated with different kinds of fluctuating multipoles: C₆ (dipole–dipole), C₈ (dipole–quadrupole), C₉ (dipole–dipole–dipole), C₁₀ (dipole–octupole and quadrupole–quadrupole).^74,82,83 The C₉ coefficients were not printed to the forcefield precursors file, because they can be readily computed⁷⁴ from the printed forcefield polarizability and QDO parameters. The MCLF method includes convenient mixing rules (based on a QDO model) to easily calculate each of these dispersion coefficients between unlike atoms using only parameters of the individual atoms.⁷⁴

Of key importance, the C₆ dispersion coefficient does not equal the r⁻⁶ coefficient of the Lennard-Jones force field.⁸⁴ Because the Lennard-Jones force field does not explicitly include higher-order dispersion (e.g., C₈, C₁₀, etc.) terms, the Lennard-Jones r⁻⁶ coefficient must be made artificially higher than C₆ to effectively compensate for the neglected C₈ and C₁₀ dispersion terms.^74,84 Near the minimum energy separation between two atoms, higher-order dispersion (e.g., C₈, C₁₀, etc.) can contribute ∼35% of the total dispersion energy.⁷⁹

A QDO is a quantum harmonic oscillator containing a pseudoelectron attracted to a pseudonucleus.^85,86 Three QDO parameters were computed for each atom in the material: (a) the pseudoelectron's effective charge, (b) the effective QDO frequency, and (c) the QDO's reduced mass.^74,85 Force fields based on QDO models describe multibody dispersion and multibody polarization beyond the dipole approximation but require advanced simulation techniques.^85–87

2.3. Quantifying electrostatic model accuracy

The root mean squared error (RMSE) of an electrostatic model quantifies its error compared to the quantum mechanically computed (e.g., DFT) electrostatic potential over a chosen set of grid points:⁸⁸

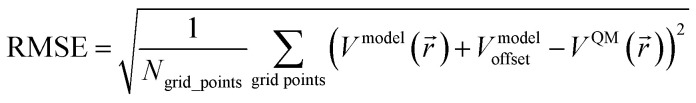2

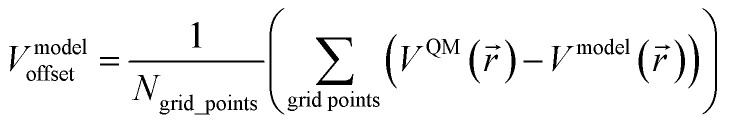3

where N_{grid_points} is the number of grid points used to compute RMSE. V^model_offset is the average difference between V^QM(r⃑) and V^model(r⃑) over these grid points.⁸⁹ These grid points are normally chosen to be outside the material's van der Waals surface.⁹⁰ For a MOF crystal, these grid points occur inside the MOF's pores.

In this study, the RMSE grid points were uniformly distributed in the volume of space that simultaneously met all three of the following criteria: (i) the material's total electron density, ρ(r⃑), was ≤10⁻⁴ e bohr⁻³, (ii) the grid point was no closer than 5 bohr to any atom in the material, and (iii) the grid point was closer than 12 bohr to at least one atom in the material. If any one of these three criteria were not met, the grid point was not used.

The relative root mean squared error (RRMSE) is the ratio of the electrostatic model's RMSE to the RMSE of a null model for which V^null_model(r⃑) = 0.⁹¹ Note that V^null_model_offset equals the average of V^QM(r⃑) over the RMSE grid points, V^QM_avg. Therefore,

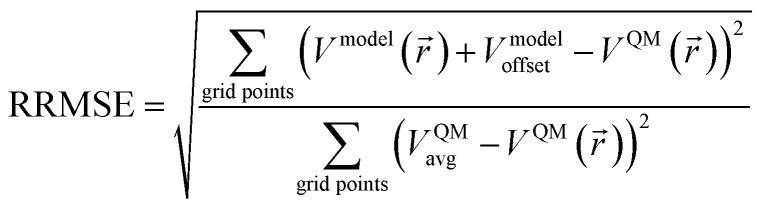4

The RRMSE quantifies the fraction of electrostatic potential variations that are not described by the model. For example, an RRMSE = 0.1 means that 90% of the electrostatic potential variations are captured by the model and 10% are not. This RRMSE definition was used in several prior studies^76,88,91,92 co-authored by one of us and differs from the even earlier literature^89,93 by including the potential offsets in this RRMSE definition. These potential offsets must be included in the RMSE and RRMSE definitions, because in periodic materials the electrostatic potential has no obvious spatial position where it approaches zero value and the energy of a system having no net charge is invariant to a constant electrostatic potential shift.

In this work, the DFT electrostatic potential V^QM(r⃑) was output from VASP using the keyword LVHAR = .true. We wrote an OpenMP parallelized Fortran program to compute RMSE and RRMSE. The RMSE and RRMSE were computed for the following four electrostatic models: (A) NACs only (aka monopole order), (B) NACs plus spherical cloud penetration, (C) NACs plus atomic dipoles (aka dipole order), and (D) NACs plus atomic dipoles plus spherical cloud penetration.

2.4. Structure acceptance or rejection

The 2014 CoRE MOF database was developed with goals of fixing disordered atoms, adding missing hydrogens, removing solvent molecules, discarding unfixable structures, and other cleaning protocols.⁷ These goals were partially but not fully achieved.

To partially address remaining structural deficiencies in the 2014 CoRE MOF database, we performed: (i) reasonability checks on our computed forcefield precursors for the calculated structures and (ii) connectivity checks for all structure categories. Table 2 lists reasons for rejecting a MOF structure.

Reasons for rejecting MOF structures.

Rejection reason	Identification method	Category
Unreasonable SBO for non-metal atom	DDEC6	Calculated
Negative NAC on metal atom	DDEC6	Calculated
RRMSE > 0.5	Direct calculation	Calculated
Isolated atom	Radii based connectivity	All
Unreasonable connectivity	Visual inspection	CSD and uncalculated

The sum of bond orders (SBO) was used as a screening criterion for reasonableness. DDEC6 bond orders and SBO for each atom in a material were computed using the Chargemol program.^69,94Table 3 lists accepted SBO ranges for non-metal elements appearing in the database. A MOF structure was rejected if the SBO for any atom in the material was outside these ranges. Since a carbon atom has four valence electrons available to share in covalent bonding, its SBO is normally expected to be ∼4. The acceptable range of SBO for C atoms was set to [3.5, 4.75]. Since F and H have one electron to share in covalent bonding, their accepted SBO ranges were set to [0.5, 1.5]. The remaining halogens (Cl, Br, and I) had accepted SBO ranges of [0.5, 5.0] to accommodate situations in which these atoms were bonded to several O atoms (e.g., ClO₄⁻, BrO₄⁻, IO₄⁻) which can give relatively large SBOs. Oxygen atom has two electrons to share in covalent bonding but can also bond via lone-pairs (e.g., Lewis acid–base interaction and hydrogen bonding); therefore, its accepted SBO range was set to [1.5, 3.0]. Boron and nitrogen atoms can exhibit variable bonding involving ∼3 or ∼4 covalent bonds (e.g., BF₃, B₂H₆, NH₃, NH₄⁺); therefore, accepted SBO ranges were set to [2.5, 4.5] for B and [2.5, 4.75] for N. The upper bound for N was slightly higher than for B to accommodate the formally higher SBO of N in nitrates than B in borates. Since Si prefers ∼4 bonds, its accepted SBO range was set to [3.5, 4.5]. The accepted SBO ranges for S, Se, and Te were set to [1.5, 6.0] to accommodate their ability to form ∼2 (e.g., H₂S, H₂Se, H₂Te) to ∼6 heuristic bonds (e.g., SO₄²⁻, SeO₄²⁻, TeO₄²⁻). The accepted SBO ranges for P and As were set to [3.0, 6.0] to accommodate their ability to form ∼3 (e.g., PF₃, AsF₃) to ∼6 heuristic bonds (e.g., H₂PO₄⁻, H₂AsO₄⁻). We do not claim these choices are perfect, but they can screen out some bad structures.

Accepted ranges of SBOs for non-metal elements.

H	[0.5, 1.5]	S	[1.5, 6.0]
B	[2.5, 4.5]	Cl	[0.5, 5.0]
C	[3.5, 4.75]	As	[3.0, 6.0]
N	[2.5, 4.75]	Se	[1.5, 6.0]
O	[1.5, 3.0]	Br	[0.5, 5.0]
F	[0.5, 1.5]	Te	[1.5, 6.0]
Si	[3.5, 4.5]	I	[0.5, 5.0]
P	[3.0, 6.0]

A calculated structure was rejected if any metal atom had negative NAC. In this article, the definition of metal atom included all elements not listed in Table 3 except rare gases (He, Ne, Ar, Kr, Xe, Rn) and At. The rational for this criterion is that metal atoms in MOFs are typically bound to more electronegative elements (e.g., N, O, etc.).

A calculated structure was rejected if any one of the four RRMSE described in Section 2.3 was greater than 0.5. This criterion ensured each of our four electrostatic models described the electrostatic potential with an error less than half of a no charges model. In other words, each electrostatic model described the majority of electrostatic potential variations in the MOF's pores.

Structures were rejected from all categories if they contained any isolated atoms. An atom was considered isolated if it was not connected to any other atom based on the radii listed in Table 5.

Radii (Å) used for atom typing. Two atoms were considered directly connected if the distance between them was no greater than the sum of these radii.

H	0.38	Cr	1.53	Pd	1.68	Er	1.80
Li	0.86	Mn	1.53	Ag	1.56	Tm	1.84
Be	0.53	Fe	1.43	Cd	1.56	Yb	1.80
B	1.01	Co	1.31	In	1.53	Lu	1.86
C	0.88	Ni	1.33	Sn	1.64	Hf	1.73
N	0.86	Cu	1.31	Sb	1.64	W	1.33
O	0.89	Zn	1.41	Te	1.65	Re	1.29
F	0.82	Ga	1.40	I	1.58	Ir	1.50
Na	1.15	Ge	1.35	Cs	1.85	Pt	1.66
Mg	1.28	As	1.39	Ba	1.52	Au	1.68
Al	1.53	Se	1.40	La	1.91	Hg	1.88
Si	1.38	Br	1.39	Ce	1.98	Pb	1.72
P	1.28	Rb	1.65	Pr	1.75	Bi	1.72
S	1.20	Sr	1.30	Nd	1.92	Th	1.97
Cl	1.17	Y	1.84	Sm	1.89	U	1.76
K	1.44	Zr	1.73	Eu	1.83	Np	1.73
Ca	1.17	Nb	1.66	Gd	1.79	Pu	1.71
Sc	1.62	Mo	1.57	Tb	1.82
Ti	1.65	Ru	1.58	Dy	1.79
V	1.51	Rh	1.63	Ho	1.63

For CSD and uncalculated structures, some structures were rejected based on strange connectivity identified by visual inspection. Because this visual inspection was not performed systematically, we do not claim all instances of bad connectivity were identified.

Table 4 lists the category breakdown for 2014 CoRE MOF structures. Calculated structures were those for which an electron density distribution was calculated using DFT. Uncalculated structures were non-CSD structures for which the electron density distribution was not calculated. This could be due to one of two factors: (i) the MOF structure was so large that DFT calculation was not practical within our computational budget or (ii) the DFT calculation did not readily converge. CSD structures were those for which the geometry came directly from the CSD database.⁷ We do not report forcefield precursors for the CSD structures, because CSD licensing terms may not allow us to publicly distribute their geometries.

Category breakdown for 2014 CoRE MOF structures.

	Total structures	Rejected	Accepted
Calculated	4445	1389	3056
Uncalculated	319	63	256
CSD	345	49	296
Total	5109	1501	3608

The second column of Table 4 lists the total number of structures in each category. The third and fourth columns list the number of rejected and non-rejected structures in each category, respectively. The ESI† contains detailed lists of MOFs in each category. For each rejected structure, the ESI† lists the specific reason(s) that structure was rejected.

3. Results and discussion

3.1. Forcefield precursors

Files containing forcefield precursors for 3056 accepted calculated structures are contained in the ESI.† The data collected for each atom in a MOF includes: the coordinates; the net atomic charge (NAC); C₆, C₈ and C₁₀ dispersion coefficients; fluctuating polarizability; forcefield polarizability; electron cloud parameters; 〈r³〉 and 〈 r⁴〉 moments; QDO parameters; atomic dipole and quadrupole; atomic screened static polarizability tensor and isotropic polarizability; atomic spin moment. The data collected for the MOF's unit cell includes: the lattice vectors, the total spin magnetic moment, the net charge, and the RRMSE of the electrostatic potential for electrostatic models including (A) NACs only, (B) NACs plus spherical cloud penetration, (C) NACs plus atomic dipoles, and (D) NACs plus atomic dipoles and spherical cloud penetration. For each MOF, these data were written to a xyz file whose chemical structure can be visualized with the Jmol^95,96 program. In the future, these forcefield precursors could be used as building blocks to construct force fields for these materials.

3.2. RRMSE of electrostatic potential

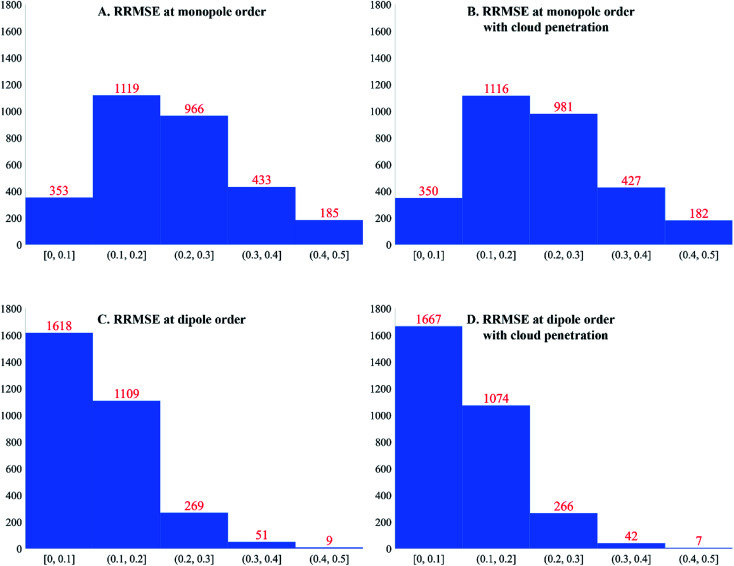
Fig. 4 plots histograms of electrostatic potential RRMSE for the accepted calculated structures. At monopole order (with or without spherical cloud penetration), the histograms peak at RRMSE = (0.1, 0.2). At both monopole and dipole orders, spherical cloud penetration had negligible effect on the histograms. Dipole order showed dramatic improvement over monopole order.

Fig. 4. Histograms of electrostatic potential RRMSE (dimensionless) for accepted calculated structures.

Some additional comments are in order. Even though spherical cloud penetration had negligible effect on the RRMSE values, this does not necessarily mean charge penetration effects are not important for constructing accurate electrostatic models. In MOF's, the RRMSE probes volume in space that is likely occupied by an adsorbate atom's nuclear position. Because charge penetration extends over the volume occupied by an adsorbate atom's full electron density distribution, it affects the electrostatic potential over a much larger volume than that probed by RRMSE calculation. For this reason, charge penetration can be more important than indicated by the RRMSE values. Prior studies demonstrated intermolecular electrostatic interaction energies are substantially improved by including charge penetration.^97–99 Therefore, including spherical cloud penetration (aka ‘charge penetration’) will likely improve the adsorbate–MOF and adsorbate–adsorbate electrostatic interaction energies even though its effects on RRMSE were negligible.

When constructing force fields, decisions have to be made about tradeoffs between simplicity and accuracy. For best accuracy, the force field should include NACs, atomic dipoles (and possibly atomic quadrupoles), and spherical charge penetration. However, the simplest force field would include NACs only and neglect atomic multipoles and charge penetration.

3.3. Atom types

Atom types are widely used in force fields.²⁹ The main idea of atom typing is to classify similar atoms into the same atom type to facilitate forcefield parameterization, where all atoms of the same atom type are normally assigned identical forcefield parameters.³² Biomolecular force fields have used atom types for several decades.^100–106 The universal force field (UFF) and its extensions to MOFs (e.g., UFF4MOF) focused on atom types for structural optimizations.^107–109

The connectivity based atom contribution (CBAC) method defined atom types in porous materials (e.g., MOFs and covalent organic frameworks) using first neighbors only.^110,111 Two significant limitations of the CBAC method are: (i) its atom types are based on first neighbors only which limits chemical transferability and (ii) the NACs for its atom types were obtained by CHELPG analysis of small fragment clusters but it is unclear how accurately these may reproduce the fully periodic electrostatic potential.^110,111

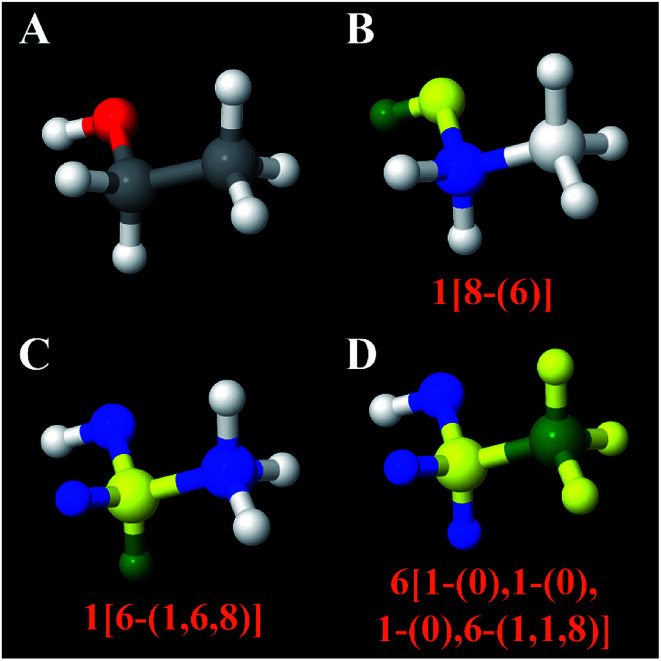
In our work, atom types are defined based on both first and second neighbors leading to better chemical transferability. Also, the NACs for our atom types were calculated using the fully periodic electrostatic potential, rather than small fragment clusters. Fig. 5 illustrates our atom typing scheme. When multiple neighbor groups are present, they are sorted by the atomic number of the neighbor atoms from smallest to largest. If a first neighbor has no second neighbors, its lack of second neighbor is indicated by (0) in the atom type label. For example, the atom type 6[1-(0),1-(0),1-(0),6-(1,1,8)] indicates a central carbon atom with four first neighbors (H, H, H, C) where each of the first neighbor H atoms is not directly bonded to any second neighbors and the first-neighbor C atom is directly bonded to H, H, and O plus the central atom. As another example, the atom type 15[6-(6),6-(6,6),6-(6,6),29-(7,7,7)] demonstrates that 6-(6) is listed prior to 6-(6,6). As another example, the atom type 7[1-(0),6-(1,1,6),6-(6,8)] demonstrates that 6-(1,1,6) is listed prior to 6-(6,8).

Fig. 5. Illustration of labeling atom types. Panel (A) shows an ethanol molecule with atoms colored by element: grey (C), red (O), white (H). Panels (B–D) illustrate the typing of different atoms in this molecule. In each panel, the chosen atom is colored green. Its first neighbors are colored yellow. Its second neighbors are colored blue. In Panel (B), the hydrogen in the hydroxy group is chosen as the central atom. It is connected to one oxygen that is connected to a carbon atom plus the central atom. In Panel (C), the α-H is chosen as the central atom. It is connected to one carbon that is connected to one hydrogen, one carbon, and one oxygen plus the central atom. In Panel (D), the β-C is chosen as the central atom. It is connected to three hydrogens and one carbon. The carbon is connected to two hydrogens and one oxygen plus the central atom.

During atom typing, two atoms were considered directly connected if the distance between them was no greater than the sum of the atom typing radii listed in Table 5. These radii have the following history. Starting with the atom connectivity radii of OpenBabel version 1.100.1, we added 0.18 Å (i.e., a skin distance was incorporated into the radii). Second, we reduced some transition metal radii to eliminate unreasonable metal–metal bonds and excessively high coordination numbers. Third, the carbon and oxygen radii were slightly increased to maintain carbon/oxygen–metal bonds after decreasing the metal radii. These radii values are unique only in an approximate sense, because small increases or decreases in the radii values may be feasible. Large changes in these radii values are not feasible, because bad atom connectivity would result.

These atom type definitions gave a total of 1313 first-neighbor atom types and 7033 second-neighbor atom types for the 3056 accepted calculated MOFs. Of these, 783 first-neighbor and 3015 second-neighbor atom types appeared in more than one MOF.

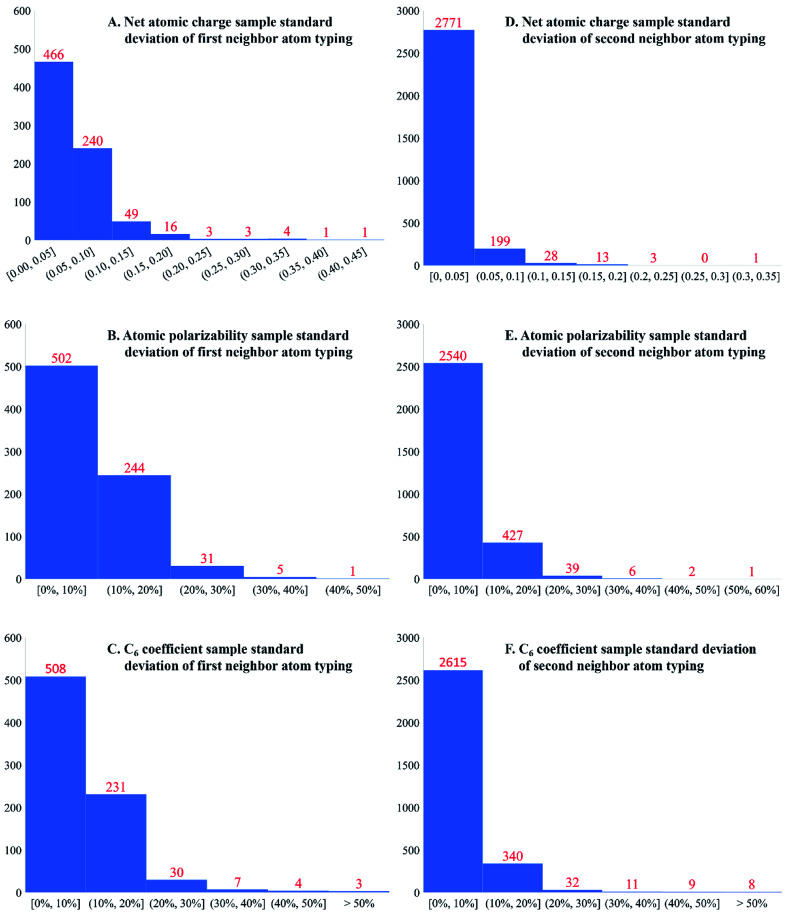
Is second-neighbor-based atom typing optimal? To explore this question, the averages and standard deviations of 17 different forcefield precursors were computed and listed in the ESI† for each first-neighbor-based and each second-neighbor-based atom type: NAC; C₆, C₈, and C₁₀ dispersion coefficients; fluctuating, forcefield, and static polarizabilities; 〈r³〉 and 〈r⁴〉 radial moments; a, b, and R² electron cloud parameters; atomic dipole moment magnitude; three QDO parameters; and atomic spin moment. Fig. 6 presents histograms of the standard deviations for NAC, forcefield polarizability, and C₆ across first-neighbor-based and second-neighbor-based atom types. Only atom types appearing in more than one accepted calculated structure were included in this analysis. Second-neighbor-based atom types showed remarkably better chemical transferability compared to first-neighbor-based atom types. For example, 91.9% of the second-neighbor-based atom types had NAC standard deviations ≤0.05e, while only 59.5% of the first-neighbor-based atom types did.

Fig. 6. Histograms of standard deviations of NACs, forcefield polarizabilities, and C₆ dispersion coefficients for first-neighbor-based and second-neighbor-based atom types. Second-neighbor-based atom types included both first and second neighbors. Each standard deviation was computed across different occurrences of the same atom type. The second-neighbor-based atom types showed much smaller standard deviations than the first-neighbor-based atom types.

This atom typing is theoretically justified, because in organic molecules electronic effects play a major role in group reactivity and induction contributes a significant portion of that effect. In organic chemistry, the inductive effect is the electron donating or withdrawing ability of a chemical group that can be transmitted to other parts of the molecule through chemical bonds.¹¹² The inductive effect usually decreases across each bond and is usually limited to 2 to 3 bonds lengths.¹¹² Our decision to base atom typing on first and second neighbors is a pragmatic one. As shown in Fig. 6, using only first neighbors leads to large standard deviations in the calculated forcefield parameters. The standard deviation is greatly reduced by incorporating second neighbors in the atom types. Incorporating third neighbors into the atom type definition would lead to an enormous number of different atom types, thus making forcefield parameterization too tedious. Therefore, second-neighbor-based atom types are optimal.

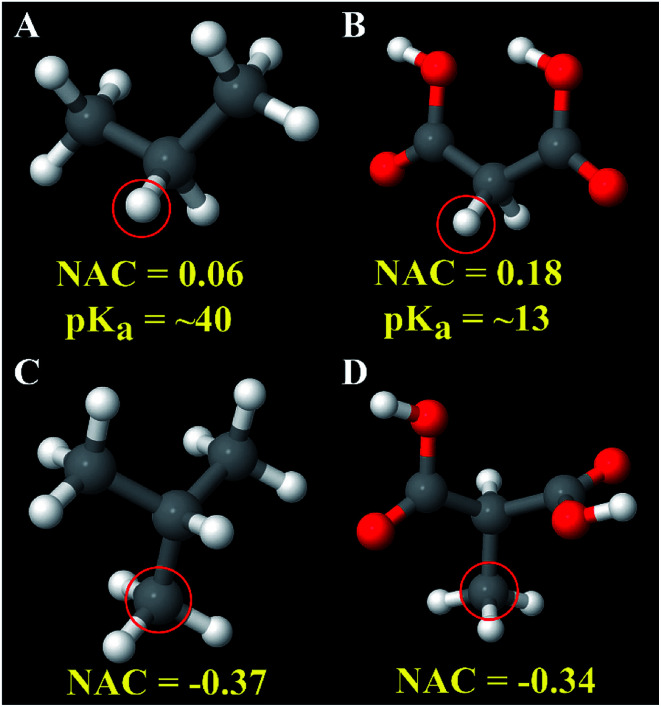
Fig. 7 explores an extreme case of third neighbor inductive effects. In malonic acid (Fig. 7B), the four highly electronegative oxygen groups withdraw electrons increasing the acidity of the circled hydrogen atom compared to the circled hydrogen in propane (Fig. 7A). Specifically, the circled hydrogen in Fig. 7B can be stripped away from the carbon atom by strong base while the one in Fig. 7A does not possess the same reactivity. The NACs of those hydrogens are 0.06 for Fig. 7A and 0.18 for Fig. 7B. If these hydrogens are replaced with a methyl group, the methyl carbon NACs are −0.37 and −0.34 respectively. These differences in NACs are within an acceptable range for atoms sharing the same atom type.

Fig. 7. Atoms of the same atom type can sometimes have different chemical reactivities. Panels (A and B) show hydrogen atoms having the same atom type but very different pK_a values. The approximate pK_a values are from ref. 113. Panels (C and D) show the good transferability of carbon atom NAC for analogous compounds in which the circled hydrogen atoms in Panels (A and B) were replaced by a methyl group.

Table 6 summarizes the breakdown of atom types in the 3608 accepted structures. A total of 8607 different atom types appeared in these structures. 3015 atom types appeared in more than one accepted calculated structure, while 4018 atom types appeared in only one accepted calculated structure. An additional 1574 atom types appeared only in the uncalculated and/or CSD structures. These results clearly show that many atom types appeared in only one MOF in the dataset. These results also show the nearly infinite chemical diversity of MOFs. For example, the 296 accepted CSD structures contained 320 new atom types that did not appear in either the calculated or uncalculated structures.

Breakdown of atom types in accepted structures.

Appeared in more than one calculated MOFs	3015
Appeared in only one calculated MOF	4018
Unique to uncalculated MOFs	1241
Unique to CSD MOFs	320
Appeared in both uncalculated and CSD MOFs but not calculated MOFs	13
Total	8607

Do a relatively small number of atom types completely describe a large percentage of the accepted calculated structures? Table 7 summarizes calculations performed to explore this question. Starting with a ‘frequency threshold’, any MOF containing any atom type that appeared in fewer than ‘frequency threshold’ different MOFs (within the 3056 accepted calculated structures) was discarded. All atom types appearing in the remaining MOFs occurred in at least ‘frequency threshold’ different MOFs in the 3056 accepted calculated structures. Then, the number of distinct atom types appearing in the remaining MOFs was counted and reported in the second column of Table 7. The results show the chemical diversity of MOFs in this dataset is well-mixed. In other words, there was not a large segregated subset of MOFs in this dataset that are completely described by a few atom types.

Exploration of most important atom types in accepted calculated structures. Each atom type appearing in the enumerated MOFs appeared in at least ‘frequency threshold’ different accepted calculated structures. The listed number of atom types is the number of different atom types in these enumerated MOFs.

Frequency threshold	# atom types	# MOFs	Frequency threshold	# atom types	# MOFs
5	1167	1120	30	166	219
10	572	682	35	138	188
15	385	508	40	120	151
20	273	334	45	106	107
25	208	268	50	94	77

Zn and Cu were the most common metal elements in the 2014 CoRE MOF database.⁷ Among the 3056 accepted calculated structures, 785 structures were built entirely of the elements Cu, Zn, C, H, N, and O. These 785 structures contained 1314 different atom types.

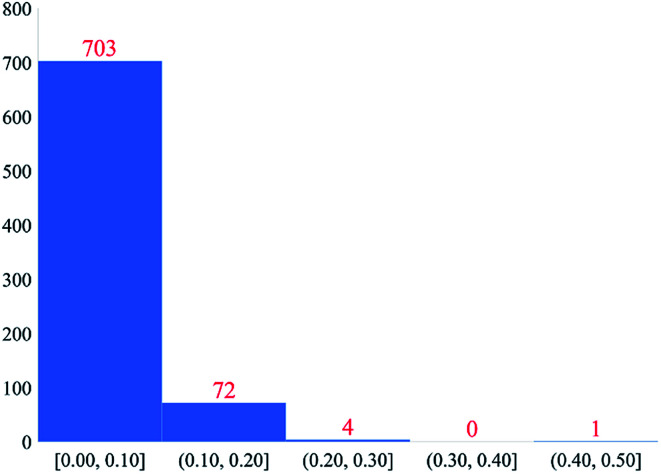
Finally, we tested the transferability of atom typing across different classes of materials. Applying the second-neighbor atom typing procedure discussed above to the molecular test set of Bleiziffer et al.,⁶² we obtained 32 530 atom types from 130 265 molecules in the dataset (aka ‘130k’ dataset). (Bleiziffer et al.'s dataset contained 130 267 structures, but we did not include the two of these structures containing unbonded atoms.) The DDEC6 NACs for these molecules are obtained from Bleiziffer et al.'s data for a dielectric constant of 4.⁶² Of the atom types from the 130k molecules and 3056 accepted calculated CoRE MOFs, 798 are shared in both datasets and 780 of these have more than one occurrence (in the same or multiple structures) in each dataset. Fig. 8 is a histogram of the absolute difference of the average DDEC6 NAC between the 130k molecules dataset and the 3056 accepted calculated MOF dataset for these 780 atom types. As shown in Fig. 8, most of these atom types had an average DDEC6 NAC absolute difference less than 0.1. This shows our atom typing scheme has good chemical transferability and can be applied to different material types. Also, Bleiziffer et al. trained a machine learning model on the 130k dataset to predict DDEC6 NACs with high accuracy.⁶² The similar DDEC6 NAC between CoRE MOF and 130k molecules datasets for a shared atom type and Bleiziffer et al.'s successful machine learning model indicate it should be feasible to train a machine learning model to predict the properties of new atom types. Due to the extremely large number of distinct atom types we found in these datasets, a machine learning model could be highly useful to assign force-field parameter values for such a large number of atom types.

Fig. 8. Histogram of absolute difference of average DDEC6 NAC between 130k molecules dataset and 3056 accepted calculated MOFs dataset. This histogram includes 780 atom types that have more than one occurrence in each dataset.

4. Conclusions

In this article, we considered the problem of how to automatically extract forcefield precursors from quantum chemistry calculations using DDEC6 atomic population analysis. We focused on calculating non-bonded parameters for each atom in the material: net atomic charge, atomic dipole and quadrupole, electron cloud parameters, atomic spin moment, dispersion coefficients, various polarizabilities, and QDO parameters. Our first main result was calculated values of these atomistic descriptors for 3056 MOFs that will serve as building blocks to construct classical force fields for these materials.

Regarding the electrostatic parameters, our results confirm the general belief that NACs can often reproduce the electrostatic potential surrounding a material with acceptable accuracy. Including atomic dipoles dramatically reduced the electrostatic potential errors; therefore, it is preferable to include atomic dipoles in the electrostatic model. Spherical cloud penetration had negligible effect on the RRMSE histograms; however, charge penetration effects can still be important at short interatomic distances.

Our second main result was the practical assessment of atom typing for MOFs. We improved values of the atom typing radii that define whether two atoms in a material are directly bonded to each other. Our results showed that atom types based on both first and second neighbors adequately captures the chemical environment, but atom types based on only first neighbors does not. Specifically, the standard deviation of calculated forcefield precursors was relatively large across atoms sharing similar first neighbor environments but relatively small across atoms sharing similar first and second neighbor environments. Including third neighbors in the atom type definition would create an unnecessarily large and burdensome number of different atom types. Therefore, atom typing including both first and second neighbors is optimal.

Our results demonstrate the large chemical diversity of MOFs. 8607 different atom types were identified in the 3608 non-rejected MOFs. These atom types should be useful to develop future force fields for MOFs. Although the MOF to atom type ratio was lower than 1.0 in our study, there are two key reasons to be believe this ratio will improve in the future: (1) the number of chemical elements from which MOFs can be synthesized is practically limited to ∼100, because heavier chemical elements undergo rapid radioactive decay. Therefore, new MOFs will reuse many of the same chemical elements. (2) There is an almost infinite number of different ways to combine common metals and common organic linkers to form MOFs.^18,19 To date, only a tiny fraction of these hypothetical MOFs have been chemically synthesized.^18,19 As more and more of these hypothetical MOFs are synthesized, many atom types will be reused leading to a higher MOF to atom type ratio. Moreover, parameterizing only the popular atom types could describe a substantial percentage of MOFs with higher MOF to atom type ratio.

In summary, more research is urgently needed to develop accurate interaction models for MOFs. Because of the large chemical diversity of real and hypothetical MOFs, it is impractical to evaluate all possible MOFs experimentally. Therefore, computational assessment is required. The interaction model is a crucial ingredient of computational assessment. Two major types of interaction models are exchange–correlation theories (e.g., DFT + dispersion) and classical force fields. The former needs orders of magnitude improvement in computational speed to yield rapid ab initio molecular dynamics. The latter requires extensive parameterization to yield accurate force fields. To actually develop working force fields, the non-bonded interaction terms studied herein will need to be combined with bonded interaction terms (e.g., bond springs, angle springs, torsion and/or out-of-plane parameters) and further parameterization of short-range exchange-repulsion. However, in simulations using a rigid framework approximation (e.g., Monte Carlo simulations of adsorption in rigid frameworks), the bonded interaction terms are not required.

Funding

National Science Foundation (NSF) CAREER Award DMR-1555376 provided financial support. Supercomputing resources were provided by the Extreme Science and Engineering Discovery Environment (XSEDE).¹¹⁴ XSEDE is funded by NSF grant ACI-1548562. XSEDE project grant TG-CTS100027 provided allocations on the Stampede2 cluster at the Texas Advanced Computing Center and the Comet cluster at the San Diego Supercomputing Center.

Authors' contributions

T. C. performed the calculations and wrote Python scripts to prepare input files, analyze output files, perform atom typing, determine whether to accept or reject structures, and write files containing force-field precursors and atom type statistics. T. A. M. wrote the programs to compute the electrostatic potential RRMSE and electron cloud parameters. T. A. M. obtained funding for the project. Both authors designed the study, interpreted data, and wrote the manuscript.

Conflicts of interest

There are no conflicts of interest to declare.