Machine learning of material properties: Predictive and interpretable multilinear models

Abstract

Machine learning models can provide fast and accurate predictions of material properties but often lack transparency. Interpretability techniques can be used with black box solutions, or alternatively, models can be created that are directly interpretable. We revisit material datasets used in several works and demonstrate that simple linear combinations of nonlinear basis functions can be created, which have comparable accuracy to the kernel and neural network approaches originally used. Linear solutions can accurately predict the bandgap and formation energy of transparent conducting oxides, the spin states for transition metal complexes, and the formation energy for elpasolite structures. We demonstrate how linear solutions can provide interpretable predictive models and highlight the new insights that can be found when a model can be directly understood from its coefficients and functional form. Furthermore, we discuss how to recognize when intrinsically interpretable solutions may be the best route to interpretability.

Revisiting material datasets reveals how specialized linear models can be both predictive and interpretable.

INTRODUCTION

Predictive models using neural networks (NNs), random forest, and kernel regression have been applied across the physical sciences, with great success in many areas (1–8). However, explaining how these types of “black box” models work can be challenging. Machine learning (ML) interpretability methods can help us understand ML models, but limitations exist with these techniques (9–16). Rather than using interpretability techniques on sophisticated ML solutions, an alternative approach is to reformulate a model into an intrinsically interpretable model (17). As long as the underlying basis remains interpretable and the solution is not overly complex (16), simple linear combination of nonlinear basis functions (which we will refer to as linear models) is an excellent approach for interpretable predictions. In this work, we highlight examples where kernel methods or NNs have been used, but alternative directly interpretable solutions exist. In doing so, we demonstrate the benefits of moving toward simpler regression models where possible. Furthermore, we discuss how to identify the set of problems that can be described without complex nonlinear solutions and the alternative approaches for creating intrinsically interpretable models.

The prediction of a material’s properties using ML has been a subject of interest in the material science community for many years (1, 18–21). Understanding how these predictive models work is also highly important (2–5, 5, 22–29). Interpretability has been considered in the development of the model itself; examples include the rule-based descriptors (5, 22) and symbolic regression (30). These are intrinsically interpretable models that do not require further processing steps to be analyzed. The development of SISSO (sure independence screening and sparsifying operator), which can automatically create analytical formulas from physical properties, has been particularly influential in this area (5, 26). Alternatively, post hoc interpretability methods can be used to analyze a nonlinear ML model after it has been fit (1, 24, 28). However, most ML regression models remain black boxes without clear explanations for their predictions.

As an example, we consider the winning model of the crowd-sourced material science Novel Materials Discovery (NOMAD) Kaggle competition discussed in (19). This competition involved in predicting the relative formation energy and electronic bandgap energy for a set of transparent conducting oxides (TCOs), specifically (Al_xGa_yIn_z)₂O₃ compounds (with x + y + z = 1). The winning group used a kernel ridge regression (KRR) model. However, while a KRR model can explain predictions in terms of similarity to other data points, models built with KRR do not provide a description of the nonlinearity or the interactions present or give a breakdown of the contribution of each variable to an outcome. We begin by considering the connection between the representation used in the winning solution of the NOMAD Kaggle competition and the cluster expansion method (31–33). We then demonstrate that linear models with pairwise interaction terms can predict the formation energy and bandgap energy of TCOs with the same accuracy as the kernel approach originally used.

We then show two further examples where simple linear models can be built. First, for the prediction of formation energies for elpasolite crystals from (21). These are quaternary crystals with the form ABC₂D₆ in the Fm3m space group. Again, KRR is not required, and a highly accurate linear model for the formation energy can be created. The existence of an accurate linear solution can be anticipated by considering both the discrete nature of the variables and the size of the dataset used. We then demonstrate that the prediction of spin splitting in transition metal complexes, as carried out in (34), can be performed with a linear solution. In the resulting model, the coefficients reflect trends in the dataset and known physical principles.

Before the datasets are revisited, it is important to consider what is meant by interpretability. Interpretability is a concept with a definition that is specific not only to a given field but even also to a given paper. Although steps have been taken to try and clarify what is meant by interpretability [see (25) for an insightful discussion], a clear general definition is lacking. In this work, we refer to the linear solutions we create as interpretable as both an overall understanding of the global model can be achieved because of the simplicity of the functional form, and individual predictions can be broken down into contributions from variables and interactions. However, as interpretability is a subjective and field-dependent concept, other viewpoints will exist, particularly regarding the required sparsity of the model. Greater consensus may be reached as the area is further developed; however, it is currently not possible to strictly define a model as interpretable or not.

The problems around interpretability extend to discussions around its benefits. Advantages can be stated such as improvement in scientific understanding, trust, new chemical and physical insights, and increased knowledge. However, rather than focus on indefinite concepts, we instead identify a set of characteristics and associated advantages:

1) By analyzing the coefficients of a linear model, it can be seen whether a model agrees or disagrees with known physical principles. As we will show, this can serve as a form of validation test for physical behavior. For example, the expected trends in the elpasolite formation energy across the periodic table can be seen from the coefficients of the linear model created.

2) With a clear functional form, the assumptions present in a model can be seen. This allows us to compare the new solution to existing predictive models and to recognize the physical assumptions present. This can indicate in which regimes a model will work or fail. By reformulating the solution for the TCOs to a specialized linear model, the similarities and differences to cluster expansion—an established method in materials modeling—can be recognized, and the systems the model will accurately describe can be predicted.

3) The coefficients of a linear model can provide information that can be used to guide future predictions. This can make property prediction faster by focusing on important variables and interactions. We use this for the elpasolite universe to perform a focused search of low formation energy structures.

While using post hoc interpretability methods on nonlinear solutions can help with the analysis, being able to use the coefficients of a linear model is much simpler and does not require further calculations. Furthermore, the functional form is stated. Visualizing the relationship between hundreds of variables and a predicted outcome is more complex than having the relationship described by a well-defined formula. Interaction detection is possible with post hoc interpretability methods but can require expensive or complex techniques (11–15, 35, 36). Approaches using symbolic regression or SISSO also have the characteristics listed (5, 22, 30). However, automated searches for analytical formula can become prohibitively expensive when there are a large number of features. In addition, analyzing a model containing hundreds of basis functions with multiple different transforms becomes extremely challenging. Therefore, these techniques have not been used for the applications studied in this work. Instead, we use a much smaller number of possible operators that are guided by physical insight. We also focus on datasets with a large number of features, where it has not been realized that simple linear combinations of nonlinear basis functions produce accurate predictive models.

The examples we revisit were innovative contributions to the field that helped to establish the power of complex nonlinear ML methods for predicting chemical and material properties. By producing specialized linear solutions for these challenging tasks, we provide new insight about how these predictive models work and demonstrate that changing the type of regression model used can be a viable route to interpretability. Generalized nonlinear solutions will offer accurate models for a wide range of problems, but the use of more specialized regression models can provide benefits beyond accuracy. This has already been seen with the development of linear interatomic potentials and the associated improvements in speed and extrapolation (37–40). Here, we show the benefits of interpretability with predictive linear solutions.

RESULTS

Transparent conducting oxides

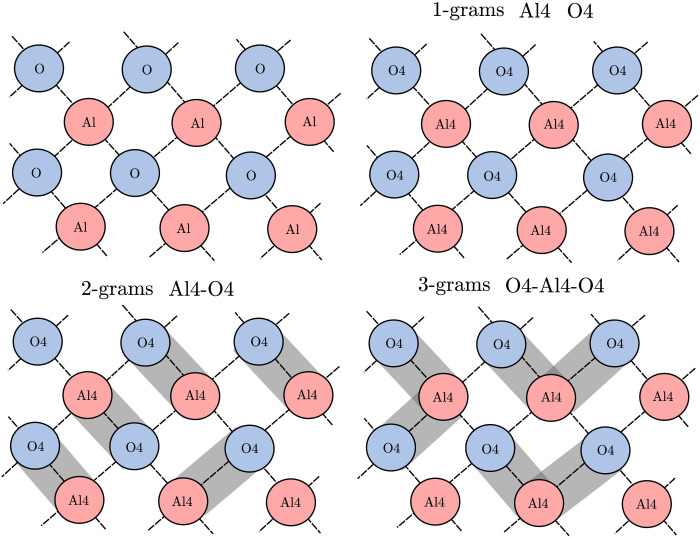
The first example that we will examine is the winning model of the NOMAD Kaggle competition and the prediction of formation energies for TCOs. The representation scheme used in this model was n-grams. The simplest form of n-grams is 1-grams, which describe each atom by its element type and coordination number (see Fig. 1). The number of each type of 1-grams in the unit cell is then counted and divided by the volume of the unit cell. Sequences of neighboring 1-grams are constructed, with up to 4-grams in this case. That is, the number of connected clusters in a given volume is used as the representation.

Fig. 1. A diagram of the n-gram representation.

The n-gram representation is shown for an example material. The 2-grams and 3-grams shown do not represent all those present in the structure.

The motivation for constructing a linear model for this case comes from considering the parallels between the n-gram representation and cluster expansion. Cluster expansion represents the elements present in a material by spin-like variables on a fixed lattice (33). Distinct clusters on a lattice are then defined, and the sum of the spin product across the clusters is calculated. Coefficients are then assigned to each distinct clusters to calculate the formation energy. The n-gram representation is not formulated from a spin-based model but effectively counts the number of unique spin configurations for small clusters. Given the similarities between the approaches, the existence of an accurate linear model using the n-gram representation can be hypothesized. Two linear models were constructed with the n-gram representation. First, a linear additive model without interactions present

$$E(\mathrm{\chi })={\sum }_i{\mathrm{\alpha }}_i\frac{{\mathrm{\chi }}_i}{V}+c$$ (1)

where χ_i is the number of n-gram clusters of type i, V is the volume of the unit cell, and the α_i coefficients are calculated by fitting to the dense functional theory (DFT) data. Second, a linear model with pairwise cluster-cluster interactions

$$E(\mathrm{\chi })={\sum }_i{\mathrm{\alpha }}_i\frac{{\mathrm{\chi }}_i}{V}+{\sum }_{j<i}{\mathrm{\beta }}_{\mathit{ij}}\frac{{\mathrm{\chi }}_i{\mathrm{\chi }}_j}{V^2}+c$$ (2)

The presence of pairwise interactions between clusters will incorporate nonlocal and higher body order effects into the model. Note that these are interactions between different n-gram clusters and not between different atoms. We will refer to Eq. 2 as a bilinear model. A KRR was retrained using the settings described in (19). In (19), it was shown that using NN or light gradient–boosting machine did not improve results. The linear model was fit to the whole training set at once and did not explicitly identify or separate a structure by its space group (six different space groups are included in the dataset $R\overline{3}c$, C2/m, Pna2₁, $\mathit{Ia}\overline{3}$, P6₃/mmc, and $\mathit{Fd}\overline{3}m$). Details of the LASSO (least absolute shrinkage and selection operator) fitting procedure are given in Materials and Methods.

The mean absolute error (MAE) for the testing and training set is shown in Table 1. The comparable performance of the bilinear model and the kernel model can be seen. The linear additive model has an error that is 51.1% higher than the bilinear model, indicating the importance of interactions between clusters for this problem.

Table 1. The training and testing set MAE of the KRR regression models and the linear regression models for the formation energy (E_f) and bandgap energy (E_bg).

The score for the bilinear model using the measure used in the NOMAD competition is 0.079 and 0.020 for the E_bg and E_f, respectively.

	MAE (eV per cation)
	E f		E bg
Model	Train	Test	Train	Test
KRR	0.011	0.015	0.088	0.107
Linear	0.022	0.022	0.143	0.143
Bilinear	0.013	0.015	0.085	0.105

Replacing a KRR model with a linear model is advantageous for a number of reasons. The functional form and coefficients of the model enable a global understanding to be achieved. The n-gram representation partitions a structure into distinct clusters that are identified by the elements present and their coordination number. The linear model then assigns a contribution to the formation energy for each of the clusters present. The interaction cluster-cluster term adds a further contribution to the formation energy if two specific kinds of clusters both occur in the material. As the nonlinearity incorporated into the KRR model is not explicitly defined, gaining a global understanding of the model is extremely challenging. As previously noted, the linear n-gram model has similarities with cluster expansion, which also identifies distinct clusters of atoms, uses a linear model, and is fit to DFT data. However, by using the coordination number of an atom to identify clusters, the n-gram model can be accurately fit to multiple space groups at once and can be used on lattices it was not explicitly fit to. This increases the number of basis functions but does not decrease performance as LASSO is used to sparsify the basis. The advantages of applying l₁ regularization for cluster expansion have previously been seen (41). An additional difference between the two approaches is that cluster expansion does not include the pairwise cluster-cluster interactions.

Understanding the link between cluster expansion and linear n-grams is not just an interesting insight but has clear practical benefits. Recognizing the assumptions present in a model, and how existing predictive models relate to one another, can help us predict the systems a model will accurately describe. The capabilities and limitations of cluster expansion are known and can be used to predict the accuracy of linear n-grams. For example, in (42), cluster expansion was shown to perform poorly for the prediction of the mixing energy, E_me, of 8043 symmetrically different Zn₈Mg₂₄O₃₂ structures in a 64 atom supercell. This is a dataset with a fixed composition, multiple space groups, and a very narrow energy range. The assumptions present in the cluster expansion model fail to describe the system accurately. In linear n-grams, the atoms are represented by the element type and the coordination number, and this allows multiple space groups to be accurately modeled. The presence of pairwise interaction terms will further improve performance as the model is not limited to localize four atom descriptions. We can therefore predict that the linear n-gram model will improve on cluster expansion and better describe the small energy differences between structures and multiple space groups. We are able to make this prediction as the physical assumptions present in linear n-grams are known, as is the link to cluster expansion. The test set MAE for cluster expansion in (42) for the E_me was 20 meV per supercell when trained to 6434 structures. However, this corresponds to an R² (coefficient of determination) of 0.39 as the energy range is very narrow. In contrast, linear n-grams have an MAE of 5.7 meV per supercell and an R² of 0.96, a substantial improvement. We can also predict that linear n-grams will accurately describe materials that cluster expansion has shown to perform well for, e.g., an AgPd system (43). When fit to 600 face-centered cubic structures from (43), linear n-grams can reach a test set accuracy of 3.6 meV per atom. This is comparable to the accuracies reached by state of the art interatomic potentials (43).

Another advantage of a linear model is that the contribution of variables to an individual prediction can be calculated. For nonlinear models, methods such as SHAP (SHapley Additive exPlanations) or LIME (Local Interpretable Model-Agnostic Explanations) can show estimated contributions from individual variables (14, 15). Linear models do not require assumptions to calculate variable contribution, and moreover, interaction and individual effects can be completely separated. As the contributions are simply calculated by the coefficient multiplied by the variable, there is also little barrier to understanding linear contributions.

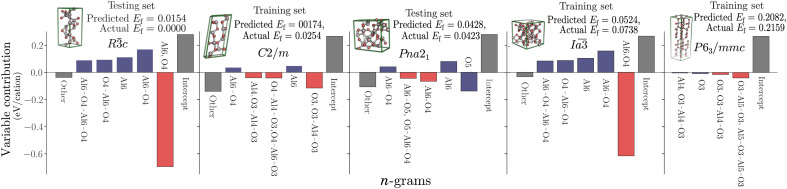
To explore variable contributions further, we examine the five polymorphs of aluminum oxide contained in the dataset (Fig. 2). The order of the formation energies for the structures are correctly recreated with the linear model, despite $R\overline{3}c$ and Pna2₁ not being present in the training set. Figure 2 shows that $R\overline{3}c$ and $\mathit{Ia}\overline{3}$ have the same variables contributing to the formation energy, demonstrating the similarity of these two structures in the n-gram representation. Despite the similarity, however, there is still a difference of 0.037 eV per atom in the predicted formation energy. This is due to the slightly higher amount of Al6 and O4, and associated n-grams, per unit volume in $R\overline{3}c$. This level of insight into individual predictions, with variable and interaction contributions identified, is another advantage of linear models.

Fig. 2. The variable contributions for the aluminum oxide polymorphs.

For the five Al₂O₃ polymorphs in the transparent conduction oxide dataset, the contributions of the top five variables to the predicted formation energy are shown, with the remaining contributions and intercept also given. These can be calculated directly from the bilinear model by α_ix_i or β_ijx_ix_j, and the predicted energy is simply the sum of all variable contributions. Interaction terms are shown in red, and main effects are shown in blue. Energies are given in electron volts per cation.

For the prediction of the bandgap energy, again, we see that a linear model with pairwise interactions is sufficient to recreate the bandgap energy with comparable accuracy to KRR (Table 1). Therefore, both the formation energy and bandgap energy can be predicted using an alternative linear model. The comparable accuracy between KRR and a linear model emphasizes the importance of representations for this problem. Although cluster expansion has previously been used for the prediction of the bandgap energies, its use has been limited compared to the wide-spread prediction of formation energies (42, 44, 45). The performance of cluster expansion for bandgap energy prediction has been varied and is dependent on the system studied (42, 44,45). It is yet to be seen whether the addition of cluster-cluster interactions using l₁ regularization and adding the coordination number of the element to identify atoms can allow linear n-grams to accurately predict bandgap energies for a wider range of materials. However, the performance for TCOs is promising.

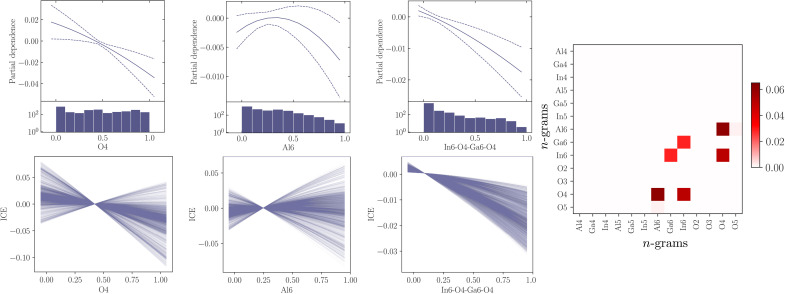
To investigate whether the kernel solution originally proposed resembles the n-gram linear model, post hoc interpretability techniques were used to visualize the kernel solution for the formation energy. Partial dependence (PD) plots show the average relationship between a variable and the outcome for an ML model; a further description is provided in Materials and Methods (9). An ensemble of KRR models is used for this analysis with the variation in the solutions shown. A measure of the uncertainty present is necessary to see if the trends are robust to small changes. The PD plots for the kernel model for three variables are shown in Fig. 3. This figure demonstrates that the predicted formation energy tends to decrease linearly with a higher percentage of O4 and In6-O4-Ga6-O4. This linear trend generally continues across other variables and higher-order n-grams, with a linear solution within the 95% confidence interval of the PD plots for the vast majority of examples.

Fig. 3. The PD, ICE, and interactions for the KRR TCO model.

PD and ICE plots for two 1-gram features (O4, Al6) and one 4-gram feature (In6-O4-Ga6-O4) for the KRR model for formation energy. The interactions between the 1-grams in the KRR model are also shown. The code required for this plot is available at https://github.com/aa840/icepd.git.

However, for many variables, the uncertainty of the PD is large, and conclusions cannot be reached, as there is not a consensus in behavior across the ensemble, as shown by Al6 in Fig. 3.

The PD plots can be supplemented by individual conditional expectation (ICE) plots to see if the behavior is consistent across all data points (Fig. 3) (10). PD plots show the averaged behavior of a variable, whereas ICE plot show the behavior at multiple data points. For O₄, the ICE plot demonstrates that while the relationship between the variable and outcome remains linear, there is variation in the gradient. For other variables, a similar trend can be seen with the relationship between the variables and the outcome following a linear trend but with inhomogeneity in the gradient across the data points. This inhomogeneity indicates that interactions are present in the model. The pairwise interactions for the 1-gram features are shown in Fig. 3. The strongest interactions present are between Al6 and O4. This interaction was also important for the aluminum oxide polymorphs and is consistently nonzero across an ensemble of linear models. The 2-gram interactions are shown in fig. S2.

The linear behavior and the presence of interactions in the kernel model suggest that not only is the linear solution as accurate as the kernel model but also the solutions have additional similarities. If the possibility of using a linear combination of nonlinear basis functions had not been previously recognized, then visualizing the relationships between the variable and outcome through ICE plots could have exposed this. Likewise, possible transforms could also have been found by examining the ICE and PD plots.

We will now demonstrate how the discovery of TCOs can be guided by information from the specialized linear models. When analyzing predictive models, it is important to consider that there may be multiple solutions to the underlying problems and not one unique solution. While analyzing individual predictive models can be useful, care has to be taken when drawing general conclusions about TCOs. The consistency of trends in the coefficients can be explored by examining the deviation in values across an ensemble of linear models. This is shown in fig. S3, where variation is seen in the coefficients across the ensemble. When two properties are being optimized, the variables that influence both are of particular interest. Their presence will positively contribute to multiple properties. If a large bandgap, low formation energy material is desired, then we want to identify variables that increase the bandgap and lower the formation energy. These variable can be found by examining the large coefficients present in both models. This is shown in fig. S3C for the ensemble linear models. Three variables result in both a high bandgap and low formation energy. Two are interactions variables between Al6,O4 and O4,Ga6 and then the single variable O5. If we wanted to design new compounds, then we could therefore concentrate on creating structures that contain these n-grams. This analysis would in theory be possible using a nonlinear model; however, using post hoc interpretability methods on all possible pairwise interaction would be prohibitively expensive. Of the three identified coefficients, the O5 variable is of particular interest as this is only present in the Pna2₁ space group. A focused searches of structures in this space group could be performed and weighted toward producing high O5 concentration structures. When suitable compounds where found, the lowest-energy polymorph could then be identified. Within the existing dataset, a very clear relationship between the bandgap energy and O5 concentration can already be observed (see fig. S3D).

By reformulating the n-grams model, we have shown how moving toward simpler regression models can expose the assumptions in a model and discussed how analyzing an ML model can guide future predictions. We have begun to demonstrate the advantages of moving away from generalized nonlinear solutions, and we will continue to do so with two further examples.

Elpasolite crystals

In (21), a predictive model for the formation energy of 10,590 elpasolite structures, with quaternary crystal structure ABC₂D₆ in the Fm3m space group, was produced using KRR. The features used to describe the structures were the principle quantum number (n) and number of valence electrons (v) at each site A, B, C, or D. The primary reason why a linear model is expected to work for this problem is the discrete nature of the variables. As there are only a discrete number of possibilities for each variable (either six or eight), the variables can be one-hot encoded (i.e., n_a can instead be represented as six separate binary variables: n_A1, n_A2, n_A3, n_A4, n_A5, and n_A6). This assigns each row and column in the periodic table a distinct contribution to the formation energy. If a variable is binary, then transforms do not need to be considered, and therefore, the set of possible solutions is greatly decreased.

A linear model was produced with interactions between up to three variables included (trilinear)

$$\begin{array}{cc}\hfill E(n,v)=& {\sum }_i{\mathrm{\alpha }}_i{n}_i+{\sum }_i{\mathrm{\beta }}_i{v}_i+{\sum }_{j<i}{\mathrm{\alpha }}_{\mathit{ij}}{n}_i{n}_j+{\sum }_{j<i}{\mathrm{\beta }}_{\mathit{ij}}{v}_i{v}_j+\hfill \\ & {\sum }_{i,j}{\mathrm{\gamma }}_{\mathit{ij}}{n}_i{v}_j+{\sum }_{k<j<i}{\mathrm{\alpha }}_{\mathit{ijk}}{n}_i{n}_j{n}_k+{\sum }_{k<j<i}{\mathrm{\beta }}_{\mathit{ijk}}{v}_i{v}_j{v}_k+\hfill \\ & {\sum }_{k<i,j}{\mathrm{\gamma }}_{\mathit{ijk}}{n}_i{v}_j{n}_k+{\sum }_{k<j,i}{\mathrm{\lambda }}_{\mathrm{ijk}}{n}_i{v}_j{v}_k\hfill \end{array}$$ (3)

where i sums over all positions (A, B, C, and D) and all one-hot encoded values. Again, LASSO was used to fit the coefficients, with further details given in Materials and Methods.

For this problem, it is clear that at least pairwise interactions will be important, as otherwise, the formation energy for an atom would be dictated purely by its group and period.

There are fundamental limits to the interaction order that can accurately be fit in a dataset of a given size. If there are 10,000 data points with around 40 different elements at four different positions, then this means that if everything is approximately uniform, there will only be around six structures in the training set for any two elements at a given position. For example, the number of training structures with Ca at A and Mg at B will be approximately 6. This means that it may be possible to include important interactions between four variables as there is adequate data. However, beyond that, the training set is not large enough to capture important interactions; the sampling is insufficient. High interaction order effects can only be important in a model if the dataset size is large enough to sample them properly.

At 10,000 data points, the trilinear model has an MAE of 0.11 eV per atom. In (21), an MAE of 0.10 eV per atom was reported for a KRR model. Therefore, the trilinear model offers comparable accuracy to the KRR model. The accuracy of the DFT data has been stated as between 0.10 eV per atom for transition metal oxides and elemental solids and 0.19 eV per atom for heats of formation for filled d shells (21, 46,47). Three variable interaction terms are necessary as the pairwise interaction model does not provide the same performance at 0.14 eV per atom. However, an MAE of 0.14 eV per atom is still relatively low and much improved on the linear additive model, which has an error of 0.46 eV per atom.

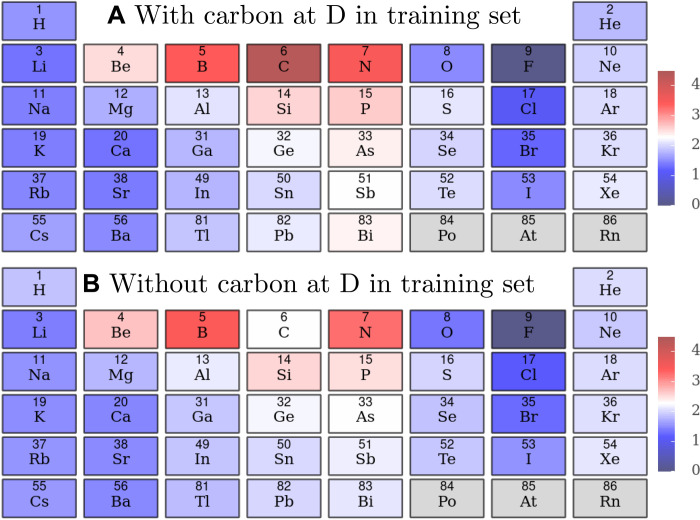
With the linear model, trends in the behavior of elpasolites can be directly seen from the model. For example, in (21), it was found that fluoride lowered the formation energy at position D the most. Carbon at position D, on the other hand, was associated with the highest formation energy. Using the coefficients of linear model (simply summing the coefficients of n_Dx and v_Dy and the pairwise interaction term n_Dx, v_Dy), the contribution of each element to the formation energy can be isolated (Fig. 4A). In Fig. 4A, it can be seen that carbon at position D has the highest contribution to the formation energy, while fluorine at position D has the smallest. This trend reflects that fluorine prefers to form heteronuclear bonds rather than homonuclear bonds, while carbon prefers to form homonuclear bonds. Therefore, we can see how the coefficients reflect known physical principles. In addition, the contribution of the individual coefficients can be calculated (fig. S4). For example, carbon’s contribution to the formation energy at position D is composed of n_D2 and v_D4 and n_D2, v_D4 with coefficients of 0.48, 0.68, and 1.39, respectively. This demonstrates the importance of the pairwise interaction term for this case, indicating that carbon does not follow the trends of its group and period.

Fig. 4. The contribution to the formation energies across the periodic table for site D.

The formation energy (in electron volts per atom) for each atom at site D for (A) a model with carbon included in the training set and (B) a model without carbon included in the training set at position D. This is calculated directly from the coefficients of the model, and the zero point is set to the lowest value of fluorine.

In addition, we can begin to understand why extrapolation to a new regime may fail. To illustrate this, we retrained the trilinear model with a training set of 10,000 structures, none of which contained carbon in position D. A test set was constructed consisting of 295 elpasolite structures with carbon in position D, and the resultant error was 2.07 eV per atom. The error on a test set without carbon in position D was 0.11 eV per atom, 20 times smaller. The contribution of each atom to the formation energy at position D for this model is shown in Fig. 4B). The trends are identical to original model, except for carbon’s formation energy, which is noticeably different, 2.24 eV per atom compared to 4.34 eV per atom. This is because the important pairwise interaction term previously discussed is zero in this new model. Generalizability and interpretability are connected concepts, and when we can understand how a model works, we can begin to understand whether a model will work or fail.

To show that the linear model is still capable of exploring the elpasolite universe, the formation energies for ~2 ×10⁶ ABC₂D₆ structures were calculated. We then examined the 250 lowest-energy structures to see if the lowest-energy structure suggested in (21), CaSrCs₂F₆, was found. In (21), the low-energy structures all contained fluorine in positions D, and the same is seen for the linear model. We also again see that CaSrCs₂F₆ is in the bottom of 250 energies identified by the linear model. As with the TCOs, the contributions of each term to an individual prediction can be calculated. However, in this case, it should be appreciated that as each value is one-hot encoded, the meaning of the zero value has changed. Therefore, we can now understand why CaSrCs₂F₆ is predicted to have a low energy (Fig. 5). Fluorine at position D lowers the formation energy as we have previously seen, and the cesium atom at position C has a negative contribution to the formation energy too. However, what is also essential is the pairwise interaction terms between v_D,v_A and v_D,v_B and v_D,v_C, which all lower the formation energy by at least −0.25 eV. Therefore, not only can a linear model be used to explore the elpasolite universe and identify low-energy structures, but it can also show the important interactions present.

Fig. 5. The variable contributions for CaSrCs₂F₆.

The variable contributions for CaSrCs₂F₆; the formation energy for this material is −3.11 eV per atom.

As previously noted, one of the benefits of interpretable ML models for materials is assisting in predictions. The coefficients of the linear model from the elpasolite structures can help us more efficiently explore regions of the elpasolite universe we wish to investigate further. For example, we may be interested in the low formation energy elpasolites. At the simplest level, this could mean exploring only materials with fluorine at position D. However, if we only used information about single sites, the optimal structure suggested would be FFBa₂F₆. This is not a low-energy structure, and the bonding between different sites is not considered. Therefore, interactions between terms must be taken into account. These interactions are not easily accessible in a nonlinear model. With a three variable linear model, we have access to a large amount of information from the coefficients. If we want to identify materials with a low formation energy, as an example, then we can exploit this information. Rather than search the full space of the elpasolites, we can instead focus on the highly negative three variable contributions and construct algorithms that will favor low-energy structures.

A set of 260 unique structures was produced using an algorithm based on three variable contributions described in Materials and Methods, with the position of these structures in the elpasolite universe shown in fig. S5. The sampled structures are consistently in the low-energy regime, with 46 of the 100 lowest structures in the elpasolite universe of 2 ×10⁶ structures being identified within this small set of proposed structures. This is far more efficient than randomly searching the elpasolite universe even when position D is constrained to containing fluorine (see fig. S5). Given that the elpasolite universe can be fully explored and has been already analyzed, improving sampling for this system is not necessary. Nonetheless, the possibility of using analysis from an ML model to guide predictions has been highlighted, and the advantages of using linear combinations of terms have been seen.

Transition metal complexes

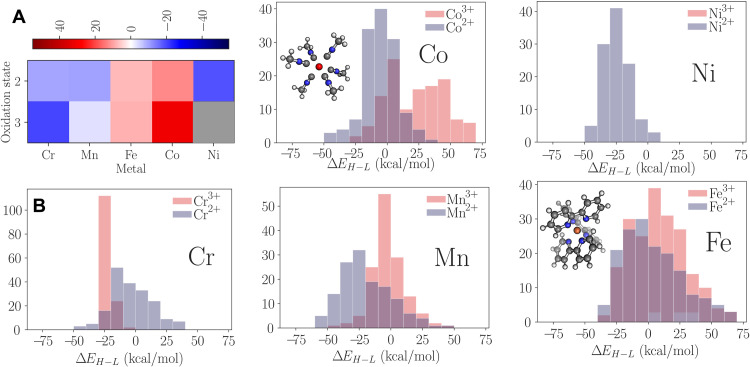
In transition metal complexes, the degeneracy of the d-orbitals of the central metal ion is broken by the presence of the surrounding ligands. For octahedral complexes, three d-orbitals are at a lower energy than the remaining two d-orbitals. This leads to the existence of two spin state configurations, a high and a low spin state. The size of the spin splitting is connected to various properties of the ligand and the metal ion, and therefore, these properties were used as variables for an NN model in (34). The Hartree-Fock exchange fraction of the B3LYP functional was also used as a variable. The energy difference between high and low spin state, ΔE_{H − L}, was predicted for a set of octahedral transition metal complexes.

For this example, continuous variables are present, but the variables describing the oxidation state/element of the metal ion and the connecting element of the ligand atoms are binary. The variables describing the charge and denticity of the ligands have only three possible values. Furthermore, spin splitting has previously been shown to be linearly dependent on the Hartree-Fock exchange fraction (48, 49). Therefore, restricting this variable to a linear form will not decrease the predictive performance. The variables mentioned are all expected to be highly important in the predictive model. Given these factors, a linear model with interactions is a viable option. A trilinear model was constructed, with three variable interaction terms included and again fit using LASSO, with details given in Materials and Methods. Interaction terms between three variables allow for contributions that are dependent on the nature of the two types of connecting ligands and the metal ion. Interactions also allow the sensitivity to the Hartree-Fock exchange to be dependent on properties of the ligand, which has been previously observed (49).

The trilinear model offers comparable accuracy to the NN result used in (34). The testing (training) set root mean square error is 2.2 (1.7) kcal/mol for the linear model and 3.1 (3.0) kcal/mol for the NN reported in (34). Figure 6A) shows how the contribution to the predicted spin splitting changes with the metal ion and its oxidation state. This can be calculated using the coefficients for the metal ion, oxidation state, and pairwise term for the metal and oxidation state together. Higher-order effects are again not considered. In Fig. 6B, the distribution of the spin splitting for different metal ions and oxidation states dataset is shown. Manganese with oxidation state 2+ is predominantly in the high spin state configuration, and therefore, the net negative contribution for the Mn²⁺ coefficients is expected. Other factors will be important for the prediction, but it would be suspect if the coefficients for Mn²⁺ were large and positive. In addition, the differences between the oxidation states can be seen. Cobalt shows this as Co³⁺ has a larger value than Co²⁺. This is then reflected in the distribution of the energy difference for cobalt, with Co³⁺ in the low-energy state more frequently than Co²⁺.

Fig. 6. The model coefficients and dataset distributions for the transition metal complexes.

The (A) contribution from the metal and oxidation state to the predicted spin splitting. The gray indicates that Ni³⁺ is not present in the dataset. The (B) distribution of ΔE_{H − L} for different metal ions in the dataset. If the difference is positive, then the spin configuration is low, and if the difference is negative, then the spin configuration is high.

The coefficients of the linear model reflect the physical principles that underpin transition metal spin splitting. The electron configuration for Cr³⁺ is [Ar]3d³, and therefore, it cannot exist in a low spin state as at least four electrons must be present in the d-orbitals. The lack of low spin states can be seen in the distribution of ΔE_{H − L} in Fig. 6B. Consequently, the coefficient contributions for Cr³⁺ are highly negative, reflecting that Cr³⁺ is always associated with the high spin state. This shows how analyzing a linear model can reveal that physical properties are reflected in the model.

DISCUSSION

One of the interesting aspects of interpretable ML is that the best route to interpretability depends on the underlying problem and dataset. Identifying if a directly interpretable regression model is available requires the consideration of a number of factors. Comparing the representation used in a nonlinear model with existing physically motivated models, as well as considering the nature and known relationships between variables, can help to identify when simplistic linear solutions can replace a nonlinear model. Another key factor is the size of the dataset, as discussed for the elpasolite structures, as the larger the dataset, the more constrained the space of possible solutions is.

Once it has been identified that complex nonlinear solutions may not be necessary, the next step is to decide how to construct an interpretable model. In this work, we have constructed linear combinations of nonlinear basis functions by applying knowledge about the physical system and variables and manually adding new terms. Although we have not used variable transforms in these examples, this could additionally be incorporated into the process. However, alternative approaches have also been used to discover intrinsically interpretable solutions.

Automated methods exist to produce physically meaningful descriptors with well-defined formula. These methods include symbolic regression and rule-based descriptors (5, 22, 30, 50, 51). Complex relationships can be recreated with these approaches, but because of poor scaling, there are difficulties in using these methods if there are a large number of variables (5, 50). However, they remain an extremely effective approach to producing physically meaningful formula. Complex linear polynomials, such as those used in interatomic potentials, can also be created with automated approaches (37–40). However, if there are tens of thousands of basis functions with varying forms, then analyzing a linear solution by its individual coefficients becomes practically impossible.

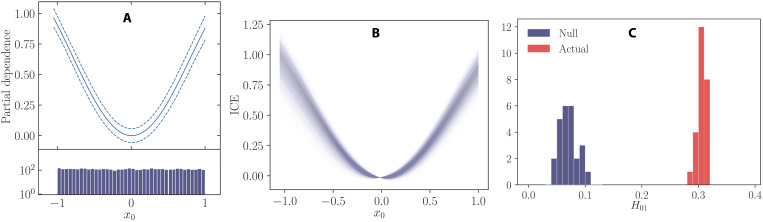
To varying degrees, the links between linear and nonlinear models can be described analytically. For example, there is a known exact equivalence between linear models and polynomial kernels, and for other kernel types, approximations to linear models can be produced. Visualizing nonlinear solutions provide an alternative way to compare the links between a linear and nonlinear solution. PD and ICE can both be used to visualize the relationship between a variable and the predicted outcome as seen for the TCOs (9, 10). If clear relationships can be seen in the nonlinear solution, then a linear model can subsequently be built that incorporates these relationships. For example, Fig. 7 shows PD and ICE plots for simulated data. The quadratic relationship of the x₀ can be observed in both plots, and if the relationship was not previously known, then the x₀ variable could be squared and used in a linear model. The ICE plot would confirm that the relationship seen was consistent across many data points in the dataset. Alternative methods exist for producing intrinsically interpretable models, such as using generalized additive models or simple decision trees. They provide another route, which also does not rely on using post hoc interpretability methods.

Fig. 7. An example of PD, ICE and interaction detection for simulated data.

The (A) PD and (B) ICE plot for x₀. The simulated data have the form $f(x)=x_0^2+0.1{\sum }_{i=1}^{N-1}{x}_i+\mathrm{ϵ}$, where x is drawn from a uniform probability distribution between −1 and 1 and ϵ ∼ N(0,0.25). The $x_0^2$ relationship can be seen in the PD. The dashed lines show the 95% confidence interval, and the solid line is the mean value for the five models fit. An NN model is used. The PD plot it centered so that PD(0) = 0 for the mean of the ensemble. The ICE plot is centered so that $\widehat{f}(0,x_c^{(i)})=0$. (C) The distribution of H statistics for the real ensemble model and null distribution for an NN ensemble model fit to f(x) = x₀ + x₁ + x₀x₁ + ϵ.

There are many problems that cannot be simplified this way. For example, intrinsically interpretable models cannot be created for interatomic potentials or for predicting the formation energy of a material purely from stoichiometric information without a large reduction in accuracy (6, 52, 53). While linear models can be created for interatomic potentials, their form is far more complex. Some understanding can still be gained given their linear form, but they cannot be as readily analyzed as the simplistic linear models described in this work (37–40). It is important to distinguish and identify those applications that require nonlinear solutions or complex linear solutions and those that do not. While the former cannot be represented by intrinsically interpretable models, the latter often can. The required complexity of the regression model for a given problem determines the best route for interpretability.

The works we have revisited were chosen as they are excellent examples of how ML can assist in material and molecular property prediction. However, remarkably simple regression models can be used for these problems. We have demonstrated that a black box model is not the only option for exploring the elpasolite universe, predicting the spin states of transition metal complexes, or even winning the NOMAD Kaggle competition. The nature of the variables present in the model, as well as knowledge of the physics of the underlying problem, can both help to identify when simplistic linear solutions will offer comparable performance. Specialized regression models can provide multiple advantages. With linear interatomic potentials, improvements in speed and extrapolation have already been observed (37–40). With simplistic linear solutions, the benefits of interpretability become apparent.

These benefits include showing how a model agrees or disagrees with known physical principles. This is reflected by the trends seen in the coefficients of the models for the elpasolites and the transition metal complexes. In addition, linear models can provide information that can guide future predictions, and this was seen with the search for low-energy elpasolite structures and the discovery of the variables responsible for large bandgap and low formation energy structure for TCOs. Furthermore, the similarities between the n-gram model and cluster expansion could be analyzed in the linear reformulation. This information could then be used to predict the systems that the linear n-gram model could accurately describe.

In this work, we have focused on examples from the material science community; however, producing interpretable predictive models by creating simple linear combinations of nonlinear basis functions is widely applicable. While certain problems require deep learning or other such techniques, this is not always the case. It is important to be able to identify when more transparent solutions are available.

MATERIALS AND METHODS

LASSO fitting

To fit the coefficients of the model, LASSO was used with the regularization optimized by a grid search (54). Fivefold cross-validation was used on the training set to find the optimal regularization parameter.

For the TCOs, features with less than 10 entries were removed to reduce the size of the dataset, resulting in 62,089 remaining variables. The final model for E_f had only 387 nonzero coefficients.

Kernel ridge regression

A radial basis kernel was used for the TCO examples as in (19). A Laplacian kernel was used for the elpasolite example as in (55). Hyperparameters controlling the length scale of the Gaussian and the regularization strength were optimized using a grid search. The Python package scikit-learn was used.

Transparent conducting oxides

The formation energy is defined relative to the binary phases and normalized per number of cations: E_f = E(Al_xGa_yIn_z)₂O₃ − xE(Al₂O₃) − yE(Ga₂O₃) − zE(In₂O₃), where $x=\frac{N_{\text{Al}}}{N_{\text{Al}}+N{a}_{\text{Ga}}+N{a}_{\text{In}}}$, $y=\frac{N_{\text{Ga}}}{N_{\text{Al}}+N{a}_{\text{Ga}}+N{a}_{\text{In}}}$ and $z=\frac{N_{\text{In}}}{N_{\text{Al}}+N{a}_{\text{Ga}}+N{a}_{\text{In}}}$. This differs from the usual definition and gives a measure of the stability of the ternary compound relative to the binary compounds. The formation energy and n-gram representation is taken from (19). For a detailed explanation of how the n-gram features were built, how the formation energy was calculated, and the contents of the dataset, see (19). The dataset consists of 3000 structures, 2400 are used in the training set and 600 are in the testing set.

Both properties were calculated using DFT with the Perdew-Burke-Ernzerhof (PBE) exchange functional in FHI-aims (56). The accuracy of the bandgap calculation is discussed in (19). The features are scaled so that 0/1 is the minimum/maximum value of the feature in the dataset. The model was then fit to the formation energy. Two other models were discussed in (19), the first one used an smooth overlap of atomic positions (SOAP) representation with an NN (52, 53) and the second one represented the local atomic environment with a variables derived from analytic bond-order potentials along with other geometric and chemical properties and used LightGBM, a form of gradient boosting (57–59). We focus here just on the n-gram model as this representation can be interpreted easily.

The n-grams for the MgZnO and AgPd systems use cutoff radii based on the covalent radii of the elements scaled by 1.5. The MgZnO model was trained to 6434 structures and tested on 1609 structures with five different test/train splits used. The AgPd model was trained to 600 structures and tested on 76 structures with five different test/train splits used.

Elpasolite dataset

The elpasolite dataset consists of ABC₂D₆ structures and contains all main-group elements up to Bi. There are 10,590 structures in the dataset, with up to 10,000 are used as training data, and it is taken from (55).

Transition metal complexes

The transition metal complexes dataset was taken from (34). There are 807 structures in the training set and 538 in the testing set. All complexes are octahedral, and the central metal ion can be Cr, Mn, Fe, Co, or Ni. Oxidation states of 2+ and 3+ are included in the set. Variables describing the electronegativity differences and the shape of the ligand are also included. The high and low spin state energy was calculated using DFT with the hybrid functional B3LYP at seven Hartree-Fock exchange fractions. The exchange fraction is also included as a variable in the model.

Post hoc interpretability methods

PD is a commonly used method for visualizing the relationship between an independent variable and the dependent variable and can be calculated by

$$\text{PD}(x_s)=\frac{1}{n}{\sum }_{i=1}^n[\hat{f}(x_{\mathrm{s}},x_{\mathrm{c}}^{(i)})]$$ (4)

where x_s is the variable of interest, x_c is all other variables excluding x_s, and $\widehat{f}$ is the ML model. Therefore, the PD is a measure of the mean value of the ML model at x_s across a dataset. A PD plot for simulated data with a quadratic form is shown in Fig. 7. The x² relationship can clearly be seen in the figure.

ICE plots help to overcome the problems associated with PD (10). PD averages the data points contributions, while ICE plots instead show all points $\widehat{f}(x_{\mathrm{s}},x_{\mathrm{c}}^{(i)})$ for a given x_s. This can be used to check for interactions and to see if the averaged trends seen in the PD plots persist across all data points. An example of an ICE plots for simulated data is shown in Fig. 7B

PD measures can also be used to determine whether an interaction exists. An interaction is said to exist between variables x_i and x_j if a function, F(x), where x = (x₁, x₂, …, x_n), cannot be expressed as two functions

$$F(x)=f_{\setminus j}(x_1,\dots ,x_{j-1},x_{j+1},\dots ,x_n)+f_{\setminus i}(x_1,\dots ,x_{i-1},x_{i+1},\dots ,x_n)$$ (5)

where f_∖j does not depend on x_i and f_∖j does not depend on x_i (35). An interaction between two variables can be quantified using H statistics (36). The interaction between two variables j and k is defined by

$$H_{\mathit{jk}}^2=\frac{{\displaystyle {\sum }_{i=1}^n}[\mathrm{P}{\mathrm{D}}_{\mathit{jk}}(x_j^{(i)},x_k^{(i)})-\mathrm{P}{\mathrm{D}}_j(x_j^{(i)})-\mathrm{P}{\mathrm{D}}_k(x_k^{(i)})]}{{\displaystyle {\sum }_{i=1}^n}\mathrm{P}{\mathrm{D}}_{\mathit{jk}}^2(x_j^{(i)},x_k^{(i)})}$$ (6)

with $H_{\mathit{jk}}=\sqrt{H_{\mathit{jk}}^2}$. For meaningful interpretation, the H statistics for $\widehat{f}(x)$ must then be compared to the distribution of H statistics if no interactions are present. The null distribution, H₀, is produced by generating artificial data from the best possible additive model (36, 60)

${\tilde{y}}_i={\widehat{f}}_A({\mathbf{x}}_{\mathbf{i}})+[y_{p(i)}-{\widehat{f}}_A({\mathbf{x}}_{p_{(\mathit{i})}})]$, where ${\widehat{f}}_{\mathrm{A}}(\mathbf{x})$ is the best additive model and p(i) represents a random permutation of integers 1,2,...,N.

The original model is then fit to the artificial data (${\tilde{y}}_i$, x_i), and H_{0, jk} is calculated. An interaction is then define as H_jk − mean(H_{0, jk}) > α × std(H_{0, jk}), where α = 4 is used in this work unless otherwise stated. An example of the distribution of the H statistics for the null distribution and the components in an ensemble NN model is shown in Fig. 7 for f(x) = x₀ + x₁ + x₀x₁ + ϵ.

By using ensemble methods to show uncertainty, checking the consistency of nonlinearity with ICE plots, and calculating the null distribution for H statistics, we have taken steps to test the robustness of conclusions drawn. The code used to calculate and produce the figures in this work is provided (https://github.com/aa840/icepd). The H statistics for the KRR were calculated using 1000 values in the dataset and 10 null data points. The convergence with respect to the number of values for Al6,O4 is shown in fig. S1.

Algorithm for exploring elpasolite universe

The algorithm that we use has the following steps:

1) The three variable values of c_ic_jc_k + c_ic_j + c_ic_k + c_jc_k + c_i + c_j + c_k, where c_i is the coefficient of variable i, are calculated for all possible combinations of n and v at each site (A, B, C, and D).

2) The minimum three variable contributions are found and define up to three of the variables present in the final structure.

3) Under the constraint of the existing variables in the final structure, the minimum in the set of remaining three variable contributions is found.

4) This process is repeated until all variables are defined.

Many different variations of this algorithm could be used, and this is not a unique solution to the problem. Performing this procedure for the elpasolite three variable model results in the structure CaSrCs₂F₆ being identified first. This is in the bottom 250 structures in the elpasolite universe and coincidentally the lowest-energy structure found by subsequent DFT calculations. Multiple structures can be created by systematically preventing low-energy three variable contributions previously identified from being used in new structures. Up to four different interactions identified from the previously produced structure were prevented from being chosen in the creation of a new candidate. The effective degenerate structure of ABC₂D₆, BAC₂D₆, was also added to the set. This resulted in the production of 260 unique structures.

Supplementary Materials

This PDF file includes:

Figs. S1 to S5