Gravimetric analysis of the autocatalytic growth of copper microparticles in aqueous solution

Abstract

The growth kinetics of copper microparticles was analysed by using the gravimetric method. The copper microparticles were synthesized in aqueous solution containing cupric ion and HCHO under various conditions (temperature, additive) and the total mass was monitored during the synthesis. The relation between the total mass and time was formularized using heterogeneous and pseudo-first order reaction kinetics of the autocatalytic surface growth of copper with a modification of the Finke–Watzky kinetic model. Fitting of theoretical curves to the experimental results with various temperatures provided the rate constants of the surface growth, and the reaction activation energy was found from the Arrhenius plot to be 105.4 kJ mol⁻¹. The obtained value was validated by comparing it with one from copper film growth. Its change was observed with the addition of 2,2′-dipyridyl during synthesis.

The growth kinetics of copper microparticles was analysed by using the gravimetric method.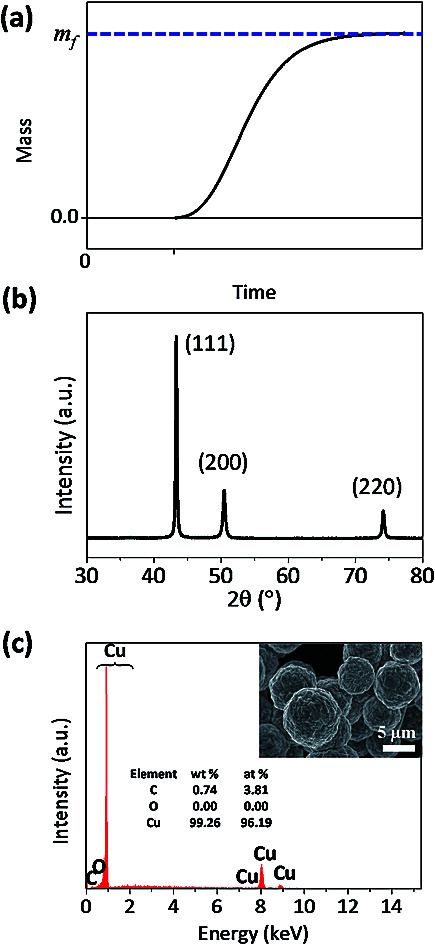

1. Introduction

Nano- or micro-particles have been of interest since C. Murray¹ published his paper on the fabrication of uniform sized nanoparticles that exhibited unusual physical and chemical properties in association with high volume/surface area ratio. Metallic particles can be synthesized in aqueous solution containing metal ions and the reducing agent. According to the LaMer mechanism,² the reduced single metal atoms are thermodynamically unstable so they agglomerate with each other to reach the critical size of a stable metal cluster.³ The critical cluster is called a monomer, which is a minimal unit of a crystal. As the concentration of monomer steadily increases and reaches supersaturation level, burst-up nucleation occurs.⁴ At burst-up nucleation step, the monomer cluster become nuclei at the minimum detectable size. The nuclei grows by consuming peripheral monomers after the nucleation step, which is termed Ostwald ripening. Thermodynamically, it is based on the minimization of the surface energy of the particle through the diffusion-limited monomers consumption. However, in the case of catalytic metals, such as copper (Cu), cobalt (Co), and nickel (Ni), metal particles grow through the reduction of metal ions on the metal surface, which refers to the autocatalytic reaction. The growth of Cu particles is a one good example of the autocatalytic reaction. Cupric ion (Cu²⁺) can be reduced by formaldehyde as a reducing agent, and reduced Cu as a reaction product catalyzes the oxidation of formaldehyde.^5,6 In alkaline solution, formaldehyde is transformed into methylene glycol, and donates electron for the reduction (the Cannizzaro reaction).⁷ The reaction of Cu²⁺ reduction in alkaline condition requires ethylenediaminetetraacetic acid (EDTA) as a complexing agent in order to prevent the precipitation of copper hydroxide,⁸ and the overall reaction can be written as:⁹

CuEDTA²⁻ + 2HCHO + 4OH⁻ → Cu⁰ + H₂ + 2H₂O + 2HCOO⁻ + EDTA⁴⁻ 1

The synthesized particles are usually analysed via TEM,^10–17 dynamic light scattering (DLS),^18,19 X-ray diffractometry,^20,21 IR or UV-Vis spectroscopy,^22–25 electrophoretic light scattering (ELS),^26,27 and so forth. TEM is the most widely used tool for the observation of the size, shape, and crystal structure of nanoparticle. However, the extremely high spatial resolution of TEM analysis sometimes causes difficulties in examining all particles, and therefore, it is often supported by other methods. In this study, we evaluated the gravimetric method for particle analysis. The gravimetric method is one of the oldest and simplest analytical methods, as it can be applied to any reaction system, regardless of the scale and uniformity.²⁸ Gravimetric analysis does not require a sampling step, so that the change in the mass of particles would directly provide the information about the averaged growth of particle. However, the sensitivity of the gravimetric analysis is often limited by the mass resolution of the weighing scale, which is about (10⁻³ to 10⁻⁵) g for a high precision balance. Subsequently, gravimetric analyses of the nanoparticles and their nucleation would be unreasonable, but analyses of particles grown to the micrometer scale would have useful information about the particle growth.

In this research, we observed the formation of Cu microparticles through the gravimetric method. During particle synthesis, gradual increase in the total mass of Cu microparticles over time is anticipated and it is associated with nucleation, followed by surface growth. The increase would quickly be accelerated, due to the enlarged surface area of the growing particle with the heterogeneous autocatalytic Cu²⁺ reduction.²⁹ Afterward, it would be quickly retarded, due to the depletion of Cu²⁺ in the solution. Consequently, the plot of mass against time would have a sigmoidal shape. In this study, the mass-time curve was simulated using pseudo-1^st order autocatalytic surface reaction kinetics for Cu²⁺ reduction, and fitted to the experimental data. Consequently, the activation barrier energy for the autocatalytic growth of Cu microparticles was estimated from the simulated and fitted mass-time curve.

2. Experimental

2.1. Chemicals

Copper(ii) sulfate pentahydrate (CuSO₄·5H₂O, ACS Reagent), cobalt(ii) sulfate heptahydrate (CoSO₄·7H₂O, Reagent-plus), citric acid (HOC(COOH)(CH₂COOH)₂, ACS Reagent), potassium hydroxide (KOH, pellet type, ACS Reagent, 85%), 2,2′-dipyridyl (C₁₀H₈N₂, Reagent-plus), hydrazine hydrate (NH₂NH₂·H₂O, Reagent grade, containing 64–65% N₂H₄), formaldehyde solution (HCHO, ACS Reagent, 37 wt% in H₂O, containing 10–15% methanol), sulfuric acid solution (H₂SO₄, 95%), and hydrogen peroxide (30 vol%, ACS Reagent) were purchased from Sigma Aldrich. EDTA ((HO₂CCH₂)₂NCH₂CH₂N(CH₂CO₂H)₂, ACS Reagent) was purchased from Junsei. All reagents were used without further purification.

2.2. Particle synthesis and gravimetric measurement

Cu particles were synthesized in aqueous solution (100 mL as a reaction volume) containing 50 mM of CuSO₄·5H₂O, 100 mM of EDTA, 150 mM of HCHO and 600 mM of KOH. If necessary, 1 μM of 2,2′-dipyridyl was added.³⁰ The measurement started by injecting HCHO into the preheated HCHO-free solution. Co particle was synthesized in 50 mM of CoSO₄·7H₂O, 300 mM of citric acid, and 10 M of KOH in 100 mL solution. The solution was pre-heated to 80 °C, and after that, hydrazine was added to form 600 mM in the whole solution.

Synthesized particles were collected for weighing by filtering the solution using filter paper (200 nm pore size). Each experiment was repeated over 3 times, and the measured mass was averaged.

2.3. Cu film growth

The reaction rate of Cu²⁺ reduction was also estimated from the growth of Cu film on Cu foil (0.8 cm × 1.0 cm, which area was similar to the total surface area of the synthesized particle) as the substrate. Cu foil was pretreated in order to remove the surface oxide by dipping in 10 vol% H₂SO₄ and 3 vol% of H₂O₂ solution for 2 min, followed by rinsing with deionized water for 10 s. All solutions were maintained at 25 °C. The pretreated Cu foil was dipped into the solution that was the same as the one used for particle synthesis, and its mass change was measured to estimate the amount of Cu film grown. In order to eliminate the effect of mass transfer of Cu²⁺, the solution was vigorously stirred during film growth.

2.4. Particle analysis

The shape and size of particles were evaluated using field emission scanning electron microscopy (FESEM, HITACHI S-4800). X-ray diffraction (XRD, D8-Advanced, Cu Kα radiation) patterns were obtained from Cu microparticles. The nonlinear least squares method was used for data fitting.

3. Results and discussion

Many studies have tried to demonstrate and simulate the sigmoidal curve for particle formation; the Smoluchowski rate equation^31,32 based on the collision of particles form a statistical perspective, the Kolmogorov–Johnson–Mehl–Avrami expression,³³ for the solid-state phase transformation, the Lifshitz–Slyozov–Wagner model³⁴ for Ostwald ripening and the relevant diffusion controlled growth model,^16,35 and the Finke–Watzky (F–W)³⁶ model, for fast autocatalytic surface growth. Since the growth of Cu microparticles has autocatalytic reaction characteristics, the model for the total mass as a function of time in this study is based on the F–W model under the assumption of the pseudo-elementary nucleation and growth steps, and it is expressed as:³⁷

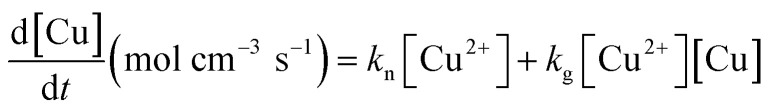2

where [Cu²⁺] is the concentration of Cu²⁺ reactant, [Cu] is the molar amount of Cu per unit reaction volume, and k_n and k_g are the rate constants for nucleation and growth, respectively. The assumption of pseudo-elementary Cu growth in this study is quite as, and was confirmed by the reaction of Cu film growth on Cu foil which is a first order in Cu²⁺ (Fig. S1 of the ESI†). The multiplication of [Cu] in the second term on the right side of eqn (2) is the contribution of product to the autocatalytic reaction. In contrast to the homogeneous reaction, the contribution might not be linearly proportional to [Cu]. In the F–W model, it has been considered as a “scaling factor”, which is the fraction of active surface³⁸ atoms gained in the growth step.³⁷ For particles of micrometer-sized scale, there would be plenty of active sites, which number is proportional to the surface area of microparticles. Accordingly, the contribution of Cu to the autocatalytic reaction might be proportional to [Cu]^2/3, rather than [Cu].

Along with this consideration, eqn (2) can be transformed in terms of mass (m = M_w[Cu], where m is the total mass of Cu particles per unit reaction volume, and M_w is the molar mass of Cu and it is 63.55 g mol⁻¹) as follows (see the ESI†)

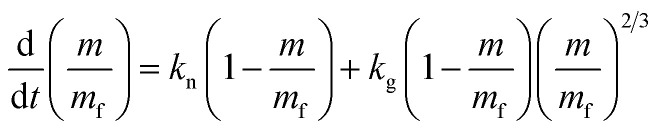3

where m_f is the total mass of Cu particles per unit reaction volume when the reaction is completed and it is equal to M_w[Cu²⁺]₀ ([Cu²⁺]₀: the initial concentration of Cu²⁺, [Cu²⁺]₀ = [Cu²⁺] + [Cu]). (m/m_f)^2/3 presents a scaling factor in this study. Eqn (3) does not consider the mass transfer of Cu²⁺ to the Cu particle surface, since the autocatalytic surface growth step is normally not diffusion limited,³⁷ and its effect is also minimized with the vigorous stirring during particle growth.

Consequently, the change in the total mass of Cu microparticles according to time can be expressed as an analytical solution of eqn (3) (see the ESI† for details):

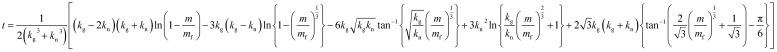4

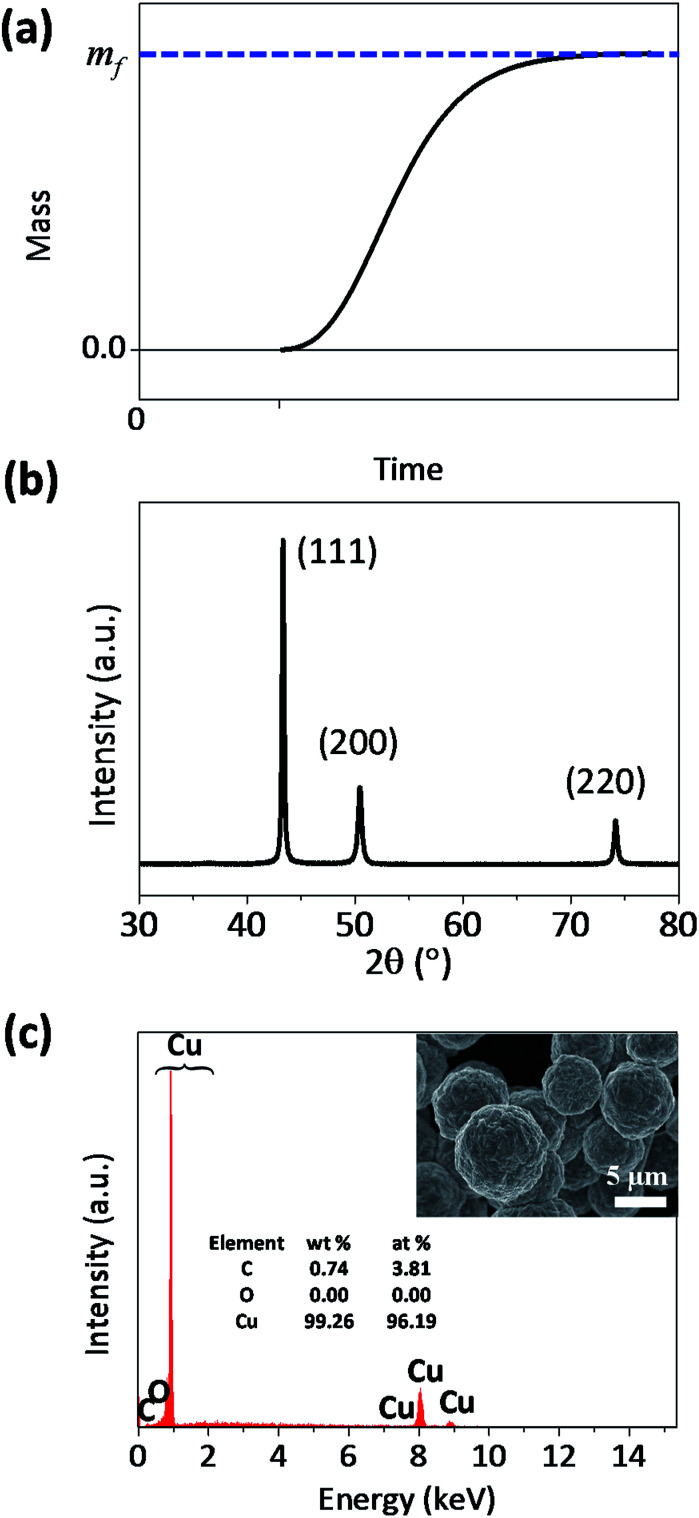
The theoretical curve from eqn (4) has a sigmoidal shape, as expected (Fig. 1a). Fig. 1b and c shows that the synthesized particle is spherical, micrometer-sized, and a polycrystalline Cu. The synthesized particles did not contain oxygen (Fig. 1c), which indicates that the Cu particle grows via the surface autocatalytic reduction of Cu²⁺ without other chemical reactions involved.³⁹

Fig. 1. (a) Theoretical sigmoidal curve of mass-time during the formation of microparticles, and (b) XRD data and (c) SEM-EDS result of the synthesized Cu microparticles.

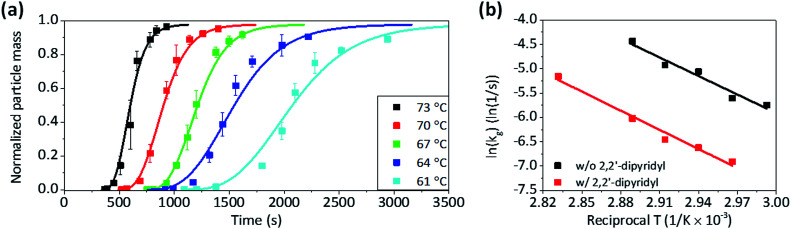
Fig. 2a plots the total mass of Cu particles synthesized over time for various solution temperatures. In all reaction temperatures, the total mass increased with the sigmoidal shape and approached m_f. At higher temperature, the mass of Cu particles was detected sooner and increased more abruptly. A fit of eqn (4) to the experimental data gives the values of various parameters such as k_g, and k_n, listed in Table 1. As expected, the values of k_g and k_n increased with the reaction temperature. It is noticeable that k_g is much bigger than k_n, and therefore, the contribution of the second term on the right side of eqn (3) is much more significant than that of the first term for the mass increase, except when m ≪ m_f. This is consistent with the condition for the F–W model, which is “slow nucleation”.³⁷ It is also supported by the observation of Fig. S2 of the ESI,† which shows that the size of each particle increases without significant increase in the population as the reaction time passes. The Arrhenius plot of k_g shows that, the activation energy (E_a) for the autocatalytic growth reaction is about 105.4 kJ mol⁻¹ (Fig. 2b).

Fig. 2. (a) The plots of mass against time for the formation of Cu microparticles under various temperatures and fitted curves according to eqn (4), and (b) Arrhenius plots of the reaction constants (k_g) for the autocatalytic surface reaction, which were obtained from curve fitting.

List of curve fit values of k_g and k_n for the formation of Cu microparticle.

Temperature (°C)	k g (s−1) × 10−3	k n (s−1) × 10−10	t ind (s)
73	11.8	9.95	365
70	7.28	4.96	505
67	6.35	2.23	753
64	3.69	2.01	839
61	3.21	1.16	1120

The Arrhenius plot of Fig. 2b shows the change in E_a that was observed with the addition of 2,2′-dipyridyl. The gravimetric analyses revealed that the increase in the mass was retarded, and k_g was reduced to one-tenth with the addition of 2,2′-dipyridyl (Fig. S3 of the ESI†). E_a was estimated to be 113.9 kJ mol⁻¹, which is 8.5 kJ mol⁻¹ larger than that without 2,2′-dipyridyl. It is reported that 2,2′-dipyridyl decreases the reaction rate of Cu²⁺ reduction via the adsorption on the Cu surface.^40–42 The contribution of 8.5 kJ mol⁻¹ to k_g is about 33% decrease in the reaction rate, indicating that the adsorbed 2,2′-dipyridyl on Cu also affect the pre-exponential factor that contains the collision rate of Cu²⁺ on the Cu surface and a steric factor (proper orientation of the collision for the reaction).

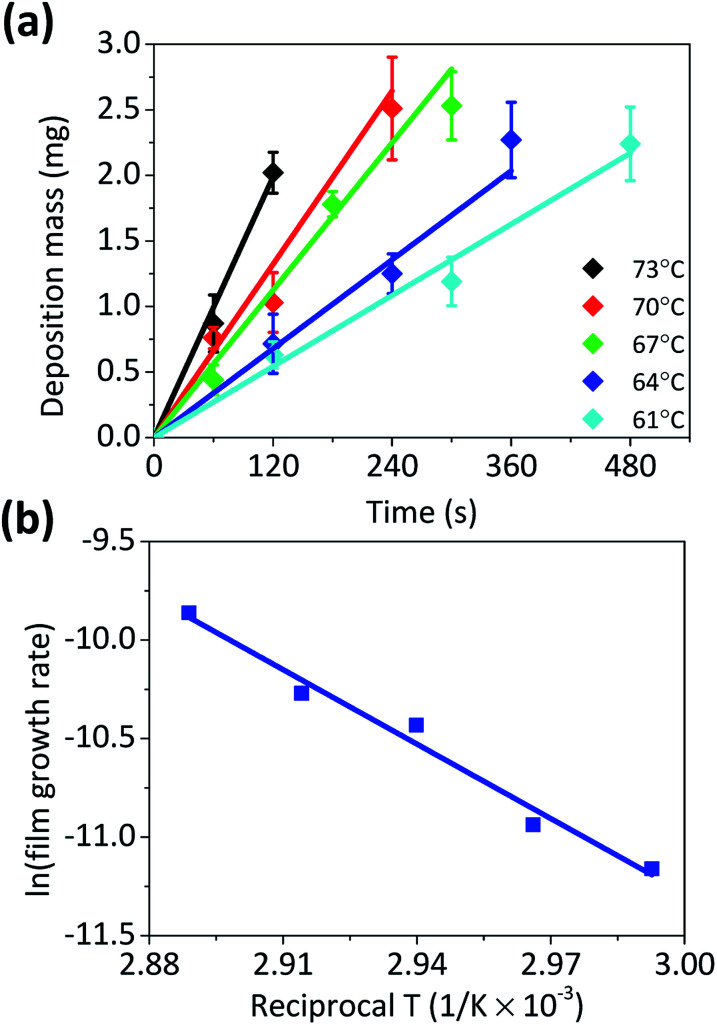
The validity of E_a was examined by comparison with the E_a value obtained from the film growth reaction on Cu foil (Fig. 3). For the Cu film growth on Cu, the growth rate is generally expressed in a similar way to eqn (3) and is roughly treated as the absence of nucleation and a scaling factor. However, as it is a pseudo-first order heterogeneous surface reaction, its rate constant has a unit of [cm s⁻¹]. Accordingly, it is not appropriate to directly compare with k_g. Nevertheless, the growth of microparticle and film would have same energetic state and the reaction pathway, and therefore, E_a for both reactions would also be identical. The growth rate of Cu film was measured in various temperatures (Fig. 3a), and Fig. 3b shows the Arrhenius plot of the rate constant. The obtained E_a of Cu film growth on Cu foil was about 104.0 kJ mol⁻¹, which value was similar to the values from previous researches.^5,9 The E_a values estimated from both the gravimetric method and the film growth are almost identical, indicating that the model used in this study interprets the autocatalytic growth kinetics of Cu microparticles well.

Fig. 3. (a) The plots of mass against time for the formation of Cu films under various temperatures and (b) the Arrhenius plot of the reaction constants for Cu film growth. The activation energy was calculated as 104.0 kJ mol⁻¹.

Consideration of the scaling factor (m/m_f)^2/3 was found to be important for the precise estimation of k_g and E_a. If the experimental results are fitted to the simple F–W model that is based on eqn (2) without the consideration of the scale factor, E_a is obtained as 137.7 kJ mol⁻¹ which shows a relatively large difference from the one from the film growth (Fig. S4 of the ESI†).

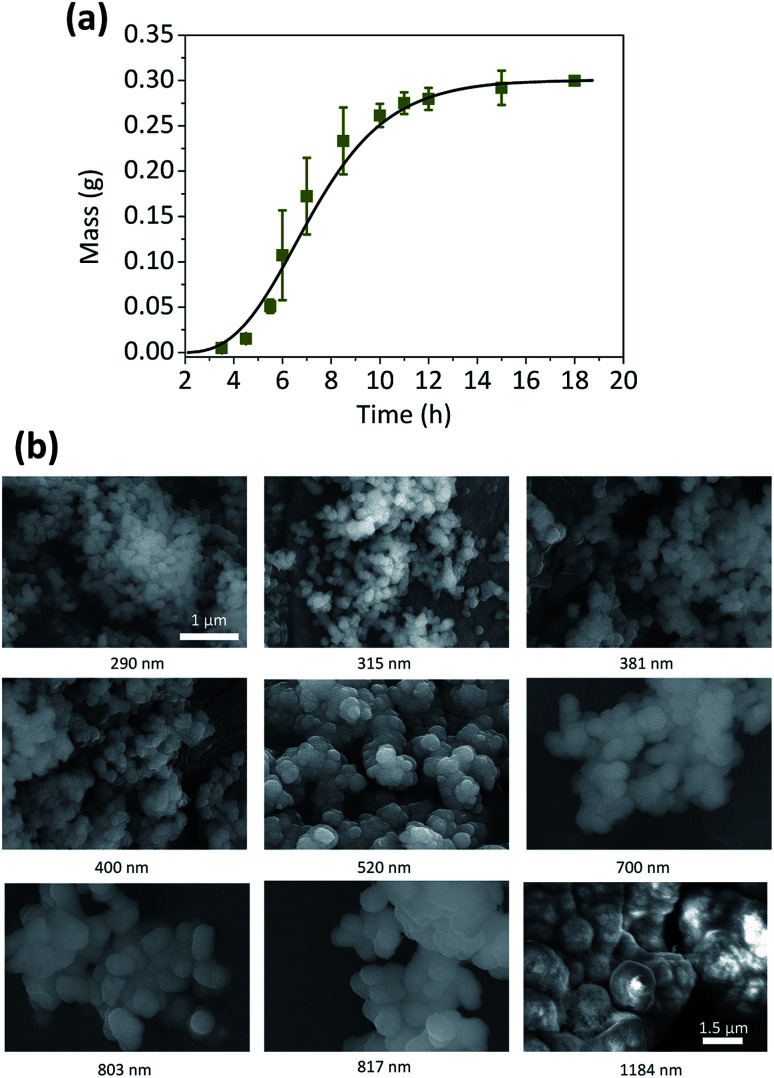
The validity of this model was not limited to the synthesis of Cu microparticles. It could also be successfully applied to the synthesis of Co spherical particles, which is an another example of the autocatalytic reaction.⁴³ The sigmoidal curve of the total amount of Co particle over time was obtained by the gravimetric method (Fig. 4) and its kinetic parameters could be evaluated (Table 2).

Fig. 4. (a) The plots of mass against time for the formation of Co microparticles, and (b) FESEM images of the synthesized Co microparticles. The number at the bottom of each figure corresponds to the average size of Co microparticle.

List of curve fit values of k_g and k_n for the formation of Co microparticle.

Fitting parameters	Value
k g (s−1) × 10−4	1.37
k n (s−1) × 10−12	9.55
t ind (s)	8000

The curve fitting also provides the information of k_n, and in this study, its change was observed with the addition of 2,2′-dipyridyl. Unfortunately, the k_n values were extremely small, and varied significantly with the mass measured at the early stage of the particle synthesis. This might be associated with the mass resolution limit in this study, and it indicates that the kinetic information on the nucleation step might be beyond the capability of gravimetric analysis. The nucleation step is critical for the control of the morphology or dimension of the synthesized particle,^44,45 and it is also closely related to scaling factor in this kinetic model. Therefore, our future study would focus on the gravimetric analysis on Cu particle with various shapes other than the sphere, synthesized by using an adequate capping agents such as ethylenediamine⁴⁶ or cetyltrimethylammonium bromide.⁴⁷

4. Conclusions

We derived the theoretical relation between the total mass of the Cu microparticle and the reaction time, which contained k_n and k_g, with the modification of the F–W autocatalytic growth model. This was verified by gravimetric analysis of the formation of Cu microparticles. The sigmoidal curve-to-fit provides k_g for the autocatalytic surface growth of Cu microparticles. From its Arrhenius plot analysis, E_a for the surface growth was estimated to be 105.4 kJ mol⁻¹, and which is almost identical to the value from the film growth (104.0 kJ mol⁻¹). The introduction of the scaling factor (m/m_f)^2/3 into the rate equation was critical for the precise estimation of E_a, and the model used in this study could be also applied to the investigation of Co particle growth. The change in the growth rate of Cu particle with the addition of 2,2′-dipyridyl was clearly manifested in the gravimetric analysis and it was associated with the decrease in k_g.

Conflicts of interest

There are no conflicts to declare.