What should be the baseline when calculating excess mortality? New approaches suggest that we have underestimated the impact of the COVID-19 pandemic and previous winter peaks

Abstract

Excess mortality has been used to measure the impact of COVID-19 over time and across countries. But what baseline should be chosen? We propose two novel approaches: an alternative retrospective baseline derived from the lowest weekly death rates achieved in previous years and a within-year baseline based on the average of the 13 lowest weekly death rates within the same year. These baselines express normative levels of the lowest feasible target death rates. The excess death rates calculated from these baselines are not distorted by past mortality peaks and do not treat non-pandemic winter mortality excesses as inevitable.

We obtained weekly series for 35 industrialized countries from the Human Mortality Database for 2000–2020. Observed, baseline and excess mortalities were measured by age-standardized death rates. We assessed weekly and annual excess death rates driven by the COVID-19 pandemic in 2020 and those related to seasonal respiratory infections in earlier years. There was a distinct geographic pattern with high excess death rates in Eastern Europe followed by parts of the UK, and countries of Southern and Western Europe. Some Asia-Pacific and Scandinavian countries experienced lower excess mortality. In 2020 and earlier years, the alternative retrospective and the within-year excess mortality figures were higher than estimates based on conventional metrics. While the latter were typically negative or close to zero in years without extraordinary epidemics, the alternative estimates were substantial. Cumulation of this "usual" excess over 2–3 years results in human losses comparable to those caused by COVID-19.

Challenging the view that non-pandemic seasonal winter mortality is inevitable would focus attention on reducing premature mortality in many countries. As SARS-CoV-2 is unlikely to be the last respiratory pathogen with the potential to cause a pandemic, such measures would also strengthen global resilience in the face of similar threats in the future.

Highlights

• •Conventional estimates of excess mortality underestimate potentially avoidable losses.
• •We propose metrics based on best weeks in the same and in earlier years.
• •Our alternative metrics estimate higher annual excess mortality in 2020 and 2005-19.
• •Mortality peaks in non-pandemic years should be regarded as potentially avoidable.

1. Introduction

The total mortality impact of outbreaks of influenza and other respiratory infections are underestimated by statistics on causes of death. This is related both to the complexity of pathological processes and interactions with pre-existing (often cardiovascular) conditions and also by issues related to diagnosis and cause-of-death coding. Although deaths attributed by official statistics to influenza and respiratory diseases (as the underlying cause) are highly correlated with all-cause mortality fluctuations (Thompson et al., 2009; Office for National Statistics, 2015), they constitute only a minor part of these fluctuations with a higher share constituted by circulatory diseases (Douglas et al., 1991; Office for National Statistics, 2012; Sprenger et al., 1993).

This underestimation by the cause-of-death statistics was also a feature of the SARS-CoV-2 pandemic in 2020 (Armstrong 2021). Therefore, the concept of excess mortality has received considerable attention since the start of the pandemic and is now used widely as a metric to quantify the impact of the pandemic, comparing observed deaths with those that would be expected if death rates had remained the same as in previous years (Iacobucci, 2021). It compares week- or month-specific death rates over a year with some baseline mortality level, such as (for example) the five years preceding the year being studied (Nepomuceno et al., 2022; Schöley, 2021). The magnitude of the deviation from previous years is taken as quantifying the deaths that would not have occurred if there had not been a pandemic. Conventional excess mortality measures mortality above what would be expected from mortality in previous years, although this includes periods when mortality was unusually high. Thus, the conventional method makes an implicit assumption (or at least is often interpreted in this way) that death rates during that period were as low as reasonably achievable. Given fluctuations in mortality, both over the course of any given year and in comparison with the same period in previous years, this is clearly not the case. It has the additional effect of normalizing high rates of seasonal mortality that, as we see from international comparisons, are not inevitable. Consequently, there is a need for an alternative approach.

The UK Office for National Statistics, other statistical agencies, many researchers and data journalists publishing these figures use as a baseline the 5 years from 2015 to 2019 (Office for National Statistics, 2021; Kontis et al., 2020). Yet in three of these five years (2015, 2017, and 2018), many countries faced particularly substantial mortality elevations in winter (Nielsen et al., 2019; Office for National Statistics, 2017, 2019). This raises the fundamental question as to what should be regarded as an acceptable or “normal” level of mortality. As seasonal increases in deaths from influenza and other causes are common, should they simply be accepted?

This question has led us to revisit the phenomenon of intra-annual mortality fluctuations especially given that their intensity varies by year and across countries. Specifically, we have looked at alternative baselines that do not assume that winter mortality excesses are inevitable and therefore implicitly acceptable.

Despite substantial progress in reducing mortality overall, increased mortality rates at certain times of the year continue to make an important contribution to the annual toll of human deaths in many countries. In the 2010s, substantial increases in winter mortality occurred in many European countries (Nielsen et al., 2019; Hiam et al., 2021) and, while these were often associated with influenza epidemics, other factors1 may have contributed (Eurowinter Group, 1997; Keatinge, 2002; Marti-Soler et al., 2014; Sartini et al., 2017; Wilkinson et al., 2001). Several countries faced life expectancy declines in 2015 followed by a rebound in 2016 and no increase or another decline in 2017 (Ho & Hendi, 2018; Leon et al., 2020; OECD, 2021; Raleigh, 2019).

Analysis of excess mortality has a long tradition in demography and epidemiology (McKee, 1989; Rau, 2006; Sakamoto-Momiyama, 1978). The current interest in excess mortality to measure the impact of the pandemic is only the latest example of this method being applied to, for example, epidemics, extreme weather events, famines, and conflicts (Dols & Van Arcken 1946; Ekamper et al., 2017). Its advantage is that it avoids problems associated with variability and incompatibility of statistics on causes of death and is accepted by researchers and health authorities as to the most reliable and objective measure of increased mortality caused by the COVID-19 pandemic (Our World in Data 2020; Beaney et al., 2020; The Health Foundation, 2020; Leon et al., 2020) and earlier epidemics (Rau, 2006; Thompson et al., 2009).

In this study, we report an investigation of weekly mortality series from 35 industrialized countries with reliable vital statistics from the beginning of 2000 until the end of 2020. All these countries have experienced intra-annual mortality fluctuations of variable amplitudes, with frequent increases in the winter season. Summer heat-wave mortality peaks are also seen in some. We examine mortality across calendar years and populations and compare levels and patterns of excess mortality in the extraordinary COVID-19 year of 2020 with earlier times. We then employ novel metrics for assessment of excess mortality based on using two alternative mortality baselines that are considered as a target corresponding to the lowest level that has been achieved in a country either in corresponding weeks in recent past years or at another period within the same year. Then we compare the resulting excess mortality estimates with commonly used measures for the period 2005–2020. Our objective is to lay out the various alternative methods that might be used in the future to construct reference or baseline mortality in each country, and in so doing contribute to the emerging debate about whether post-COVID the new normal should be less tolerant of non-pandemic mortality excesses that to an important degree may be avoidable.

2. Data and methods

2.1. Data

The Short-Term Mortality Fluctuations Database (STMF) of the Human Mortality Database (HMD) served as our prime data source (Human Mortality Database, 2021; Jdanov et al., 2021; Németh et al., 2021). All countries and regions presented in the STMF have reliable vital statistics.

We used the main STMF data file containing death counts and death rates by standardized 7-day weeks according to ISO-8601 (the international standard for the worldwide exchange and communication of date- and time-related data (ISO 8601 2019) and epidemiological weeks in Canada) by year, sex, and broad age groups 0–14, 15–64, 65–74, 75–84, and 85+. We also used the STMF input country files that provide weekly age-specific death counts by sex and 5-year age groups. For most of the country-year combinations, the 5-year age groups were 0–4, 5–9, 10–14, …. The last age group was 90+ for most countries, and 95+ or 100+ for some countries. Weekly deaths by 5-year age groups were not available for Australia, Canada, England and Wales, Germany, Israel, New Zealand, South Korea, and the USA, each of which uses their own age categories covering broader ranges of ages.

Finally, we used annual data on deaths, death rates, and population counts by single-year ages from the core HMD. All the data were retrieved from STMF and the core HMD on April 5, 2021.

Although STMF includes 38 countries and regions, we used 35 of them. Australian data were dropped as they did not include all deaths. We also excluded Luxembourg and Iceland due to low death numbers and large random fluctuations. The analysis included the constituent parts of the UK: England and Wales, Northern Ireland, and Scotland. Twenty STMF series begin from 2000 or 2001 (see Table C1 in the Supplementary Appendix C for more details on the input data). Correspondingly, we examined data series from 2000-2001 to 2020. Russian data for 2020 have not yet been delivered (as of April 5, 2021) by the Russian statistical agency Rosstat.

2.2. Data processing and computation of age-standardized death rates

Before estimating excess mortality, we checked the completeness and comparability of weekly mortality data across populations and years. Information about the measures employed has been published elsewhere (Klimkin et al., 2021) but is summarized in the next paragraph.

For the years covered by the HMD core, the annual HMD mortality data are considered a “gold standard”. However, the weekly data in the STMF are mostly labeled as “preliminary” by data providers and are somewhat incomplete by definition. Therefore, we distinguish between two parts of the HMD: STMF and HMD core. The latter provides the final, complete, and detailed data on annual mortality. Updating the HMD core is much slower than updating the STMF. Consequently, we adjusted the age-specific weekly deaths from STMF for exact compliance with the corresponding annual death counts in the HMD core, as described by Klimkin et al. (2021). In 90% of country-year cases, the adjustment factor was between 0.9998 and 1.0113. In most recent years with missing HMD core data (mostly 2019 and 2020), we adjusted the STMF weekly death counts using adjustment factors from the last year available in the HMD, again as described by Klimkin et al. (2021).

The age compositions of populations under study vary substantially across countries and time. Thus, we used the age-standardized death rate (SDR) as the main mortality measure, based on the 2013 European Standard Population. For 28 countries, the availability of weekly death rates by 5-year age bands enabled a straightforward calculation of weekly SDRs. For precise calculation of SDRs in the remaining seven countries, we applied an indirect calculation procedure that combines the weekly crude death rates by broad age groups with the annual death rates by 5-year-age death rates (Klimkin et al., 2021). Additional details are given in the Supplementary Appendix A.

2.3. Baselines defining lower mortality targets

The literature suggests two approaches to estimating intra-annual excess mortality (Nicoll et al., 2012; Rau, 2006). The first is the retrospective one, which has been commonly used to assess excess mortality during the COVID-19 pandemic. This looks at deviations of weekly death rates in an index year from a reference level based on the weekly mortality experience of previous years (Kontis et al., 2020; Nicoll et al., 2012; Nielsen et al., 2011; Thompson et al., 2009). Here baseline mortality is defined as predicted mortality for the index year derived from past mortality series (Nielsen et al., 2019; Nunes et al., 2011; Office for National Statistics, 2021; Simonsen et al., 2005). The second is a within-year approach, which focuses on the variation of mortality across weeks within the index year and is related to seasonality. Here the baseline mortality is defined as mortality during lower mortality weeks (typically in the summer season) of the same year (Andreev & Biryukov 1998; Healy, 2003; Liddell et al., 2016; Rau, 2006; Sakamoto-Momiyama, 1978). The STMF Visualization Toolkit provides simple excess mortality measures implementing both the retrospective and the within-year approaches (Németh et al., 2021).

Although excess mortality estimates based on the two approaches measure the amount of intra-annual mortality elevation, they make different assumptions. Excess mortality compared to previous years expresses an aversion to any weekly mortality increase relative to recent annual experience. This metric captures rises in all weekly death rates in the index year compared to the past. However, this approach implicitly treats within-year seasonality, especially common winter excesses, as inevitable. In contrast, when excess mortality is measured against mortality within the index year it implies an aversion to excess mortality compared to other weeks within the same year. It is related to seasonality which expresses itself in concave (Northern Hemisphere) or convex (Southern Hemisphere) intra-annual patterns. This metric is insensitive to the annual average level and to how this level compares to previous years. In practice, the two types of measures are highly correlated across time and space because the intra-annual mortality elevations contribute both to the contrast with previous years and variation within the index year.

Both the retrospective and the within-year approaches have several variants, each with its own strengths and weaknesses.

In the paragraphs below, we present a variant of each one that seeks to define a baseline that represents an achievable target minimum against which different years may be judged.

2.3.1. Alternative retrospective baseline

For an index year $y$, the baseline weekly death rate referring to past $N$ years is defined as

$$SD{R}_{aretro}^B\left(y,w\right)={\hat{\alpha }}_w+\hat{\beta }·y$$ (1)

where $w$ is the week number, $\hat{\beta }$ is an estimate of the slope of the linear regression of the annual SDR on year

$$t:SDR(t)=\beta \cdot t+{\epsilon }_t,y-N\le t\le y-1,$$

and the weekly effects ${\hat{\alpha }}_w$ are defined as ${\hat{\alpha }}_w=\underset{t}{\min 2}\left[SDR\left(t,w\right)-\hat{\beta }·t\right]$ with $\underset{t}{\min 2}$ denoting the second-lowest $SDR(t,w)$ value for week w among years $t$ running from $y-N$ to $y-1$ (see also Box 1). The use of the second minimum is a commonly used device to reduce the probability of outliers (David & Nagaraja, 2003).2

Box 1. Summary of mortality baselines.

Alternative baselines

aretro: Weekly death rates that are equal to the second-lowest weekly death rates for the same weeks within the reference period adjusted for the secular trend after smoothing of these death rates across weeks of the index year. The reference period consists of seven years preceding the index year.

within-year: Weekly death rates that are equal to the average of 13 lowest weekly death rates within the same year.

Conventional baselines

r1: Weekly death rates that are equal to averages of weekly death rates for the same weeks within the reference period.

r2: Weekly death rates that are equal to averages of weekly death rates for the same weeks within the reference period adjusted for the secular trend.

Alt-text: Box 1

According to Eq. (1), for each week w of the index year $y$ the baseline weekly death rate ${SDR}_{\mathit{aretro}}^B(y,w)$ is equal to the second-lowest value of the observed $SDR$ values for the same week in $N$ previous years with an additional shift to account for the underlying mortality trend. In this sense, the ${SDR}_{aretro}^B(y,w)$ indicates a target level of mortality referring to the lowest weekly death rates in the recent past. The baseline weekly death rates based on the previous minimal values are insensitive to past mortality peaks. This makes an important difference from more conventional metrics involving annual averaging of past weekly death rates.

In calculating the second-minimum baseline it is important to include enough “good” years in which there were no significant epidemics (Stang et al., 2020). In the countries under study in 2000–20, winter mortality peaks were seen in 12 of 21 years. We found (analysis not shown here) that a 7-year retrospective period ($N=7$) always includes at least two non-epidemic years. However, a 7-year retrospective period reduces the number of index years that can be included in the excess mortality calculation. To relax it, we additionally included in the excess mortality calculation years with data available for at least five previous years $(N\ge 5)$. Thus, with data series starting at 2000, 2005 is the first possible index year allowing for calculation ${SDR}_{aretro}^B(y,w)$.3

As mentioned earlier, the alternative retrospective baseline, which is derived from low weekly death rates in the past, is considered as a target (desirable) mortality level. In many countries and index years, the empirical second-lowest death rates display random fluctuations across neighboring weeks. However, the target mortality level (by definition) should not differ abruptly between neighboring time points so we have eliminated these fluctuations by smoothing.4 The weekly ${SDR}_{aretro}^B(y,w)$ were smoothed within every index year between 2005 and 2020 with cubic splines using the smooth.spline function from the R-package stats available in R version 4.0.3. After the smoothing, we additionally adjusted the resulting weekly SDRs for the exact compliance with the annual averages of the unsmoothed baseline death rates.

2.3.2. Within-year baseline

The baseline mortality referring to lower mortality weeks within the same (index) year $y$ is defined as

$$SD{R}_{wy}^B\left(y\right)=\left(1/13\right)·{\sum }_{w\in {\mathit{Q}}_1}SDR\left(y,w\right)$$ (2)

where the set Q₁ includes 13 weeks (a quarter of a year) constituting the lower quartile of $SDR(y,w)$ values in year $y$ (see also Box 1).

Conventional indexes of the seasonal mortality excess use a fixed calendar frame of the low mortality season (non-winter season) (Healy, 2003; Liddell et al., 2016). Eq. (2) provides a more flexible definition that is not connected to a fixed range of weeks or months.

The constant (concerning $w$) baseline death rate ${SDR}_{wy}^B\left(y\right)$ is equal to the lower-quartile of 52 or 535 weekly SDR values in year $y$. It determines a lower benchmark of mortality within the index year and highlights the amount of mortality that has to be eliminated to reach the average level of the 13 lowest mortality weeks (not necessarily consecutive).

2.3.3. Conventional baselines

For comparative purposes, we use two retrospective baselines that have been most frequently used in other studies (Box 1).6 The first one (r1) corresponds to the conventional averaging of week-specific death rates. The second one (r2) also uses the averaging with additional adjustment for secular trends. Precise mathematical definitions of baselines r1 and r2 which use fixed-effects models are given in the Supplementary Appendix B.7 The corresponding baseline death rates are denoted ${SDR}_{r1}^B(y,w)$ and ${SDR}_{r2}^B(y,w)$, respectively.

2.4. Excess standardized death rates

The excess age-standardized death rates are the differences between the observed and the baseline age-standardized death rates

$$ESDR(y,w)=SDR(y,w)-{SDR}^B(y,w)$$ (3)

In the text below, ESDRs calculated from the four baselines are denoted as ${ESDR}_{aretro}$ for the alternative retrospective baseline; ${ESDR}_{wy}$ for the within-year baseline; ${ESDR}_{r1}$ for the conventional baseline r1; ${ESDR}_{r2}$ for the conventional baseline r2.

The annual baseline and observed SDRs, as well as the annual ESDRs, are obtained by averaging the weekly SDRs and ESDRs within respective years. Such a simple calculation is correct because STMF uses the same population exposure for every week within each calendar year (Human Mortality Database, 2021).

2.5. Excess death numbers

Excess death numbers (EDNs) are counts of lives lost due to excess mortality. They were used to measure of absolute losses of human lives. We calculated ${EDN}_{aretro}$ and ${EDN}_{wy}$ by multiplying ${ESDR}_{aretro}$ and ${ESDR}_{wy}$, respectively, by population sizes. Variability of EDNs that are defined this way is determined by the intensity of death and population size, but not by population age structures.

2.6. Confidence intervals

To obtain 95% confidence limits for the baseline SDRs, ESDRs, and EDNs, and related variables, we simulated for each sex and country the year-week-country-specific deaths according to the Negative Binomial distributions with parameters equal to empirical death numbers $D(y,w)$ and empirical death rates (1000 simulations).

2.7. Heat maps

To present excess mortality graphically across space and time we built heat maps for 35 countries and regions over the period 2005–20. Excess mortality is expressed by ESDR_aretro(upper panels) and ESDR_wy(lower panels). Countries (except Russia8) are ordered according to excess mortality in 2020. The color scale has seven categories ranging from light yellow to dark brown. They correspond to seven percentiles (14.6%) of ESDR distributions across 840 male and female country-year cells in the ESDR_aretro maps and 944 cells in the ESDR_wy maps. Numeric values of ESDR_aretro and ESDR_wy with their 95% confidence intervals are reported in the Supplementary Data File D.

3. Results

3.1. Illustrative application

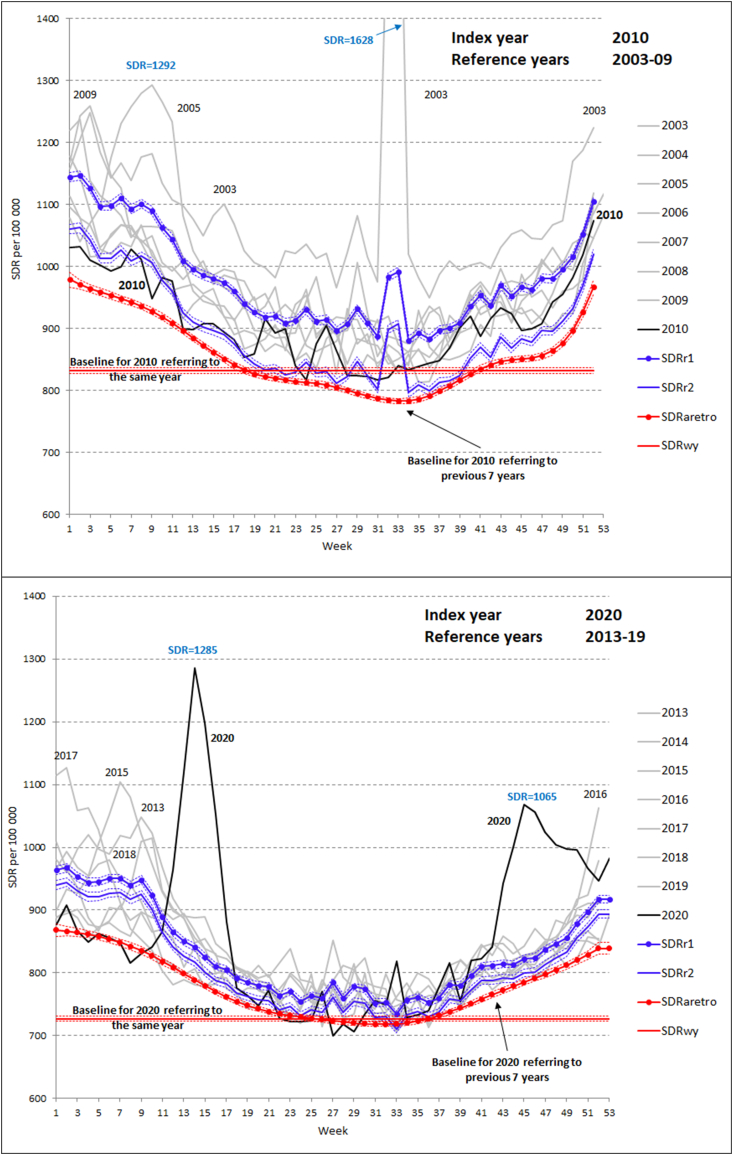
Fig. 1 shows observed weekly SDRs and the four baseline weekly SDRs in France for index years 2010 (upper panel) and 2020 (lower panel). While 2010 was a “normal” year of relatively low winter mortality, 2020 was a year of the COVID-19 pandemic.

Fig. 1.

Weekly age-standardized death rates in France per 100 000 person-years. Observed SDRs by weeks of the index years 2010 (upper panel) and 2020 (lower panel) and of the reference years 2003–2009 (upper panel) and 2013–19 (lower panel) and four baselines

Notes. Baselines: aretro – alternative retrospective baseline; wy - within-year baseline; r1 – conventional retrospective baseline (week-specific averages); r2 – conventional retrospective baseline (week-specific averages + trend).

A typical concave shape without substantial winter mortality peaks and a few moderate peaks in summer were observed in 2010. In 2003–2009, there were several mortality peaks, including huge mortality elevations in summer 2003 and winter 2005. These fluctuations were combined with a general SDR decline over years. Correspondingly, the baseline r2 that accounts for this secular trend lies substantially below baseline r1 and slightly lower than the observed weekly SDRs of 2010. As expected, the retrospective baseline referring to low (second-minimum) weekly death rates of the past lies further below r2. The horizontal within-year baseline reflects mortality in the 13 lowest mortality weeks of 2010. It lies below all other baselines with particularly pronounced gaps during cold seasons at the beginning and the end of the year.

Importantly, the alternative retrospective baseline (aretro) is insensitive both to the past mortality peaks such as the winter peaks in 2005 and 2009 and the summer peak of 2003. However, these peaks strongly influence the conventional baselines r1 and r2. This is particularly visible during the first ten weeks and weeks 32–33.

In the lower panel of Fig. 1, the index year 2020 shows sharp spring as well as autumn-winter mortality elevations due to the COVID-19 pandemic. In 2015, 2017, and 2018, France also experienced pronounced mortality elevations over the first 13–15 weeks of these years. The general mortality decline in 2013–19 was slower than that in 2003–09. For this reason, the comparator baselines r1 and r2 are closer to each other in the lower than in the upper panel. Again, the retrospective baseline (aretro) lies below baselines r1 and r2. Again, past mortality peaks do not influence the retrospective baseline but influence baselines r1 and r2.

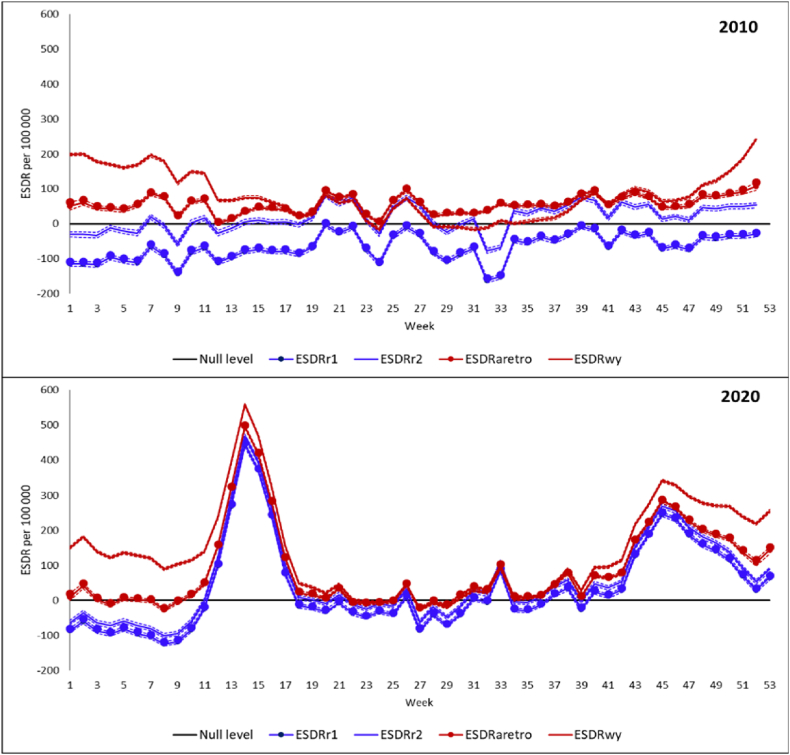
Fig. 2 displays four weekly ESDRs corresponding to the four baselines in 2010 (upper panel) and 2020 (lower panel). There are expected differences between the ESDRs depending on the baseline with the highest excess mortality corresponding to the within-year baselines and the lowest excess mortality corresponding to the comparator baseline r1.

Fig. 2.

Excess weekly age-standardized death rates per 100 000 person-years in France according to four baselines in 2010 and 2020.

3.2. Comparison between annual values of the four excess mortality measures across countries in 2005–20

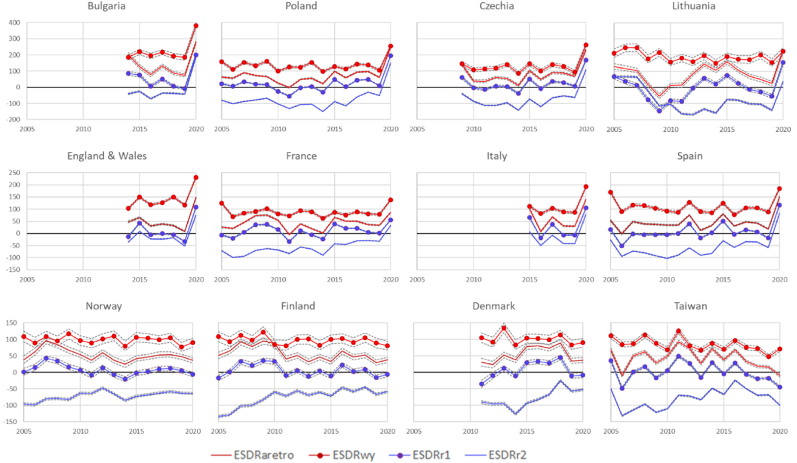
Fig. 3 presents annual trends in $ESD{R}_{aretro}$ and ${ESDR}_{wy}$ (red lines) ${ESDR}_{r1}$ and ${ESDR}_{r2}$ (blue lines) for a selection of 12 countries. Gaps in some of the trends reflect missing data in the STMF data series. The three rows of panels in the figure present countries with different levels of excess mortality in 2020. Four countries of the first row experienced the highest excess mortality in 2020 and countries of the third row experienced very low excess mortality or no excess mortality in 2020.

Fig. 3.

Excess age-standardized death rates per 100 000 person-years in 2005–20 in selected twelve countries according to the alternative retrospective, within-year, and two conventional retrospective baselines r1 and r2.

Fig. 3 highlights consistent gaps between different ESDRs. Differences between levels of the four measures of mortality excess agree with the French example in the previous section. Although weekly data, reveals excess mortality in many weeks within years before 2020 (mostly in cold seasons), but for the whole years the totals of week-specific deviations from artificially high baselines r1 and r2 are often negative (${ESDR}_{r1}$) or close to zero (${ESDR}_{r2}$). ${ESDR}_{r2}$ (that accounts for the general mortality decline) has substantial positive values in years of particularly strong flu epidemics such as 2015 or (in several countries) 2017–18. ${ESDR}_{wy}$ and ${ESDR}_{aretro}$ series lie substantially above ${ESDR}_{r2}$ with ${ESDR}_{wy}$ values being higher than ${ESDR}_{aretro}$. By contrast, ${ESDR}_{aretro}$ and ${ESDR}_{wy}$ indicate mortality excess in many years before 2020.

Table C2 in the Supplementary Appendix C provides sex-specific medians for the four measures of excess mortality in 2005–09, 2010–14, 2015–19, and 2020 across 21 countries with continuous STMF series over the period 2005–20. Despite the general SDR decline, ESDRs did not decrease between 2005–09 and 2010–14 and even somewhat increased in 2015–19 compared to previous periods (especially among females). In 2020, all ESDRs show drastic elevations in all four measures that were greater for males than females.

Table C2 in the Supplementary Appendix C provides more detailed information about medians of the four ESDRs for every single year from 2015 to 2020 for 29 countries with no data gaps during this period. One can see that in 2020 for both sexes the median values of all the four ESDRs were positive and quite high. Nevertheless, median ${ESDR}_{aretro}$ was about 90/100 000 higher than median ${ESDR}_{r1}$ and by about 50/100 000 higher than median ${ESDR}_{r2}$. In 2020, median ${ESDR}_{wy}$ was higher than median ${ESDR}_{aretro}$ by another 50/100 000. However, in “normal years” (such as 2016 or 2019) with less pronounced intra-annual mortality elevations, median ${ESDR}_{r1}$ was negative and median ${ESDR}_{r2}$ was close to zero. In such years, the gaps between ${ESDR}_{aretro}$ on one side and ${ESDR}_{r1}$ and ${ESDR}_{r2}$ on the other were by about 20–40/100 000 greater than the respective gaps in 2020. At the same time, the difference between the median values of ${ESDR}_{wy}$ and ${ESDR}_{aretro}$ in 2016 or 2019 was about the same as the one in 2020.

Fig. 3 suggests also longitudinal correlations between the four ESDRs. Compared to the other three measures, ${ESDR}_{wy}$ is somewhat different due to lower temporal variability since the within-year variation often remains high even in “normal” years without major winter peaks. Table C4 in the Supplementary Appendix C provides Pearson’s coefficients of correlation between temporal changes in the four excess mortality measures for each of 21 countries with continuous STMF data in 2005–20. Correlations among ${ESDR}_{r1}$, ${ESDR}_{r2}$, and ${ESDR}_{aretro}$ are also quite high (ranging across countries from 0.59 (CI95% 0.50; 0.67) to 0.998 (CI95% 0.997; 0.998). The maximal coefficients of correlation (ranging from 0.96 (CI95% 0.94; 0.98) to 0.998 (CI95% 0.997; 0.998)) demonstrate a tight link between ${ESDR}_{aretro}$ and ${ESDR}_{r2}$. Lower or statistically insignificant (in two countries) r values characterize links between ${ESDR}_{wy}$ on one side and ${ESDR}_{r1}$, ${ESDR}_{r2}$, and ${ESDR}_{aretro}$ on the other.9 For all 21 countries with continuous data series in 2005–20, the Pearson’s r for the ${ESDR}_{wy}$-${ESDR}_{aretro}$ pair is 0.78 (CI95% 0.74; 0.81).

To examine similarities and differences between countries’ rankings according to different ESDRs, we estimated Spearman’s correlation coefficients for different ESDR pairs for each year from 2015 to 2020 (Table C5 in the Supplementary Appendix C). In 2015–19, all cross-sectional rank correlations were substantially lower compared to the corresponding longitudinal correlations. This is especially true for links connecting ${ESDR}_{r1}$ with the other three measures and ${ESDR}_{r2}$ with ${ESDR}_{wy}$. Higher rank correlations are observed in pairs ${ESDR}_{r2}$-${ESDR}_{aretro}$ (ranging across countries from 0.53 (CI95% 0.42; 0.64) to 0.82 (CI95% 0.78; 0.87)) and ${ESDR}_{aretro}$-${ESDR}_{wy}$ (ranging from 0.63 (CI95% 0.54; 0.71) to 0.82 (CI95% 0.77; 0.86)). In 2020, countries’ ranks are much less dependent on the choice of baseline and the rank correlations linking the six pairs of ESDRs are very high (Table C5 in the Supplementary Appendix C).

3.3. Retrospective and within-year annual excess mortality in 2005–20

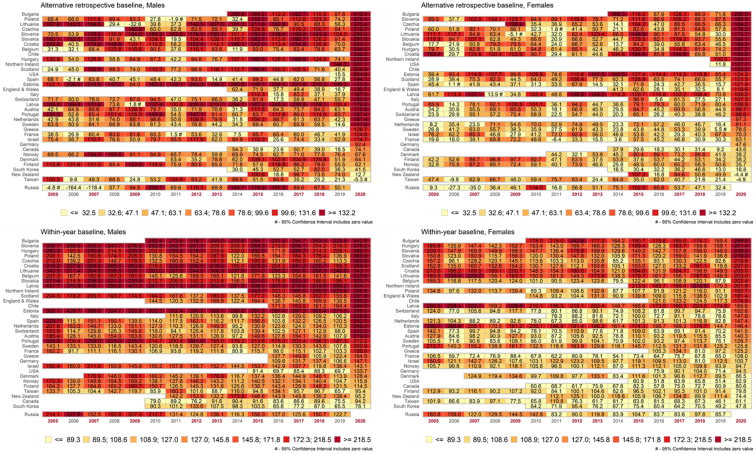
In the heat maps (Fig. 4), darker and lighter color columns in the maps indicate years of higher and lower excess mortality (e.g. “normal” and epidemic years). It appears that there are 9 epidemic years out of 16 years observed. Although the year 2020 stands out due to the dramatic increase in mortality during the pandemic, high excess mortality is seen also in earlier years such as 2015 followed by 2012 and 2007.

Fig. 4.

Heat maps of alternative retrospective and within-year excess age-standardized death rates (ESDR_aretro and ESDR_wy) per 100 000 person-years by sex from 2005 to 2020 across 35 countries and regions

Notes: Countries ordered according to ESDR values in 2020. In the maps, Russia is placed in a separate row since Russian data of 2020 is still (as of April 5, 2021) unavailable. The 7-category scales reflect 14.2% percentiles of ESDR distribution by countries and year. The scales differ between ESDR_aretro and ESDR_wy but are the same for males and females.

Darker horizontal rows in the maps mark countries and regions that tend to experience higher excess mortality compared to other countries and regions in many years. There is a distinct geographic pattern of excess mortality with higher ESDRs in countries of Eastern Europe. These are followed by parts of the UK, and countries of Southern and Western Europe. Overseas countries and Scandinavia tend to experience lower excess mortality.

There are visible similarities between the aretro and the within-year maps as one could expect from correlations presented in the previous section. Despite the similarities, the colors of many country-year cells differ between the aretro and the within-year maps. These differences are partly related to a difference between secular trends in ${ESDR}_{aretro}$ and ${ESDR}_{wy}$. While ${ESDR}_{wy}$ decreased with time in 2005–19, ${ESDR}_{aretro}$ did not. For ${ESDR}_{wy}$ the slope of the trend is −3.62 (95%CI -3.99; −3.27) and −1.69 (95%CI -1.94; −1.42) for males and females respectively in 21 countries with no data gaps in 2015–19. For ${ESDR}_{aretro}$, the corresponding values are 0.35 (CI95% −0.03; 0.71) and 0.13 (CI95% −0.10; 0.38).

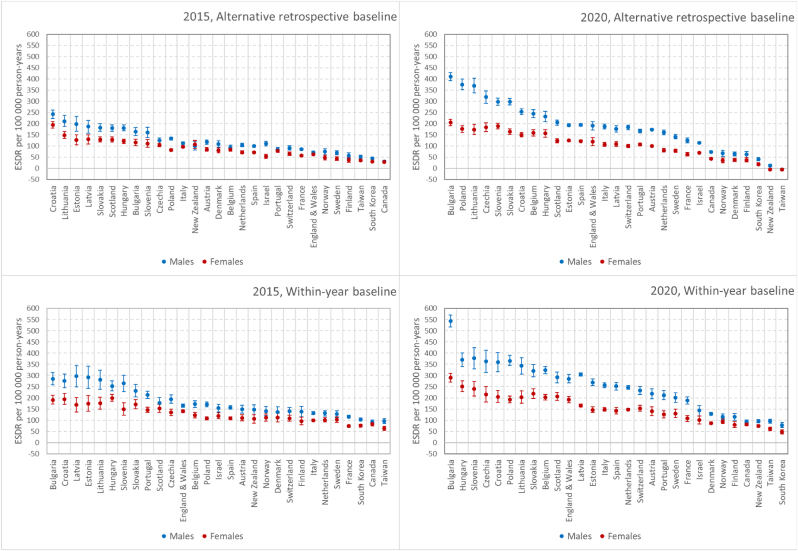
Fig. 5 compares excess mortality according to the alternative retrospective and the within-year baselines between 2020 and 2015 (an earlier year with great winter mortality elevation) and between men and women. It demonstrates much higher excess mortality and larger male-female gaps in 2020 compared to 2015 for 29 countries with no data gaps in 2008–14 and 2013–19. The 2020/2015 ratio in ${ESDR}_{aretro}$ is 1.53 (CI95% 1.49; 1.58) and 1.20 (CI95% 1.16; 1.23) for males and females, respectively. The same ratio in ${ESDR}_{wy}$ is 1.38 (CI95% 1.33; 1.42) and 1.20 (CI95% 1.17; 1.24) for males and females, respectively. Across countries, these ratios vary from about 0.8 to about 2. Despite the larger toll of excess deaths, excess mortality rankings of countries show clear similarities between 2015 and 2020. For ${ESDR}_{aretro}$, the Spearman’s rho is 0.70 (CI95% 0.64; 0.76) for males and 0.69 (CI95% 0.62; 0.74) for females. For ${ESDR}_{wy}$ the respective values are 0.79 (CI95% 0.73; 0.84) and 0.75 (CI95% 0.66; 0.82).

Fig. 5.

Alternative retrospective and within-year excess age-standardized death rates (ESDR_aretro and ESDR_wy) by sex and country per 100 000 person-years in 2015 and 2020

Notes. 29 countries with no data gaps in 2008–15 and 2013–20. Countries ordered according to the average excess mortality.

3.4. Annual excess death numbers

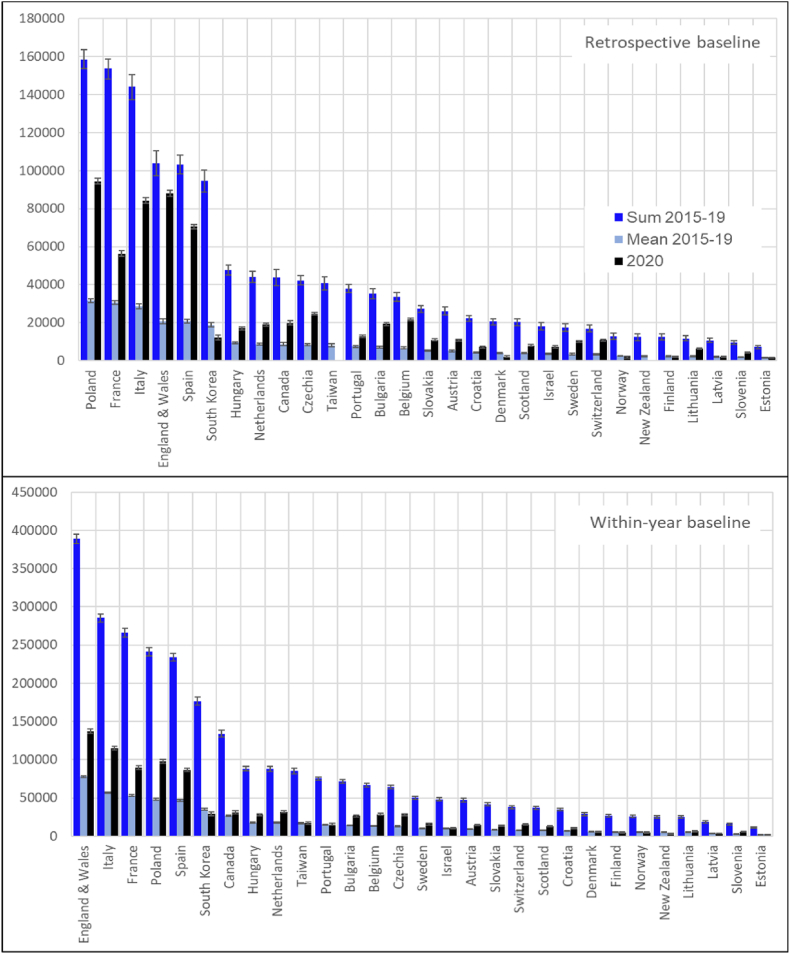
Fig. 6 shows excess death numbers (EDNs) in 2020 as well as the mean annual EDNs for the period 2015-19, and the sums of annual EDNs for this period for 29 countries with no data gaps in 2008–15 and 2013–20. In each panel, countries are ordered according to the sum of excess mortality in 2015–19. Countries’ rankings are very similar in upper and lower panels (Spearman’s rho is 0.96 (CI95% 0.95; 0.97). The USA and Germany – countries with the largest populations are not shown in the figure, since their STMF time series are too short (as of April 5, 2021) and do not allow estimating ${ESDR}_{aretro}$ in 2015–19.

Fig. 6.

Excess death numbers according to the alternative retrospective (upper panel) and within-year (lower panel) baselines: deaths in 2020, mean annual deaths, and a sum of deaths in 2015–19 for both sexes in 29 countries^#

Notes. ^# 29 countries with no data gaps in 2008–15 and 2013–20. The vertical axes scales differ between the upper and the lower panels.

The mean annual ${EDN}_{aretro}$ (upper panel) in 2015–19 ranges from 31.7 (CI95% 30.7; 32.7) thousand to 1.4 (CI95% 1.3; 1.6) thousand. In 2020, ${EDN}_{aretro}$ ranges across countries from 94.5 (CI95% 93.0; 95.9) thousand to −2.2 (CI95% −3.1; −1.8) thousand.

Mean absolute losses in 2020 exceeded the 2015–19 annual mean by 2.3 times. Nevertheless, the latter annual mean was still substantial. Therefore, the ${EDN}_{aretro}$ were cumulating over the five pre-pandemic years, and the sum of excess deaths for the period 2015–19 was (on average) 2.1 fold (CI95% 2.1; 2.2) higher than the total number of excess deaths in 2020.

The maximal ${EDN}_{aretro}$ in 2015–19 were observed in Poland, France, Italy, England and Wales, and Spain, the minimal ones – in Estonia, Slovenia, Latvia, Lithuania, and Finland. In 2020, the corresponding countries were: Poland, England and Wales, Italy, Spain, and France with the highest losses, and Taiwan, New Zealand, Estonia, Norway, and Finland with the lowest losses.

Although ${EDN}_{wy}$ values presented in the lower panel are about twice higher than ${EDN}_{aretro}$ values in the upper panel, patterns of ${EDN}_{aretro}$ variation across countries are quite similar. The annual ${EDN}_{wy}$ in 2015–19 ranges from 77.8 (CI95% 76.6; 79.0) thousand to 2.2 (CI95% 2.1; 2.4) thousand. For 2020, the corresponding numbers are 137.2 (CI95% 134.5; 139.9) thousand and 1.9 (CI95% 1.5; 2.3) thousand, respectively. The ${EDN}_{wy}$ in 2020 exceeded the 2015–19 average by about 1.62 (CI95% 1.60; 1.64) times. The five-year ${EDN}_{wy}$ losses in 2015–19 were about three-fold higher than the annual losses in 2020

The maximal ${EDN}_{wy}$ in 2015–19 were observed in England and Wales, Italy, France, Poland, and Spain, the minimal ones in Estonia, Slovenia, Latvia, Lithuania, and New Zealand. In 2020, the corresponding countries were: England and Wales, Italy, France, Poland, and Spain with the highest losses, and Estonia, New Zealand, Latvia, and Finland with the lowest losses.

The magnitude of annual excess death rates and annual absolute losses in pre-pandemic years suggest an important difference between the alternative metrics and the conventional measures of excess mortality, which were either negative (ESDR_r1) or very low positive (ESDR_r2) in most of the pre-pandemic years.

4. Discussion

This study employed the widely-used concept of excess mortality to assess intra-annual mortality fluctuations between 2000 and 2020 and then to examine fluctuations associated with the SARS-CoV-2 pandemic in 2020 and those caused by epidemics of respiratory infections in earlier years. In a departure from previous practice, we used novel measures of excess morality that are not distorted by past mortality peaks and thus avoid underestimating excess mortality. We used two alternative baselines. Our alternative retrospective baseline was derived from the lowest weekly death rates achieved in previous years and our within-year baseline used an average of 13 lowest weekly death rates within the same year. We believe that these “normative” baselines make more sense from a public health perspective than the “expected mortality” baselines currently used.

The use of our alternative baselines results in excess mortality figures that are substantially higher than estimates based on conventional metrics both in 2020 as well as in earlier years. In “normal” years without particularly pronounced mortality fluctuations, the conventional measures were mostly negative (${ESDR}_{r1}$) or very small positive (${ESDR}_{r2}$). These values are so low because baselines used in their calculation are artificially shifted upward. Conventional excess rates ${ESDR}_{r1}$ and ${ESDR}_{r2}$ understate the mortality excess because they do not account for mortality trends across years and/or are influenced by past mortality elevations during the reference period. Although in 2000–2020 substantial elevations occurred every second year, the alternative retrospective excess death rates ${ESDR}_{aretro}$ were not downshifted. Our within-year excess death rates ${ESDR}_{wy}$ tended to be higher than ${ESDR}_{aretro}$ estimates because they implement a “maximalist” desire to liquidate the circumflex pattern of within-year mortality by suppressing all weekly death rates down to minimal within-year levels that are usually observed in the summer season.

Importantly, excess mortality referring to both the alternative retrospective and the within-year baselines was exceptionally high in the pandemic year 2020 but was also substantial in previous years. Thus, even in pre-pandemic years, intra-annual mortality fluctuations contributed more to excess mortality than is often assumed.

There are some limitations to our proposed alternative approach. First, although the novel measures can be calculated from a scalar indicator of mortality (SDR) that maybe also replaced by crude death rate or life expectancy, we do not have a corresponding measurement procedure applicable to vectors of age-specific death rates. Second, the empirical analyses were completed as early as May 2021 using the STMF series as of April 5, 2021. At this time, data for 2020 was still incomplete. Subsequently, more data have been added, including weekly mortality in Germany for the period 2000–2015 and in Russia for the year 2020. A conventional analysis of the very high excess mortality in Russia in 2020 is reported elsewhere (Islam et al., 2021; Timonin et al., 2022).

The observation that intra-annual mortality fluctuations differ among countries should give cause for reflection. The appropriate response to the COVID-19 pandemic has been highly contested. Countries took different approaches, in part reflecting their experience of SARS in 2003 as well as the delayed understanding of the major importance of airborne transmission in the spread of COVID-19 (Greenhalgh et al., 2021; Han et al., 2020). However, in the mainstream and social media, where comment has often been heavily influenced by the ideology of those participating, some, and especially the so-called “lockdown skeptics” (John, 2020), have frequently invoked the annual toll of influenza-related deaths, asking why governments are responding so intensely to COVID-19 when they fail to do so when influenza epidemics occur (Oliver, 2021). Leaving aside their often highly selective and misleading use of data, for example arguing incorrectly that the lethality of COVID-19 is comparable to that of influenza (Pekosz, 2020), perhaps they have a point, even if this is the opposite of what they are advocating. Before 2020, societies tended to tolerate winter mortality peaks as an inevitable “natural” cyclic phenomenon. Indeed, some critics of restrictions during the pandemic pointed to the failure to act decisively against influenza in the past as a justification for keeping society open and argued that we should move to treating COVID-19 “just like the flu” (Javid, 2021). Indeed, one adviser to the British government said “in a bad flu season, 200–300 die a day over winter and nobody wears a mask or socially distances, that's perhaps a right line to draw in the sand” (Gallagher, 2022). However, this argument can be turned on its head. The potentially avoidable character of a large fraction of seasonal influenza deaths is underlined by the fact that levels of influenza, and associated mortality, have been extremely low in many countries in winter 2020/21 (Adlhoch et al., 2021; Sullivan et al., 2020). Now we know that we can reduce seasonal respiratory infections with basic non-pharmacological interventions (Kadambari et al., 2022), some have suggested that we might continue with some in the future (Kelly, 2020). Experience of developing interventions to reduce the impact of COVID-19 in 2020 gives a realistic hope that excess mortality from respiratory infections can be reduced greatly in the future. Thus, we should take the frequent occurrence of large numbers of influenza-related deaths more seriously.

SARS-CoV-2 and the influenza virus differ in many ways, especially in their lethality, and it is unrealistic to expect the severe restrictions necessary to curtail the spread of the former to be imposed each year in response to influenza. However, our analysis should challenge the complacency that exists with respect to seasonal influenza. In most countries the public health response, if it exists, is based on vaccination of those at greatest risk, especially older people (Smetana et al., 2018). A few also vaccinate children with a nasal vaccine, primarily to reduce their role in transmitting the infection to older relatives. Yet as the historical experience with influenza and the contemporary experience with COVID-19 show us, such an approach lacks ambition and has limited impact.

This calls for a renewed effort to understand what might work after the current pandemic to reduce the avoidable toll of deaths from newly emerging viruses such as the SARS-CoV-2, from “conventional” influenza or any other respiratory infection. It is now clear that our understanding of the transmission of COVID-19 was delayed by the failure to convene the necessary multidisciplinary expertise, in particular those with expertise in aerodynamics (Tang et al., 2021), the methodological challenges in evaluating the role of face coverings in reducing spread from those infected (as opposed to any role in protecting the wearer) (Greenhalgh, 2020), an under-appreciation of the importance of ventilation of indoor spaces (Morawska, 2021), and a failure to recognize the importance of super-spreading events. However, the magnitude of the crisis has created an imperative to address these knowledge gaps, as well as to develop innovative responses such as RNA vaccines, which some believe have potential to address the problems arising from the need for annual influenza vaccination (Freyn et al., 2020).

A rejection of the complacency that has characterized responses to seasonal influenza would, as we have shown, make an important contribution to reducing premature mortality in many countries. However, as SARS-CoV-2 is unlikely to be the last respiratory pathogen with the potential to cause a pandemic, such measures will also strengthen global resilience in the face of a similar threat in the future.

Declarations of interest

None.

Funding sources

IK, SAT, EMA were supported by funding from the Basic Research Program at the National Research University Higher School of Economics. VMS, DAJ, and DAL were partly supported by this Program. The funder had no role in study design, data collection, and analysis, decision to publish, or preparation of the manuscript.

Financial disclosure statement

There are no financial relationships between any of the authors and other organisations that may bias or influence the conclusions of this work.

Ethical statement

The study uses publicly available data, and as such it did not require ethical approval.

CRediT authorship contribution statement

Vladimir M. Shkolnikov: Conceptualization, Methodology, Investigation, Writing – original draft, Writing – review & editing, Visualization, Supervision. Ilya Klimkin: Conceptualization, Formal analysis, Software, Validation, Investigation, Data curation, Visualization, Writing – original draft, Writing – review & editing. Martin McKee: Writing – original draft, Writing – review & editing. Dmitri A. Jdanov: Conceptualization, Methodology. Ainhoa Alustiza-Galarza: Data curation, Validation, Project administration. László Németh: Methodology, Formal analysis, Visualization. Sergey A. Timonin: Conceptualization, Visualization, Validation. Marília R. Nepomuceno: Formal analysis, Investigation. Evgeny M. Andreev: Formal analysis, Investigation. David A. Leon: Conceptualization, Investigation, Writing – original draft, Writing – review & editing.

Declaration of competing interest

The authors declare no competing interests.

Supplementary data

The following are the supplementary data to this article: