Skip to main content
PMC home page
RSC Advances logoLink to RSC Advances
. 2019 Dec 5;9(69):40340–40347. doi: 10.1039/c9ra07670k

Exploring the potentials of Ti3N2 and Ti3N2X2 (X = O, F, OH) monolayers as anodes for Li or non-Li ion batteries from first-principles calculations†

Hongli Yu 1, Wei Lin 1, Yongfan Zhang 1, Yi Li 1, Kaining Ding 1, Shuping Huang 1,✉, Wenkai Chen 1,2,3,✉
PMCID: PMC9076222  PMID: 35542669

Abstract

The electronic properties and different metal ion (Li, Na, Mg) storage capabilities of the two-dimensional (2D) Ti3N2 monolayer and its Ti3N2X2 derivatives (X = O, F, and OH) as anode materials in rechargeable batteries have been systematically investigated by density functional theory (DFT) computations. Results show that the bare Ti3N2 and terminated monolayers in their most stable configurations are all metallic before and after metal ion adsorption. The relatively low diffusion barriers on the bare Ti3N2 monolayer were also confirmed, which implies faster charge and discharge rates. With respect to storage capacity, a high theoretical capacity of 1874 mA h g−1 can be provided by the Ti3N2 monolayer for Mg due to its multilayer adsorption and two-electron reaction. The existence of functional groups is proven to be unfavorable to metal ion migration and will decrease the corresponding storage capacities, which should be avoided in experiments as much as possible. These excellent performances suggest that the bare Ti3N2 is a promising anode material for Li-ion or non-Li-ion batteries.

The electronic properties and metal ion (Li, Na, Mg) storage capabilities of the two-dimensional Ti3N2 monolayer and its Ti3N2X2 derivatives (X = O, F, OH) as anode materials in rechargeable batteries are investigated by DFT computations.graphic file with name c9ra07670k-ga.jpg

1. Introduction

Energy storage has attracted extensive attention of researchers in recent years due to its widespread and varied applications, including portable electronic devices and electric vehicles.1,2 Among different energy storage systems, lithium-ion batteries (LIBs) as the most prominent representative of secondary batteries, have been widely commercialized due to their significant advantages of large energy density, long circle-life and high performance.3–5 However, the further development of LIBs is impeded by cost and safety issues, and limited natural reserves and geometric consumption will result in lithium resources being in short supply. Therefore, non-Li ion batteries in which other metal ions replace the Li ions are receiving great attention. Compared to lithium, sodium has rich reserves and low-cost, which can cover the shortcomings of lithium so that Na-ion batteries (NIBs) can become a promising candidate for next-generation rechargeable batteries.6–8 Except for monovalent elements, multivalent metal ions (Mg,9,10 Ca,11 and Al12) have also been investigated. The emphasis for developing all these various secondary batteries focuses on appropriate electrode materials that can provide satisfactory battery performance.

Two-dimensional (2D) materials have become a hot spot due to its excellent mechanical and electrical properties. One representative among them is graphene,13,14 it has been successfully applied as electrode materials for LIBs owing to its ultrahigh surface area and high cycle performance. Except for graphene, phosphorene15 and transition metal dichalcogenides16–18 are sequentially explored by researchers. Recently, a new class of two-dimensional early transition metal carbides and carbonitrides (MXenes) materials have attracted tremendous attention in many materials research fields (such as energy, optics, catalysis, etc.) due to its unique properties.19,20 The general formula of 2D transition-metal carbides and nitrides are Mn+1AXn (n = 1, 2, 3), where “M” represents an early transition metal, A represents the mostly IIIA or IVA elements. X represents C or N. Mn+1Xn was synthesized by selective etching of the A atomic layer in the three-dimensional layered compound Mn+1AXn by HF acid to obtain a two-dimensional atomic crystalline compound which have a graphene-like structure. Usually, the functional groups (–O, –F, –OH, etc.) generated during the etching process give MXene good hydrophilicity, but it does not significantly affect its conductivity.21–23 Many MXenes have been successfully synthesized in the experiment, such as Ti3C2,24 Ti3CN, Ti2C, Ta4C3 (ref. 25) and Nb2C.26 It has been demonstrated that MXenes have great potential for energy storage due to its excellent rate characteristics and cycle stability.27,28 Compared with Mn+1Cn, Mn+1Nn is relatively difficult to synthesize experimentally due to lower cohesive energy, which signifies that A layer in Mn+1ANn phase precursor is strongly bonded. Nitride MXenes exhibit better performance in electronic conductivity than its carbide counterparts.29 Therefore, low electron diffusion and good electrical conductivity making nitride MXenes are suitable candidates for battery anode materials.

In this paper, we selected Ti3N2 as the representative MXene and systematically investigated Li, Na, Mg ion storage properties and diffusion barrier of the monolayer with bare, fluorinated, hydroxylated and oxidized derivatives by using first-principles calculations. Before and after metal ions adsorption, the lowest energy configuration and corresponding electronic properties of the material have been confirmed. Then in-depth study the process of adsorbing different metal ions and the corresponding diffusion barrier. Our calculation results exhibit that the bare Ti3N2 monolayer has favorable performance as anode material, which has metallic character with relatively low band gap, low barrier energy indicating fast ion diffusion, high theoretical capacity for Mg (∼1874 mA h g−1). It's also worth mentioning that the existence of functional groups tends to hinder ions diffusion and greatly reduce the Li or non-Li storage capacities, which ought to be experimentally avoided as possible.

2. Computational details

All our calculations were based on density functional theory (DFT) by an all-electron method in the DMol3 code that a generalized gradient approximation (GGA) for the exchange–correlation term with Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional was carried out.30–32 The basis set adopted was the double numerical plus d functions (DND) and for accurately measured electrostatic interactions we used the DFT + D2 method with the Grimme vdW correction.33 The energy convergence criterion of the self-consistent field (SCF) was set to 1 × 10−6 au to ensure sufficient accuracy. The maximal force convergence criterion was set 0.002 Ha Å−1 guarantee that the forces on each atom converge. We build a vacuum space exceed 20 Å in order to eliminate the interaction between adjacent layer caused by periodic boundaries. For structure geometry optimization, the Brillouin zone was implemented by Monkhorst–Pack special k-point mesh of 4 × 4 × 1 meanwhile 12 × 12 × 1 mesh for the electronic structure calculations.34

We built a 3 × 3 × 1 supercell to systematic investigated the process of one metal atom (Li, Na, Mg) adsorption on the bare Ti3N2 and Ti3N2X2 (X = F, OH, O) monolayer. Searching for the exact transition states (energy saddle points) by computing the minimum-energy path (MEP) accomplished through using the LST/QST function in the DMol3. The energy of the barrier was defined as the energy difference between the reactant state and transition state. Phonon modes are calculated in the Phonopy with the atomic displacements of 0.01 Å.35

3. Result and discussion

3.1. Structural and electronic properties of Ti3N2, Ti3N2X2 (X = O, F, OH) monolayers

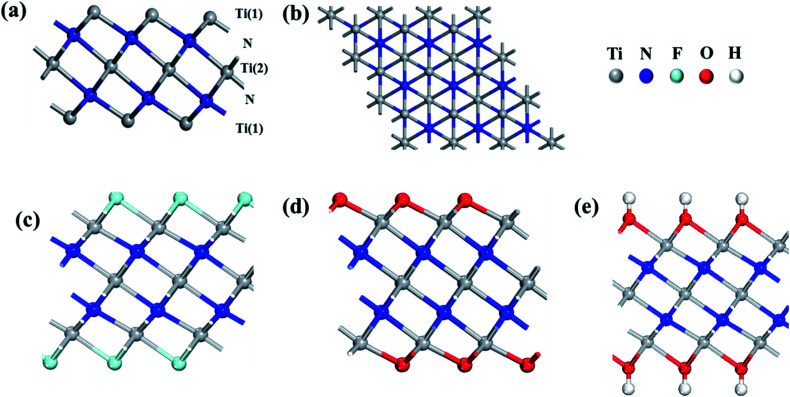
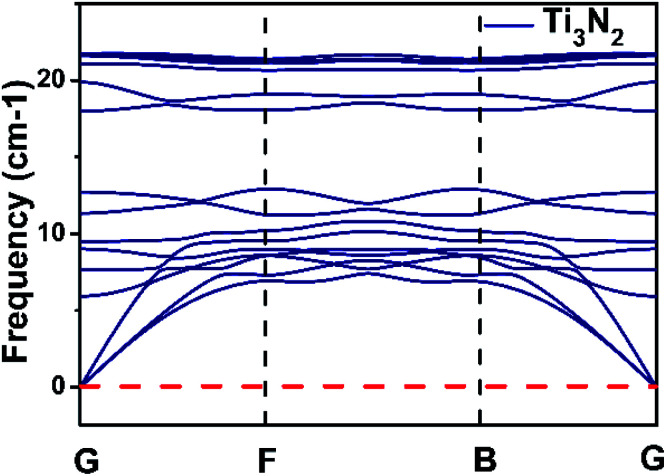
Firstly, the monolayer Ti3N2 configuration is constructed like their carbide counterparts with quintuple layers stacked in a sequence of Ti(1)–N–Ti(2)–N–Ti(1),36,37 where Ti(1) represents Ti atoms that protrude from the surface of the sheet and Ti(2) represents the atomic layer which is sandwiched by two N-atomic layers (Fig. 1a). The optimized lattice constant of Ti3N2 is 3.098 Å and the distance between the Ti(1)–N bonds is 2.048 Å in good agreement with the previous reports.35 The structures of Ti3N2X2 (X = O, F, OH) sheets are achieved by saturating the Ti atoms on the surface with the functional groups. There are three possible configurations for Ti3N2X2 (Fig. S1†): type I, the X groups are above the vertical sites of Ti(2) atoms on both sides of Ti3N2 layer; type II, the X groups are oriented above the topmost sites of N atoms on both sides of Ti3N2 layer; type III, an asymmetrical structure that can be considered as a compound of the above two types, in which X groups are above the vertical sites of Ti(2) atoms on one side and above the topmost sites of N atoms on the other side. We confirmed the most stable configuration (Fig. 1c–e) by comparing their total energies. The conclusion is that type I has the lowest energy regardless of the specific adsorption groups. The energy of type I is lower than type II and type III by about 0.22 and 0.40 eV (Ti3N2F2), 0.71 and 1.44 eV (Ti3N2O2), 0.05 and 0.11 eV [Ti3N(OH)2] per unit cell, respectively. The results distinctly show that the functional groups are more inclined to point directly toward the Ti(2) atoms. The occurrence of this phenomenon may be attributed to spatial electronic exclusion between the surface terminations with the saturated N atoms. Hence, we only consider the most stable configuration for its derivatives in the following investigations. After X groups saturation, the Ti(1)–N bond length is elongated to different degrees for various terminations: 2.059 Å (Ti3N2F2) 2.182 Å (Ti3N2O2), 2.084 Å [Ti3N2(OH)2], respectively. Phonon dispersion calculation of Ti3N2 was carried out to verify its stability and the corresponding result is shown in the Fig. 2. There is no imaginary phonon frequency which means the Ti3N2 monolayer is dynamically stable.

Fig. 1. (a) Side view of bare Ti3N2 monolayer. (b) Top view of Ti3N2 monolayer. (c–e) Side view of Ti3N2F2, Ti3N2O2, Ti3N2(OH)2, respectively.

Fig. 1

Open in a new tab

Fig. 2. Calculated phonon dispersion curves for the structure of Ti3N2.

Fig. 2

Open in a new tab

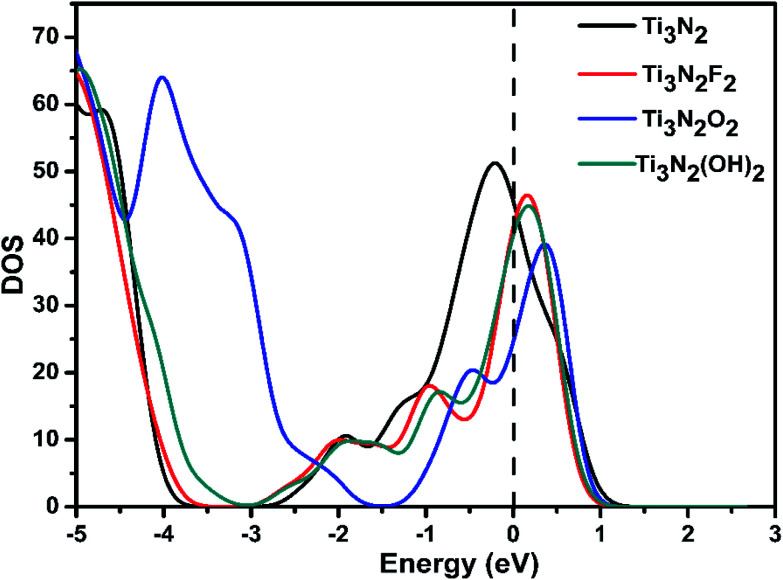
The total density of states (TDOS) of Ti3N2 and Ti3N2X2 are shown in Fig. 3. For bare Ti3N2 (Fig. 3a), the calculation result indicates that it is characterized as a metallic configuration with substantial electron states crossing the Fermi level, which is in agreement with previous work.37 With regard to surface passivated by X groups, the results demonstrate that the Ti3N2X2 monolayers still maintain metallic properties regardless of the specific adsorption configurations. The metallic character of Ti3N2 and Ti3N2X2 monolayers can guarantee their good electrical conductivity as anode materials in rechargeable batteries.

Fig. 3. Total DOS of Ti3N2, Ti3N2F2, Ti3N2O2 and Ti3N2(OH)2. The Fermi levels are set to zero and are indicated by the dashed lines.

Fig. 3

Open in a new tab

3.2. Metal atom adsorption and diffusion on Ti3N2 and Ti3N2X2 (X = F, O, OH) monolayers

We have known that the bare Ti3N2 and Ti3N2X2 monolayers possess metal electronic properties. Next we make a thorough research about the behavior of different metal species A (A = Li, Na, Mg) adsorption and diffusion on Ti3N2 and Ti3N2X2 (X = F, O, OH) monolayers. The first step is to confirm the most favorable adsorption site. We only discuss the adsorption position on the surface due to the adatoms are embedded in the inner layer and cause significant volume expansion of the system. Hence, a 3 × 3 × 1 supercell, which corresponds to a chemical stoichiometry of Ti27N18A and Ti27N18X18A (X = F, O, OH), has been adopted to systematically investigate one atom adsorbed on surface sites in order to avoid interaction between atoms. Three existing adsorption sites are considered in our calculations: (a) the site on top of the Ti(1) atom, (b) the site on top of the N atom, (c) the site on top of the Ti(2) atom (which is top site of F atom for I–Ti3N2F2, top site of O atom for I–Ti3N2O2, top site of OH group for I–Ti3N2(OH)2). The adsorption energy (Ead) of guest adatoms on the monolayer is defined as

Ead = ETi27N18X18A(F,O,OH) − ETi27N18X18(F,O,OH) − EA 1

where Ead represents that adsorption energy, ETi27N18X18A(F,O,OH) and ETi27N18X18(F,O,OH) are the total energies of Ti27N18 or Ti27N18X18 monolayers with and without atoms adsorption, and EA is the energy per atom in the bulk metal for Li, Na, and the primitive hexagonal Bravais lattice for Mg.

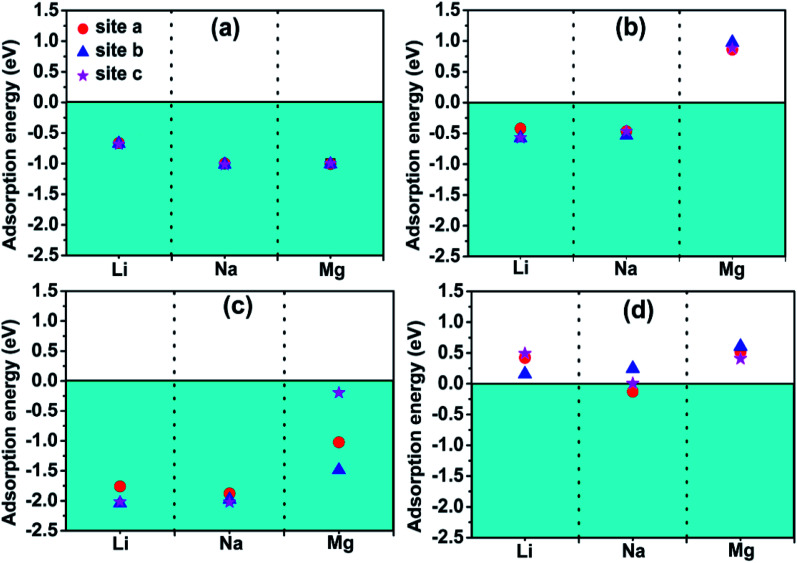
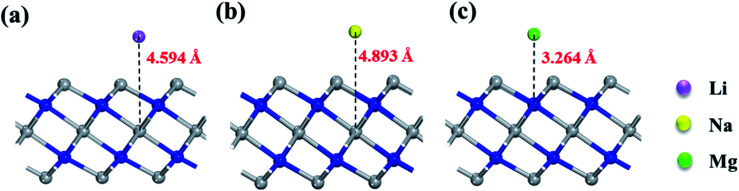
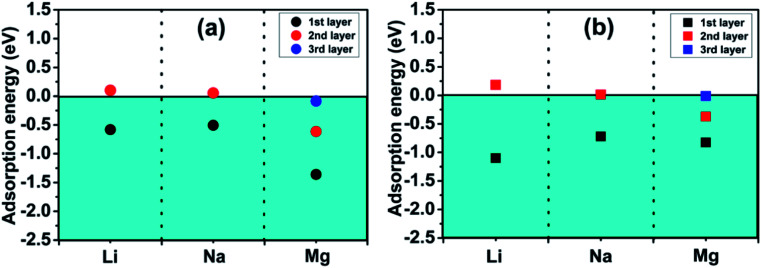
Fig. 4 exhibits the adsorption energy values of different metal atoms adsorbed at different adsorption sites. The blue portion represents negative adsorption energy, it indicates that adatoms are more willing to adsorb on the surface of the monolayer rather than clustering by itself. We observe that all the investigated adatoms can be adsorbed on the surface with little difference in adsorption energy for bare Ti3N2 monolayer. Interestingly, the adsorption energy turns more negative when the surface terminated by O group, which means the interaction between adatoms and Ti3N2O2 monolayer is strengthened. The Mg atom cannot be adsorbed on Ti3N2F2 monolayer, and only Na atom can be adsorbed on Ti3N2(OH)2 monolayer which have a relatively small adsorption energy value. Our calculations showed that the existence of terminal groups conspicuously descend the storage capacity of Ti3N2 except for O group. This is similar to the case of Ti3C2.34 For bare Ti3N2, the most favorable adsorption position for Li, Na, and Mg are the “c”, “c” and “b” site, respectively. The optimal distances along the c-axis between Ti(2) and Li/Na are 4.594/4.893 Å, with respect to the distance of N–Mg is 3.264 Å as shown in Fig. 5. For the case of Li adsorption, the average distances of Li–N (the most favorable adsorption position) are 3.357 (for Ti3N2F2) and 3.271 Å (for Ti3N2O2), respectively. We do not consider Ti3N2(OH)2 due to Li can't be adsorbed.

Fig. 4. Adsorption energies of metal atom species A (A = Li, Na, Mg) on (a) Ti3N2, (b) Ti3N2F2, (c) Ti3N2O2, (d) Ti3N2(OH)2 at different surface sites.

Fig. 4

Open in a new tab

Fig. 5. Side views of the optimized structures of (a) Li, (b) Na, (c) Mg adsorbed on Ti3N2 monolayers.

Fig. 5

Open in a new tab

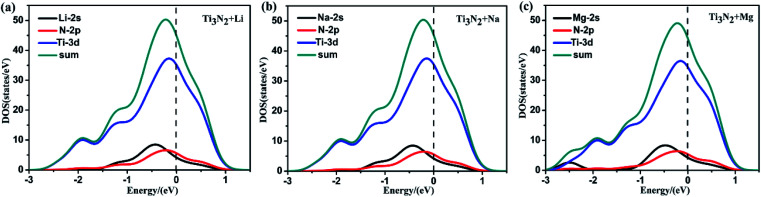
Whether the monolayer could continue to acquire a metallic character after adatoms adsorption is a key for its electrode performance. So we further calculated the corresponding DOS (Fig. S2†) to answer this question. In the case of the different metal ions adsorbed Ti3N2 monolayer, the results show that the monolayer remains metallic rather than becoming an insulator. Furthermore, the difference in PDOS exhibited by the same monolayer adsorbing different metal atoms (Li, Na, Mg) is very small (Fig. 6).

Fig. 6. Total DOS and PDOS of Ti 3d, N 2p, (a) Li 2s, (b) Na 2s (c) Mg 2s for the system of adatoms adsorbed Ti3N2 monolayer. The Fermi levels are set to zero and are indicated by the dashed lines.

Fig. 6

Open in a new tab

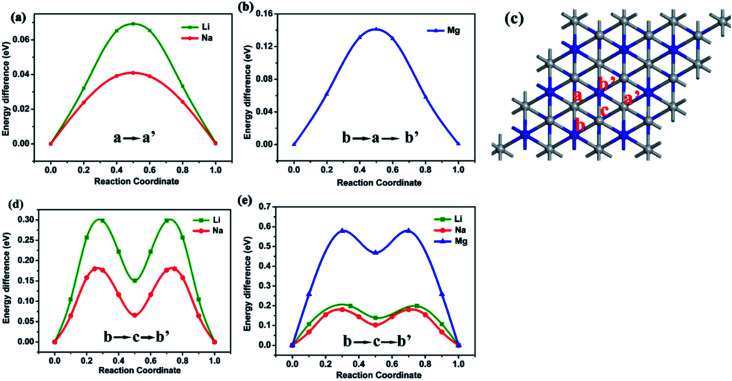
The charge and discharge rate of rechargeable batteries is determined by metal ions mobility. Therefore, we continue to study the different metal ions (Li, Na, Mg) diffusion on the surface of Ti3N2 and Ti3N2X2 monolayers. We adopted the most stable adsorption configuration as the initial state, and the configuration with adatoms adsorption at the most favorable neighboring adsorption site as the final states. The diffusion energy profiles and the corresponding pathways are shown in Fig. 7, we found that the energy of barriers for bare Ti3N2 are 0.069 eV (Li), 0.041 eV (Na), 0.103 eV (Mg), respectively. The diffusion of Na is faster than that of Li, similar to the result of MnSb2S4.44 For Li and Na, their migration paths are from the “a” site to the nearest neighboring “a′” site (Fig. 6a) with one saddle point. The vertical distances between the Ti3N2 monolayer and Li/Na are 2.956 Å/3.348 Å, respectively. The longer distance Na+ means weaker interplay and lower migration energy barrier. For Mg, the migration path is from the “b” site to the nearest neighboring “b′” site passing through the “a” site which can be described as b → a → b′, so we can clearly observed two saddle points. For Ti3N2F2 and Ti3N2O2 monolayers, their migration paths are both b → c → b′ with two saddle points. The diffusion barrier for Ti3N2F2 are 0.298 eV (for Li), 0.180 eV (for Na), and for Ti3N2O2 are 0.198 eV (for Li), 0.181 eV (for Na), 0.578 eV (for Mg), respectively. By comparing the migration energy barriers of different atoms adsorbed on the surface of Ti3N2F2 and Ti3N2O2 monolayers, we summarize the following order from lowest to highest: Na < Li < Mg, the Mg migrates relatively difficult due to its high valence state. Higher migration energy barriers than bare Ti3N2 indicate that adatoms must overcome greater resistance on the surface of Ti3N2X2, this can be interpreted as the existence of the surface terminating O or F atoms creates the strong Coulomb resistance. Compared to some traditional anode materials in the case of Ti3C2 (0.068 eV for Li,34 0.096 eV for Na, 0.118 eV for Ca), Mo2S (0.21 eV for Li,38 0.25 eV for Na,39 0.48 eV for Mg40), the commercialized graphene (0.32 eV for Li41), the values of Ti3N2 are relatively low. These low migration energy barrier values suggest that Ti3N2 monolayer is a potential candidate as electrode materials.

Fig. 7. The diffusion barrier profiles of (a) Li, Na (b) Mg on the Ti3N2 monolayer, (d) Li, Na on the Ti3N2F2 monolayer, (e) Li, Na, Mg on the Ti3N2O2 monolayer. (c) Labeling of the high symmetry points appearing in the diffusion paths. The site “a” and “a′” are on top of Ti(2) atoms for bare Ti3N2 and occupied by X for Ti3N2X2. The site “b” and “b′” are on top of N atoms. The site “c” is on top of Ti(1) atom.

Fig. 7

Open in a new tab

3.3. Average open circuit voltage and storage capacity of Ti3N2 and Ti3N2X2 monolayers

In addition to the intrinsic metallic conductivity and the low diffusion barrier, the average open circuit voltage and storage capacity are also two important characteristics which determine the performance of electrode materials. To estimate the maximum capacity of A atoms adsorption, we still adopt a 3 × 3 × 1 supercell with gradually increase the concentration of absorbed adatoms on both sides of the Ti3N2 and Ti3N2X2 monolayers. The following half-cell reaction vs. A/Ay+ are assumed during the anode charge/discharge processes:

Ti3N2[Ti3N2X2 (X = F, O)] + xAy+ + xye− ↔Ti3N2[Ti3N2X2Ax (X = F, O)] 2

The average open circuit voltage (OCV) is directly determined by the difference in total energies before and after adatoms intercalation, while the influence of volume (PΔV) and entropy (TΔS) are neglected. The change in Gibbs free energy is approximately equal to the change in internal energy at 0 K.42,43 Hence, the average open circuit voltage (OCV) is described as the following equation:

Vave = [ETi3N2/Ti3N2X2(X=F,O) + xEA − ETi3N2/Ti3N2X2Ax(X=F,O)]/xye 3

where ETi3N2[Ti3N2F2,Ti3N2O2] and ETi3N2[Ti3N2F2,Ti3N2O2]Ax are the total energies of bare Ti3N2, Ti3N2X2 without and with cations intercalation, respectively. EA is the energy of bulk metal and y stands for the valence number (y = 1 for Li, Na; y = 2 for Mg).

For the bare Ti3N2, we use Li atom adsorption as a typical case to investigate the maximum storage capacity which determines the value of x. The positions of the first Li layer situate at the most stable sites for Li adsorption that is the top sites of Ti(2) atoms, and the corresponding Li layer could form on both sides of Ti3N2 monolayer with symmetry. The second Li layer are at the top sites of N atoms on both sides after the first layer adsorption. The same to Na case, but for Mg case, the first, second and third layer are located at the top sites of N, Ti(2), Ti(1) atoms, respectively. As for Ti3N2X2, the order in which all the cations layers are located at the top sites of N, Ti(1), X atoms, respectively. To further investigate the interaction between the host material and the adsorbed cation layer, we define and compute the average layer-by-layer adsorption energy as the following equation:

Elayerad = [ETi27N18/Ti27N18X18A18n(X=F,O) − ETi27N18/Ti27N18X18A18(n−1)(X=F,O) − 18EA]/18 4

where ETi27N18/Ti27N18X18A18n(X=F,O) and ETi27N18/Ti27N18X18A18(n−1)(X=F,O) are the total energies of the supercell Ti27N18/Ti27N18X18 (X = F, O) with n and (n − 1) layers, respectively. EA is the energy per atom in bulk metal and the number ‘18’ represents the totally 18 adsorbed atoms on both sides of each monolayer. The corresponding Elayerad values are calculated and exhibited in Fig. 7. For Ti3N2F2, the calculations showed that no atoms can completely cover the first layer so we don't consider showing the results in Fig. 8. The calculated Elayerad for the first and second layers on bare Ti3N2 are −0.581, 0.102 eV for Li+ and −0.506, 0.055 eV for Na+, respectively. The positive Elayerad of the second layer indicates that the adsorbed atoms attain saturation and begin to occur cluster formation rather than regularly adsorbed on the surface of Ti3N2 monolayer. Therefore, the 3 × 3 × 1 supercell could accommodate up to 18 Li atoms and 18 Na atoms, which the corresponding chemical stoichiometry are Ti3N2Li2 and Ti3N2Na2, respectively. The evaluated average OCVs and theoretical specific capacities are 0.58 V, 312 mA h g−1 for Ti3N2Li2 and 0.51 V, 312 mA h g−1 for Ti3N2Na2. Compared with the case of Ti3C2Li2 (0.62 V, 320 mA h g−1),34 the average intercalation potentials for Ti3N2Li2 are essentially lower and the corresponding theoretical specific capacity almost the same. But for Mg, further calculations showed that there is a slightly negative Elayerad (−0.085 eV) up to entirely cover the third layer, which the chemical stoichiometry is Ti3N2Mg6 and the corresponding capacity is 1874 mA h g−1. It suggests that the strong interaction between the Ti3N2 monolayer and Mg layers.

Fig. 8. Adsorption energies of different adsorption layers on (a) Ti3N2, (b) Ti3N2O2 monolayers.

Fig. 8

Open in a new tab

For the functionalized Ti3N2 monolayers, we found that the Ti3N2F2 monolayer was severely deformed when the supercell extremely accommodate up to 12 Li atoms on both sides, and a positive adsorption energy value would occur when it accumulates 18 Na atoms, so the corresponding chemical stoichiometry are Ti3N2F2Li2/3 and Ti3N2F2Na2/3 at the maximum capacity. The average OCVs and theoretical specific capacities are 0.60 V, 85 mA h g−1 for Ti3N2F2Li2/3 and 0.06 V, 85 mA h g−1 for Ti3N2F2Na2/3. For Ti3N2O2, all the metal ions are demonstrated can completely cover the first layer, but can't achieve the second layer adsorption except for Mg case. The computed OCVs are 1.100 V (Ti3N2O2Li2) and 0.721 V (Ti3N2O2Na2), and the corresponding theoretical capacities are both 258 mA h g−1. Mg atom can achieve multilayer adsorption that it can entirely cover the third layer, the OCVs and theoretical specific capacities are 0.20 V, 1714 mA h g−1 for Ti3N2O2Mg6. The capacities of Mg adsorbed on Ti3N2O2 monolayer are slightly decline compared to Ti3N2 monolayer. The presence of surface F/OH groups significantly lower the theoretical capacities as compared with the bare Ti3N2 monolayer and the increased Li occupancy will lead to the surface instability and thus reduce the reversibility and cyclic stability of Ti3N2 anodes, so should avoid it as much as possible during the experimental synthesis.

4. Conclusions

In summary, we have investigated the electronic properties of Ti3N2 and its F/O/OH functionalized derivatives and their Li or non-Li storage capabilities based on DFT calculations. Our calculations exhibit that the bare Ti3N2 and Ti3N2X2 (X = F, OH, O) monolayers possess metallic characters whether or not atoms adsorption on it. The metallic properties guarantee strong electronic conductivity when the materials are applied as the anode material. Among them, the bare Ti3N2 monolayer could represent excellent electrochemical properties for different metal-ion adsorption. The corresponding results are various such as the relatively lowest diffusion barrier (0.041 eV) for Na-ion batteries and the highest theoretical capacity (1874 mA h g−1) for Mg-ion batteries. However, we also observed that the presence of functional groups significantly impedes ion migration and reduces theoretical capacity except for Ti3N2O2. Our calculations suggest that bare Ti3N2 has great potential as Li-ion and non-Li-ion batteries anode material with its metallic property, low diffusion barrier and high theoretical capacity through the modification of functional groups.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

RA-009-C9RA07670K-s001

Acknowledgments

This research was supported by the National Natural Science Foundation of China under No. 51574090 and No. 21703036.

†

Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra07670k

References

  1. Dunn B. Kamath H. Tarascon J.-M. Science. 2011;334:928. doi: 10.1126/science.1212741. [DOI] [PubMed] [Google Scholar]
  2. Chen H. Cong T. N. Yang W. Tan C. Li Y. Ding Y. Prog. Nat. Sci. 2009;19:291–312. doi: 10.1016/j.pnsc.2008.07.014. [DOI] [Google Scholar]
  3. Poizot P. Laruelle S. Grugeon S. Dupont L. Tarascon J. M. Nature. 2000;407:496–499. doi: 10.1038/35035045. [DOI] [PubMed] [Google Scholar]
  4. Simon P. Gogotsi Y. Dunn B. Science. 2014;343:1210. doi: 10.1126/science.1249625. [DOI] [PubMed] [Google Scholar]
  5. Wang Y. Jiao Z. Ma S. Guo Y. J. Power Sources. 2019;413:117–124. doi: 10.1016/j.jpowsour.2018.12.031. [DOI] [Google Scholar]
  6. Mortazavi M. Wang C. Deng J. Shenoy V. B. Medhekar N. V. J. Power Sources. 2014;268:279–286. doi: 10.1016/j.jpowsour.2014.06.049. [DOI] [Google Scholar]
  7. Palomares V. Casas-Cabanas M. Castillo-Martínez E. Han M. H. Rojo T. Energy Environ. Sci. 2013;6:2312–2337. doi: 10.1039/C3EE41031E. [DOI] [Google Scholar]
  8. Slater M. D. Kim D. Lee E. Johnson C. S. Adv. Funct. Mater. 2013;23:947–958. doi: 10.1002/adfm.201200691. [DOI] [Google Scholar]
  9. Ichitsubo T. Adachi T. Yagi S. Doi T. J. Mater. Chem. 2011;21:11764–11772. doi: 10.1039/C1JM11793A. [DOI] [Google Scholar]
  10. Liu B. Luo T. Mu G. Wang X. Chen D. Shen G. ACS Nano. 2013;7:8051–8058. doi: 10.1021/nn4032454. [DOI] [PubMed] [Google Scholar]
  11. Lipson A. L. Pan B. Lapidus S. H. Liao C. Vaughey J. T. Ingram B. J. Chem. Mater. 2015;27:8442–8447. doi: 10.1021/acs.chemmater.5b04027. [DOI] [Google Scholar]
  12. He Y. J. Peng J. F. Chu W. Li Y. Z. Tong D. G. J. Mater. Chem. A. 2014;2:1721–1731. doi: 10.1039/C3TA13906A. [DOI] [Google Scholar]
  13. Jing Y. Zhou Z. Cabrera C. R. Chen Z. J. Mater. Chem. A. 2014;2:12104–12122. doi: 10.1039/C4TA01033G. [DOI] [Google Scholar]
  14. Novoselov K. S. Fal'ko V. I. Colombo L. Gellert P. R. Schwab M. G. Kim K. Nature. 2012;490:192. doi: 10.1038/nature11458. [DOI] [PubMed] [Google Scholar]
  15. Sun J. Lee H.-W. Pasta M. Yuan H. Zheng G. Sun Y. Li Y. Cui Y. Nat. Nanotechnol. 2015;10:980. doi: 10.1038/nnano.2015.194. [DOI] [PubMed] [Google Scholar]
  16. Li Y. Wu D. Zhou Z. Cabrera C. R. Chen Z. J. Phys. Chem. Lett. 2012;3:2221–2227. doi: 10.1021/jz300792n. [DOI] [PubMed] [Google Scholar]
  17. Putungan D. B. Lin S.-H. Kuo J.-L. ACS Appl. Mater. Interfaces. 2016;8:18754–18762. doi: 10.1021/acsami.6b03499. [DOI] [PubMed] [Google Scholar]
  18. Wang Q. H. Kalantar-Zadeh K. Kis A. Coleman J. N. Strano M. S. Nat. Nanotechnol. 2012;7:699. doi: 10.1038/nnano.2012.193. [DOI] [PubMed] [Google Scholar]
  19. Wang J. Zhou Y. Annu. Rev. Mater. Res. 2009;39:415–443. doi: 10.1146/annurev-matsci-082908-145340. [DOI] [Google Scholar]
  20. Yang E. Ji H. Kim J. Kim H. Jung Y. Phys. Chem. Chem. Phys. 2015;17:5000–5005. doi: 10.1039/C4CP05140H. [DOI] [PubMed] [Google Scholar]
  21. Coleman J. N. Lotya M. O'Neill A. Bergin S. D. King P. J. Khan U. Young K. Gaucher A. De S. Smith R. J. Shvets I. V. Arora S. K. Stanton G. Kim H.-Y. Lee K. Kim G. T. Duesberg G. S. Hallam T. Boland J. J. Wang J. J. Donegan J. F. Grunlan J. C. Moriarty G. Shmeliov A. Nicholls R. J. Perkins J. M. Grieveson E. M. Theuwissen K. McComb D. W. Nellist P. D. Nicolosi V. Science. 2011;331:568. doi: 10.1126/science.1194975. [DOI] [PubMed] [Google Scholar]
  22. Lei J.-C. Zhang X. Zhou Z. Front. Phys. 2015;10:276–286. doi: 10.1007/s11467-015-0493-x. [DOI] [Google Scholar]
  23. Naguib M. Gogotsi Y. Acc. Chem. Res. 2015;48:128–135. doi: 10.1021/ar500346b. [DOI] [PubMed] [Google Scholar]
  24. Naguib M. Kurtoglu M. Presser V. Lu J. Niu J. Heon M. Hultman L. Gogotsi Y. Barsoum M. W. Adv. Mater. 2011;23:4248–4253. doi: 10.1002/adma.201102306. [DOI] [PubMed] [Google Scholar]
  25. Naguib M. Mashtalir O. Carle J. Presser V. Lu J. Hultman L. Gogotsi Y. Barsoum M. W. ACS Nano. 2012;6:1322–1331. doi: 10.1021/nn204153h. [DOI] [PubMed] [Google Scholar]
  26. Naguib M. Halim J. Lu J. Cook K. M. Hultman L. Gogotsi Y. Barsoum M. W. J. Am. Chem. Soc. 2013;135:15966–15969. doi: 10.1021/ja405735d. [DOI] [PubMed] [Google Scholar]
  27. Li Y.-M. Chen W.-G. Guo Y.-L. Jiao Z.-Y. J. Alloys Compd. 2019;778:53–60. doi: 10.1016/j.jallcom.2018.11.140. [DOI] [Google Scholar]
  28. Li Y. Guo Y. Chen W. Jiao Z. Ma S. J. Mater. Sci. 2019;54:493–505. doi: 10.1007/s10853-018-2854-7. [DOI] [Google Scholar]
  29. Urbankowski P. Anasori B. Makaryan T. Er D. Kota S. Walsh P. L. Zhao M. Shenoy V. B. Barsoum M. W. Gogotsi Y. Nanoscale. 2016;8:11385–11391. doi: 10.1039/C6NR02253G. [DOI] [PubMed] [Google Scholar]
  30. Delley B. J. Chem. Phys. 1990;92:508–517. doi: 10.1063/1.458452. [DOI] [Google Scholar]
  31. Delley B. J. Chem. Phys. 2000;113:7756–7764. doi: 10.1063/1.1316015. [DOI] [Google Scholar]
  32. Pham K. D. Hieu N. N. Phuc H. V. Fedorov I. A. Duque C. A. Amin B. Nguyen C. V. Appl. Phys. Lett. 2018;113:171605. doi: 10.1063/1.5055616. [DOI] [Google Scholar]
  33. Grimme S. J. Comput. Chem. 2006;27:1787–1799. doi: 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
  34. Tang Q. Zhou Z. Shen P. J. Am. Chem. Soc. 2012;134:16909–16916. doi: 10.1021/ja308463r. [DOI] [PubMed] [Google Scholar]
  35. Togo A. Oba F. Tanaka I. Phys. Rev. B: Condens. Matter Mater. Phys. 2008;78:134106. doi: 10.1103/PhysRevB.78.134106. [DOI] [Google Scholar]
  36. Chen X. Kong Z. Li N. Zhao X. Sun C. Phys. Chem. Chem. Phys. 2016;18:32937–32943. doi: 10.1039/C6CP06018H. [DOI] [PubMed] [Google Scholar]
  37. Pan H. J. Mater. Chem. A. 2015;3:21486–21493. doi: 10.1039/C5TA06259D. [DOI] [Google Scholar]
  38. Li Y. Wu D. Zhou Z. Cabrera C. R. Chen Z. J. Phys. Chem. Lett. 2012;3:2221–2227. doi: 10.1021/jz300792n. [DOI] [PubMed] [Google Scholar]
  39. Mortazavi M. Wang C. Deng J. Shenoy V. B. Medhekar N. V. J. Power Sources. 2014;268:279–286. doi: 10.1016/j.jpowsour.2014.06.049. [DOI] [Google Scholar]
  40. Yang S. Q. Li D. X. Zhang T. R. Tao Z. L. Chen J. J. Phys. Chem. C. 2012;116:1307–1312. doi: 10.1021/jp2097026. [DOI] [Google Scholar]
  41. Fan X. Zheng W. T. Kuo J.-L. ACS Appl. Mater. Interfaces. 2012;4:2432–2438. doi: 10.1021/am3000962. [DOI] [PubMed] [Google Scholar]
  42. Aydinol M. K. Kohan A. F. Ceder G. Cho K. Joannopoulos J. Phys. Rev. B: Condens. Matter Mater. Phys. 1997;56:1354–1365. doi: 10.1103/PhysRevB.56.1354. [DOI] [Google Scholar]
  43. Meng Y. S. Arroyo-de Dompablo M. E. Energy Environ. Sci. 2009;2:589–609. doi: 10.1039/B901825E. [DOI] [Google Scholar]
  44. Zhang Z. Zhang Y. Li Y. Lin J. Truhlar D. G. Huang S. Chem. Mater. 2018;30:3208–3214. doi: 10.1021/acs.chemmater.7b05311. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

RA-009-C9RA07670K-s001
RA-009-C9RA07670K-s001.pdf (357.5KB, pdf)

Articles from RSC Advances are provided here courtesy of Royal Society of Chemistry

RESOURCES