Aortic stiffness is lower when PVAT is included: a novel ex vivo mechanics study

Abstract

Perivascular adipose tissue (PVAT) is increasingly recognized as an essential layer of the functional vasculature, being responsible for producing vasoactive substances and assisting arterial stress relaxation. Here, we test the hypothesis that PVAT reduces aortic stiffness. Our model was the thoracic aorta of the male Sprague–Dawley rat. Uniaxial mechanical tests for three groups of tissue were performed: aorta with PVAT attached (+PVAT) or removed (−PVAT), and isolated PVAT (PVAT only). The output of the mechanical test is reported in the form of a Cauchy stress-stretch curve. This work presents a novel, physiologically relevant approach to measure mechanical stiffness ex vivo in isolated PVAT. Low-stress stiffness (E₀), high-stress stiffness (E₁), and the stress corresponding to a stretch of 1.2 (σ_1.2) were measured as metrics of distensibility. The low-stress stiffness was largest in the −PVAT samples and smallest in PVAT only samples. Both the high-stress stiffness and the stress at 1.2 stretch were significantly higher in −PVAT samples when compared with +PVAT samples. Taken together, these results suggest that −PVAT samples are stiffer (less distensible) both at low stress (not significant) as well as at high stress (significant) when compared with +PVAT samples. These conclusions are supported by the results of the continuum mechanics material model that we also used to interpret the same experimental data. Thus, tissue stiffness is significantly lower when considering PVAT as part of the aortic wall. As such, PVAT should be considered as a target for improving vascular function in diseases with elevated aortic stiffness, including hypertension.

NEW & NOTEWORTHY We introduce a novel and physiologically relevant way of measuring perivascular adipose tissue (PVAT) mechanical stiffness which shows that PVAT’s low, yet measurable, stiffness is linearly correlated with the amount of collagen fibers present within the tissue. Including PVAT in the measurement of the aortic wall’s mechanical behavior is important, and it significantly affects the resulting metrics by decreasing aortic stiffness.

INTRODUCTION

Perivascular adipose tissue (PVAT) studies have focused primarily on factors secreted by PVAT that either relax (adiponectin, H₂S) or contract (angiotensin II) the blood vessel (1–12). We test the hypothesis that considering PVAT as part of the aortic wall decreases the stiffness of the system as a whole, presenting the novel idea that PVAT contributes to the vessels’ mechanical function.

Thoracic aorta and the surrounding PVAT were selected for the present study because this portion of the aorta contributes significantly to pulse wave velocity (PWV). Elevated aortic stiffness increases PWV by accelerating the reflected pressure wave generated by the heart/ascending aorta during diastole and returning during systole (13, 14). A stiffer aorta increases heart work, decreasing the arterial reservoir of elastic potential energy. The increased aortic/arterial stiffness measured in vivo in aging and disease has been largely attributed to changes in the mechanics of the vascular tunicas, the intima/media/adventitia (proper artery). Aortic stiffness is an independent risk factor for stroke, heart disease, overall cardiovascular mortality, and cognitive decline (13, 15–18). In addition, increased stiffness precedes hypertension (14, 17). As such, knowing mechanisms behind the progression of arterial stiffness is important.

Although PWV is a valuable in vivo measure of arterial stiffness, it is an inherently average measure. Consequently, it does not allow us to investigate how different components of the aortic wall or different locations along the aortic tree contribute to the increase in stiffness. In other words, measuring aortic stiffness just by PWV makes it impossible to answer questions such as: Is the whole aorta stiffening equally, in every location, and simultaneously? Or is the stiffening concentrated in a specific tunica of the aortic wall? Ex vivo testing is a valuable option to investigate such questions. By testing the tissue in an isolated, ex vivo setting, it is possible to use tissue manipulations to isolate the contribution of each layer to the overall, averaged behavior of the aorta.

In the present study, we used the isolated thoracic aorta of the normal male Sprague–Dawley rat as our model for mechanical testing to measure 1) stiffness of PVAT itself and 2) whether the inclusion of PVAT lowered the stiffness measure for the artery. We conducted histological examination to determine collagen tissue content in relationship to measured stiffness parameters for PVAT itself. This artery was chosen because it is a great part of what is considered when measuring PWV and because the PVAT of this artery could be separated from the proper vessel so both could be studied independently. We have not studied females nor a large sample group because this focused study was an effort to determine if there is value to the question of whether the aortic PVAT has stiffness of its own and can modify aortic stiffness.

A common measure of material stiffness is the Young’s modulus, usually defined as the slope of the linear stress-strain response of a material (19). This metric is not always appropriate to describe the mechanics of biological tissue due to their inherent complexity and nonlinearity of biological tissue. Although in vivo aortic mechanics follows a mostly linear relationship within the physiological pressure range (i.e., pressure variation of ∼30 mmHg), ex vivo aortic tissue shows highly nonlinear mechanical response, making a single linear measure of stiffness, such as the Young’s modulus, inherently ineffective to capture the overall behavior of the tissue. In this study, we use the classic continuum mechanics theory of nonlinear elasticity in large deformations (19–22) using a two-parameter exponential material model (23–25) to capture the mechanical behavior of the aortic wall with and without PVAT as well as of isolated PVAT. This allowed us to isolate the contribution of PVAT to the mechanical behavior of the aorta.

METHODS

Animal Use

Michigan State University (MSU) Institutional Animal Care and Use Committee (https://animalcare.msu.edu/iacuc/) approved all protocols used in this study. Protocols were performed in accordance with the standards in the Guide for the Care and Use of Laboratory Animals (8th ed., Washington, D.C.: National Academies Press, 2011). MSU is an Assessment and Accreditation of Laboratory Animal Care (AAALAC) accredited institution (A3955-01); this work was specifically approved under Protocol No. PROTO201900089. Sprague–Dawley male rats (∼250–300 g) were purchased (Charles River, Portage, MI). This strain was chosen given the wide use of the Sprague–Dawley rat in basic cardiovascular studies. Only males were used given the intent of this study, to determine whether measurement of PVAT was feasible. All rats were housed in a temperature-controlled room (22°C) with 12:12-h light/dark cycles. Sprague–Dawley rats were on Teklad 22/5 Rodent diet (Madison, WI). All rats received distilled water ad libitum. The rats used were randomized to studies. Each N value represents data that came from one animal. Rings from the same rat were used for both mechanical testing and histology to minimize intraindividual variability. There were no animals excluded from the data shared.

Tissue Isolation

Rats were given pentobarbital (Vortech Pharmaceuticals, Dearborn, MI) as a deep anesthetic (80 mg·kg⁻¹ ip). A bilateral pneumothorax was created before vessel dissection. The thoracic aorta was dissected from the aortic arch to the diaphragm. Tissue dissection took place under a stereomicroscope and in a silastic-coated dish filled with physiological salt solution (PSS) containing (in mM) 130 NaCl, 4.7 KCl, 1.18 KH₂PO₄, 1.17 MgSO₄·7H₂O, 14.8 NaHCO₃, 5.5 dextrose, 0.03 CaNa₂-EDTA, and 1.6 CaCl₂ (pH 7.2). The endothelium was left intact. For creating rings of aorta (∼5 mm length) with and without PVAT, the vessel was guided onto a wire that was embedded into the dish silastic to allow for tissue revolution such that the vessel could be completely cleaned of PVAT. For creating separated rings of the vessel and its surrounding PVAT, a section of the vessel including PVAT was positioned on its end in the silastic dish, and two small insect pins inserted into the lumen of the aorta to hold the vessel open. Although holding the PVAT layer away from the adventitia with fine tip forceps, vannas scissors were used to cut connections between the PVAT and vessel/adventitia, moving around the whole circumference of the vessel. The ring was then flipped vertically, and this process was repeated. The separated ring of PVAT was then lifted off the vessel. Thus, one rat could provide the following: vessel + PVAT (called +PVAT), vessel − PVAT (called −PVAT), and PVAT alone (called PVAT only). Published work validates our ability to leave the adventitia intact with this procedure (26). Samples then were subjected to either mechanical or histological testing.

Mechanical Testing

For each animal (N = 5), we conducted uniaxial ring tests in the circumferential direction on three rings (i.e., +PVAT, −PVAT, and PVAT only). First, the rings were mounted to a custom-made manually controlled uniaxial tensile testing machine via custom-made 316H stainless steel hooks (Fig. 1A). During the test, force was measured with a 250-g capacity load cell (Futek, LSB 200, 250 g, JR S-Beam Load Cell, Irvine, CA), and the deformation was continuously recorded throughout the tests with a charge-coupled device (CCD) camera (Basler, piA1000-60gm, Exton, PA). To maintain tissue hydration, samples were dabbed with room temperature-modified calcium-free Krebs–Henseleit buffer solution (Sigma-Aldrich, St. Louis, MO) throughout the testing (19, 27). The calcium-free Krebs–Hensleit buffer used in this study contains (in g/L distilled water) 2 C₆H₁₂O₆, 0.141 MgSO₄, 0.16 KH₂PO₄, 0.35 KCl, 6.9 NaCl, and 2.1 NaHCO₃. First, a 0.1-g preload was applied; this is a common practice in mechanical testing of soft tissues, especially when testing cylindrical samples in a planar way, either uniaxial or biaxial (28). Then, four loading protocols were performed, each comprised five repeated loading-unloading cycles, for a total of 20 loading-unloading cycles for each sample. The uniaxial stretch applied was increased by 10% after every five cycles, starting from 10% stretch up to 40% stretch. Specifically, we applied a 10% stretch for the first five loading-unloading cycles, followed by 20% stretch for the next five loading-unloading cycles, followed by 30% for the next five loading-unloading cycles, and ultimately by 40% stretch for the last five loading-unloading cycles. The rings were deformed at an approximate rate of 0.16 mm/s, and the deformation rate was controlled by synchronizing machine handle rotations with a metronome. The approximate duration of each mechanical test (i.e., mechanical testing of +PVAT, −PVAT, and PVAT only rings for one animal) is 2 h.

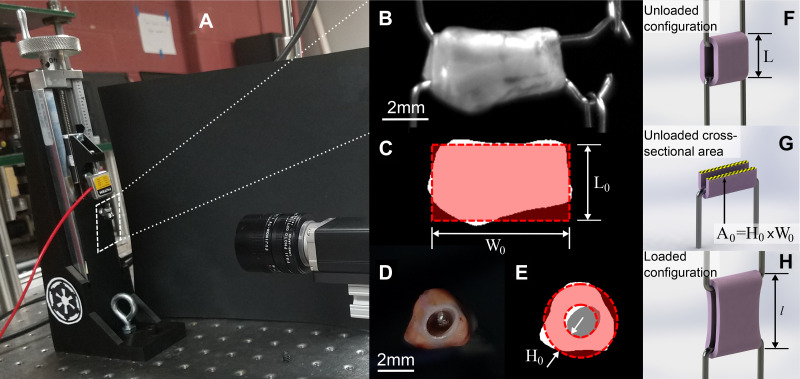
Figure 1.

Schematic of the geometric measurements relevant to the mechanical analysis. A: custom-made manually controlled uniaxial tensile testing machine. Images taken from the side (B) and from the arterial longitudinal axis (D) of a representative sample, as well as the same images after thresholding are represented in C and E, respectively. Also shown in C and E are schematic representations of how the sample’s initial width (W₀) and thickness (H₀) are estimated. Briefly, the width was defined as the widths of the rectangle fit to the side-view image of the sample (seen in C). The sample’s thickness was calculated as the difference in radii between the outer and inner effective circles—the outer effective circle was calculated by equating the areas of both the white and gray regions as shown in E and the inner effective circle was calculated by equating the area of the gray region only. F and H show schematics of the unloaded configuration’s length calculated at the end of the test (L, used to evaluate the stretch) as well as the loaded configuration’s length during the test (l). Finally, G highlights the cross-sectional area in the unloaded configuration A₀ = H₀ × W₀.

To calculate the elongations to be applied during the test to achieve the relevant percentage stretch, we needed to estimate the sample’s initial unloaded length (L₀). This was done by estimating the length of each sample, as shown in Fig. 1C, at the beginning of the mechanical test, after the preload was applied. This step is required and reasonable, yet it inherently generates a measurement error since it implies that we must choose an experimental criterion to define the unloaded state. This may seem trivial, but it is a key step in mechanically testing soft tissues, a step that may significantly affect not just the testing outcome, but also all mechanical analyses that follow. This measurement is affected by the viscoelastic behavior of the tissue, which has been significantly reported in the past (26). Briefly, due to the time-dependent viscoelastic behavior, it is to be expected that the tissue will relax throughout the test, resulting in an unloaded length that increases with testing time. Furthermore, fiber reorganization and fiber sliding, which could happen throughout an ex vivo test, can also result in an increase of the unloaded length during the test. In other words, the unloaded length of each sample (i.e., the length measured for a preload of 0.1 g) will be longer if measured at the end of the test when compared with the same length measured at the beginning of the test. Furthermore, this behavior is potentially sample dependent, since each individual sample may have different characteristics. A consequence of this behavior is that although the testing steps used are consistent between samples and the same estimated elongation is applied to all samples, it may still result in different values of effective elongation in the postprocessing, due to the change in unloaded length.

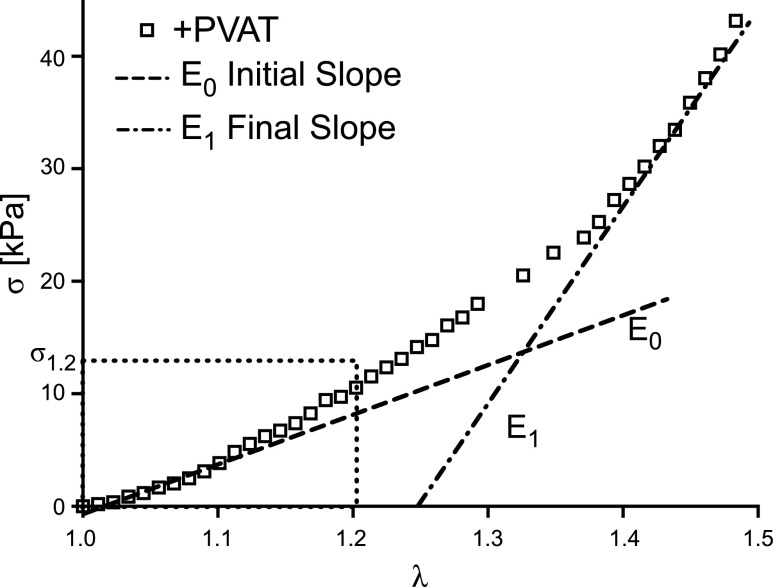
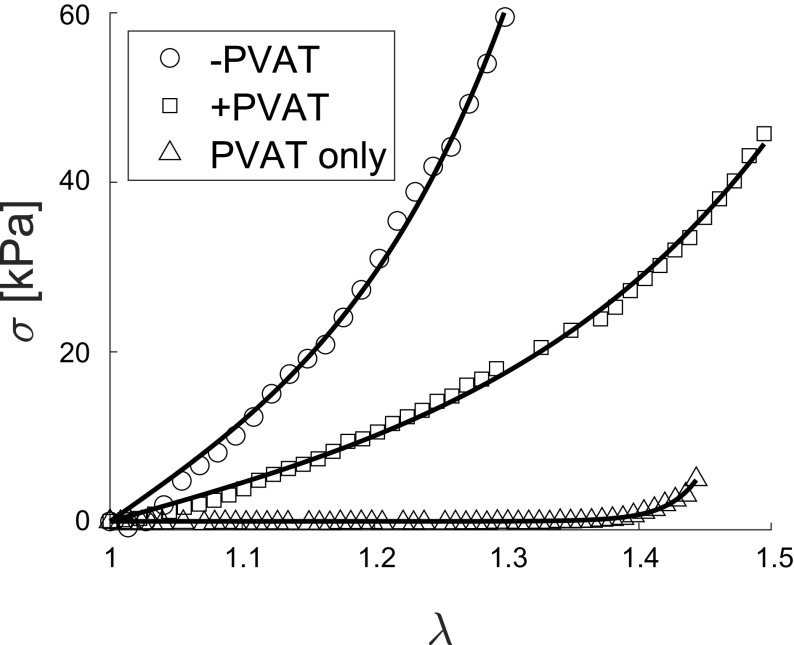
The output of the mechanical test is reported in the form of a Cauchy stress-stretch curve, as shown in Fig. 2 for a representative sample. Stretch, represented by the parameter λ on the x-axis of Fig. 2, is the measure of deformation used in this study and is defined as λ = l/L, that is the ratio between sample’s loaded length (l) and sample’s unloaded length (L), as shown in the schematic Fig. 1, F and H. The unloaded length $L$ for the stress analysis was defined as the length for a force equal to zero at the end of the test, estimated in postprocessing. The Cauchy stress, shown on the y-axis in Fig. 2, was defined as σ = F/A, where F is the force needed to apply the stretch, measure throughout the test, and A is the cross-sectional area normal to the direction of applied stretch in the loaded configuration. Under the hypothesis of isochoric deformation, the area in the loaded configuration can be defined as A= A₀/λ, where A₀ is the unloaded cross-sectional area. A₀ is calculated from side-view images taken after preload application (Basler, piA1000-60gm, Exton, PA) and images taken along the aortic longitudinal axis before testing (Dual Pixel 12MP OIS, F1.7 Basler, Exton, PA; see Fig. 1, B, D, and G, respectively). Images were converted to binary via manual thresholding to separate the sample from the background (Fig. 1, C and E). To estimate L₀ and W₀, first, the actual length and width of the sample were measured by counting the number of white pixels in the binary image at every column and at every row, respectively (Fig. 1C). Then, the total number of white pixels was used to define the sample’s actual lateral area. Assuming a rectangular shape for our model, L₀ was then quantified by minimizing the sum of squared error (SSE) between the rectangle length and the actual sample length at every pixel. Finally, the area of the rectangular model was constrained to equal the actual area of the sample, which results in W₀ being inversely related to L₀, allowing the estimation of both parameters by minimizing the SSE for one parameter only, namely L₀. The thickness H₀ is calculated as the difference between the radii of the inner and outer circles represented in Fig. 1E. With respect to Fig. 1E, the radii of the inner and outer circles are estimated by equating the area of the inner circle to the gray area, and the area of the outer circle to the sum of the white and gray areas, respectively.

Figure 2.

Representative output of mechanical test and definition of mechanical metrics. Representative stress-stretch experimental data from a +PVAT sample. Cauchy stress (σ) is represented on the y-axis and stretch (λ) is represented on the x-axis. Also shown, the graphic representation of the low-stress stiffness (E₀) and of the high-stress stiffness (E₁), namely the slope of lines fitting to the first 10% and last 10% of the stretch, respectively. Also defined is the stress for a stretch of 1.2 (σ_1.2). PVAT, perivascular adipose tissue.

As mentioned, the choice of unloaded configuration has strong implication, yet is a choice we must make. This is well demonstrated in a 2009 study of bladder tissue (29), where the authors showed how the stress-stretch curve can be affected by the choice of unloaded configuration. They considered a series of possible unloaded configurations that could be measured for each experimental data set and evaluated the resulting stress-stretch curve for each choice. What they found is that with respect to the anisotropy of the tissue, this would dramatically impact their analysis. Specifically, when considering a certain unloaded configuration, the longitudinal direction appeared to be stiffer than the circumferential direction, but this was not true for a different choice of unloaded configuration. This highlights the importance of this step.

In the following analysis, when comparing between groups, we used the final loading curve from the last loading protocol (i.e., for a maximum stretch of 1.4 as estimated at the beginning of the test). The metrics used to quantify the mechanical characteristics of each group are the low-stress stiffness (E₀), defined as the slope of the first 10% of the stress-stretch curve; the high-stress stiffness (E₁), defined as the slope of the last 10% of the stress-stretch curve; and the Cauchy stress corresponding to a stretch of 1.2 (σ_1.2), a metric of distensibility (the higher the stress, the less distensible the tissue). We decided to evaluate the stress for a stretch of 1.2 because it is representative of the circumferential stretch arteries experience in vivo (30). Figure 2 depicts the schematics of the metrics described.

Constitutive Modeling

We used an exponential continuum mechanics model to describe the mechanical behavior of the tissue, which has been introduced in Ref. 23 and used before to describe the mechanical behavior of carotid arteries (24) and left ventricle (25). For a more detailed and rigorous description of the continuum mechanics theory of nonlinear materials in large deformations we defer to prior literature (19–22). The strain energy function for this material model, W (C), is defined as

$$W\left(\mathit{C}\right)=\frac{c_1}{2c_2}\left(e^{c_2\left(tr\left(\mathit{C}\right)-3\right)}-1\right),$$ (1)

where C = F^TF is the right Cauchy–Green deformation tensor, $\mathit{F}=diag\left(\lambda ,\frac{1}{\sqrt{\lambda }},\frac{1}{\sqrt{\lambda }}\right)$ is the deformation gradient tensor for uniaxial deformation, and c₁ and c₂ are material parameters, with units of stress and dimensionless, respectively. It follows, that the Cauchy stress can be calculated as

$$\sigma =-p\mathit{I}+2\mathit{F}\frac{\partial W\left(\mathit{C}\right)}{\partial \mathit{C}}{\mathit{F}}^T,$$ (2)

where p is a Lagrange multiplier needed to enforce incompressibility (i.e., isochoric deformation) and I is the identity tensor. After applying stress-free boundary conditions on the lateral surfaces during the test, we can specify the Cauchy stress as

$$\text{σ}=\left({\text{λ}}^2-\frac{1}{\text{λ}}\right)c_1{e}^{c_2\left({\text{λ}}^2+\frac{2}{\text{λ}}-3\right)}.$$ (3)

Equation 3 highlights relation between the material parameters c₁ and c₂, and the physical shape of the stress-stretch curve. The material parameter c₁ represents the value that scales the exponential and consequently is more influential on the low-stress portions of the curve, whereas the material parameter c₂ is contained in the exponents and consequently is more influential on the high-stress portion of the curve.

We estimated the best-fitting model parameters for each sample by minimizing the sum of squared error between the experimental Cauchy stress-stretch data and the model output, using the function fminsearch in MATLAB (i.e., optimization of the parameters).

Histology

In sequential rings from the same rats which provided samples for mechanical testing, PVAT was removed as described previously, and tissues (PVAT only) fixed in 10% formalin overnight, switched to 30% ethanol and taken to Investigative Histopathology Services (https://humanpathology.natsci.msu.edu/) on the campus of MSU for section cutting to provide slides with 8 to 10-μm thick sections. Slides were imaged on an inverted Nikon Eclipse TE2000 microscope (Nikon Group, Otowara, Japan) using a TI-PS100w Nikon Power supply with Nikon NIS Elements BR 4.6 software. Light settings were maintained and consistent across all tissue images. Image analysis was performed on the PVAT-only images (4 images per sample for 5 samples) stained with Masson’s trichrome, to quantify the collagen area fraction. Briefly, using manual color thresholding, the white background of the image was removed, and blue regions were segregated, using MATLAB (RRID:SCR_013499). Collagen area fraction was then calculated as the ratio of blue pixels to total number of sample pixels (i.e., nonwhite pixels).

Blinding, Data Presentation, and Statistical Analysis

Blinding of data analyses was not possible in this study because the differences in the aorta with and without PVAT or PVAT only could not be hidden/was obvious. We performed a statistical analysis of the mechanical metrics (i.e., low-stress stiffness, high-stress stiffness, and Cauchy stress at a stretch of 1.2), and best-fit material parameters (c₁, c₂). Statistical testing consisted of one-way ANOVAs, where tissue (i.e., ±PVAT and PVAT only) was the source of variation, followed by Tukey–Kramer multiple comparisons tests for all pairwise multiple-comparison procedures. When only two data sets were available (i.e., ±PVAT) statistical testing consisted of a paired t test. Statistical significance was reached for P < 0.05; we also signaled when P < 0.01 and P < 0.001 were reached.

RESULTS

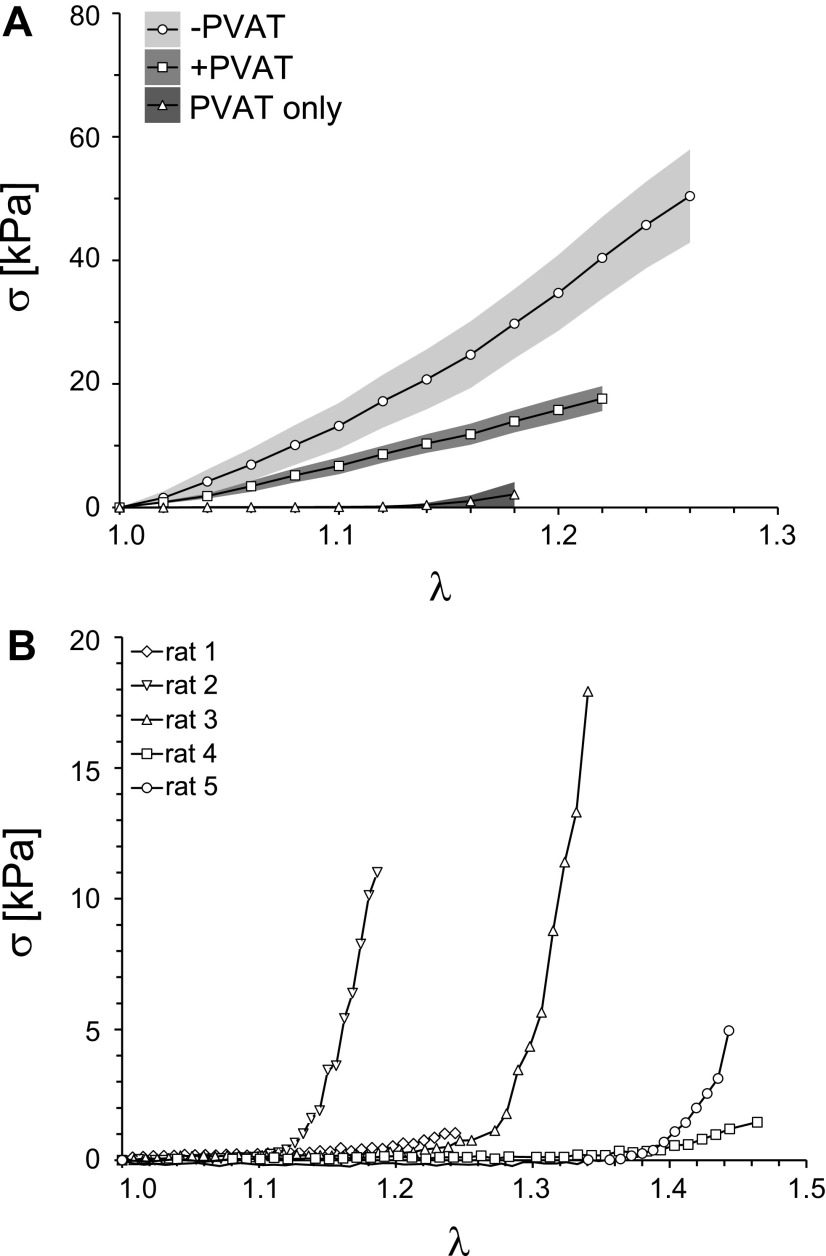
Figure 3A shows means ± SE of the Cauchy stress-stretch curves for the −PVAT, +PVAT, and PVAT only rings. In Fig. 3A, it can be appreciated how −PVAT samples appear to be the least distensible (i.e., reach the highest value of stress for a given value of stretch) and the PVAT only samples appear to be the most distensible (i.e., reach the lowest value of stress for a given value of stretch). It is important to notice that although our protocol strives to apply up to 40% stretch (a maximum stretch equal to 1.4) for every sample, some of the samples resulted in an effective lower stretch applied. This can be observed in Fig. 3A, where the horizontal axis reaches different values of stretch for different tissue groups. As discussed in the methods, this is due to how we estimate the unloaded length L in postprocessing as compared with how it is defined during testing, with the discrepancy between the two likely being a result of viscoelastic effects and fibers realignment during the test. This behavior is even more evident in Fig. 3B, where we show not the average but each individual Cauchy stress-stretch curve for all PVAT only samples tested, suggesting that isolated PVAT samples may be more sensitive to these effects. Moreover, Fig. 3B shows how two of the PVAT-only samples reached relatively high stresses (rats 2 and 3), entering in the exponential portion of the stress-stretch curve, suggesting an engagement of collagen fibers. Although, under the same loading protocol, two different PVAT only samples (rats 1 and 4) remained in the low stress, almost linear, portion of the curve, suggesting there was low collagen engagement.

Figure 3.

Mechanical data for all groups. A: mean stress-stretch curves (lines) and SE of stresses (shaded regions) for −PVAT, +PVAT, and PVAT only data. For each group, N = 5 samples were tested. B: full mechanical data set collected for PVAT only samples. In A and B, Cauchy stress (σ) is represented on the y-axis and stretch (λ) is represented on the x-axis. PVAT, perivascular adipose tissue.

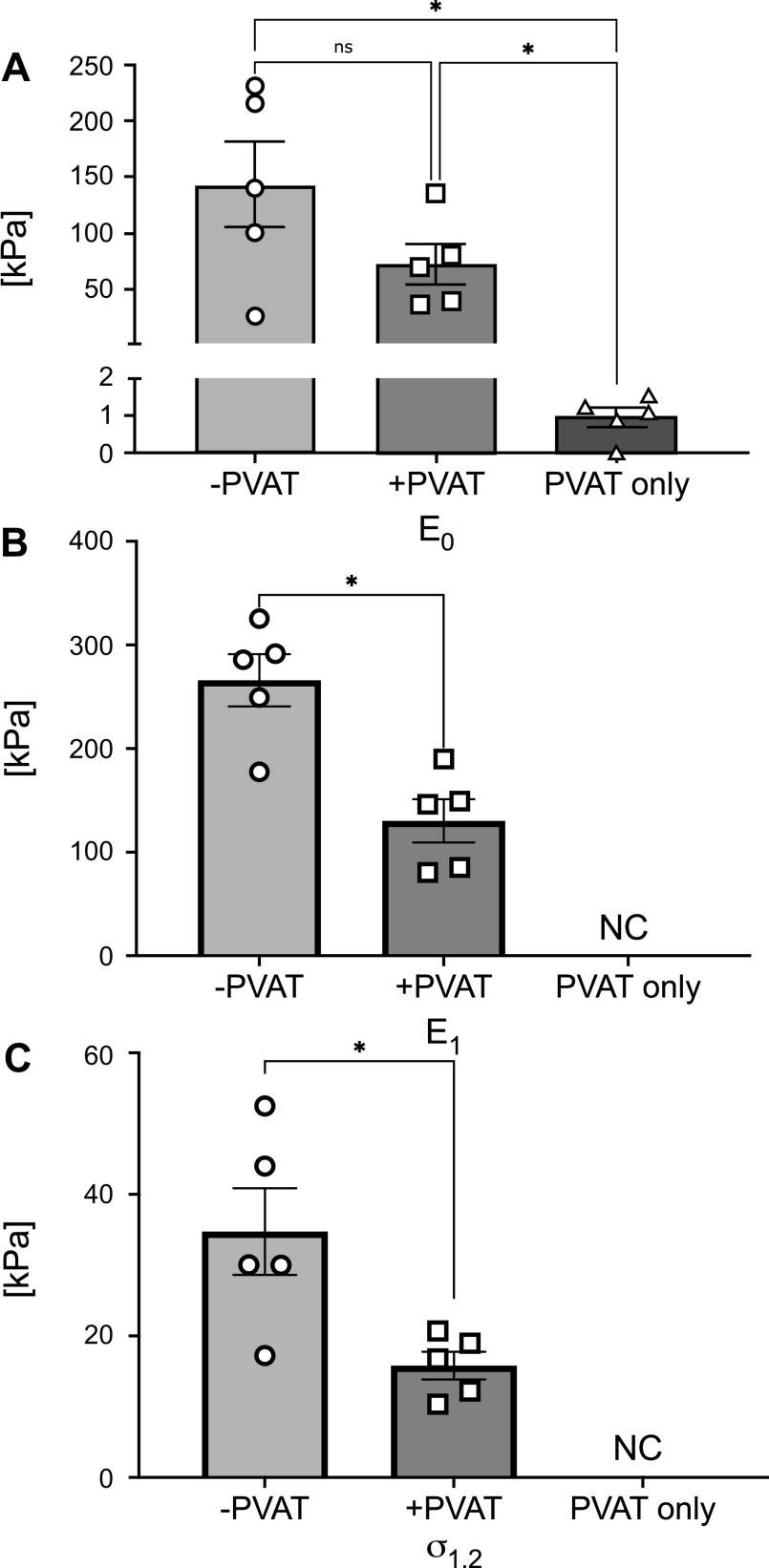
Figure 4 represents means ± SE of the metrics used here to quantify the mechanical behavior of the tissues, calculated as described in METHODS. Specifically, in Fig. 4A, the low-stress stiffness (E₀) was greatest in −PVAT samples and lowest in PVAT only samples. The statistical analysis resulted in a significant difference, when comparing both −PVAT and +PVAT to PVAT only low-stress stiffnesses (−PVAT vs. +PVAT, P = 0.213; −PVAT vs. PVAT only, P = 0.042; +PVAT vs. PVAT only, P = 0.034). In Fig. 4, B and C, high-stress stiffness, E₁, and stress at a stretch of 1.2, σ_1.2, were both significantly higher in −PVAT samples when compared with +PVAT samples (−PVAT vs. +PVAT, P = 0.019 and P = 0.022, respectively). Due to the inconsistencies in the effective stretch reached during the testing protocols, as highlighted in Fig. 3B, we were unable to calculate high-stress stiffness and stress at 1.2 stretch for samples in the PVAT only group.

Figure 4.

Mechanical metrics quantified from experimental data, for all groups. Means ± SE of the low-stress stiffness (E₀; A), the high-stress stiffness (E₁; B), and stress at a stretch of 1.2 (σ_1.2; C), represented for all groups tested. In B and C, the parameters for PVAT only could not be calculated (NC). For each group, N = 5 samples were tested. Statistical analysis for A: one-way ANOVA (−PVAT vs. +PVAT, P = 0.213; −PVAT vs. PVAT only, P = 0.042; +PVAT vs. PVAT only, P = 0.034). Statistical analysis for B and C: paired t test (−PVAT vs. +PVAT, P = 0.019 and P = 0.022, respectively). Significance is set at *P < 0.05. PVAT, perivascular adipose tissue.

Figure 5 shows a representative set of experimental stress-stretch curves of all three tissues from one animal (shown in symbols), along with the corresponding model calculated curves using the optimized material parameters for each sample (shown with lines). Figure 5 reveals how the exponential material model selected here is equally successful in capturing the behavior of all tissue groups tested. In Fig. 6, A and B, we report means ± SE of the material parameters, c₁ and c₂, estimated for all groups. The material parameter c₁ is significantly lower in samples in the PVAT only group compared with samples in the +PVAT and −PVAT groups (−PVAT vs. +PVAT, P = 0.145; −PVAT vs. PVAT only, P = 0.036; +PVAT vs. PVAT only, P = 0.009). In addition, although no significance was reached when comparing +PVAT to −PVAT, the comparison suggested a statistical trend (P = 0.145). We have also investigated differences in the parameter c₂, which assumes similar values for samples in the −PVAT and +PVAT groups, and higher values in the PVAT, yet no comparison reached statistical significance (−PVAT vs. +PVAT, P = 0.528; −PVAT vs. PVAT only, P = 0.119; +PVAT vs. PVAT only, P = 0.100). All mechanical parameters for all samples are collected in Table 1.

Figure 5.

Continuum mechanics model fit of experimental data. Stress-stretch data for −PVAT, +PVAT, and PVAT only, from a representative animal (symbols), along with the corresponding model fit (lines). Cauchy stress (σ) is represented on the y-axis and stretch (λ) is represented on the x-axis. Normalized root-mean-square error (NRMSE) is 0.030 for −PVAT, 0.040 for +PVAT, and 0.025 for PVAT only, when averaged between all samples. PVAT, perivascular adipose tissue.

Figure 6.

Continuum mechanics model parameters. Means ± SE of model parameter estimates, c₁ (A) and c₂ (B). For each group, N = 5 samples were tested. Statistical analysis for A: one-way ANOVA (−PVAT vs. +PVAT, P = 0.145; −PVAT vs. PVAT only, P = 0.036; +PVAT vs. PVAT only, P = 0.009). Statistical analysis for B: one-way ANOVA (−PVAT vs. +PVAT, P = 0.528; −PVAT vs. PVAT only, P = 0.119; +PVAT vs. PVAT only, P = 0.100). Significance is set at *P < 0.05; **P < 0.01. ns, not significant; PVAT, perivascular adipose tissue.

Table 1.

Material parameters estimated for all samples

	E0, kPa	E1, kPa	σ1.2, kPa	c1, kPa	c 2	NRMSE
Animal 1
−PVAT	101.05	249.22	30.05	35.71	2.66	0.042
PVAT only	1.10	N/A	N/A	0.58	5.30	0.069
+PVAT	39.99	85.26	12.22	13.73	3.51	0.034
Animal 2
−PVAT	216.14	291.59	43.99	62.87	1.19	0.013
PVAT only	1.25	N/A	N/A	0.61	38.28	0.041
+PVAT	70.14	149.23	18.97	25.43	1.56	0.027
Animal 3
−PVAT	26.53	177.58	17.22	13.40	5.84	0.060
PVAT only	1.54	N/A	N/A	5.16E-02	20.17	0.020
+PVAT	81.12	146.15	16.76	23.73	1.30	0.012
Animal 4
−PVAT	231.18	325.37	52.50	78.80	0.85	0.013
PVAT only	0.89	N/A	N/A	2.53E-02	7.29	0.040
+PVAT	135.89	80.39	20.71	33.92	9.05E-10	0.033
Animal 5
−PVAT	140.40	285.69	30.00	36.49	2.60	0.022
PVAT only	6.27E-03	N/A	N/A	1.64E-04	21.26	0.031
+PVAT	37.21	189.85	10.38	14.70	1.15	0.015

E₀, low-stress stiffness; E₁, high-stress stiffness; σ_1.2, stress at a stretch of 1.2; c₁, material parameter with units of stress; c₂, material parameter contained in the exponents; NRMSE, normalized root-mean-square error; PVAT, perivascular adipose tissue; N/A, not applicable.

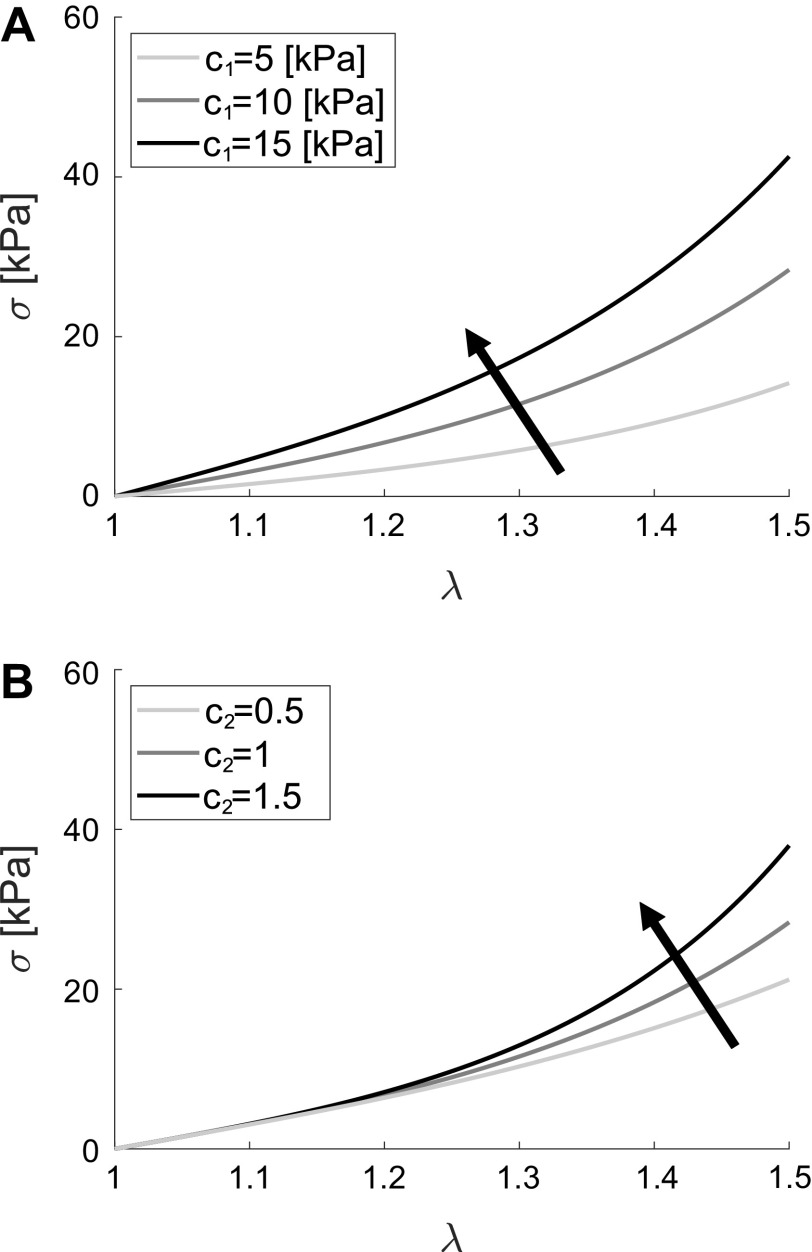
To help interpret the results shown in Fig. 6, we performed a parametric study, shown in Fig. 7, aiming to represent what is the mechanical consequence of changes in the material parameters c₁ and c₂. In Fig. 7A, one can see that for a constant value of c₂ = 1, an increase in the parameter c₁ results in an increase in the slope of the stress-stretch curve in the low-stress region. Figure 7B shows the effect of an increase in the parameter c₂, for a constant value of c₁ = 10 kPa, which results in an increase of the slope of the curve at high stresses. Taken together, Fig. 7, A and B suggests that c₁ has substantial influence on the mechanical behavior in the low-stress region, whereas c₂ has substantial influence on the mechanical behavior in the high-stress region.

Figure 7.

Parametric study of model parameters. A: mechanical consequence of an increase in material parameters c₁, when c₂ = 1. B: mechanical consequence of an increase in material parameters c₂, when c₁ = 10 kPa. In A and B, Cauchy stress (σ) is represented on the y-axis and stretch (λ) is represented on the x-axis.

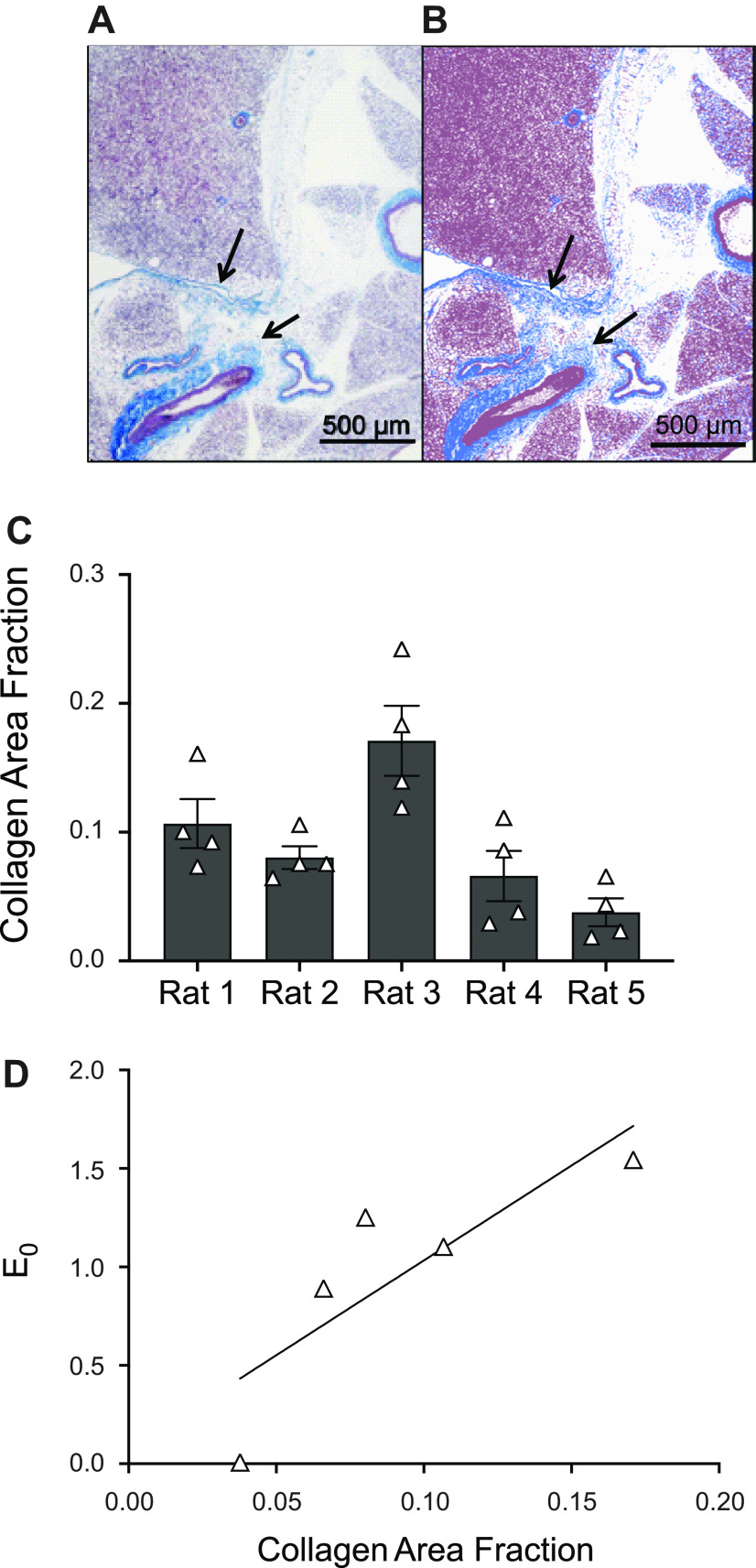
Finally, we have estimated the composition of PVAT only tissue using the histological images shown in Fig. 8. Figure 8, A and B, shows a representative image of a PVAT sample stained with Masson’s trichrome before and after color thresholding, respectively. Collagen area fraction averaged between four PVAT only images from each sample showed high variability between animals (shown in Fig. 8C, overall means ± SE across all samples is 0.092 ± 0.023). We have also performed a correlation analysis between parameters and collagen content of the PVAT only samples and found that the low-stress stiffness (E₀) is linearly, positively correlated with the collagen content for PVAT only samples (Pearson coefficient r = 0.84), as shown in Fig. 8D.

Figure 8.

Histological analysis of PVAT tissue. A and B: histological image of PVAT stained with Masson’s trichrome (magnification ×4). Image in A shows collagen in blue (highlighted by arrows in the figure), and cell nuclei and cytoplasm in red/purple. Image in B shows the segmented image after color thresholding, i.e., white background, blue collagen, and red/purple for everything else. Collagen area fraction is calculated as the ratio of blue pixels to nonwhite pixels in B. C: collagen area fraction estimated for all PVAT only samples, measurement for each animal (N = 5 animals) is represented as the means ± SE across n = 4 measures (i.e., number of locations on the histology). The means ± SE across animals is 0.092 ± 0.023. D: linear relation between collagen area fraction and low-stress stiffness (E₀) for PVAT only samples (Pearson coefficient r = 0.84, N = 5). PVAT, perivascular adipose tissue.

DISCUSSION

Thirty years ago, Soltis and Cassis published the first paper that proposed PVAT did more than simply encase the artery; PVAT affected arterial function (31). Here, we extend these functions into a measure that is enormously clinically meaningful, that of arterial/aortic stiffness.

PVAT has a Low Stiffness of its Own: a New Finding

Because of the ability to remove the PVAT ring from around the vessel, we were able to directly measure the mechanical properties of the PVAT layer, something that has not been done in mechanical testing. As Figs. 4A and 6A show, the PVAT ring has a markedly low initial stiffness. This can be observed by the eye and simple handling. Adipocytes contribute the greatest mass to PVAT and have a small but measurable stiffness defined primarily by the lipid droplets (32, 33). Important to the contributions of obesity to cardiovascular disease, adipocyte stiffness increases with lipid accumulation (33).

The histological studies were done to determine the concentration of collagen within PVAT of healthy tissue, with the idea that this would likely contribute to the measure of stiffness made (34, 35). The fact that the collagen area fraction is positively correlated with the low-stress stiffness parameter E₀ (Fig. 8D) supports the idea that the mechanical behavior is significantly affected by collagen content in PVAT only samples. Moreover, such a measure provides a baseline of sorts to ultimately determine if PVAT can become fibrotic, as occurs in non-PVAT adipose tissues (visceral, non-PVAT) in obesity, increasing tissue stiffness and decreasing metabolism of adipocytes (36–38). Finally, the high variability observed in the Cauchy stress-stretch curves for PVAT only samples (Fig. 3B) highlights how differences in collagen concentration, and potentially organization, could lead to significant differences between mechanical behavior for different animals. Another factor that could lead to significant differences in the stress-stretch curves recorded for PVAT only samples is that this tissue has very pronounced viscoelastic behavior, as shown in our prior work (26), which could lead to a more pronounced difference between the unloaded length measured at the beginning of the test and that measured at the end of the test. As mentioned before, this is a factor that can significantly affect the measured mechanical behavior of the tissue. Moreover, potential variations in PVAT removal protocol before testing could also lead to different amounts of collagen or fat on the outer portion of the aorta, thus changing the measured mechanical response. Although we have published that the aorta has a largely intact adventitia/collagen layer after PVAT removal, we cannot exclude the possibility that unequal portions of the adventitia could be dissected along with the PVAT such that this could account for the variability in collagen content.

Does PVAT Impact the Mechanics of the Aorta?

Including PVAT in the measurement of the aortic wall’s mechanical behavior is important, and it significantly affects the resulting metrics. This impact is twofold. First, including PVAT matters in terms of defining cross-sectional area of the tissue (i.e., in defining A₀) and consequently impacts the stress-range that results from the analysis. This is important, as the amount of PVAT that surrounds the artery can vary with disease. Second, PVAT seems to be stiffer in the high-stress region when compared with the low-stress region, as supported by low values of material parameter c₁ and high values for parameter c₂ for the PVAT only samples as shown in Fig. 6. This supports the idea that the major mechanical contribution of PVAT to aortic mechanics behavior happens at a level of applied stretch/stress that corresponds to an in vivo condition (i.e., the in vivo circumferential stretch for arteries is 1.2–1.3, as reported in Ref. 30). Yet, the variation in mechanical behavior observed for PVAT only samples (Fig. 3B) seems to support the idea that this contribution could be highly animal specific.

What Is the Best Metric to Quantify Aortic and PVAT Stiffness?

It is important to consider an appropriate measure of stiffness to be able to identify and comment on the contribution that PVAT has on the mechanical behavior of the artery as a whole. There are two main advantages associated with using a two-parameter continuum mechanics material model, such as the one described in Eq. 3, in combination with the single-value stiffnesses we have identified and used in this study, namely low- and high-stress stiffness, E₀ and E₁. First, Eq. 3 captures the overall behavior of the stress-stretch curve, while E₀ and E₁ capture the behavior of a specific section of the curve (i.e., the low-stress or the high-stress section, respectively). Consequently, E₀ and E₁ are affected by how we define the low-stress and high-stress sections of the curve. In this study, we have defined these sections as the first and last 10% of the applied stretch, but a different choice could have led to different values of E₀ and E₁. The continuum model expressed in Eq. 3 is independent of these definitions, therefore a more consistent metric. Second, the continuum model is somewhat independent of the consistency of the effective stretch applied during the mechanical test. As discussed, the peculiarity of the tissue tested and especially the PVAT only group, led to a variability in the mechanical data collection, as represented in Fig. 3B. This made it impossible to consistently estimate E₁, as well as σ_1.2, for the PVAT only group, which is a shortcoming of these metrics. But the continuum model shown in Eq. 3 still has the ability of capturing the overall behavior of the stress-stretch curve, resulting in estimates for both material parameters c₁ and c₂. As mentioned, these two parameters are helpful in describing the behavior of the low-stress and high-stress mechanical behavior of all tissue tested, included PVAT only, as described by Fig. 7.

Prior Research in PVAT and Arterial/Aortic Stiffness

Three studies indirectly support the idea that including PVAT in the definition of the arterial wall has a significant effect on what we measure as arterial stiffness. First, Liu et al. (39) used the healthy Yorkshire pig in vivo to demonstrate that removal of PVAT from around carotid and femoral arteries resulted in increases in circumferential stress and strain when compared with animals in which PVAT was left intact. PVAT took up part of the load, contributing to the mechanics of the artery. Second Kim et al. (40) developed computational models that emphasize the importance of surrounding tissues on the biomechanics of the thoracic aorta of the Yorkshire pig. They concluded that localized measures of aortic thickness and surrounding tissues should be included in biomechanical analysis since they may play a significant role in dictating regional adaptation both in physiological or pathological conditions. Finally, Ferruzzi et al. (41) reaffirmed that perivascular tethering impacts (lowers) the value of stress within the aortic wall in homeostatic and pathological conditions. Changes in PVAT function and structure ultimately influence arterial/aortic mechanics, such that the vessel would have to adapt in response to maintain stress. Collectively, these studies and the present one argue that mechanistically (at the tissue level), PVAT needs to be considered to understand, more wholly, blood vessel stiffness.

Study Limitations

Here, we recognize limitations of this work. First, we must limit our conclusion that PVAT reduces aortic stiffness to the thoracic aorta of the male rat with an intact endothelium. This is because PVAT is not the same around all vessels, females were not studied, and the endothelium was left intact. We focused on the thoracic aorta given its well-established contribution to PWV, the gold standard measure of arterial stiffness in the human. Moreover, the amount of tissue in the thoracic portion of the aorta in the rat is sufficient that we could readily pair the mechanical and biochemical testing in the same animal. It would clearly be ideal to perform similar studies in resistance arteries. Understanding PVAT contribution to arterial stiffness/function in these vessels responsible for determination of total peripheral resistance would underscore the physiological importance of our findings. However, such an undertaking in these small vessels is more challenging. The novel methodology presented here is optimized for vessels with diameter included in the range 0.5–1.5 mm. We have not validated the appropriate protocol in these smaller vessels, and it is less clear how to pair the mechanical with biological data within an animal, a pairing that is a strength of the current study. Finally, it will be important to both increase the number of samples and include female animals in future studies.

Second, we have not included mechanistic work as to how PVAT reduces aortic stiffness. The present study was necessary to demonstrate the basic novel fact that PVAT has a stiffness of its own and could reduce aortic stiffness. We recognize that testing this idea in vivo using PWV as an end point would be ideal. For several years, we have considered methods to remove PVAT from the thoracic aorta (surgery, genetically) without causing an inflammation that obfuscates the conclusions made in PWV studies. This is still a significant work in progress.

Third, PVAT is best known for the secreted factors it makes and their subsequent influence on the vessel it surrounds. We speculate that the effects of PVAT are independent of these secreted factors. We base this on findings that were published previously and the one shared in this manuscript. First, PVAT possess, like an artery, the ability to stress relax (26). Second, when PVAT is detached from the artery and then added back, PVAT-assisted stress-relaxation continues to occur. This suggests that direct connections that might facilitate the effects of secreted factors are not needed for PVAT to assist in stress-relaxation. Stress-relaxation is not the same as stiffness, but they are related mechanical measures. In the present study, PVAT was found to have a stiffness of its own, though profoundly low compared with the artery. Collectively, these findings suggest that the effects of PVAT on aortic stiffness may be independent of actions on the artery (e.g., release of substances). That said, we cannot exclude the possibility that stretch of PVAT results in release of vasoactive substances. Such a study has been a separate research project in the laboratory.

Fourth, the protocol presented here is geared to calculate the homogenized mechanical behavior of PVAT; in other words, it is not capable to probe the localized characteristics of PVAT. However, it is evident that PVAT is unevenly distributed around the aortic circumference which may translate to an uneven distribution of mechanical properties as well. The development of combined experimental and modeling protocols to estimate the inhomogeneity of PVAT’s properties is still a significant work in progress in our group.

Conclusions

In this work, we demonstrated how PVAT is an integral part of aortic mechanics. We introduced a novel methodology to quantify the mechanical properties of the aorta with and without PVAT as well as PVAT itself. We have shown how the inclusion of PVAT as part of the aortic wall will significantly impact several mechanical metrics by reducing the stiffness of the vessel. This work lays the foundation to reformulate what may be considered the “whole” blood vessel through the mechanistic understanding of PVAT’s contributions.

DATA AVAILABILITY

The data that support this study are available upon request.

GRANTS

This work was supported by Michigan State University Internal Funds; National Heart, Lung, and Blood Institute Grant P01HL152951 (to S.W.W.); and National Science Foundation Civil, Mechanical and Manufacturing Innovation Grant 1933768 (to S.R.).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

S.W.W. and S.R. conceived and designed research; T.T. and E.D. performed experiments; T.T., E.D., S.W.W., and S.R. analyzed data; T.T., E.D., S.W.W., and S.R. interpreted results of experiments; T.T. and E.D. prepared figures; T.T., E.D., S.W.W., and S.R. drafted manuscript; T.T., E.D., S.W.W., and S.R. edited and revised manuscript; T.T., E.D., S.W.W., and S.R. approved final version of manuscript.