A Surgeon’s Guide to Understanding Artificial Intelligence and Machine Learning Studies in Orthopaedic Surgery

Abstract

Purpose of Review

In recent years, machine learning techniques have been increasingly utilized across medicine, impacting the practice and delivery of healthcare. The data-driven nature of orthopaedic surgery presents many targets for improvement through the use of artificial intelligence, which is reflected in the increasing number of publications in the medical literature. However, the unique methodologies utilized in AI studies can present a barrier to its widespread acceptance and use in orthopaedics. The purpose of our review is to provide a tool that can be used by practitioners to better understand and ultimately leverage AI studies.

Recent Findings

The increasing interest in machine learning across medicine is reflected in a greater utilization of AI in recent medical literature. The process of designing machine learning studies includes study design, model choice, data collection/handling, model development, training, testing, and interpretation. Recent studies leveraging ML in orthopaedics provide useful examples for future research endeavors.

Summary

This manuscript intends to create a guide discussing the use of machine learning and artificial intelligence in orthopaedic surgery research. Our review outlines the process of creating a machine learning algorithm and discusses the different model types, utilizing examples from recent orthopaedic literature to illustrate the techniques involved.

Introduction

Artificial intelligence (AI) is a broad term referring to any human-like intelligence exhibited by a machine including the ability to make decisions, solve problems, and learn from experience. Through the rapid processing of large amounts of information, AI has already transformed industries such as entertainment and transportation, among others [1]. Given its increasing available and promising applications, AI is also expected to impact the practice of medicine and the delivery of healthcare.

A growing interest in AI is reflected in the increasing number of publications in the medical literature, many of which utilize AI to answer orthopaedic-specific questions [2–4]. Interpreting radiographs and predicting postoperative outcomes are areas where early AI research in orthopaedics has focused. The data-driven nature of the specialty combined with its need for high-quality and cost-effective treatment offers many targets for further improvement by Al. While technological constraints of applying AI are rapidly diminishing, a more fundamental problem may ultimately limit its impact on orthopaedic surgery: trust. The unique methodologies of AI research studies may be a significant barrier to widespread acceptance of AI into orthopaedic surgery. Without a robust understanding of AI methodology, equivalent or superior to insights in traditional statistical methods, a consistent and critical analysis of the AI literature will be hampered, and the editorial process may fail to produce robust high-quality publications. This will lead to a large number of publications with varying validity, eroding the community’s trust in the peer-review process and in the findings of the AI literature.

An understanding of fundamental methodological concepts will thus be essential moving forward so that studies can be critically evaluated as more are published. Despite its limitations, AI has the potential to meaningfully change the delivery of orthopaedic care. Until surgeons are more familiar with the methodology though, AI in the orthopaedic literature will likely be met with continued skepticism. The purpose of this guide is to facilitate understanding and development of studies within orthopaedics utilizing AI methodology.

Machine Learning

Though sometimes used interchangeably with AI, machine learning (ML) is an important subset of AI with arguably the most promising applications for medical research [5]. Much like traditional statistics, the purpose of ML is to describe the relationship between variables. To simplify, one can distinguish the methodologies by their respective goals. With traditional statistical models, the goal is to infer the relationship between variables, while with ML models, the goal is to predict these relationships. Inference involves testing a null hypothesis for an effect size and confidence measurement to calculate the probability that the observed relationship happened by chance. This is the standard way in which traditional clinical research is conducted, by retrospectively or prospectively analyzing the outcome of interest and inferring the probability of this result in the context of other given variables.

On the contrary, prediction involves assigning a known output of interest with several associated inputs, without understanding the relationship between the two or why it exists. It is important to note that neither method alone is superior to the other; each one should be considered with the research question in mind. Statistical models may be more appropriate for studies with a research question interested in assessing the effect of any one input on an output, whereas ML models may be preferred for studies with a research question interested in correctly identifying an output given a set of inputs. The relationship between individual inputs and the output is of little relevance in a ML model so long as the prediction is accurate. However, the emphasis on predictive accuracy is also what contributes to the so-called black box phenomenon, a frequently mentioned criticism of ML, in which the predictive model is undecipherable to human intuition [6•]. Without an understanding of the mechanisms and limitations within the model, the predictive outputs carry less meaning and may be dismissed by surgeons making clinical decisions.

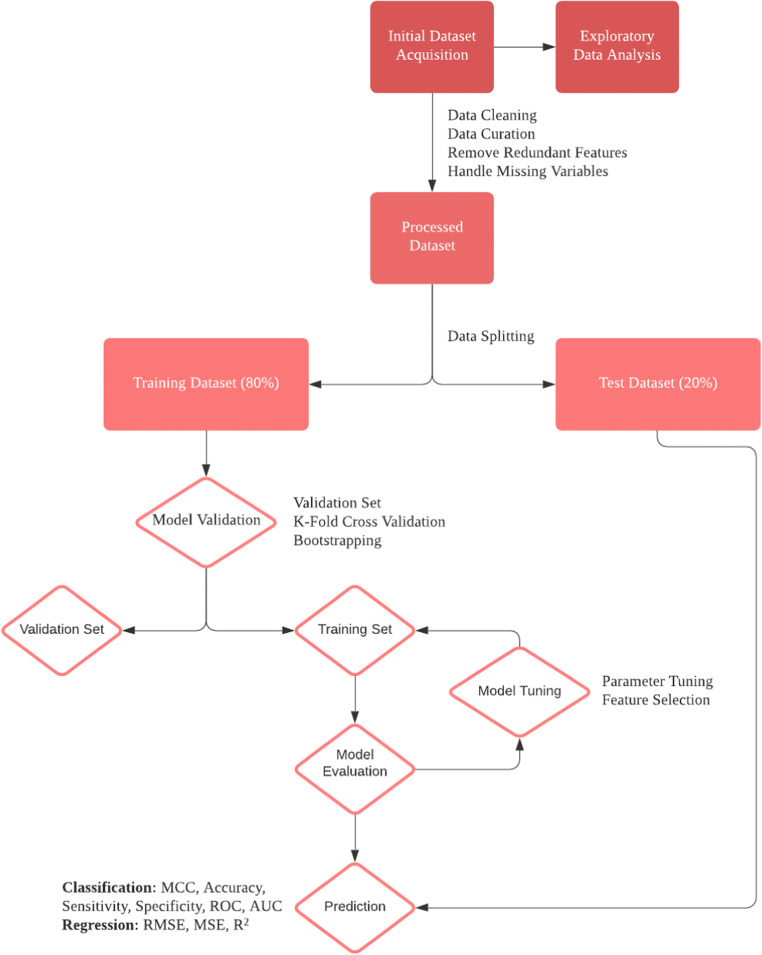
Two areas particularly suited for application of ML techniques in medicine are diagnosis and prognosis as both involve a degree of uncertainty and forecasting. In orthopaedics, ML has been used both diagnostically for the identification of pathology like osteoarthritis and fracture on radiographs and prognostically through the estimation of postoperative outcomes and healthcare costs [7–9]. The aim of this review is to delineate key ML methodological terms, concepts in study design, model choice, data collection/handling, and model development, training, testing, and interpretation. Table 1 delineates the key terminology discussed throughout this review. The process of designing, evaluating, and interpreting a machine learning algorithm is outlined in Figure 1.

Table 1.

Key terminology

Term	Definition
Black box	Models are created directly from data by an algorithm, making it difficult for humans to understand how predictions are made
Classification	Characterizes relationships between input variables and categorical outcomes
Diagnostic	Identification of a disease state or condition
Inference	The process of using a given dataset to determine how an observed output is produced as a function of input variables
Machine learning	A subset of artificial intelligence focused on using existing datasets to develop algorithms capable of prediction
Overfitting	An error that results when a model fits the training data too closely, making it difficult to generalize and apply to future data
Prediction	Using existing data to train models that can accurately utilize new measurements to select from a set of outcomes
Prognostic	Information relevant to clinical outcomes
Regression	Problems that map input variables to continuous outcome variables
Supervised	Process of training models to predict relationships between variables using datasets that include inputs and outputs
Test Data	Data used to evaluate the accuracy and efficiency of a trained model
Training Data	Data used by the model to learn to make predictions for unknown outcomes
Unsupervised	Training algorithms without labeled outputs; using the model to evaluate patterns in a dataset
Underfitting	A modeling error where the algorithm cannot fit both the training data and future datasets

Fig. 1.

Outlining the process of designing a machine learning model

Study Design

When critically evaluating or developing a study that utilizes ML methodology, the research question must first be identified. As mentioned previously, if the purpose of the research question is to make a prediction, then ML may offer advantages over traditional statistics. Because of the complexity of the model that makes interpretability one of the main challenges to its acceptance and implementation into clinical practice, it is important for authors to provide a clear justification for the use of ML and state the advantages it affords for answering the research question.

Research questions can be categorized as diagnostic or prognostic based on the goal of the prediction [10]. An example of a diagnostic question in orthopaedic research might involve developing a ML model to identify osteoarthritis from radiographic images, while a prognostic question could involve developing one to estimate healthcare costs after total knee arthroplasty (TKA) based on patient and clinical factors.

Research questions can be further categorized as a classification or regression question based on the type of output generated by the prediction. To simplify, with classification questions, the output of the model is a class, while with regression problems, the output of the model is a number [11]. Utilizing the above examples, detecting osteoarthritis on radiographs would be a classification question since the output of this prediction model is a class, i.e., either “yes” or “no” osteoarthritis. Estimating healthcare costs after total knee arthroplasty would then be an example of a regression question since the output of this prediction model is a number (i.e., healthcare dollars). Diagnostic questions are often classification questions and prognostic questions are often regression questions, but this is not always the case. Model choice is based upon the research question, which can be described further by the goal of the prediction and the type output generated by it, as well as the characteristics of the available data. Once identified, the appropriate ML model can be determined.

Model Choice

ML algorithms can be classified as either supervised or unsupervised. In supervised learning, the researchers provide the model with inputs and the desired output and the goal is to predict the relationship between these variables [12]. In unsupervised learning, there is no labeled output; therefore, the aim of this type of algorithm is to evaluate patterns within the dataset. For the purposes of this review, we will focus on supervised learning since this is the most common type of ML model used in medical research.

The next step is choosing an algorithm for the model. A number of factors impact algorithm selection—interpretability, accuracy, speed, and size of dataset. Common algorithms for classification problems include logistic regression, support vector machines (SVM), decision trees (DTs), random forest, and k-nearest neighbors (kNN). Models for regression problems include simple linear regression, multiple linear regression, support vector machine (SVM), decision trees, random forests, LASSO (least absolute shrinkage and selection operator) regression, and ridge regression. Deep learning techniques are inspired by the human brain, using artificial neural networks to learn from large datasets. These networks can be conceptualized as multiple layered algorithms working together. It is typically useful to create multiple algorithms for a problem and determine the most effective choice after evaluating the models. Table 2 outlines the different models discussed in our article, with examples of potential applications.

Table 2.

Model types and example applications

Model	Example application
Logistic regression	Logistic regression is useful for predicting categorical outcomes. In a study evaluating osteosarcoma survival, predictor variables could include age, tumor size, tumor site, metastasis, and chemotherapy.
Linear regression	Linear regression is appropriate for predicting continuous outcomes, such as the postoperative length of stay following hip replacement surgery. Predictor variables could include age, medication, blood clots, infection, and physical therapy.
Support vector machines	The SVM is commonly used in classification problems, though it can be used for regression. Mehta and Sebro developed a SVM model to identify lumbar spine (L1–L4) vertebral fractures using future DEXA studies [13].
Lasso regression	Venäläinen et al. created lasso regression models assessing the risk associated with various factors responsible for treatment failure in total hip arthroplasties [14•].
Ridge regression	Ridge regression can be used to study data with high multicollinearity. Zhao et al. used the ridge regression to predict the durations of various robot-assisted elective surgeries [15•].
Elastic net regression	The elastic net regression weights both ridge and lasso regression, and was utilized by Baca et al. to build predictive algorithms for acute postoperative pain [16].
Decision trees	Decision trees can be used for both classification and regression, with an example application being the prediction of postoperative pain scores.
Random forests	Applications of random forests include quantifying risk factors for disease, building diagnostic tools, and predicting outcomes. Zhong et al. developed a random forest to predict the length of stay in hip arthroplasty patients [17].
k-nearest neighbors	The kNN model is used to determine similarities between cases. Dolatabadi et al. used the kNN to classify gait patterns as healthy or pathological, after using kinetic skeletal tracking to observe different gait sequences [18].
Neural networks	Neural networks can make complicated decisions, with a prominent application being in the interpretation of radiographs.

Logistic Regression

Logistic regression is one of the simplest modeling techniques to predict the probability of a binary outcome variable [19]. Logistic regression is commonly used in orthopaedics research and has a broad range of applications. An example of an appropriate application would be a study determining statistically significant predictors of survival of osteosarcoma. Predictor variables might include age, tumor size, tumor site, metastasis, and chemotherapy. We can use logistic regression to determine the statistical significance of the predictors by analyzing the z-statistic and associated p-values.

Linear Regression

Linear regressions intend to model relationships between explanatory variables and a scalar response, predicting the value of the outcome [20]. Simple linear regressions include one explanatory variable; in the case that there are multiple, the process is referred to as multiple linear regression. Linear regression analyses are relatively simple to conduct and interpret, and are often used to assess quantitative variables. Linear regression is also a commonly used statistical technique in orthopaedic research as it can easily infer the relationship between several demographic and clinical variables with a scalar outcome of interest. An example application of linear regression would be to a study analyzing the significance of predictors for postoperative length of stay following hip replacement surgery. Predictor variables could include age, medication, blood clots, infection, and physical therapy. Similar to logistic regression analyses, the researcher can use linear regression to calculate t-test values and analyze the associated p-values. Linear regression differs from logistic regression in that it is used to predict continuous dependent variables, while logistic regression is utilized for categorical outcome variables. In linear regression, there may be correlation between predictor variables, while logistic regressions should not have correlation within predictors.

Polynomial regression is a form of analysis that models the relationship between independent and dependent variables as an nth-degree polynomial. Polynomial regressions are used to study nonlinear relationships. However, they are considered to be a type of multiple linear regression due to the estimate being linear in nature.

Support Vector Machines

SVM is typically employed in classification problems but can be utilized in regression as well [21]. The objective of SVM is to find a decision boundary based on the number of input features that classifies data points. Advantages of the SVM algorithm include high accuracy and low computational power. The objective of SVM is to use data points, referred to as support vectors, to find a hyperplane that classifies the data points. In a binary classification problem, data points are separated by one hyperplane and the number of hyperplanes increases with the number of features. The location and orientation of the hyperplane are chosen based on the maximum distance between the data points in different classes. Figure 2 visualizes the support vector data points in relation to the hyperplane via a coordinates transformation. Mehta and Sebro utilized an SVM algorithm to study ancillary data collected from posterior-anterior dual-energy X-ray absorptiometry (DEXA) studies, creating a tool to identify lumbar spine (L1–L4) vertebral fractures from future DEXA studies [13]. The SVM determined training vectors that differentiated patients with fractures from control patients, and was found to be accurate when tested. The SVM with the linear kernel had the best AUC in the training (AUC = 0.9258) and test (AUC = 0.8963) datasets, with an accuracy of 91.8% when evaluated in the test dataset.

Fig. 2.

Support vector machines

Lasso Regression, Ridge Regression, and Elastic Net

Linear regression is performed using ordinary least squares (OLS), through which the parameters in a model are estimated by minimizing the sum of squared residuals [22]. By minimizing this cost function, OLS regression produces a linear function with the least total squared error. Lasso, ridge, and elastic net regressions are derivatives of simple linear regressions that attempt to improve the cost function.

Lasso regression operates through shrinkage, which is a technique that shrinks data towards a central value [23]. Lasso is performed through L1 regularization, which adds a penalty using the absolute value of coefficients. Consequently, coefficients can be eliminated from the model, often resulting in sparse models that contain few predictive variables. Regularization is an approach that minimizes high variance, preferring some error in predictions instead. The technique is appropriate in datasets that contain multicollinearity, and can be useful in automating aspects of model design such as eliminating variables of interest. Lasso regression is suitable for constructing simple and interpretable models, and is resistant to outliers.

Venäläinen et al. developed lasso regression models using data for 25,919 total hip arthroplasties (THA) reported to the Finnish Arthroplasty Registry (FAR), assessing the risk of common factors responsible for treatment failure [14•]. In doing so, clinical decision-making could be optimized for improved surgical outcomes. The most frequently observed adverse outcomes within 6 months post-operation were revision procedures due to infection (1.1%), dislocation (0.7%), death (0.7%), and periprosthetic fracture (0.5%). Lasso regression was used to identify subsets of predictor variables through the training dataset, determining risk factors for treatment failure. The highest performing model predicted death (AUC = 0.84), with the algorithms for revisions (0.68), fractures (0.65), and dislocations (0.64) following.

Similarly to lasso, ridge regression is a form of linear regression with reduced complexity that can minimize the risk of poor generalizability [24]. Ridge regression performs L2 regularization, which incurs a penalty equal to the square of the coefficients’ magnitudes. As a result, ridge regression shrinks the coefficients, reducing the complexity of the model and making it appropriate for datasets with high multicollinearity. Unlike lasso models, ridge regression cannot eliminate variables since it is unable to set coefficient values to absolute zero. In Figure 3, it can be seen how ordinary regression compares to the lasso and ridge regressions.

Fig. 3.

Ordinary vs. ridge and lasso regressions

A study by Zhao et al. presents an example application of ridge regression in surgery research, using the technique to predict durations of robot-assisted surgeries [15•]. A ridge regression was used to evaluate a sample of 500 randomly selected elective robotic surgeries in conjunction with several other ML models: (1) multivariable linear regression, 2) lasso regression, (3) random forest, (4) boosted regression tree (BRT), and (5) neural networks. In their study, the boosted regression tree performed the best, with a root mean square error (RMSE) of 80.2 (95% CI: 74.0–86.4). The RMSE measures the standard deviations of residuals, with lower values indicating greater accuracy. In the study, the ridge regression model yielded a RMSE of 82.4 (95% CI: 73.3–91.5), with the baseline model having a value of 100.4 (CI: 90.5–110.3). Boosted regression trees are advantageous in managing missing data, are resistant to outliers, and can analyze complex nonlinear relationships. These factors may have contributed to the greater performance observed in the BRT compared with other models. The study performed is instructional in outlining the process of testing many different models for the highest accuracy in particular problems.

Due to the similarities between the two techniques, problems can be approached using an elastic net (EN) regression, which is a weighted combination of ridge and lasso regression [25]. All three regression models can identify variables with high predictive power and determine directional contributions through the magnitude and signs of coefficients. A study performed by Baca et al. developing predictive algorithms for acute pain after surgery is instructive [16]. In their project, authors collected data from a multinational registry containing detailed pharmacological information. The predictive model included 1008 patients that underwent lumbar surgery, with EN being selected due to its ability to manage multicollinearity. Procedures were characterized as (1) decompressions of the spinal canal, (2) disk surgery, (3) spinal fusion, and (4) other surgeries. Once validated, the model was significant (P = 8.9 E⁻¹⁵) and suggested relevant parameters for studying postoperative pain, including biological and psychological factors. However, the model only accounted for a small portion of the variance observed, indicating the presence of predictors not included in the study.

Decision Trees and Random Forests

Decision trees are a non-parametric learning method utilized in both classification and regression [26]. The objective of DTs is to predict the value of a target outcome variable using decision rules derived from features. Decision trees are advantageous because they require minimal data manipulation, can utilize categorical and quantitative data, can be validated using statistical tests, and are explainable, and results can be simply understood. Disadvantages include the potential for poorly generalizing data, instability of the model if data is slightly altered, and an inability to extrapolate from existing trends. Decision trees are best utilized in datasets with many features because we can then analyze the relative importance of each feature after generating the model.

Random forest models are used for both classification and regression problems [27]. A random forest utilizes ensemble learning, which combines classifiers to solve complicated problems. Random forest algorithms contain many decision trees, being generated using bootstrap aggregating. Bootstrapping is an ensemble aggregation tool that increases the accuracy of the model. The random forest algorithm takes the average of many decision trees’ outputs and can be made more precise by increasing the number of trees. As a consequence of utilizing many DTs, a random forest algorithm reduces the likelihood for poor generalizability. Random forest models can effectively manage missing data, providing a practical benefit for analyses. Due to their complexity, random forests typically require greater resources and time to create than many other modeling techniques. Since they are composed of decision trees, random forests are unable to effectively extrapolate from trends. The random forest model can be visualized in Figure 4 as an aggregate measure of many decision trees.

Fig. 4.

Random forest models

Applications of random forests in orthopaedics include quantifying risk factors for disorders, creating diagnostic tools, and predicting outcomes. Merali et al. utilized ML techniques to predict postoperative outcomes in patients with degenerative cervical myelopathy, with a random forest algorithm being most accurate [28••]. When evaluated, the model had a classification accuracy of 77%, sensitivity of 78%, and AUC of 0.70. Zhong et al. similarly used ML modeling, predicting length of stay (LOS) in hip arthroplasty patients by creating a logistic regression, artificial neural networks, and random forest [17]. Predictive factors included anesthesia type, age, ethnicity, body mass index, sodium levels, white blood cells, and alkaline phosphatase. The random forest model was most accurate in their study, with an AUC of 0.804 and accuracy at 81%. The logistic regression had an AUC of 0.715 and accuracy of 65%, and the neural networks yielded an AUC of 0.762 and accuracy at 73%. All models had acceptable quality, being able to effectively predict LOS based on the included clinical characteristics.

k-Nearest Neighbors

Nearest neighbor analyses are used to determine similarities between cases [29]. The kNN algorithm assumes that similar data points exist near each other. There are a few ways to calculate distance between data points, but Euclidean distance is the most common option. The first objective of developing a kNN model is to choose the optimal k-value that reduces the error rate while maintaining the algorithm’s ability to accurately make predictions. Generally, a k-value closer to 1 is less accurate because it does not suppress noise, while a larger k-value makes classification boundaries less distinct. An example use of kNN can be found in a project conducted by Dolatabadi et al. to classify gait patterns as healthy or pathological [18]. The study used kinetic skeletal tracking to observe different gait sequences. Each unique sequence was assigned a class label. The kNN model was then trained to identify whether each gait sequence showed a healthy pattern.

Neural Networks

Neural networks are inspired by human intelligence, intending to mimic the signaling patterns of biological neurons with their numerous interconnections [30]. They form the basis for deep learning, a sub-discipline within ML. The goal of deep learning is to ultimately create a computer simulation capable of recognizing patterns, learning objects and ideas, and making complicated decisions replicating human intelligence. The main advantage of a neural network is that they do not need to be programmed explicitly and they are able to accurately identify an output of interest by adjusting relationships between their interconnected neurons.

The computational units of neural networks are referred to as nodes. Each node contains an individual weight and threshold. When the threshold barrier for a node is passed, the node is activated, sending a signal to the next layer in the network. Any neural network contains an input layer, one or multiple hidden layers, and an output layer. The input layer is composed of the initial data introduced to the model for analysis, and the output is where results are produced. Predictions are made in the hidden layers, where input data is passed through a series of calculations. The number of hidden layers can depend on the type of network and complexity of the problem. Figure 5 details the neural network model, outlining the input, hidden, and output layers by depicting the interactions between individual nodes.

Fig. 5.

Neural networks

The most common neural networks are feedforward, being unidirectional towards the output. However, models can be trained to move backwards from output to input, which is a technique known as backpropagation. In doing so, the error in individual neurons can be identified for adjustment. Convolutional neural networks (CNNs) are a type of feedforward neural network that can be leveraged for computer vision, being able to classify images through pattern recognition [31]. Feedforward networks are appropriate for modeling relationships between predictor and outcomes variables. Advantages of neural networks include the ability to model nonlinear relationships and identify patterns in complicated data. Disadvantages include the need for large datasets and inability to provide explanations for calculations.

There are many applications of neural networks in orthopaedics, with the most prominent being in the interpretation of radiographs. Lindsey et al. developed a deep neural network to assist clinicians in detecting fractures in radiographs, providing an instructive example [32••]. The model was trained using 135,409 radiographs annotated by 18 senior orthopaedic surgeons. Radiographs were most commonly posterior-anterior or lateral wrist views (n = 34,990), with the remaining 100,855 images being taken of the shoulder, elbow, foot, ankle, knee, femur, tibia, pelvis, hip, humerus, and spine. Two test datasets were created for model development containing only randomly sampled wrist radiographs, with the first consisting of 3,500 and the second 1,400 images. The remaining images were used for model development, with the 100,855 images not taken from the wrist being used for bootstrapping in the training process. The 31,490 remaining wrist radiographs were used as a training dataset. Once the model was developed, a controlled experiment was performed with emergency medicine clinicians to determine the effectiveness of the diagnostic tool. When unaided by the model, the average sensitivity of a clinician was 80.8% (95% CI: 76.7–84.1%). When aided, the sensitivity increased to 91.5% (CI: 89.3–92.9%). Specificity without the model was 87.5% (CI: 85.3–89.5%), rising to 93.9% (CI: 92.9–94.9%) when aided. On average, the misinterpretation rate for clinicians was reduced by 47% (CI: 37.4–53.9%). Diagnostic accuracy was significantly improved when aided by the model, a finding that is reflective of the ability for deep learning to meaningfully transform patient care.

Data Collection and Handling

After identifying the appropriate model to be used for the clinical question that is proposed, the next step is data handling. Here, it is necessary to establish inclusion and exclusion criteria and subsequently select patients who qualify for the study. These criteria can include patients based on type of diagnosis, type of procedure, or follow-up time after surgery. Examples of exclusion criteria might include age, gender, treatment history, or stage of disease. Defining criteria in ML studies ensures more reliable and reproducible results.

Once the data is obtained, the next important step is to create a workable dataset. Data cleaning is the process of fixing or removing incorrectly formatted, duplicate, or missing data within a dataset. This step may include standardizing quantitative variables and numerically encoding categorical variables. In addition, handling missing data is necessary because several ML algorithms are unable to process datasets with missing data. One common practice to solve this issue is to impute missing data, or replace missing data with substituted values. Alternatively, observations containing any missing data can be entirely removed from the dataset.

Model Development

After choosing the model, the next step in producing an ML algorithm is to select variables. ML models consist of a primary outcome variable and multiple predictive variables. The outcome variable is selected based on the hypothesis. One way to approach predictive variable selection is through statistical tests and analyses. For instance, a linear or logistic regression can be performed to evaluate statistical significance of t-values for continuous variables. Categorical variables can be analyzed using a chi-square test. Typically, statistical significance is defined as p < 0.05.

Alternatively, feature selection can be determined using Shapley additive explanation (SHAP) values, which quantify variable importance and variable interaction effects [33]. SHAP values are calculated by connecting distributions of the total outcome to individual features. By quantifying and ranking individual features by importance, users can select highly ranked variables to include in the model. In subsequent iterations of the model, features can be added or removed to improve model accuracy on the test dataset. Analyses related to model development can be executed using software such as R, Python, or MatLab.

Model Training and Testing

Developing an ML model generally involves dividing a dataset into both training and test/validation subsets [34]. Using the training data, the learning algorithm will search for patterns, mapping the data to create a ML model that predicts the outcome of interest when it is unknown. Test data provides a subset that allows the trained model to be evaluated. Models are tested using only independent variables from “testing sets,” with predictions made being compared with the known outcomes. Parameters of the model can then be tuned to improve model accuracy. Test data should be large enough to yield meaningful results, and be representative of the overall dataset. Typically, test data includes 20–30% of the overall dataset, with the remainder being used as training data. Importantly, there should never be any overlap within the training and test data, since this will result in an inflated accuracy when testing the ML model.

The effectiveness of models is often measured using accuracy, precision, and recall. Accuracy is a measurement for how much of the data was labeled correctly, and can be determined via the ratio of correctly assigned outcomes over total outcomes evaluated. Precision is used to quantify how often outcomes marked as positive are truly positive. It is calculated by dividing the number of correctly predicted positives by all outcomes predicted to be positive. High precision reflects a low false positive rate. The difference between precision and recall is subtle, with the latter measuring the percentage of true positives that were identified by the model. Recall is derived from the ratio of positives correctly predicted by the model over the total number of true positives in the sample. High recall values represent a low false negative rate. The F1 score can weigh both precision and recall, allowing for a score that considers both false positives and false negatives. It is most appropriate to evaluate a model using accuracy when false positives and false negatives have similar effects. If either has a more dominant effect, precision and recall should be utilized. The equations for calculating accuracy, precision, and recall are outlined in Figure 6. The ROC curve (receiver operating characteristic curve) measures the performance of a classification algorithm by plotting the true and false positive rates at all decision thresholds. By measuring the area under the curve (AUC), one can determine an aggregate measure of model performance at varying thresholds. AUC values range from 0 to 1. A model that scores at 0 would produce only incorrect predictions, while a model measuring at 1 would only produce correct predictions. An AUC value of 0.7 is commonly used as a clinically discriminative threshold.

Fig. 6.

Accuracy, precision, and recall equations

The process of training and evaluating models is referred to as cross-validation, with common errors including “overfitting” and “underfitting” [35]. Overfitting occurs when a model is too complex, making it poorly generalizable to new data. When a model is too simple, underfitting is a potential concern, as there may be poor goodness-of-fit and precision through high model bias. Through the process of cross-validation after training models, the presence of these errors can be evaluated.

Model Interpretation

Though machine learning can be a powerful tool to make predictions, it is often difficult to understand the explanations behind the forecast. ML calculations can be incredibly complex, and understanding why an algorithm arrives at its results, known as explainability, can be impossible [36]. However, interpretability, which is slightly distinct from explainability, is a method of analyzing models that can be achieved. Interpretability refers to the process of determining how a ML model reached its conclusions. It is important for debugging algorithms for bias, ensuring reliability, directing the collection of future data, understanding future applications of the model, informing decision-making, and establishing trust in the model.

The simplest way of maintaining interpretability is only utilizing algorithms that create interpretable models, such as linear regression, logistic regression, and decision trees. Interpretable models have different properties, which are important in determining which to utilize. Linear models create linear associations between the target and predictors. Models with monotonicity have unidirectional relationships between predictors and outcomes (i.e., increases in individual features result in only increases or decreases in the outcome). Monotonicity can make understanding relationships between predictors and outcomes simple. Certain models are able to account for interactions between predictors when determining outcomes; however, if these interactions are too complex, interpretability may be more difficult to achieve.

Other types of ML algorithms are much more complicated, such as in deep learning using neural networks. Individual predictions can involve millions of operations in complex neural networks, making it impossible to track the mapping utilized by the model. Consequently, more complex interpretation methods must be utilized to understand the behavior of neural networks.

Natural Language Processing

Natural language processing (NLP) is a discipline concerned with developing AI algorithms capable of understanding text and spoken words [37]. Building AI models able to interpret human language is essential for the large-scale analysis of the electronic medical record (EMR). NLP is capable of recognizing both syntax and semantics by separating human language into segments, allowing the interactions between words to be understood. Using NLP, the process of acquiring structured data from the EMR can be automated, being conducted at a far greater rate than conventional manual chart reviews. If NLP algorithms can be appropriately leveraged to acquire data, they may eliminate the need for manual extraction, making research and surveillance endeavors more efficient. NLP may also be utilized to create medical records more efficiently, based on factors including speech and prior clinical notes.

Conclusion

Machine learning presents the future of medicine, having a powerful predictive capability unmatched by conventional research methods. In orthopaedics, ML modeling can be leveraged to develop diagnostic and prognostic tools, predict clinical outcomes, and create clinical decision support systems. Moving forwards, it will be increasingly important to create a consistent and critical understanding of the design of AI studies. This will lead to familiarity with AI studies and trust in the interpretation of their findings.

Author Contribution

All authors reviewed the manuscript, approved the final manuscript, and agree to be held responsible for all aspects of the work.

Data Availability

N/A

Declarations

Conflict of Interest

The authors do not have any relevant conflicts of interest, sources of financial support, corporate involvement, or patent holdings to disclose.

Human and Animal Rights and Informed Consent

This article does not contain any studies with human or animal subjects performed by any of the authors.