Hierarchical graph attention network for miRNA-disease association prediction

Abstract

Many biological studies show that the mutation and abnormal expression of microRNAs (miRNAs) could cause a variety of diseases. As an important biomarker for disease diagnosis, miRNA is helpful to understand pathogenesis, and could promote the identification, diagnosis and treatment of diseases. However, the pathogenic mechanism how miRNAs affect these diseases has not been fully understood. Therefore, predicting the potential miRNA-disease associations is of great importance for the development of clinical medicine and drug research. In this study, we proposed a novel deep learning model based on hierarchical graph attention network for predicting miRNA-disease associations (HGANMDA). Firstly, we constructed a miRNA-disease-lncRNA heterogeneous graph based on known miRNA-disease associations, miRNA-lncRNA associations and disease-lncRNA associations. Secondly, the node-layer attention was applied to learn the importance of neighbor nodes based on different meta-paths. Thirdly, the semantic-layer attention was applied to learn the importance of different meta-paths. Finally, a bilinear decoder was employed to reconstruct the connections between miRNAs and diseases. The extensive experimental results indicated that our model achieved good performance and satisfactory results in predicting miRNA-disease associations.

Graphical abstract

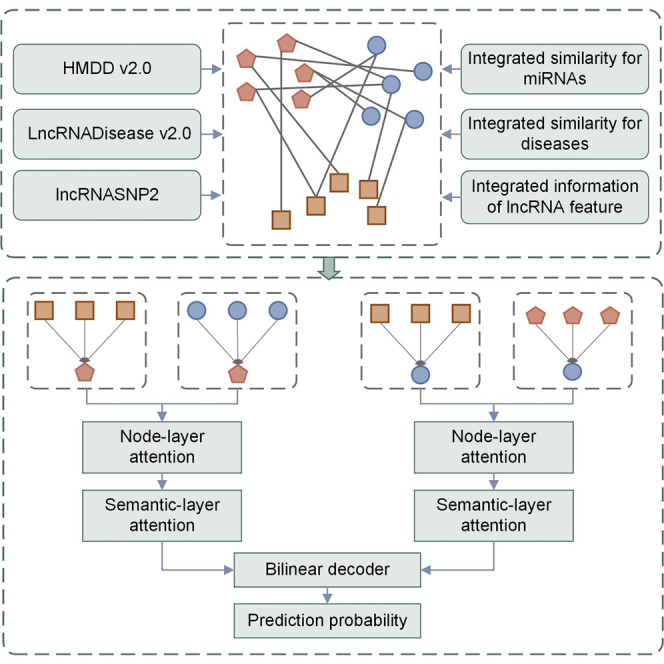
Li et al. presented a hierarchical graph attention network for miRNA-disease association prediction. Node-layer attention and semantic-layer attention were applied to extract complex structural information and rich semantic information. The model achieved the average AUC of 93.74% based on HMDD v.2.0, which outperforms various baselines.

Introduction

RNA (ribonucleic acid) is one of the important molecules commonly found in plants, animals, microorganisms and viruses.^1,2 It has a variety of important biological functions.³ MicroRNAs (miRNAs) are a class of small, non-coding RNA molecules encoded by endogenous genes that are about 22 nucleotides in length.^4,5 Since lin-4 were discovered from Caenorhabditis elegans in 1993, more and more researchers turned their attention to the function of miRNAs.⁶ Especially in recent years, many studies found that the abnormal expression of miRNAs is related to the generation and evolution of human complex diseases.⁷ For example, miR-155 has been confirmed to be a key regulator of ErbB2-induced mammary epithelial cell transformation and mediates the therapeutic response of ErbB2-positive breast cancer to trastuzumab.⁸ Therefore, it is very important to help disease researchers find the potential miRNA-disease associations.

Early researchers mainly used some biological techniques to identify the potential miRNA-disease associations, such as reverse transcription polymerase chain reaction (PCR),⁹ northern blotting,¹⁰ and microarray profiling.¹¹ However, the implementation of traditional biological technology often requires a lot of money and time, and the efficiency is relatively low.¹² With the development of biological technology and the summary of past experimental results, researchers constructed many reliable bioinformatics databases on miRNA-disease associations, such as the human miRNA-disease database (HMDD),¹³ the database of differentially expressed miRNAs in human cancers (dbDEMC),¹⁴ and the database for miRNA deregulation in human disease (miR2Disease).¹⁵ Meanwhile, the computational method and performance of computers have been greatly improved. Therefore, some researchers began to consider a computational method to realize miRNA-disease association prediction.¹⁶

Many novel and efficient computational methods have been proposed to study miRNA-disease associations over the last several years. These methods can be roughly divided into two categories: similarity-based methods and machine-learning-based methods. The similarity-based prediction methods come from a hypothesis that, if miRNAs have similar functions, they are more likely to be related to phenotypically similar diseases. Many researchers have used similarity-based methods to predict miRNA-disease associations. For example, Jiang et al. pioneered the approach of constructing a functionally relevant miRNA network and a human phenotypic miRNA network to investigate whether functionally relevant miRNAs are associated with phenotypically similar diseases.¹⁷ Due to insufficient data, they did not consider the indirect neighbor nodes, which led to the final prediction effect being not very good. Chen et al. proposed the model of combining within and between scores for predicting miRNA-disease associations, which can be used for diseases without known associated miRNAs.⁸ Besides, considering that most methods fail to predict miRNA-disease associations when their association information is unknown, Zhang et al. proposed the FLNSNLI model, which employed a weighted average strategy to predict the unknown associations between miRNAs and diseases.¹⁸ The FLNSNLI model still requires partially confirmed miRNA-disease associations to predict potential miRNA-disease associations. Then, Zhao et al. proposed the DCSMDA model, which combines proven miRNA-lncRNA associations and disease-lncRNA associations to construct a miRNA-disease-lncRNA network to predict the associations between miRNAs and diseases without using any proven miRNA-disease associations.¹⁹

Different from the similarity-based prediction methods, the machine-learning-based methods focus on classification algorithms and feature extraction methods to predict the associations between miRNAs and diseases. For example, Chen et al. used the restricted Boltzmann machine (RBMMMDA) as a classifier to predict multiple miRNA-disease associations.²⁰ Liu et al. constructed an miRNA-disease association network to connect disease similarity subnetworks and miRNA similarity subnetworks, and then used random walk to calculate association scores.²¹ Different from the method of Liu et al., Zheng et al. developed a new method called MLMDA, which applied deep autoencoder neural network for feature extraction, and then employed a random forest classifier for classification.²² Furthermore, Liu et al. proposed the SMALF model, which employed the stacked autoencoder to learn latent features and utilized XGBoost to predict unknown miRNA-disease associations.²³ Besides, Li et al. designed a diffusion-based machine learning method (DF-MDA) to extract node features in heterogeneous networks and employed a random forest classifier to judge the associations.²⁴

With the popularity of graph neural networks, researchers found that the graph structure method using graph neural networks is very suitable for predicting the miRNA-disease relationships. For example, Tang et al. presented an MMGCN model, which applied a graph convolution network and a multi-channel attention mechanism to enhance the features of miRNAs and diseases.²⁵ Wang et al. employed a graph convolution encoder to learn the potential representation of nodes and a neural multirelational decoder to obtain miRNA-disease association scores.²⁶ Ji et al. proposed the HGATMDA model, which extracts the features of miRNAs and diseases by weighted DeepWalk and a graph attention network.²⁷ Although the previous methods have shown satisfactory prediction performance, most researchers have not paid attention to the rich semantic information contained in an miRNA-disease heterogeneous graph. Meta-path is a path connecting different types of nodes, which can be employed to mine complex structure information and rich semantic information in heterogeneous networks.^28,29 Therefore, we considered combining graph neural networks with meta-path to aggregate node feature information and meta-path semantic information in heterogeneous graph networks.

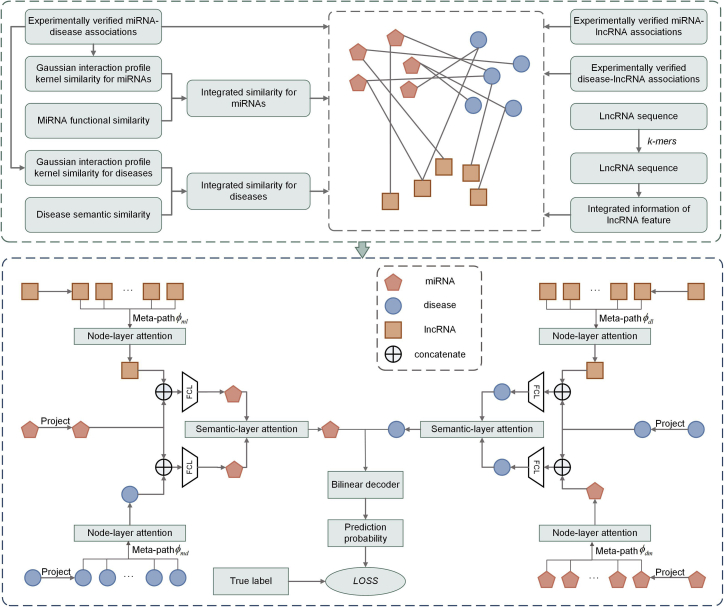
In this article, we propose a novel hierarchical graph attention network model named HGANMDA for predicting miRNA-disease associations. Specifically, we firstly integrated multiple data to construct an miRNA-disease-lncRNA heterogeneous graph. Secondly, miRNA and disease nodes were projected into the same vector space. Thirdly, node-layer attention was applied to aggregate the features of neighbor nodes based on different meta-paths. Semantic-layer attention was applied to obtain the semantic information by learning the importance of different meta-paths. The final node embedding was obtained by fusing the node aggregation feature information and semantic information in semantic-layer attention. Fourthly, a bilinear decoder was employed to decode the final embedding of miRNA and disease nodes to reconstruct the connections between miRNAs and diseases. Finally, the entire model was trained end-to-end by cross-entropy loss and back-propagation algorithm. In the experiment, we evaluated the performance of the HGANMDA model under 5-fold cross-validation and obtained the average area under the curve (AUC) of 93.74% and area under the precision-recall (AUPR) of 93.43%. In addition, we implemented the case studies of esophageal neoplasms, lymphoma, and prostate neoplasms. The results showed that 48, 46, and 46 of the top 50 miRNAs related to these diseases were verified by dbDEMC and miR2Disease databases, respectively. All experimental results demonstrated that the HGANMDA model can be an effective tool to help researchers study miRNA-disease associations.

Results

Evaluation metrics

To evaluate the performance of our proposed model from more aspects, we selected Accuracy (Acc.), Precision (Prec.), Recall, and F1 score as the evaluation metrics of HGANMDA model. These evaluation metrics are calculated as follows:

$$Accuracy=\frac{TP+TN}{TP+TN+FP+FN},$$ (Equation 1)

$$\mathit{Precision}=\frac{TP}{TP+FP},$$ (Equation 2)

$$\mathit{Re}call=\frac{TP}{TP+FN},$$ (Equation 3)

$$F1-\mathit{score}=\frac{2TP}{2TP+FP+FN},$$ (Equation 4)

where TP, TN, FP, and FN represent true positive, true negative, false positive, and false negative, respectively.

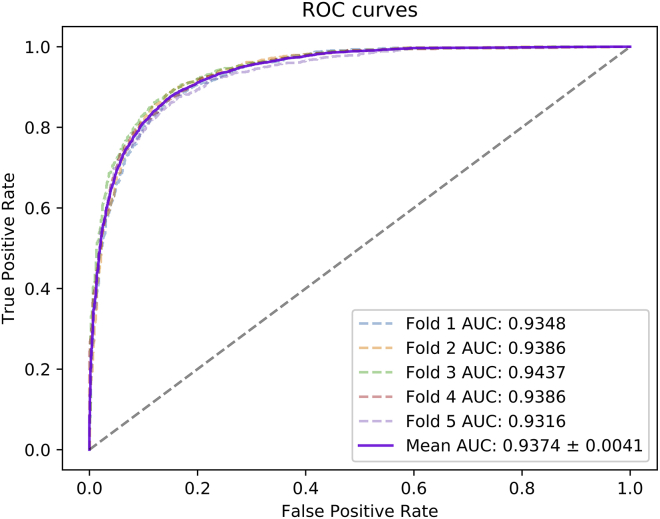
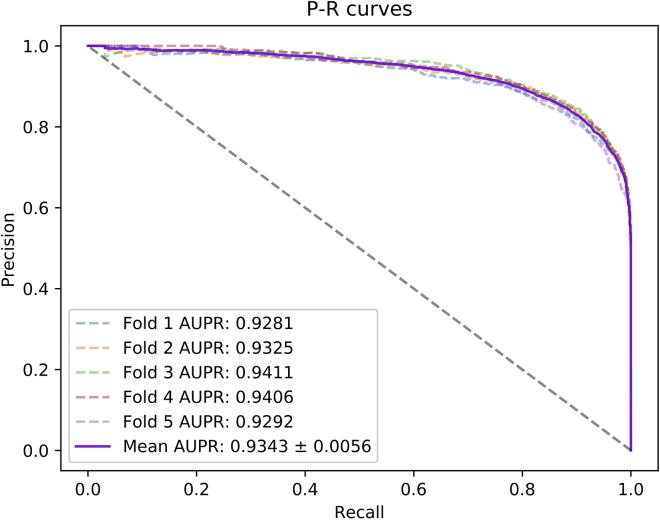
Besides, considering that the previous evaluation metrics cannot intuitively represent the research performance of our model, we plotted the receiver operating characteristic (ROC) curve and precision-recall (P-R) curve. Normally, if the area under the ROC curve is larger, the prediction performance of the model will be better.

Implementation details and performance evaluation

The HGANMDA model was implemented based on the Deep Graph Library of PyTorch. In the training phase of the experiment, we randomly initialized parameters and optimized our proposed model with Adam. Also, we set the training epochs to 1,000, the learning rate to 0.001, the weight decay to 5 × 10⁻³, the number of multi-head attention heads to 8, and the dimension of the semantic-layer attention vector q to 128 for the HGANMDA model. To reduce the occurrence of overfitting, we set dropout from 0.1 to 0.9 to train the model. Finally, we found that if dropout was set to 0.6, the model had the best prediction performance. All the experimental data and codes can be downloaded from https://github.com/ZTangBo/HGANMDA.

In this experiment, we applied 5-fold cross-validation to evaluate the performance of the HGANMDA model. For implementing 5-fold cross-validation, we randomly divided the selected miRNA-disease sample set into five subsets, where four of them were chosen as the training set and the remaining one was chosen as the test set. Next, we applied the training set to train the model and the test set to get the prediction results. Finally, according to the experimental results, we drew graphs and tables to show the effect of the model. In Table 1, we can see that HGANMDA achieves average Acc. of 86.28%, Prec. of 85.88%, Recall of 86.87%, and F1 score of 86.36% with standard deviations of 0.60%, 1.13%, 1.25%, and 0.59%, respectively. Besides, we also achieved average AUC of 93.74%, which is the average of 93.48%, 93.86%, 94.37%, 93.86%, and 93.16%, and average AUPR of 93.43%, which is the average of 92.81%, 93.25%, 94.11%, 94.06%, and 92.92%. The ROC curves of the HGANMDA model are shown in Figure 2 and the P-R curves are shown in Figure 3.

Table 1.

Five-fold cross-validation results performed by HGANMDA based on HMDD v.2.0

Testing set	Acc. (%)	Prec. (%)	Recall (%)	F1 score (%)
1	86.10	84.70	87.85	86.25
2	86.88	85.86	88.01	86.92
3	87.02	88.01	85.74	86.86
4	86.00	85.28	87.74	86.49
5	85.41	85.55	85.00	85.28
Average	86.28 ± 0.60	85.88 ± 1.13	86.87 ± 1.25	86.36 ± 0.59

Figure 2.

ROC curves performed by HGANMDA model based on HMDD v.2.0

Figure 3.

P-R curves performed by HGANMDA model based on HMDD v.2.0

Compare with other latest methods

To further confirm the performance of our model in predicting the associations between miRNAs and diseases, we compared the performance of the HGANMDA model with that of another seven of the latest models, including IMIPMF,³⁰ NMCMDA,²⁶ NCFM,³¹ DBMDA,³² CEMDA,³³ NIMCGCN,³⁴ and M2GMDA.³⁵ To make the results convincing and fair, the models we selected were all from the past 2 years, and their evaluation metrics were obtained by applying the 5-fold cross-validation method on the HMDD v.2.0 dataset. Since these models chose the AUC value as an important metric to evaluate their performance, we compared the AUC value of our proposed model with those of these models. The comparison results are shown in Table 2. We can see that, compared with other models, our model has the highest AUC value and 0.51% higher than the second highest M2GMDA model. The possible reason is that our model combines node-layer attention with semantic-layer attention, which not only considers the feature information of neighbor nodes, but also considers the semantic information of neighbor nodes, which made the final node embedding more comprehensive and the prediction results better.

Table 2.

The comparison results of HGANMDA model with other latest models according to 5-fold cross-validation on HMDD v.2.0 dataset

Models	AUC (%)
IMIPMF	89.10
NMCMDA	89.42
NCFM	91.20
DBMDA	91.29
CEMDA	92.03
NIMCGCN	92.91
M2GMDA	93.23
HGANMDA	93.74

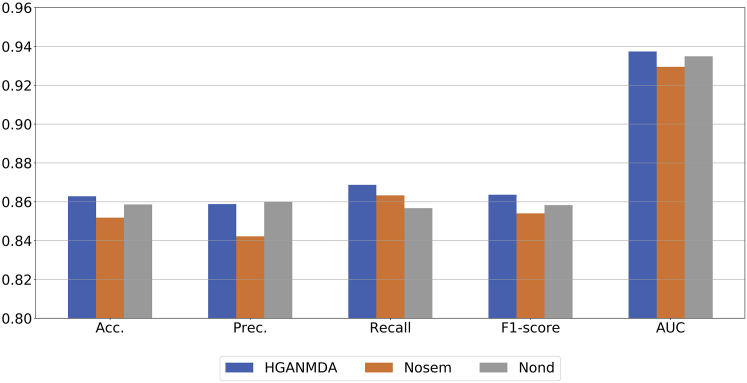
Influence of feature aggregation

In this experiment, we applied a combination of node-layer attention and semantic-layer attention to achieve the embedding of miRNA and disease nodes. For proving the feasibility of our method and convincing experimental results, we compared the prediction performance of HGANMDA with that of the method without node-layer attention and the method without semantic-layer attention. Since node-layer attention was applied to aggregate the features of neighbor nodes based on meta-paths, the same importance was assigned to each neighbor node when node-layer attention was not considered, denoted as Nond. In contrast, since semantic-layer attention was applied to obtain the importance of meta-paths, the same importance was assigned to each meta-path when semantic-layer attention was not considered, denoted as Nosem. The comparison results are shown in Figure 4. It can be seen that HGANMDA has the highest Accuracy, Recall, F1 score, and AUC among the three methods. Although the Precision of Nond is slightly higher than that of HGANMDA, Nond is significantly lower than HGANMDA in the other four evaluation metrics, which means that the semantic-layer attention is a supplement to the node-layer attention. The semantic-layer attention integrated the specific semantic information of node-layer attention to obtain more comprehensive node aggregation features. Therefore, the effect of the HGANMDA model is better than the other two methods.

Figure 4.

The average Acc., Prec., Recall, F1 score, and AUC values of HGANMDA under different feature aggregation methods according to 5-fold cross-validation

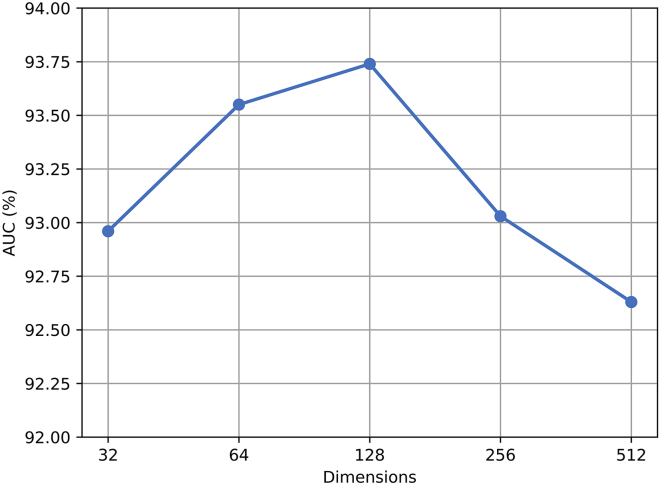
Influence of dimension of semantic-layer attention vector q

Since the dimension of semantic-layer attention vector q is a key factor affecting the performance of the semantic-layer attention, we compared the AUC value of HGANMDA under different dimensions according to 5-fold cross-validation. The comparison results are shown in Figure 5. It can be seen that the AUC value of HGANMDA initially increases with the dimension of the semantic-layer attention vector q. When the dimension of the semantic-layer attention vector q was set to 128, the AUC was the largest, and the model had the best prediction effect at that time. However, when the dimension of q was set beyond 128, the AUC started to decrease. We also found that the AUC of our model decreased significantly when the dimension is 512 compared with a value of 128, which may be due to overfitting. Therefore, we set the dimension of the semantic-layer attention vector q to 128 as our default dimension.

Figure 5.

Dimension of the semantic-layer attention vector q

Case studies

To further reflect the performance of the HGANMDA model in predicting the potential associations between miRNAs and specific diseases, we completed case studies of esophageal neoplasms, lymphoma, and prostate neoplasms. Specifically, we firstly filtered out the edges containing miRNA nodes and disease-specific nodes from the miRNA-disease-lncRNA heterogeneous graph. Then, the remaining edges containing miRNA nodes and diseases nodes were trained as training sets, and the filtered edges were tested as test sets. Finally, we ranked the results of the test set and used the dbDEMC and miR2Disease datasets to judge whether the associations between the predicted miRNAs and specific diseases were confirmed.

Esophageal neoplasms are one of the most common digestive tract neoplasms. They rank fourth among the top 10 malignant neoplasms in the world. Numerous studies show that the expression of miRNAs is significantly different between normal tissues and esophageal neoplasm tissues, and that miRNAs are involved in the occurrence, development, and prognosis of esophageal tumor. Therefore, esophageal neoplasms were selected as the first case study to test the prediction performance of the model. From Table 3, we can find that the dbDEMC and miR2Disease datasets confirmed 48 of the top 50 miRNAs related to esophageal neoplasms.

Table 3.

Top 50 miRNAs related to esophageal neoplasms predicted by HGANMDA

miRNA(1–25)	Evidence	miRNA(26–50)	Evidence
hsa-mir-18a	dbDEMC	hsa-mir-218	dbDEMC
hsa-mir-19b	dbDEMC	hsa-mir-195	dbDEMC
hsa-let-7i	dbDEMC	hsa-mir-133b	dbDEMC
hsa-let-7e	dbDEMC	hsa-mir-138	dbDEMC
hsa-mir-17	dbDEMC	hsa-mir-106b	dbDEMC
hsa-mir-200b	dbDEMC	hsa-mir-24	dbDEMC
hsa-mir-221	dbDEMC	hsa-mir-96	dbDEMC
hsa-mir-29a	dbDEMC	hsa-mir-378a	dbDEMC
hsa-let-7d	dbDEMC	hsa-mir-497	dbDEMC
hsa-let-7g	dbDEMC	hsa-mir-142	dbDEMC
hsa-let-7f	Unconfirmed	hsa-mir-181a	dbDEMC
hsa-mir-107	dbDEMC, miR2Disease	hsa-mir-181b	dbDEMC
hsa-mir-222	dbDEMC	hsa-mir-106a	dbDEMC
hsa-mir-9	dbDEMC	hsa-mir-206	dbDEMC
hsa-mir-93	dbDEMC	hsa-mir-127	dbDEMC
hsa-mir-429	dbDEMC	hsa-mir-302b	dbDEMC
hsa-mir-18b	dbDEMC	hsa-mir-182	dbDEMC
hsa-mir-125b	dbDEMC	hsa-mir-7	dbDEMC
hsa-mir-10b	dbDEMC	hsa-mir-320a	dbDEMC
hsa-mir-29b	dbDEMC	hsa-mir-151a	Unconfirmed
hsa-mir-20b	dbDEMC	hsa-mir-122	dbDEMC
hsa-mir-125a	dbDEMC	hsa-mir-302c	dbDEMC
hsa-mir-1	dbDEMC	hsa-mir-132	dbDEMC
hsa-mir-16	dbDEMC	hsa-mir-191	dbDEMC
hsa-mir-146b	dbDEMC	hsa-mir-92b	dbDEMC

Lymphoma is a malignant tumor of the lymphatic hematopoietic system. miRNAs have an important role in the pathogenesis of lymphoma and are involved in the differentiation, proliferation, and apoptosis of lymphoma cells. For example, high expression of miR-155 can block the inhibitory effect of the RhoA signaling pathway on lymphoma, which promotes the occurrence of lymphoma.³⁶ Therefore, lymphoma was selected as the second case study. From Table 4, we show that 46 of the top 50 miRNAs associated with lymphoma were confirmed by the dbDEMC and miR2Disease datasets.

Table 4.

Top 50 miRNAs related to lymphoma predicted by HGANMDA

miRNA(1–25)	Evidence	miRNA(26–50)	Evidence
hsa-mir-125b	dbDEMC	hsa-mir-214	DbDEMC
hsa-mir-221	dbDEMC, miR2Disease	hsa-mir-34b	dbDEMC
hsa-mir-34a	dbDEMC	hsa-let-7c	dbDEMC
hsa-mir-133a	dbDEMC	hsa-mir-192	dbDEMC
hsa-mir-31	dbDEMC	hsa-let-7e	dbDEMC, miR2Disease
hsa-mir-1	dbDEMC	hsa-mir-183	dbDEMC
hsa-mir-222	dbDEMC	hsa-mir-137	dbDEMC
hsa-mir-29a	dbDEMC	hsa-mir-142	Unconfirmed
hsa-mir-145	dbDEMC, miR2Disease	hsa-mir-195	dbDEMC
hsa-mir-106b	dbDEMC	hsa-let-7f	dbDEMC
hsa-let-7d	dbDEMC	hsa-mir-146b	Unconfirmed
hsa-let-7b	dbDEMC	hsa-mir-27a	dbDEMC
hsa-mir-9	dbDEMC	hsa-mir-7	dbDEMC
hsa-mir-29b	dbDEMC	hsa-mir-106a	dbDEMC, miR2Disease
hsa-mir-141	dbDEMC	hsa-let-7g	dbDEMC
hsa-let-7a	dbDEMC	hsa-mir-182	dbDEMC
hsa-mir-199a	dbDEMC	hsa-mir-429	Unconfirmed
hsa-mir-148a	dbDEMC	hsa-mir-96	dbDEMC
hsa-mir-34c	Unconfirmed	hsa-mir-206	dbDEMC
hsa-mir-223	dbDEMC	hsa-mir-196a	dbDEMC
hsa-mir-181b	dbDEMC	hsa-mir-10b	dbDEMC
hsa-mir-143	dbDEMC, miR2Disease	hsa-mir-100	dbDEMC
hsa-let-7i	dbDEMC	hsa-mir-335	dbDEMC
hsa-mir-15b	dbDEMC	hsa-mir-205	dbDEMC
hsa-mir-93	dbDEMC	hsa-mir-451a	dbDEMC

To make the experimental results more adequate, we conducted the third case study on prostate neoplasms. Prostate neoplasms include epithelial and mesenchymal neoplasms of the prostate, most of which are malignant. The reason why we chose prostate neoplasms is that their occurrence is also closely related to miRNAs. Table 5 shows that 46 of the top 50 miRNAs associated with prostate neoplasms can be confirmed by the dbDEMC and miR2Disease datasets. In conclusion, the HGANMDA model achieved satisfactory results in case studies predicting the associations between miRNAs and specific diseases.

Table 5.

Top 50 miRNAs related to prostate neoplasms predicted by HGANMDA

miRNA(1–25)	Evidence	miRNA(26–50)	Evidence
hsa-mir-21	dbDEMC, miR2Disease	hsa-mir-199a	dbDEMC, miR2Disease
hsa-mir-155	dbDEMC	hsa-mir-142	Unconfirmed
hsa-mir-146a	miR2Disease	hsa-mir-26a	dbDEMC, miR2Disease
hsa-mir-20a	miR2Disease	hsa-let-7a	dbDEMC, miR2Disease
hsa-mir-150	dbDEMC	hsa-mir-133b	dbDEMC
hsa-mir-17	miR2Disease	hsa-let-7b	dbDEMC, miR2Disease
hsa-mir-19b	dbDEMC, miR2Disease	hsa-mir-29c	dbDEMC
hsa-mir-221	dbDEMC, miR2Disease	hsa-mir-148a	miR2Disease
hsa-mir-19a	dbDEMC	hsa-mir-141	miR2Disease
hsa-mir-16	dbDEMC, miR2Disease	hsa-mir-195	dbDEMC, miR2Disease
hsa-mir-126	dbDEMC, miR2Disease	hsa-mir-200a	dbDEMC
hsa-mir-1	dbDEMC	hsa-mir-15b	dbDEMC
hsa-mir-34a	dbDEMC, miR2Disease	hsa-mir-200b	Unconfirmed
hsa-mir-29a	dbDEMC, miR2Disease	hsa-mir-210	miR2Disease
hsa-mir-18a	dbDEMC	hsa-mir-24	dbDEMC, miR2Disease
hsa-mir-122	Unconfirmed	hsa-let-7e	dbDEMC
hsa-mir-133a	dbDEMC	hsa-let-7c	dbDEMC, miR2Disease
hsa-mir-222	dbDEMC, miR2Disease	hsa-mir-206	dbDEMC
hsa-mir-15a	dbDEMC, miR2Disease	hsa-mir-181b	dbDEMC, miR2Disease
hsa-mir-92a	Unconfirmed	hsa-mir-200c	dbDEMC
hsa-mir-143	dbDEMC, miR2Disease	hsa-mir-196a	dbDEMC
hsa-mir-31	dbDEMC, miR2Disease	hsa-mir-214	dbDEMC, miR2Disease
hsa-mir-223	dbDEMC, miR2Disease	hsa-mir-9	dbDEMC
hsa-mir-29b	dbDEMC, miR2Disease	hsa-mir-124	dbDEMC
hsa-mir-181a	dbDEMC, miR2Disease	hsa-mir-192	dbDEMC

Discussion

MiRNAs have been proved to play a key role in the generation and development of human diseases. Mining some pathogenic miRNAs by computational methods cannot only solve the high cost and long cycle of biological experimental methods, but also guide researchers to conduct targeted studies on miRNAs related to specific diseases. In this paper, we propose a hierarchical graph attention network, including node-layer attention and semantic-layer attention, to predict the associations between miRNAs and diseases, which we called the HGANMDA model. The model applies node-layer attention to learn the importance of the neighbor nodes based on different meta-paths and applied semantic-layer attention to learn the importance of different meta-paths. Through the network, the HGANMDA model can make full use of the node information, structural information, and semantic information in an miRNA-disease-lncRNA heterogeneous graph. Overall, these evaluation metrics and case studies demonstrated the excellent prediction performance of the HGANMDA model in predicting miRNA-disease associations. Our proposed model should prove to be a valuable method to help researchers improve research on the miRNA-disease associations. However, in the HGANMDA model, we did not employ longer meta-paths. The reason is that when the length of meta-paths was greater than or equal to 2, the association matrix based on meta-paths becomes dense. Therefore, for further improving the prediction performance of our model, we plan to employ longer meta-paths by limiting the number of neighbor nodes in the future.

Materials and methods

Human miRNA-disease associations database

In this study, we implement the model by using the benchmark dataset HMDD v.2.0. It can be downloaded from https://www.cuilab.cn/hmdd.¹³ The dataset contains 383 diseases, 495 miRNAs, and 5,430 experimentally verified miRNA-disease associations. In the experiment, we created an adjacency matrix DM(i,j) to store miRNA-disease associations. In the matrix, 383 rows represent the number of diseases, 495 columns represent the number of miRNAs. If disease d(i) is associated with miRNA m(j), the corresponding position of the matrix is recorded as 1, otherwise 0.

miRNA functional similarity

Based on the assumption that miRNAs with similar functions are usually associated in similar diseases and vice versa, Wang et al. proposed a model to calculate miRNAs functional similarity.³⁷ Benefiting from their previous work, we can directly obtain miRNA functional similarity data from https://www.cuilab.cn/files/images/cuilab/misim.zip. Then, we constructed a matrix MFSM with 495 rows and columns, where $MFSM\left(m\left(i\right),m\left(j\right)\right)$ represents the functional similarity score between miRNA m(i) and m(j).

Disease semantic similarity

According to previous research,³⁸ we can obtain the relationships between different diseases from the medical subject headings (MeSH) database (https://www.ncbi.nlm.nih.gov/) and calculate disease semantic similarity. In the MeSH database, every disease can be represented by a directed acyclic graph (DAG). $DAG\left(d\left(i\right)\right)=\left(d\left(i\right),T\left(d\left(i\right)\right),E\left(d\left(i\right)\right)\right)$, represents a directed acyclic graph of disease d(i), which includes disease d(i), its ancestor nodes $T\left(d\left(i\right)\right)$, and the set $E\left(d\left(i\right)\right)$ of directly connected edges from the ancestor nodes to node d(i). Then, the semantic contribution value of disease d(k) to d(i) is calculated as follows:

$$\begin{array}{l}D{1}_{d\left(i\right)}\left(d\left(k\right)\right)=\{\begin{array}{ll}1\hfill & d\left(k\right)=d\left(i\right)\hfill \\ max\left\{\Delta \ast D{1}_{d\left(i\right)}\left(d{\left(k\right)}^{\prime }\right)\right\}\hfill & d\left(k\right)\ne d\left(i\right)\hfill \end{array}\hfill \end{array},$$ (Equation 5)

where $d{\left(k\right)}^{\prime }$ denotes the children node of d(k), $\Delta$ denotes the contribution factors of semantic decay and we set it to 0.5 based on the research of Xuan et al.³⁸ The contribution factor of disease d(i) to itself is set to 1. If the distance from disease d(k) to disease d(i) increases, the semantic contribution factor will decrease. Therefore, we can calculate the semantic value of disease d(i) as follows:

$$\text{DS}1\left(d\left(i\right)\right)=\sum _{d\left(k\right)\in T\left(d\left(i\right)\right)}D{1}_{d\left(i\right)}\left(d\left(k\right)\right).$$ (Equation 6)

According to the assumption that two diseases are more similar if the DAGs of two diseases share more parts, we can calculate the disease semantic similarity $DSSM1\left(d\left(i\right),d\left(j\right)\right)$ between disease d(i) and d(j) as follows:

$$DSSM1\left(d\left(i\right),d\left(j\right)\right)=\frac{{\sum }_{d\left(k\right)\in T\left(d\left(i\right)\right)\cap T\left(d\left(j\right)\right)}\left(D{1}_{d\left(i\right)}\left(d\left(k\right)\right)+D{1}_{d\left(j\right)}\left(d\left(k\right)\right)\right)}{DS1\left(d\left(i\right)\right)+DS1\left(d\left(j\right)\right)}.$$ (Equation 7)

However, the above method is not so comprehensive that the appearance times of diseases in the same layer of DAG may be different in DAGs of all diseases. We integrated the research of Pasquier and Gardès and employed another method to calculate disease semantic similarity.³⁹ The semantic contribution value of disease d(k) to d(i) is calculated as follows:

$$D{2}_{d\left(i\right)}\left(d\left(k\right)\right)=-log\left(\frac{num\left(DAGs\left(d\left(k\right)\right)\right)}{num\left(diseases\right)}\right).$$ (Equation 8)

In this way, the semantic value of disease d(i) is calculated as Equation (9) and the disease semantic similarity $DSSM2\left(d\left(i\right),d\left(j\right)\right)$ between disease d(i) and d(j) is calculated as Equation (10).

$$\begin{array}{l}DS2\left(d\left(i\right)\right)=\sum _{d\left(k\right)\in T\left(d\left(i\right)\right)}D{2}_{d\left(i\right)}\left(d\left(k\right)\right)\hfill \end{array}$$ (Equation 9)

$$DSSM2\left(d\left(i\right),d\left(j\right)\right)=\frac{{\sum }_{d\left(k\right)\in T\left(d\left(i\right)\right)\cap T\left(d\left(j\right)\right)}\left(D{2}_{d\left(i\right)}\left(d\left(k\right)\right)+D{2}_{d\left(j\right)}\left(d\left(k\right)\right)\right)}{DS2\left(d\left(i\right)\right)+DS2\left(d\left(j\right)\right)}.$$ (Equation 10)

Therefore, to obtain more reasonable and accurate disease semantic similarity, we averaged two-disease semantic similarity as the final disease semantic similarity. Finally, the disease semantic similarity $DSSM\left(d\left(i\right),d\left(j\right)\right)$ between d(i) and d(j) is calculated as follows:

$$DSSM\left(d\left(i\right),d\left(j\right)\right)=\frac{DSSM1\left(d\left(i\right),d\left(j\right)\right)+DSSM2\left(d\left(i\right),d\left(j\right)\right)}{2}.$$ (Equation 11)

Gaussian interaction profile kernel similarity for miRNAs and diseases

Based on the topology structure of verified miRNA-disease association network, we can calculate the Gaussian interaction profile kernel similarity for miRNAs and diseases.⁸ Firstly, according to a hypothesis that similar miRNAs are more likely to be associated with similar diseases, we created a binary vector $IP\left(m\left(i\right)\right)$, which is the ith column of matrix DM, representing the associations between miRNA m(i) and all other diseases. Then, we can calculate the Gaussian interaction profile kernel similarity for miRNAs $MGSM\left(m\left(i\right),m\left(j\right)\right)$ between miRNA m(i) and m(j) as follows:

$$MGSM\left(m\left(i\right),m\left(j\right)\right)=exp\left(-r_m{\Vert IP\left(m\left(i\right)\right)-IP\left(m\left(j\right)\right)\Vert }^2\right),$$ (Equation 12)

where parameter $r_m$ is used to control the bandwidth of the kernel. It can be calculated as follows:

$$r_m=\raisebox{1ex}{$r_m^{\prime }$}\!\left/ \!\raisebox{-1ex}{$\left(\frac{1}{nm}{\sum }_{i=1}^{nm}{\Vert IP\left(m\left(i\right)\right)\Vert }^2\right)$}\right.,$$ (Equation 13)

where $r_m^{\text{′}}$ is set to 1 referring to previous studies⁸ and $nm$ is set to 495, which is equal to the number of all miRNAs. Similarly, we can calculate the Gaussian interaction profile of diseases $DGSM\left(d\left(i\right),d\left(j\right)\right)$ between diseases $d\left(i\right)$ and $d\left(j\right)$ as follows:

$$DGSM\left(d\left(i\right),d\left(j\right)\right)=exp\left(-r_d{\Vert IP\left(d\left(i\right)\right)-IP\left(d\left(j\right)\right)\Vert }^2\right),$$ (Equation 14)

$$r_d=\raisebox{1ex}{$r_d^{\prime }$}\!\left/ \!\raisebox{-1ex}{$\left(\frac{1}{nd}{\sum }_{i=1}^{nd}{\Vert d\left(i\right)\Vert }^2\right)$}\right.,$$ (Equation 15)

where a binary vector $IP\left(d\left(i\right)\right)$, which is the ith row of matrix DM, represents the associations between disease d(i) and all other miRNAs. $r_d^{\text{′}}$ is set to 1 and nd is set to 383, which is equal to the number of all diseases.

Integrated similarity for miRNAs and diseases

Based on the above results, we can calculate the integrated similarity for miRNAs $IM\left(m\left(i\right),m\left(j\right)\right)$ between miRNA m(i) and m(j) as Equation (16), and the integrated similarity for diseases $ID\left(d\left(i\right),d\left(j\right)\right)$ between disease d(i) and d(j) as Equation (17).

$$IM\left(m\left(i\right),m\left(j\right)\right)=\{\begin{array}{ll}MFSM\left(m\left(i\right),m\left(j\right)\right)\hfill & m\left(i\right)\text{and}m\left(j\right)\text{have functional similarity}\hfill \\ MGSM\left(m\left(i\right),m\left(j\right)\right)\hfill & \text{otherwise}\hfill \end{array},$$ (Equation 16)

$$ID\left(d\left(i\right),d\left(j\right)\right)=\{\begin{array}{ll}DSSM\left(d\left(i\right),d\left(j\right)\right)\hfill & d\left(i\right)\text{and}d\left(j\right)\text{have semantic similarity}\hfill \\ DGSM\left(d\left(i\right),d\left(j\right)\right)\hfill & \text{otherwise}\hfill \end{array}.$$ (Equation 17)

Matrix representation of lncRNA sequences

In the experiment, the data we employed include experimentally confirmed miRNA-lncRNA associations and lncRNA-disease associations. To obtain the associated data, we introduced the lncRNASNP2⁴⁰ and LncRNADisease v.2.0⁴¹ datasets. The LncRNASNP2 dataset records 45,329 confirmed associations between 3,521 lncRNAs and 276 miRNAs, which can be download from http://bioinfo.life.hust.edu.cn/lncRNASNP.^42,43 The LncRNADisease v.2.0 dataset records 10,564 confirmed associations between 6,086 lncRNAs and 451 diseases, which can be download from http://www.rnanut.net/lncrnadisease.⁴⁴ Based on these data, we manually matched the associations between miRNAs and lncRNAs, and the associations between diseases and lncRNAs in the lncRNASNP2 dataset, the LncRNADisease v.2.0 dataset, and HMDD v.2.0 dataset. For the convenience of the experiment, we selected 467 lncRNAs associated with miRNAs and diseases. As a result, we obtained 4,352 confirmed associations between 495 miRNAs and 467 lncRNAs, and 1,486 confirmed associations between 383 diseases and 467 lncRNAs.

For getting the feature information of lncRNAs, we downloaded the sequence information of lncRNAs from NONCODE (http://www.noncode.org/) to represent the attributes of nodes.⁴⁵ Then, we converted lncRNA sequences to vectors using the k-mers method.^46,47 The k-mers could divide the lncRNA sequences into a series of subsequences with bases. Generally, a sequence of length $m$ can be divided into $m-k+1$ k-mers. In the experiment, we extracted the conjoint triads (3-mers) of lncRNAs from the sequences of lncRNAs. Four bases of lncRNA are A, C, G, and U. Therefore, 3-mers could split the sequence of lncRNA into AAA, AAC, …, UUU. Specifically, we firstly applied a sliding window to divide the sequence of lncRNA into many conjoint triads. Then, we calculated the frequency of each subsequence and normalized these data. Finally, we obtained a 64-dimension vector to represent the feature information of lncRNA. Because the number of lncRNAs is 467, we created a matrix IL with 467 rows and 64 columns to store the vectors of these lncRNAs, where $IL\left(k\right)$ represents the feature of lncRNA l(k).

HGANMDA

In this paper, we propose a hierarchical graph attention network model which combines node-layer attention, semantic-layer attention, and a bilinear decoder for miRNA-disease association prediction (HGANMDA). The flowchart of the proposed model is shown in Figure 1. HGANMDA can be described as six steps: (1) construct an miRNA-disease-lncRNA heterogeneous graph; (2) project miRNA and disease nodes into the same feature space; (3) apply node-layer attention to aggregate features of neighbor nodes based on different meta-paths; (4) employ semantic-layer attention to learn the importance of different meta-paths and fuse the node aggregation feature information and semantic information; (5) use a bilinear decoder to reconstruct the connections between miRNAs and diseases; and (6) use cross-entropy loss function to train the whole model in an end-to-end way. Next, we introduce the specific implementation process of each step.

Figure 1.

Flowchart of HGANMDA model for predicting miRNA-disease associations

Construction of the miRNA-disease-lncRNA heterogeneous graph

To implement this model, we need to construct a heterogeneous graph containing 495 miRNA nodes, 383 disease nodes, 467 lncRNA nodes, and verified associations between all nodes. In HMDD v.2.0, there are 5,430 experimentally verified miRNA-disease associations. We applied these 5,430 associations as positive samples between miRNA nodes and disease nodes, which were labeled as 1. However, the number of unknown miRNA-disease associations is far greater than the number of confirmed miRNA-disease associations. The imbalance of positive and negative samples will make the prediction results tend to the classification with more samples, which will reduce the generalization ability of the model. To solve this problem, we randomly selected 5,430 associations from all the unknown miRNA-disease associations as negative samples, which were labeled as 0 and added to the heterogeneous graph. In addition, we regarded the integrated similarity of miRNAs and diseases as miRNA and disease node features, respectively. Therefore, miRNA m(i) can be recorded as a 495-dimensions vector $F_{m\left(i\right)}$ as follows:

$$\begin{array}{l}{F}_{m\left(i\right)}=\left(x_1,x_2,x_3,\dots ,x_{494},x_{495}\right)\hfill \end{array},$$ (Equation 18)

where $F_{m\left(i\right)}$ represents the ith column of matrix IM and x_j represents the integrated similarity value between miRNA m(i) and m(j). Similarity, disease d(i) can be recorded as a 383-dimensions vector $F_{d\left(i\right)}$ as follows:

$$\begin{array}{l}{F}_{d\left(i\right)}=\left(y_1,y_2,y_3,\dots ,y_{382},y_{383}\right)\hfill \end{array},$$ (19)

where $F_{d\left(i\right)}$ represents the ith column of matrix ID and y_j represents the integrated similarity value between disease d(i) and d(j).

Node-layer attention

Since the neighbor nodes based on different meta-paths show different importance in the specific task of learning node embedding, we applied the node-layer attention to learn the importance of neighbor nodes based on different meta-paths in the heterogeneous graph and aggregate the feature information of these meaningful neighbor nodes to form a node embedding. Firstly, due to the heterogeneity of nodes in miRNA-disease-lncRNA heterogeneous graph, different nodes may be in different feature spaces. Therefore, for each type of node, we designed the type-specific transformation matrix W to project different types of nodes into the same feature space. This projection process is shown as follows:

$$H_{m\left(i\right)}=W_{m\left(i\right)}\cdot F_{m\left(i\right)},$$ (Equation 20)

$$H_{d\left(i\right)}=W_{d\left(i\right)}\cdot F_{d\left(i\right)},$$ (Equation 21)

where H_m(i) and H_d(i) are projection features of miRNA node m(i) and disease node d(i), respectively. By this projection operation, miRNA nodes and disease nodes can be projected into the 64-dimensional space. Besides, since the features of lncRNA nodes have been located in the 64-dimensional space, the feature of lncRNA l(i) is shown as follows:

$$\begin{array}{l}{H}_{l\left(i\right)}={\left(IL\left(i\right)\right)}^T\hfill \end{array},$$ (Equation 22)

where IL(i) represents the ith row of matrix IL. ${(·)}^T$ represents matrix transposition.

Secondly, we applied attention mechanism⁴⁸ to learn the weights among miRNA nodes, disease nodes, and lncRNA nodes. Given that the center node u (u is a miRNA or disease node) connects the neighbor node $v$ based on the meta-path $\varnothing$, the importance of node v to node u based on meta-path $\varnothing$ can be calculated as follows:

$$e_{uv}^{\varnothing }=LeakyReLU\left({\left({\left(H_u\right)}^T·H_v\right)}_{\varnothing }\right),$$ (Equation 23)

where $LeakyReLU(·)$ is a nonlinear activation function (the slope of negative value is set to 0.2). After obtaining the importance between center node and neighbor nodes based on different meta-paths, we applied softmax function to normalize them to obtain the attention coefficients. The specific calculation process is shown as follows:

$$a_{uv}^{\varnothing }=softmax\left(e_{uv}^{\varnothing }\right)=\frac{exp\left(e_{uv}^{\varnothing }\right)}{{\sum }_{k\in N_u^{\varnothing }}exp\left(e_{uk}^{\varnothing }\right)},$$ (Equation 24)

where $N_u^{\varnothing }$ represents the first-order neighbor node set of node $u$ based on meta-path $\varnothing$.

Then, the embedding of node $u$ based on meta-path $\varnothing$ can be aggregated by the features of neighbor nodes and the attention coefficients as follows:

$$z_u^{\varnothing }=\sigma \left(\sum _{v\in N_u^{\varnothing }}{a}_{uv}^{\varnothing }·H_v\right),$$ (Equation 25)

where $\sigma (\cdot )$ represents the ELU activation function. Since the attention coefficients $a_{uv}^{\varnothing }$ was generated by meta-path $\varnothing$, $z_u^{\varnothing }$ was a semantic-specific node embedding and contained a kind of semantic information.

Heterogeneous graph has scale-free property, which leads to high variance of graph data. To reduce the variance and make the result more stable, we introduced the multi-head-attention mechanism to expand the node-layer attention. Concretely, we calculated node-layer attention K times and connected each node embedding as the semantic-specific embedding of node $u$. The specific calculation process is shown as follows:

$$\begin{array}{l}{z}_u^{\varnothing }=\begin{array}{l}K\hfill \\ \parallel \hfill \\ k=1\hfill \end{array}\sigma \left(\sum _{v\in N_u^{\varnothing }}{a}_{uv}^{\varnothing }·H_v\right)\hfill \end{array}.$$ (Equation 26)

In our experiment, the meta-path set includes the meta-path ${\varnothing }_{md}$ connecting miRNA and disease node, the meta-path ${\varnothing }_{ml}$ connecting miRNA and lncRNA node, the meta-path ${\varnothing }_{dm}$ connecting disease and miRNA node, and the meta-path ${\varnothing }_{dl}$ connecting disease and lncRNA node. After calculating the node-layer attention, we can obtain four groups of semantic-specific node embedding, which are $z^{{\varnothing }_{md}}$, $z^{{\varnothing }_{ml}}$, $z^{{\varnothing }_{dm}}$, and $z^{{\varnothing }_{dl}}$.

Semantic-layer attention

In the miRNA-disease-lncRNA heterogeneous graph, miRNA nodes and disease nodes contain a variety of semantic information. However, semantic-specific node embedding can only reflect semantic information of nodes from one aspect. To get a more comprehensive and sufficient node embedding, we proposed a novel semantic-layer attention to learn the importance of different meta-paths and integrated them into the central node. Firstly, we transformed the semantic-specific node embedding by a nonlinear transformation to obtain the importance of each meta-path. Then, we measured the importance of the semantic-specific node embedding as the similarity of transformed node embedding with a semantic-level attention vector q. Finally, we averaged the importance of semantic-specific node embedding as the importance of each meta-path. Therefore, the importance of meta-path ${\varnothing }_i$ can be calculated as follows:

$$w_u^{{\varnothing }_i}=\frac{1}{\left|V\right|}\sum _{u\in V}{q}^T·\tanh \left(W^{{\varnothing }_i}·z_u^{{\varnothing }_i}+b\right),$$ (Equation 27)

where $W^{{\varnothing }_i}$ denotes a weight matrix, $b$ denotes a bias vector, $tanh(·)$ denotes the activation function, and q denotes the semantic-layer attention vector and its dimension is set to 128. V denotes the number of nodes, which are of the same type as node u. Then, we normalized the importance of each meta-path by softmax function. Therefore, we can obtain the weight of meta-path ${\varnothing }_i$, which is denoted as ${\beta }_u^{{\varnothing }_i}$. The calculation process is shown as follows:

$${\beta }_u^{{\varnothing }_i}=\frac{exp\left(w_u^{{\varnothing }_i}\right)}{{\sum }_{j=1}^{P}exp\left(w_u^{{\varnothing }_j}\right)},$$ (Equation 28)

where $P$ represents the number of meta-path types associated with node u, and ${\beta }_u^{{\varnothing }_i}$ represents the contribution of meta-path ${\varnothing }_i$ to the central node $u$. We can know that if ${\beta }_u^{{\varnothing }_i}$ is larger, the meta-path ${\varnothing }_i$ is more important. Finally, we took the weights of the meta-paths as coefficients to calculate the final node embedding by aggregating the semantic-specific embedding. The calculation process is shown as follows:

$$Z_u=\sum _{i=1}^P{\beta }_u^{{\varnothing }_i}·z_u^{{\varnothing }_i}.$$ (Equation 29)

By the semantic-layer attention, we obtained the final embedding Z_m of miRNAs and the final embedding Z_d of diseases. Their dimensions are 64 × 495 and 64 × 383, respectively.

Bilinear decoder

For obtaining the prediction probability of the associations between miRNAs and diseases, we reconstructed the connections between miRNA nodes and disease nodes by adopting a bilinear decoder. Therefore, the prediction probability ${\hat{y}}_{ij}$ that a miRNA node $m\left(i\right)$ will be associated with a disease node $d\left(j\right)$ can be calculated as follows:

$${\hat{y}}_{ij}=sigmoid\left({\left(Z_{m\left(i\right)}\right)}^{T}Q{Z}_{d\left(j\right)}\right),$$ (Equation 30)

where Q denotes a trainable parameter matrix, the dimension of which is 64 × 64.

Finally, we used cross-entropy loss function to calculate the difference between the predicted value of our proposed model and the training samples. The calculation process of cross-entropy loss function LOSS is shown as follows:

$$LOSS=-\left(ylog\hat{y}+\left(1-y\right)log\left(1-\hat{y}\right)\right),$$ (Equation 31)

where y represents the true association labels between miRNAs and diseases. Since the smaller the cross-entropy loss, the better the prediction performance of the model. Therefore, we employed the back-propagation algorithm to train the model end-to-end to reduce the loss of the model and get the best results.