Skip to main content
PMC home page
RSC Advances logoLink to RSC Advances
. 2018 Jan 31;8(10):5321–5330. doi: 10.1039/c7ra13209c

Towards reliable quantification of hydroxyl radicals in the Fenton reaction using chemical probes†

Burgos Castillo Rutely C 1,3,✉, Fontmorin Jean-M 1, Tang Walter Z 2, Dominguez-Benetton Xochitl 3,4, Sillanpää Mika 1,2
PMCID: PMC9078104  PMID: 35542446

Abstract

Quantification of hydroxyl radical concentration using two chemical probes was assessed through the Fenton reaction. The probes were 1,2-benzopyrone (coumarin) for fluorescence and 5,5-dimethyl-1-pyrroline-N-oxide (DMPO) for electron spin resonance (ESR). The corresponding hydroxylated species, namely 7-hydroxycoumarin (7HC) and 2-hydroxy-5,5-dimethyl-1-pyrroline-N-oxide (DMPO-OH adduct), were monitored by fluorescence and ESR-spin trapping techniques, respectively. The experiments were designed according to the theoretical conditions determined for stable fluorescence and EPR signals. The results demonstrate that: the optimal [chemical probe] : [H2O2] ratio predicted by a simplified quasi-steady-state model was in good agreement with the optimal [chemical probe] : [H2O2] ratio observed experimentally for [H2O2] : [Fe2+] = 10, and the proper adjustment of the [chemical probe] : [H2O2] ratio at a given concentration of the Fenton's reagent improves the detected amount of hydroxyl radicals. Finally, using DMPO required a higher concentration compared to coumarin to yield the same amount of ˙OH detected but resulted in a more reliable probe for detecting ˙OH under the consideration of this study.

Quantification of hydroxyl radical concentration using two chemical probes was assessed through the Fenton reaction.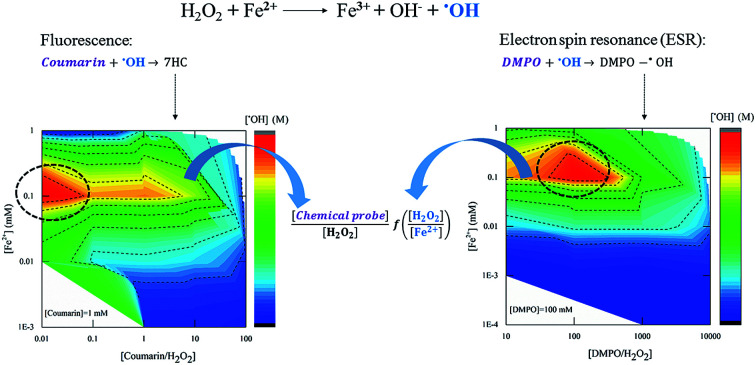graphic file with name c7ra13209c-ga.jpg

Introduction

Hydroxyl radicals (˙OH) are the most reactive oxygen species (ROS) and hence one of the most powerful oxidizing agents. ˙OH are ubiquitous in our environment and biological systems; they are also found in interstellar space,1 while they see ample industrial applicability here on Earth. For instance, ˙OH are widely recognized as atmospheric cleansers, and they are essential reaction chain initiators in most oxidation processes involving organic compounds. They play a key role as quenchers in futuristic self-propelled catalytic microjets,2 trigger destructive effects on cellular components, e.g., peroxidation of biomolecules, and are advantageous as essential components in advanced oxidation processes (AOPs) for water and wastewater treatment. Their strong oxidizing potential plays a key role in the degradation of organic pollutants and refractory compounds3–7 as well as on the precipitation of recalcitrant metal ions.8 However, their short lifetime of a few nanoseconds9 makes their direct detection and quantification challenging.

Indirect methods, such as probe-assisted spectroscopic techniques, are helpful to estimate the concentration of ˙OH.10–13 These methods follow the products formed from the reaction between ˙OH and the chemical probes, namely salicylic acid, 4-hydroxybenzoic acid, p-chlorobenzoic acid, phthalhydrazine, atrazine, deethylatrazine, p-nitrosodimethylaniline, n-propanol, coumarin, nitroxide compounds, dimethylsulfoxide (DMSO), among others.14,15 Nevertheless, since ˙OH radicals are non-selective oxidants, a large number of by-products have been detected when using those probes.14,16,17

Ideally, chemical probes to detect radicals like ˙OH would readily react with the targeted radical while remaining significantly unaffected by subsequent reactions, besides being innocuous, well-characterized and economical.18,19 Additionally, they should provide reproducibility and repeatability in the analysis of ˙OH.14 In other words, reliable detection and quantification of ˙OH require identification of conditions where the chemical probes are sensitive and selective to ˙OH while the formation of byproducts is limited, and wherein the reaction products to be measured do not react significantly with excess ˙OH or other reactive oxygen species (ROS) present in the media. Thus, providing long-term stability. The use of chemical probes for ˙OH detection and quantification should rely on the understanding of their chemical properties, their kinetic behaviour and their functionality in the conditions of interest.

The chemical environment in which ˙OH are generated is of paramount relevance.2 Its components may have an impact on the scavenging, decomposition or even on the acceleration of ˙OH production. For instance, even throughout a well-controlled Fenton's reaction (reaction (1)), wherein ferrous ions act with hydrogen peroxide to generate ˙OH, these effects have been evidenced. Peña et al. discussed the importance of the role that excess hydrogen peroxide plays as a scavenger of ˙OH (reaction (3)), thus decreasing their concentration at a faster rate than they are generated through the Fenton reaction. In addition, ferric and ferrous iron ions react with hydrogen peroxide (reaction (2) and (4)),20 thus having an ultimate impact on the generation, detection, and quantification of ˙OH.21

Fe2+ + H2O2 → Fe3+ + ˙OH + OH−, ki = 76 mol L−1 s−1 1
Fe2+ + ˙OH → Fe3+ + OH−, kt1 = 3 × 108 mol L−1 s−1 2
H2O2 + ˙OH → HO2˙ + H2O, kt2 = 2.7 × 107 mol L−1 s−1 3
Fe3+ + H2O2 → Fe2+ + H+ + HO2˙, kt3 = 3.1 × 10−3 mol L−1 s−1 4

Ciotti et al. observed an effect of the [Fe2+] : [H2O2] ratio on the amount of radicals formed. Although they employed a mathematical model to explain this behaviour, they did not consider the need of reaching a steady state to ensure the reliability of their method to quantify hydroxyl radicals,22 which leads to inaccurate results.

On the other hand, the work of Lindsey and Tarr11 pointed out at the possibility of finding optimal conditions in Fenton systems to successfully use chemical probes for ˙OH detection and quantification. However, since then, only a few works have attempted to rationalize the use of organic chemical probes in Fenton-based processes.

Organic chemical probes such as DMPO23,24 and coumarin10,25 exhibit low toxicity and good sensitivity, but their conditions of use have not yet rendered high selectivity in Fenton-based systems, showing variable behaviour from sample to sample or method to method, which needs to be calibrated every time.14 In the majority of studies, the probe concentration appears to be critical;11,13,26 skewed results can occur when chemical probes are used in concentrations at which the probability of reaction with the ˙OH available is either low or very high.11,15,16,26,27 Abou et al. investigated the use of DMSO in an electro-Fenton system. They concluded that DMSO would not be an appropriate probe because of the electrode reactions of DMSO.15

Furthermore, the sensitivity and reliability of organic chemical probes in the presence of complex matrices involving metals, anions, and cations like in AOP conditions, is not thoroughly assessed; thus, determining the concentration of radicals is still a challenging issue. Therefore, it is of significant value to investigate and predict systematically how, for specific systems and chemical environments, the key factors such as the concentrations of the major reactants and the chemical probe affect the detection of ˙OH under different operating conditions.

This study was designed as an approach to analyse and to establish appropriate relations between key parameters that influence the quantification of ˙OH: the concentrations of the Fenton's reagent and chemical probe. The detection of ˙OH was performed using two well-known chemical probes, namely coumarin and 5,5-dimethyl-1-pyrroline-N-oxide (DMPO). This information is useful to further understand in which conditions ˙OH detection and quantification can be feasible under ideal performance of Fenton systems (i.e., pH 3).28–31 Finally, this study may be immediately extrapolated to systematically investigate the use of other chemical probes which can reduce time and resources.

Experimental section

Chemicals

Ferrous sulfate heptahydrate (FeSO4·7H2O) and hydrogen peroxide (H2O2) were purchased from Merck (Darmstadt, Germany). 4-Hydroxy-2,2,6,6-tetramethylpiperidin-1-oxyl (TEMPOL), 1,2-benzopyrone (coumarin) and 7-hydroxycoumarin (umbelliferone) and catalase were purchased from Sigma-Aldrich (Darmstadt, Germany). 5,5-Dimethyl-1-pyrroline-N-oxide (DMPO) was provided by Cayman Chemical Company (Ann Arbor, USA). All reagents were of analytical grade and were used without further purification. The concentrations of stock solutions for Fenton reagents were: 4.5 M H2O2, 0.05 M FeSO4·7H2O, 1 M DMPO and 0.008 M coumarin. The pH of all stock solutions was adjusted to 3.0 ± 0.2 using concentrated sulfuric acid. All chemical solutions were prepared using ultra-pure water produced with a Millipore Milli-Q system and stored in amber flasks at laboratory +4 °C.

Sample preparation

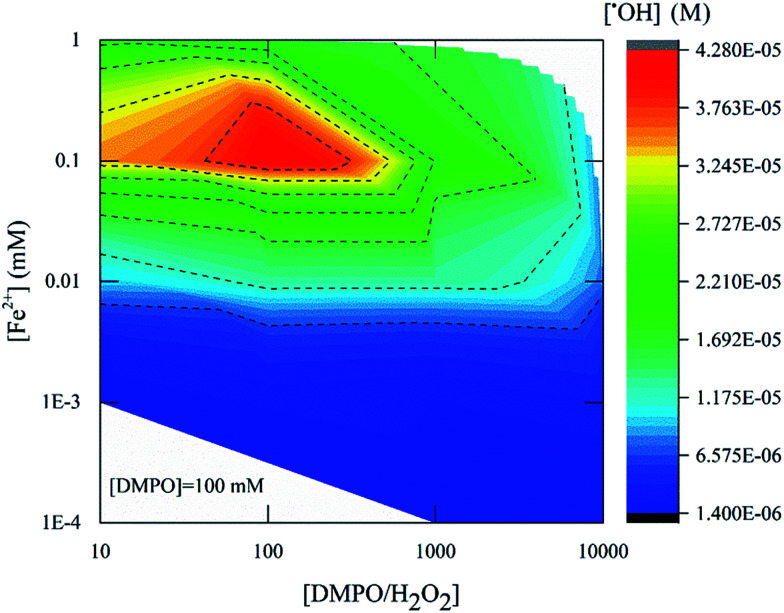
Electron Spin Resonance (ESR) experiments were conducted with H2O2 and Fe2+ concentrations varying from 0.1 mM to 10 mM, and from 0.001 mM to 1 mM, respectively. DMPO was employed at a fixed concentration of 100 mM. Different ratios of [H2O2] : [Fe2+], i.e., 10 : 1; 100 : 1; 1000 : 1; 10 000 : 1, and 100 000 : 1, were tested. Fenton reactions were performed by mixing reagents using a vortex, in the following order: ultra-pure water (adjusted to pH 3.0 ± 0.2 using concentrated sulfuric acid), H2O2, DMPO, and FeSO4·7H2O (total volume: 2 mL). The mixed reagents were allowed to react in the dark and samples were taken and analysed at times specified in the Results and discussion section.

Fluorescence experiments were conducted with H2O2, Fe2+, and coumarin concentrations varying from 1 mM to 100 mM, 0.001 mM to 10 mM, and 1 mM to 4 mM, respectively, using different ratios of [H2O2] : [Fe2+], i.e., 10 : 1; 100 : 1, and 1000 : 1. The difference in the [H2O2] : [Fe2+] ratios employed for detection with DMPO and coumarin is due to the lower solubility of coumarin compared to DMPO, as well as due to the difference in sensitivity of the fluorescence method, which is higher for coumarin. Fenton reactions were prepared by mixing reagents in desired proportions using a vortex, in the following order: ultra-pure water (adjusted to pH 3.0 ± 0.2 using concentrated sulfuric acid), H2O2, coumarin, and FeSO4·7H2O (volume: 2.5 mL). Blank experiments were recorded to verify that both ESR and fluorescence signals resulted from the reaction between the chemical probe and ˙OH. The mixed reagents were allowed to react in the dark and samples were taken at times presented in the Results and discussion section. All samples for DMPO-OH adduct were quenched by adding 100 μL of catalase dissolution immediately after taking the sample to achieve a final concentration of 0.2 mg L−1, pH of those samples increased to 5–6.24 Fluorescence samples were measured immediately thus no quencher was used as catalase decreased the signal when used.

Fluorescence and ESR analysis

Fluorescence measurements were performed using a Cary Eclipse spectrophotometer from Varian Corporation (Palo Alto, California, USA). The excitation wavelength was set at 340 nm, and the emission wavelength enveloped at 456 ± 2 nm; the excitation and emission slits were 10 and 5 nm, respectively. A calibration curve using 7-hydroxycoumarin (7HC) as a standard was constructed to quantify the 7HC formed as a result of the hydroxylation reaction between coumarin and ˙OH (reaction (5)). All samples were analysed at least in triplicate to build the calibration curves and the Fenton problem samples described in Table 2 were analysed at least in duplicate. All plots were prepared using Origin 2015.

graphic file with name c7ra13209c-t1.jpg 5

Fenton's reagent and coumarin concentrations used in this study.

Condition [H2O2] (mM) [Fe2+] (mM) [Coumarin] (mM) [Coumarin] : [H2O2]
Fenton A 1 0.1 0.5 0.5
Fenton B 1 0.1 1 1
Fenton C 1 0.1 2 2
Fenton D 1 0.1 4 4
Fenton E 1 0.1 0.05 0.05
Fenton F 1 0.1 0.1 0.1
Fenton G 0.1 0.01 0.1 1
Fenton H 0.1 0.01 0.5 5
Fenton I 0.1 0.01 1 10
Fenton J 10 0.1 1 0.1
Fenton K 1 0.01 1 1
Fenton L 10 0.01 1 0.1
Fenton M 10 1 1 0.1
Fenton N 100 0.1 1 0.01
Open in a new tab

The concentration of the DMPO-OH adduct, generated from the reaction between DMPO and ˙OH (reaction (6)), was measured with an ESR spectrometer CMS-8400 from ADANI, Minsk, Belarus. The ESR spectrometer operated at 9.450 GHz with 0.100 mT magnetic field modulation. The instrumental parameters were: center field 336.5 ± 6.0 mT, power attenuation 10 dB, sweep time 100 s, and 4096 data points.

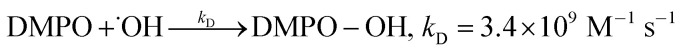graphic file with name c7ra13209c-t2.jpg 6

To analyse quantitatively the DMPO-OH adduct signal intensity, TEMPOL was used as the standard. TEMPOL was selected as an ESR standard due to its relative stability and solubility in water.32 From ESR spectra, DMPO-OH adduct and TEMPOL intensities were measured as the peak-to-peak amplitude. TEMPOL concentrations were varied from 2.5 × 10−6 M to 12.5 × 10−6 M in the same conditions as Fenton reactions, and both samples and standards were measured under non-saturating conditions. ESR parameters of the DMPO-OH adduct and TEMPOL were determined using EasySpin software 5.0.33 When required, dilution factors were applied to the samples. All plots were prepared using Origin 2015 and MATLAB R2015b software.

Calibration curves

The concentration of 7HC was quantified from the fluorescence intensity and was used to determine the ˙OH concentration. The reaction yield between coumarin and ˙OH to form 7HC (reaction (5)) was reported as 4.7% by Newton and Milligan.17 The fraction of ˙OH not leading to 7HC generates other hydroxylated compounds which are not fluorescent, and are thus not detected by the technique used.17,34 Therefore the yield fraction of 4.7% was taken into account for the calculations of radicals generated during the Fenton experiments. Typical spectra of the fluorescence intensity of 7HC standard and the constructed calibration curve are described in Fig. S1.†

The ESR signal of the DMPO-OH adduct was expressed relative to the concentration of the stable radical TEMPOL.35 All ESR spectra exhibited typical hyperfine coupling constants of the DMPO-OH quartet (aβH = aN = 1.47 mT) and the TEMPOL triplet (aN = 1.68 mT).35,36 The ESR peak-to-peak intensity of TEMPOL increased with the increasing dosage. ESR spectra recorded for DMPO-OH adduct and TEMPOL and the built calibration curve are depicted in Fig. S2 and S3,† respectively.

Equations for the determination of the chemical probe concentration

To gain insight into the use of chemical probes for measuring ˙OH generation, eqn (7) and (8)—derived from a kinetic model proposed in our earlier work—were used. The agreement between the theoretical [chemical probe] : [H2O2] ratio against the experimental one was analysed, in order to obtain a reliable signal by either fluorescence or ESR.24

The model assumed quasi-steady-state concentrations. As a consequence, some important conditions must be satisfied in order to generate stable signals: (i) the rate of change of the reaction product (i.e., DMPO-OH adduct, 7HC) with respect to time approaches zero;24 (ii) the rate of change of the reaction product with respect to time is not a function of the concentration of the chemical probe;24 (iii) the reaction product to be followed does not degrade significantly during the time frame of the analysis; otherwise, the conditions are not favorable for ˙OH detection.11,17,23

Eqn (7) and (8) were developed in terms of elementary reactions for coumarin and DMPO, respectively. The respective contributions of the reaction rates from side reactions were set at zero. Thus these equations are simplified to reflect the contribution of the [H2O2] : [Fe2+] ratio and the chemical probe concentration to produce a constant signal under quasi-steady-state conditions, as previously demonstrated.24

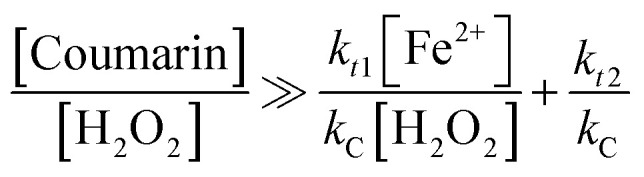graphic file with name c7ra13209c-t3.jpg 7
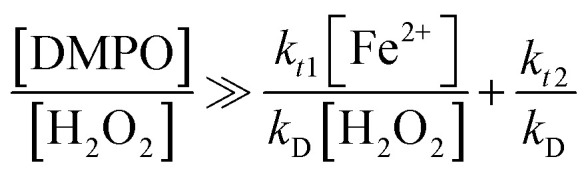graphic file with name c7ra13209c-t4.jpg 8

where: kt1 (rate constant of reaction (2)), kt2 (rate constant of reaction (3)), are rate constants of ˙OH quenching reactions in the Fenton mechanism;23kC (5.6 × 109 M−1 s−1), kD (3.4 × 109 M−1 s−1) are formation rate constants of 7HC and DMPO-OH adduct, respectively.

According to the discussions in our previous work,24 to obtain stable signals by fluorescence and ESR, the left-hand ratios from eqn (7) and (8) ([chemical probe] : [H2O2]) should be significantly greater, i.e., by at least two to three orders of magnitude higher than the corresponding right-hand ratios. In the case of DMPO, this hypothesis was already confirmed with initial concentrations of 1 mM H2O2 and 0.1 mM Fe2+ (i.e., [H2O2] : [Fe2+] = 10 and right-hand ratio of eqn (8) equals 0.0168). Experiments confirmed that [DMPO] : [H2O2] ratio should be at minimum 16.8 in order to obtain a stable DMPO-OH adduct signal.24 However, the susceptibility of the DMPO signal to change with the probe concentration was not previously validated, and thus the [chemical probe] : [H2O2] ratios and that the amount Fenton's reagent can be still optimized. Besides, this work makes progress beyond the current state of the art by: (1) providing further analysis to establish the suitable values of chemical probe which can render a stable analytical response, and (2) finding optimal concentrations of iron that can be used as catalyst for Fenton reactions in the conditions studied.

Table 1 shows the theoretical [chemical probe] : [H2O2] values predicted, at different Fenton's reagent ratios using 1 mM coumarin. In these calculations, the Fe2+ concentration was varied at given concentrations of H2O2 (from 10−2 M to 10−4 M). For example, for [H2O2] : [Fe2+] = 10, the threshold [coumarin] : [H2O2] ratio is 1.02 (Table 1) which was taken as two orders of magnitude higher than the value calculated from eqn (7) (i.e. 0.0102). Thus the experiments were designed and carried out in order to validate the hypothesis suggested by the theoretical model and to verify whether this model can also be applied to coumarin.

Theoretical [coumarin] : [H2O2] ratios predicted from eqn (7), for a set of proposed [H2O2] : [Fe2+] ratios.

Ratio Theoretical ratio
[H2O2] : [Fe2+] [Coumarin] : [H2O2]a
10 1.02
100 0.54
1000 0.49
Open in a new tab
a

From right hand side of eqn (7).

Results and discussion

Validation of the equations proposed to determine optimal chemical probe concentration

To validate the conditions suggested from eqn (7) in Fenton systems, three different sets of experiments were carried out by varying the Fenton's reagent ratio and coumarin concentration. The first set of experiments measured the concentration of 7HC with respect to time, by varying coumarin concentration. The conditions applied in this section are described in Table 2. The experiments lasted for up to 60 min at a fixed [H2O2] : [Fe2+] ratio of 10 and varying coumarin concentrations from 0.5 mM to 4 mM (Fig. 1). According to the theoretical model described above (eqn (7)), the optimal [coumarin] : [H2O2] ratio was expected to be at minimum 1 to 10. Experiments were carried out to validate the values calculated by the model.

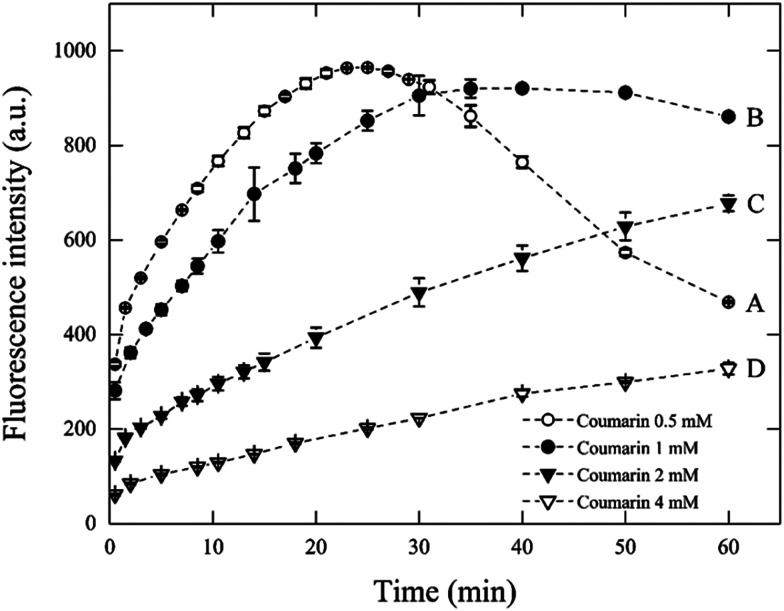
Fig. 1. Effect of coumarin concentration on fluorescence intensity during 60 min for Fenton reaction with 1 mM H2O2 and 0.1 mM Fe2+.

Fig. 1

Open in a new tab

In principle, it may be expected that the formation of ˙OH would occur at the same rate in all these four systems (A–D), given that the same concentrations and ratios of Fenton's reagent were used. However, it has been discussed that changes in initial probe concentration will result in a shift in probe response even at constant radical flux.18 Thus, these results suggest that once the ˙OH are formed, it is the rate of their reaction with coumarin which is, in fact different as the coumarin concentration changes, presumably driven by mass transfer limitations. Because for every molecule of coumarin and ˙OH to react, these must come into intimate contact with each other. Although good mixing increases the chances of interaction, the concentration of coumarin molecules implies a delayed rate for their reaction with ˙OH when coumarin appears to be in large excess (i.e., systems C and D). As depicted in Fig. 1, with condition A, the chemical probe concentration appeared to be underdosed and resulted in a non-steady state concentration of 7HC. In this system, the signal decreased fast after the first 20 min of reaction.

It is inferred that coumarin is first hydroxylated into 7HC during the first 20 min. Yet, the disappearance of 7HC can be attributed to the relative excess of homogeneous reactive oxygen species (mainly ˙OH, and to a lesser extent H2O2, HO2˙) which can further attack the π-electron-rich position of the hydroxylated primary byproducts formed to render different molecules than 7HC which either may not fluoresce or may be easily degraded to smaller molecules such as carboxylic acids.10,26,37,38 The swift degradation of 7HC is feasible, and the conditions are here clearly identified. This is a fundamental step to prevent 7HC to react significantly with ˙OH for reliable measurements.

The fluorescence response of system B ([coumarin] : [H2O2] ratio of 1), reached a maximum value after 30 min, then remained relatively stable until 50 min in contrast to the other tests. These results may indicate the establishment of a quasi-steady-state concentration of 7HC, wherein a 1 mM coumarin concentration would be suitable for the detection of radicals up to 30 min, where the accumulated concentration of 7HC could be considered constant and maximum.

From these data, the hypothetical [coumarin] : [H2O2] ratio calculated from the theoretical model (eqn (7)) appears to be in good agreement with the experimental one, i.e., for [H2O2] : [Fe2+] = 10, the right-hand ratio of eqn (7) equals 0.0102 which means that [coumarin] : [H2O2] must be at minimum 1.02 in order to obtain a stable fluorescence signal.

In conditions C and D (i.e., [coumarin] : [H2O2] > 1), the amount of 7HC was lower, thus using a higher coumarin concentration does not result in more efficient radical detection. This behaviour has been previously shown.26 However, it was overlooked by the authors, and hence it remained unexplored.

In general, as the same concentration and ratio of Fenton's reagent were kept constant in all systems, the rate-limiting step of the process is the reaction of ˙OH with coumarin. If there would be no other effects, then all cases should give the same response up to the point where either coumarin or ˙OH are exhausted. Moreover, the hypothesis derived from our model (eqn (7)) suggests that an optimum coumarin concentration to detect ˙OH must be established. The effect of coumarin concentration can be explained as follows. First, when coumarin concentration is higher as in C and D, part of the 7HC concentration may react rapidly with ˙OH and compete with reaction of ˙OH with coumarin. ˙OH can be consumed by coumarin, coumarin byproducts and scavengers. Thus, the concentration of ˙OH, [˙OH], can change with time, as the concentration of organics change. Therefore, the fluorescence response may be poorer—given that it will take a longer time for coumarin to effectively collide with a ˙OH molecule; otherwise, part of the emission energy of the fluorophores may decrease by self-quenching.18,39,40 As a consequence, a decreasing fluorescence signal resulted when coumarin increased from 2 mM (system C) to 4 mM (system D). At optimal coumarin concentrations, which may be between systems B and C, the quasi-steady-state is promoted as a stoichiometric ratio of coumarin is used. Finally, when coumarin concentration is lower, it gets rapidly exhausted from the reaction system A. Thus the fluorescence signal decay was observed, as explained before. From, these kinetic profiles we can conclude the following statements in which the profiles from Fig. 1 seem to exhibit four kinetic regimes: (i) very fast kinetic effect on the first two minutes, (ii) after the first two minutes and up to a certain point around 20 min, the profile is specific for each case, (iii) after the first 20 min, it appears a change in slope to a slower rate as coumarin concentration increases, which leads to an inflection point (system A), steady state (system B) or to a decrease in rate (systems C and D), (iv) the slower rate, may be due to a low concentration of coumarin (after 20 min) which may promote the reaction between 7HC and excess radicals. This fact is evident in the system A.

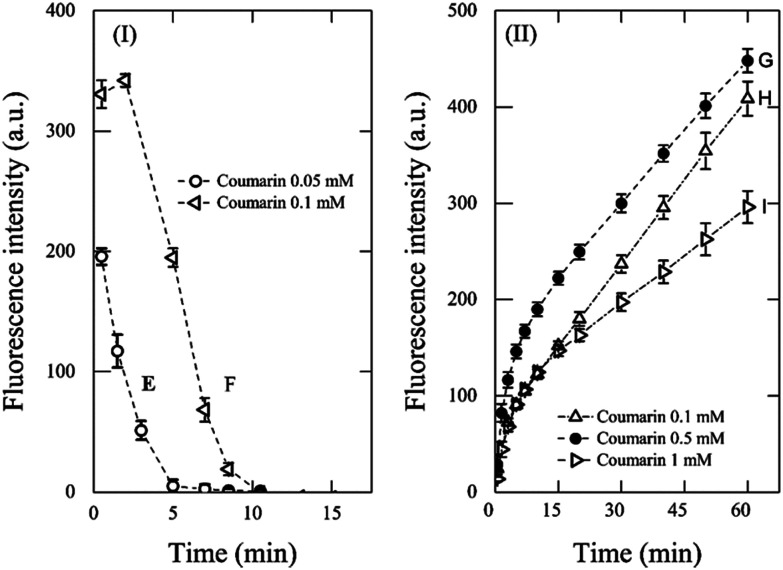
To further assess the effect of the coumarin concentration and the role of the initial concentration of Fenton's reagent on the kinetic profile, a second set of experiments was carried out using conditions E–I, with [H2O2] : [Fe2+] kept at a value of 10 (Fig. 2). In those tests, the fluorescence signal evolved into a combination of two opposite trends and was dependent on both the initial coumarin concentration and the initial concentration of Fenton's reagent. As it was expected with conditions E and F (Fig. 2I), the fluorescence intensity decreased, which occurred during the first 15 min. It confirms that the underdosed coumarin is rapidly depleted by ˙OH to form 7HC, the last being further hydroxylated to non-fluorescent species by ˙OH that kept forming as described previously.

Fig. 2. Effect of coumarin concentration on fluorescence intensity over time for Fenton reaction with [H2O2] : [Fe2+] = 10: (I) 1 mM H2O2 and 0.1 mM Fe2+ and (II) 0.1 mM H2O2 and 0.01 mM Fe2+.

Fig. 2

Open in a new tab

When the concentration of Fenton's reagent was reduced by a factor of ten (i.e., 0.1 mM H2O2 and 0.01 mM Fe2+, Fig. 2II) and the coumarin concentration used at conditions G–I, corresponded to 0.1 mM, 0.5 mM, and 1 mM, respectively, the fluorescence signals showed a tendency to increase through time. However, these systems did not reach a quasi-steady-state concentration of 7HC during 60 min of reaction. In addition, as the coumarin concentration increased from 0.1 mM to 1 mM (i.e., [coumarin] : [H2O2] > 1), the signal intensity decreased as depicted in Fig. 2. This can be explained by ineffective collisions between both Fenton's reagent to render ˙OH and coumarin to react with ˙OH, while the reason because the plateau was not reached is due to excess coumarin with respect to Fenton's reagent.

From the above discussions, 1 mM coumarin was determined to be the most suitable concentration to estimate the concentration of ˙OH (Fig. 1B) for an initial concentration of 1 mM H2O2 and 0.1 mM Fe2+, which can render suitable kinetic profiles.

Effects of Fenton's reagent ratio and coumarin concentration

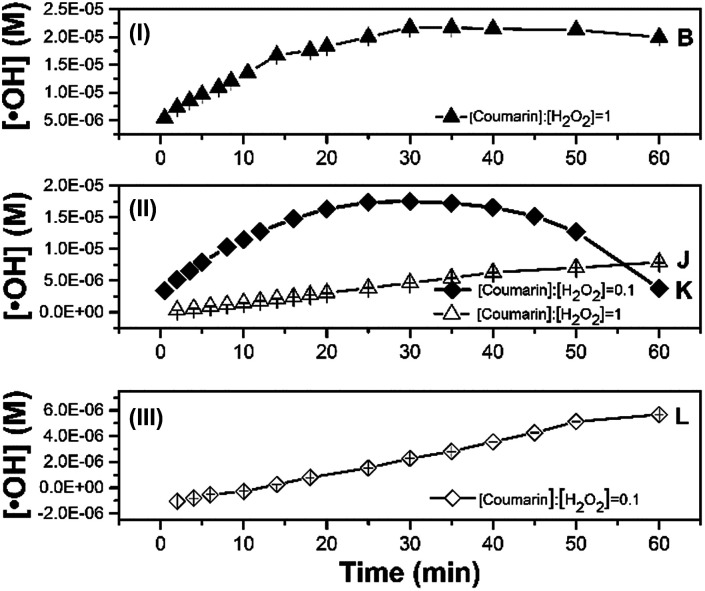
The concentration of ˙OH was determined to investigate the effect of different Fenton's reagent ratios on the optimal coumarin concentration to be applied (Fig. 3). The left-hand ratios of eqn (7), calculated with different Fenton's reagent ratios, are given in Table 1. Each experiment lasted 60 min. As the [H2O2] : [Fe2+] ratio increased (conditions B, J, K, L, M described in Table 2), the concentration profile through time for the detection of radicals changed with the [coumarin] : [H2O2] ratio (Fig. 3).

Fig. 3. Time-dependent effect of the [H2O2] : [Fe2+] ratio on molar ˙OH detection by 1 mM coumarin concentration for 60 min at Fenton's reagent ratios of (I) 10, (II) 100 and (III) 1000. The size of some error bars are in the same scale than the symbols used.

Fig. 3

Open in a new tab

At [H2O2] : [Fe2+] = 10 (Fig. 3I), the ratio [coumarin] : [H2O2] = 1 determined experimentally concurred with the [coumarin] : [H2O2] ratio calculated using eqn (7) (Table 1). From these experiments, it was noticeable that the system M exhibited a similar behaviour to conditions E and F.

In these conditions, the trend across time showed a sudden reduction of the fluorescence intensity after four minutes of reaction time (Fig. S4†). At a Fenton's ratio of 100, under conditions J and K (Fig. 3II), corresponding to [coumarin] : [H2O2] ratios of 0.1 and 1, respectively, the experimental [coumarin] : [H2O2] ratio differed from those calculated from eqn (7). In those systems, the predicted [coumarin] : [H2O2] using eqn (7) should be at least ∼0.54 (Table 1), suggesting that using 0.54 ratio as optimum [coumarin] : [H2O2] value may render a suitable concentration profile. These results also revealed that the initial amount of ˙OH detected was around 3.6 times higher with condition J than with condition K around the first four minutes. It should be noted that the maximum amount of ˙OH in both systems was of the same order of magnitude (∼10−5 M). Thus, the optimal detection of ˙OH could be achieved at optimal [coumarin] : [H2O2] ratios keeping [Fe2+] at its optimal value (∼0.1 mM in this work).

At higher Fenton's ratio of 1000, under condition L (Fig. 3III), the formation of radicals was lower, showing a behaviour similar to that under condition J. This may be related to a slow reaction rate between Fenton's reagent, resulting in less formation of ˙OH. The second order rate constant for hydroxylation of coumarin (5.6 × 109 M−1 s−1 (ref. 17)) by ˙OH may imply that a higher concentration of ˙OH has to be available to promote effective collisions with coumarin. In turn, a higher initial concentration of Fenton's reagent and the adjusted coumarin concentration are required to obtain suitable profiles for ˙OH detection and quantification. As a result, systems J and L, with a higher Fenton's reagent ratio and non-optimized [coumarin] : [H2O2] ratio, were less efficient at detection radicals over a period of 60 min, without reaching a plateau (quasi-steady-state) zone. Therefore, the fact that the [coumarin] : [H2O2] ratio needs to be optimized as the initial concentration of Fenton's reagent varies may be closely related to the different mechanisms that control the overall reaction as the [H2O2] : [Fe2+] changes.41 For example, at high [H2O2] : [Fe2+] ratios the large amount of H2O2 added can act as scavenger for the generated ˙OH (reaction (2)), while at low [H2O2] : [Fe2+] ratios the catalytic conversion of H2O2 to ˙OH may increase but not the reaction with coumarin because of the promotion of scavenging reactions (reactions (2) and (3)).42

Analysis of the amount of ˙OH detected after one minute of mixing the reagents confirmed this behaviour (Fig. S5†). At an initial H2O2 concentration of 1 mM, a higher ˙OH concentration (7.7 × 10−6 M) was achieved during the early phase of reaction (first minutes) with [H2O2] : [Fe2+] = 10 corresponding to condition B, while the amount of ˙OH detected decreased as the Fenton's reagent ratio increased from 100 to 1000 (Fig. S5I†), as observed in Fig. 3. At an initial H2O2 concentration of 10 mM, the maximum initial formation of radicals was detected under condition K, and resulted in an analogous magnitude than that obtained with 1 mM H2O2 (7.7 × 10−6 M, Fig. S5II†). This again suggests that the coumarin concentration should be optimized in relation to the initial concentration of Fenton's reagent, to achieve suitable reaction rates between ˙OH and coumarin.

It seems that reasonable predictions of the [coumarin] : [H2O2] ratio can be made using the equations derived from the simplified quasi-steady-state model proposed. These results suggest that the optimum [coumarin] : [H2O2] ratios, initial [H2O2] and iron Fe2+ amount must be adjusted to achieve suitable concentration profiles that allow greater detection of ˙OH as predicted by the model proposed (Table 1), wherein 7HC does not react significantly with ˙OH. It should be noted from these results that:

(i) The ratio of Fenton's reagent ratios to generate and detect ˙OH using fluorescence (such as [H2O2] : [Fe2+] = 10, 100 and 1000) appeared to be less significant than the [coumarin] : [H2O2] ratio as predicted. Those [H2O2] : [Fe2+] ratios have rendered good level of ˙OH and are consistent with those typically employed in water treatment processes.39

(ii) The [coumarin] : [H2O2] ratio needs to be adjusted as the initial concentration of Fenton's reagent changes; thus, in this work is suggested that the best level of detection of ˙OH is achieved at [coumarin] : [H2O2] = 1, when [H2O2] : [Fe2+] = 10 and Fe2+ concentration is 0.1 mM.

(iii) Under condition M, the theoretical [coumarin] : [H2O2] ratio was not applicable. This bias may be closely related to the fact that: (a) H2O2 was excessive compared to coumarin, thus leading to excess ˙OH formation that caused degradation of the reaction product 7HC into non-fluorescent compounds.

(iv) It was also observed that a ferrous iron concentration of 0.1 mM played a significant role in the amount of ˙OH detected. This value is in the order of magnitude that other works have found as the optimal operative condition to generate ˙OH in electro-Fenton systems.20

Response of coumarin and DMPO as probes for the detection of ˙OH

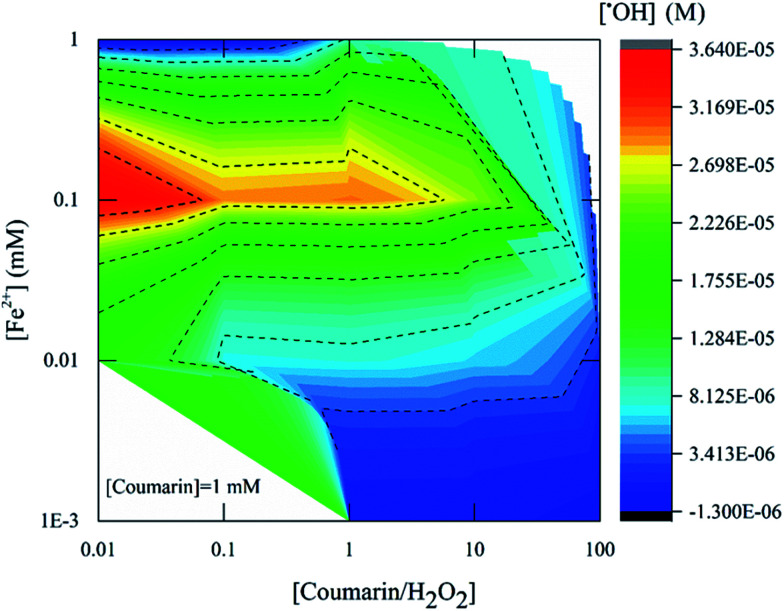
To evaluate the response of different chemical probes at conditions established as suitable from the previous analysis, two independent matrices of experiments were performed using a fixed concentration of chemical probes: 1 mM coumarin and 100 mM DMPO for fluorescence and ESR, respectively. The Fenton's reagent ratio of [H2O2] : [Fe2+] was varied from 1 to 104, and the equivalent concentration of ˙OH detected by fluorescence and ESR are depicted accordingly in Fig. 4 and 5. In our previous work, the response of DMPO under a fixed ratio of Fenton's reagent was tested.24 In this section, the concentration of chemical probe is kept constant, and the Fenton's reagent ratio is different.

Fig. 4. Equivalent concentration of ˙OH formed as a function of the Fenton's reagent ratio using 1 mM coumarin. All data were measured 22.5 min after mixing the reagents using 7-hydroxycoumarin (7HC) as a standard. The x-axis and y-axis are presented on logarithmic scales.

Fig. 4

Open in a new tab

Fig. 5. Equivalent concentration of ˙OH formed as a function of the Fenton's reagent ratio at constant DMPO adduct probe concentration (100 mM) using TEMPOL as a standard. All data were measured 4 min after mixing the reagents. The x-axis and y-axis are presented on logarithmic scales.

Fig. 5

Open in a new tab

The concentration of ˙OH detected by fluorescence using coumarin as a probe was measured 22.5 min after mixing Fenton's reagent with coumarin (Fig. 4). The highest product yield was approximately 3.0 × 10−5 M and measured with [H2O2] : [Fe2+] = 10 (condition B). For [H2O2] : [Fe2+] = 100, the highest product yield was around 3.0 × 10−5 M (condition K) while for [H2O2] : [Fe2+] = 1000 the concentration of ˙OH detected was 3.6 × 10−5 M (condition N). These results also showed that the detection of radicals involved an initial Fe2+ concentration of around 0.1 mM, which corresponds to a ratio of 10, 100 and 1000 in respect to H2O2 concentration (Fig. 5, red zone) as noted previously.

Fig. 5 presents the amount of ˙OH detected by ESR with different concentrations of Fenton's reagent and using 100 mM DMPO as a probe. The [H2O2] : [Fe2+] ratio was varied from 10 to 104, and the equivalent ˙OH amount was measured four min after mixing Fenton's reagent and DMPO. The highest product yield at [H2O2] : [Fe2+] = 10 was 4.2 × 10−5 M. With [H2O2] : [Fe2+] = 100, the highest product yield was around 1.3 × 10−5 M while for [H2O2] : [ Fe2+] = 1000, the yield was 2.7 × 10−6 M. From these results it can be concluded that an effective ˙OH detection was rendered at a Fenton's reagent ratio of 10 (Fig. 5, red zone).

Finally, a comparison between the coumarin and DMPO results revealed that the magnitude of maximum ˙OH detected was of the same order of magnitude as 3.6 × 10−5 M and 4.3 × 10−5 M respectively. This may imply that at a ratio of [H2O2] : [Fe2+] = 10 and at [chemical] : [H2O2] ratio of at least two orders of magnitude higher than the right side of eqn (7) and (8) would help acquiring a stable analytical signal for measurements of ˙OH. However, some differences can be highlighted: (i) the concentration of chemical probe required for ESR and fluorescence suggests that the ESR method consumes as much as 100 times or more DMPO concentration than the needed with coumarin and (ii) the time required to detect an equivalent molar concentration of ˙OH is longer for coumarin than for DMPO, 22.5 min and 4 min respectively. Those times were determined from the kinetic profile, where the system appeared to be stable as it reached a stable state (plateau, Fig. 1B). In addition, the coumarin concentration needed could limit its application under the conditions required in Fenton-based systems.

Therefore further analysis using this technique testing different probes other than non-modified coumarin could be useful as it involves inexpensive reagents, a wide linear range, and is user-friendly compared to the ESR technique.

These data showed the impact of [H2O2] : [Fe2+] ratio on the amount of ˙OH detected. The optimal [H2O2] : [Fe2+] ratio for detection of ˙OH in both techniques was between [H2O2] : [Fe2+] = 10 (Fig. 4 and 5). It is also suggested that the relationship between the chemical probe concentration needed and the ˙OH formed should be between values of initial concentration of Fenton's reagent that does not promote the further oxidization of the reaction byproduct to be monitored such as 7HC or DMPO-OH adduct.

Conclusions

This study investigated the application of both coumarin and DMPO as probes to measure hydroxyl radicals by fluorescence and ESR respectively. Hydroxyl radicals were produced by Fenton's reactions.

The effect of the Fenton's reagent ratio (up to 103) and the [chemical probe] : [H2O2] ratio on the quantification of hydroxyl radical concentrations was experimentally determined. On the basis of the experimental results, the following conclusions can be drawn:

• Coumarin is a good chemical probe around 1 mM and initial concentration of 1 mM H2O2 and 0.1 mM Fe2+ because excess can promote either collisions between two coumarins or two fluorophores (7HC) which will render a poor fluorescence signal.

• For reliable quantification of ˙OH, the [coumarin] : [H2O2] ratio should be two orders greater than the right-hand side of eqn (7) at [H2O2] : [Fe2+] = 10.

• Degradation of 7HC in the presence of excess ˙OH may involve a further hydroxylation reaction into non-fluorescent derivatives.

• A ferrous iron concentration of 0.1 mM independently of the chemical probes tested, played a significant role in the amount of ˙OH generated and detected.

• The optimal [H2O2] : [Fe2+] ratio used in the detection of ˙OH in both techniques fluorescence and ESR was observed to be [H2O2] : [Fe2+] = 10.

• Finally, using DMPO required a higher concentration than coumarin to yield the same amount of ˙OH detected but resulted being a more reliable probe for detecting ˙OH under the consideration of this study.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

RA-008-C7RA13209C-s001

Acknowledgments

We would like to thank the support given by the Finnish Funding Agency for Innovation. Thanks to Prof. Enric Brillas for his valuable advice. XD thanks VITO Strategic Research Funds for supporting her contributions to this article, as well as the Strategic Initiative Materials (SIM) in Flanders, within the recyclable materials MaRes program, under grant agreement no. 150626 (Get-A-Met project), and the European Union's Horizon 2020 research and innovation programme under grant agreement no. 654100 (CHPM2030 project).

†

Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra13209c

Notes and references

  1. Robinson B. J. Hydroxyl radicals in space. Sci. Am. 1965;213(1):26–33. doi: 10.1038/scientificamerican0765-26. [DOI] [Google Scholar]
  2. Zhao G. Sanchez S. Schmidt O. G. Pumera M. Poisoning of bubble propelled catalytic micromotors: the chemical environment matters. Nanoscale. 2013;5(7):2909–2914. doi: 10.1039/C3NR34213A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Chaplin B. P. Critical review of electrochemical advanced oxidation processes for water treatment applications. Environ. Sci.: Processes Impacts. 2014;16(6):1182–1203. doi: 10.1039/c3em00679d. [DOI] [PubMed] [Google Scholar]
  4. Cheng M. Zeng G. Huang D. Lai C. Xu P. Zhang C. et al., Hydroxyl radicals based advanced oxidation processes (AOPs) for remediation of soils contaminated with organic compounds: A review. Chem. Eng. J. 2016;284:582–598. doi: 10.1016/j.cej.2015.09.001. [DOI] [Google Scholar]
  5. Gligorovski S. Strekowski R. Barbati S. Vione D. Environmental Implications of Hydroxyl Radicals (˙OH) Chem. Rev. 2015;115(24):13051–13092. doi: 10.1021/cr500310b. [DOI] [PubMed] [Google Scholar]
  6. Han S.-K. Nam S.-N. Kang J.-W. OH radical monitoring technologies for AOP advanced oxidation process. Water Sci. Technol. 2002;46(11–12):7–12. [PubMed] [Google Scholar]
  7. Radjenovic J. Sedlak D. L. Challenges and Opportunities for Electrochemical Processes as Next-Generation Technologies for the Treatment of Contaminated Water. Environ. Sci. Technol. 2015;49(19):11292–11302. doi: 10.1021/acs.est.5b02414. [DOI] [PubMed] [Google Scholar]
  8. Lewinsky A. A., Hazardous Materials and Wastewater: Treatment, Removal and Analysis, Nova Publishers, 2007, p. 394 [Google Scholar]
  9. Brillas E. Sirés I. Oturan M. A. Electro-Fenton Process and Related Electrochemical Technologies Based on Fenton's Reaction Chemistry. Chem. Rev. 2009;109(12):6570–6631. doi: 10.1021/cr900136g. [DOI] [PubMed] [Google Scholar]
  10. Lin Z.-R. Zhao L. Dong Y.-H. Quantitative characterization of hydroxyl radical generation in a goethite-catalyzed Fenton-like reaction. Chemosphere. 2015;141:7–12. doi: 10.1016/j.chemosphere.2015.05.066. [DOI] [PubMed] [Google Scholar]
  11. Lindsey M. E. Tarr M. A. Quantitation of hydroxyl radical during Fenton oxidation following a single addition of iron and peroxide. Chemosphere. 2000;41(3):409–417. doi: 10.1016/S0045-6535(99)00296-9. [DOI] [PubMed] [Google Scholar]
  12. Tai C. Xiao C. Zhao T. Wu L. Han D. Determination of hydroxyl radicals photochemically generated in surface waters under sunlight by high performance liquid chromatography with fluorescence detection. Anal. Methods. 2014;6(20):8193–8199. doi: 10.1039/C4AY01300J. [DOI] [Google Scholar]
  13. Xiang Q. Yu J. Wong P. K. Quantitative characterization of hydroxyl radicals produced by various photocatalysts. J. Colloid Interface Sci. 2011;357(1):163–167. doi: 10.1016/j.jcis.2011.01.093. [DOI] [PubMed] [Google Scholar]
  14. Fernández-Castro P. Vallejo M. San Román M. F. Ortiz I. Insight on the fundamentals of advanced oxidation processes. Role and review of the determination methods of reactive oxygen species. J. Chem. Technol. Biotechnol. 2015;90(5):796–820. doi: 10.1002/jctb.4634. [DOI] [Google Scholar]
  15. Abou Dalle A. Domergue L. Fourcade F. Assadi A. A. Djelal H. Lendormi T. et al., Efficiency of DMSO as hydroxyl radical probe in an Electrochemical Advanced Oxidation Process – Reactive oxygen species monitoring and impact of the current density. Electrochim. Acta. 2017;246(suppl. C):1–8. doi: 10.1016/j.electacta.2017.06.024. [DOI] [Google Scholar]
  16. Marriott P. R. Perkins M. J. Griller D. Spin trapping for hydroxyl in water: a kinetic evaluation of two popular traps. Can. J. Chem. 1980;58(8):803–807. doi: 10.1139/v80-125. [DOI] [Google Scholar]
  17. Newton G. L. Milligan J. R. Fluorescence detection of hydroxyl radicals. Radiat. Phys. Chem. 2006;75(4):473–478. doi: 10.1016/j.radphyschem.2005.10.011. [DOI] [Google Scholar]
  18. Wardman P. Fluorescent and luminescent probes for measurement of oxidative and nitrosative species in cells and tissues: Progress, pitfalls, and prospects. Free Radicals Biol. Med. 2007;43(7):995–1022. doi: 10.1016/j.freeradbiomed.2007.06.026. [DOI] [PubMed] [Google Scholar]
  19. Workman P. Collins I. Probing the Probes: Fitness Factors For Small Molecule Tools. Chem. Biol. 2010;17(6):561–577. doi: 10.1016/j.chembiol.2010.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Brillas E. Banos M. A. Camps S. Arias C. Cabot P.-L. Garrido J. A. et al., Catalytic effect of Fe2+, Cu2+ and UVA light on the electrochemical degradation of nitrobenzene using an oxygen-diffusion cathode. New J. Chem. 2004;28(2):314–322. doi: 10.1039/B312445B. [DOI] [Google Scholar]
  21. Peña R. C. Silva V. O. Quina F. H. Bertotti M. Hydrogen peroxide monitoring in Fenton reaction by using a ruthenium oxide hexacyanoferrate/multiwalled carbon nanotubes modified electrode. J. Electroanal. Chem. 2012;686(suppl. C):1–6. doi: 10.1016/j.jelechem.2012.08.037. [DOI] [Google Scholar]
  22. Ciotti C. Baciocchi R. Tuhkanen T. Influence of the operating conditions on highly oxidative radicals generation in Fenton's systems. J. Hazard. Mater. 2009;161(1):402–408. doi: 10.1016/j.jhazmat.2008.03.137. [DOI] [PubMed] [Google Scholar]
  23. Finkelstein E. Rosen G. M. Rauckman E. J. Spin trapping. Kinetics of the reaction of superoxide and hydroxyl radicals with nitrones. J. Am. Chem. Soc. 1980;102(15):4994–4999. doi: 10.1021/ja00535a029. [DOI] [Google Scholar]
  24. Fontmorin J. M. Burgos Castillo R. C. Tang W. Z. Sillanpää M. Stability of 5,5-dimethyl-1-pyrroline-N-oxide as a spin-trap for quantification of hydroxyl radicals in processes based on Fenton reaction. Water Res. 2016;99:24–32. doi: 10.1016/j.watres.2016.04.053. [DOI] [PubMed] [Google Scholar]
  25. Liu S. Zhao J. Zhang K. Yang L. Sun M. Yu H. et al., Dual-emissive fluorescence measurements of hydroxyl radicals using a coumarin-activated silica nanohybrid probe. Analyst. 2016;141(7):2296–2302. doi: 10.1039/C5AN02261D. [DOI] [PubMed] [Google Scholar]
  26. Czili H. Horváth A. Applicability of coumarin for detecting and measuring hydroxyl radicals generated by photoexcitation of TiO2 nanoparticles. Appl. Catal., B. 2008;81(3–4):295–302. doi: 10.1016/j.apcatb.2008.01.001. [DOI] [Google Scholar]
  27. Steiner M. G. Babbs C. F. Quantitation of the hydroxyl radical by reaction with dimethyl sulfoxide. Arch. Biochem. Biophys. 1990;278(2):478–481. doi: 10.1016/0003-9861(90)90288-A. [DOI] [PubMed] [Google Scholar]
  28. Yang X. Xu X. Xu J. Han Y. Iron Oxychloride (FeOCl): An Efficient Fenton-Like Catalyst for Producing Hydroxyl Radicals in Degradation of Organic Contaminants. J. Am. Chem. Soc. 2013;135(43):16058–16061. doi: 10.1021/ja409130c. [DOI] [PubMed] [Google Scholar]
  29. Oturan M. A. Aaron J.-J. Advanced Oxidation Processes in Water/Wastewater Treatment: Principles and Applications. A Review. Crit. Rev. Environ. Sci. Technol. 2014;44(23):2577–2641. doi: 10.1080/10643389.2013.829765. [DOI] [Google Scholar]
  30. Nidheesh P. V. Gandhimathi R. Effect of solution pH on the performance of three electrolytic advanced oxidation processes for the treatment of textile wastewater and sludge characteristics. RSC Adv. 2014;4(53):27946–27954. doi: 10.1039/C4RA02958E. [DOI] [Google Scholar]
  31. Burgos-Castillo R. C. Sirés I. Sillanpää M. Brillas E. Application of electrochemical advanced oxidation to bisphenol A degradation in water. Effect of sulfate and chloride ions. Chemosphere. 2018;194:812–820. doi: 10.1016/j.chemosphere.2017.12.014. [DOI] [PubMed] [Google Scholar]
  32. Yordanov N. D. Ranguelova K. Quantitative electron paramagnetic resonance and spectrophotometric determination of the free radical 4-hydroxy-2,2,6,6-tetramethylpiperidinyloxy. Spectrochim. Acta, Part A. 2000;56(2):373–378. doi: 10.1016/S1386-1425(99)00248-6. [DOI] [PubMed] [Google Scholar]
  33. Stoll S. Schweiger A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006;178(1):42–55. doi: 10.1016/j.jmr.2005.08.013. [DOI] [PubMed] [Google Scholar]
  34. Louit G. Foley S. Cabillic J. Coffigny H. Taran F. Valleix A. et al., The reaction of coumarin with the OH radical revisited: hydroxylation product analysis determined by fluorescence and chromatography. Radiat. Phys. Chem. 2005;72(2):119–124. doi: 10.1016/j.radphyschem.2004.09.007. [DOI] [Google Scholar]
  35. Takeshita K. Saito K. Ueda J. Anzai K. Ozawa T. Kinetic study on ESR signal decay of nitroxyl radicals, potent redox probes for in vivo ESR spectroscopy, caused by reactive oxygen species. Biochim. Biophys. Acta, Gen. Subj. 2002;1573(2):156–164. doi: 10.1016/S0304-4165(02)00420-8. [DOI] [PubMed] [Google Scholar]
  36. Carolyn Mottley H. D. C. 7OJ Oxygen hyperfine structure for the hydroxyl and superoxide radical adducts of the spin traps DMPO, PBN, and 4-POBN. Biochem. Biophys. Res. Commun. 1987;141(2):622–628. doi: 10.1016/S0006-291X(86)80218-2. [DOI] [PubMed] [Google Scholar]
  37. Brillas E. A review on the degradation of organic pollutants in waters by UV photoelectro-Fenton and solar photoelectro-Fenton. J. Braz. Chem. Soc. 2014;25:393–417. [Google Scholar]
  38. Ishibashi K. Fujishima A. Watanabe T. Hashimoto K. Quantum yields of active oxidative species formed on TiO2 photocatalyst. J. Photochem. Photobiol., A. 2000;134(1–2):139–142. doi: 10.1016/S1010-6030(00)00264-1. [DOI] [Google Scholar]
  39. Pignatello J. J. Oliveros E. MacKay A. Advanced Oxidation Processes for Organic Contaminant Destruction Based on the Fenton Reaction and Related Chemistry. Crit. Rev. Environ. Sci. Technol. 2006;36(1):1–84. doi: 10.1080/10643380500326564. [DOI] [Google Scholar]
  40. Fleming K. G., Fluorescence Theory A2-Lindon, in Encyclopedia of Spectroscopy and Spectrometry, ed. C. John, G. E. Tranter and D. W. Koppenaal, Academic Press, Oxford, 3rd edn, 2017, pp. 647–653, https://www.sciencedirect.com/science/article/pii/B9780128032244003575 [Google Scholar]
  41. Crittenden J. C. and Trussell R. R., Hand DW. MWH's Water Treatment: Principles and Design. John, Wiley & Sons, 2012, p. 1921 [Google Scholar]
  42. Pliego G. Zazo J. A. Garcia-Muñoz P. Munoz M. Casas J. A. Rodriguez J. J. Trends in the Intensification of the Fenton Process for Wastewater Treatment: An Overview. Crit. Rev. Environ. Sci. Technol. 2015;45(24):2611–2692. doi: 10.1080/10643389.2015.1025646. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

RA-008-C7RA13209C-s001
RA-008-C7RA13209C-s001.pdf (1.3MB, pdf)

Articles from RSC Advances are provided here courtesy of Royal Society of Chemistry

RESOURCES