A novel adaptive ensemble classification framework for ADME prediction

Abstract

It has now become clear that in silico prediction of ADME (absorption, distribution, metabolism, and elimination) characteristics is an important component of the drug discovery process. Therefore, there has been considerable interest in the development of in silico modeling of ADME prediction in recent years. Despite the advances in this field, there remains challenges when facing the unbalanced and high dimensionality problems simultaneously. In this work, we introduce a novel adaptive ensemble classification framework named as AECF to deal with the above issues. AECF includes four components which are (1) data balancing, (2) generating individual models, (3) combining individual models, and (4) optimizing the ensemble. We considered five sampling methods, seven base modeling techniques, and ten ensemble rules to build a choice pool. The proper route of constructing predictive models was determined automatically according to the imbalance ratio (IR). With the adaptive characteristics of AECF, it can be used to work on the different kinds of ADME data, and the balanced data is a special case in AECF. We evaluated the performance of our approach using five extensive ADME datasets concerning Caco-2 cell permeability (CacoP), human intestinal absorption (HIA), oral bioavailability (OB), and P-glycoprotein (P-gp) binders (substrates/inhibitors, PS/PI). The performance of AECF was evaluated on two independent datasets, and the average AUC values were 0.8574–0.8602, 0.8968–0.9182, 0.7821–0.7981, 0.8139–0.8311, and 0.8874–0.8898 for CacoP, HIA, OB, PS and PI, respectively. Our results show that AECF can provide better performance and generality compared with individual models and two representative ensemble methods bagging and boosting. Furthermore, the degree of complementarity among the AECF ensemble members was investigated for the purpose of elucidating the potential advantages of our framework. We found that AECF can effectively select complementary members to construct predictive models by our auto-adaptive optimization approach, and the additional diversity in both sample and feature space mainly contribute to the complementarity of ensemble members.

AECF is a GA based ensemble method. It includes four components which are (1) data balancing, (2) generating individual models, (3) combining individual models, and (4) optimizing the ensemble.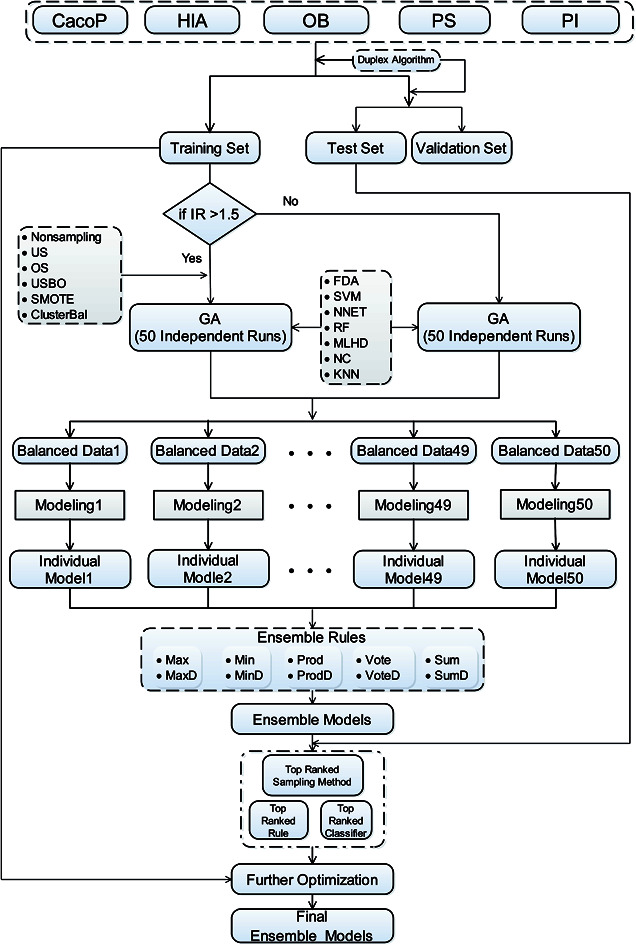

Introduction

Nowadays, it is important to introduce early absorption, distribution, metabolism and excretion (ADME) profiling in parallel with optimization of efficacy in drug discovery. The poor ADME properties are largely accountable for drug failure in the late-stage development phase. The early ADME profiling approaches allow for the prioritization of drug candidates over their biopharmaceutical properties. With the advances in combinatorial chemistry and high-throughput techniques, large libraries of chemicals are available, and can be screened at higher throughput. In silico modeling, as compared to the traditional in vitro/vivo test, is lower-cost and time-saving. Over the past few decades, more robust models have been established to predict various ADME properties, including membrane permeability,^1,2 intestinal absorption (IA),^3,4 oral bioavailability (OB),^5–7 human ether-a-go-go related gene binders,^8–10 as well as transporter binders.^11,12 Most of these models were based on quantitative-structure active relationship (QSAR) approach, ranging from simple multiple linear regression to complex machine learning techniques, such as partial least squares discriminant analysis (PLSDA),¹³ naive bayes (NB) classifier,^10,14 Kohonen self-organizing maps,¹⁵ k nearest neighbor (KNN),^5,16,17 artificial neural networks (NNET),¹⁸ support vector machine (SVM),^5,16,17,19 and random forest (RF).^5,16,17 However, there remain some challenges when developing these methods. First, unbalanced situations often occurs in ADME data due to the publications biased to the favorable property. It refers to datasets in which samples from some classes greatly outnumber samples from others.²⁰ For the binary ADME classification, the number of unfavorable compounds is much less than favorable ones. Such skewed class distribution has detrimental effects on the performance of conventional classifiers which are driven by accuracy. Several studies balanced data sets by changing the classification cutoff. For instance, Xue et al.²¹ used 70% as threshold to classify the good IA and poor IA, and 80% was used to differentiate the good OB and the poor OB.²² However, these cutoff values may be unreasonable in practice,²³ consequently limiting the application of these predictive models in drug design. In addition, a large number of molecular descriptors were calculated to quantitatively define structural and physicochemical properties when modeling. This high dimensionality makes unbalanced classification hard.²⁴ The samples of minority class tends to be sparse as dimensionality increasing, leading to amplifying the issue of skewed class distribution.²⁵ Some studies^24,26–28 reported that the classification performance heavily degenerated when using conventional classifiers for high-dimensional and unbalanced datasets.

In order to address the unbalanced problem, a number of techniques can be carried out. These methods can be divided into two main categories: the data level and the algorithm level.²⁰ The data level methods, also named sampling methods, preprocess the training data to make them balanced by increasing the minority class compounds, eliminating the majority class compounds, or the hybrid strategy. Some of the most popular ones are such as oversampling and undersampling. Sampling methods were effective in solving the class unbalanced problem. However, the benefits of these preprocess techniques may vary in characteristics of datasets.^20,29 Furthermore, some potential useful data may be omitted when modeling on a very small balanced subset from the original data by some methods such as the undersampling based approaches.³⁰ The algorithm level methods reduce the sensitiveness to class unbalance by modifications of existing classification algorithms. These cost-sensitive methods including the modified SVM,¹⁹ RF,³¹ and classification and regression tree (CART)³² were successfully used to handle the unbalanced problem of predicting IA. Recently, Hai's study³³ showed that sampling based methods displayed better performance than the cost-sensitive methods for Caco-2 cell permeability (CacoP) prediction. Moreover, it is not easy to achieve the accurate misclassification cost when applying the cost-sensitive methods.³⁰ Some recent work^29,30 found that both the data level and the algorithm level were problem dependent, and the selection of proper strategy was largely based on data characteristics.

Ensemble methods have gained popularity in recent years, and they have been used to handle the unbalanced problem in many studies.^34–37 The general idea of ensemble methods lies in the aggregation from several individual models in an attempt to obtain substantial improvement over all individual ones.³⁸ Several studies^11,33,39,40 have reported the better performance achieved by ensemble models for ADME prediction. With regard to the construction of ensemble models, some important issues need to be taken into account. The performance of ensemble models is dependent on the choice of constituent individual models. Both the accuracy and the diversity of individual models should be considered.²⁹ Then, how to generate such individual models and how to combine these models should be investigated in the ensemble. When facing high dimensionality simultaneously, it becomes more complex. On the other hand, the larger ADME datasets with higher quality are also required to enhance the generalization ability of the prediction models.

In this paper, we focus on the ensemble based approaches. We attempt to build an adaptive ensemble classification framework (AECF) for different kinds of ADME datasets. With special care to the above issues, AECF consists of four main phases: (1) data balancing, (2) generating individual models, (3) combining individual models, and (4) optimizing the ensemble. It is noted that the performance of an ensemble model can be affected by the way the modeling data are selected, the options of the base classifiers, and the final ensemble rules. The design of AECF may be formulated as a problem in which we look for the optimal combination for constructing a specific ensemble model. The adapting options to frame AECF are from a total selection pool containing five sampling methods, seven base classifiers, and ten ensemble rules. In the first phase, multiple balanced training datasets were created by a specific sampling method. Subsequently, the initial pool of multiple individual models were generated by a genetic algorithm (GA) coupled with a specific classifier from these balanced subsets in the second phase. Then a specific ensemble rule was used to aggregate the classification results of these individual models, and the ensemble model was optimized by an adaptive procedure in the following phases. To assess the effectiveness of our approach, we constructed five updated and different ADME datasets from multiple resources, and AECF was employed to perform the prediction task. The results show that AECF achieved the best performance compared to the individual prediction models, and outperformed the conventional ensemble based techniques including bagging and boosting. The main contributions of our work include:

(1) Five extensive available ADME datasets concerning CacoP, human intestinal absorption (HIA), oral bioavailability (OB), and P-glycoprotein (P-gp) binders (substrates/inhibitors) were constructed, which facilitate to enhance the generalization ability of AECF.

(2) With specially designed for the unbalanced problems, many crucial issues including choice of sample balancing methods, choice of base classifiers, choice of feature space, choice of aggregation rules, and choice of pruning individual models have been taken into account during the development of AECF. The final selection is adaptively based on the data characteristics. Thus, the adaptive characteristics of AECF make it possible to work on the different types of ADME data, and the balanced ADME data is a special case in AECF.

(3) The proposed AECF is a GA based ensemble method. In our framework, each individual model is built on a random balanced subset from the original training data by an independent GA run. Due to the stochastic of both GA and data balancing methods, the diverse and informative feature space can be achieved during evolution, which in turn, maintains the diversity and accuracy of the base classifier. Consequently, the robustness and quality of the prediction task can be improved.

(4) An adaptive procedure was used to optimize the selection of individual models for ensemble after a fitness function of individual models was designed by their diversity and accuracy. After the optimization procedure, the ensemble size was automatically decided, and the better performance was achieved.

Methods and materials

Data source

In our framework, five extensive ADME data sets containing diverse compounds from multiple resources were used for binary classification. The CacoP data set was assembled from a set of 1387 compounds mainly from 13 references. The permeability cutoff value (P_app = 2 × 10⁻⁶ cm s⁻¹) was used.⁴¹ The compounds with P_app < 2 × 10⁻⁶ cm s⁻¹ were considered as unfavorable permeability (CacoP−) group, and the others were labelled as CacoP+. As a result, this data set comprised 922 CacoP+ compounds and 465 CacoP− compounds.

The HIA data set was collected from 11 references. A reasonable cutoff value of 30% (ref. 19, 23, 42 and 43) for HIA was selected to divide the data set into unfavorable HIA (HIA−) and favorable HIA (HIA+). This leads to the data set of 734 compounds, comprising 632 HIA+ compounds and 102 HIA− compounds.

The OB data set comprising 1076 compounds was assembled from 7 references. Since the OB of most compounds is mainly dependent on absorption, the OB is lower than HIA. In this work, the cutoff value for classification was set to OB = 20%.^23,43,44 The compounds with OB < 20% were considered as lower OB (OB−) group, and the others were labelled as OB+. This resulted in the data set comprising 809 OB + compounds and 267 OB− compounds.

The P-gp substrates (PS) data set was derived from 138 references, and the same class assignments provided on the original citations was used. This leads to the data set of 894 compounds, comprising 551 P-gp substrates and 343 P-gp nonsubstrates.

The P-gp inhibitors (PI) data set of 2079 compounds that includes 1240 P-gp inhibitors and 839 P-gp noninhibitors was compiled from our previous work.¹¹ All compounds in five data sets represented by SMILES format are available in ESI Table S1.†

Calculations of molecular descriptors

To quantitatively define structural and physicochemical properties, a large number of molecular descriptors were calculated in this work. For each data set, all the two-dimensional (2D) molecular descriptors and six types of molecular fingerprint sets including MACCS fingerprints, estate fingerprints, substructure fingerprints, Pubchem fingerprints, atom pairs 2D fingerprints, and Klekota–Roth fingerprints from PaDEL⁴⁵ (version 2.20) software were used. Moreover, eight drug-likeness descriptors (DLDs) generated by desirability functions and their weighted fusion presented by Bickerton⁴⁶ were also calculated. As a result, 8526 descriptors were calculated for each compound. The descriptions of the descriptors are summarized in ESI Table S2.†

Data pre-processing and splitting

The same preprocessing strategy reported in our previous study¹¹ was employed to reduce the number of molecular descriptors for each data set. The near-zero variance descriptors were recognized and discarded. The highly correlated descriptors were sequentially removed until all pairwise correlations were below 0.85. The continuous descriptors with highly skewed distribution were Box-Cox transformed so that the skewness values were below 2.⁴⁷ Finally, all continuous descriptors were centered and scaled to unit variance for further analysis.

To choose representative compounds for modeling and ensure a sufficient number of compounds for validation, a two-step data splitting was performed by duplex algorithm⁴⁸ for each data set. In the first step, the data set was divided into two partitions of equal size, of which one was stored as training set (TRS), and then the other was further split into two subsets of equal size, which were served as test set (TES) and validation set (VAS), respectively. The division was carried out for each individual class separately in order to keep the same class distribution in different subsets. This resulted in TRS, TES, and VAS composed of 50%, 25%, and 25% of compounds for each data set, respectively.

Adaptive ensemble classification framework (AECF)

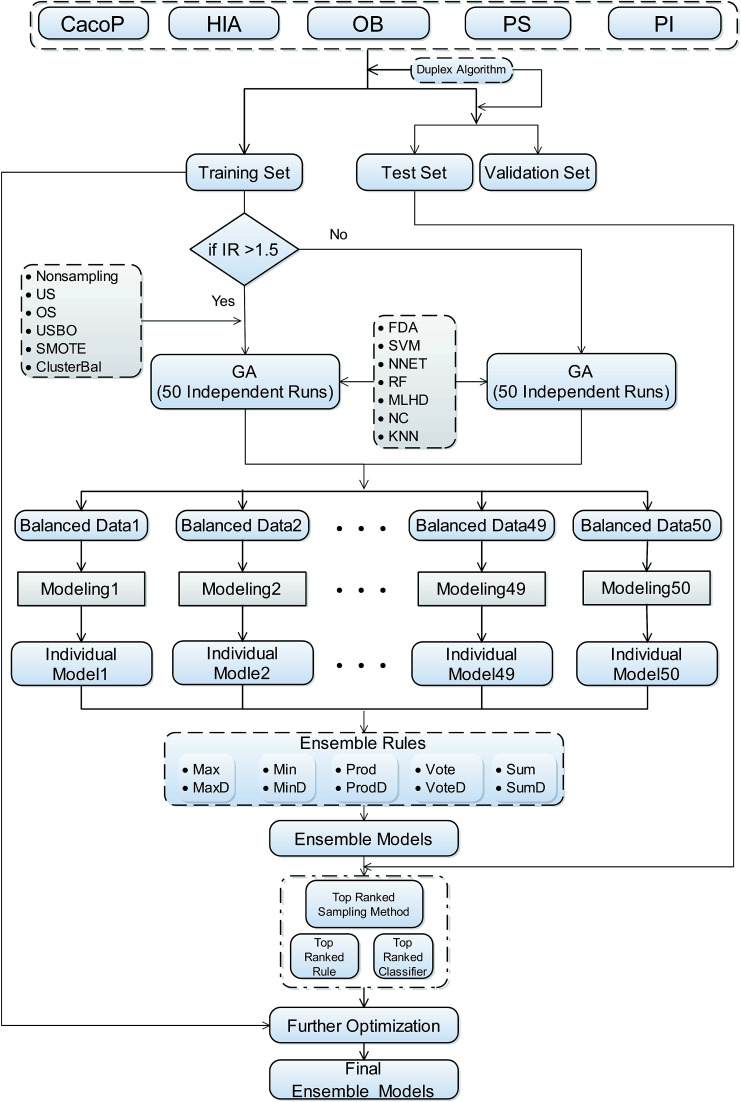
AECF is a GA based ensemble framework. The current work is strongly motivated by previously published approaches^29,49 for ensemble construction. Diversity and quality are two important issues for the performance of ensemble models. When handling the unbalanced problems, AECF maintains the diversity in both the sample space and the feature space. It is also necessary to note that in our framework the model construction process was based only on TRS, the adaptive selection was based on TES, and VAS was only used to evaluate the final generalization capabilities and performance of the optimal ensemble models. The overview of our proposed framework is illustrated schematically in Fig. 1. It can be seen that the classification framework comprises four main phases as follows.

Fig. 1. Workflow of the AECF. IR, imbalance ratio. US, undersampling. OS, oversampling. USBO, undersampling combined with bootstrapping. ClusterBal, cluster based balancing. RF, random forest. MLHD, maximum likelihood classifier. NC, nearest centroid classifier.

(1) Data balancing

After the data set was split, the skewness of class distribution of TRS was measured by the imbalance ratio (IR). IR is defined as the ratio of the number of compounds in the majority class to the number of compounds in the minority class.⁵⁰ In this framework, the TRS with IR greater than 1.5 was considered as an imbalanced data, and the data balancing methods were applied. Otherwise, to reduce the computational cost, the TRS was directly input to GA. The pool of data balancing methods includes the following five sampling techniques.

• Undersampling (US): the majority class compounds are randomly eliminated to match the size of the minority class.

• Oversampling (OS): the minority class compounds are randomly sampled with replacement to match the size of the majority class.

• Synthetic minority oversampling technique (SMOTE): the synthetic samples for the minority class are created based on the k nearest neighbors of the same class, and the number of generated samples depends on the difference in size of the two classes. In this work, five nearest neighbors of the minority class were used to generate the synthetic samples.

• Undersampling combined with bootstrapping (USBO): this is a hybrid sampling method. The majority class compounds are undersampled and the minority class compounds are sampled by bootstrapping.

• Cluster based balancing (ClusterBal): this technique was presented by Sun et al.³⁰ The idea of ClusterBal is that a balanced data set can be obtained by the combination of the subgroup of the majority class and the minority class. In this work, a k-means algorithm was employed to cluster the majority class into K groups. K depended on the IR, and K equaled the rounded IR to integer and no smaller than 2. Then one of these groups was randomly selected to be combined with the minority class, and the new balanced data set was constructed.

Further, nonsampling (NS) as a baseline method, which means that no sampling methods are applied, was also brought into the pool. Thus, after the number of balancing was predefined, multiple balanced subsets from original TRS could be acquired. However, when the TRS was judged as a balanced dataset, the multiple replications of TRS were created.

(2) Generating individual models

After data balancing, multiple balanced training sets were derived. Considering high dimensionality, a genetic algorithm coupled with a specific classifier was applied for simultaneous feature selection and individual classifier design. For each balanced training subset, the sequence of steps of GA in current scheme is as follows.

(i) Initial population of chromosomes with random descriptors: random descriptor sets were created from the original descriptor space. These selected descriptors made up a population of chromosomes, and were used as initially modelling feature vectors to develop base classifiers. Choosing too few descriptors can damage the performance of base classifiers, while using too many descriptors can lead to high computational cost as well as the potential for overfitting. In this study, the number of the selected descriptors was fixed at one twenty-fifth of the number of training instances and no larger than 20 during the GA evolution, and the population size was set to 20.

(ii) Chromosomes evaluation using fitness function: an internal 5-fold cross-validation (CV) was implemented to evaluate chromosomes' fitness during GA runs, and the AUC score (the area under the ROC curve) was taken as the fitness score of the chromosomes. The training set was randomly split into 5 non-overlapping subsets with equal size according to their categories. In each fold, one subset was held out for validation, and the rest were used to train the base classifier. Then this predictive model was applied to the validation subset. This procedure was repeated until every subset was used for validation. The pool of base classifiers includes seven popularly used machine learning techniques. The detailed information of these techniques is listed in Table 1, and the default parameters provided by the tool was used to construct classifiers.

The abbreviations and descriptions of base classifiers.

Abbreviation	Description	Package
FDA	Flexible discriminant analysis	mda52
SVM	Support vector machine with polynomial kernel	kernlab53
NNET	Neural network	nnet54
RF	Random forest	randomForest55
MLHD	Maximum likelihood	Galgo51
NC	Nearest centroid	Galgo51
KNN	k-Nearest neighbors	Galgo51

(iii) Design of the GA operator: chromosomes with higher fitness in each generation were selected and then updated by the genetic operators: crossover and mutation. These procedures were repeated until the maximum generation was reached. In this study, the maximum generation was set to 100, and the other GA parameters were default according to Galgo package.⁵¹

At the conclusion of GA search, the informative descriptor subset with the highest fitness in the last generation was saved for each balanced training subset, and the corresponding individual model was built on the discriminative descriptor subset using a specific classifier. As a result, multiple individual models were achieved. There are two main advantages of using multiple GA runs in our scheme. First, the feature space can be reduced to improve the accuracy of base classifiers, resulting in individual models with high performance. Second, due to the stochastic of both the GA and data balancing methods, running the algorithm from a different training subset from original data set each time can yield a different discriminative descriptor subset, which promotes the diversity among individual models. Therefore, AECF is able to yield multiple individual models as accurate and diverse as those obtained with wrapper-based feature selection and data balancing.

(3) Combining individual models

Another important issue in the development of ensemble models is how to combine individual models. There are various schemes to aggregate the outputs of individual models. In our framework, ten alternative rules were investigated for improving the performance of the fusion phase. They constitute the pool of ensemble rules in AECF, and their detailed strategies and descriptions are shown in Table 2. These rules are all based on predicted probabilities of each class, and can be divided into two groups. Max Rule, Min Rule, Prod Rule, Sum Rule, and Vote Rule directly use predicted probabilities for aggregation. While MaxD Rule, MinD Rule, ProdD Rule, SumD Rule, and VoteD Rule are distance based rules.³⁰ These rules use the inverse of average distance to adjust predicted probabilities. For binary classification, suppose that the class labels are G₁ and G₂. When N individual models are applied for a new compound, N predicted probabilities of each class can be derived. Let P_1i and P_2i denote the probability of being G₁ and G₂ predicted by the ith individual model, respectively. Then the fusion scores for the class G₁ and G₂ (represented as S₁ and S₂, respectively) can be achieved by the rule. For distance based rules, D_1i, and D_2i denote the average distance between the new compound and the ith training compounds with label G₁ and G₂, respectively. Finally, the new compound is labelled to the class with maximum fusion score. More details about these ensemble rules have been described elsewhere.^30,56

The strategies and descriptions for the pool of ensemble rules.

Rule	Strategy	Description
Max	S 1 = argmax1≤i≤NP1i, S2 = argmax1≤i≤NP2i	Use the maximum predicted probability of N individual models for each class label
Min	S 1 = argmin1≤i≤NP1i, S2 = argmin1≤i≤NP2i	Use the minimum predicted probability of N individual models for each class label
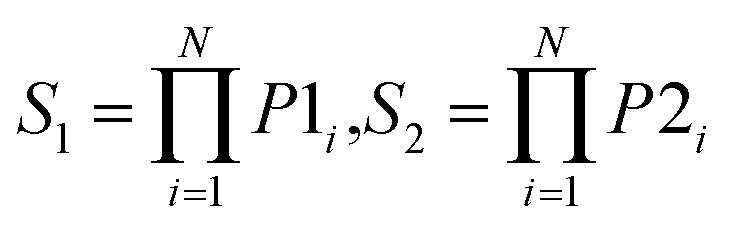
Prod		Use the product of predicted probability of N individual models for each class label
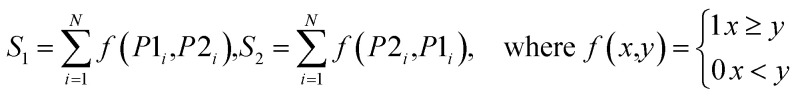
Vote		For the ith model, if P1i ≥ P2i, class G1 gets a vote, otherwise, class G2 gets a vote
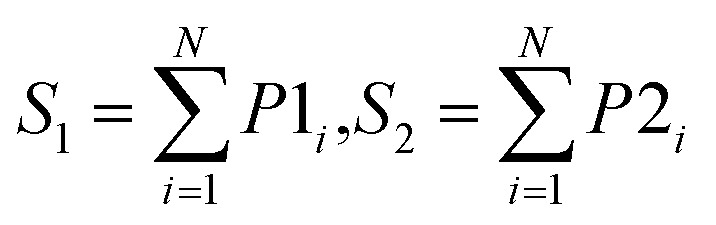
Sum		Use the summation of predicted probability of N individual models for each class label
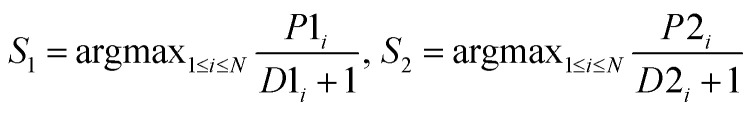
MaxD		Use the inverse of average distance to adjust the corresponding rule
MinD
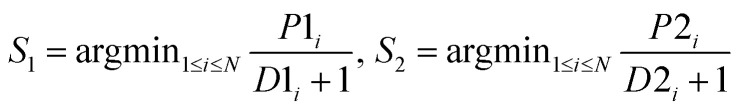
ProdD
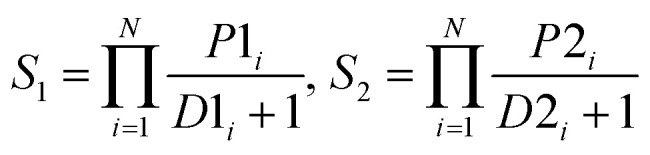
VoteD
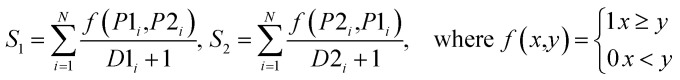
SumD

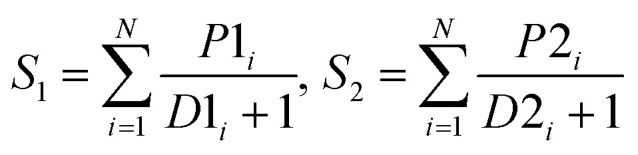
(4) Optimizing the ensemble

In the proposed framework, we focus on the optimization of ensemble classification system. There are several combination issues that need to be addressed. Given a pool of data balancing methods, a pool of base classifiers, and a pool of ensemble rules, the first problem is how to choose the best combination. Given a pool of individual models, another problem is how to effectively select which individual models to use in the final ensemble. Thus, a novel two-stage adaptive optimization method was developed in this work.

Considering that combination schemes tend to be data-specific (none produced the best results for all data sets). Therefore, in the first stage, all combinations of the methods from supplied pools including data balancing methods, base classifiers, and ensemble rules were tested. This resulted in 420 combinations for unbalanced data sets and 70 combinations for balanced data sets. For each combination, an ensemble model was established by the aggregation of multiple individual models. Then, the AUC score on TES was taken as the performance score. The combination with the highest performance was chosen as the adaptive selection. In the current investigation, the number of individual models was set to 50.

After obtaining the best combination of method pools, a further optimization can be invoked to find the best combination of individual models in the second stage, which yields the best ensemble performance. This selection of individual models focuses on finding the most efficient subset of ensembles, rather than combining all available individuals. In the second stage, a forward search algorithm (FSA) was designed. Initially, the goodness of each individual in the pool was evaluated. Individual models were ranked according to their fitness, from the best to the worse, and the top two individuals were firstly selected in the final ensemble. Then the individual model from the (sorted) input list was iteratively added into the ensemble where, at each step the ensemble was evaluated on the hold-out dataset. This procedure was repeated until no further improvements could be obtained. Here, a fitness function Q was defined for assessing the goodness of individual models as follows.

Q = f(Perf, Div) 1

where Perf and Div represents the measurement of performance and diversity, respectively. In this work, the predicted AUC score was taken as the measurement of performance, and the diversity was measured by a pairwise metric of fail/non-fail disagreement (Dis).⁵⁷ Dis was defined as the percentage of test compounds for which the individual models made different predictions but that for one of both was correct.

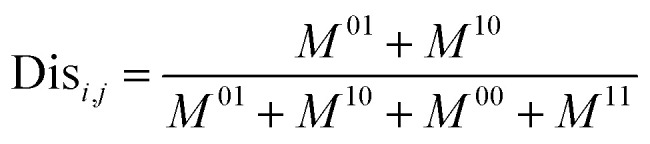2

where Dis_i,j denotes the measurement of diversity between individual model i and j. M^ab is the number of compounds, predicted correctly (a = 1) or incorrectly (a = 0) by the individual model i, and correctly (b = 1) or incorrectly (b = 0) by the individual model j. Dis_i,j varies from 0 to 1, when both models predict identically for each compound, it is equal to 0, and it is equal to 1 when the results are always different and one of them is correct. Then the diversity score of individual model i (represented as Div_i) was calculated by averaging Dis_i,j over all pairs.

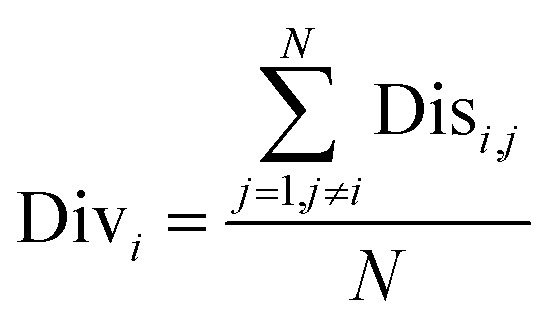3

where N is the number of individual models. Consequently, the fitness of individual model i (represented as Q_i) was calculated as follows.

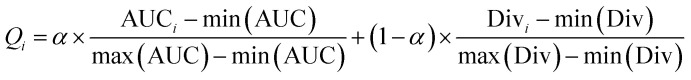4

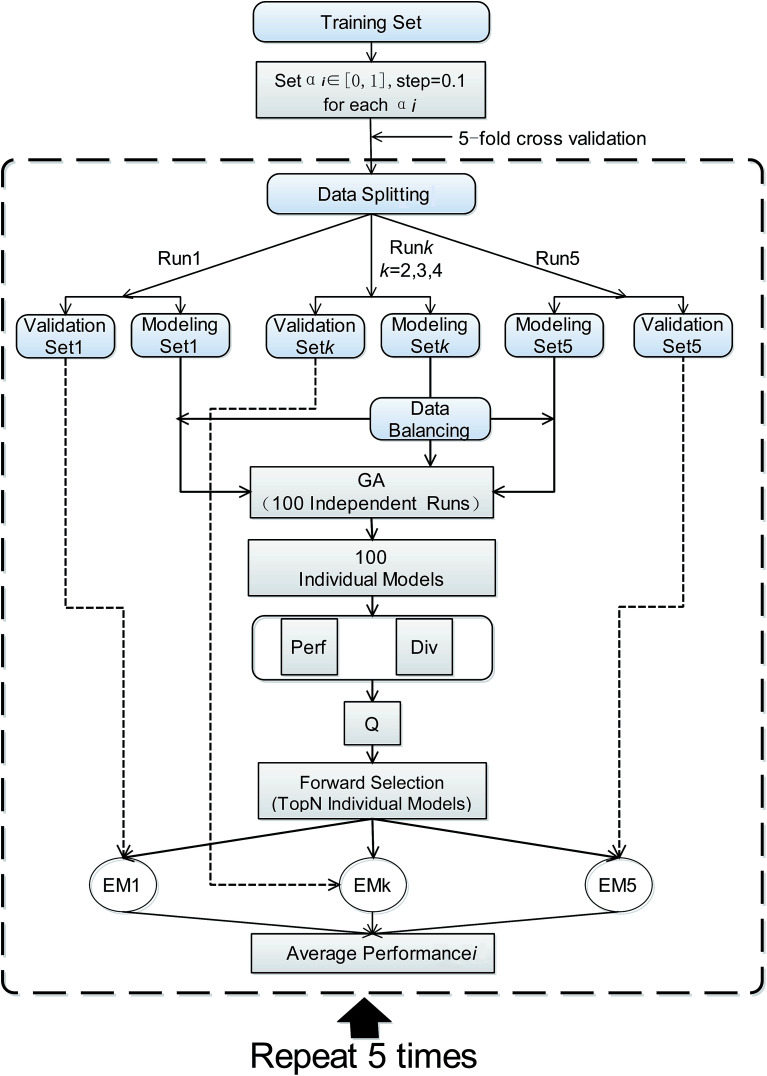
where AUC and Div represents the predicted AUC score vector and the diversity score vector of individual models, respectively. The maximum and minimum functions were used to scale the metrics. The parameter, α, was used to adjust the weights of performance and diversity, and varied from 0 to 1. Previous study⁵⁸ suggested that the status of individual models with medium performance and medium diversity could result in better ensemble performance, but the tradeoff between performance and diversity remained unclear. Different α could be needed for different data. Due to the lack of theoretical support, α should be estimated from the data. In this paper, a rigorous 5-fold cross validation combined with FSA was proposed to automatically choose the optimal α. The general workflow of this adaptive optimization process is shown in Fig. 2. It is necessary to note that TRS was only used in this process. The selection pool of α values needs to be predefined. In AECF, α began from 0 and stepped up by 0.1 in each increment until it reached 1. For each value of α, the original training data was randomly divided into five subsets with equal size according to their categories. Each time one subset was regard as the validation set and the remaining sets as modeling set. The modeling set was subsequently used to generate 100 balanced training data sets, and 100 individual models were created by multiple GA runs. Then an ensemble model was developed using the best combination of method pools derived from the previous optimizing section. This ensemble model was further optimized by FSA, and was employed to predict on the validation set. The AUC score was used to estimate the prediction ability of the ensemble model. This process was repeated for five times until each subset was used for validation. Moreover, this optimization process with 5-fold cross validation was repeated five times due to the use of stochastic search algorithm. The value of α with the highest AUC score averaged over all runs was picked up as the optimal solution. Finally, the final ensemble model was automatically rebuilt using the best combination of method pools, and was optimized by FSA using the optimal α.

Fig. 2. Auto optimization for α by a rigorous 5-fold cross validation. Perf, the performance score of individual models. Div, the diversity score of individual models. Q, the fitness of individual models.

Model evaluation

The performance of ensemble models was evaluated via the prediction of the two independent data set (test set and validation set). Considering the imbalanced classification task, several statistical metrics including specificity (SP), sensitivity (SE), overall accuracy (OA), kappa statistic, Matthews's correlation coefficient (MCC), and AUC were used as evaluation criteria. These metrics were calculated as follows:

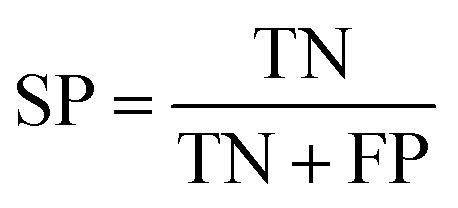5

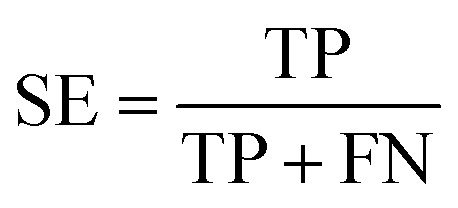6

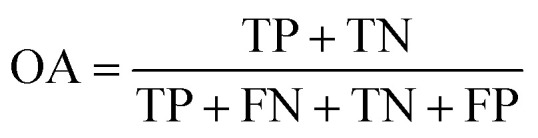7

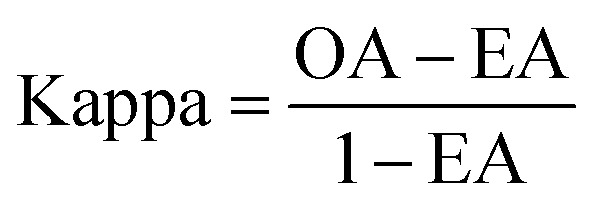8

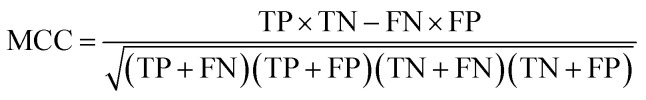9

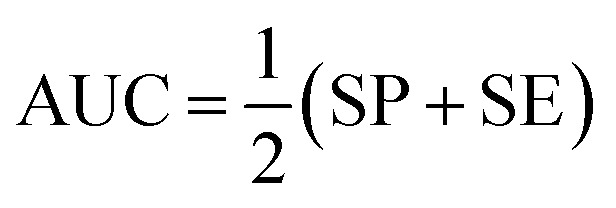10

where TP, FP, TN, and FN represents true positive, false positive, true negative, and false negative, respectively. EA is the expected accuracy based on the marginal totals of the confusion matrix. The AUC is defined as the area under the ROC curve, which has proved to be a reliable performance measure for class imbalanced problems.⁵⁹ In this work, AUC was also used to guide the construction and optimization of AECF. For binary classification, AUC is identical to the balanced accuracy.⁶⁰

Applicability domain (AD) analysis

It is necessary to define AD for delineation of interpolation space in which the model can make reliable predictions when applying a predictive model on a new dataset.⁶¹ Several different methodologies can be used for defining AD, including the projection approach⁶² and machine learning based approach.^47,52 Our previous study¹¹ showed that machine learning based approach was more appropriate for AD analysis than projection approach. In the presented work, we applied machine learning based approach to define AD. In this approach, the union of modeling descriptor sets of selected individual models were selected, and 100 shuffled training sets were created by randomly permuting these descriptors. Then 100 combined datasets were created, and each of them was constructed by merging the original training set and one shuffled set. An ensemble classification model was established to predict the probability of new compounds being members of the training set. Readers can refer to our previous work¹¹ for implementation details.

Tools

All calculations were performed with R-3.3.2 software. The packages used for implementing various base classifiers are presented in Table 1. SMOTE algorithm was implemented using DMwR package.⁶³ Galgo⁵¹ package was used to perform GA. Caret package⁶⁴ and boostr package⁶⁵ was used to implement Bagging and Boosting algorithm, respectively.

Results and discussions

Characterization of the data set

For each data set, only a small subset of calculated descriptors was remained for modeling after feature preprocessing, and data splitting resulted in fifty percent as TRS, twenty five percent as TES, and twenty five percent as VAS. The data characteristics are summarized in Table 3, where the number of compounds is listed in the parentheses following to the name of category. The calculated IRs for the different data sets are also shown. The results show that most of IRs are greater than the predefined threshold (IR = 1.5). Therefore, AECF handles these datasets (Cacop, HIA, OB, and PS) as unbalanced data except PI data.

The summarization of datasets after preprocessing and splitting.

Dataset	Subset	Descriptors	Class		IR
			Majority	Minority
CacoP	TRS	902	CacoP+(461)	CacoP−(233)	1.98
	TES		CacoP+(231)	CacoP−(116)	1.99
	VAS		CacoP+(230)	CacoP−(116)	1.98
HIA	TRS	677	HIA+(316)	HIA−(51)	6.20
	TES		HIA+(158)	HIA−(26)	6.08
	VAS		HIA+(158)	HIA−(25)	6.32
OB	TRS	940	OB+(405)	OB−(134)	3.02
	TES		OB+(202)	OB−(67)	3.01
	VAS		OB+(202)	OB−(66)	3.06
PS	TRS	880	Substrate(276)	Nonsubstrate(172)	1.60
	TES		Substrate(138)	Nonsubstrate(86)	1.60
	VAS		Substrate(137)	Nonsubstrate(85)	1.61
PI	TRS	832	Inhibitor(620)	Noninhibitor(420)	1.48
	TES		Inhibitor(310)	Noninhibitor(210)	1.48
	VAS		Inhibitor(310)	Noninhibitor(209)	1.48

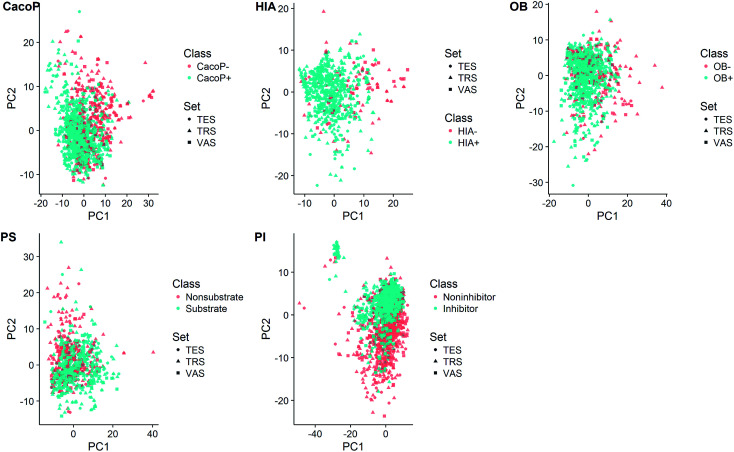
In order to inspect the coverage of the chemical space of compounds, principal component analysis (PCA) was employed on each data set to visualize the data structure (Fig. 3). The total variance explained by the first two principal components was 15.8%, 15.2%, 14.8%, 15.0%, and 15.1% for CacoP, HIA, OB, PS, and PI, respectively. The majority and minority class points were coloured in blue and red, respectively. In Fig. 3, there was a trend for separation of two groups, which urged us to develop classification models. Moreover, it can be seen from the score plots that the majority class had more dispersion of the chemical properties than the minority class in most cases. On the other hand, for each data set, the distribution of the compounds seems to be well-balanced among the three data subsets, which illuminates the representative ability of samples in all subsets during duplex algorithm for splitting.

Fig. 3. Score plot from PCA based on each data set.

For each data set, profile analysis of individual molecular property was performed using Student's t-test or Fisher's exact test, and the corresponding P-values were calculated and ranked. As a result, there were 464, 282, 358, 324, and 488 statistically significant descriptors with a low P-value (P-value < 0.01) for CacoP, HIA, OB, PS, and PI data, respectively. The distributions of the top nine relevant descriptors between groups are shown in the ESI Fig. S1–S5.† We can see that DLDs whose name ending with a suffix “_DES” show high discriminability between groups for CacoP, HIA, and OB. While descriptors related to molecular hydrophobicity (Mlog P) and the number of carbon atom in the molecule (PubchemFP12) are more discriminative for P-gp properties.

Development of AECF

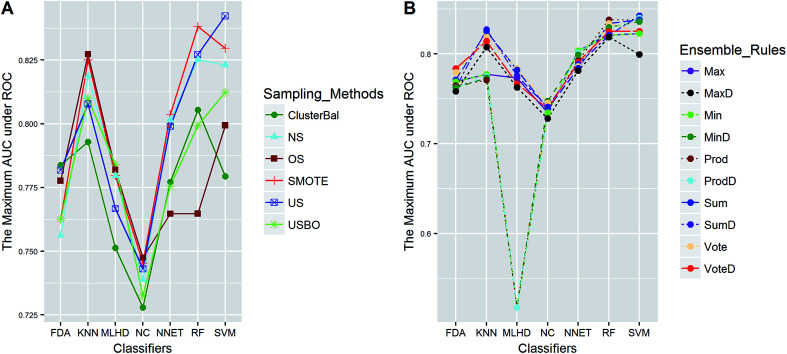
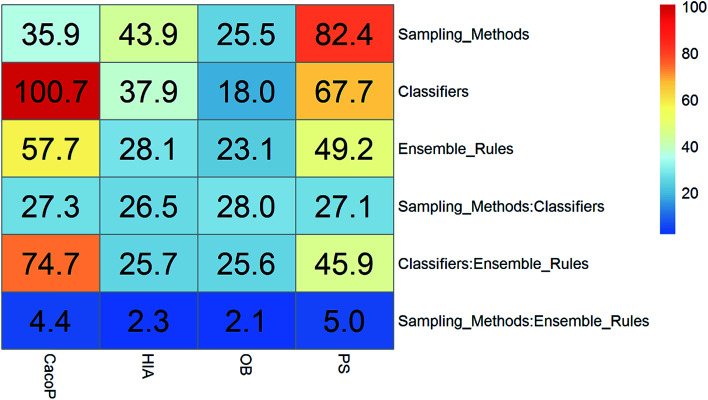
In this study, five data sets were divided into two types according to their IRs in AECF. CacoP, HIA, OB, and PS followed the route for tackling unbalanced datasets. The initial ensemble models were developed by the following procedures: data balancing, generating individual models, and combining individual models. Each method in each investigation pool was combined together to form the initial ensemble model, and the best combination in terms of AUC was picked out by AECF as the adaptive solution. In our framework, the default number of independent GA runs is 50, which means that each initial ensemble model was aggregated by 50 individual models during each combination. For unbalanced datasets, a total of 420 combinations were investigated. The maximum AUC scores of pairwise combinations for each data set are presented in Fig. 4–7. The results show that the different combination gained different performance. There were high degree of performance fluctuations among each pool of candidate methods. In order to investigate the relationships, a multiple linear regression model was built in terms of a connection between performance and methods for each data set, and the main effects and their two-way interaction effects were tested by analysis of variances. The corresponding P-values were calculated, and a term score (TS) was defined as the minus logarithm-transformed P-value.

TS = −log₁₀(P-value) 11

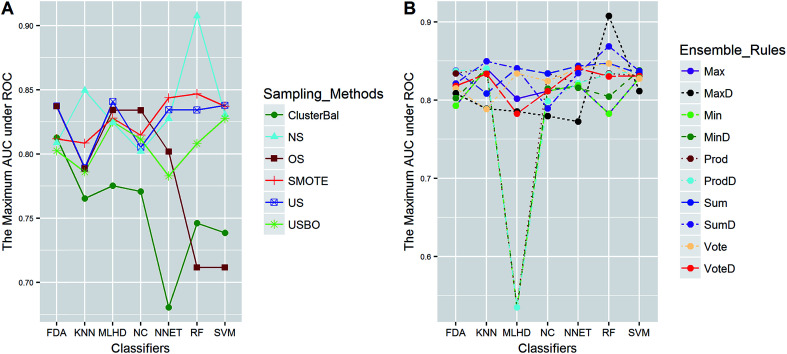
Fig. 4. The maximum AUC scores of pairwise combinations for CacoP. (A) The combination of classifier and sampling method, and (B) the combination of classifier and ensemble rule. US, undersampling. OS, oversampling. USBO, undersampling combined with bootstrapping. ClusterBal, cluster based balancing.

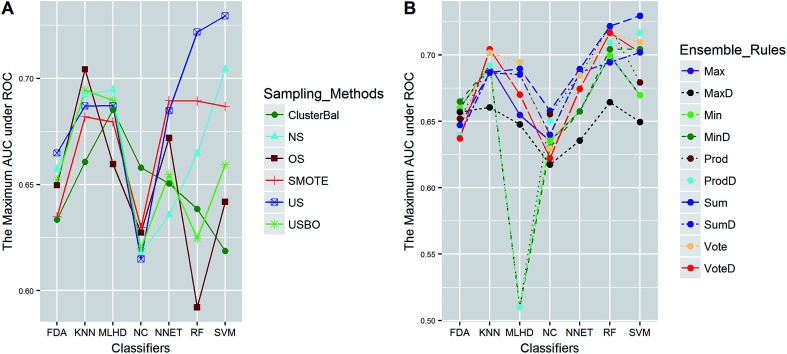
Fig. 5. The maximum AUC scores of pairwise combinations for HIA. (A) The combination of classifier and sampling method, and (B) the combination of classifier and ensemble rule. US, undersampling. OS, oversampling. USBO, undersampling combined with bootstrapping. ClusterBal, cluster based balancing.

Fig. 6. The maximum AUC scores of pairwise combinations for OB. (A) The combination of classifier and sampling method, and (B) the combination of classifier and ensemble rule. US, undersampling. OS, oversampling. USBO, undersampling combined with bootstrapping. ClusterBal, cluster based balancing.

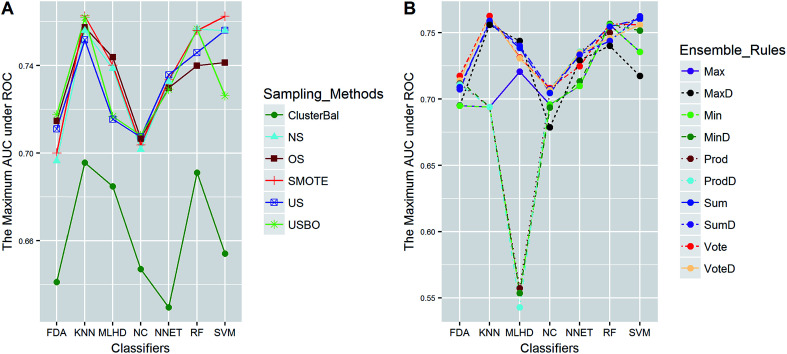
Fig. 7. The maximum AUC scores of pairwise combinations for PS. (A) The combination of classifier and sampling method, and (B) the combination of classifier and ensemble rule. US, undersampling. OS, oversampling. USBO, undersampling combined with bootstrapping. ClusterBal, cluster based balancing.

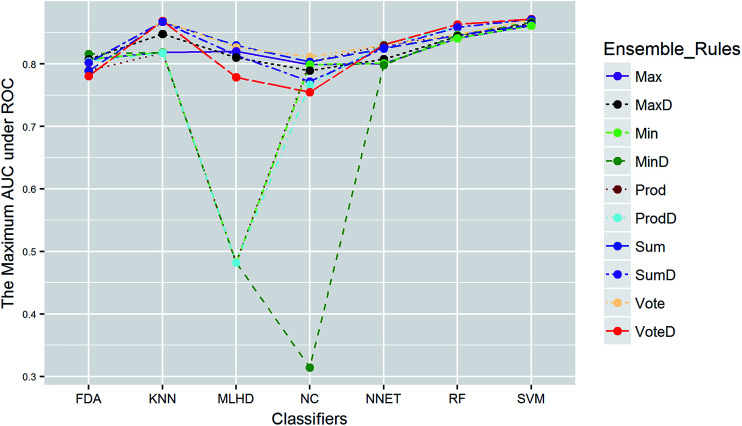
Clearly, the more significant a term is, the higher TS it will get. Particularly, a term with P-value < 0.01 will have a TS > 2. The summarization of TS for each data set was shown in Fig. 8. All terms are statistically significant with TS greater than 2, which suggests that the choices of sampling methods, classifiers, and ensemble rules are key considerations to achieve better performance for these datasets. In most cases, SVM and RF presented better scores, while MLHD and NC were worse. Sampling method also played an important role in the development of predictive models. It is interesting that the baseline method (NS) was not always worst, on the contrary, the best performance was observed when it was combined with RF for HIA. The reasonable explanation may be due to the complicated interactions among the pools of candidate methods when AECF handles the unbalanced datasets.

Fig. 8. The summarization of TS for unbalanced datasets.

The balanced dataset PI was tackled in the same way except that data balancing was skipped. The AUC scores of 70 combinations were recorded, and Fig. 9 presents the maximum scores of combinations between classifiers and ensemble rules. The main effects were also tested by the same way. The results show that the term of classifiers had a significant effect for performance with TS = 4.4, while the ensemble rules (TS = 1.0) didn't. Thus the choice of classifiers is more important than that of ensemble rules for PI data. The best score was obtained by the combination of SVM and VoteD.

Fig. 9. The maximum AUC scores of combinations between classifiers and ensemble rules for PI.

Table 4 lists the adaptive solutions selected by AECF. To summarize, the adaptive routes of AECF for the construction of ensemble models are as follows:

The auto-adaptive solutions selected by AECF.

Data set	Sampling method	Classifier	Ensemble rule
CacoP	Undersampling	SVM	SumD
HIA	Nosampling	RF	MaxD
OB	Undersampling	SVM	Sum
PS	SMOTE	KNN	Vote
PI	Nosampling	SVM	VoteD

• For CacoP data, US was used to balance the data, and individual models were generated by multiple GA-SVM runs. The ensemble model was built by aggregating individual outputs using SumD.

• For HIA data, individual models were generated by multiple GA-RF runs. The ensemble model was built by aggregating individual outputs using MaxD.

• For OB data, US was used to balance the data, and individual models were generated by multiple GA-SVM runs. The ensemble model was built by aggregating individual outputs using Sum.

• For PS data, SMOTE was used to balance the data, and individual models were generated by multiple GA-KNN runs. The ensemble model was built by aggregating individual outputs using Vote.

• For PI data, individual models were generated by multiple GA-SVM runs. The ensemble model was built by aggregating individual outputs using VoteD.

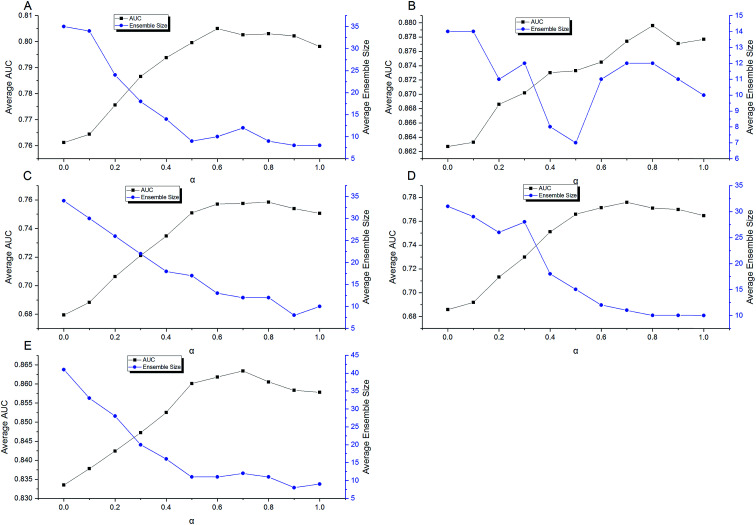
Then a five-times-repeated rigorous 5-fold cross validation combined with FSA described above was used in the second stage of optimization to find the optimal α automatically for each dataset. In the current stage, only TRS was used, and the range of α was set to [0,1]. The step was set to 0.1. With each value of α, using the adaptive routes determined previously, the ensemble models were built by aggregating 100 individual models in each fold validation. Fig. 10 shows the results of optimization procedure. It is apparent that the performance was more sensitive to the value of α. In most cases, a S-shaped-like curve was observed to describe the relationship between α and performance. In the range of α, neither the maximum nor the minimum could achieve the best performance for every data set. This indicates that the tradeoff between performance and diversity of individual models should be taken into consideration when constructing ensemble models. However, the relationships between α and ensemble size can be described as the reverse S-shaped-like curves in most cases. The larger α leads to smaller ensemble size. In other words, increasing the weight of performance in the fitness function Q helps to decrease the number of individuals to be aggregated. The α with the highest AUC was chosen automatically by AECF. Consequently, the optimal α was 0.6, 0.8, 0.8, 0.7, and 0.7 for CacoP, HIA, OB, PS, and PI, respectively. The optimal values were all greater than 0.5, which suggested that the performance was more important than the diversity during evaluating the fitness of individual models in our experiment.

Fig. 10. Optimization of α for (A) CacoP, (B) HIA, (C) OB, (D) PS, and (E) PI.

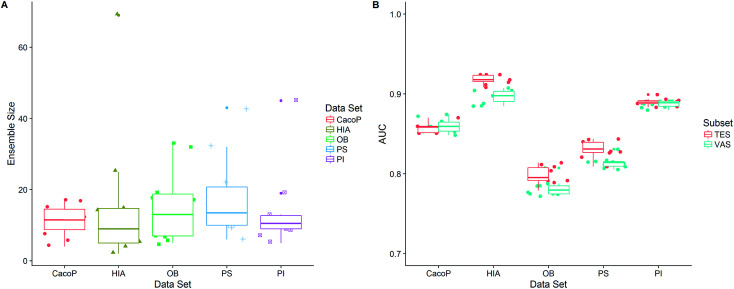
After the optimization procedure, the ensemble model was rebuilt using the best combination of method pools based on TRS. 100 individual models were generated by multiple GA runs, and the ensemble size was automatically determined by FSA using the optimal α. Then the final (optimal) ensemble model was achieved. Due to the stochastic of generation of individual models, the procedure of constructing final ensemble model was repeated ten times. All the performance measures calculated on average over ten ensemble models for TES and VAS are shown in Table 5. We can see that, for all datasets, AECF shows the most discriminative power with AUC ranging from 0.7821–0.9182, MCC ranging from 0.5137–0.7887, OA ranging from 0.7792–0.9459, and kappa ranging from 0.5004–0.7856. To demonstrate the effectiveness of the optimization approach by AECF, the performances of the individual models and suboptimal ensemble models whose second stage of optimization were skipped are also reported. We can see that the final ensemble model (AECF) achieved the best performance in terms of all metrics in each data set. In contrast, the individual models were the worst. After applying our two-step adaptive optimization approach, the AUCs were raised by 6.36–26.99% and 2.09–8.04% compared to the individual models and suboptimal ensemble models, respectively. The distributions of ensemble size and AUC of ten AECF models for each data set are shown in Fig. 11. There were no clear relationships between ensemble size and performance. Although large ranges of ensemble size of final models were observed, the similar performances were obtained, which demonstrates the robustness of our approach.

The average performance of different models.

Data	Subset	Model	AUC	MCC	SE	SP	OA	Kappa
CacoP	TES	AECF	0.8574	0.6935	0.8537	0.8612	0.8562	0.6889
		Suboptimal AECF	0.8289	0.6370	0.8320	0.8259	0.8300	0.6327
		Individual model	0.7643	0.5038	0.7396	0.7891	0.7561	0.4915
	VAS	AECF	0.8602	0.6994	0.8574	0.8629	0.8592	0.6953
		Suboptimal AECF	0.8342	0.6439	0.8235	0.8448	0.8306	0.6375
		Individual model	0.7703	0.5144	0.7362	0.8043	0.7590	0.5003
HIA	TES	AECF	0.9182	0.7887	0.9563	0.8800	0.9459	0.7856
		Suboptimal AECF	0.8994	0.7236	0.9348	0.8640	0.9251	0.7160
		Individual model	0.7953	0.686	0.9839	0.6067	0.9324	0.6715
	VAS	AECF	0.8968	0.7404	0.9437	0.8500	0.9304	0.7357
		Suboptimal AECF	0.8782	0.6586	0.9063	0.8500	0.8984	0.6442
		Individual model	0.7758	0.6737	0.9888	0.5628	0.9286	0.6501
OB	TES	AECF	0.7981	0.5295	0.7604	0.8358	0.7792	0.5027
		Suboptimal AECF	0.7387	0.4302	0.7594	0.7179	0.7491	0.4157
		Individual model	0.6285	0.2236	0.5965	0.6606	0.6125	0.1993
	VAS	AECF	0.7821	0.5137	0.7990	0.7652	0.7907	0.5004
		Suboptimal AECF	0.7327	0.4369	0.8124	0.6530	0.7731	0.4325
		Individual model	0.6413	0.2452	0.6092	0.6735	0.625	0.2194
PS	TES	AECF	0.8311	0.6738	0.8964	0.7659	0.8464	0.6709
		Suboptimal AECF	0.7860	0.5677	0.8190	0.7529	0.7937	0.5672
		Individual model	0.6772	0.3634	0.7914	0.5630	0.7039	0.3611
	VAS	AECF	0.8139	0.6458	0.9022	0.7256	0.8344	0.6420
		Suboptimal AECF	0.7534	0.5026	0.7906	0.7163	0.7621	0.5020
		Individual model	0.6848	0.3791	0.7974	0.5723	0.7109	0.3768
PI	TES	AECF	0.8898	0.7740	0.8900	0.8895	0.8898	0.7731
		Suboptimal AECF	0.8669	0.7287	0.8732	0.8605	0.8681	0.7281
		Individual model	0.8366	0.6708	0.8574	0.8157	0.8406	0.6703
	VAS	AECF	0.8874	0.7699	0.8906	0.8842	0.8881	0.7691
		Suboptimal AECF	0.8688	0.7359	0.8887	0.8488	0.8726	0.7359
		Individual model	0.8330	0.6673	0.8697	0.7962	0.8401	0.6671

Fig. 11. The distributions of (A) ensemble size and (B) AUC of ten AECF models for each data set.

In order to investigate how the individuals in the ensemble complement each other to increase performance, the degree of complementarity of AECF was evaluated. The following calculations were all based on ten final ensemble models (EM).

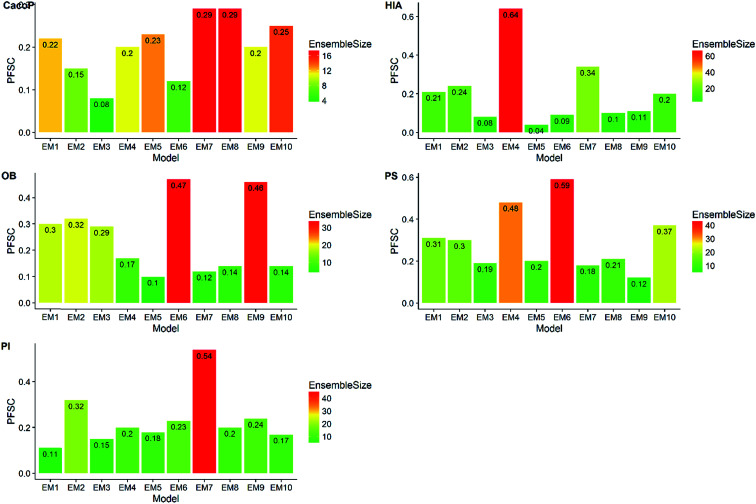
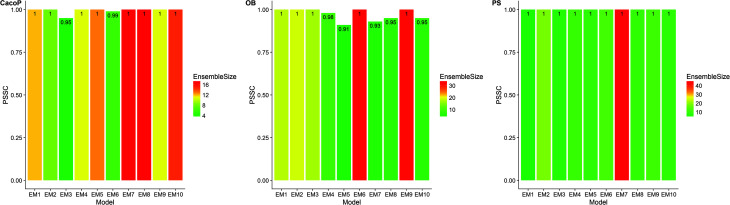
First, the degree of TRS that was utilized by AECF was analyzed. Both the sample and feature space coverage of individual models within final ensemble model were calculated for each data set. Fig. 12 presents the percentage of feature space coverage (PFSC) of each EM for each data set. We can see that there is a good linear relationship between ensemble size and the percentage of feature space coverage. Larger ensemble sizes led to larger PFSCs. The PFSCs were 0.08–0.29, 0.04–0.64, 0.10–0.47, 0.12–0.59, and 0.11–0.54 for CacoP, HIA, OB, PS, and PI, respectively. AECF achieved better performance by using only a small part (about 4–12%) of descriptors, which indicated that our approach successfully made a good optimization by eliminating the redundant features. Fig. 13 presents the percentage of sample space coverage (PSSC) of each EM for each data set (except HIA and PI where non-sampling was applied). The PSSCs were all 1.00 for PS. This means that the modeling data of AECF covered all TRS samples for PS. The PSSCs were 0.95–1.00 and 0.91–1.00 for CacoP and OB, respectively. Moreover, seven and five out of ten EMs were with the PSSC value 1.00 for CacoP and OB, respectively. Even though the ensemble sizes were small, the PSSCs were large. For instance, the PSSC of EM with the smallest ensemble size (4) for CacoP was still large (95%). The similar case could be found for OB. With the benefits of multiple data balancing and effective optimization strategy, AECF can make a better use of TRS samples despite selecting small number of individual models for aggregation.

Fig. 12. The percentage of feature space coverage of each EM for each data set.

Fig. 13. The percentage of sample space coverage of each EM for CacoP, OB and PS data set.

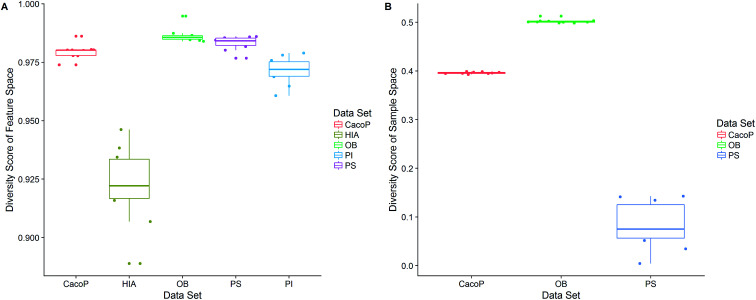
Next, the mechanism of diversity maintenance in individual models within AECF was further explored. A Jaccard distance (JD) was defined as follows to measure the diversity of both sample and feature space of individual models.

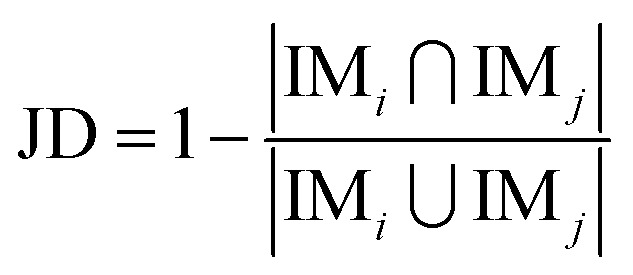12

where IM_i and IM_j denotes the sample or feature space of individual model i and j, respectively. Obviously, JD is a pairwise metric. Then the diversity score of sample or feature space of an individual model was calculated by averaging JD over all pairs within an ensemble model. The distributions of diversity scores of sample and feature space were shown in Fig. 14. Compared to sample space, the diversity of feature space was larger. The averaged diversity score of feature space was 0.9795, 0.9225, 0.9864, 0.9833, and 0.9714 for CacoP, HIA, OB, PS, and PI, respectively. This means that the individual models within AECF shared very little descriptors for each data set. For the sample space, multiple data balancing accounted for the diversity of sample space. The diversity scores of OB and CacoP were larger than that of PS. The results indicated that TRS with higher IR using US produced more diverse sample space than that with lower IR using SMOTE in the current investigation. The diverse feature space and sample space helped to keep the diversity of different individual models. These findings suggest that, for the present problem, better performance can be achieved by different feature sets and sample sets, and the information useful in classification provided by the diverse individuals help to provide complementary strength of individual models such that a more robust and predictive ensemble model can be achieved.

Fig. 14. The distributions of diversity scores of (A) feature and (B) sample space.

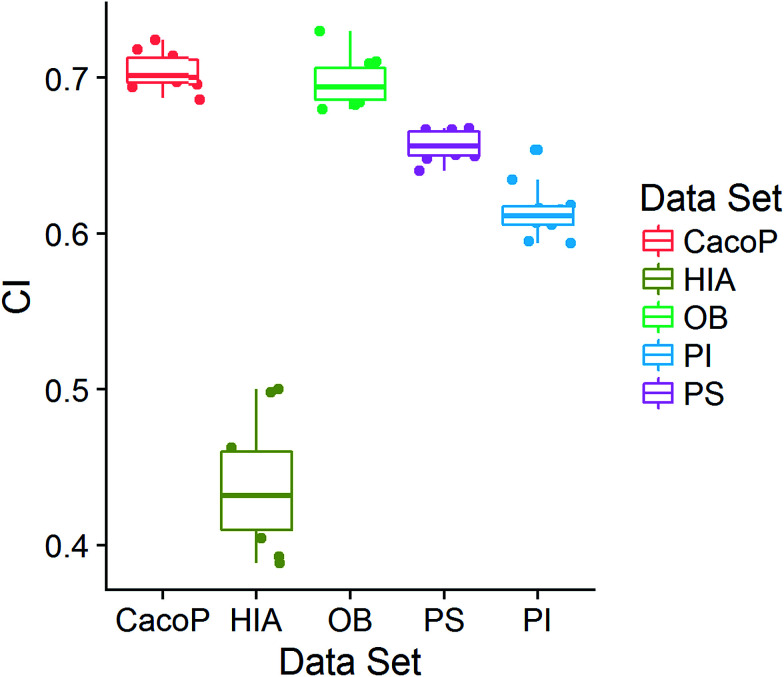
Last, a complementary index (CI)⁶⁶ was defined as follows to quantify the degree of complementarity of individual models, and the relationships between the performance of EMs and the characteristics of their individual models were explored.

13

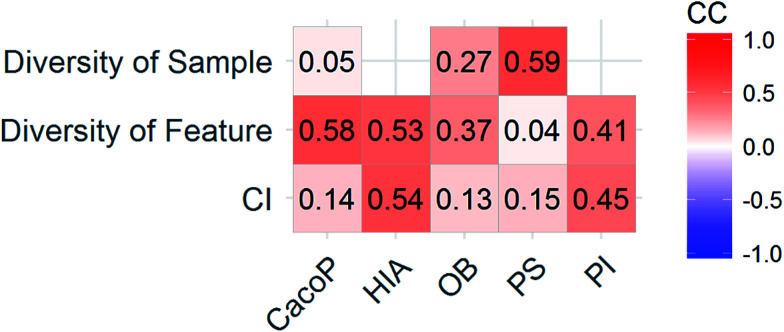
CI is a pairwise metric, where N^ij is the number of compounds with certain identification status by individual model i and j, and i,j ∈ {C,F} in which F denotes an individual model fails to classify the compound while C denotes it classify the compound correctly. In other words, CF is the number of compounds individual model i and j give inconsistent result, which is the situation of single fault. BF is the number of compounds both models fail. Then the degree of complementarity of EM can be calculated by averaging CI over all pairs. Fig. 15 presents the distribution of averaged CIs for each data set. It is observed that the averaged CIs of HIA and PI where nonsampling was applied were lower than those of others, which suggested that the additional diversity of sample space could help to promote the degree of complementarity. Moreover, a multiple linear regression model was established in terms of a connection between AUC scores and the characteristics (averaged CIs, the diversity score of sample and feature space) of EMs for the combined data set. Analysis of variance table (ESI Table S3†) of the regression model shows that all terms were statistically significant at the 0.05 level. This demonstrates that the performance of EM is associated with the complementarity and diversity of individuals. A rank based correlation analysis (Fig. 16) for each data set shows that all the correlation coefficients (CC) were positive, which indicate the positive relationships. Our findings are essentially consistent with the fact that the generation and maintenance of diversity in individuals help to improve the performance of EM, and AECF can effectively select complementary members to construct predictive models by our two-stage auto-adaptive optimization approach.

Fig. 15. The distributions of averaged CI for each data set.

Fig. 16. CCs between AUC and the characteristics of EMs for each data set.

Descriptor importance and contribution

In this work, the importance of descriptor was evaluated by the frequency that the number of times the descriptor was selected in individual models by multiple GA runs. The P-values were calculated as follows based on ten ensemble models using the binomial probabilities of descriptors being selected x times by GA runs.⁶⁷

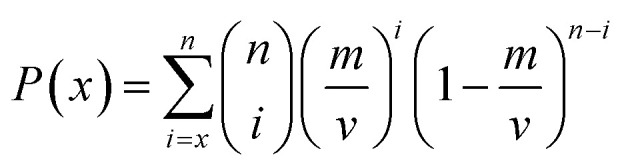14

where n was the total number of GA runs, i denotes the selected times (i is no less than x), v was the total number of descriptors, and m denotes the average number of times descriptors are selected, rounded to a whole number. Then the P-value, after being adjusted by the Bonferroni method, measures the probability of a descriptor selected more than x times in n draws whose size is m from a population of size v by random chance. In current investigation, the number of GA runs for each EM was 100, resulting in a total number of 1000 runs for ten EMs for each data set. As a result, there were 43, 37, 43, 35, and 65 statistically significant descriptors with a low P-value (P-value < 0.01) for CacoP, HIA, OB, PS, and PI, respectively. Table 6 lists the top 10 descriptors most frequently selected by GA for each data set, and their ranks based on the previous univariate statistical test (RUS) were also reported. The results show that some of the DLDs whose name ending with a suffix “_DES” were important for the classification task of CacoP, HIA, and OB, and the number of drug-likeness descriptors within the top 10 of the ranked list were 5, 3, and 2 for CacoP, HIA, and OB, respectively. Two DLD (QED_DES and PSA_DES) were most shared. PSA_DES represents the desirability function transformed molecular polar surface area, and QED_DES is a weighted composite of the other eight DLDs by the desirability function.⁴⁶ These two DLDs were also within the top 10 of RUS. These findings suggest that these DLDs can be used for the assessment of some ADME characteristics (e.g. CacoP, HIA, and OB) straightforwardly.⁴⁶ However, to make a better predictive model, they need to be combined with other informative descriptors. Hydrophobicity related descriptors (Crippenlog P, LipoaffinityIndex, and Mlog P) were more informative for identifying Pgp inhibitors, while some molecular fingerprints (PubchemFP12, MACCSFP129, PubchemFP500, KRFP18, MACCSFP49, and KRFP605) were more important for identifying Pgp substrates. It is particularly surprising that the ranks of contribution of some descriptors (e.g. MACCSFP70 and MACCSFP49) were quite different between the model based method and the univariate analysis. They were ranked lower, and even showed no significant by the univariate analysis. But they were important to construct predictive EMs, which suggests that there exists complex relationships between the descriptors and ADME characteristics. Due to the black-box property of EMs, the knowledge behind it remains unclear, and needs to be further explored in the future.

Top 10 descriptors most frequently selected by GA for each data set.

Data Set	Descriptor	Times selected	P-value	RUSa
CacoP	PSA_DES	272	<1.00 × 10−100	2
	QED_DES	226	<1.00 × 10−100	1
	HBA_DES	171	1.86 × 10−91	3
	ETA_dEpsilon_D	137	1.13 × 10−60	15
	ALOGP_DES	134	3.77 × 10−58	30
	HBD_DES	133	2.57 × 10−57	4
	Crippenlog P	119	4.84 × 10−46	10
	AATSC1c	115	5.77 × 10−43	9
	MDEN.22	89	1.01 × 10−24	101
	Xlog P	85	3.26 × 10−22	24
HIA	MACCSFP49	652	<1.00 × 10−100	30
	MDEO.11	480	<1.00 × 10−100	25
	PSA_DES	459	<1.00 × 10−100	3
	QED_DES	299	<1.00 × 10−100	1
	VC.4	452	<1.00 × 10−100	228
	HBA_DES	190	<1.00 × 10−100	2
	VC.3	148	2.24 × 10−70	83
	MATS4m	123	2.41 × 10−49	181
	MACCSFP70	108	6.69 × 10−38	672
	nAcid	105	9.93 × 10−36	122
OB	QED_DES	114	6.97 × 10−44	1
	KRFP3757	90	1.33 × 10−26	104
	SubFP85	88	2.74 × 10−25	22
	KRFP346	87	1.22 × 10−24	123
	KRFP438	85	2.33 × 10−23	309
	MACCSFP30	85	2.33 × 10−23	85
	Lipinski failures	83	4.22 × 10−22	3
	VE3_D	79	1.18 × 10−19	222
	KRFP4557	75	2.68 × 10−17	330
	PSA_DES	70	1.71 × 10−14	6
PS	PubchemFP12	116	1.04 × 10−42	2
	MACCSFP129	98	7.49 × 10−30	1
	PubchemFP500	76	2.58 × 10−16	269
	KRFP18	69	1.36 × 10−12	34
	maxHCsats	68	4.37 × 10−12	35
	MACCSFP49	66	4.28 × 10−11	467
	JGI10	63	1.17 × 10−9	60
	SpMAD_Dzs	62	3.40 × 10−9	28
	Lipoaffinity index	61	9.74 × 10−9	76
	KRFP605	60	2.74 × 10−8	36
PI	Crippenlog P	245	<1.00 × 10−100	6
	Lipoaffinity index	257	<1.00 × 10−100	3
	Mlog P	305	<1.00 × 10−100	1
	SpMin3_Bhs	200	<1.00 × 10−100	5
	WPATH	197	<1.00 × 10−100	82
	SubFP84	169	2.46 × 10−84	83
	SpMAD_Dt	145	3.21 × 10−63	31
	MDEC.23	141	6.89 × 10−60	2
	PubchemFP192	134	3.38 × 10−54	15
	ATSC0p	128	1.83 × 10−49	13

^aRUS-ranks based on the univariate statistical test.

Comparison with other algorithms and models

In the following section, our results of prediction performance were compared tentatively with those of published literatures. It was not easy to make a direct comparison between ours and those of previously published classification models because of the particularity of the data used and unbalance degree. Table 7 summarizes the previously published classification models for each property. Since many literatures developed more than one models, the best performances were reported. It is apparent that the present work was based on the largest data set, and achieved the best performance in some cases. Although some models produced better performances, they were based on a relatively small amount of compounds, and their classification cutoff values might be unreasonable in practice, or they were validated by a very small independent data set. For PI data, compared to our previously study,¹¹ AECF achieved better performances than the ensemble of different classifiers for the same independent data set.

Summary of previously published classification models.

Data set	Model	No. of compounds	Performancea	Reference
CacoP	LDA	51	88.90%	68
	KNN	712	75.5–88.5%	69
	LDA	157	84.20%	1
	LDA	146	83.30%	70
	GLDA	674	78–82%	71
	3PRule	1279	70.6–72.9%	2
	AECF	1387	85.77%	Ours
HIA	SVM	578	98.00%	19
	ANN	367	75.00%	72
	PLSDA, CART	225	84.00%	13
	SVM	578	99.00%	73
	CART, ANN	458	79.00–91.00%	3
	CART	645	74.2–85.3%	4
	AECF	734	93.82%	Ours
OB	ROC	184	74.00%	74
	21 models	969	71.00%	22
	RF,SVM,KNN	995	76.00%	5
	AECF	1076	78.49%	Ours
PS	SVM	332	69.24%	75
	SVM,RF,KNN	484	70.00%	16
	SVM,KNN,CART	195	81.00%	76
	SVM	99	80.00%	77
	SVM	332	88.00%	12
	NB	822	83.50%	78
	AECF	894	84.04%	Ours
PI	PLSDA	325	72.40%	79
	NB	609	82.20%	80
	RP,NB	1273	81.20%	14
	PLSDA,LDA	1275	85.0–86.0%	81
	KNN,SVM,RF	1935	75.00%	16
	SOM,NNET	206	80.80%	15
	SVM	1275	86.80%	82
	SVM,KNN,RF	1954	73.0–82.0%	17
	Ensemble(FDA,RF,SVM) Models	2079	85.50%	11
	AECF	2079	88.89%	Ours

^aThe accuracy of independent test data.

Moreover, our proposed approach was compared with two representative ensemble methods Bagging and Boosting. Bagging based ensemble models were built by training several classifiers with bootstrapped version of the original training data, while Boosting introduced a re-weighting technique to reduce the bias towards the majority class. In this work, the best individual model within the final AECF was picked out as the base classifier. The number of bootstrap samples and the number of iterations of boosting were optimized by a 10-fold CV, and the other parameters were set to default. Table 8 summarizes the average performances of ten models for each data set. It is clear that AECF achieved the best performances in terms of AUC, MCC, and Kappa for all data sets. Bagging and Boosting produced similar performances, and they were superior to the individual models in most cases. Then a pairwise Kruskal–Wallis rank sum test was used to clarify the difference of performances of these methods regarding to AUC. The P-values adjusted by false discovery rate are presented in ESI Table S4,† which supports AECF gains the best performance. The results indicate that there were significant differences between representative ensemble methods and AECF with low P-values (P-value < 0.001), which implied AECF significantly outperformed the others for these data sets.

Comparisons with Bagging and Boosting based ensemble models.

Data set	Subset	Model	AUC	MCC	SE	SP	OA	Kappa
CacoP	TES	SVM-Bagging	0.7785	0.5445	0.8156	0.7414	0.7908	0.5422
		SVM-Boosting	0.7866	0.5823	0.8766	0.6966	0.8164	0.5816
		AECF	0.8574	0.6935	0.8537	0.8612	0.8562	0.6889
	VAS	SVM-Bagging	0.7899	0.5650	0.8143	0.7655	0.7980	0.5616
		SVM-Boosting	0.7891	0.5847	0.8713	0.7069	0.8162	0.5840
		AECF	0.8602	0.6994	0.8574	0.8629	0.8592	0.6953
HIA	TES	RF-Bagging	0.8643	0.6432	0.9127	0.8160	0.8995	0.6316
		RF-Boosting	0.8251	0.7255	0.9823	0.6680	0.9393	0.7154
		AECF	0.8968	0.7404	0.9437	0.8500	0.9304	0.7357
	VAS	RF-Bagging	0.8430	0.5902	0.8899	0.7962	0.8766	0.5746
		RF-Boosting	0.8097	0.7012	0.9810	0.6385	0.9326	0.6905
		AECF	0.9182	0.7887	0.9563	0.8800	0.9459	0.7856
OB	TES	SVM-Bagging	0.6456	0.2776	0.7807	0.5104	0.7134	0.2757
		SVM-Boosting	0.6075	0.2546	0.8955	0.3194	0.7520	0.2442
		AECF	0.7981	0.5295	0.7604	0.8358	0.7792	0.5027
	VAS	SVM-Bagging	0.6591	0.3069	0.8015	0.5167	0.7313	0.3053
		SVM-Boosting	0.6348	0.3144	0.9030	0.3667	0.7709	0.3040
		AECF	0.7821	0.5137	0.7990	0.7652	0.7907	0.5004
PS	TES	KNN-Bagging	0.7128	0.4186	0.6930	0.7326	0.7174	0.4161
		KNN-Boosting	0.6660	0.3378	0.5616	0.7703	0.6902	0.3366
		AECF	0.8311	0.6738	0.8964	0.7659	0.8464	0.6709
	VAS	KNN-Bagging	0.6951	0.3903	0.6259	0.7642	0.7113	0.3895
		KNN-Boosting	0.6726	0.3598	0.5400	0.8051	0.7036	0.3553
		AECF	0.8139	0.6458	0.9022	0.7256	0.8344	0.6420
PI	TES	SVM-Bagging	0.8328	0.6574	0.8433	0.8223	0.8308	0.6544
		SVM-Boosting	0.8329	0.6617	0.8190	0.8468	0.8356	0.6610
		AECF	0.8898	0.7740	0.8900	0.8895	0.8898	0.7731
	VAS	SVM-Bagging	0.8407	0.6746	0.8402	0.8413	0.8408	0.6732
		SVM-Boosting	0.8260	0.6528	0.7895	0.8626	0.8331	0.6527
		AECF	0.8874	0.7699	0.8906	0.8842	0.8881	0.7691

Relationships between OB and other ADME properties

The relationships between OB and other ADME properties were analyzed by a Fisher's exact test based on the common compounds presented in the datasets. Table 9 presents the contingency table between OB and other ADME properties, and the corresponding standardized residuals are also reported. Although the number of common compounds between groups was small, the significant associations of OB–CacoP and OB–HIA were observed with low P values(<0.0001). Large positive standardized residual (3.44 greater than 1.96) of CacoP- and OB-indicated that when compounds belonged to CacoP–, they had significantly more likelihood to be OB–, and the similar occurrence was observed in OB–HIA. These finds suggested that the positive associations of OB–CacoP and OB–HIA were mainly driven by the undesirable class compounds. So the predictions of CacoP and HIA are meaningful toward the prediction of OB. However, the associations between OB and P-gp properties were not found to be statistically significant (P values more than 0.05 by Fisher's exact test).

Contingency table to explore the relationship between OB and other ADME properties^a.

ADME properties	Class	OB		P value#
		OB+	OB-
CacoP	CacoP+	123	15	1.68 × 10−5
	Std residual	1.101	−2.252
	CacoP-	36	23
	Std residual	−1.684	3.444
HIA	HIA+	133	7	1.67 × 10−7
	Std residual	0.615	−1.852
	HIA-	3	8
	Std residual	−2.194	6.608
PS	Substrate	33	6	0.557
	Std residual	0.227	−0.474
	Nonsubstrate	28	8
	Std residual	−0.237	0.494
PI	Inhibitor	1	2	0.121
	Std residual	−0.873	1.633
	Noninhibitor	41	10
	Std residual	0.212	−0.396

^a# P values were obtained using Fisher's exact test.

AD analysis

It is necessary to examine a model's predictive reliability for practical purpose. As mentioned above, an ensemble classification model was used to measure the reliability characterized by the chemical domain for each data set. This AD EM was developed based on the molecular descriptors selected by the final AECF, and the values of the predicted probability were output to distinguish Inside-AD and Outside-AD. The default cutoff value was set to 0.5, so that compounds with a predicted probability > 0.5 were labelled as Inside-AD and vice versa. As a result, all compounds from the two independent subsets (TES and VAS) were labelled as Inside-AD for each data set at the default cutoff value (COF), which illustrated that the similar chemical coverage to TRS was achieved by duplex algorithm.

Furthermore, the effect of the COFs of the AD probability on the model performance was investigated. In this way, COF varied from 0.5 to 0.9, and the performance metrics were recalculated on the Inside-AD compounds. Table 10 presents the results for each data set. We can see that higher performances were achieved when COFs were also higher. It is apparent that increasing COF decreased the number of Inside-AD compounds that the model covered, but in general, increased the performance of classification models.

Classification performance with different cutoff values of AD probability.

Dataset	Subset	COF	NCa		The performance of Inside-AD compounds
			Inside	Outside	MCC	AUC	SE	SP	OA	Kappa
CacoP	TES	0.5	347	0	0.701	0.860	0.866	0.853	0.862	0.698
		0.6	332	15	0.721	0.868	0.876	0.860	0.870	0.719
		0.7	297	50	0.729	0.873	0.870	0.875	0.872	0.726
		0.8	211	136	0.775	0.897	0.893	0.901	0.896	0.773
		0.9	76	271	0.826	0.921	0.922	0.920	0.921	0.825
	VAS	0.5	346	0	0.691	0.853	0.870	0.836	0.858	0.690
		0.6	333	13	0.713	0.865	0.874	0.856	0.868	0.711
		0.7	285	61	0.740	0.878	0.876	0.880	0.877	0.737
		0.8	198	148	0.760	0.894	0.863	0.925	0.884	0.752
		0.9	72	274	0.854	0.937	0.915	0.960	0.931	0.851
HIA	TES	0.5	184	0	0.803	0.921	0.962	0.880	0.951	0.802
		0.6	168	16	0.780	0.912	0.960	0.864	0.948	0.778
		0.7	131	53	0.838	0.951	0.964	0.938	0.960	0.834
		0.8	64	120	1.000	1.000	1.000	1.000	1.000	1.000
		0.9	21	163	1.000	1.000	1.000	1.000	1.000	1.000
	VAS	0.5	183	0	0.731	0.907	0.930	0.885	0.924	0.722
		0.6	172	11	0.742	0.906	0.938	0.875	0.929	0.736
		0.7	126	57	0.702	0.885	0.929	0.842	0.916	0.695
		0.8	66	117	0.821	0.932	0.941	0.923	0.938	0.817
		0.9	12	171	1.000	1.000	1.000	1.000	1.000	1.000
OB	TES	0.5	269	0	0.534	0.797	0.787	0.806	0.792	0.516
		0.6	234	35	0.547	0.799	0.799	0.800	0.799	0.532
		0.7	162	107	0.578	0.801	0.857	0.744	0.827	0.576
		0.8	88	181	0.529	0.795	0.773	0.818	0.784	0.506
		0.9	19	250	0.889	0.962	0.923	1.000	0.947	0.883
	VAS	0.5	268	0	0.514	0.788	0.772	0.803	0.780	0.492
		0.6	240	28	0.525	0.788	0.787	0.790	0.788	0.510
		0.7	172	96	0.616	0.840	0.823	0.857	0.831	0.598
		0.8	82	186	0.659	0.855	0.852	0.857	0.854	0.649
		0.9	16	252	0.537	0.933	0.867	1.000	0.875	0.448
PS	TES	0.5	224	0	0.677	0.840	0.812	0.869	0.847	0.677
		0.6	216	8	0.676	0.839	0.805	0.872	0.847	0.675
		0.7	177	47	0.710	0.848	0.780	0.917	0.865	0.708
		0.8	98	126	0.629	0.805	0.696	0.915	0.854	0.628
		0.9	31	193	NAb	NAb	NAb	1.000	1.000	NAb
	VAS	0.5	222	0	0.646	0.813	0.721	0.906	0.835	0.642
		0.6	215	7	0.641	0.809	0.707	0.910	0.833	0.636
		0.7	155	67	0.609	0.790	0.672	0.909	0.819	0.602
		0.8	82	140	0.693	0.813	0.656	0.970	0.867	0.675
		0.9	15	207	0.713	0.786	0.571	1.000	0.903	0.674
PI	TES	0.5	520	0	0.774	0.889	0.881	0.897	0.890	0.774
		0.6	514	6	0.779	0.891	0.879	0.902	0.893	0.778
		0.7	460	60	0.774	0.888	0.867	0.909	0.893	0.774
		0.8	290	230	0.778	0.891	0.842	0.939	0.914	0.778
		0.9	121	399	0.805	0.915	0.857	0.972	0.959	0.804
	VAS	0.5	519	0	0.757	0.880	0.866	0.894	0.882	0.757
		0.6	513	6	0.753	0.878	0.863	0.893	0.881	0.753
		0.7	461	58	0.768	0.884	0.854	0.914	0.892	0.768
		0.8	311	208	0.754	0.871	0.800	0.942	0.904	0.754
		0.9	113	406	0.637	0.771	0.563	0.979	0.920	0.623

^aThe number of compounds.

^bNot available.

External validation

After demonstrating the ADME prediction ability of AECF, we applied our models to predict ADME properties of the compounds from DrugBank 5.0 (ref. 83) (http://www.drugbank.ca) database. DrugBank database provides many ADMET related properties of compounds. In this work, 1925 approved compounds were chosen as an external database for prediction application. After removing the duplicates and overlapping compounds, 1793 unique compounds were prepared, and those compounds whose prediction probabilities are greater than or equal to 0.7 were extracted for investigation. As a result, there were 652, 1398, 1307, 814, and 974 compounds for predicting their ADME property of CacoP, HIA, OB, PS, and PI, respectively. Then the probability that the query compound was a member of the modeling data set was predicted by the corresponding AD model. Table 11 shows the predictions of our models for Inside-AD compounds based on the different COFs of the AD probability. Although classification cutoff values of CacoP and OB in DrugBank database were different from ours, overall, our predictive models achieved better concordance with DrugBank predictions. As expected, better performances were achieved based on the higher COFs at the expense of AD coverage in most cases. It is particularly surprising that the best performance in terms of AUC was obtained when COF equaled 0.6 for PS. These results suggested that an appropriate balance between the predictive reliability and the size of AD should be taken into consideration when determining a COF for practical application.

Prediction performance on DrugBank database with different Cutoff values of AD probability.

Property	COF	NCa		The performance of Inside-AD compounds
		Total	Inside-AD	MCC	AUC	SE	SP	OA	Kappa
CacoPb	0.5	652	634	0.6956	0.8237	0.6621	0.9853	0.8360	0.6624
	0.6	652	599	0.7154	0.8359	0.6873	0.9846	0.8481	0.6871
	0.7	652	450	0.7788	0.8716	0.7590	0.9843	0.8867	0.7631
	0.8	652	242	0.8680	0.9172	0.8409	0.9935	0.9380	0.8617
	0.9	652	40	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
HIA	0.5	1398	1347	0.6118	0.9015	0.9225	0.8805	0.8849	0.5683
	0.6	1398	1187	0.6314	0.9040	0.9083	0.8997	0.9006	0.5963
	0.7	1398	820	0.7293	0.9235	0.9070	0.9401	0.9366	0.7149
	0.8	1398	407	0.8176	0.9373	0.9048	0.9699	0.9631	0.8146
	0.9	1398	86	0.8622	0.9311	0.8750	0.9872	0.9767	0.8622
OBb	0.5	1307	1210	0.3384	0.7252	0.9261	0.5243	0.5917	0.2355
	0.6	1307	1036	0.3573	0.7369	0.9209	0.5530	0.6158	0.2590
	0.7	1307	667	0.4042	0.7596	0.9355	0.5838	0.6492	0.3094
	0.8	1307	291	0.5245	0.7925	0.9136	0.6714	0.7388	0.4737
	0.9	1307	33	0.5164	0.7727	0.8182	0.7273	0.7576	0.5000
PS	0.5	814	776	0.7358	0.8868	0.9221	0.8515	0.8737	0.7254
	0.6	814	737	0.7482	0.8959	0.9430	0.8487	0.8779	0.7348
	0.7	814	520	0.7355	0.8914	0.9430	0.8398	0.8712	0.7199
	0.8	814	241	0.6447	0.8694	0.9259	0.8128	0.8382	0.6135
	0.9	814	65	0.3898	0.7639	0.7778	0.7500	0.7538	0.3384
PI	0.5	974	919	0.6322	0.7329	0.4699	0.9960	0.9010	0.5821
	0.6	974	885	0.6476	0.7432	0.4906	0.9959	0.9051	0.6017
	0.7	974	708	0.7315	0.8011	0.6071	0.9950	0.9336	0.7072
	0.8	974	319	0.8429	0.8958	0.8033	0.9884	0.9530	0.8389
	0.9	974	55	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000

^aThe number of compounds.

^bClassification cutoff values of these properties in DrugBank database are different from ours.

Limitations and future work

Although AECF makes encouraging predictive performance, it has some limitations and shares common weakness associated with EM classification task. First, although our prediction work was developed based on the large databases, the compounds were actually from various literature sources, increasing the risk of erroneous judgment. So such large and compatible classification data sets are still encouraged to yield more reliable predictions. Second, AECF shows reliable performances on ADME datasets with the IR range of 1.48–6.32. However, this cannot guarantee that the same performance can be achieved on a more unbalanced dataset when a reasonable classification cutoff value is determined. Therefore, the performance on a higher degree of unbalanced dataset needs to be investigated in the future. Third, AECF is a GA based ensemble approach, and multiple runs of GA is performed in order to keep diversity and quality of individual model. The number of GA runs depends on the number of balanced datasets to construct individual models. However, the exact number is hard to decide. More runs may result in a more reliable and extensive individual model pool at a cost of more computation time. On the other hand, our results demonstrate that the optimal solutions for modeling are data-specific, so all combinations of the methods from supplied method pools including data balancing methods, base classifiers, and ensemble rules need to be investigated, resulting in hundreds of routes. It is also computationally expensive. Therefore, more computationally efficient modeling techniques need to be developed to reduce the computation time and to improve performance in future. Finally, AD problem was addressed by an ensemble classification model. Our results illustrate that this technique can define AD efficiently, while the selection of descriptors for AD analysis may be a limitation. Building AD models on each individual predictor set instead of the union set may allow more discrimination. The point is that the proposed approach achieved substantially good performance on Inside-AD compounds, and a higher classification confidence may be obtained by choosing a higher COF of AD predicted probability.

Conclusions

The in silico prediction of ADME properties has been a challenge for drug designers. In the present work, we propose a novel adaptive ensemble classification framework (AECF) for ADME prediction. AECF can deal with classification task for different kinds of ADME datasets by employing resampling and feature selection techniques. The design of AECF was motivated by the belief that the predictive performance of ensemble models can be affected by the different combination of individual classifiers and fusion rules. For this reason, we considered five sampling methods, seven base modeling techniques, and ten ensemble rules as options. For different kinds of ADME datasets, AECF automatically chose the proper route of constructing predictive models according to their IR, and the developed optimal procedure was full automatic from the selection of the optimal combinations to the optimal ensemble pruning. We evaluated the performance of AECF using five updated ADME datasets. As a result, we have achieved better performance compared with the individual models and two representative ensemble methods Bagging and Boosting. The performance of AECF was evaluated on two independent datasets, and the average AUC values were 0.8574–0.8602, 0.8968–0.9182, 0.7821–0.7981, 0.8139–0.8311, and 0.8874–0.8898 for CacoP, HIA, OB, PS and PI, respectively. Besides, the external validation by DrugBank database further confirmed our predictive results.

Particularly, we have performed a series of analysis to elucidate the potential advantages of our framework. A fitness function was defined to assess the goodness of individual models during the ensemble pruning, and results of the optimal adjustment weights further confirmed the necessity of incorporating both performance and diversity for ensemble construction. What's more, the degree of complementarity of AECF was evaluated by a complementary index analysis. We found that there were some correlations between the performance of AECF and the characteristics of its individual models. The characteristics of individual models were measured by (1) the sample and feature space coverage, and (2) the diversity score of sample and feature space. Our results demonstrate that AECF is efficient to make a better use of modeling samples and at the same time informative feature sets can be achieved by GA, and the additional diversity in both sample and feature space encouraged good cooperation among the AECF ensemble members.

An ensemble based technique was used to define AD in this paper. Our results show that Inside-AD compounds are more likely to be correctly predicted. The definition of AD has made AECF more practical and applicable. By the analysis of the effect of different COFs of AD probability on the model performance, we found that in general, better performance could be achieved based on higher COFs at the expense of AD coverage. Therefore, in order to obtain higher prediction confidence, the tradeoff between the performance and AD coverage should be taken into consideration when using AECF for application.

Conflicts of interest

The authors declare that there is no conflict of interest involved in this paper.