Nonexponential kinetics captured in sequential unfolding of polyproteins over a range of loads

Abstract

While performing under mechanical loads in vivo, polyproteins are vitally involved in cellular mechanisms such as regulation of tissue elasticity and mechano-transduction by unfolding their comprising domains and extending them. It is widely thought that the process of sequential unfolding of polyproteins follows an exponential kinetics as the individual unfolding events exhibit identical and identically distributed (iid) Poisson behavior. However, it was shown that under high loads, the sequential unfolding kinetics displays nonexponential kinetics that alludes to aging by a subdiffusion process. Statistical order analysis of this kinetics indicated that the individual unfolding events are not iid, and cannot be defined as a Poisson (memoryless) process. Based on numerical simulations it was argued that this behavior becomes less pronounced with lowering the load, therefore it is to be expected that polyproteins unfolding under lower forces will follow a Poisson behavior. This expectation serves as the motivation of the current study, in which we investigate the effect of force lowering on the unfolding kinetics of Poly-L₈ under varying loads, specifically high (150, 100 ​pN) and moderate-low (45, 30, 20 ​pN) forces. We found that a hierarchy among the unfolding events still exists even under low loads, again resulting in nonexponential behavior. We observe that analyzing the dwell-time distributions with stretched-exponentials and power laws give rise to different phenomenological trends. Using statistical order analysis, we demonstrated that even under the lowest load, the sequential unfolding cannot be considered as iid, in accord with the power law distribution. Additional free energy analysis revealed the contribution of the unfolded segments elasticity that scales with the force on the overall one-dimensional contour of the energy landscape, but more importantly, it discloses the hierarchy within the activation barriers during sequential unfolding that account for the observed nonexponentiality.

Graphical abstract

Highlights

• •Poly-L₈ unfolding shows nonexponential kinetics at forces ranging from 150 to 20 ​pN.
• •Different phenomenological trends are observed for the dwell-time distributions.
• •The unfolding events were shown to be dependent and not identically distributed.
• •Free energy analysis reveals elastic impact and hierarchy in the unfolding barriers.

1. Introduction

Polyproteins own a unique structure, in which its constituting domains are connected in tandem. In some cases, polyproteins are tethered between two physiological surfaces, and perform under mechanical loads. Some well-known examples can be found in muscle contraction (Kellermayer et al., 1997; Rief et al., 1997; Tskhovrebova et al., 1997; LeWinter and Granzier, 2010; Freundt and Linke, 2019; Rivas-Pardo et al., 2020), mechano-sensing and cell-adhesion (Oberhauser et al., 2002; Vogel and Sheetz, 2006; del Rio et al., 2009; Leckband and de Rooij, 2014; Haining et al., 2016; Klapholz and Brown, 2017; Alonso-Caballero et al., 2021). This configurational array enables polyproteins to perform under the application of loads by regulating tension and energy storage through unfolding and extending some of their domains (Fantner et al., 2006; Astley and Roberts, 2012; Roach et al., 2013; Berkovich et al., 2018; Alegre-Cebollada, 2021). For such system to maintain its integrity, a controlled hierarchical mechanism is advantageous for its efficient physiological function.

Single molecule force spectroscopy (SMFS) studies point to the existence of correlations within polyproteins (Bura et al., 2007, 2008; Chetrit et al., 2020), and history dependence (Rief et al., 1998; Zinober et al., 2002; Lannon et al., 2012; Tych et al., 2015; Sumbul et al., 2018; Elias-Mordechai et al., 2020) that manifest in the unexpected unfolding times distributions. Early dwell-times analyses of polyprotein unfolding expected their distributions to follow an exponential decay. This postulate relied on the assumption that sequential forced unfolding in polyproteins is a Poisson process, which requires the unfolding events to be independent of each other and be identically distributed (iid). However, several studies have shown that the resulting empirical distributions did not follow the Poisson distributions (Brujic et al., 2006, 2007; Garcia-Manyes et al., 2007). This observation led to an effort to explain the measured deviation from exponentiality by means of static and dynamic disorders (Kuo et al., 2010; Chatterjee and Cherayil, 2011; Zheng et al., 2014; Costescu et al., 2017; Kundu et al., 2020), corrugated energy landscapes (Brujic et al., 2006; Lannon et al., 2012), and as consequence of the polymeric nature of the proteins (Bell and Terentjev, 2016). In their pioneering computational work, Bura et al., showed how unfolding in polyproteins become less correlated when reducing the applied force from 88 to 66 ​pN (Bura et al., 2007, 2008). This led to the current understanding that high correlations (or history dependence) between unfolding events in polyproteins, which are present under high loads (Lannon et al., 2012; Chetrit et al., 2020) and under constant pulling velocities (Rief et al., 1998; Zinober et al., 2002; Tych et al., 2015; Schoeler et al., 2016; Sumbul et al., 2018), are expected to vanish or be considerably reduced under the application of low forces (Bura et al., 2007, 2008; Chetrit et al., 2020).

In this work we use Atomic Force Microscopy (AFM) and Magnetic Tweezers (MT) to apply forces ranging from 150 ​pN down to 20 ​pN to trigger unfolding in a polyprotein construct comprised of eight domains of protein L (Poly-L₈) as a model system. We first analyze the general unfolding processes using two approaches based on dwell-time analysis, and surprisingly, we observe that one of them provides a better estimation of the characteristic unfolding times with respect to the dwell-time medians at each force, and their characteristic exponents show opposite trends. To understand the latter outcome, we perform statistical correlation analysis of the individual unfolding events, and reveal that the low force applied here did not remove the correlations between unfolding events. Lastly, through the reconstruction of the Potentials of Mean Force (PMFs) from the Poly-L₈ unfolding traces, we demonstrate the effect of the applied forces on the one-dimensional morphology of the polyprotein energy landscape.

2. Materials and methods

2.1. Protein expression and purification

All chemicals were purchased from Sigma-Aldrich, unless otherwise specified. For AFM measurements, eight repeats of protein L (B1 domain of Finegoldia magna) were inserted in a pQE80 with a His-tag at the N-terminus and a cysteine at the C-terminus. For magnetic tweezers measurements, eight repeats of protein L (were inserted into a pFN18a expression vector (Promega) modified to introduce a HaloTag at the N-terminus and a His-tag and a cysteine at the C-terminus (Popa et al., 2013b). The His-tag was utilized for protein purification. The plasmids were transformed into E. coli BLR(DE3) competent cells which were then grown in Luria Broth (LB) in presence of 50 ​μg/mL carbenicilin at 37 ​°C until OD⁶⁰⁰ reached 0.6–0.8. The protein overexpression was induced with 1 ​mM Isopropyl β-D-1-thiogalactopyranoside (IPTG) overnight at 25 ​°C. The induced cells were then pelleted and re-suspended in E/W buffer (50 ​mM NaH₂PO₄, 300 ​mM NaCl, 1 ​mM DTT, 5% glycerol, pH 7), followed by lysis using lysozyme, 1% Triton X-100, DNase, and RNase, in presence of protease inhibitors. Cells were further lysed using sonicator, and the soluble protein fractions were filtered using 0.45 ​μm and 0.22 ​μm PES membrane filters, or separated using high-speed centrifugation. The soluble fraction was passed through a chemical affinity purification Ni-NTA column. The column with adsorbed protein was washed with E/W buffer containing 7 ​mM Imidazole, while the elution of protein was done using E/W buffer with 250 ​mM Imidazole. Subsequently, the protein was injected into size exclusion chromatography column (S-300, Akta GE) and eluted with a HEPES buffer (50 ​mM HEPES, 150 ​nM NaCl, 5% glycerol, pH 7.2). For magnetic tweezers measurements, the construct was further conjugated with a 604 base pairs DNA linker, which was cloned from λ-phase DNA (Thermo Scientific) with a di-Biotin at the 3′ end and amine at the 5’ end. The conjugation was done using a 30 ​min reaction between a Sulfosuccinimidyl-trans-4-(N-maleimidomethyl)cyclohexane-1-carboxylate (Sulfo-SMCC) bifunctional ligand, (EMD Millipore) and the amine group on the DNA in Borax buffer (50 ​mM Na₂B₄O₇, 150 ​mM NaCl, pH 8.5), followed by a cleaning-up step using a Macherey-Nagel NucleoSpin kit (Fisher Scientific), and reaction with the protein at 4 ​°C, overnight (Popa et al., 2016).

2.2. Surface functionalization

For AFM experiments, circular glass coverslips (15 ​mm in diameter, Ted Pella) were cleaned using the Piranha cleaning procedure, which consists of a 3:1 mixture of concentrated H₂SO₄ (EMD Chemicals) and 30% (wt/vol) H₂O₂ (Fisher Scientific) for 30 ​min at 80 ​°C (caution: Piranha solution is corrosive and can lead to violent reactions with organic solvents) (Popa et al., 2013a). After cleaning, the surfaces were dried in the oven for >1 ​h at 100 ​°C. Following the drying step, a layer of 10 ​nm of Ni–Cr (GoodFellow) was deposited, followed by a layer of 20–30 ​nm of gold (GoodFellow), using an Edwards Auto 306 evaporator.

The fluid chambers used for single-molecule magnetic tweezers measurements were assembled by sandwiching two glass coverslips (Ted Pella) separated by parafilm strips. The bottom surfaces were cleaned thoroughly by sonicating in 1% Hellmanex solution for 20 ​min, followed by successive sonication in acetone and methanol. After drying in oven at 100 ​°C, the surfaces were activated using air plasma for 20 ​min, and immersed in 0.1% (3-aminopropyl)-trimethoxysilane solution in methanol, for 20 ​min. Following the wash with methanol to remove the excess silane, the surfaces were cured for >1 ​h at 100 ​°C. The bottom surfaces were cleaned by sonicating in 1% Hellmanex solution for 20 ​min and then rinsing with ethanol. The assembled fluid chambers were incubated with a mixture of 1% v/v glutaraldehyde and 0.05% w/v amine-terminated polystyrene beads (2.6 ​μM, Spherotech) in PBS buffer (50 ​mM Na₂HPO₄/NaH₂PO₄, 150 ​mM KCl, and pH 7.2) for 1 ​h. Washing the chamber with PBS buffer to remove non-adsorbed glutaraldehyde and polystyrene beads, next, it was incubated with a solution of 10 ​μg/mL amine-terminated chloroalkane ligand (HaloTag Ligand, Promega) in PBS, for 4 ​h at room temperature. The final step involved washing the chambers and then passivating them with 1% BSA in Tris-KCl solution (1% w/v sulfhydryl blocked-BSA, 20 ​mM TRIS, 150 ​mM KCl, pH 7.4). To apply magnetic force to the biomolecules, superparamagnetic beads functionalized with Streptavidin (Dyna beads M-270, Thermo Fisher Scientific) were used. The Dyna beads were first washed three times with PBS buffer and then passivated with Casein solution (Fisher Scientific, 1.5% w/v in PBS) at 4 ​°C. After washing the beads with PBS three times, the beads were resuspended in the same buffer.

2.3. Single Molecule Force spectroscopy experimental setup

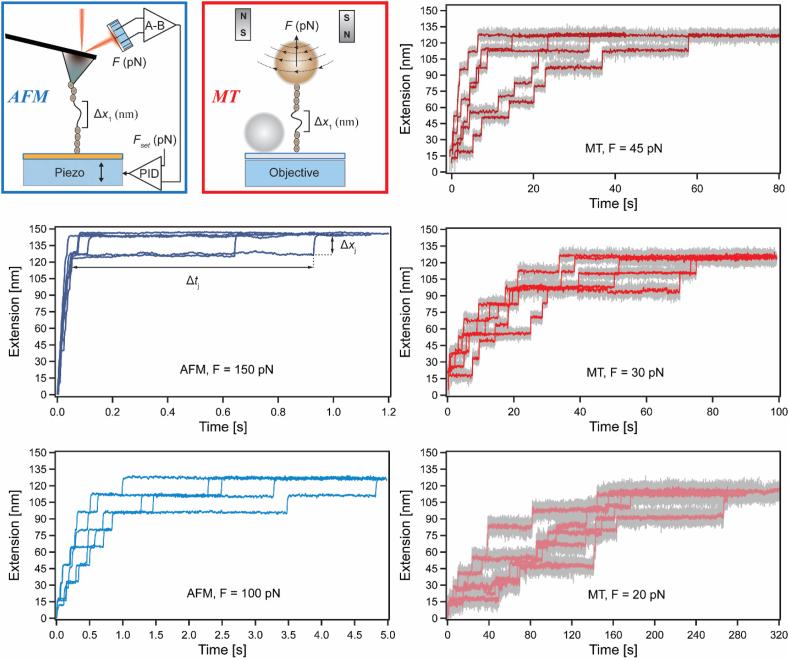
The AFM measurements were done on a custom-built AFM setup, as described in reference (Berkovich et al., 2012; Popa et al., 2013a). Following ∼10 ​min protein-adsorption onto the gold-functionalized surface (diluted to ∼100 ​nM), the surface was gently washed with PBS buffer and mounted on the piezo-element of the AFM (PicoCube, Physik Instrumente). An AFM probe with a sharp cantilever tip (MLCT, Bruker) was mounted on the instrument and the laser beam was aligned, before approaching the surface to seal the measurement chamber. The force experienced by the cantilever was measured through the change in the position of the reflected laser beam, using a quadrant photodiode (PD, First Sensor). The cantilever was first calibrated using its nominal resonant frequency and its deflection while in-contact with the surface, and had a typical spring constant of ∼15 ​pN/nm (Popa et al., 2013a). Force-clamp operation, where the force is maintained constant at a given setpoint, was accomplished using a proportional-differential-integral (PID) active system (Analog PID Controller - Stanford Research Systems). During operation, the piezo actuator continually approached and retracted the protein-covered slide to and from the cantilever. When a protein attached to the cantilever, the position of the piezo actuator was continuously adjusted by the PID to ensure constant tension on the protein. Following each unfolding event, the piezo moved to restore the tension decrease due to increasing contour length, with a time response of ∼1 ​ms. Possible inaccuracies in the applied force may be introduced to the AFM experiments when the calibration is performed on different sets of measurements or using different cantilevers (Pimenta Lopes et al., 2019). The number of independent force measurements that were analyzed from data measured (only 5 out of the 22 unfolding traces at 150 ​pN) are reported in Table S1 in the supporting information.

Our custom-made magnetic tweezers instrument is built on top of an inverted microscope (Olympus, using 100× oil-immersion objective); details can be found in reference (Dahal et al., 2020). The chloro-alkane functionalized chamber was first incubated with ∼100 ​nM of protein solution for 10 ​min. The fluid chamber was then washed with PBS buffer, to remove non-adsorbed molecules. After mounting the chamber on the inverted microscope, the paramagnetic beads were added to the chamber and were left to sediment for ∼1 ​min. The permanent magnets (N52, K&J Magnetics) were then approached the low force position (∼2 ​pN), which resulted in detachment of non-specifically attached beads, without unfolding the tethered protein molecules. Single-molecule measurements were performed by approaching the permanent magnets using a voice-coil (Equipment Solutions). The positions of the beads were monitored using live-image processing. First, two region-of-interest (ROIs) of 128 ​× ​128 pixels, centering a tethered paramagnetic bead and a surface-glued non-magnetic reference bead, were selected. Vertical-stack libraries of both beads were acquired by moving the objective in steps of 20 ​nm with the help of piezo actuator (Physik Instrumente). These stack libraries were then used during the measurement to determine the relative position of the paramagnetic bead with respect to the reference bead, which gave the relative extension of the tethered molecule.

The live-image processing consisted of calculating the 2D-fast Fourier transform (FFT) of the selected ROIs, followed by a radial profile around the center (Popa et al., 2016). The absolute positions of a beads were determined from the Gaussian fit of the Pearson correlation between the radial profile obtained during measurement and the profiles stored in the stack library. Any drift was actively corrected during the measurement, by moving the position of the piezo actuator, to maintain the reference bead in-focus. Due to the slow decay of the magnetic field gradient (proportional to the experienced force) with separation from the magnets, which is on the mm scale (Popa et al., 2016), magnetic tweezers effectively operate in a passive force-clamp mode, whereas the change in the position of the paramagnetic bead due to unfolding events has a negligible effect on the applied force. The used covalent attachment chemistry, based on HaloTag, together with the active correction of the focal drift, enabled hour-long measurements, where the same molecule was exposed repeatedly to cycles of low and high force (Popa et al., 2016).

3. Results and discussion

3.1. Forced sequential unfolding of Poly-L₈ reveals nonexponential/asymptotic kinetics

We measured the sequential unfolding dynamics of protein-L (O'Neill et al., 2001) within its eight-repeat polyprotein construct under high loads of 150 (N ​= ​22 sequences with 8 unfolding events, n ​= ​176 unfolding events in total) and 100 ​pN (N ​= ​112, n ​= ​856) using AFM, and under moderately-low forces of 45 (N ​= ​91, n ​= ​728), 30 (N ​= ​28, n ​= ​224) and 20 ​pN (N ​= ​21, n ​= ​188) with MT. Fig. 1 shows several representative traces from each of these measurements, all displaying characteristic “staircase” unfolding pattern comprised of eight unfolding events. In this figure, and in those to follow, AFM related data are color coded with shades of blue, and MT with shades of red. The dwell-times of the unfolding events, Δt_j were taken as the time difference between unfolding events, characterized by an extension Δx_j. The unfolding length (step sizes) were characteristic to Poly-L₈ (contour length 18.6 ​nm), and proportional to the applied loads (see Fig. S1 in supporting information). For this analysis we considered only traces with eight sequential unfolding events, displaying force dependent characteristic Δx, within the same experimental timeframe (during which, none of the measured polyproteins detached) (Popa et al., 2013b, 2016).

Fig. 1.

Unfolding of Poly-L₈ under constant stretching forces. The upper left panel illustrates the unfolding traces measured in Force-Clamp AFM (left-side, blue frame) and MT (right-side, red frame) settings, with seven folded domains of the Poly-L₈ constructs portrayed by dark gray spheres, and an unfolded domain chain marked with its Δx extension. Exemplary unfolding traces displaying eight events under loads of 150 ​pN (dark blue), with arrows marking the unfolding dwell-time of the 8th event (Δt₈) and its corresponding extension (Δx₈), 100 ​pN (blue), 45 ​pN (dark red), 30 ​pN (red), and 20 ​pN (light red). (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

The unfolding dwell-times measurements were fitted to either a stretched-exponential (SE), also referred to as “Weibull distribution“ (Frauenfelder et al., 1991; Lannon et al., 2012; Costescu et al., 2017), or a truncated power law (TPL) (Chetrit et al., 2020). Compared with several approaches, the SE distribution was shown to be the best functional model that quantifies sequential unfolding data (Lannon et al., 2012). It is known to reliably describe relaxation kinetics in disordered systems (Klafter and Shlesinger, 1986) and transition rates within the complex energy landscape of proteins (Frauenfelder et al., 1991). The power law ansatz is a generalization of the exponential distribution, which was shown to adequately model simulated sequential unfolding dwell-time distributions (Bura et al., 2007, 2008). This approach was extended as TPL (truncated by physical limitations of the system), and leans on the parametrization of systems that display subdiffusive behavior (here in the context of crossing energy barriers), which are characterized by coexisstence of short dwell times along with the extremely long ones (Metzler and Klafter, 2000; Burov et al., 2011; Dentz et al., 2004; Chetrit et al., 2020). In our previous work (Chetrit et al., 2020) we explored the SE and TPL approaches for the analysis of the dwell-time distributions under a single force. Here we expand this analysis to study the parametrization behavior of these models over a range of applied loads.

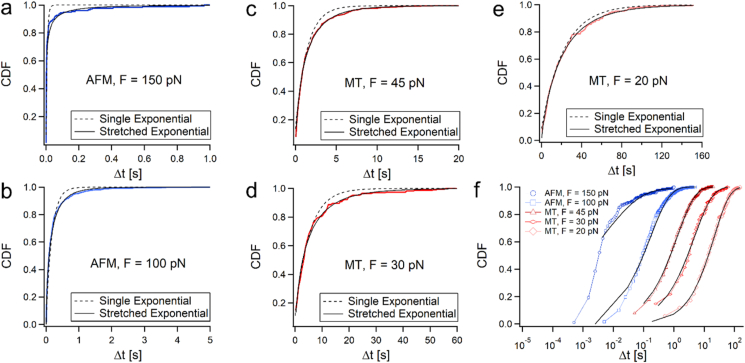
We begin with calculating the empirical cumulative distribution functions (CDFs) per applied load (Fig. 2, colored lines). We used these distributions for the evaluation of their medians, μ_½(Δt), as their characteristic times. Due to the nonexponential/asymptotic nature of the dwell-times distributions, the median serves as a better characteristic time than the mean, as it is more statistically resistant in the sense that it is not unduly influenced by outliers, of either exceptionally fast or slow dwell-time measurements. The details of the statistical analysis of the data (medians and quartile values) are given in Table S1 in the supporting information. Each data set was then fitted with SE of the form:

$${\phi }_{SE}\left(\text{Δ}t;\tau ,\beta \right)=1-e^{-{\left(\frac{\text{Δ}t}{\tau }\right)}^{\beta }}$$ (1)

Fig. 2.

Unfolding dwell-time CDFs for (a) 150 ​pN, (b) 100 ​pN, (c) 45 ​pN, (d) 30 ​pN, (e) 20 ​pN, and (f) all the CDFs on the same timescale, demonstrating their stretch over several decades.

for Δt ​≥ ​0. In this model, τ signifies the timescale of the unfolding process, and β, the exponential constant, describes the stretching of the data when it expands over several decades. At β ​= ​2 Eq. (1) describes a Gaussian distribution, and at β ​= ​1, it reduces to the Poissonian single exponential dependency.

Fig. 2 shows the five empirical CDFs calculated at each load, and their SE fittings (continuous lines). The CDFs exhibited excellent fitting statistics when using Eq. (1) (0.006 ​< ​χ² ​< ​0.410). For comparison with the non-iid (Poissonian) behavior, the CDFs were also fitted with a single exponential, φ_{single exponential}(Δt; τ) ​= ​1 – exp(–Δt/τ) (dashed lines in Fig. 2a–e). The single exponential fits (dashed lines) were not as good as the SE fits (0.085 ​< ​χ² ​< ​1.156), however their fitting improved at the lowest force. All the fitting parameters and their goodness of fits (with additional statistics) are given in Table S2 in the supporting information.

The second approach is based on Continuous Time Random Walk (CTRW) formalism (Montroll and Weiss, 1965), according to which we describe the time dependent position of the consecutive unfolding trajectories as transport between traps. These traps represent structural heterogeneities manifesting as local wells in the overall energy landscape of the polyprotein. The externally applied force gradient induces the motion from one local well to the other by tilting the barriers between them, and consequently affecting the flux and velocity distributions. The overall transport can then be expressed by the PDFs of the dwell-times, ψ(Δt), and step-sizes, p(Δx) (Metzler and Klafter, 2000). When these distributions behave asymptotically, anomalous dynamics are conveyed. If the transport process is of Poisson nature, which means that the time events are iid, then the dwell-times density function is conveniently described by a single exponential decay, τ⁻¹exp(Δt/τ) (here τ ​= ​⟨Δt⟩), and is associated with normal (Gaussian) transport. The algebraic decay form, ∼(τ/Δt)^1+α, can be used when asymptotic behavior appears (Metzler and Klafter, 2000; Metzler et al., 2014). Here the disorder exponent, α, varies between 0 and 1, where anomalous transport is characterized with α ​< ​1 (Metzler and Klafter, 2000), and is used to describe crossing over varying energy barriers (Ben Arous et al., 2002; Burov and Barkai, 2007).

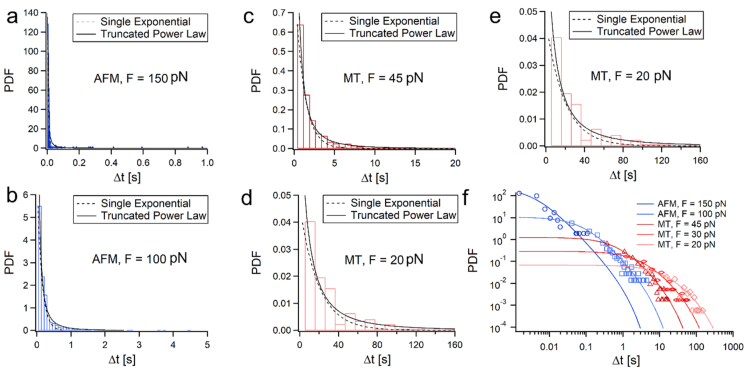
In the case of forced consecutive unfolding in polyproteins, the time distributions were reported not to follow the exponential decay, while the step-size distributions did not exhibit any asymptotic behavior (Brujic et al., 2006, 2007; Garcia-Manyes et al., 2007). In our previous work, based on the CTRW approach, we showed that under high load the unfolding dwell-time distributions of poly-(I91)₈ sample times that span over several orders of magnitude, and therefore could be represented with the heavy-tailed asymptotic form of ψ(Δt) (Chetrit et al., 2020), using a TPL ansatz (Dentz et al., 2004; Burov et al., 2011):

$${\psi }_{TPL}\left(\text{Δ}t;\tau ,\alpha ,t_c\right)=C{\left(1+\frac{\text{Δ}t}{\tau }\right)}^{-1-\alpha }{e}^{-\frac{\text{Δ}t}{t_c}}$$ (2)

where C is a normalization factor (Dentz et al., 2004), and t_c is the cutoff time (the longest dwell-time measured), which reflects the maximal barrier formed at the energy landscape of the polyprotein. This description implies that during the transition times (τ ​< ​Δt ​< ​t_c), ψ_PDF behaves as a power-law with an exponent –(1 ​+ ​α), and decays exponentially at Δt ​> ​t_c.

For the calculation of the dwell-times probability density functions (PDFs), we estimated the bin-size for each PDF with the Freedman-Diaconis rule (Freedman and Diaconis, 1981), Δb ​= ​2^.IQR^.n^–/13, where n is the number of events, and the interquartile range is given by IQR ​= ​Q₃ – Q₁, in which Q₁ is the 1st quartile and Q₃ is the 3rd quartile. This measure provides an extent of the spread in a data set, and is useful for clustering the bulk of the values (located around the mean). The calculated dwell-time PDFs for the five loads, fitted with Eq. (2) are shown in Fig. 3. Here, apart from the 150 ​pN poor fit (χ² ​= ​1947), all the other PDFs exhibited excellent fitting with Eq. (2) (5.293∗10⁻⁵ ​< ​χ² ​< ​0.1885).

Fig. 3.

Poly-L₈ unfolding dwell-time PDFs and their TPL fits for (a) 150 ​pN, (b) 100 ​pN, (c) 45 ​pN, (d) 30 ​pN, (e) 20 ​pN, and (f) all the PDFs on the same timescale, demonstrating their stretch over several decades (the PDFs are given by the empty symbols, and the fits with the lines).

We additionally fitted the PDFs with a single exponential, ψ_{single exponential}(Δt; τ) ​= ​τ⁻¹exp(–Δt/τ) (dashed lines in Fig. 3a–e). The single exponential fits (dashed lines) showed comparable goodness of fits to the TPL model, in which 6.31∗10⁻⁵ ​< ​χ² ​< ​0.5212 (with the similar exception at 150 ​pN: χ² ​= ​1296). However, their Kolmogorov-Smirnov (K–S) test did not show agreement with the single exponential, while the TPL showed better fitting with the lowering of the force (see Table S3 in the supporting information). All the fitting parameters and their goodness of fits (with additional statistics) are given in Table S3 in the supporting information.

From a model fitting perspective, the SE model describes the unfolding dwell-time CDFs better than the single exponential (although this difference somewhat reduces at 20 ​pN), and the TPL model fits the empirical PDFs slightly better than a single exponential. Yet, as previously mentioned, the physically significant parameter is the characteristic dwell-time, given by μ_½(Δt). We therefore focus on its model-dependent parametric estimation, τ, as a comparative measure between the hypothesized parametric distributions, i.e., SE, TPL and single exponential distributions.

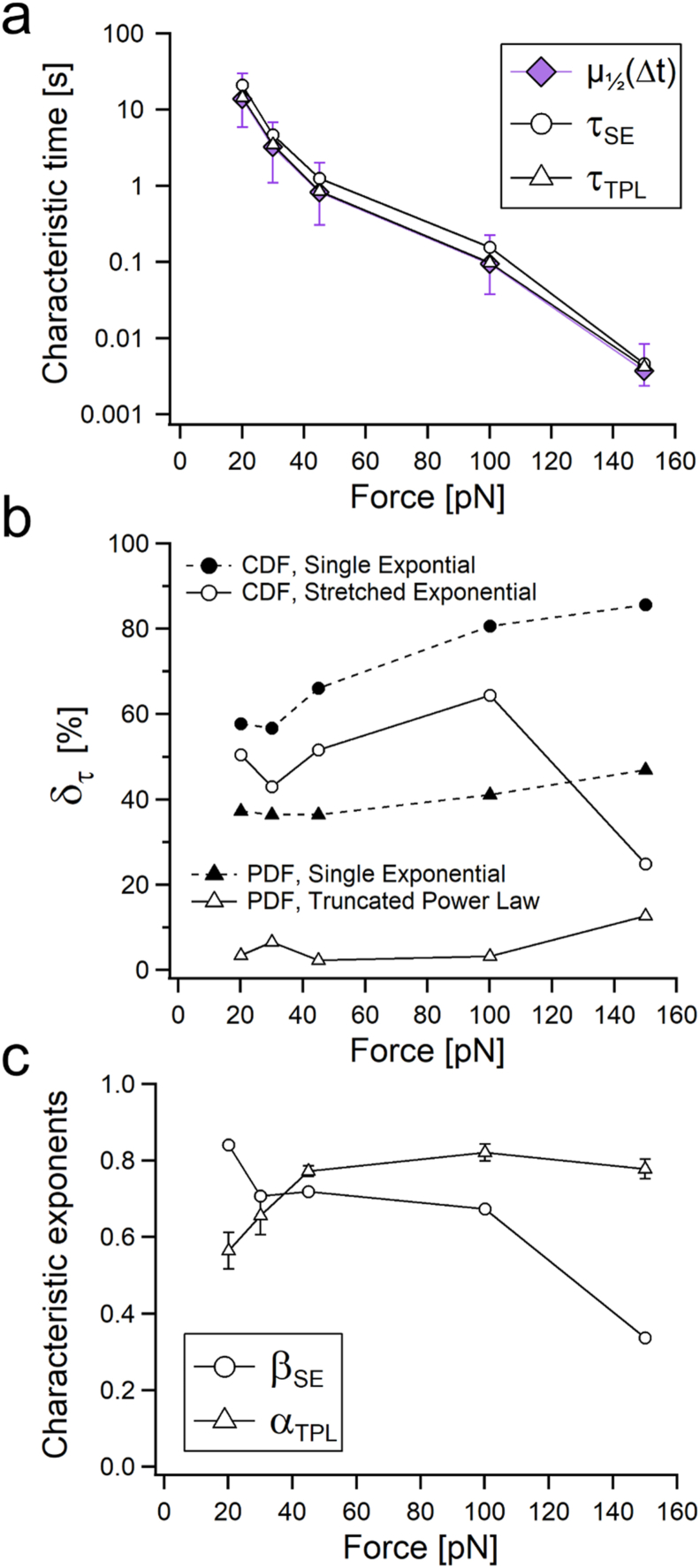
Fig. 4 summarizes the resulting parametric fits of the unfolding dwell-times CDFs and PDFs with SE and the TPL, given by Eqs. (1), (2) respectively (as shown in Fig. 2, Fig. 3). The characteristic dwell-times are shown in Fig. 4a. To put these times in perspective, we added the experimental characteristic dwell-times, given by their medians, μ_½(Δt) to Fig. 4a. These dwell-times were calculated directly from the data without any model assumption, along with their corresponding IQRs as a statistical measure of spread (marked with purple diamonds). Generally, as one expects, all the characteristic times become smaller with the applied load, which indicate the increase of unfolding rates as the load increases (Schlierf et al., 2004; Liu et al., 2009). Comparing the values of τ_CDF and τ_PDF with the medians shows that while both model-based characteristic time evaluations follow the same trend and order of magnitude, τ_TPL is considerably closer to the median values at every force than τ_SE.

Fig. 4.

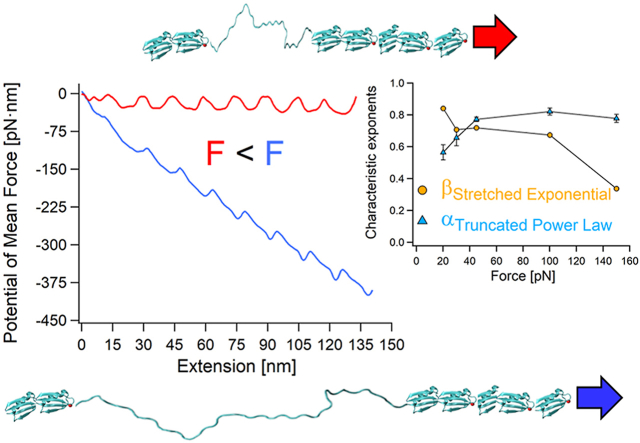
Force variation of the unfolding dwell-time parametrization obtained from the SE (from CDFs, empty circles) and the TPL (from PDF, empty triangles) approaches. (a) Characteristic times obtained from CDFs, PDFs, and dwell-time medians (purple diamonds). The error bars to the fitted τ are given by the standard deviation of the fitting numerical error, and the medians error bars are given by the IQRs according to the distribution of the data at each force. (b) Characteristic-time percent relative errors of the parametric estimations of τ with respect to the medians for the CDFs (SE, empty circles; Single Exponential, filled circles), and for the PDFs (TPL, empty triangles; Single Exponential, filled triangles). (c) Characteristic exponents obtained from the fittings of the SE (β_SE, empty circles) and TPL (α_TPL, empty triangles). (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

We evaluated the relative percent error between the fitted τ in the three models, δ_τ ​= ​100 ​× ​|1 – τ/μ_½(Δt)|, for the SE and single-exponential CDFs, and for the TPL and single exponential PDFs, and plotted them as a function of the applied force in Fig. 4b. It is evident that while the SE slightly better estimates the characteristic-times than single exponential in the CDFs, the error in the characteristic-time estimation in the TPL model for the PDFs is considerably better. Generally, the error of the TPL characteristic-time estimation is better in an order of magnitude than both the SE and single exponential distributions in the CDFs and PDFs.

Regarding the characteristic exponents, all their values are smaller than one, even at low forces. This is an interesting indication that although the applied loads are considerably reduced, the forced unfolding still deviates from being iid, even at 20 ​pN. The charactersitic exponents display opposing trends (Fig. 4c). The CDF force dependent exponentials, β, grow with the reduction of the applied load from ∼0.4 ​at 150 ​pN to ∼0.9 ​at 20 ​pN, which indicates that the deviation from exponentiality decreases with the amount of perturbation. Given this trend, it is reasonable to assume that under lower loads β will reach one, and the unfolding along the polyprotein domains will become iid, which means that each unfolding will behave as an individual and independent event. In contrary and quite surprisingly, the TPL (PDF force dependent) exponentials, α, show an opposing trend, where they change very little with the initial reduction of the force (even increase very slightly), and then considerably reduce from ∼0.8 down to ∼0.55.

3.2. Correlations and non-identically in the dwell-time distributions between events

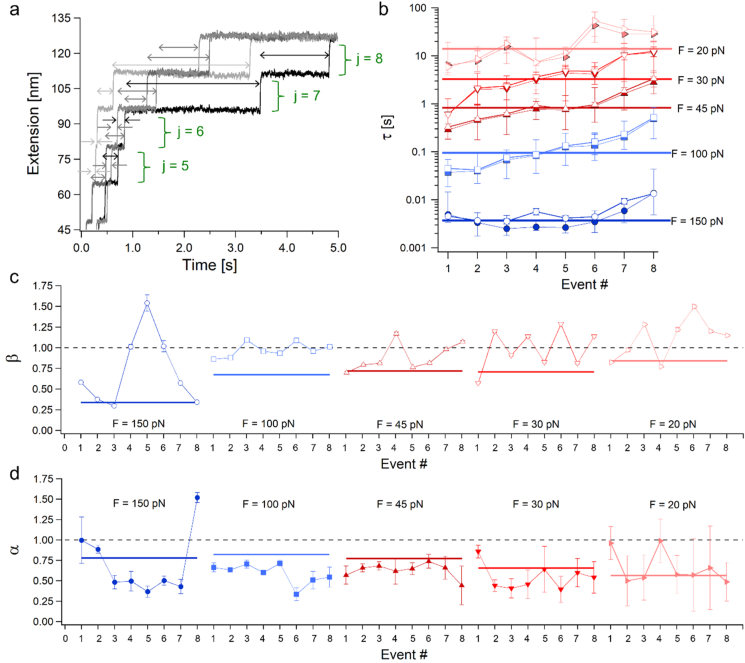
The overall time distributions shown above displayed nonexponential behavior that signify processes with several time scales that emerge into collective behaviors (Klafter and Shlesinger, 1986; Palmer et al., 1984). In order to gain better understanding of the features of the overall distributions, we calculated the distributions per each unfolding event, i.e., for all the first events, all second events, etc. (illustrated in Fig. 5a). The relation between the individual unfolding dwell-times events can assist to understand the discrepancy between the exponents of the two approaches, and particularly the decrease in α. We begin by calculating their j-CDFs and j-PDFs (the CDFs/PDFs for each j unfolding event at a given force, F, when j ​= ​1–8), and fitting them respectively with the SE and the TPL distributions (see Fig. S2 – S7 in the supporting information). The fitted SE exponents, β(j, F), and TPL exponents, α(j, F), obtained from the individual event distributions at the given forces are plotted in Fig. 5a and 5b respectively in empty and colored symbols. For comparison, β(F) and α(F) values of the overall distributions (shown also in Fig. 4b) are plotted as horizontal thick lines. Fig. 5c plots the characteristic times τ(j, F) that were estimated by fitting the individual j-PDFs (see Fig. S3 – S7 in the supporting information), and the overall distributions τ(F) (shown also in Fig. 4a) with Eq. (2). We calculated the medians for all the individual events at the given forces (Fig. 5c, filled colored symbols). Similar to the behavior of τ(F) and μ_½(Δt) of the overall PDFs (Fig. 4b), the individual τ(j, F) displays very close proximity to the medians of the individual events.

Fig. 5.

Individual unfolding events within poly-L₈ at different forces. (a) Schematics of the unfolding dwell-times by event. (b) Characteristic time-intervals τ(j, F) fitted for each event j-PDF (empty symbols) and for all-events PDFs, τ(F) (horizontal thick lines), with medians of each event j-PDF (colored symbols). (c) Fitted values of the SE exponents, β(j, F), obtained for each event j-CDF (empty symbols) and for all-events CDFs, β(F) (horizontal thick lines). (d) Fitted values of the TPL exponent, α(j, F), obtained for each event j-PDF (filled symbols) and for all-events PDFs, α(F) (horizontal thick lines).

It should be noted that while the sample size used to calculate the overall empirical distribution functions at each force is sufficient, it becomes less satisfying for estimating the individual probability densities at F ​= ​150 (N ​= ​22), 30 (N ​= ​28), and 20 ​pN (N ​= ​21). Additionally, unfolding events at F ​= ​150 ​pN were considerably fast, leading to large inaccuracies in the estimations of Δt, particularly for the initial unfolding events, as evident from their characteristic times (Fig. 5c), and exponents (Fig. 5a and b). Under these reservations, we observe that in general ⟨β(j, F)⟩ ≠ β(F) and ⟨α(j, F)⟩ ≠ α(F), while ⟨τ(j, F) ⟩ ​∼ ​τ(F). This behavior of the exponents can indicate that the individual j-PDFs are not iid (Bura et al., 2007; Chetrit et al., 2020), a possibility that will be further tested below.

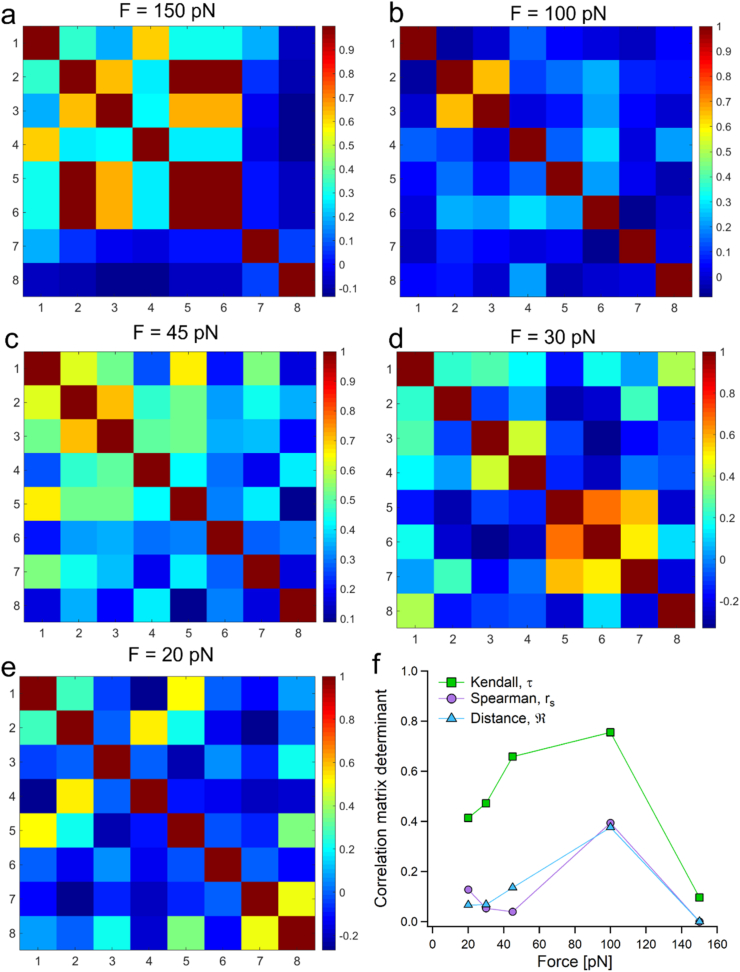
To examine whether under a given stretching force a dependence exists between the measured dwell-times for each of the eight unfolding events, three measures of correlation were calculated. These are the Spearman's rank order correlation coefficient, r_s, Kendall's rank (τ_Kendall) correlation coefficient, and distance correlation, $\mathcal{R}$ (see supporting material and Fig. S8 – S13 for details). Fig. 6a – 6e show heatmaps of the Spearman correlation matrices. The color coding indicates the span of correlation degree ranging from high correlation (dark red ​= ​= ​1) to no correlation (deep blue ​= ​= ​0). The highest force, 150 ​pN shows strong dependency between the unfolding events dwell-times that decays with the number of events. This dependency reduces with the reduction of the force to 100 ​pN, however increases at 45 ​pN (although to less extent compared to 150 ​pN, from which it continues to decrease at 30 ​pN and 20 ​pN. Yet, it does not vanish.

Fig. 6.

Spearman rank correlation coefficient matrices between unfolding dwell-times at each event at (a) 150 ​pN, (b) 100 ​pN, (c) 45 ​pN, (d) 30 ​pN, and (e) 20 ​pN. (f) Determinants of the correlation matrices for three measures of correlation. Here, unlike in the correlation matrices shown in (a)–(e), lower determinant value indicates higher correlation.

We calculated the determinants of the three correlation matrices, and plotted them in Fig. 6f as a function of the applied force. The possible values of the correlation matrices’ determinants are within the range of 0–1, where 0 (singularity) is a manifestation of total interdependence between the variables, and 1 means absolute independence (orthogonality). Therefore, as the value of the determinant increases, the interdependency among the variables decreases (Rockwell, 1975). It should be noted that such determinants exhibit an opposite behavior to the absolute values of correlation coefficients. For example, 0 means complete absence of correlation regarding a given correlation coefficient, but manifests total interdependence when a determinant of correlation matrix is concerned. In this study, we notice that all the determinants of the three kinds of correlation matrices (each for a different coefficient: r_s, τ_Kendall and $\mathcal{R}$) show a similar trend. Moreover, r_s and $\mathcal{R}$ range within proximity. The correlation at 150 ​pN is the highest (lowest determinant values), it decreases at 100 ​pN, and then increases again at 45 ​pN, from which the Kendall and distance correlation coefficients indicate an increase of the correlations, while the Spearman coefficient displays a moderate decrease. Interestingly, this behavior resembles to the way in which α varies with the force, slightly growing from 150 to 100 ​pN (when the correlations decrease), and then decreasing from 45 ​pN, with the increase in the correlations.

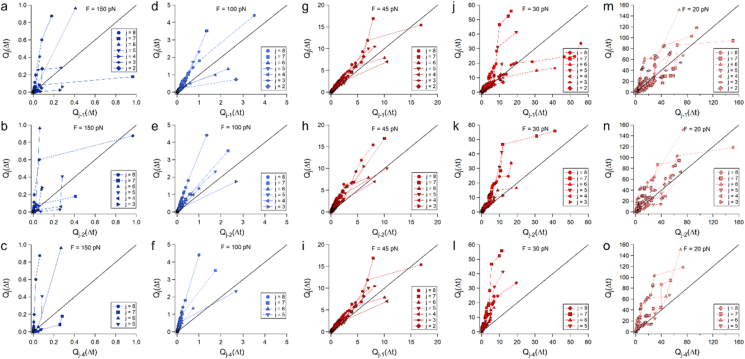
To establish if the individual event dwell-times originate from a common population distribution, we used the Q–Q (quantile–quantile) graphical representation. The quantiles are calculated by first choosing a set of percentiles, then for each percentile the corresponding quantile values in each of the compared individual events dwell-times distributions were calculated. Therefore, each percentile links together two quantiles from the compared datasets, which form a point that is then plotted in the Q-Q plot. The dwell-times of the two events are considered identically distributed, or originate from a common distribution if the quantile points fall on the diagonal (reference) line. A deviation from the reference line means that the distributions of the two data sets are different form each other, where a larger distance from the reference line indicates larger differences in the distributions.

Fig. 7 plots the dwell-time quantiles of the j event, Q_j(Δt) at every force (columns), versus the dwell-time quantiles of their previous event, Q_j-1(Δt) (first row), preceding two events, Q_j-2(Δt) (second row), and preceding four events, Q_j-4(Δt) (third row). At F ​= ​150 ​pN (first column, Fig. 7a–c), the Q-Q plots displayed a substantial deviation from the reference line. The 100 ​pN Q-Q plots (second column, Fig. 7d–f) shows very small similarities at short times (<∼0.5 ​s) between two consecutive events (Fig. 6d row), that strays and deviates from the reference line at intermediate and longer times (∼0.5–5 ​s). When looking at the relation between two and four consecutive events (Fig. 7e and f) the quantiles deviate from the reference line. At 45 ​pN (third column, Fig. 7g–i), we observe similarity at short times (<∼3 ​s), while for the rest of the times (∼3–20 ​s), they deviate and scatter around the reference lines. At 30 ​pN (fourth column, Fig. 7j–l) we see a similarity in short times (<∼8 ​s), and deviations from the reference line for the rest of the times (∼8–60 ​s) for consecutive events (Fig. 7j). For quantiles separated by two events (Fig. 7k), this trend is maintained, although the scattering varies, and for four distant events (Figures 7l) the similarity is reduced to shorter times (<∼5 ​s). Lastly, at 20 ​pN (fifth column, Figures 7m–°) the quantiles show large scattering around the reference line, that shifts above the reference line with event separation. For comparison, the step-size extension shows high similarity in their distributions as evident from their Q-Q plots shown in Fig. S14 in the supporting information.

Fig. 7.

Q–Q plots of forces unfolding dwell-times at separate event combinations (rows) with the applied forces (columns). The dwell-time quantiles of the j event, Q_j(Δt), versus the dwell-time quantiles of their previous event, Q_j-1(Δt) are plotted along the first row, versus preceding two events, Q_j-2(Δt) (second row), and versus preceding four events, Q_j-4(Δt) (third row).

All these indicate that under all the measured forces, over the majority of the times, there are differences between the recorded dwell-time distributions. This, in addition to the correlation coefficient matrices, demonstrates that even under the low loads applied in this study, the measured sequential unfolding is not iid. As such, this explains the asymptotic (or nonexponential) behavior that is observed even under the application of the low forces applied here.

This can partially account for the unexpected reduction of α with the reduction of the applied force, that alludes, within the framework of the CTRW approach, to an increase of the anomalous subdiffusivity in the sequential unfolding process (smaller α indicates a more dispersive transport). Such behavior can be associated with the concept of aging and ergodicity breaking (Metzler and Klafter, 2000). The term aging in the context of sequential unfolding relates to the decrease of rate with time, which means that as time progresses, the dwell-times become substantially longer, as if the unfolding process gets “stuck“ (i.e., dependence of the temporal correlation functions on the initial time of the measurement) (Barkai, 2003; Barkai and Cheng, 2003).

3.3. Free energy perspective

The free energy of the polyproteins under the applied loads can provide additional understanding on the correlations and non-Poissonian behavior that was observed even at low forces. We first examine the PMF of the whole unfolding polyproteins. The PMF represents the one-dimensional projection of the multi-dimensional free energy landscape of the polyprotein over its extension (end-to-end) reaction coordinate (Kawai and Komatsuzaki, 2013). We reconstructed the PMF of the polyprotein under the applied loads using the following relation (Berkovich et al., 2018):

$$E\left(x\right)=-\frac{k_{B}T}{D}\underset{x_i}{\overset{x_f}{\int }}\dot{x}\left(x\right)dx-k_{B}Tln\left[P\left(x\right)\right]$$ (3)

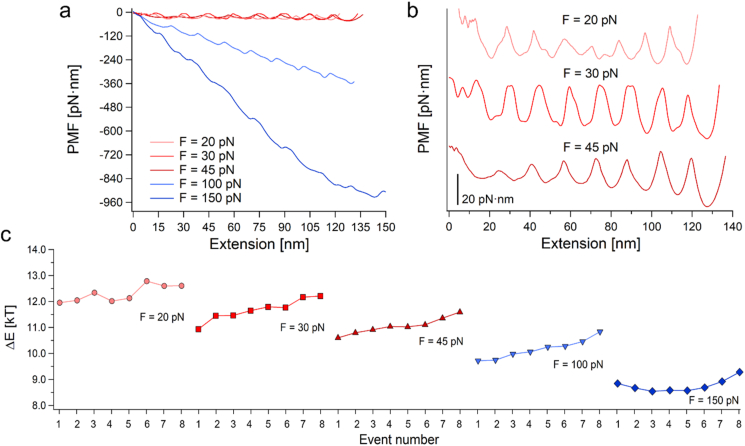
where k_B is Boltzmann's constant, T is the absolute temperature, D is the effective diffusion coefficient of the system (polyprotein and probe) (Janovjak et al., 2005; Berkovich et al., 2012), ẋ(x) is the position-dependent velocity (x_i and x_f set the boundary conditions), and P(x) is the quasi-equilibrium PDF (Zhang et al., 2011). For the PMF reconstructions we used the measured data to calculate ẋ(x) and P(x), and took D as 1500 ​nm²/s for the AFM data (Berkovich et al., 2010, 2012; Chetrit et al., 2020), and 1.5^.10⁵ ​nm²/s for the MT (Cossio et al., 2015; Shmilovich and Popa, 2018). The reconstructed PMFs of the Poly-L₈ under different forces are plotted in Figures 8a and b. These PMFs experimentally affirm the theoretical prediction of the contractive “accordion”-like behavior with lowering of the applied force (Valle-Orero et al., 2015, 2017) due to the effect of conformational entropy of the unfolded domains (Valle-Orero et al., 2017; Makarov, 2009; Bonilla et al., 2014). The “accordion” effect is a manifestation of the stretching of unfolded domain that scales with the applied force. It is also interesting to observe that the overall contour of the PMF becomes less steep and less curved as the applied force becomes smaller. This is related to the mechanical work that the pulling apparatus performs on the tethered molecule (Berkovich et al., 2018; Valle-Orero et al., 2015). As unfolding progresses, the loose chain segments become less stiff, and consequently increase the effective barriers along the energy landscape of the polyprotein (Kawakami et al., 2006; Elias-Mordechai et al., 2020; Shoham and Givli, 2020).

Fig. 8.

The effect of the applied force on Poly-L₈ free energy reflected by its PMF along its extension coordinate. (a) Reconstructed PMFs of Poly-L₈ under varying loads of 150, 100, 45, 30 and 20 ​pN. (b) Separated PMFs of Poly-L₈ at low forces. (c) Activation barrier heights, calculated from the unfolding dwell-times.

From Fig. 8a it is clear that if the applied load is smaller, the overall contour of the PMF becomes shallower and straightens. Since the low force PMFs are close in energy, we also plotted them separately in Fig. 8b. The insufficient statistics at the low forces (as well as for the high 150 ​pN load) takes its toll on the reconstructed PMFs, particularly the unsatisfactory sampling during the actual transitioning. These barrier crossings are related to the ẋ(x) term in Eq. (3). The experimental data acquisition rate (7.2–2.2 ​kHz for the AFM and 0.5–1 ​kHz for MT) poses a limitation on the required sampling spatial resolution for an adequate reconstruction, as it artificially smooths the region of the barriers peaks (Hummer and Szabo, 2010).

Due to this insufficient temporal resolution, the activation energy barriers at each event were calculated from the unfolding dwell-times, ΔE(j, F) ​= ​k_BTln[τ(j, F)/A] (Fig. 8c). The attempt frequency at zero force was estimated as A ​= ​k₀exp(ΔE₀/k_BT) ​= ​1.4∗10¹¹ s⁻¹, where k₀ ​= ​2.22∗10⁻³ s⁻¹ is the off-rate measured for Poly-L₈ (Dahal et al., 2020), and ΔE₀ ​= ​13.8 ​kT (Valle-Orero et al., 2017). As can be observed in Fig. 8c, the activation barriers calculated from τ(j, F) show two main consistent behaviors: first, their relative values decrease with the increase of the force, which is expected, and second, their relative heights grow with event number (j). The latter trend, the so-called j-effect (sometimes N-effect), was reported in the literature for polyprotein unfolding under the application of high forces (Rief et al., 1998; Zinober et al., 2002; Lannon et al., 2012; Tych et al., 2015; Sumbul et al., 2018; Chetrit et al., 2020; Elias-Mordechai et al., 2020), yet it exists even at forces as low as 20 ​pN. This behavior, together with the conformational entropy effects that are evidenced in the local elastic curvature of the PMFs at the applied loads, account for the phenomenological behavior of α.

In light of the statistical and energetic analyses that clarify the observed trend in α, revisiting Fig. 5c can provide a better understanding of the opposite trend observed for β. MD simulation of (a single) NuG2 under reducing constant load showed that β increases with the reduction of the force until it reaches 1 (at which the distribution becomes exponential) (Costescu et al., 2017). β obtained from our measured data (of Poly-L₈), did not reach 1 for the overall CDFs (Fig. 4c). However, they displayed values higher than 1 for the individual events (Fig. 5c), while following the same trend in which it increases with the lowering of the applied load. Hence, β that signifies the extent of deviation from exponentiality, behaves as expected for both individual NuG2 protein and Poly-L₈ polyprotein. This behavior can question the capability of the SE model to capture unfolding kinetics, particularly as its inclination towards exponentiality counters the non-iid nature disclosed from the unfolding dwell-times. Another question that may arise from the current study concerns the possible effect of the measuring apparatus. Here we studied and compared kinetic data obtained by two methodologies (AFM and MT); however, these technologies reported different characteristics of the same polyprotein. For instance, unfolding studies of Poly-L₈ with AFM reported a distance from the transition state of 0.22 ​nm (Brockwell et al., 2005), where a distance of ∼0.4 ​nm were reported with MT (Dahal et al., 2020; Valle-Orero et al., 2017). While AFM has better sampling rate and better resolution for determining ẋ(x), its larger probe diffuses three orders of magnitude slower than in MT. Hence, one can also wonder whether the different hydrodynamic drag exerted by the AFM cantilever tip or the MT magnetic bead, reflected by their different diffusion coefficients (Berkovich et al., 2010, 2012; Chetrit et al., 2020; Cossio et al., 2015; Shmilovich and Popa, 2018) and their different acquisition rates can play important roles during the measured conformational transitions of the studied molecules (Janovjak et al., 2005; Cossio et al., 2015). At this point, these remain open questions that invite additional investigation of the unfolding kinetics under forces lower than 20 ​pN, with their correlative behavior, and comparative study of the unfolding under the same load using different apparatuses.

4. Conclusions

Nonexponential kinetics of polyprotein unfolding under constant load have been documented for more than a decade and a half. While several theories were used to account for this nonexponentiality, the general hypothesis was that for sufficiently lower applied loads, the unfolding kinetics will become exponential. In this study we measure the unfolding kinetics of Poly-L₈ under loads of 150 and 100 ​pN using AFM, and 45, 30 and 20 ​pN with MT. We fitted the unfolding dwell-time measurements with two different types of theoretical distributions: Stretched exponential, SE, and truncated power law, TPL, which were fitted to the empirical CDFs and PDFs respectively. The fitted characteristic times displayed a trend which was similar to the medians calculated from the data (in which the characteristic time decreased with the increasing of the force). The fitted τ_TPL were however closer to the medians than τ_SE. The exponents of the two distributions displayed opposing tendencies, where β, the SE exponent increased with the reduction of the force, in accord with the hypothetical expectancy, while surprisingly α, the TPL exponent decreased with decrease of the applied load. To better understand these behaviors, we performed statistical analysis of the unfolding time-intervals for all the events, and per event, and observed that the unfolding times are correlated, and depend on each other, even at 20 ​pN (although to a lesser extent than 150 ​pN). Moreover, the general trend of α was concert with the correlation statistics of the data. By calculating the PMFs of the unfolding polyprotein we observed the contribution of the entropic elasticity of each unfolded domain segment on the overall curvature of the PMF contours (the “accordion” effect). This experimentally demonstrates the strong association of the polyprotein to its polypeptide polymeric properties. Since temporal limitations of the measurements inhibited full resolution of the unfolding barriers, we calculated them using chemical kinetic theory. Surprisingly, the unfolding activation barriers displayed increasing hierarchy with event number even at the lowest applied force of 20 ​pN. Although we report here that unfolding kinetics still displays asymptotic behavior at low forces as 20 ​pN, we do not exclude the possibility that they will become decorrelated at lower forces, however, at such low forces the probability to refold might influence the correlations of the unfolding events as well.

CRediT authorship contribution statement

Einat Chetrit: Investigation, Formal analysis, Writing – original draft. Sabita Sharma: Investigation. Uri Maayan: Investigation, Formal analysis. Maya Georgia Pelah: Formal analysis. Ziv Klausner: Formal analysis, Writing – review & editing. Ionel Popa: Conceptualization, Resources, Investigation, Supervision, Writing – review & editing. Ronen Berkovich: Conceptualization, Investigation, Formal analysis, Supervision, Project administration, Writing – original draft, Writing – review & editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Handling editor. chandra shekhar verma

Appendix A. Supplementary data

The following is the Supplementary data to this article: