A microfluidic method to measure bulging heights for bulge testing of polydimethylsiloxane (PDMS) and polyurethane (PU) elastomeric membranes

Abstract

Thin and flexible elastomeric membranes are frequently used in many microfluidic applications including microfluidic valves and organs-on-a-chip. The elastic properties of these membranes play an important role in the design of such microfluidic devices. Bulge testing, which is a common method to characterize the elastic behavior of these membranes, involves direct observation of the changes in the bulge height in response to a range of applied pressures. Here, we report a microfluidic approach to measure the bulging height of elastic membranes to replace direct observation of the bulge height under a microscope. Bulging height is measured by tracking the displacement of a fluid inside a microfluidic channel, where the fluid in the channel was designed to be directly in contact with the elastomeric membrane. Polydimethylsiloxane (PDMS) and polyurethane (PU) membranes with thickness 12–35 μm were fabricated by spin coating for bulge testing using both direct optical observation and the microfluidic method. Bulging height determined from the optical method was subject to interpretation by the user, whereas the microfluidic approach provided a simple but sensitive method for determining the bulging height of membranes down to a few micrometers. This work validates the proof of principle that uses microfluidics to accurately measure bulging height in conventional bulge testing for polydimethylsiloxane (PDMS) and polyurethane (PU)eElastomeric membranes.

A unique microfluidic platform to rapidly and accurately measure the bulging heights of polymeric membranes.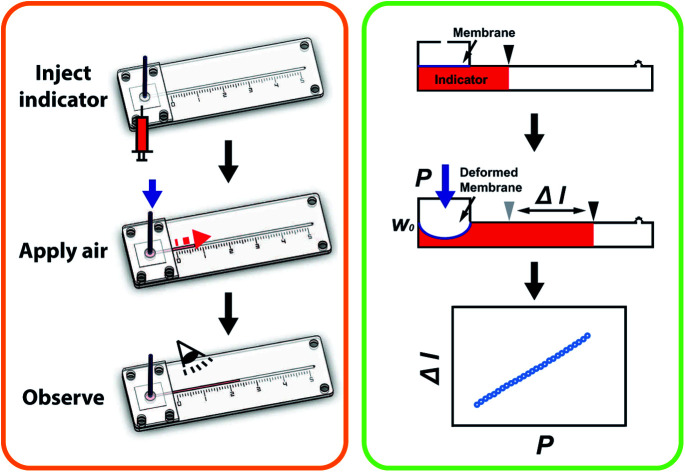

Introduction

Elastic thin membranes integrated into microfluidic devices have been widely used for cell biology, tissue engineering, and drug discovery.¹ Some of these thin membranes are elastically deformable and have been used in different platforms such as micro-valves,^2,3 micro-pumps,^4–6 pressure sensors,^7,8 and optofluidic devices.^9,10 For biological applications, elastic membranes have also been used for tissue engineering,¹¹ lung-on-a-chip,¹² and gut-on-a-chip.¹³ The elastic properties of these membranes are important parameters to determine their functionality and modes of operation in these particular micro-environments.

Typically, the elastic properties of polymeric membranes are characterized by pressure loading such as bulge test or blister test^14–18 and point loading techniques such as indentation and microtensile tests.^19–22 These membrane characterization processes involve multiple steps, which include: (1) handling and mounting the membranes to the measuring device; (2) controlling the applied force to obtain deformation; (3) observation and data processing to determine the deformation characteristic; (4) using developed mathematics to calculate the elastic modulus. However, these techniques currently require specialized tools such as indenters, high amplification microscopes, and interferometers to carry out the characterization. For example, use of interferometers is common in the semiconductor industry to accurately determine the deformation characteristic of the membrane (bulging height). However, the dynamic range of these instruments is limited to account for large deflections, especially for highly elastic membranes. Moreover, these dedicated tools are very sensitive to vibrations. Alternately, high amplification microscopes integrated with high-resolution cameras have also been used to observe the deformation of the elastic membrane.^16,20 Nevertheless, translucent or reflective samples may not be compatible with these imaging techniques. These instruments may also not be readily accessible due to cost concerns. A recent study has shown the use of a liquid displacement approach in a microfluidic device to determine the peak deflection of the membrane without using expensive equipment.²³ The peak deflection can be altered by modifying the dimension of the embedded membrane in the device. However, the results are still preliminary and were not validated against a common elastic modulus characterization method. Furthermore, the fabrication of microfluidic device and membrane still involves the photolithography process, limiting the types of the membrane.

As indicated above, the handling of the elastic membranes during testing is also an important consideration so that they can be mounted on a measuring device. Thin (<35 μm) elastic membranes tend to become wrinkled when removed from the substrate. Typically, they are clamped using a special screw-based clamping tool, which sometimes can cause air leaks between the mounting gaskets.¹⁷

The objective of this work is to present a simple, microfluidic method that can rapidly and accurately measure the bulging height of elastomeric membranes and validate the method by comparing results with a typical microscopic observation based bulging test. The platform utilizes displacement of fluids inside a microfluidic channel caused by the deformation of the elastic membrane. By measuring the displacement of the fluid, the elastic modulus of the membrane can be estimated. Proof of concept was demonstrated by measuring the stress–strain relationship of thin PDMS and PU membranes.

Theory

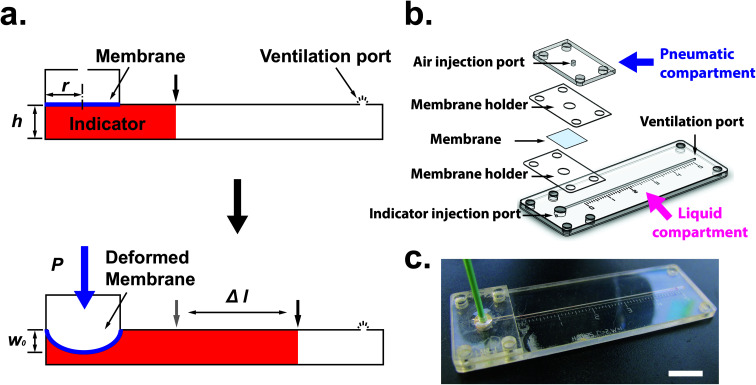
Fig. 1(a) shows the principle of measuring the elastic modulus of thin polymeric membranes using the current approach. The platform is composed of two compartments. The first compartment (liquid compartment) is connected to a microfluidic channel that is partially filled with an indicator liquid. The microfluidic channel is designed such that movement of the indicator liquid is visible with the naked eye or via an easily accessible digital microscope. The second compartment (pneumatic compartment) is connected to a pressure source that can allow the users to determine the applied force on the membrane. The membrane is installed between the two compartments. As the membrane is deformed by a known pressure (P), the deformation of the membrane is indicated by the displacement of the indicator inside the microfluidic channel. The indicator displacement length due to the membrane deformation is noted as Δl and the bulging height of membrane at the center is noted as w₀. The bulging volume is equal to the displaced indicator volume (Δl × h × w, where h is the height of the microchannel and w is the width). If the bulging volume (V_sp) was assumed as a spherical cap, it will be equal to 1/3 × π × w₀² × (3r − w₀), where r is the radius of the opening for bulging membrane. The bulging height (w₀) can then be calculated using the length of the displaced fluid:

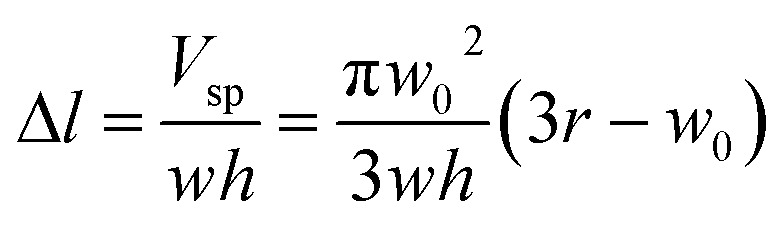1

Fig. 1. (a) The principle of elastic modulus measurement in a microfluidic device. (b) Schematic showing the individual components of the device. (c) Image of membrane elastic modulus measurement device. Scale bar = 1 cm.

Now, the material elastic properties can be then obtained from eqn (2), which is governed by the equi-biaxial expression of Hooke's Law:

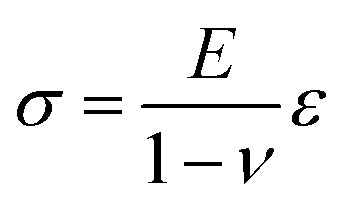2

where σ is the stress applied to the membrane, E is the elastic modulus of the membrane, ν is Poisson ratio of membrane and ε is strain on the membrane. For the thin-wall sphere, the stress on the thin membrane can be expressed as:¹⁴

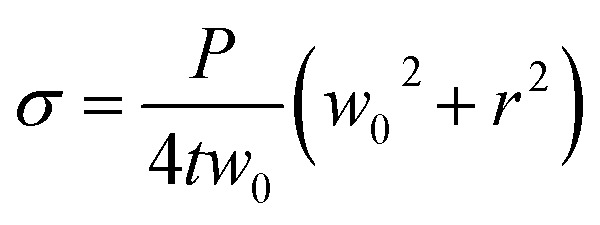3

where t is the membrane thickness. The strain on the membrane derived from circular membrane can be expressed in terms of bulging height:¹⁴

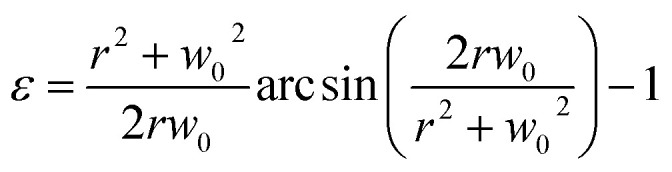4

Therefore, the elastic modulus of the membrane can be obtained by plotting the stress–strain curve with the known Poisson ratio.

In this case, w₀ is determined by measuring the liquid displacement (Δl) in our microfluidic channel. Even the smallest bulging in the membrane can cause sufficiently large displacement in the microchannel. For example, if we assume that a displacement of 1 mm can be seen with the naked eye in a channel having the width of 1 mm, a 50 μm deep channel can allow the detection of a bulging height about 3 μm (Table. S1†).

Design and fabrication

One challenge of integrating membranes into microfluidic devices is the requirement of placing and fixing flexible membranes into planar systems. Although thin polydimethylsiloxane (PDMS) membranes can be fabricated in situ and assembled in the measurement device,¹⁵ it is not trivial to integrate flexible membranes using common fabrication techniques available for microfluidics. To integrate the membrane into the microfluidic devices, we use layer-by-layer stacking technique to sandwich membrane layer between the liquid and pneumatic compartments. Fig. 1(b) shows the different layers of the measurement device. The patterns for each layer were designed using Solid Edge 2D Drafting ST4 software (Siemens PLM Software). The membrane holder and microfluidic channel portion were cut with a CO₂ laser cutter (M-360, Universal Laser Systems) on PET film (0.25 mm; McMaster-Carr) laminated with adhesive tapes (9122, 3M Company) on both sides. PDMS thin membranes were fabricated by mixing of degassed pre-polymer and curing agent (10 : 1 ratio; Sylgard 184; Dow Corning) and spin coating on a polycarbonate (PC) film (0.125 mm; McMaster-Carr) temporarily bonded to a rigid substrate such as acrylic. Typically, thin PDMS membranes (<25 μm) are molded or spin coated on rigid substrates such as glass or silicon. To remove a thin membrane from the substrate and to place it onto the measurement device may require precise handling. The bonding between the substrate and PDMS elastic membrane can be sufficiently strong that it makes peeling the thin material challenging without tearing. In addition, once the membrane is peeled off from the substrate, we found that the thin membranes less than 50 μm also tend to crumple together [Fig. S1(a)†] and it is difficult to stretch the membranes back to their original state. These handling and fixation issues may cause instability, require more samples for the measuring process, and eventually affect the results of the measurement.

To address these challenges, we used a rapid prototyping method based on laser-based micro-patterning and lamination techniques as described previously.^11,24 This technique can allow us: (1) to fix the radius of the window (r) for membrane elasticity measurement [Fig. S1(b)†]; (2) peel off the membrane from the PC substrate rapidly and easily using an adhesive layer due to the adhesion of the PDMS film on the PC is weaker than on silicon or glass substrates [Fig. S1(c)†]; (3) transport the membrane with the rigid holder [Fig. S1(d)†]; and (4) integrate the membrane into the microfluidic device to perform the measurement. Currently, the free-standing ultrathin PDMS membrane (less than 1 μm in thickness) is possible to be fabricated and transferred to a ring support for the ease of handling.²⁵ It is also applicable to use the lamination approach mentioned here to transfer the ultrathin membrane into the microfluidic-based measurement device.

Polyurethane (PU) membranes were fabricated by mixing two components (1 : 1 ratio; 1552-2; GS Polymers, Inc.) and spin coating on the silicon wafer. Here silicon wafers were used as the substrate because the adhesion of PU to PC films was too strong for follow-on processing. On the other hand, it was simple to peel the PU membrane from the silicon substrate after soaking in water for 24 hours. Different thicknesses of PDMS membranes and PU membranes were fabricated and tested in this work. The thickness of each membrane was confirmed using a scanning electron microscope (Fig. S2†).

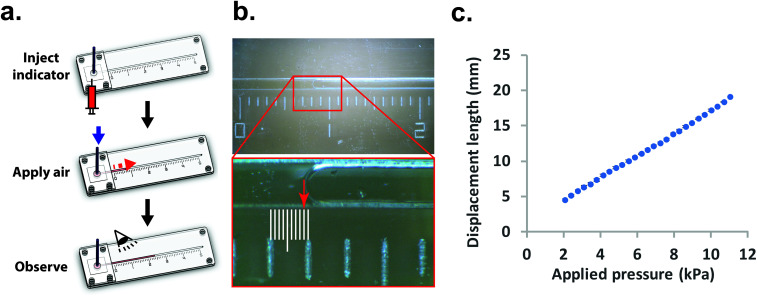
Once the measurement device was assembled by using layer-by-layer stacking fabrication technique, PEEK (polyether ether ketone) tubing was placed and glued to the air injection port [Fig. 1(b)] to complete the device [Fig. 1(c)]. The device was designed with the specific dimensions so that the displacement of the indicator can be easily observed under a stereomicroscope (h = 0.35 mm, w = 1 mm and r = 2 mm). The liquid compartment was partially filled with a fluorinated oil (Novec 7500, 3M) solution as a liquid indicator to reduce the friction in the microchannel. The fluorinated oil is a lubricant with excellent thermal stability and chemical resistance. Thus, it can reduce the interaction between the membrane and liquid and avoid the evaporation during the operation. However, if bubbles are trapped during the filling of the channels with the oil – it can have a significant impact on the experimental result. Therefore, care needs to be taken while filling the device with the fluorinated oil. The design of the platform integrates this requirement by including a liquid injection port and a vent port [Fig. 1 (b)] in the liquid channel such that no air bubble is trapped during filling. To ensure reproducibility, the device is held vertically with the injection port connected with a syringe during the filling operation. The oil is injected using the syringe against the gravity, which can simply push any air bubble out through the vent port. With this arrangement, it was simple to fill the channel with the desired amount of oil in a reproducible and rapid fashion. The membrane was deformed by applying a known pressure using a pneumatic pump (PneuWave Pump; CorSolutions, LLC). The deformation of the membrane causes the indicator to be displaced along the microchannel. The displacement of the indicator can be recorded from the difference of length based on a scale imprinted on the device [Fig. 2(a)]. The scale with millimeter range was engraved using the laser cutter on the surface of the device [Fig. 2(b)]. When a digital microscope is used, the displacement of the indicator can be recorded more accurately (down to 0.01 cm). Therefore, the sensitivity of this platform can be tailored to measure the elastic modulus of membranes with very small deflection. In order to validate the measurements with the microfluidic method, the membranes were also subjected to a conventional bulging test under a stereo microscope.¹⁶ After the images were captured, the bulging height was determined using ImageJ software (National Institutes of Health).

Fig. 2. (a) The procedure of measurement. (b) Photograph of microfluidics with liquid under a light microscope. The liquid volume can be precisely measured according to the engraved scale (unit in centimeter). In this example, the distance would be measured as 0.79 cm. (c) Increased length of liquid displacement corresponds to applied pressure. N = 3.

Results and discussion

Conventionally, bulging height of membrane can be directly measured using high amplification microscopes.^15,16 The bulging shape is in a form of spherical cap and the bulging height is determined by measuring the length between the peak point and base point (Fig. S3†). Although the measurement technique can be viewed as a straightforward method, this imaging technique is sometimes not suitable for reflective or transparent samples. For example, planar PDMS still has about 5% reflectance of light.²⁶ Light reflection can affect the observation as well. Fig. S3† shows an example of our membrane under the inflated condition where it is difficult to pinpoint the exact peak and base points of the bulged membrane. In addition, the determination of these points can also vary depending on the observation angle. Due to these reasons, the bulging height might vary with experimental setup or the observer's judgment that can cause measurement errors between samples.

On the other hand, using our microfluidic-based technique enabled interpretation of the bulging magnitude to obtain a stable and quantitative measurement. Fig. 2(c) shows the applied pressure-displacement curve for thin PDMS membrane (35 μm of thickness) integrated into the measurement device. The result demonstrates that the displacement length in the liquid compartment is proportional to the applied pressure in the pneumatic compartment.

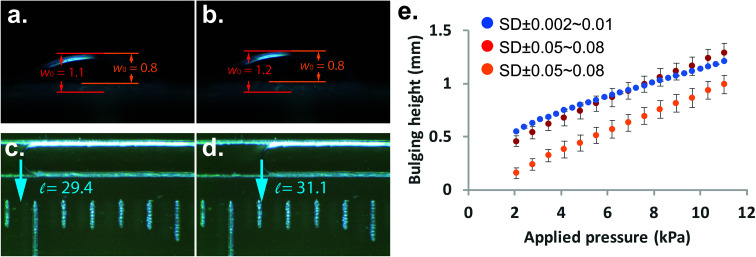
The main task of a bulging test is to obtain the bulging height of the membrane. In our study, we can simply translate the length of displacement into the bulging height of membrane using eqn (1). In order to validate the bulging height obtained from the microfluidic-based device, we used the conventional bulging test to observe the change of bulging height under a microscope as well. Initially, the colorless membrane/substrate made it difficult to determine the peak and base points of the bulging membrane under the microscope. We have used one fixed peak and two base points (as indicated by the orange line in Fig. 3 and Fig. S3†) to determine the observed bulging height. Fig. 3(a) and (b) shows the comparison between the microfluidic-based measurement device and the conventional bulging test. We were able to confidently observe the movement of the indicator fluid and obtain the length of displacement [Fig. 3(c) and (d)], whereas one could obtain different bulging height depending on their selection of base/peak point in the conventional bulging test [indicated by orange and red lines in Fig. 3(a)]. A range of pressure was then applied to obtain load-deflection curves for the membranes. The result shows that although the same setup of conventional bulging height was observed, the standard deviation of each measurement varied by 50–80 μm. The microfluidic-based measurement, on the other hand, the standard deviation was only within 2–10 μm. Furthermore, the load-deflection curve obtained from the conventional approach varied significantly based on where we chose the location of the base/peak points [Fig. 3(e)]. Therefore, we found that our microfluidic-based approach revealed results that are more reliable and repeatable eliminating human errors and light reflection effects. For the materials with a higher elastic modulus (e.g. PU), the microfluidic-based technique might be a useful tool to measure very small bulging of the membranes. The microfluidic-based approach can be made more sensitive by reducing the dimension of the channel in a microfluidic chip.

Fig. 3. Slightly changes of pressure were applied between 1.2 (left column) psi and 1.3 psi (right column) using (a), (b) microscope-based observation and (c), (d) microfluidic-based bulging tests to obtain bulging height and liquid displacement of PDMS membrane, respectively. Unit of length is in centimeter. (e) Bulging height plots with applied pressure for the conventional bulging test with base point 1 (red dots), conventional bulging test with base point 2 (orange dots), and microfluidic-based bulging tests (blue dots). N = 3.

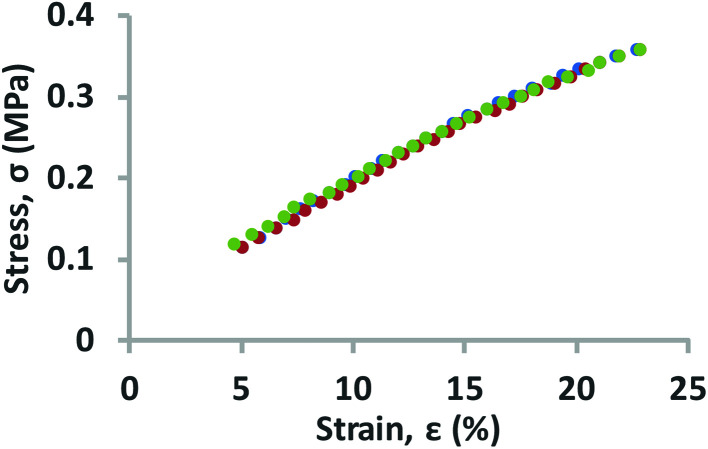
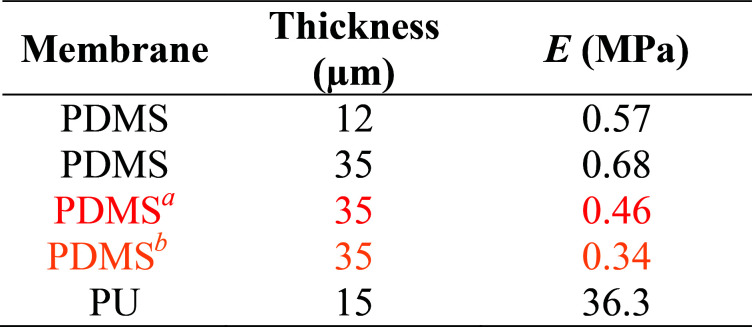
In this work, the elastic modulus of PDMS membrane was measured by analyzing the bulging height of membrane integrated into the microfluidic-based measurement device. First, the stress–strain curve of each membrane was plotted by calculating the applied stress and strain of the membrane from eqn (3) and (4) (Fig. 4). The elastic modulus of each test membrane was then determined by fitting the slope of the stress–strain curve to eqn (2) (assuming ν = 0.5).²⁷Table 1 shows the elastic modulus results for the PDMS membrane with 12 and 35 μm of thicknesses. We have obtained two different elastic moduli of the PDMS membrane for the two different thicknesses. It is not uncommon to obtain different elastic modulus for PDMS depending on the processing conditions and fabrications method.²⁸ Thickness-dependent arises from shear stress during fabrication, which can be dependent on the processing conditions and surface energy of the substrate. Unfortunately, it is difficult to compare literature data with our findings as the processing conditions and substrates used in our work is unique.

Fig. 4. Stress–strain curves for PDMS membrane. All data were obtained using the measurement devices (N = 3) with known dimensions (h = 0.25 mm, w = 1 mm, r = 2 mm). The PDMS membranes used for this experiment have a thickness of 35 μm.

The calculated elastic modulus for various samples.

^aElastic modulus obtained based on the optical measurement with base point 1 in Fig. 3.

^bElastic modulus obtained based on the optical measurement with base point 2 in Fig. 3.

The same method was also used to measure the elastic modulus of PU membrane (assuming ν = 0.49)²⁹ with 15 μm of thickness (Table 1 and Fig. S4†). The high elastic modulus of PU meant lower bulging height for the same applied pressure compared to PDMS. We were able to detect PU bulging height differences that were as a little as 10 μm, which were not detectable using the conventional bulging test performed under the same condition. The elastic moduli obtained by using microscope-based observation were also calculated to demonstrate the range of inaccuracy if different base points were chosen.

The microfluidic method to measure the bulging height follows a simple principle. The platforms in this work were fabricated using a rapid prototyping method that uses laser cutters and lamination method. However, the basic working principle is independent of the fabrication technique used in this work and should be amenable for integration with other common fabrication methods. One unique attribute of our method is the bulging test is carried out in a microfluidic environment. Therefore, the current method is capable of producing testing conditions which are similar to the ultimate applications of the membranes (e.g. microfluidics valves, organ on a chip etc.). This provides a great advantage over other bulging tests since mechanical properties of polymeric membranes. However, the microfluidic method in its current form may not be suitable for testing porous membranes or highly air permeable membranes. Similarly, care should be taken to utilize this technique with materials that can interact with the indicator fluid. Since the objective of this work was to validate the proof of principle that uses microfluidics to accurately measure bulging height in conventional bulge testing, we have used fluorinated oil as the indicator fluid. Nevertheless, we believe that the current method will provide new opportunities for mechanical characterization of a wide range of materials.

Conclusion

We have demonstrated the ability to characterize elastic modulus of polymeric membranes using a simple microfluidic platform. In spite of its simplicity, our platform showed higher precision compared to conventional bulging tests. This method will be suitable to perform precise and sensitive measurements with a wide range of polymeric membranes applications including micro-valves and organs-on-a-chip. The ability to incorporate various types of elastic membranes in our platform and rapidly obtain the elastic properties can also be an important quality control step to verify fabrication variation, batch to batch consistency, and membrane stability.

Conflicts of interest

There are no conflicts to declare.