Reconstruction of three-dimensional tomographic patient models for radiation dose modulation in CT from two scout views using deep learning

Abstract

Background:

A tomographic patient model is essential for radiation dose modulation in x-ray computed tomography (CT). Currently, two-view scout images (also known as topograms) are used to estimate patient models with relatively uniform attenuation coefficients. These patient models do not account for the detailed anatomical variations of human subjects, and thus may limit the accuracy of intra-view or organ-specific dose modulations in emerging CT technologies.

Purpose:

The purpose of this work was to show that 3D tomographic patient models can be generated from two-view scout images using deep learning strategies, and the reconstructed 3D patient models indeed enable accurate prescriptions of fluence-field modulated or organ-specific dose delivery in the subsequent CT scans.

Methods:

CT images and the corresponding two-view scout images were retrospectively collected from 4,214 individual CT exams. The collected data were curated for the training of a deep neural network architecture termed ScoutCT-NET to generate 3D tomographic attenuation models from two-view scout images. The trained network was validated using a cohort of 55,136 images from 212 individual patients. To evaluate the accuracy of the reconstructed 3D patient models, radiation delivery plans were generated using ScoutCT-NET 3D patient models and compared with plans prescribed based on true CT images (gold-standard) for both fluence-field modulated CT and organ-specific CT. Radiation dose distributions were estimated using Monte Carlo simulations and were quantitatively evaluated using the Gamma analysis method. Modulated dose profiles were compared against state-of-the-art tube current modulation schemes. Impacts of ScoutCT-NET patient model-based dose modulation schemes on universal-purpose CT acquisitions and organ-specific acquisitions were also compared in terms of overall image appearance, noise magnitude, and noise uniformity.

Results:

The results demonstrate that (1) The end-to-end trained ScoutCT-NET can be used to generate 3D patient attenuation models and demonstrate empirical generalizability. 2) The 3D patient models can be used to accurately estimate the spatial distribution of radiation dose delivered by standard helical CTs prior to the actual CT acquisition; compared to the gold-standard dose distribution, 95.0% of the voxels in the ScoutCT-NET based dose maps have acceptable gamma values for 5 mm distance-to-agreement and 10% dose difference. 3) The 3D patient models also enabled accurate prescription of fluence-field modulated CT to generate a more uniform noise distribution across the patient body compared to tube current modulated CT. 4) ScoutCT-NET 3D patient models enabled accurate prescription of organ-specific CT to boost image quality for a given body region-of-interest under a given radiation dose constraint.

Conclusion:

3D tomographic attenuation models generated by ScoutCT-NET from two-view scout images can be used to prescribe fluence-field modulated or organ-specific CT scans with high accuracy for the overall objective of radiation dose reduction or image quality improvement for a given imaging task.

I. INTRODUCTION

The year 2021 marks the 50th anniversary of the first CT scan of a human patient. Over a half-century journey, CT imaging has demonstrated an unprecedented positive impact on the diagnosis and treatment of symptomatic patients. Continuous technological advances in CT have made it an integral component of modern medicine.¹ However, the issue of the small, but non-zero, theoretical cancer risk associated with the use of ionizing radiation in CT remains a public concern despite its invaluable contributions to modern patient care.^2,3 To address the public concerns regarding ionizing radiation risks due to the use of CT in diagnosis and image-guided therapeutic procedures, low dose CT and radiation dose optimization have become a key task in clinical medical physics practices and a central topic of research in the CT imaging community.^4,5

The research and development efforts from academic, industrial, and clinical societies in the past decade have resulted in the development of a variety of radiation dose reduction strategies for CT exams. Software-related techniques include noise reduction reconstruction or image processing algorithms that operate on either raw data, reconstructed image data, or both.^6–13 The initial anticipation for these iterative reconstruction (IR) algorithms was to reduce radiation dose by 60–70%, with the potential for even further reduction.^14,15 However, recent clinical results have concluded that, after a decade-long effort to reduce CT radiation dose with IR software techniques, the status quo is up to 25% dose reduction with IR techniques, far short of the originally expected 60–70% or even 90% claims.^16,17 On the other hand, hardware improvements aim to effectively improve the dose efficiency of CT systems. Namely, given the necessary diagnostic image performance with the improved dose efficiency offered by the scanner hardware, the required radiation dose to a patient can be reduced with improvements in hardware. Current hardware dose reduction strategies include 1) newer generations of CT detectors (such as photon-counting detectors) with improved radiation dose efficiency,^18–24 2) beam shaping filters and dynamic z-axis collimators that limit dose at the periphery of the patient and edge of the scan range²⁵, 3) automatic exposure control systems with the flexibility to modulate tube potential and tube current along the projection view angle direction.^26–29, and 4) intra-view fluence-field modulation schemes and devices have been extensively studied in recent years to better account for the heterogeneous nature of human anatomy to further reduce dose.^30–40

Earlier researches on intra-view fluence-field modulated CT demonstrated a promising 30–50% radiation reduction compared to the current standard-of-care when the entrance fluence field is properly modulated based on the x-ray attenuation properties of the image objects.^32,33,35 The success of fluence-field modulated CT-based dose reduction relies on the availability of an accurate 3D tomographic attenuation model for prescription of a personalized dose modulation scheme before the actual CT scan is executed. In the current clinical CT imaging workflow, the needed patient attenuation information for dose modulations is estimated from the planar scout images (also known as topograms) acquired at two orthogonal view angles (e.g., 90° and 180°) under a scanning-beam acquisition to overcome the narrow coverage of the CT detector along the superior-inferior (SI) direction. During a scout scan, the x-ray beam is narrowly collimated (e.g. to 5 mm); the patient table translates continuously while the detector is read out at a uniform frame rate. The recorded frames are stitched together based on the frame rate and table speed and then scaled to generate the overall scout image that covers the desired patient anatomy for the purpose of patient positioning and generation of the patient model for dose modulations. After the scout images are acquired, patient attenuation information for other view angles can be estimated by interpolating two-view scout images based on a cosine function or other models.⁴¹ However, these estimation strategies do not account for the heterogeneous patient attenuation distributions and thus are not able to provide sufficiently accurate patient information necessary for prescribing more detailed and accurate dose modulations. The concept of ultra-low-dose “3D CT scout” has been investigated^42,43 to obtain the needed 3D patient models for prescribing intra-view or organ-specific CT dose modulations. Despite its conceptual simplicity, a wide adoption of 3D CT scout strategies in practice encountered several challenges: 1) Additional radiation dose is introduced to the patient by this additional CT acquisition; 2) Noise streaks caused by strong photon starvation in these ultra-low-dose CT are often too severe to allow reliable estimations of patient- and organ-specific attenuation distributions; 3) The quantitative accuracy of CT numbers, which is important for the calculation of radiologic paths in intra-view dose modulation schemes, is significantly compromised at ultra-low-dose levels.^44,45 Besides using 3D CT scout images and two-view 2D scouts, tube current modulations can also be prescribed using online feedback of the previously-measured 180° conjugate projection data at a different but nearby z-location (helical or step-and-shoot axial acquisitions) or at the same z-location but at a prior time (dynamic CT scans). These inter-view tube current modulation schemes have been successfully implemented by different CT manufacturers to enable their own vendor-specific tube current modulation schemes to reduce dose while maintaining the overall image quality.^46,47 The limitation of the online feedback strategy lies in the fact that it is not applicable to most task- or organ-based dose deliveries which require the optimization of the modulation schemes ahead of the actual CT scan. Additionally, for scan applications with a single axial gantry rotation (e.g., coronary CT performed on 256- or 320-slice scanners with 16 cm z coverage), the online feedback strategy is not applicable even for inter-view tube current modulations.

In summary, there remains an unmet need for a robust method to generate 3D tomographic patient models to account for the heterogeneous attenuation distributions of individual patients. It is highly desirable to generate a 3D tomographic patient attenuation model from two 2D scout images to leverage its clinically favorable features: super low radiation dose (about 0.04mGy) and broad anatomical coverage along the SI direction. To accomplish this overall objective, the following two scientific challenges must be addressed: 1) Technically, what is the reconstruction method that enables tomographic reconstruction using two scout images stitched together from many small pieces? 2) If a technical solution is available, given the severe ill-posedness of the two-view reconstruction problem itself, it is anticipated that the reconstruction accuracy may be limited. Therefore, the practical value of the reconstructed 3D patient attenuation model in radiation dose modulations must be evaluated to carefully examine whether the 3D patient model generated from two-view scout images provides sufficient information for the purpose of prescribing intra-view or organ-specific dose-modulated CT.

Regarding the technical feasibility to reconstruct a 3D tomographic attenuation patient model from two projection view angles, it would be extremely challenging, if not impossible, to use traditional analytical or iterative image reconstruction strategies due to the difficulty of hand-crafting the appropriate regularizers to regularize the severe ill-posedness of this reconstruction problem. However, recent advances in data-driven deep learning approaches offer a new hope to regularize ill-posed inverse problems by learning the needed regularizers from well-curated training data sets. As a matter of fact, by leveraging the improved regression capabilities of deep neural networks, deep learning-based methods have been introduced into the CT image processing and reconstruction field in recent years and have demonstrated immense promise towards addressing difficult problems previously not solvable with traditional analytical and iterative methods. Earlier works focused primarily on the use of image-to-image neural network models under a supervised learning paradigm to reduce image noise.^48–53 Recent works in the context of image reconstruction have integrated model-based iterative reconstruction methods with neural networks via learned regularizers.^54–58 Direct learning of CT reconstruction from projection data acquired under a wide variety of conditions has also been demonstrated: Li et al. showed promising results for low-dose CT and sparse-view CT reconstructions,⁵⁹ but not under the extreme condition of only one or two projection views.

Recently, several groups have pioneered tomographic reconstruction from one or two views projection images.^60–63 It has been shown that under the condition that a prior CT or cone-beam CT volume of the same patient is available, digitally reconstructed radiographs (DRRs) can be generated from prior CT volumes by a numerical forward cone-beam projection operation. These DRRs and their corresponding image volumes can be used to generate synthetic training data pairs to train a variety of deep neural network architectures to accomplish 3D reconstruction from one or two synthetic views of projection data. For example, in the context of four-dimensional cone-beam CT (4D CBCT), using the DRRs and the corresponding image volumes from six out of ten respiratory phases, a deep learning model was trained to reconstruct 3D image volumes using DRRs from a single view angle.⁶⁴ The performance of the proposed reconstruction strategy was evaluated by applying the trained model to the DRRs of the remaining four respiratory phases of the same patient. However, it has not been shown that the proposed strategy can be used to reconstruct 4D CBCT images from the experimentally acquired cone-beam projection data yet. It is also unclear how the proposed strategy would generalize from one patient to another. In another interesting work, Ying et al.⁶⁵ trained a deep learning model termed the X2CT-GAN network to reconstruct a CT image volume from DRRs. Due to the differences between DRRs and the available chest x-ray radiography images in public databases that were acquired using x-ray cone-beam image acquisitions, the authors used a cycle-GAN to perform style transfer from available chest x-ray radiography images to DRRs and then used the output DRRs to reconstruct the CT-like images. Due to the differences between the slit-scanning acquisitions used in scout imaging⁶⁶ and the cone-beam acquisitions used in x-ray radiography, the authors in Ref. 65 were not able to generate CT-like images from actual scout images. Additionally, there is no reference CT image volume of the patient available to evaluate the accuracy of the reconstructed CT-like images. Similarly, Henzler et al. also trained a network using paired DRRs and CT images to generate volumetric images and rendering of high-contrast structures (e.g. skulls) inside the image objects from single-view DRR images.⁶⁷ However, there is no soft tissue reconstruction demonstrated yet in their work. In another work by Liu et al.,⁶⁸ the AUTOMAP neural network⁶⁹ was adapted for sparse-view reconstruction using two-view or four-view DRRs. Some good initial results have also been achieved despite the encountered challenges of severe organ distortions in reconstructed images as pointed out by the authors.

To summarize, despite the amazing progress made, the aforementioned two scientific questions remain to be answered in an attempt to reconstruct a 3D patient attenuation model for radiation dose prescription in CT. This motivated the purpose of this work: 1) To develop a deep learning-based method referred to as ScoutCT-NET to generate 3D patient attenuation models directly from two-view scout images acquired in clinical CT exams; 2) To demonstrate the trained ScoutCT-NET can be used to directly reconstruct patient-specific 3D patient models from 2D scout images, and 3) To demonstrate both intra-view dose modulations and organ-specific dose modulations can be accurately prescribed based on ScoutCT-NET 3D patient models.

II. METHODS

A. ScoutCT-NET Image Formation – Problem Formulation

Classical statistical image tomographic reconstruction techniques aim to solve the following optimization problem:

$${\overrightarrow{x}}^{\ast }=\arg \underset{\overrightarrow{x}}{\min }[L(\overrightarrow{y}-A\overrightarrow{x})+\lambda R(\overrightarrow{x})],$$ (1)

where $\overrightarrow{x}$ denotes a vectorized image matrix to be reconstructed, $\overrightarrow{y}$ denotes the vectorized projection data, and A denotes the CT system matrix. In general, $L(\overrightarrow{y}-A\overrightarrow{x})$ is considered a function that quantifies data consistency (e.g weighted least squares), and $\lambda R(\overrightarrow{x})$ represents a regularization function whose strength is controlled by the parameter λ. From a statistical inference perspective, the classical statistical image reconstruction techniques aimed to seek for a set of statistical parameters that maximize the a posteriori probability.

In contrast, the central objective of ScoutCT-NET aims to directly learn a transform G to generate a 3D attenuation model of each patient using two orthogonal-view scout images as inputs. To parameterize the desired target transform G, a deep neural network was used to leverage its powerful expression capacities. The proposed two-view ScoutCT-NET 3D patient model estimation problem is formulated as the following optimization problem:

$$\begin{gathered} G^{\ast }=\arg \underset{G}{\min }\underset{D}{\max }\{\underset{\overrightarrow{y}}{\mathbb{E}}\left[\parallel \overrightarrow{y}-AG(\overrightarrow{y}){\parallel }_2^2\right]+\lambda \underset{\overrightarrow{y},{\overrightarrow{x}}_p}{\mathbb{E}}\left[{\Vert {\overrightarrow{x}}_p-G(\overrightarrow{y})\Vert }_1\right] \\ +\underset{{\overrightarrow{x}}_p}{\mathbb{E}}\left[\ln D\left({\overrightarrow{x}}_p\right)\right]+\underset{\overrightarrow{y}}{\mathbb{E}}[1-\ln D(G(\overrightarrow{y}))]\} \end{gathered}$$ (2)

In the above equation, $\mathbb{E}$ denotes the expected value using the empirical statistical distribution, $\overrightarrow{y}$ is the vector representation of the input two-view scout images, the 3D model of the image object is given by $\overrightarrow{x}=G(\overrightarrow{y})$, and ${\overrightarrow{x}}_p$ denotes true CT images for the purpose of learning the neural network transform G. The factor λ is a scalar that controls the strength of the L1 regularization term and D represents a discriminator deep neural network that serves as a learned regularizer to enforce G to approximate the distribution of ${\overrightarrow{x}}_p$. The needed mapping $\overrightarrow{x}=G(\overrightarrow{y})$ can be learned in an end-to-end manner using the well-established adversarial neural network training methodology, in which G aims to minimize the data consistency loss and the L1-norm between the resulting image and the prior image; at the same time, a cross-entropy loss is maximized to enforce G to approximate the distribution of ${\overrightarrow{x}}_p$. This prevents the model from simply learning an identity function that only minimizes a data consistency loss.

B. Neural Network Architecture and Implementation

The overall architecture of ScoutCT-NET is shown in Fig. 1. In this architecture, the deep neural network G in Eq. (2) takes a 888 × 5 section from each of the two scout images as input to generate a sub-volume of tomographic images with 288×288×5 voxels. This is based on the fact that in reality, scout images are acquired under a narrow-beam scanning mode on MDCT scanners. This is different from the cone-beam acquisition geometry used by most x-ray radiography and fluoroscopy systems. In order to map the narrow section of the scout images onto the 3D image space, the first layer of the network consists of a direct backprojection operation which is then followed by 24 convolutional layers that are arranged in a simplified U-Net architecture with four vertical levels⁷⁰. The network was trained using a conditional adversarial loss^71,72 with a 24-layer convolutional discriminator using a ResNet architecture^73,74.

Figure 1:

ScoutCT-NET deep neural network architecture. The network takes a 888×5 narrow section from each of the two scout images as input to generate a sub-volume of tomographic images with 288 × 288 × 5 voxels. This process is repeated for each section of the scout images. In order to map the 2D projections into the 3D image space, the first layer of the network performs a direct backprojection operation which is then followed by 24 convolutional layers arranged into a simplified U-Net architecture with four vertical levels (only 3 vertical levels are shown for diagram simplicity).

The exact neural network layer configuration is as follows: the U-Net encoder uses C64C64-sc1-MPs2-C128-C128-sc2-MPs2-C256-C256-sc3-MPs2-C512-C512-sc4-MPs2-C1024-C1024, where Ck stand for a convolutional layer with k filters, sci represents a skip connection at level i and MPs2 represents a max-pooling operation with stride 2. Similarly, the U-Net decoder layers are as follows: TC512-sc4-C512-C512-TC256-sc3-C256-C256-TC128-sc2-C128-C128-TC64-sc1-C64-C64-C64-C5, where TCk represents a transpose convolution operation with k filters. All convolutional layers use a 3×3 spatial filter configuration with ReLU activations and no batch normalization. Backprojection and forward projection layers are implemented as fully connected layers with weights predefined by the system geometry and no trainable parameters. The ResNet configuration for the discriminator network used only during training is the following: C32s2-C32-C64-sc-C64-C64-sc-C64-C64-sc-C64C64-sc-(C128s2,AP-C128)-C128-sc-C128-C128-sc-C128-C128-sc-(C256s2, AP-C256)-C256sc-C256-C256-sc-C256-C256-sc-FC1, where Ck stand for a convolutional layer with k filters and Cks2 represents a convolutional layer with k filters and stride 2. sc represents the characteristic skip connection of the ResNet architecture. Finally, the AP-Ck notation represents an auxiliary layer consisting of a 3 × 3 average pooling operation with stride 2 followed by a convolutional layer of 1×1×k filter to match the size and number of channels when spatial downsampling occurs in the network. The final FC1 layer represents a fully connected layer with one output. The first layer uses a 5 × 5 receptive field and all other convolutional layers use a 3 × 3 spatial filter configuration with ReLU activations and no batch normalization.

The model was implemented using TensorFlow⁷⁵ version 1.3. Network parameters were initialized using the variance scaling method⁷⁶ and trained from scratch using stochastic gradient descent with the Adam optimizer with a learning rate of 2.0 × 10⁻⁴, momentum parameters of β₁ = 0.9 and β₂ = 0.999 and batch size of 32. To avoid exploding gradients, we adopted gradient clipping in the range [−1.0,1.0]. The model was pretrained for 4 epochs to optimize the generator loss and then we used early stopping when the adversarial loss reached equilibrium in the testing cohort after an additional 4 epochs. The model was trained using two GTX 1080 Ti (NVIDIA, CA) GPUs.

C. Training data collection and curation

More than 1.1 million CT images and their corresponding scout image data from 4,214 clinically indicated CT studies were retrospectively collected. The dataset was used to train the ScoutCT-NET in order to reconstruct 3D patient attenuation models from 2-view scout images. Once the ScoutCT-NET model was trained, it was used to generate 3D attenuation models for patients in the testing cohort. Based on the 3D attenuation model, intra-view or organ-based dose modulation plans were prescribed and virtually delivered. The overall study schema is shown in Fig. 2.

Figure 2:

Overall study schema. More than 1.1 million CT images and their corresponding scout image data from 4,214 clinically indicated CT studies were retrospectively collected. Data were split into three cohorts consisting of 3,790 (90%), 212 (5%) and 212 (5%) CT studies for training, validation and testing of the deep learning model, respectively. The total number of unique data samples used was 1,001,496 for training, 55,136 for validation, and 55,136 for testing. After the ScoutCT-NET model was trained, 3D image localizers were calculated for the 212 testing patients and image analysis was performed.

1. Data collection

All image data were deidentified and collected under an Institutionally Review Board approved protocol. The requirement for informed consent was waived for this retrospective study. Scout and CT images from 4,214 clinically indicated CT exams acquired over the period of nine months at our institution were retrospectively collected from PACS. Inclusion criteria were 1) CT exams acquired without contrast media, 2) Scanned with the anatomical region of the chest, and 3) Patients scanned in a supine position. To avoid potential data inconsistency, CT exams that presented significant image artifacts from metallic objects or data truncation caused by anatomical regions outside the scanning field of view were excluded.

2. Data curation

Each CT exam included in this work consisted of two orthogonal-view scout images and one volume of CT images. Scout and CT images are typically acquired under the same tube potential to assure consistent attenuation measurements in the scout images for the purpose of dose-modulated CT prescriptions. The two CT scanner models used to acquire the data are Discovery CT750 HD and Revolution CT (GE Healthcare, Waukesha, WI). Tube potentials used to acquire the data range from 70 to 140 kV and were determined based on the scan protocol and actual patient size. In order to account for possible differences in CT image reconstruction parameters (i.e. image thickness, voxel size and field of view position), each CT image volume was translated and scaled to the CT system global coordinates using an affine transformation. The matrix size of every image was 288×288 with 1.89 mm × 1.89 mm × 1.00 mm voxel size. There is no special reason for using a matrix size of 288 × 288; instead, it was just a convention used in our work and one can also choose to use a matrix size of 256 × 256 if it is preferred. However, the physical size of the image voxel needs to accommodate the following practical considerations: 1) First is to reduce the computational burden of Monte Carlo simulations; 2) Second is to meet the condition of charged particle equilibrium (CPE) for dose calculations. Note that the range of the secondary electrons for the energies used in diagnostic CT is typically less than 0.5 mm in human tissue, thus the choice of a 1.89 mm × 1.89 mm × 1.00 mm voxel size satisfies the CPE condition.

3. Data partition for training, validation, and testing

Data were split into three cohorts consisting of 3,790 (90%), 212 (5%) and 212 (5%) of the total number of CT studies for training, validation and testing of the ScoutCT-NET deep learning model respectively. The validation and testing cohorts were randomly selected from the subset of patients who underwent a single CT exam with one study per exam in order to avoid potential overlap between the training and validation/testing data.

D. Quantitative evaluation of 3D patient attenuation model generated from ScoutCT-NET (I): Comparison of radiation dose distribution generated from the ScoutCT-NET 3D patient model in Monte Carlo dose simulations

After training, ScoutCT-NET was used to process scout images from the testing cohort to generate 3D patient models. As the first step of evaluating the ScoutCT-NET based 3D patient models, standard helical CT scans were virtually delivered to both the 3D patient models and the corresponding gold-standard patient models to evaluate whether the absorbed dose distributions in the ScoutCT-NET based attenuation model match that of the gold standard. The virtual CT scan was performed using the Monte Carlo platform (MC-GPU version 1.3).⁷⁷ A standard chest CT with a helical pitch of 1.375, a tube potential of 120 kV, 4 mm of Al filtration, and a scanner geometry matching that of the GE Discovery CT750 HD scanner was simulated. After the virtual CT scans were delivered and radiation dose distributions were calculated for both the ScoutCT-NET patient model and the CT-based gold-standard patient model, the gamma analysis method⁷⁸ was used to evaluate the quantitative agreement between their dose distribution maps.

To quantify the agreement between CT and ScoutCT-NET dose distributions and to test the empirical generalizability of the ScoutCT-NET, the percentage of voxels with a passing gamma value (≤ 1) was calculated for each of the 212 testing patients. The median and inter-quartile range (IQR) for the percentage were calculated. Three passing criteria were used: 1) Δd_m = 5mm, ΔD_m = 5%; 2) Δd_m = 5mm, ΔD_m = 10%; and 3) Δd_m = 10mm, ΔD_m = 10%, where ΔD_m denotes the dose difference and Δd_m denotes the distance to agreement (DTA) as defined in Ref. 78.

E. Quantitative evaluation of 3D patient attenuation models generated from ScoutCT-NET (II): Accuracy of radiation dose prescription in fluence-field modulated CT applications

With the 3D patient model generated from ScoutCT-NET, the expected x-ray attenuation along an arbitrary ray direction was calculated by forward-projecting the 3D patient model using the Siddon method and the geometry of a given CT system.⁷⁹ Based on the attenuation information and the “minimal mean FBP noise variance method”,^27,80,81 fluence-field modulation plans were calculated. The plans were determined by solving the following constrained optimization problem:

$$\underset{n_{j,\theta }}{\text{min}}\overline{{\sigma }^2}\left(n_{j,\theta }\right),\text{s . t.}{n}_{\text{total}}=\sum _{\theta }\sum _j{n}_{j,\theta },$$ (3)

where n_j,θ represents the expected x-ray number for detector element j at projection angle θ, $\overline{{\sigma }^2}$ is the mean noise variance of a reconstructed CT image determined by n_j,θ, and n_total is the total photon number budget. The well-known Lagrange multiplier method can be used to find a closed-form solution as shown by Harpen:⁸¹

$$n_{j,\theta }=\frac{{\text{e}}^{\frac{l(j,\theta )}{2}}}{{\sum }_{j,\theta }{\text{e}}^{\frac{l(j,\theta )}{2}}}{n}_{\text{total}}.$$ (4)

In Eq. (4), l(j,θ) denotes the line integral of the patient’s linear attenuation coefficient along a ray corresponding to the jth detector element and a projection angle of θ. Once the fluence-field modulation plan was determined by solving Eq. (3), it was used to modulate the x-ray fluence for each ray, which will be virtually delivered to the patient using the geometry of the Discovery CT750 HD CT scanner (GE Healthcare, Waukesha, WI). The voxelized ground truth “patient” used for virtual delivery was established based on the true CT image volume. FBP was applied to the acquired projection dataset to reconstruct CT images resulted from the virtual fluence-field modulated CT scans. The radiation dose distribution map was also provided by the Monte Carlo method (MC-GPU version 1.3).

Using a similar workflow, we also generated images and dose distributions for 1) Interview modulated CT prescribed using the average of the central 100 detector channels from two-view scouts and the cosine interpolation method⁴¹ and 2) Inter-view modulated CT prescribed using online feedback from the 180° conjugate projection measurements^46,47. Specifically, the “online 180°” method used a bi-dimensional moving average of the projection data and stored the maximum patient attenuation of each angle over the previous half rotation for tube current modulation. All simulations were performed at matched overall patient dose levels. The results were assessed using noise-only image and noise standard deviation (STD) maps generated from 50 repeated virtual CT scans. Radiation dose distribution maps were also compared. The similarity of the dose distributions between the dose modulation plans calculated using ScoutCT-NET images and the actual CT images was assessed using the gamma analysis method previously described. Two passing criteria were used: 1) Δd_m = 1mm, ΔD_m = 1%; 2) Δd_m = 3mm, ΔD_m = 3%.

F. Quantitative evaluation of 3D patient attenuation model generated from ScoutCT-NET (III): Accuracy of radiation dose prescription in organ-specific CT dose delivery applications

Image data of a female patient were used to demonstrate the potential application of the ScoutCT-NET based 3D patient model in organ-specific CT dose delivery. The selected organs-of-interest are breast, spinal canal, and ascending aorta. Each virtual dose delivery focuses on one of the three organs. As a proof-of-concept, the objective of the dose prescription was to obtain the highest image quality within the organ-of-interest while keeping radiation dose delivered to other body regions as low as possible. No matter which organ was chosen, the overall dose delivered to the patient was fixed at 1.6 mGy. For each organ, two dose modulation plans were prescribed: one based on the 3D patient model generated from ScoutCT-NET; the other one based on the reference CT images. During the dose prescription, an ROI was placed on the organ identified based on the 3D patient model (or CT images). Next, the tube current for a given projection view was determined based on the standard that rays intersecting the ROI have a reference entrance photon fluence; all other non-intersecting rays were kept at only 6% of the reference fluence. The quality of the organ-specific modulation plans was assessed using noise-only images and noise STD maps generated from 50 repeated virtual scans. Dose distribution maps were compared between plans prescribed using the ScoutCT-NET 3D patient model and those using true CT images.

G. Empirical studies of generalizability of ScoutCT-NET

One potential challenge with the existing deep learning studies lies in the fact that there is no theoretical guarantee in their generalizability at this time. Therefore, it is important to extensively test the generalizability of a trained deep learning model despite the caveat that there is no general principle to guide this empirical generalizability test. In this study, empirical generalizability was tested from two aspects: as shown in sub-section IID, Monte Carlo dose distributions have been computed using the output of the trained ScoutCT-NET over the entire test patient cohort (212 patients). To further test how well the network model can be generalized in practice, qualitative evaluations have also been performed to determine whether the trained model can be applied to extremal cases such as pediatric patients and anthropomorphic chest phantoms.

III. RESULTS

A. 3D tomographic patient model accuracy studies: Qualitative and quantitative assessment of ScoutCT-NET based dose distribution maps

Table I summarizes the results of the gamma analysis for the agreement between the radiation dose distributions virtually delivered to the ScoutCT-NET 3D patient model and those to the CT images for all 212 testing subjects. Median values for the percent of voxels with satisfactory gamma values (γ(r_m) ≤ 1) across the 212 testing patients were 97.9%, 95.0% and 92.8% for the (Δd_m = 10mm, ΔD_m = 10%), (Δd_m = 5mm, ΔD_m = 10%), and (Δd_m = 5mm, ΔD_m = 5%) criteria, respectively. These results indicate that one could estimate the radiation dose from a helical chest CT using ScoutCT-NET images with 95.0% of the patient’s voxels being within 5 mm and 10% dose difference of the actual CT scan. This is important because it opens up the possibility of having accurate patient-specific and organ-specific x-ray modulation prescriptions.

Table I.

Percent of voxels with passing gamma criteria (γ(r_m) ≤ 1) across the entire testing cohort with 212 patients. DTA: distance to agreement (DTA).

DTA/Dose Difference	Median	IQR	Min	Max
5 mm/5%	92.8 %	89.7% – 94.2 %	78.1 %	96.8 %
5 mm / 10%	95.0 %	93.2% – 96.0 %	83.1 %	97.6 %
10 mm / 10%	97.9 %	97.4% – 98.3 %	93.3 %	99.1 %

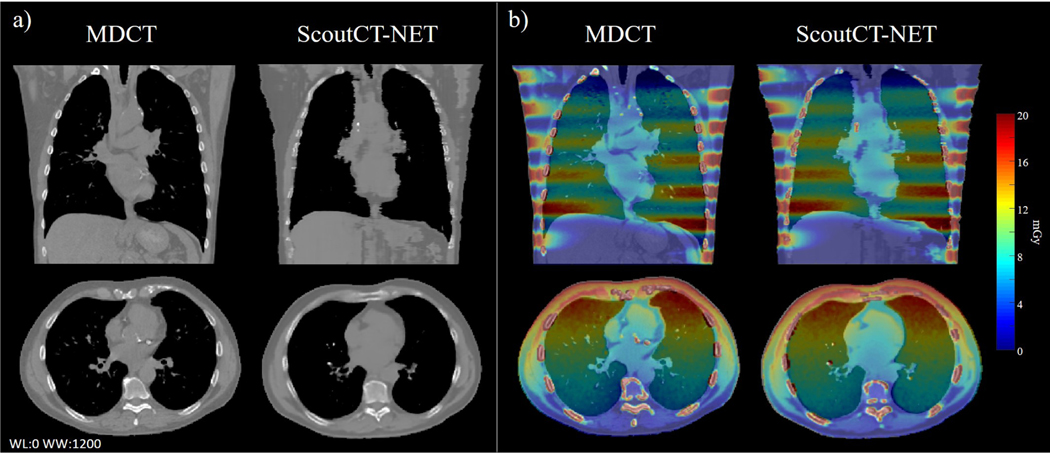
Figure 3 shows axial and coronal slices through the ScoutCT-NET 3D attenuation model of a patient from the testing cohort. A similar image impression between the ScoutCT-NET patient model and CT images was achieved with all major anatomical structures and organs clearly delineated in the ScoutCT-NET patient model. In addition, the radiation dose distribution from a virtual helical CT scan delivered to the 3D attenuation model closely matched the radiation dose distribution calculated based on the CT image volume. For this subject, the gamma analysis demonstrated that 96.0% of image voxels had a gamma value ≤ 1 based on the Δd_m = 5mm distance to agreement and ΔD_m = 10% criterion.

Figure 3:

(a) Coronal and axial slices through the ScoutCT-NET 3D patient attenuation model and the corresponding CT images. (b) Comparison of the spatial distribution of absorbed doses from a virtual helical CT scan delivered to the ScoutCET-NET attenuation model with those to the CT-based attenuation model. 96.0% of the voxels had a gamma value ≤ 1 based on the Δd_m = 5mm distance to agreement and ΔD_m = 10% criterion.

B. 3D tomographic patient model accuracy studies: Accuracy in radiation dose prescription in fluence-field modulated CT applications

Figure 4 compares x-ray fluence profiles used in the inter-view and intra-view dose modulated CT prescribed and virtually delivered to a patient from the testing cohort. For each projection angle, the x-ray fluence fields prescribed based on the ScoutCT-NET 3D attenuation model closely matched those prescribed based on CT images. The figure also demonstrates that, even with the use of the bowtie beam filter, the two-view scout based “cosine” inter-view modulation and the “online 180°” inter-view scheme generated less conformal fluence profiles: for example, for projection views with an overall high attenuation due to the presence of the spine, the breast tissue also receive more doses.

Figure 4:

Comparison of x-ray fluence profiles for different CT dose delivery techniques applied to a test subject. These techniques include the “cosine” tube current modulation (TCM) combined with a bowtie filter, “online 180°” TCM with a bowtie filter, intra-view fluence-field modulation prescribed based on the CT image volume, and intra-view fluence-field modulation prescribed based on the ScoutCT-NET 3D patient model. The sub-figure (a) on the upper left plots the maximal fluence of each view as a function of projection angle. Other sub-figures in (b) show x-ray fluence profiles for 9 representative projection angles. For the ”cosine” and the ”online 180” methods, the modulation within the fan beam for each projection view was caused by the bowtie filter while both methods used angular TCMs. Each detector element has a physical size of 1 mm×1 mm.

Figure 5 shows imaging outcomes from virtual deliveries of four different CT dose modulation schemes, which includes two-view scout image-based “cosine” tube current modulation, “online 180°” tube current modulation, reference CT image based intra-view fluence-field modulation, and ScoutCT-NET 3D patient model-based intra-view fluence-field modulation. The results were simulated at matched overall absorbed dose level (1.6 mGy). For each dose delivery scheme, the reconstructed CT image, noise-only image, noise STD map, and absorbed dose map are provided. The noise-only images and STD images show highly non-uniform noise distributions for both the “cosine” and the “online 180°” tube current modulation methods: while lower noise can be observed in the lungs, much higher noise can be found in the periphery region of the body where the bowtie shape mismatched the actual patient attenuation. In contrast, intra-view fluence-field modulation led to much more uniform noise patterns across the entire body cross-section with significantly fewer noise streaks. The spatially uniform image quality provided by fluence-field modulated CT can benefit the detection of lesions both within and outside the lungs as well as detection of other incidental findings. As shown by the third and fourth columns of Fig. 5, both the image quality and dose distributions of the ScoutCT-NET patient model-based fluence-field modulated CT matched those prescribed using the true CT volume: the percent of voxels within the patient with satisfactory gamma values are 98.4% and 100.0% for the 1) Δd_m = 1mm, ΔD_m = 1% and 2) Δd_m = 3mm, ΔD_m = 3% criteria, respectively. As a reminder, in reality, the true CT volume is generally unavailable before the fluence-field modulated CT is performed. In this case, only ScoutCT-NET enabled fluence-field modulated CT with uniform image quality.

Figure 5:

Comparison of four different dose modulation techniques that were virtually applied to a female patient from the test cohort. The four techniques are “cosine” tube current modulation prescribed based on two-view 2D scout images (column 1), “online 180°” tube current modulation prescribed based on conjugate projections (column 2), intra-view (fluence-field) modulation prescribed based on the reference CT images (column 3), and intra-view (fluence-field) modulation prescribed based on the ScoutCT-NET 3D patient model (column 4). The first row shows CT images from different dose modulation schemes; the second row shows noise-only images; the third row displays noise standard deviation (STD) maps calculated from 50 repeated virtual experiments; the fourth row shows radiation dose distributions.

C. 3D tomographic patient model accuracy studies: Accuracy in radiation dose prescription in organ-specific dose prescription CT applications

Figure 6 shows imaging outcomes of organ-specific CT dose deliveries. Plans of these deliveries were prescribed using the ScoutCT-NET 3D patient attenuation model, or using the CT volume as the reference standard. For each virtual dose delivery, one of the following three organs was chosen: breast, the ascending aorta, or the spinal canal. For the ScoutCT-NET-based plan, the ROIs of these organs were drawn based on the 3D patient attenuation model without using any information from the CT image volume. As demonstrated by Row (1) in Fig. 6, organ ROIs determined based on the ScoutCT-NET patient model matched those based on the CT image volume. Even for glandular tissues in the breast, its ROI can be easily drawn based on the ScoutCT-NET patient model. Fig. 6 Row (2) and Row (3) show the differing image quality between the ROIs and the rest of the body cross-section. When the CT dose modulation was prescribed for a given ROI, noise in that ROI is significantly lower. The noise-only images in Row (4) and the STD maps in Row (5) further confirm the much lower noise magnitude in the selected ROI of each plan. The radiation dose maps in Row (6) demonstrate that the dose distribution was substantially modulated: the organ-of-interest received higher (but not overly high) dose while the rest of the patient body received significantly less radiation. The overall dose was maintained at a constant level of 1.6 mGy. These results demonstrate that ScoutCT-NET 3D patient model can be used to prescribe organ-specific dose modulated CT to enhance the image quality of specific regions in the patient body while meeting the radiation dose constraint. The results also confirm that the ScoutCT-NET patient model generated equivalent imaging outcomes as the gold-standard patient attenuation model.

Figure 6:

Results from organ-specific CT dose deliveries. The region-of-interest (ROI) is in the breast (a), the ascending aorta (b), or the spinal canal (c). Row (1) illustrates the locations of the ROI selected based on the ScoutCT-NET 3D patient model or the reference CT image volume. Row (2) shows the CT image virtually acquired using different organ-specific dose modulation plans and reconstructed using FBP. Row (3) shows zoomed-in images at three locations for each dose modulation plan. Row (4) shows noise-only images corresponding to the results in Row (2). Row (5) shows noise standard deviation (STD) maps calculated from 50 repeated virtual deliveries of each dose modulation plan. Row (6) shows radiation dose distribution of each dose modulation plan. The dose levels are reported within the organ-of-interest and excluding the organ-of-interest. All modulation plans are conducted with the overall dose delivered to the patient being matched.

D. Generalizability test

To demonstrate the generalizability of ScoutCT-NET, the network was applied not only to adult patients, but also to a pediatric patient and an anthropomorphic chest phantom. Fig. 7 shows multiplanar reformatted images and volume renderings of 3D attenuation models for the generalizability-testing image objects: although some anatomical structures in the lung were not perfectly reproduced in the ScoutCT-NET attenuation models due to the low attenuation contrast of these structures in the planar scout images, the overall image impression and organ locations of ScoutCT-NET patient models accurately resemble the corresponding CT images even for patients with abnormal anatomy in addition to a 2-year-old pediatric patient.

Figure 7:

Coronal and volume rendering of (a) MDCT and (b) ScoutCT-NET images of an anthropomorphic phantom. The ScoutCT-NET images reconstructed in (b) served as the basis 3D patient attenuation model to calculate the optimal intra-view dose modulation plan. (c) Shows axial MDCT and ScoutCT-NET images of a patient with pleural effusion as pointed by the arrow and (d) shows axial and coronal images of a 2-years old pediatric patient. These images show the generalization of the ScoutCT-NET model to patients with different medical conditions as well as pediatric patients, despite being trained using images from adult patients.

IV. DISCUSSION AND CONCLUSIONS

In this paper, the following key results have been obtained: 1) It has been shown that the proposed ScoutCT-NET can be trained in an end-to-end manner to generate 3D patient attenuation models directly from true clinical two-view scout (i.e. topogram) images. Once the ScoutCT-NET model is trained, it can be directly used to reconstruct 3D patient attenuation models without any prior knowledge of the patient anatomy. 2) One trained model using a large training data set with diverse data conditions can be applied to reconstruct 3D patient tomographic models for patients with a similar anatomical coverage. 3) The reconstructed 3D patient attenuation models provided the needed accuracy to prescribe radiation dose in both fluence-field modulated CT and organ-specific dose deliveries. 4) Since the 3D patient model is directly reconstructed from two-view scout images with a long z-coverage, the reconstructed patient tomographic model can be readily used to perform nearly optimal inter-view tube current modulations similar to that achieved in online modulation schemes. In addition, the ScoutCT-NET patient model does not depend on the CT scan modes employed in various applications.

Towards reconstructing CT images from one or two planar x-rays, prior efforts have been made to train deep neural networks using CT images and their digital forward-projections, namely DRRs.^82–84 The majority of the validations of these networks used DRRs (over which the developers have precise control and knowledge during the forward-projection process) instead of real x-ray images, not to mention real scout images. To our knowledge, the only prior work that performed evaluations using real x-ray radiography images, but not actual scout images, is Ref. 65. However, no reference-standard CT images were provided to validate the “quite plausible”⁶⁵ images generated from real x-ray images and thus their values in medical applications remain unclear due to the potential challenges between DRRs and scout images. It is worth mentioning that, in reality, there exist multiple differences between DRRs, x-ray radiography images, and scout images: for example, the signal intensity of scout images is scaled differently from radiography images; both the pixel size and material of CT detectors are different from the flat panel detectors used in radiography and the idealized detector used in generating DRRs; x-ray radiography images are usually acquired under the wide-cone geometry with much poorer scatter rejection capability and stronger x-ray heel effect compared to CTs. In contrast, scout images are acquired by operating the MDCT scanner under a scanning-beam acquisition mode with narrowly collimated beams. The scout images were stitched from a series of image segments along the scanning direction. Therefore, as shown in Fig. 2 in Subsection IIB, a proper preparation/curation of the scout images during the training phase of ScoutCT-NET is essential for its initial success. In the context of 4D CBCT acquisitions, it is also worth mentioning that earlier work⁸⁵ has demonstrated the possibility to estimate the motion field from a single view of DRR. If the estimated motion field is accurate enough, one can potentially generate a new image volume that is consistent with the single view DRR. However, there is no study to look into this possibility in a systematic way yet.

Our study also has some limitations. First, we only studied the application of ScoutCT-NET for anatomical regions in the chest. This deliberate choice is partially due to the fact that the chest anatomy is highly heterogeneous and contains important radiosensitive organs with major differences in density, e.g. lung tissue vs soft tissue. As a result, this anatomic region has a great potential for intra-view dose modulation CT to offer greater potential for radiation dose reduction. But our general methodology is not limited to chest scans and in principle, one could easily extend and re-train a ScoutCT-NET network for other anatomical regions. Second, we have only validated our methodology using images from a single CT vendor, meaning that our trained ScoutCT-NET model might not be directly generalizable to other vendors’ scout image data without further re-training or network fine-tuning. However, it is important to notice that the general methodology of ScoutCT-NET does not make any assumptions about the equipment used to acquire the scout images and CT images or any vendor proprietary data processing steps other than the CT system geometry. Therefore, in principle, the ScoutCT-NET should be able to be implemented under multiple manufacturers’ platforms without significant drawbacks. Finally, an inherent limitation of the presented methodology is the fact that both the AP and LAT scout images, as well as the CT scans used as prior images for network training and data analysis, come from separated scans acquired at different patient breath holds with CT table translation between scans. This means that the scout images used as input of the ScoutCT-NET network might not be perfectly registered to the exact same anatomy or the target images used during network training regularization. This limitation is somewhat alleviated by the use of a data consistency term in the objective function, but at the same time it prevents us from drawing even stronger conclusions regarding the accuracy of the reconstructed images and their potential diagnostic value. Also, at the current research stage, neural network architecture design is purely empirical, and we did not perform any ablation studies or neural architecture search optimization, as these problems will often be NP-hard in order to determine the minimal required amount of data and the neural network architecture needed to achieve the desired performance. However, it is important to notice that we did not observe any case in our cohort where this limitation had a significant adverse effect on the practical use of ScoutCT-NET for radiation dose optimization purposes.

In conclusion, a deep learning-based method has been developed in this work to generate 3D patient attenuation models directly from real two-view scout images without requiring any prior knowledge of the patients. This method opens a new way for prospectively prescribing dose delivery schemes for fluence-field modulated and organ-specific dose modulated CT towards accomplishing personalized medicine.

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.