Structural, magnetic and electronic properties of CrO₂ at multimegabar pressures

Abstract

As the only half-metallic ferromagnetic material in 3d transition metal dioxides, CrO₂ has attracted great scientific interest from materials science to physical chemistry. Here, an investigation into the structural, magnetic and electronic properties of CrO₂ under high pressure has been conducted by first-principles calculations based on density functional theory. Static calculations have predicted that CrO₂ undergoes structural transitions with the sequence of rutile-type → CaCl₂-type → pyrite-type → Pnma → (Fe₂P-type→) I4/mmm at high pressures. In addition, a transition from the ferromagnetic state to the non-magnetic state with the magnetic collapse of Cr is observed in CrO₂ at the pyrite–Pnma transition. This transition also delocalizes the 3d electrons of Cr and leads to a metallic character of CrO₂. The equation of state, elasticity and band gap for each energetically favorable phase of CrO₂ are determined. Our results not only bridge the gap about the high-pressure behavior of CrO₂ in previous studies but also extend our understanding of its properties up to multimegabar conditions. According to previous data and present results, we further discuss and summarize the high-pressure behavior of various AO₂ compounds. This can contribute to investigating properties of other AO₂ compounds or exploring novel materials at high pressures.

CrO₂ can undergo the pressure-induced phase transition sequence of rutile-type → CaCl₂-type → pyrite-type → Pnma → (Fe₂P-type→) I4/mmm.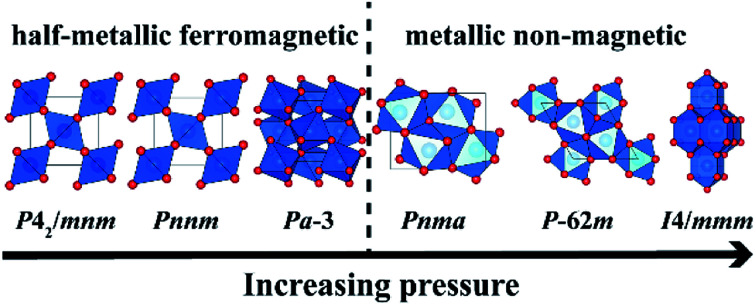

1. Introduction

The high-pressure behavior of AO₂ compounds, especially transition metal dioxides such as TiO₂, VO₂, CrO₂ and FeO₂, has attracted considerable interest in the field of materials science, condensed matter physics and geoscience.^1–10 For example, as a very important technological wide-gap semiconductor widely applied in photo-catalysts and electrochemical solar cells,^1,3 the band gap of TiO₂ can be modified by pressure, which extends its application in the industry.^11–13 The possibility to quench high-pressure forms of AO₂ compounds with different properties to ambient conditions is also potentially important to explore novel materials.¹⁴ In addition, pressure-induced structural and electronic transitions of the simple compound VO₂ provide a good example to deeply understand and interpret the complicated Mott-like metal–insulator transition.^15,16 On the other hand, pressure-induced phase transitions of transition metal dioxides can serve as lower-pressure analogs to SiO₂, a critical component in the Earth's interior, especially when investigating ultrahigh-pressure polymorphs of SiO₂ in super-Earths’ or extrasolar planets' interiors.^17–20

In particular, CrO₂ attracts special interest since it is the only half-metallic (HM) ferromagnetic (FM) material in 3d transition metal dioxides. At ambient conditions, CrO₂ adopts the tetragonal rutile-type structure consisting of distorted edge-sharing CrO₆ octahedra similar to other transition metal dioxides [Fig. 1(a)]. Due to the crystal field of distorted CrO₆ octahedra, Cr t_2g states are split into d_xy with lower energy and d_yz–d_xz with higher energy. The double-exchange interaction between the localized 3d electron occupying the d_xy state and the delocalized 3d electron occupying half of the d_yz–d_xz state near the Fermi level accounts for its HM and FM nature. The previous Andreev reflection experiment demonstrated that the spin polarization of the conduction electrons was more than 90%.²¹ The saturation magnetization at 10 K was experimentally determined to be 1.92 μB per Cr.²² Compared with other half-metals, the FM CrO₂ possesses a high Curie temperature of 390 K, which is also of technological importance to develop spintronic devices.²³ It is thus evident that these intriguing technological applications are associated with the structural, magnetic and electronic configurations of CrO₂. The properties are originated from the arrangement and interaction of electrons of CrO₂ within a typical structure.

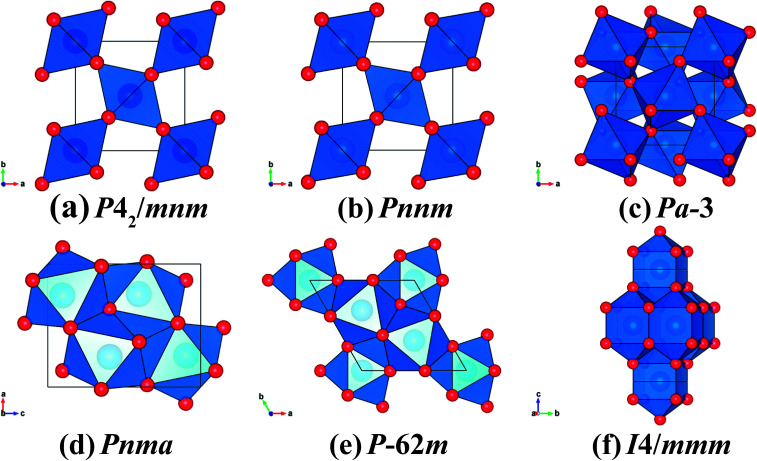
Fig. 1. The crystal structures of CrO₂ with (a) rutile-type, (b) CaCl₂-type, (c) pyrite-type, (d) Pnma, (e) Fe₂P-type and (f) I4/mmm. The blue and red spheres represent Cr and O atoms, respectively.

High pressure, as one important thermodynamic parameter provides a unique way to decipher materials' structural, magnetic and electronic properties. The previous synchrotron X-ray diffraction (XRD) experiment and first-principle simulations both confirmed a second-order structural transition of CrO₂ from rutile-type to CaCl₂-type at ∼12 GPa.^24–26 Theoretical computations predicted a further transition to the CaF₂-type structure at 89.6 GPa.²⁵ Recently, Wu et al.²⁷ predicted a pressure-induced phase transition sequence of rutile-type → CaCl₂-type → pyrite-type → CaF₂-type for CrO₂ whereas calculated results by the GGA method demonstrated that CrO₂ underwent a transition sequence of rutile-type → CaCl₂-type → PbO₂-type → pyrite-type at high pressures.²⁸ Obviously, there exists considerable discrepancy between different computational studies on CrO₂. It is worthwhile to note that heretofore the highest coordination number of Cr of various CrO₂ phases considered in previous investigations is eight whereas denser structures with higher coordination number are not included. In terms of magnetic properties of CrO₂ at high pressures, Kuznetsov et al.²⁹ predicted a magnetic transition from the FM state to the non-magnetic (NM) state accompanied by a half-metal to metal transition at ∼53 GPa. Whereas another theoretical study showed that the energetically favorable pyrite-type CrO₂ kept FM and HM up to ∼100 GPa.²⁸ In the meanwhile, Kim et al.²⁶ indicated that the phonon softening led to the FM–NM transition across a structural transition from the CaCl₂-type to a monoclinic structure at ∼61 GPa. Beyond ∼89 GPa, the CaF₂-type structure had the lowest enthalpy and correspondingly CrO₂ became a FM insulator. Therefore, the effect of pressure on the magnetic and electronic properties of CrO₂ still remains elusive and the physical properties of CrO₂ with much denser structures are poorly understood.

In this paper, we have performed first-principle calculations based on density functional theory (DFT) to fully investigate the structural, magnetic and electronic properties of CrO₂ at high pressures aiming to bridge the gap about the high-pressure behavior of CrO₂ between previous studies. Furthermore, we extend the pressure range to investigate stable structures and properties of CrO₂ up to multimegabar conditions. Finally, comparing previous data with present results, we summarize the high-pressure behavior of various AO₂ compounds such as the phase transition sequence, elasticity and electronic properties.

2. Methods

High pressure can generally reduce bond distances and lead to the structural transition of one compound to form a denser structure. In addition, transition metal dioxides might undergo a similar phase transition sequence upon compression due to similar properties of transition metal elements. Thus, based on this empirical rule of the high-pressure crystal chemistry and extensive experimental and computational data, twelve candidate structures (rutile-type (P4₂/mnm), CaCl₂-type (Pnnm), PbO₂-type (Pbcn), pyrite-type (Pa3̄), CaF₂-type (Fm3̄m), Pnma, Fe₂P-type (P6̄2m), CuAl₂-type (I4/mcm), R3̄m, I4/mmm, AlB₂-type (P6/mmm), and Ni₂In-type (P6₃/mmc)) for CrO₂ were considered in the present study. First-principle calculations were performed based on DFT with the projected augmented wave method (PAW) implemented in Vienna ab-initio simulation package (VASP).^30–32 The Perdew–Burke–Ernzerhof (PBE) version of the generalized gradient approximations (GGA) was selected to treat the exchange correlation potential.³³ The kinetic energy cut-off was set to 1000 eV. The energy convergence criterion for the electronic self-consistent calculation was 10⁻⁶ eV. The total energy difference was converged to 1 × 10⁻⁵ eV per formula unit (f.u.) with respect to the energy cutoff or k-points. The force difference was converged to 1 × 10⁻³ eV Å⁻¹ (less than 0.1 GPa). The spin-polarization of Cr without spin–orbit coupling in CrO₂ with various structures was included in the present study to obtain accurate physical information of CrO₂. The calculated sub-lattice magnetic moment per Cr in the rutile-type CrO₂ at 0 GPa was 2.04 μB in agreement with previous results and the HM property of the rutile-type CrO₂ could be accurately depicted.²² The structural, elastic and magnetic properties of the rutile-type CrO₂ at 0 GPa could be reproduced by means of the GGA method. But Korotin et al.³⁴ suggested that the correlated effect of 3d electrons should be considered in CrO₂. Whether this system is strongly correlated is still an open question. On the one hand, comparing DFT results with low-temperature experimental data, Toropova et al.³⁵ concluded that the ordered phase of CrO₂ was weakly correlated. On the other hand, the calculated band gap of the rutile-type CrO₂ at 0 GPa was ∼1.3 eV by the GGA method, much lower than the normal value ∼2 eV.³⁴ Thus, in the present study, we used both the GGA and GGA + U methods to perform electronic density of state (DOS) calculations.³⁶ We applied U = 3 eV (the on-site Coulomb interaction parameter) and J = 0.9 eV (the Hund coupling constant) for Cr in GGA + U calculations as previous simulations did.^34,37

For each crystalline phase, the atomic positions, unit-cell parameters and individual magnetic moments were allowed to relax at each given volume to obtain the minimum total energy. Energy-volume results were then fitted to the third-order Birch–Murnaghan equation of state (EoS) to obtain the corresponding parameters (volume per formula unit (V₀), bulk modulus (K₀), its pressure derivative 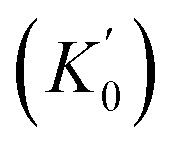and energy (E₀) at zero pressure).^38,39 In addition, the enthalpy (H = E + PV) of each phase was compared with each other to identify the most stable structure at the given pressure. Furthermore, the DOS of various CrO₂ phases under selected pressure conditions were obtained by the static calculation, utilizing the tetrahedral smearing method with Blöchl corrections. The k-points grids were set as 12 × 12 × 20 for rutile-type, 12 × 12 × 20 for CaCl₂-type, 16 × 16 × 16 for pyrite-type, 16 × 24 × 12 for Pnma, 13 × 13 × 29 for Fe₂P-type and 24 × 24 × 12 for I4/mmm CrO₂ in DOS calculations. The phonon dispersion was calculated using the phonopy code by the supercell method.⁴⁰ 2 × 3 × 2, 2 × 2 × 3 and 3 × 3 × 2 supercells were constructed for the Pnma, Fe₂P-type and I4/mmm CrO₂, respectively. The k-points grids in phonon calculations were set as 3 × 5 × 3 for Pnma, 3 × 3 × 5 for Fe₂P-type and 5 × 5 × 3 for I4/mmm CrO₂, respectively.

3. Results and discussion

3.1. Structural stability and phase transitions

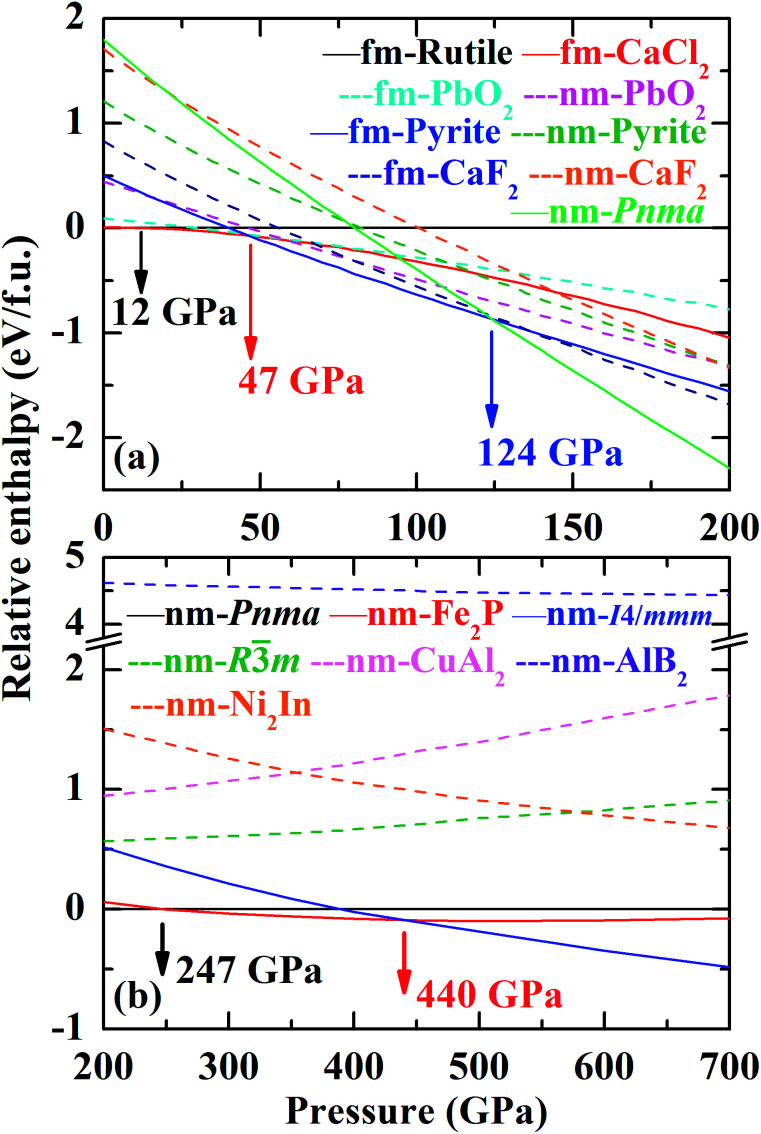
The corresponding EoS parameters of various candidate phases of CrO₂ are listed in Table 1. The present results of the FM rutile-type CrO₂ are consistent with previous high-pressure XRD data.²⁴ Calculated static enthalpy differences among various candidate phases of CrO₂ are plotted in Fig. 2 as a function of pressure up to 700 GPa based on aforementioned parameters. The present static calculations predict that CrO₂ will undergo five structural transitions upon compression with the sequence of rutile-type → CaCl₂-type → pyrite-type → Pnma → Fe₂P-type → I4/mmm. Calculated lattice constants and atomic coordinates of six phases at selected pressures are listed in Table 2.

Calculated parameters of the third-order Birch–Murnaghan equation of state (energy per formula unit E₀, volume per formula unit V₀, bulk modulus K₀ and its pressure derivative 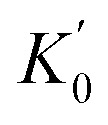at zero pressure) of different CrO₂ phases. FM and NM represent ferromagnetic and non-magnetic, respectively. The previous experimental and theoretical data are extracted for comparison.

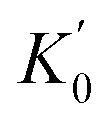
Phase	E 0/f.u. (eV)	V 0/f.u. (Å3)	K 0 (GPa)		Method and reference
FM-rutile	−25.231	29.13	228	4.7	This study
Rutile	—	28.50	235	5.0	Exp.24
Rutile	—	28.09	283	4.6	LDA27
FM-CaCl2	−25.225	29.15	205	3.7	This study
CaCl2	—	29.05	162	4.0	Exp.24
CaCl2	—	28.32	179	4.3	LDA27
FM-PbO2	−25.138	28.69	219	4.2	This study
NM-PbO2	−24.785	27.57	213	4.7	This study
FM-pyrite	−24.727	26.85	249	4.4	This study
Pyrite	—	26.12	272	4.6	LDA27
NM-pyrite	−24.021	26.12	272	4.3	This study
FM-CaF2	−24.401	26.35	254	4.4	This study
CaF2	—	25.26	289	4.5	LDA27
NM-CaF2	−23.523	25.60	276	4.3	This study
NM-Pnma	−23.434	24.95	254	4.0	This study
NM-Fe2P	−22.844	23.98	286	4.1	This study
NM-CuAl2	−22.533	24.79	262	4.3	This study
NM-R3̄m	−22.861	24.88	254	4.2	This study
NM-I4/mmm	−21.742	23.13	310	4.1	This study
NM-AlB2	−18.704	24.97	241	4.1	This study
NM-Ni2In	−21.203	24.28	240	4.3	This study

Fig. 2. Static enthalpy differences among various candidate phases of CrO₂ as a function of pressure. FM and NM represent ferromagnetic and non-magnetic, respectively. Structural transitions have been indicated by arrows.

Calculated lattice parameters and atomic coordinates of rutile-type, CaCl₂-type, pyrite-type, Pnma, Fe₂P-type and I4/mmm CrO₂ under different conditions. The previous experimental and theoretical data are given for comparison.

Phase	Pressure (GPa)	a (Å)	b (Å)	c (Å)	Site	Wyckoff symbol	Internal coordinates			Method and reference
							x	y	z
Rutile (P42/mnm)	0	4.459	4.459	2.929	Cr	2a	0	0	0	This study
					O	4f	0.3037	0.3037	0
Rutile	0	4.421	4.421	2.916	Cr	2a	0	0	0	Exp.24
					O	4f	0.301	0.301	0
Rutile	0	4.456	4.456	2.829	Cr	2a	0	0	0	LDA27
					O	4f	0.2999	0.2999	0
CaCl2 (Pnnm)	12	4.409	4.334	2.893	Cr	2a	0	0	0	This study
					O	4g	0.3105	0.2945	0
CaCl2	14	4.387	4.282	2.878	Cr	2a	0	0	0	Exp.24
					O	4g	0.299	0.272	0
CaCl2	14	4.393	4.291	2.881	Cr	2a	0	0	0	GGA28
					O	4g	0.312	0.291	0
Pyrite (Pa3̄)	47	4.538	4.538	4.538	Cr	4a	0	0	0	This study
					O	8c	0.3533	0.3533	0.3533
Pyrite	46	4.524	4.524	4.524	Cr	4a	0	0	0	GGA28
					O	8c	0.353	0.353	0.353
Pnma	128	4.876	2.541	6.066	Cr	4c	0.2551	1/4	0.9049	This study
					O1	4c	0.3676	1/4	0.5979
					O2	4c	0.4815	1/4	0.1494
Fe2P (P6̄2m)	286	4.866	4.866	2.308	Cr1	1b	0	0	0.5	This study
					Cr2	2c	1/3	2/3	0
					O1	3f	0.2698	0	0
					O2	3g	0.6045	0	0.5
I4/mmm	463	2.220	2.220	5.605	Cr	2b	0.5	0.5	0	This study
					O	4e	0	0	0.1603

The predicted rutile–CaCl₂ transition at 12 GPa is consistent with the experimental observation at 12 ± 3 GPa by high-pressure XRD and Raman spectroscopy.²⁴ The second structural transition is calculated to occur at 47 GPa whereas Wu et al.²⁷ predicted it to be 23.9 GPa. As shown in Table 1, data from Wu et al. are perfectly consistent with our results of the NM pyrite-type CrO₂. However, our calculations demonstrate that the FM pyrite-type CrO₂ is more stable than the NM phase up to at least 200 GPa (Fig. 2). This may explain the difference mentioned above. The previous study predicted an intermediate PbO₂-type phase between the CaCl₂-type and pyrite-type CrO₂.²⁸ Though Fig. 2 presents that the enthalpy difference between the PbO₂-type and pyrite-type CrO₂ is marginal, our results imply a direct transition from CaCl₂-type to pyrite-type. This can be also supported by the previous high-pressure XRD experiment, which has revealed that the CaCl₂-type CrO₂ is stable up to about 50 GPa.²⁴ In addition, previous studies simply considered the CaF₂-type structure as the high-pressure post-pyrite phase of CrO₂ neglecting other structures.²⁵ The present simulation demonstrates that neither the FM CaF₂-type nor the NM CaF₂-type is a stable high-pressure phase. Instead, the Pnma structure becomes energetically favorable compared with the pyrite-type structure above 124 GPa. We further predict that at ultra-high pressures the Fe₂P-type and I4/mmm structures are energetically stable for CrO₂, both of which have been also identified as the post-Pnma phases for many AX₂ compounds.^{17–19,41–43} It is to be noted that neither the AlB₂-type nor Ni₂In-type CrO₂ is an energetically stable phase compared with the ten-fold coordinated I4/mmm structure in the calculated pressure range. The enthalpy difference between AlB₂-type (or Ni₂In-type) and I4/mmm is considerable. That is there is no tendency to transform to a structure where the coordination number of Cr is beyond 10 up to at least 700 GPa.

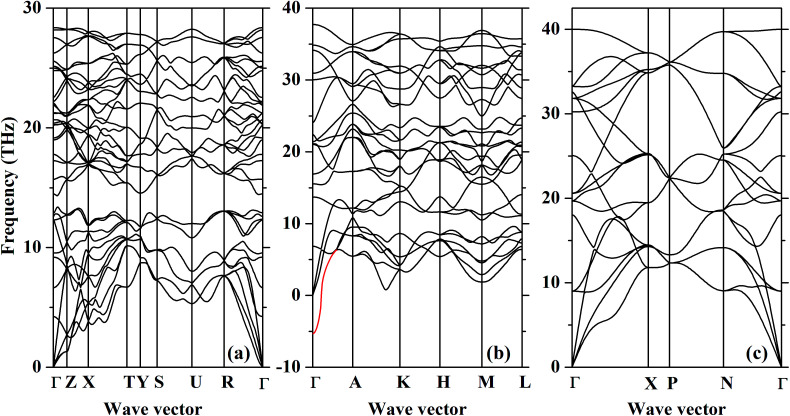
To investigate the dynamic stability of three new phases predicted here, the Pnma, Fe₂P-type and I4/mmm structures at ultra-high pressures, we have performed ab initio lattice-dynamics calculations (Fig. 3). The resultant phonon spectra, lacking any imaginary frequencies imply that the Pnma and I4/mmm phases are dynamically stable. But for the Fe₂P-type phase, the phonon softens below zero around the gamma point in the Brillion zone indicating that it is dynamically unstable. Combining H–P relations and phonon spectra, we might modify the high-pressure phase transition sequence of CrO₂ with rutile-type → CaCl₂-type → pyrite-type → Pnma → I4/mmm. It is worthwhile to mention that although recent first-principle calculations have shown that the energetically favorable Fe₂P-type ZrO₂ is dynamically unstable,⁴⁴ the high-pressure and high-temperature XRD experiments have successfully synthesized the Fe₂P-type ZrO₂.⁴³ This may indicates that the Fe₂P-type phase is dynamically unstable at 0 K, and it can be stable at high temperature and quenched to the ambient temperature. Furthermore, the recent high-pressure experiment has found that VO₂ partially undergoes the Pnma–Fe₂P transition at ∼100 GPa at room temperature without laser heating.⁴⁵ Thus, the Fe₂P-type structure can still be a candidate as an intermediate high-pressure phase between the Pnma and I4/mmm phases. It definitely requires further experimental verification.

Fig. 3. The phonon dispersions of the (a) Pnma, (b) Fe₂P-type and (c) I4/mmm CrO₂ at 128 GPa, 386 GPa and 463 GPa, respectively. The red line indicates the phonon softening.

3.2. Equation of state and elasticity

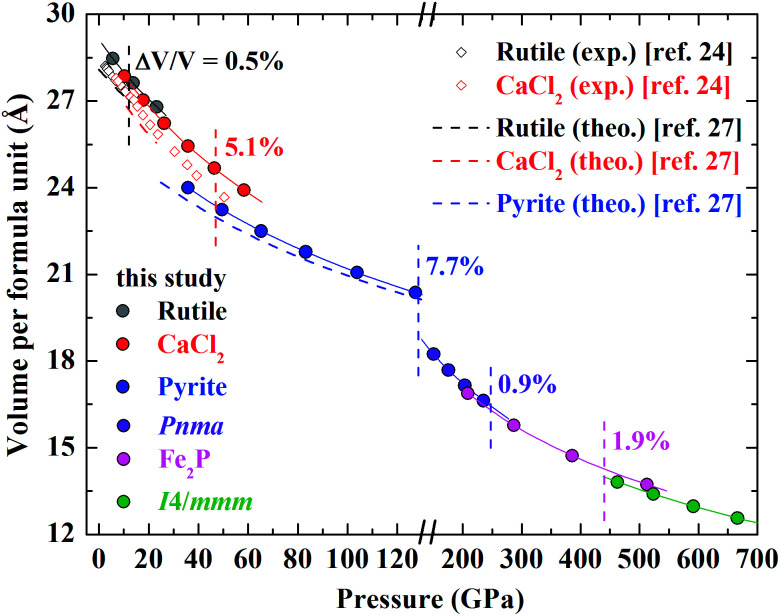
Fig. 4 displays the compression of volumes of various phases as a function of pressure and previous experimental and theoretical data are plotted for comparison.^24,27 Our results are generally larger than those obtained by experiments and calculated from simulations. It is widely accepted that GGA tends to overestimate the experimental volume whereas LDA underestimates it. In addition to different exchange correlation potentials, the spin-polarization of Cr is introduced in the present study, which can also cause a larger calculated volume of one compound.

Fig. 4. Calculated volume per formula unit of the rutile-type, CaCl₂-type, pyrite-type, Pnma, Fe₂P-type and I4/mmm CrO₂ as a function of pressure. The solid lines are fitted by the third-order Birch–Murnaghan equation of state. The volume collapse through the structural transition is marked. The previous experimental (black and red open diamonds²⁴) and theoretical (black, red and blue dashed lines²⁷) data are plotted for comparison.

The volume reduction through the rutile–CaCl₂ transition is marginal, specifically less than 0.5%, corresponding to the strain-driven distortive phase transition [Fig. 1(a) and (b)].²⁴ This can also be supported by the calculated average Cr–O bond distance (d_av) shown in Fig. 5, where the evolution of Cr–O bond distances is continuous through the rutile–CaCl₂ transition at 12 GPa. (The average bond distance is defined as 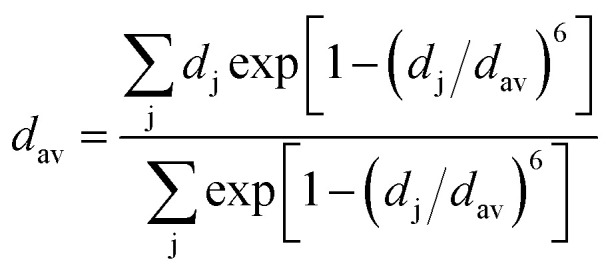.^46,47d_av is obtained self-consistently.). The volume collapse is 5.1% for the CaCl₂–pyrite transition, and 7.7% for the pyrite–Pnma transition (Fig. 4). It indicates that two transitions are both first-order. Fig. 5 and Table 2 demonstrate that the large volume collapse at the CaCl₂–pyrite transition is due to the reconstruction of ions but not to the compression of the nearest-neighbor Cr–O distances [Fig. 1(b) and (c)]. The compression of Cr–O distances at high pressures leads to the abrupt volume change at the pyrite–Pnma transition [Fig. 1(d), 4 and 5]. The effective coordination number (ECoN) of Cr in the Pnma phase increases rapidly from 7.24 at ∼128 GPa to 7.73 at ∼235 GPa. (The effective coordination number is defined as ^46,47). ECoN of Cr in the Fe₂P-type phase is 8.3–8.5 closer to the ideal value 9. Thus, d_av decreases through the Pnma–Fe₂P transition. The volume variation from Pnma to Fe₂P-type and further to I4/mmm is 0.9% at 247 GPa and 1.9% at 440 GPa, respectively. It is comparable to that of structural transitions in similar compounds.^{17,19,41–43} Though the volume reduction is typically smaller than the aforementioned ones, it may have important contributions to stabilize the high-pressure polymorphs of CrO₂. As displayed in Fig. 5, both the dense polyhedral packing and the compression of the nearest-neighbor Cr–O bond distances contribute to the volume variation [Fig. 1(e) and (f)].

Fig. 5. Calculated (a) average Cr–O bond distance and (b) effective coordination number (ECoN) of different CrO₂ phases as a function of pressure. The vertical dashed lines represent phase transitions. The horizontal dotted lines represent ideal coordination numbers for different structures.

As for the zero-pressure bulk modulus K₀ of different polymorphs of CrO₂, none of them are less than 200 GPa (Table 1). K₀ of CrO₂ generally increases after transforming into a new high-pressure phase except K₀ of the CaCl₂-type CrO₂. The distortion of the CaCl₂-type structure upon compression mainly accounts for such a reduction. It is worthwhile to note that K₀ of the ten-fold coordinated I4/mmm CrO₂ exceeds 300 GPa, which might be a potential super-hard material or could be utilized to explore novel super-hard materials.

3.3. Magnetic and electronic properties

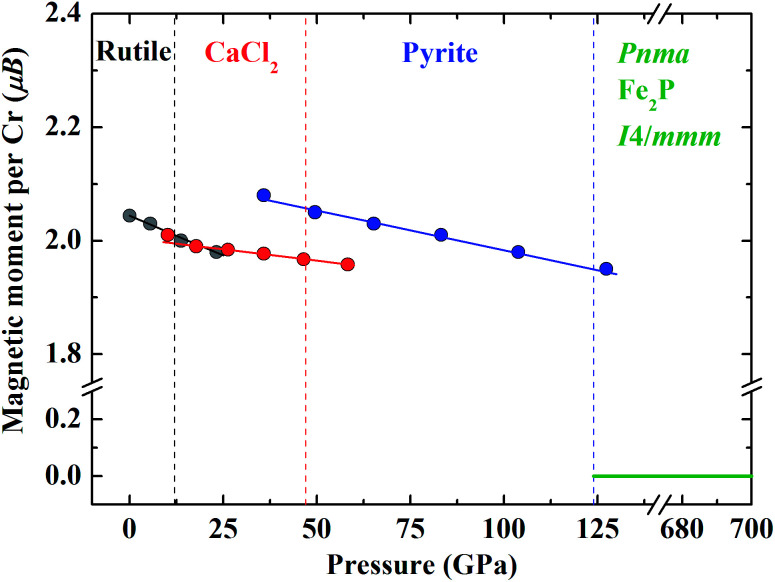
As reported by previous studies, the rutile-type CrO₂ is FM at ambient conditions.²³ CrO₂ keeps FM through the rutile–CaCl₂–pyrite transition upon compression up to about 120 GPa (Fig. 6). The variation of the magnetic moment per Cr is continuous through the rutile–CaCl₂ transition and there is slight increase of the magnetic moment by 0.08 μB at the CaCl₂–pyrite transition. As shown in Fig. 6, the pressure slightly affects the magnetic moment of Cr of the FM state. Specifically, the slopes of magnetic moment reductions versus pressure are −0.0028 for rutile-type, −0.0008 for CaCl₂-type and −0.0014 for pyrite-type, respectively. A magnetic collapse where the sub-lattice magnetic moment per Cr drops from ∼1.95 μB to 0 μB is observed at the transition from pyrite-type to Pnma at 124 GPa indicating an FM–NM transition (Fig. 6). CrO₂ keeps NM up to 700 GPa considered in the present study. Our results do not support the FM–NM–FM transition proposed by Kim et al.²⁶ Comparing previous investigations with our data, we are able to find out that magnetism affects not only the structural stability of CrO₂ at high pressures but also other physical properties such as elasticity.^26–28

Fig. 6. Calculated sub-lattice magnetic moment per Cr in different CrO₂ phases as a function of pressure.

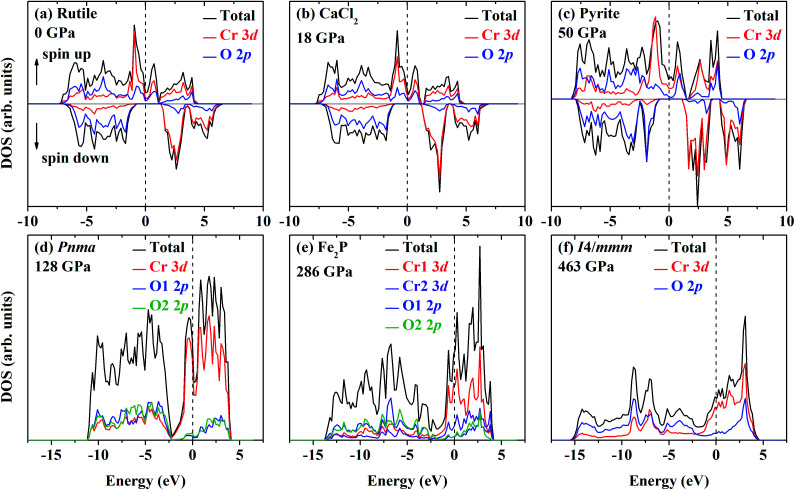
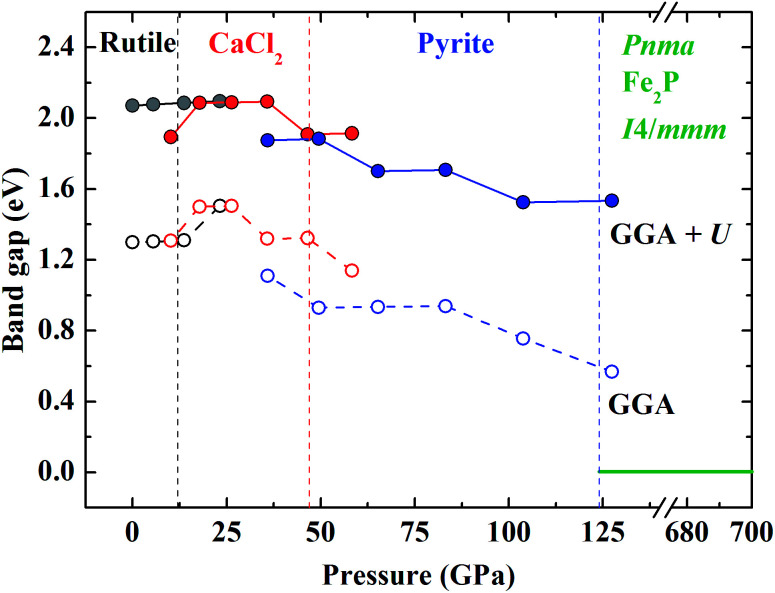
The DOS of various energetically favorable CrO₂ phases at high pressures calculated by the GGA + U method are plotted in Fig. 7. In the rutile-type structure at ambient pressure [Fig. 7(a) and 8], the total DOS in the spin-up state crosses the Fermi level exhibiting metallic whereas there is a gap of 2.07 eV in the spin-down state indicating the semiconducting property. These confirm the HM character of the rutile-type CrO₂ at ambient pressure. Upon compression, CrO₂ keeps its half-metallicity at the transition to CaCl₂-type, even further to pyrite-type (Fig. 7b and c). There is no discontinuity in the variation of the gap in the spin-down state across the rutile–CaCl₂ transition (Fig. 8). The gap of the CaCl₂-type CrO₂ drops ∼0.2 eV at ∼35 GPa. It may be related to the softening of the B_1g phonon mode as observed in the high-pressure Raman experiment.²⁴ The gap in the spin-down state of the pyrite-type CrO₂ reduces gradually upon compression implying the decrease of its half-metallicity at high pressures. At the transition to the Pnma structure, CrO₂ becomes metallic demonstrating that its half-metallicity is destroyed by pressure [Fig. 7(d) and 8]. The Fe₂P-type and I4/mmm CrO₂ still exhibit metallic at least in the calculated pressure range [Fig. 7(e) and (f) and 8]. The contribution of 2p electrons of O to the conducting band is more pronounced in the Fe₂P-type or I4/mmm structure than that in the Pnma structure. Compared with the first three structures (rutile-type, CaCl₂-type and pyrite-type), the 3d electrons of Cr and 2p electrons of O both become more delocalized within the last three structures (Pnma, Fe₂P-type and I4/mmm) resulting in an enhancement of the hybridization between 3d electrons of Cr and 2p electrons of O. As mentioned above, an FM–NM transition with the magnetic collapse of Cr is observed at the pyrite–Pnma transition. In combination with the analysis of DOS of various CrO₂ phases, we may propose that with increasing pressure an FM–NM transition accompanied by a magnetic collapse delocalizes the 3d electrons of Cr leading to the metallic character of CrO₂.

Fig. 7. Calculated DOS of various CrO₂ phases under different conditions by the GGA + U method. The total DOS, partial DOS of Cr and O at each equivalent atomic site are marked. The Fermi level is indicated by the vertical dashed line. (a) Rutile-type at 0 GPa, (b) CaCl₂-type at 18 GPa, (c) pyrite-type at 50 GPa, (d) Pnma at 128 GPa, (e) Fe₂P-type at 286 GPa and (f) I4/mmm at 463 GPa.

Fig. 8. Calculated band gaps in the spin-down state of various CrO₂ phases as a function of pressure by the GGA and GGA + U methods.

3.4. Comparison with other AO₂ compounds

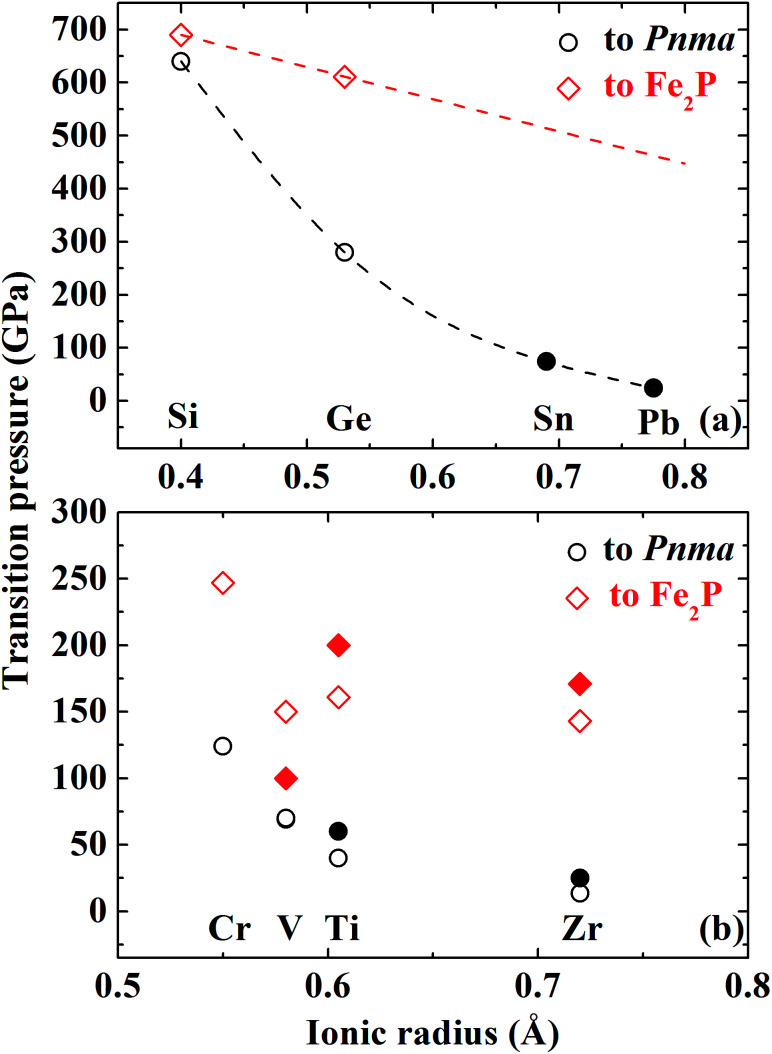
Extensive experimental and theoretical simulations have been performed on AO₂ compounds to investigate their stable high-pressure polymorphs. For the fourth main-group element dioxides except CO₂, they can undergo a transition to the Pnma structure at relevant high-pressure conditions.^42,48–51 SiO₂ and GeO₂ are predicted to undergo the Pnma–Fe₂P transition upon further compression.^17,18,42 The Pnma–Fe₂P transition of TiO₂ is predicted to occur at 161 GPa by the GGA method and confirmed by in situ XRD at 200 GPa and 3000 K.⁴¹ Experimental and theoretical studies have also verified similar transitions in ZrO₂.⁴³ According to these available data and our results, we have plotted the transition pressure to the Pnma or Fe₂P-type structure (noted by P_P or P_F) for AO₂ compounds versus the ionic radius of cations (noted by I_r) (Fig. 9). The ionic radius is the value of the six-fold coordinated cation with the chemical valence of +4.⁵² These dioxides can be divided into two groups: main-group element dioxides with unoccupied d orbitals and transition metal dioxides. As shown in Fig. 9, P_P or P_F for transition metal dioxides is much lower than that for main-group element dioxides. For main-group element dioxides, P_P decreases significantly with I_r compared with P_F [Fig. 9(a)]. For transition metal dioxides, P_P or P_F can be roughly considered to reduce linearly with I_r [Fig. 9(b)]. Either theoretical or experimental P_F of VO₂ is much lower than that of TiO₂ or CrO₂. At room temperature, VO₂ crystallizes in the monoclinic P2₁/c structure, a distorted rutile-type form. The distortion significantly affects the structural characteristics and physical properties of VO₂ upon compression. The quasi-hydrostatic or non-hydrostatic condition in high-pressure diamond anvil cell experiments may contribute to or even promote the transition to the Fe₂P-type structure.⁴⁵P_P and P_F of CrO₂ are a little larger. It may be related to the fact that CrO₂ have unpaired 3d electrons. The existence of magnetism in CrO₂ may stabilize the pyrite-type phase, postponing the transition to the Pnma phase. Xie et al.⁴⁵ also take the high-pressure structural evolution of RuO₂ as an example to illustrate the phase transition route of CaCl₂–pyrite–CaF₂. The difference of oxygen coordination between VO₂ and RuO₂ leads to different evolution patterns. In the present study, the FM CaF₂-type CrO₂ is much more stable than the NM phase (Fig. 2). But the NM Pnma CrO₂ is energetically favorable compared with aforementioned two phases. The magnetic collapse of Cr can make contributions to favor the pyrite–Pnma transition rather than the pyrite–CaF₂ transition. The available data for the pressure-induced phase transition to the I4/mmm structure are too limited and there is no significant relation between the transition pressure to the I4/mmm structure and I_r. In terms of FeO₂ in the recent study, we have predicted a transition sequence of pyrite–R3̄m–I4/mmm at high pressures, different from present calculated results.⁵³ And the stable region of the R3̄m FeO₂ has a span of ∼1200 GPa whereas the R3̄m CrO₂ is energetically unfavorable in the present calculated pressure range. Therefore, this can serve as an indirect evidence that the chemical valence of iron cation is not +4 in FeO₂ under ultra-high pressure.

Fig. 9. Correlation plot between the transition pressure to the Pnma or Fe₂P-type structure for AO₂ compounds and the ionic radius of cations. The ionic radius of the horizontal ordinate is the value of the six-fold coordinated cation with the chemical valence of +4.⁵¹ The circle and diamond marks represent the transition pressure to Pnma and Fe₂P-type, respectively. The open and solid marks represent results obtained by simulations and experiments, respectively.^{17,41–43,45,50,51}.

The EoS of the Pnma TiO₂ and ZrO₂ have been also obtained by means of high-pressure XRD experiments.^54,55 These results show that K₀ of either TiO₂ or ZrO₂ is larger than 400 GPa. However, recent first-principle calculations or updated XRD data demonstrate that they are both smaller than 300 GPa, i.e. 250–290 GPa for TiO₂ and ∼286 GPa for ZrO₂.^12,41,43 It is thus worthwhile to mention that K₀ of the Pnma phase slightly increases with I_r. As displayed in Fig. 5(b), ECoN of Cr in the Pnma phase is much smaller than nine. It increases rapidly upon compression, indicating the rapid compression of the longest Cr–O bond as a function of pressure. This may result in a smaller K₀. Whereas those with high ECoN may have a larger K₀.

As for the electronic property, the HM CrO₂ is predicted to become metallic through the pyrite–Pnma structural transition and keep its metallicity up to 700 GPa. Lyle et al.¹⁹ have predicted the closure of the band gap in TiO₂ and SiO₂ through the Fe₂P–I4/mmm transition at 650 GPa and 9800 GPa, respectively. While FeO₂ is metallic even in the deep lower mantle conditions.^10,56 These thus lead to the conclusion that many of the I4/mmm AO₂ compounds can exhibit metallic, to some extent, independent of their chemical valence and ionic radii of cations. That is the structural character of I4/mmm itself strongly affects the electronic property of AO₂ compounds with the I4/mmm structure upon compression. This can provide an alternative method to explore and synthesize metallic AO₂ materials at high pressures.

4. Conclusions

In conclusion, the high-pressure behavior of CrO₂ has been studied based on first-principle density functional theory. CrO₂ is predicted to undergo a structural transition sequence of rutile-type → CaCl₂-type → pyrite-type → Pnma→ (Fe₂P-type→) I4/mmm at high pressures. Through the pyrite–Pnma transition, a magnetic collapse in CrO₂ where the magnetic moment drops from ∼2 μB to 0 μB is observed accompanied by a half-metal to metal crossover. The equation of state for different phases of CrO₂ are determined and the elasticity of CrO₂ at high pressures is also discussed in detail. Finally, we summarize the high-pressure behavior of various AO₂ compounds, such as the phase transition pressure, elastic and electronic properties.

Conflicts of interest

There are no conflicts to declare.