Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Apr 5;94(15):5901–5908. doi: 10.1021/acs.analchem.2c00110

Experimental Voltammetry Analyzed Using Artificial Intelligence: Thermodynamics and Kinetics of the Dissociation of Acetic Acid in Aqueous Solution

Haotian Chen †, Danlei Li †, Enno Kätelhön ‡, Ruiyang Miao †, Richard G Compton †,*
PMCID: PMC9082489  PMID: 35381175

Abstract

graphic file with name ac2c00110_0005.jpg

Artificial intelligence (AI) is used to quantitatively analyze the voltammetry of the reduction of acetic acid in aqueous solution generating thermodynamic and kinetic data. Specifically, the variation of the steady-state current for the reduction of protons at a platinum microelectrode as a function of the bulk concentration of acetic acid is recorded and analyzed giving data in close agreement with independent measurements, provided the AI is trained with accurate and precise knowledge of diffusion coefficients of acetic acid, acetate ions, and H+.

Introduction

Machine learning has, despite its enormous potential, been used only sporadically in the quantification of analytes in different electroanalytical contexts and less in fundamental electrochemistry. For example, in food chemistry, a support vector machine approach was used to distinguish ale from lager based on cyclic voltammetry, and a neural network was able to estimate alcoholic content.1 In environmental chemistry, along with cyclic square-wave voltammetry, neural networks were applied to quantify the concentration of various pollutants in seawater, including copper, lead, mercury, paraquat (PQ), and Bisphenol-A (BPA).2 In biosensor development, by integrating with fast-scan cyclic voltammetry (FSCV) and an autoencoder, a variant of an artificial neural network, Mao et al. impressively achieved in vivo quantification of the concentration of dopamine, ascorbate, and NaCl in rat brains.3 Multicomponent detection of insulin and glucose in serum with the help of neural networks was also reported by Liu et al. recently.4 Beyond chemical analysis, in fundamental electrochemistry, Bond et al. reported the successful classification of electrode reaction mechanisms (specifically E-, EE-, and EC-type processes) using a convolutional neural network5 and claimed recognition of electrode kinetic between Butler–Volmer and Marcus–Hush types using Bayesian inference.6 More generally, at least in principle, when electrochemistry is equipped with machine learning for data analysis, the latter allows correlation and analysis of electrochemical data (including voltammograms and chronoamperograms) without the need for deploying mathematically analytical expressions.

Despite the emerging reports on the application to quantification of analytes, the study of electrochemical reactions and mechanisms with machine learning is still largely lacking. Bond and colleagues recently communicated the need for quantification of confidence limits and errors in parameter estimation when making a comparison of experimental data and simulated data. They attributed such absences to possible computational limitations.7 In response to the desirability for machine learning of parameters in electrochemical reactions, we recently communicated the theoretical study of training neural networks on simulated voltammograms to infer rate/equilibrium constants from the voltammograms of a dissociative CErev reaction and the reverse process of predicting voltammograms from such constants without recourse to further simulation.8 The general scheme of the dissociative CE reaction is

graphic file with name ac2c00110_m001.jpg 1

where kf and kb are forward and reverse reaction rate constants, respectively, and the equilibrium constant, Inline graphic.

In this paper, we next develop this work in the context of experiment and apply the approach to the extraction of thermodynamic and kinetic parameters for the acetic acid dissociation reaction in aqueous solution enabling comparison with extensive independent reports in the literature so permitting verification and critical evaluation of the AI approach including limitations. In particular, authentic experimental data will contain finite background currents and possible contributions from migration and/or convection and/or double-layer charging, which inevitably distort, to a greater or lesser extent, the voltammetry from that predicted via simulation. Accordingly, it is important to address the question of whether the AI approach to the analysis of voltammetry can “live with” the inevitable imperfections of authentic experimental data.

Specifically, to facilitate proving the power of machine learning on parameter extraction from experiments, we quantitatively analyze current–concentration data to extract the thermodynamic and kinetic parameters (Keq and kf) of acetic acid dissociation using machine learning. The predicted parameters are then checked via simulation and comparison of the results with experiments. Electro-reduction of acetic acid is known to follow a dissociative CE process9,10

graphic file with name ac2c00110_m003.jpg 2

Table 1 shows the reported Keq and kf values at 298 K in different aqueous environments where the presence of the added electrolyte is known to cause both kinetic and thermodynamic salt effects, albeit relatively small in magnitude (see Table 1). Keq values of acetic acid are readily measured, for example, most simply from the pH of acetic acid solutions and reported as 1.754 × 10–5 M in pure water.11 Higher values are seen when the electrolyte is present (i.e., 2.82 × 10–5 M in 0.1 M KCl solution12). Measurement of kf has been made by a variety of methods.

Table 1. Literature Values of the Equilibrium and the Rate Constants of the Acetic Acid Dissociation Reaction.

constant solution composition value and reference
Keq, M CH3COOH in pure water 1.754 × 10–5,11
CH3COOH, CH3COONa in pure water 1.743 × 10–5 to 1.784 × 10–5,19
CH3COOH/0.1106 M KCl(aq) 2.805 × 10–5,20
CH3COOH/0.1 M of KCl, NaCl or LiCl respectively 2.82 × 10–5, 2.79 × 105, 2.85 × 10–5,12
CH3COOH/1 M KCl(aq) 3.06 × 10–5,21
kf, s–1, nonelectrochemical methods 0.1 × 10–3 M CH3COOH in pure water 8 × 105,13
8.3 × 10–5 M CH3COOH in pure water 8.7 × 105,14
CH3COOH in pure water 1.91 × 105,15
CH3COOH coupled with bromocresol blue in pure water 1.3 × 106,16
kf, s–1, electrochemical methods 2.7 × 10–3 M CH3COOH, 0.03 M CH3COONa/1 M KCl 3.46 × 106,9
2.17 × 10–3 M CH3COOH/1.475 M (CH3) 4N(Cl) 1.58 × 106,10
20 × 10–3 M CH3COOH/0.1 and 0.3 M KCl 9.1 × 105,18
CH3COOH/1 M KCl(aq) 3 × 105,22
2.5 × 10–3 M CH3 COOH, 5 × 10–3 M CH3 COONa/50:50 water-ethanol. Ionic strength adjusted to 1 M with KCl 2.9 × 105,23
CH3COOH/LiCl(aq). Ionic strength adjusted to 1 M with LiCl 1.39 × 106,24,25
Open in a new tab

Nonelectrochemical methods reported include the electrical pulse methods,13 the high field dispersion and temperature jump method,14 and the electric field jump (E-jump) relaxation technique.15 Although acetic acid does not absorb at visible wavelength, a colored acid–base indicator, Bromocresol green, was coupled in solution to enable spectroscopic detection using a square-wave field-effect apparatus.16

Electrochemical methods reported include voltammetry using a hydrodynamic modulated rotating disk electrode and analysis using the modified Koutecky–Levich equation,9,17 the polarography on acetate-acetic acid solution of low buffering capacity,10 and a two-cell technique, each with a rotating electrode connected by a Wheatstone bridge circuit.18 A table of individually measured kf and Keq values is shown in Table 1. The values of kf range widely from 1.91 × 105 to 3.46 × 106 s–1 in different solution compositions.

In the following, we report a simple three-step electrochemical approach for estimating these two constants. This paper follows the work flow of method A reported before,8 but the technical implementation is bespoke to account for the exact experimental data.

First, measurements are made of the steady-state current for the reduction of protons as a function of the bulk acetic acid concentration cCH3COOH,total* at a platinum microdisk electrode. This approach was preferred to cyclic voltammetry because the steady-state currents obtained at a microelectrode are independent of electrochemical rate constants and transfer coefficients, whereas understanding and simulating a full voltammogram either at a macroelectrode or a microelectrode for the reduction of H+ from acetic acid dissociation would require a confident knowledge of the mechanism and the kinetic parameters of the hydrogen evolution reaction on the Pt electrode, which remains controversial.26,27 Under the conditions employed in the present study, the steady-state current depends only on kf, Keq, and cCH3COOH,total assuming prior knowledge of diffusion coefficients.

Second, a simulation of the expected limiting currents with different kf, Keq, and bulk concentrations of acetic acids was conducted to obtain the steady-state current under different conditions and a neural network was trained and tested with simulated data. The features used for training were the steady-state currents at different bulk concentrations of acetic acid and targets were the kf and Keq values for the acetic acid CE process.

Third, steady-state currents obtained from experiments were fed into the trained network to give predictions of kf and Keq values, which were compared with those in Table 1 facilitating generic insights into the AI approach. More generally, the latter offers the prospect of simulation-free approaches to the quantitative analysis of voltammetric data in which simulations are only used to initially train the AI but thereafter there is no resort to expensive, commercial software, as the exact implementation of which can be user sensitive. The methodology thus promotes the analysis of data in a manner that is easily comparable between laboratories. To this end, we provide the simulation and machine learning programs for acetic acid reduction reported, along with raw experimental data, at https://github.com/nmerovingian/Acetic-Acid-Dissociation-AI. The simulation and machine learning programs for the theoretical study reported before8 can be found at https://github.com/nmerovingian/dissociativeCE-Simulation-MachineLearning. The resources provided will enable the users to fully reproduce the results reported and possibly further explore the application of AI using the training data provided.

Theory

In this section, we first discuss the formal potential of the H+/H2 couple and the expected half-wave potential for the reduction of protons in the case that the proton reduction reaction is electrochemically reversible. Second, we outline the simulation of the expected transport-limited currents for the proton reduction as a function of Keq and kf, noting that the computational approach is given in ref (8) apart from small changes in boundary conditions as outlined below.

Formal Potential and Half-Wave Potential of the H+/H2 Couple

The formal potential, Ef,H+/H20 of the H+/H2 couple has been shown to be given by

graphic file with name ac2c00110_m004.jpg 3

where EH+/H20 is the standard electrochemical potential and γH+ is the activity coefficient of H+ ion in solution; ks and cs are the salt parameter and salt concentration, respectively, which account for the salt-out effect in an electrolytic solution; p0 and a0 are standard pressure and standard activity, which are 1 bar and 1 M, respectively; KH2 is Henry’s law constant for H2; and R, T, and F are the gas constant, temperature, and Faraday constant, respectively. Using parameters from Table 2, Ef,H+/H2 is calculated as −0.341 V vs saturated calomel electrode (SCE).28

Table 2. Parameters Used for Calculation of the Formal Potential of the H+/H2 Redox Couple and for Simulation.

parameter explanation value
EH+/H20 vs SCE standard potential of H+/H2 vs saturated calomel electrode –0.241 V,30
DCH3COOH– diffusion coefficient of acetic acid 1.29 × 10–9 m2 s–1,11
DCH3COO– diffusion coefficient of acetate 1.089 × 10–9 m2 s–1,11
DH+ diffusion coefficient of hydrogen ion 9.311 × 10–9 m2 s–1,11
DH2 diffusion coefficient of hydrogen 5.11 × 10–9 m2 s–1,11
γH+ activity coefficient of hydrogen ion 0.754,31
KH2 Henry’s law constant of hydrogen 1292 bar M–1,32
cKNO3 concentration of KNO3 electrolyte in experiment 0.1 M
kKNO3 salt parameter of KNO3 0.07 M–1,33
Open in a new tab

The half-wave potential assuming an electrochemically reversible H+/H2 couple for the reduction of protons at a uniformly accessible electrode has been derived previously28

graphic file with name ac2c00110_m005.jpg 4

where E1/2 is the half-wave potential and cH+* and c0 are the bulk concentration of acetic acid and reference concentration (1 M), respectively. The dependence of the half-wave potential on the bulk proton concentration arises from the nonunity stoichiometry of the reaction.28,29 The formal potential Ef,H+/H2 as derived above is −0.341 V vs SCE. Using the reported pKa value of 4.756 of acetic acid11 and bulk concentration of acetic acid as 10 mM, cH+* is calculated to be 4.10 × 10–4 M and E1/2 is estimated as −0.448 V vs SCE. On the other hand, assuming cH+ as the bulk concentration of acetic acid, the calculated E1/2 is −0.408 V vs SCE. Clearly, from the CE process of describing the acetic acid reduction with the hypothetical assumption of reversible electrochemistry, the half-wave potential would be expected to lie between −0.408 and −0.448 V.

Simulation Equations

The mass transport is assumed to be exclusively diffusive, and the diffusion equations coupled with chemical reactions are solved to show how the steady-state limiting current at a microelectrode depends on the parameters kf and Keq for different acetic acid concentrations. Note that the electrochemical reaction on a microdisk electrode of radius r can be approximated as a hemispherical electrode with radius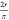Inline graphic to reduce the diffusion problem from two dimensions to one dimension. The relevant steady-state diffusion equations can be formulated as

graphic file with name ac2c00110_m007.jpg 5

where Dj is the diffusion coefficient for species j.

If re is the radius of the hemispherical electrode, the boundary conditions at the surface of the electrode for the steady-state reduction of protons are

graphic file with name ac2c00110_m008.jpg 6

The boundary conditions for the outer boundary of simulation are

graphic file with name ac2c00110_m009.jpg 7

where cT = cCH3COOH,total is the concentration of acetic acid added to the solution before chemical equilibrium forming proton and acetate, which are assumed absent in the initial solution. In the absence of electrolysis, cCH3COOH,total = cCH3COOH* + cCH3COO– and rsim is the outer boundary of the simulation as discussed in ref (8).8

Experimental Section

Chemicals

Acetic acid (CH3COOH, 99.8%), potassium nitrate (KNO3, 99%), potassium chloride (KCl, 99%), and hexaammineruthenium (III) chloride (Ru(NH3)6Cl3, 98%) were purchased from Sigma-Aldrich (Dorset, UK) and used as received. All solutions were prepared with deionized water (of resistivity 18.2 MΩ cm at 298 K, Millipore).

Voltammetry and Chronoamperometry of Acetic acid at a Pt Microdisk Electrode

All electrochemical measurements were performed with a μAutolab Type III potentiostat analyzer using a standard three-electrode arrangement in an optimized and thermostatted electrochemical cell34 in a Faraday cage. A Pt microdisk electrode (diameter: approximately 10 μm) was polished with three grades of successively finer aluminum powder (1.0, 0.3, and 0.05 μm), washed with deionized water, dried with N2 flow, and served as the working electrode. The counter and reference electrodes were a platinum wire and a saturated calomel electrode (SCE), respectively. The radius of the Pt microdisk electrode was calibrated electrochemically as 4.97 ± 0.05 μm by analyzing the steady-state voltammetry of 1.0 mM [Ru(NH3)6]3+ in 0.1 M KCl aqueous solution, using the reported diffusion coefficient for [Ru(NH3)6]3+ of 8.43 × 10–10 m2 s–1 at 298 K in 0.1 M KCl solution.35

Linear sweep voltammetry of 10 mM acetic acid in 0.1 M KNO3 was performed in the potential range of −0.15 to −1.0 V vs SCE at a scan rate of 800 mV s–1, as shown in Figure 1. The half-wave potential is measured at −0.570 V vs SCE, significantly smaller than the half-wave potential of the electrochemically reversible H+/H2 couple at different concentrations (−0.408 to −0.448 V), suggesting that the reduction of H+ on the Pt microdisk electrode was at least partly electrochemically irreversible.28

Figure 1.

Figure 1

Open in a new tab

Linear sweep voltammetry of 10 mM acetic acid in 0.1 M KNO3 at a scan rate of 800 mV s–1 from −0.15 to −1.0 V vs SCE. Dashed lines show the calculated half-wave potentials at different bulk concentrations of H+.

Acetic acid solutions with four concentrations (10, 20, 40, and 100 mM) were prepared in the 0.1 M KNO3 supporting electrolyte. The solution was degassed for 10 min with N2 before voltammetric or chronoamperometric measurements, and the temperature was stabilized at 298 ± 1 K via a digital temperature controller (SCT1 Digital contact thermometer).34 Current time transients for analysis via AI were recorded at an applied potential of −1.0 V vs SCE for a duration of 10 sec. The working electrode was polished with 0.05 μm aluminum powder and washed with deionized water between each experiment. Three repeated chronoamperometries were performed for each concentration.

Simulation and Machine Learning

The simulation program was written in Python. Multiprocessing was used for parallel computing of the working surfaces on an Intel E5 processor. The nonlinear diffusion equations were solved using the finite difference method by discretizing the diffusion equations using both expanding space grid and time grid. The resulting multidiagonal matrix was solved using the Newton–Raphson method for at most 10 iterations.36 If the mean absolute error in dimensionless concentration was smaller than 10–12, additional iterations were skipped to save time without significant compromise of accuracy. The convergence of the simulation was checked, and the results can be found in Testing and Verification of the Simulations section in the Supporting Information.37−39

The working surfaces from simulations were used to train a multiheaded Dense Neural Network (DNN) written in TensorFlow.40 The DNN was trained by using the simulated steady-state currents at different concentrations as features to predict the corresponding log10kf and log10Keq as targets. Note that the targets were in logarithm form to reduce the exploding/diminishing gradient problem.41 The DNN has only 4 hidden layers with relatively small numbers of neurons (<100) to avoid overfitting: a smaller network forced itself to predict rate constants instead of “memorizing” them.

The implementation of simulation and machine learning programs along with scripts for visualization and feature engineering can be found at https://github.com/nmerovingian/Acetic-Acid-Dissociation-AI. Raw experimental data is also provided in the repository. The more general simulation and machine learning programs for dissociative CE reaction reported before8 can be found at https://github.com/nmerovingian/dissociativeCE-Simulation-MachineLearning. Note that because of the stochastic nature of the neural network, and different hardware and operating systems from our workstation, the users’ machine learning results may vary slightly from the authors’, but generally to less than 0.1 on the log10 scale for prediction of rate and equilibrium constants. The simulation results are expected to be consistent in a different computing environment.

Results and Discussion

Figure 1 shows the voltammogram for which measurements were made. Current data was measured at a potential of −1.0 V vs SCE corresponding to the limiting current and the attainment of the steady-state current assessed by chronoamperometry as described in the next section. Specifically, the measurement of the limiting current as a function of the bulk concentration of acetic acid is used to avoid the need for any electrode kinetic data or assumption.

Chronoamperometry of Acetic Acid

To identify the steady-state currents, current–time transients for four different concentrations of acetic acid between 10 and 100 mM in 0.1 M KNO3 were recorded at a Pt microdisk electrode by stepping the potential from a value where no current flowed to an applied potential of −1.0 V vs SCE, corresponding to a sufficiently negative potential for a diffusion-limited reduction of protons. The corresponding chronoamperograms at four concentrations are reported in the Chronoamperogram section in the Supporting Information, which showed that steady-state behavior is observed after 2 s. Erring on the side of caution, currents at t = 10 s were chosen for quantitative analysis, assumed to be steady state and measured as −30.5 ± 0.4, −55.2 ± 0.3, −102 ± 1, and −238 ± 4 nA for 10.0, 20.0, 40.0, and 100 mM of acetic acid with three separate chronoamperograms averaged for each concentration. The steady-state currents did not scale proportionally with the concentration of acetic acid since the reduction of acetic acid obeys the dissociative CE mechanism. The concentrations of acetic acid and the measured steady-state currents were utilized as experimental features for machine learning to predict rate and equilibrium constant as described below.

Simulation of Steady-State Limiting Currents

A wide range of kf (1–108 s–1) and Keq (10–3–10–8 M) values were applied to simulate the steady-state limiting currents at four different bulk concentrations of acetic acid (10, 20, 40, and 100 mM). The diffusion coefficients of all species reported in the literature are given in Table 2. Note that some combinations of Keq and kf values would generate kb values exceeding a reasonable magnitude, so simulations were only performed if kb ≤ 1013 M–1 s–1 with the latter values selected to give a considerable margin of error. The steady-state currents at different kf and Keq values are represented on the working surfaces such as the one shown in Figure 2 for a bulk concentration of acetic acid of 10 mM. Figure 2 shows that the steady-state current increases in magnitude with increasing Keq and kf. Increasing Keq can increase the magnitude of steady-state current since higher Keq increases the bulk concentration of electroactive H+ at equilibrium. Higher kf increases the extent of acetic acid dissociation on the voltammetric timescale to replenish H+ consumed during electrochemical reduction. The working surfaces for bulk concentrations of acetic acid of 20, 40, and 100 mM can be found in the Working Surfaces for the Steady-State Limiting Current section in the Supporting Information.

Figure 2.

Figure 2

Open in a new tab

Working surface showing the steady-state currents at different kf and Keq values for a bulk concentration of acetic acid of 10 mM. Note: the apparent “kink” in the left of the surface is because it is not parallel to the log10Keq axis but rather cross (kf and Keq) space at an angle. The smooth continuity of the surface is emphasized by the contour plot.

Training and Testing the Neural Network

Using the working surfaces, the neural network was trained to predict log10kf and log10Keq using steady-state currents at four different concentrations of acetic acid and trained for 2000 epochs. The loss function was the mean absolute error (MAE) and the optimizer was Adam (learning rate = 0.001).42 To evaluate the performance of the neural network model after training, it was tested with independent testing datasets and the results are shown in Figure 3, as 90.5% predictions of log10kf were within 10% error and 100% predictions of log10Keq were within 5% error. The lower accuracy of predictions of log10kf compared to log10Keq arises because log10kf had a relatively smaller effect on the steady-state current but the network was judged sufficient for the prediction of constants from experimental results. The performance was benchmarked with a third-degree polynomial regression, which results in 61.2% prediction of log10kf within 10% error and 86.7% prediction of log10Keq within 5% error. Details are shown in the Benchmark section in the Supporting Information.

Figure 3.

Figure 3

Open in a new tab

Error of predicting the rate and equilibrium constants from an independent testing dataset composed of simulated steady-state currents. (a) Errors of predicting log10kf 90.5% predictions of log10kf were within 10% errors and (b) errors of predicting log10Keq 100% predictions of log10Keq were within 5% errors.

Predicting Rate and Equilibrium Constants with Experimental Data

Using the steady-state current at the four different concentrations as the input of the neural network trained in the last step, the neural network predicted kf and Keq values in the logarithmic scale as 6.47 and −4.77, which convert to 2.95 × 106 s–1 and 1.70 × 10–5 M. The 95% prediction intervals for the neural network were estimated using the bootstrap method.43 First, 500 observations were sampled from testing datasets and repeated 100 times to obtain 100 bootstrapped samples. Second, each bootstrap sample was trained in an independent neural network to obtain an empirical distribution of bootstrap predictions. At the 5% significance level, the upper and lower limits were, respectively, 97.5 and 2.5% quantile obtained from the bootstrap distribution. The 95% prediction intervals were calculated as 2.78 × 106–3.13 × 106 s–1 and 1.67 × 10–5–1.71 × 10–5 M for predicted kf and Keq, respectively. These values are fully consistent with the accepted literature values shown in Table 1 showing the power of the proposed AI approach in extracting kinetic and thermodynamic data.

Testing the Approach with Different Diffusion Coefficients

Not all systems under study will have as well-characterized diffusion coefficient as the acetic acid dissociation reaction described above. Sometimes, diffusion coefficients are unknown and frequently uncertain. It is therefore pertinent to ask how well the AI approach responds to variations in the diffusion coefficients used for the proton, acetic acid, and acetate ions.

To address this question, we compared the performance of the three-step electrochemical approach with five different sets of diffusion coefficients and the predicted constants using simulated steady-state currents, as shown in Table 3. The values of kf and Keq obtained for the wrong diffusion coefficients that deviate from the accepted values give noticeably wrong answers.

Table 3. Five Cases Considered When Varying Diffusion Coefficients of Species and the Predicted kf and Keq Values.

case # description predicted kf, s–1 predicted Keq, M
1 diffusion coefficients shown in Table 2 2.95 × 106 1.70 × 10–5
2 increasing diffusion coefficients in Table 2 by 10% 3.02 × 103 5.13 × 10–6
3 decreasing diffusion coefficients in Table 2 by 10% >1010 3.47 × 10–6
4 all diffusion coefficients set to 10–9 m2 s–1 9.05 × 102 1.56 × 10–3
5 DH+ = 9.311 × 10–9 m2 s–1, other species 10–9 m2 s–1 >1010 1.07 × 10–5
Open in a new tab

In cases 2 and 3, the diffusion coefficients were arbitrarily set higher or lower than the accepted values by 10%. The effect is that for lowered diffusion coefficients, the Keq and kf values increase to provide more or more rapid dissociation, while for increased diffusion coefficients, the opposite occurs and the two parameters decrease to reduce the number of protons formed through dissociation on the voltammetric timescale. These trends are exactly what is expected since we are using the limiting current to probe the two parameters of interest and so the inferred values will be very sensitive to the rate of diffusion in addition to kf and Keq. The steady-state concentration profile can be found in the Concentration Profile section in the Supporting Information.

It is interesting first that the values of kf and Keq are changed so markedly, highlighting a limitation of the electrochemical method for their measurement, and second that the AI approach stresses the requirement for the accurate parameter input in a way that is much more emphatic than using traditional curve-fitting approaches.

In the example chosen for study, all three diffusion coefficients are well known and the used ones in case 1 are considered to be reliable especially as they are measured via conductivity or Gouy interferometry.44 In some cases, where the diffusion coefficients are unknown, an experimenter might be tempted to estimate or guess the relevant parameters. Thus, in cases 4 and 5, we investigate this approach and fix some or all of the diffusion coefficients as 10–9 m2 s–1. This set of low values significantly underestimates the D of H+ and therefore leads to high kf estimates. The steady-state concentration profiles of CH3COO–, H+, and CH3COOH in cases 1, 4, and 5 are shown in the Supporting information when (a) cCH3COOH,total* = 100 mM and (b) cCH3COOH,total = 10 mM and are to be contrasted with those generated from more reliable diffusion coefficients.

The five cases discussed above showed that incorrect simulation parameters notably diffusion coefficients lead to incorrect input data for the neural network training and generate unreliable predictions. Thus, in practice, we recommend major caution with simulation parameters for accurate simulations and predictions.

Conclusions

We have shown how artificial intelligence methods can be developed and trained to analyze electrochemical data and extract reliable kinetic and thermodynamic parameters, which compare well with those independently measured both by electrochemical and nonelectrochemical methods given a mechanism for the electrode reaction is known. The specific approach previously advocated8 has been shown to be effective when using simulation to train and validate AI programs and then applied to authentic experimental data. However, it is useful to assess the strengths and especially the limitations of the approach. We note that the method meets the challenge presented by Bond and colleagues of giving a well-defined and experimenter-independent method of data analysis. However, it must be recognized that we have applied it to a well-defined system where the mechanism of the electrode process under evaluation is known. This is required to perform the simulation necessary to train the AI. Moreover, because the chemistry is clear, it is possible to simplify the number of parameters needed for training by adopting the reliable literature data for the diffusion coefficients of the three species controlling the magnitude of the current, acetic acid, acetate ions, and protons. Even so, from the analysis using deliberately wrong diffusion coefficients, it is clear that even relatively small errors in the values lead to significant errors in the inferred kf and Keq values. That said, AI allows the sensitivity of the values to be readily checked and the inferences caveated in a way that is not always easily adopted in conventional analysis of voltammogram.

It is evident that the approach of using simulation to train the AI requires a clear understanding of the likely chemistry even if the experimenter is willing to simulate and train AI for different possible mechanisms. Overall, this points to a possible need to make complementary measurements, notably spectro-electrochemistry, and/or good chemical intuition to identify realistic chemistry. In the above, we deliberately selected to focus our analysis on the limiting current data from our experiments to make our conclusion independent of the mechanism and electrode kinetics of the H+/H2 redox couple, which would influence cyclic voltammetric data (peak current and peak potentials). The speculative application of a trained network for more complex chemistry is fraught with risk, possibly extreme risk. Thus, in the context of the dissociative CE mechanism, such a process undoubtedly underpins the oxidation of hydrazine in aqueous solution where deprotonation of N2H5+ prior to oxidation of N2H4 is required at some electrodes; however, the oxidation process is self-inhibiting since it produces nitrogen and protons45,46

graphic file with name ac2c00110_m010.jpg

which act to change the pH of the solution local to the electrode. The application of an AI program trained for a simple dissociative CE process could not capture the essential content of the voltammetry/chronoamperometry and requires chemical expertise from the experimenter. Similarly, the voltammetry of blood reveals signals attributed to the electro-reduction of oxygen released from oxy-hemoglobin close to an electrode.47−49 Again, the chemistry is not simple: four oxygen molecules are bound to each hemoglobin and have different kinetics and thermodynamics of release. A chemically over-simplified analysis using AI trained for a simple mechanism would likely give erroneous or misleading output. Further, it is evident that the use of low-quality training data presents implantation risk and that this grows with the complexity of the mechanism because of the number of parameters required. Knowledge of accurate diffusion coefficients is one specific problem and, of course, is intrinsic to all electrochemical data analysis problems. We predict that the role of human intelligence (“HI”) will remain dominant over the artificial form for the foreseeable future in electrochemistry at least except for some niche applications. One such immediate niche lies in the analysis of electrode reaction mechanisms where the experimentalist is confident of the generic nature of the reaction, for example, CE, EC, ECE, etc. As we have shown, the AI approach allows for simulation-free data analysis and hence makes the extraction of parameters independent of the experimenter so better facilitating interlaboratory comparisons.

Acknowledgments

Haotian Chen thanks Lady Margaret Hall for a 2020/2021 Postgraduate Scholarship Award.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.analchem.2c00110.

  • Testing and verification of the simulations; working surfaces of the steady-state limiting current; benchmark; chronoamperogram; concentration profile (PDF)

Author Contributions

All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

ac2c00110_si_001.pdf (1.4MB, pdf)

References

  1. Roselló A.; Serrano N.; Díaz-Cruz J. M.; Ariño C. Discrimination of Beers by Cyclic Voltammetry Using a Single Carbon Screen-printed Electrode. Electroanalysis 2021, 33, 864–872. 10.1002/elan.202060515. [DOI] [Google Scholar]
  2. Dean S. N.; Shriver-Lake L. C.; Stenger D. A.; Erickson J. S.; Golden J. P.; Trammell S. A. Machine Learning Techniques for Chemical Identification Using Cyclic Square Wave Voltammetry. Sensors 2019, 19, 2392. 10.3390/s19102392. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Mao L.; Xue Y.; Ji W.; Jiang Y.; Yu P. Deep learning for voltammetric sensing in living animal brain. Angew. Chem., Int. Ed. 2021, 60, 23777–23783. 10.1002/anie.202109170. [DOI] [PubMed] [Google Scholar]
  4. Zhao Y.; Zhang H.; Li Y.; Yu X.; Cai Y.; Sha X.; Wang S.; Zhan Z.; Xu J.; Liu L. AI powered electrochemical multi-component detection of insulin and glucose in serum. Biosens. Bioelectron. 2021, 186, 113291 10.1016/j.bios.2021.113291. [DOI] [PubMed] [Google Scholar]
  5. Kennedy G. F.; Zhang J.; Bond A. M. Automatically Identifying Electrode Reaction Mechanisms Using Deep Neural Networks. Anal. Chem. 2019, 91, 12220–12227. 10.1021/acs.analchem.9b01891. [DOI] [PubMed] [Google Scholar]
  6. Li J.; Kennedy G. F.; Gundry L.; Bond A. M.; Zhang J. Application of Bayesian Inference in Fourier-Transformed Alternating Current Voltammetry for Electrode Kinetic Mechanism Distinction. Anal. Chem. 2019, 91, 5303–5309. 10.1021/acs.analchem.9b00129. [DOI] [PubMed] [Google Scholar]
  7. Bond A. M. A perceived paucity of quantitative studies in the modern era of voltammetry: prospects for parameterisation of complex reactions in Bayesian and machine learning frameworks. J. Solid State Electrochem. 2020, 24, 2041–2050. 10.1007/s10008-020-04639-6. [DOI] [Google Scholar]
  8. Chen H.; Kätelhön E.; Le H.; Compton R. G. Use of Artificial Intelligence in Electrode Reaction Mechanism Studies: Predicting Voltammograms and Analyzing the Dissociative CE Reaction at a Hemispherical Electrode. Anal. Chem. 2021, 93, 13360–13372. 10.1021/acs.analchem.1c03154. [DOI] [PubMed] [Google Scholar]
  9. Kanzaki Y.; Tokuda K.; Bruckenstein S. Dissociation rates of weak acids using sinusoidal hydrodynamic modulated rotating disk electrode employing Koutecky-Levich equation. J. Electrochem. Soc. 2014, 161, H770. 10.1149/2.0221412jes. [DOI] [Google Scholar]
  10. Schroeder R. R.; Shain I. Application of the potentiostatic method. Determination of the rate constant for the dissociation of acetic acid. J. Phys. Chem. A 1969, 73, 197–206. 10.1021/j100721a032. [DOI] [Google Scholar]
  11. Haynes W. M.CRC Handbook of Chemistry and Physics; CRC Press, 2014. [Google Scholar]
  12. Kilpatrick M.; Eanes R. D. The dissociation constants of acids in salt solutions. II. Acetic acid. J. Am. Chem. Soc. 1953, 75, 586–587. 10.1021/ja01099a019. [DOI] [Google Scholar]
  13. Eigen M.; Schoen J. Stoßspannungsverfahren zur Untersuchung sehr schnell verlaufender Ionenreaktionen in wässeriger Lösung. Ber. Bunsen. Phys. Chem. 1955, 59, 483–494. [Google Scholar]
  14. Eigen M.; Eyring E. M. Fast protolytic reactions in aqueous solutions of aminobenzoic acids. J. Am. Chem. Soc. 1962, 84, 3254–3256. 10.1021/ja00876a008. [DOI] [Google Scholar]
  15. Staples† B. R.; Turner‡ D. J.; Atkinson G. An Apparatus for the Determination of Rates of Proton Transfer and Other Very Fast Reactions. Instrum. Sci. Technol. 1969, 2, 127–147. 10.1080/10739146908543273. [DOI] [Google Scholar]
  16. Eyring E. M.; Auborn J. J.; Warrick P. Jr Spectrophotometric dissociation field effect kinetics of aqueous acetic acid and bromocresol green. J. Phys. Chem. B 1971, 75, 2488–2492. 10.1021/j100685a013. [DOI] [Google Scholar]
  17. Levich V. G.Physicochemical hydrodynamics, 1962.
  18. Albery W. J.; Bell R. P. The Kinetics of the Dissociation of Weak Acids measured by a Rotating Platinum Disc Electrode. Proc. Chem. Soc. 1963, 157–188. [Google Scholar]
  19. Cohn E. J.; Heyroth F. F.; Menkin M. F. The Dissociation Constant of Acetic Acid And the Activity Coefficients of the Ions in Certain Acetate Solutions. J. Am. Chem. Soc. 1928, 50, 696–714. 10.1021/ja01390a012. [DOI] [Google Scholar]
  20. Ferra M. I. A.; Graça J. R.; Marques A. M. M. Ionization of Acetic Acid in Aqueous Potassium Chloride Solutions. J. Chem. Eng. Data 2011, 56, 3673–3678. 10.1021/je200584a. [DOI] [Google Scholar]
  21. Bruckenstein S.; Nelson D. Acid-Base Dissociation Constants in 1.0 M Sodium Chloride. J. Chem. Eng. Data 1961, 6, 605–606. 10.1021/je60011a037. [DOI] [Google Scholar]
  22. Vielstich W.; Jahn D. II7. Zur Messung schneller Reaktionen in Lösung mit Hilfe der rotierenden Scheibenelektrode. Ber. Bunsen. Phys. Chem. 1960, 64, 43–44. [Google Scholar]
  23. Delahay P.; Vielstich W. Kinetics of the Dissociation of Weak Acids and Bases—Application of Polarography and Voltammetry at Constant Current. J. Am. Chem. Soc. 1955, 77, 4955–4958. 10.1021/ja01624a002. [DOI] [Google Scholar]
  24. Barker G.; Nürnberg H. W. On the study of very rapid homogeneous chemical reactions by new electrochemical methods. Naturwissenschaften 1964, 51, 191. 10.1007/BF00600719. [DOI] [Google Scholar]
  25. Nürnberg H. W.; Barker G. The determination of the rate constants for the dissociation and recombination of weak acids by high level faradaic rectification. Naturwissenschaften 1964, 51, 191–192. 10.1007/BF00600720. [DOI] [Google Scholar]
  26. Zwaschka G.; Tong Y.; Wolf M.; Kramer Campen R. Probing the Hydrogen Evolution Reaction and Charge Transfer on Platinum Electrodes on Femtosecond Timescales. ChemElectroChem 2019, 6, 2675–2682. 10.1002/celc.201900336. [DOI] [Google Scholar]
  27. Tavares M. C.; Machado S. A. S.; Mazo L. H. Study of hydrogen evolution reaction in acid medium on Pt microelectrodes. Electrochim. Acta 2001, 46, 4359–4369. 10.1016/S0013-4686(01)00726-5. [DOI] [Google Scholar]
  28. Jiao X.; Batchelor-McAuley C.; Kätelhön E.; Ellison J.; Tschulik K.; Compton R. G. The subtleties of the reversible hydrogen evolution reaction arising from the nonunity stoichiometry. J. Phys. Chem. C 2015, 119, 9402–9410. 10.1021/acs.jpcc.5b01864. [DOI] [Google Scholar]
  29. Gómez-Gil J. M.; Laborda E.; Molina A. General Explicit Mathematical Solution for the Voltammetry of Nonunity Stoichiometry Electrode Reactions: Diagnosis Criteria in Cyclic Voltammetry. Anal. Chem. 2020, 92, 3728–3734. 10.1021/acs.analchem.9b05023. [DOI] [PubMed] [Google Scholar]
  30. Bard A.Standard Potentials in Aqueous Solution; Routledge, 2017. [Google Scholar]
  31. Robinson R. A.; Stokes R. H.. The Measurements and Interpretations of Conductance, Chemical Potential and Diffusion in Solutions of Simple Electrolytes. In Electrolyte Solutions; Courier Corporation, 2002. [Google Scholar]
  32. Wilhelm E.; Battino R.; Wilcock R. J. Low-pressure solubility of gases in liquid water. Chem. Rev. 1977, 77, 219–262. 10.1021/cr60306a003. [DOI] [Google Scholar]
  33. Long F.; McDevit W. Activity coefficients of nonelectrolyte solutes in aqueous salt solutions. Chem. Rev. 1952, 51, 119–169. 10.1021/cr60158a004. [DOI] [Google Scholar]
  34. Li X.; Batchelor-McAuley C.; Novev J. K.; Compton R. G. A thermostated cell for electrochemistry: minimising natural convection and investigating the role of evaporation and radiation. Phys. Chem. Chem. Phys. 2018, 20, 11794–11804. 10.1039/C8CP01360H. [DOI] [PubMed] [Google Scholar]
  35. Wang Y.; Limon-Petersen J. G.; Compton R. G. Measurement of the diffusion coefficients of [Ru(NH3)6]3+ and [Ru(NH3)6]2+ in aqueous solution using microelectrode double potential step chronoamperometry. J. Electroanal. Chem. 2011, 652, 13–17. 10.1016/j.jelechem.2010.12.011. [DOI] [Google Scholar]
  36. Compton R. G.; Laborda E.; Kaetelhoen E.; Ward K. R.. Understanding Voltammetry: Simulation of Electrode Processes, 2nd ed.; World Scientific: London, 2020. [Google Scholar]
  37. Kätelhön E.; Compton R. G. Testing and validating electroanalytical simulations. Analyst 2015, 140, 2592–2598. 10.1039/C4AN02276A. [DOI] [PubMed] [Google Scholar]
  38. Kätelhön E.; Compton R. G. Correction: Testing and validating electroanalytical simulations. Analyst 2015, 140, 3290. 10.1039/C5AN90033F. [DOI] [PubMed] [Google Scholar]
  39. Kätelhön E.; Compton R. G. Correction: Testing and validating electroanalytical simulations. Analyst 2016, 141, 1154. 10.1039/C6AN90007K. [DOI] [PubMed] [Google Scholar]
  40. Abadi M.; Barham P.; Chen J.; Chen Z.; Davis A.; Dean J.; Devin M.; Ghemawat S.; Irving G.; Isard M. In Tensorflow: A System for Large-scale Machine Learning, 12th Symposium on Operating Systems Design and Implementation, 2016; pp 265–283.
  41. Philipp G.; Song D.; Carbonell J. G.. The Exploding Gradient Problem Demystified-Definition, Prevalence, Impact, Origin, Tradeoffs, and Solutions, arXiv:1712.05577. arXiv.org e-Print archive. https://arxiv.org/abs/1712.05577 (accessed Dec 15, 2017).
  42. Kingma D. P.; Ba J.. Adam: A Method for Stochastic Optimization, arXiv:1412.6980. arXiv.org e-Print archive. https://arxiv.org/abs/1412.6980. (accessed Dec 22, 2014).
  43. Efron B.Bootstrap Methods: Another Look at the Jackknife. In Breakthroughs in Statistics; Springer, 1992; Vol. 62, pp 569–593. [Google Scholar]
  44. Dunn L.; Stokes R. The diffusion of monocarboxylic acids in aqueous solution at 25°. Aust. J. Chem. 1965, 18, 285–296. 10.1071/CH9650285. [DOI] [Google Scholar]
  45. Miao R.; Compton R. G. The Electro-Oxidation of Hydrazine: A Self-Inhibiting Reaction. J. Phys. Chem. Lett. 2021, 12, 1601–1605. 10.1021/acs.jpclett.1c00070. [DOI] [PubMed] [Google Scholar]
  46. Miao R.; Shao L.; Compton R. G. Single entity electrochemistry and the electron transfer kinetics of hydrazine oxidation. Nano Res. 2021, 14, 4132–4139. 10.1007/s12274-021-3353-8. [DOI] [Google Scholar]
  47. Li D.; Batchelor-McAuley C.; Compton R. G. Voltammetry in sheep’s blood: Membrane-free amperometric measurement of O2 concentration. Talanta 2021, 123127 10.1016/j.talanta.2021.123127. [DOI] [PubMed] [Google Scholar]
  48. Gibson Q. H.; Roughton F. J. W. The kinetics of dissociation of the first oxygen molecule from fully saturated oxyhaemoglobin in sheep blood solutions. Proc. R. Soc. London 1955, 143, 310–334. 10.1098/rspb.1955.0014. [DOI] [PubMed] [Google Scholar]
  49. Roughton F. J. W.; Otis A.; Lyster R. The determination of the individual equilibrium constants of the four intermediate reactions between oxygen and sheep haemoglobin. Proc. R. Soc. London 1955, 144, 29–54. 10.1098/rspb.1955.0032. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ac2c00110_si_001.pdf (1.4MB, pdf)

Articles from Analytical Chemistry are provided here courtesy of American Chemical Society

RESOURCES