Abstract
Thermal noise and acoustic clutter signals degrade ultrasonic image quality and contribute to unreliable clinical assessment. When both noise and clutter are prevalent, it is difficult to determine which one is a more significant contributor to image degradation because there is no way to separately measure their contributions in vivo. Efforts to improve image quality often rely on an understanding of the type of image degradation at play. To address this, we derived and validated a method to quantify the individual contributions of thermal noise and acoustic clutter to image degradation by leveraging spatial and temporal coherence characteristics. Using Field II simulations, we validated the assumptions of our method, explored strategies for robust implementation, and investigated its accuracy and dynamic range. We further proposed a novel robust approach for estimating spatial lag-one coherence. Using this robust approach, we determined that our method can estimate the signal-to-thermal noise ratio (SNR) and signal-to-clutter ratio (SCR) with high accuracy between SNR levels of −30 to 40 dB and SCR levels of −20 to 15 dB. We further explored imaging parameter requirements with our Field II simulations and determined that SNR and SCR can be estimated accurately with as few as two frames and sixteen channels. Finally, we demonstrate in vivo feasibility in brain imaging and liver imaging, showing that it is possible to overcome the constraints of in vivo motion using high-frame rate M-Mode imaging.
Index Terms—: image quality, image degradation, coherence, clutter, signal-to-noise ratio, signal-to-clutter ratio
I. Introduction
Image quality is highly variable in medical ultrasound. Poor image quality is common in many applications, often leading to a high failure rate of clinical exams. For example, clinical failure rates range from 11% to 64% in obstetrics and 9% to 64% in transthoracic echocardiography [1]–[7]. High failure rates in these challenging clinical scenarios are due to various forms of image degradation such as thermal noise and acoustic clutter which obscure or confound on-axis signals of interest.
Measuring the contributions of each type of image degradation is crucial to the development of better beamforming and signal processing algorithms and for the optimization of pulse sequences to achieve higher success rates in clinical exams. Depending on whether thermal noise or acoustic clutter dominates, different approaches can be taken to achieve the greatest improvements. For example, when thermal noise dominates, coded excitation or contrast agents may be the most appropriate next steps, whereas when clutter dominates, adaptive beamforming approaches or harmonic imaging may be more appropriate [8]–[16]. Although both thermal noise and clutter contribute to image degradation, it is not always straight-forward to determine which one is more significant for a given scenario because there is currently no way to separately measure their contributions in vivo. This work proposes a solution based on spatiotemporal coherence to separate and quantify sources of image degradation in order to shed light on their role in reducing image quality. These sources include attenuation, reverberation or multiple scattering, phase aberration, and off-axis scattering [13], [17]–[23].
Attenuation leads to a low signal-to-noise ratio (SNR) which causes thermal noise from the electronic components of the imaging system to dominate and reduces image quality. Phase aberration also leads to a reduction in SNR due to focusing errors [24]. SNR can be estimated using temporal correlation since thermal noise is incoherent across repeated acquisitions [25], [26]. Another approach to estimating thermal noise involves acquiring a “noise frame” with no prior ultrasonic transmission [27]. However, it is not known for sure if the noise characteristics of the imaging system are the same when it is not transmitting, which limits this approach. Furthermore, none of these techniques are able to separately measure both thermal noise and acoustic clutter and as such cannot be used to understand the relative contributions of each.
Other forms of image degradation such as reverberation create acoustic clutter, a temporally stable haze that reduces visibility and contrast of structures [13], [17]–[20]. For the purposes herein, acoustic clutter will be defined in the anatomical imaging sense, meaning that it will refer to sources of non-diffraction limited image degradation that arise due to interactions between the sound waves and the imaging medium instead of from the imaging system itself. High amounts of clutter lead to a low signal-to-clutter ratio (SCR) which also reduces image quality. Reverberation, also known as multiple scattering, is the largest source of clutter in fundamental frequency imaging [18], [28]. Reverberation is incoherent across the aperture (channel) dimension [29]. Note that throughout this work, spatial coherence will refer to coherence measured across the aperture dimension, i.e., across the transducer elements on the delayed channel data.
Since both thermal noise and acoustic clutter lead to spatial decorrelation, aperture domain techniques that leverage the coherence properties of acoustic backscatter have been used to assess sources of image degradation [12], [26], [29], [30]. These methods are sensitive to thermal noise and most acoustic clutter but do not fully characterize the relative contribution of each [12], [30]. Clever simulation approaches and well-designed phantom or ex vivo experiments can accomplish this by imaging a medium with and without a layer of material (such as an abdominal wall) that creates clutter, but this cannot be performed in vivo noninvasively [18], [31]–[33].
Currently, the only technique to measure clutter magnitude in vivo requires measuring signal power within a large anechoic or hypoechoic region such as the bladder, a large fluid-filled cyst, or a large blood vessel [17]. This will suffice if such a region can be manually identified, but that is not always the case in many clinical imaging scenarios. Furthermore, this measurement of clutter is not generally representative of all types and sources of clutter [23]. In addition, this approach only provides information about clutter at that particular depth or region of the image rather than throughout the entire field of view. This makes it difficult to understand the spatial distribution of clutter in a given imaging scenario.
More recently, Long et al. reported a spatial coherence-based approach to measure incoherent noise and phase aberration, but this approach groups thermal noise with incoherent clutter rather than separating them [20]. Morgan et al. also reported a method based on spatial coherence to estimate signal components for image formation, but again they grouped thermal noise together with incoherent acoustic clutter [12].
Herein, we present a technique to separately measure the thermal noise power and the incoherent acoustic clutter power [34]. Instead of relying on the presence of an anechoic region, our approach only requires the presence of speckle. This simplification makes our method more practical for in vivo application. In the following sections, we present the theoretical framework on which this technique is based and we validate it across a wide range of clinically relevant noise and clutter levels using simulations. We further explore strategies for robust implementation and study how the number of available frames and channels affects accuracy. Finally, we demonstrate in vivo feasibility in the presence of motion.
II. Theory
A. Components of the Observed Signal
The acoustic signal measured by the transducer during an in vivo image acquisition will be a combination of uncorrupted tissue signal , thermal noise , and acoustic clutter . This observed signal is given by Eq. (1).
| (1) |
The power of the observed signal, , can be written according to Eq. (2).
| (2) |
Assuming that the tissue, noise, and clutter signals are uncorrelated spatially and temporally [25], [29], the cross-terms in Eq. (2) go to zero and the power of the observed signal can be written according to Eq. (3), where , , and are the power of the signal, noise, and clutter, respectively.
| (3) |
B. Spatial Coherence of Signals
The van Cittert-Zernike (VCZ) theorem describes the coherence of a wave emitted from an incoherent source such as ultrasonic echoes backscattered from a random field of diffuse sub-resolution scatterers. This spatial coherence can be described by the autocorrelation of the aperture function or the scaled Fourier transform of the transmitted intensity field [35]–[37]. For a rectangular aperture and apodization, this becomes a triangle function with a base twice the width of the aperture. The VCZ theorem is therefore able to predict the spatial coherence of a signal reflected from a diffusely scattering medium across the aperture domain, i.e., the time-delayed channel data. In the absence of thermal noise and acoustic clutter, the tissue speckle signal is expected to have a spatial coherence at the focus given by the triangle function, Λ[m/M], where m is the channel separation or lag and M is the total number of channels used for transmit focusing (blue curve of Fig. 1a).
Fig. 1.
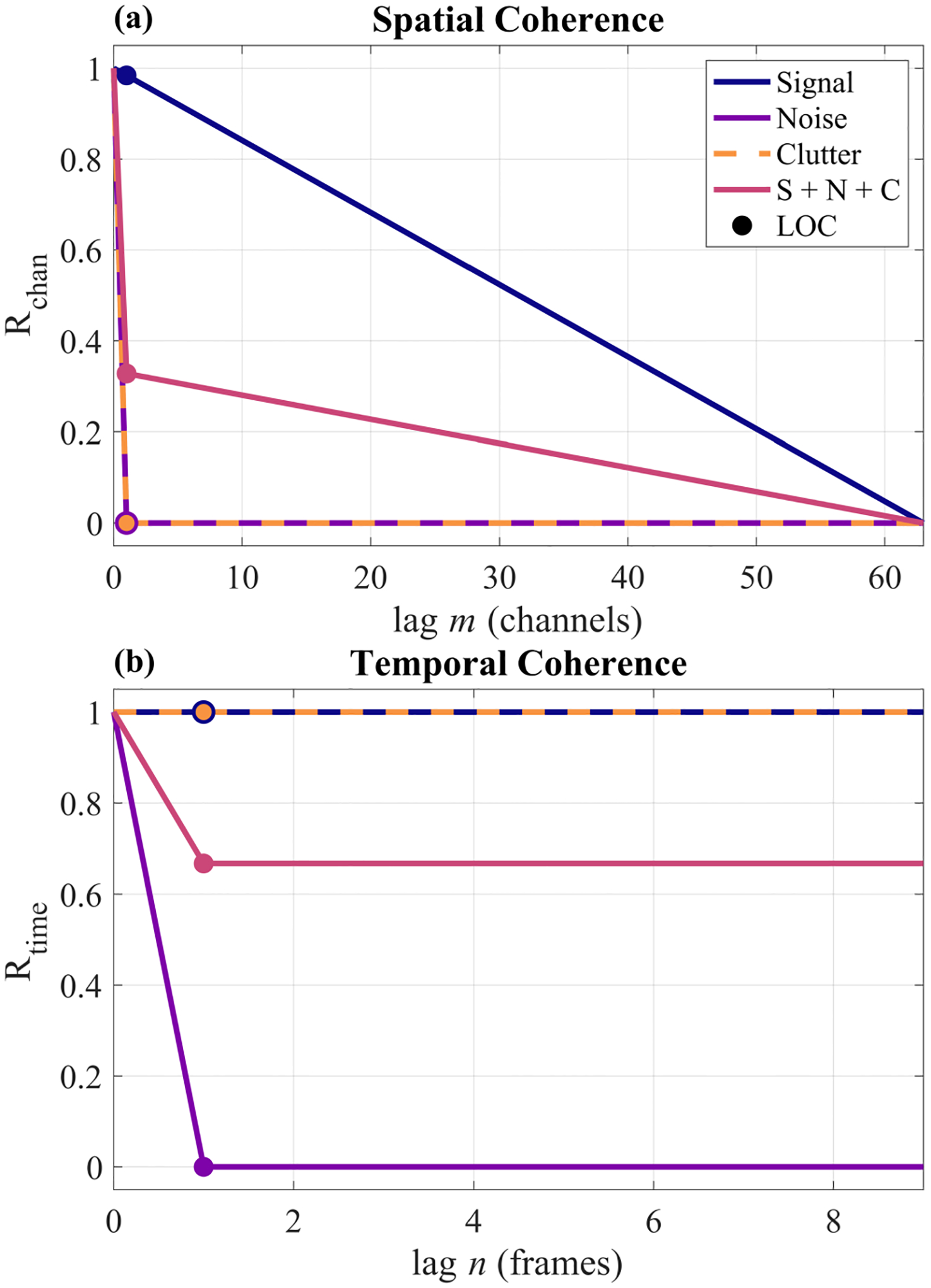
Theoretical spatial (a) and temporal (b) coherence curves for each signal component and their coherent summation (S + N + C). The noise and clutter components were each coherently added to the signal component at a 0 dB magnitude, i.e., an SNR of 0 dB and an SCR 0 dB. LOC corresponds to the lag-one coherence points that are estimated by Eqs. (5) and (9).
For zero-mean Gaussian noise, the spatial coherence is a delta function on average (purple curve of Fig. 1a) [26]. Acoustic clutter has also been shown to rapidly decorrelate across the aperture, producing an approximate delta function as well (orange curve of Fig. 1a) [29]. Provided that Eq. (3) holds, the spatial coherence of such a signal is therefore given by Eq. (4) and the pink curve of Fig. 1a [26], [29].
| (4) |
Equation (4) implies that the spatial coherence curve will have a drop at lag one proportional to the combined noise and clutter power. The lag-one coherence therefore encapsulates the total power of the noise and clutter [13], [26], [30].
The lag-one coherence (LOC) is calculated from the real-valued delayed channel data, denoted by s, according to Eq. (5), where the lag m is equal to 1, M is the total number of channels, i indexes the channel dimension, b indexes the beam dimension, j indexes the frame dimension, k indexes the axial dimension, and k1, k2 are the bounds of the axial kernel.
| (5a) |
| (5b) |
The function in Eq. (5b) represents computing the mean or median over axial samples, beams, and frames. Alternatively, the ensemble spatial coherence estimate proposed by Hyun et al. could be computed instead according to Eq. (6) [38].
| (6a) |
| (6b) |
Eq. (6b) is evaluated by computing the mean or the median over axial samples, beams, and frames. As compared to the spatial coherence estimator in Eq. (5), the ensemble estimator in Eq. (6) applies normalization differently to improve the stability and robustness of the estimate [38]. The use of Eq. (5) versus Eq. (6) as well as the mean versus the median is discussed further in Section IV-B.
After estimating the lag-one spatial coherence, it can then be used to calculate the channel SNR according to Eq. (7) [30].
| (7) |
From Eq. (4) and Fig. 1a, it is evident that tissue is partially coherent across the aperture whereas clutter and noise are incoherent across the aperture. In other words, the noise and clutter are indistinguishable from each other across the aperture dimension and will both contribute to the “noise” term in the channel SNR calculation. From this result, we can further write channel SNR in terms of tissue, noise, and clutter power according to Eq. (8).
| (8) |
Together, Eqs. (7) and (8) suggest a relation between the spatial lag-one coherence and the tissue, noise, and incoherent clutter power.
C. Temporal Coherence of Signals
Across repeated acquisitions, stationary tissue signal is coherent since speckle is temporally deterministic (blue curve of Fig. 1b). In addition, acoustic clutter is also temporally stable, making tissue and clutter indistinguishable in this dimension (orange curve in Fig. 1b) [19], [29]. However, thermal noise is uncorrelated and can be modeled as a delta function (purple curve of Fig. 1b). The temporal lag-one coherence therefore encapsulates the thermal noise power only (pink curve of Fig. 1b). The temporal lag-one coherence can be calculated according to Eq. (9), where the lag n is equal to 1, N is the total number of frames, and all other variables have been defined previously. Note that this is still computed on the delayed channel data to facilitate comparison with the spatial lag-one coherence defined in Eq. (5).
| (9a) |
| (9b) |
The function in Eq. (9b) represents computing the mean or median over axial samples, channels, and beams. Alternatively, an ensemble temporal coherence estimate analogous to Eq. (6) could be computed according to Eq. (10).
| (10a) |
| (10b) |
Again, to evaluate Eq. (10b), the mean or the median is computed across axial samples, channels, and beams (see Section IV-B).
After estimating the temporal lag-one coherence, it can then be used to calculate the temporal SNR according to Eq. (11) [25].
| (11) |
Since tissue and clutter are temporally stable and thermal noise is temporally uncorrelated as shown in Fig. 1b, we note that tissue and clutter are indistinguishable from each other across this dimension and as such will both contribute to the “signal” term in the temporal SNR calculation. From this result, we can further write temporal SNR in terms of signal, noise, and clutter power according to Eq. (12).
| (12) |
Equations (11) and (12) relate temporal lag-one coherence to signal, noise, and clutter power.
D. Solving for Signal, Noise, and Clutter Power
Equations (3), (8), and (12) can be algebraically manipulated to solve for the three unknowns (, , and ). is given by Eq. (13), where is estimated directly by computing the power of the channel data and SNRchan is estimated from the channel data according to Eq. (7).
| (13) |
Either or can be solved for next, and either approach leads to equivalent results. Solving for first yields Eq. (14), where and SNRchan are estimated from the channel data as explained above and SNRtime is estimated from the channel data according to Eq. (11).
| (14) |
Finally, can be solved for according to Eq. (3). Once , , and are solved for, the signal-to-thermal-noise ratio (15), signal-to-clutter ratio (16), and signal-to-clutter-plus-noise ratio (17) can be calculated.
| (15) |
| (16) |
| (17) |
Note that Eq. (17) is equivalent to Eq. (8), but Eqs. (15) and (16) would be impossible to estimate without first separating the thermal noise and acoustic clutter. Using Eqs. (15) and (16), the contributions of thermal noise and acoustic clutter can be evaluated separately and compared to determine which one contributes more to image degradation in any in vivo scenario and throughout any field of view, assuming valid application of the VCZ theorem.
III. Methods
A. Field II Simulations
In order to validate the theory presented in Section II as well as determine the accuracy and dynamic range of this method, simulations were conducted using Field II in MATLAB R2021a (Mathworks, Natick, Massachusetts) [39], [40]. Simulations are advantageous in this scenario because they offer a ground truth; by simulating the tissue, clutter, and thermal noise separately and coherently combining them with known relative magnitudes, the accuracy of this technique can be tested over a wide range of SNR and SCR levels.
To create the uncorrupted channel data (Fig. 2a), a 20 mm × 50 mm (xz) tissue phantom with uniform speckle was first created. The tissue phantom speed of sound was 1540 m/s and there were 16 scatterers per resolution cell. Imaging was simulated with a 64-element linear array with 0.3 mm pitch (0.53λ) and 65% fractional bandwidth operating at a center frequency of 2.72 MHz. The Field II sampling frequency was 80 MHz. The imaging procedure consisted of 128 focused transmissions and receptions with a transmit focal depth of 4 cm. The 128 beams were evenly spaced across the 20 mm aperture. Dynamic receive beamforming with uniform apodization was performed. Ten frames were simulated.
Fig. 2.
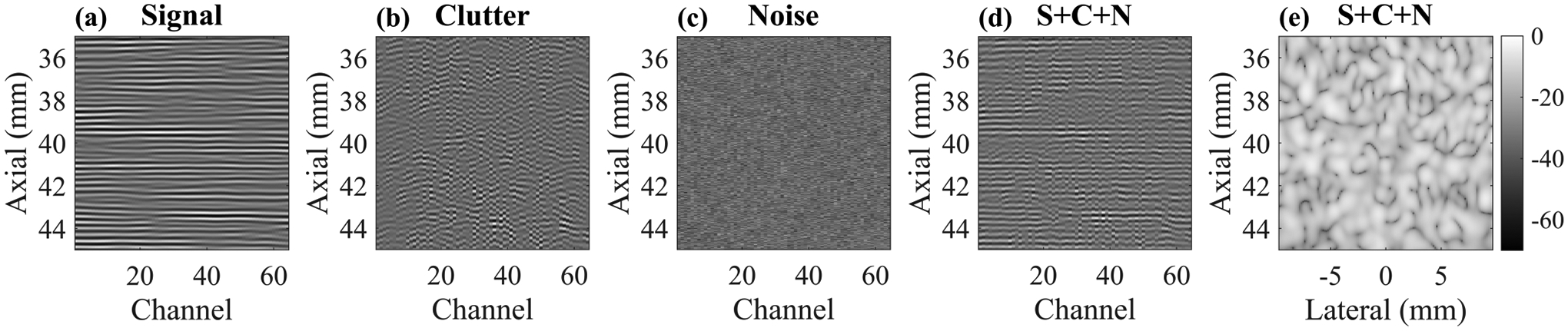
Channel data (a)-(c) for each signal component. Transmit focus was 40 mm. The SNR and SCR were each 10 dB for the combined channel data set (S + C + N) shown in (d). The resulting B-Mode image is shown in (e) on a 70 dB dynamic range.
The clutter channel data were created using a previously reported pseudo-nonlinear approach to simulating reverberation with Field II [33]. Briefly, this approach involves simulating single-path scattering from a set of points whose axial locations are drawn from an exponential distribution such that most of them are close to the surface of the transducer. This distribution led to simulation outcomes that match well with in vivo measurements. Additionally, this is conceptually similar to in vivo imaging through the abdominal wall or the skull where most of the clutter generation occurs in near-field tissue layers or near-field skull bone.
Each point was simulated individually in Field II. However, an extra delay was applied to the received channel data for each individual point to simulate multipath scattering, making it appear as though the echoes arrived from deeper locations. The shifted channel data from each point were summed coherently before applying standard dynamic receive focusing. This results in delayed channel data with remaining curvature as opposed to properly delayed and focused channel data that appears flat (see Fig. 2b). The reverberation scatterers were placed with a density of ten scatterers per resolution cell and their axial locations were distributed exponentially with a mean of 0.5 mm. As discussed by Byram et al. and verified empirically herein (see Section IV-A), these parameters led to spatial coherence curves with near delta function appearance, thereby serving as a sufficient model of clutter for these purposes [33].
After creating the signal and clutter channel data, the noise channel data (Fig. 2c) were created by sampling the normal distribution. Ten independent frames were generated. To create the frames for the signal and clutter data, the channel data were simply replicated since signal and clutter are temporally stable. The signal, clutter, and noise channel data were then combined via coherent summation at all possible combinations of signal-to-noise levels and signal-to-clutter levels ranging from −30 to 40 dB in increments of 5 dB (225 different combinations). Note that the scaling was performed on the channel data by calculating power within a 2 mm ROI centered about the transmit focus. An example channel data set with 10 dB SNR and 10 dB SCR is shown in Fig. 2d and the B-Mode is shown in Fig. 2e. This process was repeated for 10 independent realizations of signal + clutter + noise phantoms.
B. Verification of Assumptions
To verify that the simulated signal, clutter, and noise components meet the assumptions of our method, the spatial and temporal coherence curves for each image component were calculated for representative noise and clutter levels and compared to the theoretical spatial and temporal coherence curves. Next, the spatial normalized cross-correlation (NCC) between each of the signal pairings (signal and clutter, clutter and noise, signal and noise) was also computed to assess signal independence. Temporal NCC curves were not computed since the signal and clutter data are simply replicated to create each frame so computing NCC across additional temporal lags would be redundant.
C. Method Implementation
Spatial and temporal coherence were calculated on delayed, real-valued channel data using a 2 mm ROI centered about the transmit focus to ensure coherence behavior as predicted by the VCZ theorem [41]. Real-valued data were used in this work to reduce computational complexity, but complex-valued coherence calculations using the complex IQ data could be performed as well. Importantly, the axial kernel for coherence calculations was 10λ.
While previously the mean has been used to compute a spatial coherence estimate [13], [20], [30], [38], we evaluated alternative approaches to estimating a metric of centrality since spatial and temporal coherence are not normally distributed. Alternatives include using the median or using the Fisher z-transform to normalize the lag-one coherence data before computing the mean and taking the inverse Fisher z-transform. For the purposes of this work, another option would be to compute channel and temporal SNR before computing the mean or median of lag-one coherence, which would amount to not evaluating Eqs. (5b) or (9b) before evaluating Eqs. (7) and (11). We also evaluated estimating the temporal and spatial coherence values with the standard equations (Eqs. (5) and (9)) versus the ensemble equations (Eqs. (6) and (10)) to determine if the ensemble equations provided improved stability.
We additionally designed a “robust” approach to estimating spatial lag-one coherence. The robust approach involved estimating the entire spatial coherence curve (lags 1 through M) using the median as a centrality metric, fitting a first degree polynomial to the coherence curve from lag one to lag M in the least-squares sense, and then using the equation of that line to estimate the coherence at lag one. To take into account the higher variance of the coherence estimate at higher lags, 1/variance was computed for each lag and used as a weight for the fit routine so that the higher lags with more variance were weighted less than the lower lags with less variance. Variance was calculated according to (1 − ρ2)2/(Nsamp − 1), where ρ is the coherence value and Nsamp is the number of samples used to form one estimate of ρ [42].
All of the approaches described above were investigated using the signal + clutter + noise phantoms described in Section III-A to evaluate their effect on coherence, SNR, and SCR estimation accuracy as well as the dynamic range of the method.
D. Minimum Requirements for Data Acquisition
We further evaluated the SNR and SCR accuracy as a function of the number of frames used for the calculation and the number of channels used for the calculation. SNR and SCR were estimated on the signal + clutter + noise phantoms described in Section III-A for representative SNR and SCR values. Frame numbers ranging from fifty frames to two frames and channel numbers ranging from all sixty-four down to eight channels were tested.
E. In Vivo Demonstration
To investigate the influence of frame rate and in vivo motion on temporal decorrelation, M-Mode acquisitions were acquired in two representative in vivo imaging scenarios: transabdominal liver imaging, which is expected to have a moderate amount of motion due to proximity to the diaphragm, and transcranial neuroimaging, which is expected to have less motion. Two datasets in the liver and two datasets in the brain were acquired on a healthy adult human volunteer under protocols approved by the local IRB.
For data acquisition, a P4-2v phased array transducer operating at 2.72 MHz (pitch = 0.3 mm) and a Verasonics Vantage 128 system (Verasonics, Kirkland, WA) were used. For guidance, focused B-Mode images were acquired using 129 evenly spaced focused transmissions and receptions spanning an angle of 45 degrees. The transmit focal depth was 8 cm. Dynamic receive beamforming with uniform apodization was applied. M-Mode acquisitions with a two second ensemble and 1000 Hz pulse repetition frequency (2000 total RF lines) were acquired for measuring coherence. M-Mode acquisitions had a transmit focal depth of 8 cm and a steering angle of 0 degrees, i.e. the central beam from the B-Mode sequence was repeatedly interrogated.
To investigate how motion influenced temporal decorrelation, normalized temporal correlation matrices were computed on the beam-summed data to measure similarity across the two second ensemble [43]. Subsets of contiguous frames with maximal normalized temporal correlation were also identified and temporal LOC was computed within these subsets. The data were also downsampled at factors of two, five, ten, and twenty-five to determine how frame rate impacts temporal coherence estimation in the presence of differing degrees of in vivo motion.
IV. Results
A. Verification of Assumptions
Fig. 3 shows the ground truth and simulated spatial and temporal coherence curves for the signal, clutter, and noise components. For these representative cases, the coherence curve values from the simulated data were all within ±0.05 of the theoretical values, demonstrating good agreement with theory as others have confirmed before [20], [33].
Fig. 3.
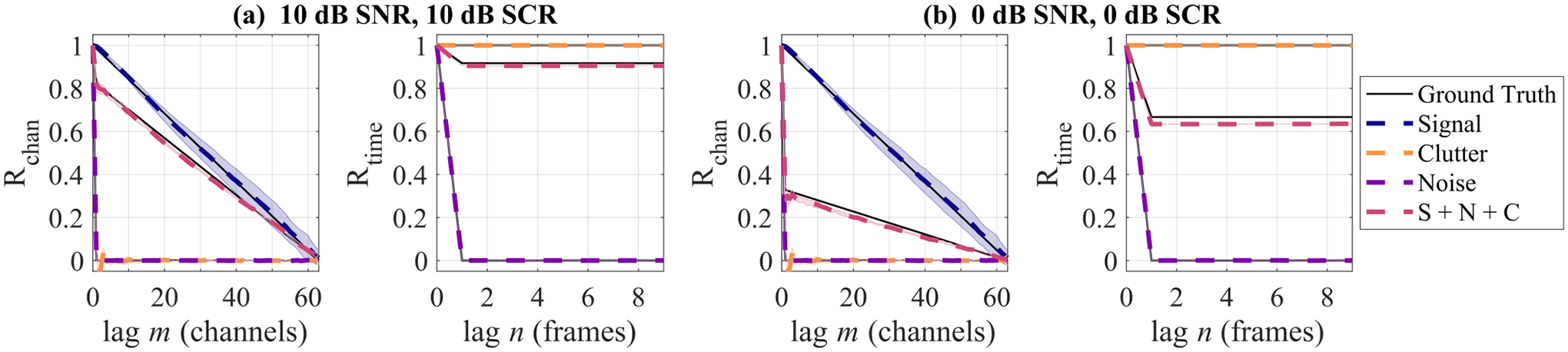
Spatial and temporal coherence curves for simulated signal + clutter + noise phantoms at (a) 10 dB SNR and 10 dB SCR and (b) 0 dB SNR and 0 dB SCR. Shaded regions for simulation coherence curves indicate standard deviation across phantom realizations (shading is not always apparent due to low standard deviation).
We next validated our assumption that the signal, noise, and clutter components are uncorrelated by computing the spatial normalized cross-correlation (NCC) between each of these pairs as shown in Fig. 4. Since these NCC curves are all near zero (within ±0.02), we can assume that our simulated signal, clutter, and noise are uncorrelated across the aperture on average. Furthermore, this demonstrates that our simulations satisfied the assumptions used to derive Eq. (3) from Eq. (1). We expect this assumption to hold true in vivo as well: The large axial kernel of 10λ that is used for the coherence calculations provides more independent samples to average over, leading to near-zero cross-correlations despite the finite aperture size and kernel size [29], [38].
Fig. 4.
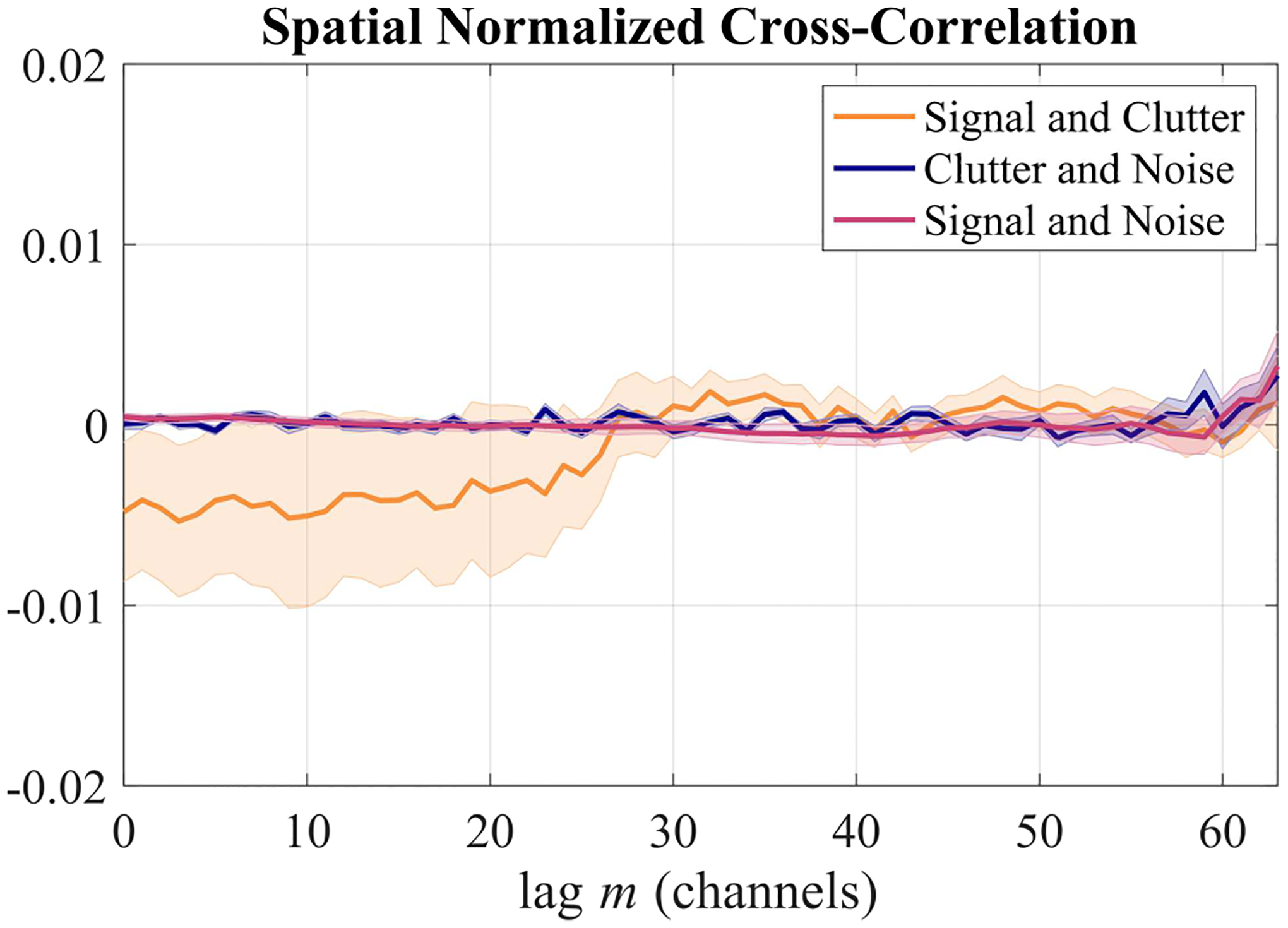
Spatial normalized cross-correlation between signal, clutter, and noise components. The shaded regions indicate standard error of the mean over the 10 simulated signal + clutter + noise phantoms.
However, it should be noted that this assumption may break down for more extreme (and likely not clinically relevant) SCR values: When either or is very large, it is possible that the non-normalized cross-correlation between signal and clutter becomes more significant in relation to or , leading to errors. This is explored in detail in Appendix A.
B. Method Accuracy and Dynamic Range
To determine the best way to implement our method, we started by comparing ground truth LOC and SNR values to those estimated with our method using the approaches described in Section III-C. In Fig. 5, the distributions of LOC and SNR are shown for a simulated signal + clutter + noise phantom with 20 dB SNR and 10 dB SCR. The different centrality metrics are provided in Table I and are also shown in the relevant histograms of Fig. 5.
Fig. 5.
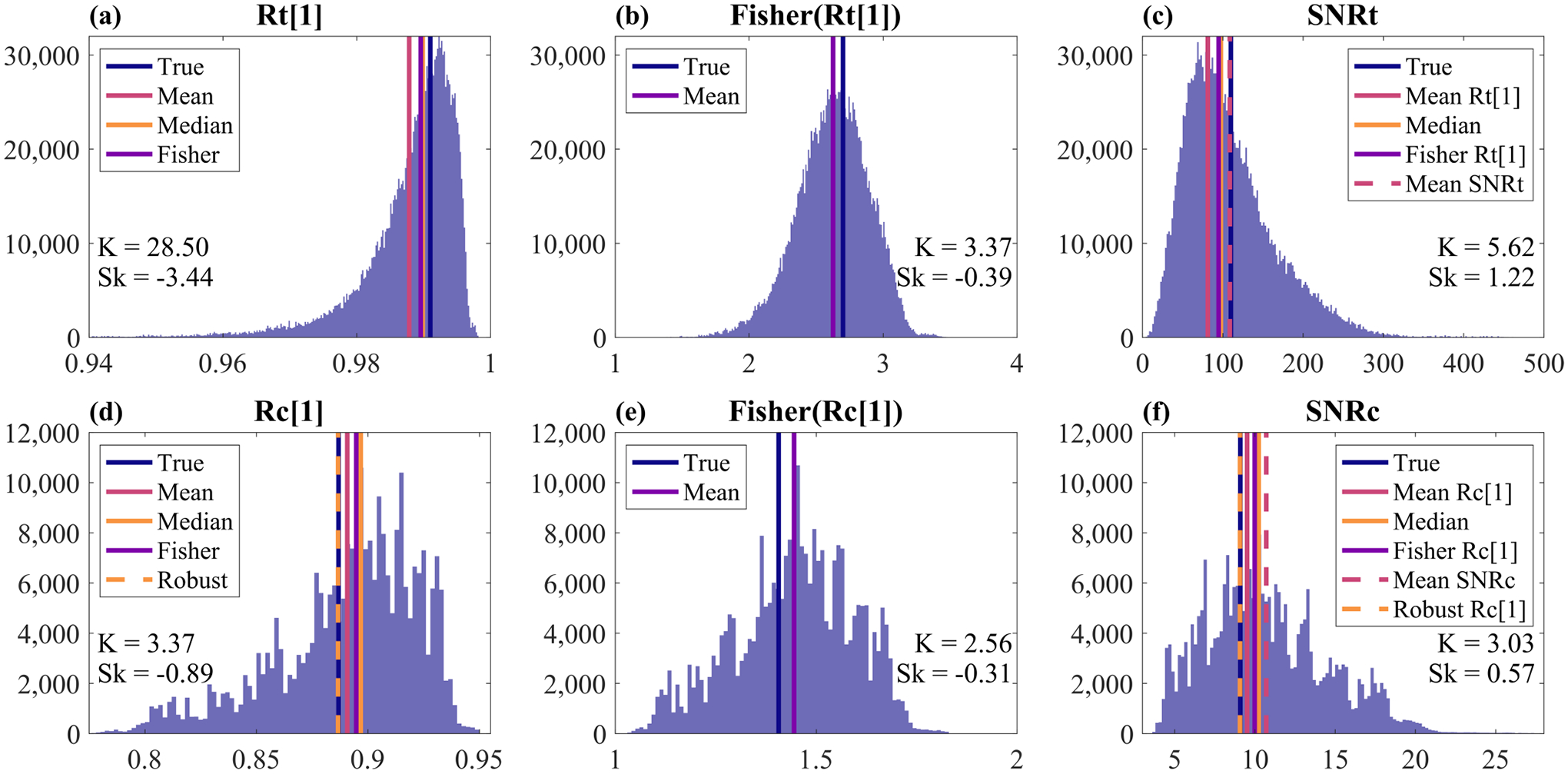
Histograms for (a) temporal LOC, (b) the Fisher z-transform of temporal LOC, (c) temporal SNR, (d), spatial LOC, (e) the Fisher z-transform of spatial LOC, and (f) channel SNR. Distributions were derived from a 2 mm ROI about the transmit focus of one simulated signal + clutter + noise phantom with 20 dB SNR and 10 dB SCR. Kurtosis (K) and skewness (Sk) are indicated in each panel. Note that the shapes of these distributions and subsequently the skewness and kurtosis will change for different SNR and SCR levels. Colored lines show the true values as well as distribution centrality as determined by various approaches (see Section IV-B). Note that the temporal and spatial coherence estimators used here were the ensemble estimators, i.e. Eqs. (6) and (10).
TABLE I.
Comparison of Centrality Metrics
| Rtime [1] | Rchan [1] | SNRtime | SNRchan | |
|---|---|---|---|---|
| True | 0.9910 | 0.8868 | 110.00 | 9.09 |
| Mean R (ens) | 0.9878 | 0.8907 | 81.23 | 9.51 |
| Mean R (non-ens) | 0.9879 | 0.8891 | 81.65 | 9.33 |
| Median R (ens) | 0.9898 | 0.8968 | 97.53 | 10.24 |
| Median R (non-ens) | 0.9899 | 0.8998 | 98.01 | 10.63 |
| Fisher Mean R (ens) | 0.9896 | 0.8948 | 94.79 | 9.99 |
| Fisher Mean R (non-ens) | 0.9896 | 0.8947 | 95.28 | 9.98 |
| Robust R (ens) | – | 0.8866 | – | 9.07 |
| Robust R (non-ens) | – | 0.8905 | – | 9.48 |
| Mean SNR (ens) | – | – | 108.50 | 10.71 |
| Mean SNR (non-ens) | – | – | 109.18 | 10.98 |
First considering the various approaches to calculating temporal LOC as shown in Table I and Fig. 5a, we see that the median is the most accurate. This makes sense considering the high kurtosis and skewness of this distribution. However, the median of temporal LOC does not yield the most accurate estimation of SNRtime. Instead, the mean of SNRtime is most accurate. Interestingly, even though the Fisher z-transform of temporal and spatial LOC improved the Gaussianity of the distributions (Figs. 5b and 5e), taking the mean of the z-transformed LOC distributions did not yield the most accurate results for any quantity (Table I).
Next considering the different approaches to estimating spatial LOC and SNRchan as shown in Table I and Fig. 5d, we see that using the robust spatial LOC estimation technique described in Section III-C yielded the most accurate estimations for both. The mean of spatial LOC was the next most accurate, followed by the median. However, we observed when plotting full coherence curves that the median of spatial or temporal coherence provides the most accurate coherence estimation for lags greater than 1, inspiring the selection of the median as the centrality metric for the robust line-fitting approach for spatial LOC estimation described in Section III-C.
Finally, comparing the use of the ensemble coherence estimators (ens) versus the standard ones (non-ens), we see in Table I that the choice makes little difference for temporal LOC and SNRtime (at least for the tested SNR and SCR values). However, for Rchan[1] and SNRchan, there was a more notable difference between the estimators. The most accurate estimation of Rchan[1] was achieved with the ensemble estimator and the robust approach, but the next most accurate estimator was the mean of Rchan[1] with the non-ensemble estimator. The same trend can be seen for SNRchan.
We further investigated the differences between the ensemble and non-ensemble estimators in terms of SNR and SCR accuracy over a wider range of noise and clutter levels. Fig. 6 shows the average SNR and SCR accuracy in ten simulated signal + clutter + noise phantoms over noise and clutter levels ranging from −30 to 40 dB using either the ensemble or non-ensemble coherence estimators as well as either the mean of spatial LOC or the robust approach for spatial LOC. The mean of temporal SNR was used in each case. Again, the largest difference was between using or not using the robust approach as opposed to using the ensemble estimators or not. In the SCR accuracy plot (Fig. 6b), there is a very clear improvement using the robust spatial LOC approaches over the mean spatial LOC approaches for SCR levels of −15 dB or lower. Differences on the higher end of the SCR accuracy curve are more subtle, and all approaches have high accuracy within the mid-range SCR values between about −15 dB and 15 dB.
Fig. 6.
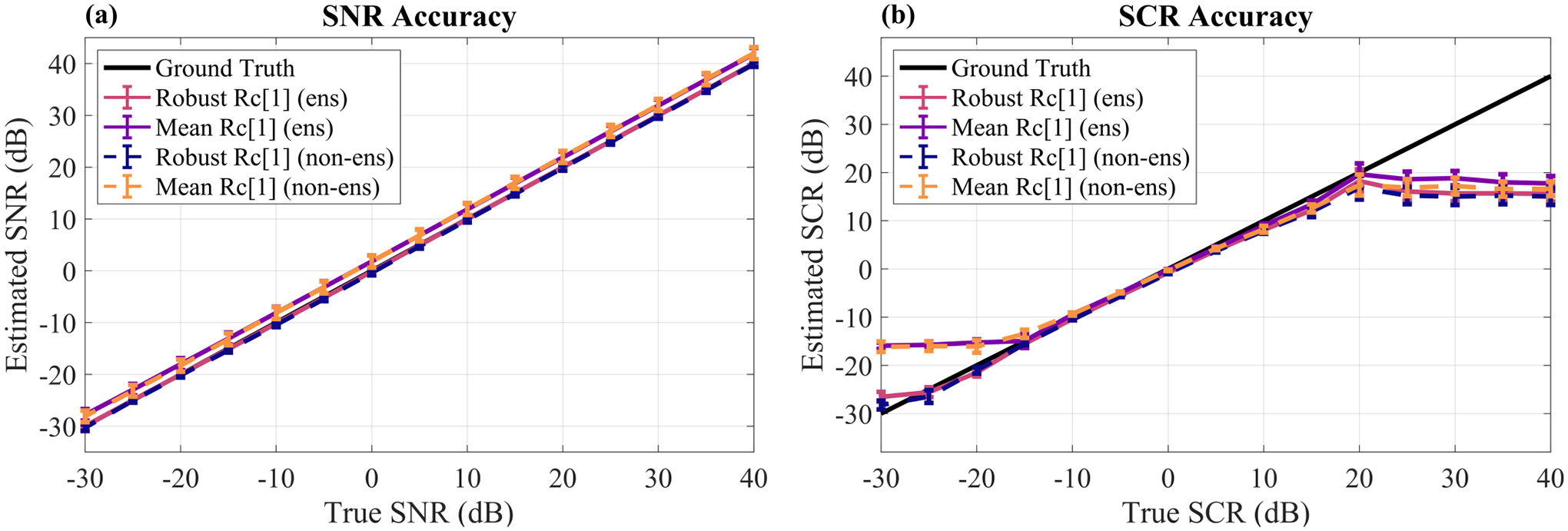
SNR (a) and SCR (b) estimation accuracy of various approaches for method implementation. The Robust Rc[1] approach refers to using the robust line fitting technique to estimate spatial LOC as opposed to using the mean of spatial LOC. The lines labeled with ‘ens’ denote usage of the ensemble estimators for spatial and temporal coherence (Eqs. (6) and (10)) whereas the lines labeled with ‘non-ens’ denote usage of the standard estimators for spatial and temporal coherence (Eqs. (5) and (9)). All cases use the mean of temporal SNR. For SNR accuracy in (a), each point shows the mean ± standard error of the mean across clutter levels ranging from −30 to 40 dB SCR. For SCR accuracy in (b), each point shows the mean ± standard error of the mean across noise levels ranging from −30 to 40 dB SNR.
To better understand the influence of these approaches on the effective dynamic range of the method, the dynamic range was defined as the range of ground truth SNR and SCR values for which no complex estimations of SNRdB or SCRdB resulted. Note that in Fig. 6, any complex values were displayed using the real part only. For more details about when and why this method may sometimes produce complex SNRdB or SCRdB estimations, see Appendix B. From the dynamic ranges shown in Table II, we see that the ensemble estimator approach improves the lower and upper end of the SCR dynamic range when using the mean of spatial LOC, but has no effect on the robust spatial LOC approach. Furthermore, the benefit of using the robust approach instead of the mean is highlighted by improved dynamic range on the lower end for SCR and for SNR.
TABLE II.
Dynamic Range
| SNR Range (dB) | SCR Range (dB) | |
|---|---|---|
| Mean Rchan [1] (ens) | [−25, 40] | [−15, 15] |
| Robust Rchan [1] (ens) | [−30, 40] | [−20, 15] |
| Mean Rchan [1] (non-ens) | [−25, 40] | [−10, 10] |
| Robust Rchan [1] (non-ens) | [−30, 40] | [−20, 15] |
C. Minimum Requirements for Data Acquisition
Figure 7 shows the SNR and SCR mean squared logarithmic error (MSLE) as a function of number of frames or number of channels for three representative SNR and SCR levels. MSLE is defined according to Eq. (18),
| (18) |
where y and are the true and estimated SNR or SCR values on a linear scale and the resulting metric is in units of dB. Looking first at the error versus number of frames in Figs. 7a and 7b, we see that the values stabilize at approximately ten frames, but even with as few as two or five frames the error is very comparable.
Fig. 7.
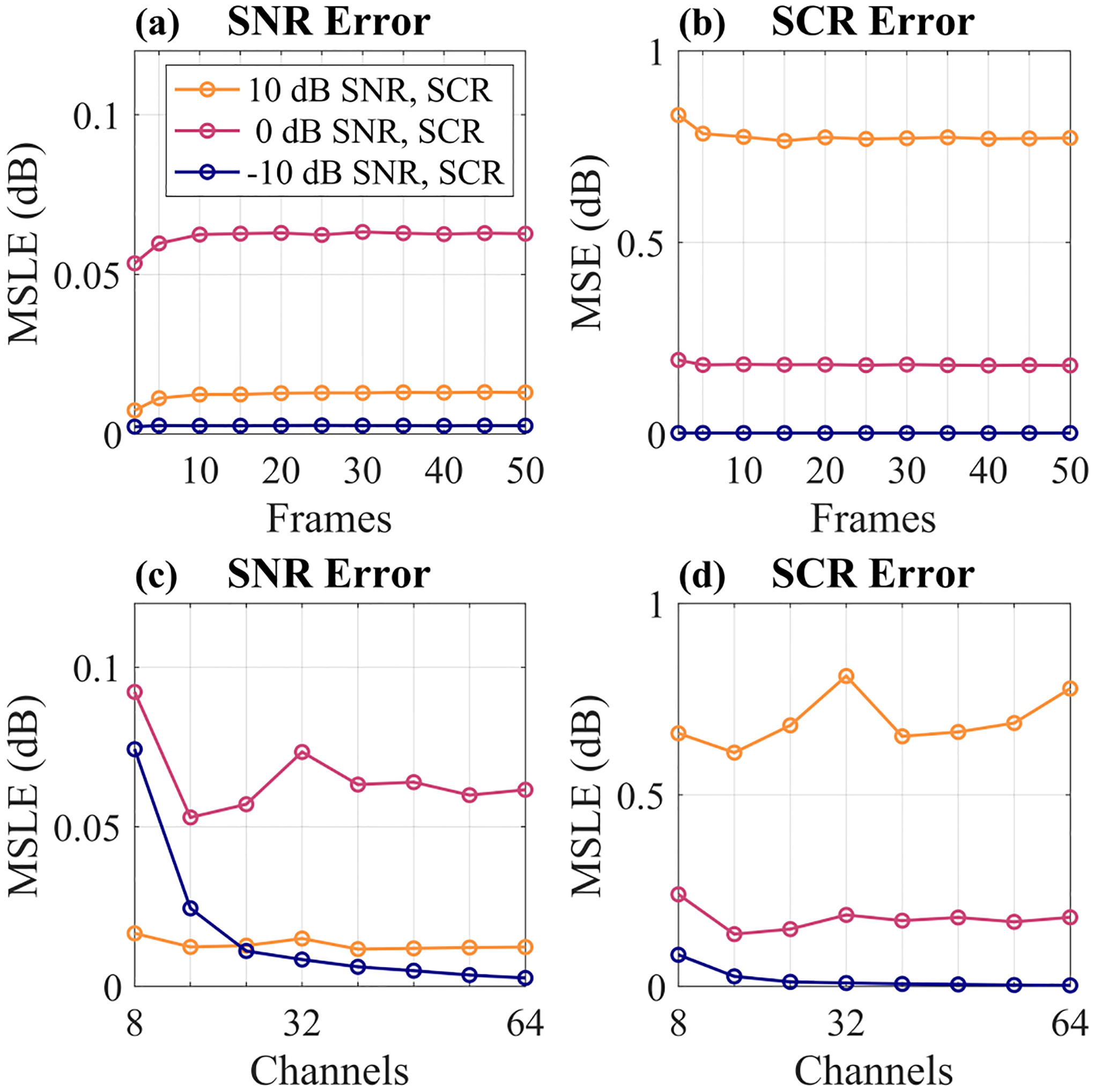
SNR and SCR mean squared logarithmic error (MSLE) versus number of frames used in (a) and (b) and number of channels used in (c) and (d). For (a) and (b), all 64 channels were used. For (c) and (d), 10 frames were used. All data points are averages across 10 independently simulated signal + clutter + noise phantoms.
Considering next the error as a function of the number of channels in Figs. 7c and 7d, we see that, in general, SNR and SCR can be estimated accurately with as few as 16 channels. However, in the lower signal environments, more channels are needed to maintain SNR estimation accuracy. Interestingly, there is a slight increase in SCR error for the 10 dB SNR and SCR case when all 64 channels were used. This may be due to the choice of using the channels in the middle of the aperture for the reduced channel number measurements. When almost all of the channels were being used, the edge elements which may have lower quality data were being included as well, which could have contributed to the slight increase in error.
D. In Vivo Demonstration
Finally, we investigated in vivo application of our method in two representative imaging environments to determine the effects of motion on temporal coherence estimation and to show how we can overcome its confounding effects. An overview of this study is shown in Fig. 8. Normalized temporal correlation matrices were calculated on the beam-summed M-Mode data to visualize temporal decorrelation across the ensemble and to select a contiguous group of RF lines with maximal temporal correlation under the assumption that high correlation between RF lines is indicative of minimal motion between them [43].
Fig. 8.
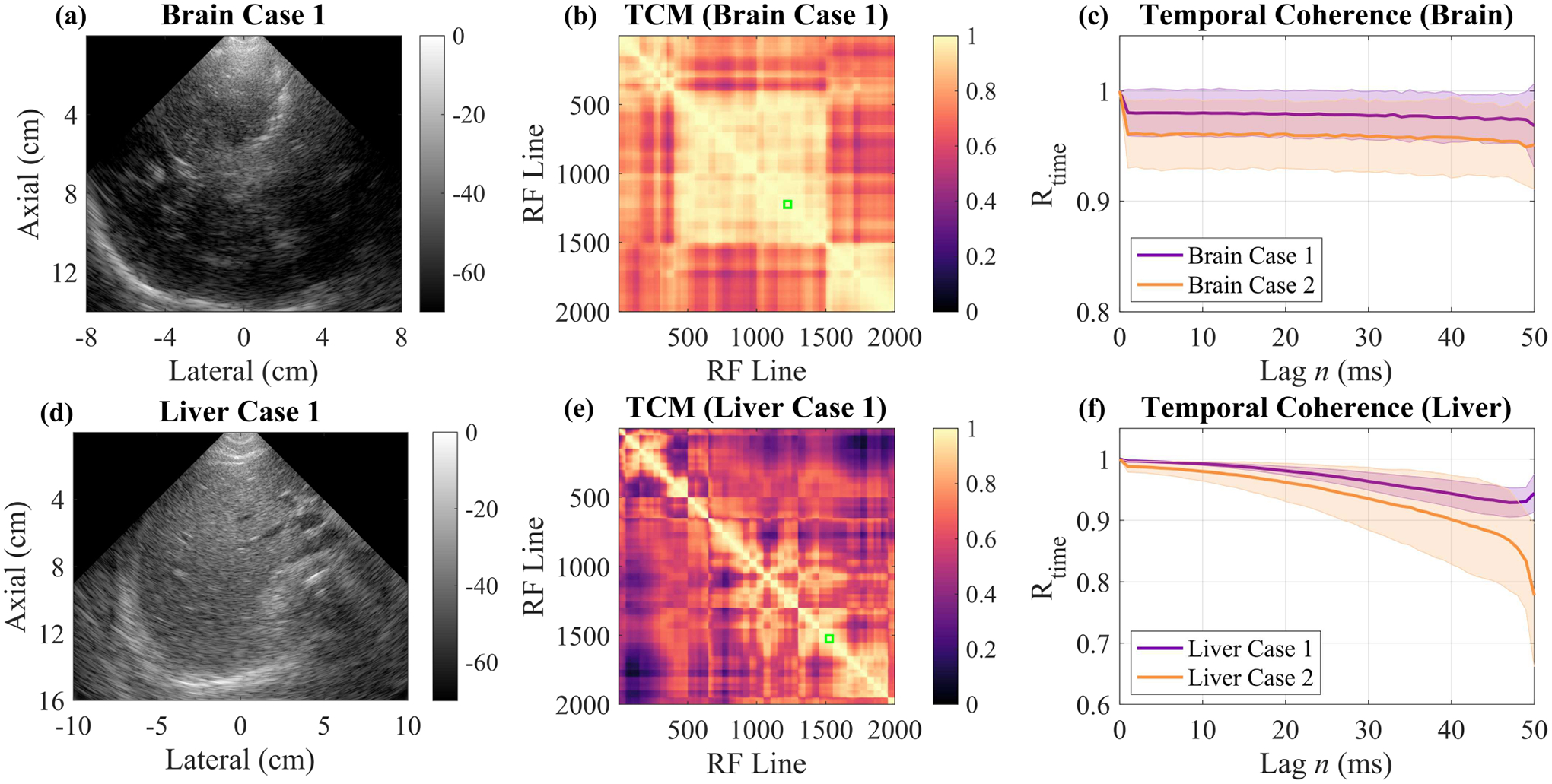
In vivo case studies investigating the effects of motion on temporal coherence in two representative imaging environments, the brain (a)-(c) and the liver (d)-(f). (a) B-Mode of brain imaging Case 1. (b) Temporal Correlation Matrix (TCM) for the M-Mode acquisition for Brain Case 1. Green box indicates the 50 RF line ensemble with maximal correlation which was used to calculate temporal coherence. (c) Temporal coherence curves for the two Brain Cases calculated over their respective 50 RF line ensembles with maximal coherence. (d) B-Mode of the liver imaging Case 1. (e) Temporal correlation matrix for the M-Mode acquisition for Liver Case 1 with the green box indicating the 50 RF line ensemble with maximal correlation. (f) Temporal coherence curves for the two liver cases calculated over their respective 50 RF line ensembles with maximal coherence.
From Fig. 8b, the temporal correlation matrix for the brain imaging case shown in Fig. 8a, we see a relatively high amount of correlation throughout the two second ensemble as compared to the temporal correlation matrix for one of the liver imaging cases (Fig. 8e). This observation confirms our expectations that there was more motion present in the liver imaging case than the brain imaging case. Using these temporal correlation matrices, we selected a contiguous group of 50 RF lines for each imaging case and computed temporal coherence curves as shown in Figs. 8c and 8f. For the two brain cases, the temporal coherence was approximately stable for the entire 50 lags (50 ms), but the liver cases showed motion-induced decorrelation with increasing lags. This highlights the need for either short ensembles or fast frame rates (or both).
We first investigated the effect of reducing the ensemble size on temporal LOC calculation as shown in Table III. Here we see that, in general, reducing the ensemble size leads to an increase in temporal LOC since there is less time for motion to cause decorrelation. With only two RF lines in the M-Mode sequence, temporal LOC was the highest. Since we showed in Section IV-C that very few frames are required for accurate SNR and SCR estimation accuracy, we can conclude that as few as two frames is likely sufficient.
TABLE III.
Temporal LOC vs Ensemble Size
| PRF (Hz) | RF Lines | Brain #1 | Brain #2 | Liver #1 | Liver #2 |
|---|---|---|---|---|---|
| 1000 | 50 | 0.9788 | 0.9605 | 0.9983 | 0.9950 |
| 1000 | 25 | 0.9790 | 0.9612 | 0.9983 | 0.9950 |
| 1000 | 10 | 0.9802 | 0.9598 | 0.9983 | 0.9952 |
| 1000 | 5 | 0.9817 | 0.9578 | 0.9984 | 0.9952 |
| 1000 | 2 | 0.9842 | 0.9615 | 0.9985 | 0.9960 |
We next investigated temporal LOC as a function of pulse repetition frequency (PRF) as shown in Table IV. In this experiment, the number of RF lines was kept constant and the M-Mode data were down-sampled to emulate lower PRFs. For the two brain cases, temporal LOC fluctuated for each PRF but did not markedly decrease as PRF decreased, indicating that 40 Hz is likely sufficient for this imaging scenario. For the two liver cases, temporal LOC steadily decreased with decreasing PRF and experienced a large decrease between 100 Hz and 40 Hz, indicating that 40 Hz is not sufficient to overcome the amount of motion present in this scenario.
TABLE IV.
Temporal LOC vs Pulse Repetition Frequency
| PRF (Hz) | RF Lines | Brain #1 | Brain #2 | Liver #1 | Liver #2 |
|---|---|---|---|---|---|
| 1000 | 2 | 0.9842 | 0.9615 | 0.9985 | 0.9960 |
| 500 | 2 | 0.9849 | 0.9647 | 0.9983 | 0.9956 |
| 200 | 2 | 0.9828 | 0.9634 | 0.9977 | 0.9941 |
| 100 | 2 | 0.9830 | 0.9654 | 0.9945 | 0.9898 |
| 40 | 2 | 0.9838 | 0.9637 | 0.9769 | 0.9512 |
Using two frames of the fully-sampled (1000 Hz) data, we calculated the SNR and SCR for each imaging case as shown in Table V. Due to poor spatial coherence curve behavior at later lags, we were unable to use our robust spatial LOC estimation technique and instead used the mean of spatial LOC. The liver cases had higher SNR than the brain cases, most likely due to the higher attenuation of the skull. The SCR of the first liver case was higher than the brain cases, but not the second liver case in which the transmit focus was near a blood vessel.
TABLE V.
In Vivo SNR and SCR
| Brain #1 | Brain #2 | Liver #1 | Liver #2 | |
|---|---|---|---|---|
| SNR (dB) | 18.89 | 14.00 | 28.29 | 23.58 |
| SCR (dB) | 8.83 | 5.98 | 11.98 | 6.28 |
Overall, the results of this in vivo study have shown that motion is a significant factor to take into account and that the frame rate requirements are dependent upon the amount of motion present. To better understand how much motion may be in a given imaging environment and therefore select an adequate PRF, the temporal correlation matrix and the temporal coherence curve are useful tools.
V. DISCUSSION
A. Method Accuracy and Dynamic Range
In Section IV-B, we showed that our method accurately estimates SNR across the entire range tested (−30 to 40 dB SNR) but that it only accurately estimates SCR within mid-range SCR values (−20 to 15 dB SCR). The reduction in SCR estimation accuracy (and the occurrence of complex SCRdB estimations) at more extreme values of SCR is related to two reasons explored in Appendices A and B.
The first issue described in Appendix A involves partial correlations between signal and clutter. One of the assumptions of our method described in Section II was that the signal, clutter, and noise components are uncorrelated. We showed in Section IV-A with Fig. 4 that the normalized cross-correlation between these components was very small. However, for the short- and mid-lag region, the NCC between signal and clutter was non-zero, albeit small. We show in Appendix A that the non-normalized magnitude of this small partial correlation can become more significant with respect to either clutter power or signal power at the more extreme levels of SCR (when either clutter power or signal power are very low). These partial correlations lead to extra errors terms in the derivations of SNRchan and SNRtime as a function of spatial or temporal LOC which in turn lead to small errors in the calculation of clutter power and signal power from LOC measurements. However, we also showed in Appendix A that, for our simulated data, this power estimation mean squared error is very small (below 0 dB) for any clinically relevant SCR values, indicating that this is not a major source of error in our results and likely not a major source of error in many applications.
Although partial correlations between signal and clutter may lead to very small errors in power estimation, they do not explain why this method produces negative estimates of power that lead to complex-valued SNRdB and SCRdB estimations at the more extreme levels of SCR. This issue, described in Appendix B, stems from inaccuracies in measuring coherence due to inherent variance in the coherence estimator. For example, it is well-known in the coherence literature that negative estimates of spatial LOC occasionally occur in low signal environments [13], [44]. As shown in Appendix B, negative estimates of spatial LOC lead to a negative estimate of with our method, which leads to a negative estimate of SNR and SCR (or complex-valued SNRdB and SCRdB after taking the logarithm). This explains the dynamic range limitation of −20 dB SCR for our method.
On the flip side, our method also has an upper bound for lag-one coherence defined by the inequality Rchan[1] > Rtime[1](1 − 1/M) (derived in Appendix B). If the spatial LOC and/or temporal LOC estimations violate this inequality, then our method estimation of becomes negative which leads to a complex SCRdB estimation. Again, this can happen due to inherent variance in the coherence estimator. Appendix B also shows that this LOC boundary creates a vertical asymptote for SCR defined as a function of temporal or spatial LOC; as SCR increases, it tends towards infinity as it approaches this asymptote. This explains the upper dynamic range limitation of 15 dB for our method.
B. Robust Estimation
In this work, we presented a new robust technique described in Section III-C for estimating spatial LOC based on computing an entire spatial coherence curve (lags 1 through M) using Eq. (6) and using the median as a centrality metric and then performing a weighted fit of the line to estimate the lag-one coherence value. In addition to improving the spatial LOC, SNR, and SCR estimation accuracy, this approach also extended the dynamic range of this framework to lower SCR and SNR values as shown in Fig. 6 and Table II. In effect, this robust spatial LOC estimation approach was able to reduce occurrences of negative spatial LOC estimations, thereby eliminating negative estimations. This is how the robust approach was able to improve the lower dynamic range of both SNR and SCR. Interestingly, it has been previously identified that at −15 dB and lower, the variance of estimating spatial LOC is too high [13]. This is corroborated by the plateau in SCR accuracy at low SCR values using the mean of spatial LOC instead (Fig. 6b and Table II). However, we were unable to use the robust spatial LOC estimation approach on our in vivo datasets due to poor spatial coherence behavior at higher lags which is a limitation of this approach.
The robust line-fitting approach for estimating spatial LOC may be useful for improving the performance of other clutter estimation or suppression techniques that rely on computing spatial LOC such as LoSCAN (Lag-one Spatial Coherence Adaptive Normalization) [13], [45]. It may additionally provide a simple mechanism for accounting for low-frequency phase aberration with the proposed noise separation framework. Since low-frequency phase aberration affects the lower lags in addition to lag one, if the starting lag for the line fitting procedure were chosen appropriately (e.g., 10% or 20% of the aperture), the resulting “lag-one” value that would be extrapolated would incorporate the loss in coherence from the phase aberration at those short lags. By estimating coherence with a starting lag of 1 and then again with a starting lag of 10–20% of the aperture, the contributions of phase aberration could be assessed separately from those of incoherent clutter such as reverberation. Future work should explore the ability of this robust spatial LOC estimation technique to account for low-frequency phase aberration.
Although it was not explored in this work, another strategy that may provide increased robustness to phase aberration would be to perform the coherence calculations on complex-valued data and then take the magnitude of the result instead of the real part. In the real-valued data, phase aberration manifests as time shifts, but in the complex-valued data, phase aberration manifests as phase rotations, which do not affect the magnitude. Future work should explore the significance of the increased robustness provided by complex-valued coherence calculations in the face of high in vivo phase aberration.
C. Clinical Relevance of Noise and Clutter Levels
While there is limited data on the expected range of clutter levels in vivo, partially due to the lack of a method to fully assess clutter in vivo, we believe these SNR and SCR ranges to be clinically relevant. Bladder wall to clutter magnitudes have been measured in vivo and were found to be between 0 and 35 dB [17]. Other studies of clutter also fall within this range [18], [23]. In simulation studies, SCNR and SCR ranges were varied from −20 to 20 dB and showed perceptually realistic levels of clutter, further confirming that the ranges simulated herein are more than adequate [20], [46]. In terms of SNR, previous reports indicate that −20 to 40 dB is a reasonable range to model effects seen in vivo [47]. Furthermore, our in vivo results in the liver and the brain also fall within the dynamic range of our method.
D. Limitations
One of the primary challenges in applying a temporal coherence-based approach in vivo is the assumption that the signal is stationary. Patient respiration, pulsatile blood flow, and sonographer hand motion (if applicable) can all lead to motion and therefore decorrelation across repeated acquisitions. This would lead to an overestimation in the amount of thermal noise present which in turn would lead to an underestimation in the amount of clutter present. High frame rate imaging with focused transmits or plane wave synthetic focusing is one possible solution to this [48], [49]. We employed high frame-rate M-Mode imaging to ensure we performed our calculations on data with minimal frame-to-frame motion. We found our 1 kHz frame rate to be more than sufficient for accurate temporal coherence estimation and additionally showed that the frame rate requirements are dependent upon the amount of motion present. For the brain imaging scenario, two frames with a 40 Hz PRF was sufficient, but for the liver imaging scenario, 40 Hz was too slow and a higher PRF would be required.
Another limitation of this approach is the need for adequate transmit focusing to ensure valid application of the VCZ theorem. For typical focused B-Mode imaging sequences, only one or a few transmit focal depths are used, meaning that this analysis can only be performed within ROIs centered about those transmit foci. However, synthetic focusing can be used to create transmit focusing throughout the full field of view, thereby providing an opportunity for full-field assessment [41]. Moreover, since as few as two frames are needed for accurate coherence estimation, it would be trivial to design a sequence that acquires a few frames at many different transmit focal depths. This would facilitate evaluation of the image quality across the entire field-of-view, allowing SNR and SCR “images” to be displayed or overlaid on the B-Mode images similar to how Offerdahl et al. displayed pixel-wise maps of spatial LOC alongside B-Mode images [50]. Future work will incorporate such sequences and analysis.
An additional underlying assumption for this derivation of the VCZ theorem is that the coherence calculations are performed in a region of speckle. Alternative non-speckle targets would include specular reflections or highly coherent targets such as kidney stones and anisotropic muscle fibers, which could lead to increased spatial coherence, and anechoic or very hypoechoic regions such as inside a large fluid filled cavity which would lead to decreased spatial coherence. In the case of highly increased spatial coherence, this may cause the method to fail as the boundary of Rchan[1] > Rtime[1](1 − 1/M) may become violated, leading to a complex SCRdB value as discussed in Appendix B. In the case of reduced spatial coherence, the method may again fail if the spatial LOC estimate drops below zero, causing both a complex SCRdB value and a complex SNRdB value as discussed in Appendix B. Although, if off-axis scattering is prevalent within the anechoic region, then this may not occur. In practice, these limitations could be circumvented using real-time B-Mode guidance to avoid placing the transmit focus within a non-speckle target.
Additionally, it should be pointed out that off-axis clutter sources such as side lobes are not explicitly removed from the Field II simulations and as such are grouped in with the signal term, . This is consistent with the VCZ theorem derivation of the triangle function for the signal spatial coherence curve which includes the presence of side lobes. In order to separate their small contributions from that of the main lobe in a uniform scattering medium, the spatial coherence curve corresponding to the main lobe could be used instead of the triangle function [12]. However, in mediums with inhomogeneous scattering functions (e.g., strong off-axis scattering from a neighboring hyperechoic region), the spatial coherence may be further altered from theoretical predictions [36]. As it stands, our method is most sensitive to reverberant clutter which is largely incoherent [29] whereas phase aberration and off-axis scattering can be weakly coherent [13], [20], [36].
Finally, other limitations of this approach include the reliance on channel data as opposed to beamformed RF data or log-compressed pixel data which may be more readily available from commercial scanners. However, we showed in Section IV-C that accurate SNR and SCR estimations can be made with only a small number of channels available which may allow our approach to be more readily utilized in commercial scanners. Despite these minor limitations, this work still provides an important and unique contribution to the study of image degradation in ultrasonic imaging.
E. Future Applications
Our technique is most relevant to those interested in distinguishing between the contributions of thermal noise and acoustic clutter. This is of particular importance in especially challenging imaging scenarios such as transcranial imaging, transthoracic echocardiography, and abdominal imaging of high habitus patients where there remains significant work to be done improving image quality as well as in blood flow imaging where blood echogenicity and sensitivity are low. If thermal noise is found to be the dominating factor, then contrast agents or coded excitation would be possible ways to overcome that limitation [8], [9]. If acoustic clutter is found to be the dominating factor, then harmonic imaging and/or advanced beamforming approaches such as ADMIRE, SLSC, MIST, LoSCAN, minimum variance, or deep neural network approaches may be more applicable [10]–[16]. In addition, with real-time spatial and temporal lag-one coherence implementations, SNR and SCR estimations could be used for adaptive transmit parameter selection [51]–[54].
VI. Conclusion
In summary, we have presented a method and implementation strategy for separating the contributions of thermal noise and acoustic clutter to image degradation by leveraging coherence properties of signals. We validated this framework in realistic simulations across an extensive range of clutter and noise levels and found that it can estimate SNR and SCR with high accuracy over a wide range of clinically relevant noise and clutter levels. We further showed that this method maintains accurate estimations of SNR and SCR with a small number of frames and channels, suggesting feasibility of implementation on commercial scanners. Finally, we proposed a strategy to circumvent the effects of motion in vivo, further demonstrating the suitability of our method for quantifying the effects of in vivo image degradation. This work has the potential to greatly impact the study of improving image quality in challenging clinical imaging scenarios.
Acknowledgment
The authors would like to acknowledge the staff at Vanderbilt University’s Advanced Computing Center for Research and Education (ACCRE) for their continued support.
This work was supported in part by the National Institute of Biomedical Imaging and Bioengineering through NIH Grants T32EB021937 (to E.P.V. and K.A.O.) and R01EB020040 (to B.C.B.). This work was also supported in part by the National Heart, Lung, and Blood Institute under Grant R01HL156034 (to B.C.B.). This material is based upon work supported by the National Science Foundation CAREER award under grant number IIS-1750994 (to B.C.B.) and by the National Science Foundation Graduate Research Fellowship Program under grant number 1937963 (to E.P.V.). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Biographies
Emelina P. Vienneau (IEEE Graduate Student Member) received the B.S.E. degree in biomedical engineering from Duke University, Durham, NC, USA in 2018. She is currently a Ph.D. candidate in biomedical engineering at Vanderbilt University, Nashville, TN, USA. She is an NSF Graduate Research Fellow and a recipient of the Provost Graduate Fellowship as well as the Harold Stirling Vanderbilt Award. She is affiliated with the Vanderbilt Institute for Surgery and Engineering (VISE) and holds the Graduate Certificate in Surgical and Interventional Engineering. She is also affiliated with the Vanderbilt University Institute of Imaging Science (VUIIS). Her research interests include ultrasound imaging, signal processing, and functional neuroimaging.

Kathryn A. Ozgun (IEEE Member) received the B.S. degree in biomedical engineering from North Carolina State University, Raleigh, NC, USA in 2016 and the Ph.D. degree in biomedical engineering from Vanderbilt University, Nashville, TN, USA in 2021. She holds a Graduate Certificate in Surgical and Interventional Engineering and is an affiliate of the Vanderbilt Institute for Surgery and Engineering (VISE). Her research interests include adaptive beamforming and filtering methods for ultrasound imaging. She is currently an Ultrasound Systems Engineer at Rivanna Medical in Charlottesville, VA, USA.

Brett C. Byram (IEEE Member) is an associate professor at the Vanderbilt University School of Engineering. He received his B.S.E. degree in biomedical engineering and mathematics from Vanderbilt University and his Ph.D. in biomedical engineering from Duke University in 2011. He’s spent time in Mountain View, California working at Siemens’ Ultrasound Business Unit, and he spent a year working with Jorgen Jensen’s Center for Fast Ultrasound in Lyngby, Denmark. Brett served as an Assistant Research Professor at Duke University from 2012–2013. Brett is part of the Vanderbilt Institute for Surgery and Engineering (VISE) and is an affiliate of the Vanderbilt University Institute of Imaging Science (VUIIS).

APPENDIX A. Derivation of SNR with Partial Correlations
In previous derivations of SNR based on the correlation coefficient, the signal is assumed to be uncorrelated with the noise sources [25], [41]. We used the same assumptions and showed in Fig. 4 that the normalized cross-correlation between the signal, clutter, and noise was small, indicating that they are approximately orthogonal. However, as shown in Fig. 4, the signal and clutter cross-correlation is non-zero for the lower lags. In this Appendix, we investigate what happens when small cross-terms remain and hypothesize that, when either the signal power or the clutter power is very small (as is the case for very high or very low SCR values), the magnitude of the non-normalized partial correlations may become more significant.
First, to understand how these partial correlations would manifest in the definitions of SNRtime and SNRchan, the derivation of SNR from the cross-correlation coefficient, ρ, must be revisited. Consider the correlation between two real-valued signals, and , that are each corrupted with thermal noise ( and ) and clutter :
| (19) |
Note that previous derivations have only considered signal and noise, but here we are explicitly considering noise and clutter separately [25], [41]. For clarity, we start by considering the expansions of the numerator and denominator separately. First considering the numerator, we have
where we have assumed that all of the noise terms are zero since Gaussian white noise is uncorrelated with a sufficient window size. The following analysis could be extended to include small correlations of noise as well, but this is a much smaller effect. Replacing with , we have the following expression for the numerator:
Note that we would typically assume the clutter is uncorrelated with the signal and with itself, but here we are considering the case that those terms may not be completely zero. Considering next the expansion of the denominator and zeroing out the noise terms, we have:
We can re-write the denominator as follows, subbing in power terms where appropriate:
Using the binomial series expansion defined below,
we eliminate the square roots with a first-order approximation:
Multiplying through and eliminating a higher-order term yields:
which further reduces to
Bringing together the numerator and denominator, we have:
| (20) |
Before continuing to derive an expression for SNR, we first define our error terms for convenience, where ϵ1 is the cross-correlation (lag > 0) between the signal and the clutter, ϵ0 is the lag-zero cross-correlation between signal and clutter, and ϵc is the cross-correlation (lag > 0) between clutter and itself. We can consider the lag to be across either the channel dimension or the frame dimension.
| (21) |
| (22) |
| (23) |
We can now write:
| (24) |
Finally, dividing through by yields:
| (25) |
We can write Eq. (25) in terms of temporal LOC by considering that the relationship between the correlation of the noise-free signal at lag n, , is related to the correlation of signal + noise + clutter, i.e. ρ[n], by the signal-to-clutter-plus-noise ratio. That is,
| (26) |
Since the noise-free signal is temporally stable, and we can write Eq. (26) in terms of temporal LOC:
| (27) |
Alternatively, we could write Eq. (25) in terms of spatial LOC by again considering that the relationship between correlation of the noise-free signal at lag m, , is related to the correlation of signal + noise + clutter, i.e. ρ[m], by the signal-to-clutter-plus-noise ratio. That is,
| (28) |
The VCZ theorem for a rectangular aperture and M transmit focusing elements relates and ρ[m] according to (1 − m/M), allowing us to write
| (29) |
Finally, rearranging terms in Eqs. (27) and (29) yields equations for the SCNR as a function of lag-one coherence and signal power. Starting with Eq. (27), we have
| (30) |
where ϵtime ≡ (ϵ1 + ϵc − ϵ0Rtime[1])/PS. Note that the lags in ϵ0, ϵ1, and ϵc are across the frame dimension in this case. Considering next Eq. (29), we have
| (31) |
where and we are now considering lags across the channel dimension. Note that if ϵ0, ϵ1, and ϵc are zero, then Eq. (30) reduces to Eq. (11) and Eq. (31) reduces to Eq. (7).
We next analyzed ϵ0, ϵ1, and ϵc across the channel dimension and frame dimension as a function of SCR level. From Fig. 9a, we see that ϵ0 and ϵ1 are nearly indistinguishable from each another. We also observe that as clutter power becomes small (SCR is high), the magnitude of ϵ0 and ϵ1 relative to clutter power becomes large. Conversely, as signal power becomes small (SCR is low), the magnitude of ϵ0 and ϵ1 relative to signal power becomes large. On the other hand, is not dependent upon SCR. It is also nonzero in this example, indicating that non-zero partial correlations between clutter and itself (over lags > 0) is possible and can also contribute to error.
Fig. 9.
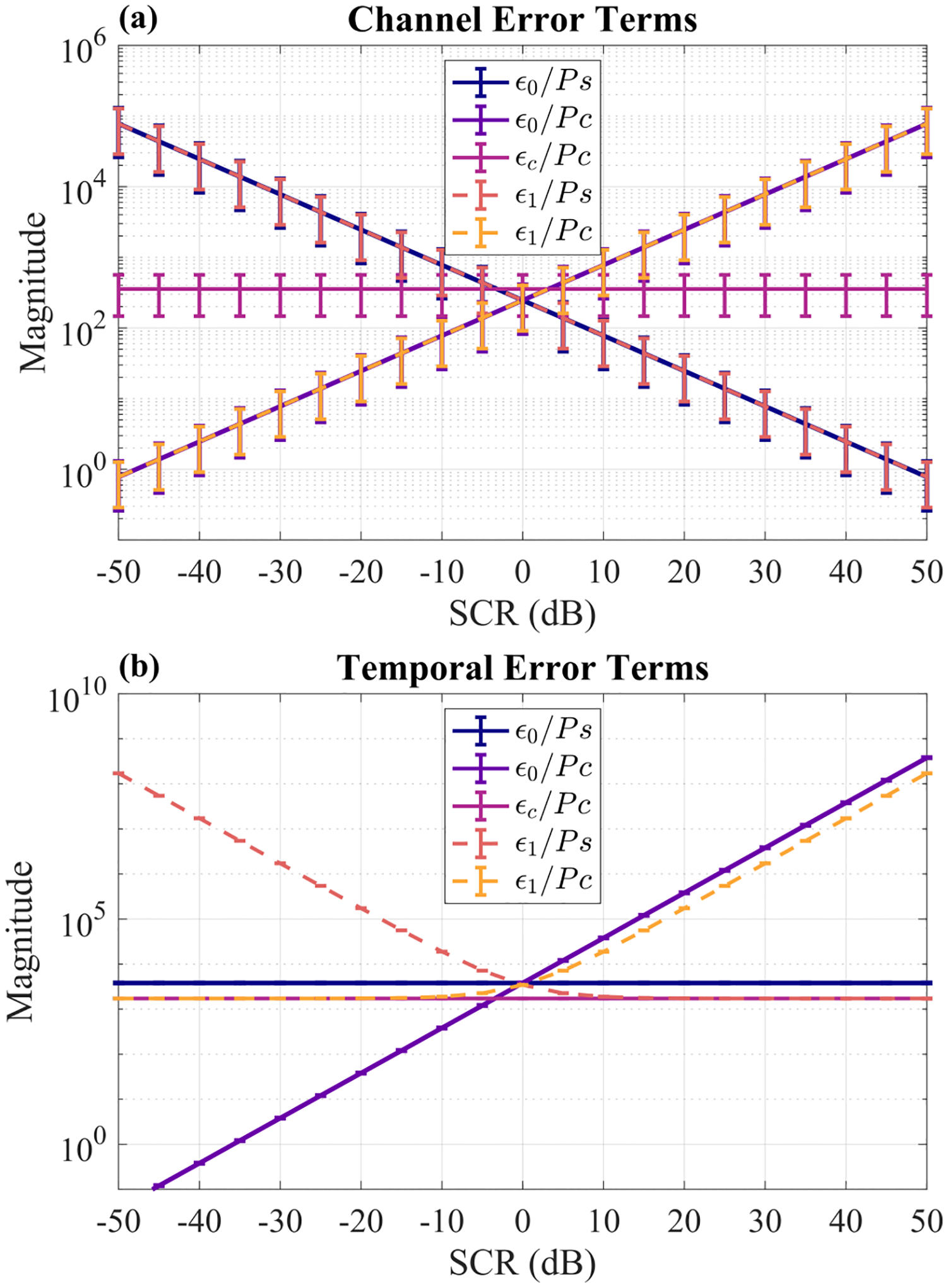
Epsilon error terms normalized by either signal power or clutter power as a function of SCR. (a) Error terms with cross-correlation lags across channels. (b) Error terms with cross-correlation lags across frames. Each point is the mean ± standard deviation across 10 independent simulated signal + clutter phantoms (no noise added).
Considering next the error terms across the temporal dimension shown in Fig. 9b, we see similar trends, with and both increasing with increasing SCR and with increasing with decreasing SCR. In summary, as either signal power or clutter power becomes too small, the magnitude of their cross-correlation begins to matter and errors in estimating SNRtime and SNRchan occur. Partial correlations within the clutter itself may also contribute to error, though this will vary across scenarios.
Finally, we computed the signal power and clutter power mean-squared error (MSE) as a function of SCR in Fig. 10. Here we observe that MSE steadily increases as SCR (and therefore ) decreases. For high SCR values, MSE remains very low. MSE increases for either very low or very high SCR values and remains small for the mid-range SCR values. This corroborates with previous observations showing that SCR estimation is most accurate within mid-range SCR values. Importantly, and MSE remain very low (below 0 dB) within a clinically relevant range of SCR values, indicating that, in general, this is not a major source of error for most practical applications.
Fig. 10.
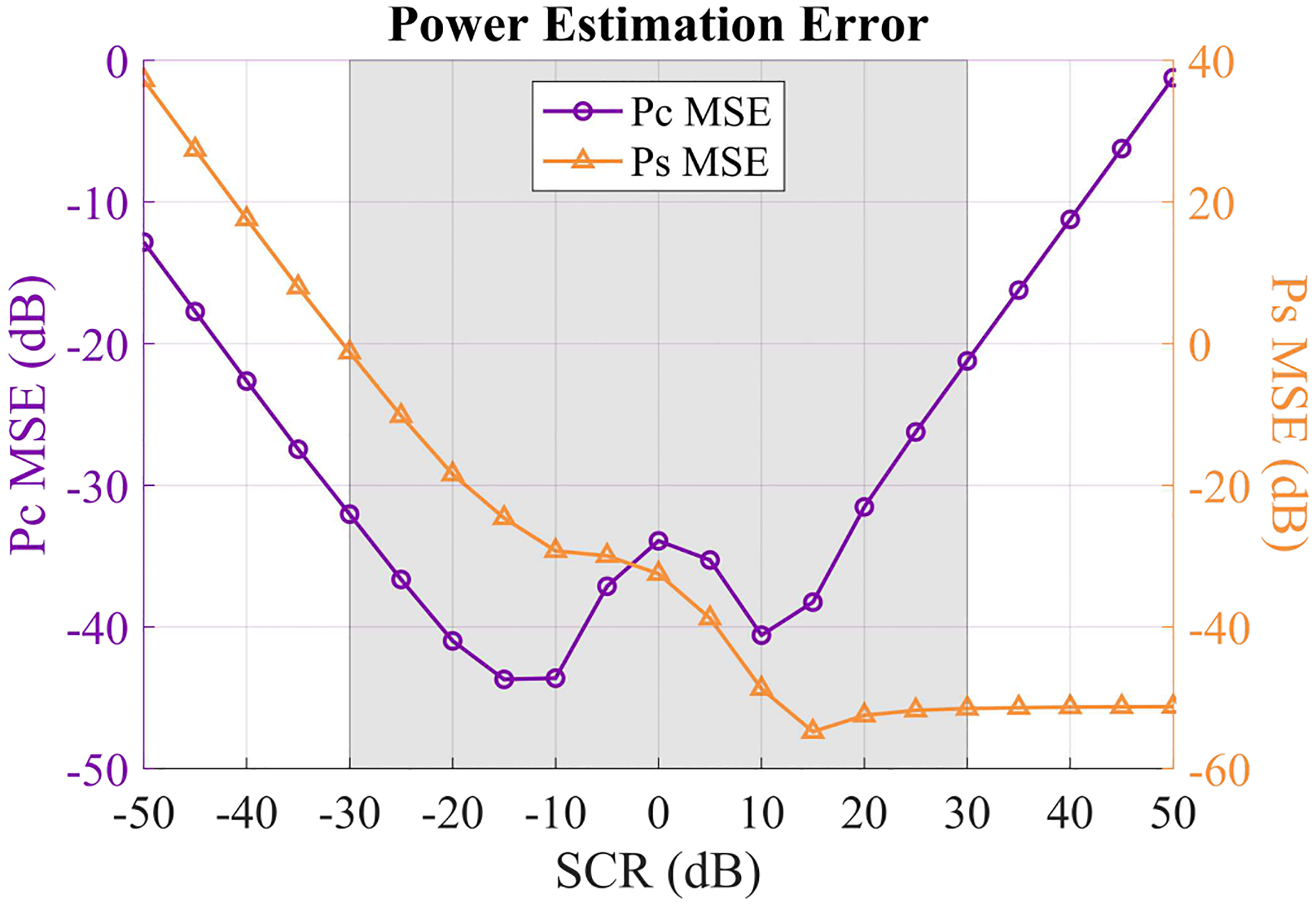
Mean squared error (MSE) for and across 10 independent signal + clutter + noise phantoms with varying SCR. SNR was set to 30 dB. and MSE were calculated on a linear scale, normalized by or , respectively, and then converted to units of dB for plotting. The gray shaded region indicates the range of SCR values that are relevant for in vivo imaging.
Appendix B. Derivation of Lag-One Coherence Bounds
Here we take a closer look at why our method may fail to produce numerically valid estimates of SNR or SCR in certain ranges. For instance, within some ranges of SCR levels, the estimated SNR or SCR may be negative (and complex after taking the logarithm) even though this is not physically possible. Based on Eq. (16), SCRdB can only be complex if the estimated or is negative. If , then SNRchan > SNRtime based on Eqs. (13) and (14). This would further imply based on Eqs. (7) and (11) that, for to be negative, Rchan[1] > Rtime[1](1 − 1/M) would have to be true.
Considering instead what would need to happen for , we see by considering Eq. (13) and assuming that SNRchan would need to be less than zero. This would further imply via Eq. (7) that Rchan[1] would need to be less than zero. From this analysis, we see that SCRdB will be complex if either Rchan[1] < 0 or Rchan[1] > Rtime[1](1 − 1/M), which should not happen but nevertheless does happen due to estimation error. Interestingly, we confirmed with our simulation data that each occurrence of a negative estimation was accompanied by a negative Rchan[1] estimation and each negative estimation was accompanied by a violation of the inequality Rchan[1] > Rtime[1](1 − 1/M).
Considering now what would need to occur for SNRdB estimation to be complex, we see from Eq. (15) that either or would need to be negative. From analysis of Eqs. (3), (7), (8), (13), and (14), it can be shown that, for to be negative, either M < 1 or would need to be true, neither of which is possible. Therefore, the only way for this method to produce a complex SNRdB value is if Rchan[1] < 0.
We next visualized SNR and SCR as a function of spatial LOC and temporal LOC in Fig. 11 to understand how they are related to these bounds on LOC. In Figs. 11a and 11c, we see that SNR and SCR decrease rapidly as spatial LOC goes to zero. In Fig. 11b, SNR increases rapidly as temporal LOC goes to 1 which is expected based on Eq. (11). In Figs. 11c and 11d, the SCR curves each approach a vertical asymptote defined by Rchan[1] = Rtime[1](1 − 1/M) and Rtime[1] = Rchan[1]/(1 − 1/M), respectively. If Rchan[1] or Rtime[1] pass this threshold due to errors in estimating coherence, SCR is undefined. As discussed above, this leads to a negative estimation of and therefore a complex estimation of SCRdB. In comparison, SNR is defined for any values of spatial or temporal LOC within (0, 1). This makes the method estimations of SNRdB less susceptible to becoming complex than estimations of SCRdB.
Fig. 11.
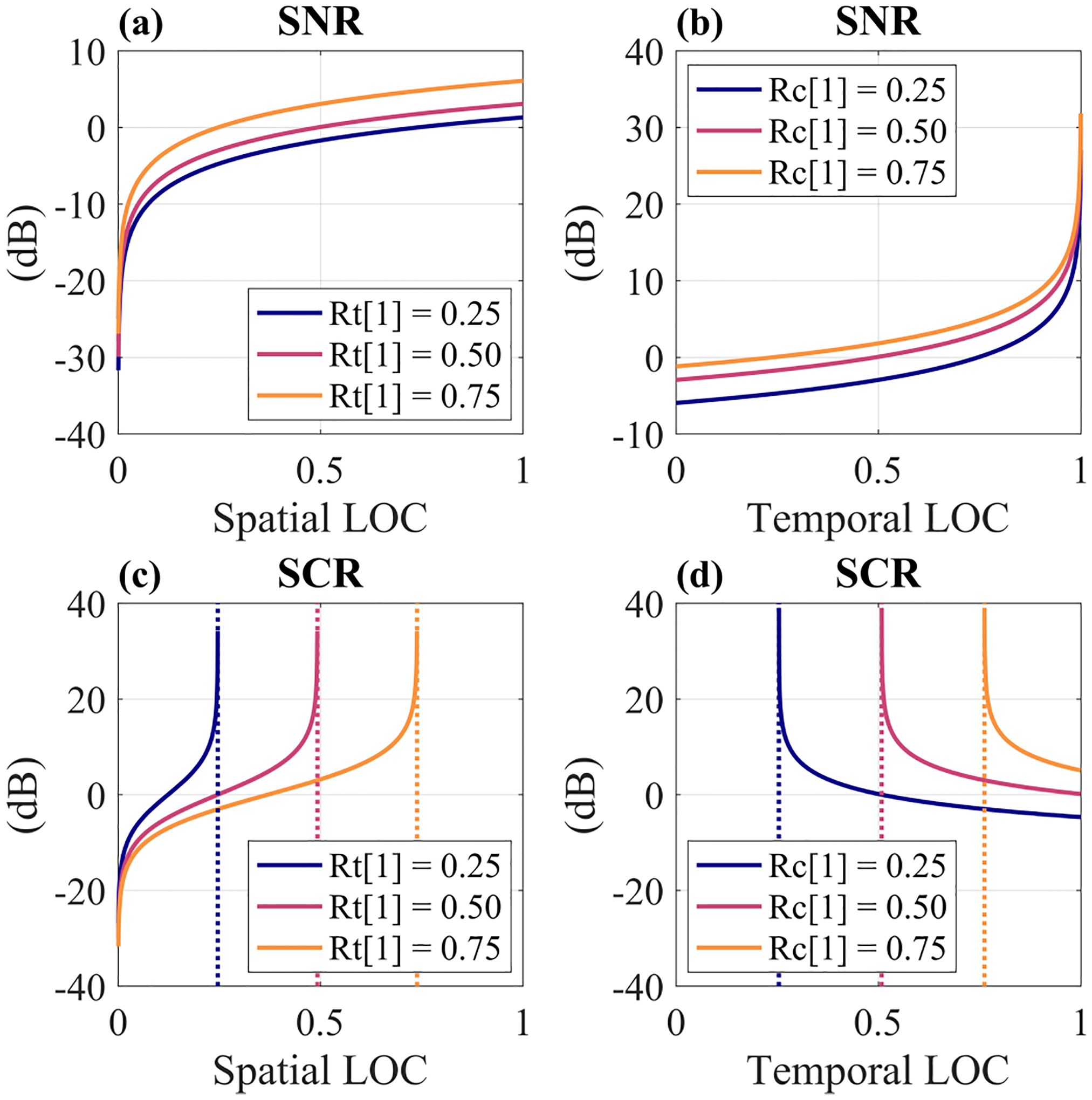
SNR (a), (b) and SCR (c), (d) as a function of spatial LOC (“Rc[1]”) and temporal LOC (“Rt[1]”). Temporal and Spatial LOC were computed by Eqs. (10) and (6), respectively. Dotted lines in (c) and (d) correspond to asymptotes defined by Rchan[1] = Rtime[1](1 − 1/M) and Rtime[1] = Rchan[1]/(1 − 1/M), respectively.
Contributor Information
Emelina P. Vienneau, Department of Biomedical Engineering, Vanderbilt University, Nashville, TN, 37235, USA.
Kathryn A. Ozgun, Department of Biomedical Engineering, Vanderbilt University, Nashville, TN, 37235, USA. She is now with Rivanna Medical, Charlottesville, VA, 22911, USA.
Brett C. Byram, Department of Biomedical Engineering, Vanderbilt University, Nashville, TN, 37235, USA.
References
- [1].Hendler I, Blackwell SC, Bujold E, Treadwell MC, Wolfe HM, Sokol RJ, and Sorokin Y, “The impact of maternal obesity on midtrimester sonographic visualization of fetal cardiac and craniospinal structures,” International Journal of Obesity and Related Metabolic Disorders, vol. 28, no. 12, pp. 1607–1611, 2004. [DOI] [PubMed] [Google Scholar]
- [2].Hendler I, Blackwell SC, Bujold E, Treadwell MC, Mittal P, Sokol RJ, and Sorokin Y, “Suboptimal second-trimester ultrasonographic visualization of the fetal heart in obese women: Should we repeat the examination?” Journal of Ultrasound in Medicine, vol. 24, no. 9, pp. 1205–1209, 2005. [DOI] [PubMed] [Google Scholar]
- [3].Hendler I, Blackwell SC, Treadwell MC, Bujold E, Sokol RJ, and Sorokin Y, “Does advanced ultrasound equipment improve the adequacy of ultrasound visualization of fetal cardiac structures in the obese gravid woman?” American Journal of Obstetrics and Gynecology, vol. 190, no. 6, pp. 1616–1619, 2004. [DOI] [PubMed] [Google Scholar]
- [4].Khoury FR, Ehrenberg HM, and Mercer BM, “The impact of maternal obesity on satisfactory detailed anatomic ultrasound image acquisition,” Journal of Maternal-Fetal & Neonatal Medicine, vol. 22, no. 4, pp. 337–341, 2009. [DOI] [PubMed] [Google Scholar]
- [5].Flynn BC, Spellman J, Bodian C, and Moitra VK, “Inadequate visualization and reporting of ventricular function from transthoracic echocardiography after cardiac surgery,” Journal of Cardiothoracic and Vascular Anesthesia, vol. 24, no. 2, pp. 280–284, 2010. [DOI] [PubMed] [Google Scholar]
- [6].Garrett JV, Passman MA, Guzman RJ, Dattilo JB, and Naslund TC, “Expanding options for bedside placement of inferior vena cava filters with intravascular ultrasound when transabdominal duplex ultrasound imaging is inadequate,” Annals of Vascular Surgery, vol. 18, no. 3, pp. 329–334, 2004. [DOI] [PubMed] [Google Scholar]
- [7].Heidenreich PA, Stainback RF, Redberg RF, Schiller NB, Cohen NH, and Foster E, “Transesophageal echocardiography predicts mortality in critically ill patients with unexplained hypotension,” Journal of the American College of Cardiology, vol. 26, no. 1, pp. 152–158, 1995. [DOI] [PubMed] [Google Scholar]
- [8].Feinstein SB, Coll B, Staub D, Adam D, Schinkel AF, ten Cate FJ, and Thomenius K, “Contrast enhanced ultrasound imaging,” Journal of Nuclear Cardiology, vol. 17, no. 1, pp. 106–115, 2010. [DOI] [PubMed] [Google Scholar]
- [9].Chiao RY and Hao X, “Coded excitation for diagnostic ultrasound: a system developer’s perspective,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 52, no. 2, pp. 160–170, 2005. [DOI] [PubMed] [Google Scholar]
- [10].Lediju MA, Trahey GE, Byram BC, and Dahl JJ, “Short-lag spatial coherence of backscattered echoes: imaging characteristics,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 58, pp. 1377–1388, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Byram B, Dei K, Tierney J, and Dumont D, “A model and regularization scheme for ultrasonic beamforming clutter reduction,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 62, no. 11, pp. 1913–1927, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Morgan MR, Trahey GE, and Walker WF, “Multi-covariate imaging of sub-resolution targets,” IEEE Transactions on Medical Imaging, vol. 38, no. 7, pp. 1690–1700, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Long W, Bottenus N, and Trahey GE, “Incoherent clutter suppression using lag-one coherence,” IEEE Transactions in Ultrasonics, Ferroelectrics, and Frequency Control, vol. 67, no. 8, pp. 1544–1557, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Holfort IK, Gran F, and Jensen JA, “Broadband minimum variance beamforming for ultrasound imaging,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 56, no. 2, pp. 314–325, 2009. [DOI] [PubMed] [Google Scholar]
- [15].Tierney J, Luchies A, Khan C, Byram B, and Berger M, “Domain adaptation for ultrasound beamforming,” in International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, 2020, pp. 410–420. [Google Scholar]
- [16].Tranquart F, Grenier N, Eder V, and Pourcelot L, “Clinical use of ultrasound tissue harmonic imaging,” Ultrasound in Medicine & Biology, vol. 25, no. 6, pp. 889–894, 1999. [DOI] [PubMed] [Google Scholar]
- [17].Lediju MA, Pihl MJ, Dahl JJ, and Trahey GE, “Quantitative assessment of the magnitude, impact and spatial extent of ultrasonic clutter,” Ultrasonic Imaging, vol. 30, no. 3, pp. 151–168, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Pinton GF, Trahey GE, and Dahl JJ, “Erratum: Sources of image degradation in fundamental and harmonic ultrasound imaging: a nonlinear, full-wave, simulation study,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 58, no. 6, pp. 1272–1283, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Dahl JJ and Sheth NM, “Reverberation clutter from subcutaneous tissue layers: simulation and in vivo demonstrations,” Ultrasound in Medicine & Biology, vol. 40, no. 4, pp. 714–726, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Long J, Long W, Bottenus N, and Trahey G, “Coherence-based quantification of acoustic clutter sources in medical ultrasound,” The Journal of the Acoustical Society of America, vol. 148, no. 2, pp. 1051–1062, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Dahl J, “Coherence beamforming and its applications to the difficult-to-image patient,” in 2017 IEEE International Ultrasonics Symposium (IUS), 2017, pp. 1–10. [Google Scholar]
- [22].Dei K and Byram B, “The impact of model-based clutter suppression on cluttered, aberrated wavefronts,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 64, no. 10, pp. 1450–1464, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Fatemi A, Berg EAR, and Rodriguez-Molares A, “Studying the origin of reverberation clutter in echocardiography: in vitro experiments and in vivo demonstrations,” Ultrasound in Medicine & Biology, vol. 45, no. 7, pp. 1799–1813, 2019. [DOI] [PubMed] [Google Scholar]
- [24].Lindsey BD and Smith SW, “Pitch-catch phase aberration correction of multiple isoplanatic patches for 3-D transcranial ultrasound imaging,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 60, no. 3, pp. 463–480, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Friemel BH, Bohs LN, Nightingale KR, and Trahey GE, “Speckle decorrelation due to two-dimensional flow gradients,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 45, no. 2, pp. 317–327, 1998. [DOI] [PubMed] [Google Scholar]
- [26].Bottenus NB and Trahey GE, “Equivalence of time and aperture domain additive noise in ultrasound coherence,” The Journal of the Acoustical Society of America, vol. 137, no. 1, pp. 132–138, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Huang C, Song P, Gong P, Trzasko JD, Manduca A, and Chen S, “Debiasing-based noise suppression for ultrafast ultrasound microvessel imaging,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 66, no. 8, pp. 1281–1291, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Pinton GF, Trahey GE, and Dahl JJ, “Sources of image degradation in fundamental and harmonic ultrasound imaging using nonlinear, full-wave simulations,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 58, no. 4, pp. 754–765, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Pinton G, Trahey G, and Dahl J, “Spatial coherence in human tissue: implications for imaging and measurement,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 61, no. 12, pp. 1976–1987, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Long W, Bottenus N, and Trahey GE, “Lag-one coherence as a metric for ultrasonic image quality,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 65, no. 10, pp. 1768–1780, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Hinkelman LM, Mast TD, Metlay LA, and Waag RC, “The effect of abdominal wall morphology on ultrasonic pulse distortion. Part I. Measurements,” The Journal of the Acoustical Society of America, vol. 104, no. 6, pp. 3635–3649, 1998. [DOI] [PubMed] [Google Scholar]
- [32].Mast TD, Hinkelman LM, Orr MJ, and Waag RC, “The effect of abdominal wall morphology on ultrasonic pulse distortion. Part II. Simulations,” The Journal of the Acoustical Society of America, vol. 104, no. 6, pp. 3651–3664, 1998. [DOI] [PubMed] [Google Scholar]
- [33].Byram B and Shu J, “Pseudononlinear ultrasound simulation approach for reverberation clutter,” Journal of Medical Imaging, vol. 3, no. 4, p. 046005, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Vienneau E, Ozgun K, and Byram B, “A coherence-based technique to separate and quantify sources of image degradation in vivo with application to transcranial imaging,” in 2020 IEEE International Ultrasonics Symposium (IUS), 2020, pp. 1–4. [Google Scholar]
- [35].Goodman Joseph W., Statistical Optics. Hoboken, NJ, USA: John Wiley & Sons, 2015. [Google Scholar]
- [36].Mallart R and Fink M, “The van Cittert-Zernike theorem in pulse echo measurements,” The Journal of the Acoustical Society of America, vol. 90, no. 5, pp. 2718–2727, 1991. [Google Scholar]
- [37].Liu DL and Waag RC, “About the application of the van Cittert-Zernike theorem in ultrasonic imaging,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 42, no. 4, pp. 590–601, 1995. [Google Scholar]
- [38].Hyun D, Crowley ALC, and Dahl JJ, “Efficient strategies for estimating the spatial coherence of backscatter,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 64, no. 3, pp. 500–513, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Jensen JA, “A model for the propagation and scattering of ultrasound in tissue,” The Journal of the Acoustical Society of America, vol. 89, no. 1, pp. 182–190, 1991. [DOI] [PubMed] [Google Scholar]
- [40].Jensen JA and Svendsen NB, “Calculation of pressure fields from arbitrarily shaped, apodized, and excited ultrasound transducers,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 39, no. 2, pp. 262–267, 1992. [DOI] [PubMed] [Google Scholar]
- [41].Bottenus N, Byram BC, Dahl JJ, and Trahey GE, “Synthetic aperture focusing for short-lag spatial coherence imaging,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 60, no. 9, pp. 1816–1826, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Fisher RA, Statistical Methods for Research Workers, Crew FAE and Cutler DW, Eds. Edinburgh: Oliver and Boyd, 1925. [Google Scholar]
- [43].Nayak R, MacNeill J, Flores C, Webb J, Fatemi M, and Alizad A, “Quantitative assessment of ensemble coherency in contrast-free ultrasound microvasculature imaging,” Medical Physics, vol. 48, no. 7, pp. 3540–3558, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Ozgun K, Tierney J, and Byram B, “A spatial coherence beamformer design for power Doppler imaging,” IEEE Transactions on Medical Imaging, vol. 39, no. 5, pp. 1558–1570, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Ahmed R, Bottenus N, Long J, and Trahey G, “Reverberation clutter suppression using 2D spatial coherence analysis,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 69, no. 1, pp. 84–87, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Schlunk S, Dei K, and Byram B, “Iterative model-based beamforming for high dynamic range applications,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 68, no. 3, pp. 482–493, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Bell MAL, Dahl JJ, and Trahey GE, “Resolution and brightness characteristics of short-lag spatial coherence (SLSC) images,” IEEE Transactions in Ultrasonics, Ferroelectrics, and Frequency Control, vol. 62, no. 7, pp. 1265–1276, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Montaldo G, Tanter M, Bercoff J, Benech N, and Fink M, “Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 56, no. 3, pp. 489–506, 2009. [DOI] [PubMed] [Google Scholar]
- [49].Tierney J, Coolbaugh C, Towse T, and Byram B, “Adaptive clutter demodulation for non-contrast ultrasound perfusion imaging,” IEEE Transactions on Medical Imaging, vol. 36, no. 9, pp. 1979–1991, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Offerdahl K, Huber M, Long W, Bottenus N, Nelson R, and Trahey G, “Occult regions of suppressed coherence in liver B-Mode images,” Ultrasound in Medicine & Biology, vol. 48, no. 1, pp. 47–58, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Bottenus N, Long W, Long J, and Trahey G, “A real-time lag-one coherence tool for adaptive imaging,” in 2018 IEEE International Ultrasonics Symposium (IUS), 2018, pp. 1–4. [Google Scholar]
- [52].Hyun D, Trahey GE, and Dahl JJ, “Real-time high-frame rate in vivo cardiac SLSC imaging with a GPU-based beamformer,” in 2015 IEEE International Ultrasonics Symposium (IUS), 2015, pp. 1–4. [Google Scholar]
- [53].Long J, Long W, Bottenus N, Pinton GF, and Trahey GE, “Implications of lag-one coherence on real-time adaptive frequency selection,” in 2018 IEEE International Ultrasonics Symposium (IUS), 2018, pp. 1–4. [Google Scholar]
- [54].Flint K, Bottenus N, Bradway D, McNally P, Ellestad S, and Trahey G, “An automated ALARA method for ultrasound: an obstetric ultrasound feasibility study,” Journal of Ultrasound in Medicine, vol. 40, pp. 1863–1877, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]


