Age- and sex-dependent clinical equations to estimate glomerular filtration rates in children and young adults with chronic kidney disease

Abstract

Using data (2655 observations from 928 participants) from the Chronic Kidney Disease in Children Study, we developed and internally validated new glomerular filtration rate estimating equations for clinical use in children and young adults: two forms of K × [heigh(ht) / serum creatinine(sCr)] and two forms of K × [1 / cystatin C(cysC)]. For each marker, one equation used a sex-dependent K; in the other, K is sex-and age-dependent. Glomerular filtration rate (GFR) was measured directly by plasma iohexol disappearance. The equations using ht/sCr had sex-specific constants of 41.8 for males and 37.6 for females. In the age- dependent models, K increased monotonically for children 1–18 years old and was constant for young adults 18–25 years. For males, K ranged from 35.7 for one-year-olds to 50.8 for those 18 and older. For females, the values of K ranged from 33.1 to 41.4. Constant K values for cystatin-C equations were 81.9 for males and 74.9 for females. With age-dependency, K varied non-monotonically with the highest values at age 15 for males (K of 87.2) and 12 years for females (K of 79.9). Use of an age-dependent K with ht/sCr models reduced average bias, notably in young children and young adults; age-dependent cystatin-C models produced similar agreement to using a constant K in children under 18 years, but reduced bias in young adults. These age-dependent proposed equations were evaluated alongside estimated GFRs from 11 other published equations for pediatrics and young adults. Only our proposed equations yielded non- significant bias and within 30% accuracy values greater than 85% in both the pediatric and young adult subpopulations.

Valid estimation of glomerular filtration rate (GFR) by serum biomarkers is critical for optimal clinical care. In 1976, Schwartz et al.¹ developed plasma creatinine-based equations for pediatric use, which incorporated heterogeneity by age and sex in the quantitative relationship between directly measured GFR (mGFR) and a child’s height-to-serum creatinine ratio (height/sCr). In 2009, investigators from the Chronic Kidney Disease in Children (CKiD) Study developed an updated pediatric “bedside” equation (GFR = 41:3 × [height (in m)/sCr (in mg/dl)], which has found common use both clinically and in research.² This equation was derived from serum creatinine (sCr) measured enzymatically and standardized using isotope dilution mass spectrometry reference material.³ The equation benefits from its simplicity—a single constant independent of age and sex—and its clinical accessibility—it uses only the sCr biomarker that is available in a basic metabolic panel. The data used to develop this equation came primarily from children aged 8 to 15 years and lacked an adequate sample of both young children (e.g., aged <5 years) and young adults (e.g., aged ≥18 years) to evaluate its validity across a broader age range.

Since the original publication of the CKiD bedside equation, nearly 200 additional children aged <5 years with chronic kidney disease (CKD) have been enrolled in the CKiD Study. In addition, participants remaining in the study up to the age of 25 years have contributed data as young adults. Previous work demonstrated that the bedside equation underestimates mGFR in young adult CKiD participants.⁴

In addition, since the original publication, cystatin-C (cysC) has been shown to be a strong predictor of kidney function,^5–7 and its clinical availability and use have substantially increased. Moreover, calibration using International Federation of Clinical Chemistry–approved reference material is now available, and all cysC measurements in CKiD are now aligned to this standard.⁸ Given the data available from a wider age range within CKiD and new laboratory calibrations since the first CKiD equations were published, we consider it timely to revisit the estimating equations for clinical use.

The aim of this study was to revisit the CKiD bedside estimated GFR (eGFR) equation to assess whether the “one-size-fits-all” K = 41.3 for height/sCr should be modified by sex and age to yield less biased estimates of mGFR, most notably in young children (aged <5 years) and young adults (aged 18–25 years). We also sought to develop a complementary estimating equation based on cysC. We refer to these new equations collectively as the “CKiD under 25 (U25)” eGFR equations (where 25 refers to age in years). Finally, we internally validated these equations and compared them with previously published eGFR equations for children and young adults.

RESULTS

Complete data for mGFR, sCr, sex, age, height, and CKD diagnosis were available for 2670 visits from 929 CKiD participants. To minimize potential influential observations, we excluded 1 observation with an mGFR >140 ml/min per 1.73 m², 1 observation with an mGFR <7 ml/min per 1.73 m², and 13 observations with low outlying values (<3) of log[mGFR × (sCr =height), leaving 2655 observations from 928 participants for the analysis.

The training data comprised 1093 person-visits from 387 male participants and 671 person-visits from 231 female participants (Table 1). Male and female observations were similar with respect to age (median, 13 years old for both), race (approximately 1/5 of participants were of Black race), and mGFR (median, 49 vs. 46 ml/min per 1.73 m²). Males and females had similar median heights. A greater percentage of female observations came from participants with glomerular CKD (32% vs. 22%). Approximately 50% of person-visits contributed by males and 60% of person-visits contributed by females were peripubertal/postpubertal. Observations from male participants had higher levels of sCr, cysC, and the 2 primary outcomes, mGFR × (sCr =height) and mGFR × cysC. The validation data set consisted of 570 observations from 194 male participants and 321 observations from 116 female participants. Characteristics were similar in the validation data, with the exception that relatively fewer observations came from participants of Black race: 18% and 12% for males and females, respectively.

Table 1|.

Demographic and clinical characteristics of 2655 pv by training/validation data status and participant sex

	Training data		Validation data
	Male	Female	Male	Female
Characteristics	(N = 387; 1093 pv)	(N = 231; 671 pv)	(N = 194; 570 pv)	(N = 116; 321 pv)
Age, yr Race	13 (9–16)	13 (10–16)	13 (8–16)	13 (9–16)
White	66 (720)	68 (453)	70 (400)	74 (238)
Black	23 (246)	20 (135)	18 (104)	12 (38)
Other	12 (127)	12 (83)	12 (66)	14 (45)
Height, m	1.51 (1.29–1.69)	1.49 (1.32–1.60)	1.49 (1.26–1.69)	1.49 (1.29–1.61)
Height percentilea	33 (14–61)	26 (6–57)	36 (13–63)	35 (10–66)
Weight percentilea	53 (24–83)	44 (15–79)	53 (25–84)	57 (21–91)
BMI percentilea	64 (36–89)	62 (31–88)	65 (34–91)	68 (34–94)
Premature at birth	10 (110)	15 (98)	9 (52)	10 (32)
Peripubertal/postpubertal	52 (509)	62 (379)	47 (242)	61 (182)
Glomerular CKD	22 (239)	32 (212)	21 (119)	32 (103)
mGFR, ml/min per 1.73 m2	49 (34–66)	46 (35–62)	47 (32–62)	41 (30–58)
sCr, mg/dl	1.23 (0.85–1.90)	1.11 (0.85–1.60)	1.25 (0.90–1.90)	1.30 (0.90–1.80)
CysC, mg/dl	1.69 (1.28–2.45)	1.59 (1.23–2.12)	1.77 (1.36–2.45)	1.84 (1.30–2.62)
Height/sCr	1.20 (0.78–1.61)	1.29 (0.94–1.65)	1.16 (0.81–1.54)	1.12 (0.81–1.59)
mGFR × sCr/height	41.8 (35.8–49.1)	37.5 (32.4–43.2)	41.0 (34.7–48.4)	38.6 (32.6–43.9)
mGFR × cysC	82.9 (73.0–93.6)	74.8 (66.7–85.8)	82.4 (72.4–93.2)	76.4 (64.7–86.1)

BMI, body mass index; CKD, chronic kidney disease; CysC, cystatin-C; mGFR, measured glomerular filtration rate (based on plasma iohexol disappearance); pv, person-visits; sCr, serum creatinine.

^aStandardized by age and sex using Centers for Disease Control and Prevention normative values for US children and adolescents.Continuous (quantitative) variables are summarized using median (interquartile range); categorical variables are summarized using percentage (frequency). Missing data: height percentile, n = 45; weight percentile, n = 124; BMI percentile, n = 149; prematurity status, n = 81; pubertal status, n = 244; cystatin-C, n = 129.

Estimating values of K for the U25 equations

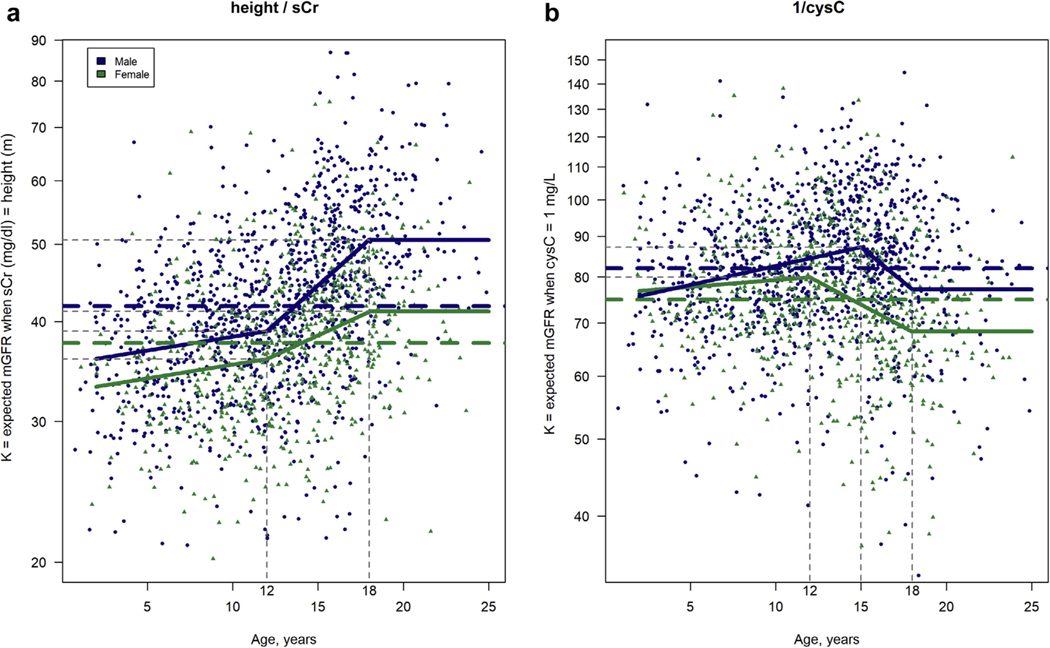
Table 2 and Figure 1 present the results of 2 sex-specific models for the biomarkers height/sCr and 1/cysC, a constant model and an age-dependent model. The constant models have a single sex-specific value for K applied to all ages; the age-dependent models allow age to modify K using a piecewise linear parameterization of age. For the estimating equations, using height, the sex-specific constants were 41.8 for males and 37.6 for females. These values translate into the estimated mGFR of males and females, respectively, for whom height (m) is equal to sCr (mg/dl), independent of age. For the purpose of consistency between males and females, both sex-specific, age-dependent models for height/sCr contained 3 linear pieces with knots at 12 and 18 years and a constant value for K for subjects aged ≥18 years (see Methods, Statistical analysis, for model parameterization). For males, the value of K ranged from 35.7 (39:0 × 1:008^(1–12)) for those aged 1 year to 50.8 for those aged ≥18 years. For boys aged 1 to 12 years, K increased by a factor of 1.008 per year of age; for boys aged 12 to 18 years, K increased more rapidly (1.045 per year of age). For females, the values of K were systematically lower and less variable, ranging from 33.1 (36:1 1:008^(1–12)) for those aged 1 year to 41.4 for those aged ≥18 years. For girls aged 1 to 12 years, K increased at the same rate as in boys of the same age. For girls aged 12 to 18 years, K increased by 1.023 for each year increase in age. For both males and females, the age-dependent models provided significantly overall better goodness of fit to the training data than the constant models (Akaike information criterion [AIC] for males: −275.6 vs. −491.5 for the constant and age-dependent models, respectively; AIC for females: −329.8 vs. −385.7 for the constant and age-dependent models, respectively [lower values indicate a statistically better fit of the model to the data]). The fit of these models to the training data is visualized in Figure 1a.

Table 2|.

Sex-specific values of K in constant and age-dependent models for height/sCr and 1/cysC glomerular filtration rate estimating equations

	K for height / sCr				K for 1 / cysC
	Male (N = 387; 1093 pv)a		Female (N = 231; 671 pv)a		Male (N = 387; 1039 pv)a		Female (N = 231; 644 pv)a
Age, yr	Constant	Age dependent	Constant	Age dependent	Constant	Age dependent	Constant	Age dependent
1–12	41.8	39.0×1.008(age-12)	37.6	36.1×1.008(age-12)	81.9	87.2×1.011(age-15)	74.9	79.9×1.004(age-12)
12–15		39.0×1.045(age-12)		36.1×1.023(age-12)				79.9×0.974(age-12)
15–18						87.2×0.960(age-15)
18–25		50.8		41.4		77.1		68.3

CysC, cystatin-C; pv, person-visits; sCr, serum creatinine.

^aThe number of participants and pv in the model training data set. CysC was missing for 81 pv in the training data. Height is measured in meters; sCr, mg/dl; and cysC, mg/L.

Figure 1|. Sex-specific values of K by age from the Chronic Kidney Disease in Children (CKiD) Study CKiD under 25 constant (dashed line) and age-dependent (solid line) models.

(a) The height/serum creatinine (sCr) models. (b) The cystatin-C (cysC) models. Scatterplot of training data (n = 1764 measurements from 618 participants) is superimposed. mGFR, measured glomerular filtration rate.

For the 1/cysC-based equations, the sex-specific constants were 81.9 for males and 74.9 for females and translate into the eGFR for males and females, respectively, with cysC (mg/L) equal to 1, independent of age. The model with sex-specific values of K offered an improved fit of the training data (P < 0.0001 using a likelihood ratio test comparing with a single-intercept model only) and reduced residual error in the validation data (test root mean square error, 10.68 for sex specific vs. 10.83 for a single intercept). For the age-dependent models, parameterization was piecewise linear, with knots at the ages of 15 and 18 years for males and 12 and 18 years for females; and like the sCr models, they estimated a constant value for K for subjects aged ≥18 years. For the youngest children (aged <5 years), values of K for boys and girls were similar. For boys aged 1 to 15 years, K increased by 1.1% per year of age from 74.8 to 87.2. For girls aged 1 to 12 years, K increased more modestly at 0.4% per year of age from 76.5 to 79.9. From those aged 15 to 18 years, K for boys decreased by a factor of 0.960 for each 1-year increase in age to 77.1 (87:2 × 0:960^(18−15) ) for those aged 18 years and remained constant for those aged 18 to 25 years. For girls aged 12 to 18 years, K decreased by a factor of 0.974 per year increase in age from 79.9 to 68.3 (79.9 × 0:974^(18−12)) and remained constant for young women aged 18 to 25 years. For males, the AIC values were −289.2 and −321.8 for the constant and age-dependent models, respectively; for females, the same 2 AIC values were −142.8 and −179.1. The fit of the cysC models to the training data is visualized in Figure 1b.

Internal validation for U25 equations

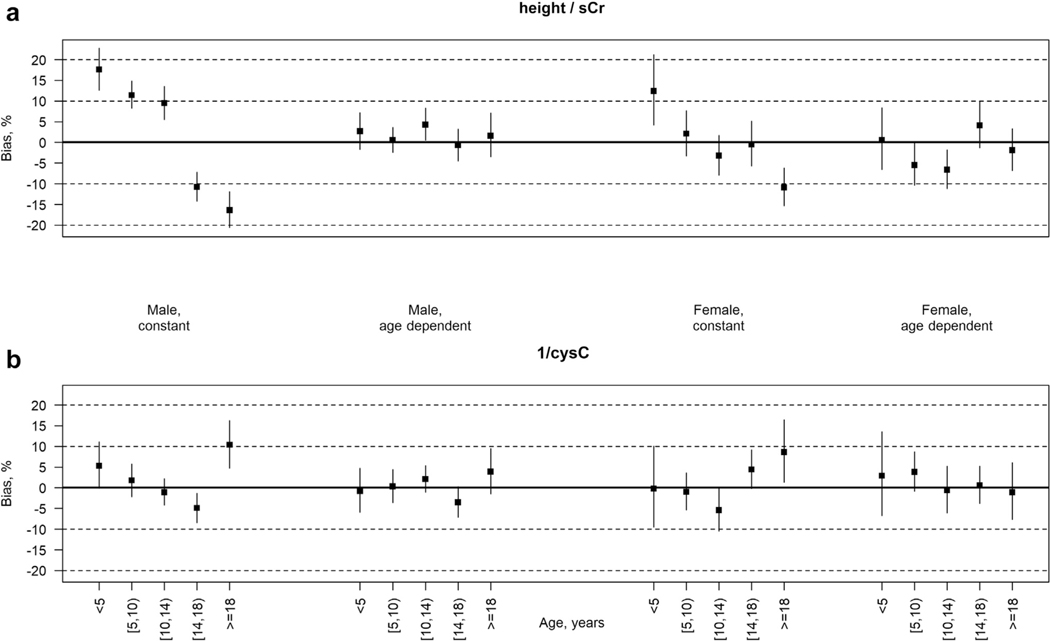
All models provided strong discrimination, with correlation coefficients of ≥0.89. Figure 2a shows the mean relative bias of the height/sCr-based eGFR compared with mGFR by sex and in 5 age subgroups of the validation data set: aged <5, 5 to 10, 10 to 14, 14 to 18, and ≥18 years. For both males and females, use of a single, constant K across all ages demonstrated statistically significant mean bias in both the youngest and oldest age groups. For children aged <5 years, the mean bias was 17.6% (95% confidence interval [CI], 12.6%–22.8%) for males and 12.4% (95% CI, 4.2%–21.2%) for females. For young adults, aged ≥18 years, the equation underestimated mGFR on average by 16.4% (95% CI, −20.6% to −11.9%) in males and by 10.9% (95% CI, −15.3% to −6.2%) in females. In fact, for males, all 5 age-specific mean bias measures were significantly different from zero, suggesting poor calibration from the constant model across all ages. This bias was markedly reduced using the age-dependent K model. All age-specific mean bias estimates were <5% for males and <7% for females (largest, −6.6% for those aged 10–14 years). Sex-specific scatterplots of arithmetic bias (eGFR – mGFR) for the U25 age-dependent height/sCr equations against age are available in the Supplementary Material (Supplementary Figure S1 A and B).

Figure 2|. Mean bias (percentage) of Chronic Kidney Disease in Children (CKiD) Study CKiD under 25 estimated glomerular filtration rate (GFR) versus iohexol-measured GFR by age and sex in the validation data set (n = 891 observations from 310 participants) for models using a constant K and an age-dependent K.

(a) Equations based on height/serum creatinine (sCr). (b) Equations based on cystatin-C (cysC). Solid squares represent point estimates; vertical bars represent the 95% confidence interval.

Figure 2b shows the age- and sex-specific mean relative biases of the cysC-based equations. For males and females, the age-constant model yielded average mean bias of <6% for the 4 pediatric (aged <18 years) age groups. However, these models overestimated mGFR in both young men (10.4% [95% CI, 4.7%–16.3%]) and women (8.6% [95% CI, 1.3%–16.4%]) aged ≥18 years. Use of an age-dependent K reduced mean bias estimates notably for young men (from 10.4% to 3.9%) and women (from 8.6% to −1.1%). For both sexes, all age-specific mean bias estimates were <4%, and none was statistically different from zero. Supplementary Figure S1C and D provide sex-specific scatterplots of arithmetic bias for the U25 age-dependent cysC equations against age.

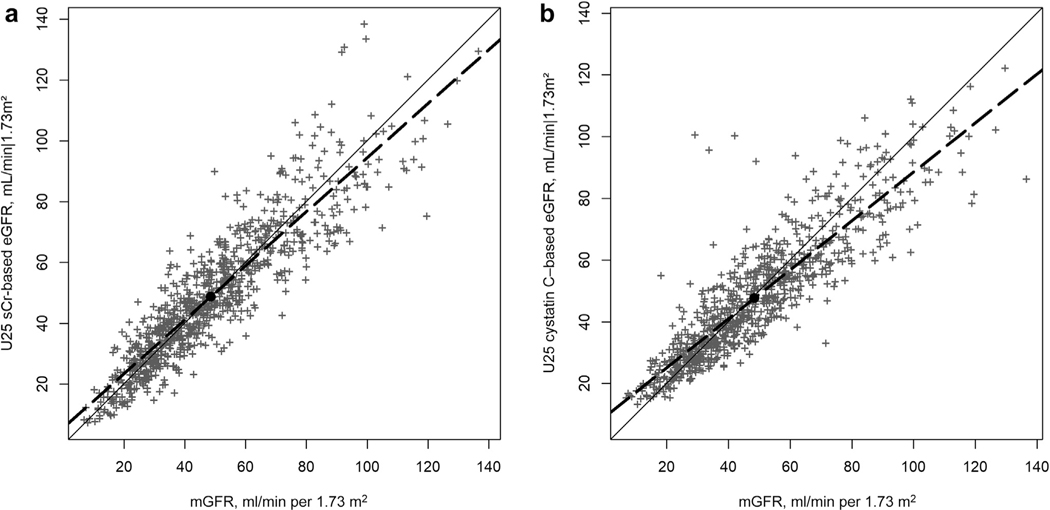
Scatterplots of U25 age-dependent eGFR versus mGFR over the full range of possible values in the validation data, with a reference line of equality and a linear regression line, are presented in Figure 3 (Figure 3a shows data for sCr, and Figure 3b shows data for cysC). For the sCr and the cysC equations, the mean biases were 0.2 (95% CI, −0.8 to 1.15) and −0.8 (95% CI, −1.6 to 0.0) ml/ min per 1.73 m², respectively. The corresponding ratios of the SDs (SD_eGFR/SD_mGFR) were 0.99 (95% CI, 0.96–1.03) and 0.89 (95% CI, 0.86–0.93). Regression to the mean— proportional with the SD ratio departure from 1 and the linear regression line in the scatterplots departing from the line of equality—was more present in the U25 cysC model than in the sCr model. Correlations between eGFR and mGFR were similar for the 2 equations: 0.90 for sCr and 0.89 for cysC.

Figure 3|. Scatterplot of sex- and age-dependent Chronic Kidney Disease in Children (CKiD) Study CKiD under 25 (U25) estimated glomerular filtration rate (eGFR) versus iohexol-measured glomerular filtration rate (mGFR) in the validation data set.

(a) Height/serum creatinine (sCr)–based eGFR (n = 891 observations from 310 participants). (b) Cystatin-C–based eGFR (n = 843 observations from 304 participants). Solid line is reference line of equality; dashed line is regression line. Black dot marks the mean mGFR and mean U25 eGFR.

Bias was also assessed within racial subgroups of the validation data. For the U25 age-dependent sCr equation, the mean arithmetic bias (eGFR – mGFR) for White, Black, and other racial groups was 1.1 (95% CI, 0.2–2.1), −3.2 (95% CI, −5.6 to −0.8), and 0.9 (95% CI, −1.4 to 3.3) ml/min per 1.73 m², respectively; for the cysC age-dependent equation, the corresponding bias estimates were −0.8 (95% CI, −1.8 to 0.1), 1.0 (95% CI, −1.1 to 3.1), and −1.6 (95% CI, −4.2 to 0.9) ml/ min per 1.73 m².

Comparison to other published equations

Table 3 presents bias and agreement metrics using the validation data for the U25 age-dependent equations, 2 previously published CKiD equations (the bedside and the 2012 cysC equations), and 9 other non-CKiD published equations (6 sCr based and 3 cysC based) for children and young adults. Full formulas are provided in the Supplementary Material (Item S1). Analyses were stratified by age: aged 1 to 18 years (children) and aged 18 to 25 years (young adults). Among children, all 13 equations produced mean absolute bias levels of <5 ml/min per 1.73 m², 3 of which were not significantly different from zero: the 2 CKiD U25 age-dependent equations and the Flanders metadata equation. All but 1 equation (Gao quadratic) yielded percentage of eGFR values that were within 30% of their corresponding mGFR (p30) values >75% among children; 3 had p30 values >85% in this age group (the 2 CKiD U25 age-dependent and the Schwartz-Lyon equations). Among young adults, mean bias varied more across equations. Of 13 equations, 7 produced mean absolute bias levels <5 ml/min per 1.73 m², of which 4 were not significantly different from zero: the 2 U25 equations, the full age spectrum (FAS) equation using Q based on height, and the Gao quadratic equation. All but 1 equation (FAS for cysC) yielded p30 values >75% among young adults; 7 had p30 values >85% in this age group (the 2 CKiD U25 age-dependent, the CKiD bedside, FAS using Q [height], Lund-Malmö revised for sCr and those <18 years old [LMR18], Flanders metadata, and Gao quadratic equations). The U25 age-dependent cysC equation was the only cysC-based equation to reach this threshold. Test root mean square error values ranged from 9.9 (CKiD U25 age-dependent equation using sCr) to 13.5 (Caucasian, Asian, pediatric and adult [CAPA] equation for cystatin C) for participants aged <18 years and from 9.6 (CKiD U25 age-dependent equation using sCr) to 15.0 (Berg-cysC) in young adults.

Table 3|.

Side-by-side validation measures for the CKiD U25 eGFR equations and other published eGFR equations for children, adolescents, and young adults

	Arithmetic bias, eGFR - mGFR (95% CI)a		p10: eGFR within 10% of mGFR		p30: eGFR within 30% of mGFR		Test RMSEb
eGFR equation	Aged <18 yr	Aged ≥18 yr	Aged <18 yr	Aged ≥18 yr	Aged <18 yr	Aged ≥18 yr	Aged <18 yr	Aged ≥18 yr
Plasma/sCr-based equations
CKiD U25 age and sex dependent	0.0 (−0.9 to 1.0)	0.7 (−1.6 to 3.0)	36.4	44.9	86.2	90.7	9.9	9.6
CKiD “bedside”	2.3 (1.1 to 3.5)	−5.4 (−7.7 to −3.1)	34.6	33.6	77.2	86.0	12.0	11.7
Full age spectrum (FAS)
Q(age)	3.8 (2.7 to 4.9)	5.9 (3.4 to 8.3)	36.9	36.4	77.8	77.6	12.1	11.6
Q(height)	2.2 (1.1 to 3.2)	0.5 (−2.1 to 3.2)	38.0	43.0	82.1	87.9	10.6	11.0
Lund-Malmö revised for sCr, including those aged <18 yr (LMR18)	−2.3 (−3.5 to −1.2)	−3.8 (−5.9 to −1.6)	29.8	36.4	81.3	88.8	11.6	10.1
Schwartz-Lyon	−2.0 (−3.0 to −0.9)	−7.4 (−9.8 to −5.1)	36.6	30.8	85.6	83.2	10.4	12.7
Flanders metadata (FM)	0.3 (−0.8 to 1.4)	−4.2 (−6.5 to −1.8)	40.2	35.5	83.7	89.7	10.8	11.0
Gao quadratic (GQ)	2.9 (1.7 to 4.1)	−2.1 (−4.3 to 0.1)	28.7	40.2	69.6	89.7	12.4	9.8
IFCC cysC-based equations
CKiD U25, age and sex dependent	−0.8 (−1.7 to 0.1)	−0.9 (−3.1 to 1.3)	39.3	45.7	86.6	85.7	10.5	10.8
Full age spectrum (FAS)	4.1 (3.2 to 5.1)	8.7 (6.6 to 10.8)	36.9	22.9	79.8	71.4	11.8	13.9
Caucasian, Asian, pediatric and adult (CAPA)	2.2 (1.0 to 3.3)	3.0 (0.6 to 5.3)	30.9	32.4	76.4	81.0	13.5	12.1
Berg	1.4 (0.4 to 2.4)	7.1 (4.5 to 9.8)	35.4	27.6	82.2	76.2	12.5	15.0
Non-IFCC cysC-based equations CKiD 2012c	1.9 (1.0 to 2.9)	5.8 (3.7 to 7.8)	38.3	27.6	82.0	75.2	10.9	11.9

CysC, cystatin-C; CI, confidence interval; CKiD, Chronic Kidney Disease in Children; eGFR, estimated glomerular filtration rate; IFCC, International Federation of Clinical Chemistry; mGFR, measured glomerular filtration rate; p10, percentage of eGFR values within 10% of mGFR values; p30, percentage of eGFR values within 30% of mGFR values; RMSE, root mean square error; sCr, serum creatinine; U25, CKiD under 25.

^aCalculated using the estimated fixed effect intercept of an intercept-only linear mixed effects model with a random intercept (participant) with the difference of eGFR – mGFR as the outcome.

^b $\text{Test}\text{RMSE}=\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(eGF{R}_i-mGF{R}_i\right)}^2}.$

^cEquation was developed using non-IFCC standardized cysC measurements. Therefore, “unstandardized” cysC measurements were derived from IFCC standardized cysC by dividing by 1.17.⁸

Presented metrics (mean arithmetic bias, p10, p30, and test RMSE) derived from the validation data set. Metrics are presented stratified by age: children and adolescents aged 1 to 18 years (n = 784 person-visits from 308 participants) and young adults aged 18 to 25 years (n = 107 person-visits from 69 participants). Missing data: n = 48 person-visits missing cysC. Full formulas of each of the listed equations can be found in the Supplementary Material (Item S1).

DISCUSSION

We developed and internally validated 4 GFR estimating equations, 2 that use sex-specific constant values of K as a multiplier of height/sCr and 1/cysC, respectively, and 2 that use age- and sex-specific values of K. We refer to these collectively as the “CKiD under 25 (U25)” GFR estimating equations. These equations yielded improved estimates of mGFR compared with the 2009 CKiD bedside equation, which generates biased estimates of GFR in young children (e.g., aged <5 years) and young adults (aged ≥18 years),⁴ and the CKiD 2012 cysC equation. The equations we present herein—for both height/sCr and cysC—overcome these limitations by using sex- and age-specific values of K and offer a single equation that can be used without bias across the full pediatric age spectrum and into young adulthood (to the age of 25 years).

Existing published pediatric GFR estimating equations have recognized the benefit of sex- and age-dependent multipliers of height/sCr^1,9–12 and, to a lesser extent, cysC.^13,14 Our CKiD U25 models are piecewise linear and capture a gradual change with age in the relationship between height/ sCr (or 1/cysC) and mGFR without gaps or discontinuities. Both kidney function and muscle mass affect sCr levels, the latter of which differs between males and females and across ages. Indeed, significant changes in muscle mass occur during puberty, particularly in boys. Our proposed U25 eGFR equations now reflect the age and sex developmental dynamics between kidney function and height/sCr. For males, K ranges from 36.0 for those aged 2 years to 50.8 for young adults aged ≥18 years, with the greatest change occurring between the ages of 12 and 18 years, coinciding with traditional ages of pubertal growth. For females, the value of K is lower than for males across all ages, ranging from 33.3 for those aged 2 years to 41.4 for young adults aged ≥18 years, with the greatest increases occurring between the ages of 12 and 18 years.

Likewise, we constructed sex-specific equations using cysC without and with age-dependent values of K. Although cysC has been shown to be less influenced by muscle mass than sCr and most published equations based only on cysC do not include age or height,^{5–7,15–17} some association with sex, age, and height in children has been demonstrated.^13,18,19 In our cysC U25 models, allowing K to depend on age provided marginal improvement in agreement and reduced bias, mostly in young adults. For both males and females, the constant equations demonstrated average bias within 6% for all pediatric age-specific subgroups (aged <18 years). In comparison, the age-dependent cysC models reduced average bias in 7 of the 10 age- and sex-based subgroups, most notably for young adults aged 18 to 25 years. Clinicians may find benefit estimating GFR using cysC in children and young adults with atypical body habitus stemming from higher or lower than expected muscle mass for a given height.

An analysis of bias within racial subgroups of our validation data revealed underestimation of mGFR by 3.2 ml/min per 1.73 m² on average when using the age-dependent sCr-based U25 equation among participants identifying as Black race. No significant bias was observed with the age-dependent cysC equation in the 3 racial subgroups. Race is a complex construct composed of both social and biological elements. Its use in clinical diagnostic tools, including GFR estimation, is an ongoing discussion within the field.^20–22 Our validation analysis suggests that cysC may offer a slightly more accurate estimate of GFR in children and young adults of Black race.

The age-dependent U25 models we propose are unified across ages to calculate unbiased estimates of GFR across childhood, adolescence, and young adulthood, as demonstrated in Figure 2 and Table 3. Most of the equations we evaluated in Table 3 yielded p30 agreement levels >75%, a threshold recognized as “good for clinical decision making.”²³ However, only the 2 U25 equations yielded p30 estimates >85% in both age groups (<18 and ≥18 years). In addition, all of the equations we examined yielded absolute mean bias levels <5 ml/min per 1.73 m² in the participants aged <18 years, but a subset had significant bias in the older participants. Of the equations for which we performed an external validation, several stood out. The Flanders metadata equation yielded no significant bias in participants aged <18 years. The FAS equation using Q derived from height performed with minimal bias and strong p30 agreement in both age groups. Although the U25 equations performed well, we recognize the limitation that no formal external validation was performed and the results should be interpreted accordingly.

Many of the non-CKiD equations we evaluated in the side-by-side validation analysis of Table 3 were developed in non-CKD populations. A unique strength of our U25 models is that they were developed and validated in a population of children and young adults with mild to moderate CKD with median (interquartile range) mGFR of 48 (34–64) ml/min per 1.73 m². A valid estimation of GFR is critical for clinical management in this high-risk population. In all 10 age/sex subgroups, the average bias for both U25 age-dependent K equations was well within 10%.

Compared with earlier CKiD-derived GFR estimating equations, more data were available for young children, aged <5 years, and young adults, aged ≥18 years. This was a major strength of the U25 equations. Indeed, we were able to identify systematic biases in the earlier published equations for estimating GFR in these age groups and correct these with sex- and age-specific values of K.

Our study and proposed equations have several limitations. First, our validation analyses used a subset of CKiD data, not external data. As a result, our comparison of eGFR equations for children and young adults is an internal validation for our U25 equations and an external validation for all other non-CKiD equations evaluated. These results should be interpreted in that context. Second, our study population did not include children and young adults free of CKD. Therefore, we cannot speak to the validity of our equations for estimating GFR in healthy patients or to their clinical utility for screening otherwise healthy patients for kidney problems. Third, our U25 sCr-based equations require knowledge of a patient’s height, which may not always be available to laboratories. Neither the FAS sCr equation based on age nor the LMR18 sCr equation requires height, and each may therefore facilitate GFR estimation when height is unavailable. That said, both of these equations had significant levels of bias in both the older and younger participants, and the FAS with Q (age) equation had lower p30 values than the U25 equations.

The U25 equations presented herein have been internally validated across the pediatric and young adult age spectrum of our CKiD data and are accessible for clinical use. And although K differs by sex and age, once identified, one need simply multiply either height/sCr or 1/CysC, depending on data availability. When the 2 estimates are available, the average of them preserves the unbiasedness, is more accurate (i.e., higher P10 and P30) and more precise (i.e., lower RSME) than either of the single-marker estimates, and yields a sex- and age-dependent linear combination of the biomarkers as the estimate of GFR. To facilitate this process, we have developed a CKiD U25 GFR calculator that can be accessed online (https://ckid-gfrcalculator.shinyapps.io/eGFR/ ) and have provided a supplementary table of sex- and age-specific values of K (Supplementary Table S1). Appropriate next steps will be to quantify their validity externally in other pediatric and young adult CKD populations. In addition, exploring more flexible models (e.g., allowing exponents for the 2 markers to be different than 1, and including both markers in a multivariate model) could further improve estimation of GFR. This is beyond the scope of the present analysis, which aimed to develop age- and sex-specific multipliers of the raw values of height/sCr and cysC for the most common clinical scenario in which only one marker is present.

In conclusion, by using the largest resource of standardized, directly measured GFR in children and young adults with CKD to date, we propose new sCr- and cysC-based equations that include younger children and young adults that were not previously available. These equations overcome limitations in earlier equations and demonstrated internal validity to provide the most up-to-date tools for clinical use.

METHODS

This analysis is based on data from the CKiD Study, a longitudinal cohort study of children and young adults (aged 1–25 years) with mild to moderate CKD recruited from 63 sites across the United States and Canada. Study enrollment of children aged 1 to 16 years with an eGFR <90 ml/min per 1.73 m² began in 2005.^2,24 Two additional recruitment periods, beginning in 2011 and 2016, recruited children with higher GFRs and younger ages than the original enrollment, respectively. Demographic and clinical data were collected at annual visits. For the current analysis, variables of interest included a participant’s sex, age, height, self-reported race, CKD diagnosis, sCr, cysC, and mGFR.

The GFR was measured directly (mGFR) by plasma disappearance of iohexol longitudinally.²⁵ Before 2018, all laboratory measurements of plasma iohexol concentration were performed at the CKiD central biochemistry laboratory at the University of Rochester Medical Center (New York, NY, USA). Beginning in 2018, these operations were moved to the University of Minnesota, and iohexol measurements from the 2 sites have been calibrated.²⁶ sCr, assayed enzymatically (Advia 2400; Siemens Diagnostics, Malvern, PA), and cysC, assayed nephelometrically (Siemens Diagnostics), were measured at the CKiD central biochemistry laboratory at each annual visit and calibrated to International Federation of Clinical Chemistry standards.^3,8 Analysis was restricted to person-visits contributed before end-stage kidney disease.

Statistical analysis

The first objective of this study was to reexamine the CKiD bedside eGFR equation to determine if the constant, K, in the equation GFR = K × height/sCr needs modification by sex, age, or height to reduce bias and improve accuracy of eGFRs in children and young adults. The second objective was to develop a complementary cysC-based equation of the form GFR = K × 1=cysC.

Data were randomly split into training and validation data sets in a 2:1 ratio within strata of sex and CKD diagnosis and at the participant level. For the j^th visit of the i^th individual, the dependent variable of interest for the sCr-based equations was the value of mGFR × sCr/height in the log scale, with sCr measured in mg/dl and height measured in meters. Linear regression of this quantity against sex and age assured an exponent value of one for the height/sCr term of the equation when reconfigured to the arithmetic scale. Moreover, $\log (K)=E\{\log [mGFR\times (sCr/height)]\}$ and K can be interpreted as the expected mGFR of an individual whose sCr = height.

Although height and age were considered candidate modifiers of K, these 2 variables are highly correlated in the pediatric setting, and early analysis suggested minimal utility in including both variables in the estimating equations. Using the training data and stratifying by sex, we regressed $\log [mGFR\times (sCr/height)]$ against various parameterizations of age using linear mixed-effects models with a random intercept to account for repeated measures:

$$\log {[mGFR\times (sCr/height)]}_{ij}=\alpha +\mu \left(ag{e}_{ij};{\beta }_1,\dots ,{\beta }_p\right)+a_i+e_{ij}$$

where μ(age_ij; β₁;…;β_p) corresponds to the dependencies on age modeled by p parameters, a_i is the random intercept, and e_ij is the residual error term. For a simple linear relationship μ(age_ij; β₁;.;β_p) = β₁age_ij and for a piecewise linear with a constant value after, say, age 18 years and 2 slopes with one between aged 12 and 18 years and another before age 12 years,μ(age_ij; β₁;.;β_p) = β₁(age_ij −12) (age_ij < 12) + β₂[(age_ij −12)−(age_ij −18)(age_ij ≥ 18)(age_ij ≥ 12) so that α= log(K) for an individual aged 12 years, β₁ is the slope before the age of 12 years, b₂ is the slope from the age of 12 to 18 years, and the value after 18 years stays constant at α + β₂ × 6. As part of model development, various age-defined knots and linear piecewise parameterizations as well as cubic splines were explored, although model parsimony was also considered. Model selection and goodness of fit were assessed using AIC.²⁷

Development of cysC-based models followed the same framework, replacing log[mGFR × (sCr/height)] with log[mGFR × cysC]. For these models, K can be interpreted as the expected mGFR of an individual whose cysC = 1 mg/L.

Candidate models were validated within age- and sex-specific subgroups of the validation data set. Using generalized estimating equations, we calculated average relative bias by regressing log(eGFR/mGFR) against the average value of log-transformed eGFR and mGFR centered at the mean of these averaged values.^4,25,28 Agreement between the age-dependent model-based eGFRs and mGFRs across the GFR spectrum was summarized with scatterplots, correlations, ratios of SDs (SD_eGFR/SD_mGFR), and mean arithmetic bias derived from regression models of the 2 GFR markers using methods as described above for the relative bias, except that the dependent variable was the arithmetic difference, eGFR – mGFR, and the independent variable was the mean of the raw eGFR and mGFR values. Bias for the age-dependent models was also assessed in racial subgroups (White, Black, and other individuals; participants who identified as multiracial, including Black race, were classified as Black race). In addition, we performed a side-by-side validation analysis that included the age-dependent candidate models presented herein and 11 single-marker (sCr or cysC, not both) eGFR equations for pediatric and young adult populations that have been published over the past 15 years (Table 3 and Supplementary Item S1 provide a listing of the equations).^{2,5,10–13,16,17,29–31} With the exception of the CKiD 2012 cysC equation, we restricted assessment of cysC-based equations to those developed with International Federation of Clinical Chemistry standardized values. Agreement was quantified as mean arithmetic bias (eGFR – mGFR), the percentage of eGFR values that were within 10% and 30% of their corresponding mGFR value, and the test root mean square error calculated in the original scale (i.e., not log transformed).

All analysis was performed in SAS version 9.4 and R version 3.6.1 statistical software.

Supplementary Material

1

Figure S1. Sex-specific scatterplots of difference between sex- and age-dependent U25 estimated GFR and iohexol-measured GFR (eGFR – mGFR) versus age in years. (A,B) U25 height/serum creatinine–based eGFR for males (n = 570 observations from 194 participants) and females (n = 321 observations from 116 participants), respectively. (C,D): U25 cystatin-C–based eGFR for males (n = 534 observations from 190 participants) and females (n = 300 observations from 114 participants), respectively. Loess regression curves shown in black with 95% confidence intervals (in gray). Note: n = 4 male and n = 1 female data points do not appear in the cystatin-C scatterplots because of absolute difference >40 ml/min per 1.73 m². These points are included in the loess regressions.

Table S1. Age- and sex-specific values of K for the GFR estimating equations GFR = K × [height (m)=sCr (mg =dL) and GFR = K [1=cysC (mg =L). Values of K shown are for integer ages and can be used for ages 0.5 years from the listed integer age (e.g., for children between 12.5 and 13.5 years, use the K reported herein for age 13 years).

Item S1. Listing of eGFR equations included in the side-by-side validation analysis (Table 3).